Efficient Discrete Optimal Transport Algorithm by Accelerated Gradient Descent

Abstract

Optimal transport (OT) plays an essential role in various areas like machine learning and deep learning. However, computing discrete OT for large scale problems with adequate accuracy and efficiency is highly challenging. Recently, methods based on the Sinkhorn algorithm add an entropy regularizer to the prime problem and obtain a trade off between efficiency and accuracy. In this paper, we propose a novel algorithm based on Nesterov’s smoothing technique to further improve the efficiency and accuracy in computing OT. Basically, the non-smooth c-transform of the Kantorovich potential is approximated by the smooth Log-Sum-Exp function, which smooths the original non-smooth Kantorovich dual functional. The smooth Kantorovich functional can be efficiently optimized by a fast proximal gradient method, the fast iterative shrinkage thresholding algorithm (FISTA). Theoretically, the computational complexity of the proposed method is given by $O(n^{\frac{5}{2}}\sqrt{\log n}∕ϵ)$, which is lower than current estimation of the Sinkhorn algorithm. Experimentally, compared with the Sinkhorn algorithm, our results demonstrate that the proposed method achieves faster convergence and better accuracy with the same parameter.

Introduction

Optimal transport (OT) is a powerful tool to compute the Wasserstein distance between probability measures and widely used to model various natural and social phenomena, including economics (Galichon 2016), optics (Glimm and Oliker 2003), biology (Schiebinger et al. 2019), physics (Jordan, Kinderlehrer, and Otto 1998) and in other scientific fields. Recently, OT has been successfully applied in machine learning and statistics, such as parameter estimation in Bayesian non-parametric models (Nguyen 2013), computer vision (Arjovsky, Chintala, and Bottou 2017; Courty et al. 2017; Tolstikhin et al. 2018; An et al. 2020; Lei et al. 2020), and natural language processing (Kusner et al. 2015; Yurochkin et al. 2019). In these areas, the complex probability measures are approximated by summations of Dirac measures supported on the samples. To obtain the Wasserstein distance between the empirical distributions, we then solve the discrete OT problems.

Discrete Optimal Transport

In discrete OT problem, where both the source and target measures are discrete, the Kantorovich functional becomes a convex function defined on a convex domain. Due to the lack of smoothness, conventional gradient descend method can not be applied directly. Instead, it can be optimized with the sub-differential method (Nesterov 2005), in which the gradient is replaced by the sub-differential. To achieve an approximation error less than $\epsilon$, the sub-differential method requires $O(1∕{\epsilon }^2)$ iterations. Recently, several approximation methods have been proposed to improve the computational efficiency. In these methods (Cuturi 2013; Benamou et al. 2015; Altschuler, Niles-Weed, and Rigollet 2017), a strongly convex entropy function is added to the prime Kantorovich problem and thus the regularized problem can be efficiently solved by the Sinkhorn algorithm. More detailed analysis shows that the computational complexity of the Sinkhorn algorithm is $\tilde{O}(n^2∕{\epsilon }^2)$ (Dvurechensky, Gasnikov, and Kroshnin 2018) by setting $\lambda =ϵ∕4\log n$. Also, a series of primal-dual algorithms are proposed, including the APDAGD (adaptive primal-dual accelerated gradient descent) algorithm (Dvurechensky, Gasnikov, and Kroshnin 2018) with computational complexity $\tilde{O}(n^{2.5}∕ϵ)$, the APDAMD (adaptive primal-dual accelerated mirror descent) algorithm (Lin, Ho, and Jordan 2019) with $\tilde{O}(n^2\sqrt{r}∕ϵ)$ where $r$ is a complex constant of the Bregman divergence, and the APDRCD (accelerated primal-dual randomized coordinate descent) algorithm (Guo, Ho, and Jordan 2020) with $\tilde{O}(n^{2.5}∕ϵ)$. But all of the three methods need to build a matrix with space complexity $O(n^3)$, making them difficult to compute when $n$ is large.

Our Method

In this work, instead of starting from the prime Kantorovich problem like the Sinkhorn based methods, we directly deal with the dual Kantorovich problem. The key idea is to approximate the original non-smooth c-transform of the Kantorovich potential by Nesterov’s smoothing technique. Specifically, we approximate the max function by the Log-Sum-Exp function, which has also been used in (Schmitzer 2019; Peyré and Cuturi 2018), such that the original non-smooth Kantorovich functional is converted to an unconstrained ($n-1$)-dimensional smooth convex energy. By using the Fast Proximal Gradient Method named FISTA (Beck and Teboulle 2009), we can quickly optimize the smoothed energy to get a precise estimate of the OT cost. In theory, the method can achieve the approximate error $\epsilon$ with the space complexity $O(n^2)$ and computational complexity $O(n^{2.5}\sqrt{\log n}∕\epsilon )$. Additionally, we show that the induced approximate OT plan by our algorithm is equivalent to that of the Sinkhorn algorithm. The contributions of our work are as follows.

• We convert the dual Kantorovich problem to an unconstrained smooth convex optimization problem by approximating the non-smooth c-transform of the Kantorovich potential with Nesterov’s smoothing idea.

• The smoothed Kantorovich functional can be efficiently solved by the FISTA algorithm with computational complexity $\tilde{O}(n^{2.5}∕\sqrt{\epsilon })$. At the same time, the computational complexity of the Kantorovich functional itself is given by $\tilde{O}(n^{2.5}∕\epsilon )$.

• The experiments demonstrate that compared with the Sinkhorn algorithm, the proposed method achieves faster convergence and better accuracy with the same parameter $\lambda$.

Notation

In this work, ${\mathbb{R}}_{\ge 0}$ represents the non negative real numbers, $0$ and $1$ represents the all-zeros and all-ones vectors of appropriate dimension. The set of integers $\{1,2,\dots ,n\}$ is denoted as $[n]$. And ${\mid \cdot \mid }_1$ and $\Vert \cdot \Vert$ are the ${\ell }_1$ and ${\ell }_2$ norms, ${\mid v\mid }_1={\sum }_i\mid v_i\mid$ and $\Vert v\Vert =\sqrt{{\sum }_i{v}_i^2}$, respectively. $R(C)$ is the range of the cost matrix $C=(c_{ij})$, namely $C_{\max }-C_{\text{min}}$, where $C_{\max }$ and $C_{\text{min}}$ represent the maximum and minimum of the elements of $C$ with $c_{ij}>0$. We use ${\nu }_{\text{min}}$ to denote the minimal element of $\nu$ and $\oslash$ to denote element wise division.

Related Work

Optimal transport plays an important role in various kinds of fields, and there is a huge literature in this area. Here we mainly focus on the most related works. For detailed overview, we refer readers to (Peyré and Cuturi 2018).

When both the source and target measures are discrete, the OT problem can be treated as a standard linear programming (LP) task and solved by interior-point method with computational complexity $\tilde{O}(n^{5∕2})$ (Lee and Sidford 2014). But this method requires a practical solver of the Laplacian linear system, which is not currently available for large dataset. Another interior-point based method to solve the OT problem is proposed by Pele and Werman (Pele and Werman 2009) with complexity $\tilde{O}(n^3)$. Generally speaking, it is unrealistic to solve the large scale OT problem with the traditional LP solvers.

The prevalent way to compute the OT cost between two discrete measures involves adding a strongly convex entropy function to the prime Kantorovich problem (Cuturi 2013; Benamou et al. 2015). Most of the current solutions for the discrete OT problem follow this strategy. Genevay et al. (Genevay et al. 2016) extend the algorithm in its dual form and solve it by stochastic average gradient method. The Greenkhorn algorithm (Altschuler, Niles-Weed, and Rigollet 2017; Abid and Gower 2018; Chakrabarty and Khanna 2021) is a greedy version of the Sinkhorn algorithm. Specifically, Altschuler et al. (Altschuler, Niles-Weed, and Rigollet 2017) show that the complexity of their algorithm is $\tilde{O}(\frac{n^2}{{ϵ}^3})$. Later, Dvurechensky et al. (Dvurechensky, Gasnikov, and Kroshnin 2018) improve the complexity bound of the Sinkhorn algorithm to $\tilde{O}(\frac{n^2}{{ϵ}^2})$, and propose an APDAGD method with complexity $\tilde{O}(\text{min}\{\frac{n^{9∕4}}{ϵ},\frac{n^2}{{ϵ}^2}\})$. Jambulapati et al. (Jambulapati, Sidford, and Tian 2019) introduce a parallelelizable algorithm to compute the OT problem with complexity $\tilde{O}(\frac{n^2{\Vert C\Vert }_{\max }}{ϵ})$. Through screening the negligible components by directly setting them at that value before entering the Sinkhorn problem, the screenkhorn (Alaya et al. 2019) method solves a smaller Sinkhorn problem and improves the computation efficiency. Based on a primal-dual formulation and a tight upper bound for the dual solution, Lin et al. (Lin, Ho, and Jordan 2019) improve the complexity bound of the Greenkhorn algorithm to $\tilde{O}(\frac{n^2}{{ϵ}^2})$, and propose the APDAMD algorithm, whose complexity bound is proven to be $\tilde{O}(\frac{n^2\sqrt{r}}{ϵ})$, where $r\in (0,n]$ refers to some constants in the Bregman divergence. Recently, a practically more efficient method called APDRCD (Guo, Ho, and Jordan 2020) is proposed with complexity $\tilde{O}(n^{2.5}∕ϵ)$. But all these three primal-dual based methods need to build a matrix with space complexity $O(n^3)$, which makes them impractical when $n$ is large. By utilizing Newton-type information, Blanchet et al. (Blanchet et al. 2018) and Quanrud (Quanrud 2018) propose algorithms with complexity $\tilde{O}(\frac{n^2}{ϵ})$. However, the Newton-based methods only give the theoretical upper bound and provide no practical algorithms.

Besides the entropy regularizer based methods, Blondel et al. (Blondel, Seguy, and Rolet 2018) use the squared 2-norm and group LASSO (least absolute shrinkage and selection operator) to regularize the prime Kantorovich problem and then use the quasi-Newton method to accelerate the algorithm. Xie et al. (Xie et al. 2019b) develop an Inexact Proximal point method for exact optimal transport. By utilizing the structure of the cost function, Gerber and Maggioni (Gerber and Maggioni 2017) optimize the transport plan from coarse to fine. Meng et al. (Meng et al. 2019) propose the projection pursuit Monge map, which accelerates the computation of the original sliced OT problem. Xie et al. (Xie et al. 2019a) also use the generative learning based method to model the optimal transport. But the theoretical analysis of these algorithms is still nascent.

In this work, we introduce a method based on Nesterov’s smoothing technique, which is applied to the dual Kantorovich problem with computational complexity $O(n^{2.5}\sqrt{\log n}∕\epsilon )$ (or equivalently $\tilde{O}(n^{2.5}∕\epsilon )$ and approximation error bound $2\lambda \log n$.

Optimal Transport Theory

In this section, we introduce some basic concepts and theorems in the classical optimal transport theory, focusing on Kantorovich’s approach and its generalization to the discrete settings via c-transform. The details can be found in Villani’s book (Villani 2008).

Optimal Transport Problem

Suppose $X\subset {\mathbb{R}}^d$, $Y\subset {\mathbb{R}}^d$ are two subsets of the Euclidean space ${\mathbb{R}}^d,\mu ,\nu$ are two probability measures defined on $X$ and $Y$ with equal total measure, $\mu (X)=\nu (Y)$.

Kantorovich’s Approach

Depending on the cost functions and the measures, the OT map between ($X,\mu$) and ($Y,\nu$) may not exist. Thus, Kantorovich relaxed the transport maps to transport plans, and defined joint probability measure $\pi :X\times Y\to {\mathbb{R}}_{\ge 0}$, such that the marginal probability of $\pi$ equals to $\mu$ and $\nu$, respectively. Formally, let the projection maps be ${\rho }_x(x,y)=x$, ${\rho }_y(x,y)=y$, then we define

$$\pi (\mu ,\nu )≔\{P:X\times Y\to {\mathbb{R}}_{\ge 0}:{({\rho }_x)}_{\#}P=\mu ,{({\rho }_y)}_{\#}P=\nu \}.$$ (1)

Problem 1 (Kantorovich Problem). Given the transport cost function $X\times Y\to \mathbb{R}$, find the joint probability measure $P:X\times Y\to \mathbb{R}$ that minimizes the total transport cost

$$M_c(\mu ,\nu )=\underset{P\in \pi (\mu ,\nu )}{\text{min}}{\int }_{X\times Y}c(x,y)dP(x,y)$$ (2)

Problem 2 (Dual Kantorovich Problem). Given two probability measures $\mu$ and $\nu$ supported on $X$ and $Y$, respectively, and the transport cost function $c:X\times Y\to \mathbb{R}$, the Kantorovich problem is equivalent to maximizing the following Kantorovich functional:

$$M_c(\mu ,\nu )=\max \left\{-{\int }_X\varphi d\mu +{\int }_Y\psi d\nu \right\}$$ (3)

where $\varphi \in L^1(X,\mu )$ and $\psi \in L^1(Y,\nu )$ are called Kantorovich potentials and $-\varphi (x)+\psi (y)\le c(x,y)$. The above problem can be reformulated as the following minimization form with the same constraints:

$$M_c(\mu ,\nu )=-\text{min}\left\{{\int }_X\varphi d\mu -{\int }_Y\psi d\nu \right\}$$ (4)

Definition 3 (c-transform). Let $\varphi \in L^1(X,\mu )$ and $\psi \in L^1(Y,\nu )$, we define

$$\varphi (x)={\psi }^c(x)=\underset{y\in Y}{\text{sup}}\psi (y)-c(x,y).$$

With c-transform, Eqn. (4) is equivalent to solving the following optimization problem:

$$M_c(\mu ,\nu )=-\text{min}\left\{{\int }_X{\psi }^c(x)d\mu (x)-{\int }_Y\psi (y)d\nu (y)\right\}$$ (5)

where $\psi \in L^1(Y,\nu )$. When $\mu ={\sum }_{i=1}^m{\mu }_i\delta (x-x_i)$ and $\nu ={\sum }_{j=1}^n{\nu }_j\delta (y-y_j)$, $\psi ={({\psi }_1,{\psi }_2,\dots ,{\psi }_n)}^T$, Eqn. (5) gives the unconstrained convex optimization problem:

$$M_c(\mu ,\nu )=-\underset{\psi }{\text{min}}E(\psi )=-\underset{\psi }{\text{min}}\{\sum _{i=1}^m{\mu }_i{\psi }^c(x_i)-\sum _{j=1}^n{\nu }_j{\psi }_j\}$$ (6)

where the c-transform of $\psi$ is given by:

$${\psi }^c(x_i)=\underset{j}{\max }\{{\psi }_j-c_{ij}\}$$ (7)

where $c_{ij}=c(x_i,y_j)$. Suppose ${\psi }^{\ast }$ is the solution to Eqn. (6), then it has the following properties:

1. If the cost function is $\widehat{c}(x,y)=c(x,y)-k$, where $k$ is a constant, the corresponding optimal solution is ${\widehat{\psi }}^{\ast }$, then ${\widehat{\psi }}^{\ast }={\psi }^{\ast }$. At the same time, we have $M_c(\mu ,\nu )=M_{\widehat{c}}(\mu ,\nu )+k$.

2. ${\psi }^{\ast }+k1$ is also an optimal solution for Eqn. (6).

In order to make the solution unique, we add a constraint $\psi \in H$ using the indicator function $I_H$, where $H=\{\psi \mid {\sum }_{j=1}^n{\psi }_j=0\}$, and modify the Kantorovich functional $E(\psi )$ in Eqn. (6) as:

$$\tilde{E}(\psi )=E(\psi )+I_H(\psi ),I_H(\psi )=\{\begin{array}{cc}0\hfill & \psi \in H\hfill \\ \infty \hfill & \psi \notin H\hfill \end{array}\phantom{\}}$$ (8)

Then solving Eqn. (6) is equivalent to finding the solution to:

$$\begin{gathered} M_c(\mu ,\nu )=-\underset{\psi }{\text{min}}\tilde{E}(\psi ) \\ =-\underset{\psi }{\text{min}}\left\{\sum _{i=1}^m{\mu }_i{\psi }^c(x_i)-\sum _{j=1}^n{\nu }_j{\psi }_j+I_H(\psi )\right\} \end{gathered}$$ (9)

which is essentially an ($n-1$)-dimensional unconstrained convex problem. According to the definition of $c$-transform in 7), ${\psi }^c$ is non-smooth with respect to $\psi$.

Nesterov’s Smoothing of Kantorovich functional

Following Nesterov’s original strategy (Nesterov 2005), which has also been applied in the OT field (Peyré and Cuturi 2018; Schmitzer 2019), we smooth the non-smooth discrete Kantorovich functional $E(\psi )$. We approximate ${\psi }^c(x)$ with the Log-Sum-Exp function to get the smooth Kantorovich functional $E_{\lambda }(\psi )$. Then through the FISTA algorithm (Beck and Teboulle 2009), we can easily induce that the computation complexity of our algorithm is $O(n^{2.5}\sqrt{\log n}∕\epsilon )$, with $\tilde{E}({\psi }^t)-\tilde{E}({\psi }^{\ast })\le ϵ$. By abuse of notation, in the following we call both $E(\psi )$ and $\tilde{E}(\psi )$ the Kantorovich functional and both $E_{\lambda }(\psi )$ and ${\tilde{E}}_{\lambda }(\psi )$ the smooth Kantorovich functional.

Definition 4 ($(\alpha ,\beta )$-smoothable). A convex function $f$ is called ($\alpha ,\beta$)-smoothable if, for any $\lambda >0$, $\exists a$ a convex function $f_{\lambda }$ such that

$$\begin{gathered} f_{\lambda }(x)\le f(x)\le f_{\lambda }(x)+\beta \lambda \\ {f}_{\lambda }(y)\le f_{\lambda }(x)+\langle \nabla f_{\lambda }(x),y-x\rangle +\frac{\alpha }{2\lambda }{(y-x)}^T{\nabla }^2{f}_{\lambda }(x)(y-x) \end{gathered}$$

Here $f_{\lambda }$ is called a $\frac{1}{\lambda }$-smooth approximation of $f$ with parameters ($\alpha ,\beta$).

In the above definition, the parameter $\lambda$ defines a trade-off between the approximation accuracy and the smoothness, where the smaller the $\lambda$, the better approximation and the less smoothness we obtain.

Lemma 5 (Nesterov’s Smoothing). Given $f:{\mathbb{R}}^n\to \mathbb{R}$, $f(x)=\max \{x_j:j=1,\dots ,n\}$, for any $\lambda >0$, we have its $\frac{1}{\lambda }$-smooth approximation with parameters ($1,\log n$)

$$f_{\lambda }(x)=\lambda \log \left(\sum _{j=1}^n{e}^{x_j∕\lambda }\right)-\lambda \log n,$$ (10)

Proof. We have $\forall x\in R^n$,

$$\begin{gathered} f_{\lambda }(x)\le \lambda \log (n\underset{j}{\max }{e}^{x_j∕\lambda })-\lambda \log (n)=f(x) \\ f(x)=\lambda \log \underset{j}{\max }{e}^{x_j∕\lambda }<\lambda \log \sum _{j=1}^n{e}^{x_j∕\lambda }=f_{\lambda }(x)+\lambda \log n \end{gathered}$$

Furthermore, it is easy to prove that $f_{\lambda }(x)$ is $\frac{1}{\lambda }$-smooth. Therefore, $f_{\lambda }(x)$ is an approximation of $f(x)$ with parameters ($1,\log n$).

Recalling the definition of c-transform of the Kantorovich potential in Eqn. (7), we obtain the Nesterov’s smoothing of ${\psi }^c$ by applying Eqn. (10)

$${\psi }_{\lambda }^c=\lambda \log \left(\sum _{j=1}^n{e}^{({\psi }_j-c_{ij})∕\lambda }\right)-\lambda \log n.$$ (11)

We use ${\psi }_{\lambda }^c$ to replace ${\psi }^c$ in Eqn. (9) to approximate the Kantorovich functional. Then the Nesterov’s smoothing of the Kantorovich functional becomes

$$E_{\lambda }(\psi )=\lambda \sum _{i=1}^m{\mu }_i\log \left(\sum _{j=1}^n{e}^{({\psi }_j-c_{ij})∕\lambda }\right)-\sum _{j=1}^n{\nu }_j{\psi }_j-\lambda \log n$$ (12)

and its gradient is given by

$$\frac{\partial E_{\lambda }}{\partial {\psi }_j}=\sum _{i=1}^m{\mu }_i\frac{e^{({\psi }_j-c_{ij})∕\lambda }}{{\sum }_{k=1}^n{e}^{({\psi }_k-c_{ik})∕\lambda }}-{\nu }_j,\forall j\in [n]$$ (13)

Furthermore, we can directly compute the Hessian matrix of $E_{\lambda }(\psi )$. Let $K_{ij}=e^{-c_{ij}∕\lambda }$ and $v_j=e^{{\psi }_j∕\lambda }$, and set $E_{\lambda }^i≔\lambda \log {\sum }_{j=1}^n{K}_{ij}{v}_j$, $\forall i\in [m]$. Direct computation gives the following gradient and Hessian matrix:

$$\begin{gathered} \nabla E_{\lambda }=diag(v)K^T(\mu \oslash Kv)-\nu \\ {\nabla }^2{E}_{\lambda }=\sum _{i=1}^m{\mu }_i{\nabla }^2{E}_{\lambda }^i, \\ {\nabla }^2{E}_{\lambda }^i=\frac{1}{\lambda }\left(\frac{1}{1^T{V}_i}{\Lambda }_i-\frac{1}{{(1^T{V}_i)}^2}{V}_i{V}_i^T\right) \end{gathered}$$ (14)

where $V_i={(K_{i1}{v}_1,K_{i2}{v}_2,\dots ,K_{in}{v}_n)}^T$, and ${\Lambda }_i=\text{diag}(K_{i1}{v}_1,K_{i2}{v}_2,\dots ,K_{in}{v}_n)$. By the Hessian matrix, we can show that $E_{\lambda }$ is a smooth approximation of $E$.

Lemma 6. $E_{\lambda }(\psi )$ is a $\frac{1}{\lambda }$-smooth approximation of $E(\psi )$ with parameters ($1,\log n$).

Proof. From Eqn. (14), we see ${\nabla }^2{E}_{\lambda }^i$ has $K=\{k1:k\in \mathbb{R}\}$ as its null space. In the orthogonal complementary space of $K$, ${\nabla }^2{E}_{\lambda }^i$ is diagonal dominant, therefore strictly positive definite.

Weyl’s inequality (Horn and Johnson 1991) states that the eigen value of $A=B+C$ is no greater than the maximal eigenvalue of $B$ minus the minimal eigenvalue of $C$, where $B$ is an exact matrix and $C$ is a perturbation matrix. Hence the maximal eigenvalue of ${\nabla }^2{E}_{\lambda }^i$, denoted as ${\sigma }_i$, has an upper bound,

$$0\le {\sigma }_i\le \frac{1}{\lambda }\frac{1}{1^T{V}_i}\underset{j}{\max }\{K_{ij}{v}_j\}\le \frac{1}{\lambda }.$$

Thus the maximal eigenvalue of ${\nabla }^2{E}_{\lambda }(\psi )$ is no greater than ${\sum }_{i=1}^n{\mu }_i{\sigma }_i\le \frac{1}{\lambda }$. It is easy to find that $E_{\lambda }(\psi )\le E(\psi )\le E_{\lambda }(\psi )+\lambda \log n$. Thus, $E_{\lambda }(\psi )$ is a $\frac{1}{\lambda }$-smooth approximation of $E(\psi )$ with parameters ($1,\log n$).

Lemma 7. Suppose $E_{\lambda }(\psi )$ is the $\frac{1}{\lambda }$-smooth approximation of $E(\psi )$ with parameters $1,\log n$, ${\psi }_{\lambda }^{\ast }$ is the optimizer of $E_{\lambda }(\psi )$, then the approximate OT plan is unique and given by

$${(P_{\lambda }^{\ast })}_{ij}={\mu }_i\frac{e^{({({\psi }_{\lambda }^{\ast })}_j-c_{ij})∕\lambda }}{{\sum }_{k=1}^n{e}^{({({\psi }_{\lambda }^{\ast })}_k-c_{ik})∕\lambda }}=\frac{{\mu }_i{K}_{ij}{v}_j^{\ast }}{K_i{v}^{\ast }}$$ (15)

where $K_i$ is the $ith$ row of $K$ and $v^{\ast }=e^{{\psi }_{\lambda }^{\ast }∕\lambda }$.

Proof. By the gradient formula Eqn. (13) and the optimizer ${\psi }_{\lambda }^{\ast }$, we have

$$\frac{\partial E_{\lambda }({\psi }^{\ast })}{\partial {\psi }_j}=\sum _{i=1}^m{(P_{\lambda }^{\ast })}_{ij}-{\nu }_j=0\forall j=1,\cdots ,n.$$

On the other hand, by the definition of $P_{\lambda }^{\ast }$, we have

$$\sum _{j=1}^n{(P_{\lambda }^{\ast })}_{ij}={\mu }_i,\forall i=1,\dots ,m,$$

Combing the above two equations, we obtain that $P_{\lambda }^{\ast }\in \pi (\mu ,\nu )$ and it is the approximate OT plan.

Similar to the discrete Kantorovich functional in Eqn. (6), the optimizer of the smooth Kantorovich functional in Eqn. (12) is also not unique: given an optimizer ${\psi }_{\lambda }^{\ast }$, then ${\psi }_{\lambda }^{\ast }+k1$, $k\in \mathbb{R}$ is also an optimizer. We can eliminate the ambiguity by adding the indicator function as Eqn. (8), ${\tilde{E}}_{\lambda }(\psi )=E_{\lambda }(\psi )+I_H(\psi )$,

$$\begin{gathered} {\tilde{E}}_{\lambda }(\psi )=\lambda \sum _{i=1}^m{\mu }_i\log \left(\sum _{j=1}^n{e}^{({\psi }_j-c_{ij})∕\lambda }\right) \\ -\sum _{j=1}^n{\nu }_j{\psi }_j-\lambda \log n+I_H(\psi ) \end{gathered}$$ (16)

This energy can be optimized effectively through the following FISTA iterations (Beck and Teboulle 2009).

$$\begin{gathered} z^{t+1}={\Pi }_{{\eta }_t{I}_H}({\psi }^t-{\eta }_t\nabla E_{\lambda }({\psi }^t)) \\ {\psi }^{t+1}=z^{t+1}+\frac{{\theta }_t-1}{{\theta }_{t+1}}(z^{t+1}-z^t) \end{gathered}$$ (17)

with initial conditions ${\psi }^0=v^0=0$, ${\theta }_0=1$, ${\eta }_t=\lambda$ and ${\theta }_{t+1}=\frac{1}{2}\left(1+\sqrt{1+4{\theta }_t^2}\right)$. Here ${\Pi }_{{\eta }_t{I}_H}(z)=z-\frac{1}{n}{\sum }_{j=1}^n{z}_j$ is the projection of $z$ to $H$ (the proximal function of $I_H(x)$ (Parikh and Boyd 2014). Similar to the Sinkhorn’s algorithm, this algorithm can be parallelized, since all the operations are row based.

Theorem 8. Given the cost matrix $C=(c_{ij})$, the source measure $\mu \in R_{+}^m$ and target measure $\nu \in R_{+}^n$ with ${\sum }_{i=1}^m{\mu }_i={\sum }_{j=1}^n{\nu }_j=1$, ${\psi }^{\ast }$ is the optimizer of the discrete dual Kantorovich functional $\tilde{E}(\psi )$, and ${\psi }_{\lambda }^{\ast }$ is the optimizer of the smooth Kantorovich functional ${\tilde{E}}_{\lambda }(\psi )$. Then the approximation error is

$$\mid \tilde{E}({\psi }^{\ast })-{\tilde{E}}_{\lambda }({\psi }_{\lambda }^{\ast })\mid \le 2\lambda \log n$$

Proof. Assume ${\psi }^{\ast }$ and ${\psi }_{\lambda }^{\ast }$ are the minimizers of $E(\psi )$ and $E_{\lambda }(\psi )$ respectively. Then by the inequality in Eqn. (10)

$$\begin{gathered} E_{\lambda }({\psi }^{\ast })\le E({\psi }^{\ast })\le E({\psi }_{\lambda }^{\ast })\le E_{\lambda }({\psi }_{\lambda }^{\ast })+\lambda \log n \\ {E}_{\lambda }({\psi }_{\lambda }^{\ast })\le E_{\lambda }({\psi }^{\ast })\le E({\psi }^{\ast })\le E_{\lambda }({\psi }^{\ast })+\lambda \log n \end{gathered}$$

This shows $\mid E_{\lambda }({\psi }^{\ast })-E_{\lambda }({\psi }_{\lambda }^{\ast })\mid \le \lambda \log n$. Removing the indicator functions, we can get

$$\begin{gathered} \mid \tilde{E}({\psi }^{\ast })-{\tilde{E}}_{\lambda }({\psi }_{\lambda }^{\ast })\mid \\ =\mid E({\psi }^{\ast })-E_{\lambda }({\psi }_{\lambda }^{\ast })\mid \\ \le \mid E({\psi }^{\ast })-E_{\lambda }({\psi }^{\ast })\mid +\mid E_{\lambda }({\psi }^{\ast })-E_{\lambda }({\psi }_{\lambda }^{\ast })\mid \\ \le 2\lambda \log n \end{gathered}$$

This also shows that $E({\psi }_{\lambda }^{\ast })$ converges quickly to $E({\psi }^{\ast })$ as the decrease of $\lambda$. The convergence analysis of FISTA is given as follows:

Theorem 9 (Thm 4.4 of (Beck and Teboulle 2009)). Assume $(1)g(x)$ is convex and differentiable with $dom(g)={\mathbb{R}}^n$, $\nabla g$ is Lipschitz continuous with Lipschitz constant $L>0$; and $(2)h(x)$ is convex and its proximal function can be evaluated. Then from the minimization of $f(x)=g(x)+h(x)$ by FISTA with fixed step size ${\eta }_t=\frac{1}{L}$, we can get

$$f(x^t)-f(x^{\ast })\le \frac{2L}{{(t+1)}^2}{\Vert x^0-x^{\ast }\Vert }^2$$ (18)

Corollary 10. Suppose $\lambda$ is fixed and ${\psi }^0=0$, then for any $t\ge \sqrt{\frac{2{\Vert {\psi }_{\lambda }^{\ast }\Vert }^2}{\lambda \epsilon }}$, we have

$${\tilde{E}}_{\lambda }({\psi }^t)-{\tilde{E}}_{\lambda }({\psi }_{\lambda }^{\ast })\le \epsilon ,$$ (19)

where ${\psi }_{\lambda }^{\ast }$ is the optimizer of ${\tilde{E}}_{\lambda }(\psi )$.

Proof. Under the settings of the smoothed Kantorovich problem Eqn. (12), $E_{\lambda }(\psi )$ is convex and differentiable with ${\nabla }^2{E}_{\lambda }(\psi )\underset{¯}{\prec }\frac{1}{\lambda }I$, $I_H(\psi )$ is convex and its proximal function is given by ${\Pi }_H(v)$. Thus, directly applying Thm. 9 and setting $L=\frac{1}{\lambda }$, we can get ${\tilde{E}}_{\lambda }({\psi }^t)-{\tilde{E}}_{\lambda }({\psi }_{\lambda }^{\ast })\le \frac{2}{\lambda {(t+1)}^2}\Vert {\psi }_{\lambda }^{\ast }-{\psi }^0{\Vert }^2$. Set ${\psi }^0=0$ and $\frac{2}{\lambda {(t+1)}^2}\Vert {\psi }_{\lambda }^{\ast }{\Vert }^2\le \epsilon$, then we get that, when $t\ge \sqrt{\frac{2\Vert {\psi }_{\lambda }^{\ast }{\Vert }^2}{\lambda \epsilon }}$, we have ${\tilde{E}}_{\lambda }(\psi {}^t)-{\tilde{E}}_{\lambda }(\psi {}_{\lambda }^{\ast })\le \epsilon$.

With the above analysis of the convergence of the smooth Kantorovich functional ${\tilde{E}}_{\lambda }(\psi {}^t)$, in the following we give the convergence analysis of the original Kantorovich functional $\tilde{E}(\psi {}^t)$ in Eqn. (9), where ${\psi }^t$ is obtained by FISTA.

Theorem 11. If $\lambda =\frac{\epsilon }{2\log n}$, then for any $t\ge \frac{\sqrt{8\Vert \overline{C}{\Vert }^{2}n\log n}}{ϵ}$, with $\overline{C}=C_{\max }-\lambda \log {\nu }_{min}$, we have

$$\tilde{E}({\psi }^t)-\tilde{E}({\psi }^{\ast })<\epsilon ,$$ (20)

where ${\psi }^t$ is the solver of ${\tilde{E}}_{\lambda }(\psi )$ after $t$ steps in the iterations in Alg. 1, and ${\psi }^{\ast }$ is the optimizer of $\tilde{E}(\psi )$. Then the total computational complexity is $O(\frac{n^{2.5}\sqrt{\log n}}{\epsilon })$.

Algorithm 1: Accelerated gradient descent for OT

$$\begin{array}{cc}\hfill & 1:\mathrm{Input}:\text{The cost matrix}C=(c_{ij}),\text{the corresponding source}\hfill \\ \hfill & \text{weights}\mu \text{and target weights}\nu ,\text{the approximate parameter}\lambda ,\hfill \\ \hfill & \text{and the step length}\eta .\hfill \\ \hfill & 2:\mathrm{Output}:\text{The smoothed Kantorovich functional}{\psi }_{\lambda }.\hfill \\ \hfill & 3:\text{Initialize}\psi =({\psi }_1,{\psi }_2,\dots ,{\psi }_n)\leftarrow (0,0,\dots ,0).\hfill \\ \hfill & 4:\text{Initialize}z\leftarrow (0,0,\dots ,0).\hfill \\ \hfill & 5:\text{Initialize}K=e^{-C∕\lambda },{\theta }_0=1\hfill \\ \hfill & 6:\mathbf{repeat}\hfill \\ \hfill & 7:v^t=e^{{\psi }^t∕\lambda }.\hfill \\ \hfill & 8:\nabla E_{\lambda }({\psi }^t)=diag(v)K^T(\mu \mid \oslash Kv)-\nu .\hfill \\ \hfill & 9:z^{t+1}={\psi }^t-\eta \nabla E_{\lambda }({\psi }^t)\hfill \\ \hfill & 10:z^{t+1}=z^{t+1}-mean(z^{t+1}).\hfill \\ \hfill & 11:{\psi }^{t+1}=z^{t+1}+\frac{{\theta }_t-1}{{\theta }_{t+1}}(z^{t+1}-z^t).\hfill \\ \hfill & 12:{\theta }_{t+1}=\frac{1}{2}(1+\sqrt{1+4{\theta }_t^2}).\hfill \\ \hfill & 13:t=t+1\hfill \\ \hfill & 14:\mathbf{until}\text{Converge}\hfill \\ \hfill & 15:\text{The OT cost}E({\psi }^t)={\sum }_{i+1}^m{\mu }_i{\psi }^c(x_i)-{\sum }_{j=1}^n{\psi }_j^t{\nu }_j.\hfill \end{array}$$

Proof. We set the initial condition ${\psi }^0=0$. For any given $\epsilon >0$, we choose iteration step $t$, such that $\frac{2}{\lambda {(t+1)}^2}\Vert {\psi }_{\lambda }^{\ast }{\Vert }^2\le \frac{\epsilon }{2}$, $t\ge \frac{\sqrt{8\Vert {\psi }_{\lambda }^{\ast }{\Vert }^2\log n}}{ϵ}$, where ${\psi }_{\lambda }^{\ast }$ is the optimizer of ${\tilde{E}}_{\lambda }(\psi )$. By theorem 9, we have

$$\begin{gathered} {\tilde{E}}_{\lambda }({\psi }^t)-\tilde{E}({\psi }^{\ast })\le {\tilde{E}}_{\lambda }({\psi }^t)-{\tilde{E}}_{\lambda }({\psi }^{\ast }) \\ \le {\tilde{E}}_{\lambda }({\psi }^t)-{\tilde{E}}_{\lambda }({\psi }_{\lambda }^{\ast }) \\ \le \frac{2}{{\lambda (t+1)}^2}{\Vert {\psi }_{\lambda }^{\ast }\Vert }^2 \\ \le \frac{\epsilon }{2} \end{gathered}$$

By Eqn. (16), we have

$$\begin{gathered} \tilde{E}({\psi }^t)-\tilde{E}({\psi }^{\ast })=E({\psi }^t)+I_H({\psi }^t)-E({\psi }^{\ast })-I_H({\psi }^{\ast }) \\ =(E({\psi }^t)-E_{\lambda }({\psi }^t))+(E_{\lambda }({\psi }^t)+I_H({\psi }^t)) \\ -(E({\psi }^{\ast })+I_H({\psi }^{\ast })) \\ \le \mid E({\psi }^t)-E_{\lambda }({\psi }^t)\mid +({\tilde{E}}_{\lambda }({\psi }^t)-\tilde{E}({\psi }^{\ast })) \\ \le \lambda \log n+\frac{\epsilon }{2} \\ =\epsilon \end{gathered}$$

Next we show that $\Vert {\psi }_{\lambda }^{\ast }{\Vert }^2\le n\Vert \overline{C}{\Vert }^2$ by proving $\mid {({\psi }_{\lambda }^{\ast })}_j\mid \le \overline{C}\forall j\in [n]$. According to Eq. (15),

$$\begin{gathered} {\nu }_j=\sum _{i=1}^m{\mu }_i\frac{e^{({({\psi }_{\lambda }^{\ast })}_j-c_{ij})∕\lambda }}{{\sum }_{k=1}^n{e}^{({({\psi }_{\lambda }^{\ast })}_k-c_{ik})∕\lambda }} \\ =\sum _{i=1}^m{\mu }_i\frac{e^{{({\psi }_{\lambda }^{\ast })}_j∕\lambda }}{{\sum }_{k=1}^n{e}^{{({\psi }_{\lambda }^{\ast })}_k∕\lambda }{e}^{(c_{ij}-c_{ik})∕\lambda }} \end{gathered}$$ (21)

Assume ${({\psi }_{\lambda }^{\ast })}_{\max }$ is the maximal element of ${\psi }_{\lambda }^{\ast }$, we have ${\sum }_{k=1}^n{e}^{{(\psi {}_{\lambda }^{\ast })}_k∕\lambda }{e}^{(c_{ij}-c_{ik})∕\lambda }\ge e^{{({\psi }_{\lambda }^{\ast })}_{\max }∕\lambda }{e}^{-C_{\max }∕\lambda }$, where $C_{\max }$ is the maximal element of the matrix $C$. Thus,

$$\begin{gathered} {\nu }_j\le \sum _{i=1}^n{\mu }_i\frac{e^{{({\psi }_{\lambda }^{\ast })}_j∕\lambda }}{e^{{({\psi }_{\lambda }^{\ast })}_{\max }∕\lambda }{e}^{-C_{\max }∕\lambda }} \\ =\frac{e^{{({\psi }_{\lambda }^{\ast })}_j∕\lambda }}{e^{{({\psi }_{\lambda }^{\ast })}_{\max }∕\lambda }{e}^{-C_{\max }∕\lambda }} \end{gathered}$$

Then, ${({\psi }_{\lambda }^{\ast })}_{\max }\le ({{\psi }_{\lambda }^{\ast })}_j+C_{\max }-\lambda \log v_j$ and

$$\begin{gathered} {({\psi }_{\lambda }^{\ast })}_{\max }\le \frac{1}{n}\sum _{j=1}^n\{{({\psi }_{\lambda }^{\ast })}_j+C_{\max }-\lambda \log {\nu }_j\} \\ \le C_{\max }-\lambda \log {\mu }_{min} \end{gathered}$$ (22)

According to the inequality of arithmetic and geometric means, we have ${\sum }_{k=1}^n{e}^{({\psi {}_{\lambda }^{\ast })}_k∕\lambda }\ge {ne}^{\frac{1}{n}({\sum }_{k=1}^n({\psi }_{\lambda }^{\ast }){}_k∕\lambda )}=n$. Thus, ${\nu }_j\le \frac{e^{({\psi {}_{\lambda }^{\ast })}_j∕\lambda }}{n{e}^{-C{}_{\max }∕\lambda }}$.

$$\begin{gathered} {({\psi }_{\lambda }^{\ast })}_j\ge \lambda \log n-C_{\max }+\lambda \log {\nu }_j \\ \ge \lambda \log {\nu }_{min}-C_{\max } \end{gathered}$$ (23)

Combine Eqn. (22) and (23), we have $\mid {({\psi }_{\lambda }^{\ast })}_j\mid \le C_{\max }-\lambda \log {\nu }_{min}=\overline{C}$. Hence, we obtain that when $t\ge \frac{\sqrt{8{\Vert \overline{C}\Vert }^{2}n\log n}}{ϵ},\tilde{E}({\psi }^t)-\tilde{E}({\psi }^{\ast })<\epsilon$.

For each iteration in Eqn. (17), we need $O(n^2)$ times of operations, thus total the computational complexity of the proposed method is $O(\frac{n^{2.5}\sqrt{\log n}}{\epsilon })$.

Relationship with Softmax

If there exists an OT map from $\mu$ to $\nu$, then each sample $x_i$ of the source distribution is classified into the corresponding $y_j=T(x_i)$. If there does not exist an OT map, we can only get the OT plan, which can be treated as a soft classification problem: each weighted sample $x_i$ with weight ${\mu }_i$ will be sent to the corresponding $y_j\mathrm{s}$ with weight ${\mu }_i\frac{P_{ij}}{{\sum }_{k=1}^n{P}_{ik}}$ where $P_{ij}>0$. Here $P_{ij}={\mu }_i\frac{P_{ij}}{{\sum }_{k=1}^n{P}_{ik}}$ gives the OT plan from the source to the target distribution. The smoothed OT plan given by minimizing the smooth Kantorovich functional can be further treated as a relaxed OT plan. Instead of sending the weights of a specific sample to several target samples, the smooth solver tends to send each source sample to all of the target samples weighted by $\frac{e^{({\psi }_j^{\ast }-c_{ij})∕\lambda }}{{\sum }_{k=1}^n{e}^{({\psi }_k^{\ast }-c_{ik})∕\lambda }}$. Sample $x_j$ weighted by ${\mu }_i$ will be sent to $y_j$ with weight ${\mu }_i\frac{e^{({\psi }_j^{\ast }-c_{ij})∕\lambda }}{{\sum }_{k=1}^n{e}^{({\psi }_k^{\ast }-c_{ik})∕\lambda }}$.

Relationship with entropy regularized OT problem

The Sinkhorn algorithm is deduced from minimizing the entropy regularized OT problem (Cuturi 2013): $\langle P,C\rangle +\lambda KL(P\mid \mu \otimes \nu )$ with $P\in \pi (\mu ,\nu )$. Its dual is given by (Genevay et al. 2016):

$$\begin{gathered} W_{\lambda }(\mu ,\nu )=-\underset{\psi }{\text{min}}\{\lambda \sum _{i=1}^m{\mu }_i\log \left(\sum _{j=1}^n{\nu }_j{e}^{({\psi }_j-c_{ij})\lambda }\right) \\ -\sum _{j=1}^n{\nu }_j{\psi }_j+\lambda \} \end{gathered}$$ (24)

with gradient $\frac{\partial W_{\lambda }}{\partial {\psi }_j}={\sum }_{i=1}^m{\mu }_i\frac{{\nu }_j{e}^{({\psi }_j-c_{ij})∕\lambda }}{{\sum }_{k=1}^n{\nu }_k{e}^{({\psi }_k-c_{ik})∕\lambda }}-{\nu }_j$. With the optimal solver ${\psi }^{\ast }$, the approximate OT plan is given by $P_{ij}={\mu }_i\frac{{\nu }_j{e}^{({\psi }_j-c_{ij})∕\lambda }}{{\sum }_{k=1}^n{\nu }_k{e}^{({\psi }_k-c_{ik})∕\lambda }}$. We can compare them with our gradient Eqn. (13) and approximated OT plan Eqn. (15) to see the subtle differences. Actually, by setting $\psi ≔\psi -\log \nu$, the minimizing problem in Eqn. (24) is equivalent to our smoothed semi-discrete problem of Eqn. (16) with a different constant term.

Furthermore, if we set $u={(u_1,u_2,\dots ,u_m)}^T$ with $u_i=\frac{{\mu }_i}{K_{i}v}$ in Eqn. (15), the computed approximate OT plan can be rewritten as $P_{\lambda }=diag(u)Kdiag(v)$, which is the same as the form of the Sinkhorn solution (Cuturi 2013). Since the solution of the Sinkhorn algorithm is unique, we conclude that the induced approximate optimal transport plan Eqn. (15) by our algorithm is equivalent to that of the Sinkhorn.

Experiments

In this section, we investigate the performance of the proposed algorithm under different parameters, and then compare it with the Sinkhorn algorithm (Cuturi 2013). In the following, we first introduce the various settings of the experiments including the parameters, the cost matrix and the evaluation metrics. Then we show the experimental results. All of the codes were written in MATLAB with GPU acceleration, including the proposed method and the Sinkhorn algorithm (Cuturi 2013). The experiments are also conducted on a Windows laptop with Intel Core i7-7700HQ CPU, 16 GB memory and NVIDIA GTX 1060Ti GPU.

Parameters

There are two parameters involved in the proposed algorithm, $\lambda$ and ${\eta }_t$. The former is used to control the approximate accuracy between the Log-Sum-Exp function and the Kantorovich potential ${\psi }^c$ in Eqn. (11), and the latter controls the step size of the FISTA algorithm in Eqn. (17). Basically, smaller $\lambda$ gives better approximation.

In our experiments, to get $\lambda$ as small as possible, based on the Property 1 of the Eqn. (6), we set the median of the cost matrix $C$ equal to zero, so that the full range of the exponential of the floating-point numbers can be used, instead of only the negative part¹. Thus we set $C=C-\frac{C_{\max }+C_{\text{min}}}{2}$ and call it the translation trick. If the range of $C$ is denoted as $R$, then the accuracy parameter is set to be $\lambda =\frac{R}{T}$, where $T$ is a positive constant. For the FISTA algorithm, the ideal step size should be ${\eta }_t=\frac{1}{{\sigma }_{\max }}$, where ${\sigma }_{\max }$ is the maximal eigenvalue of the Hessian matrix ${\nabla }^2{\tilde{E}}_{\lambda }(\psi )$ in Eqn. (14). By Nesterov smoothing, we know ${\sigma }_{\max }\le \frac{1}{\lambda }$, so we set the step length ${\eta }_t=\eta \lambda$, where $\eta$ is a constant². In practice we use ($T,\eta$) as control parameters instead of ($\lambda ,{\eta }_t$).

Cost Matrix

In the following experiments, we test the performance of the algorithm with different parameters under different metrics. Specifically, we set $\mu ={\sum }_{i=1}^m{\mu }_i\delta (x-x_i)$, $\nu ={\sum }_{j=1}^n{\nu }_j\delta (y-y_j)$. Note that after the settings of ${\mu }_i\mathrm{s}$ and ${\nu }_j\mathrm{s}$, they are normalized by ${\mu }_i=\frac{{\mu }_i}{{\sum }_{k=1}^m{\mu }_k}$ and ${\nu }_j=\frac{{\nu }_j}{{\sum }_{k=1}^n{\nu }_k}$. To build the cost matrix, we use the Euclidean distance, squared Euclidean distance, spherical distance, and random cost matrix.

• For Euclidean distance (ED) and the squared Euclidean distance (SED) experiments, in experiment 1, $x_i’\mathrm{s}$ are randomly generated from the Gaussian distribution $𝒩(31_{\mathbf{d}},I_d)$ and $y_j’\mathrm{s}$ are randomly sampled from the uniform distribution $Uni({[0,1]}^d)-5$. Both ${\mu }_i$ and ${\nu }_j$ are randomly generated from the uniform distribution $Uni([0,1])$. Experiment 3 also uses a similar sampling strategy to build the discrete source and target measures. In experiment 2, like (Altschuler, Niles-Weed, and Rigollet 2017), we randomly choose one pair of images from the MNIST dataset (LeCun and Cortes 2010), and then add negligible noise 0.01 to each background pixel with intensity 0. ${\mu }_i$ and $x_i$ (${\nu }_j$ and $y_j$) are set to be the value and the coordinate of each pixel in the source (target) image. Then the Euclidean distance and squared Euclidean distance between $x_i$ and $y_j$ are given by $c(x_i,y_j)=\Vert x_i-y_j\Vert$ and $c(x_i,y_j)={\Vert x_i-y_j\Vert }^2$, respectively.

• For the spherical distance (SD) experiment, both ${\mu }_j$ ${\nu }_j$ are randomly generated from the uniform distribution $Uni([0,1])$. $x_i’\mathrm{s}$ are randomly generated from the Gaussian distribution $𝒩(31_{\mathbf{d}},I_d)$ and $y_j’\mathrm{s}$ are randomly generated from the uniform distribution $Uni({[0,1]}^d)$. Then we normalize $x_i$ and $y_j$ by $x_i=\frac{x_i}{{\Vert x_i\Vert }_2}$ and $y_j=\frac{y_j}{{\Vert y_j\Vert }_2}$. As a result, both $x_i’\mathrm{s}$ and $y_j’\mathrm{s}$ are located on the sphere. The spherical distance is given by $c(x_i,y_j)=\text{arccos}(\langle x_i,y_j\rangle )$.

• For the random distance (RD) matrix experiment, both ${\mu }_i$ and ${\nu }_j$ are randomly generated from the uniform distribution $Uni([0,1])$. Also, to build $C$, we randomly sample $c_{ij}$ from the Gaussian distribution $𝒩(0,1)$, then $C$ is defined as $C=C-C_{\text{min}}+1.0$.

Evaluation Metrics

We use two metrics to evaluate the proposed method: the first one is the transport cost, which is defined by Eqn. (6) and is given by $-E(\psi )$; and the second is the $L_1$ distance from the computed transport plan $P_{\lambda }$ to the admissible distribution space $\pi (\mu ,\nu )$ defined in Eqn. (1), and the distance is defined as $D(P_{\lambda })={\Vert P_{\lambda }1-\mu \Vert }_1+{\Vert P_{\lambda }^{T}1-\nu \Vert }_1$.

Experiment 1: The influence of different parameters

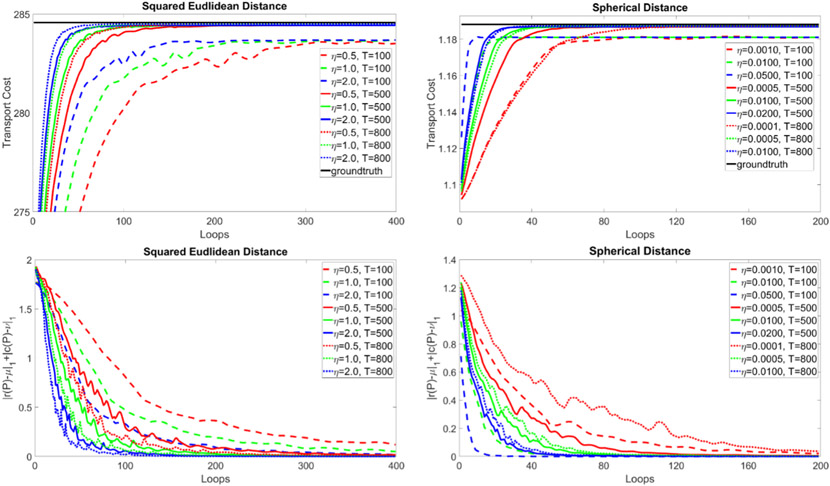
We test the performance of the proposed algorithm with different parameters under the SED and SD with $m=n=100$ and $d=5$, as shown in Fig. 1. The left column shows the results for SED and the right column is the result for SD. The top row illustrates the transport costs over iterations, and the bottom row is the distance $D(P_{\lambda })$.

Figure 1:

The performance of the proposed algorithm with different parameters.

In the top row of Fig. 1, the black lines give the groundtruth transport costs, which are computed by linear programming. It is obvious that for the same $\eta$, by increasing $T$ (decreasing $\lambda$, see the different types of the lines with the same color), the approximate accuracy is improved, and the convergence rate is increased; if $T$ (equivalently $\lambda$) is fixed, by increasing $\eta$ (see the different colors of the lines with the same type), we increase the convergence speed.

Experiment 2: Faster Convergence

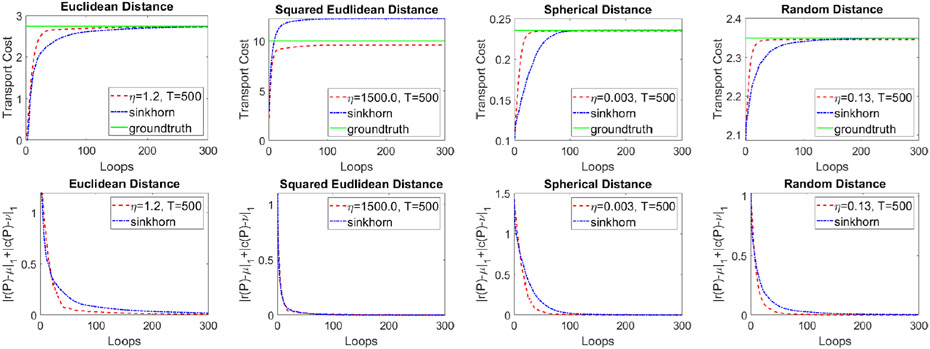
For the experiments with ED and SED, the distributions come from the MNIST dataset (LeCun and Cortes 2010), as illustrated in the Cost Matrix. For the the experiments with SD and RD, we set $m=n=500$ and $d=5$. Then we compare with the Sinkhorn algorithm (Cuturi 2013) with respect to both the convergence rate and the approximation accuracy. We manually set $T=500$ to get a good estimate of the OT cost, and then adjust $\eta$ to get the best convergence speed of the proposed algorithm. For the purpose of fair comparison, we use the same cost matrix with the same translation trick and the same $\lambda$ for the Sinkhorn algorithm, where we treat each update of $v$ as one step. We summarize the results in Fig. 2, where the green curves represent the groundtruth computed by linear programming, the blue curves are for the Sinkhorn algorithm, and the red curves give the results of our method. It is obvious that in all of the four experiments, our method achieves faster convergence than the Sinkhorn algorithm. Note that the computed approximate transport plan of the Sinkhorn algorithm is intrinsically equivalent to our induced transport plan in Eqn. (15).

Figure 2:

Comparison with the Sinkhorn algorithm (Cuturi 2013) under different cost matrix.

In Tab. 1, we report the running time of our method, Sinkhorn (Cuturi 2013), its variants algorithms, including Greenkhorn (Altschuler, Niles-Weed, and Rigollet 2017) and Screenkhorn (Alaya et al. 2019), and APDAMD (Lin, Ho, and Jordan 2019) for the four experiments shown in Fig. 2 with $T=700$. The stop condition is set to be $\mid E({\psi }^{t+1})-E({\psi }^t)\mid ∕\mid E({\psi }^t)\mid \le {10}^{-3}$. For all of the experiments, we can see that our proposed method achieves the fastest convergence.

Table 1:

Running time (s) of our method, Sinkhorn (Sink) (Cuturi 2013), Greenkhorn (Green) (Altschuler, Niles-Weed, and Rigollet 2017), Screenkhorn (Screen) (Alaya et al. 2019) and APDAMD (Lin, Ho, and Jordan 2019).

	Sink	Green	Screen	APDAMD	Ours
ED	0.0596	0.0923	0.0541	3.76	0.0404
SED	0.0431	0.0870	0.0328	3.21	0.0197
SD	0.0564	0.0862	0.0400	2.29	0.0142
RD	0.0374	0.0726	0.0313	2.88	0.0227

Experiment 3: Better Accuracy

From Fig. 2, we can observe that $-E({\psi }_{\lambda }^{\ast })$ gives a comparable or better approximate of the OT cost than $\langle P_{\lambda }^{\ast },C\rangle$ with the same small $\lambda$, especially for the $L_p$ cost function $c(x,y)={\Vert x-y\Vert }^p$ with $p>1$, see the second column of Fig. 2 for an example of $p=2$. To achieve $ϵ$ precision, $\langle P_{\lambda }^{\ast },C\rangle$ (equivalent to the Sinkhorn result) needs to set $\lambda =\frac{ϵ}{4\log n}$ (Dvurechensky, Gasnikov, and Kroshnin 2018), which is smaller than our requirement of $\lambda =\frac{ϵ}{2\log n}$ according to Thm. 11. Thus, with the same $\lambda$, the results of our algorithm should be more accurate than the Sinkhorn solutions. To verify this point, we give more examples in Tab. 2 with $p=1.5$, 2, 3 and 4. Here we use the discrete measures similar to the squared Euclidean distance as stated in the Cost Matrix part, and set $m=n=500$, $d=5$. From the table, we can see that our method obtains more accurate results than Sinkhorn.

Table 2:

Comparison among the OT cost (GT) by linear programming, the Sinkhorn results (Cuturi 2013) denoted as ’Sink’ and the results of the proposed method denoted as ’Ours’ with $T=500$ and different $p$.

p	GT	Sink	Ours	$\mid \text{Sink-GT}\mid$	$\mid \text{Ours-GT}\mid$
1.5	103.33	103.51	103.27	0.18	0.06
2	281.7	282.5	281.6	0.8	0.1
3	2189.8	2197.1	2187.5	7.3	2.3
4	16951.4	17038.5	16932.0	87.1	19.4

Conclusion

In this paper, we propose a novel algorithm based on Nesterov’s smoothing technique to improve the accuracy for solving the discrete OT problem. The c-transform of the Kantorovich potential is approximated by the smooth Log-Sum-Exp function, and the smoothed Kantorovich functional can be solved by FISTA efficiently. Theoretically, the computational complexity of the proposed method is given by $O(n^{2.5}\sqrt{\log n}∕\epsilon )$, which is lower than current estimation of the Sinkhorn method. Experimentally, our results demonstrate that the proposed method achieves faster convergence and better accuracy than the Sinkhorn algorithm.