Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2023 Nov 3;35(21):9064–9072. doi: 10.1021/acs.chemmater.3c01771

How Does Local Strain Affect Stokes Shifts in Halide Double Perovskite Nanocrystals?

Saar Shaek †,‡, Sasha Khalfin †, Emma Hasina Massasa †, Arad Lang †, Shai Levy †, Lotte T J Kortstee §, Betty Shamaev †, Shaked Dror †, Rachel Lifer †, Reut Shechter †, Yaron Kauffmann †, Rotem Strassberg †,⊥, Iryna Polishchuk †, Andrew Barnabas Wong ∥, Boaz Pokroy †, Ivano E Castelli §, Yehonadav Bekenstein †,‡,⊥,*
PMCID: PMC10653075  PMID: 37982006

Abstract

graphic file with name cm3c01771_0006.jpg

Lead-free perovskite nanocrystals are of interest due to their nontoxicity and potential application in the display industry. However, engineering their optical properties is nontrivial and demands an understanding of emission from both self-trapped and free excitons. Here, we focus on tuning silver-based double perovskite nanocrystals’ optical properties via two iso-valent dopants, Bi and Sb. The photoluminescence quantum yield of the intrinsic Cs2Ag1–yNayInCl6 perovskite increased dramatically upon doping. However, the two dopants affect the optical properties very differently. We hypothesize that the differences arise from their differences in electronic level contributions and ionic sizes. This hypothesis is validated through absorption and temperature dependence photoluminescence measurements, namely, by employing the Huang–Rhys factor, which indicates the coupling of the exciton to the lattice environment. The larger ionic size of Bi also plays a role in inducing significant microstraining verified via synchrotron measurements. These differences make Bi more sensitive to doping concentration over antimony which displays brighter emission (QY ∼40%). Such understanding is important for engineering optical properties in double perovskites, especially in light of recent achievements in boosting the photoluminescence quantum yield.

Lead halide perovskites (LHPs) APbX3 (where A = CH3NH3+, Cs+; X = Cl–, Br–, I–) are attracting much interest due to their potential in optoelectronic applications, such as light-emitting diodes, photovoltaic cells, photodetectors, etc.(1) LHPs have major challenges, such as the toxicity of Pb and instability of the organic–inorganic LHPs.2 One of the main strategies to overcome those challenges is by replacing the divalent Pb ion with altering monovalent and trivalent ions.3 The structure of double perovskite (DP) A2BIBIIIX6 is obtained, where A is Cs+, BI is a monovalent cation (for example, Ag+, Na+, and K+), BIII is a trivalent cation (for example, In3+, Bi3+, Sb3+, Fe3+, and Tl3+), and X is a halide.4,5 Although lead-free DPs are less toxic and more stable, their photoluminescence quantum yield (PLQY) is lower compared to that of LHPs due to parity-forbidden or slow transitions; thus, further emission enhancement strategies are required.6,7 Some reported enhancement strategies include alloying and doping in the BI and BIII sites.8−11 Jahn–Teller lattice distortion is caused by excitonic state defects, induced by alloying, and doping can break the symmetry to allow the transitions. Additional optoelectronic characteristic manipulation and enhancement strategy include lanthanide doping and codoping.12 Using Bi doping and Na alloying in bulk Cs2AgInCl6 DP crystals, Luo et al. achieved a PLQY of 86%, and Li et al. achieved 87% with emission peaks centered around 560 nm. Emission enhancements in DP nanocrystals (NCs) have also been reported, with a PLQY of up to 64% and emission peaks centered around 620, 570, and 550 nm.9,13−16 Many of those lead-free DPs' emission is due to the self-trapped exciton (STE) mechanism.17,18 STEs are strongly bound excitons affected by the matrix phonons and distortion of the structure. The Huang–Rhys factor reflects the strength of exciton–phonon interaction.19 Two-dimensional (2D) LHPs also exhibit broad emission characteristics assigned to the STE mechanism because of strong exciton–phonon coupling, as well as Stokes shifts of the free excitons due to quantum confinement effects.20−22 However, this explanation for broad emission is currently strongly debated, citing the existence of halide vacancy trap states. Using a combined experimental–computational study, Kahmann et al. demonstrated that the broad emission in 2D LHP originates both from halide vacancies' trapped states and STE. Their claim is further supported by demonstrating no contribution of STE in iodine 2D LHP.23 According to the STE mechanism behavior, the emission peak features a large Stokes shift and large full-width half-maximum (fwhm) depending on the Huang–Rhys factor. The large fwhm of the STE mechanism is of interest for white light emission applications and luminescent solar concentrators.9,17,24 Recent works investigate the Sb-doped Cs2NaInCl6 DP. Sb-doped Cs2NaInCl6 exhibits the STE emission mechanism with a smaller Stokes shift than the Bi-doped Cs2Ag1–yNayInCl6 DP.25−27 In the work of Gray et al., the Stokes shift was 112 nm with an emission peak centered at 455 nm and a PLQY of 79%.28 Zhang et al. investigated the STE mechanism in Sb-doped 2D (PEA)4NaInCl8 (PEA = phenethylamine) and (PEA)2CsNaInCl7 DP with emission peaks centered at 555 and 676 nm and PLQYs of 48.7 and 29.3% according to the monolayer and bilayer, respectively.29 Zeng et al. achieved a PLQY of 75.89%, with an emission peak centered at 442 nm.30 Noculak et al. investigated the alloying between Na and K in Sb-doped Cs2NaInCl6 DP, achieving a PLQY of 93% and an emission peak centered in the range of 440–492 nm with respect to the alloying concentrations.31 The work of Wu et al. expands Sb-doped to organic–inorganic hybrid systems emphasizing the STE emission mechanism.32 While those works describe the behavior of Bi-doped Cs2Ag1–yNayInCl6 and Sb-doped Cs2NaInCl6, a further detailed comparison is needed, which is addressed in this present study.

Results and Discussion

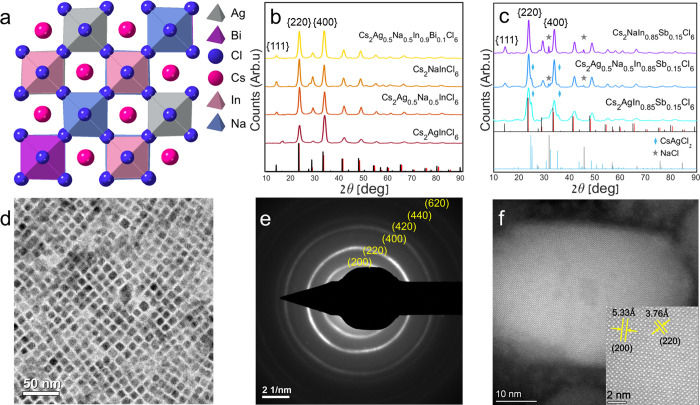
Here, we compare the Bi-doped and Sb-doped Cs2Ag1–yNayInCl6 DP systems. We synthesized NCs in an ambient environment using ligand passivation to control our colloidal reactions. Using DFT methods, we calculate the structure of alloyed and doped DP, and the structural model is presented in Figure 1a. A TEM micrograph of the DP NCs is shown in Figure 1d. To confirm the obtained structure of the NC’s, X-ray diffraction (XRD) patterns (Figure 1b,c), selected area diffraction (SAD), and high-angle annular dark-field scanning transmission electron microscopy (HAADF-STEM) micrographs were acquired (Figure 1e,f). The obtained experimental patterns of the DPs are compatible with the theoretical XRD patterns. Additionally, alloying between Ag and Na, as already reported by others, maintains the cubic Fm3̅m structure and creates a solid solution between the two DP matrixes.15 Furthermore, when alloying with Na atoms, the diffraction peak of the {111} planes appears at ∼14o, and the intensities of {220} and {400} diffraction peaks alter, as shown in Figure 1b. A clean XRD pattern of a single phase is obtained by doping Bi to the alloyed matrix. Chemical analysis using scanning electron microscopy (SEM) micrographs with energy-dispersive X-ray spectroscopy (EDS) was performed to validate the insertion of alloying and doping into the samples (Figure S1). In Figure 1c, the XRD patterns of Sb-doped systems are shown. Additional peaks of unwanted products are evident, including NaCl while alloying with Na and CsAgCl2 while alloying with Ag. These unwanted minor products probably formed, while the precipitants were deposited and dried on the XRD glass substrate. The Cs2AgSbCl6 system is less stable than Cs2AgInCl6 and Cs2AgBiCl6 systems, as reported by J. C. Dahl et al.33 Therefore, unwanted products might be obtained due to degradation of the DPs with Sb doping. For further verification of the structure of Cs2Ag0.5Na0.5In0.9Bi0.1Cl6, SAD was taken, and the diffraction rings with the corresponding indexed lattice plane spacings are seen in Figure 1e. The area at which the SAD was acquired is presented in Figure 1d. To verify the structure of Cs2NaIn0.85Sb0.15Cl6, the HAADF-STEM micrograph is shown in Figure 1f, including the lattice structure d-spacing (inset). The NCs of Cs2Ag0.5Na0.5In0.9Bi0.1Cl6 present a cubic shape with an edge length of 8.1 ± 0.8 nm (see Figure S2). However, the NCs of Cs2NaIn0.85Sb0.15Cl6 compositions present less faceted shapes, even though the crystal structure and ligand passivation are the same (see Figure S2). According to our previous work, this might be related to the role of Ag nanoparticles as nucleation sites in the DP NCs.34 This could also be a surface energy consideration. As the DP’s matrix is different, the energy of facets dictates different morphologies of the nanoparticles. The NCs without Ag are larger, typically 11.2 ± 1.4 nm in length.

Figure 1.

Figure 1

Open in a new tab

(a) Calculated structure diagram (using DFT, see Supporting Information) of the Bi-doped Cs2Ag1–yNayInCl6 DP (graphic designed using CrystalMaker).35 XRD patterns (using 1.54 Å (Cu Kα) wavelength) of (b) Cs2AgInCl6, Cs2Ag0.5Na0.5InCl6, Cs2NaInCl6, and Cs2Ag0.5Na0.5In0.9Bi0.1Cl6 nanoparticles (theoretical red lines for Cs2AgInCl6 ICCD no. 01–085–7533,36 theoretical black lines for Cs2NaInCl6 CIF no. 4003575)31 and (c) Cs2AgIn0.85Sb0.15Cl6, Cs2Ag0.5Na0.5In0.85Sb0.15Cl6, and Cs2NaIn0.85Sb0.15Cl6 nanoparticles. NaCl peaks marked with gray stars (and theoretical gray lines for ICDD no. 04-020-4596)37 and CsAgCl2 peaks marked with a light blue rhombus (and theoretical light blue lines for ICCD Card -04–014–2739).38 (d) TEM micrograph of Bi-doped Cs2Ag0.5Na0.5InCl6 NCs. (e) SAD pattern of Cs2Ag0.5Na0.5In0.9Bi0.1Cl6. (f) HAADF-STEM micrograph of Cs2NaIn0.9Sb0.1Cl6. Inset: zoomed-in micrograph with labeled d-spacings of {200} and {220}.

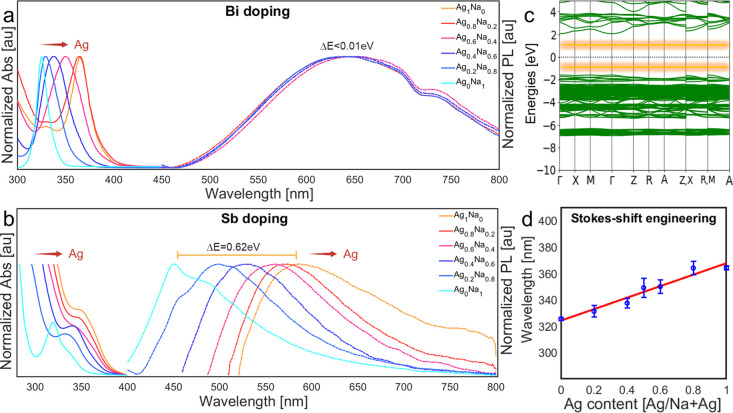
The most apparent differences between the doping systems are the optical characteristic results. The optical band gap absorption occurs between matrix octahedra (for example, [AgCl6], [NaCl6], and [InCl6]) and dopant octahedra ([BiCl6] or [SbCl6]). The excited energy states and the relaxed states are determined differently according to the dopant system, as shown by the works of Locardi et al. and Zeng et al.15,19,30,31 In our discussion, we will refer to it as absorption between the valence band (VB) and the conduction band (CB) for simplicity. The Bi-doped Cs2Ag1–yNayInCl6 absorption peak position is related to the Ag/Na ratio, as presented in Figure 2a, and in agreement with others.8,15 This is similar to the Sb-doped system, as seen in Figure 2b, suggesting that the absorption mechanism strongly depends on the matrix for both systems. The Na/Ag ratio was confirmed using 42 syntheses of Bi-doped Cs2Ag1–yNayCl6 with different Na/Ag ratios to fit a linear curve for absorption peak position versus Ag concentration, as shown in Figure 2d.

Figure 2.

Figure 2

Open in a new tab

Normalized absorption (Abs) and PL of (a) Cs2Ag1–yNayIn0.9Bi0.1Cl6 (y = 0, 0.2, 0.4, 0.5, 0.6, 0.8, 1) and (b) Cs2Ag1–yNayIn0.9Sb0.1Cl6 (y = 0, 0.2, 0.4, 0.6, 0.8, 1). For emphasis, the absorption data were collected only around the peak, omitting high-level absorption. Note in (a) that there is no emission for y = 1. (c) Simulated band diagram of intrinsic Cs2Ag0.4Na0.6InCl6 (the graphic designed using atomic simulation environment [ASE]).41 The STE energy levels (yellow) are added by hand (not part of the DFT simulation) according to the literature.15 (d) Absorption peak position averaged on 42 synthetic reactions plotted against the Ag loading ratio in the reaction flask (y = 0, 0.2, 0.4, 0.5, 0.6, 0.8, 1). 0% and a 100% are without Ag addition and only Ag addition to the reaction flask, respectively. The obtained Ag ratio is calibrated using a linear fit based only on the absorption (R2=0.95).

The differences in the STE emission are related to the dopant identity (Figure 2a,b). The STE states of the Bi-doped DP are deep inside the band gap, as illustrated (by hand) in the calculated band diagram of Cs2Ag0.4Na0.6InCl6 (Figure 2c), related to the dopant octahedrons and the Ag octahedrons.13,15 The STE states are not included in the DFT calculation. The states are situated (by hand) with equal distance from the zero-energy line, and with a total gap of ∼2 eV (according to the literature15), to demonstrate the deeper energy levels of the STE. Adding the dopant and forming [SbCl6] or [BiCl6] octahedra introduces strain and electronic effects to the native perovskite, which promotes an extrinsic STE mechanism. The STEs are coupled to the matrix phonons and include vibrational modes, broadening the emission. The Huang–Rhys factor describes the excitons’ coupling to the matrix. As the Huang–Rhys factor S increases, the coupling is stronger, and the Stokes shift (ΔE) is more prominent, according to

(1) ΔEStokes shift = 2Sℏωphonon, while ℏ is the reduced Planck constant and ℏω the phonon frequency.13,39 Doping with Bi distorts the matrix octahedrons due to the large size of the Bi ions, which increases the Huang–Rhys factor, as reported by Siddique et al.19 A smaller Huang–Rhys factor of Sb-doped Cs2NaInCl6 can explain the difference in the emission peak position and fwhm (Figure 2a,b). For the Bi-doped system’s normalized photoluminescence (PL), changing the matrix almost does not influence the emission peak position, contrary to the absorption, as shown in Figure 2a. However, for the Sb-doped system, the PL peak position is strongly influenced by changing the matrix from 450 to 580 nm, as shown in Figure 2b. The PL peak becomes broader while increasing the Ag content. This result agrees with the reformulated Duffy’s model of Philippe Boutinaud.40 Larger atom mass in BI sites increases the Stokes shift; thus, the Huang–Rhys factor depends on the octahedron’s reduced mass μ through (2) 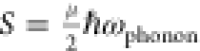Inline graphic. This model confirms the assumption that only Ag and Bi localize the holes and electrons in the Bi-doped system. This assumption explains the fixed PL position in our results (Figure 2a) while changing the Ag/Na ratio and agrees with the hypothesis15 that the Bi-doped system holes are localized in the Bi octahedra, and the electrons are localized in the Ag octahedra. Furthermore, there is no emission in the Bi-doped system without alloying with Ag atoms (y = 1 in Figure 2a). On the contrary, the Sb-doped system emits without alloying with Ag atoms (y = 1 in Figure 2b), and Sb and In localize both the holes and electrons octahedra, as depicted by Noculak et al.31 According to our hypothesis, by alloying Ag atoms into the matrix, the localization of holes is mixed between Sb and Ag octahedra, and as a result, a robust change in the emission occurs, from 450 to 580 nm; thus, enhanced Stokes shift is induced.

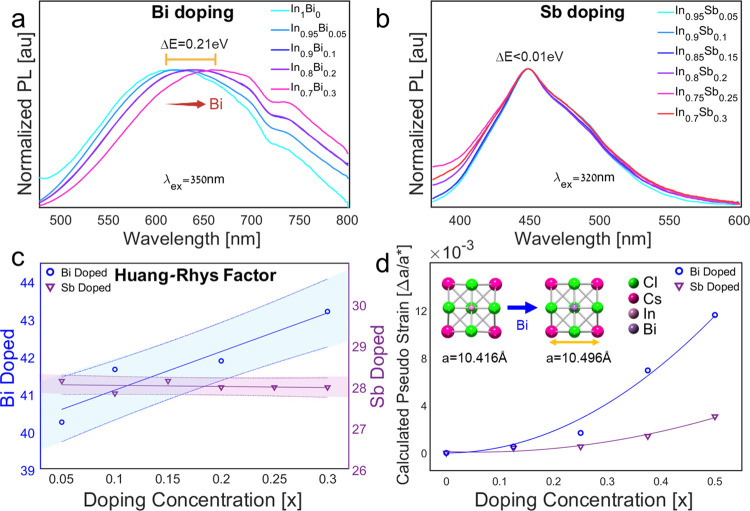
Changing the doping concentration does not affect the absorption peak position for both systems (see Figures S3 and S4). This observation agrees with the absorption mechanism as discussed above. The absorption of undoped Cs2Ag1–yNayInCl6 is excluded because there is no excitonic absorption peak. We assign the fluctuations in absorption peak positions of Bi-doped samples to deviations in Ag/Na ratios between reaction batches (Figures S3 and S4). The emission peak position of the Bi-doped system is red-shifted while increasing the Bi content from 610 nm without Bi addition to 680 nm with 30% of Bi (Bi–In ratio), as shown in Figure 3a and others.19

Figure 3.

Figure 3

Open in a new tab

Normalized PL of (a) Cs2Ag0.4Na0.6In1–xBixCl6 (x = 0, 0.05, 0.1, 0.2, 0.3) and (b) Cs2NaIn1–xSbxCl6 (x = 0.05, 0.1, 0.15, 0.2, 0.25, 0.3). (c) Huang–Rhys factor and (d) calculated pseudo strain of Cs2Ag0.4Na0.6In1–xBixCl6 (x = 0.05, 0.1, 0.2, 0.3) and Cs2NaIn1–xSbxCl6 (x = 0.05, 0.1, 0.15, 0.2, 0.25, 0.3), inset: changes of the lattice parameter with Bi doping. See the Supporting Information for the absorption and PLE of these compositions (Figures S3 and S4).

The different influences on the emission peak position for those doped systems are related to two reasons: dopant size and electronic character. First, in terms of size, Bi is significantly larger than In, while Sb is about the same size.42 Therefore, the Sb system does not experience any shift in the emission wavelength with increasing dopant concentration (Figure 3b). Indeed, we measured an increase in the lattice spacing with the addition of Bi content (Figure S5). This is also supported in DFT modeling. A calculated pseudostrain comparison of Bi and Sb doping appears in Figure 3d. The larger Bi cation is reflected in a significant dependence of the Huang–Rhys factor on Bi concentration. In comparison, the Sb concentration makes little difference (Figure 3c). The Stokes shift dependence is derived from absorption and emission data, as seen in Figures 2, 3, and S3. From this, we calculate the Huang–Rhys factor using eq 1, Stokes shift values, and a phonon energy of ℏωphonons = 20 meV (from literature19). There might be small variations in the phonon energy with doping and alloying, but it is less significant to the calculated Huang–Rhys factor trend, shown with the Stokes shift.13,19,43

To experimentally verify the dopant size effect (strain), we performed synchrotron high-resolution powder XRD (HR-PXRD) measurements on samples with increasing Bi or Sb concentrations (Figure 4a,b). We then fitted the (400) diffraction peak of each sample to a Voigt function and extracted the averaged microstrain fluctuations from the Gaussian contribution of fit using 3) 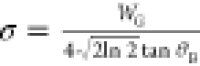Inline graphic, where WG is the Gaussian fwhm and θB is the Bragg’s angle (see Figure S6).44 The results described in Figure 4c show that for Bi doping, the averaged microstrain fluctuations are larger than that of Sb doping. Similarly, we extracted the lattice parameters from the position of the (400) diffraction peak of each sample (see Figure S7). While the lattice parameter increases linearly with concentration for both dopants, it is more significant in the case of Bi.

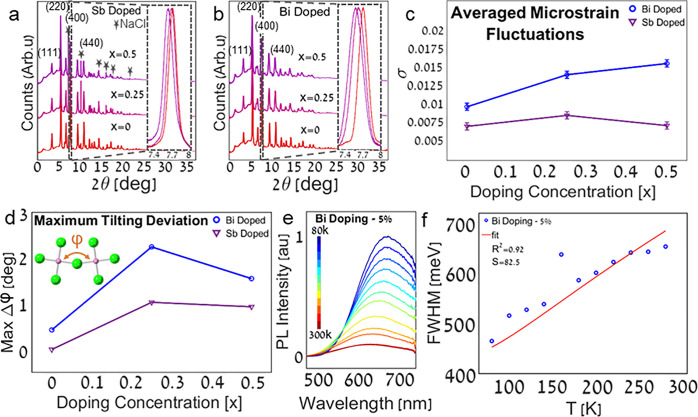
Figure 4.

Figure 4

Open in a new tab

Synchrotron HR-PXRD (λ = 0.35423 Å wavelength) of (a) Cs2NaIn1–xSbxCl6 (x = 0, 0.25, 0.5) and (b) Cs2Ag0.4Na0.6In1–xBixCl6 (x = 0, 0.25, 0.5); inset: normalized (400) diffraction peaks. Diffraction peaks that stem from NaCl are marked with stars (ICDD no. 04–020–4596). TEM and HRTEM micrographs of the samples could be found in the Supporting Information (Figure S10). (c) Microstrain fluctuations of Cs2NaIn1–xSbxCl6 and Cs2Ag0.4Na0.6In1–xBixCl6 (x = 0, 0.25, 0.5). The microstrain fluctuations were calculated from fitting the (400) diffraction peaks to a Voigt function (Figure S6). (d) Maximum tilting deviation of Cs2NaIn1–xSbxCl6 and Cs2Ag0.4Na0.6In1–xBixCl6 (x = 0, 0.25, 0.5). The tilting angles were extracted based on the DFT modeling, and the deviations were calculated from the difference from the original non tilted angles. The maximum rotation deviations can be found in the Supporting Information (Figure S8). Temperature-dependent (e) PL and (f) fwhm measurements of Cs2Ag0.4Na0.6In0.95Bi0.05Cl6. The Huang–Rhys factor S was extracted from the fitted model temperature-dependent fwhm (R2=0.92) as described at the Supporting Information (Figure S11). SEM-EDS images of the Cs2Ag0.4Na0.6In0.95Bi0.05Cl6 NCs could be found in the Supporting Information (Figure S1).

The DFT results below show that the strained octahedra are tilted and rotated compared to the undoped unstrained system. This is analogous to LHPs, where significant octahedral tilting due to interstitial iodine in methylammonium lead iodide (MAPbI3) leads to a giant Huang–Rhys factor of above 300.45 In our case, doping with Bi or Sb introduces angle deviations from the cubic unstrained intrinsic perovskite. While the effect exists for both Bi and Sb, the maximum tilting and rotation deviations are more pronounced for Bi doping (Figures 4d and S8).

Here, a clear structure function is observed. The pronounced angle deviations for Bi over Sb doping are aligned with observed microstrain fluctuations and red-shifted emission for increased dopant concentration.

We point to a curious result. The strain seems to decrease for doping concentrations greater than 50%, for both dopants (Figure 4d). We assign this to a configurational more symmetric and therefore more stable rearrangement of dopants in the In sites for a given unit cell.46

We now move to analyze the temperature-dependent PL for this system. Since the extrinsic STE is strongly coupled to the phonon modes of the lattice, it stands to reason that the large fwhm of the emission will depend on the temperature. Figure 4e shows that in a Bi-doped system, there is a visible decrease in the fwhm at lower temperatures as expected for an exciton that is strongly coupled to lattice vibrations. The trend of the concentration dependence of the Huang–Rhys factor is discussed above (Figure 3c), while the pronounced effect of the temperature on the fwhm is presented in Figure 4.

We note the influence of the electronic mixing of excitonic states, which differs between Bi and Sb once Ag is added to alloy the Cs2NaInCl6 matrix. This ultimately affects the emission peak position. In the case of Sb doping, we see that the concentration of Ag in the matrix is critical. It significantly changes the Huang–Rhys factor and decreases the overall PLQY. This aligns with reports regarding the electronic nature of Ag/Sb electronic hybridization which supports excitons with localized holes (Figure S9).15,47,48 Contrary to this, the dependence of the Huang–Rhys factor of the Bi system on the Ag/Na ratio is only due to the redshifts of the absorption peak with Ag addition.

Alloying with Ag atoms significantly decreases the PLQY in the case of Sb-doping (Figure 5a). In contrast, with Bi-doping without Ag present in the matrix, there is no emission as was also observed by others.15 We suggested this outcome is related to the identity of the octahedron, which localized the STE holes in each doped system. While for Bi-doping, alloying of Ag is essential for high PLQY, the Sb-doped system is different, and the highest PLQY is achieved without any Ag addition (Figure 5a). This is because, for the Bi-doped system, alloying between Na and Ag breaks the symmetry and helps with the charge localization of the STE, together with the Bi doping.

Figure 5.

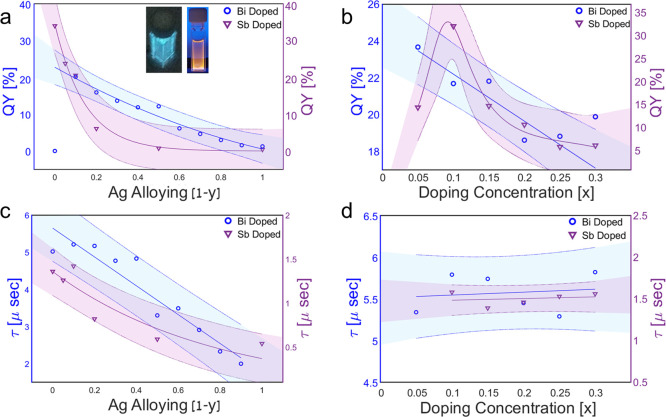
Figure 5

Open in a new tab

Comparison of alloying ratios (Ag–Na) and doping concentrations (Bi or Sb). (a) PLQY and (c) lifetime. The compositions of alloying ratios are as follows: (Ag–Na), [Cs2Ag1–yNayIn0.9Bi0.1Cl6 (y = 0, 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1), and Cs2Ag1–yNayIn0.9Sb0.1Cl6 (y = 0, 0.5, 0.8, 0.9, 0.95, 1)] and (b) PLQY and (d) lifetime for doping concentrations of (Bi or Sb) of [Cs2Ag0.4Na0.6In1–xBixCl6 (x = 0.05, 0.1, 0.15, 0.2, 0.25, 0.3), and Cs2NaIn1–xSbxCl6 (x = 0.05, 0.1, 0.15, 0.2, 0.25, 0.3)], inset: Cs2NaIn0.9Sb0.1Cl6 and Cs2Ag0.4Na0.6In0.9Bi0.1Cl6 under UV light. Note that one data point is excluded in (a) for Bi doping (no Ag alloying) because the PLQY is zero.

In our results, while the Huang–Rhys factor of the Bi-doped system is increased, the PLQY decreases (Figure 5b), contrary to previous works.19 This outcome might relate to the alloying of Na and Ag atoms. According to the Franck–Condon factor, a higher Huang–Rhys factor induces a lower transition probability. The vibrational overlap integral is decreased with higher distortion and Huang–Rhys factor.13 This explains the PLQY decrease for a higher Bi content (Figure 5b). While the large Bi3+ ions distort the structure and affect the Huang–Rhys factor, the structure distortion while doping with Sb3+ ions is negligible due to the almost similar size of the Sb3+ and In3+ ions.

The STE emission of the Sb-doped system is determined by the 5P and 5S states and related to the Sb atoms.28 Increasing the Sb content does not influence the size of the octahedra nor the emission trapping states, and there is no change in the peak position since the Sb and In ions have the same size. Nevertheless, the Sb/In ratio influences the PLQY, as shown in Figure 5b. And in both the Bi and Sb cases, a high dopant concentration reduces the emission intensity (Figure 5b). To understand the effect of doping and alloying on the emission dynamics, we examine the decay lifetime for both systems. The decay lifetimes of all the examined DPs are in a microsecond scale. Longer lifetimes are observed for alloying with Na, as shown in Figure 5c. This is related to the tendency of Na to suppress nonradiative decay channels and consequently increase the lifetime.15 Lifetimes are weakly affected by the doping concentration, as opposed to alloying between Ag and Na, as shown in Figure 5d. This result suggests that decay lifetimes are more sensitive to the matrix composition of DPs, contrary to the binding energy. For 5 and 25% Bi doping, the binding energy increased from ∼69 meV to ∼87 meV, respectively. This result aligns with increased phonon–exciton coupling (Huang–Rhys factor) for higher Bi doping, also reflected in increased excitonic binding energy (Figure S11).

Based on these results, it is, therefore, tempting to continue the development of the DP nanocrystals around dominantly Na–In compositions instead of Ag–In, as this work clearly demonstrates that with Na–In DP, better Stokes-shift engineering and higher PLQYs are possible.

Conclusions

To conclude our study for tuning the optical properties of silver-based DP NCs via two iso-valent dopants, Bi and Sb, we can clearly state that when incorporated into a DP NC matrix, the matrix influences the dopant’s energy level and transition in a very different way for each system. In the case of the Bi-doped system, alloying of the matrix will introduce a Stokes shift, which is influenced only by absorption peak shifts, while the central emission wavelength remains fixed. In contrast, for the Sb-doped system, increasing alloying of Na concentration in the matrix leads to a decrease in the Stokes shift. This is due to the different octahedra localizing the holes and electrons. In both systems, the holes are localized by the dopant’s octahedra. In the Bi system, the electrons are localized by the Ag octahedra, while in the Sb system, the electrons are localized by both the Sb and Ag octahedra.

The situation is completely different for changing the concentration of the doping species. In the case of the Sb-doped system, the doping concentration has a negligible effect on the Stokes shift, contrary to the Bi-doped system, where increasing the Bi concentration increases the Stokes shift. This outcome exemplifies the effect of dopants with different sizes than the ion that they generally substitute. The larger the difference, the higher the lattice straining and resulting octahedral tilting, resulting in an increased Stokes shift. A better understanding of doping effects emphasizing the difference between Bi and Sb species and other dopants will improve Stokes shift engineering of colloidal DP NCs.

Methods

Materials

The materials used are as follows: antimony(III) acetate (99.9%, Aldrich), benzoyl chloride (99.9%, Alfa Aesar), bismuth(III) acetate (99.9%, Aldrich), cesium carbonate (99.9%, Aldrich), hexane (A.R. Aldrich or 99.9%, Fischer Scientific), indium(III) acetate (99.9%, Aldrich), octadecene (90%, Aldrich), oleic acid (90%, Aldrich), oleylamine (70%, Aldrich), silver acetate (99.9%, Aldrich), and sodium acetate (99.9%, Aldrich). All chemicals were used as purchased with no further purifications.

Synthesis of the 0.5 M Cs-oleate Precursor

1.63 g (5 mmol) of Cs2CO and 20 mL (63.37 mmol) of oleic acid were inserted into a 50 mL three-necked round-bottom flask and degassed under vacuum and at 100 °C for 30 min or until there were no bubbles. Then, the temperature was raised to 150 °C under nitrogen and stirred for 3 h. The product obtained was a clear yellow solution.

Synthesis of 0.25 M Sb-oleate, 0.25 M In-oleate, and 0.5 M Na-oleate Precursors

0.7472 g (2.5 mmol) of Sb(ac)3 or 0.7299 g (2.5 mmol) of In(ac)3 or 0.4102 g (5 mmol) of Na(ac), and 10 mL (31.7 mmol) of oleic acid were inserted into a 20 mL glass vile. The reaction was stirred for 45 min at 90 °C in an open-air environment. The Sb-oleate and Na-oleate products obtained were slightly yellow, clear solutions. The In-oleate product obtained was a clear solution while warm and a solid white paste when cold (room temperature).

Synthesis of Cs2Ag1–yNayIn1–xBixCl6 NC’s

0.24 mmol of Ag(ac) and Na(ac), 0.25 mmol of In(ac)3 and Bi(ac)3, 1 mL of 0.5 M Cs-oleate solution (0.5 mmol), 0.5 mL of oleylamine (1.52 mmol), and 4.5 mL of ODE were inserted into a 20 mL glass vile. The mixture was stirred for 5 min at 100 °C in an open-air environment. Then, 200 μL of Bz-Cl (1.72 mmol) was swiftly injected. The reaction was then cooled in a cold water bath. The solution was then centrifuged at 7000 rpm for 10 min, and the precipitation was redispersed in 5 mL of hexane and then centrifuged at 3500 rpm for 5 min. The solution was transferred to a new tube and centrifuged again at 7000 rpm for 10 min and separated from the residue.

Synthesis of Cs2Ag1–yNayIn1–xSbxCl6 NCs

0.24 mmol of Ag(ac) and 0.5 M Na-oleate solution, 0.25 mmol of 0.25 M In-oleate solution and Sb-oleate solution, 1 mL of 0.5 M Cs-oleate solution (0.5 mmol), 0.5 mL of oleylamine (1.52 mmol), and 4.5 mL of ODE were inserted into a 20 mL glass vile. The synthesis procedure is the same as described for Cs2Ag1–yNayIn1–xSbxCl6 NCs.

Optical Characterizations

The absorption, emission, and PLE characterizations were performed using a Gen5 Synergy H1 hybrid multimode reader spectrophotometer with 99-well plates. All of the measurements were performed with the products inside the hexane emulsion solution and with a reference blank well of clean hexane.

Lifetime and PLQY characterizations were performed using an Edinburgh FLS1000 photoluminescence spectrometer. All of the samples were loaded into a quartz cuvette. The lifetime measurements were performed in a multichannel scaling (MCS) mode and conducted using a variable pulse laser (VPL). The PLQY measurements were performed with an integrated sphere holder inside the spectrometer.

Temperature-dependent photoluminescence was performed using the Edinburgh FLS1000 photoluminescence spectrometer coupled to the Nikon Eclipse UPRIGHT Ni–U architecture light microscope with a THMS350 V temperature-controlled vacuum system stage with LNP95. The NC’s solution in hexane was centrifuged at 12000 rpm for 10 min, and the residue was drop-cast onto p-type silicon wafer slice (10 × 10 mm2).

See the Supporting Information for information regarding characterizations and calculations.

Acknowledgments

Special thanks to the scientific staff of our microscopy center (MIKA) and, specifically, Dr. Maria Koifman for discussing the XRD analysis. We thank the EuroTech alliance program for their kind support. Y.B. thanks the Nancy and Stephen Grand Technion Energy Program for their generous support and support of the Technion Russel Berrie Nanotechnology Institute and of the Technion Helen Diller quantum center. We acknowledge the European Synchrotron Radiation Facility (ESRF) for provision of synchrotron radiation facilities, and we would like to thank Dr. Catherine Dejoie for assistance and support in using beamline ID22.

Data Availability Statement

All data are available in the main text or the Supporting Information.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.chemmater.3c01771.

  • Materials; methods descriptions, including syntheses, optical, XRD, HRPXRD, TEM, HAADF-STEM, SEM, EDS characterization, and DFT calculations; SEM-EDS spectra and data; TEM micrographs and size distribution of nanoparticles; additional absorption and emission spectra; additional XRD patterns and extracted lattice parameter; Voigt function fits of HRPXRD and data; additional DFT-calculated rotation and tilting deviation data; additional Huang–Rhys factor data; additional TEM and HRTEM micrographs; and additional temperature-dependent PL emission spectra, fwhm, and integrated intensity, including calculations of Huang–Rhys factor and binding energy (PDF)

Author Contributions

The manuscript was written through the contributions of all authors.

This work is supported by the Israel Science Foundation grant number 890015. This project has received funding from the European Union’s Horizon 2020 research and innovation program under grant agreement No 949682-ERC-HeteroPlates.

The authors declare no competing financial interest.

Supplementary Material

cm3c01771_si_001.pdf (1.9MB, pdf)

References

  1. Lin W.; Hu X.; Mo L.; Jiang X.; Xing X.; Shui L.; Priya S.; Wang K.; Zhou G. Progresses on Novel B-Site Perovskite Nanocrystals. Adv. Opt. Mater. 2021, 9, 2100261 10.1002/adom.202100261. [DOI] [Google Scholar]
  2. Heidari Gourji F.; Velauthapillai D. A Review on Cs-Based Pb-Free Double Halide Perovskites: From Theoretical and Experimental Studies to Doping and Applications. Molecules 2021, 26 (7), 2010. 10.3390/molecules26072010. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Cucco B.; Pedesseau L.; Katan C.; Even J.; Kepenekian M.; Volonakis G. Silver–Bismuth Halide Double Salts for Lead-Free Photovoltaics: Insights from Symmetry-Based Modeling. Sol. RRL 2022, 6 (12), 2200718 10.1002/solr.202200718. [DOI] [Google Scholar]
  4. Volonakis G.; Filip M. R.; Abbas Haghighirad A.; Sakai N.; Wenger B.; Snaith H. J.; Giustino F. Lead-Free Halide Double Perovskites via Heterovalent Substitution of Noble Metals. J. Phys. Chem. Lett. 2016, 7, 1254. 10.1021/acs.jpclett.6b00376. [DOI] [PubMed] [Google Scholar]
  5. McClure E. T.; Ball M. R.; Windl W.; Woodward P. M. Cs2AgBiX6 (X = Br, Cl): New Visible Light Absorbing, Lead-Free Halide Perovskite Semiconductors. Chem. Mater. 2016, 28 (5), 1348–1354. 10.1021/acs.chemmater.5b04231. [DOI] [Google Scholar]
  6. Khalfin S.; Bekenstein Y. Advances in Lead-Free Double Perovskite Nanocrystals, Engineering Band-Gaps and Enhancing Stability through Composition Tunability. Nanoscale 2019, 11 (18), 8665–8679. 10.1039/C9NR01031A. [DOI] [PubMed] [Google Scholar]
  7. Liu Y.; Nag A.; Manna L.; Xia Z. Lead-Free Double Perovskite Cs2AgInCl6. Angew. Chem. Int. Ed. 2021, 60, 11592–11603. 10.1002/anie.202011833. [DOI] [PubMed] [Google Scholar]
  8. Singh Lamba R.; Basera P.; Bhattacharya S.; Sapra S. Band Gap Engineering in Cs2(NaxAg1–x)BiCl6 Double Perovskite Nanocrystals. J. Phys. Chem. Lett. 2019, 10, 5173–5181. 10.1021/acs.jpclett.9b02168. [DOI] [PubMed] [Google Scholar]
  9. Hu Q.; Niu G.; Zheng Z.; Li S.; Zhang Y.; Song H.; Zhai T.; Tang J. Tunable Color Temperatures and Efficient White Emission from Cs2Ag1–xNaxIn1–yBiyCl6 Double Perovskite Nanocrystals. Small 2019, 15 (44), 1903496 10.1002/smll.201903496. [DOI] [PubMed] [Google Scholar]
  10. Locardi F.; Cirignano M.; Baranov D.; Dang Z.; Prato M.; Drago F.; Ferretti M.; Pinchetti V.; Fanciulli M.; Brovelli S.; De Trizio L.; Manna L. Colloidal Synthesis of Double Perovskite Cs2AgInCl6 and Mn-Doped Cs2AgInCl6 Nanocrystals. J. Am. Chem. Soc. 2018, 140 (40), 12989–12995. 10.1021/jacs.8b07983. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Liu Y.; Jing Y.; Zhao J.; Liu Q.; Xia Z. Design Optimization of Lead-Free Perovskite Cs2AgInCl6:Bi Nanocrystals with 11.4% Photoluminescence Quantum Yield. Chem. Mater. 2019, 31 (9), 3333–3339. 10.1021/acs.chemmater.9b00410. [DOI] [Google Scholar]
  12. Arfin H.; Kaur J.; Sheikh T.; Chakraborty S.; Nag A. Bi3+-Er3+ and Bi3+-Yb3+ Codoped Cs2AgInCl6 Double Perovskite Near-Infrared Emitters. Angew. Chem. Int. Ed. 2020, 59 (28), 11307–11311. 10.1002/anie.202002721. [DOI] [PubMed] [Google Scholar]
  13. Luo J.; Wang X.; Li S.; Liu J.; Guo Y.; Niu G.; Yao L.; Fu Y.; Gao L.; Dong Q.; Zhao C.; Leng M.; Ma F.; Liang W.; Wang L.; Jin S.; Han J.; Zhang L.; Etheridge J.; Wang J.; Yan Y.; Sargent E. H.; Tang J. Efficient and Stable Emission of Warm-White Light from Lead-Free Halide Double Perovskites. Nature 2018, 563 (7732), 541–545. 10.1038/s41586-018-0691-0. [DOI] [PubMed] [Google Scholar]
  14. Li S.; Shi Z.; Zhang F.; Lintaowang L.; Ma Z.; Wu D.; Yang D.; Chen X.; Tian Y.; Zhang Y.; Shan C.; Li X. J.; Wang L.; Li X. Ultrastable Lead-Free Double Perovskite Warm-White Light-Emitting Devices with a Lifetime Above 1000 h. ACS Appl. Mater. Interfaces 2020, 12 (41), 46330–46339. 10.1021/acsami.0c14557. [DOI] [PubMed] [Google Scholar]
  15. Locardi F.; Sartori E.; Buha J.; Zito J.; Prato M.; Pinchetti V.; Zaffalon M. L.; Ferretti M.; Brovelli S.; Infante I.; De Trizio L.; Manna L. Emissive Bi-Doped Double Perovskite Cs2Ag1-XNaxInCl6 Nanocrystals. ACS Energy Lett. 2019, 4 (8), 1976–1982. 10.1021/acsenergylett.9b01274. [DOI] [Google Scholar]
  16. Yang B.; Mao X.; Hong F.; Meng W.; Tang Y.; Xia X.; Yang S.; Deng W.; Han K. Lead-Free Direct Band Gap Double-Perovskite Nanocrystals with Bright Dual-Color Emission. J. Am. Chem. Soc. 2018, 140 (49), 17001–17006. 10.1021/jacs.8b07424. [DOI] [PubMed] [Google Scholar]
  17. Cong M.; Yang B.; Hong F.; Zheng T.; Sang Y.; Guo J.; Yang S.; Han K. Self-Trapped Exciton Engineering for White-Light Emission in Colloidal Lead-Free Double Perovskite Nanocrystals. Sci. Bull. 2020, 65 (13), 1078–1084. 10.1016/j.scib.2020.03.010. [DOI] [PubMed] [Google Scholar]
  18. Liao Q.; Chen J.; Zhou L.; Wei T.; Zhang L.; Chen D.; Huang F.; Pang Q.; Zhang J. Z. Bandgap Engineering of Lead-Free Double Perovskite Cs2AgInCl6 Nanocrystals via Cu 2+-Doping. J. Phys. Chem. Lett. 2020, 11, 8392. 10.1021/acs.jpclett.0c02553. [DOI] [PubMed] [Google Scholar]
  19. Siddique H.; Xu Z.; Li X.; Saeed S.; Liang W.; Wang X.; Gao C.; Dai R.; Wang Z.; Zhang Z. Anomalous Octahedron Distortion of Bi-Alloyed Cs2AgInCl6 Crystal via XRD, Raman, Huang–Rhys Factor, and Photoluminescence. J. Phys. Chem. Lett. 2020, 11 (22), 9572–9578. 10.1021/acs.jpclett.0c02852. [DOI] [PubMed] [Google Scholar]
  20. Guo B.; Luo C.; Yan C.; Sun B.; Li W.; Yang W. Understanding Excitonic Behavior in Light Absorption and Recombination Process. J. Phys. Chem. C 2020, 124 (47), 26076–26082. 10.1021/acs.jpcc.0c09334. [DOI] [Google Scholar]
  21. Thomaz J. E.; Lindquist K. P.; Karunadasa H. I.; Fayer M. D. Single Ensemble Nonexponential Photoluminescent Population Decays from a Broadband White-Light-Emitting Perovskite. J. Am. Chem. Soc. 2020, 142 (39), 16622–16631. 10.1021/jacs.0c05636. [DOI] [PubMed] [Google Scholar]
  22. Vurgaft A.; Strassberg R.; Shechter R.; Lifer R.; Dahl J. C.; Chan E. M.; Bekenstein Y. Inverse Size-Dependent Stokes Shift in Strongly Quantum Confined CsPbBr3 Perovskite Nanoplates. Nanoscale 2022, 14 (46), 17262–17270. 10.1039/D2NR03275A. [DOI] [PubMed] [Google Scholar]
  23. Kahmann S.; Meggiolaro D.; Gregori L.; Tekelenburg E. K.; Pitaro M.; Stranks S. D.; De Angelis F.; Loi M. A. The Origin of Broad Emission in ⟨100⟩ Two-Dimensional Perovskites: Extrinsic vs Intrinsic Processes. ACS Energy Lett. 2022, 7 (12), 4232–4241. 10.1021/acsenergylett.2c02123. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Li S.; Luo J.; Liu J.; Tang J. Self-Trapped Excitons in All-Inorganic Halide Perovskites: Fundamentals, Status, and Potential Applications. J. Phys. Chem. Lett. 2019, 10 (8), 1999–2007. 10.1021/acs.jpclett.8b03604. [DOI] [PubMed] [Google Scholar]
  25. Jing Y.; Liu Y.; Li M.; Xia Z. Photoluminescence of Singlet/Triplet Self-Trapped Excitons in Sb3+-Based Metal Halides. Adv. Opt. Mater. 2021, 9, 2002213 10.1002/adom.202002213. [DOI] [Google Scholar]
  26. Arfin H.; Kshirsagar A. S.; Kaur J.; Mondal B.; Xia Z.; Chakraborty S.; Nag A. Ns2 Electron (Bi3+ and Sb3+) Doping in Lead-Free Metal Halide Perovskite Derivatives. Chem. Mater. 2020, 32 (24), 10255–10267. 10.1021/acs.chemmater.0c03394. [DOI] [Google Scholar]
  27. Ahmad R.; Zdražil L.; Kalytchuk S.; Naldoni A.; Rogach A. L.; Schmuki P.; Zboril R.; Kment Š. Uncovering the Role of Trioctylphosphine on Colloidal and Emission Stability of Sb-Alloyed Cs2NaInCl6 Double Perovskite Nanocrystals. ACS Appl. Mater. Interfaces 2021, 13 (40), 47845–47859. 10.1021/acsami.1c10782. [DOI] [PubMed] [Google Scholar]
  28. Gray M. B.; Hariyani S.; Strom T. A.; Majher J. D.; Brgoch J.; Woodward P. M. High-Efficiency Blue Photoluminescence in the Cs2NaInCl6:Sb3+ double Perovskite Phosphor. J. Mater. Chem. C 2020, 8 (20), 6797–6803. 10.1039/D0TC01037E. [DOI] [Google Scholar]
  29. Zhang Y.; Liu X.; Sun H.; Zhang J.; Gao X.; Yang C.; Li Q.; Jiang H.; Wang J.; Xu D. Strong Self-Trapped Exciton Emissions in Two-dimensional Na-In Halide Perovskites Triggered by Antimony Doping. Angew. Chem., Int. Ed. 2021, 60 (14), 7587–7592. 10.1002/anie.202015873. [DOI] [PubMed] [Google Scholar]
  30. Zeng R.; Zhang L.; Xue Y.; Ke B.; Zhao Z.; Huang D.; Wei Q.; Zhou W.; Zou B. Highly Efficient Blue Emission from Self-Trapped Excitons in Stable Sb3+ -Doped Cs2NaInCl6 Double Perovskites. J. Phys. Chem. Lett. 2020, 11, 2053–2061. 10.1021/acs.jpclett.0c00330. [DOI] [PubMed] [Google Scholar]
  31. Noculak A.; Morad V.; Mccall K. M.; Yakunin S.; Shynkarenko Y.; Wö M.; Kovalenko M. V. Bright Blue and Green Luminescence of Sb(III) in Double Perovskite Cs2MInCl6 (M = Na, K) Matrices. Chem. Mater. 2020, 32 (12), 5118–5124. 10.1021/acs.chemmater.0c01004. [DOI] [PMC free article] [PubMed] [Google Scholar]
  32. Wu Y.; Shi C.-M.; Xu L.-J.; Yang M.; Chen Z.-N. Reversible Luminescent Vapochromism of a Zero-Dimensional Sb3+-Doped Organic–Inorganic Hybrid. J. Phys. Chem. Lett. 2021, 12 (13), 3288–3294. 10.1021/acs.jpclett.1c00418. [DOI] [PubMed] [Google Scholar]
  33. Dahl J. C.; Osowiecki W. T.; Cai Y.; Swabeck J. K.; Bekenstein Y.; Asta M.; Chan E. M.; Alivisatos A. P. Probing the Stability and Band Gaps of Cs2AgInCl6 and Cs2AgSbCl6 Lead-Free Double Perovskite Nanocrystals. Chem. Mater. 2019, 31 (9), 3134–3143. 10.1021/acs.chemmater.8b04202. [DOI] [Google Scholar]
  34. Levy S.; Khalfin S.; Pavlopoulos N. G.; Kauffmann Y.; Atiya G.; Shaek S.; Dror S.; Shechter R.; Bekenstein Y. The Role Silver Nanoparticles Plays in Silver-Based Double-Perovskite Nanocrystals. Chem. Mater. 2021, 33 (7), 2370–2377. 10.1021/acs.chemmater.0c04536. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Palmer D. C. Visualization and Analysis of Crystal Structures Using CrystalMaker Software. Z. Krist. - Cryst. Mater. 2015, 230 (9–10), 559–572. 10.1515/zkri-2015-1869. [DOI] [Google Scholar]
  36. Volonakis G.; Amir; Haghighirad A.; Milot R. L.; Sio W. H.; Filip M. R.; Wenger B.; Johnston M. B.; Herz L. M.; Snaith H. J.; Giustino F. Cs2InAgCl6: A New Lead-Free Halide Double Perovskite with Direct Band Gap. J. Phys. Chem. Lett. 2017, 8 (4), 772–778. 10.1021/acs.jpclett.6b02682. [DOI] [PubMed] [Google Scholar]
  37. Ming L. C.; Shieh S. R.; Jayaraman A.; Sharma S. K.; Kim Y. H. High-Pressure Phase Transformations of CuGeO3. J. Phys. Chem. Solids 1999, 60, 69–81. 10.1016/S0022-3697(98)00244-3. [DOI] [Google Scholar]
  38. Hull S.; Berastegui P. Crystal Structures and Ionic Conductivities of Ternary Derivatives of the Silver and Copper Monohalides-II: Ordered Phases within the (AgX)x-(MX)1-x and (CuX)x-(MX)1-x (M = K, Rb and Cs; X = Cl, Br and I) Systems. J. Solid State Chem. 2004, 177, 3156–3173. 10.1016/j.jssc.2004.05.004. [DOI] [Google Scholar]
  39. Huang K.; Rhys A. Theory of Light Absorption and Non-Radiative Transitions in F-Centres. Proc. R. Soc. London. Ser. A. Math. Phys. Sci. 1950, 204 (1078), 406–423. 10.1098/rspa.1950.0184. [DOI] [Google Scholar]
  40. Boutinaud P. Revisiting Duffy’s Model for Sb3+ and Bi3+ in Double Halide Perovskites: Emergence of a Descriptor for Machine Learning. Opt. Mater. X 2021, 11, 100082 10.1016/j.omx.2021.100082. [DOI] [Google Scholar]
  41. Larsen A. H.; Mortensen J. J.; Blomqvist J.; Castelli I. E.; Christensen R.; Dułak M.; Friis J.; Groves M. N.; Hammer B.; Hargus C.; Hermes E. D.; Jennings P. C.; Jensen P. B.; Kermode J.; Kitchin J. R.; Kolsbjerg E. L.; Kubal J.; Kaasbjerg K.; Lysgaard S.; Maronsson J. B.; Maxson T.; Olsen T.; Pastewka L.; Peterson A.; Rostgaard C.; SchiØtz J.; Schütt O.; Strange M.; Thygesen K. S.; Vegge T.; Vilhelmsen L.; Walter M.; Zeng Z.; Jacobsen K. W. The Atomic Simulation Environment—a Python Library for Working with Atoms. J. Phys.: Condens. Matter 2017, 29 (27), 273002. 10.1088/1361-648X/aa680e. [DOI] [PubMed] [Google Scholar]
  42. Shannon R. D.; Prewitt C. T.; IUCr Effective Ionic Radii in Oxides and Fluorides. Acta Crystallogr. B 1969, 25 (5), 925–946. 10.1107/S0567740869003220. [DOI] [Google Scholar]
  43. Manna D.; Kangsabanik J.; Kumar T.; Das K.; Das D.; Alam A.; Yella A. Lattice Dynamics and Electron–Phonon Coupling in Lead-Free Cs2AgIn1–xBixCl6 Double Perovskite Nanocrystals. J. Phys. Chem. Lett. 2020, 11 (6), 2113–2120. 10.1021/acs.jpclett.0c00206. [DOI] [PubMed] [Google Scholar]
  44. Boaz Pokroy B.; Fitch A. N.; Zolotoyabko E.; Zolotoyabko E.; Pokroy B.; Fitch A. N. The Microstructure of Biogenic Calcite: A View by High-Resolution Synchrotron Powder Diffraction. Adv. Mater. 2006, 18 (18), 2363–2368. 10.1002/adma.200600714. [DOI] [Google Scholar]
  45. Whalley L. D.; Van Gerwen P.; Frost J. M.; Kim S.; Hood S. N.; Walsh A. Giant Huang–Rhys Factor for Electron Capture by the Iodine Intersitial in Perovskite Solar Cells. J. Am. Chem. Soc. 2021, 143 (24), 9123–9128. 10.1021/jacs.1c03064. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Gwalani B.; Alam T.; Miller C.; Rojhirunsakool T.; Kim Y. S.; Kim S. S.; Kaufman M. J.; Ren Y.; Banerjee R. Experimental Investigation of the Ordering Pathway in a Ni-33 at.%Cr Alloy. Acta Mater. 2016, 115, 372–384. 10.1016/j.actamat.2016.06.014. [DOI] [Google Scholar]
  47. Tran T. T.; Panella J. R.; Chamorro R. J.; Morey R. J.; McQueen T. M. Designing Indirect-Direct Bandgap Transitions in Double Perovskites. Mater. Horiz. 2017, 4, 688–693. 10.1039/C7MH00239D. [DOI] [Google Scholar]
  48. Lan C.; Zhao S.; Luo J.; Fan P. First-Principles Study of Anion Diffusion in Lead-Free Halide Double Perovskites. Phys. Chem. Chem. Phys. 2018, 20 (37), 24339–24344. 10.1039/C8CP04150D. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

cm3c01771_si_001.pdf (1.9MB, pdf)

Data Availability Statement

All data are available in the main text or the Supporting Information.

Articles from Chemistry of Materials are provided here courtesy of American Chemical Society

RESOURCES