Integrated Molecular Modeling and Machine Learning for Drug Design

Abstract

Modern therapeutic development often involves several stages that are interconnected, and multiple iterations are usually required to bring a new drug to the market. Computational approaches have increasingly become an indispensable part of helping reduce the time and cost of the research and development of new drugs. In this Perspective, we summarize our recent efforts on integrating molecular modeling and machine learning to develop computational tools for modulator design, including a pocket-guided rational design approach based on AlphaSpace to target protein–protein interactions, delta machine learning scoring functions for protein–ligand docking as well as virtual screening, and state-of-the-art deep learning models to predict calculated and experimental molecular properties based on molecular mechanics optimized geometries. Meanwhile, we discuss remaining challenges and promising directions for further development and use a retrospective example of FDA approved kinase inhibitor Erlotinib to demonstrate the use of these newly developed computational tools.

Introduction

The cost of research and development of new drugs has risen over the past decade.¹⁻³ There is great interest in advancing computational methods, including molecular modeling and machine learning (ML), to greatly accelerate the process of drug discovery and development.⁴⁻¹⁰ The goal of drug discovery is to find small molecules that inhibit the disease-related target and, therefore, modulate the disease. Meanwhile, the pharmacokinetic properties including absorption, distribution, metabolism, excretion, and toxicity (ADME/T) of small molecules also need to be considered in the drug development process.¹¹ The success of drug development requires both good efficacy and the desired pharmacokinetic properties of the drug molecules. Computer-aided drug design (CADD) offers valuable tools in finding candidate compounds in all stages of drug discovery and development.

It should be noted that a modern therapeutic development process often involves multiple nonlinearly interconnected stages.¹²Figure 1A shows a simplified “pipeline” of therapeutic development where CADD tools are playing important roles. Hit identification is the first step which involves finding the compounds with desired bioactivity.¹³ Ligand based methods use prior knowledge to predict new drug compounds with similar bioactivities (Figure 1B).¹⁴ Similarity search,¹⁵ pharmacophore modeling,^16,17 and quantitative structure–activity relationships^18,19 are common tools for ligand based drug screening. Structure based methods such as molecular docking²⁰⁻²⁶ and molecular dynamics simulations²⁷⁻³² are common computational tools used to predict the binding affinity between the protein and ligand (Figure 1C). Binding site prediction tools³³⁻³⁹ offer information on the protein surface where a ligand molecule binds to produce the desired output (activation, inhibition, or modulation).⁵ If the structure of the protein is not solved experimentally, homology modeling⁴⁰⁻⁴³ and ab initio protein structure modeling⁴⁴⁻⁴⁷ approaches can be used to predict the protein structure.

Figure 1.

Roles of computational models at the stages of drug discovery and development.

After discovering the hit compounds, subsequent steps involve producing more potent and selective compounds with desirable physicochemical properties.¹³ It is estimated that over 40% of drug candidates are withdrawn in preclinical tests due to ADME/T concerns.⁴⁸ To address the problem, a number of computational models have been developed to predict the ADME/T properties of small molecules.⁴⁹⁻⁶⁰ The accurate prediction of molecular properties requires models to learn more robust molecular representations for 1D SMILES,⁶¹ 2D graph,⁶² and 3D geometry.⁶³

As computational tools at all stages of drug discovery and development have been extensively reviewed recently,^64,65 in this perspective, we focus on the recent progress related to our group. Specifically, we first summarize protein pocket identification and analysis methods based on fragment-centric topographical mapping. Subsequently, we discuss recent advances and promising directions in developing ML and deep learning (DL)-based molecular docking models. Finally, we describe our recent efforts to improve small molecule representation learning and explore chemical space⁶⁶ more efficiently.

1. Protein Pocket Identification and Representation

1.1. Protein Pocket Identification: Fragment-Centric Topographical Mapping

In contemporary approaches to structure-based drug design, focus is placed on the analysis of concave regions found on biomolecular surfaces. These regions can vary from well-defined small-molecule binding sites to extensive protein–protein interaction (PPI) interfaces.⁶⁷ Gaining a deeper understanding of concave biomolecular surfaces holds immense potential for various applications in modulator design, such as lead optimization, enhanced ligand screening, and even the identification of previously undiscovered druggable sites.⁶⁷⁻⁶⁹ Furthermore, comparisons of these surfaces investigate ligand selectivity, off-target effects, and polypharmacological activity.^70,71

One of the main tasks in analyzing the protein surfaces is identifying binding sites. There are a number of algorithms that do this, and these can be broadly classified as geometry-^{35,37,72−76} or energy-based methods.^68,77−81 Geometry-based methods map out the concavities on the surface using grids or alpha-spheres, while energy-based methods calculate the interaction energy or surface accessibility between the protein and diverse small-molecule probes. The next step usually requires ML methods to characterize the binding site. For example, some methods use clustering to agglomerate data points into binding pockets and others use regression to score the concavities on the protein surface for their ligandability.⁸² Most methods can correctly predict and rank the voluminous and well-defined ligand binding pockets in holo structures.^72,83,84

The alpha-sphere geometry-based representation of the concavities is an established strategy that relies on Voronoi diagrams.^{34,35,73,74,85−87} Voronoi diagrams form polyhedra defined by the planes that bisect adjacent atoms, resulting in a tessellation of the concave region. Alpha-spheres are placed at the vertices of the Voronoi diagram. These alpha-spheres are then clustered to represent binding pockets. Rooklin et al. developed a python program named AlphaSpace, an alpha-sphere-based method developing on the popular method fpocket,³⁵ that leverages concepts of fragment-based drug discovery and caters to the analysis of PPI (Figure 2).³⁴ To this aim, AlphaSpace uses a tuned clustering method to demarcate pockets that reflect on average one fragment per pocket and defines alpha-atoms, a theoretical ligand atom whose properties reflect a docked fragment. It represents entire PPI surfaces by retaining shallower fragment-centric pockets during the evaluation stage and suggests targetable pockets near the binding partner for ligand optimization. Furthermore, Katigbak et al. developed AlphaSpace 2.0, a python package that clusters the alpha-atoms to a β-cluster, a pseudomolecular representation of the concave site comprised of β-atoms (Figure 2).³³ Each β-atom is replaced with a probe atom that iterates through different Vina atom types. The AutoDock Vina score is calculated for each atom type of each probe atom. Then the best Vina score for each probe atom is summed to generate the overall β-score. This β-score reflects the maximum theoretical docking score of the β-cluster.

Figure 2.

Workflow of AlphaSpace to optimize a ligand to bind to a protein begins with a selected PDB structure and follows the purple arrows until the optimization is validated experimentally. The additions introduced by AlphaSpace2.0 follow the orange arrows.

Both AlphaSpace and AlphaSpace2 offer alignment-free and alignment-based pocket matching protocols, respectively, allowing for comparisons of binding sites between structures within the alpha-sphere framework.^33,34 Both methods assess the change in the inhibitor binding site of PPI interfaces using the curated 2P2I database, which provides structures of a protein in the apo, PPI complex, or inhibitor bound PPI complex states. In both cases they can observe the binding pockets on the apo structure that corresponds to the inhibitor binding site, and AlphaSpace2 reports similar ligand-ability estimates of that binding site across structures. However, on the CryptoSite database consisting of structures where a pocket forms in the holo state but not the apo state, AlphaSpace2 reports differences in ligand-ability estimates.

DL methods are also gaining prominence due to their ability to learn complex relationships from raw protein data and predict binding surfaces.^82,88 DL architectures can learn the representation and functional roles of the binding pockets without first preprocessing the data to explicitly detect the pockets. Mylonas et al. developed DeepSurf, a 3D-convolutional neural network (CNN) trained on voxels placed on the protein surface.⁸⁹ It had superior performance compared to other methods tested in the SHREC 2022 contest at identifying druggable sites on diverse data sets of apo and holo structures.^83,89 Gainza et al. proposed MaSIF, a surface representation framework that uses overlapping radial patches characterized by a chemical and geometric fingerprint.^90,91 These patches can be input into geometric neural network architectures and trained to perform particular tasks, including predicting PPI and ligand sites. Most recently, Smith et al. developed Graph Attention Site Prediction (GrASP) which uses a graph attention network (GAT) architecture to encode the binding site from a protein structure graph. This model is trained on a modified version of sc-PDB to predict the likelihood of an atom to be part of the binding site. These atoms are then clustered and aggregated into binding sites with ligand-ability scores.⁹² This results in superior precision and recall compared to another graph neural network (GNN)-based method, P2Rank, on the COACH420 and HOLO4K benchmarks.⁹²

1.2. Experimentally Validating Predictions of Underutilized but Targetable Regions

AlphaSpace has guided the optimization of minimal protein mimetics that target PPIs by expanding mimetics to target secondary binding sites and incorporating noncanonical amino acids to reach untargeted binding pockets

(93−95) Guided by the binding pocket analysis, researchers introduced a terminal tryptophan of a p53 mimetic to interact with a previously untargeted secondary site which resulted in an ∼10-fold improvement of binding affinity to MdmX and Mdm2.⁹⁵ This interaction was verified to bind to the secondary site through NMR. In another case, optimization steps were able to reverse the loss of binding affinity resulting from truncating the full length protein to a minimal mimetic. The truncated helical MML-mimetic bound poorly to the KIX domain of the p300/CBP coactivator (K_d: >100 μm), but a MML mimetic mutated with noncanonical amino acids was optimized to a similar binding affinity (K_d: 3.3 ± 0.5 μm) as the full-length wildtype MML (K_d: 1.0 ± 0.3 μm).⁹³ Moreover, suggested mutations to the cross-linked helix dimers of the NEMO coiled coil reversed the binding affinity loss due to the aforementioned. These mimetics were also able to inhibit the native PPI in vivo.⁹⁴ In these cases, the role of AlphaSpace was to suggest initial fragments for improvement, but expertise and further experimental optimization were necessary to generate stable mimetics and maximize protein–ligand binding affinity.⁹³⁻⁹⁶

AlphaSpace has also guided the analysis of protein structures for targetable binding sites to design small molecule inhibitors and understand their binding mechanisms. Some computational experiments qualitatively studied the interaction mechanisms and binding modes by docking inhibitors to the most targetable pockets of the transmembrane protein ABCG2 and by running molecular dynamics (MD) simulations of the complexes.^97,98 Other binding pocket analyses led to successful prospective docking studies. Hou et al. detected a cryptic pocket in a metastable state of the apo striatal-enriched protein tyrosine phosphatase (STEP) from MD simulations. Ensemble docking to this state at the cryptic pocket resulted in 11 novel inhibitors (IC₅₀ = 9.7–47.7 μm).⁹⁹ These experimental validations highlight the utility and role that AlphaSpace can play in identifying pockets to develop ligands with improved binding.

2. Protein–Ligand Docking in the Machine-Learning Era

Employing computational methods to discover bioactive compounds is becoming an indispensable technique to accelerate the process of drug discovery,^100−107 leading to the successful discovery of several approved drugs.^{104,108−110} The drug discovery process encompasses two major categories: ligand-based drug discovery (LBDD) and structure-based drug discovery (SBDD). LBDD is an indirect approach that employs quantitative structure–activity relationship methods, molecular similarity, and pharmacophore modeling to predict various properties of compounds.¹⁴ On the other hand, SBDD involves using the three-dimensional structures of the protein and small molecule to identify or optimize drug compounds.^101,111 SBDD focuses on recognizing binding sites and essential interactions crucial to the biological functions of the target. By doing so, it suggests therapeutic compounds that can compete with these crucial interactions, thereby disrupting biological pathways effectively.

Virtual screening (VS) is a method within SBDD where extensive libraries of commercially available, druglike chemical compounds are computationally screened against target proteins with known or predicted 3D structures in a high-throughput manner. The primary goal of VS is to identify potential compounds that exhibit a high predicted binding affinity for the target protein. These selected compounds are then subjected to experimental testing to validate their actual binding capabilities.^112,113

Molecular docking is a widely used computational procedure in VS protocols.^114−117 It operates based on the lock-and-key¹¹⁸ model of drug action and predicts the noncovalent interactions between the target and small molecules. In structure-based VS, molecular docking methods are commonly used to assess large libraries of molecules.²⁶

2.1. Protein–Ligand Scoring Functions

Molecular docking programs rely on a scoring function to evaluate the binding affinity and optimize the binding orientation between protein and ligand.^{21−23,25,119−121} The scoring function plays a pivotal role in accurately predicting how well the ligand binds to the target protein. Consequently, developing a robust, efficient, and accurate scoring function is a critical component of molecular docking.¹⁰⁷

A rigorous theoretical prediction of protein–ligand binding affinity requires the calculation of the free energy difference between the bound and unbound state. However, existing methods for free energy calculation, such as free energy perturbation^122,123 and thermodynamic integration,^124,125 are computationally expensive, making them impractical for virtual screening over a large set of compounds. To overcome this limitation, scoring functions serve as fast and approximate computational methods to evaluate the strength of noncovalent interactions between proteins and ligands, based on their 3D binding poses.^126−128 They are widely used in SBDD to determine the binding mode of ligands (docking power), predict the binding affinity between proteins and ligands (scoring power), identify hits from a large compound library for given protein targets (screening power), and perform structure–activity relationship analyses for hit-to-lead and lead optimization.^105,129,130 It is important to note that scoring functions provide estimations of ligand binding affinity, and these predicted scores may not align closely with binding affinities determined through rigorous methods, such as free energy perturbation. For an in-depth understanding of terms such as “scoring power”, “docking power”, and “screening power”, we direct readers to the comprehensive definitions provided in the paper “Comparative Assessment of Scoring Functions: The CASF-2016 Update”.¹³¹

Classical scoring functions use a linear combination of force-field or interaction descriptors to evaluate the binding affinity between proteins and ligands. They can be categorized into different types based on their underlying principles. Physics-based scoring functions use the fundamental molecular physics terms derived from experimental data and/or QM calculations;^21,119,121 knowledge-based scoring functions use the statistical potentials derived from experimentally determined protein–ligand structures;^132−135 and empirical scoring functions make predictions by fitting experimentally measured binding affinity data using linear regression on a set of physical descriptors.^{21−23,120,136−139}

In recent years, ML-based scoring functions have garnered increasing attention due to the rapid growth of experimental data and advancements in computational infrastructure.^140,141 Unlike classical scoring functions that adopt linear forms, ML-based scoring functions have the capability to learn more complex functional forms using ML algorithms such as support vector machine (SVM),¹⁴² random forest (RF),¹⁴³ and extreme gradient boosting (XGB).¹⁴⁴ In 2010, Ballester et al. introduced RF-score which is the first ML-based scoring function that outperforms classical scoring functions in terms of scoring power.¹⁴⁵ In 2013, Zillian et al. developed SFCscore^RF which achieved significantly higher scoring power on common benchmarks.¹⁴⁶ However, both models performed much worse when performing docking and screening tasks compared to classical scoring functions.^147,148 The reader is directed to this review by Chao et al.¹⁰⁷ for more in-depth discussion on scoring functions.

The Δ-ML strategy improves the scoring-ranking-docking-screening power of ML-based scoring functions

To address this problem, Wang et al. applied a Δ-ML strategy, which involves using ML to predict the correction between experimental binding affinity and computationally predicted binding affinity. The final predicted score is obtained by adding this ML correction to classical scoring functions. The first model to employ this strategy is Δ_VinaRF₂₀,¹⁴⁹ a random forest model that predicts the corrections to the Vina score. It uses pharmacophore-based solvent-accessible surface area descriptors and AutoDock Vina features as input. Δ_VinaRF₂₀ demonstrated superior performance in all power tests on both CASF-2013 and CASF-2007 benchmarks compared to classical scoring functions.^150,151 Subsequently, Lu et al. have proposed the Δ_VinaXGB model which uses XGB trees.^152,153 This model incorporates features from explicit water molecules, metal ions, and ligand conformational stability in addition to the Δ_VinaRF₂₀ features.¹⁵² The Δ_VinaXGB model outperformed other scoring functions on the CASF-2016 benchmark data set.¹³¹ Recently, Yang et al. have developed the Δ_Lin__F9XGB model¹⁵⁴ based on a classical scoring function named Lin_F9.¹³⁹ Lin_F9 is a linear empirical scoring function that builds on AutoDock Vina, overcoming some of Vina’s limitations by introducing new empirical terms for better scoring accuracy. By applying the Δ-ML strategy to the Lin_F9 scoring function, and improving feature selection and the training set, Δ_Lin__F9XGB achieves superior scoring, ranking, and screening performance on the CASF-2016 benchmark.¹⁵⁴

In addition to the CASF-2016 benchmark data set, previous models have undergone extensive testing on the LIT-PCBA data set, specifically designed for virtual screening and ML purposes.¹⁵⁵ Preliminary results have shown that the LIT-PCBA data set is challenging due to the high imbalance of active/inactive compounds, common molecular properties shared between active and inactive compounds, and weak potencies of the active compounds.^154,156 The average top 1% enrichment factor achieved by Δ_Lin__F9XGB is 5.55, which outperforms other scoring methods such as AutoDock Vina, Δ_VinaRF₂₀, and Lin_F9.

Learning distance likelihood potential boosts the docking and screening performance of DL-based scoring functions

Aside from traditional ML-based scoring functions, the emergence of DL methods has introduced new strategies for developing scoring functions in drug discovery. Neural network-based models use hand-crafted features as input, including protein–ligand interactions and ligand-dependent descriptors.^147,157,158 Convolutional neural network (CNN)-based scoring functions adopt a different approach by using vectorized 3D grids that cover the protein–ligand binding region as input. These grids are processed through CNN layers, followed by readout layers to make predictions about the binding affinity.^159−164 Graph neural networks (GNNs) represent molecules as graphs and can learn on the protein–ligand binding system through graph convolutions.^165−169 However, despite the increasing popularity of DL-based scoring functions, it is worth noting that these models have not significantly outperformed traditional ML-based scoring functions on well-established benchmark data sets like CASF.¹⁰⁷

Recently, Méndez-Lucio et al. proposed a geometric DL-based model named DeepDock¹⁷⁰ which learns the probability density distribution of the distance between ligand atom and the protein surface. This approach showed competitive performance in docking and screening tasks when compared to those with well-established scoring functions. Building on the concept of distance likelihood, Shen et al. developed RTMScore.¹⁷¹ Unlike DeepDock, RTMScore overcomes the need for protein surface triangulation by using the probability density distribution of distances between ligand atoms and protein amino acids at the residue level. To achieve this, RTMScore represents proteins as undirect graphs at the residue level and leverages graph transformers to learn the representation of both proteins and ligands. As a result, RTMScore achieves top docking and screening power on the CASF-2016 data set, outperforming state-of-the-art ML- and DL-based scoring functions.

However, RTMScore utilizes biased protein pockets generated from known binder structures as the input protein structure. For example, when evaluating the binding score of the ligand 1A30 on the protein 1E66 (Figure 3A), only the protein structure within 10 Å of the binder ligand 1E66 is used along with the docked ligand 1A30 structure as model input (Figure 3B). This selection method may lead to two potential problems. First, this method requires the binder structure to cut the protein, while in real world virtual screening scenarios, the protein may not have a known binder, or the binder structure may be unknown. Second, the selected pocket is biased toward the binder ligand, potentially neglecting essential interactions between the decoy ligands and the protein when the decoy structures are far from the binder ligand (Figure 3B and C).

Figure 3.

Biased protein pockets when evaluating the docking power and screening power on the CASF-2016 data set. (A) Protein and ligand structures. (B) The biased protein pocket resulting from using the binder ligand structure to cut the protein. (C) The unbiased protein pocket without using the binding structure.

The influence of the biased pocket selection was investigated by using docked decoy structures to cut the proteins (Figure 3C) and retesting RTMScore on the CASF-2016 data set. The results, as presented in Table 1, revealed a performance drop when the unbiased pocket was used as the model input for RTMScore models. Despite this drop in performance, the unbiased model still outperformed most of the state-of-the-art models in terms of docking and screening power. This finding highlights the importance of addressing the issue of biased pocket selection in DL-based scoring functions. Although the performance of RTMScore was affected by the unbiased pocket, the fact that it still outperformed many state-of-the-art models indicates that learning distance likelihood potential is a promising direction to improve the docking and screening performance of DL scoring functions.

Table 1. Docking Power and Screening Power of RTMScore on CASF-2016 Data Set When Using the Unbiased Pocket Selection Method, Compared with Other State-of-the-Art Models.

	Docking Power (Success Rate)		Forward Screening Power
Model Name	Without native poses	With native poses	EF1%	Top1 success rate	Reference
RTMScore1-unBiased	0.877	0.909	24.84	0.509	This work
RTMScore1-Biased	0.937	0.986	28.78	0.737	(171)
DeepDock	0.870	–	16.41	0.439	(170)
PIGNet	0.870	–	19.6	0.554	(172)
DeepBSP	0.872	0.885	–	–	(173)
OnionNet-SFCT	–	0.937	15.50	0.421	(174)
ΔLin_F9XGB	–	0.867	12.61	0.404	(154)
ΔVinaXGB	–	0.916	13.14	0.368	(152)
ΔVinaRF20	0.849	0.891	11.73	0.421	(149)
KORP-PL	0.856	0.891	22.23	0.421	(175)
GlideScore-SP	0.846	0.877	11.44	0.368	(23)
ChemPLP@GOLD	0.832	0.860	11.91	0.351	(176)
AutoDock Vina	0.846	0.902	7.70	0.298	(22)

The very recent work by Shen et al. extends the RTMScore model to the GenScore framework.¹⁷⁷ By introducing an adjustable binding affinity term during the training of the probability density distribution, GenScore successfully addresses the issue of low scoring and ranking power experienced by RTMScore, achieving balanced scoring, ranking, docking, and screening power on the CASF-2016 data set. Furthermore, the evaluation of GenScore on the LIT-PCBA data set for real-world screening power is particularly noteworthy. Their best-performing GenScore model exhibits an impressive average top 1% enhancement factor of 6.80 among all targets, demonstrating an excellent screening power.

However, it is important to acknowledge that the biased pocket problem, as mentioned earlier, is not explicitly addressed by GenScore. The reliance on pocket selection using binder ligand structures limits its applicability in real-world virtual screening protocols, especially for novel targets for which binder ligands might not be known or available. Addressing the biased pocket problem would undoubtedly enhance the utility and versatility of RTMScore, GenScore, and other DL-based scoring functions in real-world virtual screening scenarios, making them more effective in identifying potential drug candidates for novel targets with unknown binder structures. Future research in this direction may help overcome this limitation and further establish DL-based scoring functions as valuable tools in drug discovery efforts.

2.2. Molecular Docking in the Deep Learning Era

Traditional molecular docking methods such as AutoDock Vina²² and Lin_F9¹³⁹ rely on the scoring functions and optimization algorithms that search for the global maximum of the scoring functions. The optimization algorithm rotates the rotatable bonds in the molecule, translates the molecule, and rotates the whole molecule until it finds the best conformation with the highest score predicted by the scoring function. In principle, the optimization algorithms can also be applied to DL-based scoring functions. However, in practice, the optimization algorithms often fail to converge when using DL-based scoring functions, especially for those compounds with a high number of rotatable bonds.¹⁷⁰ Recently, researchers have developed DL-based docking models to predict binding poses in one shot by treating molecular docking as a regression task.^178,179 Although these models are faster than traditional docking methods, they do not significantly outperform traditional docking methods in terms of accuracy.

In late 2022, Corso et al. introduced DiffDock,¹⁸⁰ a diffusion generative model which learns the ligand pose distribution from ligand and protein structures. The model employs a diffusion process over the ligand center position, orientation, and torsional angles of each rotatable bond. By iteratively refining ligand poses through updates of translations, rotations, and torsion angles, DiffDock can sample binding poses from random initial ligand conformations.

On the PDBBind blind docking task, DiffDock achieves a 38% top-1 accuracy, significantly outperforming state-of-the-art molecular docking models.¹⁸⁰ This success demonstrates the potential of DL methods in improving the ligand binding pose prediction. By combination of DiffDock with modern DL-based scoring functions, a more robust virtual screening protocol can be developed for real-world drug discovery applications.

3. Molecular Representation Learning with Deep Learning Methods

3.1. Exploring Chemical Space Efficiently with Force-Field Optimized 3D Geometry and 2D Molecular Graphs

In theoretical chemistry, the Schrödinger equation (SE) serves as the “standard model” because it represents the physics of the charged particles that make up almost all of the molecules and materials. Unfortunately, the analytical solution to SE is only available for systems with a few degrees of freedom. Numerical solutions such as high-accurate quantum mechanics (QM) calculations impose prohibitive computational cost.^181−184 To overcome this challenge, ML approaches to predict molecular energies have been crafted to circumvent the task of solving SE of the system 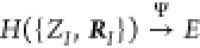by learning the mapping from the geometry to the energy through supervised learning.^185−191 With advances in computer infrastructure and the availability of organized chemistry data sets, DL¹⁹² methods are gaining popularity. DL methods utilize the atomic coordinates {R_I} and atom types {Z_I} to predict molecular energetics directly, avoiding the need for hand-crafted molecular descriptors used in ML methods.^193−203 In the past few years, many DL models^204−213 with distinct model architectures have been developed for the prediction of molecular energetics with better performance on the QM9 benchmark data set.^214−216 This data set contains minimized structures and molecular properties calculated using the density functional theory²¹⁷ (DFT) method for 133,885 molecules composed of H, C, N, O, and F atoms with up to nine heavy atoms. However, despite the progress, many DL models developed on the QM9 data set still require DFT-optimized geometries as input for prediction, which leads to the original problem of computational expense not being fully addressed.

Force-field optimized geometries can be used to predict DFT-level molecular energetics

In 2019, Lu et al. have demonstrated the feasibility of using Merck Molecular Force Field (MMFF)¹⁸³ optimized geometry for gas phase DFT-level electronic energy prediction.²⁰⁹ They first train a model called DTNN_7ib on the QM9 data set using DFT-optimized geometries as input and then retrain the readout layer of the model on their prepared MMFF-optimized geometries. The trained DTNN_7ib achieves a mean-absolute-error (MAE) of 0.79 kcal/mol on DFT-level electronic energy by using MMFF-optimized geometry.

In 2021, Lu et al. extended the effectiveness of MMFF-optimized geometry beyond the QM9 benchmark data set by constructing the Frag20 data set.⁶³ These data consisted of DFT-calculated properties for over half a million molecules, with both MMFF and DFT-optimized geometries, and consisted of elements H, B, C, O, N, F, P, S, Cl, and Br, with no more than 20 heavy atoms. They train a model named sPhysNet on the Frag20 data set and achieve better than or close to chemical accuracy (1 kcal/mol) on multiple test sets, including two external test sets based on experimental crystal structures. The work indicated the potential of using MMFF-optimized geometries as a more computationally efficient alternative to explore chemical space⁶⁶ compared to solely relying on DFT-optimized geometries.

MMFF geometry also proves useful for predicting experimental properties

In 2022, Xia et al.⁵¹ developed a DL model named sPhysNet-MT-ens5 for predicting experimental hydration free energy and octanol/water partition coefficient (logP) using MMFF optimized geometry. Figure 4 shows the overall workflow using the model for prediction. For each compound, up to 300 conformations are generated using EDKTG²¹⁸ implemented in RDKit²¹⁹ and then optimized with MMFF. The conformation with the lowest MMFF energy is then selected as the input geometry for the prediction of experimental hydration free energy and logP, as well as other properties of the compound. An ensemble of five independently trained sPhysNet-MT models is used for prediction, and the average of the five predictions is used as the ensemble prediction. The model achieves a root-mean-square error (RMSE) of 0.620 kcal/mol on the FreeSolv²²⁰ data set for experimental hydration free energy prediction, as well as an RMSE of 0.393 on the PHYSPROP^18,221−223 data set for experimental logP prediction.

Figure 4.

Overall workflow using sPhysNet-MT-ens5 for energetics prediction. (A) MMFF geometry generation protocol. (B) The prediction of electronic energies and transfer free energies with sPhysNet-MT-ens5.

Spatial information computed from MMFF geometry enhances 2D molecular representations

Unlike models that use 3D molecular geometry as input, many DL models use 2D molecular graphs to predict various chemical properties.^224−231 While they have shown success in these tasks, their limitations in representing molecules with 2D graphs have been widely discussed.^232−236 This is because models based solely on 2D connection graphs may not distinguish between molecules with 3D spatial structures. For example, message passing GNNs cannot distinguish decaprismane²³⁷ C₂₀H₂₀ from dodecahedrane²³⁸ C₂₀H₂₀ purely based on their 2D graphs.²³⁵

To address this limitation, models that incorporate geometry information can achieve better performance.^52,239 In 2022, Zhang et al. developed A3D-PNAConv⁵² which uses both 2D and 3D information on molecules. They demonstrate that incorporating 3D atomic features obtained from MMFF-optimized geometries enhances the learning power of GNN models in predicting calculated solvation free energies. The 3D atomic features are calculated by atom-centered symmetry functions (ACSFs),²⁰⁰ which are sets of many-body interaction functions encoding atomic environments in 3D structures. The GNNs use the 3D atomic features as the initial atomic embedding and then perform several iterations of message passing on the 2D molecular graphs. In comparison, they have also trained GNNs without 3D atomic features. The GNNs with 3D atomic features as initialization outperform their 2D counterpart for predicting calculated water solvation free energy on their Frag20-Aqsol-100k data set. This indicates that using 3D atomic features obtained from MMFF geometries can enhance the learning capability of GNN-based models.

3.2. Enhancing Downstream Tasks through Transfer Learning with Pretrained Molecular Modeling Data

In the early stages of the drug discovery process, data scarcity is the most common issue for DL models in the prediction of experimental physicochemical properties. DL models heavily rely on the size and quality of the training data, and they tend to overfit on small data sets, leading to poor generalizability and performance.²⁴⁰ In contrast, molecular modeling data can be obtained in larger quantities within a reasonable time frame, thanks to advancements in high-performance computing. As shown in Table 2, publicly available data sets generated using molecular modeling methods are significantly larger than experimental data sets in terms of size. To address the scarcity of experimental values, calculated data sets should be fully utilized when training DL models on experimental data.

Table 2. Overview of Common Experimental and Calculated Data Sets for Energetic-Related Properties.

Type	Name	Data set size	#Heavy Atoms	Properties	Reference
Calculated	QM9	133,885	1–9	Electronic energy, HOMO, LUMO, etc.	(215)
	ANI-1	24,687,809	1–8	Electronic energy	(241)
	Frag20	566,296	1–20	Electronic energy	(63)
	Frag20-solv-678k	678,916	1–20	Electronic energies (gas water and octanol)	(51)
Experimental	FreeSolv	643	1–24	Hydration Free Energy	(220)
	PHYSPROP-logP	14,174	3–85	Water/octanol partition coefficient	(221,223)
	MNSOL	3,037	0–28	Solvation free energies and transfer free energies in 92 solvents	(242)

Pretraining on DFT-calculated energetics aids in improving the prediction of downstream tasks on related experimental properties

The fine-tuning strategy is commonly employed in training DL models. First, a model is pretrained on a source task, and then, its trained weights are transferred as the initialization for a related target task. This fine-tuning approach often yields better performance compared to random initialization.²⁴³ For instance, Zhang et al. developed a data set named Frag20-Aqsol-100k which contains 100k diverse molecules sampled from Frag20 and CSD20 data sets, along with their calculated hydration free energy using their SMD_B3LYP protocol.⁵² They pretrained DL models on the Frag20-Aqsol-100k data set and fine-tuned the models on the FreeSolv data set, which contains 640 compounds with experimentally measured hydration free energy. Their fine-tuned model achieved state-of-the-art performance and can even achieve chemical accuracy with a very small training data size of just 100 molecules.⁵²

Xia et al.⁵¹ extended the work and develop Frag20-solv-678k which contains 678,916 conformations and their calculated energetics in gas, water, and octanol phases. They pretrained a DL model on all three electronic energetics and the transfer free energies between the three phases, and fine-tuned the model on a combined data set composed of molecules from FreeSolv with experimental hydration free energy and PHYSPROP with experimental logP. The fine-tuned model predicts experimental hydration free energy with an RMSE of 0.620 kcal/mol on the FreeSolv data set, as well as experimental logP with an RMSE of 0.393 on the PHYSPROP data set, achieving state-of-the-art performance on both tasks simultaneously (Figure 5).

Figure 5.

Model performance comparison between sPhysNet-MT and other state-of-the-art models on the experimental hydration free energy and logP prediction. Results are adapted from the sPhysNet-MT manuscript.⁵¹

3.3. Improving Molecular Representations through Mutual Learning with Multitask Training

There are a wide range of ML and DL models that have been developed for a variety of chemical tasks. Although some chemical tasks are related, they are treated by different models with distinct model architectures. For example, the models developed for the prediction of high-level QM calculated molecular energetics^204−212 and the models for predicting of experimental transfer free energies^{52,225,228,229,239,244,245} are often developed separately. While separate models may be more effective for accurate predictions for weakly related tasks,^210,211 multitask models can be advantageous when tasks are well-related.^246,247

Multitask training on related tasks leads to more robust molecular representation learning

Motivated by the fact that many molecular modeling methods use the direct relationship between absolute energies and transfer energies to predict experimental properties with satisfactory results,^248−251 Xia et al. developed a multitask DL model named sPhysNet-MT.⁵¹ This model simultaneously predicts electronic energies of molecules in gas, water, and octanol as well as the transfer free energies between these phases. On their calculated data set, which includes molecules with energetics computed at the DFT-level, the sPhysNet-MT model achieves chemical accuracy on all tasks. Additionally, on the experimental data set containing molecules with experimental hydration free energy and logP, the model achieves state-of-the-art performance on both tasks simultaneously (Figure 5).

Similarly, Lu et al. developed the T5Chem model for multitask reaction prediction, which encompasses forward reaction prediction, reactant prediction, reagent prediction, reaction yield prediction, and reaction type classification.²⁵² On the test set of their reaction prediction data set called USPTO_500_MT, T5Chem achieves top-1 accuracy of 97.5%, 72.9%, and 24.9% for forward prediction, retrosynthesis, and reagents prediction, respectively. The model also achieves an accuracy of 99.4% in reaction type classification, R² of 0.22, and MAE of 17.8 in reaction yield prediction, showing competitive performance compared to models trained solely on individual tasks.

4. Case Study: 1M17

To illustrate the computational tools described in this paper, we show a case study using the crystal structure of the FDA approved inhibitor Erlotinib bound to the kinase domain of the epidermal growth factor receptor (EGFR) from PDB 1M17 (Figure 6).

Figure 6.

Case study of PDB 1M17 with models mentioned in the paper. (A) AlphaSpace and AlphaSpace 2.0 binding pocket analysis. (B) Binding affinity prediction was done using Lin_F9 and Δ_LinF9XGB. (C) Prediction of physicochemical properties of the ligand molecule using sPhysNet-MT.

We first use AlphaSpace to analyze the binding of Erlotinib to EGFR kinase. The crystal receptor and crystal ligand are the inputs for AlphaSpace and AlphaSpace2.0 analysis. To calculate the AlphaSpace 2.0 β-score, hydrogens and partial charges are added to the ligand and protein input files. The AlphaSpace output characterizes the pockets that are in contact with the ligand, provides a binding score, and suggests undertargeted pockets (Figure 6A). The alpha-atoms and β-atoms are colored by the pockets which they belong to.

We then apply Δ_{Lin_F9}XGB for the prediction of the binding affinity. Similarly to the preparation of the AlphaSpace 2.0 input files, we add hydrogens and generate the partial charges to the crystal ligand and crystal protein input files. We apply Lin_F9 local optimization on the ligand binding orientation and get the Lin_F9 binding score. The Vina, solvent accessible surface area, water, metal, and ligand descriptors are calculated for the optimized geometry. These are input to an ensemble of 10 XGB models, the average output of which is used as correction of the Lin_F9 binding affinity. The sum of the Lin_F9 and XGB correction is the final Δ_{Lin_F9}XGB score or the predicted binding affinity. The predicted binding affinity of Erlotnib to EGFR kinase from the structure 1M17 (pK^pred_d = 8.46, K^pred_d = 3.5 nM, Figure 6B) closely matches the experimental binding affinity found in BindingDB (with an average of pK^exp_d and pK^exp_i = 8.9 ± 0.9).²⁵³ It is worth noting that BindingDB contains 45 entries for K_i (ranging from 0.1 to 136 nM) and K_d (ranging from 0.35 to 190 nM), indicating a wide range of experimentally measured binding affinities. Our predicted K_d value of 3.5 nM falls comfortably within this spectrum of binding affinities.

Finally, we use sPhysNet-MT to predict the physicochemical properties of the ligand molecule Erlotinib. Starting from the SMILES of Erlotinib, we first generate up to 300 conformations using EDKTG and optimize them with MMFF. 291 conformations are successfully generated, and the one with the lowest MMFF energy is selected as the input geometry for sPhysNet-MT. The average output of an ensemble of 5 independently trained sPhysNet-MT models is used as the final prediction. The model predicts the logP of the molecule to be 2.76 which is close to the experimental measured value queried from the DrugBank database, 2.7 (Figure 6C).²⁵⁴ The detailed scripts to carry out these calculations and analysis can be found at: https://github.com/SongXia-NYU/drug_discovery_perspective.

5. Concluding Remarks and Perspective

The success of developing computational tools for drug design requires the integration of both molecular modeling and ML techniques. Models for small molecules, protein surfaces, and protein–ligand interactions are all required during different stages of the drug design process, and there is still room for development and research in these methods.

The AlphaSpace methods can be more robust and applicable. Further improvements can account for the role of protein conformational stability in pocket ligand-ability. This can make pocket comparisons more robust, especially when large conformational changes or comparisons between apo and holo structures are involved. When apo structures result in lower ligand-ability estimates, it limits confidence in using apo structures for downstream structure-based design. Quantified comparisons between different proteins and between orthosteric and allosteric pockets can also provide insights into ligand selectivity and off-target effects. Future versions can address these limitations by leveraging deep learning approaches to learn the representation of these relationships and improve ligand-ability estimates. Smith et al. suggest that there are opportunities to apply advanced deep learning image vision techniques to this research question.⁹² AlphaSpace2 and future versions can be tested on recently developed benchmarks for protein–ligand binding site prediction such as SHREC,⁸³ HOLO4K, COACH420,⁷⁸ and for binding site comparisons such as ProSPECCTs.^70,255 Additionally, a Web server can be developed to give medicinal chemists a more user-friendly experience.

Despite the improved performance of ML- and DL-based molecular docking and scoring methods on the CASF-2016 data set, these methods tend to have a high false positive rate and lack generalizability on real-world VS data sets. More consideration should be given to the curation of the training data sets and to introducing regularization techniques to current VS protocol. Computationally generated decoy poses and training data sets should be generated carefully to prevent the model from having noncausal bias, an issue where the model learns specific data patterns instead of meaningful ligand–protein interactions.^256,257 Training data sets tend to have many positive labels that lack diversity and have few or biased negative labels.^{83,88,258,259} Non- and poor-binders are under-reported, and computationally selected nonbinders should be verified experimentally.^260,261 There is a lack of quality and standardized data for some targets. Methods such as data set debiasing²⁶² and introducing specific models to classify and rank actives from inactives^{171,263−265} are promising regularization techniques to tackle this problem. Furthermore, it is necessary to test models in fair benchmarking data sets akin to real-world conditions.^155,266

The size and quality of the training data are also important considerations for the prediction of molecular properties with DL models. More diverse data sets are required to further explore the chemical space. The Frag20 data preparation protocol⁶³ can be used to carefully select diverse molecules, and modern high performance computing platforms can with the help generate labels for DFT calculations for calculated data sets. Collaboration with experimental groups is needed to enlarge and standardize experimental training sets. More careful pretraining protocols and model architecture designs should be developed to fully take advantage of the existing experimental data. Another disadvantage of sPhysNet-MT as well as many other DL-based models is that they can run into problems when considering charged molecules, because they do not explicitly express molecular charge in the model. For example, when predicting pK_a, the molecule may be ionized and the model may have problems learning the molecular representation without knowing the total charge of the system.

Additionally, structure-based drug design methods are limited by the exclusion of protein dynamics in most current protein–ligand representations. Protein flexibility can range from slight perturbation of the ligand binding pockets to reconstitution of the binding site to large-scale conformational changes. In the case of binding site prediction, the introduction of the protein dynamics to the model can lead to the detection of cryptic pockets that are not seen in the static crystal structures and to better predictors of binding site ligandability.⁸² Cryptic pockets can be teased out using standard MD simulations or specialized MD simulations where the solvent molecules are altered to act as probes to tease out these pockets.⁸⁰ Researchers are also using ML models that have learned the aspects of protein flexibility that lead to cryptic pockets from MD simulations to predict cryptic sites.^267,268

Researchers have addressed this limitation of protein flexibility within the context of docking and binding affinity prediction as well.²⁶⁹ Some methods introduce side chain flexibility to the receptor binding pocket,²⁷⁰ others include MD simulations to probe the stability of the predicted binding pose,²⁷¹ while some DL methods learn the features that drive protein–ligand interactions in MD simulations to predict binding affinity.²⁷² The most common method is ensemble docking, which performs docking on a diverse selection of static receptor structures.^273,274 Although rigorous in concept, ensemble docking can actually lead to a decrease in performance when using too many structures and thus researchers propose additional ML methods to select the best subset of structures.^275−277 The use of technology, like cryo-EM that can determine diverse receptor structures, enhanced sampling MD simulations that speed conformational sampling, and DL protein structure prediction methods that can predict previously undetermined protein structures and conformations will drive the research in understanding the role of protein conformation in ligand binding. The decision to introduce protein flexibility to structure-based drug design comes with additional computational cost, a factor that must be aligned with the scope and goals of every screening campaign and currently does not guarantee improved performance.

Author Contributions

^∥ S.X. and E.C. contributed equally.

The authors declare no competing financial interest.