Abstract
Understanding what controls global leaf type variation in trees is crucial for comprehending their role in terrestrial ecosystems, including carbon, water and nutrient dynamics. Yet our understanding of the factors influencing forest leaf types remains incomplete, leaving us uncertain about the global proportions of needle-leaved, broadleaved, evergreen and deciduous trees. To address these gaps, we conducted a global, ground-sourced assessment of forest leaf-type variation by integrating forest inventory data with comprehensive leaf form (broadleaf vs needle-leaf) and habit (evergreen vs deciduous) records. We found that global variation in leaf habit is primarily driven by isothermality and soil characteristics, while leaf form is predominantly driven by temperature. Given these relationships, we estimate that 38% of global tree individuals are needle-leaved evergreen, 29% are broadleaved evergreen, 27% are broadleaved deciduous and 5% are needle-leaved deciduous. The aboveground biomass distribution among these tree types is approximately 21% (126.4 Gt), 54% (335.7 Gt), 22% (136.2 Gt) and 3% (18.7 Gt), respectively. We further project that, depending on future emissions pathways, 17–34% of forested areas will experience climate conditions by the end of the century that currently support a different forest type, highlighting the intensification of climatic stress on existing forests. By quantifying the distribution of tree leaf types and their corresponding biomass, and identifying regions where climate change will exert greatest pressure on current leaf types, our results can help improve predictions of future terrestrial ecosystem functioning and carbon cycling.
Subject terms: Ecology, Biogeography
Integrating inventory data with machine learning models reveals the global composition of tree types—needle-leaved evergreen individuals dominate, followed by broadleaved evergreen and deciduous trees—and climate change risks.
Main
Forest ecosystems, which contain 80–90% of global terrestrial plant biomass1,2 and a large proportion of terrestrial biodiversity3, regulate global biogeochemical cycles, and provide critical ecosystem services4. Leaves mediate forest energy and carbon inputs via photosynthesis, respiration, transpiration5,6 and litterfall7,8, thereby regulating ecosystem structure and function, and water, nutrient and carbon cycles9–11. Leaves of trees are highly diverse but can be broadly classified into four major types on the basis of leaf habit (evergreen vs deciduous) and form (broadleaved vs needle-leaved). These characteristics are linked to a vast array of functional traits associated with resource-use strategies and strongly depend on local growing conditions12–15. Therefore, understanding variation in leaf types along environmental gradients is critical to predicting global biogeochemical cycles and ecosystem functioning in a changing world. Yet, we still lack a global, quantitative understanding of forest leaf habit and form, informed by field-based observations.
Deciduous tree species evolved to tolerate seasonal climates and maximize the use of a short growing season16,17. They usually have higher photosynthetic rates18 than evergreen species and reduce transpiratory water loss due to respiration by shedding their leaves during unfavourable seasons11. Evergreen trees with longer leaf lifespans, by contrast, tend to have greater leaf construction costs19 and lower nutrient cycling rates20. Growing season water-use strategy commonly differs between broadleaved and needle-leaved species21, with needle-leaved species often showing conservative strategies22, such as lower stomatal conductance23 and higher hydraulic safety margins24, resulting in low photosynthesis rates25. A spatially explicit understanding of tree leaf types is therefore critical for estimating the sensitivity and resilience of forests to future climate and soil conditions26–28, and understanding the ecological consequences of such changes.
Theoretical models29 and remote sensing observations30,31 have shown general trends in how climate and soil conditions affect the geographic occurrence of broadleaved and needle-leaved tree species at regional and global scales32. These relationships form the foundation of dynamic global vegetation models31,33–37. Yet, the relative importance of various environmental characteristics on leaf habit and form remains to be determined. Furthermore, until now, these vegetation models have lacked the ground data needed to build tree-density-based ‘bottom-up’ models. Such models are crucial for validating satellite-derived trends on a global scale and for providing a comprehensive, high-resolution depiction of forest leaf-type variation across environmental gradients.
Here we analyse the global distribution of needle-leaved, broadleaved, evergreen and deciduous tree species, by integrating ground-sourced information from 9,781 standardized forest inventory plots in the Global Forest Biodiversity initiative (GFBi)38 database with species-level leaf habit (evergreen vs deciduous) and leaf form (broadleaf vs needle-leaf) information accessed from the TRY plant trait database39 (Fig. 1a). The 9,781 forest inventory plots represented a subsample of the full GFBi data of >1 million records to ensure an equal representation of different forest biomes across the globe and avoid modelling bias caused by uneven spatial sampling (see Methods). Using information on both the occurrences of individual trees per plot and the basal-area weighted occurrences of each individual, we calculated plot-level leaf-type proportions (1) on the basis of the leaf type of each individual tree (tree-based leaf type) and (2) by weighting each tree by its basal area (area-based leaf type) (see Methods section 'Tree leaf-type data'). The first estimate allowed us to map the tree densities of each leaf type, while the second estimate allowed us to map the leaf types represented by the largest trees in a plot. To interpolate patterns across the globe, we combined our plot-level forest leaf information with 58 environmental variables, representing vegetation characteristics, climate, topography, vegetation, soil conditions and human-related features. We also tested the relative importance of 29 commonly studied variables on leaf-type variation and characterized the relationships between environmental features and leaf type.
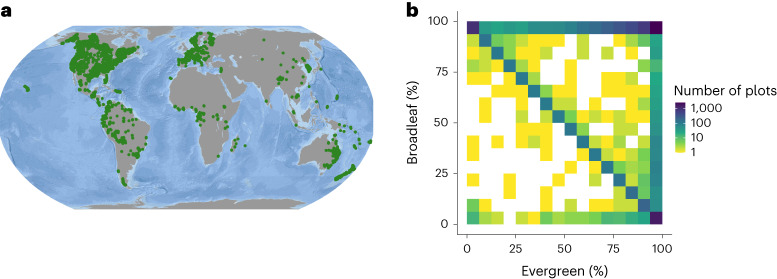
Fig. 1. Global coverage of forest inventory locations (GFBi data) and plot-level leaf-type proportions.
a, A total of 9,781 forest inventory plots (green points) were used for geospatial modelling of forest leaf types. b, Number of plots in relation to their proportion of evergreen vs deciduous and broadleaved vs needle-leaved individuals.
Mapping global forest leaf types
To characterize the variation in forest leaf type, we first summarized the proportion of evergreen vs deciduous (leaf habit) and broadleaved vs needle-leaved (leaf form) individuals within each plot (Fig. 1a). Across all 9,781 forest plots, 13% contain exclusively broadleaved evergreen trees, 7% contain exclusively broadleaved deciduous trees, 12% contain exclusively needle-leaved evergreen trees, and the remaining 68% contain a mixture of leaf habits and forms (Fig. 1b).
Our random forest model predicted 75% of the global variation of forest leaf-type classes (10-fold cross-validation , see Methods). We also ran spatially buffered leave-one-out cross-validation (LOO-CV) to account for the potential effect of spatial autocorrelation on model evaluation statistics, which resulted in a coefficient of determination (R2) of 0.56 at a buffer radius of 300 km (see Methods and Supplementary Fig. 1). Within each class, our model explained 90%, 59%, 75% and 29% (10-fold cross-validation R2) of the global variation in the proportion of broadleaved evergreen, broadleaved deciduous, needle-leaved evergreen and needle-leaved deciduous trees within forests, respectively. These predictive relationships were then used to upscale the observations across the global extent of forest coverage (Fig. 2).
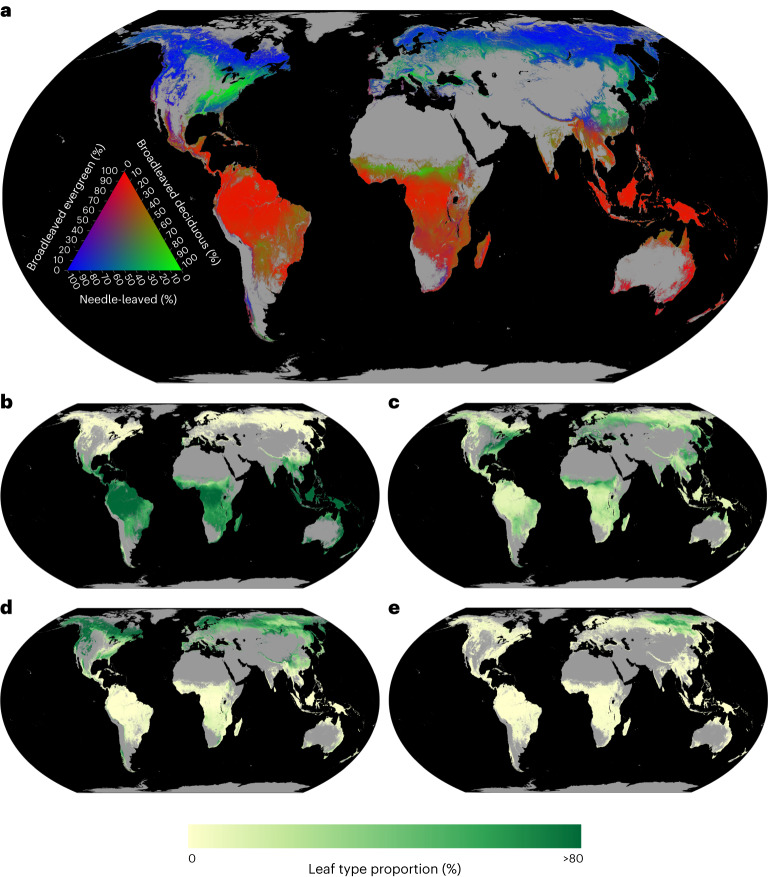
Fig. 2. The global distribution of forest leaf types.
a, The global distribution of tree leaf type as predicted by a random forest model built from area-based leaf-type data (see Methods). Pixels are coloured in the red, green and blue spectrum according to the percentage of total tree basal area occupied by broadleaved evergreen, broadleaved deciduous and needle-leaved tree types, as indicated by the ternary plot. Needle-leaved evergreen and needle-leaved deciduous forests were combined due to the low global coverage of needle-leaved deciduous trees. b–e, Predicted relative coverage of each leaf type from random forest models. Ref. 81 was used to mask non-forest areas. b, Broadleaved evergreen coverage. c, Broadleaved deciduous coverage. d, Needle-leaved evergreen coverage. e, Needle-leaved deciduous coverage.
To evaluate model robustness, we tested its performance on an independent validation dataset containing 3,895 sites across the globe40, resulting in an R2 of 0.47 (see Methods section 'Cross-validation using external data'). In addition, we compared our model output with annual land cover maps from the European Space Agency’s Climate Change Initiative (ESA CCI LC)41. Across all leaf types, our model showed high correlations with the ESA CCI LC outputs, with an of 0.61. Within each leaf type class, our model explained 78% of the variation in the proportion of broadleaved evergreen trees, 31% of broadleaved deciduous tree proportions, 64% of needle-leaved evergreen tree proportions and 19% of needle-leaved deciduous tree proportions (R2).
While considerable uncertainties exist for individual predictions at the pixel level, these uncertainties rapidly decrease as the model is projected to a larger area (<5% at 250 km2; Supplementary Fig. 2). Our model shows high confidence in tropical and boreal forests, whereas predictive confidence is lower in mixed forests and ecotones between different types of forest (Supplementary Figs. 3 and 4). For example, models for broadleaved evergreen and deciduous species share low predictive confidence in central African savanna regions. Similarly, low predictive confidence can be found across eastern Russian mixed forests. The low predictive confidence for these regions can be attributed to low sample size and mixed occurrence of broadleaved evergreen and deciduous species, as well as differences in the year of observation across forest survey plots, which may lead to larger uncertainties in ecotones where forest types can shift in relatively short time periods.
Global environmental drivers of forest leaf-type variation
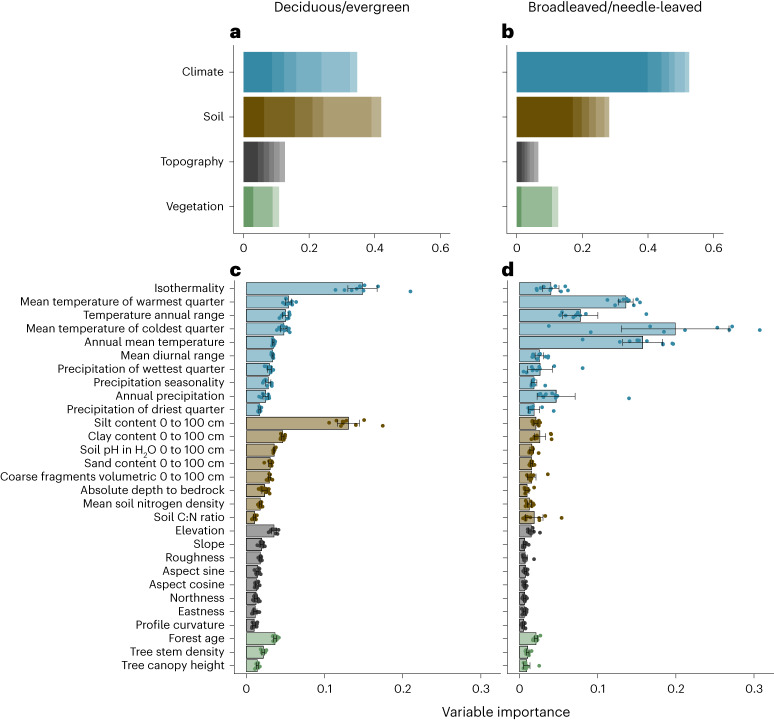
To assess the relative importance of environmental features on variation in leaf types, we ran random forest models including a range of environmental variables (see Methods). We combined these environmental factors into three groups (climate, soil and topography). To test for the relative importance of climate, soil and topographic characteristics, we ran a principal component analysis (PCA) for each of these variable groups and selected the first six principal components, which explained ≥90% of the total variation across all variables. Our analyses show that climate and soil characteristics jointly determine the global leaf-type distribution (Fig. 3a). With respect to variation in leaf habit, temperature fluctuations, that is, isothermality and temperature seasonality, were the most important variables (Fig. 3c). Yet, the entire combination of soil features (first six principal components of soil variables) was as important as climate for predicting leaf habit in our random forest model (Fig. 3a), suggesting that soil characteristics play an important role in the global distribution of evergreen ‘vs’ deciduous species. Especially soil texture, in combination with pH, appears to affect global variation in tree leaf habit. Acidic soils, commonly found in tropical and boreal regions, inhibit nutrient (N and P) supply by reducing cation availability and limiting tree growth rates16. This might explain why broadleaved deciduous species that require high nutrient supply are less abundant in regions with acidic soil. Broadleaved evergreen species, by contrast, may better cope with nutrient poor, acidic soils42. Similarly, needle-leaved evergreen species that can maintain growth even under low nutrient supply are more abundant in regions with acidic soil16. The high tannin and phenol contents of needle leaves further contribute to the acidification of soils16, probably creating a positive feedback towards coniferous dominance. Overall, our results point towards a feedback between tree leaf habits and soil conditions, highlighting the connection between physical soil features and soil water43 and nutrient44 availability.
Fig. 3. Variable importance of environmental covariates on forest leaf-type variation.
a,b, Cumulative importance of the first six principal components of climate, soil, topographic and vegetation covariates in the variation of leaf habit (a) and leaf form (b). c,d, Variable importance of selected environmental features on variation in leaf habit (c) and leaf form (d). Bars in c and d represent the mean ± 95% CI; relative importance based on the 10 best random forest models (n = 10; see Methods). Area-based leaf-type proportions were used to represent forest (plot-level) leaf-type variation.
Variation in leaf form was best predicted by climate variables (Fig. 3b), with the most important variable being temperature of the coldest quarter (Fig. 3d). By contrast to leaf habit, soil, topographic and vegetation features were less important in driving variation in leaf form, indicating adaptation to extreme climates, cold winters or extended dry seasons, as a major determinant of leaf form. This supports previous studies indicating that diverse leaf forms evolved to adapt to different climates45,46.
Computation of tree densities with different leaf types
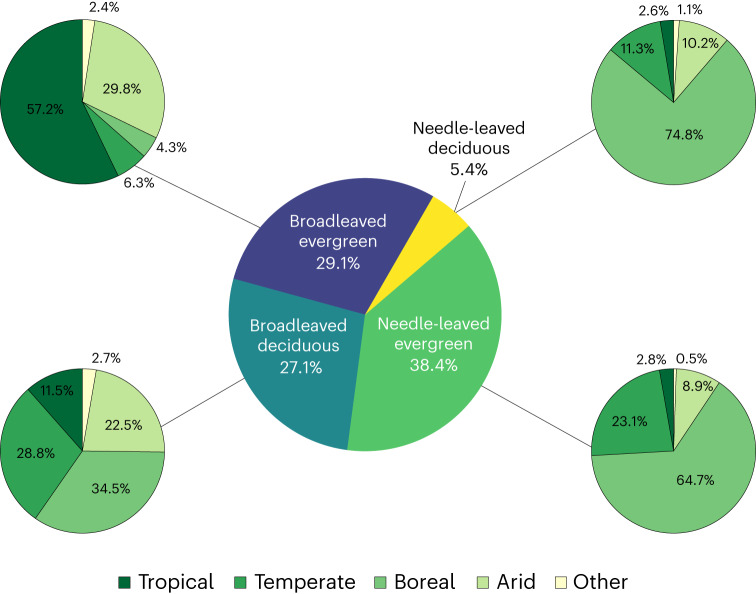
To quantify the proportions of different leaf types across global forests, we combined a global tree density distribution map47 with our individual-based leaf type models (see Methods and Supplementary Fig. 5). At the global scale, we estimate that of the ∼3 trillion adult trees presently existing, 29.1% (95% CI = 27.5–30.7%) are broadleaved evergreen, 27.1% (23.8–30.6%) are broadleaved deciduous, 38.4% (35.2–41.6%) are needle-leaved evergreen and 5.4% (4.3–6.6%) are needle-leaved deciduous (Fig. 4 and Supplementary Fig. 6). Even though needle-leaved tree species comprise less than 2% of the world’s estimated 73,000 tree species48, this small fraction of diversity represents around 44% of individual trees on Earth.
Fig. 4. The global proportion of evergreen broadleaved, deciduous broadleaved, needle-leaved evergreen and needle-leaved deciduous trees.
The relative proportions of trees that occur within tropical, temperate, boreal and arid regions are shown as separate pie charts for each leaf type.
Of the 1.15 trillion needle-leaved evergreen trees growing worldwide, the majority (64.7%) are found in boreal regions, while 23.1%, 8.9%, 2.8% are found in temperate, arid and tropical regions, respectively (Fig. 4). In contrast, of the 0.87 trillion broadleaved evergreen trees growing worldwide, the majority exists in tropical (57.2%) and arid (29.8%) regions, with 6.3% and 4.3% existing in temperate and boreal regions, respectively (Fig. 4). Broadleaved deciduous trees show the widest range of occurrences. Of the 0.81 trillion broadleaved deciduous trees, 34.5% are found in boreal regions, 28.8% in temperate regions, 22.5% in arid regions and 11.5% in tropical regions (Fig. 4). We further estimate that there are 0.16 trillion needle-leaved deciduous trees across the globe, the vast majority of which grow in boreal regions.
Using our basal-area-based model of leaf types, we were able to estimate the biomass contribution of each leaf type within individual forest pixels by integrating our data with a recently published aboveground biomass map49. Our analysis revealed that broadleaved evergreen trees store the largest proportion of global forest biomass, accounting for 54.4% (335.7 Gt) out of the total biomass of 617 Gt. Broadleaved deciduous trees contribute 22.1% (136.2 Gt), needle-leaved evergreen trees contribute 20.5% (126.4 Gt) and needle-leaved deciduous trees contribute 4% (18.7 Gt) (Supplementary Fig. 7). Interestingly, despite there being 42% more evergreen needle-leaved trees compared with broadleaved evergreen trees, their biomass contribution is 62% (209.3 Gt) lower. This distribution of biomass across different leaf types provides valuable insights into the carbon storage capacity of diverse forest ecosystems.
Climatic risk assessment of future leaf types
Climate change will strongly affect the functioning of terrestrial ecosystems by altering growth, mortality and reproduction of trees and their interactions with leaf form and habit16. Our models allowed us to highlight areas of potential risk by identifying the regions where future climates will shift to conditions that currently support leaf types different from the prevailing ones. In these regions, trees are likely to experience more climatic stress in the future. To assess the extent and distribution of future changes in forest leaf-type climate envelopes, we projected our leaf-type models into the future using three climate change scenarios (low-emission scenario (SSP1–RCP2.6), business-as-usual scenario (SSP3–RCP7) and high-emission scenario (SSP5–RCP8.5))50. To do so, we used our random forest models of present leaf type distributions and replaced all climate variables reflecting the 1979–2013 climate (see Supplementary Fig. 1) with climate model projections for 2071–2100 while keeping soil, topographic, vegetative and anthropogenic characteristics constant.
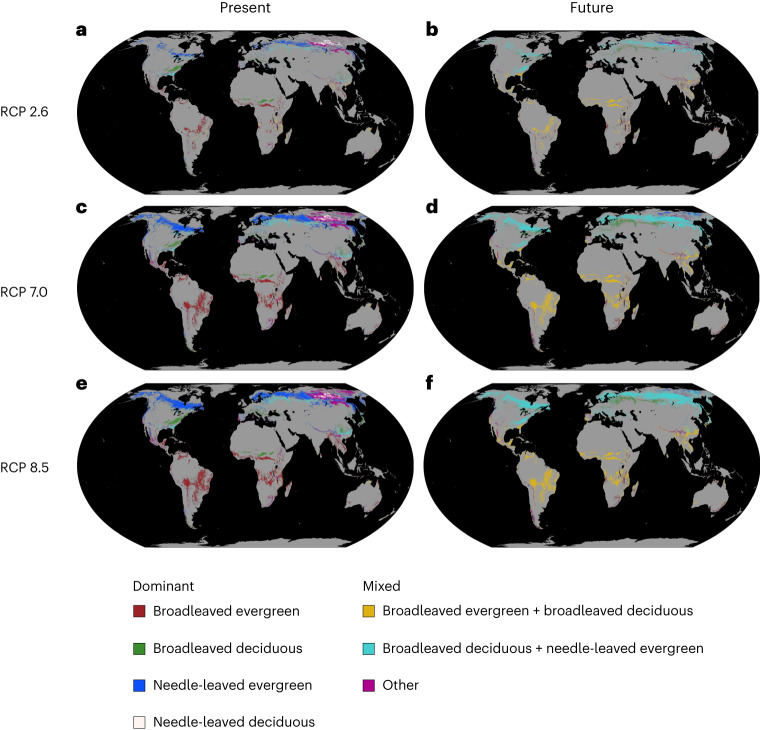
The results suggest that forests will experience substantial shifts in leaf-type climate conditions. Depending on future emissions pathways, 17 to 34% of future forested regions are projected to experience a climate by the end of the century that currently supports leaf types different from the prevailing ones (Fig. 5 and Supplementary Fig. 8; see Supplementary Fig. 9 for an alternative definition of forest types). The climate conditions that have historically supported evergreen forests are declining as global conditions shift towards those that have historically supported more deciduous forests, and this appears to be the case for both broadleaved and needle-leaved species (Supplementary Fig. 10). Specifically, 7–20% of the broadleaved evergreen forests are likely to experience changes towards conditions that currently support deciduous species (Fig. 5). Similarly, 29–67% of the needle-leaved evergreen forests will experience changes towards climate conditions that currently support mixed or deciduous forests (Fig. 5 and Supplementary Figs. 8–12). If these climate projections are realized, plants in those regions must either tolerate more stressful environmental conditions or shift their distributions, causing changes in forest composition51. Previous studies predicting ecoregion shifts have also shown a heightened vulnerability to changing climate conditions, surpassing even the susceptibility of leaf types52.
Fig. 5. Forested areas where future climates may no longer support prevailing leaf types.
If a pixel’s forest area was predominantly (>60%) covered by one leaf type, it was classified as that specific leaf type. Pixels where no leaf type exceeded 60% coverage were classified as mixed forest. To determine the relative proportion of each leaf type per plot, we considered the basal area of individual trees (area-based leaf type). Coloured pixels on the map indicate areas that, by the end of the century (2071–2100), will face climate conditions that currently support a different forest type. The future climate conditions were represented using three climate change scenarios: low-emission (SSP1–RCP2.6; a,b), business-as-usual (SSP3–RCP7; c,d) and high-emission (SSP5–RCP8.5; e,f) for the period 2071–2100. Panels a, c and e show the present forest types. In contrast, panels b, d and f show the type of forest expected under the projected future climate of each respective pixel.
It is important to acknowledge that linking forest leaf types to climate alone cannot fully capture the complex interactions of other influential factors, including CO2 concentration53,54 and nutrient availability26. Consequently, the analysis presented in this study does not project actual changes in forest leaf types. Instead, its focus is on identifying regions where future climates will shift to conditions that currently support different leaf types than what is currently observed. Different species may exhibit varying tolerance thresholds and responses to CO2 fertilization, leading to divergent outcomes. Moreover, it is possible that species sharing the same leaf habit or form but with broader climatic tolerance ranges could replace the present species, potentially mitigating leaf-type changes.
Our analysis serves as a risk assessment, highlighting regions where climate poses a potential threat to the existing forest composition. Further research is necessary to gain a deeper understanding of the intricate interactions between climatic changes, elevated atmospheric CO2 concentrations and nutrient availability. These interactions play a pivotal role in determining essential aspects of forest ecology, such as germination rates, seedling survival, growth rates and tree mortality, which ultimately shape forest composition. Nonetheless, the analysis underscores the substantial and rapid changes in climatic conditions that forests are already experiencing and will continue to experience even more profoundly in the future, on timescales ranging from decades to centuries.
Methodological considerations
Our models successfully captured a substantial portion of the observed spatial variation in forest leaf types, with an overall explained variation of 75%. However, the accuracy of our predictions varied across different leaf types. Among them, our model achieved the highest accuracy in predicting the spatial distribution of broadleaved evergreen tree species, with an explained variation of 90%. Conversely, our model explained only 29% of the variation in needle-leaved deciduous trees, which can be attributed to the limited availability of data from plots containing needle-leaved deciduous species.
To address the uncertainties associated with our predictions, we employed a subsampling approach, running 100 independent models. This allowed us to assess the range of variability in our predictions and identify areas with lower predictive confidence. The resulting maps of model uncertainty (Supplementary Fig. 3) highlight regions where caution should be exercised when interpreting our predictions.
While our study supports many of the mechanisms identified in previous research, our correlative analyses do not necessarily establish causal relationships. To map leaf-ype variation across the globe on the basis of the relationships with environmental features, we used global layers. This approach was necessary as point-level predictor variables cannot be used to interpolate predictions across the globe. While the majority of these layers effectively capture local variations, soil layers may not fully reflect point-level soil observations due to the inherent spatial heterogeneity of soil conditions. In addition, soil layers are typically derived from interpolation methods using environmental information and may thus be correlated with climate variables. While our random forest model predictions are not affected by multicollinearity, this could impact the quantification of variable importance related to environmental, soil, topographic and vegetation features.
Incorporating local point observations into the model training was not feasible because the ground-based forest inventory data we used did not include field-measured environmental and soil characteristics. Although we examined additional point-level observations from the World Soil Information Service (WOSIS) dataset (see next paragraph), these observations often did not align spatially with the forest inventory plots, resulting in a reduced sample size (>80% reduction) and geographic bias (Fig. 1 and Supplementary Fig. 14). Moreover, training the model using point observations while relying on soil layers for model prediction could introduce further uncertainties and biases. To avoid these limitations, we conducted both model training and predictions using the same soil layers.
Nevertheless, we conducted analyses to determine the agreement between results based on global soil layers and point-level soil observations. We matched our forest inventory dataset55 with the WOSIS dataset56, which contains local point observations of soil features. These analyses indicated that: (1) model predictions remained consistent when using point observations instead of global layers of soil characteristics (97–99% similarity in predictions), (2) the global soil layers exhibited good agreement with point observations for most soil variables, particularly the four most important variables (R2 = 0.42–0.62; Fig. 3c and Supplementary Fig. 13) and (3) the inferred importance of soil features in leaf type variation remained similar (<5% difference) when using point observations instead of soil layers as predictors (Supplementary Fig. 14). These analyses underscore the crucial role of soil features in determining global leaf-type variation.
Conclusions
By characterizing the environmental controls of forest leaf-type variation and integrating this information with tree density data, our analysis reveals that 38% of global tree individuals are needle-leaved evergreen, 29% are broadleaved evergreen, 27% are broadleaved deciduous and 5% are needle-leaved deciduous. We further show predictable global patterns in forest leaf varieties, with the relative abundance of leaf forms mainly correlating with temperature variation. In contrast, leaf habit is jointly controlled by climate and soil characteristics. These global relationships between environmental factors and forest leaf types largely agree with local experimental and modelling studies57–59, which also highlight the dual role of climate and soil conditions in driving variation in forest types.
Our analysis of the spatial variation of forest leaf types refines our understanding of forest composition and structure60,61 at a global scale. While satellite-derived approaches have been foundational for the characterization of spatial variation in canopy structure62, our bottom-up model, derived from empirical inventory data, allowed us to create models of forest leaf type at the individual tree level to provide novel insights into forest composition. This can help benchmark satellite-derived models of forest structure and inform ecological models of plant productivity, biogeochemical cycling, carbon storage and species distribution31,63,64. By identifying the main environmental characteristics that determine habitat suitability, such as annual mean temperature, climate seasonality and water and nutrient supplies, our baseline estimates of leaf-type densities are also critical for projecting population- and community-level tree demographics under current and future climate change. Ultimately, these insights can help make informed decisions to guide global efforts to conserve, restore and sustainably manage forest ecosystems that are so vital for the wellbeing of all organisms on Earth.
Methods
Data collection
Forest inventory data
To obtain empirical information on tree occurrences, we extracted a total of 1.1 million forest inventory plots with more than 50 million individual occurrence records, covering all continents except Antarctica from the GFBi dataset38. To avoid modelling bias caused by uneven spatial sampling across biomes, we downsampled the dataset so that the relative proportion of plots in each biome in the dataset approximately matched the proportion of forested area within each biome65. This was done by retaining all tropical forest plots in GFBi (n = 11,367) and randomly downsampling the remaining biomes in proportion to this number. Individuals with stem diameters <10 cm were excluded as the focus was on adult trees, and only plots with ≥10 adult individuals were included in the final analysis. For each plot, the dataset contains information on the location (coordinates), the year(s) when the inventory took place, stem diameter at breast height (DBH) and species identity of each individual. For plots with time series data, only the most recent observation year was included in the analysis. The average year of observation across all plots was 2005. This resulted in a total of 9,781 plots with a median size of ∼500 m2 and 817,091 individual tree records, with 20.3% of the plots in the boreal biome (vs 21% of forested land globally), 20.4% in temperate biomes (vs 22%), 54% in tropical biomes (vs 50%) and 3% in Mediterranean woodland, tundra, xeric shrubland or mangrove biomes (vs 7% globally).
Tree leaf-type data
Information on leaf habit (evergreen vs deciduous) and leaf type (broadleaved vs needle-leaved) was extracted from the TRY plant trait database39. For each species and genus, we assigned the most common leaf habit across all TRY observations, treating leaf habit as a binary variable of whether it is evergreen or not. Species names were standardized using the Taxonstand R package66. We then assigned leaf-type information to the individuals included in the GFBi dataset using species-level information or genus-level information in case species-level information was not available. Plots in which <50% of all individuals had a leaf-type record in TRY were excluded. Out of 10,274 species recorded globally in the GFBi dataset, leaf-type records could be assigned to 8,642 tropical tree species, 453 temperate tree species, 46 boreal tree species and 1,124 tree species in dry areas. Next, we calculated the proportion of each leaf-type combination (evergreen broadleaved, deciduous broadleaved, needle-leaved evergreen or needle-leaved deciduous) within a plot, either by dividing the sum of individuals featuring the respective leaf type by the total number of individuals within the plot (individual-based leaf type) or by dividing the basal area featuring the respective leaf type by the total basal area of all trees in the plot (area-based leaf type).
Environmental covariates
In total, 58 global environmental layers reflecting climate50, topography, vegetation, anthropogenic and soil67 (at 0 cm to 100 cm depth) characteristics were used as covariates in our analyses (Supplementary Fig. 1). Climate variables reflect the average climate between 1979–2013. All layers were standardized to 30-arc-second resolution (∼1 km2 at the equator).
Geospatial modelling
Random forest modelling
To predict the occurrence probabilities of the four forest leaf types (broadleaved evergreen, broadleaved deciduous, needle-leaved evergreen and needle-leaved deciduous), we ran random forest models in Google Earth Engine68. In random forest, unlike traditional regression, correlation among variables does not affect model accuracy. Indeed, the ability to use many correlated predictors is one of the key benefits of machine learning models69. When variables are correlated, the effect of these variables is ‘shared’ across the trees in the random forest. Because random forest does not estimate coefficients as in regression, this correlation does not hinder model fit or performance, but rather complicates efforts to quantify variable importance, which is also shared across correlated variables. Thus, by including numerous variables, even if correlated, we can improve our predictive power of the model to accurately quantify current carbon.
To run the models, we set the output mode to ‘MULTIPROBABILITY’ and randomly sampled 10 individuals from each plot 100 times, weighting individuals by their basal area to model area-based leaf types. The following equation was used to transform DBH to basal area: . To model individual-based leaf types, individuals were sampled without weighting them. This resulted in 100 training datasets, each containing 98,330 rows. After extracting pixel values from 58 environmental covariates, we then modelled leaf types for each training dataset with a random forest model, using the 58 environmental covariates. The correlation between our point-level response variable (leaf type) and spatially contiguous covariates then allowed us to map the global distribution of leaf types.
To train global models of forest leaf types, we first ran a grid-search procedure, exploring the results of a suite of random forest models with different hyperparameters. The hyperparameters that were allowed to vary were the number of random trees (10, 20, 50, 100 and 250), the number of variables sampled at each split (1, 2, 4, 5, 8, 10, 15, 20 and 30) and the minimum sample size at the end of the nodes (1, 2, 5, 10, 15, 20 and 30); subsampling rate was constant at 0.632. To quantify predictive accuracy, we used the Bhattacharyya coefficient to compare the predicted and observed probabilities for each pixel, as is commonly used in image processing and feature extraction70–73. Because four probability classes within a pixel are not independent, we cannot use standard loss functions to estimate predictive accuracy. Instead, we used the Bhattacharyya coefficient, given by , which quantifies the similarity between two vectors, O and P, with n categories. The Bhattacharyya coefficient falls within (0,1), equalling one only when for all i within a pixel (that is, when the predictions exactly match the observed) and zero when the vectors are completely disjoint. To evaluate overall model performance, we then adopted a similar approach to that of ref. 74 for multinomial data75, using the Bhattacharyya coefficients to calculate a pseudo-R2 () (equations 1∼5) on the basis of 10-fold cross-validation:
| 1 |
in which
| 2 |
| 3 |
and
| 4 |
| 5 |
where, MAE is the mean absolute error, Oi is the observed coverage of leaf type i, Pi is the predicted coverage of leaf type i (on out-of-fit data via cross-validation), is the average coverage of leaf type i across all the observations and n is the number of forest leaf types (here, n = 4). Note that the summation terms in equations (3) and (5) are the Bhattacharyya coefficients between the observed multinomial distribution and the predicted distribution (equation 3) and the average distribution (equation 5). Thus, equation (3) is the predictive loss term for each pixel, with the MAEmodel in equation (2) giving the average across all pixels, which equals zero only when the predictions perfectly match the observations. Similarly, equation (5) is the loss term for each pixel when using group-level means, with MAEmean in equation (4) giving the average loss across all pixels. By comparing MAEmodel to MAEmean, we follow the standard approach for computing R2 by quantifying performances relative to human predictions, with R2 = equalling 1 only when our predictions are perfect (MAEmodel = 0) and R2 being 0 when our predictions are equal to or worse than the mean. Importantly, as suggested in ref. 74, equation (1) is estimated using out-of-fit cross-validated data, where the predicted values are estimated by omitting the corresponding observed values from the training data, with the resulting pseudo-R2 used to assess our four-element model output.
To create the final maps (Fig. 2 and Supplementary Fig. 5), we used the random forest model for each training dataset with the optimal suite of hyperparameters based on the from the grid search. Extrapolation of our predictions across global forest areas resulted in 100 four-band global layers, with each band representing the global probability of one forest leaf type. We averaged the predictions from these 100 model outputs by taking the mean for the final map. We calculated the 95% confidence intervals across the 100 model layers76 to represent sampling uncertainty.
As an alternative mapping approach, we used an independent tree-based classification and regression trees (CART) model77 (Supplementary Fig. 15). This approach was used to test whether model performance depends on model type. If the two models (random forest and CART) show similar results, this indicates that predictions are not biased by model selection. Using the same independent ‘Tallo’ dataset40 used for testing the robustness of the random forest model, the CART model had an explanatory power of 0.46, which is similar to the of 0.47 of the random forest model. When directly comparing both models, the CART model showed 87% similarity () with the random forest model. This suggests that our maps and predictions do not depend on the type of model, and we report the random forest model results throughout the main text since it showed slightly higher accuracy55.
Cross-validation using external data
We tested for the performance and correlation between the predictions of the area-based and individual-based random forest models. When using the same independent ‘Tallo’ dataset40 for testing the robustness of the random forest models, the tree-based and area-based models had an explanatory power of 46% and 47%, respectively. When directly comparing both models, the area-based model showed 89% similarity () with the individual-based model, showing that both metrics result in similar predictions of leaf-type variation.
To further evaluate the performance of our models, we additionally compared the model predictions with satellite-derived leaf type estimates from annual land cover maps from the ESA CCI LC41. We used land cover layers for the years 2000, 2005, 2010 and 2015, each with a spatial resolution of 300 m × 300 m. To assign each pixel to forest leaf-type classes, we recalculated the leaf-type proportions for each layer as these represented leaf-type proportions across all ecosystem types, including grasslands. For example, we recalculated forest leaf-type proportions for pixels with 30% broadleaf deciduous forest cover, 20% needle-leaf evergreen forest cover, 10% needle-leaf deciduous forest cover and 40% non-forest cover by dividing each forest cover percentage by the total area covered by forest, resulting in 50% broadleaved deciduous, 33.3% needle-leaved evergreen and 16.7% needle-leaved deciduous. We then calculated the average values across the four years for each pixel and compared the results with our model outputs. Our area-based models explained 61% of the spatial variation in the ESA CCI LC models, with an explanatory power of 78% for broadleaved evergreen leaf-type proportions, 31% for broadleaved deciduous, 64% for needle-leaved evergreen and 19% for needle-leaved deciduous.
To generate global layers of soil features, the Soil Grids dataset relies on machine learning models informed by global, spatially explicit information on various climate variables. This global interpolation of soil information using climate data may thus lead to an overestimation of the covariation between climate and soil layers while reducing small-scale heterogeneity in soil features. To assess whether this potential caveat affects our results, we used point-level soil measurements from the WOSIS dataset, including clay content, silt content, pH and sand content. To spatially match this dataset with the full GFBi dataset containing more than 1.1 million plots across the globe55, we used the ‘geosphere’78 R package. We then selected the nearest soil observation that fell within 250 m or 1,000 m of the centre of each forest plot. This resulted in a spatial match between soil measurements and forest plots in 146 cases for the 250 m radius and in 1,893 cases for the 1,000 m radius (Supplementary Fig. 14a). To test whether model performance and predictions change when using point observations of soil features instead of global layers, we then trained random forest models using either WOSIS or Soil Grids soil data along with information on climate, topography, human and vegetation characteristics (Supplementary Fig. 14b–d). For both the 250 m and 1,000 m buffer radii, the models showed a high degree of agreement () between model predictions.
In a second step, we then tested whether the use of point observations vs global layers of soil features affects the estimated importance of variables in driving leaf-type variation. The analysis showed a slight reduction in the importance of soil variables of 5–6% when using point observations rather than Soil Grids data (Supplementary Fig. 13), which is probably driven by the slightly lower covariation of soil point data with climate variables (Supplementary Fig. 16). Nevertheless, the results remain similar, showing that this difference is unlikely to affect the conclusions of our study.
Interpolation vs extrapolation in model predictions
To evaluate how well our training dataset represents the full multivariate environmental covariate space, we performed a principal-component-analysis-based approach following refs. 76,79. We projected the covariate composite into the same space using the centreing values, scaling values and eigenvectors from the principal component analysis of the training data. We created the convex hulls for each of the bivariate combinations from the top principal components and classified whether each pixel falls in or outside each of these convex hulls. We used 24 principal components with 276 combinations for all covariates for the sampling dataset. This analysis showed that 99.2% of land pixels (778,975,911 of 785,150,461) cover at least 90% of the environmental variables present in our training data locations (Supplementary Fig. 17).
LOO-CV
To account for the potential effect of spatial autocorrelation in model residuals on model validation statistics, we ran spatially buffered LOO-CV for a series of buffer radii from 10 m to 500 km. In LOO-CV, each observation is predicted on the basis of a model that includes all data outside the respective buffer radius. This results in 9,781 (=total number of observations) separate models for each buffer radius. Model performance was evaluated on the basis of . To assess the range of spatial autocorrelation, we ran semi-variograms for random cross-validation and LOO-CV model residuals in each forest type, showing that regardless of buffer radius or validation type, our residuals show weak spatial autocorrelation (Supplementary Fig. 1). Nevertheless, when eliminating any potential effects of spatial autocorrelation on model performance by applying large buffer radii of 300 km and 500 km, the out-of-sample remained high (0.56 and 0.53, respectively).
Global tree density and biomass calculation of leaf types
Tree leaf-type densities were estimated by integrating a map of the global tree density distribution47 with our individual-based forest leaf-type maps. For each pixel, we multiplied tree density values with modelled forest leaf-type proportions to obtain the pixel-level stem density of each leaf type. We then summed up these pixel-level abundances across the globe to estimate the total abundances of each forest leaf type. To obtain the total number of trees of each leaf type for the major forest types, we defined tropical forests as pixels falling in the biomes tropical and subtropical moist broadleaf forest (WWF80 biome 1), tropical and subtropical coniferous forest (biome 3) and mangroves (biome 14). Temperate forests were defined as pixels in the biomes temperate broadleaf and mixed forest (biome 4) and temperate coniferous forest (biome 5). Boreal forests were defined as pixels in the biomes boreal forest or taiga (biome 6), montane grasslands and shrublands (biome 10) and tundra (biome 11). Dry forests were defined as pixels in the biomes tropical and subtropical dry broadleaf forest (biome 2), tropical and subtropical grasslands, savannas and shrubland (biome 7), temperate grasslands, savannas and shrubland (biome 8), Mediterranean forests, woodlands and scrub (biome 12), and deserts and xeric shrubland (biome 13).
Forest biomass for each leaf type was computed by incorporating a map of global forest biomass49 with our area-based leaf-type models. We calculated the absolute biomass by scaling biomass density with tree canopy cover81 and pixel area within each pixel. This absolute biomass per pixel was then partitioned by leaf-type proportions, derived from our area-based models. By summing up the pixel-level biomass across the globe, we were able to approximate the total amount of biomass stored in each of the leaf types.
Environmental drivers of forest leaf-type variations
To evaluate the relative importance of environmental features on forest leaf-type variation, out of the total 58 environmental covariates, we tested the effects of 29 commonly used environmental characteristics using random forest models (see Supplementary Fig. 1). We separated the environmental features into four major groups: climate, soil, topography and vegetation. To equally represent each of the three groups in the model and minimize collinearity, we selected the first six principal components from climate, soil and topography groups. These six principal components explained ≥90% of the total variation across all group variables. We included all the three vegetation characteristics, which are forest age, tree density and canopy height, into the analysis without computing the principal components. We then computed the variance inflation factors (VIFs) across all 21 principal components using the R package HH82. All VIFs were lower than 4, suggesting sufficient independence among covariates. The principal components were then used as predictors in random forest models with different combinations of hyperparameters (that is, 1 to 12 samples per split and a minimum sample size at the end of the nodes of 1 to 10), and we selected the ten best models with the highest coefficient of determining variation (R2). Variable importance was determined by calculating the relative influence of each variable, expressed by the variable’s attributed reduction in squared error. To quantify the importance of individual environmental factors, we used the same combinations of hyperparameters. Based on R2, the ten best random forest models were again chosen to explore the relative importance of each factor. The random forest models were run via the R package h2o83.
Forest types and their future climate envelopes
To assess the extent and distribution of future changes in forest leaf-type climate envelopes, we projected our leaf-type models into the future using CMIP6 climate models for the time interval of 2071–2100 and three emission scenarios (SSP1–RCP2.6, SSP3–RCP7 and SSP5–RCP8.5)50. The CMIP6 climate models were extracted following the ISIMIP3b protocol and included five models (gfdl-esm4, ukesm1-0-II, mpi-esm1-2-hr, ipsl-cm6a-lr and mri-esm2-0). We projected the global forest leaf-type distribution for each emission scenario on the basis of each of the five climate models using our random forest models. To do so, we used our 100 random forest models of present leaf-type distributions and replaced the climate variables (‘bioclim’ variables from the CHELSA dataset, marked with hashtags in Supplementary Fig. 1) with CMIP6 climate model projections while keeping soil, topographic, vegetative and anthropogenic characteristics constant. For each emission scenario and CMIP6 model, we aggregated the 100 layers by taking the mean. We then aggregated the five CMIP6 model projections by taking the mean. For both evergreen vs deciduous and broadleaf vs needle-leaf proportions, we then subtracted the present predictions by the averaged model projections for the three climate change scenarios. We then summarized the predictions for each of the three climate change scenarios across latitude, aggregating predictions for each half degree. This allowed us to identify areas where future climates will shift to conditions that currently support leaf types different from the prevailing ones (Fig. 5 and Supplementary Fig. 9). To do so, we first obtained information on the forest type that currently is most abundant in each pixel (using area-based leaf-type proportions). Pixels in which > 60% of the forest area was covered by a single leaf type were assigned to that respective leaf type. Pixels in which none of the leaf types covered > 60% of the forest area were categorized as mixed forest (Fig. 5). The analysis was also conducted for a forest-area threshold of 80% to ensure that the results are not driven by the choice of the threshold (Supplementary Fig. 9). Following these definitions, we categorized forest pixels into groups using present and future climate scenarios. By scaling pixels by canopy cover, we could then calculate the total areas in which the climate is expected to shift to conditions that currently support a different forest type.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Supplementary information
Supplementary Table 1 and Figs. 1–17.
Acknowledgements
We thank the Global Forest Biodiversity Initiative (GFBi) for establishing the data standards and collaborative framework; TRY database managers and countless researchers who contributed open-access data. This work was supported by grants to C.M.Z. from the Ambizione fellowship (PZ00P3_193646), L.M. from the China Scholarship Council, and T.W.C. from DOB Ecology and the Bernina Foundation. O.B. acknowledges funding from the Romania National Council for Higher Education, CNFIS, project number CNFIS-FDI-2023-F-0579. We thank the French National Forest Inventory (NFI campaigns; raw data 2005 and subsequent annual surveys were downloaded by GFBI at https://inventaire-forestier.ign.fr/spip.php?rubrique159, accessed on 1 January 2015) and the Italian Forest Inventory (NFI campaigns; raw data 2005 and subsequent surveys were downloaded by GFBI at https://inventarioforestale.org/, accessed on 27 April 2019); G.A. was supported by the Italian National Recovery Plan through the National Biodiversity Future Center. M.B. thanks the BOS Foundation, the Indonesian Institute of Sciences (LIPI), the Direktorat Fasilitasi Organisasi Politik dan Kemasyarakatan, Departamen Dalam Negri, and the BKSDA Palangkaraya for permission to work in the MAWAS region of Indonesia, and acknowledges funding from The American Society of Primatologists, the Duke University Graduate School, the L.S.B. Leakey Foundation, the National Science Foundation (Grant No. 0452995) and the Wenner-Gren Foundation for Anthropological Research (Grant No. 7330). K.S. thanks the IBL for supporting this work by internal funds under project no. 261509 “AFTER FBS - maintenance of ForBioSensing project performance indicators”. Plot data collection from Białowieża Forest was supported by Project LIFE+ ForBioSensing (contract number LIFE13ENV/PL/000048) and Poland’s National Fund for Environmental Protection and Water Management (contract number 485/2014/WN10/OPNMLF/D). Plot data collection from Central Siberia was supported by Russian Science Foundation project no 21-46-07002. Contributions from ForestPlots.net and RAINFOR were supported by numerous sources, including the European Research Council (ERC Advanced Grant 291585 – ‘T-FORCES’), the Gordon and Betty Moore Foundation (1656 ‘RAINFOR’), the Natural Environment Research Council (including NE/B503384/1, NE/N012542/1) and the Royal Society (ICA/R1/180100 - ‘FORAMA’). We also thank the National Council for Science and Technology Development of Brazil (CNPq) for support to the Cerrado/Amazonia Transition Long-Term Ecology Project (PELD/441244/2016-5). J.D. was funded by the Czech Science Foundation (project no. 21-26883S).We are grateful to all the ministries and agencies from the Government of Spain and to all the people that supported the collection, compilation, and coordination of forest inventory data, also including the Spanish National Forest Inventories. Sergio de Miguel benefitted from a Serra-Húnter fellowship provided by the Government of Catalonia (Generalitat de Catalunya). J.C.S. considers this work a contribution to Center for Ecological Dynamics in a Novel Biosphere (ECONOVO), funded by the Danish National Research Foundation (grant DNRF173) and his VILLUM Investigator project ‘Biodiversity Dynamics in a Changing World’, funded by VILLUM FONDEN (grant 16549). The exploratory plots of FunDivEUROPE were established through funding from the European Union Seventh Framework Programme FP7/2007-2013 under Grant 265171. Plot data collection from the Brazilian Atlantic Forest was supported by the State of São Paulo Research Foundation/FAPESP (BIOTA Grants 2003/12595-7; 2012/51509-8 and 2012/51872-5) and by the Brazilian National Research Council/CNPq (PELD Grant 403710/2012-0). H.V was funded by FCT - Portuguese Foundation for Science and Technology, project UIDB/04033/2020 and ICNF-Instituto da Conservação da Natureza, Portugal, National Forest Inventory. Financial support for the Monafor network in Mexico came from many projects, including the National Forestry Commission (CONAFOR), Council of Science and Technology of the State of Durango (COCYTED), the Natural Environment Research Council, UK (NERC; NE/T011084/1), and local support of Ejidos and Comunidades. We also directly acknowledge the use of data drawn from the Natural Forest plot data collected between January 2009 and March 2014 by the LUCAS programme for the New Zealand Ministry for the Environment. Data were sourced via the NZ National Vegetation Survey (NVS) Databank.
Author contributions
H.M. and C.M.Z. conceived, developed and wrote the paper, with input from T.W.C., L.M., D.S.M., S.S.R., and Y.Z. H.M. performed the analyses with assistance from C.M.Z., Y.Z., J.v.d.H., D.S.M. and L.M. All authors contributed to data collection and/or curation and reviewed and/or provided input on the manuscript.
Peer review
Peer review information
Nature Plants thanks Helena Vallicrosa and the other, anonymous, reviewer(s) for their contribution to the peer review of this work.
Funding
Open access funding provided by Swiss Federal Institute of Technology Zurich.
Data availability
Tree occurrence data from the Global Forest Biodiversity initiative (GFBi) is available upon request via Science-I (https://science-i.org) or the GFBi website (https://www.gfbiinitiative.org/). Information on leaf habit (evergreen vs deciduous) and leaf form (broadleaved vs needle-leaved) came from the TRY database (https://www.try-db.org). Additional, leaf-type data came from the Tallo dataset (https://zenodo.org/record/6637599). Plot-level soil information came from the World Soil Information Service (WOSIS) dataset (https://www.isric.org/explore/wosis).
Code availability
All code is available at 10.5281/zenodo.7967245.
Competing interests
The authors declare no competing interests.
Footnotes
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
The online version contains supplementary material available at 10.1038/s41477-023-01543-5.
References
- 1.Pan Y, Birdsey RA, Phillips OL, Jackson RB. The structure, distribution, and biomass of the world’s forests. Annu. Rev. Ecol. Evol. Syst. 2013;44:593–622. [Google Scholar]
- 2.Pan Y, et al. A large and persistent carbon sink in the world’s forests. Science. 2011;333:988–993. doi: 10.1126/science.1201609. [DOI] [PubMed] [Google Scholar]
- 3.The State of the World’s Forests 2020. Forests, Biodiversity and People (FAO and UNEP, 2020).
- 4.Bonan GB. Forests and climate change: forcings, feedbacks, and the climate benefits of forests. Science. 2008;320:1444–1449. doi: 10.1126/science.1155121. [DOI] [PubMed] [Google Scholar]
- 5.Wright IJ, et al. The worldwide leaf economics spectrum. Nature. 2004;428:821–827. doi: 10.1038/nature02403. [DOI] [PubMed] [Google Scholar]
- 6.Schulze ED. Biological control of the terrestrial carbon sink. Biogeosciences. 2006;3:147–166. [Google Scholar]
- 7.Sayer EJ. Using experimental manipulation to assess the roles of leaf litter in the functioning of forest ecosystems. Biol. Rev. Camb. Phil. Soc. 2006;81:1–31. doi: 10.1017/S1464793105006846. [DOI] [PubMed] [Google Scholar]
- 8.Ollinger SV, Aber JD, Reich PB, Freuder RJ. Interactive effects of nitrogen deposition, tropospheric ozone, elevated CO2 and land use history on the carbon dynamics of northern hardwood forests. Glob. Change Biol. 2002;8:545–562. [Google Scholar]
- 9.Nicotra AB, et al. The evolution and functional significance of leaf shape in the angiosperms. Funct. Plant Biol. 2011;38:535–552. doi: 10.1071/FP11057. [DOI] [PubMed] [Google Scholar]
- 10.Díaz S, et al. The global spectrum of plant form and function. Nature. 2016;529:167–171. doi: 10.1038/nature16489. [DOI] [PubMed] [Google Scholar]
- 11.Baldocchi DD, et al. On the differential advantages of evergreenness and deciduousness in mediterranean oak woodlands: a flux perspective. Ecol. Appl. 2010;20:1583–1597. doi: 10.1890/08-2047.1. [DOI] [PubMed] [Google Scholar]
- 12.Arora VK, Boer GJ. A parameterization of leaf phenology for the terrestrial ecosystem component of climate models. Glob. Change Biol. 2005;11:39–59. [Google Scholar]
- 13.Schweitzer JA, et al. Genetically based trait in a dominant tree affects ecosystem processes. Ecol. Lett. 2004;7:127–134. [Google Scholar]
- 14.Tian F, et al. Coupling of ecosystem-scale plant water storage and leaf phenology observed by satellite. Nat. Ecol. Evol. 2018;2:1428–1435. doi: 10.1038/s41559-018-0630-3. [DOI] [PubMed] [Google Scholar]
- 15.Méndez-Alonzo R, Pineda-García F, Paz H, Rosell JA, Olson ME. Leaf phenology is associated with soil water availability and xylem traits in a tropical dry forest. Trees. 2013;27:745–754. [Google Scholar]
- 16.Givnish TJ. Adaptive significance of evergreen vs. deciduous leaves: solving the triple paradox. Silva Fenn. 2002;36:703–743. [Google Scholar]
- 17.Axelrod DI. Origin of deciduous and evergreen habits in temperate forests. Evolution. 1966;20:1–15. doi: 10.1111/j.1558-5646.1966.tb03339.x. [DOI] [PubMed] [Google Scholar]
- 18.Reich PB, Walters MB, Ellsworth DS. From tropics to tundra: global convergence in plant functioning. Proc. Natl Acad. Sci. USA. 1997;94:13730–13734. doi: 10.1073/pnas.94.25.13730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Villar R, Merino J. Comparison of leaf construction costs in woody species with differing leaf life‐spans in contrasting ecosystems. New Phytol. 2001;151:213–226. doi: 10.1046/j.1469-8137.2001.00147.x. [DOI] [PubMed] [Google Scholar]
- 20.Chabot BF, Hicks DJ. The ecology of leaf life spans. Annu. Rev. Ecol. Syst. 2003;13:229–259. [Google Scholar]
- 21.Augusto L, et al. Influences of evergreen gymnosperm and deciduous angiosperm tree species on the functioning of temperate and boreal forests. Biol. Rev. 2015;90:444–466. doi: 10.1111/brv.12119. [DOI] [PubMed] [Google Scholar]
- 22.Flo V, et al. Climate and functional traits jointly mediate tree water-use strategies. New Phytol. 2021;231:617–630. doi: 10.1111/nph.17404. [DOI] [PubMed] [Google Scholar]
- 23.Lin YS, et al. Optimal stomatal behaviour around the world. Nat. Clim. Change. 2015;5:459–464. [Google Scholar]
- 24.Choat B, et al. Global convergence in the vulnerability of forests to drought. Nature. 2012;491:752–755. doi: 10.1038/nature11688. [DOI] [PubMed] [Google Scholar]
- 25.Lusk CH, Wright I, Reich PB. Photosynthetic differences contribute to competitive advantage of evergreen angiosperm trees over evergreen conifers in productive habitats. New Phytol. 2003;160:329–336. doi: 10.1046/j.1469-8137.2003.00879.x. [DOI] [PubMed] [Google Scholar]
- 26.Mekonnen ZA, Riley WJ, Randerson JT, Grant RF, Rogers BM. Expansion of high-latitude deciduous forests driven by interactions between climate warming and fire. Nat. Plants. 2019;5:952–958. doi: 10.1038/s41477-019-0495-8. [DOI] [PubMed] [Google Scholar]
- 27.Baltzer JL, et al. Increasing fire and the decline of fire adapted black spruce in the boreal forest. Proc. Natl Acad. Sci. USA. 2021;118:e2024872118. doi: 10.1073/pnas.2024872118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Mack MC, et al. Carbon loss from boreal forest wildfires offset by increased dominance of deciduous trees. Science. 2021;372:280–283. doi: 10.1126/science.abf3903. [DOI] [PubMed] [Google Scholar]
- 29.Kikuzawa K. A cost-benefit analysis of leaf habit and leaf longevity of trees and their geographical pattern. Am. Nat. 1991;138:1250–1263. [Google Scholar]
- 30.Huechacona-Ruiz AH, et al. Mapping tree species deciduousness of tropical dry forests combining reflectance, spectral unmixing, and texture data from high-resolution imagery. Forests. 2020;11:1234. [Google Scholar]
- 31.Sitch S, et al. Evaluation of ecosystem dynamics, plant geography and terrestrial carbon cycling in the LPJ dynamic global vegetation model. Glob. Change Biol. 2003;9:161–185. [Google Scholar]
- 32.Woodward FI, Williams BG. Climate and plant distribution at global and local scales. Vegetatio. 1987;69:189–197. [Google Scholar]
- 33.Smith B, et al. Implications of incorporating N cycling and N limitations on primary production in an individual-based dynamic vegetation model. Biogeosciences. 2014;11:2027–2054. [Google Scholar]
- 34.Bondeau A, et al. Modelling the role of agriculture for the 20th century global terrestrial carbon balance. Glob. Change Biol. 2007;13:679–706. [Google Scholar]
- 35.Gerten D, Schaphoff S, Haberlandt U, Lucht W, Sitch S. Terrestrial vegetation and water balance - hydrological evaluation of a dynamic global vegetation model. J. Hydrol. 2004;286:249–270. [Google Scholar]
- 36.Krinner G, et al. A dynamic global vegetation model for studies of the coupled atmosphere-biosphere system. Glob. Biogeochem. Cycles. 2005;19:GB1015. [Google Scholar]
- 37.Sato H, Itoh A, Kohyama T. SEIB-DGVM: a new dynamic global vegetation model using a spatially explicit individual-based approach. Ecol. Modell. 2007;200:279–307. [Google Scholar]
- 38.Liang J, et al. Positive biodiversity-productivity relationship predominant in global forests. Science. 2016;354:aaf8957. doi: 10.1126/science.aaf8957. [DOI] [PubMed] [Google Scholar]
- 39.Kattge J, et al. TRY-a global database of plant traits. Glob. Change Biol. 2011;17:2905–2935. [Google Scholar]
- 40.Jucker T, et al. Tallo: a global tree allometry and crown architecture database. Glob. Change Biol. 2022 doi: 10.1111/gcb.16302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Land Cover Classification Gridded Maps from 1992 to Present Derived From Satellite Observations (Copernicus Climate Change Service (C3S) Climate Data Store (CDS), accessed 24 March 2023); 10.24381/cds.006f2c9a
- 42.Goldberg DE. The distribution of evergreen and deciduous trees relative to soil type: an example from the Sierra Madre, Mexico, and a general model. Ecology. 1982;63:942–951. [Google Scholar]
- 43.Reichert JM, et al. Estimation of water retention and availability in soils of Rio Grande do Sul. Rev. Bras. Cienc. Solo. 2009;33:1547–1560. [Google Scholar]
- 44.Duong TTT, Penfold C, Marschner P. Amending soils of different texture with six compost types: impact on soil nutrient availability, plant growth and nutrient uptake. Plant Soil. 2012;354:197–209. [Google Scholar]
- 45.Yang J, et al. Leaf form-climate relationships on the global stage: an ensemble of characters. Glob. Ecol. Biogeogr. 2015;24:1113–1125. [Google Scholar]
- 46.Allen CD, et al. A global overview of drought and heat-induced tree mortality reveals emerging climate change risks for forests. Ecol. Manage. 2010;259:660–684. [Google Scholar]
- 47.Crowther TW, et al. Mapping tree density at a global scale. Nature. 2015;525:201–205. doi: 10.1038/nature14967. [DOI] [PubMed] [Google Scholar]
- 48.Gatti, R. C. et al. The number of tree species on Earth. Proc. Natl Acad. Sci. USA119, (2022).
- 49.Santoro, M. & Cartus, O. ESA Biomass Climate Change Initiative (Biomass_cci): Global Datasets of Forest Above-ground Biomass for the Years 2010, 2017 and 2018 v.3 (NERC EDS Centre for Environmental Data Analysis, 2021).
- 50.Karger DN, et al. Climatologies at high resolution for the earth’s land surface areas. Sci. Data. 2017;4:170122. doi: 10.1038/sdata.2017.122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Reich PB, et al. Even modest climate change may lead to major transitions in boreal forests. Nature. 2022;608:540–545. doi: 10.1038/s41586-022-05076-3. [DOI] [PubMed] [Google Scholar]
- 52.Elsen PR, et al. Accelerated shifts in terrestrial life zones under rapid climate change. Glob. Change Biol. 2022;28:918–935. doi: 10.1111/gcb.15962. [DOI] [PubMed] [Google Scholar]
- 53.Graham RL, Turner MG, Dale VH. How increasing CO2 and climate change affect forests. Bioscience. 1990;40:575–587. [Google Scholar]
- 54.Keenan T, Maria Serra J, Lloret F, Ninyerola M, Sabate S. Predicting the future of forests in the Mediterranean under climate change, with niche- and process-based models: CO2 matters! Glob. Change Biol. 2011;17:565–579. [Google Scholar]
- 55.Liang J, et al. Co-limitation towards lower latitudes shapes global forest diversity gradients. Nat. Ecol. Evol. 2022;6:1423–1437. doi: 10.1038/s41559-022-01831-x. [DOI] [PubMed] [Google Scholar]
- 56.Batjes NH, Ribeiro E, Van Oostrum A. Standardised soil profile data to support global mapping and modelling (WoSIS snapshot 2019) Earth Syst. Sci. Data. 2020;12:299–320. [Google Scholar]
- 57.Condit R, Engelbrecht BMJ, Pino D, Pérez R, Turnera BL. Species distributions in response to individual soil nutrients and seasonal drought across a community of tropical trees. Proc. Natl Acad. Sci. USA. 2013;110:5064–5068. doi: 10.1073/pnas.1218042110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Álvarez-Yépiz JC, et al. Resource partitioning by evergreen and deciduous species in a tropical dry forest. Oecologia. 2017;183:607–618. doi: 10.1007/s00442-016-3790-3. [DOI] [PubMed] [Google Scholar]
- 59.Aerts R. The advantages of being evergreen. Trends Ecol. Evol. 1995;10:402–407. doi: 10.1016/s0169-5347(00)89156-9. [DOI] [PubMed] [Google Scholar]
- 60.Ouédraogo D-Y, et al. The determinants of tropical forest deciduousness: disentangling the effects of rainfall and geology in central Africa. J. Ecol. 2016;104:924–935. [Google Scholar]
- 61.Chave J, et al. Towards a worldwide wood economics spectrum. Ecol. Lett. 2009;12:351–366. doi: 10.1111/j.1461-0248.2009.01285.x. [DOI] [PubMed] [Google Scholar]
- 62.Simard M, Pinto N, Fisher JB, Baccini A. Mapping forest canopy height globally with spaceborne lidar. J. Geophys. Res. Biogeosci. 2011;116:G04021. [Google Scholar]
- 63.Sitch S, et al. Recent trends and drivers of regional sources and sinks of carbon dioxide. Biogeosciences. 2015;12:653–679. [Google Scholar]
- 64.Pugh TAM, et al. Understanding the uncertainty in global forest carbon turnover. Biogeosciences. 2020;17:3961–3989. [Google Scholar]
- 65.Hansen MC, et al. High-resolution global maps of 21st-century forest cover change. Science. 2013;342:850–853. doi: 10.1126/science.1244693. [DOI] [PubMed] [Google Scholar]
- 66.Cayuela L, Granzow-de la Cerda Í, Albuquerque FS, Golicher DJ. Taxonstand: an R package for species names standardisation in vegetation databases. Methods Ecol. Evol. 2012;3:1078–1083. [Google Scholar]
- 67.Hengl T, et al. SoilGrids250m: global gridded soil information based on machine learning. PLoS ONE. 2017;12:e0169748. doi: 10.1371/journal.pone.0169748. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Gorelick N, et al. Google Earth Engine: planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017;202:18–27. [Google Scholar]
- 69.Strobl C, Boulesteix AL, Kneib T, Augustin T, Zeileis A. Conditional variable importance for random forests. BMC Bioinformatics. 2008;9:307. doi: 10.1186/1471-2105-9-307. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Simin C, Rongqun Z, Wenling C, Hui Y. Band selection of hyperspectral images based on Bhattacharyya distance. WSEAS Trans. Inf. Sci. Appl. 2009;6:1165–1175. [Google Scholar]
- 71.Ning J, Zhang L, Zhang D, Wu C. Interactive image segmentation by maximal similarity based region merging. Pattern Recognit. 2010;43:445–456. [Google Scholar]
- 72.Choi E, Lee C. Feature extraction based on the Bhattacharyya distance. Pattern Recognit. 2003;36:1703–1709. [Google Scholar]
- 73.El Merabet Y, et al. Maximal similarity based region classification method through local image region descriptors and Bhattacharyya coefficient-based distance: application to horizon line detection using wide-angle camera. Neurocomputing. 2017;265:28–41. [Google Scholar]
- 74.Li J. Assessing the accuracy of predictive models for numerical data: not r nor r2, why not? Then what? PLoS ONE. 2017;12:e0183250. doi: 10.1371/journal.pone.0183250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Bhattacharyya A. On a measure of divergence between two multinomial populations. Sankhyā Indian J. Stat. 1946;7:401–406. [Google Scholar]
- 76.Ma H, et al. The global distribution and environmental drivers of aboveground versus belowground plant biomass. Nat. Ecol. Evol. 2021;5:1110–1122. doi: 10.1038/s41559-021-01485-1. [DOI] [PubMed] [Google Scholar]
- 77.Breiman, L., Friedman, J., Stone, C. J. & Olshen, R. A. Classification Algorithms and Regression Trees (Chapman & Hall, 1984).
- 78.Hijmans, R. J. et al. Package geosphere (CRAN, 2019).
- 79.van den Hoogen J, et al. Soil nematode abundance and functional group composition at a global scale. Nature. 2019;572:194–198. doi: 10.1038/s41586-019-1418-6. [DOI] [PubMed] [Google Scholar]
- 80.Olson DM, et al. Terrestrial ecoregions of the world: a new map of life on Earth. Bioscience. 2001;51:933–938. [Google Scholar]
- 81.Tuanmu MN, Jetz W. A global 1-km consensus land-cover product for biodiversity and ecosystem modelling. Glob. Ecol. Biogeogr. 2014;23:1031–1045. [Google Scholar]
- 82.Heiberger, R. M. HH: Statistical Analysis and Data Display: Heiberger and Holland (CRAN, 2020).
- 83.Erin, L. et al. h2o: R Interface for the ‘H2O’ Scalable Machine Learning Platform. R package v.3.32.0.2 (GitHub, 2020).
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary Table 1 and Figs. 1–17.
Data Availability Statement
Tree occurrence data from the Global Forest Biodiversity initiative (GFBi) is available upon request via Science-I (https://science-i.org) or the GFBi website (https://www.gfbiinitiative.org/). Information on leaf habit (evergreen vs deciduous) and leaf form (broadleaved vs needle-leaved) came from the TRY database (https://www.try-db.org). Additional, leaf-type data came from the Tallo dataset (https://zenodo.org/record/6637599). Plot-level soil information came from the World Soil Information Service (WOSIS) dataset (https://www.isric.org/explore/wosis).
All code is available at 10.5281/zenodo.7967245.