Water Stress Deforms Tracheids Peripheral to the Leaf Vein of a Tropical Conifer

Abstract

Just as a soggy paper straw is prone to yielding under the applied suction of a thirsty drinker, the xylem tracheids in leaves seem prone to collapse as water potential declines, impeding their function. Here we describe the collapse, under tension, of lignified cells peripheral to the leaf vein of a broad-leaved rainforest conifer, Podocarpus grayi de Laub. Leaves of Podocarpus are characterized by an array of cylindrical tracheids aligned perpendicular to the leaf vein, apparently involved in the distribution of water radially through the mesophyll. During leaf desiccation the majority of these tracheids collapsed from circular to flat over the water potential range −1.5 to −2.8 MPa. An increase in the percentage of tracheids collapsed during imposed water stress was mirrored by declining leaf hydraulic conductivity (K_leaf), implying a direct effect on water transport efficiency. Stomata responded to water stress by closing at −2.0 MPa when 45% of cells were collapsed and K_leaf had declined by 25%. This was still substantially before the initial indications of cavitation-induced loss of hydraulic conductance in the leaf vein, at −3 MPa. Plants droughted until 49% of tracheids had collapsed were found to fully recover tracheid shape and leaf function 1 week after rewatering. A simple mechanical model of tracheid collapse, derived from the theoretical buckling pressure for pipes, accurately predicted the collapse dynamics observed in P. grayi, substantiating estimates of cell wall elasticity and measured leaf water potential. The possible adaptive advantages of collapsible vascular tissue are discussed.

Leaves employ the strong cohesive properties of water to do the work of pulling water from the soil to prevent leaf desiccation during gas exchange (Dixon and Joly, 1895). Of course this mode of water transport does not come without attendant costs, the most profound of which is the generation of hydraulic tension or negative pressure in the plumbing of vascular plants. The magnitude of this tension is generally large due to subzero soil water potential and substantial resistances to hydraulic flow through the vascular system of plants (Jeje and Zimmermann, 1979; Pockman et al., 1995). As such, it is common to measure hydraulic tensions (negative water potentials) of the order of −2 MPa in plants exposed to moderate water stress. In nonliving xylem cells conducting dilute sap, such tension will exert a large mechanical force on cell walls wherever they are bordered by air spaces. To place this force into perspective, if it were possible to reproduce a tension of −2 MPa inside a stainless steel tube it would be capable of crushing a pipe of 60 mm radius and 2 mm wall thickness.

To resist megapascals of crushing pressure across the cell wall, xylem conduits have evolved thick secondary walls incorporating lignin as a means of fortifying their tangential elastic modulus against collapse (Raven, 1977). However, given that both lignin and celluloses are costly to synthesize, it is likely that plants minimize xylem wall thickness and lignin content. Hence it is conceivable that only a narrow safety margin may prevent xylem collapse during normal transpiration and that under water stress, cell collapse may occur. Indeed, the collapse of fibers and tracheids by hydrostatic tension has long been recognized in the timber industry as a cause of deformation during the early seasoning of some dense hardwoods such as Eucalyptus (Tiemann, 1915; Cuevas, 1969). Whether or not xylem conduits ever collapse in living trees is an important question with profound implications for our understanding of the performance and evolution of the vascular system.

To date, physiological work on xylem dysfunction has focused almost exclusively on cavitation as the process responsible for reduced hydraulic efficiency in plants under water stress. The assumption is that increasing water tension in plants exposed to drying soil or elevated transpiration leads to cavitation of the water in xylem conduits before water potential falls sufficiently low to collapse cells. Indeed, several papers have specifically addressed this issue and concluded that xylem conduits of soft and hardwoods are twice as resistant to collapse as they are to cavitation (Hacke et al., 2001, 2004; Sperry and Hacke, 2004). However, recent work demonstrating xylem deformation under water stress in pine needles has suggested that these conclusions may not hold true for Pinus needles (Cochard et al., 2004). Cochard et al. (2004) showed good evidence that xylem tracheids in the vascular cylinder of Pinus nigra needles became crushed at low water potentials and that this deformation of cells would lead to a progressive decline in hydraulic efficiency.

Leaves are the obvious place to look for evidence of xylem dysfunction by collapse under hydrostatic tension. Leaves experience the lowest water potentials in the plant while containing a large proportion of air, thus creating conditions for maximum pressure differentials across xylem cell walls. Also it is commonly the case that leaf veins terminate in large collapse-prone tracheids with thin, highly pitted walls (Esau, 1977). Hence it could be imagined that the collapse of such cells under tension may explain observed patterns of midday depression of leaf hydraulic conductance (Brodribb and Holbrook, 2004a). The advantage of a collapse-mediated decline in leaf hydraulic conductivity is that once collapsed, only a small relaxation in the lumen water potential is required to restore hydraulic flow, assuming cell wall bending remains elastic. In contrast, the repair of embolized xylem conduits requires that leaf water potential increase to near atmospheric pressure or that metabolic energy is used to drive some (as yet unknown) refiling process.

In attempting to quantify the extent of tracheid cell collapse in living leaves we focus here on the leaves of a member of the genus Podocarpus, the most common conifer genus south of the equator. Podocarpus is an unusual genus that produces the largest of all conifer leaves (up to 45 × 300 mm) while relying on a single vein per leaf for hydraulic supply. Podocarpus leaves depend on a network of extravenous tracheids (Bucholtz and Gray, 1948; Griffith, 1957) called accessory transfusion tissue (ATT) that carry water radially from the midrib toward the leaf margin (Fig. 1). Tracheids in the ATT lie perpendicular to the leaf midrib and form an interconnected matrix between the palisade and the spongy mesophyll. This leaf anatomy is ideal for studies of cell collapse because the accessory transfusion tracheids are not surrounded by endodermis or bundle sheath cells and, as such, interface directly with airspaces in the leaf. Hence the walls of these tracheids are exposed to a pressure differential from atmospheric pressure in the airspaces to the negative water potential in the lumen. Also the accessory transfusion trachieds are round in cross section, aligned parallel, and show a minimum range in diameter, greatly simplifying the task of quantifying shape change due to crushing.

Figure 1.

A, Distal half of a 12-mm wide P. grayi leaf showing single vein. B, Fluorescence image of a paradermal section of leaf after infusion with Texas red. Tissues from left to right are leaf vein metaxylem (MX; red), transfusion tissue (TT; red), and ATT (yellow). Those ATT tracheids not containing dye appear blue due to lignin autofluorescence. C and D, Frozen cross sections of the leaf cut along the axis marked in B, showing ATT tracheids in blue (due to autofluorescence) and chlorophyll as red. Tracheids under small tensions appeared round in cross section (C) while those in water stressed leaves (D) became highly flattened. Scale bars in B = 200 μm and in C and D = 100 μm).

Here we examine the response of cell geometry and leaf hydraulic conductance to water potential to determine whether cell collapse is likely to interfere with water conduction under field conditions in this species. A structural mechanical model is used to predict theoretical collapse pressures for conduits, assuming they behave as cylindrical pipes. The model, based on Timshenko's equation relating pipe size and wall properties to buckling pressure, is applied to the measured dimensions of ATT tracheids in the leaves of Podocarpus specimens.

RESULTS

Tracheid Collapse

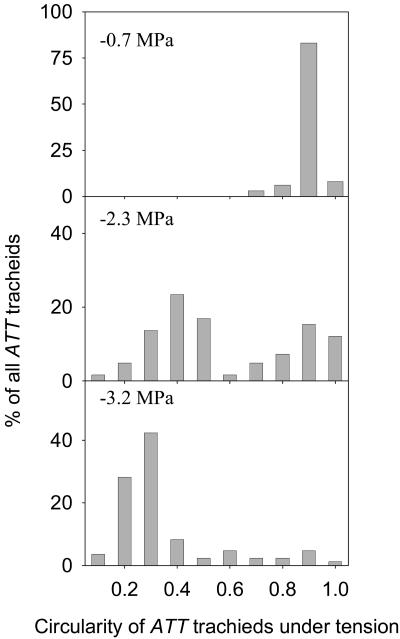
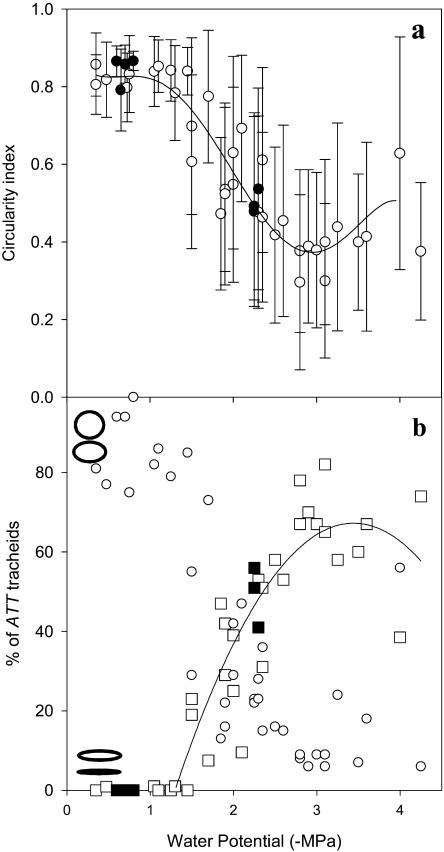
Declining leaf water potential had a marked effect on the geometry of ATT tracheids as quantified by the circularity index (C). At water potentials above −1.5 MPa very little conduit deformation was observed, with 75% to 92% of tracheids exhibiting a round geometry (C > 0.8), while no cells appeared flattened (Figs. 2 and 3). At water potentials below −1.5 MPa, however, a sharp increase in the proportion of collapsed cells led to a drop in the mean C (Fig. 3) of ATT tracheids in the leaf. A strongly bimodal distribution of cell geometries existed in leaves at between −1.5 and −2.8 MPa (Fig. 2) with >75% of cells either circular (C > 0.8) or flattened (C < 0.4). This led to a high sd in mean cell circularity for leaves dehydrated below −1.5 MPa. A better index of the impact of cell collapse on water transport capacity of the ATT is the percentage of collapsed (and presumably dysfunctional) tracheids (C < 0.4). The percentage of collapsed cells was found to increase steeply as Ψ_l dropped below −1.5 MPa, saturating at −3.0 MPa (Fig. 3B). The percentage of uncollapsed cells mirrored this trend, indicating again that cell geometries tended to be collapsed or uncollapsed with few intermediates (Fig. 3B). Leaves dehydrated below −3 MPa showed a small decline in the percentage of collapsed cells presumably due to some cavitation of cells allowing a relaxation in the cell wall to an uncollapsed state.

Figure 2.

Distributions of ATT tracheid cross-sectional geometry using a circularity index (C) that describes perfectly round cells as 1 and approaches zero as cells become flattened. At low tension (−0.7 MPa) nearly all cells were round while at high tension (−3.2 MPa) cells were mostly flattened. At intermediate tensions (−2.3 MPa) the frequency distribution of tracheid circularity was always strongly bimodal with 75% of cells either round (C ≥ 0.8) or strongly flattened (C ≤ 0.4). The three distributions shown are from representative leaves at the pressures shown (n = 140–150 tracheids/leaf).

Figure 3.

A, Mean values (±sd; n = 140) of ATT tracheid C for 40 leaves desiccated to a range of water potentials. A polynomial curve is fitted to the data indicating the decline in C at water potentials below −1 MPa to a minimum at −2.8 MPa followed by a small increase in C below −2.8 MPa, probably indicating initial cavitation. Very large sds indicate the bimodal distribution of tracheid shape. Values from whole plants droughted to −2.3 MPa and then rewatered are shown as black circles. B, Increasing percentage of collapsed ATT tracheids (C ≤ 0.4; squares) and decreasing percentage of uncollapsed tracheids (C ≥ 0.8; circles) in the same leaves as A. Leaves from droughted trees are shown as black squares. Ellipses at the left end of the graph show the range of shapes within the uncollapsed (top) and collapsed (bottom) catagories.

Leaves frozen in situ while attached to trees exhibited identical behavior to those detached prior to desiccation. One sample tree was subjected to drought by withholding water, and after 3 weeks of drought, leaves were found to be at −2.25 to −2.3 MPa and stomata remained closed during the day. Tracheid collapse was observed at 49% ± 8%, which recovered to 0% 1 week after rewatering (Fig. 3).

Occasional sectioning of tracheids in the midvein of leaves suggested that this xylem tissue was not prone to collapse (T.J. Brodribb, unpublished data).

Leaf Vulnerability and Stomatal Function

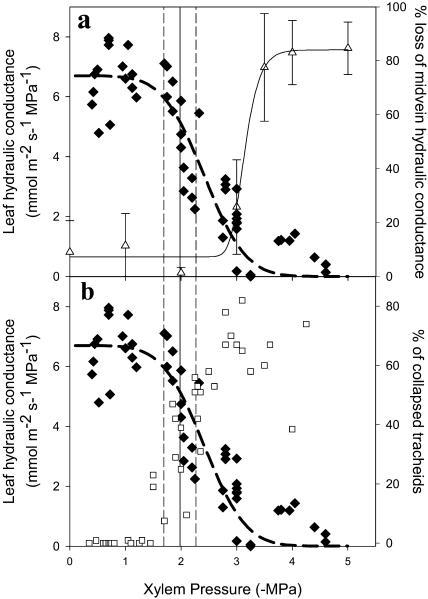
Leaf hydraulic conductance declined rapidly from a mean maximum of 6.7 mmol m⁻² s⁻¹ MPa⁻¹ in leaves above −1.8 MPa to less than 1 mmol m⁻² s⁻¹ MPa⁻¹ in leaves at water potentials more negative than −3.0 MPa (Fig. 4). The leaf vein was found to be substantially more resistant to dysfunction under simulated xylem tension than the leaf lamina, illustrating a transition from 24% to 80% loss of hydraulic conductance over the range −3 to −4 MPa (Fig. 4A). Tracheid collapse on the other hand was much better correlated with the loss of whole-leaf hydraulic conductance. Declining K_leaf was closely mirrored by the increase in the percentage of collapsed tracheids in the ATT (Fig. 4B).

Figure 4.

A, The response of leaf hydraulic conductance: K_leaf (black diamonds) and percentage loss of leaf-vein hydraulic conductance (white triangles) to leaf water potential. Mean water potential (±sd; n = 8) at stomatal closure is indicated by a vertical line (sd by dotted lines) showing that stomata closed after a 25% loss of K_leaf and significantly in advance of any cavitation in the vein xylem. B, Comparison of the response of K_leaf and percentage collapse of ATT tracheids (white squares) to water potential during leaf desiccation. Strong correspondence between hydraulic conductance and cell collapse suggest a causal relationship. Stomatal closure corresponded with a 45% collapse rate of tracheids.

Stomatal conductance responded to a range of water potentials depending on the humidity to which leaves were exposed during desiccation. Despite this, the water potential resulting in 90% stomatal closure was consistent among all replicates, occurring at a mean water potential of −2.0 ± 0.25 MPa. This number was also independent of the rate of desiccation and the time after cutting from the tree (T.J. Brodribb, unpublished data). The timing of stomatal closure corresponded with the early stages of tracheid collapse (45%) and the initial decline of K_leaf (25% depression). The water potential of 90% stomatal closure did not appear related to the vulnerability of the vein xylem (Fig. 4A).

Tracheid Dimensions and Structural Modeling

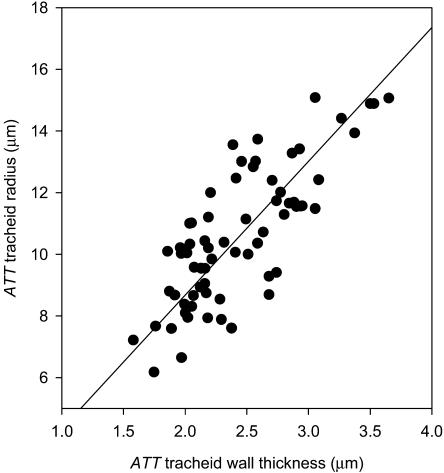
Tracheid wall thickness and cell radius were highly correlated in the ATT (r² = 0.61; P < 0.001). Tracheid cell sizes ranged from a minimum diameter of 12 μm to a maximum slightly over 30 μm (Fig. 5). A similar range of tracheid diameters was observed in the midvein xylem where the largest cells were 24 μm (data not shown). Pitting in ATT tracheids was found to be frequent in cells bordering spongy mesophyll, while among the bulk of tracheids only endwalls were densely pitted. Lateral walls exhibited single rows of pits in regions of contact between tracheids.

Figure 5.

Relationship between the cell radius and cell wall thickness of ATT tracheids (n = 80) from five leaves. Wall thickness and cell radius varied in proportion over the range of cell sizes. A highly significant linear regression is fitted (r² = 0.61; P < 0.001).

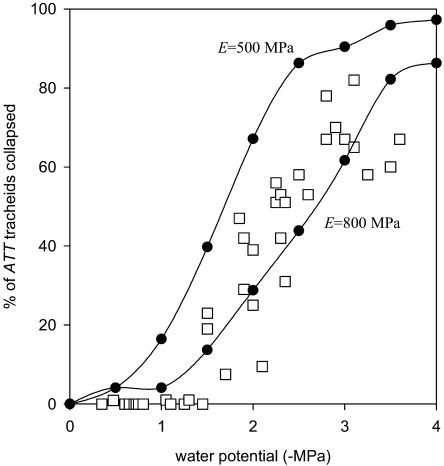
By treating tracheids as pipes (ignoring areas of structural weakening such as pitted regions of the wall) it was possible to estimate the collapse behavior of a representative sample of 80 tracheids using the theoretical buckling pressure given in Equation 2. The predicted distribution of collapse pressures (assuming no cavitation in tracheids) was very close to the observed pattern when an elastic modulus of M = 800 MPa was used for the tracheid wall (Fig. 6). The lower value of 500 MPa for M underestimated the wall strength, predicting cells to collapse at less negative water potentials.

Figure 6.

Observed versus modeled cell collapse of ATT tracheids in P. grayi. Observed collapse data are the same as shown in Figure 3B (squares) while modeled values are shown as curves. Cell wall elastic modulus is unknown for tracheids, and hence two values for the radial modulus of Picea abies green wood are used for comparison. The larger of these estimates appears to be close to the real value for the tracheids observed here.

DISCUSSION

The collapse of tracheids under water tension is shown here to be an important feature of the physiology of the conifer Podocarpus grayi. The tracheids prone to collapse (ATT) were those occurring outside the leaf vein and were involved in the delivery of water radially from the vein toward the leaf margin. It is significant to note that a great many gymnosperms, particularly those in the southern hemisphere, possess similar accessory xylem either in the form of ATT (Podocarpaceae and Cycas) or as elongate idiosclerieds oriented radially (Papuacedrus) or parallel (Agathis) to the leaf vein. Given that xylem in the needles of several Pinus species has also recently been shown to collapse under tension (Cochard et al., 2004), it appears that this feature may dictate the limits of water supply to many gymnosperm leaves.

The data presented strongly suggest that the collapse of ATT tracheids in P. grayi is likely to have directly caused the decline in K_leaf in this species. The pattern of decreasing K_leaf in P. grayi under water stress closely matched the percentage of tracheids observed to be collapsed in the ATT (Fig. 4B). Hydraulic flow through tracheids crushed to the collapsed category (geometrically defined by a value of C < 0.4) would be <6% of the conductance of uncollapsed conduits (assuming that tracheids collapse into an ellipse shape), effectively deactivating them as water-conducting tissues. Deactivation of the ATT by cell collapse must greatly impede the flow of water through the leaf as a whole, given that water would be forced to travel many thousands of microns through nonspecialized cells before reaching the sites of evaporation. For this reason it is not surprising that stomatal closure in P. grayi was correlated with the process of cell collapse rather than the subsequent process of xylem cavitation in the midrib (Fig. 4A).

Interestingly, we found stomatal closure in response to leaf desiccation to occur midway through the loss of K_leaf and tracheid collapse (Fig. 4, A and B). Closure of stomata after the onset of xylem dysfunction has been shown to occur in some tropical angiosperms but appears to require some sort of refiling process to repair embolized xylem (Bucci et al., 2003; Brodribb and Holbrook, 2004a). It was imagined that conifers might display more conservative stomatal regulation similar to ferns, which close their stomata before the onset of xylem dysfunction (Brodribb and Holbrook, 2004b). Such apparently risky behavior in conifers may be enabled by the large capacitance typically displayed by conifer leaves (Brodribb et al., 2005).

In fact it may be the case that the collapse of ATT tracheids is an adaptive means of regulating leaf water potential without risking embolism. Being a mechanical process, the collapse of tracheids is likely to release the bulk of the lumen water over a small range of water potentials (i.e. at the point of buckling of the cell wall). Given that most tracheids buckled under a tension of 1.5 to 2.5 MPa, this would provide a specific capacitance to the leaf over the water potential range of stomatal closure. From cross sectional area measurements we calculated that an average of 2,300 mmol m⁻² of water was present in nondeformed ATT tracheids. This is a significant volume when it is considered that only 1,450 mmol m⁻² is required to hydrate an average P. grayi leaf from −2 MPa to 0 MPa (T.J. Brodribb, unpublished data). Under conditions of rapidly declining vapor-pressure difference, the release of ATT water during collapse of cells would significantly delay water potential decline in the leaf, given that maximum rates of E in P. grayi were close to 1 mmol m⁻² s⁻¹ (T.J. Brodribb, unpublished data). This might provide a water potential buffer, enabling complete stomatal closure before leaf water potential is allowed to fall to a point where vein (or stem) embolism is initiated. Such a process would be energetically preferable to a system of diurnal embolism and refiling because, unlike conduit embolism, tracheid collapse appears to be readily reversed once water supply is reestablished (Fig. 3) making for a cost-free recovery of K_leaf post stress. A system of collapse-dependent capacitance may be important in a great many leaves of both conifers and angiosperms, given that many species from both groups possess nonliving lignified tissues outside the leaf vascular bundle (Esau, 1977).

Collapse of tracheid cells in the leaf attests to the existence of large negative pressures in the xylem. Although the application of Equation 2 should accurately predict collapse pressures in tubes, there is some uncertainty in the magnitude of the elastic modulus for the tracheid wall and the weakening effect of pitting. Although the presence of (unbordered) pits in the walls of ATT tracheids reduces its resistance to crushing, SEM examination revealed that only a small percentage of the tracheids measured were sectioned through the pit aperture. Hence most of the cells observed were of uniform wall thickness and, as such, should adhere to the buckling equation (2) used here (Timoshenko, 1930). Other considerations such as imperfections in circular (unstressed) geometry might also reduce the resistance to collapse. However, the close agreement between observed and predicted cell collapse suggests that an elastic modulus of 800 MPa is a good estimate for these individual tracheids (Fig. 6). Xylem cells arranged in matrices of ±rectangular cells would be likely to be more resistant to collapse due to the reinforced geometry of the xylem (Hunter, 2001) as well as the probable exclusion of air from around many cells. This perhaps explains why collapse was not observed in the leaf vein of P. grayi.

In many plant groups including conifers, cycads, and many angiosperm families, the final delivery of water from xylem cells to mesophyll tissue takes place through lignified cells with large lumens and highly developed pitting. It is these cells, rather than the xylem in vascular bundles that seems most prone to dysfunction by collapse. Their irregular geometry, proximity to air spaces, and exposure to the highest tensions in the plant make their cell walls prone to buckling, but by the same token, their geometry will also make collapse difficult to observe under tension. On the other hand these cells may also be prone to cavitation, alleviating hoop stress on the cells prior to collapse. Whatever the story, we believe more attention should be focused upon tracheids within the leaf if we are to achieve a better understanding of the delivery of water to leaves under tension.

MATERIALS AND METHODS

Plant Material

All measurements were carried out on two 8-year-old specimens of Podocarpus grayi grown from seed under ambient glasshouse conditions (temperature range 5°C to 36°C, maximum light intensity 950 μmol m⁻² s⁻¹) at the University of Tasmania, Hobart. Although the genus Podocarpus is found throughout the southern hemisphere in moist forest and subalpine scrub, P. grayi is restricted to the far northeast of Australia where it grows as a small subcanopy tree in rainforest from sea level to approximately 600-m altitude. Leaves of P. grayi are linear, typically 80 to 150 mm in length and 10 to 15 mm in diameter with only a single midrib for venation.

Leaf Hydraulic Conductance

Leaf hydraulic conductance (K_leaf) was measured using a leaf rehydration technique (Brodribb and Holbrook, 2003). The advantage of this technique is that hydraulic conductances of leaves can be measured under tension, thus allowing the possible effects of xylem crushing to be assessed. Fifty leaves were detached from the two study plants and dehydrated on the laboratory bench for periods ranging from 10 min to 2 d resulting in a range of water potentials from −0.4 MPa to −4.6 MPa. Leaves were cut in half such that one half was used for an initial reference water potential (Ψ_o) and the other half rehydrated and measured to give the final water potential (Ψ_f ). Rehydration times were typically between 50 and 200 s and managed in such a way as to produce a drop in water potential of 3 to 5 bars. Water potentials were measured using a Scholander pressure chamber (PMS Instrument, Corvallis, OR) and leaf hydraulic conductance calculated from the equation:

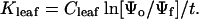(1)

Mean leaf capacitance (C_leaf) for each species was measured from six fully expanded leaves using the slope of the leaf pressure-volume relationship (PV; Tyree and Hammel, 1972). Branches were cut underwater in the morning and rehydrated until Ψ_leaf was > −0.05 MPa, after which leaves were detached for determination of PV relations on the leaf tissue. Leaf weight and water potential were measured periodically during slow desiccation of sample leaves in the laboratory. The initial (linear) slopes of the relative water content (RWC) versus Ψ_leaf curves yielded the leaf capacitance function in terms of RWC. Calculation of K_leaf (mmol m⁻² s⁻¹ MPa⁻¹) requires that leaf capacitance be calculated in absolute terms and normalized by leaf area. To do this, the capacitance calculated from the PV relationship was multiplied by the saturated mass of water in the leaf and then divided by leaf area (Koide et al., 1991; Brodribb and Holbrook, 2003). Leaf areas were measured as projected areas with a digital camera and the public domain NIH ImageJ program (developed at the United States National Institutes of Health and available on the Internet at http://rsb.info.nih.gov/nih-image).

Midrib Hydraulic Vulnerability

Five leaves were excised under water and two longitudinal cuts made parallel to the midrib (5 mm either side) along the length of the leaf. These cuts were designed to minimize resistance to radial leakage of water out of the midrib during flow measurements. Leaves were attached to a steady-state flow meter (Zwieniecki et al., 2000) and the resistance to the flow of a 0.01 m KCl solution under a small positive pressure was measured for each sample leaf. The initial hydraulic conductance (flow/pressure gradient) of the midrib was calculated using the length of the segment. The cut end of the midrib was then placed into a pressure bomb and pressurized to 1 MPa for 10 min while the rest of the leaf remained outside the chamber. Five mm of the proximal end of the petiole was then excised under water and hydraulic conductance remeasured. This process was repeated in 1 MPa steps up to 5 MPa for each leaf, and the hydraulic conductance was expressed as a percentage of the maximum for each leaf midrib.

Xylem Collapse

Twenty-five leaves from each of the two P. grayi individuals were cut from trees during the morning while plants were hydrated and allowed to dry for different periods to yield a range of leaf water potentials from −0.35 MPa to −4MPa. For each leaf specimen, leaf water potential was determined by cutting off the lower third of the leaf for pressure bomb measurement while the upper two-thirds of the leaf were sealed in plastic bags to prevent further water loss and used for microscope examination. The proportion of collapsed cells was determined on leaves snap frozen in liquid nitrogen to preserve the tissue conformation under tension. Leaves were placed into a small aluminum specimen holder and submerged in liquid nitrogen. Each leaf was then trimmed to about 20 mm in length and placed in a shallow polystyrene well such that the leaf remained submerged in liquid nitrogen. The ATT runs perpendicular to the midrib, so leaves were cut 5 mm from the margin, parallel to the midrib to expose the ATT tracheids in cross section. Sectioned leaves were examined at 20× magnification under a fluorescence microscope (Axioscop, Carl Zeiss, Oberkochen, Germany) while still partially submerged in liquid nitrogen, and photographed using a digital camera (Axiocam, Carl Zeiss) attached to a photographic tube.

Ten images per leaf were taken at approximately 2-mm intervals along the 20-mm leaf section, each containing approximately 15 tracheids. Tracheid outlines were later traced in Adobe Photoshop (Adobe Systems, Mountain View, CA) and transferred to ImageJ for analysis. Degree of cell collapse was expressed as a C described by Equation 1.

(1) C = 4 π (a/p²), where a = tracheid cross-sectional area and p = tracheid cross-sectional perimeter. The resulting parameter ranges from 1 in a perfect circle toward zero as the circle becomes squashed.

Circularity data were first analyzed as a mean value per leaf (±sd, n = 150); however, geometries were found to exhibit a strongly bimodal distribution of highly collapsed or uncollapsed cells. For this reason the percentage of collapsed cells (C < 0.4) and uncollapsed cells (C > 0.8) was also calculated for each leaf sample.

To test whether collapse occurred while leaves were attached to the tree, a single tree was left unwatered for 3 weeks to simulate drought. Once leaf water potential had dropped sufficiently to prevent stomatal opening during the day (−2.3 MPa), three leaves were dipped into liquid nitrogen while attached to the tree and harvested for shape analysis as above. The tree was then rewatered and, once photosynthesis had recovered to 90% of predrought levels, another three leaves were frozen on the plant and harvested for tracheid shape determination.

Stomatal Closure

Leaf water potential at stomatal closure was determined on detached leaves under a range of evaporative gradients to test the consistency of the stomatal response to leaf water potential (Brodribb and Holbrook, 2004a). Five leaves from each tree were detached and hydrated overnight in moist plastic bags. Next morning leaves were placed under lights (200 μmol photons m⁻² s⁻¹) above a water bath at 40°C to create a stable leaf temperature of 30°C and a relative humidity range from 30% to 80%. Leaf mass was measured every 5 to 10 min on a digital balance. E typically fell after 2 to 3 h due to stomatal closure. Once E had stabilized at a minimum rate (g_s < 5 mmol m⁻² s⁻¹ as measured with a porometer) for at least 2 h, leaves were placed in a drying oven at 70°C for a week, and dry weight measured. Plots of E versus time generally showed clear transitions from declining E to stable minimum E (assumed to be 100% closed stomata), and the water potential at this transition was calculated from the previously established relationship between RWC and Ψ_leaf. The water potential at stomatal closure (Ψ_sc) was defined as the leaf water potential at which E was reduced by 90% from the E maximum recorded with stomata open. Three additional leaves were dehydrated as above, until E reached 10% of the maximum, at which point leaves were placed in plastic bags and Ψ_sc measured directly with a pressure chamber.

Tracheid Dimensions

A sample of five leaves were hydrated and sectioned 3 mm from the margin to expose the ATT in cross section as above. These sections were then serially dehydrated in alcohol and placed in an automated critical point drier where they were dried and gold coated. Samples were then examined under an ESEM (Quanta 200, Philips, Eindhoven, The Netherlands) and 30 images of ATT tracheids were photographed at 1,500× magnification along the length of the five sample sections. Images were then analyzed using graphics software to measure cell diameter and cell wall thickness of 80 ATT tracheids.

Modeling Tracheid Collapse

In hydrated leaves the ATT tracheids were very close to circular in cross section with only small regions of contact between cells. Hence in this case tracheid geometry approximates a cylindrical tube (rather than a deflecting plate as is the case with neighboring vessels; Hacke et al., 2001). The pattern of ATT tracheid collapse under tension was modeled using Timoshenko's equation (2) for pipe buckling under pressure as the basis for predicting the water potential at which tracheids should deform.

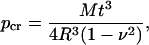(2)

where p_cr = theoretical collapse strength for a round tube; M = elastic modulus (MPa); v = Poisson ratio; R = tracheid diameter; and t = wall thickness. Due to the complex anisotropic nature of the xylem secondary cell wall, the best approximation for the elastic modulus of tracheids is to use the radial modulus for compression of green wood (Innes, 1995). Such data are unavailable for any species of Podocarpus, and hence we used two values to indicate the likely range within which ATT tracheids fell. The low end of the range (500 MPa) was for Picea abies wood (Guitard, 1987), while the upper end (800 MPa) was an estimate for the elastic modulus of tracheid cells based on the structural model using properties of the S layers of a cell with a 2-μm-thick secondary wall (Bergander and Salmén, 2002). The Poisson ratio for lignin (0.28) was used (Innes, 1995) while R and t were taken from the survey of 80 cells described above.

For each of the 80 cells surveyed, a critical collapse pressure (P_cr) was predicted from Equation 2. This range of pressures was taken to represent the mean behavior of tracheids in the leaf and used to model the progress of cell collapse in response to decreasing leaf water potential. This modeled response was then compared with direct observations of frozen leaves described above.

Statistical Analysis

When present, curves were fitted to the data to show pattern rather than mechanism, and hence best fit models were adopted. For K_leaf vulnerability a cumulative normal distribution was fitted as described previously (Brodribb and Hill, 1999). Stem vulnerability was best described by a sigmoid function, while collapse data were best fitted by polynomial functions. All statistical analyses were performed using JMP software (SAS Institute, Cary, NC).