Abstract
In the ongoing pursuit of novel and efficient NLO materials, the potential of alkali metal-doped {6}cycloparaphenylene ({6}CPP) and methylene bridged {6} cycloparaphenylene (MB{6}CPP) nanohoops as excellent NLO candidates has been explored. The geometric, electronic, linear, and nonlinear optical properties of designed systems have been investigated theoretically. All the nanohoops demonstrated thermodynamic stability, with remarkable interaction energies reaching up to −1.39 eV (−0.0511 au). Notably, the introduction of alkali metals led to a significant reduction in the HOMO-LUMO energy gaps, with values as low as 2.92 eV, compared to 6.80 eV and 6.06 eV for undoped {6}CPP and MB{6}CPP, respectively. Moreover, the alkali metal-doped nanohoops exhibited exceptional NLO response, with the K@r6-{6}CPP complex achieving the highest first hyperpolarizability of 56,221.7 × 10−30 esu. Additionally, the frequency-dependent first hyperpolarizability values are also computed at two commonly used wavelengths of 1550 nm and 1907 nm, respectively. These findings highlight the potential of designed nanohoops as promising candidates for advanced NLO materials with high-tech applications.
Keywords: {6}Cycloparaphenylene, Methylene bridged {6}cycloparaphenylene, Density functional theory (DFT), Nanohoops, Nonlinear optical
Graphical abstract

Highlights
-
•
Alkali metals doped nanohoops have been investigated for better NLO response.
-
•
All complexes are stable, with interaction energies up to −1.39 eV.
-
•
Non-covalent interactions are confirmed through NCI & QTAIM analyses.
-
•
K@r6-{6}CPP has exhibited the highest first hyperpolarizability of 56,221.7 × 10−30 esu.
-
•
Frequency dependent analysis and βHRS also reflect their high NLO response.
1. Introduction
The emergence of nonlinear optical (NLO) materials can be traced back to the realization of the frequency doubling phenomenon achieved through the interaction of electromagnetic radiations with a non-centrosymmetric material [1]. Over time, the fabrication of materials with a large NLO response has gained tremendous importance due to their multiple applications in different fields, including optical computing, data storage [2], molecular switches [3], laser technology [4], telecommunication [5] and biological imaging [6]. Different strategies have been proposed to amplify the NLO response, such as extended π-electron system [7], a donor acceptor π conjugated system [8], bond length alternation (BLA) [9], diradical character [10], and the introduction of diffuse excess electrons [11]. Nowadays, the diffuse excess electron strategy has proven to be an efficient way to enhance NLO response of materials [12]. These excess electrons may lead to an increase in hyperpolarizability in resulting electrides [13], metalides [14], alkalides [15], and alkaline earthides [16]. Over the last two decades, metal doping has emerged as a promising strategy for introducing excess electrons to enhance the NLO response of both organic and inorganic systems.
Organic NLO materials have gained significant attention due to their low cost, less toxicity, simple processing, nonlinearity [17,18] and fast response [19,20] in contrast to inorganic ones. In this regard, Dye and coworkers carried out successful synthesis of an organic cavity based alkalide in 1974 [21]. They have also synthesized K+(Me6Aza222)Na− and K+(Me6Aza222)K− alkalides which are stable at room temperature. Similarly, Redko et al., achieved the synthesis of the Ba2+(H5Azacryptand [2.2.2]−)Na−, a barium-based sodide, thereby expanding the scope of research within the realm of nano-sized cavity based materials [22]. In another study, Li doped calix{4}pyrrole electride has exhibited the highest first hyperpolarizability (βo) as compared to the pristine calix{4}pyrrole [23]. The alkali metals doped six-membered cyclic thiophene (6CT) has shown a βo value of 4 × 104 au for Na@6CT as compared to 2 × 102 au for pristine 6CT [24]. Similarly, the NLO response of alkali metals (AM=Li, Na and K) doped graphene (GE), graphyne (GY) and graphdiyne (GDY) was evaluated, and the results illustrated exceptionally high βₒ values (8.57 × 104 to 3.93 × 105 au) for AM@GDY as compared to AM@GE and AM@GY [25].
In the search for novel organic systems, scientists have uncovered a class of structurally tunable cyclic organic compounds known as cycloparaphenylenes (CPPs) or nanohoops. These nanohoops contain fully conjugated benzenes in various sizes [26]. Furthermore, they exhibit strain [27] and size-dependent optoelectronic [28], photophysical [29] and host-guest properties due to π-electron density, or cyclic π-conjugation [30]. These properties have rendered them as a class with emerging applications in electronics [31], bioimaging/fluorophores [32], as building blocks of carbon nanomaterials [33] and supramolecular chemistry [34]. Within this category, a specific subclass known as {6}cycloparaphenylene ({6}CPP) has been synthesized, exhibiting a tubular packed structure similar to nanotubes and featuring a nano-sized cavity [35]. Notably, {6}CPP possesses a distinctive benzenoid structure characterized by significantly bent benzene rings. This molecule has potential applications in material science, sensors, capturing of pollutant gases [36], fabrication of fluorescent system [37], energy absorption and thermal insulation [38].
Recently, a non-alternative aromatic belt shaped, crystal packed, methylene bridged {6}cycloparaphenylene (MB{6}CPP) has also been synthesized [39]. Its structure comprises alternating five- and six-membered rings. The presence of methylene bridges co-planarizes the neighboring phenylene units, resulting in a high degree of π-conjugation. The nanohoops exhibit a unique size/aromaticity dependent NLO behavior; specifically, there is an increase in the third order NLO behavior with decrease in aromaticity [40].The NLO study on bipyridine-{8}CPP has shown a 3.8 times larger βₒ value after the incorporation of the transition metal Pd(II) as compare to pure bipyridine-{8}CPP [41]. Furthermore, the introduction of electron donor and acceptor groups in CPPs has resulted the highest βHRS value of 11.6 × 10−30 esu for –NH2 and 7,7,8,8-tetracyanoquinodimethane (TCNQ) substituted moieties [42]. Additionally, the CPP molecular lemniscular (CPPL) and its derivatives have exhibited the highest βHRS value of 34.99 × 10−30 esu for the structure with a combination of donor-acceptor (NO2, NH2) [43]. In a recent work, pristine and halogen (F, Cl and Br) substituted CPPs have been examined via DFT simulations and it was revealed that the halogen-substituted CPPs have exhibited a remarkable increment in their NLO response in terms of first order hyperpolarizability tensors values [44].
Various studies have revealed that cyclic and bent conjugated macromolecules exhibit tunable optical behavior distinct from their linear counterparts [[45], [46], [47]]. Therefore, the idea of investigating the NLO properties of {6}CPP and MB{6}CPP is highly intriguing. Guided by the merits of cyclic and bent molecules, our aim is to theoretically explore the exohedrally and endohedrally alkali metals doped {6}CPP and MB{6}CPP. This investigation will focus on the geometric, electronic and NLO properties of these nanohoops. The primary goal of this study is to assess the NLO potential of alkali metals doped nanohoops, with the aim of utilizing them for the fabrication of advanced NLO materials in the future.
2. Computational methodology
Geometry optimization of pristine and alkali metals doped {6}CPP and MB{6}CPP are carried out at ωB97XD/6-31G (d, p) level of theory. The ωB97XD is a highly reliable, full range separated, widely used dispersion corrected DFT method and results in satisfactory accuracy for thermochemistry and kinetics [48]. Full range separated functionals possess the correct 1.00 fraction of nonlocal exchange. Previous studies have demonstrated that a full range separated functional exhibits nonlinear optical properties comparable to those calculated using highly accurate methods [49,50]. It is widely used for accurate calculations of hyperpolarizability [51], non-covalent interaction energies [52] and potential energy surfaces [53]. Moreover, frequency analysis is also performed at the same level of theory to confirm that theses optimized structures correspond to true minima (absence of imaginary frequency). Interaction energies (Eint), natural bond orbital (NBO) analysis, HOMO-LUMO energy gaps and vertical ionization energies (VIE) are also computed at the same level of theory. In addition, density of state (DOS), quantum theory of atoms in molecules (QTAIM) and non-covalent Interaction (NCI) analyses are also performed and visualized by Multiwfn [54] and VMD [55] software programs.
The interaction energy to predict the thermal stability of doped moieties is defined as;
| (1) |
| (2) |
where (EM@ {6}CPP, EM@MB {6}CPP), EM and (E{6}CPP, EMB{6}CPP) are the total electronic energies of the doped molecules, the alkali metal and the undoped species respectively.
The HOMO-LUMO energy gap (EH-L) of doped systems are calculated as
| (3) |
where the EH is the energy of HOMO and EL is the energy of LUMO.
The time dependent-density functional theory (TD-DFT) calculations are performed at TD-ωB97XD/6-311+G(d) level of theory to evaluate the absorption spectra of all complexes. Moreover, the polarizability (α), static and dynamic hyperpolarizability (βo, βvec and βHRS) are carried out at ωB97XD/6–311++G (2d, 2p) level of theory [56].
The dipole moment, static polarizability and first hyperpolarizability are described as
| (4) |
| (5) |
| (6) |
where , , .
The βvec is denoted as:
| (7) |
The frequency dependent NLO response in terms of the second harmonic generation (SHG) β(−2ω, ω, ω) and the electro-optical Pockels effect (EOPE) β(−ω, ω, 0) are calculated at two standard Nd:YAG laser frequencies: 1550 nm and 1907 nm by using coupled-perturbed SCF method.
The dynamic (frequency dependent) first hyperpolarizability can be represented by using the following equation:
| (8) |
The hyper-Rayleigh scattering (βHRS) values are estimated from the following equation:
| (9) |
All the calculations are performed by using GAUSSIAN 16 [57] software package and the results are viewed by GaussView 6.1.1 [58] software.
3. Results and discussion
3.1. Geometrical parameters
Pristine {6}CPP has D3d symmetry and ring shaped benzenoid structure (containing six membered rings). The calculated diameter of this CPP is 8.06 Å, while the C–C bond length connecting the benzene rings (b66) is about 1.49 Å, consistent with the reported one [35]. Moreover, the dihedral angle between the adjacent benzene rings is 31.5°. All of these parameters are mentioned in Table 1. Furthermore, the averaged bond lengths of C–H and C–C bonds are 1.08 Å and 1.39 Å, respectively. The MB{6}CPP has C1 symmetry and a diameter of 7.78 Å, which is smaller than {6}CPP. The phenylene units connected by methylene bridges resulted in the decrease in diameter with condensed belt structure. Moreover, the methylene bridging has increased its structural conjugation. In addition, for MB{6}CPP, the calculated values of dihedral angle between the adjacent phenylene units and the C–C bond (b56) are 0.0° and 1.48 Å, respectively, and are in consistent with the previously reported literature [39]. The C–H and C–C averaged bond lengths are 1.08 and 1.39 Å, respectively. The optimized structures of both CPPs are shown in Fig. 1.
Table 1.
Geometrical parameters of {6}CPP and MB{6}CPP.
| Compound | Diameter (Å) | Dihedral angle (◦) | C–C (Å) | C–C (Å) of benzenoid (Average) | C–H (Å) of benzenoid (Average) |
|---|---|---|---|---|---|
| {6}CPP | 8.06 | 31.5 | 1.49 | 1.39 | 1.08 |
| MB{6}CPP | 7.78 | 0.00 | 1.48 | 1.39 | 1.08 |
Fig. 1.
Optimized geometries of {6}CPP and MB{6}CPP.
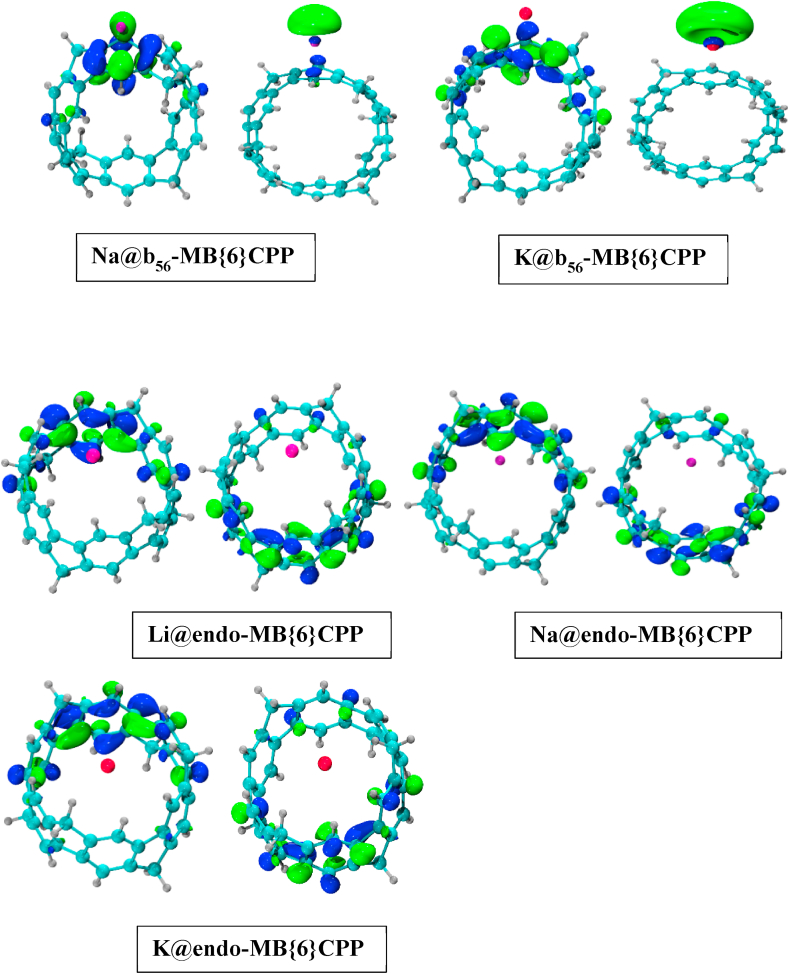
In the present work, these two substrates including {6}cycloparaphenylene ({6}CPP) and methylene bridged {6}cycloparaphenylene (MB{6}CPP) nanohoops have been doped with alkali metals (Li, Na and K) to tune their NLO responses. All the possible doping positions including two exohedral i.e., r6 (above the center of six membered ring), b66 (at the bond between two hexagonal rings) and endohedral at center of the substrate are explored for {6}CPP. After optimization, some of these structures converged to other structures. Two most stable positions are obtained for metals doped {6}CPP complexes including M@r6-{6}CPP (exohedral) and M@endo-{6}CPP (endohedral). In case of exohedral complexes, the r6 position is the stable one as six carbon atoms are interacting with the alkali metal atoms from all sides as compared to the b66 where metal atom interacts with only two carbon atoms at the bonding region. The interaction of decorated alkali metals with the {6}CPP has reduced the interaction distance of metal atoms with the C atoms of the {6}CPP. For M@endo-{6}CPP complexes, significant interaction between metal atoms and nanohoop has resulted in an interaction distance of 2.25–3.02 Å. In case of M@r6-{6}CPPs, the interaction distances are 2.32 Å, 3.17 Å and 3.44 Å for Li@r6-{6}CPP, Na@r6-{6}CPP and K@r6{6}CPP complexes, respectively (Table 2). It is interesting to note that the interaction distance between metal and the substrate increases with the increase in metal atom size, which is in accordance with the previously reported studies [59]. The observed geometrical symmetry of all M@-{6}CPP complexes is C1 as compared to D3d of pristine {6}CPP. The optimized geometries of all above mentioned complexes are given in Fig. 2.
Table 2.
Optimized pristine and alkali metals doped complexes of {6}CPP with first frequencies ν1 (cm−1), average bond lengths of alkali metal-C bond (Å) and interaction energies (eV).
| Complexes | ν1 (cm−1) | X M-C (Å) | Eint (eV)∗ |
|---|---|---|---|
| {6}CPP | 42.88 | – | – |
| Li@r6 | 32.52 | 2.32 | −0.68 (−0.025) |
| Li@endo | 34.20 | 2.25 | −1.24 (−0.045) |
| Na@r6 | 33.14 | 3.17 | −0.22 (−0.008) |
| Na@endo | 26.80 | 2.66 | −0.99 (−0.0366) |
| K@r6 | 29.13 | 3.44 | −0.21 (−0.007) |
| K@endo | 15.48 | 3.02 | −1.39 (−0.0511) |
Energy values in atomic units (au) are expressed in the bracket.
Fig. 2.
Optimized geometries of alkali metals (Li, Na and K) doped M@-{6}CPP complexes.
In case of MB{6}CPP complexes, three exohedral positions such as r6, r5 (above the five-membered ring), b56 (on bond between two phenylene rings) and one endohedral position at the center of the molecule are considered. In case of Li@MB{6}CPP complexes, despite of distinct input structures, Li@r5-MB{6}CPP and Li@b56-MB{6}CPP are converged to a single structure. While for Na doped systems four complexes are obtained, namely, Na@r6-MB{6}CPP, Na@r5-MB{6}CPP, Na@b56-MB{6}CPP and Na@endo-MB{6}CPP. In case of K doped systems, the optimized complexes obtained are; K@r6-MB{6}CPP, K@r5-MB{6}CPP, K@b56-MB{6}CPP and K@endo-MB{6}CPP. In case of exohedral complexes, the r6 position has the highest interaction as six carbon atoms are interacting with the alkali metal atoms from all sides as compared to the r5 where five carbon atoms are interacting and the b56 where only two carbon atoms interact. The geometrical symmetry of all these considered complexes is C1 and their complexes are shown in Fig. 3.
Fig. 3.
Optimized structures of alkali metals (Li, Na and K) doped M@-MB{6}CPP complexes.
The results depict that the interaction distance increases monotonically with the increase in size of alkali metal atoms. The interaction distances of metal atoms from the MB{6}CPP are in the range of 2.25–3.64 Å. For example, the interaction distances are 2.30, 3.16 and 3.44 Å for Li@r6-MB{6}CPP, Na@r6-MB{6}CPP and K@r6-MB{6}CPP complexes, respectively as mentioned in Table 3. This trend is quite similar to the already reported interaction distance for M@r6-Al1P12, where the interaction distance for Li@r6-Al1P12, Na@r6-Al1P12 and K@r6-Al1P12 complexes are 2.75, 3.09 and 3.54 Å, respectively [60]. However, for M@endo-MB{6}CPP complexes, the interaction distances are 2.25, 2.71 and 3.08 Å for Li@endo-MB{6}CPP, Na@endo-MB{6}CPP and K@endo-MB{6}CPP complexes respectively. For M@r5-MB{6}CPP complexes, the interaction distances are in the range of 3.34–3.64 Å whereas in case of M@b56 doping site, the observed interaction distances lie in the range of 2.66–2.97 Å.
Table 3.
Optimized pristine and alkali metals doped complexes of MB{6}CPP with first frequencies ν1 (cm−1), average bond lengths of M–C bond (Å) and interaction energies (eV).
| Complexes | ν1 (cm−1) | X M-C (Å) | Eint (eV)∗ |
|---|---|---|---|
| MB{6}CPP | 45.50 | – | – |
| Li@r6 | 42.72 | 2.30 | −0.64 (−0.023) |
| Li@endo | 30.38 | 2.25 | −1.07 (−0.039) |
| Na@r5 | 10.22 | 3.34 | −0.13 (−0.005) |
| Na@r6 | 38.78 | 3.16 | −0.24 (−0.008) |
| Na@b56 | 41.85 | 2.66 | −0.14 (−0.005) |
| Na@endo | 18.52 | 2.71 | −0.86 (−0.03) |
| K@r5 | 10.20 | 3.64 | −0.12 (−0.004) |
| K@r6 | 33.88 | 3.44 | −0.22 (−0.008) |
| K@b56 | 41.49 | 2.97 | −0.22 (−0.008) |
| K@endo | 6.45 | 3.08 | −1.29 (−0.04) |
Energy values in atomic units (au) are expressed in the bracket.
The thermodynamic stability is an important factor for the fabrication and practical applications of NLO materials [61]. To analyze the thermodynamic stability of all the CPP complexes, their interaction energies (Eint) are calculated. The nature of interactions between metal atoms and cycloparaphenylene is physiosorption as reflected from the calculated interaction energies ranging from −0.12 to −1.39 eV. All alkali metals doped {6}CPP complexes exhibit negative values of interaction energies, confirming their thermodynamic stability. Their Eint values are in the range of −0.21 eV (−0.007 au) to −1.39 eV (−0.0511 au) as listed in Table 2. In case of exohedral M@r6-{6}CPP complexes, it is observed that the interaction energies decrease with the increase in size of metal atom. The observed energies are −0.68 eV (−0.025 au), −0.22 eV (−0.008 au) and −0.21 eV (−0.007 au) for Li@r6-{6}CPP, Na@r6-{6}CPP and K@r6-{6}CPP complexes, respectively. The findings for M@r6-{6}CPP indicate that the Li atom has a strong interaction with the {6}CPP as compared to Na and K. One potential reason for this strong interaction could be attributed to the smaller atomic size of Li, which likely leads to a greater extent of charge transfer (vide infra) from Li to the {6}CPP at this specific doping site, in contrast to Na and K. Moreover, a comparable pattern of interaction energies with respect to the atomic size of alkali metal atoms has been observed earlier in alkali metal-doped M@C6O6Li6 complexes [62]. In case of M@endo-{6}CPP complexes, the interaction energies for Li@endo-{6}CPP, Na@endo-{6}CPP and K@endo-{6}CPP complexes are −1.24 eV (−0.045 au), −0.99 eV (−0.0366 au) and −1.39 eV (−0.0511 au), respectively.
The interaction energies of all alkali metals doped MB{6}CPP complexes are also negative and exothermic in nature, ranging from −0.12 eV to −1.29 eV (Table 3). For exohedral (M@r6-MB{6}CPPs & M@r5-MB{6}CPP) complexes, the interaction energy values decrease with the increase in atomic size of metal atoms as follows: Li > Na > K. The values of Eint are −0.64 eV (−0.023 au), −0.24 eV (−0.008 au) and −0.22 eV (−0.008 au) for Li@r6-MB{6}CPP, Na@r6-MB{6}CPP and K@r6-MB{6}CPP complexes, respectively and are also in consistent with the results of M@r6-{6}CPP complexes (vide supra). In case of M@r5-MB{6}CPP complexes, these lie in the range of −0.12 to −0.13 eV. In addition, for M@b56 position, the observed interaction energies are −0.14 eV and −0.22 eV for Na@b56-MB{6}CPP and K@b56-MB{6}CPP complexes, respectively. On the other hand, for M@endo-MB{6}CPP complexes, the interaction energies are −1.07 eV (−0.039 au), −0.86 eV (−0.03 au) and −1.29 eV (−0.04 au) for Li, Na and K doped complexes, respectively. These negative values of Eint energies illustrated that doping of alkali metals on CPP is more exothermic process as compared to the alkali metals encapsulation in aluminium nitride nanocages such as Li@Al12N12 and Na@ Al12N12 as reported earlier [63]. These results suggest that both alkali metals doped CPP complexes have exhibited the higher thermodynamic stability.
The chemical stability of alkali metals doped CPP complexes is calculated by their vertical ionization energies. The M@-{6}CPP complexes have VIE values ranging from 3.32 to 4.51 eV (Table 4). In M@endo-{6}CPP complexes, the highest VIE value of 4.51 eV is observed for Li@endo-{6}CPP complex whereas the VIE values of Na@endo-{6}CPP and K@endo-{6}CPP are 4.29 and 4.17 eV, respectively. For M@r6-{6}CPP complexes, the obtained VIE values are 4.23, 3.82 and 3.32 eV for Li@r6-{6}CPP, Na@r6-{6}CPP and K@r6-{6}CPP complexes, respectively. It is noticed that, in general, VIE values are decreased with the increase in alkali metal atomic size i.e., Li@-{6}CPPs > Na@-{6}CPPs > K@-{6}CPPs. In case of M@-MB{6}CPP complexes, the VIEs ranged from 3.25 to 4.15 eV (Table 5). For Li@-MB{6}CPP complexes, the Li@endo-MB{6}CPP complex has the highest VIE value of 4.15 eV followed by 4.13 eV for Li@r6-MB{6}CPP. Furthermore, for Na@-MB{6}CPP complexes, the VIEs are 3.88, 3.73, 3.82 and 3.96 eV for Na@r5-MB{6}CPP, Na@r6-MB{6}CPP, Na@b56-MB{6}CPP and Na@endo-MB{6}CPP complexes, respectively. In addition, the values of VIE for K doped MB{6}CPP complexes are in the range of 3.25–3.82 eV. It is observed that, just like alkali metals doped {6}CPP complexes, the VIEs of M@-MB{6}CPP are also decreased with the increase in metal size. This behavior is also observed in previously reported alkali metals doped cubane having VIEs of 4.49, 4.41 and 3.75 eV for Li@Cubane, Na@Cubane and K@Cubane, respectively [64]. Herein, it is established that alkali metals doped {6}CPP complexes are more stable in comparison to alkali metals doped MB{6}CPP complexes.
Table 4.
NBO charges Q (|e|), energies of frontier molecular orbitals EHOMO (eV), ELUMO (eV), H-L energy gaps (eV), % EH-L, Fermi level energies EFL (eV), and vertical ionization energies (eV) of M@-{6}CPP complexes.
| Complexes | Q (|e|) | EHOMO (eV) | ELUMO (eV) | EH-L (eV) | % EH-L | EFL (eV) | VIE (eV) |
|---|---|---|---|---|---|---|---|
| {6}CPP | – | −6.82 | −0.01 | 6.80 | – | −3.41 | 6.78 |
| Li@r6 | 0.919 | −4.52 | −0.09 | 4.43 | 34.85 | −2.31 | 4.23 |
| Li@endo | 0.909 | −4.77 | −0.33 | 4.43 | 34.85 | −2.55 | 4.51 |
| Na@r6 | 0.014 | −3.99 | −0.37 | 3.63 | 46.62 | −2.18 | 3.82 |
| Na@endo | 0.912 | −4.54 | −0.29 | 4.25 | 37.5 | −2.41 | 4.29 |
| K@r6 | 0.021 | −3.48 | −0.41 | 3.07 | 62.17 | −1.95 | 3.32 |
| K@endo | 0.940 | −4.42 | −0.25 | 4.17 | 39.70 | −2.33 | 4.17 |
Table 5.
NBO charges Q (|e|), energies of frontier molecular orbitals EHOMO (eV), ELUMO (eV), H-L energy gaps (eV), % EH-L, Fermi level energies EFL (eV), and vertical ionization energies (eV) of M@-MB{6}CPP complexes.
| Complexes | Q (|e|) | EHOMO (eV) | ELUMO (eV) | EH-L (eV) | % EHL | EFL (eV) | VIE (eV) |
|---|---|---|---|---|---|---|---|
| MB{6}CPP | – | −6.17 | −0.12 | 6.06 | – | −3.14 | 6.09 |
| Li@r6 | 0.895 | −4.44 | 0.33 | 4.76 | 21.45 | −2.06 | 4.13 |
| Li@endo | 0.893 | −4.42 | 0.42 | 4.84 | 20.13 | −1.99 | 4.15 |
| Na@r5 | 0.011 | −4.09 | −0.43 | 3.67 | 39.43 | −2.26 | 3.88 |
| Na@r6 | 0.003 | −3.93 | −0.46 | 3.46 | 42.90 | −2.20 | 3.73 |
| Na@b56 | 0.842 | −4.11 | −0.18 | 3.93 | 35.14 | −2.15 | 3.82 |
| Na@endo | 0.881 | −4.20 | 0.39 | 4.59 | 24.25 | −1.90 | 3.96 |
| K@r5 | 0.007 | −3.53 | −0.45 | 3.08 | 49.17 | −1.99 | 3.35 |
| K@r6 | 0.002 | −3.43 | −0.50 | 2.92 | 51.82 | −1.97 | 3.25 |
| K@b56 | 0.961 | −3.80 | −0.41 | 3.39 | 35.15 | −2.10 | 3.49 |
| K@endo | 0.914 | −4.04 | 0.36 | 4.41 | 27.23 | −1.84 | 3.82 |
3.2. Natural bond orbital (NBO) analysis
The NBO analysis has been conducted to assess the influence of doping on the electronic charge characteristics and charge transfer within a system. It provides significant information about transfer of net charge in a system [65]. In alkali metals doped {6}CPP complexes, the NBO charges on alkali metals lie in the range of 0.014–0.940 |e| (Table 4). The positive charges are due to electropositive nature of alkali metals. These positive charges have confirmed that the charge is transferred from alkali metal atom to the nanohoops. For M@r6-{6}CPP complexes, the highest charge of 0.919 |e| is observed for Li@r6-{6}CPP complex where as Na@r6-{6}CPP and K@r6-{6}CPP complexes have charges of 0.014 and 0.021 |e|, respectively. The higher charge on Li metal atom can be attributed to its smaller size. For M@endo-{6}CPP complexes, the charge on metals falls within the range of 0.909–0.940 |e|. It is observed that in the case of M@endo-{6}CPP complexes, the charge on alkali metals increases with the size of the metal inside the CPP surface. This trend can be attributed to the greater ease of ionization of alkali metals down the group [66].
In case of M@-MB{6}CPPs, the NBO charges on alkali metals range from −0.003 to 0.961 |e| (Table 5). For Li@-MB{6}CPP complexes, the observed charges are 0.895 and 0.893 |e| for Li@r6-MB{6}CPP and Li@endo-MB{6}CPP complexes, respectively. Regarding Na@-MB{6}CPP systems, the highest charge of 0.881 |e| is observed for Na@endo-MB{6}CPP complex, whereas for K@-MB{6}CPP complexes, the charges on metals range from 0.002 to 0.914 |e.| This analysis establishes that the alkali metals doped CPP complexes exhibit a high charge transfer ability, which depends not only on the metal atoms and doped position, but also on the nature of the substrate.
3.3. Electronic properties
Frontier molecular orbitals are analyzed in order to examine the electronic properties of both alkali metals doped CPP systems. In this regard, energies of HOMOs (EH), LUMOs (EL), differences in HOMO-LUMO energy gaps (EH–L), percentage reduction in EH–L (% EH–L) and Fermi level energies (EFL) of M@-{6}CPP and M@-MB{6}CPP complexes are calculated.
The computed EH–L of pristine {6}CPP is 6.80 eV, which limits its potential applications in electronics and optoelectronic devices. It is revealed that doping of alkali metals on {6}CPP has significantly reduced its EH–L up to 3.07 eV (Table 4). The delocalized π electrons of {6}CPP has influenced the outer ns electrons of alkali metals that resulted the generation of diffuse excess electrons. These diffuse excess electrons have contributed towards the increase in HOMO energies, which results the formation of new HOMO, while the previous HOMO becomes HOMO-1. This newly generated HOMO has contributed towards the reduction of EH–L. It is noticed that the decreasing order in EH–L is K > Na > Li for all metals doped {6}CPP complexes, possibly due to the low ionization potential of K [64]. For M@r6-{6}CPP complexes, the values of EH–L are 4.43, 3.63 and 3.07 eV for Li, Na and K doped complexes, respectively. While for M@endo-{6}CPP complexes, the values of EH–L are 4.43, 4.25 and 4.17 eV for Li@endo-{6}CPP, Na@endo-{6}CPP and K@endo-{6}CPP, respectively. It is noticed that major decrease in EH–L is achieved for M@r6-{6}CPP complexes as compared to M@endo-{6}CPP complexes because of having higher values of HOMO energy that resulted the decrease in band gap. Moreover, the % EH-L of M@-{6}CPP complexes are from 34.85 to 62.17 %. In addition, the values of EFL for alkali metals doped {6}CPP complexes are from 34.85 to −1.95 eV.
The calculated EH-L of pure MB{6}CPP is 6.06 eV which decreased from 4.84 to 2.92 eV on alkali metal atoms doping, as mentioned in Table 5. Moreover, the decreasing order in EH-L is also similar to M@-{6}CPP complexes i.e., K > Na > Li. For M@r6-MB{6}CPP complexes, the values of EH-L are 4.76, 3.46 and 2.92 eV for Li, Na and K doped complexes, respectively. It is noteworthy that, just like M@-{6}CPP complexes, the major decrease in EH-L is achieved for M@r6-{6}CPP complexes because the energies of HOMO are higher for these complexes which take part to decrease the values of EH-L. For M@endo-MB{6}CPPs, the lowest value of EH-L of 4.41 eV is observed for K@endo-MB{6}CPP complex. Furthermore, M@r5-MB{6}CPP and M@r6-MB{6}CPP complexes, the major decrease in EH-L observed are 3.08 and 3.39 eV, respectively. In addition, the % EH-L is attained from 20.13 to 51.82 %. Moreover, the highest value of EFL i.e., −1.84 eV is observed for K@endo-MB{6}CPP complex. The lower EH-L is obtained for M@-MB{6}CPP as compared to M@-{6}CPP.
Moreover, for all the M@-{6}CPP complexes, the shape and densities of HOMOs and LUMOs are exhibited in Fig. 4. It is revealed that HOMOs electron density is spread over the atoms of {6}CPP except in the case of Na@r6-{6}CPP and K@r6-{6}CPP complexes, where it is located on Na and K atoms, respectively. It exhibited that Na and K have played major role in the formation of new HOMOs in case of Na@r6-{6}CPP and K@r6-{6}CPP, respectively [64]. Furthermore, it is revealed from Fig. 5 that the electron densities of HOMOs are spread over the atoms of MB{6}CPP except for M@r5-MB{6}CPP, Na@r6-MB{6}CPP and K@r6-MB{6}CPP complexes. Herein, it is established that diffuse excess electrons generated by doping of alkali metals has played an important role to alter the electronic properties (reduce the EH-L) of both alkali metals doped CPP systems. Therefore, these metals doped CPP complexes can be utilized in optoelectronic devices.
Fig. 4.
HOMOs and LUMOs of M@-{6}CPP complexes.
Fig. 5.
HOMOs and LUMOs of M@-MB{6}CPP complexes.
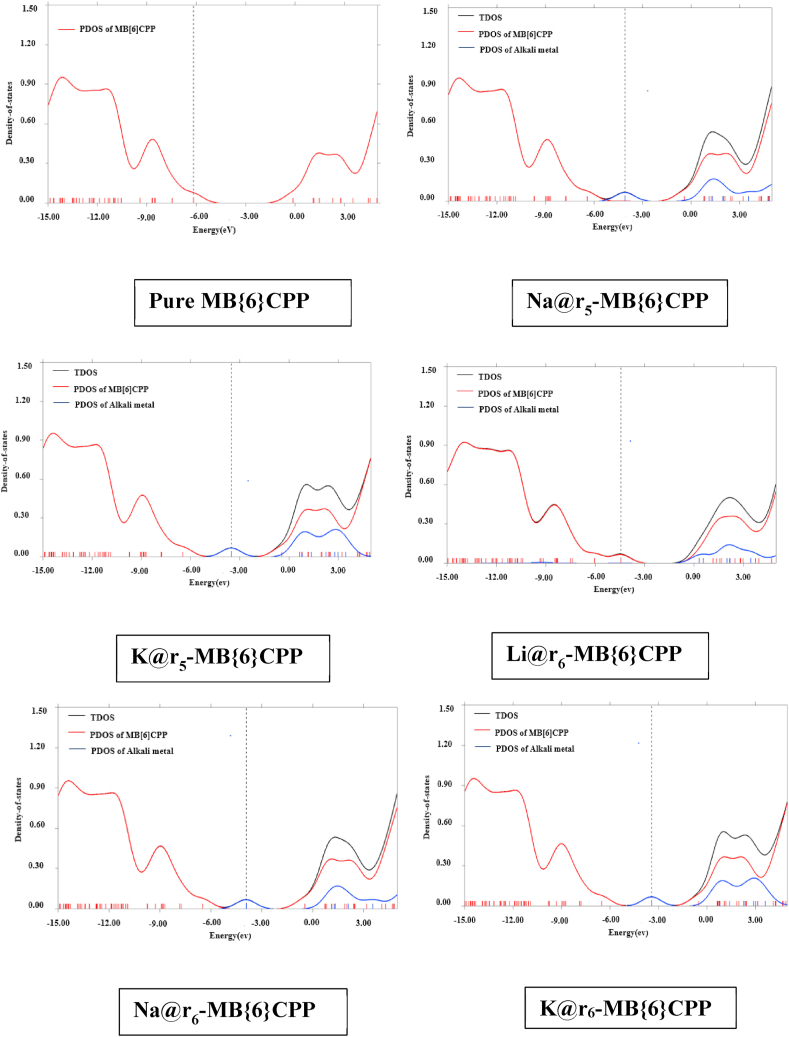
To further elaborate the effect of alkali metals doping on {6}CPP and MB{6}CPP, the TDOS and PDOS for pure and doped CPPs are plotted. It is revealed from the DOS spectra that new HOMO is generated in both M@-{6}CPP and M@-MB{6}CPP complexes as compared to pristine ones and are indicated by vertical dotted line in Fig. 6, Fig. 7. It is revealed that energy of new HOMOs in all the complexes is larger as compared to pristine CPPs/nanohoops that contributed towards the reduction in H-L energy gap [67]. The PDOS spectra elaborated that both alkali metals as well as CPPs have played role for the formation of new HOMO. Hence, it is observed that after doping of alkali metals the electronic properties of both {6}CPP and MB{6}CPP has been improved in order to make them valuable for optoelectronic industry.
Fig. 6.
TDOS and PDOS spectra of M@-{6}CPP Complexes.
Fig. 7.
TDOS and PDOS spectra of M@-MB{6}CPP Complexes.
3.4. NCI-RDG analysis
This analysis has been carried out to elucidate the type and nature of inter and intra-molecular interactions. It consists of 3D iso-surfaces and graphical portrayal of 2D-RDG graphs, based on the electron density function and its derivatives [68]. It helps to give more insight about the non-covalent interactions such as steric repulsion, hydrogen bonding and van der Waals interactions [69,70]. For all the alkali metals doped CPP complexes, the 3D iso-surfaces and 2D-RDG graphs are given in Figs. S1 and S2. The term sign (λ2)ρ in graphs has exhibited the electron density (ρ) into the sign of second Hessian eigen value λ2. To figure out the nature of interactions, the values of sign (λ2)ρ are critical such as for repulsive (non-bonded) and attractive (bonded) interactions the expressions are; sign (λ2)ρ > 0 and sign (λ2)ρ < 0, respectively [68]. Furthermore, patches of different colors in iso-surfaces have demonstrated different kind of interactions. For example, the green region exhibits the van der Waals interactions, red color represents the steric repulsion and blue one depicts the strong attractive bonding interactions.
It is revealed that all M@-{6}CPP complexes have low density, low gradient spikes at −0.01 au and 0.03 au, respectively, which are evident of noncovalent interactions and steric repulsion. Similar spikes are seen in M@-MB{6}CPP complexes at −0.01 au and 0.03 au. Additionally, blue-green 3D isosurfaces between metals and nanohoops reveal weak dispersive interactions, particularly van der Waals interactions as shown in Figs. S1 and S2. The data from the NCI analysis matches well with the interaction energies.
3.5. QTAIM analysis
The QTAIM analysis has been conducted for a more in-depth elucidation of the type and nature of the bonding [71]. This analysis relies on the electron density () and its derivatives at bond critical points (BCPs) involved in inter- or intramolecular interactions [72]. For both M@-{6}CPP and M@-MB{6}CPP complexes, all QTAIM variables at BCPs are listed in Tables S1 and S2. The value of electron density provides information about the strength of the bond; a higher value of electron density indicates a stronger bond. Additionally, the Laplacian of electron density (), kinetic electron density G(r) and potential electron density V(r) are employed to assess the nature of interactions. The topological images for both alkali metals doped CPP complexes are depicted in Figs. S3 and S4. It is established that for covalent interactions, value is either negative or 0 and > 0.1au (large), whereas for non-covalent interactions, the value of is positive or >0 and = 0.002 to 0.034 au (small). Furthermore, for electrostatic and covalent interactions, the values of -G(r)/V(r) > 0.5 and -Gr/Vr < 0.5, respectively [71].
For covalent and electrostatic interactions, the BCP values can be exhibited as;
| (10) |
| (11) |
The topological investigation of electron density in both alkali metals doped CPP systems has confirmed the presence of BCPs between the metal atom and the nanohoops. Moreover, the small and positive values of and further confirm the presence of non-covalent interactions within all the complexes as indicated in Tables S1 & S2. The highest value for both and is observed for Li@endo-{6}CPP ( = 0.017, = 0.101) and Li@endo-MB{6}CPP ( = 0.018, = 0.104), respectively, indicating the presence of strong van der Waals interactions and these results are also in consistent with the interaction energies data. Similarly, the value of -Gr/Vr value is greater than 0.5, providing additional evidence for the presence of van der Waals interactions.
Furthermore, a correlation between the electron density in BCPs of selected bonds and XM-C bond distances has also been observed in the exohedral complexes. The complexes with the shortest interaction distance (metal atom to surface bond lengths) exhibit the largest value of electron density as observed previously by Dimic et al., [73]. The Li@r6-{6}CPP and Li@r6-MB{6}CPP complexes exhibit the highest electron density values of 0.020 and 0.021 at BCPs with the shortest interaction distances of 2.32 Å and 2.30 Å among the M@r6-{6}CPP and M@r6-MB{6}CPP complexes. These results provide an extra evidence for the greater stability of these complexes as compared to their Na and K counterparts, complementing their smaller size and higher charge transfer characteristics.
3.6. UV–Visible analysis
The UV–Visible analysis has been performed to gain further insights into the absorbance properties of metal doped CPP complexes. The TD-DFT calculations have been carried out to compute the transition energies, oscillator strength (fo) and λmax values.
It is revealed from the UV–Visible spectra of all alkali metals doped {6}CPP complexes that red shift is achieved as compared to the pristine {6}CPP as shown in Fig. 8 and S5. This bathochromic shift has contributed to a decrease in the values of excitation energies (ΔE). The absorption values of metal doped {6}CPP complexes fall in the range of 326–1086 nm, significantly higher than the 291 nm for the pure one, as given in Table 6. In the exohedral complexes, the K@r6-{6}CPP complex attains the highest λmax value at 1086 nm, owing to its remarkably low H-L energy gap of 3.07 eV. Conversely, the Li@r6-{6}CPP complex exhibits the lowest λmax value at 326 nm, corresponding to the highest H-L energy gap of 4.43 eV. Moreover, the shift in the absorption spectra of the designed complexes is also influenced by the size and charge distribution of alkali metal atoms. Small sized, and highly charged Li metal, has led to a shift in λmax towards a lower wavelength (326 nm). In contrast, the larger size K metal, with less charge distribution, has shifted the absorption wavelength towards a longer wavelength (1086 nm).
Fig. 8.
UV–Vis spectra of M@r6-{6}CPP Complexes.
Table 6.
Dipole moment (Debye), mean polarizability (×10−24 esu), first hyperpolarizability (×10−30 esu), oscillation strength, transition energy (eV), difference in dipole moment (Debye) and maximum absorption λmax (nm) of pristine and M@-{6}CPP complexes.
| Complexes | μo (D) | αo (×10−24 esu) | β◦ (×10−30 esu) | βVec (au) | fo | ΔE (eV) | Δμ (D) | λmax (nm) |
|---|---|---|---|---|---|---|---|---|
| {6}CPP | – | – | 0.00 | – | 0.845 | 4.26 | – | 291 |
| Li@r6 | 8.55 | 74.4 | 24.3 | 4.70 × 103 | 0.134 | 3.80 | 0.11 | 326 |
| Li@endo | 0.46 | 73.4 | 51.8 | 1.00 × 104 | 0.408 | 3.73 | 0.08 | 332 |
| Na@r6 | 4.23 | 112.9 | 1641.1 | 3.16 × 105 | 0.256 | 2.16 | 0.17 | 574 |
| Na@endo | 1.35 | 77.1 | 92.8 | 1.79 × 104 | 0.287 | 3.69 | 0.05 | 336 |
| K@r6 | 2.25 | 300.3 | 56,221.7 | 1.08 × 107 | 0.220 | 1.14 | 0.18 | 1086 |
| K@endo | 1.95 | 80.2 | 120.6 | 2.32 × 104 | 0.374 | 3.62 | 0.06 | 342 |
In case of M@-MB{6}CPP complexes, the absorption wavelengths fall within the range of 336 nm–1181 nm, higher compared to the pristine form at 318 nm (Table 7). Similar to M@-{6}CPP complexes, a red shift is also observed in M@-MB{6}CPP complexes as shown in Fig. 9 & S6. For M@r6-MB{6}CPP complexes, there is an increasing trend in absorption wavelength with the increase in size of metal atoms, having values of 388, 580 and 781 nm for Li@r6-MB{6}CPP, Na@r6-MB{6}CPP and K@r6-MB{6}CPP complexes, respectively. Apart from their smaller size, the charge distribution and H-L energy gap also contribute to the shift in the absorption spectra (vide supra). However, the trend is inverse in the case of M@endo-MB{6}CPP, with values of 366, 361 and 336 nm for Li@endo-MB{6}CPP, Na@endo-MB{6}CPP and K@endo-MB{6}CPP complexes, respectively. In summary, both M@{6}CPP and M@MB{6}CPP complexes demonstrate absorbance from UV–Visible to infrared region, whereas pristine nanohoops have absorption peaks primarily in UV region. The estimated results further indicate that both M@-{6}CPP and M@-MB{6}CPP complexes exhibit perfect transparency in the deep UV region (<200 nm).
Table 7.
Dipole moment (Debye), mean polarizability (×10−24 esu), first hyperpolarizability (×10−30 esu), oscillation strength, transition energy (eV), difference in dipole moment (Debye) and maximum absorption λmax (nm) of pristine and M@-MB{6}CPP complexes.
| Complexes | μo (D) | αo (×10−24 esu) | β◦ (×10−30 esu) | βVec (au) | fo | ΔE (eV) | Δμ (D) | λmax (nm) |
|---|---|---|---|---|---|---|---|---|
| MB{6}CPP | 0.00 | – | 0.00 | – | 0.623 | 3.89 | – | 318 |
| Li@r6 | 6.51 | 80.1 | 15.4 | 2.97 × 103 | 0.096 | 3.19 | 0.01 | 388 |
| Li@endo | 0.33 | 81.6 | 81.1 | 1.56 × 104 | 0.311 | 3.38 | 0.00 | 366 |
| Na@r5 | 4.17 | 113.6 | 685.2 | 1.32 × 105 | 0.339 | 2.22 | 0.14 | 559 |
| Na@r6 | 5.46 | 109.9 | 727.6 | 1.40 × 105 | 0.402 | 2.14 | 0.00 | 580 |
| Na@b56 | 9.62 | 86.6 | 305.1 | 5.88 × 104 | 0.079 | 1.05 | 0.00 | 1181 |
| Na@endo | 0.46 | 77.3 | 92.8 | 2.39 × 104 | 0.196 | 3.43 | 0.00 | 361 |
| K@r5 | 5.44 | 150.1 | 2769.9 | 5.34 × 105 | 0.303 | 1.64 | 0.12 | 757 |
| K@r6 | 16.76 | 159.1 | 31,099.8 | 5.99 × 106 | 0.114 | 1.59 | 0.00 | 781 |
| K@b56 | 13.74 | 83.6 | 64.2 | 1.24 × 104 | 0.125 | 2.06 | 0.00 | 600 |
| K@endo | 0.95 | 89.7 | 176.9 | 3.41 × 104 | 0.286 | 3.68 | 0.00 | 336 |
Fig. 9.
UV/Vis spectra of M@-MB{6}CPP Complexes.
3.7. Nonlinear optical properties
From literature it is established that excess electrons have played an important role to enhance the NLO response of molecules [74]. It is clear from the charge analysis that excess electrons generated by alkali metal atoms, which may take part to increase the NLO response of these complexes. To confirm this, dipole moment (μo) and the indicators of NLO response such as static polarizability (α◦) and first hyperpolarizability (β◦) of both metals doped CPP systems are computed.
The dipole moment of undoped {6}CPP is computed to be zero because of its centrosymmetric nature. The dipole moments of complexes have been increased from 0.46 to 8.55 D on the doping of alkali metals atoms and are mentioned in Table 6. The increase in dipole moment of doped complexes is due to the breakage of the centrosymmetric nature of the {6}CPP and creation of positive and negative poles. In addition, an increase in polarizability is also observed from 112.9 to 300.3 × 10−24 esu. For M@endo-{6}CPP complexes, the increasing trend in polarizability is observed with the increase in metals size such as; 73.4, 77.1 and 80.2 × 10−24 esu for Li, Na and K doped complexes, respectively. The centrosymmetric {6}CPP has exhibited zero first hyperpolarizability but metals doped complexes of {6}CPP shown noticeable values of first hyperpolarizability. The first hyperpolarizability of alkali metals doped {6}CPP complexes lie in the range of 24.3 × 10−30 esu to 56, 221.7 × 10−30 esu as indicated in Table 6. The highest hyperpolarizability of 56, 221.7 × 10−30 esu is achieved for K@r6-{6}CPP complex which is larger than NLO response of earlier reported alkali metals doped cyclic systems such as Na@6CT [24] and K@calix{4}pyrrole [75]. An increasing trend of K > Na > Li in first hyperpolarizability is noticed for M@r6-{6}CPP complexes. The β◦ values of 24.3 × 10−30 esu, 1641.1 × 10−30 esu and 56,221.7 × 10−30 esu are observed for Li, Na and K doped complexes, respectively. Whereas, for M@endo-{6}CPP complexes, the values of β◦ are 51.8 × 10−30 esu, 92.8 × 10−30 esu and 120.6 × 10−30 esu for Li, Na and K doped complexes, respectively. This trend exhibited that the doping of metals on organic systems is more efficient way to increase the β◦ values. For example, in case of alkali metals doped calix{4}pyrrole the values of β◦ for Li@calix{4}pyrrole, Na@calix{4}pyrrole and K@calix{4}pyrrole are 7320, 7500 and 173,304 au, respectively [75]. This behavior is due to the fact that with the increase in atomic number, the ionization potential decreases down the group and the valence electrons are easily pushed out from alkali metal atoms to generate excess electrons. The VIE is also an important factor that has influence on first hyperpolarizability values, such as the complexes with large metal size and small VIE value exhibits notable values of first hyperpolarizability [64,76]. For example, the complex K@r6-{6}CPP having the largest hyperpolarizability also possessed the smallest VIE of 3.32 eV.
The pure MB{6}CPP has depicted the zero dipole moment but after doping the dipole moments are significantly increased from 0.33 to 16.76 D and are mentioned in Table 7. For all the doped complexes, the polarizability is also enhanced from 77.3 × 10−24 esu to 159.1 × 10−24 esu. Furthermore, the β◦ values of M@-MB{6}CPP complexes are increased from 15.4 × 10−30 esu to 31,099.8 × 10−30 esu as compared to pristine one as listed in Table 7. The highest response in terms of β◦ i.e., 31,099.8 × 10−30 esu is observed for K@r6-MB{6}CPP complex having the smallest VIE (3.25 eV) and H-L energy gap (2.92 eV). However, the hyperpolarizability value of K@r6-MB{6}CPP complex is lower in contrast of K@r6-{6}CPP. The possible reason for this might be the high stain energy of MB{6}CPP (110.9 kcal/mol) as compared to {6}CPP (4.2 kcal/mol) [39]. The increasing trend in first hyperpolarizability is observed i.e., K > Na > Li except for M@r6-MB{6}CPP complexes. For example, the first hyperpolarizability values of M@r6-MB{6}CPP complexes are 15.4 × 10−30 esu, 727.6 × 10−30 esu and 31,099.8 × 10−30 esu for Li, Na and K doped MB{6}CPP complexes, respectively.
To gain an insight into the increased hyperpolarizability values, TD-DFT simulations at “two-level model” are applied [77,78]. According to the two-level model
| (12) |
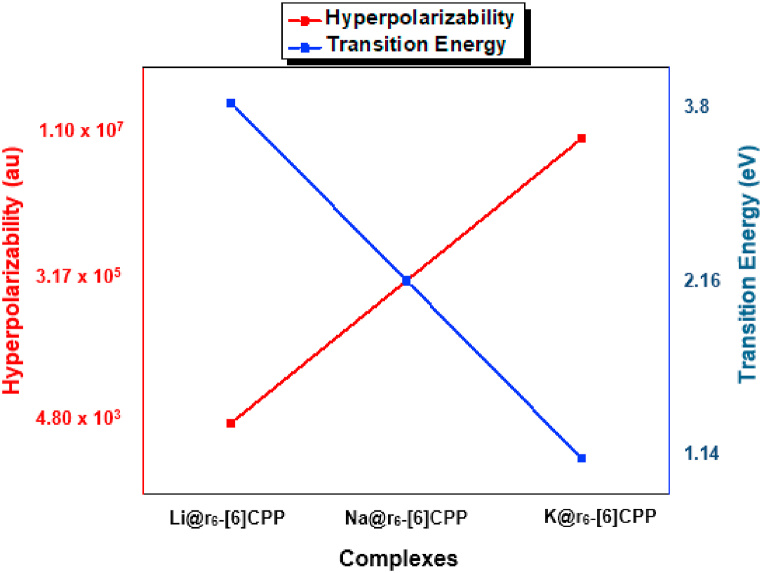
where is the largest oscillation strength, is difference of dipole moments between the ground state and the crucial excited state and is crucial transition energy. It is clear from the equation that β◦ is inversely proportional to the third power of the . It is an important factor to examine the NLO properties as previous studies revealed that a smaller transition energy will lead to an increase in the first hyperpolarizability [79]. For all the alkali metals doped {6}CPP complexes, the prominent decrease in is observed from 3.80 to 1.14 eV. Moreover, the increase in β◦ with the decrease in is achieved for all M@-{6}CPP complexes as depicted in Fig. 10. The complex of K@r6-{6}CPP that shown the maximum β◦ has exhibited the smaller of 1.14 eV. In addition, the consistent decrease in from 1.05 to 3.68 eV is achieved for metal doped MB{6}CPP complexes. Herein, the inverse relation between the hyperpolarizability and transition energy is also observed as shown in Fig. 11 for M@r6-MB{6}CPP complexes.
Fig. 10.
Correlation between first hyperpolarizability and crucial excitation energies for M@r6-{6}CPP Complexes.
Fig. 11.
Correlation between first hyperpolarizability and crucial excitation energies for M@r6-MB{6}CPP Complexes.
Furthermore, the projection of hyperpolarizability on dipole moment vector (βvec) is also explored. The calculated values of βvec for M@-{6}CPP complexes are from 4.70 × 103 to 1.08 × 107 au. These results are compatible with the values of β◦ and exhibited the same trend of increment as that of the first hyperpolarizability. The highest value of 1.08 × 107 au is observed for K@r6- [66]CPP. Moreover, the computed values of βvec for M@-MB{6}CPP complexes are from 2.97 × 103 to 5.99 × 106 au that are quite similar to their β◦ values. Therefore, it is established that both alkali metals doped CPP systems have remarkable NLO response in terms of hyperpolarizability and can be utilized in optoelectronics.
Nowadays, hyper Rayleigh scattering hyperpolarizability (HRS) is emerged both theoretically and experimentally as an efficient technique in fast electro-optic modulation, frequency doubling high-resolution microscopy and to measure the hyperpolarizability of molecules directly [79]. For further elucidation of nonlinearity, we have computed hyper Rayleigh scattering hyperpolarizability (βHRS) of M@r6-{6}CPP and M@r6-MB{6}CPP complexes. In addition, depolarization ratio is also calculated to elucidate the symmetry of molecules in tensorial space. The off-resonant nonlinear tensors are divided into dipolar and octupolar components. Octupolar molecules have large SHG which is important for their use in optical devices [80].
The βHRS values of M@r6-{6}CPP complexes are from 1.98 × 105 to 5.28 × 106 au as tabulated in Table 8. The largest value of βHRS is achieved for K@r6-{6}CPP complex. Furthermore, their depolarization ratio values are from 0.341 to 2.082 DR, indicating their octupolar nature. These octupolar molecules have significant importance in optoelectronics because of their ability to exhibit large SHG [80]. While in case of M@r6-MB{6}CPP complexes the βHRS are in the range of the 7.09 × 104 to 4.49 × 105 au as mentioned in Table 8. Moreover, they also exhibited octupolar nature because the depolarization ratio values are from 0.546 to 2.137 DR. It is noticed that in case of both M@r6-{6}CPP and M@r6-MB{6}CPP complexes the values of βHRS are higher than β◦ except for complexes where K is doped above the benzene ring of the nanohoops.
Table 8.
Hyper Rayleigh scattering (βHRS, au) and depolarization ratio (DR) of M@r6-{6}CPPs and M@r6-MB{6}CPP complexes.
| Complexes | βHRS (au) | DR |
|---|---|---|
| Li@r6-{6}CPP | 1.98 × 105 | 2.082 |
| Na@r6-{6}CPP | 5.26 × 105 | 0.577 |
| K@r6-{6}CPP | 5.28 × 106 | 0.341 |
| Li@r6-MB{6}CPP | 1.16 × 105 | 2.137 |
| Na@r6-MB{6}CPP | 4.49 × 105 | 0.546 |
| K@r6-MB{6}CPP | 7.09 × 104 | 1.466 |
Frequency dependent first hyperpolarizability (β(ω)) calculations are performed for M@r6-{6}CPP and M@r6-MB{6}CPP complexes at two routinely used laser wavelengths of 1550 nm and 1907 nm. The SHG values of M@r6-{6}CPP complexes at 1550 nm range from 3.62 × 105 to 1.84 × 106 au, while at 1907 nm, the values fall within the range of 4.05 × 102 to 4.81 × 104 au as indicated in Table 9. Therefore, it is established that the SHG values at 1550 nm are larger than those at 1907 nm. In addition, the EOPE has exhibited a maximum response of 1.30 × 108 au at 1907 nm.
Table 9.
Frequency dependent first hyperpolarizability (β(ω)) of M@r6-{6}CPP complexes.
| Parameters | Frequency | Li@r6-{6}CPP | Na@r6-{6}CPP |
|---|---|---|---|
| β (−ω, ω,0) (au) | 0.00 | 2.82 × 103 | 1.89 × 105 |
| 1550 nm | 2.69 × 103 | 5.92 × 105 | |
| 1907 nm | 2.82 × 103 | 1.30 × 108 | |
| β (−2ω, ω, ω) (au) | 0.00 | 2.82 × 103 | 1.89 × 105 |
| 1550 nm | 1.84 × 106 | 3.62 × 105 | |
| 1907 nm | 4.05 × 102 | 4.81 × 104 |
For M@r6-MB{6}CPP complexes, the SHG values range from 2.74 × 104 to 5.61 × 105 au at 1907 nm, whereas the SHG response at 1550 nm falls in the range of 1.23 × 105 to 4.24 × 105 au (Table 10). Furthermore, the EOPE has exhibited the maximum response of 6.08 × 106 au at 1907 nm. It is established from the above discussion that these alkali metals doped CPP complexes have exhibited remarkably enhanced NLO response in the presence of different operating wavelengths.
Table 10.
Frequency dependent first hyperpolarizability (β(ω)) of M@r6-MB{6}CPP complexes.
| Parameters | Frequency | Li@r6-MB{6}CPP | Na@r6-MB{6}CPP | K@r6-MB{6}CPP |
|---|---|---|---|---|
|
β (−ω, ω,0) (au) |
0.00 | 1.78 × 103 | 8.42 × 104 | 3.59 × 106 |
| 1550 nm | 5.29 × 103 | 1.05 × 105 | 9.57 × 104 | |
| 1907 nm | 3.54 × 103 | 6.08 × 106 | 1.04 × 105 | |
|
β (−2ω, ω, ω) (au) |
0.00 | 1.78 × 103 | 8.42 × 104 | 3.59 × 106 |
| 1550 nm | 4.01 × 105 | 1.23 × 105 | 4.24 × 105 | |
| 1907 nm | 2.74 × 104 | 5.61 × 105 | 1.15 × 105 |
4. Conclusion
In the present work, the geometrical, electronic and NLO properties of alkali metals doped {6}CPP and MB{6}CPP complexes are studied via DFT simulations. The NBO analysis has revealed charge transfer from metal atoms to the nanohoops and values of adsorption energies have indicated the thermodynamic stability of designed complexes. For M@-{6}CPP complexes, the maximum interaction energy of −1.39 eV is achieved for K@endo-{6}CPP while, for M@-MB{6}CPP complexes the observed interaction energies are −0.12 eV to −1.29 eV. A significant decrease in H-L energy gap is achieved in doped complexes such as, 3.07 eV and 2.92 eV for K@r6-{6}CPP and K@r6-MB{6}CPP complexes respectively. The major decrease in H-L energy gap is observed because of the formation of new HOMO which is confirmed by DOS spectra. Moreover, the enhanced NLO response in terms of hyperpolarizability is achieved from all metals doped CPP complexes. The highest β◦ values of 56,221.7 × 10−30 esu and 31,099.8 × 10−30 esu are attained for K@r6-{6}CPP and K@r6-MB{6}CPP complexes, respectively. In addition, frequency dependent first hyperpolarizability is computed at two routinely used laser wavelengths (1550 nm and 1907 nm) for M@r6-{6}CPP and M@r6-MB{6}CPP complexes. The maximum response of 1.30 × 108 au is observed for Na@r6-{6}CPP at 1907 nm. It is envisaged that these improved properties of alkali metals doped {6}CPP and MB{6}CPP will pay a way to explore them as potential organic candidates for modern NLO applications.
CRediT authorship contribution statement
Ruqiya Rasul: Data curation. Tariq Mahmood: Formal analysis. Khurshid Ayub: Conceptualization. Khurram Saleem Joya: Investigation. Farooq Anwar: Validation, Writing – original draft. Nazamid Saari: Validation, Writing – review & editing. R. Nawaz: Formal analysis, Visualization. Mazhar Amjad Gilani: Resources, Software, Supervision.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Footnotes
Supplementary data to this article can be found online at https://doi.org/10.1016/j.heliyon.2023.e21508.
Appendix A. Supplementary data
The following is the Supplementary data to this article:
References
- 1.Li Y., Liu P., Hu L., Chen L., Lin H., Zhou L., Wu L. Strong IR NLO material Ba4MGa4Se10Cl2: highly improved laser damage threshold via dual ion substitution synergy. Adv. Opt. Mater. 2015;3:957–966. [Google Scholar]
- 2.Iliopoulos K., Krupka O., Gindre D., Sallé M. Reversible two-photon optical data storage in coumarin-based copolymers. J. Am. Chem. Soc. 2010;132:14343–14345. doi: 10.1021/ja1047285. [DOI] [PubMed] [Google Scholar]
- 3.Castet F., Rodriguez V., Pozzo J.-L., Ducasse L., Plaquet A., Champagne B. Design and characterization of molecular nonlinear optical switches. Acc. Chem. Res. 2013;46:2656–2665. doi: 10.1021/ar4000955. [DOI] [PubMed] [Google Scholar]
- 4.Ahsin A., Ayub K. Theoretical investigation of superalkali clusters M2OCN and M2NCO (where M= Li, Na, K) as excess electron system with significant static and dynamic nonlinear optical response. Optik (Stuttg). 2021;227 [Google Scholar]
- 5.Kuang L., Chen Q., Sargent E.H., Wang Z.Y. [60] fullerene-containing polyurethane films with large ultrafast nonresonant third-order nonlinearity at telecommunication wavelengths. J. Am. Chem. Soc. 2003;125:13648–13649. doi: 10.1021/ja0376240. [DOI] [PubMed] [Google Scholar]
- 6.Zheng C., Huang J., Lei L., Chen W., Wang H., Li W. Nanosecond nonlinear optical and optical limiting properties of hollow gold nanocages. Appl. Phys. B. 2018;124:17. [Google Scholar]
- 7.Bredas J.L., Meyers F., Pierce B.M., Zyss J. On the second-order polarizability of conjugated. pi.-electron molecules with octupolar symmetry: the case of triaminotrinitrobenzene. J. Am. Chem. Soc. 1992;114:4928–4929. [Google Scholar]
- 8.Bai Y., Zhou Z.-J., Wang J.-J., Li Y., Wu D., Chen W., Li Z.-R., Sun C.-C. New acceptor–bridge–donor strategy for enhancing NLO response with long-range excess electron transfer from the NH2...M/M3O donor (M = Li, Na, K) to inside the electron hole cage C20F19 acceptor through the unusual σ chain bridge (CH2)4. J. Phys. Chem. A. 2013;117:2835–2843. doi: 10.1021/jp3120594. [DOI] [PubMed] [Google Scholar]
- 9.Murugan N.A., Kongsted J., Rinkevicius Z., Ågren H. Breakdown of the first hyperpolarizability/bond-length alternation parameter relationship. Proc. Natl. Acad. Sci. USA. 2010;107:16453–16458. doi: 10.1073/pnas.1006572107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Nakano M., Kishi R., Nakagawa N., Ohta S., Takahashi H., Furukawa S., Kamada K., Ohta K., Champagne B., Botek E. Second hyperpolarizabilities (γ) of bisimidazole and bistriazole benzenes: diradical character, charged state, and spin state dependences. J. Phys. Chem. A. 2006;110:4238–4243. doi: 10.1021/jp056672z. [DOI] [PubMed] [Google Scholar]
- 11.Zhong R.-L., Xu H.-L., Li Z.-R., Su Z.-M. Role of excess electrons in nonlinear optical response. J. Phys. Chem. Lett. 2015;6:612–619. doi: 10.1021/jz502588x. [DOI] [PubMed] [Google Scholar]
- 12.Ullah F., Kosar N., Ayub K., Mahmood T. Superalkalis as a source of diffuse excess electrons in newly designed inorganic electrides with remarkable nonlinear response and deep ultraviolet transparency: a DFT study. Appl. Surf. Sci. 2019;483:1118–1128. doi: 10.1016/j.apsusc.2019.04.042. [DOI] [Google Scholar]
- 13.Hou N., Wu Y.Y., Wu H.S., He H.M. The important role of superalkalis on the static first hyperpolarizabilities of new electrides: theoretical investigation on superalkali-doped hexamethylenetetramine (HMT) Synth. Met. 2017;232:39–45. doi: 10.1016/j.synthmet.2017.07.021. [DOI] [Google Scholar]
- 14.Li X.-H., Zhang X.-L., Chen Q.-H., Zhang L., Chen J.-H., Wu D., Sun W.-M., Li Z.-R. Coinage metalides: a new class of excess electron compounds with high stability and large nonlinear optical responses. Phys. Chem. Chem. Phys. 2020;22:8476–8484. doi: 10.1039/c9cp06894e. [DOI] [PubMed] [Google Scholar]
- 15.Sun W., Wu D., Li Y., Li Z. Novel alkalides with considerably large first Theoretical study on superalkali (Li3) in ammonia: hyperpolarizabilities. Dalton Trans. 2014;43:486–494. doi: 10.1039/c3dt51559a. [DOI] [PubMed] [Google Scholar]
- 16.Bano R., Arshad M., Mahmood T., Ayub K., Sharif A., Perveen S., Tabassum S., Yang J., Gilani M.A. Face specific doping of Janus all-cis-1,2,3,4,5,6-hexafluorocyclohexane with superalkalis and alkaline earth metals leads to enhanced static and dynamic NLO responses. J. Phys. Chem. Solid. 2022;160 doi: 10.1016/j.jpcs.2021.110361. [DOI] [Google Scholar]
- 17.Shobana D., Sudha S., Ramarajan D., Dimić D. Synthesis, crystal structure, spectral characterization and Hirshfeld surface analysis of (E)-N′-(3-ethoxy-4-hydroxybenzylidene)-4-fluorobenzohydrazide single-crystal–a novel NLO active material. J. Mol. Struct. 2022;1250 [Google Scholar]
- 18.Kavitha E., Ramarajan D., Rakić A., Dimić D., Sudha S., Nirmala P.N. Structural, spectroscopic, quantum chemical, and molecular docking investigation of (E)-N’-(2, 5-dimethoxybenzylidene) picolinohydrazide. J. Mol. Struct. 2022;1253 [Google Scholar]
- 19.Jauhar R.O.M.U., Viswanathan V., Vivek P., Vinitha G., Velmurugan D., Murugakoothan P. A new organic NLO material isonicotinamidium picrate (ISPA): crystal structure, structural modeling and its physico-chemical properties. RSC Adv. 2016;6:57977–57985. [Google Scholar]
- 20.Bano R., Ayub K., Mahmood T., Arshad M., Sharif A., Tabassum S., Gilani M.A. Diamondoid as potential nonlinear optical material by superalkali doping: a first principles study. Diam. Relat. Mater. 2023;135 doi: 10.1016/j.diamond.2023.109826. [DOI] [Google Scholar]
- 21.Tehan F.J., Barnett B.L., Dye J.L. Alkali anions. Preparation and crystal structure of a compound which contains the cryptated sodium cation and the sodium anion. J. Am. Chem. Soc. 1974;96:7203–7208. [Google Scholar]
- 22.Redko M.Y., Vlassa M., Jackson J.E., Misiolek A.W., Huang R.H., Dye J.L. “Inverse sodium hydride”: a crystalline salt that contains H+ and Na. J. Am. Chem. Soc. 2002;124:5928–5929. doi: 10.1021/ja025655+. [DOI] [PubMed] [Google Scholar]
- 23.Chen W., Li Z., Wu D., Li Y., Sun C., Gu F.L. 2005. The Structure and the Large Nonlinear Optical Properties of Li @ Calix [4] Pyrrole; pp. 10977–10981. [DOI] [PubMed] [Google Scholar]
- 24.Sajid H., Ayub K., Mahmood T. A comprehensive DFT study on the sensing abilities of cyclic oligothiophenes (nCTs) New J. Chem. 2019;43:14120–14133. doi: 10.1039/C9NJ01894H. [DOI] [Google Scholar]
- 25.Li X., Li S. Investigations of electronic and nonlinear optical properties of single alkali metal adsorbed graphene, graphyne and graphdiyne systems by first-principles calculations. J. Mater. Chem. C. 2019;7 [Google Scholar]
- 26.Guo Y.-D., Zeng H.-L., Hu L.-Z., Yan X.-H., Mou X.-Y., Yang M.-S. Multiple spin-resolved negative differential resistance and electrically controlled spin-polarization in transition metal-doped [6] cycloparaphenylenes. Phys. Lett. 2018;382:2763–2768. [Google Scholar]
- 27.Kayahara E., Patel V.K., Yamago S. Synthesis and characterization of [5] cycloparaphenylene. J. Am. Chem. Soc. 2014;136:2284–2287. doi: 10.1021/ja413214q. [DOI] [PubMed] [Google Scholar]
- 28.Darzi E.R., Jasti R. The dynamic, size-dependent properties of [5]–[12] cycloparaphenylenes. Chem. Soc. Rev. 2015;44:6401–6410. doi: 10.1039/c5cs00143a. [DOI] [PubMed] [Google Scholar]
- 29.Matsui K., Segawa Y., Itami K. Synthesis and properties of cycloparaphenylene-2, 5-pyridylidene: a nitrogen-containing carbon nanoring. Org. Lett. 2012;14:1888–1891. doi: 10.1021/ol3005112. [DOI] [PubMed] [Google Scholar]
- 30.Iwamoto T., Watanabe Y., Takaya H., Haino T., Yasuda N., Yamago S. Size‐and orientation‐selective encapsulation of C70 by cycloparaphenylenes. Chem. Eur J. 2013;19:14061–14068. doi: 10.1002/chem.201302694. [DOI] [PubMed] [Google Scholar]
- 31.Hu L., Guo Y., Yan X., Zeng H., Zhou J. Electronic transport properties in [n] cycloparaphenylenes molecular devices. Phys. Lett. 2017;381:2107–2111. [Google Scholar]
- 32.White B.M., Zhao Y., Kawashima T.E., Branchaud B.P., Pluth M.D., Jasti R. Expanding the chemical space of biocompatible fluorophores: nanohoops in cells. ACS Cent. Sci. 2018;4:1173–1178. doi: 10.1021/acscentsci.8b00346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Omachi H., Nakayama T., Takahashi E., Segawa Y., Itami K. Initiation of carbon nanotube growth by well-defined carbon nanorings. Nat. Chem. 2013;5:572–576. doi: 10.1038/nchem.1655. [DOI] [PubMed] [Google Scholar]
- 34.Ueno H., Nishihara T., Segawa Y., Itami K. Cycloparaphenylene‐based ionic donor–acceptor supramolecule: isolation and characterization of Li+@ C60⊂[10] CPP. Angew. Chem. 2015;127:3778–3782. doi: 10.1002/anie.201500544. [DOI] [PubMed] [Google Scholar]
- 35.Xia J., Jasti R. Synthesis, characterization, and crystal structure of [6] cycloparaphenylene. Angew. Chem. Int. Ed. 2012;51:2474–2476. doi: 10.1002/anie.201108167. [DOI] [PubMed] [Google Scholar]
- 36.Vidal Á.V., López C.S., Faza O.N. Nitrogen doped nanohoops as promising CO 2 capturing devices. Phys. Chem. Chem. Phys. 2018;20:8607–8615. doi: 10.1039/c7cp08498f. [DOI] [PubMed] [Google Scholar]
- 37.Zhang F., Du X., Zhang D., Wang Y., Lu H., Chen C. A green fluorescent nitrogen‐doped aromatic belt containing a [6] cycloparaphenylene skeleton. Angew. Chem. Int. Ed. 2021;60:15291–15295. doi: 10.1002/anie.202104259. [DOI] [PubMed] [Google Scholar]
- 38.Zhang J. Cycloparaphenylene crystals: packed carbon nanorings for energy absorption and thermal insulation. Comput. Mater. Sci. 2019;168:96–103. [Google Scholar]
- 39.Li Y., Segawa Y., Yagi A., Itami K. A nonalternant aromatic belt: methylene-bridged [6] cycloparaphenylene synthesized from pillar [6] arene. J. Am. Chem. Soc. 2020;142:12850–12856. doi: 10.1021/jacs.0c06007. [DOI] [PubMed] [Google Scholar]
- 40.Wang L., Chen S.-H., He D., Li Q.-J., Liu Y.-L., Wang M.-S. Size dependence of [n] cycloparaphenylenes (n= 9–20): relationship between aromaticity and third-order nonlinear optical properties. J. Phys. Chem. C. 2020;124:11081–11091. [Google Scholar]
- 41.Zhang Y., Wang H.-Q., Zhao Y.-Y., Qiu Y.-Q. Novel cyclic and linearizing cyclic Pd (II) nanohoop-based coordination complexes achieving nonlinear optical activity transparency trade-off optimization. Org. Electron. 2020;78 [Google Scholar]
- 42.Si Y., Yang G. The photophysical properties of cycloparaphenylene-based compounds with figure-eight configurations. New J. Chem. 2020;44:12185–12193. [Google Scholar]
- 43.Gong L., Ma C., Lin W., Lv J., Zhang X. Electronic structure and second-order nonlinear optical properties of lemniscular [16] cycloparaphenylene compounds. RSC Adv. 2020;10:13984–13990. doi: 10.1039/d0ra01323d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Seal P. Nonlinear optical properties of the hula hoop [n]‐Cycloparaphenylenes and their halo derivatives at Nd: YAG laser frequency. ChemistrySelect. 2017;2:8393–8401. [Google Scholar]
- 45.Nishihara T., Segawa Y., Itami K., Kanemitsu Y. Excited states in cycloparaphenylenes: dependence of optical properties on ring length. J. Phys. Chem. Lett. 2012;3:3125–3128. doi: 10.1021/jz3014826. [DOI] [PubMed] [Google Scholar]
- 46.Rodriguez-Hernandez B., Ondarse-Alvarez D., Oldani N., Martinez-Mesa A., Uranga-Piña L., Tretiak S., Fernandez-Alberti S. Modification of optical properties and excited-state dynamics by linearizing cyclic paraphenylene chromophores. J. Phys. Chem. C. 2018;122:16639–16648. [Google Scholar]
- 47.Li P., Sisto T.J., Darzi E.R., Jasti R. The effects of cyclic conjugation and bending on the optoelectronic properties of paraphenylenes. Org. Lett. 2014;16:182–185. doi: 10.1021/ol403168x. [DOI] [PubMed] [Google Scholar]
- 48.Chai J.-D., Head-Gordon M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008;10:6615–6620. doi: 10.1039/b810189b. [DOI] [PubMed] [Google Scholar]
- 49.Wang L., Wang W.-Y., Fang X.-Y., Zhu C.-L., Qiu Y.-Q. Intramolecular photo-induced electron transfer in nonlinear optical chromophores: fullerene (C60) derivatives. Org. Electron. 2016;33:290–299. [Google Scholar]
- 50.Oviedo M.B., V Ilawe N., Wong B.M. Polarizabilities of π-conjugated chains revisited: improved results from broken-symmetry range-separated DFT and new CCSD (T) benchmarks. J. Chem. Theor. Comput. 2016;12:3593–3602. doi: 10.1021/acs.jctc.6b00360. [DOI] [PubMed] [Google Scholar]
- 51.Bano R., Ayub K., Mahmood T., Arshad M., Sharif A., Tabassum S., Gilani M.A. Mixed superalkalis are a better choice than pure. Dalton Trans. 2022;51:8437–8453. doi: 10.1039/d2dt00321j. [DOI] [PubMed] [Google Scholar]
- 52.Rad A.S., Ayub K. Adsorption properties of acetylene and ethylene molecules onto pristine and nickel-decorated Al12N12 nanoclusters. Mater. Chem. Phys. 2017;194:337–344. [Google Scholar]
- 53.Savarese M., Bremond E., Adamo C. Exploring the limits of recent exchange–correlation functionals in modeling lithium/benzene interaction. Theor. Chem. Acc. 2016;135:1–11. [Google Scholar]
- 54.Lu T., Chen F. Multiwfn: a multifunctional wavefunction analyzer. J. Comput. Chem. 2012;33:580–592. doi: 10.1002/jcc.22885. [DOI] [PubMed] [Google Scholar]
- 55.Humphrey W., Dalke A., Schulten K. VMD: visual molecular dynamics. J. Mol. Graph. 1996;14:33–38. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 56.Ullah F., Kosar N., Arshad M.N., Gilani M.A., Ayub K., Mahmood T. Design of novel superalkali doped silicon carbide nanocages with giant nonlinear optical response. Opt Laser. Technol. 2020;122 doi: 10.1016/j.optlastec.2019.105855. [DOI] [Google Scholar]
- 57.Frisch M.J., Trucks G.W., Schlegel H.B., Scuseria G.E., Robb M.A., Cheeseman J.R., Scalmani G., Barone V., Petersson G.A., Nakatsuji H., Li X., Caricato M., Marenich A.V., Bloino J., Janesko B.G., Gomperts R., Mennucci B., Hratchian H.P., Ortiz J.V., Izmaylov A.F., Sonnenberg J.L., Williams-Young D., Ding F., Lipparini F., Egidi F., Goings J., Peng B., Petrone A., Henderson T., Ranasinghe D., Zakrzewski V.G., Gao J., Rega N., Zheng G., Liang W., Hada M., Ehara M., Toyota K., Fukuda R., Hasegawa J., Ishida M., Nakajima T., Honda Y., Kitao O., Nakai H., Vreven T., Throssell K., Montgomery J.A., Peralta J.E., Ogliaro F., Bearpark M.J., Heyd J.J., Brothers E.N., Kudin K.N., Staroverov V.N., Keith T.A., Kobayashi R., Normand J., Raghavachari K., Rendell A.P., Burant J.C., Iyengar S.S., Tomasi J., Cossi M., Millam J.M., Klene M., Adamo C., Cammi R., Ochterski J.W., Martin R.L., Morokuma K., Farkas O., Foresman J.B., Fox D.J. Gaussian, Inc.; Wallingford CT: 2016. Gaussian 16, Revision B. 01. [Google Scholar]
- 58.Dennington R., Keith T., Millam J. Semichem Inc.; Shawnee Mission. KS.: 2019. GaussView, Version 6.1.1. [Google Scholar]
- 59.Niu M., Yu G., Yang G., Chen W., Zhao X., Huang X. Doping the alkali atom: an effective strategy to improve the electronic and nonlinear optical properties of the inorganic Al12N12 nanocage. Inorg. Chem. 2014;53:349–358. doi: 10.1021/ic4022917. [DOI] [PubMed] [Google Scholar]
- 60.Munsif S., Khan S., Ali A., Gilani M.A., Iqbal J., Ludwig R., Ayub K. Remarkable nonlinear optical response of alkali metal doped aluminum phosphide and boron phosphide nanoclusters. J. Mol. Liq. 2018;271:51–64. [Google Scholar]
- 61.Sohail M., Khaliq F., Mahmood T., Ayub K., Tabassum S., Gilani M.A. Influence of bi-alkali metals doping over Al12N12 nanocage on stability and optoelectronic properties: a DFT investigation. Radiat. Phys. Chem. 2021;184 doi: 10.1016/j.radphyschem.2021.109457. [DOI] [Google Scholar]
- 62.Wajid S., Kosar N., Ullah F., Gilani M.A., Ayub K., Muhammad S., Mahmood T. Demonstrating the potential of alkali metal-doped cyclic C6O6Li6 organometallics as electrides and high-performance NLO materials. ACS Omega. 2021;6:29852–29861. doi: 10.1021/acsomega.1c04349. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Ayub K. Are phosphide nano-cages better than nitride nano-cages? A kinetic, thermodynamic and non-linear optical properties study of alkali metal encapsulated X 12 Y 12 nano-cages. J. Mater. Chem. C. 2016;4:10919–10934. [Google Scholar]
- 64.Naeem J., Bano R., Ayub K., Mahmood T., Tabassum S., Arooj A., Gilani M.A. Assessment of alkali and alkaline earth metals doped cubanes as high-performance nonlinear optical materials by first-principles study. J. Sci. Adv. Mater. Devices. 2022;7 [Google Scholar]
- 65.Kavitha E., Sundaraganesan N., Sebastian S., Kurt M. Molecular structure, anharmonic vibrational frequencies and NBO analysis of naphthalene acetic acid by density functional theory calculations. Spectrochim. Acta Part A Mol. Biomol. Spectrosc. 2010;77:612–619. doi: 10.1016/j.saa.2010.06.034. [DOI] [PubMed] [Google Scholar]
- 66.Maria J. Iqbal, Ludwig R., Ayub K. Phosphides or nitrides for better NLO properties? A detailed comparative study of alkali metal doped nano-cages. Mater. Res. Bull. 2017;92:113–122. doi: 10.1016/j.materresbull.2017.03.065. [DOI] [Google Scholar]
- 67.Bano R., Arshad M., Mahmood T., Ayub K., Sharif A., Tabassum S., Gilani M.A. Superalkali (Li2F, Li3F) doped Al12N12 electrides with enhanced static, dynamic nonlinear optical responses and refractive indices. Mater. Sci. Semicond. Process. 2022;143 [Google Scholar]
- 68.Johnson E.R., Keinan S., Mori-Sánchez P., Contreras-García J., Cohen A.J., Yang W. Revealing noncovalent interactions. J. Am. Chem. Soc. 2010;132:6498–6506. doi: 10.1021/ja100936w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Lefebvre C., Rubez G., Khartabil H., Boisson J.-C., Contreras-García J., Hénon E. Accurately extracting the signature of intermolecular interactions present in the NCI plot of the reduced density gradient versus electron density. Phys. Chem. Chem. Phys. 2017;19:17928–17936. doi: 10.1039/c7cp02110k. [DOI] [PubMed] [Google Scholar]
- 70.Firme C.L., V Monteiro N.K., Silva S.R.B. QTAIM and NCI analysis of intermolecular interactions in steroid ligands binding a cytochrome P450 enzyme–Beyond the most obvious interactions. Comput. Theor. Chem. 2017;1111:40–49. [Google Scholar]
- 71.Bader R.F.W. Atoms in molecules. Acc. Chem. Res. 1985;18:9–15. [Google Scholar]
- 72.Esrafili M.D. Investigation of H-bonding and halogen-bonding effects in dichloroacetic acid: DFT calculations of NQR parameters and QTAIM analysis. J. Mol. Model. 2012;18:5005–5016. doi: 10.1007/s00894-012-1496-y. [DOI] [PubMed] [Google Scholar]
- 73.Dimić D., Petković M. Control of a photoswitching chelator by metal ions: DFT, NBO, and QTAIM analysis. Int. J. Quant. Chem. 2016;116:27–34. [Google Scholar]
- 74.Sun W.M., Fan L.T., Li Y., Liu J.Y., Wu D., Li Z.R. On the potential application of superalkali clusters in designing novel alkalides with large nonlinear optical properties. Inorg. Chem. 2014;53:6170–6178. doi: 10.1021/ic500655s. [DOI] [PubMed] [Google Scholar]
- 75.Chen W., Yu G., Jin P., Li Z.-R., Huang X.-R. The heavier, the better—increased first hyperpolarizabilities in M@ Calix [4] pyrrole (M= Na and K) J. Comput. Theor. Nanosci. 2011;8:2482–2487. [Google Scholar]
- 76.Gilani M.A., Tabassum S., Gul U., Mahmood T., Alharthi A.I., Alotaibi M.A., Geesi M., Sheikh R., Ayub K. Copper-doped Al12N12 nano-cages: potential candidates for nonlinear optical materials. Appl. Phys. A. 2018;124:1–9. [Google Scholar]
- 77.Datta A., Pati S.K. Dipolar interactions and hydrogen bonding in supramolecular aggregates: understanding cooperative phenomena for 1st hyperpolarizability. Chem. Soc. Rev. 2006;35:1305–1323. doi: 10.1039/b605478a. [DOI] [PubMed] [Google Scholar]
- 78.d Oudar J.L. Optical nonlinearities of conjugated molecules. Stilbene derivatives and highly polar aromatic compounds. J. Chem. Phys. 1977;67:446–457. [Google Scholar]
- 79.Li X., Zhang Y., Lu J. Remarkably enhanced first hyperpolarizability and nonlinear refractive index of novel graphdiyne-based materials for promising optoelectronic applications: a first-principles study. Appl. Surf. Sci. 2020;512 [Google Scholar]
- 80.Zyss J., Brasselet S., Thalladi V.R., Desiraju G.R. Octupolar versus dipolar crystalline structures for nonlinear optics: a dual crystal and propagative engineering approach. J. Chem. Phys. 1998;109:658–669. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.