A broadly applicable approach to enrich electronic-health-record cohorts by identifying patients with complete data: a multisite evaluation

Abstract

Objective

Patients who receive most care within a single healthcare system (colloquially called a “loyalty cohort” since they typically return to the same providers) have mostly complete data within that organization’s electronic health record (EHR). Loyalty cohorts have low data missingness, which can unintentionally bias research results. Using proxies of routine care and healthcare utilization metrics, we compute a per-patient score that identifies a loyalty cohort.

Materials and Methods

We implemented a computable program for the widely adopted i2b2 platform that identifies loyalty cohorts in EHRs based on a machine-learning model, which was previously validated using linked claims data. We developed a novel validation approach, which tests, using only EHR data, whether patients returned to the same healthcare system after the training period. We evaluated these tools at 3 institutions using data from 2017 to 2019.

Results

Loyalty cohort calculations to identify patients who returned during a 1-year follow-up yielded a mean area under the receiver operating characteristic curve of 0.77 using the original model and 0.80 after calibrating the model at individual sites. Factors such as multiple medications or visits contributed significantly at all sites. Screening tests’ contributions (eg, colonoscopy) varied across sites, likely due to coding and population differences.

Discussion

This open-source implementation of a “loyalty score” algorithm had good predictive power. Enriching research cohorts by utilizing these low-missingness patients is a way to obtain the data completeness necessary for accurate causal analysis.

Conclusion

i2b2 sites can use this approach to select cohorts with mostly complete EHR data.

Background and significance

Electronic health records (EHRs) contain billions of data points, which have been utilized in tens of thousands of studies and initiatives to accelerate research, and various consortiums and networks have done this at a national or international scale.^1–6 The use of EHRs for high-impact research is, however, hampered by data quality issues.^7,8 The problem of missing data is among the most urgent and pervasive.^9–13 Patients may receive care at multiple healthcare institutions and it is frequently impossible to aggregate patient data from all these locations. This is due to both the complexity of the healthcare regulatory environment and the difficulty of linking patients across institutions.^14–18 For instance, a patient may have no record of diabetes in an institution’s EHR; however, this does not imply that the patient does not have diabetes. The patient might have received their diabetes care at another institution that is not included in the EHR. This can result in many false negative data points, creating significant biases in EHR-based research that could misrepresent, for instance, the prevalence of a disease or its treatment.^11,19 Consequently, it is essential to ensure that patients included in EHR data analyses have a reasonable likelihood of complete data, also known as “low EHR discontinuity.”^20–22 In cases where pooling data across healthcare systems is not possible, a solution can be through cohort selection, enriching research cohorts to include only patients with complete-enough data to not result in false negatives due to missing data. Since these patients are “loyal” to the healthcare system, we refer to them as a loyalty cohort. Not all missingness is false missingness—a patient might be relatively healthy and only seek healthcare at a bi-annual physical. A robust loyalty cohort would consist of both healthy and chronically ill patients, but only those who primarily utilize the same healthcare system.

It is important to note that this approach uses one of several approaches to adjust for missing data (cohort selection), which can alter the biases in the data. Hospital data are inherently biased (eg, because of missingness; toward people who seek medical care) and the loyalty cohort approach will shift that bias toward patients with complete data, moving the cohort demographics away from the mean. More detailed information can be found in the “Discussion” section under “Loyalty cohorts and bias.”

Lin et al²⁰ developed a machine-learning method for constructing such a loyalty cohort. They chose 20 EHR-derived proxy variables to construct a model that predicts loyalty, using claims data as the gold standard for model training and evaluation. Their model was highly correlated with Mean Proportion of Encounters Captured by the EHR system compared with the claims data. The researchers later found that the proportion of misclassifications in a machine-learning task was reduced by more than half after applying their loyalty cohort filter.¹¹ Although the Lin model was successful at 2 institutions and the EHR proxy selections can guide future work, the implementation and possibly the regression model are not generally applicable to the vast majority of EHR data warehouses. Institution-specific data collection workflows, local medical coding systems, and practice variation all make it difficult to develop generalized EHR-based algorithms. Complex institution-specific data models further complicate the development of programs that can be shared.

Fortunately, several projects have developed common data models (CDMs) and harmonized concept dictionaries for EHR data warehousing and networking. The widely used Informatics for Integrating Biology and the Bedside (i2b2) platform is a well-established open-source clinical data warehousing and analytics platform that has been in use for over 15 years, presently at over 200 locations worldwide.^3,23,24 It is designed to simplify data ingestion for local institutions, and it is also used in large, federated research networks where the Shared Health Research Informatics NEtwork (SHRINE) software links the institutional i2b2s.^25,26 The Evolve to Next-gen Accrual to Clinical Trials (ENACT) network that links 57 CTSA hubs uses i2b2 and SHRINE and has developed and maintains a harmonized concept dictionary called the ENACT ontology.^2,27 In i2b2, an ontology organizes patient-related concepts (eg, International Classification of Diseases Tenth Edition [ICD-10] and Logical Observation Identifiers Names and Codes [LOINC]) into a searchable hierarchy. This ontology provides an “information model” for the i2b2 instance, defining all possible concepts that can be represented. The ontology allows local datasets to be queried using shared concepts.²⁸ Our goal was to develop a program to compute loyalty cohorts using the i2b2 and ENACT infrastructure, such that it could be used by any site in the ENACT network “out-of-the-box.”

Objective

In this study, we utilize the variables and coefficients defined by Lin et al²⁹ as the scaffolding for a robust, widely applicable loyalty cohort calculation tool that can be implemented by any site in the ENACT network. The objective of our loyalty score strategy is to select enriched cohorts that are not biased by missingness. Because patients who are loyal will have a return visit, we evaluate the score by its ability to accurately predict patients that return to the healthcare system during a follow-up period. This provides a silver standard without manually evaluating patient charts. This also allows us to tune the algorithm at each performance site. We further use the Charlson Comorbidity Index to ensure that the loyalty score is not biased toward capturing only patients with heavy healthcare utilization due to end-of-life care or chronic disease. The Charlson index is a validated indicator of chronic disease severity in EHR diagnosis data.³⁰ Three healthcare systems comprising 52 hospitals participated in this analysis.

Materials and methods

Loyalty cohort algorithm

Lin’s approach to predicting patients with complete data (a “loyalty cohort”) involved scoring each patient via a regression equation utilizing 20 high-level binary variables (or features) that were clinically determined to be proxies of patient loyalty.²⁹ Because the features were defined only at an abstract level, our first task was to quantify them using patient EHR data by mapping them to the ENACT i2b2 ontology. The mapping was performed in the following manner. An i2b2 ontology is a hierarchically arranged concept dictionary to which all sites in a network map their EHR data. The ENACT ontology provides a comprehensive set of Current Procedural Terminology (CPT), Healthcare Common Procedure Coding System (HCPCS), ICD, LOINC, and RxNorm terms, which we used in our mappings. We mapped each variable to one or more “folders” or leaf nodes in the ontology. As an example of leaf nodes, we mapped “Flu Shot” to a set of 18 nodes, corresponding to CPT, HCPCS, and ICD codes. As an example of folders, we mapped “Medication Use” to the “All Medications Alphabetical” folder. This allowed us to reuse concept sets (folders) and nodes previously defined for the ENACT network and it ensured data harmonization across sites. These mappings were performed initially by the authors using the i2b2 Terminology Search tool to find relevant elements, and then these were verified and expanded by a clinical expert who had familiarity with medical terminologies. Each variable could then be computed by looking for the presence of facts defined in the appropriate concept folder in the ENACT ontology. The default set of codes associated with the 20 variables is included in Table S2. This set has been expanded to include children of the ontology folders. Note that our tool allows individual sites to customize the code list to reflect site-specific practices. (In the analysis described below, Site B included a local code for BMI.)

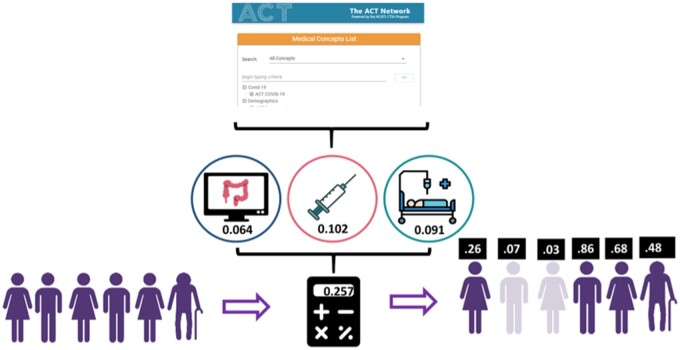
We translated the methodology described in Lin et al²⁰ into a series of programmatic steps and then implemented the steps and the mapped concepts as a SQL Server stored procedure and equivalent Oracle script to compute a “loyalty score” on all patients, using a regression equation that utilizes the 20 binary variables. The equation (including variables and coefficients) is as described in Lin et al.^20,29 The program allows the coefficients to be customized by changing a SQL data table if the equation is retrained, such as described in “Evaluation” below. The variables include: healthcare utilization metrics such as multiple visits to the same provider, an emergency department visit, multiple medication or diagnosis codes; and specific measures indicating a patient’s primary care home, such as PSA tests, Pap tests, and mammograms. A listing of the concepts and the coding systems we mapped them to can be found in Table S1. The list of concepts with coefficients can be found in Table 2 in Lin et al.²⁹ A graphical depiction of the application of the equation to mapped data is depicted in Figure 1.

Table 2.

The loyalty cohort algorithm’s performance in predicting return, shown as AUC and Youden’s J

	Site A	Site B	Site C
Original coefficients
Score AUC	0.778	0.739	0.810
Youden sensitivity	0.638	0.578	0.679
Youden specificity	0.811	0.779	0.802
Youden point threshold	0.321	0.328	0.291
Score minimum and maximum	−0.026, 1.048
Percent of patients with a return in the HER	73.1%	47.5%	58.4%
Percent of patients predicted to be loyal	51.7%	39.1%	47.9%
Retrained coefficients
MLHO (LASSO) AUC	0.819	0.772	0.827
MLHO CV AUC	0.819	0.770	0.825
Youden sensitivity	0.637	0.627	0.676
Youden specificity	0.811	0.799	0.832
Youden point threshold	0.321	0.532	0.614
Score minimum/maximum	−1.10, 4.52	−1.03, 2.03	−0.8, 3.78
Percent of patients predicted to be loyal	56.9%	40.3%	46.6%

Notes: The top section shows each site’s results with the original coefficients and the bottom section shows the retrained coefficients. Also shown is the percent of patients predicted to be loyal vs the percent who actually return when using Youden’s J as the threshold, in both the original and retrained models.

Figure 1.

The algorithm uses ENACT’s medical concept list to quantify important indicators of patient loyalty and it uses these along with a regression equation to compute a score for every patient. Scores above a certain threshold indicate that a patient is more likely to have complete data.

The loyalty cohort program builds 3 tables: one with patient-level flags and loyalty score, one with summary output to be used by implementers to check their local loyalty cohort at their site, and a table of the Charlson Comorbidity Index for each patient. A technical step-by-step description of the algorithm’s process can be found in the Supplementary Appendix.

Evaluation design

We evaluated the original loyalty score algorithm and its regression coefficients by performing a prediction task, where an individual’s loyalty score derived from 2 years of EHR data is used to predict the probability of return to the healthcare system for care in year 3. We felt that a return within a year is a reasonable proxy of loyalty and therefore lower data missingness. Three hospital systems, Mass General Brigham, University of Pittsburgh, and University of Kentucky, comprising a total of 52 hospitals, participated in the evaluation. More information on the sites can be found in Table 1. Each of the 3 hospital systems (hereafter referred to as sites) have a pre-existing i2b2 clinical data warehouse that pools and links patient data from their multiple hospitals, with data elements already mapped to the ENACT network ontology. The sites extracted data on a cohort including all patients with any encounter (including inpatient, outpatient, and other types such as telephone encounters) between January 1, 2017 and December 31, 2018 who were over 18 as of January 1, 2017. Only patients over 18 are used because a pediatric population would require different proxies and measurements of utilization that are likely not generalizable to adults and was not considered in the original model. This study period was selected to avoid the changes in healthcare utilization during the peaks of the COVID-19 pandemic. Data were extracted on each patient over the 2-year measure period and these data were used to compute the loyalty score and binary variables. A 2-year window was selected because, during development of the evaluation protocol, we found 2 years gave the best balance of performance and data requirements. As a target variable for evaluation, we computed “return,” defined as a binary variable indicating whether the patient had at least 1 visit during the 1-year follow-up period January 1, 2019–December 31, 2019. If a patient had died during the 3-year period, they were excluded from further analysis.

Table 1.

Overview of the 3 healthcare systems participating and the cohort selected for this study

Healthcare system	Number of hospitals	Number of inpatient discharges per year	Evaluation cohort size	Evaluation cohort sex distribution	Evaluation cohort age distribution
Mass General Brigham (Partners Healthcare)	10	∼150 000	1.4 million patients	41% Male, 59% Female	19–34: 20% 35–64: 51% ≥65: 29%
University of Pittsburgh/UPMC	39	∼350 000	2.3 million patients	44% Male, 56% Female	19–34: 24% 35–64: 48% ≥65: 28%
University of Kentucky	3	∼40 000	∼300 000 patients	41% Male, 59% Female	19–34: 23% 35–64: 51% ≥65: 26%

Each site ran the loyalty cohort program on its evaluation cohort, which calculated a score based on the 20 binary flags. From this we created R datasets consisting of patient identifiers, loyalty score and the binary flags of which it is composed, return indicator label, limited demographics (sex and age), and Charlson score and comorbidities. We wrote an analysis script in R using standard statistical packages as well as the previously published Machine Learns Health Outcomes (MLHO) machine-learning toolkit.³¹

To test the tool’s ability to predict patient loyalty to the respective healthcare system, we examined its performance in predicting return to receive care. At each site, we computed the area under the receiver operating characteristics curve (AUROC) and associated statistics using the loyalty score as the predictor variable and return as the outcome. We also computed the Youden’s J statistic (Youden’s index) as an operating point that maximizes potential effectiveness of a model.³²

We also compared the loyalty score to the Charlson Comorbidity Index to ensure that the loyalty cohort is not composed solely of the extremely ill. Using linear correlation tests, we compared the Charlson Index to loyalty score deciles to determine whether the Charlson score is distributed independently of loyalty score.

We used MLHO to re-train the loyalty score algorithm at each site to fine-tune and validate the transferability of the coefficients from the original algorithm to other institutions. This process produced new site-specific coefficients for the 20 binary features. (See Supplementary Appendix for technical step-by-step description.) We compared prediction performance of the re-trained local loyalty algorithm and evaluated the covariates’ coefficients. To retrain, we split the data into a training and holdout test set with a 30–70 ratio because of the large sample size and trained the algorithm using a Least Absolute Shrinkage and Selection Operator (LASSO) model—a penalized estimation method—with 5-fold cross-validation, controlling for age and sex.³³ We chose LASSO for comparability with the original equation coefficients, which were also computed using LASSO regression.³³ We then repeated the same calculation of AUROC in predicting return, which we report along with the cross-validation AUC (CVAUC), which is useful in detecting overfitting. A CVAUC value comparable to the AUC indicates no overfitting.

We then compared the relative feature importance at each site using both models (MLHO and original). We plotted the square root of the odds ratios associated with the regression equations on a logarithmic scale.

Finally, we performed a demographic shift analysis, comparing cohort demographics between the population and the loyalty cohort (after retraining with MLHO), to ascertain biases that could arise by using the loyalty cohort tool.

Each site ran the analysis locally and shared only the results presented in this manuscript. This project was approved by the Institutional Review Boards of each individual site.

Results

As reported in Table 1, the 3 hospital systems that participated, comprising 52 hospitals, included Mass General Brigham, University of Pittsburgh/UPMC, and University of Kentucky/UK HealthCare. To preserve institutional privacy, they are labeled as Sites A, B, and C, in random order. The sites extracted a cohort as described in the “Materials and Methods” with the size shown in Table 1. Each site executed the script to compute a loyalty score for each patient in the cohort and loaded this cohort into R locally for further analysis. No patient-level data were shared across sites.

Comparison with Charlson Comorbidity Index

First, we compared the Charlson Comorbidity Index of patients with loyalty scores in various deciles and found that in general the Charlson score varies independently of loyalty score, indicating that loyalty is measuring something more than chronic illness. We saw a similar distribution of Charlson Comorbidity Index scores across all deciles of loyalty. Pearson’s correlation coefficients were as follows: Site A—0.263, Site B—0.231, Site C—0.203.

Patient return analysis

Original and retrained scores

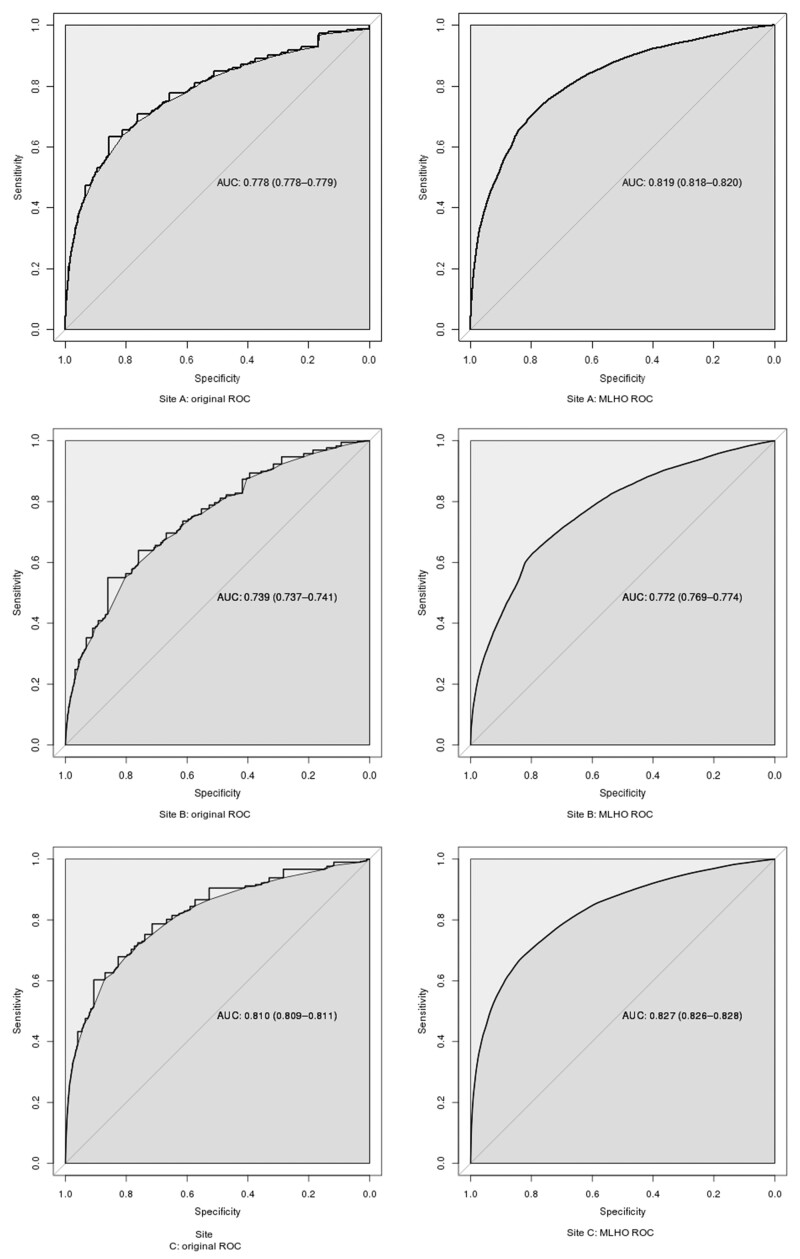
We studied the ability of the loyalty score to predict any visit (“return”) over the course of 1 year, as a proxy of loyalty and therefore low data missingness. In the top half of Table 2, we display the score’s predictive ability as measured by a ROC curve (including area under the curve—AUC—and Youden point). The actual ROC curves can be found in Figure 2. The Youden point is reported as a loyalty score, which, if exceeded, would qualify patients for inclusion in the cohort. In addition, the size of both the predicted loyalty cohort and the actual return cohort is presented.

Figure 2.

ROC curves of original and retrained loyalty algorithm at each site, showing ability to predict return within a year as an indicator of complete data.

After retraining the regression equation at each site using MLHO with a LASSO model, performance improved at every site compared to the previously published regression equation. The AUC and Youden sensitivity/specificity after retraining are shown in the bottom half of Table 2, and the actual ROC curves in Figure 2.

Predictive power of loyalty flags

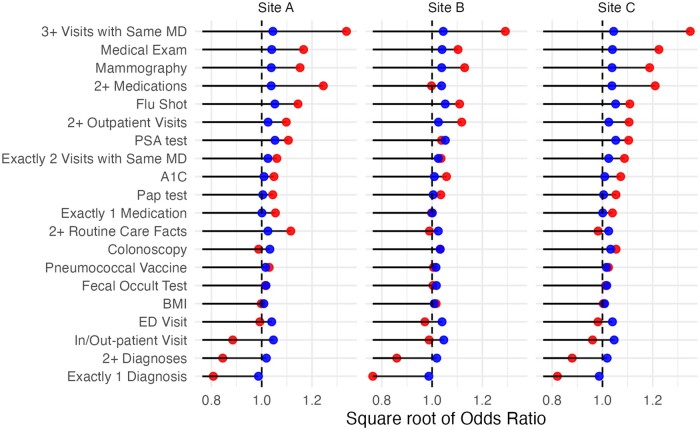
We also examined the relative contribution of the 20 features by plotting the square root of the odds ratios for each feature, both using the original equation (which is static across sites) and the performance-tuned equation (which is site-specific). These are shown in Figure 3, and the odds ratios are also repeated in Table 3, for clarity. Blue is the original equation and red is the tuned equation. A line is shown at 1.0, because points below this threshold indicate the feature is inversely predictive of loyalty. The prevalence of each flag in each site’s patient population is shown in Table 4, which is another dimension of the flag’s importance. The full descriptive name of the feature labels can be found in Table S1. The odds ratios are somewhat smaller in the original equation, which could be because a different LASSO penalization parameter was used (this was not given in Lin’s manuscript).

Figure 3.

Feature importance of the 20 binary variables, shown as square root of odds ratio. Original coefficients are blue, tuned coefficients are red. The output is sorted by the mean of the tuned (red) coefficients. The line at 1.0 shows the delineation of a positive vs negative predictor of loyalty.

Table 3.

Odds ratios (ORs) of each loyalty flag in the original equation and after being retrained at each site (shown in graphical form in Figure 3)

Loyalty flag	Original OR	Site A OR	Site B OR	Site C OR
PSA test	1.11	1.27	1.08	1.22
Flu shot	1.11	1.25	1.23	1.23
In/out-patient visit	1.10	0.75	0.98	0.92
3+ visits with same MD	1.09	1.81	1.67	1.82
Medical exam	1.08	1.25	1.22	1.50
ED visit	1.08	0.98	0.94	0.96
Mammography	1.08	1.39	1.28	1.41
2+ medications	1.08	1.56	1.00	1.46
Colonoscopy	1.07	0.98	1.07	1.11
2+ outpatient visits	1.05	1.21	1.25	1.22
Exactly 2 visits with same MD	1.05	1.12	1.07	1.18
2+ Routine care facts	1.05	1.20	0.98	0.97
2+ Diagnoses	1.04	0.70	0.74	0.77
Fecal occult test	1.03	1.03	1.01	1.02
Pneumococcal vaccine	1.03	1.10	1.01	1.05
A1C	1.02	1.12	1.12	1.15
BMI	1.02	1.00	1.03	1.01
Pap test	1.01	1.14	1.07	1.11
Exactly 1 medication	1.00	1.12	1.00	1.08
Exactly 1 diagnosis	0.97	0.64	0.58	0.67

Note: The odds ratios are sorted by the “Original OR” column.

Table 4.

Frequency of each flag at each site, as the percentage of patients having at least 1 instance of the flagged event

Loyalty flag	Site A frequency (%)	Site B frequency (%)	Site C frequency (%)
In/out-patient visit	92.3	88.1	97.5
2+ Outpatient visits	81.1	66.6	86.6
2+ Diagnoses	69.3	63.6	73.9
2+ Medications	70.9	53.9	51.1
3+ Visits with same MD	41.9	31.9	35.3
BMI	9.5	79.5	4.6
2+ Routine care facts	34.4	28.5	22.8
ED visit	24.7	28.1	21.9
Exactly 1 diagnosis	17.5	30.6	22.2
Medical Exam	26.0	14.9	25.1
Exactly 1 medication	10.4	21.8	16.5
A1C	15.2	15.8	16.8
Exactly 2 visits the same MD	12.3	12.7	11.3
Flu Shot	15.9	7.7	11.2
Mammography	13.9	5.8	13.7
Pap test	8.3	5.2	7.3
Colonoscopy	8.5	2.4	5.4
PSA test	6.0	2.1	4.4
Pneumococcal vaccine	3.8	2.9	3.7
Fecal occult test	3.7	0.7	0.8

Notes: The table is sorted by average frequency. Note that “In/out-patient visit” is not 100%, because sites can define other types of visits (such as telephone calls to patients). 2+ routine care facts refer to any 2 types of facts boldfaced in the table.

Finally, we compared loyalty cohort demographics between the population and the loyalty cohort after retraining with MLHO at each site (see Table 5). There were small shifts in the demographics that were largely consistent across sites.

Table 5.

Change in demographics after applying the loyalty filter, at each site

		Site A			Site B			Site C
Var.	Cat	All	Loyal	Δ	All	Loyal	Δ	All	Loyal	Δ
Gender	Female	57.0%	62.0%	4.9%	59.6%	65.5%	5.9%	58.6%	61.3%	2.7%
Gender	Male	42.9%	38.0%	−4.9%	40.4%	34.5%	−5.9%	41.4%	38.7%	−2.7%
Age Group	18–34	23.8%	17.0%	−6.8%	23.1%	16.8%	−6.3%	19.9%	14.9%	−5.0%
Age Group	35–44	13.3%	11.8%	−1.5%	15.6%	14.3%	−1.3%	13.9%	13.1%	−0.8%
Age Group	45–54	15.1%	15.8%	0.7%	16.7%	17.6%	0.9%	16.5%	17.3%	0.8%
Age Group	55–64	19.1%	21.9%	2.8%	19.1%	22.4%	3.3%	19.7%	21.6%	1.9%
Age Group	63–84	24.7%	29.2%	4.5%	23.2%	27.0%	3.8%	26.4%	29.6%	3.2%
Age Group	>84	4.0%	4.3%	0.3%	2.4%	1.9%	−0.5%	3.7%	3.5%	−0.2%
Race	American Indian	3.9%	2.4%	−1.5%	0.1%	0.2%	0.1%	0.1%	0.1%	0.0%
Race	Asian	1.2%	1.0%	−0.2%	1.4%	1.8%	0.4%	4.2%	4.3%	0.1%
Race	Black	7.6%	7.1%	−0.5%	7.9%	8.6%	0.7%	5.9%	5.9%	0.0%
Race	No information	0.3%	0.2%	−0.1%	3.1%	1.5%	−1.6%	9.4%	3.7%	−5.7%
Race	Other	3.6%	2.1%	−1.5%	0.0%	0.1%	0.1%	6.5%	6.5%	0.0%
Race	White	85.8%	88.7%	2.9%	87.3%	87.8%	0.5%	74.0%	79.4%	5.4%
Charlson	Index	1.7	2.12	0.42	1.96	2.46	0.5	1.72	2.14	0.41
Charlson	10 year survival probability	83.8%	79.1%	−4.7%	80.5%	75.1%	−5.4%	84.0%	78.9%	−5.2%

Note: The delta column is the shift after applying the filter (eg, Loyal-All).

Discussion

We used a novel heuristic algorithm based on a previously published method to identify patients with high data completeness. We call this a “loyalty cohort,” because patients with complete data in one EHR must be loyal to the association healthcare system. We created an evaluation tool that assigns a completeness-likelihood score (“loyalty score”) to any EHR dataset using the i2b2 data model and data mapped to the ENACT network ontology. While the original approach required claims data for evaluation, we developed a method to evaluate and then tune the algorithm’s performance at specific sites without the use of additional data sources, by examining whether the patient returned for care during a follow-up period. Return within a year was chosen as a proxy for loyalty because, while it does not demonstrate that the patient receives care exclusively at the site, it does demonstrate that the patient receives regular care at the site. This is a silver standard, which is a reasonable guess at the truth. Silver standards are used when gold standard truth is impossible or impractical to obtain. Here, the gold standard would be either manual chart review (but reviewing thousands of records by hand is impractical) or claims data (which is also impractical to obtain).

Our algorithm performed similarly at all 3 institutions. This demonstrates that the original coefficients may be sufficiently transferable to other institutions without even requiring local retraining. This was significant because the implemented loyalty score was initially trained and tested on data from only 1 institution.

Using a 2-year period to compute loyalty score, we measured the AUC for identifying patients who returned during a 1-year follow-up in 2019. Sites had an average AUC of 0.77 when using the original regression equation, but after site-specific tuning, the average AUC increased to 0.80. The CVAUC was similar to the AUC on the holdout set, indicating that the model’s parameters were not overfitting. Both models reduced the cohort size by >40%, which can reduce the computational burden of answering research questions while improving data quality. When the original method was validated, the authors used the 20% of patients with the highest loyalty score as the loyalty cohort. Here, we used a statistically determined method (the Youden point), which selected between 39% and 52% of patients. We used this approach because we found that this accounted dynamically for the differences in populations and hospital characteristics that influenced the likelihood of loyalty at each site. Of course, if a different balance of sensitivity and specificity is desired, a different point on the ROC curve can be chosen.

Variation in loyalty flag importance

The top contributors to patient loyalty were generally similar across sites, but the specific top contributors varied. Factors such as multiple visits and some screening measures like mammography were significant contributors at all sites. However, the impact of other screening measures such as PSA tests and Pap smears varied across sites. Also, at one site, medication use was not a large contributor, but at the other sites, 2 or more medication records played an important role. These differences are most likely due to differences in coding and mapping between sites (see Limitations) or to different age distributions in the population (eg, one would not expect a colonoscopy to appear for patients under 45).

Before and after retraining, the strong and weak predicators of loyalty remained stable in many cases, but in some cases the magnitude changed significantly (eg, 2+ Medications, 3+ Visits with Same MD) or even reversed direction to become a negative predictor. This highlights the importance of retraining on local data. The reversals likely all follow from a similar reasoning, so we take “In/Out-patient Visit” flag as an exemplar. Over 90% of the population had an in-person visit but it had a negative impact on score at all sites after retraining. This is likely because patients with a single visit are likely not loyal, thus the regression algorithm picks a negative coefficient for “1+ visit” but large positive coefficients for “2+ visits.” Reversals also occurred for 1+ Diagnosis, 1+ Visits, and ED Visit, which could also indicate the patient had only a single visit.

The flags with the most average impact (high or low odds ratios) across sites tended to have a high frequency in the population, whereas the flags that varied across sites the most had much lower prevalence in the population. The high variance was therefore likely to be caused by overfitting on small population prevalence. For example, medication usage and multiple visits were present in much of the population at all sites, whereas fecal occult tests and pneumococcal vaccines were in a very small percentage of patient records. This is good news for the applicability of the loyalty score, because it shows that the most common EHR data elements are the most important in predicting loyalty.

Our comparison of the loyalty score to the Charlson Comorbidity Index confirmed that loyalty captures a different characteristic of patients than chronic disease. At all 3 sites, the distribution of Charlson scores was similar across all loyalty deciles. This was significant because, while the most obvious naive approach to selecting patients with high data completeness would be to select patients with the highest disease burden, loyalty cohorts should also include patients with lower disease burdens.

Loyalty cohorts and bias

Loyalty cohorts are just one of many imperfect approaches to dealing with missing data, and it is one that by definition introduces a bias to the cohort—toward patients who are loyal. This subset of patients will have different population characteristics than the whole. Previous work by several of the authors specifically explored how different types of loyalty cohort filters introduce particular cohort biases,¹⁹ and how unrecognized bias can change the performance characteristics of analyses.³⁴ Weber et al’s conclusion was that in choosing a loyalty cohort, there is a trade-off between missingness (which creates biases in the data) and biases in the selected cohort. Both manuscripts suggest that this can be adjusted to remove known cohort biases based on the needs of the application. Some options for adjustment include: changing the loyalty threshold to be more inclusive; sub-sampling the loyalty cohort to choose, eg, the same demographic mix as the whole population; or weighting patients by the loyalty score in a particular machine-learning task, rather than removing them entirely.

A demographic analysis, as we performed in this study, can detect potential biases. Here, the loyalty cohort at all sites was more female (2.7%–5.9%) and older than the general population. They were also mildly sicker, with mean increase in Charlson Index by 0.45 and mean decrease in Charlson 10-year survival probability by 5.1%. This is consistent with known trends in healthcare, especially that young-to-middle-age men who are healthy tend not to use the healthcare system (and are therefore not loyal).³⁵ These small but consistent and explainable differences give confidence that the loyalty score approach does not introduce obvious biases.

Additionally, to further account for hidden bias, a sensitivity analysis can be performed when applying the loyalty cohort method to specific machine-learning tasks. Sensitivity analysis is an established approach to understanding the sensitivity of particular analyses to biases, including hidden biases.^36,37 (Interestingly, Rosenbaum finds that even cohorts with hidden biases can frequently be used to draw correct or mostly correct conclusions.)

Hospital data are already full of biases without any cohort selection, because it is not a random sample of the population.³⁸ Demographic biases could exist from the hospital’s location and reputation, information biases can be introduced by particular EHR workflows, and the time of day introduces bias as well.³⁹ However, bias due to incomplete data is one of the most important to address, because it directly results in false negatives in the data.^10,11 The goal in the present manuscript is to find the most important factors in predicting completeness and a method for training an AI approach for filtering based on these characteristics. The resulting loyalty cohort could then be filtered to match the needs of the application.

Alternative approaches to missing data

The loyalty algorithm combats the missing data problem by cohort selection. By finding patients who have “complete-enough” data, the approach leverages an enriched subset of the available data. There are many other approaches to dealing with missing data. The optimal approach would be to pool data across many sites and link the patients’ records across all of them. Although there are some successful linked datasets and interesting technical approaches to linking data, record linkage is frequently not feasible due to regulatory issues, privacy concerns, and the technical challenges of linking patient identifiers.^14,16–18 A third approach to missing data is imputation, which adds information to a patients’ record based on other factors in the record—for example, imputation might add a diabetes diagnosis to all patients with high hemoglobin A1C regardless of what was in the record. Imputation has been used successfully when there is some latent information that can be leveraged to impute a value, but because EHR data missingness is not at random, the application must be designed very carefully.⁴⁰ With time-series data (eg, waveform data such as blood oxygen monitoring or repeated laboratory measurements), imputation is more often used, frequently relying on emergent or known patterns due to frequent sampling.^41,42 Imputation could be a possible alternative approach to cohort selection if the expected eventual use-case involves time-series measurements. A fourth approach is to generate synthetic data that try to mimic the statistical properties of the real data, eg, with Generative Adversarial Networks.⁴³ This approach is only applicable to research at the population level because the data represent statistical correlations, not real patients. It also has other limitations, such as algorithmic challenges in generating realistic EHR data (which is an irregularly sampled time-series),⁴⁴ and a tendency for synthetic data to drift from real data over time.⁴⁵

Limitations

One must be aware of potential biases in any cohort selection task, as outlined in the “Discussion” section. Although our analysis suggests that the loyalty score does not introduce any obvious bias, analysis of additional demographic variables (eg, home zip code and social determinants of health) were not available in the datasets we used for this study. We acknowledge that these are important factors that should be included in future research on this topic.

Also, the broadly defined flags like medication record are likely to be consistent across sites, but a variety of issues could prevent a specific measure from being counted correctly. The code used at a site might not be included in the ENACT ontology, either due to nonstandard terminologies or unusual coding choices. Similarly, the code might not have been imported from the source system due to unavailability of an external interface or a bug in the import process. These types of data quality issues stem from a systematic missingness in the EHR rather than actual missingness due to multisystem healthcare utilization and must be addressed through other means.⁴⁶ However, even noting this limitation, overall performance of the algorithm was quite good across sites.

Future directions

Now that the tool has been developed, we plan to disseminate it widely within the ENACT network and through posting to the i2b2 community. We will also make changes to the tool’s database tables so the loyalty score is visible in an i2b2 ontology and can be used directly in the graphical query tool. We acknowledge that many enterprise data warehouses use platforms other than i2b2, such as the popular Observational Medical Outcomes Partnership (OMOP) data model. There is current work to develop a version of i2b2 with the ENACT ontology that can interact with OMOP databases. After this feature is released in late 2023, it will allow straightforward adaptation of our tool (which relies on the ENACT ontology) to support OMOP.^47,48

We also plan to enhance the loyalty score by: considering removal of some flags with low influence and/or low population prevalence at all sites in this study (such as BMI or fecal occult stool tests); and adding some of the additional metadata proposed by Weber et al,¹⁹ such as whether the patient lives near the performance site and age-adjusted visit frequency. Many more additional flags could be considered, such as laboratory results and vital signs; these could be assessed through a feature selection algorithm such as Minimize Sparsity, Maximize Relevance, which is included in MLHO.³¹

Another reason to revisit the specific proxy variables is that the previously published equation was validated only on a Medicare population (age ≥65) and our work used the same set of 20 proxy variables for all patients over 18. Although we controlled for age and sex when retraining on local data, and we found that the algorithm (with existing proxy variables) performs well 19+ on all adults, in the future we could consider additional variables, as some are applicable only to an aging population. At present, sites can customize the age cutoff to meet their individual needs or to remove additional flags from the analysis. We specifically excluded pediatric patients, because utilization patterns and common tests in this population are very different than in adults and a pediatric version would require a completely different approach.

In addition, we hope to apply our loyalty cohort tool to enhance the population for phenotyping algorithms.^13,49

Conclusion

This open-source implementation and site-specific tuning of a “loyalty score” can be used immediately to enrich research cohorts by reducing biases introduced by missing data, which can skew research by underestimating disease prevalence and treatment effects.¹⁴ It successfully identifies patients with more complete data using AUCs around 0.80, which will help ensure that EHR research cohorts are not biased by missing data. At present, the tool can be used by any i2b2 site that employs the ENACT ontology. As discussed above, OMOP users might soon be able to utilize our tool with few changes, using i2b2-on-OMOP tools currently in development.

Author contributions

All authors participated in the design and execution of the study. Jeffrey G. Klann drafted the article and all authors edited it. Jeffrey G. Klann, Darren W. Henderson, and Michele Morris developed the study, managed the data, performed the software development, and executed the study. Hossein Estiri contributed to study design and development, especially around visualizations and the MLHO framework. Griffin M. Weber contributed guidance and expertise from his own research on similar topics. Shyam Visweswaran provided overall support, guidance, and supervision. SNM convened the study group, formulated the core ideas of the study, and guided the methodological design and writing.

Supplementary material

Supplementary material is available at Journal of the American Medical Informatics Association online.

Funding

This work was supported by the National Library of Medicine of the National Institutes of Health under award number R01 LM013345, National Center for Advancing Translational Sciences of the National Institutes of Health under award number U24 TR004111, and National Institute of Allergy & Infectious Diseases under award number R01 AI165535.

Conflict of interest

The authors declare they have no competing interests.

Data availability

All software code that was developed for this study is freely available through GitHub at https://github.com/i2b2plugins/loyalty_cohort. The EHR datasets utilized during this study cannot be made publicly available due to regulations for protecting patient privacy and confidentiality. Access to these datasets is restricted to IRB-approved investigators at the individual institutions. Any questions about the dataset can be directed to the corresponding author.