Robust Alternatives to ANCOVA for Estimating the Treatment Effect via a Randomized Comparative Study

Abstract

In comparing two treatments via a randomized clinical trial, the analysis of covariance (ANCOVA) technique is often utilized to estimate an overall treatment effect. The ANCOVA is generally perceived as a more efficient procedure than its simple two sample estimation counterpart. Unfortunately, when the ANCOVA model is nonlinear, the resulting estimator is generally not consistent. Recently, various nonparametric alternatives to the ANCOVA, such as the augmentation methods, have been proposed to estimate the treatment effect by adjusting the covariates. However, the properties of these alternatives have not been studied in the presence of treatment allocation imbalance. In this article, we take a different approach to explore how to improve the precision of the naive two-sample estimate even when the observed distributions of baseline covariates between two groups are dissimilar. Specifically, we derive a bias-adjusted estimation procedure constructed from a conditional inference principle via relevant ancillary statistics from the observed covariates. This estimator is shown to be asymptotically equivalent to an augmentation estimator under the unconditional setting. We utilize the data from a clinical trial for evaluating a combination treatment of cardiovascular diseases to illustrate our findings.

1. Introduction

In comparing two treatment groups, let $\theta$ be the parameter of interest for quantifying the between-group difference with respect to the study endpoint. For example, let $Y$ be the outcome variable, $Z$ be the binary treatment indicator, ${\mu }_0=E(Y\mid Z=0),{\mu }_1=E(Y\mid Z=1)$, and $\theta ={\mu }_1-{\mu }_0$. Let $\hat{\theta }$ be the corresponding two-sample estimator based on the data from a randomized clinical trial with the proportions of the patients assigned to Groups 1 and 0 being $\pi$ and $1-\pi$, respectively. If $Y$ is a binary outcome, $\theta$ may be the risk ratio or odds ratio (OR). In general, with a large sample size, the distribution of $\hat{\theta }$ is approximately normal with mean $\theta$. Inferences about $\theta$ can be made accordingly.

When the patient’s potentially predictive baseline covariate vector $\mathbf{X}$ is available, we routinely utilize an analysis of covariance (ANCOVA) procedure to estimate $\theta$. A typical ANCOVA model is a multicovariate regression model relating the outcome to the treatment assignment indicator $Z$ and covariate vector $\mathbf{X}$. The estimated regression coefficient of $Z$ or a transformation thereof is interpreted as an estimator of $\theta$. Unfortunately, when the ANCOVA model is nonlinear (e.g., a logistic or proportional hazard model), the resulting estimator of the treatment effect is generally not consistent for $\theta$ of our interest (Gail, Wieand, and Piantadosi 1984; Struthers and Kalbfleisch 1986; Lin and Wei 1989). For example, the treatment effect for binary outcome is often measured by log OR

$$\theta =\text{log}\left[\frac{\text{pr}\left(Y=1∣Z=1\right)\text{pr}\left(Y=0∣Z=0\right)}{\text{pr}\left(Y=0∣Z=1\right)\text{pr}\left(Y=1∣Z=0\right)}\right].$$ (1)

The multivariable logistic regression model assumes that the conditional log OR for given covariates $\mathbf{X}$,

$$\text{log}\left[\frac{\text{pr}\left(Y=1∣Z=1,\mathbf{X}\right)\text{pr}\left(Y=0∣Z=0,\mathbf{X}\right)}{\text{pr}\left(Y=0∣Z=1,\mathbf{X}\right)\text{pr}\left(Y=1∣Z=0,\mathbf{X}\right)}\right],$$

is a constant independent of $\mathbf{X}$. This quantity is the regression coefficient of $Z$ in the model but, in general, is different from $\theta$ in (1). Therefore, it is inappropriate to use the regression coefficient of $Z$ to estimate $\theta$. However, ANCOVA may still be useful for two reasons: first, as a testing procedure for the presence of treatment effect, ANCOVA is generally valid without requiring the correct model specification and often more powerful than its simple two sample counterpart; second, when correctly specified, a version of ANCOVA can be used to estimate $\theta$ indirectly. Specifically, the potential outcomes of each individual is linked with his/her baseline covariates via appropriate regression model in both arms and the finite sample contrast of “predicted” outcomes measuring the treatment effect can be constructed accordingly. For example, noting that log OR equals to

$$\text{log}\left[\frac{E\{\text{pr}(Y=1\mid Z=1,\mathbf{X}\left)\right\}E\{\text{pr}(Y=0\mid Z=0,\mathbf{X}\left)\right\}}{E\{\text{pr}(Y=0\mid Z=1,\mathbf{X}\left)\right\}E\{\text{pr}(Y=1\mid Z=0,\mathbf{X}\left)\right\}}\right],$$

one may estimate $\theta$ by

$${\hat{\theta }}_{\text{ANCOVA}}=\text{log}\left[\frac{\widehat{E}\left\{\text{pr}\left(Y=1∣Z=1,\mathbf{X}\right)\right\}\widehat{E}\left\{\widehat{pr}\left(Y=0∣Z=0,\mathbf{X}\right)\right\}}{\widehat{E}\left\{\text{pr}\left(Y=0∣Z=1,\mathbf{X}\right)\right\}\widehat{E}\left\{\text{pr}\left(Y=1∣Z=0,\mathbf{X}\right)\right\}}\right],$$

where

$$\widehat{E}\left\{\text{pr}\left(Y=y∣Z,\mathbf{X}\right)\right\}=\int \frac{\text{exp}\left\{y\left({\hat{\beta }}_0+{\hat{\gamma }}_{Z}Z+{\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_{\mathbf{X}}^{\text{T}}\mathbf{x}\right)\right\}}{1+\text{exp}\left({\hat{\beta }}_0+{\hat{\gamma }}_{Z}Z+{\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_{\mathbf{X}}^{\text{T}}\mathbf{x}\right)}d{\widehat{F}}_{\mathbf{X}}\left(\mathbf{x}\right),$$

${\widehat{F}}_{\mathbf{X}}(\cdot )$ is the empirical cumulative distribution function of observed covariates and ${\hat{\beta }}_0,{\hat{\gamma }}_Z$, and ${\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_{\text{X}}^{\text{T}}$ are the estimators of the intercept, coefficient of the treatment indicator, and coefficient of $\mathbf{X}$ in the logistic regression model, respectively.

Since ANCOVA model is likely misspecified in practice, it is desirable to develop robust, nonparametric covariate-adjusted estimation procedures for $\theta$, which are well summarized in a recent article by Rosenblum and van der Laan (2010). For instance, an augmentation estimation procedure with covariate adjustment provides a consistent estimator for $\theta$ (Robins, Rotnitzky, and Zhao 1994; Robins 1999; Leon, Tsiatis, and Davidian 2003; Bang and Robins 2005; Tsiatis 2006; Van Der Laan and Rubin 2006; Tsiatis et al. 2008; Lu and Tsiatis 2008; Zhang, Tsiatis, and Davidian 2008; Gilbert et al. 2009; Zhang and Gilbert 2010; Tian et al. 2012). Such an estimator, say, ${\hat{\theta }}_{\text{aug,}}$ is asymptotically equivalent to a linear combination of $\hat{\theta }$ and ${\widehat{\Delta }}_{\mathbf{X}}={\stackrel{-}{\mathbf{X}}}_1-{\stackrel{-}{\mathbf{X}}}_0$, where ${\stackrel{-}{\mathbf{X}}}_k$ is the sample mean of the covariate vectors or a transformation thereof for treatment $k,k=\mathrm{0,1}$ (see Appendix A for details). The distribution of ${\hat{\theta }}_{\text{aug}}$ is also approximately normal with mean $\theta$. The standard error estimate for ${\hat{\theta }}_{\text{aug}}$ can be substantially smaller than that based on $\hat{\theta }$ when the augmented covariates are highly correlated with the response endpoint. Unlike the ANCOVA, the augmentation method is a model-free technique. Note that the stochastic properties of the above estimators were studied only under an unconditional setting in the literature, that is, with the study size $n$, their sample space is generated by all possible realizations of a random sample consisting of $n$ independent, identically distributed copies of ${\left(Y,Z,{\mathbf{X}}^{\text{T}}\right)}^{\text{T}}$. Under this unconditional setting, $\hat{\theta }$ is asymptotically unbiased.

Another important goal of using the covariate-adjustment technique for estimating the treatment difference is to reduce bias of $\hat{\theta }$ when, by chance, the observed distributions of the covariate vectors are dissimilar between two groups. Intuitively, $\hat{\theta }$ can be severely biased for this case. As discussed above, however, $\hat{\theta }$ is asymptotically unbiased unconditionally. Therefore, the bias of $\hat{\theta }$ needs to be discussed in a conditional sense. Note that the study subjects’ covariates and their functions are ancillary statistics, that is, they are not directly related to the treatment difference $\theta$. One may consider to make more “relevant” inference about $\hat{\theta }$ by conditioning on summary ancillary statistics. Such a conditional approach helps us to study the stochastic behavior of $\hat{\theta }$ with realizations of ${\left(Y,Z,{\mathbf{X}}^{\text{T}}\right)}^{\text{T}}$ whose ancillary statistics would be similar to their observed counterparts (Cox 1958; Cox and Hinkley 1979; Fraser and McDunnough 1980; Berger et al. 1988; Casella 1992; Fraser 2004; Ghosh, Reid, and Fraser 2010). Unbiased estimator conditional on all observed individual covariates, which incorporate all aspects of covariate imbalance, can be constructed by regression modelling. The aforementioned estimator ${\hat{\theta }}_{\text{ANCOVA}}$ is one such example. Unfortunately, it is a parametric approach in nature and prone to model misspecification. For a nonparametric procedure, it is infeasible to make inference conditional on such a fine level. In this article, we consider a coarser procedures only conditional on certain ancillary statistics, which quantify the imbalance between two treatment groups with respect to covariates. The choice of the conditioning ancillary statistic is not unique (Basu 1959; Cox 1971; Ghosh, Reid, and Fraser 2010). For the present case, instead of conditioning on the entire set of observed covariates, a relevant ancillary statistic for studying the stochastic behavior of estimators for $\theta$ would be the aforementioned ${\widehat{\Delta }}_{\mathbf{X}}$, which is a natural, and commonly used summary measure of covariate-imbalance in clinical studies (Pocock et al. 2002). This statistic is also routinely used for evaluating covariate imbalance after matching, for example, via the propensity score (PS) method (Resa and Zubizarreta 2016). With this ancillary statistic, the sample space considered consists of all realizations of a random sample consisting of $n$ independent copies of ${\left(Y,Z,{\mathbf{X}}^{\text{T}}\right)}^{\text{T}}$, whose imbalance measured by the two-sample covariate mean difference is identical to the observed counterpart. Figure 1 is a schematic plot of aforementioned sample spaces from the biggest to the smallest:

1. all realizations of $n$ copies of ${\left(Y,Z,{\mathbf{X}}^{\text{T}}\right)}^{\text{T}}$;

2. all realizations of $n$ copies of ${\left(Y,Z,{\mathbf{X}}^{\text{T}}\right)}^{\text{T}}$ with the same ${\widehat{\Delta }}_{\mathbf{X}}$ as observed;

3. all realizations of $n$ copies of ${\left(Y,Z,{\mathbf{X}}^{\text{T}}\right)}^{\text{T}}$ with the same observed individual covariates in two groups.

The naive estimator is asymptotically unbiased only in the largest sample space. When correctly specified, ${\hat{\theta }}_{\text{ANCOVA}}$ is asymptotically unbiased in all three, including the smallest sample space. Our bias-correction proposal operates in the intermediate sample space.

Figure 1.

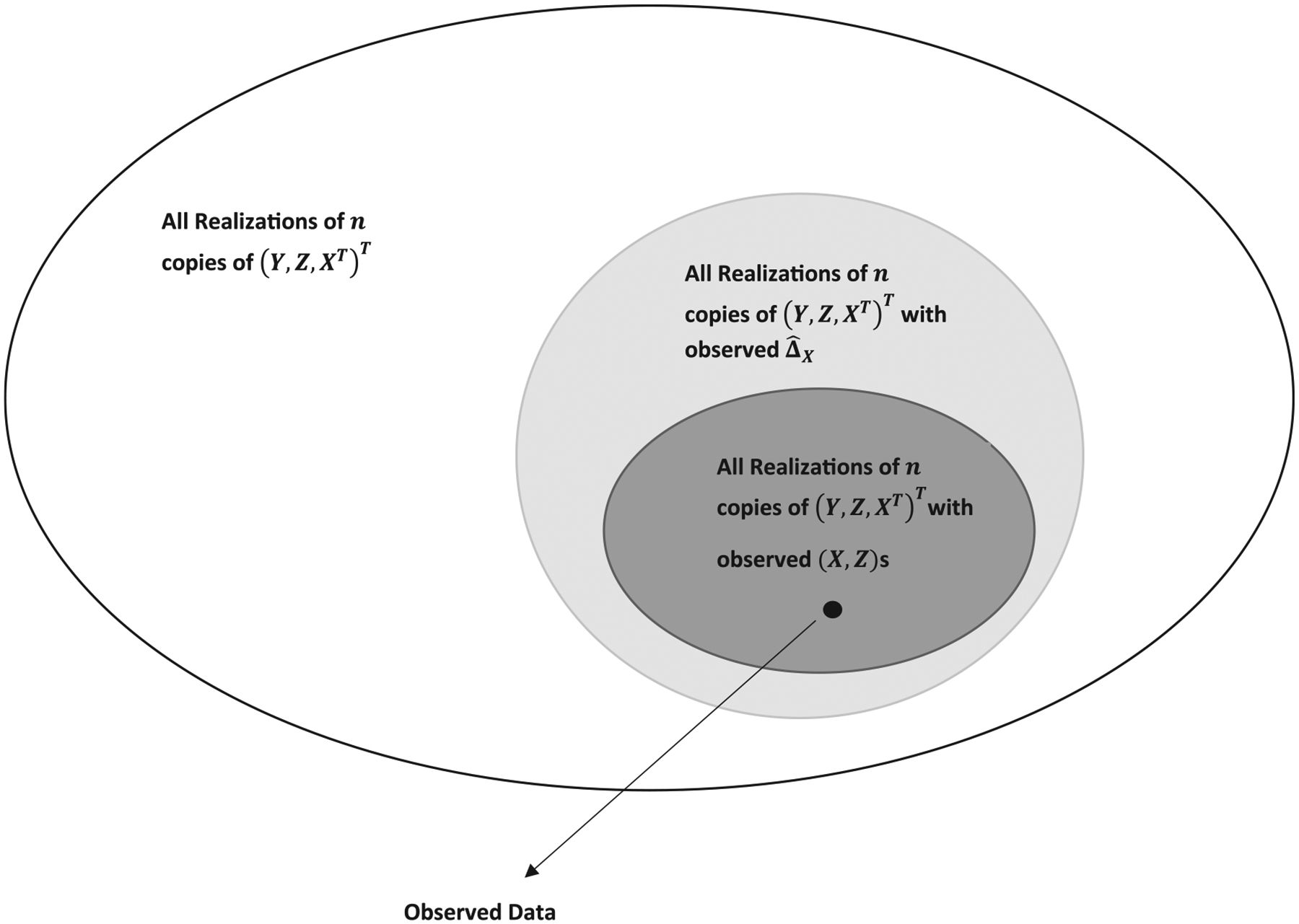
The sample spaces within which the statistical inference is made.

In this article, we show that based on this conditional inference principle, a bias-adjusted estimator ${\hat{\theta }}_{\text{adj}}$ reduces the bias of $\hat{\theta }$. We also show that unconditionally, ${\hat{\theta }}_{\text{adj}}$ is asymptotically equivalent to ${\hat{\theta }}_{\text{aug}}$ and can be viewed as an efficiency augmented estimator itself. We used the data from a comparative clinical trial to evaluate treatments for cardiovascular diseases to illustrate our findings. Furthermore, a numerical study is conducted to examine the performance of ${\hat{\theta }}_{\text{adj.}}$. We find via this study that if the covariates of the ancillary statistics are highly correlated with the outcome variable and/or the treatment allocation proportions, ${\hat{\theta }}_{\text{adj}}$ can be substantially better than two sample estimator $\hat{\theta }$.

2. The Distributions of $\stackrel{\mathit{ˆ}}{\mathit{\theta }}$ Conditioning on ${\widehat{\mathbf{\Delta }}}_{\mathbf{X}}$ and a Bias-Adjusted Estimator ${\stackrel{\mathit{ˆ}}{\mathit{\theta }}}_{\text{adj}}$

Let $\theta =g\left({\mu }_0,{\mu }_1\right)$, where $g$ is a smooth function characterizing the contrast between ${\mu }_0$ and ${\mu }_1$. Then $\hat{\theta }=g\left({\hat{\mu }}_0,{\hat{\mu }}_1\right)$ is the two sample naive estimator for $\theta$, where ${\hat{\mu }}_0$ and ${\hat{\mu }}_1$ are the simple naive estimators for ${\mu }_0$ and ${\mu }_1$, respectively. Under the random treatment assignments for designing the study, $\hat{\theta }-\theta$ and ${\widehat{\Delta }}_{\mathbf{X}}$ are approximately normal with mean 0 and covariance matrix

$$\hat{\Sigma }=\left(\begin{array}{cc}{\hat{\Sigma }}_{11}& {\hat{\Sigma }}_{12}\\ {\hat{\Sigma }}_{12}& {\hat{\Sigma }}_{22}\end{array}\right),$$

where

$${\hat{\Sigma }}_{11}\approx {\dot{g}}_1^2\left({\mu }_0,{\mu }_1\right)\text{var}\left({\hat{\mu }}_0\right)+{\dot{g}}_2^2\left({\mu }_0,{\mu }_1\right)\text{var}\left({\hat{\mu }}_1\right),$$

$${\hat{\Sigma }}_{12}\approx {\dot{g}}_2\left({\mu }_0,{\mu }_1\right)\text{cov}\left({\hat{\mu }}_1,{\stackrel{-}{\mathbf{X}}}_1\right)-{\dot{g}}_1\left({\mu }_0,{\mu }_1\right)\text{cov}\left({\hat{\mu }}_0,{\stackrel{-}{\mathbf{X}}}_0\right),\text{ and}$$

$${\hat{\Sigma }}_{22}\approx \text{var}\left({\stackrel{-}{\mathbf{X}}}_0\right)+\text{var}\left({\stackrel{-}{\mathbf{X}}}_1\right),$$

are the estimated variance of $\hat{\theta }-\theta$, the estimated covariance matrix between ${\widehat{\Delta }}_{\mathbf{X}}$ and $\hat{\theta }-\theta$, and the estimated covariance matrix of ${\widehat{\Delta }}_{\mathbf{X}}$, respectively. Here ${\dot{g}}_1$ and ${\dot{g}}_2$ are the partial derivatives of $g$ with respect to the first and second argument, respectively. Now, let ${\mathbf{d}}_n$ be the observed value of ${\widehat{\Delta }}_{\mathbf{X}}$. Then for large $n$, the distribution of $\hat{\theta }-\theta$ given ${\widehat{\Delta }}_{\mathbf{X}}={\mathbf{d}}_n$ is approximately normal with mean ${\hat{\Sigma }}_{12}{\hat{\Sigma }}_{22}^{-1}{\mathbf{d}}_n$ and variance ${\hat{\Sigma }}_{11}-{\hat{\Sigma }}_{12}{\hat{\Sigma }}_{22}^{-1}{\hat{\Sigma }}_{21}$.

The following theorem summarizes this large sample approximation under mild assumptions.

Theorem. Let ${\left(Y_i,Z_i,{\mathbf{X}}_i^{\text{T}}\right)}^{\text{T}},i=1,\dots ,n$, be the iid copies of ${\left(Y,Z,{\mathbf{X}}^{\text{T}}\right)}^{\text{T}}$ and $\pi =\text{pr}(Z=1)$. Assume that $\text{cov}\left\{{\left(Y,{\mathbf{X}}^{\text{T}}\right)}^{\text{T}}\right\}$ is a finite, nondegenerate matrix; the characteristic function of $\mathbf{X}$ is integrable; and $\hat{\theta }$ is a regular estimator for $\theta$, that is, $\sqrt{n}(\hat{\theta }-\theta )$ is asymptotically equivalent to a sum of iid random quantities. Then

$$\sqrt{n}(\hat{\theta }-\theta )\mid \left({\widehat{\Delta }}_{\mathbf{X}}={\mathbf{d}}_n\right)$$

converges weakly to a Gaussian distribution with mean ${\Sigma }_{12}{\Sigma }_{22}^{-1}{\mathit{\delta }}_0$ and variance ${\Sigma }_{11}-{\Sigma }_{12}{\Sigma }_{22}^{-1}{\Sigma }_{21}$, where ${\mathit{\delta }}_0={\text{lim}}_{n\to \infty }\sqrt{n}{\mathbf{d}}_n$, and ${\Sigma }_{11},{\Sigma }_{12}$, and ${\Sigma }_{22}$ are the population counterparts of ${\hat{\Sigma }}_{11},{\hat{\Sigma }}_{12}$, and ${\hat{\Sigma }}_{22}$, respectively.

Note that the assumptions under which the theorem holds are rather mild. For instance, the second assumption holds if the component of covariates $\mathbf{X}$ is either discrete or continuous with a squared integrable density function. The proof of the theorem is given in Appendix B. It follows from the theorem that, when ${\mathit{\delta }}_0$ is not zero, $\hat{\theta }$ is not $\sqrt{n}$ consistent under this conditional argument. A bias-adjusted estimator for $\theta$ is

$${\hat{\theta }}_{\text{adj}}=\hat{\theta }-{\hat{\Sigma }}_{12}{\hat{\Sigma }}_{22}^{-1}{\mathbf{d}}_n.$$

To illustrate how the inference procedure based on ${\hat{\theta }}_{\text{adj}}$ behaves asymptotically under various scenarios, let us consider a simple case of $\theta ={\mu }_1-{\mu }_0$ with a single covariate $X$. Here, the bias is

$$\left[\frac{\text{cov}(Y,X\mid Z=1)(1-\pi )}{\text{var}\left(X\right)}+\frac{\text{cov}(Y,X\mid Z=0)\pi }{\text{var}\left(X\right)}\right]d_n.$$

If the correlation between the covariate and response is weak, the bias can be negligible. On the other hand, if a covariate is strongly associated with the response in at least one arm, then the bias would not be trivial. Furthermore, if ${\mathbf{d}}_n$ is small, then ${\hat{\theta }}_{\text{adj}}$ is almost identical to $\hat{\theta }$. On the other hand, if the distributions of ${\mathbf{X}}_0$ and ${\mathbf{X}}_1$ do not overlap much, ${\mathbf{d}}_n$ can be quite large, and ${\hat{\theta }}_{\text{adj}}$ may be fairly different from $\hat{\theta }$. In general, if the observed distributions of ${\mathbf{X}}_0$ and ${\mathbf{X}}_1$ are similar and ${\hat{\Sigma }}_{12}$ is small, ${\hat{\theta }}_{\text{adj}}$ and $\hat{\theta }$ would have similar variances. The term ${\hat{\Sigma }}_{12}{\hat{\Sigma }}_{22}^{-1}{\hat{\Sigma }}_{21}$ represents the reduction from $\text{var}\left(\hat{\theta }\right)$ to $\text{var}\left({\hat{\theta }}_{\text{adj}}\right)$.

As a general example to illustrate how to construct ${\hat{\theta }}_{\text{adj}}$, suppose that $\theta$ is the log-transformed OR, that is, $g\left({\mu }_0,{\mu }_1\right)=\text{log}\left\{\frac{{\mu }_1\left(1-{\mu }_0\right)}{{\mu }_0\left(1-{\mu }_1\right)}\right\}$, then

$${\hat{\theta }}_{\text{adj }}=\text{log}\left\{\frac{{\hat{\mu }}_1\left(1-{\hat{\mu }}_0\right)}{{\hat{\mu }}_0\left(1-{\hat{\mu }}_1\right)}\right\}-{\hat{\Sigma }}_{12}{\hat{\Sigma }}_{22}^{-1}{\widehat{\Delta }}_{\mathbf{X}},$$

$${\hat{\Sigma }}_{11}=\frac{1}{n_1{\hat{\mu }}_1}+\frac{1}{n_1\left(1-{\hat{\mu }}_1\right)}+\frac{1}{n_0{\hat{\mu }}_0}+\frac{1}{n_0\left(1-{\hat{\mu }}_0\right)},$$

$${\hat{\Sigma }}_{12}=\frac{{\hat{\Sigma }}_{121}}{n_1{\hat{\mu }}_1\left(1-{\hat{\mu }}_1\right)}+\frac{{\hat{\Sigma }}_{120}}{n_0{\hat{\mu }}_0\left(1-{\hat{\mu }}_0\right)},\text{ and}$$

$${\hat{\Sigma }}_{22}=\frac{{\hat{\Sigma }}_{221}}{n_1}+\frac{{\hat{\Sigma }}_{220}}{n_0},$$

where $n_k,{\hat{\Sigma }}_{12k}$, and ${\hat{\Sigma }}_{22k}$ are the sample size, empirical covariance between $Y$ and $\mathbf{X}$, and the variance-covariance matrix of $\mathbf{X}$ in the $k$th group, $k=0,1$, respectively.

Note that ${\hat{\theta }}_{\text{adj}}$ is equivalent or asymptotically equivalent to augmentation estimators (Tsiatis et al. 2008; Tian et al. 2012). The justification of this unconditional equivalence is given in Appendix A. Note that in this article, the dimension of the covariate vector is small relative to the sample size. It is interesting to explore how to deal with the case with a high-dimensional covariate vector for future research.

Remark 1. For the continuous outcome, the treatment effect can be assessed by the mean difference between two groups. For the survival outcome, the treatment effect can be measured by the difference in restricted mean survival time (RMST, Zhao et al. 2016). In both cases, the naive estimator for the treatment effect can be easily constructed. The construction of the bias adjusted estimator follows the same procedure as that used for the log OR with minor modifications on the relevant variance and covariance estimations. We illustrate the bias adjustment as well as relevant statistical inference procedure in Appendix C.

3. Example

In this section, we used the data from a cardiovascular trial: “Valsartan in acute myocardial infarction” (VALIANT) study (Pfeffer et al. 2003) to illustrate our findings. The study patients were equally randomized to three groups: ARB valsartan, captopril, and a combination of these two drugs. Here, we consider a binary outcome as the endpoint, which indicates whether the patient had hospitalization/death by month 18. Since the 18-month incidence rates of hospitalization/death from two mono-therapies are almost identical, we combined the data from these two mono-therapy groups to evaluate the effect of combo-therapy. Note that pooling two groups is not a common practice and for illustrative purpose only. The study enrolled a total of 14,703 patients. The observed event rates for mono- and combo are 0.58 and 0.57, indicating that there was no benefit from the combo with respect to this outcome. On the other hand, with the data from 302 patients in Australia, the mono-therapy somehow appears to be statistically significantly better than its combo counterpart based on the simple two sample estimate (the observed event rates for combo and mono are 0.80 and 0.67, respectively). Now, let $\theta$ be the log OR, and $\hat{\theta }$ be its naive estimate. The point estimate of OR (combo vs. mono), that is, $\text{exp}\left(\hat{\theta }\right)$ and 0.95 confidence interval are 1.99 and (1.12, 3.51), respectively. Among 24 countries participated in the VALIANT study, Australia was the only one whose patients appear to have better outcomes for the mono-therapy. It is not clear whether Australian patients were quite different from those from the rest of world to have such a discrepancy on the treatment effect. On the other hand, since the sizable treatment by country interaction is rare in practice, the statistically significant OR for Australian patients may be a false discovery. To explore this further for Australia patients, we found that there was treatment allocation imbalance between these two treatment groups with respect to, for example, the patient’s binary preexisting diabetes status (DIAS) and baseline heart rate (HR), which is a potential source of the bias of the naive estimator. In Figure 2, we show the fitted curves stratified by DIAS via two logistic regression models with the treatment assignment being the outcome and standardized $\text{HR},{\text{HR}}^2$ and ${\text{HR}}^3$ as the independent variables. If the randomization treatment allocation scheme were working for Australia patients, these two curves would be flat around 2/3. Figure 2 indicates that there was indeed nontrivial treatment allocation imbalance between the mono and combo groups. Now, let ${\hat{\theta }}_{\text{adj}}$ be the biased-adjusted estimate for the log OR. The corresponding bias-adjusted estimator of OR, that is, $\text{exp}\left({\hat{\theta }}_{\text{adj}}\right)$ and the 0.95 confidence interval conditional on the observed imbalance in DIAS, $\text{HR},{\text{HR}}^2$ and ${\text{HR}}^3$ are 1.68 and (0.95, 2.94), respectively. Here, the point estimator is closer to 1 and the confidence interval contains the null value. In view of the data from other countries, the adjustment toward the null is likely in the right direction. Note that one of the reasons we considered the HR variable to the third order for the conditioning inference is that most distributions can be characterized with their first three moments. This conditioning setting would be approximately the same as that with the entire distribution of HR.

Figure 2.

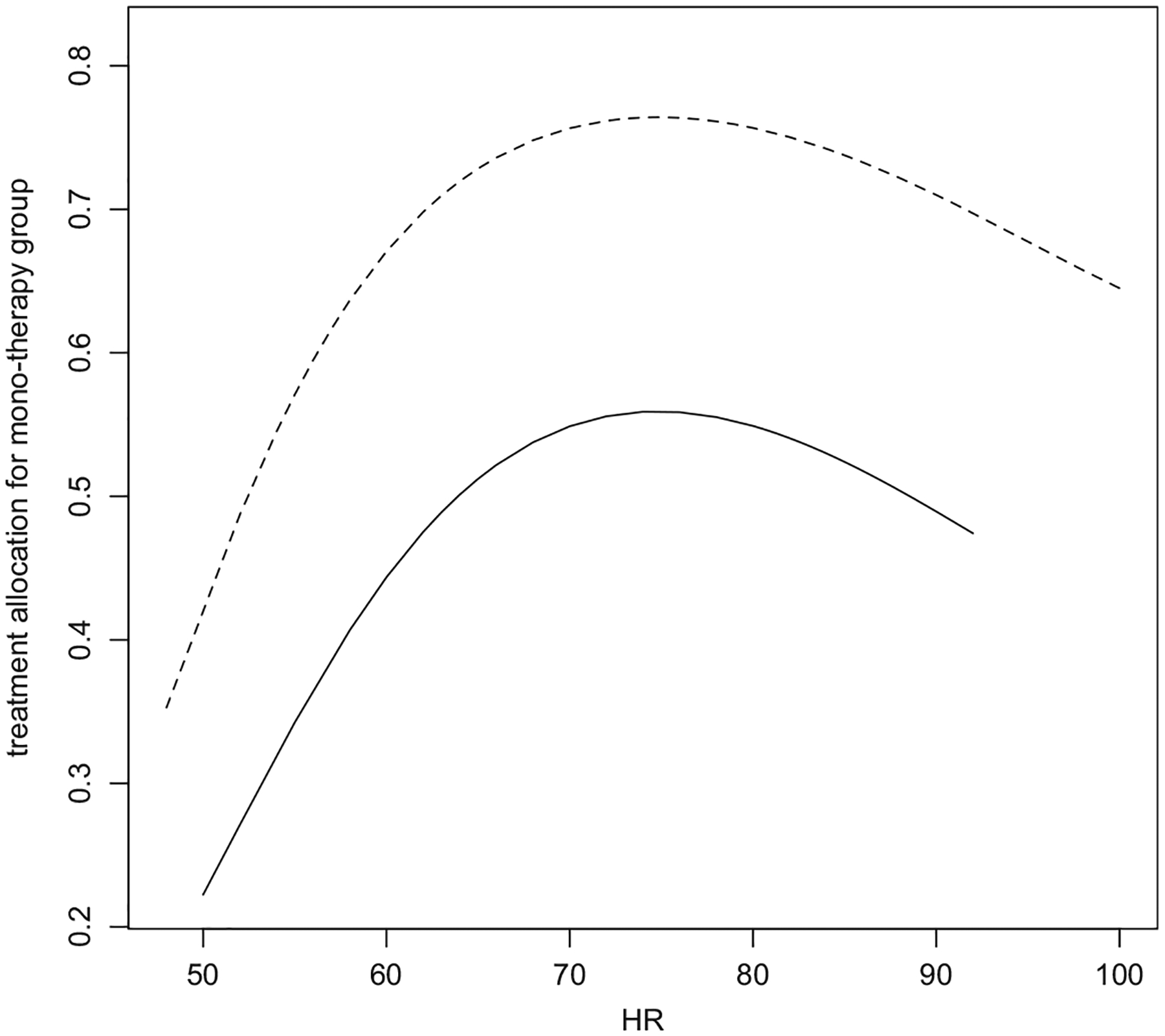
The treatment allocation proportions to mono-therapy group: solid line is for DIAS = 1; dashed line is for DIAS = 0. HR stands for heart rate.

4. Simulation Study

We further explore the finite sample properties of the proposed estimator via simulation studies. Mimicking the VALIANT study, we first generate the binary diabetes status and standardized heart rate, (DIAS, HR), for 300 patients via the following distributions

$$\text{pr}(\text{DIAS}=1)=0.22,$$

$$\text{HR }\mid \text{DIAS}=1~N\left(\mathrm{0.042,1.4}\right),\text{ and}$$

$$\text{HR }\mid \text{DIAS}=0~N(-\mathrm{0.045,1.1}),$$

which are estimated using the observed Australia data. We then randomly assign 300 simulated patients into two groups with 200 patients in the mono-therapy group and 100 patients in the combo-therapy group. The four-dimensional covariate vector of interest is $\mathbf{X}={\left(\text{DIAS},\text{HR},{\text{HR}}^2,{\text{HR}}^3\right)}^{\text{T}}$. To examine the finite sample performance of the proposed method, we need to perform the conditional inference only among samples with a given imbalance in covariates. To this end, we examine ${\widehat{\Delta }}_{\mathbf{X}}={\stackrel{-}{\mathbf{X}}}_1-{\stackrel{-}{\mathbf{X}}}_0$, the mean difference in covariates between two groups, in each of the simulated datasets and only keep those with approximately the “same” covariates imbalance as that observed in Australian patients. Specifically, we require that the observed ${\widehat{\Delta }}_{\mathbf{X}}\in [0.155,0.165]\times [-0.06,-0.04]\times [0.26,0.30]\times [-0.33,-0.21]$. The center and width of these intervals are the corresponding component of observed ${\widehat{\Delta }}_{\mathbf{X}}$ in Australian patients and 20% of the (unconditional) standard deviation thereof, respectively. After obtaining 5000 such datasets, we generate the binary outcome via the logistic regression model

$$\text{pr}(Y=1\mid \mathbf{X},Z)=h\left\{{\beta }_0+{\gamma }_{0}Z+m\left(\mathbf{X}\right)\right\}$$

where

$$m\left(\mathbf{X}\right)=\kappa \left\{{\beta }_1\left(\text{DIAS}-{\mu }_D\right)+{\beta }_2\left(\text{HR}-{\mu }_1\right)\left.+{\beta }_3\left({\text{HR}}^2-{\mu }_2\right)+{\beta }_4\left({\text{HR}}^3-{\mu }_3\right)\right\}\right.,$$

$h(\cdot )=\text{expit}(\cdot ),{\left({\beta }_0,{\beta }_1,{\beta }_2,{\beta }_3,{\beta }_4\right)}^{\text{T}}=(\mathrm{0.69,0.78},-0.25,0.33,-0.02{)}^{\text{T}}$ is the maximum likelihood estimator (MLE) of the regression coefficient based on Australia data, ${\mu }_D$ and ${\mu }_j$ are expectation of DIAS and ${\text{HR}}^j$, respectively, and $\kappa =\mathrm{0,2}$, or 4 is the tuning parameter to control the size of the covariate effect. For each simulated dataset, we obtain the naive and bias adjusted estimators for $\theta =\text{log}\left(\text{OR}\right)$. In the first setting, we let ${\gamma }_0=0$, that is, the distribution of $Y$ does not dependent $Z$ and there is no treatment effect. In the second setting, we let ${\gamma }_0=1$, representing a higher incidence rate in group $Z=1$. In this case, the true value of $\theta$ can be obtained by computing

$$\text{log}\left[\frac{E\left\{h\left({\gamma }_0+\xi \right)\right\}E\left\{1-h\left(\xi \right)\right\}}{E\left\{1-h\left({\gamma }_0+\xi \right)\right\}E\left\{h\left(\xi \right)\right\}}\right],$$

where the expectation is with respect to $\xi ={\beta }_0+m\left(\mathbf{X}\right)$. Based on 5000 such simulated datasets with approximately the same covariates imbalance, we obtain the empirical biases of estimators with and without adjusting covariates imbalance and the empirical coverage level of the corresponding 95% confidence intervals. The results are summarized in Table 1. When the covariates effect is strong $(\kappa =4)$, the naive estimator has a nontrivial bias, especially relative to its standard error. The estimated variance of the naive estimator overestimates the conditional variability and yields wide confidence intervals. Even with this upward bias in variance estimation, the 95% confidence interval based on the naive estimator fails to cover the truth at the nominal level, since the interval is centered at a biased location. On the other hand, the estimated variance of the adjusted estimator approximates the underlying conditional variance and the empirical coverage level of the 95% confidence interval is fairly close 0.95. When there is no covariates effect $(\kappa =0)$, two estimators have a comparable performance as anticipated. If we consider unconditional distribution of these two estimators, we don’t need to restrict to the generated data with the given covariate imbalance and the bias-adjusted estimator becomes a version of efficiency augmented estimator in the literature. In such a case, one may expect that both estimators are asymptotically unbiased but the variance of the bias-adjusted estimator is smaller than that of the naive estimator. The results based on 5000 simulations are summarized in Table 2, which confirms the efficiency improvement reported in the literature. We have also compared the “bias-adjusted” estimator with the efficiency augmented counterpart proposed by Tsiatis et al. (2008) and Zhang, Tsiatis, and Davidian (2008) unconditionally and obtained almost identical results as shown in Figure 3, which is consistent with their asymptotic equivalence. In Figure 4, we have plotted the density functions of the naive estimator (both unconditional and conditional on the covariates imbalance, $\kappa =0$) to highlight the fact that the distribution of an estimator can be substantially altered by conditioning on an ancillary statistics. In the same figure, we have also plotted the density functions of the bias adjusted estimator for comparison purpose. It is clear that the biased-adjusted estimator is unbiased both conditionally and unconditionally.

Table 1.

The simulation results for the log-transformed OR with binary endpoints based on 5000 simulations conditional on the observed imbalance in baseline covariates.

	$\mathit{\kappa }$	$\mathit{\theta }$	|Bias|	ESE	SEE	ECP	$\mathit{\theta }$	|Bias|	ESE	SEE	ECP
		${\mathit{\gamma }}_0=0$					${\mathit{\gamma }}_0=1$
${\hat{\theta }}_{\text{adj}}$	0	0	0.012	0.313	0.295	0.941	1.00	0.005	0.363	0.343	0.939
$\hat{\theta }$	0	0	0.012	0.302	0.297	0.951	1.00	0.004	0.353	0.346	0.950
${\hat{\theta }}_{\text{adj}}$	2	0	0.017	0.261	0.252	0.946	0.90	0.003	0.296	0.288	0.949
$\hat{\theta }$	2	0	0.259	0.259	0.270	0.841	0.90	0.261	0.294	0.302	0.872
${\hat{\theta }}_{\text{adj}}$	4	0	0.016	0.208	0.210	0.952	0.69	0.005	0.229	0.230	0.953
$\hat{\theta }$	4	0	0.404	0.210	0.250	0.657	0.69	0.391	0.231	0.264	0.705

ESE: empirical standard error; SEE: average standard error estimator; ECP: empirical coverage level of the 95% confidence intervals.

Table 2.

Unconditional distribution: the simulation results for the log-transformed OR with binary endpoints based on 5000 simulations.

	$\mathit{\kappa }$	$\mathit{\theta }$	|Bias|	ESE	SEE	ECP	$\mathit{\theta }$	|Bias|	ESE	SEE	ECP
		${\mathit{\gamma }}_0=0$					${\mathit{\gamma }}_0=1$
${\hat{\theta }}_{\text{adj}}$	0	0	0.011	0.296	0.294	0.949	1.00	0.009	0.348	0.343	0.949
$\hat{\theta }$	0	0	0.011	0.295	0.297	0.954	1.00	0.009	0.347	0.346	0.952
${\hat{\theta }}_{\text{adj}}$	2	0	0.010	0.258	0.254	0.950	0.90	0.005	0.290	0.287	0.949
$\hat{\theta }$	2	0	0.003	0.276	0.272	0.948	0.90	0.014	0.305	0.302	0.949
${\hat{\theta }}_{\text{adj}}$	4	0	0.009	0.214	0.209	0.945	0.69	0.004	0.228	0.227	0.951
$\hat{\theta }$	4	0	0.000	0.254	0.251	0.950	0.69	0.003	0.263	0.263	0.953

ESE: empirical standard error; SEE: average standard error estimator; ECP: empirical coverage level of the 95% confidence intervals.

Figure 3.

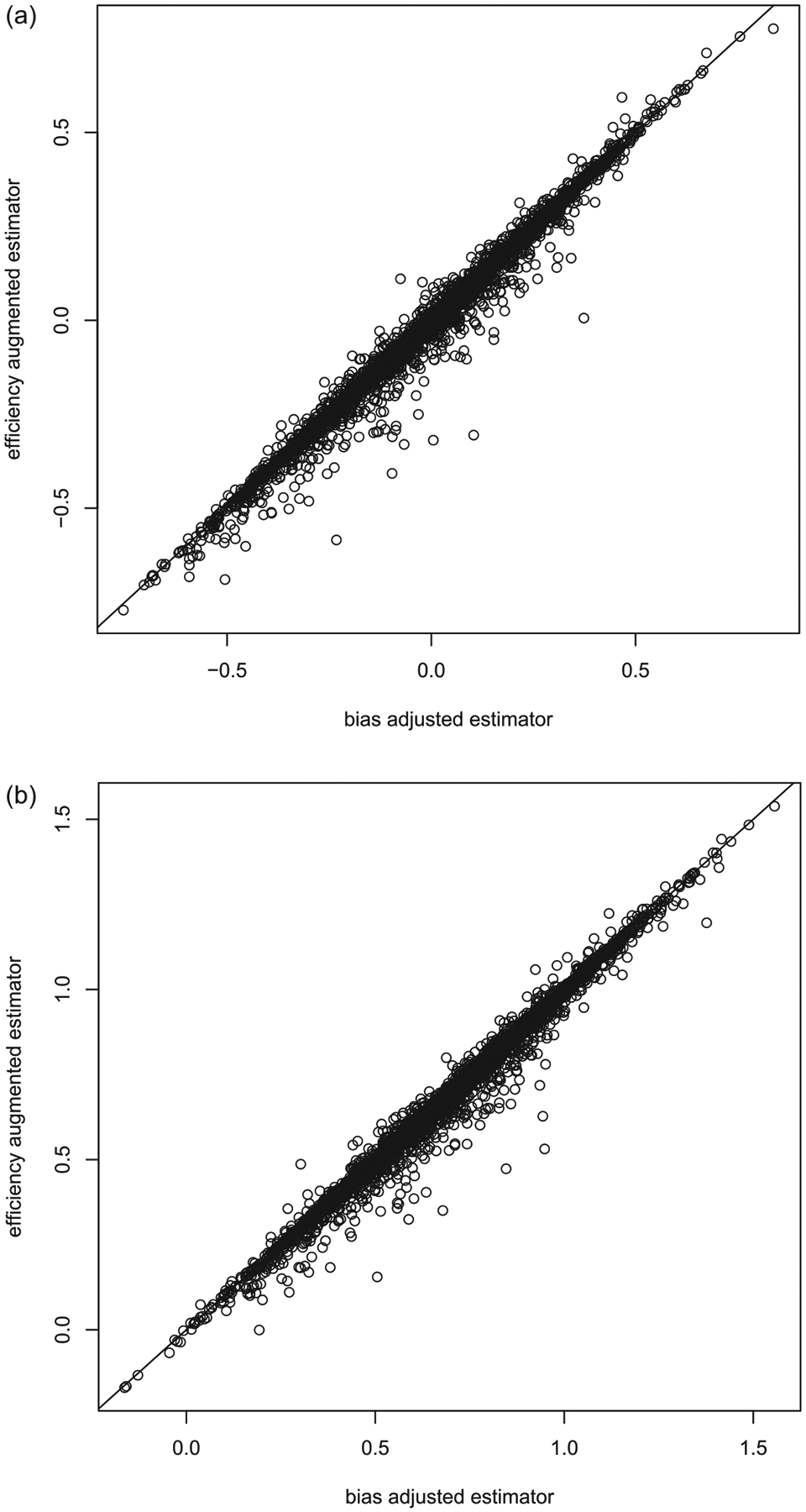
(a) The comparison between the efficiency augmented and bias adjusted estimators for binary outcomes when $\left({\gamma }_0,\kappa \right)=\left(\mathrm{0,4}\right)$. Here the median of $\mid {\widehat{\theta }}_{\text{aug}}-{\widehat{\theta }}_{\text{adj}}|/{\text{esd}}_{\text{adj}}$ over 5000 simulations is 0.02 with ${\text{esd}}_{\text{adj}}$ being the empirical standard deviation of ${\widehat{\theta }}_{\text{adj}}$ over 5000 simulations. (b) The comparison between the efficiency augmented and bias adjusted estimators for binary outcomes when $\left({\gamma }_0,\kappa \right)=\left(\mathrm{1,4}\right)$. Here the median of $\left|{\widehat{\theta }}_{\text{aug}}-{\widehat{\theta }}_{\text{adj}}\right|/{\text{esd}}_{\text{adj}}$ over 5000 simulations is 0.02 with ${\text{esd}}_{\text{adj}}$ being the empirical standard deviation of ${\widehat{\theta }}_{\text{adj}}$ over 5000 simulations.

Figure 4.

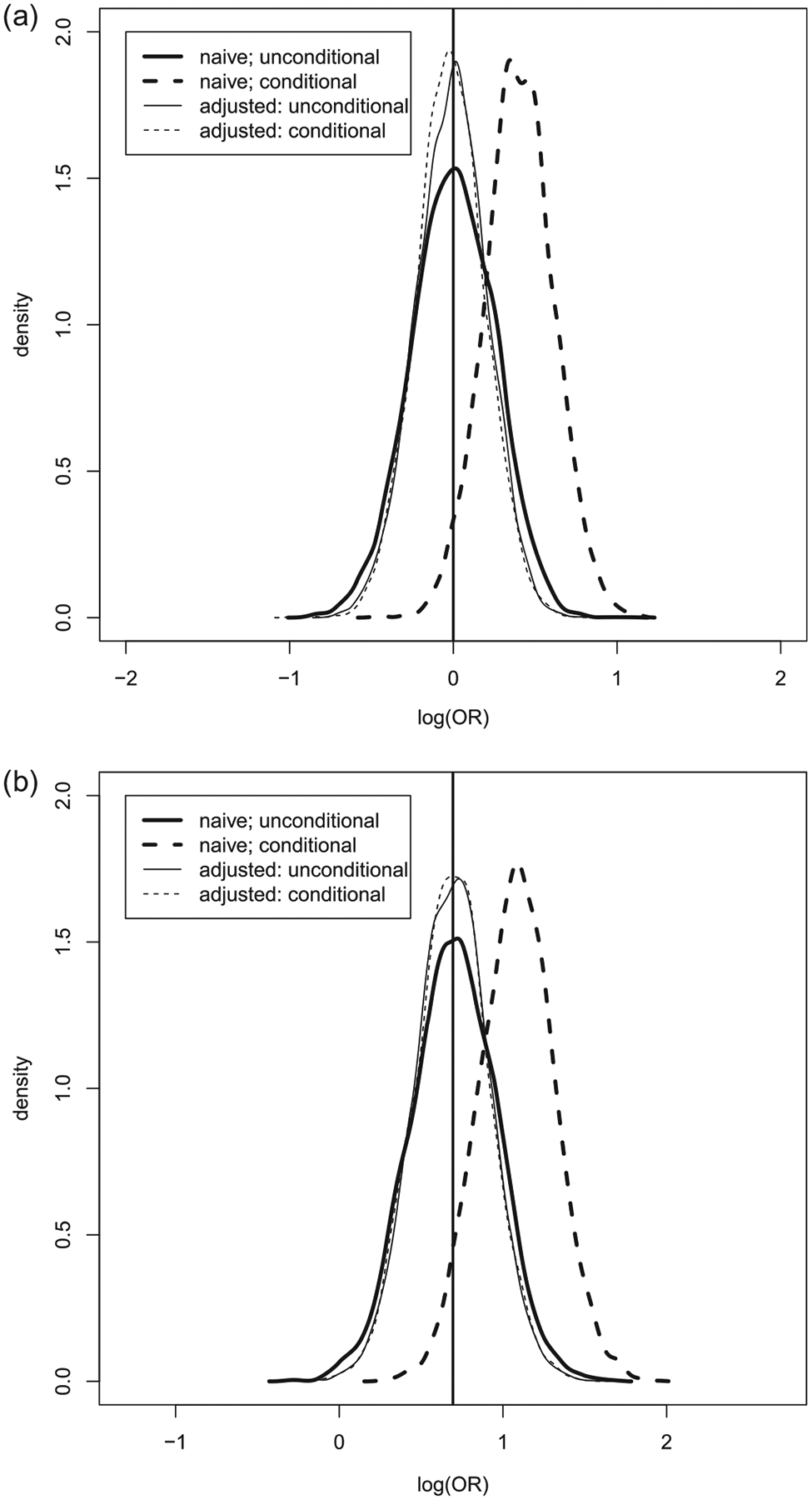
(a) The empirical density functions for $\hat{\theta }$ and ${\hat{\theta }}_{\text{adj}}$ when $\left({\gamma }_0,\kappa \right)=\left(\mathrm{0,4}\right)$. (b) The empirical density functions for $\hat{\theta }$ and ${\hat{\theta }}_{\text{adj}}$ when $\left({\gamma }_0,\kappa \right)=\left(\mathrm{1,4}\right)$.

We have repeated the simulation for continuous as well as survival outcomes. In the former case, the outcome $Y_i$ is generated via

$$Y={\beta }_0-{\gamma }_{0}Z+m\left(\mathbf{X}\right)+N\left(0,{\sigma }_0^2\right),$$

where ${\left({\beta }_0,{\beta }_1,{\beta }_2,{\beta }_3,{\beta }_4\right)}^{\text{T}}=(2.23,-0.45,-0.01,-\mathrm{0.38,0.05}{)}^{\text{T}}$ and ${\sigma }_0=2.04$ are MLEs of the log-normal regression model based on Australia data. For the latter case, the survival time is the exponential of the generated continuous outcome. The censoring time is generated uniformly between 18 and 39 months, corresponding to the minimal and maximal censoring time in the VALIANT data, respectively. For the survival outcome, the parameter of interest is the difference in RMST

$$\theta =E\left\{\text{min}\left(Y,\tau \right)∣Z=1\right\}-E\left\{\text{min}\left(Y,\tau \right)∣Z=0\right\},$$

where $\tau =33$ months is the maximum observed survival time in the Australia data. The results for the continuous endpoints are presented in Tables 3 and 4 for the conditional and unconditional distributions, respectively. Likewise, the results for the survival endpoints are presented in Tables 5 and 6. The results are similar to those for binary outcomes.

Table 3.

The simulation results for the mean difference with continuous endpoints based on 5000 simulations conditional on the observed imbalance in baseline covariates.

	$\mathit{\kappa }$	$\mathit{\theta }$	|Bias|	ESE	SEE	ECP	$\mathit{\theta }$	|Bias|	ESE	SEE	ECP
		${\mathit{\gamma }}_0=0$					${\mathit{\gamma }}_0=1$
${\hat{\theta }}_{\text{adj}}$	0	0	0.002	0.254	0.247	0.945	−1	0.002	0.254	0.247	0.945
$\hat{\theta }$	0	0	0.003	0.246	0.249	0.956	−1	0.003	0.246	0.249	0.956
${\hat{\theta }}_{\text{adj}}$	1	0	0.002	0.254	0.247	0.945	−1	0.000	0.254	0.247	0.945
$\hat{\theta }$	1	0	0.384	0.246	0.294	0.775	−1	0.384	0.246	0.294	0.775
${\hat{\theta }}_{\text{adj}}$	4	0	0.002	0.254	0.247	0.945	−1	0.002	0.254	0.247	0.945
$\hat{\theta }$	4	0	0.766	0.247	0.400	0.529	−1	0.766	0.247	0.400	0.529

ESE: empirical standard error; SEE: average standard error estimator; ECP: empirical coverage level of the 95% confidence intervals.

Table 4.

Unconditional distribution: the simulation results for the mean difference with continuous endpoints based on 5000 simulations.

	$\mathit{\kappa }$	$\mathit{\theta }$	|Bias|	ESE	SEE	ECP	$\mathit{\theta }$	|Bias|	ESE	SEE	ECP
		${\mathit{\gamma }}_0=0$					${\mathit{\gamma }}_0=1$
${\hat{\theta }}_{\text{adj}}$	0	0	0.002	0.253	0.247	0.942	−1	0.002	0.253	0.247	0.942
$\hat{\theta }$	0	0	0.003	0.250	0.249	0.947	−1	0.003	0.250	0.249	0.947
${\hat{\theta }}_{\text{adj}}$	2	0	0.002	0.253	0.247	0.942	−1	0.002	0.253	0.247	0.942
$\hat{\theta }$	2	0	0.009	0.308	0.304	0.944	−1	0.009	0.308	0.304	0.944
${\hat{\theta }}_{\text{adj}}$	4	0	0.002	0.253	0.247	0.942	−1	0.002	0.253	0.247	0.942
$\hat{\theta }$	4	0	0.015	0.435	0.427	0.943	−1	0.015	0.435	0.427	0.943

ESE: empirical standard error; SEE: average standard error estimator; ECP: empirical coverage level of the 95% confidence intervals.

Table 5.

The simulation results for the difference in RMST with survival endpoints based on 5000 simulations conditional on the observed imbalance in baseline covariates.

	$\mathit{\kappa }$	$\mathit{\theta }$	|Bias|	ESE	SEE	ECP	$\mathit{\theta }$	|Bias|	ESE	SEE	ECP
		${\mathit{\gamma }}_0=0$					${\mathit{\gamma }}_0=1$
${\hat{\theta }}_{\text{adj}}$	0	0	0.019	1.553	1.511	0.941	−4.77	0.002	1.470	1.420	0.938
$\hat{\theta }$	0	0	0.022	1.501	1.524	0.951	−4.77	0.000	1.418	1.433	0.948
${\hat{\theta }}_{\text{adj}}$	2	0	0.045	1.514	1.512	0.949	−4.66	0.029	1.456	1.451	0.950
$\hat{\theta }$	2	0	1.144	1.494	1.612	0.878	−4.66	1.324	1.441	1.531	0.880
${\hat{\theta }}_{\text{adj}}$	4	0	0.115	1.483	1.479	0.951	−4.45	0.058	1.470	1.457	0.949
$\hat{\theta }$	4	0	2.360	1.467	1.711	0.749	−4.45	2.180	1.453	1.651	0.763

ESE: empirical standard error; SEE: average standard error estimator; ECP: empirical coverage level of the 95% confidence intervals.

Table 6.

Unconditional distribution: The simulation results for the difference in RMST with survival endpoints based on 5000 simulations.

	$\mathit{\kappa }$	$\mathit{\theta }$	|Bias|	ESE	SEE	ECP	$\mathit{\theta }$	|Bias|	ESE	SEE	ECP
		${\mathit{\gamma }}_0=0$					${\mathit{\gamma }}_0=1$
${\hat{\theta }}_{\text{adj}}$	0	0	0.034	1.551	1.511	0.941	−4.77	0.014	1.472	1.419	0.935
$\hat{\theta }$	0	0	0.036	1.537	1.525	0.945	−4.77	0.016	1.456	1.434	0.943
${\hat{\theta }}_{\text{adj}}$	2	0	0.020	1.522	1.494	0.945	−4.66	0.018	1.466	1.431	0.939
$\hat{\theta }$	2	0	0.035	1.615	1.603	0.948	−4.66	0.041	1.545	1.525	0.947
${\hat{\theta }}_{\text{adj}}$	4	0	0.062	1.482	1.465	0.950	−4.45	0.037	1.471	1.442	0.945
$\hat{\theta }$	4	0	0.033	1.708	1.711	0.947	−4.45	0.020	1.665	1.656	0.946

ESE: empirical standard error; SEE: average standard error estimator; ECP: empirical coverage level of the 95% confidence intervals.

5. Discussion

For the conventional causal inference procedures, for example, the PS method, we assume that the underlying population distributions of the covariate vectors between two groups are expected to be different. Then unconditionally, the naive two sample estimator is not consistent. The PS method tries to reduce this systematic bias. Under our setting, the underlying distributions of the covariate vectors between two groups are the same due to treatment allocation randomization, but the corresponding observed distributions may be different by chance. For this situation, the parametric ANCOVA is a standard practice for obtaining an estimator for the treatment effect to reduce bias. Note that the ANCOVA is a conditional inference procedure (i.e., conditional on all the individual patients’ covariates). However, if a nonlinear ANCOVA model is not correctly specified, it is not clear how to interpret the resulting treatment effect estimate. Our nonparametric approach cannot consider this fine level of conditioning. We derived the new procedure by taking advantage of study randomization and using a conditional inference argument based on an ancillary summary statistic reflecting the observed covariate imbalance. As far as we know, there are no such methods similar to our proposal in the literature. On the other hand, it is a pleasant surprise that this conditional procedure turns out to be asymptotically equivalent to a class of augmentation methods unconditionally. This connection may enhance the usage of the augmentation procedures in practice. Now, we may claim that the new estimator improves the asymptotic efficiency unconditionally and is “unbiased” conditional on observed covariates imbalance at the same time.

Like ANCOVA or efficiency augmentation methods, the choice of covariates in our conditional procedure can be crucial. The bias adjusted estimators conditional on different covariates imbalances are all valid but have different interpretations. Thus, we suggest identifying those covariates before implementing the conditional analysis. Empirically, one may first include variables, which show imbalances via the standard two-sample test. Since the bias reduction can be substantial if the covariates of concern are highly correlated with the outcome, we suggest to additionally include covariates empirically associated with the outcome based on univariate analysis. The number of covariates in the bias adjustment procedure may be determined a priori based on the sample size to avoid over adjustment. In practice, one may examine the conditional number of the matrix ${\hat{\Sigma }}_{22}$, which would be near-singular if over adjusted. Note that theoretically, the procedures proposed by Zhu et al. (2011) and Tian et al. (2012), which have built-in variable selection algorithms, are only valid under the unconditional setting. For the unconditional case, the two sample naive and any augmented estimators are consistent, therefore, the choice of augmentation terms is solely driven by their variance. On the other hand, when we deal with the current (conditional) case, the naive estimator may not be consistent. It is not clear how to generalize these variable selection methods to the conditional setting. Further research along this line is needed.

The generalization to more general observational studies is possible by considering the new ancillary statistics

$$\frac{1}{n_1}\sum _{i=1}^n\frac{Z_i}{\pi \left({\mathbf{X}}_i\right)}{\mathbf{X}}_i-\frac{1}{n_0}\sum _{i=1}^n\frac{\left(1-Z_i\right)}{\left\{1-\pi \left({\mathbf{X}}_i\right)\right\}}{\mathbf{X}}_i,$$

where $\pi \left({\mathbf{X}}_i\right)$ is the correct PS. However, such an extension requires the knowledge of the PS, which is a difficult task by itself. Furthermore, the bias associated with the ancillary statistics is merely the “residual bias” after the PS adjustment, which removes the systematic bias between two groups. Thus, it is less important than, for example, developing a good PS model at the first place. If we can correctly specify the conditional distribution of outcome given covariates in both groups, the model-based ANCOVA method can be used to construct an unbiased estimator even for data from an observational study. However, such a model-based method may be rather sensitive to model misspecification. Covariate matching, such as the one based on PS, is also a common approach to recover the balance in baseline covariates, and ${\hat{\Delta }}_{\mathbf{X}}$ is often used to quantify imbalance after matching (Stuart 2010). This further justifies the usage of this type of ancillary statistic in our conditional inference.

Stratified analysis can be regarded as a special case of the covariate-adjusted procedure. On the other hand, due to its discrete nature of possible values of the covariates, using the present conditioning approach, one may consider the ancillary statistics consisting of the entire observed covariate vectors for stratified analysis. For the general case when some of the covariates are continuous, however, such a fine level of conditioning would be difficult, if not impossible to implement.

Appendix A: Equivalence Between ${\stackrel{\mathit{ˆ}}{\mathit{\theta }}}_{\text{aug}}$ and ${\stackrel{\mathit{ˆ}}{\mathit{\theta }}}_{\text{adj}}$

Let ${\left(Y_i,Z_i,{\mathbf{X}}_i^{\text{T}}\right)}^{\text{T}},i=1,\dots ,n$, be the iid copies of ${\left(Y,Z,{\mathbf{X}}^{\text{T}}\right)}^{\text{T}}$. The efficiency-augmented estimator for $\theta =g\left({\mu }_0,{\mu }_1\right)$ studied by Tsiatis et al. (2008) and Zhang, Tsiatis, and Davidian (2008) is given by

$${\hat{\theta }}_{\text{aug}}=g\left({\mu }_0^{†},{\mu }_1^{†}\right),$$

where

$${\mu }_1^{†}={\hat{\mu }}_1-\sum _{i=1}^n\left(1-\pi \right)\left\{n_1^{-1}{\hat{a}}_1\left({\mathbf{X}}_i\right)Z_i-n_0^{-1}{\hat{a}}_1\left({\mathbf{X}}_i\right)\left(1-Z_i\right)\right\},$$

$${\mu }_0^{†}={\hat{\mu }}_0-\sum _{i=1}^{n_0}\pi \left\{n_0^{-1}{\hat{a}}_0\left({\mathbf{X}}_i\right)\left(1-Z_i\right)-n_1^{-1}{\hat{a}}_0\left({\mathbf{X}}_i\right)Z_i\right\}.$$

Here, $n_k$ is the sample size for the $k$th group, ${\hat{a}}_k\left(\mathbf{x}\right)={\hat{\alpha }}_k+{\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_k^{\text{T}}\mathbf{x}$ and ${\hat{\alpha }}_k$ and ${\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_k$ are the least squares estimators of ${\alpha }_k$ and ${\mathit{\beta }}_k$ in regression model $E\left(Y_i\mid {\mathbf{X}}_i,Z_i=k\right)={\alpha }_k+{\mathit{\beta }}_k^{\text{T}}{\mathbf{X}}_i,k=\mathrm{0,1}$, respectively. Using the fact that ${\sum }_{i=1}^{n}I\left(Z_i=k\right)\left({\hat{\alpha }}_k+{\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_k^{\text{T}}{\mathbf{X}}_i\right)={\hat{\mu }}_k$, we have

$${\mu }_1^{†}=\pi {\hat{\mu }}_1+(1-\pi )\left({\hat{\alpha }}_1+{\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_1^{\text{T}}{\stackrel{-}{\mathbf{X}}}_0\right)\text{ and}$$

$${\mu }_0^{†}=(1-\pi ){\hat{\mu }}_0+\pi \left({\hat{\alpha }}_0+{\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_0^{\text{T}}{\stackrel{-}{\mathbf{X}}}_1\right).$$

Since ${\hat{\alpha }}_k={\hat{\mu }}_k-{\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_k^{\text{T}}{\stackrel{-}{\mathbf{X}}}_k$ and ${\left({\hat{\mu }}_k-{\mu }_k\right)}^2+{\left({\mu }_k^{†}-{\mu }_k\right)}^2=o_{\text{a.s.}}\left(n^{-1/2}\right)$,

$$\begin{gathered} {\hat{\theta }}_{\text{aug }}-\hat{\theta }= -\left(1-\pi \right){\dot{g}}_2\left({\hat{\mu }}_0,{\hat{\mu }}_1\right)\left\{{\hat{\mu }}_1-\left({\hat{\alpha }}_1+{\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_1^{\text{T}}{\stackrel{-}{\mathbf{X}}}_0\right)\right\}{-\pi \dot{g}}_1\left({\hat{\mu }}_0,{\hat{\mu }}_1\right)\left\{{\hat{\mu }}_0-\left({\hat{\alpha }}_0+{\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_0^{\text{T}}{\stackrel{-}{\mathbf{X}}}_1\right)\right\}+o_{\text{a.s.}}\left(n^{-1/2}\right) \\ =-{\left\{(1-\pi ){\dot{g}}_2\left({\hat{\mu }}_0,{\hat{\mu }}_1\right){\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_1-\pi {\dot{g}}_1\left({\hat{\mu }}_0,{\hat{\mu }}_1\right){\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_0\right\}}^{\text{T}}\widehat{\Delta }\mathbf{X}+o_{\text{a.s. }}\left(n^{-1/2}\right). \end{gathered}$$

Now, ${\stackrel{\mathit{ˆ}}{\mathit{\beta }}}_k={\hat{\Sigma }}_{22k}^{-1}{\hat{\Sigma }}_{12k}^{\text{T}}$. It follows that

$${\hat{\theta }}_{\text{aug }}=\hat{\theta }-\left\{\left(1-\pi \right){\dot{g}}_2\left({\hat{\mu }}_0,{\hat{\mu }}_1\right){\hat{\Sigma }}_{121}{\hat{\Sigma }}_{221}^{-1}\right.\left.-\pi {\dot{g}}_1\left({\hat{\mu }}_0,{\hat{\mu }}_1\right){\hat{\Sigma }}_{120}{\hat{\Sigma }}_{220}^{-1}\right\}{\widehat{\Delta }}_{\mathbf{X}}+o_{\text{a.s. }}\left(n^{-1/2}\right),$$

where ${\hat{\Sigma }}_{22k}$ is the empirical estimate for $\text{var}(\mathbf{X}\mid Z=k)$ and ${\hat{\Sigma }}_{12k}$ is the empirical estimate for $\text{cov}(Y,\mathbf{X}\mid Z=k),k=\mathrm{0,1}$. Note that in constructing the bias-adjusted estimator,

$${\hat{\Sigma }}_{12}=n^{-1}\left\{\frac{{\dot{g}}_2\left({\hat{\mu }}_0,{\hat{\mu }}_1\right){\hat{\Sigma }}_{121}}{\pi }-\frac{{\dot{g}}_1\left({\hat{\mu }}_0,{\hat{\mu }}_1\right){\hat{\Sigma }}_{120}}{1-\pi }\right\}\text{ and}$$

$${\hat{\Sigma }}_{22}=n^{-1}\left\{\frac{{\hat{\Sigma }}_{221}}{\pi }+\frac{{\hat{\Sigma }}_{220}}{1-\pi }\right\}.$$

This, coupled with the fact that ${\hat{\Sigma }}_{221}-{\hat{\Sigma }}_{220}=o_{\text{a.s.}}\left(1\right)$, implies that

$$\left\{(1-\pi ){\dot{g}}_2\left({\hat{\mu }}_0,{\hat{\mu }}_1\right){\hat{\Sigma }}_{121}{\hat{\Sigma }}_{221}^{-1}-\pi {\dot{g}}_1\left({\hat{\mu }}_0,{\hat{\mu }}_1\right){\hat{\Sigma }}_{120}{\hat{\Sigma }}_{220}^{-1}\right\}-{\hat{\Sigma }}_{12}{\hat{\Sigma }}_{22}^{-1}=o_{\text{a.s. }}\left(1\right),$$

and

$${\hat{\theta }}_{\text{aug}}-{\hat{\theta }}_{\text{adj}}=o_{\text{a}.\text{s}.}\left({\widehat{\Delta }}_{\mathbf{X}}+n^{-1/2}\right).$$

Therefore

$$\text{pr}\left\{n^{1/2}\left|{\hat{\theta }}_{\text{aug }}-{\hat{\theta }}_{\text{adj }}\right|\ge \delta \mid {\widehat{\Delta }}_{\mathbf{X}}\right\}=o_{\text{a.s. }}\left(1\right)$$

as $n\to \infty$ for any positive $\delta$.

Appendix B: Proof of Theorem

In Appendix B, we will drive the limiting distribution of

$$n^{1/2}\left(\hat{\theta }-\theta \right),$$

given ${\widehat{\Delta }}_{\mathbf{X}}$ under the following three conditions that

(A1) $\text{cov}\left\{{\left(Y,{\mathbf{X}}^{\text{T}}\right)}^{\text{T}}\right\}$ is a finite, nondegenerate matrix;

(A2) the characteristic function of $\mathbf{X}$ is integrable;

(A3) $\hat{\theta }$ is a regular estimator for $\theta$, that is,

$$\hat{\theta }-\theta =n^{-1}\sum _{i=1}^n{U}_i+{\xi }_{\theta },$$

where

$$U_i={\dot{g}}_2\left({\mu }_0,{\mu }_1\right)\frac{Z_i\left(Y_i-{\mu }_1\right)}{\pi }+{\dot{g}}_1\left({\mu }_0,{\mu }_1\right)\frac{\left(1-Z_i\right)\left(Y_i-{\mu }_0\right)}{(1-\pi )},i=1,\dots ,n,$$

are iid random variables, $\pi =\text{pr}(Z=1)=1/(M+1)$, and ${\xi }_{\theta }=o_{\text{a.s. }}\left(n^{-1/2}\right)$.

Under Condition (A3),

$$\left(\begin{array}{c}\hat{\theta }-\theta \\ {\widehat{\Delta }}_{\mathbf{X}}-{\Delta }_{\mathbf{X}}\end{array}\right)=n^{-1}\sum _{i=1}^n\left(\begin{array}{c}{U}_i\\ {\mathbf{V}}_i\end{array}\right)-\left(\begin{array}{c}{\xi }_{\theta }\\ {\xi }_{\mathbf{X}}\end{array}\right),$$ (B.1)

where ${\mathbf{V}}_i={\pi }^{-1}{Z}_i\left({\mathbf{X}}_i-\mathit{\tau }\right)+(1-\pi {)}^{-1}\left(1-Z_i\right)\left({\mathbf{X}}_i-\mathit{\tau }\right),\mathit{\tau }=E(\mathbf{X})$ and ${\xi }_{\mathbf{X}}=o_{\text{a.s.}}\left(n^{-1/2}\right)$. Let ${𝒰}_n=n^{-1/2}{\sum }_{i=1}^n{U}_i$ and ${𝒱}_n=n^{-1/2}{\sum }_{i=1}^n{\mathbf{V}}_i$. Then ${\left({𝒰}_n,{𝒱}_n^{\text{T}}\right)}^{\text{T}}$ converges weakly to ${\left(𝒰,{𝒱}^{\text{T}}\right)}^{\text{T}}$, a Gaussian vector with mean $0$ and a finite covariate matrix $n\Sigma$, where

$$\Sigma =\left(\begin{array}{cc}{\Sigma }_{11}& {\Sigma }_{12}\\ {\Sigma }_{12}& {\Sigma }_{22}\end{array}\right).$$

Here

$${\Sigma }_{11}=n^{-1}{\dot{g}}_1^2\left({\mu }_0,{\mu }_1\right)\frac{\text{var}(Y\mid Z=1)}{\pi }+n^{-1}{\dot{g}}_2^2\left({\mu }_0,{\mu }_1\right)\frac{\text{var}(Y\mid Z=0)}{1-\pi },$$

$${{\Sigma }_{12}=n}^{-1}{\dot{g}}_1\left({\mu }_0,{\mu }_1\right)\frac{\text{cov}(Y,\mathbf{X}\mid Z=1)}{\pi }-n^{-1}{\dot{g}}_2\left({\mu }_0,{\mu }_1\right)\frac{\text{cov}(Y,\mathbf{X}\mid Z=0)}{1-\pi },\text{ and }$$

$${\Sigma }_{22}{=n}^{-1}\frac{\text{var}\left(\mathbf{X}\right)}{\pi (1-\pi )}.$$

Now, let $\left\{{\mathbf{v}}_n\in {\mathbf{A}}_n\right\}$ be a sequence of vectors such that ${\mathbf{v}}_n\to {\mathbf{v}}_0$, a constant vector, as $n\to \infty$, where ${\mathbf{A}}_n$ is the support of ${𝒱}_n$. It follows from Steck (1957) that under Conditions (A1) and (A2),

$$\underset{u}{\text{sup}}\left|F_n^{{\mathbf{v}}_n}\left(u\right)-F^{{\mathbf{v}}_0}\left(u\right)\right|=o_{\text{a.s. }}\left(1\right),$$ (B.2)

where $F_n^{\mathbf{v}}\left(u\right)$ is the cumulative distribution function of the conditional distribution of ${𝒰}_n$ given ${𝒱}_n=\mathbf{v}$, and $F^{\mathbf{v}}\left(u\right)$ is the cumulative distribution function of the conditional Gaussian distribution of $𝒰$ given $𝒱=\mathbf{v}$.

Let ${\mathbf{B}}_n$ be the support of $n^{1/2}\widehat{\Delta }\mathbf{X}$. For any sequence of vectors ${\mathit{\delta }}_n\in {\mathbf{B}}_n$, such that ${\mathit{\delta }}_n-{\mathit{\delta }}_0=o\left(1\right),{\tilde{\mathit{\delta }}}_n$ also converges to ${\mathit{\delta }}_0$, as $n\to \infty$, where ${\tilde{\mathit{\delta }}}_n={\mathit{\delta }}_n-{\xi }_{\mathbf{X}}\in {\mathbf{A}}_n$. Therefore,

$$\begin{gathered} \text{Pr}\left\{n^{1/2}(\hat{\theta }-\theta )\le u\mid n^{1/2}\widehat{\Delta }\mathbf{X}={\mathit{\delta }}_n\right\} \\ =\text{Pr}\left({𝒰}_n\le u-n^{1/2}{\xi }_{\theta }\mid {𝒱}_n={\tilde{\mathit{\delta }}}_n\right)+o_{\text{a.s. }}\left(1\right) \\ =F_n^{{\mathit{\delta }}_0}\left(u-n^{1/2}{\xi }_{\theta }\right)+o_{\text{a.s. }}\left(1\right) \\ =F^{{\mathit{\delta }}_0}\left(u\right)+o_{\text{a.s. }}\left(1\right). \end{gathered}$$ (B.3)

Note that the first equality is a direct consequence of (B.1), and the last equality is implied by (B.2) and the fact that $F^{\mathit{\delta }}\left(u\right)$ is uniform continuous in $u$.

Now, let ${\mathit{\delta }}_n=n^{1/2}{\mathbf{d}}_n$. Since $F^{{\mathit{\delta }}_0}(\cdot )$ is a conditional Gaussian distribution function with mean ${\Sigma }_{12}{\Sigma }_{22}^{-1}{\mathit{\delta }}_0$, (B.3) implies $n^{1/2}(\hat{\theta }-\theta )$ given $n^{1/2}{\widehat{\Delta }}_{\mathbf{X}}={\mathit{\delta }}_n$ converges to a conditional Gaussian distribution with mean $n^{1/2}{\Sigma }_{12}{\Sigma }_{22}^{-1}{\mathit{\delta }}_0$ almost surely. Since ${\mathit{\delta }}_0-n^{1/2}{\mathbf{d}}_n=o\left(1\right)$ and ${\hat{\Sigma }}_{ij}-{\Sigma }_{ij}=o_{\text{a.s.}}\left(1\right)$, the bias-adjusted estimator $\hat{\theta }-{\hat{\Sigma }}_{12}{\hat{\Sigma }}_{22}^{-1}{\mathbf{d}}_n$ is an asymptotically unbiased estimator for $\theta$ under the conditional setting with asymptotic variance ${\Sigma }_{11}-{\Sigma }_{12}{\Sigma }_{22}^{-1}{\Sigma }_{21}$.

Appendix C: The Adjusted Estimators for the Continuous and Survival Endpoints

For the continuous endpoint, the parameter of interest is the mean difference

$$\theta =E\left(Y∣Z=1\right)-E\left(Y∣Z=0\right),$$

where $g(a,b)=b-a$. A commonly used estimator for $\theta$ can be constructed as $\hat{\theta }={\widehat{\mu }}_1-{\widehat{\mu }}_0$. The components used in the bias adjustment can be estimated as

$${\hat{\Sigma }}_{11}=\frac{1}{n}\sum _{i=1}^n\left\{\frac{Z_i}{\pi }{\left(Y_i-{\widehat{\mu }}_1\right)}^2+\frac{1-Z_i}{1-\pi }{\left(Y_i-{\widehat{\mu }}_0\right)}^2\right\}$$

$${\hat{\Sigma }}_{12}=\frac{1}{n}\sum _{i=1}^n\left\{\frac{Z_i}{\pi }\left(Y_i-{\widehat{\mu }}_1\right){\left({\mathbf{X}}_i-{\stackrel{-}{\mathbf{X}}}_1\right)}^{\text{T}}-\frac{1-Z_i}{1-\pi }\left(Y_i-{\widehat{\mu }}_0\right){\left({\mathbf{X}}_i-{\stackrel{-}{\mathbf{X}}}_0\right)}^{\text{T}}\right\}.$$

For the survival endpoint $Y$ subject to right censoring, we observe $(T,D)$, where $T=\text{min}(Y,C),D=I(Y\le C)$ and $C$ is the censoring time. The treatment effect is measured by the difference in RMST

$$\theta =E\left\{\text{min}\left(Y,\tau \right)∣Z=1\right\}-E\left\{\text{min}\left(Y,\tau \right)∣Z=0\right\},$$

for fixed $\tau$, and $g(a,b)=b-a$. The naive estimator of $\theta$ can be constructed as

$$\hat{\theta }={\int }_0^{\tau }{\hat{S}}_1\left(t\right)dt-{\int }_0^{\tau }{\hat{S}}_0\left(t\right)dt,$$

where ${\hat{S}}_j(\cdot )$ is the Kaplan–Meier (KM) estimator for the survival function of $T\mid Z=j$ based on observations from group $j,j=\mathrm{0,1}$. Note that $\hat{\theta }$ is a nonparametric estimator for $\theta$ in that its validity does not depend on any specific parametric or semiparametric assumption in contrast to the hazard ratio. It follows from the classical results about the KM estimator in survival analysis,

$$\hat{\theta }-\theta =-\frac{1}{n}\sum _{i=1}^n\left\{\frac{Z_i}{\pi }{\int }_0^{\tau }\frac{{\int }_s^{\tau }{S}_1\left(t\right)dt}{p_1\left(s\right)}d{M}_i\left(s\right)\left.+\frac{1-Z_i}{1-\pi }{\int }_0^{\tau }\frac{{\int }_s^{\tau }{S}_0\left(t\right)dt}{p_0\left(s\right)}d{M}_i\left(s\right)\right\}+o_p\left(n^{-1/2}\right),\right.$$

where $M_i\left(t\right)=I\left(T_i\le t\right)D_i-{\int }_0^{t}I\left(T_i\ge s\right)d\Lambda \left(s\mid Z_i\right),\Lambda (t\mid Z)$ is the cumulative hazard function of $Y\mid Z$, and $p_j\left(t\right)=\text{pr}(T\ge t\mid Z=j),j=1,2.$ Therefore, the variance components used in the bias adjustment can be estimated as

$${\hat{\Sigma }}_{11}=\frac{1}{n}\sum _{i=1}^n\left[\frac{Z_i}{\pi }{\left\{{\int }_0^{\tau }\frac{{\int }_s^{\tau }{\hat{S}}_1\left(t\right)dt}{{\hat{p}}_1\left(s\right)}d{\hat{M}}_i\left(s\right)\right\}}^2\left.+\frac{1-Z_i}{1-\pi }{\left\{{\int }_0^{\tau }\frac{{\int }_s^{\tau }{\hat{S}}_0\left(t\right)dt}{{\hat{p}}_0\left(s\right)}d{\hat{M}}_i\left(s\right)\right\}}^2\right]\right.$$

and

$${\hat{\Sigma }}_{12}=\frac{1}{n}\sum _{i=1}^n\left\{\frac{Z_i}{\pi }{\int }_0^{\tau }\frac{{\int }_s^{\tau }{\hat{S}}_1\left(t\right)dt}{{\hat{p}}_1\left(s\right)}d{\hat{M}}_i\left(s\right){\left({\mathbf{X}}_i-{\stackrel{-}{\mathbf{X}}}_1\right)}^{\text{T}}\left.-\frac{1-Z_i}{1-\pi }{\int }_0^{\tau }\frac{{\int }_s^{\tau }{\hat{S}}_0\left(t\right)dt}{{\hat{p}}_0\left(s\right)}d{\hat{M}}_i\left(s\right){\left({\mathbf{X}}_i-{\stackrel{-}{\mathbf{X}}}_0\right)}^{\text{T}}\right\}\right.,$$

where ${\hat{M}}_i\left(t\right)=I\left(T_i\le t\right)D_i-{\int }_0^{t}I\left(T_i\ge s\right)d\hat{\Lambda }\left(s\mid Z_i\right),\hat{\Lambda }(t\mid Z)$ is the Nelson–Aalen estimator for the cumulative hazard function of $Y\mid Z$, ${\hat{p}}_1\left(t\right)=n_1^{-1}{\sum }_{i=1}^n{Z}_{i}I\left(T_i\ge t\right)$, and ${\hat{p}}_0\left(t\right)=n_0^{-1}{\sum }_{i=1}^n\left(1-Z_i\right)I\left(T_i\ge \right. t)$.