Algorithms for Sparse Support Vector Machines

Abstract

Many problems in classification involve huge numbers of irrelevant features. Variable selection reveals the crucial features, reduces the dimensionality of feature space, and improves model interpretation. In the support vector machine literature, variable selection is achieved by ${\ell }_1$ penalties. These convex relaxations seriously bias parameter estimates toward 0 and tend to admit too many irrelevant features. The current paper presents an alternative that replaces penalties by sparse-set constraints. Penalties still appear, but serve a different purpose. The proximal distance principle takes a loss function $L(\mathit{\beta })$ and adds the penalty $\frac{\rho }{2}\text{dist}{\left(\mathit{\beta },S_k\right)}^2$ capturing the squared Euclidean distance of the parameter vector $\mathit{\beta }$ to the sparsity set $S_k$ where at most k components of $\mathit{\beta }$ are nonzero. If ${\mathit{\beta }}_{\rho }$ represents the minimum of the objective $f_{\rho }(\mathit{\beta })=L(\mathit{\beta })+\frac{\rho }{2}\text{dist}{\left(\mathit{\beta },S_k\right)}^2$, then ${\mathit{\beta }}_{\rho }$ tends to the constrained minimum of $L(\mathit{\beta })$ over $S_k$ as $\rho$ tends to $\infty$. We derive two closely related algorithms to carry out this strategy. Our simulated and real examples vividly demonstrate how the algorithms achieve better sparsity without loss of classification power.

1. Introduction

Support vector machines (SVMs) are powerful pattern recognition tools (Cortes and Vapnik, 1995) with a wide range of applications across machine learning and statistics. Success stories in supervised learning include optical character recognition (Decoste and Schölkopf, 2002), image segmentation (Barghout, 2015), text categorization (Joachims, 1998; Pradhan et al., 2004), protein structure prediction (Dunbrack, 2006), and early detection and classification of human cancers (Sewak et al., 2007). It is possible to extend SVM to online algorithms for resource-limited computing environments (Cauwenberghs and Poggio, 2000; Laskov et al., 2006) and beyond classification to unsupervised learning problems (Ben-Hur et al., 2002).

Part of the success of SVMs is due to their flexible decision boundaries. SVMs are often sparse in the sense that they depend on relatively few training samples. Sparsity enhances the ability of SVMs to label unlabeled cases. Existing research on fitting SVMs largely focuses on this strength by devising methods that improve prediction quality or accelerate the fitting process on large-scale datasets. Speed and prediction are worthy goals, but some application domains also require model interpretability. Indeed, in biological sciences and biomedical applications most variables are uninformative. One naturally desires to extract the informative variables because these drive further discovery and hypothesis generation. Thus, variable selection for SVMs is a topic of considerable interest in the literature. Lasso penalization is the primary tool for inducing sparsity (Zhu et al., 2003). Unfortunately, lasso penalization also induces shrinkage in model selection and tends to admit many irrelevant features. In contrast to penalization and shrinkage, screening methods originally developed for lasso problems eliminate variables prior to model fitting (El Ghaoui et al., 2012; Tibshirani et al., 2012; Wang et al., 2013). Ogawa et al. (2013) implement screening in SVMs, and Jaggi (2014) forges further connections between SVMs and the lasso.

The aim of this work is to present a flexible framework that addresses parsimony in both variable selection and prediction. We focus on (a) primal problems under the squared-hinge loss, (b) novel proximal distance algorithms for parameter fitting and model selection (Chi et al., 2014; Lange, 2016, the latter is a good reference), and (c) extensions to kernel machines for nonlinear data. Our key strategy replaces sparsity inducing penalties with projection onto sparsity constraint sets. The SVM proximal distance algorithm comes in two closely related flavors. Both exhibit comparable, and often superior, predictive accuracy to existing SVM methods. Although the proximal distance algorithms are sometimes slower than competing methods, their output is both easier to interpret and better at revealing sparse signals hidden in high-dimensional data.

2. Sparse SVMs via Distance Penalization

In this section we develop the theory underpinning our sparse SVM algorithms. We begin with a brief overview of SVM loss models, specifically L₂ SVMs, and derive a quadratic surrogate for squared hinge losses. We also add a squared distance penalty to the L₂ SVM loss to guide fitting toward sparsity. By projecting model coefficients onto different sparsity sets, one can directly control the number of active features in a model. We explore this idea in linear classifiers to selecting potentially informative features and to nonlinear classifiers to select potentially informative support vectors. These vectors define a classifier’s decision boundary. Readers may consult Keys et al. (2019), for a broad overview of the proximal distance principle and its connection to proximal methods in convex optimization.

2.1. Background

Many variations on supervised SVMs have been proposed. For example, the class of soft-margin L_p SVMs are based on convex programs of the form

$$\begin{array}{ll}\underset{\mathit{w},b,\xi }{\min }& \frac{1}{2}{\mathit{w}}^{\top }\mathit{w}+\frac{C}{np}\sum _{i=1}^n{\xi }_i^p\\ y_i\left({\mathit{w}}^{\top }{\mathit{x}}_i+b\right)& \ge 1-{\xi }_i,\text{for}i=1,2,\dots ,n\\ {\xi }_i& \ge 0,\end{array}$$

where $p\ge 1$, the polarities $y_i\in \{-1,+1\}$ serve as class labels, and features (predictors) are denoted ${\mathit{x}}_i\in {ℝ}^d$. Here the parameters $(\mathit{w},b)\in {ℝ}^{d+1}$ determine a hyperplane $\left\{\mathit{x}:{\mathit{w}}^{\top }\mathit{x}+b=0\right\}$ separating two classes, and the slack variables ${\xi }_i$ quantify margins in inactive constraints $y_i\left({\mathit{w}}^{\top }{\mathit{x}}_i+b\right)>1$. Typically, $C>0$ is treated as a hyperparameter that mediates a compromise between maximizing the separating margin (${\Vert \mathit{w}\Vert }_2^{-1}$) and minimizing empirical risk. Taking $C\to 0$ recovers a hard-margin model and requires data to be linearly separable.

Rewriting the margin constraints as ${\xi }_i\ge 1-y_i\left({\mathit{w}}^{\top }{\mathit{x}}_i+b\right)$ and multiplying the objective by $\lambda =1/C$ allows one to state the constrained minimization problem as an equivalent unconstrained problem

$$\begin{array}{l}\underset{\mathit{\beta }}{\min }{f}_{\lambda }(\mathit{\beta }\mid \mathit{y},\mathit{X})=\lambda \psi (\mathit{\beta })+\frac{1}{n}\sum _{i=1}^n{R}_i(\mathit{\beta }\mid \mathit{y},\mathit{X}),\\ \text{where}{R}_i(\mathit{\beta }\mid \mathit{y},\mathit{X})=p^{-1}\max {\left\{0,1-y_i\left({\mathit{w}}^{\top }{\mathit{x}}_i+b\right)\right\}}^p,\end{array}$$ (1)

with model parameters $\mathit{\beta }=(\mathit{w},b)$, penalty $\psi (\mathit{\beta })=\frac{1}{2}{\Vert \mathit{w}\Vert }_2^2$, and misclassification cost $R_i(\mathit{\beta })$ per sample $i=1,2,\dots ,n$. We adopt this version of SVM fitting and note a few connections to the existing literature. First, under this formulation the loss $\frac{1}{n}\sum _{i=1}^n{R}_i(\mathit{\beta }\mid \mathit{y},\mathit{X})$ can be interpreted as a measure of empirical risk when the functional form of R_i is chosen appropriately. When p = 1 the SVM is the classic soft-margin classifier, sometimes called the L₁ SVM, in which the ${\ell }_2$ penalty term on model coefficients enables classification even when data are not linearly separable. The ridge penalty can be replaced by a lasso penalty $\psi (\mathit{\beta })={\Vert \mathit{w}\Vert }_1$ to induce variable selection (Zhu et al., 2003). Other loss functions, such as quadratic and Huber hinge errors, have been proposed as alternatives to the hinge loss $u_{+}=\max \{0,u\}$ to promote better prediction and robustness to outliers (Groenen et al., 2008). Taking p = 2 leads to the L₂ SVM family which achieves differentiability and strict convexity at the expense of overemphasizing misclassification errors in outliers. In addition, clever formulations of convex primal programs often lead to dual programs that are easier to solve and thus accelerate the fitting process. The last point is especially pertinent to the L₂ family as the dual program reduces to maximization of a quadratic over a simplex. This brief review is hardly exhaustive. Nevertheless, in all their variations, the defining property of SVMs is their parsimonious decision boundaries driven by a small number of support vectors.

2.2. Mathematical Formulation

Our starting point is a L₂ SVM with a squared hinge-loss $\max {\{0,1-u\}}^2$. The SVM takes the form

$$\underset{\mathit{\beta }}{\min }{f}_{\lambda }(\mathit{\beta }\mid \mathit{y},\mathit{X})=\frac{\lambda }{2}{\Vert \mathit{w}\Vert }_2^2+\frac{1}{2n}\sum _{i=1}^n\max {\left\{0,1-y_i{\mathit{x}}_i^{\top }\mathit{\beta }\right\}}^2.$$ (2)

Here the n labeled samples $\left(y_i,{\mathit{x}}_i\right)$ consist of a binary label $y_i\in \{-1,1\}$ and a feature vector ${\mathit{x}}_i\in {ℝ}^{p+1}$ occupying a row of the matrix $\mathit{X}\in {ℝ}^{n\times p+1}$. The parameter vector $\mathit{\beta }=(\mathit{w},b){\in }^{{ℝ}^{p+1}}$ defines a hyperplane separating the two classes, with the first p components corresponding to weights $\mathit{w}\in {ℝ}^p$ and the last component b representing an intercept. The last component ${\mathit{x}}_{i,p+1}$ of each ${\mathit{x}}_i$ is accordingly 1. Our notation $\mathit{\beta }$ is insensitive to the inclusion or exclusion of an intercept term in describing the primal model (2).

Rather than directly minimize $f_{\lambda }(\mathit{\beta }\mid \mathit{y},\mathit{X})$ defined by equation (2), we turn to the MM principle (Lange et al., 2000; Lange, 2016) and invoke the quadratic majorization

$$\max {\{0,1-u\}}^2\le \{\begin{array}{ll}{\left(u_m-u\right)}^2,\hfill & u_m\ge 1\hfill \\ {(1-u)}^2,\hfill & u_m<1\hfill \end{array}$$

at iteration m suggested by Groenen et al. (2008). Note the two sides of the majorization agree when $u=u_m$. Given that all $y_i^2=1$, the term by term application of the majorization creates the overall quadratic surrogate

$$\begin{array}{l}{g}_{\lambda }\left(\mathit{\beta }\mid {\mathit{\beta }}_m\right)=\frac{\lambda }{2}{\Vert \mathit{w}\Vert }_2^2+\frac{1}{2n}\Vert {\mathit{z}}_m-X\mathit{\beta }{\Vert }^2,\\ \text{where}{z}_{mi}=\{\begin{array}{ll}{\mathit{x}}_i^{\top }{\mathit{\beta }}_m& \text{if}{y}_i{\mathit{x}}_i^{\top }{\mathit{\beta }}_m\ge 1\\ y_i& \text{if}{y}_i{\mathit{x}}_i^{\top }{\mathit{\beta }}_m<1.\end{array}\end{array}$$ (3)

This maneuver reduces the original minimization problem to a sequence of easier minimization problems that can be solved by repeated least squares. Nguyen and McLachlan (2017) also apply the MM principle to support vector machines and make a connection to iteratively reweighted least squares (IRLS), albeit with a different majorization. The surrogate (3) is appealing compared to surrogate (12) of Nguyen and McLachlan (2017) because the former avoids changing weights. In any case, the MM principle implies that every iteration decreases the objective function (2) via the chain of inequalities

$$f_{\lambda }\left({\mathit{\beta }}_{m+1}\right)\stackrel{\text{majorize}}{\le }{g}_{\lambda }\left({\mathit{\beta }}_{m+1}\mid {\mathit{\beta }}_m\right)\stackrel{\text{minimize}}{\le }{g}_{\lambda }\left({\mathit{\beta }}_m\mid {\mathit{\beta }}_m\right)\stackrel{\text{tangency}}{=}{f}_{\lambda }\left({\mathit{\beta }}_m\right).$$

2.3. Variable Selection

The objective (2) employs the quadratic penalty to control the size of a SVM’s separating margin, $1/\Vert \mathit{w}\Vert$, but the penalty shrinks parameters rather than selects them. Thus, we append an explicit sparsity constraint to (2) and consider constrained problems of the form

$$\underset{\mathit{\beta }}{\min }{f}_{\lambda }(\mathit{\beta }\mid \mathit{y},\mathit{X})\text{such that}{\Vert \mathit{w}\Vert }_0\le k,$$

where ${\Vert \mathit{w}\Vert }_0=\sum _{j}1\left\{w_j\ne 0\right\}$ counts the number of nonzero components in w. Note that the restriction ${\Vert \mathit{w}\Vert }_0\le k$ makes the sparsity set

$$S_k=\left\{\mathit{\beta }{\in }^{{ℝ}^{p+1}}:\mathit{\beta }=(\mathit{w},b)\text{and}{\Vert \mathit{w}\Vert }_0\le k\right\},$$

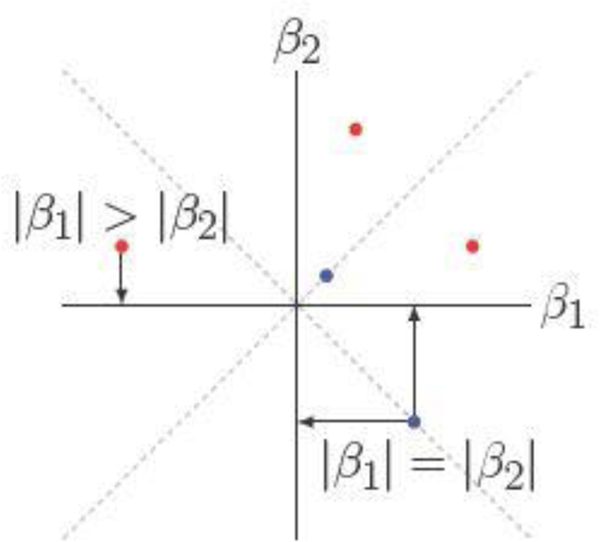
closed. For any dataset with $p\ge k$ predictors, $S_k={ℝ}^{p+1}$. Fortunately, Euclidean projection onto S_k is straightforward. The projection operator $P_{S_k}(\mathit{\beta })$ sets to zero all but the largest k entries in magnitude of ${\beta }_1$ through ${\beta }_p$. This goal can be achieved efficiently by a partial sort of these entries. Figure 1 illustrates the Euclidean projection that selects one variable in a two-dimensional problem. The projection may fail to be unique when some or all coefficients are tied, but such events occur on lower dimensional subspaces and therefore have measure zero.

Fig. 1.

Euclidean projections of points in ${ℝ}^2$ onto ${𝓢}_1$. Red points have a unique projection whereas blue points may have multiple valid projections.

In light of the simplicity of projections onto sparsity sets, we follow the penalty method of constrained optimization (Beltrami, 1970; Courant, 1943) and minimize the unconstrained objective

$$h_{\rho }(\mathit{\beta })=f_{\lambda }(\mathit{\beta }\mid \mathit{y},\mathit{X})+\frac{\rho }{2}\text{dist}{\left(\mathit{\beta },S_k\right)}^2,$$ (4)

for a large value of the annealing parameter $\rho \ge 0$. The squared distance penalty enforces near sparsity and is continuously differentiable wherever the underlying projection is single valued. In the limit as $\rho$ tends to $\infty$, the solution vector ${\mathit{\beta }}_p$ tends to a solution of the constrained problem. Combining our previous majorization (3) with distance majorization

$$\text{dist}{(\mathit{u},S)}^2\le \Vert \mathit{u}-P_S{\left({\mathit{u}}_m\right)\Vert }^2,$$

yields the sum of squares surrogate

$$g_{\rho }\left(\mathit{\beta }\mid {\mathit{\beta }}_m\right)=\frac{\lambda }{2}{\Vert \mathit{w}\Vert }_2^2+\frac{1}{2n}{\Vert {\mathit{z}}_m-\mathit{X}\mathit{\beta }\Vert }^2+\frac{\rho }{2}{\Vert P_{S_k}\left({\mathit{\beta }}_m\right)-\mathit{\beta }\Vert }_2^2.$$ (5)

Note that because no projection is applied to the intercept, when present, projection does not touch the $(p+1)$-th component. Sparsity constraints permit identification of features driving a classifier’s decision boundary in spite of sacrificing convexity. Our previous experience supports the value of the proximal distance principle in building parsimonious models with nonconvex set constraints (Xu et al., 2017; Keys et al., 2019; Landeros et al., 2022).

2.4. Support Vector Selection

While soft-margin classifiers are known to perform decently even on datasets that are not linearly separable, they do not generalize well to inherently nonlinear data. Transforming the feature vectors ${\mathit{x}}_i$ into an abstract feature space via an implicit mapping, $\varphi \left({\mathit{x}}_i\right)$, is sufficient to induce nonlinear decision boundaries. Careful design of a primal problem then allows one to invoke the kernel trick (Schölkopf and Smola, 2018), which reduces further calculations to the formation of inner products $\kappa \left({\mathit{x}}_i,{\mathit{x}}_j\right)={\langle \varphi \left({\mathit{x}}_i\right),\varphi \left({\mathit{x}}_j\right)\rangle }_{𝓗}$ in a Hilbert space $𝓗$. Thus, the functional form of the nonlinear transformation $\varphi (\cdot )$ is immaterial, and one can instead focus on choosing a positive semidefinite kernel $\kappa \left({\mathit{x}}_i,{\mathit{x}}_j\right)$ induced by the transformation.

The L₂ SVM considered in (2) has a well-known dual program (Frieß and Harrison, 1998a,b; Mangasarian and Musicant, 2001)

$$\begin{array}{ll}\underset{\mathit{\alpha }}{\min }{f}_{\lambda }(\mathit{\alpha }\mid \mathit{y},\mathit{X})& =\frac{n}{2}{\Vert \mathit{\alpha }\Vert }_2^2+\frac{1}{2\lambda }{\mathit{\alpha }}^{\top }\mathit{Y}\mathit{K}\mathit{Y}\mathit{\alpha }-{\mathbf{1}}^{\top }\mathit{\alpha }\\ \text{such that}{\mathit{y}}^{\top }\mathit{\alpha }& =0\text{and}\mathit{\alpha }\ge \mathbf{0},\end{array}$$ (6)

where $\mathit{Y}=\text{diag}(\mathit{y})$ and $\mathit{\alpha }\in {ℝ}^n$. The choice $\mathit{K}=\mathit{X}{\mathit{X}}^{\top }$ corresponds to the standard linear kernel, but in practice one may substitute $K_{ij}=\kappa \left({\mathit{x}}_i,{\mathit{x}}_j\right)$ for any positive semidefinite kernel $\kappa (\cdot ,\cdot )$ satisfying Mercer’s condition (Mercer, 1909; Kimeldorf and Wahba, 1971; Cortes and Vapnik, 1995; Schölkopf et al., 2001). One can show that the original parameters $\mathit{\beta }=(\mathit{w},b)$ are given by

$$\mathit{w}={\lambda }^{-1}\sum _i{\alpha }_i{y}_i\varphi \left({\mathit{x}}_i\right),\text{and}b=-{(n\lambda )}^{-1}{\mathit{y}}^{\top }\mathit{Y}\mathit{K}\mathit{Y}\mathit{\alpha }+\overline{y}.$$

The relationship between w and $\mathit{\alpha }$ suggests that, in general, one cannot hope to induce sparsity in w using a simple distance penalty in the dual problem. Instead, we note that the combination of constraints ${\mathit{y}}^{\top }\mathit{\alpha }=0$ and $\mathit{\alpha }\ge 0$ already imply some level of sparsity in $\mathit{\alpha }$. Thus, let $\mathit{\alpha }=(\mathit{a},b)$ for some coefficients $\mathit{a}\in {ℝ}^n$. Substituting $\mathit{w}=\sum _i{a}_i{y}_i\varphi \left({\mathit{x}}_i\right)$ in the squared hinge term of (2) leads to the alternative model

$$\begin{array}{l}{\underset{\mathit{a}}{\min }\frac{\lambda }{2}{\Vert \mathit{a}\Vert }_2^2+\frac{1}{2n}\sum _{i=1}^n\max \{0,1-y_i[\sum _{j=1}^n\kappa \left({\mathit{x}}_i,{\mathit{x}}_j\right)y_j{a}_j+b]\}}^2,\\ \text{such that}{\Vert \mathit{a}\Vert }_0\le k,\end{array}$$ (7)

which directly controls the number of support vectors in a SVM’s decision boundary. The set of support vectors equals $\left\{{\mathit{x}}_i:a_i\ne 0\right\}$. This nonlinear model, denoted by $f_{\lambda }^{\text{NL}}(\mathit{\alpha }\mid \mathit{y},\mathit{X})$, combines the advantages of a the squared hinge in the primal problem (2) with the kernel trick but, crucially, it is not anchored by any duality theory or related to the dual problem (6). Nevertheless, we will see that this model successfully fits nonlinear decision boundaries with additional flexibility in selecting support vectors.

Adding a distance penalty to (7) leads to the objective

$$h_{\rho }(\mathit{\alpha },b)=f_{\lambda }^{\text{NL}}(\mathit{\alpha }\mid \mathit{y},\mathit{X})+\frac{\rho }{2}\text{dist}{\left(\mathit{\alpha },S_k\right)}^2.$$ (8)

To recapitulate, define $\mathit{Y}=\text{diag}(\mathit{y})$ as a diagonal matrix and majorize the squared hinge and distance penalty to arrive at the quadratic surrogate

$$g_{\rho }\left(\mathit{\alpha }\mid {\mathit{\alpha }}_m\right)=\frac{\lambda }{2}{\Vert \mathit{a}\Vert }_2^2+\frac{1}{2n}{\Vert {\mathit{z}}_m+\mathit{K}\mathit{Y}\mathit{a}\Vert }_2^2+\frac{\rho }{2}{\Vert P\left({\mathit{\alpha }}_m\right)-\mathit{a}\Vert }_2^2.$$ (9)

One can verify this surrogate by identifying KY with X and $\mathit{\alpha }$ with $\mathit{\beta }$ in the function (3) majorizing the squared hinge.

3. Algorithms

In this section we derive practical algorithms for minimizing the criteria (4) and (8) via their surrogate functions (5) and (9), respectively. We begin by outlining a general strategy, proximal distance iteration, that overcomes the technical requirement that $\rho >0$ should be sufficiently large in minimizing constrained objectives functions. Convergence results are discussed. Next, we derive iterative maps specific to minimization of (4) and (8) that apply to fitting sparse linear and nonlinear classifiers, respectively. Finally, we conclude by discussing strategies to tune the level of sparsity via cross validation.

3.1. Proximal Distance Iteration

Let us briefly discuss proximal distance iteration in a general. Driving the distance penalty $\text{dist}(\mathit{x},S)$ in $h_{\rho }(\mathit{x})$ towards 0 requires setting $\rho >0$ sufficiently large. Propositions 1 through 4 of Keys et al. (2019) provide guidance on how large ρ should be. Unfortunately, taking $\rho$ arbitrarily large necessarily slows convergence. Thus, in practice one minimizes a sequence of penalized objectives $\left\{h_{\rho }(\mathit{x}):\rho ={\rho }_0,{\rho }_1,{\rho }_2,\dots \right\}$ parameterized by an increasing sequence of penalty coefficients ${\rho }_t$. The annealing path $\mathit{x}(\rho )$ is typically continuous in ρ, so that warm starting the current suproblem from the solution of the previous subproblem accelerates convergence. One can assess convergence by checking the criteria

$$\Vert h_{\rho }(\mathit{x})\Vert {\le }_g^{ϵ},\text{and}$$ (10)

$$\text{dist}(\mathit{x},S){\le }_d^{ϵ},$$ (11)

for positive tolerances ${\mathit{ϵ}}_g$ and ${\mathit{ϵ}}_d$. Note that in the initial phase of proximal distance iteration when condition (11) is violated, one does not need strict satisfaction of the gradient condition (10) before increasing ρ. On the other hand, enforcing the gradient check (10) compounds the benefits of warm starts. Algorithm 1 summarizes proximal distance iteration applied to a generic problem. According to the MM principle, the algorithm map ${𝓜}_{\rho }(\mathit{x})$ guarantees descent for fixed $\rho$. Note that the final projection step is justified when condition (11) is satisfied.

Algorithm 1.

Proximal Distance Iteration

Require: An objective $h_{\rho }(\mathit{x})$, gradient $\nabla h_{\rho }(\mathit{x})$, and algorithm map ${𝓜}_{\rho }(\mathit{x})$.
1:	Set tolerances ${\mathit{ϵ}}_d$ and ${\mathit{ϵ}}_g$; fix hyperparameters λ and k.
2:	Set maximum number of $\rho$ values, $t_{\text{max}}$; maximum inner iterations $m_{\text{max}}$.
3:	Initialize the estimate X and define an increasing sequence ${\{\rho (t)\}}_{t\ge 0}$.
4:	for $t\leftarrow 0,1,\dots ,t_{\max }$ do
5:	Set ${\mathit{x}}_0\leftarrow \mathit{x}$ using the current estimate and take $\rho \leftarrow \rho (t)$.
6:	for $m\leftarrow 1,\dots ,m_{\max }$ do
7:	Iterate the algorithm map,$x_{m+1}\leftarrow {𝓜}_{\rho }\left({\mathit{x}}_m\right)$.
8:	if ${\Vert \nabla h_{\rho }\left({\mathit{x}}_{m+1}\right)\Vert }_2\le {ϵ}_g$ then
9:	Break.
10:	end if
11:	end for
12:	Update $\mathit{x}\leftarrow {\mathit{x}}_{m+1}$
13:	if $\text{dist}(\mathit{x},S){ϵ}_d$ then
14:	Break.
15:	end if
16:	end for
17:	Project the final estimate $\mathit{x}\leftarrow P_{S_k}(\mathit{x})$.

3.2. Iteration Maps

We now derive algorithm maps for minimizing the penalized loss (4) using Algorithm 1. The MM strategy repeatedly minimizes the surrogate (5) anchored at the current estimate ${\mathit{\beta }}_m$. Updating $\mathit{\beta }$ amounts to solving the linear system

$$\begin{array}{ll}{\mathit{\beta }}_{m+1}& =\text{argmin}{g}_{\rho }\left(\mathit{\beta }\mid {\mathit{\beta }}_m\right)\\ & ={\left[n^{-1}{\mathit{X}}^{\top }\mathit{X}+(\lambda +\rho )\mathit{I}\right]}^{-1}\left[n^{-1}{\mathit{X}}^{\top }{\mathit{z}}_m+\rho P_{s_k}\left({\mathit{\beta }}_m\right)\right].\end{array}$$ (12)

Observe that the solution is non-unique if there are multiple admissible projections $P_{S_k}\left({\mathit{\beta }}_m\right)$ of ${\mathit{\beta }}_m$ onto S_k. Fortunately, the linear system can be solved efficiently using a single thin singular value decomposition (SVD) $\mathit{X}=\mathit{U}\mathbf{\Sigma }{\mathit{V}}^{\top }$ across all iterates. This approach may be expensive if the number of samples n or predictors p is large, but it keeps the factorization independent of $\rho$ and λ. We document our implementation of this strategy in Appendix A.

Alternatively, differentiability of $h_{\rho }(\mathit{\beta })$ implies the first-order tangency condition $\nabla g_{\rho }(\mathit{\beta }\mid \mathit{\beta })=\nabla h_{\rho }(\mathit{\beta })$, which in turn suggests implementing gradient descent. Minimizing the surrogate $g_{\rho }\left(\mathit{\beta }\mid {\mathit{\beta }}_m\right)$ in the direction $-\nabla h_{\rho }\left({\mathit{\beta }}_m\right)$ leads to the update

$$\begin{gathered} {\mathit{\beta }}_{m+1}={\mathit{\beta }}_m-t_m\nabla h_{\rho }\left({\mathit{\beta }}_m\right) \\ {t}_m=\frac{{\Vert \nabla h_{\rho }\left({\mathit{\beta }}_m\right)\Vert }^2}{n^{-1}{\Vert \mathit{X}\nabla h_{\rho }\left({\mathit{\beta }}_m\right)\Vert }^2+(\rho +\lambda ){\Vert \nabla h_{\rho }\left({\mathit{\beta }}_m\right)\Vert }^2} \end{gathered}$$ (13)

derived in the Appendix. A single steepest descent step cannot, in general, achieve exact minimization of $g_{\rho }\left(\mathit{\beta }\mid {\mathit{\beta }}_m\right)$, but one step always drives the surrogate $h_{\rho }(\mathit{\beta })$ downhill. In any event, the iterates generated by the MM update (12) are generally different from those generated by the steepest descent update (13). Multiple steps of steepest descent can achieve exact minimization of $g_{\rho }\left(\mathit{\beta }\mid {\mathit{\beta }}_m\right)$ and bring steepest descent into alignment with MM. However, exact minimization via steepest descent is costly and unlikely to offer any advantages in precision or computational cost over minimizing the surrogate by conjugate gradients. Fortunately, the algorithm maps (12) and (13) are easily adapted to the nonlinear setting. Simply substitute KY and $\mathit{\alpha }$ for X and $\mathit{\beta }$, respectively.

3.3. Convergence Theory

In this section we briefly address the convergence properties of our proximal distance algorithms for SVM. Convergence theory for gradient descent is more standard and is omitted. Readers mainly interested in applications can skip this discussion and return to it later as desired.

The loss $f_{\lambda }(\mathit{\beta }\mid \mathit{y},\mathit{X})$ defined in (2) is convex by the standard closure properties of convex functions. Without loss of generality, let us assume that the intercept b = 0 and identify $\mathit{\beta }=\mathit{w}$. In this regard note that the scalar function $u_{+}^2=\max {\{0,u\}}^2$ is convex in u. To prove that $f_{\lambda }(\mathit{\beta }\mid \mathit{y},\mathit{X})$ is coercive, one can invoke the fact that a convex function on ${ℝ}^p$ is coercive if and only if it is coercive along all nontrivial rays $\left\{\mathit{\beta }{\in }^{{ℝ}^p}:\mathit{\beta }=t\mathit{v},t\ge 0\right\}$ emanating from the origin (Lange et al., 2000). It is obvious that $f_{\lambda }(t\mathit{v}\mid \mathit{y},\mathit{X})$ tends to $\infty$ as t tends to $\infty$ if and only if at least one vector $-y_i{\mathit{x}}_i$ satisfies $-y_i{\mathit{x}}_i^{\top }\mathit{v}>0$. In other words, $f_{\lambda }(t\mathit{v}\mid \mathit{y},\mathit{X})$ is coercive if and only if the polar cone

$$C=\left\{\mathit{v}:-y_i{\mathit{x}}_i^{\top }\mathit{v}\le 0\text{; for all;}i\right\}$$

consists of the trivial vector 0 alone. Under these circumstances X also has full column rank. In practice, the polar cone condition is difficult to check, so we rely on the ridge penalty $\frac{\lambda }{2}{\Vert \mathit{w}\Vert }^2$ to enforce coercivity. The SVM loss $f_{\lambda }(\mathit{\beta }\mid \mathit{y},\mathit{X})$ is also continuously differentiable because $u_{+}^2$ is so with derivative 0 at u = 0. Furthermore, the gradient

$$\nabla f_{\lambda }(\mathit{\beta }\mid \mathit{y},\mathit{X})=\lambda \mathit{\beta }-\frac{1}{n}\sum _{i=1}^n{\left(1-y_i{x}_i^{\top }\mathit{\beta }\right)}_{+}{y}_i{\mathit{x}}_i$$

is locally bounded and Lipschitz because $u_{+}$ is so and the class of such functions is closed under the formation of sums and functional compositions. It follows that the surrogate (3) is continuous, strongly convex, and satisfies the Lipschitz condition

$$\Vert \nabla g_{\rho }\left(\mathit{\beta }\mid {\mathit{\beta }}_n\right)-\nabla g_{\rho }\left(\alpha \mid {\mathit{\beta }}_n\right)\Vert \le L\Vert \mathit{\beta }-\mathit{\alpha }\Vert$$

for some L on the compact set $\left\{\mathit{\beta }:f_{\lambda }(\mathit{\beta }\mid \mathit{y},\mathit{X})\le f_{\lambda }\left({\mathit{\beta }}_0\mid \mathit{y},\mathit{X}\right)\right\}$ whenever $f_{\lambda }(\mathit{\beta }\mid \mathit{y},\mathit{X})$ is coercive. Strong converge results apply in the convex settings as summarized in the survey Lange et al. (2021) and in Propositions 5 through 11 of (Keys et al., 2019).

Even if the SVM loss functions $f_{\lambda }(\mathit{\beta }\mid \mathit{y},\mathit{X})$ and $f_{\lambda }^{\text{NL}}(\mathit{\alpha }\mid \mathit{y},\mathit{X})$ are strictly convex, the addition of a nonconvex set constraint S_k sacrifices convexity in the penalized losses $h_{\rho }(\mathit{\beta })$ and $h_{\rho }(\mathit{\alpha })$. Thus, convergence is governed by nonconvex theory. One issue is the multivalent nature of projections onto sparsity sets. Fortunately, such pathological behavior occurs only on a set of Lebesgue measure 0. Furthermore, Zangwill’s Global Convergence Theorem also covers multivalent algorithm maps (Luenberger, 1984, see Section 7.7). To establish convergence to a stationary point, we rely on results from our companion papers (Keys et al., 2019; Landeros et al., 2022). There we define the necessary concepts of semialgebraic sets and functions and stationary points. Proposition 4.1 of Landeros et al. (2022) proves that the sparsity set S_k is semialgebraic. In the current context the fusion matrix D is just the identity I. Moreover, our arguments there show that our current loss and penalty are semialgebraic. Because our surrogates $g_{\rho }\left(\mathit{\beta }\mid {\mathit{\beta }}_m\right)$ are continuous, μ-strongly convex, and L-smooth, Proposition 4.4 of Landeros et al. (2022) demonstrates a linear rate of convergence to a stationary point ${\mathit{\beta }}_{\infty }$ when ${\mathit{\beta }}_{\infty }$ has k unambiguous largest components in magnitude. The complementary set of points $\mathit{\beta }$ with k ambiguous largest components in magnitude has Lebesgue measure 0.

3.4. Decision Functions and Multiclass SVM

In linear binary classification, SVMs typically use the decision rule

$$\mathit{x}\mapsto \mathrm{sgn}\left({\mathit{x}}^{\top }\mathit{w}\right)=\{\begin{array}{cc}+1,& \text{if}{\mathit{x}}^{\top }\mathit{w}>0\\ 0,& \text{if}{\mathit{x}}^{\top }\mathit{w}=0,\\ -1,& \text{if}{\mathit{x}}^{\top }\mathit{w}<0\end{array}$$

to assign an instance x a binary label using the SVM’s coefficients w. The signed decision rule can be extended to multiclass problems using the One-Versus-One (OVO) paradigm (Hsu and Lin, 2002). In OVO, one partitions a dataset with c classes into $\left(\begin{array}{c}c\\ 2\end{array}\right)$ subsets such that each subset only contains samples from two classes. One then fits $\left(\begin{array}{c}c\\ 2\end{array}\right)$ SVMs to discriminate between two classes within each subset. After fitting models to each subproblem, one constructs a decision rule through a voting system so that the assigned label of X is given by

$$\mathit{x}\mapsto \underset{j}{\text{argmax}}\left\{v_j:v_j=\sum _{\ell }1\left\{{\text{SVM}}_{\ell }(\mathit{x})=j\right\}\right\},$$

where ${\text{SVM}}_{\ell }(\mathit{x})$ is the label assigned by binary SVM $\ell$ using, for example, the signed decision rule. Thus, the class receiving the most votes is used as the predicted label for X.

Alternatively, one may interpret ${\mathit{x}}^{\top }\mathit{w}$ as a confidence value indicating the strength of a SVM’s prediction. This is useful in the One-Versus-Rest (OVR) paradigm which constructs c SVMs to distinguish one class from the rest (Hsu and Lin, 2002). In this setting, one assigns a label by aggregating confidence values from each SVM

$$\mathit{x}\mapsto \underset{j}{\text{argmax}}\left\{v_j:v_j=\sum _{\ell }{\mathit{x}}^{\top }{\mathit{w}}_{\ell }\cdot 1\left\{{\text{SVM}}_{\ell }(\mathit{x})=j\right\}\right\}.$$

In this case, OVR assigns a class based on the highest confidence value. OVR reduces the number of SVMs required to fit a multiclass classifier and, therefore also reduces the number of model parameters, but is known to suffer from worse ambiguity issues when ties occur compared to OVO (van den Burg and Groenen, 2016, see Figure 1).

In our classifiers we favor the OVO paradigm using a weighted voting system based on confidence values. We prefer to avoid the potentially ambiguous decision boundaries of OVR, although it often yields similar results to OVO (Hsu and Lin, 2002).

3.5. Tuning Sparsity with Cross Validation

Without prior knowledge of the true number of causal features, one must tune the sparsity level of the solutions. This amounts to selecting $k\in \{0,1,2,\dots ,p\}$ to restrict the number of active variables through sparsity constraints $\mathit{w}\in S_k$ or $\mathit{a}\in S_k$ in fitting linear or nonlinear SVM, respectively. Note that decreasing k increases the number of structural zeros as measured by the sparsity level $s=1-k/p$.

We examine the viability of composing K-fold cross validation (CV) with our algorithms. In each fold we initialize model parameters and then minimize the criterion (4) or the criterion (8) on a training set with fixed λ but no sparsity penalty (k = p). We then gradually increase sparsity $s=1-k/n$ to construct a solution path from the fully dense models (s = 0) to fully sparse models (s = 1). Fitted classifiers in cross validation are parameterized by an ordered pair $(s,\lambda )$. Order is important here because each λ is associated with a solution path over s. We do not consider $\rho$ as a hyperparameter in cross validation because it is already tuned by proximal distance iteration.

In principle there are various performance metrics that may be used to evaluate a classifier. A natural criterion is the minimum value of the regularized empirical risk, but this has two issues. First, it becomes difficult to compare across different loss models such as (2) versus (4) or even (8). Second, it is well-known that penalty methods reach a compromise in minimizing of f(x) or g(x) in a penalized objective $h(x)=f(x)+\rho g(x)$ (Lange, 2016). In fact, we expect that minimization of (4) or (8) will inflate the original loss model (2) or (7), respectively. This may even be desirable since our estimators for model parameters are necessarily biased compared to the standard L₂ SVM. Thus, we focus on maximizing prediction accuracy. The following describes how we fit and evaluate classifiers for each pair of hyperparameters $(s,\lambda )$.

1. Any feature standardization or normalization is based on the training set and applied to the training, validation, and test subsets. For example, if one wishes to standardize the data, then we estimate $(\mathit{\mu },\sigma )$ from the training subset ${\mathit{X}}_{\text{train}}$ and apply the transformation $x^{\mapsto }(x-\mu )/\sigma$ to all instances of feature X in each of the three data subsets. This is essential to ensure both the validity of cross validation results and the fitting of SVMs because the latter is not invariant under affine transformations.

2. In each fold, a training set is used to fit model parameters. The fitted classifier is evaluated on a validation set and a test set. The training and validation sets are shuffled between folds, whereas the test set is fixed and never participates in fitting.

3. In a linear SVM the size of a separating margin is given by $1/\Vert \mathit{w}\Vert$. Thus, smaller values of λ induce smaller margins and may lead to overfitting. Moderate values of λ are desirable and tend to avoid overfitting. Average predication accuracy on validation sets is measured by

   $$S_{\text{CV}}=\frac{1}{K}\sum _{j=1}^K\frac{1}{n_j}\sum _{i=1}^{n_j}1\left\{{\widehat{L}}_{ij}=L_{ij}\right\}.$$

   Here L_ij is the label of a validation sample i in fold j and ${\widehat{L}}_{ij}$ is its predicted label.

4. To select an optimal pair $(s,\lambda )$, we maximize $S_{\text{CV}}$ as a function of s and λ. This choice prioritizes maximizing prediction accuracy $\left(S_{\text{CV}}\right)$ over parsimony (s) and generalizability (λ).

In addition, repeated K-fold cross validation can be used to assess stability of variable selection. This involves shuffling samples between the training and validation sets and repeating the K-fold cross validation procedure. Ideally, each replicate should select a similar pair $(s,\lambda )$ with similar prediction accuracies on validation and test subsets. Algorithm 2 summarizes the flow of our cross validation procedure.

Algorithm 2.

Repeated Cross Validation

1:	Split dataset into test and cross validation subsets $𝓣$ and $𝓓$, respectively.
2:	for each replicate $r\leftarrow 1,R$ do
3:	Shuffle subset $𝓓$.
4:	for each $\text{fold}\leftarrow 1$, $K$ do
5:	Split $𝓓$ into training and validation subsets, ${𝓓}_1$ and ${𝓓}_2$.
6:	Estimate transformation parameters from the training set ${𝓓}_1$.
7:	Apply the transformation to ${𝓓}_1$, ${𝓓}_2$ and $𝓣$ to standardize/normalize data.
8:	for each λ do
9:	Initialize model parameters $\mathit{\beta }$ or $\mathit{\alpha }$ by fitting a L2 SVM using (2) or (7).
10:	for each s do
11:	Fit a sparse classifier with $k=\lfloor p(1-s)\rfloor$ active features.
12:	Evaluate prediction accuracy on subsets ${𝓓}_1$, ${𝓓}_2$ and $𝓣$.
13:	end for
14:	end for
15:	end for
16:	Evaluate average scores $S_{\text{CV}}\left({𝓓}_1\right)$, $S_{\text{CV}}\left({𝓓}_2\right)$ and $S_{\text{CV}}(𝓣)$ for each subset.
17:	Rank models by their augmented scores ($S_{CV}\left({𝓓}_2\right)$, $s$, $\lambda$).
18:	Identify and record the optimal hyperparameters s, k, and λ.
19:	end for

4. Numerical Experiments

We assess the proposed SVM algorithms by testing them on both our own simulated examples (see Appendix B) and datasets from the UCI Machine Learning Repository (Dua and Graff, 2019). The chosen datasets, which address both overdetermined and underdetermined problems, are listed in Table 1. We use the DataDeps.jl package (White et al., 2019) to process datasets and make them reproducible in our experiments. We begin by demonstrating that our sparse SVMs can recover sparse models in various high-dimensional settings. Next, we report repeated cross validation results on selected datasets and compare against SVMs fitted using all or a reduced subset of variables. Finally, we conclude with a comparison to classical SVMs implemented in LIBSVM and LIBLINEAR.

Table 1.

Summary of datasets, classifier choices, and cross validation settings used in numerical experiments.

Dataset	Classes	Samples	Features	Model	Replicates	Folds	Train	Test
synthetic	2	1000	500	Linear	10	5	800	200
synthetic-hard	2	1000	500		10	5	800	200
iris	3	150	4		10	3	120	30
bcw	2	683	9		10	3	546	137
splice	3	3176	180		10	5	2541	635
optdigits	10	5620	64		10	5	4496	1124
letters	26	20000	16		1	5	16000	4000
TCGA-HiSeq	5	801	20531		1	3	641	160
spiral	3	1000	2	Nonlinear	10	5	800	200
spiral-hard	3	1000	2		10	5	800	200

4.1. Sparse Recovery in High-Dimensional Scenarios

Let us first characterize the behavior of our sparse SVMs in two regimes, overdetermined and underdetermined, by a simulation study. Given target sample and variable sizes n and p, respectively, we generate X by sampling row vectors from a standard multivariate distribution, ${\mathit{x}}_i\sim 𝓝\left({\mathbf{0}}_{p\times 1},{\mathit{I}}_{p\times p}\right)$, and set

$$w_{0j}\sim \{\begin{array}{ll}\text{Uniform}(2,10),& j\text{is causal}\\ 0,& \text{otherwise,}\end{array}$$

for k randomized components in the support of ${\mathit{w}}_0\in {ℝ}^p$; that is $\left|\text{supp}\left({\mathit{w}}_0\right)\right|=k$. Binary labels are then assigned via the linear SVM decision rule $y_i={\mathit{x}}_i^{\top }{\mathit{w}}_0$. Overdetermined and underdetermined scenarios are generated by fixing n = 500 or p = 500 and then varying the remaining problem dimension. We also fix λ = 1 and control parameters ${ϵ}_d={10}^{-3}$ and ${ϵ}_g={10}^{-4}$. For each simulation, we fit multiple classifiers by varying the target number of active features k, using both MM and SD, and measure iterations to convergence, wall time, and prediction accuracy on a separate test set. Fitted solutions w are compared against the ground truth ${\mathit{w}}_0$ in terms of accuracy, positive predictive value (PPV), and negative predictive value (NPV). In this context we have the following definitions of true and false positives/negatives (TP/FP/TN/FN)

	$\left\{{\widehat{w}}_j\ne 0\right\}$	$\left\{{\widehat{w}}_j=0\right\}$
$\left\{w_{0j}\ne 0\right\}$	TP	FN
$\left\{w_{0j}=0\right\}$	FP	TN

from which we derive PPV and NPV. Prevalence adjustment is important for our simulation study because we fix k = 50 and expect the proportion of causal variables to shrink.

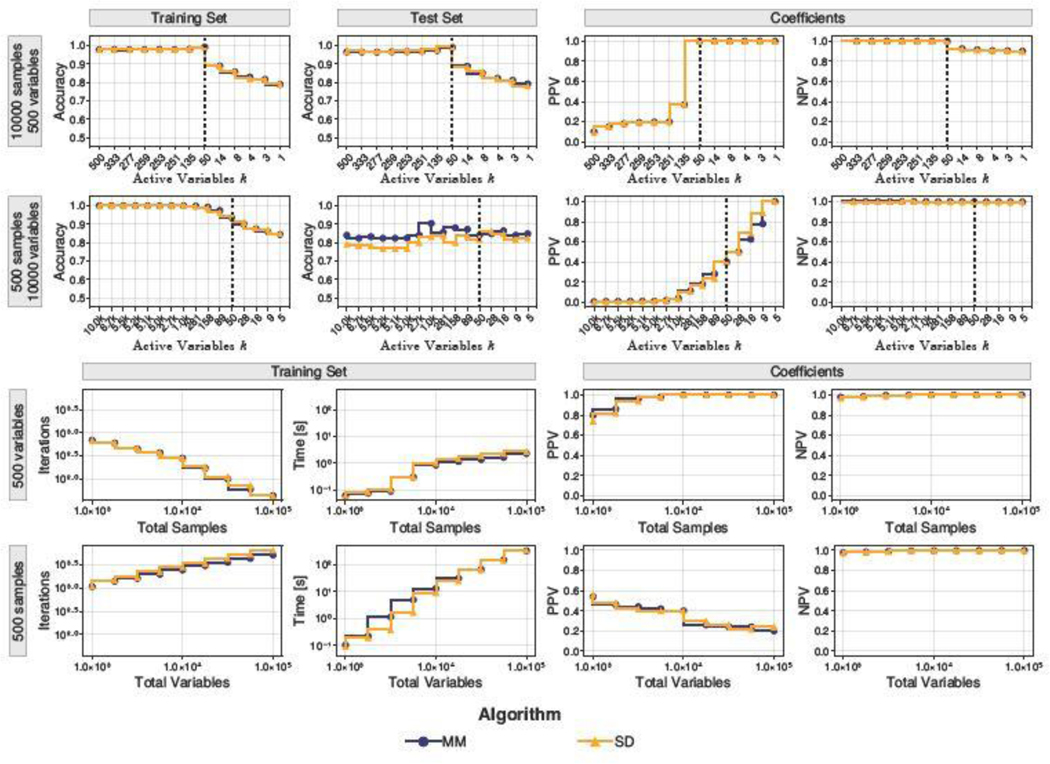
Figure 2 summarizes our results. In the two cases $(n,p)=\left({10}^4,500\right)$ and $(n,p)=\left(500,{10}^4\right)$, it is clear that our classifiers achieve acceptable performance on test sets, regardless of which algorithm is used to fit models. Moreover in the former case, maximal prediction accuracy is achieved near k = 50, which also aligns with high PPV and NPV in identifying the correct subset of causal variables. These positive results are more difficult to achieve when $p\gg n$, but the outlook is not so pessimistic. The fact that PPV increases monotonically as the number of causal variables shrinks suggests that failure to recover all the causal variables may be due to their exchangeability. In terms of scaling behavior, it is somewhat remarkable that the number of required iterations decreases as one increases n. However, the wall time does increase consistently. It should be noted that we do not include the cost of extracting the SVD of X in Algorithm MM, which would shift its time curve upwards.

Fig. 2.

Performance characteristics of sparse SVM classifiers fitted using algorithms MM (blue circles) and SD (orange triangles) across various simulated high-dimensional scenarios (row labels). Black vertical lines highlight the number of causal variables used to simulate data. In the bottom two rows, results correspond to the ideal case with k = 50.

4.2. Cross Validation Results

We our report results of using Algorithm 2 in combination with Algorithm 1 to select sparse SVMs across selected datasets. Table 2 illustrates the performance of Algorithm MM on the synthetic example in detail, and Table 3 reports the highlights across all 10 examples. Results for Algorithm SD are similar. Appendix D records distributions of the hyperparameters s, k, and λ along with validation prediction accuracy over 10 replicates of K-fold cross validation.

Table 2.

Partial solution path in 5-fold cross validation on the synthetic example with various active variables k. Reported metrics are averages over 5 folds with standard errors in parentheses. The highlighted row corresponds to results for the true sparsity level s = 0.996, or equivalently k = 2. Here λ = 1 is fixed.

				Accuracy (%)
k	Iterations	Loss	Support Vectors	Train	Validation	Test
500	7	0.300	623	98	77	72
	(0)	(0.004)	(1)	(0)	(2)	(1)
375	210	0.301	622	98	77	73
	(4)	(0.004)	(2)	(0)	(2)	(1)
250	421	0.313	622	98	77	74
	(7)	(0.004)	(1)	(0)	(2)	(1)
125	599	0.351	619	97	79	76
	(9)	(0.004)	(2)	(0)	(1)	(1)
73	696	0.388	622	97	82	79
	(11)	(0.004)	(1)	(0)	(2)	(1)
43	747	0.421	625	96	85	82
	(4)	(0.005)	(1)	(0)	(2)	(1)
25	813	0.450	627	95	86	85
	(4)	(0.004)	(1)	(0)	(2)	(1)
15	820	0.471	626	95	87	88
	(6)	(0.003)	(1)	(0)	(2)	(1)
9	866	0.488	627	95	91	91
	(9)	(0.002)	(1)	(0)	(2)	(1)
5	885	0.503	628	96	94	93
	(3)	(0.002)	(1)	(0)	(2)	(0)
3	891	0.513	628	97	96	95
	(2)	(0.002)	(1)	(0)	(1)	(0)
				Accuracy (%)
2	896	0.519	627	99	100	100
	(3)	(0.002)	(1)	(0)	(0)	(0)
1	946	0.747	640	76	73	76
	(3)	(0.002)	(0)	(0)	(0)	(1)

Table 3.

Summary of repeated cross validation results across our selected examples. We select an optimal pair $(\lambda ,k)$ by averaging CV scores over folds and replicates and fit (i) a sparse SVM based on our framework, (ii) a reduced SVM using only the active variables, and (iii) the full L₂-regularized SVM. In multiclass problems, the total and average number of active variables is taken across each binary SVM to account for overlaps.

				Active Variables				Accuracy (%)
Example	Model	λ	k	Total	Average	SVs	Margin	Train	Test
synthetic	(i)	0.10	2	2	2	518	0.95	100	100
	(ii)	0.10	2	2	2	518	0.94	100	100
	(iii)	0.10	500	500	500	527	0.96	100	76
synthetic-hard	(i)	10.00	2	2	2	800	15.30	94	96
	(ii)	10.00	2	2	2	800	15.28	94	96
	(iii)	10.00	500	500	500	800	10.69	90	70
bcw	(i)	1.00	9	9	9	215	6.09	97	98
	(ii)	1.00	9	9	9	215	6.09	97	98
	(iii)	1.00	9	9	9	215	6.09	97	98
iris	(i)	0.10	1	2	1	117	0.98	98	90
	(ii)	0.10	1	2	2	109	1.14	98	93
	(iii)	0.10	4	4	4	98	1.24	98	93
splice	(i)	0.10	145	209	145	2027	1.04	97	96
	(ii)	0.10	145	209	209	2031	1.04	98	95
	(iii)	0.10	240	240	240	2025	1.04	98	95
optdigits	(i)	1.00	48	56	48	1544	8.71	99	96
	(ii)	1.00	48	56	56	1544	8.71	99	96
	(iii)	1.00	64	64	64	1544	8.71	99	96
letters	(i)	0.10	16	16	16	13945	1.80	84	82
	(ii)	0.10	16	16	16	13945	1.80	84	82
	(iii)	0.10	16	16	16	13945	1.80	84	82
TCGA-HiSeq	(i)	10.00	5066	15778	5066	320	38.58	100	100
	(ii)	10.00	5066	15778	15778	271	41.85	100	100
	(iii)	10.00	20264	20258	20258	273	42.90	100	100
spiral	(i)	1.00	400	561	267	561	2.97	97	98
	(ii)	1.00	400	561	374	561	2.99	97	98
	(iii)	1.00	800	800	533	800	3.32	97	98
spiral-hard	(i)	1.00	669	771	446	771	3.82	89	90
	(ii)	1.00	669	771	514	771	3.85	90	89
	(iii)	1.00	800	800	533	800	3.84	89	90

In Table 2 it is clear that, for fixed λ, including extraneous variables may lead to overfitting training data in binary classification. The summary in Table 3 compares results for (i) our sparse classifiers that target a specific number of active variables k, (ii) a reduced model using the same active variables as the optimal sparse model, and (iii) the full L₂ SVM using all available variables. Rows corresponding to the synthetic, synthetic-hard, and bcw examples cover binary classification with a linear model. In these examples all 3 models deliver model coefficients of similar magnitude based on the size of the margin $1/\Vert \mathit{w}\Vert$, but our sparse classifiers better generalize to classifying novel instances when a sparse signal is present.

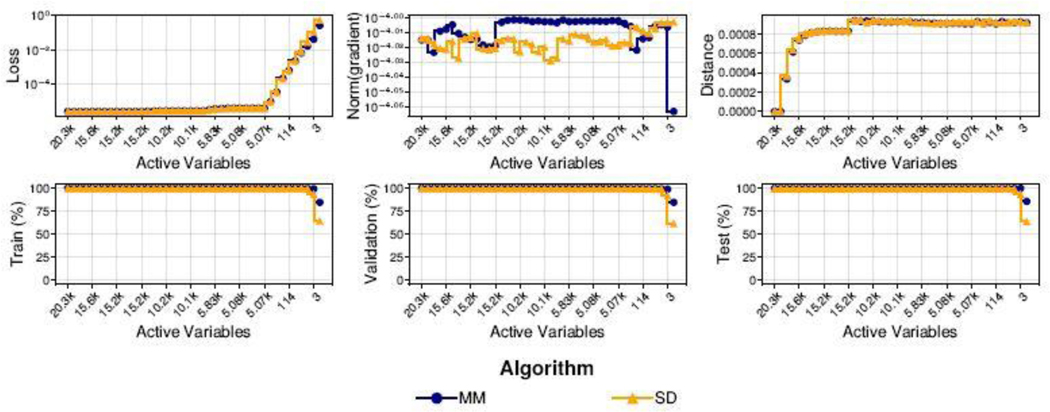
In multiclass classification, one must partition data into subsets to fit binary SVMs discriminating between two classes. This increases the total number of model parameters and makes it possible for the number of active variables to exceed the target model size k. With this in mind, our examples of multiclass problems with linear classifiers (iris, splice, optdigits, leters, and TCGA-HiSeq) echo the results for linear binary classification. However, it is now more challenging to successfully recover a sparse model because each nested binary SVM targets the same number of variables k. Comparing total number of active variables across all SVMs against average active variables per SVM illustrates this point in the iris, splice, optdigits, and TCGA-HiSeq examples. The splice junction data, in which variables are binary indicators for nucleotides T, C, G, and A within DNA sequences of 60 base pairs, shows that a uniform sparsity constraint only modestly reduces the number of selected variables from 240 to 209 because there is only some overlap between SVMs (145 variables per SVM). In image data such as the optdigits example, dropped variables correspond mainly to pixels at the boundary of images that are more likely to be black pixels. This is somewhat disappointing behavior because in the gene expression example, TCGA-HiSeq, repeated CV selects the model size k = 5066 per SVM resulting in 15778 genes discriminating between 5 cancer types. This is still a large number of genes to consider compared to the original set of 20264 genes. To our credit, Figure 3 illustrates that it may be possible to select significantly smaller values for k, thereby decreasing the total number of model parameters, in exchange for small decreases in prediction accuracy. Finally, it is interesting to note that our nonlinear SVM model successfully controls the number of support vectors while maintaining good classification accuracy in the spiral examples despite suffering from the same sparsity deficiency in multiclass problems.

Fig. 3.

Convergence metrics (top) and performance metrics (bottom) for MM and SD on the TCGA-HiSeq example. Control parameters were set to and ${\delta }_g=2\times {10}^{-4}$ and ${\delta }_d={10}^{-3}$ for gradient norms and distances, respectively.

4.3. Comparison to Existing Models

We compare our sparsity-based models to well-known classics using LIBLINEAR (Fan et al., 2008) through the Julia wrapper package LIBSVM.jl. Specifically, we compare to

1. L2R, an option from LIBLINEAR for the standard L₂ (2), and

2. L1R, an option from LIBLINEAR for the L₁-regularized version of (2).

The models used in LIBLINEAR impose regularization on the hinge term, rather than the penalty term, through a tuning constant $C={(n\lambda )}^{-1}$.

Table 4 reports our results in repeated cross validation. Our SVM training algorithms are comparable to existing approaches, albeit slower across all examples. To our credit the synthetic example underscores the superiority of sparsity constraints over shrinkage-based penalties. Namely, algorithms MM and SD successfully fit sparse classifiers with fewer variables and achieve superior prediction capability as reflected in validation and test accuracies. Specifically, our sparse approach compares favorably against the L₂-regularized SVM in our synthetic datasets, designed to have only two informative variables, even when the data are not linearly separable. Moreover, it is clear that our approach gives similar classification predictions to the L₁-regularized SVM on the synthetic examples. Similarities in performance scores disappear on multiclass problems, indicating that our algorithms converge to distinct solutions. It is not immediately clear whether our L₀ approach recovers sparser solutions, controls false positives, or mitigates shrinkage compared to the lasso. The L₁-regularized SVM is arguably too aggressive in selecting variables on the splice and letters examples but it achieves superior selection on the TCGA-HiSeq example. This suggests that, while the L₁ classifier also imposes a uniform penalty on each nested binary SVM, the continuous penalty can be more flexible on some problems. Thus, our sparse classifiers are conservative compared to shrinkage-based methods.

Table 4.

Comparison of our algorithms (MM and SD) against existing approaches implemented in LIBLINEAR (L2 and L1) in cross validation. In multiclass problems, the total and average number of active variables is taken across each binary SVM to account for overlaps. Results are based on repeated K-fold cross validation with 10 replicates in all examples except the letters and TCGA-HiSeq examples which only use 1 replicate.

					Active Variables			Accuracy (%)
Example	Algorithm	λ	k	Total Time [s]	Total	Average	SVs	Train	Validation	Test
synthetic	MM	10	2	3.98	2	2	573	99	99	100
	SD	0.1	2	4.05	2	2	506	99	99	100
	L2	0.55	500	0.05	500	500	529	99	78	74
	L1	0.1	500	0.025	271	271	471	99	99	100
synthetic-hard	MM	10	2	4.13	2	2	640	94	94	96
	SD	10	2	4.16	2	2	640	94	94	96
	L2	1	500	0.055	500	500	627	97	74	70
	L1	0.1	500	0.021	271	271	567	94	94	96
bcw	MM	0.56	6	0.64	6	6	156	97	97	96
	SD	0.32	8	2.35	8	8	129	98	98	95
	L2	0.78	9	0.007	9	9	387	87	87	87
	L1	0.04	9	0.02	9	9	369	87	86	87
iris	MM	0.02	4	0.254	4	3	45	99	98	94
	SD	0.03	3	0.282	4	3	47	98	98	95
	L2	0.02	4	0.002	4	4	80	86	85	85
	L1	0.01	4	0.006	4	3	80	85	85	84
					Active Variables			Accuracy (%)
splice	MM	0.1	144	9.51	208	150	1628	98	96	95
	SD	0.1	102	12.5	178	104	1661	97	96	97
	L2	0.1	240	0.125	240	240	1779	97	96	95
	L1	0.1	240	0.056	30	11	2032	85	84	85
optdigits	MM	0.1	36	17.1	55	36	901	100	98	96
	SD	1	34	192	54	36	1082	100	98	96
	L2	0.1	64	0.216	62	62	1693	98	96	95
	L1	0.1	64	0.534	43	17	3022	95	94	92
letters	MM	0.1	16	362	16	16	11157	84	83	82
	SD	0.1	14	3000	16	14	11174	84	83	82
	L2	0.1	16	2.38	16	16	12800	67	67	65
	L1	0.1	16	8.81	14	6	12800	46	46	45
TCGA-HiSeq	MM	10	5066	9980	15878	5066	249	100	100	100
	SD	0.1	1964	7710	8727	1964	240	100	100	100
	L2	10	20264	72	20237	20237	427	100	100	100
	L1	0.1	20264	2.78	79	16	427	100	100	100

5. Discussion

We have demonstrated the benefits of conceptually simple proximal distance algorithms for binary and multiclass classification problems on both linear SVMs and nonlinear kernel SVMs. The proximal distance principle makes it possible to attack parsimony directly through squared distance penalties. This direct approach (a) restores differentiability via quadratic surrogate functions, (b) potentially avoids the shrinkage inherent in lasso-based algorithms, (c) identifies sparser models with good predictive power, and (d) substitutes a discrete interpretable sparsity level for the continuous hyperparameters of competing methods. To our surprise, the more expensive Algorithm MM scales better on high-dimensional data due to its ability to quickly drive solutions close to a desired sparsity set.

Algorithm acceleration is essential in overcoming the unfortunate cost of (repeated) cross validation. We found experimentally that inclusion of ridge regularization is essential in preventing coefficients from diverging to $\pm \infty$. Fortunately, addition of the ridge penalty convexifies our distance penalized objectives and accelerates convergence overall. We noticed a few other tactics that lower computational costs.

In multiclass classification, Algorithm MM greatly benefits from the OVO paradigm because it reduces the dimensions of each required singular value decomposition. The OVR paradigm only requires a single, albeit large decomposition, provided the classifier is linear. It also noteworthy that our implementation uses dense linear algebra operations, so it may be possible to speed up model fitting by tracking the active parameter set. In contrast, it is not clear whether the SD variant is truly a viable alternative to MM unless the required SVD is prohibitively expensive to compute. We observe that SD benefits from Nesterov acceleration in cutting down the number of iterations, but further work is needed to make it useful in cross validation. Other computational tricks may further lower computational costs (Schölkopf and Smola, 2018); these warrant further experimentation.

While we are pleased with our results, particularly for binary classification tasks, much is left to be desired for multiclass problems. Relying on multiple SVMs to handle multiclass problems introduces $\left(\begin{array}{c}c\\ 2\end{array}\right)$ subproblems for c classes. Furthermore, different decision boundaries in the OVO paradigm may be driven by different features, obscuring the universal features that discriminate between classes. Hence, it is natural to investigate multiclass methods beyond hyperplane separation. Our previous research on multivertex discriminant analysis (MVDA) (Lange and Wu, 2008) explored a multiclass model that represents classes geometrically as vertices of a regular simplex embedded in Euclidean space rather than binary choices from $\{-1,1\}$. MVDA takes advantage of ϵ-insensitive norms and generalizes to nonlinear classification via the kernel trick (Wu and Lange, 2010). We plan to revisit MVDA and incorporate sparsity based on the proximal distance principle and possibly Huber hinge errors (van den Burg and Groenen, 2016). Given the length of the current paper and the many unresolved challenges ahead, this goal is best left to a future paper.