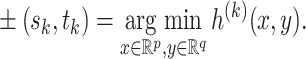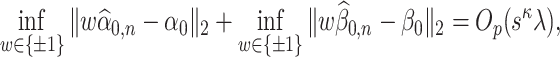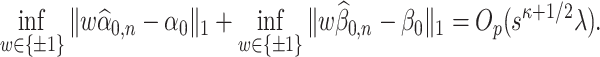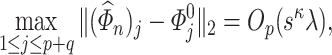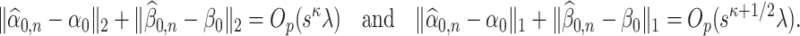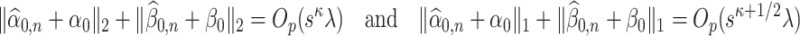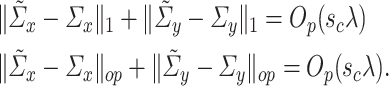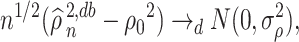Abstract
We consider asymptotically exact inference on the leading canonical correlation directions and strengths between two high-dimensional vectors under sparsity restrictions. In this regard, our main contribution is developing a novel representation of the Canonical Correlation Analysis problem, based on which one can operationalize a one-step bias correction on reasonable initial estimators. Our analytic results in this regard are adaptive over suitable structural restrictions of the high-dimensional nuisance parameters, which, in this set-up, correspond to the covariance matrices of the variables of interest. We further supplement the theoretical guarantees behind our procedures with extensive numerical studies.
Keywords: sparse canonical correlation analysis, asymptotically valid confidence intervals, one-step bias correction, high-dimensional nuisance parameters
1. Introduction
Statistical analysis of biomedical applications requires methods that can handle complex data structures. In particular, formal and systematic Exploratory Data Analysis (EDA) is an important first step when attempting to understand the relationship between high-dimensional variables. Key examples include eQTL mapping and [20, 66] epigenetics [26, 29, 30, 57]. In greater generality, EDA can be an essential part of any study involving the integration of multiple biological datasets including as genetic markers, gene expression and disease phenotypes [37, 45]. In each of these examples, it is critically important to understand the relationships between the high-dimensional variables of interest. Linear relationships are often the most straightforward and intuitive models used in this regard, lending themselves well to interpretation. Consequently, a large volume of statistical literature has been devoted to exploring linear relationships through variants of the classical statistical toolbox of Canonical Correlation Analysis (CCA) [28]. We focus in this paper on some of the most fundamental inferential questions in the context of high-dimensional CCA.
To formally set up these inferential questions in the CCA framework, we consider i.i.d. data 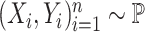 on two random vectors
on two random vectors 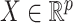 and
and 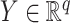 with joint covariance matrix
with joint covariance matrix
 |
The first canonical correlation 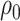 is defined as the maximum possible correlation between two linear combinations of
is defined as the maximum possible correlation between two linear combinations of  and
and 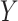 . More specifically, consider the following optimization problem:
. More specifically, consider the following optimization problem:
 |
(1.1) |
The maximum value attained in (1.1) is 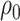 , and the solutions to (1.1) are commonly referred to as the first canonical directions, which we will denote by
, and the solutions to (1.1) are commonly referred to as the first canonical directions, which we will denote by 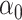 and
and 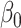 , respectively. This paper considers inference on
, respectively. This paper considers inference on 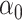 ,
, 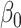 , and associated quantities of interest. In most scientific problems, the first canonical correlation coefficient is of prime interest as it summarizes the ‘maximum linear association’ between
, and associated quantities of interest. In most scientific problems, the first canonical correlation coefficient is of prime interest as it summarizes the ‘maximum linear association’ between  and
and 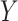 , thereby motivating our choice of inferential target.
, thereby motivating our choice of inferential target.
Early developments in the theory and application of CCA have been well documented in the statistical literature, and we refer the interested reader to [1] and the references therein for further details. These classical results have been widely used to provide statistical inference (i.e. asymptotically valid hypothesis tests, confidence intervals and p-values) across a vast range of disciplines, such as psychology, agriculture, oceanography and others. However, the current surge of interest in CCA, motivated by modern high-throughput biological experiments, requires re-thinking several aspects of the traditional theory and methods. In particular, in many contemporary datasets, the number of samples is often comparable with, or much smaller than, the number of variables in the study. This renders vanilla CCA inconsistent and inadequate without further structural assumptions [3, 13, 48]. A natural constraint that has gained popularity is that of sparsity, i.e. when an (unknown) small collection of variables is relevantly associated with each other rather than the entire collection of high-dimensional variables. Sparse Canonical Correlation Analysis (SCCA) [66] has been developed to target such low-dimensional structures and subsequently provide consistent estimation in the context of high-dimensional CCA. Although such structured CCA problems have witnessed a renewed enthusiasm from both theoretical and applied communities, most papers have heavily focused on the key aspects of estimation (in suitable norms) and relevant scalable algorithms—see, for example, [19, 24, 25, 48, 49]. However, asymptotically valid inference is yet to be explored systematically in the context of SCCA. In particular, none of the existing estimation methods for SCCA lend themselves to uncertainty quantification, i.e. inference on 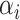
 ,
, 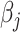
 or
or 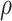 . This is unsurprising, given that the existing estimators are based on penalized methods. Thus, they are asymptotically biased, super-efficient for estimating zero coordinates and not tractable in terms of estimating underlying asymptotic distributions.[42–44, 55]. This complicates the construction of asymptotically valid confidence intervals for
. This is unsurprising, given that the existing estimators are based on penalized methods. Thus, they are asymptotically biased, super-efficient for estimating zero coordinates and not tractable in terms of estimating underlying asymptotic distributions.[42–44, 55]. This complicates the construction of asymptotically valid confidence intervals for 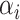 ,
, 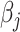 ’s and
’s and 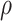 . In the absence of such intervals, bootstrap or permutation tests are typically used in practice [66]. However, these methods are often empirically justified and might suffer from subtle pathological issues that underlie standard re-sampling techniques in penalized estimation frameworks [16–18]. This paper takes a step in resolving these fundamental issues with inference in the context of SCCA.
. In the absence of such intervals, bootstrap or permutation tests are typically used in practice [66]. However, these methods are often empirically justified and might suffer from subtle pathological issues that underlie standard re-sampling techniques in penalized estimation frameworks [16–18]. This paper takes a step in resolving these fundamental issues with inference in the context of SCCA.
1.1 Main contribution
The main result of this paper is a method to construct asymptotically valid confidence intervals for 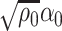 and
and 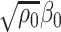 . Our method is based on a one-step bias correction performed on preliminary sparse estimators of the canonical directions. The resulting bias-corrected estimators have an asymptotic linear influence function type expansion (see e.g. [60] for asymptotic influence function expansions) with
. Our method is based on a one-step bias correction performed on preliminary sparse estimators of the canonical directions. The resulting bias-corrected estimators have an asymptotic linear influence function type expansion (see e.g. [60] for asymptotic influence function expansions) with 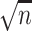 -scaling (see Theorem 4.1 and Proposition 4.2) under suitable sparsity conditions on the truth. This representation is subsequently exploited to build confidence intervals for a variety of relevant lower dimensional functions of the top canonical directions; see Corollary 1 and Corollary 3 and the discussions that follow. Finally, we will show that the entire de-biased vector is asymptotically equivalent to a high-dimensional Gaussian vector in a suitably uniform sense; see Proposition 4.2, which enables the control of family-wise error rates.
-scaling (see Theorem 4.1 and Proposition 4.2) under suitable sparsity conditions on the truth. This representation is subsequently exploited to build confidence intervals for a variety of relevant lower dimensional functions of the top canonical directions; see Corollary 1 and Corollary 3 and the discussions that follow. Finally, we will show that the entire de-biased vector is asymptotically equivalent to a high-dimensional Gaussian vector in a suitably uniform sense; see Proposition 4.2, which enables the control of family-wise error rates.
The bias correction procedure crucially relies on a novel representation of  and
and 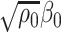 as the unique maximizers (up to a sign flip) of a smooth objective (see Lemma 3.1), which may be of independent interest. The uniqueness criteria are indispensable here since otherwise, a crucial local convexity property (see Lemma 3.2) is not guaranteed, which we exploit to deal with the high dimensionality of the problem. We also discuss why the commonly used representations of the top canonical correlations are difficult to work with owing to either the lack of such local convexity properties or the lack of a non-cumbersome derivation of the one-step bias correction. We elaborate on these subtleties in Section 3.2.
as the unique maximizers (up to a sign flip) of a smooth objective (see Lemma 3.1), which may be of independent interest. The uniqueness criteria are indispensable here since otherwise, a crucial local convexity property (see Lemma 3.2) is not guaranteed, which we exploit to deal with the high dimensionality of the problem. We also discuss why the commonly used representations of the top canonical correlations are difficult to work with owing to either the lack of such local convexity properties or the lack of a non-cumbersome derivation of the one-step bias correction. We elaborate on these subtleties in Section 3.2.
Further, we pay special attention to adapting to underlying sparsity structures of the marginal precision matrices (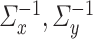 ) of the high-dimensional variables (
) of the high-dimensional variables ( ) under study. These serve as high-dimensional nuisance parameters in the SCCA problem. Consequently, our construction of asymptotically valid confidence intervals for top canonical correlation strength and directions are agnostic over the structures (e.g. sparsity of the precision matrices of
) under study. These serve as high-dimensional nuisance parameters in the SCCA problem. Consequently, our construction of asymptotically valid confidence intervals for top canonical correlation strength and directions are agnostic over the structures (e.g. sparsity of the precision matrices of  and
and 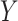 ) of these complex nuisance parameters. The de-biasing procedure can be implemented using our R package [31].
) of these complex nuisance parameters. The de-biasing procedure can be implemented using our R package [31].
Finally, we supplement our methods for inference with suitable constructions of initial estimators of canonical correlation directions as well as nuisance parameters under suitable sparsity assumptions. The construction of these estimators, although motivated by existing ideas, requires careful modifications to tackle inference on the first canonical correlation strength and directions while treating remaining directions as nuisance parameters.
2. Mathematical formalism
In this section, we collect some assumptions and notations that will be used throughout the rest of the paper.
2.1 Structural assumptions
Throughout this paper, we will assume that 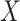 and
and 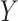 are centred sub-Gaussian random vectors (see [63] for more details) with joint covariance matrix
are centred sub-Gaussian random vectors (see [63] for more details) with joint covariance matrix 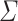 and sub-Gaussian norms bounded by some constant
and sub-Gaussian norms bounded by some constant 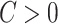 (see p. 28 of [62] for the definition). The sub-Gaussianity assumption is a standard requirement that can be found in various related literature [5, 25, 32, 39, 49]. Assuming that the data are sub-Gaussian, we can obtain tighter concentration bounds on the sample covariance matrix. Although we are not aware of any efficient method for testing the sub-Gaussianity of a random vector
(see p. 28 of [62] for the definition). The sub-Gaussianity assumption is a standard requirement that can be found in various related literature [5, 25, 32, 39, 49]. Assuming that the data are sub-Gaussian, we can obtain tighter concentration bounds on the sample covariance matrix. Although we are not aware of any efficient method for testing the sub-Gaussianity of a random vector 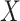 or
or 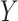 , there are several well-known examples of sub-Gaussian vectors. For instance, a multivariate Gaussian distribution is sub-Gaussian if the maximum eigenvalue of its variance matrix is bounded [38]. Moreover, random vectors uniformly distributed on the Euclidean sphere in
, there are several well-known examples of sub-Gaussian vectors. For instance, a multivariate Gaussian distribution is sub-Gaussian if the maximum eigenvalue of its variance matrix is bounded [38]. Moreover, random vectors uniformly distributed on the Euclidean sphere in  with the origin as their centre and radius
with the origin as their centre and radius 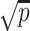 are also sub-Gaussian. Another example is when a vector’s elements are independent and have uniformly bounded sub-Gaussian norms, which is satisfied when each element is uniformly bounded [63]. We refer the readers to [63] for more examples.
are also sub-Gaussian. Another example is when a vector’s elements are independent and have uniformly bounded sub-Gaussian norms, which is satisfied when each element is uniformly bounded [63]. We refer the readers to [63] for more examples.
We will let  have a fixed rank
have a fixed rank 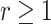 (implying that apart from
(implying that apart from  , there are
, there are 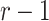 additional canonical correlations [1]). Since the cross-covariance matrix
additional canonical correlations [1]). Since the cross-covariance matrix  has rank
has rank  , it it can be shown that [cf. 19, 25]
, it it can be shown that [cf. 19, 25]
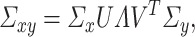 |
(2.1) |
where 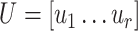 and
and  are
are  and
and 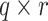 dimensional matrices satisfying
dimensional matrices satisfying 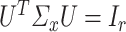 and
and 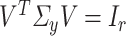 , respectively. The
, respectively. The 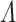 in (2.1) is a diagonal matrix, whose diagonal entries are the canonical correlations, i.e.
in (2.1) is a diagonal matrix, whose diagonal entries are the canonical correlations, i.e.
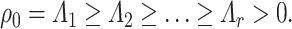 |
The matrices 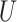 and
and  need not be unique unless the canonical correlations, i.e. the
need not be unique unless the canonical correlations, i.e. the 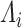 ’s, are all unique. Indeed, we will at the least require the uniqueness of
’s, are all unique. Indeed, we will at the least require the uniqueness of 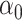 and
and 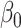 . Otherwise, these quantities are not even identifiable. To that end, we will make the following assumption that is common in the literature since it grants uniqueness of
. Otherwise, these quantities are not even identifiable. To that end, we will make the following assumption that is common in the literature since it grants uniqueness of 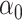 and
and 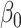 up to a sign flip [cf. 19, 25, 49].
up to a sign flip [cf. 19, 25, 49].
Assumption 2.1.
(Eigengap Assumption) There exists
so that
for all
and
.
Note that Assumption 2.1 also implies that 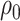 stays bounded away from zero. There exist formal tests for verifying the eigengap assumption in the asymptotic regime when
stays bounded away from zero. There exist formal tests for verifying the eigengap assumption in the asymptotic regime when  [3, 68]. However, to the best of our knowledge, no such tests currently exist for
[3, 68]. However, to the best of our knowledge, no such tests currently exist for 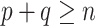 . A possible way to inspect the eigengap in this scenario is to estimate the canonical correlations and plot them against their index, which is called a screeplot. However, even the methods that consistently estimate the canonical correlations in the
. A possible way to inspect the eigengap in this scenario is to estimate the canonical correlations and plot them against their index, which is called a screeplot. However, even the methods that consistently estimate the canonical correlations in the 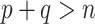 setting require the eigengap assumption [49]. Therefore, using a screeplot to assess the eigengap in this scenario may be unreliable.
setting require the eigengap assumption [49]. Therefore, using a screeplot to assess the eigengap in this scenario may be unreliable.
Our next regularity assumption, which requires 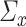 and
and 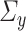 to be positive definite and bounded in operator norm, is also common in the SCCA literature [24, 25, 39, 49]. If
to be positive definite and bounded in operator norm, is also common in the SCCA literature [24, 25, 39, 49]. If 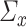 and
and  are not bounded in the operator norm, it can be shown that our sub-Gaussianity assumption will be violated [63].
are not bounded in the operator norm, it can be shown that our sub-Gaussianity assumption will be violated [63].
Assumption 2.2.
(Bounded eigenvalue Assumption) There exists
such that the eigenvalues of
and
are bounded below by
and bounded above by
for all
and
.
Although we require assumptions 2.1 and 2.2 to hold for all  and
and  , since our results are asymptotic in nature, it suffices if these assumptions hold for all sufficiently large
, since our results are asymptotic in nature, it suffices if these assumptions hold for all sufficiently large 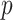 and
and  . Checking whether
. Checking whether  and
and 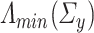 are bounded away from zero in high-dimensional settings can be challenging but it can be done under structural assumptions such as sparsity [8, 10]. In the context of proportional asymptotics (i.e. dimensions proportional to sample size) one can also appeal to results in classical random matrix theory concerning the largest eigenvalue [2] to check whether
are bounded away from zero in high-dimensional settings can be challenging but it can be done under structural assumptions such as sparsity [8, 10]. In the context of proportional asymptotics (i.e. dimensions proportional to sample size) one can also appeal to results in classical random matrix theory concerning the largest eigenvalue [2] to check whether 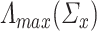 and
and  are bounded above without additional sparsity assumptions on them. However, rigorous treatment of the above is beyond the scope of this paper.
are bounded above without additional sparsity assumptions on them. However, rigorous treatment of the above is beyond the scope of this paper.
However, if  has some certain structures, Assumption 2.2 follows. We list a few examples below. (1)
has some certain structures, Assumption 2.2 follows. We list a few examples below. (1) 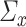 is a spike covariance matrix with finitely many spikes. This model has gained extensive attention in recent high-dimensional literature [36]. (2)
is a spike covariance matrix with finitely many spikes. This model has gained extensive attention in recent high-dimensional literature [36]. (2) 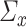 is an autoregressive matrix of order one, i.e.
is an autoregressive matrix of order one, i.e.  . In this case, the eigenvalues lie in the interval
. In this case, the eigenvalues lie in the interval 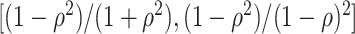 (cf. [59]). (3)
(cf. [59]). (3) 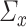 is a banded Toeplitz matrix, i.e.
is a banded Toeplitz matrix, i.e.  , where
, where 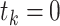 for
for 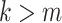 for some finite
for some finite  . This model has seen use in high-dimensional statistics literature [11]. In this case, Assumption 2.2 can be proved using Gershgorin circle theorem [27].
. This model has seen use in high-dimensional statistics literature [11]. In this case, Assumption 2.2 can be proved using Gershgorin circle theorem [27].
2.2 Notation
We will denote the set of all positive integers by 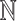 . For a matrix
. For a matrix  , we denote its
, we denote its 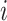 th row and
th row and 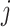 th column by
th column by 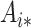 and
and 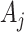 , respectively. Also, let
, respectively. Also, let  and
and 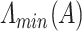 denote the largest and smallest eigenvalue of
denote the largest and smallest eigenvalue of  , respectively. We denote the gradient of a function
, respectively. We denote the gradient of a function 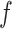 by
by 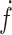 or
or  , where we reserve the notation
, where we reserve the notation 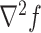 for the hessian. The
for the hessian. The  th element of any vector
th element of any vector 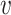 is denoted by
is denoted by  . We use the notation
. We use the notation 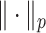 to denote the usual
to denote the usual 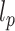 norm of a p-dimensional vector for any
norm of a p-dimensional vector for any  . For a matrix
. For a matrix  ,
, 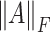 and
and 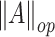 will denote the Frobenius and the operator norm, respectively. We denote by
will denote the Frobenius and the operator norm, respectively. We denote by 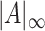 the elementwise supremum of
the elementwise supremum of  . The norm
. The norm 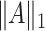 will denote
will denote  . For any
. For any 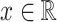 ,
,  will denote the largest integer smaller than or equal to
will denote the largest integer smaller than or equal to  .
. 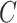 will denote a positive constant whose value may change from line to line throughout the paper.
will denote a positive constant whose value may change from line to line throughout the paper.
The results in this paper are mostly asymptotic (in  ) in nature and thus require some standard asymptotic notations. If
) in nature and thus require some standard asymptotic notations. If 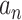 and
and  are two sequences of real numbers then
are two sequences of real numbers then 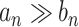 (and
(and 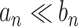 ) implies that
) implies that  (and
(and  ) as
) as 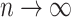 , respectively. Similarly
, respectively. Similarly 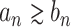 (and
(and  ) implies that
) implies that 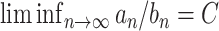 for some
for some 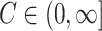 (and
(and  for some
for some 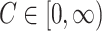 ). Alternatively,
). Alternatively, 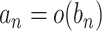 will also imply
will also imply 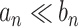 and
and 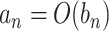 will imply that
will imply that  for some
for some  ).
).
We will denote the set of the indices of the non-zero rows in 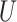 and
and 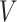 by
by 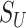 and
and  , respectively. We let
, respectively. We let  and
and  be the cardinalities of
be the cardinalities of  and
and  and use
and use  to denote the total sparsity. We further denote by
to denote the total sparsity. We further denote by  and
and 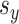 the number of non-zero elements of
the number of non-zero elements of  and
and 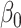 , respectively. The supports of
, respectively. The supports of 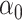 and
and  will similarly be denoted by
will similarly be denoted by  and
and  , respectively. We will discuss the precise requirements on these sparsities and the necessities of such assumptions in detail in Section 4.1.
, respectively. We will discuss the precise requirements on these sparsities and the necessities of such assumptions in detail in Section 4.1.
Our method requires initial estimators of  ,
, 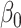 , and
, and 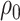 . We let
. We let 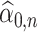 and
and 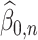 be the initial estimators of
be the initial estimators of 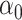 and
and  , respectively. Also, we denote the empirical estimates of
, respectively. Also, we denote the empirical estimates of 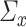 ,
, 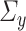 , and
, and  , by
, by  ,
, 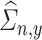 , and
, and 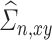 , respectively. The estimate
, respectively. The estimate  of
of 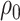 is
is
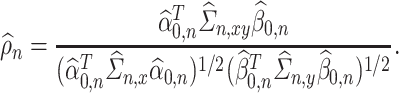 |
(2.2) |
The quantity 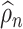 may not be positive for any
may not be positive for any 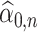 and
and 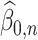 . Therefore, mostly we will use
. Therefore, mostly we will use 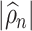 as an estimate of
as an estimate of  .
.
This paper provides many rate results that involve the term  . This term arises due to the union bound and is equivalent to the
. This term arises due to the union bound and is equivalent to the 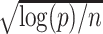 term in the asymptotic rate results of high-dimensional Lasso. To simplify notation, we will denote this term as
term in the asymptotic rate results of high-dimensional Lasso. To simplify notation, we will denote this term as  , using the following equation:
, using the following equation:
 |
(2.3) |
3. Methodology
This section discusses the intuitions and details of the proposed methodology that we will analyse in later sections. The discussions are divided across three main subsections. The first Subsection 3.1 presents the driving intuition behind obtaining de-biased estimators of general parameters of interest, defined through a generic optimization framework. Subsequently, Subsection 3.2 translates this intuition to a working principle in the context of SCCA. In particular, we design a suitable optimization criterion that allows a principled application of the general de-biasing method and lends itself to rigorous theoretical analyses. Finally, our last Subsection 3.3 elaborates on the benefit of designing this specific optimization objective function over other possible choices of optimization problems that define the leading canonical directions.
3.1 The De-biasing method in general
We first discuss the simple intuition behind reducing the bias of estimators defined through estimating equations. Suppose we are interested in estimating  , which minimizes the function
, which minimizes the function  . If
. If  is smooth, then
is smooth, then 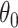 solves the equation
solves the equation  . Suppose
. Suppose 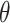 is in a small neighbourhood of
is in a small neighbourhood of 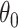 . The Taylor series expansion of
. The Taylor series expansion of 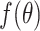 around
around 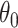 yields
yields  , where
, where 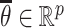 lies on the line segment joining
lies on the line segment joining  and
and 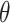 . If
. If 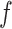 has finitely many global minima, then
has finitely many global minima, then 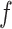 cannot be flat at
cannot be flat at 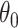 . In that case,
. In that case,  is strongly convex at some neighbourhood of
is strongly convex at some neighbourhood of 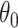 . Therefore
. Therefore 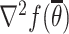 is positive definite, leading to
is positive definite, leading to 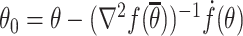 . Suppose
. Suppose 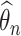 and
and 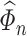 are reliable estimators of
are reliable estimators of 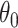 and
and  , respectively. Correcting the first-order bias of
, respectively. Correcting the first-order bias of  then yields the de-biased estimator
then yields the de-biased estimator  . Thus, to find a bias-corrected estimator of
. Thus, to find a bias-corrected estimator of 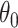 , it suffices to find a smooth function which is minimized at
, it suffices to find a smooth function which is minimized at  and has at most finitely many global minima. This simple intuition is the backbone of our strategy.
and has at most finitely many global minima. This simple intuition is the backbone of our strategy.
Remark 3.1.
(Positive definiteness of
) The positive definiteness of
is important as this is a requirement for most existing methods for estimating the inverse of a high-dimensional matrix. These methods proceed via estimating the columns of
separately through a quadratic optimization step. Unless the original matrix is positive definite, these intermediate optimization problems are unbounded. Therefore, the associated algorithms are likely to diverge even with many observations. For more details, see section 1 of [32] (see also section 2.1 of 69].
3.2 The De-biasing method for SCCA
To operationalize the intuition described above in Section 3.1, we begin with a lemma which represents 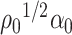 and
and 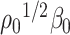 as the unique minimizers (upto a sign flip) of a smooth objective function. We defer the proof of Lemma 3.1 to Supplement E.
as the unique minimizers (upto a sign flip) of a smooth objective function. We defer the proof of Lemma 3.1 to Supplement E.
Lemma 3.1.
Under Assumption 2.1, for any
, we have
where
.
The proof of Lemma 3.1 hinges on a seminal result in low rank matrix approximation dating back to [23], which implies that for any matrix  with singular value decomposition
with singular value decomposition 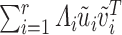 ,
,
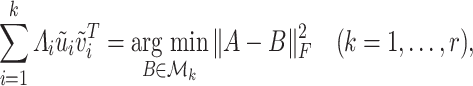 |
(3.1) |
where 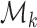 is the set of all
is the set of all 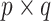 matrices with rank
matrices with rank 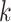 . We will use this result with
. We will use this result with  in the proof of Lemma 3.1. In that case, if
in the proof of Lemma 3.1. In that case, if 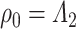 , then the minimizer in (3.1) is not unique, which is the reason why it is necessary to impose Assumption 2.1 in Lemma 3.1. Our primary inferential method for leading canonical directions builds on Lemma 3.1, and consequently, corrects for the bias of estimating
, then the minimizer in (3.1) is not unique, which is the reason why it is necessary to impose Assumption 2.1 in Lemma 3.1. Our primary inferential method for leading canonical directions builds on Lemma 3.1, and consequently, corrects for the bias of estimating 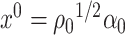 and
and 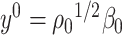 using preliminary plug-in estimators from literature. It is worth noting that we focus on the the leading canonical directions up to a multiplicative factor since from our inferential point of view, this quantity is enough to explore the nature of projection operators onto these directions. In particular, the test
using preliminary plug-in estimators from literature. It is worth noting that we focus on the the leading canonical directions up to a multiplicative factor since from our inferential point of view, this quantity is enough to explore the nature of projection operators onto these directions. In particular, the test 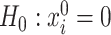 is equivalent to tests for no-signal such as
is equivalent to tests for no-signal such as  .
.
Remark 3.2.
Suppose
is as in Lemma 3.1. It can be shown that the other stationary points of
, to be denoted by
, correspond to the canonical pairs with correlations
,
. Moreover, the hessian of
at
has both positive and negative eigenvalues, indicating that the function is neither concave nor convex at these points. Therefore, all these stationary points are saddle points. Consequently, any minimum of
is a global minimum irrespective of the choice of
.
Now note that
 |
(3.2) |
and hence by symmetry, the hessian, 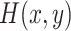 , of
, of 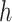 at
at 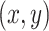 is given by
is given by
 |
We note the flexibility of our approach with regard to the choice of 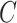 . This allows us to work with a more amenable form of the hessian and its inverse that we need to estimate. We subsequently set
. This allows us to work with a more amenable form of the hessian and its inverse that we need to estimate. We subsequently set  so that the estimation of the cross term
so that the estimation of the cross term 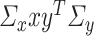 can be avoided. In particular, when
can be avoided. In particular, when  and
and  , then
, then 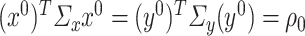 . We denote the hessian in this case as
. We denote the hessian in this case as
 |
(3.3) |
A plug-in estimator 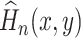 of
of  is given by
is given by
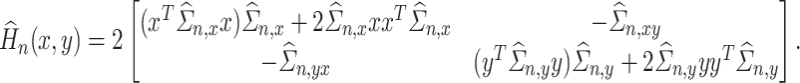 |
Because our  is a sufficiently well-behaved function, it possesses a positive definite hessian at the minima
is a sufficiently well-behaved function, it possesses a positive definite hessian at the minima  , thereby demonstrating the crucial strong convexity property mentioned in Remark 3.1. This property of
, thereby demonstrating the crucial strong convexity property mentioned in Remark 3.1. This property of  is the content of our following lemma, the proof of which can be found in Supplement E.
is the content of our following lemma, the proof of which can be found in Supplement E.
Lemma 3.2.
Under Assumptions 2.1 and 2.2, the matrix
defined in (3.3) is positive definite with minimum eigenvalue
where
is as in Assumption 2.2.
Lemma 3.1 and Lemma 3.2 subsequently allows us to construct de-biased estimators of the leading canonical directions as follows. Suppose  and
and  are estimators of
are estimators of 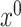 and
and 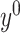 , where
, where 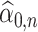 and
and  are the preliminary estimators of
are the preliminary estimators of 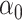 and
and  , and
, and 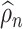 is as defined in (2.2). Our construction of de-biased estimators for SCCA now relies on two objects: (a) estimators of
is as defined in (2.2). Our construction of de-biased estimators for SCCA now relies on two objects: (a) estimators of 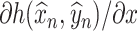 and
and 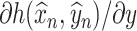 , which are simply given by
, which are simply given by
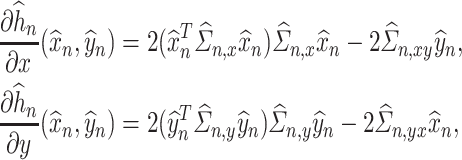 |
(3.4) |
and (b) an estimator 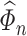 of
of  , the inverse of
, the inverse of 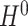 . Construction of such an estimator can be very involved. To tackle this challenge, we develop a version of the nodewise Lasso algorithm (see Supplement C.4 for details) popularized in recent research [61].
. Construction of such an estimator can be very involved. To tackle this challenge, we develop a version of the nodewise Lasso algorithm (see Supplement C.4 for details) popularized in recent research [61].
Following the intu itions discussed in Section 3.1, we can then complete the construction of the de-biased estimators, whose final form can be written as
 |
(3.5) |
In Section 5, we will discuss how our proposed method connects to the broader scope of de-biased inference in high-dimensional problems. Regarding the targets of our estimators, we note that if 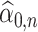 estimates
estimates 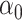 , then
, then 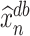 also estimates
also estimates 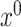 . However, if
. However, if 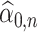 approximates
approximates  instead, then
instead, then 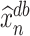 instead approximates
instead approximates  . A similar phenomenon can be observed for
. A similar phenomenon can be observed for  as well. Our theoretical analyses of these estimators will be designed accordingly.
as well. Our theoretical analyses of these estimators will be designed accordingly.
Next, we will construct a de-biased estimator of  using
using 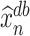 and
and  . As we will see in Section 4, we will require stricter assumptions on the nuisance parameters to correct the first-order bias of
. As we will see in Section 4, we will require stricter assumptions on the nuisance parameters to correct the first-order bias of  . In particular, we will require the columns of
. In particular, we will require the columns of  and
and 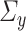 to be sparse. We will also require estimators of
to be sparse. We will also require estimators of 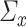 and
and 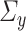 that are column sparse. Section 4 will provide a more detailed discussion of the sparsity requirements on
that are column sparse. Section 4 will provide a more detailed discussion of the sparsity requirements on 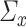 and
and 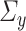 and their corresponding sparse estimators. For now, we will assume that we have access to
and their corresponding sparse estimators. For now, we will assume that we have access to 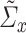 and
and  , which are column-sparse estimators of
, which are column-sparse estimators of  and
and 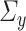 , respectively.
, respectively.
Recall that  denotes the estimator of
denotes the estimator of 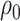 based on
based on 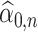 and
and 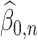 . Our estimator of
. Our estimator of 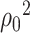 can be constructed as
can be constructed as  , where
, where
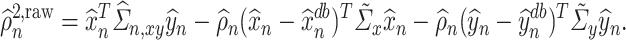 |
We want to clarify that in constructing  and
and 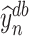 , we use
, we use  and
and  as before. We do not use
as before. We do not use  and
and  there.
there.
Before moving onto the theoretical properties of our proposed methods, we make a slight relevant digression to note that there exist many formulations of the optimization program in (1.1) so that 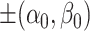 are the global optima. We therefore close this current section with a discussion on why the particular formulation in Lemma 3.1 is beneficial for our purpose.
are the global optima. We therefore close this current section with a discussion on why the particular formulation in Lemma 3.1 is beneficial for our purpose.
3.3 Subtleties with other representations of 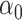 and
and 
The most intuitive approach to characterize  is to conceptualize it as the maximizer of the constrained maximization problem (1.1). This leads to the Lagrangian
is to conceptualize it as the maximizer of the constrained maximization problem (1.1). This leads to the Lagrangian
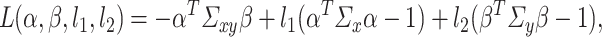 |
(3.6) |
where 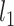 and
and 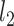 are the Lagrange multipliers. Denoting
are the Lagrange multipliers. Denoting  , it can be verified that since
, it can be verified that since  is a stationary point of (1.1),
is a stationary point of (1.1), 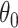 also solves
also solves  . Using the first-order Taylor series expansion of
. Using the first-order Taylor series expansion of 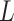 , one can then show that any
, one can then show that any  in a small neighbourhood of
in a small neighbourhood of 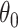 has the approximate expansion
has the approximate expansion
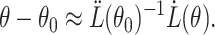 |
If we then replace 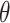 by an estimator of
by an estimator of 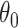 , we can use the above expansion to estimate the first-order bias of this estimator provided
, we can use the above expansion to estimate the first-order bias of this estimator provided  is suitably well-behaved and estimable. However, by strong max-min property [cf. Section 5.4.1 6],
is suitably well-behaved and estimable. However, by strong max-min property [cf. Section 5.4.1 6], 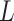 satisfies
satisfies
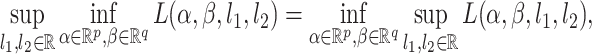 |
(3.7) |
which implies  is a saddle point of
is a saddle point of 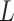 . Thus
. Thus 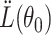 fails to be positive definite. In fact, any constrained optimization program fails to provide a Lagrangian with positive definite hessian, and thus violates the requirements outlined in Section 3.1. We have already pointed out in Remark 3.1 that statistical tools for efficient estimation of the inverse of a high-dimensional matrix are scarce unless the matrix under consideration is positive definite. Therefore, we refrain from using the constrained optimization formulation in (1.1) for the de-biasing procedure.
fails to be positive definite. In fact, any constrained optimization program fails to provide a Lagrangian with positive definite hessian, and thus violates the requirements outlined in Section 3.1. We have already pointed out in Remark 3.1 that statistical tools for efficient estimation of the inverse of a high-dimensional matrix are scarce unless the matrix under consideration is positive definite. Therefore, we refrain from using the constrained optimization formulation in (1.1) for the de-biasing procedure.
For any 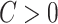 , the function
, the function
 |
however, is a valid choice for the  outlined in Subsection 3.1 since its only global minimizers are
outlined in Subsection 3.1 since its only global minimizers are 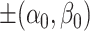 , which also indicates strong convexity at
, which also indicates strong convexity at  . However, the gradient and the hessian of this function takes a complicated form. Therefore, establishing asymptotic results for the de-biased estimator based on this
. However, the gradient and the hessian of this function takes a complicated form. Therefore, establishing asymptotic results for the de-biased estimator based on this 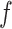 is significantly more cumbersome than its counterpart based on the
is significantly more cumbersome than its counterpart based on the  in Lemma 3.1. Hence, we refrain from using this objective function for our de-biasing procedure as well.
in Lemma 3.1. Hence, we refrain from using this objective function for our de-biasing procedure as well.
3.4 Possible extension to higher order canonical directions
Let us denote by  where we remind the readers that
where we remind the readers that 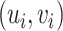 were the canonical direction pairs corresponding to
were the canonical direction pairs corresponding to  for
for  . Till now, we discussed the estimation of
. Till now, we discussed the estimation of  . In this section, we will briefly outline the de-biased estimation of of
. In this section, we will briefly outline the de-biased estimation of of 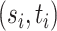 for
for 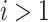 because they may be of interest in some applications. To this end, we first present a lemma that generalizes Lemma 3.1 to higher order canonical directions. The proof of Lemma 3.3 can be found in Supplement E. This lemma shows that similar to
because they may be of interest in some applications. To this end, we first present a lemma that generalizes Lemma 3.1 to higher order canonical directions. The proof of Lemma 3.3 can be found in Supplement E. This lemma shows that similar to 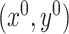 , the scaled higher order canonical directions can be presented as the minimizer of an unconstrained optimization problem up to a sign flip.
, the scaled higher order canonical directions can be presented as the minimizer of an unconstrained optimization problem up to a sign flip.
Lemma 3.3.
Suppose
for some
, where we take
. Then for any
, we have
Here
where
As in Lemma 3.1, the condition 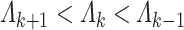 is required to ensure that
is required to ensure that  is identifiable up to a sign flip. The proof of Lemma 3.3 is similar to Lemma 3.1 and relies on (3.1).
is identifiable up to a sign flip. The proof of Lemma 3.3 is similar to Lemma 3.1 and relies on (3.1).
An important observation from Lemma 3.3 is that the formula for 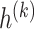 is identical to that of
is identical to that of  in Lemma 3.1, except the
in Lemma 3.1, except the 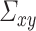 in Lemma 3.1 has been replaced by
in Lemma 3.1 has been replaced by  . Therefore, the gradient and hessian of
. Therefore, the gradient and hessian of 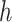 and
and  are the same, except the
are the same, except the 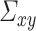 in the former case is replaced by
in the former case is replaced by  in the latter case. Since
in the latter case. Since 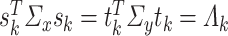 , we can proceed as in the case of
, we can proceed as in the case of 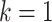 and show that when
and show that when  , the hessian of
, the hessian of  takes the form
takes the form
 |
When 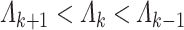 , similar to Lemma 3.2, we can show that
, similar to Lemma 3.2, we can show that 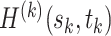 is positive definite.
is positive definite.
In light of the previous discussion, we can construct a bias-corrected estimator of  by following the same approach as in (3.5), provided that we can obtain a reliable estimate of
by following the same approach as in (3.5), provided that we can obtain a reliable estimate of 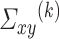 and we have
and we have 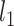 and
and 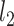 consistent preliminary estimators of
consistent preliminary estimators of 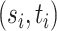 for
for  . To obtain such preliminary estimators, we may extend our modified COLAR algorithm to the rank
. To obtain such preliminary estimators, we may extend our modified COLAR algorithm to the rank  case, which will basically implement [25]’s COLAR algorithm with a rank parameter of
case, which will basically implement [25]’s COLAR algorithm with a rank parameter of  . The estimation of
. The estimation of  requires estimators of all canonical directions up to order
requires estimators of all canonical directions up to order  . Therefore we will estimate
. Therefore we will estimate  recursively. To do so, let us assume that we already have at our disposal bias-corrected estimators of
recursively. To do so, let us assume that we already have at our disposal bias-corrected estimators of  for
for  , denoted by
, denoted by 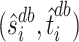 . An estimator of
. An estimator of 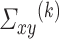 can then be obtained using the following formula:
can then be obtained using the following formula:
 |
We can then use  to obtain the de-biased estimator of
to obtain the de-biased estimator of 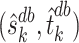 . Note that, for
. Note that, for 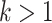 , the de-biased estimators of the canonical correlations will depend on the nuisance matrices
, the de-biased estimators of the canonical correlations will depend on the nuisance matrices 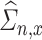 and
and  in a more complicated manner. Therefore, the
in a more complicated manner. Therefore, the 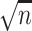 -consistency of
-consistency of  may require stronger restrictions on
may require stronger restrictions on  and
and 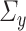 than those imposed by Assumptions 2.1 and 2.2. Although theoretical analysis of the higher order bias-corrected estimator
than those imposed by Assumptions 2.1 and 2.2. Although theoretical analysis of the higher order bias-corrected estimator 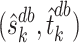 is beyond the scope of this paper, we leave it as a topic for future research.
is beyond the scope of this paper, we leave it as a topic for future research.
4. Asymptotic theory for the de-biased estimator
In this section, we establish the theoretical properties of our proposed estimators under a high-dimensional sparse asymptotic framework. To set up our main theoretical results, we present assumptions on sparsities of the true canonical directions and desired conditions on initial estimators of  in Subsection 4.1. The construction of estimators with these desired properties is discussed in Supplement B and Supplement C. Subsequently, we present the main asymptotic results and their implications for the construction of confidence intervals of relevant quantities of interest in Subsection 4.2.
in Subsection 4.1. The construction of estimators with these desired properties is discussed in Supplement B and Supplement C. Subsequently, we present the main asymptotic results and their implications for the construction of confidence intervals of relevant quantities of interest in Subsection 4.2.
4.1 Assumptions on  ,
, 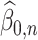 and
and 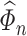
For the de-biasing procedure to be successful, it is important that 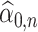 and
and  are both
are both 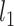 and
and  consistent for
consistent for 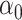 and
and  with suitable rates of convergence. In particular, we will require them to satisfy the following condition.
with suitable rates of convergence. In particular, we will require them to satisfy the following condition.
Condition 4.1.
(Preliminary estimator condition) The preliminary estimators
and
of
and
satisfy the following for some
,
, and
as defined in (2.3):
and
We present discussions regarding the necessity of the rates mentioned above as well as the motivation behind the exponent  in Section 6. Moreover, we also discuss the construction of estimators satisfying Condition 4.1 in Supplement B. Our method for developing these initial estimators is motivated by the recent results in [25], who jointly estimate
in Section 6. Moreover, we also discuss the construction of estimators satisfying Condition 4.1 in Supplement B. Our method for developing these initial estimators is motivated by the recent results in [25], who jointly estimate 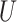 and
and 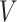 up to an orthogonal rotation with desired
up to an orthogonal rotation with desired  guarantees. However, our situation is somewhat different since we need to estimate
guarantees. However, our situation is somewhat different since we need to estimate 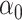 and
and 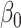 up to a sign flip, which might not be obtained from the joint estimation of all the directions up to orthogonal rotation. This is an important distinction since the remaining directions act as nuisance parameters in our set-up. The asymptotics of the sign-flipped version require crucial modification of the arguments of [25]. The analysis of this modified procedure presented in Supplement 1 allows us to extract both the desired
up to a sign flip, which might not be obtained from the joint estimation of all the directions up to orthogonal rotation. This is an important distinction since the remaining directions act as nuisance parameters in our set-up. The asymptotics of the sign-flipped version require crucial modification of the arguments of [25]. The analysis of this modified procedure presented in Supplement 1 allows us to extract both the desired 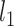 and
and  guarantees.
guarantees.
We will also require an assumption on the sparsities 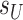 and
and 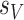 , the number of non-zero rows of
, the number of non-zero rows of 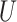 and
and 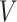 , respectively. We present this next while deferring the discussions on the necessity of such assumptions to Section 6.
, respectively. We present this next while deferring the discussions on the necessity of such assumptions to Section 6.
Assumption 4.1.
(Sparsity Assumption) We assume
,
and
where
and
is as in Condition 4.1.
In high-dimensional settings, low-dimensional structure is often necessary to estimate elements at 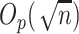 -rate. Sparsity is one common and convenient form of low-dimensional structure that is frequently assumed in high-dimensional statistics [19, 24, 32, 49]. However, verifying this assumption mathematically can be a challenging information-theoretic question [14]. Therefore, subject matter knowledge is often required to justify the sparsity assumption. For instance, in genetic studies, only a small number of genetic variants or features are typically associated with a particular disease or phenotype of interest, which justifies the sparsity assumption for the canonical covariates between the genetic features and phenotypes [67]. We defer the discussion on the specific rates appearing in Assumption 4.1 to Section 6.
-rate. Sparsity is one common and convenient form of low-dimensional structure that is frequently assumed in high-dimensional statistics [19, 24, 32, 49]. However, verifying this assumption mathematically can be a challenging information-theoretic question [14]. Therefore, subject matter knowledge is often required to justify the sparsity assumption. For instance, in genetic studies, only a small number of genetic variants or features are typically associated with a particular disease or phenotype of interest, which justifies the sparsity assumption for the canonical covariates between the genetic features and phenotypes [67]. We defer the discussion on the specific rates appearing in Assumption 4.1 to Section 6.
Finally, our last condition pertains to the estimator 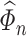 on
on 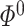 . Most methods for estimating precision matrices can be adopted to estimate
. Most methods for estimating precision matrices can be adopted to estimate  using an estimator of
using an estimator of  . However, care is needed since
. However, care is needed since 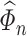 needs to satisfy certain rates of convergence for the de-biased estimators in (3.5) to be
needs to satisfy certain rates of convergence for the de-biased estimators in (3.5) to be 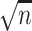 -consistent. We present this condition below.
-consistent. We present this condition below.
Condition 4.2.
Inverse hessian Conditions. The estimator
satisfies
and
where
is as in Condition 4.1.
We defer the discussion on the construction of 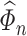 to Supplement C, where, in particular, we will show that the nodewise Lasso type estimator, which appeals to the ideas in [61], satisfies Condition 4.2.
to Supplement C, where, in particular, we will show that the nodewise Lasso type estimator, which appeals to the ideas in [61], satisfies Condition 4.2.
4.2 Theoretical analyses
In what follows, we present only the results on inference for 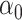 . Results for
. Results for 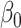 can be obtained in a parallel fashion. Before stating the main theorem, we introduce a few additional notations. We partition the
can be obtained in a parallel fashion. Before stating the main theorem, we introduce a few additional notations. We partition the 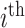 column of
column of 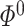 comfortably w.r.t. the dimensions of
comfortably w.r.t. the dimensions of 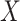 and
and 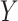 as
as 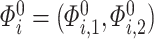 , where
, where 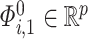 and
and 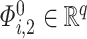 . We subsequently define the random variable
. We subsequently define the random variable
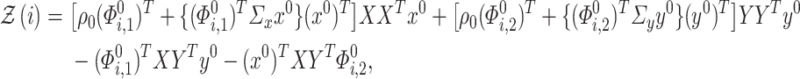 |
(4.1) |
and its associated variance as
 |
(4.2) |
Since 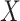 and
and 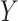 are sub-Gaussian, it can be shown that all moments of
are sub-Gaussian, it can be shown that all moments of 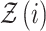 , and in particular the
, and in particular the  ’s are finite under Assumption 2.2. Indeed, we show the same through the proof of Theorem 4.1. Finally define
’s are finite under Assumption 2.2. Indeed, we show the same through the proof of Theorem 4.1. Finally define
 |
(4.3) |
With this we are ready to state the main theorem of this paper. This theorem is proved in Supplement F.
Theorem 4.1.
(Asymptotic representation of
) Suppose
and
are centred sub-Gaussian vectors, and Assumptions 2.1, 2.2 and 4.1 hold. Further suppose
satisfies Condition 4.2, and
and
satisfy Condition 4.1. In particular, suppose
and
satisfy
(4.4) Then the estimator
defined in (3.5) satisfies
, where
is as defined in (4.3), and
is a random vector satisfying
. Here
and
are as in (2.3) and Condition 4.1, respectively. If
and
satisfy
(4.5) instead, then
satisfies
, where
.
A few remarks are in order about the statement and implications of Theorem 4.1. First, (4.4) and (4.5) correspond to the cases when  concentrate around
concentrate around 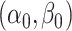 and
and 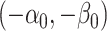 , respectively. We point out that (4.4) and (4.5) essentially do not impose extra restrictions on top of Condition 4.1. If
, respectively. We point out that (4.4) and (4.5) essentially do not impose extra restrictions on top of Condition 4.1. If  are reasonable estimators satisfying Condition 4.1, and they are chosen so as to ensure
are reasonable estimators satisfying Condition 4.1, and they are chosen so as to ensure  , then we can expect either (4.4) or (4.5) to hold. However, Condition 4.1 and
, then we can expect either (4.4) or (4.5) to hold. However, Condition 4.1 and 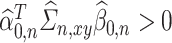 alone are not sufficient to eliminate pathological cases where
alone are not sufficient to eliminate pathological cases where  and
and  do not converge anywhere. For example, consider the trivial case where
do not converge anywhere. For example, consider the trivial case where  for even
for even  , and
, and 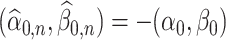 for odd
for odd 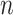 . In this case,
. In this case,  and
and 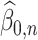 satisfy Condition 4.1 and
satisfy Condition 4.1 and  , but they do not converge in
, but they do not converge in  for any
for any 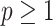 . The purpose of (4.4) and (4.5) is to disentangle the sign flip from the asymptotic convergence of
. The purpose of (4.4) and (4.5) is to disentangle the sign flip from the asymptotic convergence of 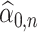 and
and  , which helps to eliminate such uninteresting pathological cases from consideration.
, which helps to eliminate such uninteresting pathological cases from consideration.
Second, we note that under Assumption 4.1, 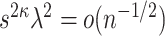 . The importance of Theorem 4.1 subsequently lies in the fact that it establishes the equivalence between
. The importance of Theorem 4.1 subsequently lies in the fact that it establishes the equivalence between 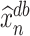 and the more tractable random vector
and the more tractable random vector  under Assumption 4.1. In particular, one can immediately derive a simple yet relevant corollary about the asymptotically normal nature of the distribution of our de-biased estimators.
under Assumption 4.1. In particular, one can immediately derive a simple yet relevant corollary about the asymptotically normal nature of the distribution of our de-biased estimators.
Proof outline of Theorem 4.1. For the sake of simplicity, we only consider the case when (4.4) holds. The key step of proving Theorem 4.1 is to decompose 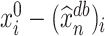 into four terms as follows:
into four terms as follows:
 |
(4.6) |
The first term, i.e. the  -term, is the main contributing term in the above expansion because, as the name suggests, it is asymptotically equivalent to
-term, is the main contributing term in the above expansion because, as the name suggests, it is asymptotically equivalent to 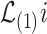 (up to a term of order
(up to a term of order  ). To show this, the main tool we use is the concentration of the sample covariance matrices around their population versions in the
). To show this, the main tool we use is the concentration of the sample covariance matrices around their population versions in the 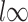 norm (see Lemma D.5), which is an elementary result for sub-gaussian random vectors (cf. 7, 32]. The remaining three terms on the right-hand side (RHS) of (4.6) are error terms of order
norm (see Lemma D.5), which is an elementary result for sub-gaussian random vectors (cf. 7, 32]. The remaining three terms on the right-hand side (RHS) of (4.6) are error terms of order 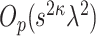 .
.
First, we encounter the cross-product term because we approximate 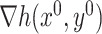 and
and 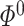 by
by 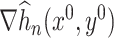 and
and  , respectively. We control the error in estimating
, respectively. We control the error in estimating 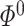 using Condition 4.2. To control the estimation error of
using Condition 4.2. To control the estimation error of 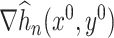 , we observe that its random elements are basically sample covariance matrices, which, as previously mentioned, concentrate in the
, we observe that its random elements are basically sample covariance matrices, which, as previously mentioned, concentrate in the  norm.
norm.
Second, the Taylor series approximation term occurs because our de-biasing method is essentially based on the first-order Taylor series approximation 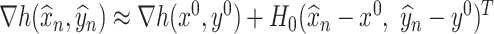 . The error due to this approximation is small because
. The error due to this approximation is small because  and
and  are asymptotically close to
are asymptotically close to  and
and  in the
in the  and
and  norms; see Condition 4.1.
norms; see Condition 4.1.
The final term, i.e. the preliminary estimation error term, is again a cross-product term. To show that this term is of order 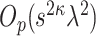 , we exploit the
, we exploit the  -consistency of
-consistency of 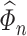 and
and  .
.
Now we will present an important corollary of Theorem 4.1, which underscores that 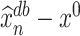 equals
equals 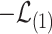 and an error term of smaller order. Using the central limit theorem, it can be shown that the marginals of
and an error term of smaller order. Using the central limit theorem, it can be shown that the marginals of  converge in distribution to centred gaussian random variables. In particular, we can show that
converge in distribution to centred gaussian random variables. In particular, we can show that
 |
(4.7) |
However, in Corollary 1, we decide to provide inference on 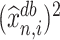 instead of
instead of 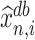 , because (a) the former is unaffected by the sign flip of
, because (a) the former is unaffected by the sign flip of 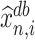 and (b) the sign of
and (b) the sign of 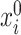 is typically of little interest. As a specific example, testing
is typically of little interest. As a specific example, testing  is equivalent to testing
is equivalent to testing 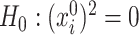 . More importantly, one of the central objects of interest in low-dimensional representations obtained through SCCA is the projection operators onto the leading canonical directions. It is easy to see that for this operator, it is sufficient to understand the squared
. More importantly, one of the central objects of interest in low-dimensional representations obtained through SCCA is the projection operators onto the leading canonical directions. It is easy to see that for this operator, it is sufficient to understand the squared 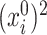 and the cross-terms
and the cross-terms 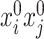 , respectively. The proof of Corollary 1 is deferred to Supplement H.
, respectively. The proof of Corollary 1 is deferred to Supplement H.
Corollary 1.
Under the set up of Theorem 4.1, for any
, the following assertions hold:
(a). If
, then
converges in distribution to a centred Gaussian random variable with variance
where the
’s are as defined in (4.2).
(b). If
, then
converges in distribution to a central Chi-squared random variable with degrees of freedom one and scale parameter
.
Next, we present results on the uniform nature of the joint asymptotically normal behaviour for the entire vector  . To this end, we verify in our next proposition that if
. To this end, we verify in our next proposition that if 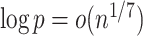 , the convergence in (4.7) is uniform across
, the convergence in (4.7) is uniform across  when restricted to suitably well-behaved sets. A proof of Proposition 4.2 is in Section G.
when restricted to suitably well-behaved sets. A proof of Proposition 4.2 is in Section G.
Proposition 4.2.
Let
be the set of all hyperrectangles in
and let
be the covariance matrix of the
-variate random vector
. Assume the set-up of Theorem 4.1 Suppose the
’s defined in (4.2) satisfy
for some
and
. Then if (4.4) holds,
and if (4.5) holds (the sign-flip case), then
where
is a random vector distributed as
.
Proof outline of Proposition 4.2. The proof of Proposition 4.2, which can be found in Supplement H, relies on a Berry–Esseen-type result. As indicated earlier, 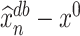 decomposes into
decomposes into 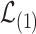 and a reminder term of smaller order. The marginals of
and a reminder term of smaller order. The marginals of  converge weakly to centred Gaussian distributions, which ultimately leads to (4.7). We apply a Berry–Esseen-type result from [21] on
converge weakly to centred Gaussian distributions, which ultimately leads to (4.7). We apply a Berry–Esseen-type result from [21] on  to show that the weak convergence of marginals can be strengthened to establish convergence over rectangular sets.
to show that the weak convergence of marginals can be strengthened to establish convergence over rectangular sets.
The lower bound requirement on the variance of the marginal limiting distribution, i.e. 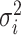 ’s, is typical for Berry–Esseen-type theorems—see e.g. [21]. As a specific example, we provide Corollary 2 below to establish the validity of
’s, is typical for Berry–Esseen-type theorems—see e.g. [21]. As a specific example, we provide Corollary 2 below to establish the validity of  for some
for some 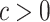 when
when 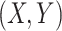 is jointly Gaussian. The proof of Corollary 2 can be found in Supplement G.
is jointly Gaussian. The proof of Corollary 2 can be found in Supplement G.
Corollary 2.
Suppose
are jointly Gaussian, and
is bounded away from zero and one. Further suppose
. Then under the set-up of Theorem 4.1, the assertion of
for some
used in Proposition 4.2 holds.
Proposition 4.2 can be used, as mentioned earlier, for inference on the non-diagonal elements of the matrix 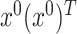 . This is the content of the following corollary—the proof of which can be found in Supplement H.
. This is the content of the following corollary—the proof of which can be found in Supplement H.
Corollary 3.
Consider the set-up of Proposition 4.2. Suppose
is positive definite. Let
, and
. Denote by
the covariance between
and
, where
’s are as defined in (4.1). Then the following assertions hold:
. Then
. Then
where
,
and
.
Here once again, we observe that the de-biased estimators of  have different asymptotic behaviour depending on whether
have different asymptotic behaviour depending on whether 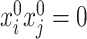 or not, which parallels the behaviour of the de-biased estimators of the diagonal elements we demonstrated earlier through Corollary 1.
or not, which parallels the behaviour of the de-biased estimators of the diagonal elements we demonstrated earlier through Corollary 1.
Remark 4.1.
Proposition 4.2 can also be used to simultaneously test the null hypotheses
. The uniform convergence in Proposition 4.2 can be used to justify multiple hypothesis testing for the coordinates of
whenever the corresponding p-values are defined through rectangular rejection regions based on
. To this end, one can use standard methods like Benjamini and Hochberg (BH) and Benjamini and Yekutieli (BY) procedures for FDR control. The simultaneous testing procedure can thereby also be connected to variable selection procedures. However, we do not pursue it here since specialized methods are available for the latter in SCCA context [39].
We end our discussions regarding the inference of 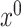 with a method for consistent estimation of the
with a method for consistent estimation of the  ’s. Indeed, this will allow us to develop tests for the hypotheses
’s. Indeed, this will allow us to develop tests for the hypotheses  or to build confidence intervals for
or to build confidence intervals for 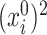 . To this end, we partition
. To this end, we partition  , where
, where 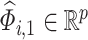 and
and  . Because
. Because  for
for  , we estimate
, we estimate  using the pseudo-observations
using the pseudo-observations 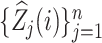 , which are defined by
, which are defined by
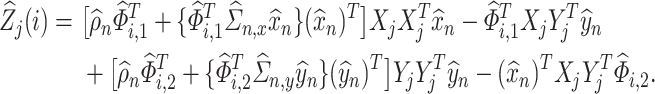 |
To this end, we propose to use a sample-splitting technique to estimate  ,
,  ,
,  ,
,  and
and  from one half of the sample, and construct the pseudo-observations using the other half of the sample. Then we can estimate
from one half of the sample, and construct the pseudo-observations using the other half of the sample. Then we can estimate  as the sample variance of the pseudo-observations. Since
as the sample variance of the pseudo-observations. Since 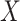 and
and 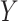 are sub-Gaussians, under the set-up of Theorem 4.1, it can be shown that the resulting estimator is consistent.
are sub-Gaussians, under the set-up of Theorem 4.1, it can be shown that the resulting estimator is consistent.
4.2.1 Inference on 
Our final theoretical result pertains to the asymptotic distribution of  . However, we require
. However, we require  and
and 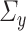 to be column-sparse (see Assumption 4.2 below) to establish the
to be column-sparse (see Assumption 4.2 below) to establish the 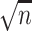 -consistency of
-consistency of  .
.
Assumption 4.2.
A column of
or
can have a maximum of
many non-zero elements, where
is a positive integer. In other words,
or
are bounded by
for each
and
.
We provide an explanation for the need behind Assumption 4.2. The assumption is crucial because the first-order bias of 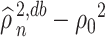 contains terms like
contains terms like 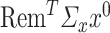 , where
, where 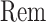 is as defined in Theorem 4.1. These terms cannot be effectively controlled under the weaker Assumption 2.2 as
is as defined in Theorem 4.1. These terms cannot be effectively controlled under the weaker Assumption 2.2 as 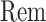 may not be sparse or small in
may not be sparse or small in 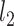 norm, which necessitates stronger assumptions on
norm, which necessitates stronger assumptions on  . Also, to control the first-order bias of
. Also, to control the first-order bias of  , we require estimators of
, we require estimators of  and
and  with
with  and
and  guarantees—see Condition 4.3. In high dimensions, the existence of such estimators is not guaranteed without structural assumptions on
guarantees—see Condition 4.3. In high dimensions, the existence of such estimators is not guaranteed without structural assumptions on  and
and 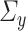 [5].
[5].
Assumption 4.2 implies a low degree of within-group association among the  and
and  variables. If the number of
variables. If the number of  and
and  variables are large, and they are also highly associated within themselves, decoding the association between
variables are large, and they are also highly associated within themselves, decoding the association between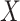 and
and 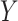 becomes difficult. To overcome this challenge, we require sparsity assumptions on the covariance matrices to precisely estimate the strength of the association between
becomes difficult. To overcome this challenge, we require sparsity assumptions on the covariance matrices to precisely estimate the strength of the association between 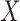 and
and 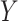 in high dimensions. Sparse covariance matrices are also a common assumption in high-dimensional statistics [5, 9, 11]. In fact, many methods have been developed specifically to estimate sparse covariance matrices in high-dimensional settings [5, 9, 11]. The sparsity assumption on
in high dimensions. Sparse covariance matrices are also a common assumption in high-dimensional statistics [5, 9, 11]. In fact, many methods have been developed specifically to estimate sparse covariance matrices in high-dimensional settings [5, 9, 11]. The sparsity assumption on 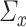 and
and  can often be justified for genetic and network data by utilizing subject-matter knowledge (cf. [15, 53, 56]). Also,
can often be justified for genetic and network data by utilizing subject-matter knowledge (cf. [15, 53, 56]). Also,  and
and  will automatically satisfy Assumption 4.2 if they are banded matrices, a widely used structural assumption for high-dimensional covariance matrices [5, 11, 58].
will automatically satisfy Assumption 4.2 if they are banded matrices, a widely used structural assumption for high-dimensional covariance matrices [5, 11, 58].
The analog of 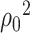 in the context of principal component analysis (PCA) is the square of the largest eigenvalue [32], for which a de-biased estimator can be derived without column-sparsity assumptions, as in Assumption 4.2. This discrepancy is explained by the fact that in PCA,
in the context of principal component analysis (PCA) is the square of the largest eigenvalue [32], for which a de-biased estimator can be derived without column-sparsity assumptions, as in Assumption 4.2. This discrepancy is explained by the fact that in PCA, 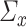 is not a nuisance parameter; its information on principal components is solely stored in
is not a nuisance parameter; its information on principal components is solely stored in 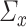 . However, for CCA, both
. However, for CCA, both 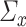 and
and 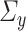 are nuisance parameters, thus implying the need for different assumptions in sparse PCA compared with sparse CCA. It might be possible to find an
are nuisance parameters, thus implying the need for different assumptions in sparse PCA compared with sparse CCA. It might be possible to find an 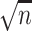 -consistent estimator of
-consistent estimator of  with less restrictive assumptions. However, since our goal here is to obtain de-biased estimators of canonical covariates, further investigation in this direction is beyond the scope of this paper.
with less restrictive assumptions. However, since our goal here is to obtain de-biased estimators of canonical covariates, further investigation in this direction is beyond the scope of this paper.
The following condition states the consistency requirements of 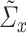 and
and 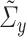 .
.
Condition 4.3.
and
satisfy the following conditions:
(4.8)
Condition 4.3 requires operator norm consistency, but this can be relaxed to the condition that
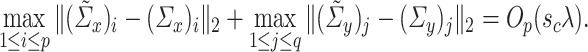 |
However, we choose to state the condition in terms of operator norm consistency because this form is more prevalent in the sparse covariance matrix estimation literature [5, 8].
Example: Under our assumptions, the coordinate-thresholding estimator proposed by [5] satisfies Condition 4.3. Specifically, we define the estimators  and
and  as
as  and
and 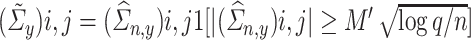 , where
, where 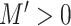 . Theorem 1 of [5] guarantees the operator norm consistency of these estimators, while their
. Theorem 1 of [5] guarantees the operator norm consistency of these estimators, while their  norm consistency is ensured by Theorem 4 of [9] for sufficiently large
norm consistency is ensured by Theorem 4 of [9] for sufficiently large 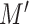 .
.
We are now ready to state our final theorem, a proof of which can be found in Supplement H.
Theorem 4.3.
Suppose
and
satisfy Assumption 4.2 and the conditions of Theorem 4.1 are met. Suppose, in addition,
, where
is as in Assumption 4.2. Further suppose either (4.4) or (4.5) holds.
Then for
,
where
. When
,
weakly converges to a random variable with distribution function
where
Here
is the distribution function of the standard Gaussian random variable. Moreover, when the observations are Gaussian,
.
We note several points concerning the statement of Theorem 4.3.
(1) variance of the parametric MLE: In the Gaussian case, the value of
 matches the variance of the parametric MLE of
matches the variance of the parametric MLE of 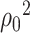 under the Gaussian model [1, p.505]. This alignment is often seen in de-biased estimators, e.g. the de-biased estimator of the principal eigenvalue [32].
under the Gaussian model [1, p.505]. This alignment is often seen in de-biased estimators, e.g. the de-biased estimator of the principal eigenvalue [32].(2) Extreme
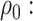 When
When 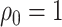 , the limiting distribution of
, the limiting distribution of  is discontinuous because it is a truncated estimator, where the truncation is applied at
is discontinuous because it is a truncated estimator, where the truncation is applied at  . When
. When 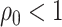 , unlike the
, unlike the  case, the truncation does not affect the asymptotic distribution of
case, the truncation does not affect the asymptotic distribution of 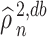 .
.(3) Sparsity condition: Theorem 4.3 imposes stricter conditions on
 than those specified in Theorem 4.1. Although we have not investigated the strictness of this assumption, a similar stricter sparsity requirement can be found in [32], where a
than those specified in Theorem 4.1. Although we have not investigated the strictness of this assumption, a similar stricter sparsity requirement can be found in [32], where a  -consistent estimator of the maximum eigenvalue is constructed for the sparse PCA problem. To compare our set-up with the PCA case, we consider our nuisance parameters
-consistent estimator of the maximum eigenvalue is constructed for the sparse PCA problem. To compare our set-up with the PCA case, we consider our nuisance parameters 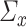 and
and 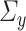 as identity matrices, which implies
as identity matrices, which implies  . In such a case, our sparsity condition reduces to
. In such a case, our sparsity condition reduces to  , which is similar to that of [32].
, which is similar to that of [32].(4) Interplay between
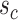 and
and 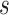 : The condition for sparsity,
: The condition for sparsity, 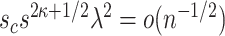 , necessitates that either
, necessitates that either 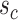 or
or  be of a smaller order. It is worth noting that
be of a smaller order. It is worth noting that 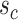 tends to be large in cases where the elements of
tends to be large in cases where the elements of  and
and 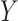 are highly correlated with each other. Hence, we can interpret the interplay between
are highly correlated with each other. Hence, we can interpret the interplay between  and
and 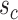 in the following manner: either the correlation within the variables
in the following manner: either the correlation within the variables 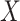 and
and 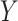 or the correlation between these variables must be sufficiently low-dimensional for our bias correction method to be effective.
or the correlation between these variables must be sufficiently low-dimensional for our bias correction method to be effective.
To construct an estimator of 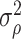 , we use a sample splitting procedure. First, we split the sample into two parts of roughly equal size:
, we use a sample splitting procedure. First, we split the sample into two parts of roughly equal size:  and
and  . We use the sample part
. We use the sample part 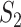 to estimate
to estimate 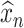 ,
,  and
and  . Next, we use these estimators to construct the pseudo-observations
. Next, we use these estimators to construct the pseudo-observations 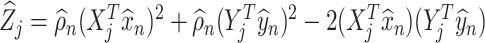 , where the
, where the  ’s and
’s and 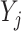 ’s (
’s (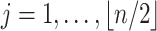 ) come from
) come from 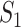 . Finally, we obtain the estimator of
. Finally, we obtain the estimator of 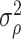 by averaging the squares of these pseudo-observations, i.e.
by averaging the squares of these pseudo-observations, i.e.  . This estimator will be consistent under the Conditions of Theorem 4.1, and hence can be used in combination with Theorem 4.3 to construct confidence intervals for
. This estimator will be consistent under the Conditions of Theorem 4.1, and hence can be used in combination with Theorem 4.3 to construct confidence intervals for 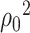 . To improve the efficiency of this estimator, we can repeat its construction by swapping the sample parts, and take average of the two estimators resulting from a sample split.
. To improve the efficiency of this estimator, we can repeat its construction by swapping the sample parts, and take average of the two estimators resulting from a sample split.
Proof outline of Theorem 4.3. The key step of this proof is to show that 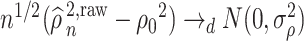 for all
for all 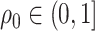 . For
. For  , we immediately obtain Theorem 4.3 because it can be easily shown that, in this case,
, we immediately obtain Theorem 4.3 because it can be easily shown that, in this case,  with probability approaching one. When
with probability approaching one. When 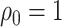 , weak convergence follows after some additional algebraic manipulations.
, weak convergence follows after some additional algebraic manipulations.
To show the weak convergence of 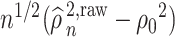 , we need to express
, we need to express  as the sum of a Lindeberg–Feller CLT term and an
as the sum of a Lindeberg–Feller CLT term and an  term. Our first step is to express
term. Our first step is to express 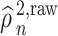 in terms of
in terms of  ,
, 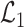 and
and 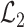 as follows:
as follows:
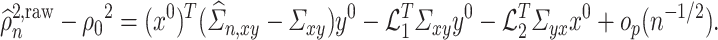 |
(4.9) |
This representation is useful as it shows that the random part of 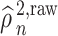 depends only on
depends only on 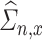 ,
,  and
and  . The second step is to show that the right-hand side of (4.9) can be written as an average of independent, centred random variables that allows us to apply the Lindeberg–Feller CLT.
. The second step is to show that the right-hand side of (4.9) can be written as an average of independent, centred random variables that allows us to apply the Lindeberg–Feller CLT.
5. Connection to related literature
The study of asymptotic inference in the context of SCCA naturally connects to the popular research direction of de-biased/de-sparsified inference in high-dimensional models [4, 12, 32–35, 50–52, 61, 71]. This line of research, starting essentially from the seminal work of [71], more or less follows the general prescription laid out in Section 3.1. Similar to our case, these methods also often depend on potentially high-dimensional parameters, thereby requiring sufficiently well-behaved initial estimators. For example, asymptotically valid confidence interval for the coordinates of a sparse linear regression vector relies critically on good initial estimators of the regression vector and nuisance parameter in the form of the precision matrix of the covariates [35, 61, 71]. The construction of a suitable estimating equation is, however, somewhat case-specific and can be involved, depending on the nature of the high-dimensional nuisance parameters. Since SCCA involves several high-dimensional nuisance parameters, including the covariance matrices 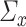 and
and 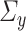 , special attention is required in deriving inferential procedures.
, special attention is required in deriving inferential procedures.
Among the methods mentioned above, our approach bears the greatest resemblance to the method recently espoused by [32] in the context of sparse principal component analysis. However, due to the presence of high-dimensional nuisance parameters  and
and  , the CCA problem is, in general, more challenging than that of PCA [24, 25]. Although the main idea of de-biasing stays the same, our method crucially differs from [32] in two key steps: (a) development of a suitable objective function and (b) construction of preliminary estimators. We elaborate on these two steps below.
, the CCA problem is, in general, more challenging than that of PCA [24, 25]. Although the main idea of de-biasing stays the same, our method crucially differs from [32] in two key steps: (a) development of a suitable objective function and (b) construction of preliminary estimators. We elaborate on these two steps below.
(a) Section 3.1 highlights the significance of selecting an appropriate objective function 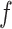 for any de-biasing technique. The objective function used in [32] is based on the well-established fact that the first principal component extraction problem can be expressed as an unconstrained Frobenius norm minimization problem. However, no such analogous representation was previously available in the CCA literature. Therefore, we had to construct such an objective function, described in Lemma 3.1, which serves as the basis for our de-biasing process.
for any de-biasing technique. The objective function used in [32] is based on the well-established fact that the first principal component extraction problem can be expressed as an unconstrained Frobenius norm minimization problem. However, no such analogous representation was previously available in the CCA literature. Therefore, we had to construct such an objective function, described in Lemma 3.1, which serves as the basis for our de-biasing process.
(b) Similar to our approach, [32] applies the de-biasing process to preliminary estimators. However, they solve a penalized version of the non-convex PCA optimization problem, where the search space is limited to a small neighbourhood of a consistent estimator of the first principal component. Any stationary point of their resulting optimization program consistently estimates the first principal component, avoiding the need to find global minima, but the program is non-convex. In contrast, our SCCA method, inspired by [25], obtains preliminary estimators by solving a convex program instead.
Compared with [32]’s PCA case or the linear regression case [35, 61], the presence of high-dimensional nuisance parameters in CCA makes proving the 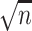 -consistency of the debiased estimators more technically involved. In particular, to prove the
-consistency of the debiased estimators more technically involved. In particular, to prove the 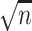 -consistency of the de-biased estimator of
-consistency of the de-biased estimator of 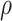 , we needed to introduce sparsity assumptions on the nuisance matrices
, we needed to introduce sparsity assumptions on the nuisance matrices 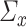 and
and 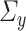 .
.
Another important direction of high-dimensional CCA concerns the proportional regime, i.e. when 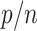 and
and  converge to a constant [3, 47, 68]. In [3], the authors analyse the behaviour of the sample canonical correlation coefficient
converge to a constant [3, 47, 68]. In [3], the authors analyse the behaviour of the sample canonical correlation coefficient  for Gaussian data. They demonstrate that there exists a threshold value
for Gaussian data. They demonstrate that there exists a threshold value  , such that if the population canonical correlation
, such that if the population canonical correlation 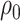 is greater than
is greater than  , then there exists
, then there exists 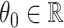 so that
so that  converges weakly to a centred normal distribution whose variance depends on
converges weakly to a centred normal distribution whose variance depends on  ,
,  and
and 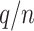 . On the other hand, if
. On the other hand, if  , then
, then  exhibits Tracy–Widom limits and concentrates at the right edge of the Tracy–Widom Law, specifically at
exhibits Tracy–Widom limits and concentrates at the right edge of the Tracy–Widom Law, specifically at  . Subsequent works such as [47] and [68] have relaxed the normality assumptions of the data to fourth- or eighth-moment conditions. However, these studies focus on inferring
. Subsequent works such as [47] and [68] have relaxed the normality assumptions of the data to fourth- or eighth-moment conditions. However, these studies focus on inferring 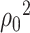 , whereas our paper deals with the inference on coordinates of
, whereas our paper deals with the inference on coordinates of 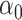 and
and  . Moreover, our analyses are motivated by
. Moreover, our analyses are motivated by  regime in contrast to the proportional asymptotic regimes considered in [3, 47, 68]. Our numerical experiments show that vanilla CCA is well-suited for scenarios with moderate dimensions and high signal-to-noise ratio, but may struggle when dealing with high dimensions without additional regularity assumptions. In contrast, the proposed de-biased CCA method is specifically designed to handle high-dimensional data under sparsity assumptions.
regime in contrast to the proportional asymptotic regimes considered in [3, 47, 68]. Our numerical experiments show that vanilla CCA is well-suited for scenarios with moderate dimensions and high signal-to-noise ratio, but may struggle when dealing with high dimensions without additional regularity assumptions. In contrast, the proposed de-biased CCA method is specifically designed to handle high-dimensional data under sparsity assumptions.
6. On the conditions and assumptions of section 4
In this section, we provide a detailed discussion on assumptions made for the sake of theoretical developments in Section 4.1.
Discussion on Condition 4.1. First, some remarks are in order regarding the range of 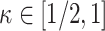 in Condition 4.1. Theorem 3.2 of [25] implies that it is impossible for
in Condition 4.1. Theorem 3.2 of [25] implies that it is impossible for  to be strictly less than
to be strictly less than  since the minimax rate of the
since the minimax rate of the 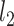 error is roughly
error is roughly 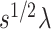 under Assumption 2.1 and Assumption 2.2. If
under Assumption 2.1 and Assumption 2.2. If 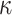 is larger, i.e.
is larger, i.e. 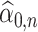 and
and  have slower rates of convergence, we pay a price in terms of the sparsity restriction
have slower rates of convergence, we pay a price in terms of the sparsity restriction 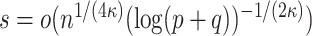 in Assumption 4.1. Supplement B shows that estimators satisfying Condition 4.1 with
in Assumption 4.1. Supplement B shows that estimators satisfying Condition 4.1 with  exist. In fact, most SCCA estimators with theoretical guarantees have an
exist. In fact, most SCCA estimators with theoretical guarantees have an  error guarantee of
error guarantee of  with
with 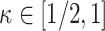 . The interested reader can refer to [19, 24, 25] and references therein. In view of the above, we let
. The interested reader can refer to [19, 24, 25] and references therein. In view of the above, we let 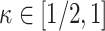 .
.
In light of Condition 4.1,  and
and  with a faster rate of convergence, i.e.
with a faster rate of convergence, i.e. 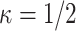 , is preferable. COLAR and [19]’s estimator attain this minimax rate when
, is preferable. COLAR and [19]’s estimator attain this minimax rate when 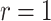 . We do not yet know if there are SCCA estimators which attain the minimax rate for
. We do not yet know if there are SCCA estimators which attain the minimax rate for  while only estimating the first canonical direction. For
while only estimating the first canonical direction. For 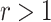 , the estimation problem becomes substantially harder because the remaining
, the estimation problem becomes substantially harder because the remaining 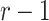 canonical directions start acting as high-dimensional nuisance parameters. A trade-off between computational and estimation efficiency likely arises in the presence of these additional nuisance parameters. In particular, it is plausible that the minimax rate of
canonical directions start acting as high-dimensional nuisance parameters. A trade-off between computational and estimation efficiency likely arises in the presence of these additional nuisance parameters. In particular, it is plausible that the minimax rate of  may not be achievable by polynomial-time algorithms in this case. To gather intuition about this, it is instructive to look at the literature on estimating the first principal component direction in high dimensions under sparsity. In this case, to the best of our knowledge, polynomial-time algorithms attain the minimax rate only in the single spike model or a slightly relaxed version of the latter. We refer the interested reader to [64] for more details. The algorithms that do succeed in estimating the first principal component under multiple spikes at the desired minimax rate attempt to solve the underlying non-convex problem, and hence are not immediately clear to be polynomial-time [32, 46, 70]. In this case, [70] and [46]’s methods essentially reduce to power methods that induce sparsity by iterative thresholding. [19]’s method tries to borrow this idea in the context of SCCA in the rank one case; see Remark B.2 for a discussion on the problems that their method may face in the presence of nuisance canonical directions.
may not be achievable by polynomial-time algorithms in this case. To gather intuition about this, it is instructive to look at the literature on estimating the first principal component direction in high dimensions under sparsity. In this case, to the best of our knowledge, polynomial-time algorithms attain the minimax rate only in the single spike model or a slightly relaxed version of the latter. We refer the interested reader to [64] for more details. The algorithms that do succeed in estimating the first principal component under multiple spikes at the desired minimax rate attempt to solve the underlying non-convex problem, and hence are not immediately clear to be polynomial-time [32, 46, 70]. In this case, [70] and [46]’s methods essentially reduce to power methods that induce sparsity by iterative thresholding. [19]’s method tries to borrow this idea in the context of SCCA in the rank one case; see Remark B.2 for a discussion on the problems that their method may face in the presence of nuisance canonical directions.
Finally for the inferential question, it is natural to consider an extension of ideas from sparse PCA as developed in [32]. When translated to SCCA, their approach will aim to solve
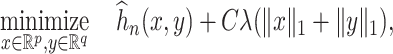 |
(6.1) |
where  is a constant, and
is a constant, and
 |
We conjecture that for a suitably chosen  , the resulting estimators will satisfy Condition 4.1 with
, the resulting estimators will satisfy Condition 4.1 with  . However, (6.1) is non-convex and solving (6.1) is computationally challenging for large
. However, (6.1) is non-convex and solving (6.1) is computationally challenging for large  and
and  . Analogous to [32], one can simplify the problem by searching for any stationary point of (6.1) over a smaller feasible set, namely a small neighbourhood of a consistent preliminary estimator of
. Analogous to [32], one can simplify the problem by searching for any stationary point of (6.1) over a smaller feasible set, namely a small neighbourhood of a consistent preliminary estimator of  and
and  . However, while this first stage does guarantee good initialization, the underlying optimization problem still remains non-convex. Since the aim of the paper is efficient inference of
. However, while this first stage does guarantee good initialization, the underlying optimization problem still remains non-convex. Since the aim of the paper is efficient inference of  and
and  with theoretically guaranteed computational efficiency, we remain with the modified COLAR estimators and refrain from exploring the route mentioned above.
with theoretically guaranteed computational efficiency, we remain with the modified COLAR estimators and refrain from exploring the route mentioned above.
Discussion on Assumption 4.1: It is natural to wonder whether the condition 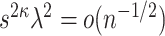 is at all necessary, especially since it is much stricter than
is at all necessary, especially since it is much stricter than 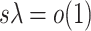 , which is sufficient for the
, which is sufficient for the  consistency of
consistency of  and
and  presented in Theorem B.1 of Supplement B. However, current literature on inference in high-dimensional sparse models bears evidence that the restriction
presented in Theorem B.1 of Supplement B. However, current literature on inference in high-dimensional sparse models bears evidence that the restriction  might be unavoidable. In fact, this sparsity requirement is a staple in most de-biasing approaches whose preliminary estimators are minimax optimal, including sparse PCA [32] and sparse generalized linear models [35, 61]. Indeed, in case of sparse linear regression, [12] shows that this sparsity is necessary for adaptive inference. We believe similar results hold for our case as well. However, further inquiry in that direction is beyond the scope of this paper.
might be unavoidable. In fact, this sparsity requirement is a staple in most de-biasing approaches whose preliminary estimators are minimax optimal, including sparse PCA [32] and sparse generalized linear models [35, 61]. Indeed, in case of sparse linear regression, [12] shows that this sparsity is necessary for adaptive inference. We believe similar results hold for our case as well. However, further inquiry in that direction is beyond the scope of this paper.
It is also natural to ask why Assumption 4.1 involves sparsity restrictions not only on  and
and 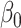 , but also on the other columns of
, but also on the other columns of  and
and  . This restriction stems from the initial estimation procedure of
. This restriction stems from the initial estimation procedure of 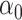 and
and  . Although we estimate only the first pair of canonical directions, the remaining canonical directions act as nuisance parameters. Thus, to efficiently estimate
. Although we estimate only the first pair of canonical directions, the remaining canonical directions act as nuisance parameters. Thus, to efficiently estimate 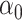 and
and  , we need to separate the other covariates from
, we need to separate the other covariates from 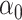 and
and 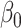 . Therefore, we need to estimate the other covariates’ effect efficiently enough. Consequently, we require some regularity assumptions on these nuisance parameters as precisely quantified by Assumption 4.1.
. Therefore, we need to estimate the other covariates’ effect efficiently enough. Consequently, we require some regularity assumptions on these nuisance parameters as precisely quantified by Assumption 4.1.
Discussion on Condition 4.2: This is a standard assumption in de-biasing literature with similar assumptions appearing in the sparse PCA [32] and sparse generalized linear models literature [61]—both of whom use the nodewise lasso algorithm to construct 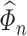 . We remark in passing that [35]’s construction of the de-biased lasso does not require the analog of
. We remark in passing that [35]’s construction of the de-biased lasso does not require the analog of 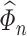 , which is the precision matrix estimator in their case, to satisfy any condition like Condition 4.2. Instead, it requires the
, which is the precision matrix estimator in their case, to satisfy any condition like Condition 4.2. Instead, it requires the  ’s to be small. It is unknown whether such constructions work in the more complicated scenario of CCA or PCA.
’s to be small. It is unknown whether such constructions work in the more complicated scenario of CCA or PCA.
7. Numerical experiments
7.1 Preliminaries
In this section, we explore aspects of finite sample behaviour of the methods discussed in earlier sections. Further numerical experiments are collected in Supplement A where we compare the bias of our method with popular SCCA alternatives. We start with some preliminary discussions on the choice for the set-up, initial estimators and tuning parameters.
Set-up: The set-up, under which we will conduct our comparisons, can be described by specifying the nuisance parameters (marginal covariance matrices of 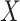 and
and  ) along with the strength (
) along with the strength (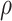 ), sparsity, rank and the joint distribution of
), sparsity, rank and the joint distribution of  . For the marginal covariance matrices of
. For the marginal covariance matrices of 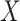 and
and 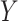 , motivated by previously studied cases in the literature [25, 49] we shall consider two cases as follows:
, motivated by previously studied cases in the literature [25, 49] we shall consider two cases as follows:
Identity. This will correspond to the case where
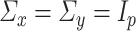
- Sparse-inverse.This will correspond to the case where
 is the correlation matrix obtained from
is the correlation matrix obtained from  , where
, where 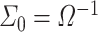 , and
, and  is a sparse matrix with the form
is a sparse matrix with the form
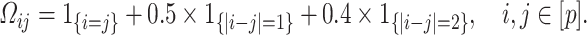
Analogous to [49] and [25], we shall also take  to be a rank one matrix, where we consider the canonical vectors
to be a rank one matrix, where we consider the canonical vectors 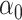 and
and  with sparsity
with sparsity  as follows:
as follows:
 |
The canonical correlation 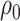 depicts the signal strength in our set-up. We will explore three different values for
depicts the signal strength in our set-up. We will explore three different values for  : 0.2, 0.5 and 0.9, which will be referred to as the small, medium and high signal strength settings, respectively. The joint distribution of
: 0.2, 0.5 and 0.9, which will be referred to as the small, medium and high signal strength settings, respectively. The joint distribution of 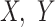 is finally taken to be Gaussian with mean
is finally taken to be Gaussian with mean  . Also, throughout we set the
. Also, throughout we set the  combination to be
combination to be  ,
, 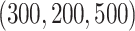 and
and 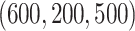 , which correspond to
, which correspond to 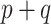 being small, moderate and moderately high, respectively. Finally, we will always consider
being small, moderate and moderately high, respectively. Finally, we will always consider 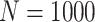 Monte Carlo samples.
Monte Carlo samples.
Initial Estimators and Tuning Parameters: We construct the preliminary estimators using the modified COLAR algorithm (see Algorithm 1). For the rank one case, the latter coincides with [25]’s COLAR estimator. Recall that throughout we set the  combination to be
combination to be 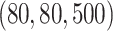 ,
,  and
and  . One of the reasons we do not accommodate higher
. One of the reasons we do not accommodate higher  and
and  is that the COLAR algorithm does not scale well with
is that the COLAR algorithm does not scale well with  and
and  (This was also noticed by 49]. Also, we do not consider smaller values of
(This was also noticed by 49]. Also, we do not consider smaller values of  since it is expected that de-biasing procedures generally require
since it is expected that de-biasing procedures generally require  to be at least moderately large [32, cf.].
to be at least moderately large [32, cf.].
In our proposed methods, tuning parameters arise from two sources: (a) estimation of the preliminary estimators and (b) precision matrix estimation. To implement the modified COLAR algorithm, we mostly follow the code for COLAR provided by the authors [25]. The COLAR penalty parameters,  and
and  , were left as specified in the COLAR code, namely
, were left as specified in the COLAR code, namely  and
and 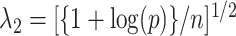 . The tolerance level was fixed at
. The tolerance level was fixed at  with a fixed maximum of 200 iterations for the first step of the COLAR algorithm. Next, consider the tuning strategy for the nodewise lasso algorithm (Algorithm 2), which involves the lasso penalty parameter
with a fixed maximum of 200 iterations for the first step of the COLAR algorithm. Next, consider the tuning strategy for the nodewise lasso algorithm (Algorithm 2), which involves the lasso penalty parameter  and the parameter
and the parameter 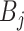 (
(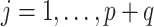 ). Theorem C.1 proposes the choice
). Theorem C.1 proposes the choice 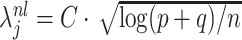 for all
for all 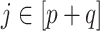 . In our simulations, the parameter
. In our simulations, the parameter  is empirically determined to minimize
is empirically determined to minimize  . For the settings
. For the settings  and
and  , this parameter is set at
, this parameter is set at  and
and  for the identity and sparse inverse cases, respectively. For the moderately high
for the identity and sparse inverse cases, respectively. For the moderately high 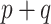 setting, this parameter is set at
setting, this parameter is set at  . The nodewise lasso parameter
. The nodewise lasso parameter 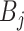 is taken to be
is taken to be 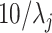 , which is in line with [32], who recommends taking
, which is in line with [32], who recommends taking 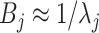 .
.
Targets of Inference: We present our results for the first and the 20th element of  . The former stands for a typical non-zero element, where the latter represents a typical zero element. For each element, we compute confidence intervals for
. The former stands for a typical non-zero element, where the latter represents a typical zero element. For each element, we compute confidence intervals for 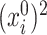 , and test the null
, and test the null 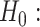

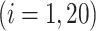 . For the latter, we use a
. For the latter, we use a  -squared test based on the asymptotic null distribution of
-squared test based on the asymptotic null distribution of 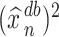 given in part two of Corollary 1. As mentioned earlier, this test is equivalent to testing
given in part two of Corollary 1. As mentioned earlier, this test is equivalent to testing 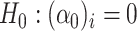 . The construction of the confidence intervals, which we discuss next, is a little more subtle.
. The construction of the confidence intervals, which we discuss next, is a little more subtle.
We construct two types of confidence interval. For any  , the first confidence interval, which will be referred as the ordinary interval from now on, is given by
, the first confidence interval, which will be referred as the ordinary interval from now on, is given by
 |
(7.1) |
Here,  is the
is the  quantile of the standard Gaussian distribution. Corollary 1 shows that the asymptotic coverage of the above confidence interval is
quantile of the standard Gaussian distribution. Corollary 1 shows that the asymptotic coverage of the above confidence interval is  when
when 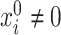 . For
. For 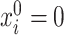 , however, the above confidence interval can have asymptotic coverage higher than
, however, the above confidence interval can have asymptotic coverage higher than 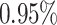 . To see why, note that
. To see why, note that 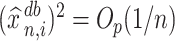 by Corollary 1 in this case. Since both the length and the centre of the ordinary interval depend on
by Corollary 1 in this case. Since both the length and the centre of the ordinary interval depend on  , the coverage can suffer greatly if
, the coverage can suffer greatly if  underestimates
underestimates  . Therefore, we construct another confidence interval by relaxing the length of the ordinary intervals. This second interval, to be referred to as the conservative interval from now on, is obtained by simply substituting the
. Therefore, we construct another confidence interval by relaxing the length of the ordinary intervals. This second interval, to be referred to as the conservative interval from now on, is obtained by simply substituting the  in the standard deviation term
in the standard deviation term  in (7.1) by
in (7.1) by  . Clearly, the conservative interval can have potentially higher coverage than
. Clearly, the conservative interval can have potentially higher coverage than 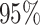 , which motivates our nomenclature.
, which motivates our nomenclature.
Comparator: We compare our de-biasing procedure with the vanilla CCA analysis. In this case, we can do inference directly on 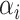 ’s and we do not need to scale them by
’s and we do not need to scale them by 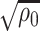 . To derive the confidence intervals of the
. To derive the confidence intervals of the 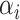 ’s using the vanilla canonical CCA, we employed the formula for the finite
’s using the vanilla canonical CCA, we employed the formula for the finite 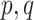 case with
case with 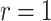 provided by [1]. As usual, we use 1000 Monte Carlo samples. The formula depends on
provided by [1]. As usual, we use 1000 Monte Carlo samples. The formula depends on  ,
,  , and
, and  . We estimated
. We estimated 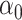 and
and  using the vanilla CCA estimators as presented in [1]. However, we observed that the vanilla CCA estimator for
using the vanilla CCA estimators as presented in [1]. However, we observed that the vanilla CCA estimator for 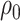 performed poorly as the signal strength increased, which is unsurprising because this estimator is known to be inconsistent in the high-dimensional case [3, 47, 68]. Therefore, we utilized the estimator proposed by [3] for estimating
performed poorly as the signal strength increased, which is unsurprising because this estimator is known to be inconsistent in the high-dimensional case [3, 47, 68]. Therefore, we utilized the estimator proposed by [3] for estimating  . It’s worth noting that [3]’s estimator is known to be consistent in the asymptotic regime [3, 68]. Since vanilla CCA does not run when
. It’s worth noting that [3]’s estimator is known to be consistent in the asymptotic regime [3, 68]. Since vanilla CCA does not run when 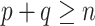 , we could produce the aforementioned confidence intervals only in the
, we could produce the aforementioned confidence intervals only in the  setting. We collect the numerical results in Fig. 1.
setting. We collect the numerical results in Fig. 1.
Fig. 1.

Confidence intervals obtained by the vanilla (ordinary) CCA for the first 100 replications. The rejection probability and the coverage are calculated based on all 1000 replications. Here,  ,
,  and
and 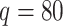 . The left column corresponds to
. The left column corresponds to  , which is non-zero, and the right column corresponds to
, which is non-zero, and the right column corresponds to  , which is zero. The top row corresponds to
, which is zero. The top row corresponds to  and
and  being the identity covariance matrix, and the bottom corresponds to them being the sparse inverse matrix.
being the identity covariance matrix, and the bottom corresponds to them being the sparse inverse matrix.
7.2 Results
We divide the presentation of our results on coordinates with and without signal, followed by discussions about issues regarding distinctions between asymptotic and finite sample considerations of our method.
Inference when there is no signal: If  , both confidence intervals (CI) exhibit high coverage, often exceeding
, both confidence intervals (CI) exhibit high coverage, often exceeding  , across all settings; see Figures M.1 and M.2 in Supplement M.1. This is unsurprising in view of the discussion in the previous paragraph. Also, Fig. 1 implies that in the no signal case, the performance of the de-biased CCA confidence intervals are significantly better than those based on vanilla CCA. The conservative confidence intervals have substantially larger lengths, which is understandable because the ratio between the ordinary and the conservative CI length is
, across all settings; see Figures M.1 and M.2 in Supplement M.1. This is unsurprising in view of the discussion in the previous paragraph. Also, Fig. 1 implies that in the no signal case, the performance of the de-biased CCA confidence intervals are significantly better than those based on vanilla CCA. The conservative confidence intervals have substantially larger lengths, which is understandable because the ratio between the ordinary and the conservative CI length is  in this case. Also, the length of the confidence intervals generally decreases as the signal strength increases, as expected. The rejection frequency of the tests (the type I error in this scenario) generally stays below
in this case. Also, the length of the confidence intervals generally decreases as the signal strength increases, as expected. The rejection frequency of the tests (the type I error in this scenario) generally stays below  , especially at medium to high signal strength.
, especially at medium to high signal strength.
Inference when there is signal: When 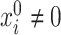 , the ordinary intervals exhibit poor coverage at the low and medium signal strength regardless of the underlying covariance matrix structure, although the performance seems worse for sparse inverse matrices. Figure 2 entails that this underperformance is due to the underestimation of small signals
, the ordinary intervals exhibit poor coverage at the low and medium signal strength regardless of the underlying covariance matrix structure, although the performance seems worse for sparse inverse matrices. Figure 2 entails that this underperformance is due to the underestimation of small signals  , which is tied to the high negative bias of the preliminary estimator in these cases; see the histograms in Fig. M.3 in Supplement M.1. This issue will be discussed in more detail in Supplement A. Figure 2 also implies that if
, which is tied to the high negative bias of the preliminary estimator in these cases; see the histograms in Fig. M.3 in Supplement M.1. This issue will be discussed in more detail in Supplement A. Figure 2 also implies that if 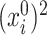 is small, the confidence intervals crowd near the origin. Also, at the high signal strength, the coverage of the ordinary intervals fails to reach the desired
is small, the confidence intervals crowd near the origin. Also, at the high signal strength, the coverage of the ordinary intervals fails to reach the desired  level. Figure 1 demonstrates that when the signal-to-noise ratio is high, vanilla CCA achieves comparable performance with our method. However, as the signal strength becomes moderate (
level. Figure 1 demonstrates that when the signal-to-noise ratio is high, vanilla CCA achieves comparable performance with our method. However, as the signal strength becomes moderate ( ), vanilla CCA’s performance is outperformed by de-biased CCA, and in the low signal-to-noise ratio regime, vanilla CCA performs equally poorly as de-biased CCA. These results highlight the limitations of vanilla CCA in scenarios with moderate to low signal strength.
), vanilla CCA’s performance is outperformed by de-biased CCA, and in the low signal-to-noise ratio regime, vanilla CCA performs equally poorly as de-biased CCA. These results highlight the limitations of vanilla CCA in scenarios with moderate to low signal strength.
Fig. 2.

Ordinary confidence intervals for 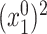 .
.
The relaxation of the ordinary confidence interval length, which leads to the conservative intervals, substantially improves the coverage, with the improvement being dramatic at a low signal. In the latter case, the conservative intervals enjoy high coverage, which is well over  for moderate or higher
for moderate or higher 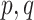 . In this case, the relaxation generally results in a four-fold or higher increase in the confidence interval length. As signal strength increases, the increase in the confidence interval length gets smaller, and consequently, the increase in the coverage slows down. This is unsurprising, noting the ratio between the length of the conservative and the ordinary interval is proportional to
. In this case, the relaxation generally results in a four-fold or higher increase in the confidence interval length. As signal strength increases, the increase in the confidence interval length gets smaller, and consequently, the increase in the coverage slows down. This is unsurprising, noting the ratio between the length of the conservative and the ordinary interval is proportional to  . One should be cautious with the relaxation, however, because it may lead to the inclusion of not only the true signal, as desired, but also zero. This can be clearly seen in the medium signal strength case of the sparse inverse matrix; compare the middle column of Fig. 2(b) with that of Fig. 3(b). The inclusion of origin does not bring any advantage for the relaxed intervals in the no-signal case either, because, as discussed earlier, in the latter case, the ordinary intervals are themselves efficient, with the relaxed versions hardly making any improvements.
. One should be cautious with the relaxation, however, because it may lead to the inclusion of not only the true signal, as desired, but also zero. This can be clearly seen in the medium signal strength case of the sparse inverse matrix; compare the middle column of Fig. 2(b) with that of Fig. 3(b). The inclusion of origin does not bring any advantage for the relaxed intervals in the no-signal case either, because, as discussed earlier, in the latter case, the ordinary intervals are themselves efficient, with the relaxed versions hardly making any improvements.
Fig. 3.

Conservative confidence intervals for 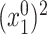 .
.
Discussion on Asymptotics: The performance of the confidence intervals improve if 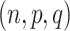 increase. See, for example, the illustration in Fig. M.4 in Supplement M.1 where the triplet has been doubled. Interestingly, the asymptotics successfully kick in for the corresponding tests as soon as the signal strength reaches the medium level. The test attains power higher than
increase. See, for example, the illustration in Fig. M.4 in Supplement M.1 where the triplet has been doubled. Interestingly, the asymptotics successfully kick in for the corresponding tests as soon as the signal strength reaches the medium level. The test attains power higher than  at the medium signal strength, and the perfect power of one at high signal strength. This phenomenon is the result of the super-efficiency of the de-biased estimator at
at the medium signal strength, and the perfect power of one at high signal strength. This phenomenon is the result of the super-efficiency of the de-biased estimator at 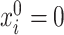 , as expounded upon by Corollary 1. Since the test exploits the knowledge of this faster convergence under the null hypothesis, it has better precision than the confidence interval, which is oblivious to this fact. The test may get rejected in many situations, but the confidence intervals, even the ordinary one, may include zero. During implementation, if one faces such a situation, they should conclude that either the signal strength is too small or the sample size is insufficient for the confidence intervals to be very precise.
, as expounded upon by Corollary 1. Since the test exploits the knowledge of this faster convergence under the null hypothesis, it has better precision than the confidence interval, which is oblivious to this fact. The test may get rejected in many situations, but the confidence intervals, even the ordinary one, may include zero. During implementation, if one faces such a situation, they should conclude that either the signal strength is too small or the sample size is insufficient for the confidence intervals to be very precise.
Discussions on Performance of De-biased SCCA: We conclude that since the de-biased estimators work on sparse estimators which are super efficient at zero, the inference does not face any obstacle if the true signal 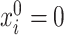 . In the presence of a signal, the tests are generally reliable if the signal strength is at least moderate. In contrast, the ordinary confidence intervals, which are blindly based on Corollary 1, struggle whenever the initial COLAR estimators incur a bias too large for the de-biasing step to overcome. This is generally observed at low to medium signal strength. The conservative intervals can solve this problem partially at the cost of increased length. At present, the
. In the presence of a signal, the tests are generally reliable if the signal strength is at least moderate. In contrast, the ordinary confidence intervals, which are blindly based on Corollary 1, struggle whenever the initial COLAR estimators incur a bias too large for the de-biasing step to overcome. This is generally observed at low to medium signal strength. The conservative intervals can solve this problem partially at the cost of increased length. At present, the  and
and  guarantees as required by Condition 4.1 are only available for COLAR type estimators. The performance of the ordinary confidence intervals may improve if one can construct an SCCA preliminary estimator with similar strong theoretical guarantees but better empirical performance in picking up small signals. Searching for a different SCCA preliminary estimator is important for another reason—COLAR is not scalable to ultra-high dimensions. This problem occurs because COLAR relies on semidefinite programming, whose scalability issues are well noted [22].
guarantees as required by Condition 4.1 are only available for COLAR type estimators. The performance of the ordinary confidence intervals may improve if one can construct an SCCA preliminary estimator with similar strong theoretical guarantees but better empirical performance in picking up small signals. Searching for a different SCCA preliminary estimator is important for another reason—COLAR is not scalable to ultra-high dimensions. This problem occurs because COLAR relies on semidefinite programming, whose scalability issues are well noted [22].
8. Real data application
Physiological functions in human bodies are controlled by complex pathways, whose deregulation can lead to various diseases. Therefore, it is important to understand the interaction between different factors participating in these biological pathways, such as proteins, genes, etc. We consider two important pathways: (a) Cytokine-cytokine receptor interaction pathway and (b) Adipocytokine signaling pathway. Cytokines are released in response to inflammation in the body, and pathway (a) is thus related to viral infection, cell growth, differentiation, and cancer progression [40]. Pathway (b) is involved in fat metabolism and insulin resistance, thus playing a vital role in diabetes [54]. We wish to study the linear association between the genes and proteins involved in these pathways. To that end, we use the microarray and proteomic datasets analysed by [41], which are originally from the National Cancer Institute, and available at http://discover.nci.nih.gov/cellminer/.
The dataset contains 60 human cancer cell lines. We use  of the sixty observations because one has missing microarray information. Although the microarray data have information on many genes, we considered only those involved in pathways (a) and (b), giving
of the sixty observations because one has missing microarray information. Although the microarray data have information on many genes, we considered only those involved in pathways (a) and (b), giving  and
and  miRNAs, respectively. To this end, we use genscript.com (https://www.genscript.com/) to get the list of genes involved in these pathways. The dataset contains
miRNAs, respectively. To this end, we use genscript.com (https://www.genscript.com/) to get the list of genes involved in these pathways. The dataset contains 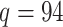 proteins. We center and scale all variables prior to our analysis. If one gene or protein had more than one measurement, we averaged across all the measurements.
proteins. We center and scale all variables prior to our analysis. If one gene or protein had more than one measurement, we averaged across all the measurements.
It is well known that certain biological pathways involve only a small number of interacting genes and proteins, which justifies the possibility of 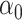 and
and 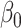 being low-dimensional [41]. Additionally, Fig. M.7 in Supplement M.2 shows that the majority of genes and proteins exhibit negligible correlation, further supporting this biological fact. On the other hand, Fig. M.8 in Supplement M.2 hints at the existence of low dimensional structures in the variance matrices of both the genes and the proteins, which is required for the consistency of our nodewise lasso estimator. However, it seems unlikely that they are totally uncorrelated among themselves, which questions the applicability of popular methods only suited for diagonal variance matrices, e.g. PMA [66].
being low-dimensional [41]. Additionally, Fig. M.7 in Supplement M.2 shows that the majority of genes and proteins exhibit negligible correlation, further supporting this biological fact. On the other hand, Fig. M.8 in Supplement M.2 hints at the existence of low dimensional structures in the variance matrices of both the genes and the proteins, which is required for the consistency of our nodewise lasso estimator. However, it seems unlikely that they are totally uncorrelated among themselves, which questions the applicability of popular methods only suited for diagonal variance matrices, e.g. PMA [66].
Apart from the de-biased estimators, we also look into the SCCA estimates of the leading canonical covariates using [49], [25], [66] and [65]’s methods. The first three methods were implemented as discussed in Supplement A. To apply [65]’s methods, we used the code provided by the authors with the default choice of tuning parameters. Among these methods, only [66]’s method requires  and
and  to be diagonal. For these methods, we say a gene or protein is ‘detected’ if the corresponding loading, i.e. the estimated
to be diagonal. For these methods, we say a gene or protein is ‘detected’ if the corresponding loading, i.e. the estimated  or
or 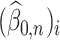 , is non-zero.
, is non-zero.
We construct confidence intervals, both ordinary and conservative, and test the null hypothesis that 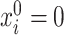 or
or 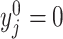 for each
for each  and
and  , as discussed in Section 7. We apply the false discovery rate corrections of Benjamini and Hochberg (BH) as well as Benjamini and Yekutieli (BY), the latter of which does not assume independent p-values. Table 1 tabulates the number of detections by the above-mentioned methods. Even after false discovery rate adjustment, most discoveries seem to include zero in the confidence intervals. We discussed this situation in Section 7, where it was indicated that the former can occur if the signal strength is small or the sample size is insufficient. To be conservative, we consider only those genes and proteins whose ordinary interval excludes zero. These discoveries are reported in Tables 2 and 3 along with the confidence intervals. The pictorial representation of the confidence intervals can be found in Fig. M.9 and Fig. M.10 in Supplement M.2.
, as discussed in Section 7. We apply the false discovery rate corrections of Benjamini and Hochberg (BH) as well as Benjamini and Yekutieli (BY), the latter of which does not assume independent p-values. Table 1 tabulates the number of detections by the above-mentioned methods. Even after false discovery rate adjustment, most discoveries seem to include zero in the confidence intervals. We discussed this situation in Section 7, where it was indicated that the former can occur if the signal strength is small or the sample size is insufficient. To be conservative, we consider only those genes and proteins whose ordinary interval excludes zero. These discoveries are reported in Tables 2 and 3 along with the confidence intervals. The pictorial representation of the confidence intervals can be found in Fig. M.9 and Fig. M.10 in Supplement M.2.
Table 1.
Number of detections: number of non-zero loadings in different SCCA estimators and number of detections by our tests (DB) after BH and BY false discovery rate correction. For the SCCA estimators, size of their intersection with DB+BY are given in parentheses
| Variable | Mai and Zhang | Wilms and Croux | Gao et al. | Witten et al. | DB+BH | DB+BY |
|---|---|---|---|---|---|---|
| Pathway (a) | ||||||
| Genes | 2 (2) | 1 (1) | 3 (3) | 41 (5) | 13 | 6 |
| Proteins | 4 (3) | 1 (1) | 7 (5) | 13 (5) | 36 | 22 |
| Pathway (b) | ||||||
| Genes | 2 (1) | 1 (1) | 4 (3) | 11 (2) | 8 | 5 |
| Proteins | 7 (1) | 1 (1) | 9 (1) | 12 (1) | 22 | 2 |
Table 2.
Discovered genes and protein from pathway (a). The confidence intervals are obtained using the methods described in Section 7. The P-values are the original P-values before false discovery rate correction. All genes and proteins were also detected by Benjamini and Yekutieli method
| Gene | P-value | 95% CI | Relaxed CI | Discovered by |
|---|---|---|---|---|
| CLCF1 | 2.0E-07 | (0.055, 0.39) | (0, 0.58) | Witten et al. |
| EGFR | 8.8E-09 | (0.11, 0.58) | (0,0.74) | Mai and Zhang, Witten et al., |
| Gao et al. | ||||
| LIF | 1.6E-05 | (0.022, 0.45) | (0, 0.68) | Witten et al., Gao et al. |
| PDGFC | 1.4E-07 | (0.094, 0.64) | (0, 0.82) | Witten et al. |
| TNFRSF12A | 7.8E-11 | (0.15, 0.60) | (0.01, 0.75) | Mai and Zhang, Witten et al., |
| Gao et al., Wilms and Croux | ||||
| Protein | P-value | 95% CI | Relaxed CI | Discovered by |
| ANXA2 | 1.3E-15 | (0.13, 0.38) | (0.01, 0.51) | Mai and Zhang, Witten et al., |
| Gao et al., Wilms and Croux | ||||
| CDH2 | 5.1E-09 | (0.22, 1.1) | (0.12, 1.23) | Mai and Zhang, Witten et al., |
| Gao et al. | ||||
| FN1 | 4.2E-07 | (0.96, 7.6) | (0.96, 7.6) | none |
| GTF2B | 6.7E-05 | (0.034, 4.0) | (0.034, 4.0) | none |
| KRT20 | 1.2E-05 | (0.015, 0.27) | (0, 0.48) | none |
| MVP | 2.6E-05 | (0.021, 0.59) | (0, 0.82) | Witten et al. |
Table 3.
Discovered genes and protein from pathway (b). The confidence intervals are obtained using the methods described in Section 7. The P-values are the original P-values before false discovery rate correction. The displayed genes and proteins were also detected by Benjamini and Yekutieli method
| Gene | P-value | 95% CI | Relaxed CI | Discovered by |
|---|---|---|---|---|
| ACSL5 | 2.9E-05 | (0.014, 0.45) | (0, 0.68) | none |
| RXRG | 4.1E-10 | (0.073, 0.32) | (0, 0.47) | Wilms and Croux, Gao et al., |
| Mai and Zhang | ||||
| TNFRSF1B | 1.1E-09 | (0.49, 2.2) | (0.49, 2.2) | none |
| Protein | P-value | 95% CI | Relaxed CI | Discovered by |
| ANXA2 | 2.7E-74 | (1.1, 1.7) | (1.1, 1.7) | none |
Using the Gene Ontology toolkit available at http://geneontology.org/, we observe that our discovered genes from pathway (a) are mainly involved in biological processes like positive regulation of gliogenesis and molecular function like growth factor activity, where the selected proteins play a role in regulating membrane assembly, enzyme function, and other cellular functions. The Gene Ontology toolkit also suggests that the discovered genes from pathway (b) are involved in positive regulation of cellular processes and molecular function like growth factor activity. The only discovered protein in pathway (b) is ANXA2, which, according to UNIPORT at https://www.uniport.org, is a membrane-binding protein involved in RNA binding and host-virus infection.
Supplementary Material
Contributor Information
Nilanjana Laha, Department of Statistics, Texas A&M, College Station, TX 77843, USA.
Nathan Huey, Department of Biostatistics, Harvard T. H. Chan School of Public Health, Boston, MA 02115, USA.
Brent Coull, Department of Biostatistics, Harvard T. H. Chan School of Public Health, Boston, MA 02115, USA.
Rajarshi Mukherjee, Department of Biostatistics, Harvard T. H. Chan School of Public Health, Boston, MA 02115, USA.
Funding
The research of Rajarshi Mukherjee is partially supported by National Institutes of Health grant P42ES030990. The work of Nilanjana Laha is partially supported by National Science Foundation grant DMS 2311098. The research of Brent Coull is supported by National Institute of Health Grants ES000002 and ES030990.
Data availability statement
No new data were generated or analysed in support of this review.
References
- 1. Anderson, T. (2003) An Introduction to Multivariate Statistical Analysis Wiley Series in Probability and Statistics.Wiley. [Google Scholar]
- 2. Bai, Z. D. (2008) Methodologies in spectral analysis of large dimensional random matrices, a review. Advances in statistics. World Scientific, pp. 174–240. [Google Scholar]
- 3. Bao, Z., Hu, J., Pan, G. & Zhou, W. (2019) Canonical correlation coefficients of high-dimensional gaussian vectors: finite rank case. Ann. Stat., 47, 612–640. [Google Scholar]
- 4. Bellec, P. C. & Zhang, C.-H. (2019) De-biasing the lasso with degrees-of-freedom adjustment. arXiv preprint arXiv:1902.08885.
- 5. Bickel, P. J. & Levina, E. (2008) Covariance regularization by thresholding. Ann. Stat., 36, 2577–2604. [Google Scholar]
- 6. Boyd, S., Boyd, S. P. & Vandenberghe, L. (2004) Convex optimization. Cambridge university press. [Google Scholar]
- 7. Bühlmann, P. & Van De Geer, S. (2011) Statistics for high-dimensional data: methods, theory and applications. Springer Science & Business Media. [Google Scholar]
- 8. Cai, T. & Liu, W. (2011) Adaptive thresholding for sparse covariance matrix estimation. J. Am. Stat. Assoc., 106, 672–684. [Google Scholar]
-
9.
Cai, T. T. & Zhou, H. H. (2012a) Minimax estimation of large covariance matrices under
 -norm. Stat. Sin., 1319–1349. [Google Scholar]
-norm. Stat. Sin., 1319–1349. [Google Scholar] - 10. Cai, T. T. & Zhou, H. H. (2012b) Optimal rates of convergence for sparse covariance matrix estimation. Ann. Stat., 40, 2389–2420. [Google Scholar]
- 11. Cai, T. T., Ren, Z. & Zhou, H. H. (2013) Optimal rates of convergence for estimating toeplitz covariance matrices. Probab. Theory Relat. Fields, 156, 101–143. [Google Scholar]
- 12. Cai, T. T., Guo, Z., et al. (2017) Confidence intervals for high-dimensional linear regression: minimax rates and adaptivity. Ann. Stat., 45, 615–626. [Google Scholar]
- 13. Cai, T. T., Zhang, A., et al. (2018) Rate-optimal perturbation bounds for singular subspaces with applications to high-dimensional statistics. Ann. Stat., 46, 60–89. [Google Scholar]
- 14. Carpentier, A. & Verzelen, N. (2019) Adaptive estimation of the sparsity in the gaussian vector model. Ann. Stat., 47, 93–126. [Google Scholar]
- 15. Carvalho, C. M., Chang, J., Lucas, J. E., Nevins, J. R. & Wang, Q. (2010) Dissecting high-dimensional phenotypes with bayesian sparse factor analysis of genetic covariance matrices. Bioinformatics, 26, 2680–2688. [Google Scholar]
- 16. Chatterjee, A. & Lahiri, S. (2010) Asymptotic properties of the residual bootstrap for lasso estimators. Proc. Am. Math. Soc., 138, 4497–4509. [Google Scholar]
- 17. Chatterjee, A. & Lahiri, S. N. (2011) Bootstrapping lasso estimators. J. Am. Stat. Assoc., 106, 608–625. [Google Scholar]
- 18. Chatterjee, A. & Lahiri, S. N. (2013) Rates of convergence of the adaptive lasso estimators to the oracle distribution and higher order refinements by the bootstrap. Ann. Stat., 41, 1232–1259. [Google Scholar]
- 19. Chen, M., Gao, C., Ren, Z. & Zhou, H. H. (2013) Sparse cca via precision adjusted iterative thresholding. arXiv preprint arXiv:1311.6186.
- 20. Chen, X., Han, L. & Carbonell, J. (2012) Structured sparse canonical correlation analysis. Artificial intelligence and statistics. PMLR, pp. 199–207. [Google Scholar]
- 21. Chernozhukov, V., Chetverikov, D. & Kato, K. (2017) Central limit theorems and bootstrap in high dimensions. Ann. Probab., 45, 2309–2352. [Google Scholar]
- 22. Dey, S. S., Mazumder, R. & Wang, G. (2018) A convex integer programming approach for optimal sparse pca. arXiv preprint arXiv:1810.09062.
- 23. Eckart, C. & Young, G. (1936) The approximation of one matrix by another of lower rank. Psychometrika, 1, 211–218. [Google Scholar]
- 24. Gao, C., Ma, Z., Ren, Z. & Zhou, H. H. (2015) Minimax estimation in sparse canonical correlation analysis. Ann. Stat., 43, 2168–2197. [Google Scholar]
- 25. Gao, C., Ma, Z. & Zhou, H. H. (2017) Sparse cca: adaptive estimation and computational barriers. Ann. Stat., 45, 2074–2101. [Google Scholar]
- 26. Holm, K., Hegardt, C., Staaf, J., Vallon-Christersson, J., Jönsson, G., Olsson, H., Borg, Å. & Ringnér, M. (2010) Molecular subtypes of breast cancer are associated with characteristic dna methylation patterns. Breast Cancer Res., 12, 1–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Horn, R. A. & Johnson, C. R. (2012) Matrix analysis. Cambridge university press. [Google Scholar]
- 28. Hotelling, H. (1992) Relations between two sets of variates. Breakthroughs in statistics. Springer, pp. 162–190. [Google Scholar]
- 29. Hu, W., Lin, D., Calhoun, V. D., and Wang, Y.-P. (2016). Integration of snps-fmri-methylation data with sparse multi-cca for schizophrenia study. In 2016 38th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), pages 3310–3313. IEEE. [DOI] [PubMed] [Google Scholar]
- 30. Hu, W., Lin, D., Cao, S., Liu, J., Chen, J., Calhoun, V. D. & Wang, Y.-P. (2017) Adaptive sparse multiple canonical correlation analysis with application to imaging (epi) genomics study of schizophrenia. IEEE Trans. Biomed. Eng., 65, 1–399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Huey, N. and Laha, N. (2021). R package for computing de-biased estimators. de.bias.cca. https://github.com/nilanjanalaha/de.bias.CCA.
- 32. Janková, J. & van de Geer, S. (2021) De-biased sparse pca: inference for eigenstructure of large covariance matrices. IEEE Trans. Inf. Theory, 67, 2507–2527. [Google Scholar]
- 33. Janková, J. & Van De Geer, S. (2016) Confidence regions for high-dimensional generalized linear models under sparsity. arXiv preprint arXiv:1610.01353.
- 34. Janková, J. & van de Geer, S. (2017) Honest confidence regions and optimality in high-dimensional precision matrix estimation. Test, 26, 143–162. [Google Scholar]
- 35. Javanmard, A. & Montanari, A. (2014) Confidence intervals and hypothesis testing for high-dimensional regression. J. Mach. Learn. Res., 15, 2869–2909. [Google Scholar]
- 36. Johnstone, I. M. & Lu, A. Y. (2009) On consistency and sparsity for principal components analysis in high dimensions. J. Am. Stat. Assoc., 104, 682–693. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Kang, M., Zhang, B., Wu, X., Liu, C., and Gao, J. (2013). Sparse generalized canonical correlation analysis for biological model integration: a genetic study of psychiatric disorders. In 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), pages 1490–1493. IEEE. [DOI] [PubMed] [Google Scholar]
- 38. Kuchibhotla, A. K. & Chakrabortty, A. (2022) Moving beyond sub-gaussianity in high-dimensional statistics: applications in covariance estimation and linear regression. Inf. Inference, 11, 1389–1456. [Google Scholar]
- 39. Laha, N. & Mukherjee, R. (2022) On support recovery with sparse cca: Information theoretic and computational limits. IEEE Transactions on Information Theory, 69, 1695–1738. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Lee, M. & Rhee, I. (2017) Cytokine signaling in tumor progression. Immune Netw., 17, 214–227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Lee, W., Lee, D., Lee, Y. & Pawitan, Y. (2011) Sparse canonical covariance analysis for high-throughput data. Stat. Appl. Genet. Mol. Biol., 10. [Google Scholar]
- 42. Leeb, H. & Pötscher, B. M. (2005) Model selection and inference: facts and fiction. Econometric Theory, 21, 21–59. [Google Scholar]
- 43. Leeb, H. & Pötscher, B. M. (2006) Can one estimate the conditional distribution of post-model-selection estimators? Ann. Stat., 34, 2554–2591. [Google Scholar]
- 44. Leeb, H. & Pötscher, B. M. (2008) Sparse estimators and the oracle property, or the return of Hodges’ estimator. J. Econometrics, 142, 201–211. [Google Scholar]
- 45. Lin, D., Zhang, J., Li, J., Calhoun, V. D., Deng, H.-W. & Wang, Y.-P. (2013) Group sparse canonical correlation analysis for genomic data integration. BMC Bioinformatics, 14, 1–16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Ma, Z., et al. (2013) Sparse principal component analysis and iterative thresholding. Ann. Stat., 41, 772–801. [Google Scholar]
- 47. Ma, Z. & Yang, F. (2021) Sample canonical correlation coefficients of high-dimensional random vectors with finite rank correlations. arXiv preprint arXiv:2102.03297.
- 48. Ma, Z. & Li, X. (2020) Subspace perspective on canonical correlation analysis: dimension reduction and minimax rates. Bernoulli, 26, 432–470. [Google Scholar]
- 49. Mai, Q. & Zhang, X. (2019) An iterative penalized least squares approach to sparse canonical correlation analysis. Biometrics, 75, 734–744. [DOI] [PubMed] [Google Scholar]
- 50. Mitra, R. & Zhang, C.-H. (2016) The benefit of group sparsity in group inference with de-biased scaled group lasso. Electron. J. Stat., 10, 1829–1873. [Google Scholar]
- 51. Neykov, M., Ning, Y., Liu, J. S. & Liu, H. (2018) A unified theory of confidence regions and testing for high-dimensional estimating equations. Stat. Sci., 33, 427–443. [Google Scholar]
- 52. Ning, Y. & Liu, H. (2017) A general theory of hypothesis tests and confidence regions for sparse high dimensional models. Ann. Stat., 45, 158–195. [Google Scholar]
- 53. Peng, Y., Gao, F. & Zhang, J. (2015) Sparse inverse covariance matrix estimation for functional connectivity analysis of fmri data. Brain Connect., 5, 607–621. [Google Scholar]
- 54. Pittas, A. G., Joseph, N. A. & Greenberg, A. S. (2004) Adipocytokines and insulin resistance. J. Clin. Endocrinol. Metab., 89, 447–452. [DOI] [PubMed] [Google Scholar]
- 55. Pötscher, B. M. & Leeb, H. (2009) On the distribution of penalized maximum likelihood estimators: the lasso, scad, and thresholding. J. Multivariate Anal., 100, 2065–2082. [Google Scholar]
- 56. Ravikumar, P., Wainwright, M. J. & Lafferty, J. D. (2008) Covariance estimation in high-dimensional sparse gaussian graphical models. J. Mach. Learn. Res., 9, 2579–2607. [Google Scholar]
- 57. Sofer, T., Maity, A., Coull, B., Baccarelli, A. A., Schwartz, J. & Lin, X. (2012) Multivariate gene selection and testing in studying the exposure effects on a gene set. Stat. Biosci., 4, 319–338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58. Sun, T. & Zhang, C.-H. (2012) Banded and sparse covariance matrices: estimation and applications. J. Multivariate Anal., 110, 149–165. [Google Scholar]
- 59. Trench, W. F. (1999) Asymptotic distribution of the spectra of a class of generalized kac–Murdock–szegö matrices. Linear Algebra Appl., 294, 181–192. [Google Scholar]
- 60. Tsiatis, A. (2007) Semiparametric theory and missing data. Springer Science & Business Media. [Google Scholar]
- 61. van de Geer, S., Bühlmann, P., Ritov, Y. & Dezeure, R. (2014) On asymptotically optimal confidence regions and tests for high-dimensional models. Ann. Stat., 42, 1166–1202. [Google Scholar]
- 62. Vershynin, R. (2010) Introduction to the non-asymptotic analysis of random matrices. arXiv preprint arXiv:1011.3027.
- 63. Vershynin, R. (2018) High-dimensional probability: An introduction with applications in data science, vol. 47. Cambridge university press. [Google Scholar]
- 64. Wang, T., Berthet, Q. & Samworth, R. J. (2016) Statistical and computational trade-offs in estimation of sparse principal components. Ann. Stat., 44, 1896–1930. [Google Scholar]
- 65. Wilms, I. & Croux, C. (2015) Sparse canonical correlation analysis from a predictive point of view. Biom. J., 57, 834–851. [DOI] [PubMed] [Google Scholar]
- 66. Witten, D. M., Tibshirani, R. & Hastie, T. (2009) A penalized matrix decomposition, with applications to sparse principal components and canonical correlation analysis. Biostatistics, 10, 515–534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67. Wu, Y. & Liu, Y. (2014) Sparse modeling and estimation for high-dimensional genetic data. Cambridge University Press. [Google Scholar]
- 68. Yang, F. (2022) Limiting distribution of the sample canonical correlation coefficients of high-dimensional random vectors. Electron. J. Probab., 27, 1–71. [Google Scholar]
- 69. Yuan, M. (2010) High dimensional inverse covariance matrix estimation via linear programming. J. Mach. Learn. Res., 11, 2261–2286. [Google Scholar]
- 70. Yuan, X.-T. & Zhang, T. (2013) Truncated power method for sparse eigenvalue problems. J. Mach. Learn. Res., 14, 899–925. [Google Scholar]
- 71. Zhang, C.-H. & Zhang, S. S. (2014) Confidence intervals for low dimensional parameters in high dimensional linear models. J. R. Stat. Soc. B, 76, 217–242. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Data Availability Statement
No new data were generated or analysed in support of this review.