Skip to main content
NCBI home page
Cerebral Cortex (New York, NY) logoLink to Cerebral Cortex (New York, NY)
. 2023 Jul 11;33(17):9802–9814. doi: 10.1093/cercor/bhad245

Temporal fingerprints of cortical gyrification in marmosets and humans

Qiyu Wang 1,2, Shijie Zhao 3,4,✉, Tianming Liu 5, Junwei Han 6,✉, Cirong Liu 7,✉
PMCID: PMC10656951  PMID: 37434368

Abstract

Recent neuroimaging studies in humans have reported distinct temporal dynamics of gyri and sulci, which may be associated with putative functions of cortical gyrification. However, the complex folding patterns of the human cortex make it difficult to explain temporal patterns of gyrification. In this study, we used the common marmoset as a simplified model to examine the temporal characteristics and compare them with the complex gyrification of humans. Using a brain-inspired deep neural network, we obtained reliable temporal-frequency fingerprints of gyri and sulci from the awake rs-fMRI data of marmosets and humans. Notably, the temporal fingerprints of one region successfully classified the gyrus/sulcus of another region in both marmosets and humans. Additionally, the temporal-frequency fingerprints were remarkably similar in both species. We then analyzed the resulting fingerprints in several domains and adopted the Wavelet Transform Coherence approach to characterize the gyro-sulcal coupling patterns. In both humans and marmosets, sulci exhibited higher frequency bands than gyri, and the two were temporally coupled within the same range of phase angles. This study supports the notion that gyri and sulci possess unique and evolutionarily conserved features that are consistent across functional areas, and advances our understanding of the functional role of cortical gyrification.

Keywords: cortical folding, convolutional neural network, Marmoset, functional connectivity, resting-state fMRI

Introduction

Cortical gyrification is the most striking but poorly understood gross morphological feature of human brains (Rakic 1988; Welker 1990; Fernández et al. 2016; Van Essen 2020). The complexity of gyrification has been linked to intellectual and cognitive functions (Barkovich et al. 2012; Fernández et al. 2016), implying the functional roles of gyrification. Recent neuroimaging studies in humans have shown that gyri and sulci are temporally coupled but exhibit distinct temporal patterns in resting-state functional networks (Liu et al. 2018; Zhang et al. 2019; Wang et al. 2023) with gyri possibly serving as global functional hubs and sulci exhibiting more local connectivity (Deng et al. 2014). These temporal patterns indicate potential communication and different roles between gyri and sulci, which may be the connectomic basis driving gyrification functions. However, previous discoveries on the temporal patterns of gyri and sulci were based solely on human fMRI studies, which may be confounded by the complexity of the human brain’s architectural structure. The human cerebral cortex has variable folding patterns with large, deep fissures surrounded by numerous small gyri/sulci located in various functional areas (Welker 1990). The combination of small and large gyri/sulci and various functional areas complicates explanations of the temporal dynamics of gyrification; thus, a simplified model of gyrification is warranted to examine the temporal and frequency patterns of gyri and sulci.

The common marmoset, a small non-human primate (NHP) species, has emerged as an ideal simplified model for investigating the temporal dynamics and connectivity patterns of gyrification. With an almost smooth brain, the marmoset cerebral cortex has two major fissures: the calcarine sulcus and the lateral fissure. While the calcarine sulcus is located exclusively in the primary visual cortex, the lateral fissure is surrounded by multiple distinct functional areas, including auditory areas and the insular cortex. The two fissures provide comparable models for extracting the temporal features of gyri and sulci and studying their functional connectivity patterns. By comparing these temporal patterns to those of human gyri and sulci, the marmoset’s gyri and sulci also provide crucial evolutionary insight into the functional roles of gyrification.

Here, we investigated the gyro-sulcal temporal characteristics of marmosets and humans. Using the resting-state fMRI datasets of Marmoset Brain Mapping Project (Tian et al. 2022) and the Human Connectome Project (Van Essen et al. 2012), we extracted the representative functional features of the gyri and sulci by using ptFCN (pooling-trimmed fully convolutional neural network). The ptFCN is a recently developed brain-inspired deep neural network that is an effective method for extracting spatial and temporal features of brain dynamics (Wang et al. 2023). We then analyzed the temporal features of the gyri and sulci in time, frequency, and phase domains and adopted the WTC (Wavelet Transform Coherence) approach to characterize the gyri-sulci synchrony. The WTC allowed us to detect the temporal dynamics in different frequency spectra, which temporal correlation or phase coherence could not measure (Liu 1994; Torrence and Compo 1998; Muller et al. 2004). These results revealed that the gyri and sulci possess unique temporal features that are stable across different functional areas and exhibit similar gyro-sulcal coupling patterns in marmosets and humans. This study provides new insights into the functional organization and roles of cortical gyrification.

Materials and methods

Data collection and preprocessing

Marmoset

The marmoset data were from the version-4 resource of the Marmoset Brain Mapping Project (https://www.marmosetbrainmapping.org),includingawake resting-state fMRI data from two research institutes (Institute of Neuroscience, ION; and National Institutes of Health, NIH) (Tian et al. 2022). This dataset includes 39 marmosets with 110 sessions, 709 fMRI runs, and 12,053-min total scan time. For more detailed demographic information, please refer to (Tian et al. 2022). All 39 marmosets were imaged using similar rs-fMRI protocols and pulse sequences, except for a minor adjustment in the echo time (TE) made to accommodate hardware differences between the ION and the NIH gradient sets. The marmosets were scanned in a 9.4 T/30 cm (ION) and 7 T/30 cm (NIH) horizontal MRI (Bruker, Billerica, USA). Two sets of spin-echo EPI with opposite phase-encoding directions (LR and RL) were collected for EPI-distortion correction. The acquisition parameters of rs-fMRI data are as follows: TR = 3,000 ms, TE = 37.69 ms (ION)/36 ms (NIH), flip angle = 90°, FOV = 28 × 36 mm, matrix size = 56 × 72, 38 axial slices, slice thickness = 0.5 mm, 8 volumes for each set. The preprocessing steps of marmoset fMRI data were similar with the HCP minimal preprocessing pipline (Glasser et al. 2013), mainly including spatial artifact/distortion removal and ICA-fix denoising. Then the preprocessed data were spatially normalized to the template space of the Marmoset Brain Atlas Version-3 (MBMv3) (Liu et al. 2021) and mapped to the standard surface mesh of the MBMv3. The mesh had 37,974 vertices for the left hemisphere and 38,094 vertices for the right hemisphere. To ensure test-retest reliability and mitigate the multi-site effect for subsequent analysis, we selected 26 marmosets (11 from ION, 15 from NIH; see Supplementary Table 1) from the dataset using the following criteria: (i) each marmoset underwent at least two fMRI scan sessions; and (ii) if a marmoset had only two scan sessions, each session must include at least five fMRI runs.

Human

The grayordinate fMRI data from Human Connectome Project 900 subjects release dataset (HCP S900) (Glasser et al. 2013) were used for this study (https://www.humanconnectome.org/). HCP S900 provides high-quality multi-modal MRI neuroimaging data with high spatial and temporal resolution and high contrast between gyri and sulci, allowing accurately locating of the position of gyri and sulci and getting reliable gyral/sulcal features. For statistical comparability with marmoset data, we randomly selected 26 subjects (the same number as the marmoset data) from 897 healthy adults for the main and the reproducibility experiments, respectively. The acquisition parameters of fMRI scans are as follows: 90 × 104 matrix, 72 slices, TR = 0.72 s, TE = 33.1 ms, FOV = 220 mm, flip angle = 52°, BW = 2,290 Hz/Px, in-plane FOV = 208 mm × 180 mm and 2.0 mm isotropic voxels. The grayordinate fMRI data were preprocessed by the HCP minimal preprocessing pipelines, including spatial artifact/distortion removal, ICA-fix denoising, cortical surface generation, within-subject multi-modal surface matching registration, and cross-subject alignment to standard space. Under the 2-mm resolution, all the gray matter was represented by 91,282 grayordinates, including ~ 30,000 surface vertices for each hemisphere and ~ 30,000 subcortical gray matter voxels (Barch et al. 2013; Robinson et al. 2014). Only cortical surface vertices in the whole-brain grayordinates were considered in our study. As the human data have higher temporal resolution than the marmoset data, and thus the two species possess different ranges of frequency domains. To make the frequency domain comparable to both species, we down-sampled the preprocessed fMRI signals of human data by the “Sinc” resampling function (Woodward 1953; Higgins 1996; Meijering 2002).

Cortical surfaces parcellation and signal extraction

As illustrated in Fig. 1(A), regions of interest (the lateral fissure and the calcarine sulcus) were identified on the cortical surfaces. To obtain identical signal fingerprints specific to gyri or sulci, it is necessary to narrow down the transition region between the gyral crown and sulcal fundi in order to capture the most representative fMRI signals. Therefore, we aimed to identify the representative regions of gyri and sulci with the help of the skeleton. For each fissure, we selected the vertices with local maximum and minimum curvature values to construct the gyral and sulcal skeleton, respectively (Fig. 1A, left row). Subsequently, we applied a three-ring neighborhood selection around the skeleton. Then, we sifted the three-ring neighboring vertices around the skeleton (Fig. 1A, right row) following the empirical setting (Deng et al. 2014; T. Zhang et al. 2016). For marmosets, 2,562 vertices were selected as gyral (1,867) and sulcal (695) vertices in the lateral fissure, and 3,452 vertices as gyral (2,166) and sulcal (1,286) vertices in the calcarine sulcus. For humans, due to the complex gyrification, the cortical surface was first inflated, and then the skeletons and vertices of interest were selected on the inflated surface. It is worth noting that all vertices of the calcarine sulcus of marmosets belong to the primary visual cortex (Liu et al. 2021), whereas the calcarine sulcus of the human brain extends to other areas (Brodmann 1909). Thus, gyral/sulcal vertices of the calcarine sulcus in human primary visual cortex were used for our following experiments to remove the influence of different functional areas (Fig. 1A, right row). In total, 4,825 vertices were identified as gyral (2,722) and sulcal (2,103) vertices in the lateral fissure region, and 717 vertices as gyral (361) and sulcal (356) vertices in the calcarine sulcus region of human brains.

Fig. 1.

Fig. 1

Open in a new tab

Overview of our study for extracting and characterizing temporal fingerprints of gyri and sulci. (A) Extraction of gyral and sulcal skeletons and their regions. Left: the gyral and sulcal skeleton of the lateral fissure (top) and the calcarine sulcus (bottom) of humans and marmosets, respectively. Right: Gyral regions and sulcal regions that are defined as adjacent vertices with a Euclidean distance of 3 to the skeleton. (B) The resting-state fMRI timeseries from gyral/sulcal regions are fed into ptFCN to extract their temporal features. The ptFCN consists of three convolutional layers (represented as series filters) and generates probability vectors representing the likelihood that each filter belongs to the category of gyri or sulci. Based on these probability vectors, these convolutional filters are defined as gyral and sulcal temporal fingerprints. The probability vector corresponding to the selected representative features is marked in the box. Dropout layers, shown with dashed lines, act as regulators to avoid overfitting. (C) the resultant temporal fingerprints are transformed into a complex plane (by Hilbert transform) and time-frequency domain (by wavelet transform). (D) The correlation and coherence of gyral and sulcal fingerprints are analyzed and compared cross-species in different domains.

The architecture of deep neural networks and training strategy

A recently developed brain-inspired deep neural network (Wang et al. 2023) was adopted to extract representative gyral/sulcal temporal features from the preprocessed fMRI time series (Fig. 1B). Our neural network consisted of the three convolutional layers. The first two convolutional layers with ReLU activation were used to learn local features. The last convolutional layer was for feature integration and prediction. Because the convolutional filters of the last layer corresponded to gyri or sulci, we mainly concentrated on the last convolutional layer. A dropout layer acted as a regulator to avoid overfitting. Instead of using activation functions for classification, we adopted a top-k-mean strategy to pool the class-wise activations and obtained a probability mass function over the categories for gyral-sulcal fMRI signal classification. The proposed ptFCN network was implemented using PyTorch (https://pytorch.org/). To ensure the stability of our results under different training strategies, we employed two distinct approaches: subject-level training and group-level training. For subject-level training, a dedicated ptFCN model was trained using fMRI signals from a specific brain region and tested on a different region. This process yielded subject-specific ptFCN models. For group-level training, we randomly split all subjects into two non-overlapping subsets. During training, gyral and sulcal fMRI signals from the training subset were utilized to train a single ptFCN model. The remaining subset was excluded from the training dataset and employed for testing the trained model.

Hyperparameter settings

Before training the brain-inspired deep neural network, preprocessing steps were applied to the input signals. One-hot encoding method was used for signal labeling, in which sulcal and gyral signals were encoded as [1 0] and [0 1], respectively. The fMRI time series of each vertex was normalized by removing the mean of per time point. We applied the random undersampling method (Kotsiantis and Pintelas 2003; Chawla 2009) on the majority class to avoid the imbalance of the training data. Then the preprocessed signals and its label were used for neural network training. Each convolution layer of our network had a filter length of 33, and the output channels for three convolutional layers were 64, 64, and 2, respectively, to extract the hierarchical features. The stride of the convolutional layer was 1, and the padding was set to 16 to ensure the identical size of the input and output. The dropout layer randomly discarded 20% of hidden nodes to mitigate overfitting. For the top-k-mean strategy, k was set to 0.875 for the feature selection. Our model used an Adam (Kingma and Ba 2014) optimizer with a base learning rate of 0.01, 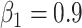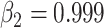Inline graphic, Inline graphic, and the L2 weight decay coefficient = 0.0005. Training batch size was set to 128, and epoch was set to 200 to ensure the convergence of the training process. The “CrossEntropyLoss” function from PyTorch toolbox was used to construct the loss function.

Features analysis methods in time and frequency space

Time domain correlation calculation

A slide-time window approach was used to measure the temporal correlation between gyri and sulci in the time domain. After extracting gyral and sulcal features by the neural network, we obtained averaged gyral and sulcal filters with 33 time points for each time window. Then, the dynamic functional correlation coefficient (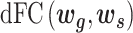Inline graphic) was calculated by moving the time window:

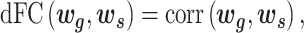graphic file with name DmEquation1.gif (1)

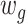where Inline graphic and Inline graphic were the time window segments of extracted gyral and sulcal features, respectively. The time-window length was set to 7 with a step of 2.

Frequency domain coherence calculation

Coherence in frequency space was assessed for the gyral-sulcal relationship. The magnitude squared coherence 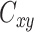Inline graphic of discrete-time signals gyri (g) and sulci (s) in the frequency domain was calculated using Welch’s method (Welch 1967), as shown in Equation (2):

graphic file with name DmEquation2.gif (2)

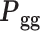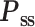where Inline graphic and Inline graphic are power spectral densities of gyral and sulcal signals, and Inline graphic is the cross spectral density of gyri and sulci. Both power spectral densities and cross spectral density were calculated by the complex conjugate multiplication, see Equations (3) and (4):

graphic file with name DmEquation3.gif (3)
graphic file with name DmEquation4.gif (4)

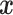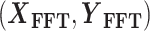Original signals Inline graphic and Inline graphic are first transformed into the frequency domain Inline graphic before spectral density calculation. 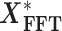Inline graphic is the complex conjugate of Inline graphic.Hilbert transformation and phase domain coherence calculation

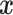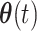Phase coherence is a phenomenon where a constant phase difference exists between any two signals or waves of the same frequency. Here, Hilbert transform was performed on the extracted fMRI features of the gyri and sulci, which expressed the given signal Inline graphic in polar coordinates, i.e. Inline graphic After transformation, the features were represented by its time-varying amplitude Inline graphic and its phase Inline graphic. 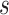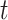To yield the phase evolution of each time point, the dynamic phase coherence Inline graphic between each gyral filter Inline graphic and sulcal filter Inline graphic at time Inline graphic was estimated by calculating the cosine of the phase difference (Equation 5):

graphic file with name DmEquation5.gif (5)

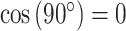Thus, gyral and sulcal filters which were temporarily aligned (i.e. with similar angles) at a given repetition time (TR) had a phase coherence value close to 1 (i.e.Inline graphic), whereas orthogonalized filters (e.g. one increasing at 45° and the other decreasing at 45°) had zero-phase coherence (i.e. Inline graphic). The resulting 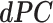Inline graphic for each representative gyro-sulcal characteristic was a vector with size Inline graphic, where T was the total number of time points (T = 33) of the extracted filters.

Wavelet transform coherence

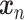Wavelet transform coherence (WTC) is a time-frequency domain method for analyzing the coherence and phase lag between two timeseries (Torrence and Compo 1998). Based on the continuous wavelet transform, the WTC decomposes a single time series into time-frequency space by successively convolving the time series with scaled and translated versions of a wavelet function Inline graphic (Stéphane Mallat 1999). The continuous wavelet transform of a time series Inline graphic of length Inline graphic, sampled from an underlying continuous waveform at equal time steps of size 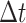Inline graphic, is defined as

graphic file with name DmEquation6.gif (6)

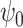where Inline graphic is a time index, and Inline graphic denotes the wavelet scale. The function Inline graphic is chosen to be the complex Morlet wavelet:

graphic file with name DmEquation7.gif (7)

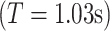where the parameter Inline graphic governs the relative time and frequency resolution. In this study, Inline graphic was set to 6, providing a good trade-off between time and frequency localization (Grinsted et al. 2004; Muller et al. 2004). Under this setting, the Fourier period Inline graphic was approximately equal to the value of s Inline graphic. Note that 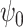Inline graphic was normalized to unit energy at each scale in Equation (7), so that the wavelet transforms at each scale were directly comparable. The wavelet transform 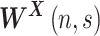Inline graphic is a complex quantity. 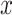The modulus of Inline graphic, expresses the amount of power in Inline graphic as a function of time and frequency, and the angle of 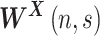Inline graphicrepresents the local phase in time-frequency domain. Similarly, the cross-wavelet transform is defined for two time series as

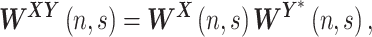graphic file with name DmEquation8.gif (8)

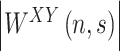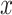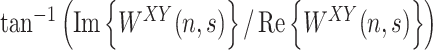whose modulusInline graphic, known as the cross-wavelet power, represents the amount of joint power between Inline graphic and Inline graphic as a function of time and frequency and whose angle Inline graphic, named cross-wavelet phase, describes their relative phase. The wavelet transform coherence is defined as (Torrence and Compo 1998)

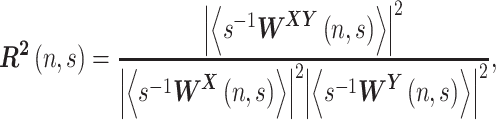graphic file with name DmEquation9.gif (9)

which reveals localized regions of phase-locked behavior. The range of Inline graphic is from 0 to 1 and can be conceptualized as a localized correlation coefficient in time-frequency space (Grinsted et al. 2004). The brackets Inline graphicindicate smoothing process in both time and frequency spaces. We adopted Gaussian function as the temporal smoothing filter, which is matched to the Morlet wavelet. We used boxcar filter for frequency smoothing. For more discussion about frequency smoothing, please refer to (Torrence and Compo 1998).

Phase entropy calculation

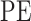Entropy is the measure of the disorder of a system. To evaluate the evolutional characteristics between marmosets and humans in the phase domain. Phase entropy (Rohila and Sharma 2019) Inline graphic of each WTC map was calculated as follows. First, the entire phase plot was divided into k sections with an angle span of Inline graphic radians for each section. The parameter k serves as a coarse-graining parameter defining how fine a sector is. In this study, k was set to 4 following the traditional analysis (Inline graphic). Then, Inline graphic is calculated by applying the Shannon entropy formula to the distribution of the phase patterns:

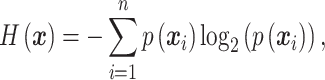graphic file with name DmEquation10.gif (10)

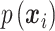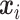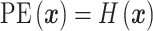where Inline graphic defines the probability of the random event Inline graphic, which is the four sections of the phase lag angle plot and then Inline graphic.

Phase lag trend entropy calculation

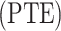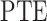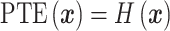Although PE can measure the phase domain complexity, this measurement overlooked the phase lag angle change trend. Thus, we calculate phase lag trend entropy Inline graphic. Before calculating the Inline graphic, we first defined the phase plot states by considering four neighboring phase lag plots (a Inline graphic window) in the time-frequency domain. In this observation window, four different states were defined to depict the trend of phase lag angles: (i) four phase lag angles were in the same phase section; (ii) three phase lag angles were in the same phase section, and the other phase lag angle was in a different phase section; (iii) four phase lag angles were grouped into two different phase sections; and (iv) four phase lag angles in the observation window were in four different phase sections. Formally, the phase trend entropy was then calculated with the Shannon entropy formulation as Equation (10), where Inline graphic when Inline graphic corresponds to the four different states in this section.

Results

Deep neural network detected reliable temporal features for classifying gyri and sulci within species and cross-species

To effectively extract the temporal features of gyri and sulci, we employed a brain-inspired deep neural network (ptFCN) to learn and classify the temporal characteristics of these structures in one fissure (the calcarine sulcus or the lateral fissure) and then applied the trained network to classify gyri and sulci in the other fissure (Fig. 1). The existence of unique temporal features (temporal fingerprints) in gyri and sulci would enable the neural network to classify them across regions.

We reconstructed corresponding gyral/sulcal skeletons of the calcarine sulcus and the lateral fissure in humans and marmosets, and then extracted the preprocessed fMRI time series from the two regions as training and test datasets for the ptFCN (Fig. 1A–B). We executed this process on both subject-level (Fig. 2A) and group-level (Supplementary Fig. 7). The ptFCN achieved a high training accuracy for both the calcarine sulcus (subject-level: humans: 85.67%, marmosets: 75.05%; group-level: humans: 70.31%, marmosets: 73.84%) and the lateral fissure (subject-level: humans: 84.56%, marmosets: 79.21%; group-level: humans: 88.70%, marmosets: 68.60%), which demonstrated that distinct temporal fingerprints existed and were effectively extracted for gyri and sulci (Fig. 2A, right panel, gray bar; Supplementary Fig. 7, left panel). To exclude the influence from functional areas, we tested the trained neural network on the other fissure on the subject-level training process (Fig. 2A, right panel, blue and red bars). When using the calcarine sulcus for network training and the lateral fissure for testing, we obtained a classification accuracy of 66.73% in humans and 65.13% in marmosets (Fig. 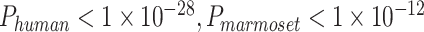2A, two-sample t-test, significantly above chance level: Inline graphic). When training on the lateral fissure and testing on the calcarine sulcus, the average classification accuracy is 65.10% in humans and 63.55% in marmosets (Fig. 2A; two-sample t-test, significantly above chance level: Inline graphic). The classification accuracy suggests that the extracted temporal fingerprints of gyrification are reliable across functional areas.

Fig. 2.

Fig. 2

Open in a new tab

Evaluation of gyro-sulcal classification performance in marmosets (blue) and humans (red). (A) Cross-regional classification. Neural networks are trained on the calcarine-sulcus area or lateral-fissure area, and then tested on the other regions, respectively (left panel). Training (gray) and testing accuracies of marmosets (blue) and humans (red) are shown in the right panel. ACC: accuracy. (B) Gyral and sulcal temporal-frequency fingerprints transformed from the prediction convolutional filters of ptFCN by wavelet transform. Fingerprints of the calcarine sulcus are shown here, and those of the lateral fissure are shown in Supplementary Fig. 1(A). Gyri and sulci exhibit distinct temporal features, and the temporal-frequency fingerprints are similar across species. (C) Classification results after applying the trained ptFCN on whole brain gyral and sulcal data of humans. The left panel shows the test results of the ptFCN trained on calcarine sulcus. The right panel shows the test results of the ptFCN trained on lateral fissure.

To visualize and compare the temporal features of gyri and sulci, we extracted the convolutional filters from the prediction convolutional layer of the ptFCN (Fig. 1B, Supplementary Fig. 7). These convolutional filters function as feature operators, reflecting the temporal characteristics used by the trained networks to differentiate between gyri and sulci (Wang et al. 2017;Liu et al. 2018 ; Zhang et al. 2019 ; Wang et al. 2023) while disregarding the signal variance in the original space. As such, these filters provide a consistent framework for comparing cross-species temporal fingerprints of gyrification. As each node of the prediction convolutional layer is a filter, we averaged the activated filters of gyri and sulci, respectively, to represent the overall and most prominent features. We subsequently applied Fourier transform and wavelet transform to convert each filter, including the averaged filters, into the frequency domain (Figs. 3C and 1C). Our findings demonstrated that while gyral and sulcal patterns exhibited inter-individual variability (Fig. 3C and Supplementary Fig. 6), but all participants exhibited a higher frequency band within the sulci compared to the gyri. These findings highlight the consistent temporal and frequency characteristics shared by filters associated with gyri and sulci, aligning with the average results (Figs. 3A, 3C, and Supplementary Fig. 6) and previous studies (Liu et al. 2018; Zhang et al. 2019; Wang et al. 2023). We further validated the extracted fingerprints on other gyri and sulci of the human brain. The classification results demonstrated that these fingerprints can effectively serve as representative whole-brain gyral/sulcal fingerprints (Fig. 2C). Notably, the distinctive temporal-frequency patterns between the gyri and the sulci were remarkably similar in humans and marmosets (Fig. 2B), suggesting the existence of evolutionary conservative features of gyrification. Consistently, by training the neural network on one species (marmoset or human) and testing on the other (human or marmoset), we achieved a significant above-the-chance level of classification accuracies (P < 1 × 10^−32) for both the calcarine sulcus and the lateral fissure (Supplementary Fig. 2).

Fig. 3.

Fig. 3

Open in a new tab

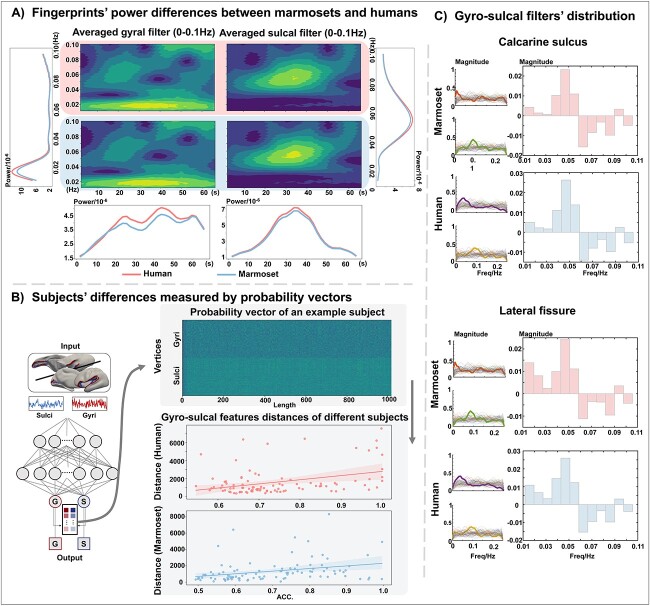
Cross-species comparison of temporal fingerprints and inter-subject variability. (A) Cross-species comparison of temporal fingerprints. To measure the differences between humans (red line) and marmosets (blue line), we calculated the wavelet power of the filters (temporal fingerprints) in frequency and time space. Humans and marmosets have similar power magnitude distributions, but the magnitude of humans is higher than that of marmosets. Fingerprints of the calcarine sulcus are shown here, and those of the lateral fissure are shown in Supplementary Fig. 1(B). The vertical plots show the average wavelet power over all time points, and the horizontal plots show the average wavelet power over all frequency bands. (B) Inter-subjects’ variability measured by probability vectors. We measured inter-subject variability by calculating the distance between the probability vectors of gyri and sulci (left panel). The top row of the right panel visualizes the probability vectors of each input vertex. The distances between the gyral and sulcal vectors were calculated using dynamic time wrapping. The regression of the distances and the classification accuracy of different subjects are plotted in the bottom panel. The magnitude of the distance indicates the differences in gyral and sulcal probability vectors: The longer the distance, the higher the classification accuracy. (C) The detailed gyral and sulcal filters of a randomly selected subject. In each panel, the left column shows the frequency distribution of all gyral (the upper plot) or sulcal (the lower plot) filters, the right column shows the histogram differences between gyral and sulcal filters. The magnitude of histogram higher than zero indicates gyral filters distributed more in this frequency band compare to sulcal filters. The magnitude of histogram lower than zero indicates sulcal filters distributed more in this frequency band compare to gyral filters.

However, we also observed differences in the power magnitude of convolutional filters between marmosets and humans (Fig. 3A). The filters of humans displayed higher power magnitude in both frequency and time space, indicating that humans may involve more complicated tasks with specific frequency bands or time points. These filters serve as representations of how our ptFCN discerns between gyri and sulci, similar to the functionality of the “Sobel” operator. Filters exhibit analogous characteristics when they are employed for similar tasks. Consequently, filters can capture the fundamental distinctions between gyri and sulci while mitigating the influence of inter-subject variability. To validate the effectiveness and robustness of these filters, we visualized the probability vectors of different subjects (Fig. 3B, top panel) and subsequently calculated the distance between the gyral and sulcal probability vectors. The probability vectors represent the output of the last convolutional layers and provide insights into the likelihood of a vertex being classified as either gyrus or sulcus. The distances between probability vectors were found to correlate directly with the classification accuracy across different subjects (Fig. 3B, bottom panel). This result suggests that the distances are related to the differences in gyral and sulcal features of different subjects, and the gyral and sulcal fingerprints can effectively reflect the common features of different subjects. These unique temporal fingerprints of gyri and sulci, revealed by the filters, underlied the accuracy of cross-regional and cross-species classification, and the individual variability contributed to the classification errors of the neural networks.

Highly consistent gyro-sulcal temporal-frequency coupling in marmosets and humans

Separate analysis of gyro-sulcal coupling in different domains

Previous studies have suggested that the gyri and sulci are temporally coupled for information processing (Liu et al. 2018; Jiang et al. 2021, 2016; Wang et al. 2023). To characterize the coupling, we calculated the correlation and coherence of the filters of gyri and sulci in the time, frequency, and phase domains (Fig. 4A). The time-domain dynamic correlation and the frequency- and phase-domain coherence were nonstationary, suggesting the dynamic communication and coupling patterns between gyri and sulci. The dynamic coupling patterns were strikingly similar between humans and marmosets for both gyrification, consistent with the similar fingerprints described in (Fig. 2B). We also observed a higher cross-subject variance of the coupling dynamics in the lateral fissure than in the calcarine sulcus (Fig. 4A). We evaluated the correlation and coherence with other configurations, including the window size and the moving step, and found similar coupling relationships between gyri and sulci in marmosets and humans (Supplementary Figs. 3 and 4). The results may be due to the different complexities of the two gyrifications: the calcarine sulcus is located on the primary visual cortex, but the lateral fissure is surrounded by more brain regions with different functions. Similarly, the human (red dots in Fig. 4A) had a higher cross-subject variance of the coupling dynamics than the marmoset (blue dots in Fig. 4A), consistent with the more complicated gyrification of humans than marmosets.

Fig. 4.

Fig. 4

Open in a new tab

Evaluation of the gyro-sulcal coupling in time, frequency, and phase domains. (A) Within-regional gyro-sulcal relationship. Dynamic correlation coefficient (top row), frequency coherence magnitude (second row), and phase coherence (third row) of extracted gyral and sulcal temporal fingerprints for the calcarine sulcus (left) and the lateral fissure (right), respectively. Dynamic correlation coefficients are calculated using a sliding-window method, frequency coherences using Welch’s method, and phase coherences using the Hilbert transformation. The X-axis shows the frequency band or time points, and the Y-axis shows the magnitude of coherence or the correlation coefficients. The dots represent the correlation/coherence magnitude of different subjects, and the line represents the average magnitude of different subjects. Red lines and dots represent human data, and blue represents marmoset data. The bottom row shows the phase lag angles distribution of gyro-sulcal coupling. (B) Cross-regional relationship. The coupling patterns between the gyri (top row) or the sulci (bottom row) of the calcarine sulcus (left) and the lateral fissure (right) are displayed, respectively.

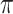The gyro-sulcal phase coherence had a full range (−Inline graphic to Inline graphic) but an un-even phase lag distribution (Fig. 4A, bottom row). For both humans and marmosets, the phase lag angles 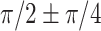Inline graphic accounted for 35.9~39.28% of time points of filters, followed by the angles of 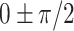Inline graphic (26.57~30.19%), suggesting that most of the gyral signals alternated with the sulcal. We also examined the cross-regional coupling of the same gyrification structure (gyri-gyri or sulci-sulci) and revealed similar coupling patterns across regions (Fig. 4B), with higher individual variability in humans than in marmosets. These results describe gyro-sulcal temporal coupling patterns in different aspects and reveal the higher variability of humans in the coupling patterns due to their more complicated gyrification.

Integrated analysis of gyro-sulcal coupling

Correlation, frequency coherence, and phase angles depicted the gyro-sulcal temporal coupling from different domains. However, these domains are not independent of each other for describing temporal signals. To achieve an integrated view, we used the WTC to characterize the gyro-sulcal temporal relationship. WTC is a method for analyzing the coherence and phase lag between two timeseries as a function of both time and frequency, and has higher temporal resolution compared to other time-frequency analysis methods. Consistent with previous results, the WTC revealed highly consistent time-frequency coupling patterns of gyri and sulci in humans and marmosets. In order to validate the stability of our results, we also trained ptFCN on group-level and got the similar coupling patterns (Supplementary Fig. 7). With a higher PE (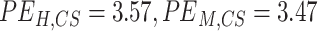Inline graphic) and phase lag trend entropy (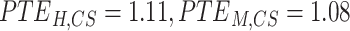Inline graphic), the gyro-sulcal phase lag angles of humans were more disorganized than those of marmoset (Fig. 5B). This indicates that the gyro-sulcal coupling patterns in humans exhibit greater complexity compared to those observed in marmoset. By plotting time-averaged coherence on each frequency, we found that gyri and sulci coupled in different frequencies with different phase lag angles, with two dominated phase-angle ranges in specific frequency bands for both species (Fig. 5B, bottom). 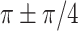Specifically, gyri and sulci were coupled at 0.111–0.056 Hz with a phase lag Inline graphic (peaking at 0.1 and 0.07 Hz), and in a lower frequency band (0.059–0.039 Hz) with a phase lag of Inline graphic (peaking at 0.04 Hz), respectively. For cross-regional comparisons (Fig. 5C), the gyrification structure (gyri-gyri or sulci-sulci) was often coupled with a phase lag angle of Inline graphic for both species. The across-regional coupling of the sulci exhibited more variability than the gyri (Inline graphic), suggesting that sulci may be varied in different regions.

Fig. 5.

Fig. 5

Open in a new tab

Evaluation of the gyro-sulcal coupling by WTC. (A) The procedure for calculating WTC involves wavelet transforming gyral and sulcal fingerprints to obtain wavelet transform coherence (WTC; Inline graphic). (B) Gyro-sulcal wavelet coherence maps of the calcarine sulcus are shown for marmosets (left) and humans (right), and those of the lateral fissure are shown in Supplementary Fig. 5. For each WTC map, the color scale represents the magnitude of coherence, and arrows indicate phase angles in the time-frequency plane. A rightward-pointing arrow indicates in-phase or positive correlation (Inline graphic), a leftward-pointing arrow indicates anti-correlation (Inline graphic), and the downward- and upward-pointing arrows indicate phase-lag angles of Inline graphic and Inline graphic, respectively. Data outside the “cone of influence” (COI) are removed because they may be susceptible to edge effects and thus less accurate during wavelet transformation. (C) Inter-regional gyral/sulcal wavelet coherence maps of marmosets and humans. Gyral/sulcal coherence maps between different regions are displayed. The first two rows show gyral coherence and sulcal coherence between the calcarine sulcus (CS) and lateral fissure (LF) of marmosets, respectively. The bottom two rows show gyral coherence and sulcal coherence between CS and LF of humans, respectively.

Given the smoothness characteristics during the computation, the WTC can be treated independently on each frequency band while not on the time scale. This makes it challenging to directly compare coherence between the integrated analysis and the separate analysis on the time scale. However, when evaluating average coherence within each frequency band, the integrated analysis exhibits a similar gyro-sulcal coupling tendency compared to the separate analysis (Supplementary Fig. 8). In addition, both separate and integrated analyses reveal a predominant coupling with a phase lag of 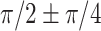Inline graphic. These findings demonstrate that the integrated analysis aligns with the previous separate signal analysis and effectively combines different aspects of the signal. In summary, by integrating the three domains (time, frequency, and phase), the WTC analysis fully characterized the unique patterns of gyro-sulcal coupling patterns, which are consistent cross-region and cross-species.

Discussion

Investigating the gross gyrification features may offer insight into the functional organization and complexity of the cerebral cortex. In this study, we used the marmoset brain as a model to examine temporal features of gyrification. By implementing ptFCN, we removed redundant non-gyrification features from the original fMRI signals and subsequently performed integrated signal analysis on the extracted representative features. Through a comparison between marmosets and humans, we found that the gyro-sulcal coherence fingerprints were conserved across species during evolution. In marmosets, which have a simpler gyrification, gyro-sulcal coherences are more consistent among different subjects, indicating a smaller individual variability. The relationship between gyri and sulci varied in the time and frequency domains and exhibited different phase lag angles. The phase lag angle, as determined by phase coherence, showed no distinct pattern of variability in the time domain, but displayed a discernible pattern in the frequency domain, with gyri and sulci coherence at various frequencies exhibiting different dominant phase lag angles. Although marmosets and humans exhibited a highly consistent overall gyro-sulcal coherence pattern, the phase lag trend entropy indicates that humans possess more complex phase lag angles of gyro-sulcal interaction. The species-conserved gyro-sulcal fingerprint implies that gyri and sulci may fulfill fixed functional tasks and can be regarded as the fundamental functional unit of the cerebral cortex.

Traditionally, analysis of fMRI signals has been conducted in the original signal space (Chang and Glover 2010; Margulies et al. 2016; Belloy et al. 2018), but interindividual variability can make it difficult to identify common features (Mars et al. 2021; Beauchamp et al. 2022). In recent years, deep learning methods have been utilized for their ability to effectively extract features from fMRI data to represent the distinctive characteristics of gyri and sulci (Liu et al. 2018; Zhang et al. 2019; Wang et al. 2023). However, these features can vary across different subjects and are difficult to compare between different species. To address this issue, we used convolutional layers in neural networks to extract local features in the temporal axis, acting as filters that extract specific features along this axis. These filters reflect the features used for classification by the neural network (Liu et al. 2018; Zhang et al. 2019; Wang et al. 2023; Wang, Yan, and Oates 2017). To establish a common comparative space for cross-species gyro-sulcal temporal-frequency analysis, we used the averaged filter features as the temporal fingerprint for analyzing gyro-sulcal coherences, and found that these fingerprints are remarkably conserved across species.

Oscillations within the brain often occur concurrently and interact with one another within or across different brain structures, forming a hierarchical and universal system of brain dynamics (Buzsáki and Wang 2012; Bragin et al. 1995; Csicsvari et al. 2003; Buzsáki 2006; Buzsaki, Logothetis, and Singer 2013; Buzsáki and Llinás 2017). Our previous studies have suggested that gyri, which tend to oscillate at lower frequencies, may be involved in long-distance communication and global functional integration, whereas sulci, which tend to oscillate at higher frequencies, may be typically responsible for local information processing and play a critical role in the functional segregation of different brain areas (Deng et al. 2014; Liu et al. 2018; Zhang et al. 2019; Wang et al. 2023). In this study, we examined the coupling patterns between gyri and sulci by measuring the relationship between their fingerprints in the time-frequency domain. We found that gyri and sulci coupled in different frequency bands with different phase lag angles. Given that the phase of slower oscillations can modulate the faster ones (Buzsáki and Wang 2012; Bragin et al. 1995; Csicsvari et al. 2003; Buzsáki 2006; Buzsaki, Logothetis, and Singer 2013; Buzsáki and Llinás 2017), it is possible that gyral oscillations (low frequency), as global hubs (Deng et al. 2014; Liu et al. 2018; Wang et al. 2023), may modulate sulcal signals (high frequency) through phase lag angles in a specific frequency band. This finding improves our understanding of the functional roles and interactions of gyri and sulci in the brain.

Recent studies have posited that the spatial–temporal patterns of the brain can be conceptualized as a blend of standing and traveling wave dynamics (Bolt et al. 2022; Gonzalez-Castillo 2022). This theory is able to explain the majority of large-scale functional topologies (Bolt et al. 2022; Gonzalez-Castillo 2022). 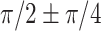For temporal patterns of gyrification, gyro-sulcal coupling phase lag angles in marmosets and humans were primarily distributed in Inline graphic and Inline graphic (Figs. 4A and 5B). According to the definitions of standing waves and traveling waves, a key feature that distinguishes traveling waves from standing waves is the presence of phase lag (Hannachi et al. 2007; Feeny 2008). Therefore, the gyro-sulcal coupling phase lag angles can be divided into standing waves (zero-lag synchrony, Inline graphic) and the traveling waves (time-lag synchrony, Inline graphic and the others). This observation suggests that the interaction between gyri and sulci may involve a combination of standing and traveling waves, leading to mixed synchronization patterns (Bolt et al. 2022). Specifically, zero-lag synchrony predominantly peaks in the lower frequency band (0–0.06 Hz), whereas time-lag synchronization exhibits a peak in the higher frequency band (0.06–0.1 Hz). Based on previous studies of cortical folding and brain rhythms (Buzsaki et al. 2013; Deng et al. 2014; Liu et al. 2018; Wang et al. 2023), high-frequency brain activity reflects local cortical processing domains, whereas low-frequency brain activity synchronizes across distributed brain regions. These pieces of evidence indicate that gyri and sulci primarily employ standing waves for global modulation and traveling waves for local modulation.

Although possessing a small and almost smooth brain, the marmoset, as a primate, shares similar white-matter fiber pathways and functional brain areas as the human (Xu et al. 2010; Nie et al. 2012; Budde and Annese 2013; Chen et al. 2013; Zhang et al. 2014; Liu et al. 2019; Kaneko et al. 2020). Previous primate studies found that long-range axons are radially distributed in the gyri and circumferentially course along the deep boundaries of the sulci (Xu et al. 2010; Nie et al. 2012; Budde and Annese 2013; Chen et al. 2013; Zhang et al. 2014). This similarity in anatomical and functional brain architecture may contribute to the conserved gyro-sulcal temporal-frequency fingerprints in marmosets and humans. Humans also display higher variability in sulcal depth than marmosets (Hayashi et al. 2021). Given that inter-subject functional connectivity variability is related to variability in sulcal depth (Mueller et al. 2013) and structural architecture (Passingham et al. 2002; de Schotten Michel et al. 2011; Popovych et al. 2021), human brains exhibit higher inter-subject variability when measuring the temporal-frequency fingerprints of gyri and sulci.

This study employed a brain-inspired deep neural network to identify the distinctive temporal fingerprints of gyri and sulci in marmosets and humans, improving our understanding of the functional properties of gyrification. However, the underlying anatomical basis and functional mechanisms of these fingerprints, as well as the biological functions of gyro-sulcal coupling, remain to be explored. It is also worth noting that our study only examined marmosets and humans, who have the simplest and most complex gyrification among all primates, respectively. Thus, other primates may also possess similar fingerprints. Finally, previous research has shown that abnormalities or changes in gyrification morphology can lead to brain disorders and problems in intellectual and cognitive function (Levitt 2003; Narr et al. 2004; Barkovich et al. 2012; Fernández et al. 2016). Therefore, it is important to further investigate how morphological changes in gyrification affect its fingerprints and gyro-sulcal coupling to better understand these intellectual and cognitive dysfunctions.

Supplementary Material

Supplementary_qiyu_final_bhad245
Click here for additional data file. (3.8MB, zip)

Acknowledgment

We thank the 9.4T core facility and Marmoset Animal Facility of the CEBSIT for their assistance in the study. Human data used in this paper were provided by the Human Connectome Project, WU-Minn Consortium (Principal Investigators: David Van Essen and Kamil Ugurbil; 1U54MH091657) funded by the 16 National Institutes of Health (NIH) Institutes and Centers that support the NIH Blueprint for Neuroscience Research and by the McDonnell Center for Systems Neuroscience at Washington University.

Contributor Information

Qiyu Wang, School of Automation, Northwestern Polytechnical University, Xi'an 710072, China; CAS Center for Excellence in Brain Science and Intelligence Technology, Institute of Neuroscience, Chinese Academy of Sciences, Shanghai 200031, China.

Shijie Zhao, School of Automation, Northwestern Polytechnical University, Xi'an 710072, China; Research & Development Institute of Northwestern Polytechnical University in Shenzhen, Shenzhen 518063, China.

Tianming Liu, Cortical Architecture Imaging and Discovery Lab, Department of Computer Science and Bioimaging Research Center, The University of Georgia, Athens, GA 30602, United States.

Junwei Han, School of Automation, Northwestern Polytechnical University, Xi'an 710072, China.

Cirong Liu, CAS Center for Excellence in Brain Science and Intelligence Technology, Institute of Neuroscience, Chinese Academy of Sciences, Shanghai 200031, China.

Author contributions

Q.W., S.Z., C.L., T.L., and J.H. designed the study; Q.W., S.Z., C.L., and T.L. analyzed and interpreted the data; Q.W., C.L., S.Z., and T.L. wrote the manuscript; and C.L., J.H., and S.Z. supervised the study.

CRediT author statement

Qiyu Wang (Conceptualization, Formal analysis, Investigation, Methodology, Writing—original draft, Writing—review and editing), Shijie Zhao (Conceptualization, Investigation, Supervision, Writing—review and editing), Tianming Liu (Conceptualization, Investigation, Writing—review and editing), Junwei Han (Conceptualization, Supervision, Writing—review and editing), Cirong Liu (Conceptualization, Formal analysis, Funding acquisition, Supervision, Writing—review and editing).

Funding

This work was supported in part by the National Science and Technology Innovation 2030 Major Program of China (No. STI2030-2021ZD0203900, 2022ZD0205000), the National Natural Science Foundation of China (No. 32171088 to C.L.), the Lingang Laboratory Grant (No. LG-QS-202201-02 to C.L.), the Shanghai Municipal Science and Technology Major Project (No. 2018SHZDZX05 to C.L.), the National Key R&D Program of China (Grant 2020AAA0105702), the National Natural Science Foundation of China (Grants 42271315，82060336, 62036011, 6202781, 62136004), Guangdong Basic and Applied Basic Research Foundation (2214050008706), Science and Technology Support Project of Guizhou Province (Grant [2021]432), and ShenzhenScience and Technology Program (JCYJ20220530161409021).

Conflict of interest statement

None declared.

Data avaliability

This paper analyzes existing and publicly available data. The HCP dataset is publicly available at https://www.humanconnectome.org/. The marmoset data is publicly available at https://www.marmosetbrainmapping.org.

References

  1. Barch  DM, Burgess  GC, Harms  MP, Petersen  SE, Schlaggar  BL, Corbetta  M, Glasser  MF, Curtiss  S, Dixit  S, Feldt  C, et al.  Function in the human connectome: task-FMRI and individual differences in behavior. NeuroImage. 2013:80(October):169–189. [DOI] [PMC free article] [PubMed] [Google Scholar]
  2. Barkovich  AJ, Guerrini  R, Kuzniecky  RI, Jackson  GD, Dobyns  WB. A developmental and genetic classification for malformations of cortical development: update 2012. Brain. 2012:135(Pt 5):1348–1369. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Beauchamp  A, Yee  Y, Darwin  BC, Raznahan  A, Mars  RB, Lerch  JP. Whole-brain comparison of rodent and human brains using spatial transcriptomics. Edited by Alex Fornito, Kate M Wassum, and Bratislav Misic. Elife. 2022:11(November):e79418. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Belloy  ME, Naeyaert  M, Abbas  A, Shah  D, Vanreusel  V, van Audekerke, Keilholz  SD, Keliris  GA, Van der Linden, Verhoye  M. Dynamic resting state FMRI analysis in mice reveals a set of quasi-periodic patterns and illustrates their relationship with the global signal. NeuroImage Brain Connect Dyn. 2018:180(October):463–484. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bolt  T, Nomi  JS, Bzdok  D, Salas  JA, Catie Chang  BT, Yeo  T, Uddin  LQ, Keilholz  SD. A parsimonious description of global functional brain organization in three spatiotemporal patterns. Nat Neurosci. 2022:25(8):1093–1103. [DOI] [PubMed] [Google Scholar]
  6. Bragin  A, Jando  G, Nadasdy  Z, Hetke  J, Wise  K, Buzsaki  G. Gamma (40-100 Hz) oscillation in the hippocampus of the behaving rat. J Neurosci. 1995:15(1):47–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Brodmann  K. Vergleichende Lokalisationslehre Der Grosshirnrinde in Ihren Prinzipien Dargestellt auf Grund des Zellenbaues. Barth: Springer Science+Business Media, Inc.; 1909. [Google Scholar]
  8. Budde  MD, Annese  J. Quantification of anisotropy and Fiber orientation in human brain histological sections. Front Integr Neurosci. 2013:7:3. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Buzsáki  G. Rhythms of the brain. New York: Oxford University Press; 2006. [Google Scholar]
  10. Buzsáki  G, Llinás  R. Space and time in the brain. Science. 2017:358(6362):482–485. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Buzsáki  G, Wang  X-J. Mechanisms of gamma oscillations. Annu Rev Neurosci. 2012:35(1):203–225. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Buzsaki  G, Logothetis  N, Singer  W. Scaling brain size, keeping timing: evolutionary preservation of brain rhythms. Neuron. 2013:80(3):751–764. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Chang  C, Glover  GH. Time-frequency dynamics of resting-state brain connectivity measured with FMRI. NeuroImage. 2010:50(1):81–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Chawla  NV. Data mining for imbalanced datasets: an overview. In: Maimon  O, Rokach  L, editors. Data mining and knowledge discovery handbook. Boston, MA: Springer US; 2009. pp. 875–886. [Google Scholar]
  15. Chen  H, Zhang  T, Guo  L, Li  K, Yu  X, Li  L, Hu  X, Han  J, Hu  X, Liu  T. Coevolution of Gyral folding and structural connection patterns in primate brains. Cereb Cortex. 2013:23(5):1208–1217. [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Csicsvari  J, Jamieson  B, Wise  KD, Buzsáki  G. Mechanisms of gamma oscillations in the hippocampus of the behaving rat. Neuron. 2003:37(2):311–322. [DOI] [PubMed] [Google Scholar]
  17. de  Schotten Michel  T, Ffytche  DH, Bizzi  A, Dell’Acqua  F, Allin  M, Walshe  M, Murray  R, Williams  SC, Murphy  DGM, Catani  M. Atlasing location, asymmetry and inter-subject variability of white matter tracts in the human brain with MR diffusion tractography. NeuroImage. 2011:54(1):49–59. [DOI] [PubMed] [Google Scholar]
  18. Deng  F, Jiang  X, Zhu  D, Zhang  T, Li  K, Guo  L, Liu  T. A functional model of cortical gyri and sulci. Brain Struct Funct. 2014:219(4):1473–1491. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Feeny  BF. A complex orthogonal decomposition for wave motion analysis. J Sound Vib. 2008:310(1):77–90. [Google Scholar]
  20. Fernández  V, Llinares-Benadero  C, Borrell  V. Cerebral cortex expansion and folding: what have we learned?  EMBO J. 2016:35(10):1021–1044. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Glasser  MF, Sotiropoulos  SN, Wilson  JA, Coalson  TS, Fischl  B, Andersson  JL, Xu  J, et al.  The minimal Preprocessing pipelines for the human connectome project. NeuroImage. 2013:80(October):105–124. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Gonzalez-Castillo  J. Traveling and standing waves in the brain. Nat Neurosci. 2022:25(8):980–981. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Grinsted  A, Moore  JC, Jevrejeva  S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Process Geophys. 2004:11(5/6):561–566. [Google Scholar]
  24. Hannachi  A, Jolliffe  IT, Stephenson  DB. Empirical orthogonal functions and related techniques in atmospheric science: a review. Int J Climatol. 2007:27(9):1119–1152. [Google Scholar]
  25. Hayashi  T, Hou  Y, Glasser  MF, Autio  JA, Knoblauch  K, Inoue-Murayama  M, Coalson  T, et al.  The nonhuman primate neuroimaging and neuroanatomy project. NeuroImage. 2021:229(April):117726. [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Higgins  JR. Sampling theory in Fourier and signal analysis: foundations. Oxford Science Publications. Oxford, New York: Clarendon Press ; Oxford University Press; 1996. [Google Scholar]
  27. Jiang  X, Li  X, Lv  J, Zhao  S, Zhang  S, Zhang  W, Zhang  T, Liu  T. Modeling functional dynamics of cortical gyri and sulci. Cham, Switzerland: Springer; 2016. pp. 19–27. [Google Scholar]
  28. Jiang  X, Zhang  T, Zhang  S, Kendrick  KM, Liu  T. Fundamental functional differences between gyri and sulci: implications for brain function, cognition, and behavior. Psychoradiology. 2021:1(1):23–41. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Kaneko  T, Takemura  H, Pestilli  F, Silva  AC, Ye  FQ, Leopold  DA. Spatial organization of occipital white matter tracts in the common marmoset. Brain Struct Funct. 2020:225(4):1313–1326. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Kingma  DP, Ba  JL. Adam: a method for stochastic optimization. In: 3rd International Conference on Learning Representations, ICLR. San Diego, CA, USA; 2015.
  31. Kotsiantis  S, Pintelas  P. Mixture of expert agents for handling imbalanced data sets. Annals of Mathematics, Computing & Teleinformatics. 2003:1(1):46–55. [Google Scholar]
  32. Levitt  JG. Cortical sulcal maps in autism. Cereb Cortex. 2003:13(7):728–735. [DOI] [PubMed] [Google Scholar]
  33. Liu  PC. Wavelet Spectrum analysis and ocean wind waves. Vol. 4. Amsterdam, The Netherlands: Elsevier; 1994, pp. 151–166. [Google Scholar]
  34. Liu  H, Zhang  S, Jiang  X, Zhang  T, Huang  H, Ge  F, Zhao  L, Li  X, Hu  X, Han  J, et al.  The cerebral cortex is bisectionally segregated into two fundamentally different functional units of gyri and sulci. Cereb Cortex. 2018:29(10):4238–4252. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Liu  C, Yen  CC, Szczupak  D, Ye  FQ, Leopold  DA, Silva  AC. Anatomical and functional investigation of the marmoset default mode network. Nat Commun. 2019:10(1):1975. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Liu  C, Yen  CC, Szczupak  D, Tian  X, Glen  D, Silva  AC. Marmoset brain mapping V3: population multi-modal standard volumetric and surface-based templates. NeuroImage. 2021:226(February):117620. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Mallat  S. A wavelet tour of signal processing. London, UK: Academic Press; 1999. [Google Scholar]
  38. Margulies  DS, Ghosh  SS, Goulas  A, Falkiewicz  M, Huntenburg  JM, Langs  G, Bezgin  G, Eickhoff  SB, Castellanos  FX, Petrides  M, et al.  Situating the default-mode network along a principal gradient of macroscale cortical organization. Proc Natl Acad Sci USA. 2016:113(44):12574–12579. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Mars  RB, Jbabdi  S, Rushworth  MFS. A common space approach to comparative neuroscience. Annu Rev Neurosci. 2021:44(1):69–86. [DOI] [PubMed] [Google Scholar]
  40. Meijering  E. A chronology of interpolation: from ancient astronomy to modern signal and image processing. Proc IEEE. 2002:90(3):319–342. [Google Scholar]
  41. Mueller  S, Wang  D, Fox  MD, Yeo  BT, Sepulcre  J, Sabuncu  MR, Shafee  R, Lu  J, Liu  H. Individual variability in functional connectivity architecture of the human brain. Neuron. 2013:77(3):586–595. [DOI] [PMC free article] [PubMed] [Google Scholar]
  42. Muller  K, Lohmann  G, Neumann  J, Grigutsch  M, Mildner  T, von  Cramon  DY. Investigating the wavelet coherence phase of the BOLD signal. J Magn Reson Imaging. 2004:20(1):145–152. [DOI] [PubMed] [Google Scholar]
  43. Narr  KL, Bilder  RM, Kim  S, Thompson  PM, Szeszko  P, Robinson  D, Luders  E, Toga  AW. Abnormal Gyral complexity in first-episode schizophrenia. Biol Psychiatry. 2004:55(8):859–867. [DOI] [PubMed] [Google Scholar]
  44. Nie  J, Guo  L, Li  K, Wang  Y, Chen  G, Li  L, Chen  H, et al.  Axonal Fiber terminations concentrate on gyri. Cereb Cortex. 2012:22(12):2831–2839. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Passingham  RE, Stephan  KE, Kotter  R. The anatomical basis of functional localization in the cortex. Nat Rev Neurosci. 2002:3(8):606–616. [DOI] [PubMed] [Google Scholar]
  46. Popovych  OV, Jung  K, Manos  T, Diaz-Pier  S, Hoffstaedter  F, Jan Schreiber  BT, Yeo  T, Eickhoff  SB. Inter-subject and inter-parcellation variability of resting-state whole-brain dynamical modeling. NeuroImage. 2021:236(August):118201. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Rakic  P. Specification of cerebral cortical areas. Science. 1988:241(4862):170–176. [DOI] [PubMed] [Google Scholar]
  48. Robinson  EC, Jbabdi  S, Glasser  MF, Andersson  J, Burgess  GC, Harms  MP, Smith  SM, Van Essen  DC, Jenkinson  M. MSM: a new flexible framework for multimodal surface matching. NeuroImage. 2014:100(October):414–426. [DOI] [PMC free article] [PubMed] [Google Scholar]
  49. Rohila  A, Sharma  A. Phase entropy: a new complexity measure for heart rate variability. Physiol Meas. 2019:40(10):105006. [DOI] [PubMed] [Google Scholar]
  50. Tian  X, Chen  Y, Majka  P, Szczupak  D, Perl  YS, Yen  CC-C, Tong  C, et al.  An integrated resource for functional and structural connectivity of the marmoset brain. Nat Commun. 2022:13(1):7416. [DOI] [PMC free article] [PubMed] [Google Scholar]
  51. Torrence  C, Compo  GP. A practical guide to wavelet analysis. Bull Am Meteorol Soc. 1998:79(1):61–78. [Google Scholar]
  52. van Essen  D, Ugurbil  K, Auerbach  E, Barch  D, Behrens  TE, Bucholz  R, Chang  A, Chen  L, Corbetta  M, Curtiss  SW, et al.  The human connectome project: a data acquisition perspective. NeuroImage. 2012:62(4):2222–2231. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Van Essen  DC. A 2020 view of tension-based cortical morphogenesis. Proc Natl Acad Sci USA. 2020:117(52):32868–32879. [DOI] [PMC free article] [PubMed] [Google Scholar]
  54. Wang, Z. G., W. Z.  Yan, and T.  Oates. Time series classification from scratch with deep neural networks: a strong baseline. In: 2017 International Joint Conference on Neural Networks (IJCNN), IEEE, Anchorage, AK, USA. 2017:1578–1585.
  55. Wang  Q, Zhao  S, He  Z, Zhang  S, Jiang  X, Zhang  T, Liu  T, Liu  C, Han  J. Modeling functional difference between gyri and sulci within intrinsic connectivity networks. Cereb Cortex. 2023:33(4):933–947. [DOI] [PubMed] [Google Scholar]
  56. Welch  P. The use of fast Fourier transform for the estimation of power spectra: a method based on time averaging over short, modified Periodograms. IEEE Trans Audio Electroacoust. 1967:15(2):70–73. [Google Scholar]
  57. Welker  W. Why Does Cerebral Cortex Fissure and Fold? In: Jones EG, Peters A. (eds) Cerebral Cortex, vol 8B. Boston, MA: Springer; 1990, pp. 3–136. [Google Scholar]
  58. Woodward  PM. Probability and information theory, with applications to radar. 2nd ed ed. International Series of Monographs on Electronics and Instrumentation 3.  Burlington, VT: Elsevier Science Pergamon Press; 1953. [Google Scholar]
  59. Xu  G, Knutsen  AK, Dikranian  K, Kroenke  CD, Bayly  PV, Taber  LA. Axons pull on the brain, but tension does not drive cortical folding. J Biomech Eng. 2010:132(7):071013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Zhang  T, Chen  H, Guo  L, Li  K, Li  L, Zhang  S, Shen  D, Hu  X, Liu  T. Characterization of U-shape streamline Fibers: methods and applications. Med Image Anal. 2014:18(5):795–807. [DOI] [PMC free article] [PubMed] [Google Scholar]
  61. Zhang  T, Zhu  D, Jiang  X, Zhang  S, Kou  Z, Guo  L, Liu  T. Group-Wise consistent cortical parcellation based on connectional profiles. Med Image Anal. 2016:32(August):32–45. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Zhang  S, Liu  H, Huang  H, Zhao  Y, Jiang  X, Bowers  B, Guo  L, Hu  X, Sanchez  M, Liu  T. Deep learning models unveiled functional difference between cortical gyri and sulci. IEEE Trans Biomed Eng. 2019:66(5):1297–1308. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary_qiyu_final_bhad245
Click here for additional data file. (3.8MB, zip)

Articles from Cerebral Cortex (New York, NY) are provided here courtesy of Oxford University Press

RESOURCES