Hierarchical Harris hawks optimizer for feature selection

Graphical abstract

Highlights

• •An improved Harris hawks optimization (EHHO) is proposed to deal with feature selection task.
• •By adding the hierarchy mechanism, the algorithm can achieve better convergence speed and accuracy.
• •EHHO performed well on classic test sets of CEC.
• •EHHO can obtain better performance than the original HHO with less features.

Abstract

Introduction

The main feature selection methods include filter, wrapper-based, and embedded methods. Because of its characteristics, the wrapper method must include a swarm intelligence algorithm, and its performance in feature selection is closely related to the algorithm's quality. Therefore, it is essential to choose and design a suitable algorithm to improve the performance of the feature selection method based on the wrapper. Harris hawks optimization (HHO) is a superb optimization approach that has just been introduced. It has a high convergence rate and a powerful global search capability but it has an unsatisfactory optimization effect on high dimensional problems or complex problems. Therefore, we introduced a hierarchy to improve HHO's ability to deal with complex problems and feature selection.

Objectives

To make the algorithm obtain good accuracy with fewer features and run faster in feature selection, we improved HHO and named it EHHO. On 30 UCI datasets, the improved HHO (EHHO) can achieve very high classification accuracy with less running time and fewer features.

Methods

We first conducted extensive experiments on 23 classical benchmark functions and compared EHHO with many state-of-the-art metaheuristic algorithms. Then we transform EHHO into binary EHHO (bEHHO) through the conversion function and verify the algorithm's ability in feature extraction on 30 UCI data sets.

Results

Experiments on 23 benchmark functions show that EHHO has better convergence speed and minimum convergence than other peers. At the same time, compared with HHO, EHHO can significantly improve the weakness of HHO in dealing with complex functions. Moreover, on 30 datasets in the UCI repository, the performance of bEHHO is better than other comparative optimization algorithms.

Conclusion

Compared with the original bHHO, bEHHO can achieve excellent classification accuracy with fewer features and is also better than bHHO in running time.

Introduction

With the advent of the information age, the supervision and classification of high-dimensional data have emerged in many fields, such as life and scientific research. Theoretically, more feature numbers can provide better discrimination ability, but with the increase of feature numbers, the algorithm's running time will also increase. In addition, due to irrelevant or redundant features, excessive features not only reduce the efficiency of the learning algorithm but also may lead to overfitting, resulting in a decrease in the model's generalization ability [1]; this will harm the classification accuracy. As a data preprocessing technology in machine learning, feature selection can remove the irrelevant, noisy and redundant features in the data set, extract important features and reduce the data dimension, to speed up the execution of the machine learning algorithm and improve the classification accuracy. Its basic premise is to identify some of the most beneficial features from the original feature set based on certain assessment criteria in order to minimize the dimensionality of subspace and achieve comparable or even higher performance of the classifier. At present, feature selection plays a vital role in medical information processing [2], [3], [4], financial data analysis [5], [6], [7], [8], and biological data analysis [9], [10].

Feature selection is a combinatorial optimization problem in classification tasks. For data with $\text{n}$ features, the search space may produce ${\text{2}}^{\text{n}}$ results. Feature selection is mainly divided into the filtering method [11], the embedding method [12], and the wrapping method [13]. The embedding method takes the feature selection process as a part of model training and selects features in the model training process. The wrapped feature selection method uses a certain learning algorithm to evaluate the candidate feature subsets and a certain prediction model to score the selected feature subsets. Each time a new set of feature subsets is selected, it is used for model training. Finally, the model is used to test on the test set to directly select the optimal feature subset from all the features in the sample data set. Because of the features of wrapped feature selection, this algorithm includes many heuristic algorithms.

Optimization methods often need some gradient info and detail of the topography of the feature space to calculate the better solution in a deterministic approach [14], [15]. Meta-heuristic algorithms (MAs) are simple, flexible, easy to implement, and do not need gradient calculation. At present, more and more people are gradually concerned about this field. MAs can be roughly divided into four categories. One is the evolutionary algorithm, such as genetic algorithm (GA) [17], differential evolution (DE) [17], etc. The inspiration for the evolutionary algorithm is drawn from the evolutionary operation of organisms in nature [16]. Basic operations such as gene coding, population initialization, cross variation operator, operation retention strategy, and so on are included. When compared with conventional optimization techniques like calculus-based and rigorous approaches, evolutionary computation has the characteristics of high robustness characteristics and is particularly widely applicable. The second is the swarm intelligence algorithm, such as particle swarm optimization (PSO) [17], equilibrium optimizer (IEO) [18], whale optimization algorithm (WOA) [17], slime mould algorithm (SMA)¹ [19], artificial bee colony algorithm (ABC) [20], etc. The third is physical or chemical algorithms, such as sine cosine algorithm (SCA) [21], simulated annealing algorithm (SA) [22], gravitational search algorithm (GSA) [17], multi-verse optimizer (MVO) [17], etc. The fourth is an algorithm based on human behavior, such as teaching–learning-based optimization (TLBO) [23], colony predation algorithm (CPA) [24], Harris hawks optimization (HHO)² [25], hunger games search (HGS)³ [26], Runge Kutta optimizer (RUN)⁴ [27], the weighted mean of vectors (INFO)⁵ [28], brain storm optimization (BSO) [29], etc. In addition, they have been successful in many fields, such as resource allocation [30], image segmentation [31], [32], train scheduling [33], feature selection [34], [35], complex optimization problem [36], economic emission dispatch problem [37], medical diagnosis [38], [39], bankruptcy prediction [40], [41], gate resource allocation [42], [43], multi-objective problem [44], [45], expensive optimization problems [46], [47], robust optimization [48], [49], fault diagnosis [50], airport taxiway planning [51], and solar cell parameter identification [52].

However, according to the free lunch (NFL) theorem [53], there is no unified algorithm to solve all problems, which requires us to conduct different analyses for different problems [54]. The traveling salesman problem is a typical NP-hard problem. Cross-docking distribution is a relatively new logistics strategy. A group of trucks is used to transport products from suppliers to customers through the cross-docking center. Each supplier and customer node can only be visited once. Direct shipment from suppliers to customers is not allowed. The study aims to determine the vehicle route that minimizes the total distance. To solve this problem, kucukoglu et al. [55] integrated the tabu search algorithm (TS) [56] into a simulated annealing algorithm (SA) [22]. Solar photovoltaic (PV) system is challenging to accurately extract PV parameters because of their multi-modal and nonlinear characteristics.

Xu et al. [57] introduced the quantum revolving gate strategy and the Nelder-Mead simplex [58] strategy into the Hunger Games search (HGS) [59] and achieved good results in extracting unknown parameters in the photovoltaic system. In order to accurately predict the power load and promote the rational integration of clean energy resources, Zhang et al. [60] combined the cuckoo search (CS) [61] with the self-recurrent (SR) mechanism and proposed a hybrid self-circulation support vector regression model. Job shop scheduling problem (JSSP) has always been a hot problem in the manufacturing industry. In order to better solve this problem, Liu et al. [62] combined Levy and DE into WOA. Dewangan et al. [63] applied GWO to the three-dimensional path planning of UAVs, which is also a typical NP-hard problem. Traveling Salesman Problem (TSP) is proved to be NP-hard. Although many heuristic techniques exist, this problem is still a complex combinatorial optimization problem. Kanna et al. [64] put forward a hybrid optimization algorithm by combining Deer Hunting Optimization Algorithm (DHOA) [65] and Earthworm Optimization Algorithm (EWA) [66]. When solving the TSP problem, the computational complexity is low, the convergence is good, and the optimal result is significantly improved. In order to overcome the shortcomings of the bat algorithm (BA) [67], Chen et al. [68] adopted the Boltzmann selection and monitoring mechanism to enable BA to maintain an appropriate balance between exploration capability and development capability. Hussain et al. [69] used the adaptive guided DE (AGDE) equivalent heuristic algorithm to solve the parameter problem of the quantum cloning circuit to improve the cloning fidelity. It can be seen that what we need to do is to develop algorithms that are competent for different types of problems, rather than one algorithm that can solve all problems.

HHO [25] is one of the excellent algorithms proposed in recent years. It has a robust global search ability and has few parameters to adjust. However, like other algorithms, HHO quickly falls into local optimization and needs to be changed in dealing with specific problems. Shao et al. [70] proposed the improvement of HHO (VHHO) to optimize the rolling bearing fault diagnosis method. Fu et al. [71] combined de and HHO to predict short-term wind speed accurately and effectively reduce a wind farm's adverse impact on the power system. In order to accurately predict the unknown parameters in the photovoltaic cell module, Chen et al. [72] added the opposite learning strategy to the HHO. Yang et al. [73] used HHO in multi-objective optimization. Zhang et al. [74] improved the ability of HHO in global optimization by improving the escape energy parameter E in HHO. Hussain et al. [75] proposed a hybrid optimization method for numerical optimization and feature selection by combining the sine–cosine algorithm (SCA) and HHO. This can avoid invalid exploration in HHO and enhance local development by dynamically adjusting candidate schemes to avoid later stagnation of HHO. Sihwail et al. [76] introduced opposite-based learning into HHO and proposed a new IHHO method. Balaha et al. [77] used HHO to optimize the super parameters in the depth learning model, which significantly affects the CT image detection of COVID-19. It can be seen that HHO has an extensive range of application scenarios in various fields, which also proves that HHO has great improvement potential and is worth further research.

The purpose of feature selection is to reduce the number of features and the time required for training the Model. Using MAs to deal with feature selection tasks belongs to solving discrete optimization problems. Although HHO can deal with discrete problems, the time cost is very high, which also leads to the slow running time of HHO when performing feature selection tasks. Furthermore, algorithms often spend much time on high-dimensional datasets, but the results are very few. At present, improving the meta-heuristic algorithm often increases the algorithm's time complexity, increasing the cost of the high-dimensional feature selection task. Therefore, our goal is to enhance the performance of the algorithm and reduce the running time of the algorithm without increasing the time complexity. For this reason, we will divide HHO into different levels to carry out local development for outstanding individuals. At the same time, it can strengthen communication between outstanding individuals. We name it EHHO.

We have conducted sufficient experiments on CEC 23 classic test sets and compared EHHO with other 7 original MAs, 8 advanced algorithms, 2 latest improved algorithms and 1 HHO improvement. In addition, for more systematic data analysis, we used Wilcoxon signed rank test [78] and the Friedman test [79] for a comprehensive comparison. The results show that EHHO is superior to other optimization algorithms in convergence speed and accuracy. In addition, bivariate EHHO (bEHHO) is obtained using the transformation function. The performance of bEHHO was evaluated on thirty datasets in the UCI repository. The experimental results show that the performance of bEHHO is better than the original HHO and other optimizers. The running speed is also significantly improved, especially in the high-dimensional feature selection dataset, which is significantly better than the original HHO. The contributions and work of this paper are as follows:

• •By classifying the Harris hawks, the speed and convergence of the algorithm are improved.
• •A new HHO improved algorithm (EHHO) is proposed, which can effectively deal with complex problems and high-dimensional feature selection problems.
• •A feature selection method for binary EHHO (bEHHO) based on KNN is proposed.
• •Compared with 7 original optimizers, 8 excellent improved optimization algorithms, 2 optimizers proposed in recent years and 1 excellent improved HHO, the excellent performance of EHHO is verified.
• •Compared to the original bHHO, bEHHO can achieve higher classification accuracy with fewer features and less running time.

The structure of the rest of this paper is as follows: in the basic theories section, the HHO and the added hierarchy are introduced in detail. The introduction to HHO that enhances the hierarchy section introduces the binary EHHO method for the feature selection task in detail. In the experiments and analysis of results section, we conduct a comprehensive experimental verification and analyze the experimental results. In the conclusions and future directions section, we summarize this paper's work and point out future research work.

Basic theories

This chapter introduces the basic knowledge of HHO, and the motivation to improve HHO and the newly proposed mechanism are described.

Harris hawks optimizer

HHO is a computational intelligence tool that replicates Harris hawk predator–prey dynamics. It is divided into three sections: exploring, transformation and exploitation. The algorithm has the capability of doing global searches and requires fewer parameters to be tweaked. Therefore, it has great mining potential.

Search phase

Harris hawks live in a random places and find its prey through the following two strategies:

$$X(t+1)\left\{\begin{array}{cc}{X}_{\mathit{rand}}\left(t\right)-r_1|X_{\mathit{rand}}\left(t\right)-2r_{2}X\left(t\right)|,& q⩾0.5\\ |X_{\mathit{rabbit}\left(t\right)}-X_m\left(t\right)|-r3\left[\mathit{lb}+r_4(ub-lb)\right],& q<0.5\end{array}\right)$$

where $X(t+1)$ is the position of the next iteration and $X\left(t\right)$ is the position of the current iteration. $t$ is the current iteration number. $X_{\mathit{rand}}\left(t\right)$ is an individual chosen at random, and $X_{\mathit{rabbit}\left(t\right)}$ is the prey position, that is, the individual position with the best fitness. Both$r_1$,$r_2$,$r_3$,$r_4$ and $q$ are random numbers between$\left[\text{0,1}\right]$, where $q$ is used to randomly select the strategy to be adopted. $X_m\left(t\right)$ is the average position of individuals, and the expression is shown in Eq. (2).

$$X_m\left(t\right)=\sum _{k=1}^N{X}_k\left(t\right)/N$$

where, $X_k\left(t\right)$ is the position of the k-th individual in the population. $N$ is the population size.

The transformation of search and development

HHO converts between search and different development behaviors according to the escape energy of prey. The definition of escape energy is shown in Eq. (3).

$$E=2E_0(1-\frac{t}{T})$$

where, $E_0$ is the random number between$\left[\text{- 1,1}\right]$, $t$ is the number of iterations, and $T$ is the maximum number of iterations. Enter the search phase when$\left|E\right|⩾1$, and enter the development phase when$\left|E\right|<1$.

Development phase

Define $r$ as a random number between $\left[\text{0,1}\right]$ to select different development strategies.

• •When $0.5⩽\left|E\right|<1$ and$r⩾0.5$, adopt the soft siege strategy to update the position, as shown in Eq. (4).

$$X(t+1)=△X\left(t\right)-E\left|J{X}_{\mathit{rabbit}}\left(t\right)-X\left(t\right)\right|$$

where, $△X\left(t\right)=X_{\mathit{rabbit}}\left(t\right)-X\left(t\right)$ represents the difference between the prey position and the current position of the individual, and $J$ is the random number between$\left[\text{0,2}\right]$.

• •When $\left|E\right|<0.5$ and$\left|E\right|<0.5$, adopt the hard siege strategy to update the position, as shown in Eq. (5).

$$X(t+1)=X_{\mathit{rabbit}\left(t\right)}-E\left|△X\left(t\right)\right|$$

• •When $0.5⩽\left|E\right|<1$ and$r<0.5$, adopt the soft surrounding strategy of asymptotic fast subduction to update the position, as shown in Eq. (6), Eq. (7) and Eq. (8).

$$X(t+1)=\left\{\begin{array}{cc}Y,& f\left(Y\right)<f\left(X\right(t\left)\right)\\ Z,& f\left(Z\right)<f\left(X\right(t\left)\right)\end{array}\right)$$

$$Y=X_{\mathit{rabbit}}\left(t\right)-E\left|J{X}_{\mathit{rabbit}}\left(t\right)-X\left(t\right)\right|$$

$$Z=Y+S\left(Dim\right)\ast Levy\left(Dim\right)$$

where, $f\left(\right)$ is the fitness function, $\mathit{Dim}$ is the dimension of the problem, $S$ is the random vector of $\mathit{Dim}$ dimension, the elements therein are the random numbers between$\left[\text{0,1}\right]$, and $\mathit{Levy}$ is Levi's flight.

• •When $\left|E\right|<0.5$ and$r<0.5$, adopt the hard surrounding strategy of asymptotic fast subduction to update the position, as shown in Eq. (9), Eq. (10) and Eq. (11).

$$X(t+1)=\left\{\begin{array}{cc}Y,& f\left(Y\right)<f\left(X\right(t\left)\right)\\ Z,& f\left(Z\right)<f\left(X\right(t\left)\right)\end{array}\right)$$

$$Y=X_{\mathit{rabbit}}\left(t\right)-E\left|J{X}_{\mathit{rabbit}}\left(t\right)-X_m\left(t\right)\right|$$

$$Z=Y+S\left(Dim\right)\ast Levy\left(Dim\right)$$

We give the pseudo-code of HHO in Algorithm 1. It can be seen that HHO can transfer from exploration to development according to the escape energy of prey and then change between different development behaviors. In the escape behavior, the energy of prey is significantly reduced.

Algorithm 1 Pseudo-code of HHO —

1. Initialize the parameters$\mathit{popsize}$,$\mathit{MaxFes}$;
2. Initialize a set of search agents (solutions) ($X$);
3. While ($t⩽MaxFes$).
4.  Calculate each of the search hawks by the objective function;
5.  Update$X_{\mathit{rabbit}}$(best loaction) and$\mathit{bestfitness}$;
6.  For i = 1 to$\mathit{popsize}$.
7.   Update the $E$ by Eq. (3);
8.   Update the$J$;
9.   If ($\left|E\right|⩾1$).
10.    Update the position of search agents using Eq. (1);
11.   End If.
12.   If ($\left|E\right|<1$).
13.    If ($0.5⩽\left|E\right|<1$ and $r⩾0.5$).
14.     Update the position of search agents using Eq. (4);
15.    End If.
16.    If ($\left|E\right|<0.5$ and $r⩾0.5$).
17.     Update the position of search agents using Eq. (5);
18.     End If.
19.    If ($0.5⩽\left|E\right|<1$ and $r<0.5$).
20.     Update the position of search agents using Eq. (6), Eq. (7), Eq. (8);
21.    End If.
22.    If ($\left|E\right|<0.5$ and $r<0.5$).
23.     Update the position of search agents using Eq. (9), Eq. (10), Eq. (11);
24.    End If.
25.   End If.
26.  End For.
27. End While.
28. Return$X_{\mathit{rabbit}}$ and$\mathit{bestfitness}$.

Enhanced hierarchy

HHO simulates various behaviors of harris hawks in the predation process, but it does not reflect other intelligent behaviors. In nature, many animals or creatures have certain social behavior and certain hierarchy. Therefore, we introduced a hierarchy to strengthen the individual connections in the HHO population so that the individuals with good fitness can play a leading role and lead the whole population to update their positions accordingly.

First, we rank the fitness of all individuals ($\mathit{fitness}$), and name the three individuals with the best fitness as A, B, and C, respectively. Then these individuals are updated separately.

• •The first is individual A, whose position update formula is shown in Eq. (12). It can be seen that comparing the ratio of the remaining running times of the algorithm to the total running times with the Cauchy random number, the current position has a certain probability to move closer to the optimal position, and the later the replacement probability is more negligible, which can effectively ensure that the algorithm can effectively avoid falling into local optimization.

$$X^j(t+1)=\left\{\begin{array}{cc}{X}_{\mathit{rabbit}\left(t\right)}^j& \left(\tan \right(pi\ast (rand-0.5))<(1-t/MaxFEs\left)\right)\\ X_{\mathit{rabbit}\left(t\right)}^j+G\ast (X_m^j\left(t\right)-X_n^j\left(t\right))& \mathit{other}\end{array}\right)$$

where, $j$ represents dimension. $X^j(t+1)$ represents the value of the next iteration of the $j$-th dimension of individual A, and $X_{\mathit{rabbit}\left(t\right)}^j$ represents the j-th dimension of the optimal position of the t-th iteration. $X_m^j$ and $X_n^j$ indicate that two individuals are randomly selected in the population, $m$ and $n$ cannot be equal, and $m$ and $n$ cannot be individual A. $\mathit{rand}$ is a random number of$\left[\text{0,1}\right]$. $t$ is the current number of iterations, and $\mathit{MaxFEs}$ is the maximum number of iterations. The value of $G$ is given by Eq. (13).

$$G=(4-t\ast \left(\frac{4}{\mathit{MaxFes}}\right))\ast rand$$

• •For individual B, its position update formula is shown in Eq. (14).

$$X^j(t+1)=\left\{\begin{array}{cc}{X}^j\left(t\right)& \text{rand > 0.5}\\ (X_A^k\left(t\right)+X_B^k\left(t\right))/2& \mathit{other}\end{array}\right)$$

where, $X^j(t+1)$ represents the value of the next iteration of the $j$ dimension of individual B, $X^j\left(t\right)$ represents the value of the current iteration of the $j$ dimension of individual B, $k$ represents the random selection of a dimension from the dimensions, $X_A^k\left(t\right)$ represents the value of the $j$ dimension of the current iteration of individual A, and $X_B^k\left(t\right)$ represents the value of the $j$ dimension of the current iteration of individual B.

• •Finally, there is individual C, whose position update formula is shown in Eq. (15).

$$X^j(t+1)=\left\{\begin{array}{cc}(X_Q^j\left(t\right)+X_R^j\left(t\right))/2& \text{rand > 0.5}\\ (X_A^k\left(t\right)+X_B^k\left(t\right)+X_C^k\left(t\right))/3& \mathit{other}\end{array}\right)$$

where, $X^j(t+1)$ represents the value of the next iteration of the $j$ dimension of individual C, $Q$ and $R$ represent two individuals randomly selected from the population, and $X_Q^j\left(t\right)$ and $X_R^j\left(t\right)$ represent the value of the $j$ dimension of the current iteration of the randomly selected individuals. Similarly, $X_A^k\left(t\right)$ represents the value of the $j$ dimension of the current iteration of individual A, $X_B^k\left(t\right)$ represents the value of the $j$ dimension of the current iteration of individual B, and $X_C^k\left(t\right)$ represents the value of the $j$ dimension of the current iteration of individual C.

It can be seen that we let three outstanding individuals carry out local development, and other individuals carry out HHO original update. At the same time, we assign the optimal position to individual a in the form of decreasing; the later the algorithm is, the smaller the replacement probability is so that the algorithm can be fully developed locally in the explored field. Both individuals B and C are related to individual A, which can strengthen the communication between excellent individuals. It can be seen that the update strategy of these three excellent individuals is simpler than the original HHO. In other words, EHHO runs faster than HHO. This is also the purpose of our algorithm improvement, which can not only make the algorithm have faster convergence speed and accuracy but also make the algorithm run faster and have better accuracy in processing feature selection tasks without increasing the time complexity.

c) An introduction to HHO that enhances hierarchy.

This section details EHHO and binary EHHO (bEHHO).

HHO based on enhanced hierarchy (EHHO)

Algorithm 2 is the pseudocode of EHHO.

Algorithm 2 Pseudo-code of EHHO. —

1. Initialize the parameters$\mathit{popsize}$,$\mathit{MaxFes}$;
2. Initialize a set of search agents (solutions) ($X$);
3. While ($t⩽MaxFes$).
4.  Calculate each of the search hawks by the objective function;
5.  Update$X_{\mathit{rabbit}}$(best loaction) and$\mathit{bestfitness}$;
6.  For i = 1 to$\mathit{popsize}$.
7.   Update the $E$ by Eq. (3);
8.   Update the$J$;
9.   If ($X\Rightarrow A$).
10.    Update the position of search agents using Eq. (12), Eq. (13);
11.   ElseIf ($X\Rightarrow B$).
12.    Update the position of search agents using Eq. (14);
13.   ElseIf ($X\Rightarrow C$).
14.    Update the position of search agents using Eq. (15);
15.   Else.
16.    If ($\left|E\right|⩾1$).
17.     Update the position of search agents using Eq. (1);
18.    End If.
19.    If ($\left|E\right|<1$).
20.     If ($0.5⩽\left|E\right|<1$ and $r⩾0.5$).
21.      Update the position of search agents using Eq. (4);
22.     End If.
23.     If ($\left|E\right|<0.5$ and $r⩾0.5$).
24.      Update the position of search agents using Eq. (5);
25.     End If.
26.     If ($0.5⩽\left|E\right|<1$ and $r<0.5$).
27.      Update the position of search agents using Eq. (6), Eq. (7), Eq. (8);
28.     End If.
29.     If ($\left|E\right|<0.5$ and $r<0.5$).
30.      Update the position of search agents using Eq. (9), Eq. (10), Eq. (11);
31.     End If.
32.    End If.
33.   End If.
34.  End For.
35. End While.
36. Return$X_{\mathit{rabbit}}$ and$\mathit{bestfitness}$.

Binary EHHO for feature selection problems

In order to make up for the weakness of HHO in local development, we propose EHHO, which can not only improve the convergence speed of the algorithm but also improve the algorithm's accuracy by classifying the population and performing different positions for different levels. In the application of feature selection, EHHO can accelerate the speed of feature selection and improve classification accuracy. At the same time, the running time is better than the original HHO. Next, we apply EHHOto feature selection.

K-nearest neighbour classifier

K-Nearest Neighbor (KNN) [80] is a common simple classification method. Its central premise is that if the majority of the K samples closest to a sample fall into a particular category, the sample likewise corresponds to that group and shares the features of the samples in that category. Generally speaking, it is “The minority obeys the majority”. Because the KNN method is simple, easy to understand and implement, and not susceptible to small error probability, it is widely used in text classification [81], [82], [83], image recognition [84], [85], medical processing [86], and water resources management [87]. The most commonly used Euclidean distance is selected in this paper, and the specific mathematical formula is shown in Eq.(16).

$$distance\left(M,Q\right)=\sqrt{\sum _{k=1}^n{\left(M_k-Q_k\right)}^2}$$

where $M$ represents the samples in the training set. $Q$ represents the samples in the test set. $n$ represents the dimension of the sample.

Binary EHHO

The feature selection problem can be regarded as a discrete combinatorial optimization problem. We express the solution through binary “0″ and ”1″, where “0″ means that the feature is not selected and ”1″ means that the feature is selected [88], [89]. This requires us to convert the proposed algorithm into an algorithm that can handle binary problems. The mathematical definition of the transfer function we use is shown in Eq. (17).

$$T\left(X_i^j\left(t\right)\right)=\left|tanh\left(X_i^j\left(t\right)\right)\right|$$

At the same time, we use ten cross-validations to segment the data set to ensure the fairness of the experiment and use Eq. (18) to update the position.

$$X_i^j\left(t+1\right)\left\{\begin{array}{cc}1& \mathit{if}\text{rand}⩾\text{T(}{X}_i^j\left(t\right))\\ 0& \mathit{if}\text{rand < T(}{X}_i^j\left(t\right))\end{array}\right)$$

If a very high classification accuracy is achieved with a small number of features in an experiment, the classification effect is very good [90]. However, effective algorithms are generally not easy to observe directly through the data, which requires an indicator to evaluate the accuracy of the selected features and classification. We choose Eq. (19), Eq. (20), and Eq. (21) as the objective function.

$$\mathit{Fitness}=\alpha ·{\gamma }_R+\beta ·\frac{\left|\mathit{SL}\right|}{\left|\mathit{FN}\right|}$$

$${\gamma }_R=1-Accuracy$$

$$\alpha +\beta =1$$

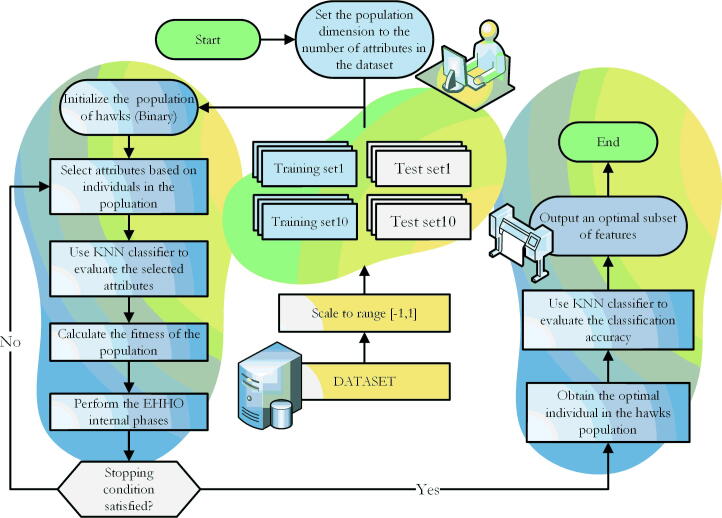
where the parameter $\alpha$ is set to 0.95, $\mathit{Accuracy}$ represents the classification accuracy of the KNN classifier, ${\gamma }_R$ is the classification error rate, $\left|\mathit{SL}\right|$ represents the number of selected features. $\left|\mathit{FN}\right|$ represents the total number of features in this data set. The flowchart of bEHHO is shown in Fig. 1.

Fig. 1.

The feature selection process using the bEHHO on the UCI dataset.

Computational complexity analysis

The time complexity of EHHO is mainly affected by the initialization population, fitness assessment, and individual location update. For better analysis, we define $\text{N}$ as the population size, $\text{D}$ as the dimension of the problem and $M$ as the maximum number of iterations. The population size and problem dimension affect the time complexity of initializing population, so the time complexity of initializing population is$O\left(N\ast D\right)$. Fitness evaluation is carried out at each iteration, so the time complexity of fitness evaluation is$O\left(\text{N}\ast D\ast M\right)$. Individuals will update their positions at each iteration, starting with the first three individuals whose time complexity of position update is$O\left(3\ast \text{D}\ast M\right)$. And then the other individuals, their position update is the original HHO position update, time complexity is$O\left((N-3)\ast D\ast M\right)$. Therefore, the time complexity required by EHHO for individual location update is$O\left(N\ast D\ast M\right)$. In summary, the total time complexity of EHHO is$O\left(2\ast N\ast D\ast M+N\ast D\right)$.

Experiments and analysis of results

In order to evaluate the performance of EHHO, a large number of experiments have been carried out in this section. First, we compare EHHO with 7 classic optimizers, 8 advanced improved algorithms, 2 newly proposed improved algorithms, and 1 HHO improvement on 23 classic test sets. At the same time, in order to evaluate the algorithm more objectively, we use the nonparametric statistical test Wilcoxon signed rank test to estimate whether the improved algorithm has statistical significance. The statistical significance level of the test is set to 0.05, and the symbol “+ / = / -” indicates that EHHO is better than, equal to, and lower than other optimizers, respectively. Finally, the Friedman test further analyzes the average performance of all test algorithms. The feature selection problem is used to evaluate the optimization ability of EHHO to deal with discrete problems.

We compared EHHO with 7 original optimizers, 8 excellent improved optimization algorithms, 2 optimizers proposed in recent years, and 1 excellent improved HHO on 23 classic test sets and verified the excellent performance of EHHO.

In comparison with other algorithms section, we compared EHHO with 7 original optimizers, 8 excellent improved optimization algorithms, 2 optimizers proposed in recent years, and 1 excellent improved HHO on 23 classic test sets, and verified the excellent performance of EHHO. In real-world optimization of feature selection section experiments, EHHO is used to deal with the feature selection problem of thirty datasets from the UCI machine learning library, including more than 10 high-dimensional datasets.

Ethics statement

All tests are run in MATLAB R2018b on Windows 11 with 16 GB memory and i7-11800H CPU (2.30 GHz). To avoid the influence of random conditions, when evaluating 23 classic test sets, the overall size of the evaluated optimizer is uniformly set to 30, the maximum evaluation times are set to 300,000, and all algorithms run 30 times. The feature selection experiment's data sets are all UCI public data sets. The iteration times of bEHHO and the other six algorithms are 50, the population size is 20, and 10 cross-validations are carried out.

Comparison with other algorithms

To verify the performance of EHHO, we compared EHHO with 7 original optimizers, 8 excellent improved optimization algorithms, 2 optimizers proposed in recent years, and 1 excellent improved HHO on 23 classic test sets. The 7 original optimizers include DE, ABC [20], SSA, PSO, MFO, GWO and HHO [25]. The 8 excellent improved optimization algorithms include BLPSO [91], ALCPSO [92], CLPSO [93], LSHADE [94], JDE [95], JADE [96], SADE [97] and SHADE [98]. The 2 recently proposed algorithms and an improved HHO algorithm are RDWOA [99], RDSSA [100], and CCNMHHO [101], respectively. We use 23 classical functions as test functions. Their final results are shown in Table 1.

Table 1.

Comparison results with other algorithms.

	Rank	+/=/-	ARV
EHHO	1	∼	5.3043
DE	4	8/10/5	6.5652
ABC	10	13/6/4	7.7391
SSA	17	17/2/4	13.6087
PSO	19	20/0/3	17.8261
MFO	18	16/7/0	15
GWO	14	15/5/3	10.87
HHO	13	14/8/1	8.8696
BLPSO	3	9/9/5	5.6522
ALCPSO	15	14/6/3	10.9565
CLPSO	2	8/11/4	5.5652
LSHADE	16	14/5/4	11.3913
JDE	6	12/7/4	6.7826
JADE	5	9/10/4	6.6522
SADE	8	12/5/6	7.6522
SHADE	11	12/7/4	8.087
RDWOA	12	7/11/5	8.3043
RDSSA	7	10/9/4	6.9565
CCNMHHO	9	11/6/6	7.6957

It can be seen from Table 1 that EHHO ranks first among all algorithms and has reached the optimal value in F1, F2, F3, F4, F6, F9, and F11. Compared with the original HHO, 15 of the 23 functions are better than HHO, which shows that EHHO has a very strong optimization ability.

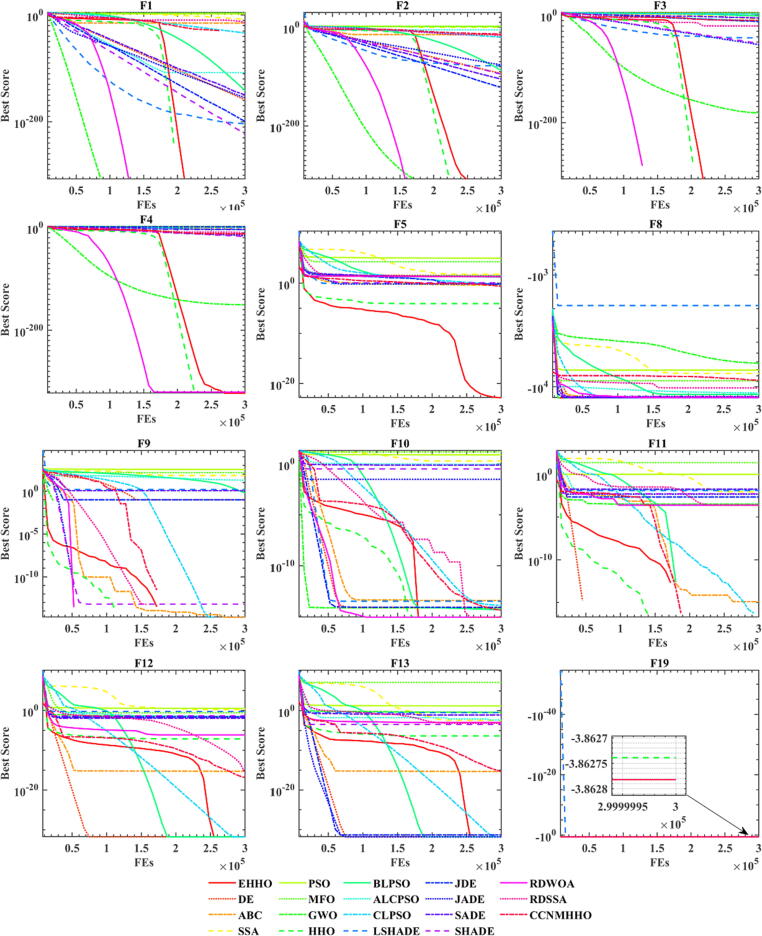
In order to more intuitively and visually show the specific changes of EHHO and other algorithms and the changes of the optimal value in the iterative process, it can be reflected by the changes of the convergence curve in the iterative process. The specific iteration diagram is shown in Fig. 2. The abscissa represents the number of iterations of the algorithm, and the ordinate represents the optimal solution value obtained by the running algorithm. As the number of iterations increases, the algorithm will gradually converge according to the calculation formula and find the minimum value of the objective function. The smaller the minimum value obtained by the algorithm and the faster the convergence speed, the better the algorithm's performance.

Fig. 2.

Convergence curves of the EHHO and other algorithms on 12 functions.

It can be seen from Fig. 2 that although EHHO has not had the fastest convergence speed in some functions, it has the lowest convergence value. Most algorithms have fallen into local optimization on functions such as F5, F12, and F13, but EHHO can avoid local optimization. It can also be seen that compared with the original HHO, EHHO significantly improved convergence speed. This is because the addition of hierarchy can make the algorithm exploration and development more balanced, and strengthen the exchange of excellent individuals, making the algorithm better jump out of local optimization. It can be seen that the hierarchy can make up for the defects of the algorithm in local development.

It can be seen from Table 1 and Fig. 2 that although EHHO has not had the fastest convergence speed in many functions, almost all of them have the smallest convergence value. In some functions, such as F5 and F19, all algorithms have fallen into local optimization, but EHHO can still converge. This is why EHHO can get first place in Table 1. Moreover, compared with CLPSO, which ranked second, EHHO has 19 functions superior to or equal to CLPSO. Compared with the original HHO, there are 22 better than or equal to the original HHO, and the running speed will be faster (in the section Experiences on real-world optimization of feature selection, the running time will be compared). That is to say, EHHO can achieve good optimization effects and accuracy with less running time.

Experiments on real-world optimization of feature selection

We have verified the application of EHHO in feature selection on thirty famous UCI datasets [102] and compared EHHO with six optimizers, including the original HHO. Similarly, high-dimensional datasets can best reflect the performance and robustness of an algorithm. In order to reflect the performance of EHHO and other algorithms, we have selected more than ten high-dimensional datasets. For the fairness of the experiment, as per rules in previous works [103], [104], [105], each data set is divided into two groups, namely, the training set and the test set. The test adopts the ten cross-validation technology to evaluate the results.

Standard of evaluation of experiments

In order to prove the optimization effect of the optimization algorithm in the feature selection process and intuitively reflect each algorithm's advantages and disadvantages, we use the following criteria to evaluate each optimization algorithm [106].

• •Average fitness ($\overline{\mathit{Fitness}}$): The average fitness value of the solution run $M$ times for each classification method on its test set. The calculation formula is shown in Eq. (22).

$$\overline{\text{Fitness}}\text{=}\frac{1}{M}\sum _{i=1}^M\text{fitness}\left(\text{i}\right)$$

• •Average classification error rate ($\overline{\mathit{Error}}$): The average classification error rate of each classification method running $M$ solutions. The calculation formula is shown in Eq. (23).

$$\overline{\text{Error}}\text{=}\frac{1}{M}\sum _{i=1}^M\left(1-Accuracy\left(i\right)\right)$$

• •Average number of selected features ($\overline{Features\_num}$): Number of selected features for each classification method to run $M$ times. The calculation formula is shown in Eq. (24).

$$\overline{Features\_num}\text{=}\frac{1}{M}\sum _{i=1}^M\text{S}ize\left(i\right)$$

• •Average running time ($\overline{\mathit{Time}}$): The average running time of the classification method for each test sample. The calculation formula is shown in Eq. (25).

$$\overline{\mathit{Time}}\text{=}\frac{1}{M}\sum _{i=1}^M\text{Runtime}\left(i\right)$$

where, $\text{fitness}\left(\text{i}\right)$ represents the fitness value obtained for the i-th time of method operation; $Accuracy\left(i\right)$ represents the classification accuracy of the i-th operation of the method; $\text{S}ize\left(i\right)$ is the number of features selected for the i-th solution of method operation; $\text{Runtime}\left(i\right)$ represents the time consumed by the method for the i-th time.

Experimental results and analysis of feature selection

To further verify the performance of the proposed EHHO, we compared EHHO with bPSO [107], bBA [108], bSSA [109], bWOA [110], bSMA [111], bHHO [112], and thirty classic data sets of UCI. In order to better represent the experimental results, we evaluated the results according to the classification error rate, average fitness, number of selected features, and running time. In addition, the Freidman test was used to sort the average value of the results, column rank was used for statistics, and average ranking value (ARV) was used for comparison. We set all tests based on fair comparison rules following past works in AI literature [[113], [114]]. Table 2 shows the fitness comparison between bEHHO and the other six optimizers.

Table 2.

Comparison between the developed bEHHO and other binary meta-heuristic algorithms on average fitness values.

Dataset	Metric	bEHHO	bPSO	bBA	bSSA	bWOA	bSMA	bHHO
Australian	Avg	9.7585E−02	1.0257E−01	1.4246E−01	1.0752E−01	1.0515E−01	1.0827E−01	1.0577E−01
	Std	3.0484E−02	2.7547E−02	2.5905E−02	1.7704E−02	1.6514E−02	1.9314E−02	2.6000E−02
blood	Avg	6.2500E−03	7.1023E−03	4.7565E−02	8.2386E−03	8.5227E−03	1.1648E−02	7.6705E−03
	Std	5.5338E−03	4.2843E−03	6.2941E−02	6.4211E−03	1.6071E−03	2.2523E−−03	5.4244E−03
Brain_Tumor1	Avg	4.5855E−02	7.3951E−02	1.0087E−01	6.1337E−02	7.8288E−02	6.5463E−02	6.1516E−02
	Std	6.6811E−02	6.9885E−02	6.2155E−02	5.6040E−02	5.4523E−02	5.3100E−02	5.1299E−02
Brain_Tumor2	Avg	9.6672E−02	1.4479E−01	1.0252E−01	1.3076E−01	1.3044E−01	7.5781E−02	9.6672E−02
	Std	9.7414E−02	9.4463E−02	1.2496E−01	9.8261E−02	1.0213E−01	1.4158E−01	8.8423E−02
Breastcancer	Avg	2.6457E−02	3.0819E−02	4.5088E−02	3.2732E−02	3.2563E−02	3.3817E−02	3.0936E−02
	Std	9.5983E−03	1.8343E−−02	1.5741E−02	1.6129E−02	6.6384E−03	1.6487E−02	1.6988E−02
CNS	Avg	8.9650E−02	1.3237E−01	2.0577E−01	1.2422E−01	1.1431E−01	1.0750E−01	1.2220E−01
	Std	8.2063E−02	1.2957E−01	1.6377E−01	1.1169E−01	8.4105E−02	1.1483E−01	7.7362E−02
Congress	Avg	2.2670E−02	2.5343E−02	4.0520E−02	2.9980E−02	2.7297E−02	3.0577E−02	2.3759E−02
	Std	2.1543E−02	1.8567E−02	1.8227E−02	1.1569E−02	2.2028E−02	2.0530E−02	1.9739E−02
DLCBL	Avg	6.2242E−03	3.6820E−02	5.7800E−02	2.0457E−02	2.5768E−02	3.5907E−02	1.8290E−02
	Std	1.1271E−03	4.2972E−02	8.8813E−02	3.5972E−02	3.8475E−02	3.7499E−02	3.7113E−02
glass	Avg	1.0954E−01	1.2505E−01	1.7949E−01	1.1728E−01	1.4524E−01	1.2021E−01	1.3146E−01
	Std	6.2248E−02	4.9067E−02	5.7804E−02	5.0693E−02	5.0082E−02	5.1540E−02	5.2557E−02
Heart	Avg	8.5641E−02	1.0279E−01	1.7745E−01	1.1758E−01	1.0202E−01	9.2621E−02	9.9274E−02
	Std	4.4378E−02	4.4304E−02	4.0053E−02	1.8850E−02	3.0193E−02	4.5428E−02	3.0570E−02
hepatitisfulldata	Avg	2.2253E−02	2.2649E−02	7.6516E−02	3.2930E−02	3.0692E−02	2.9376E−02	2.8717E−02
	Std	1.9113E−02	2.2079E−02	3.3453E−02	2.3419E−02	2.6034E−02	2.2053E−02	2.5375E−02
Ionosphere	Avg	2.0866E−02	2.6530E−02	7.0488E−02	3.5118E−02	3.3874E-02	3.8719E−02	3.1887E−02
	Std	1.2822E−02	1.9478E−02	1.6041E−02	1.3229E−02	1.2704E−02	1.4975E−02	1.6200E−02
JPNdata	Avg	2.4771E−02	5.1208E−02	1.0509E−01	4.0542E−02	3.5000E−02	3.3208E−02	5.2765E−02
	Std	2.6084E−02	4.5137E−02	3.9127E−02	4.5743E−02	4.4375E−02	3.1234E−02	3.2475E−02
Leukemia	Avg	6.9236E−03	2.3511E−02	1.7214E−02	1.0087E−02	1.5095E−02	2.4175E−02	7.1157E−−03
	Std	2.4916E−−03	2.1302E−04	2.1385E−03	8.0844E−03	2.7639E−03	2.0171E−04	1.4686E−03
Leukemia1	Avg	7.3972E−03	2.3271E−02	3.2656E−02	7.9566E−03	1.4242E−02	2.4024E−02	7.6816E−03
	Std	1.9700E−03	3.7594E−04	4.0773E−02	8.1800E−03	2.4269E−03	1.3090E−04	1.7517E−03
Leukemia2	Avg	5.8281E−03	3.5639E−02	4.3521E−02	8.4009E−03	2.7319E−02	3.7881E−02	6.8477E−03
	Std	1.3690E−03	3.7610E−02	5.3762E−02	7.4337E−03	4.1967E−02	4.2908E−02	1.8683E−03
Lung_Cancer	Avg	2.6674E−02	5.1853E−02	4.7733E−02	4.0110E−02	4.3534E−02	5.4129E−02	3.2199E−02
	Std	2.2560E−02	3.2091E−02	2.5160E−02	2.9712E−02	4.1052E−02	5.0094E−02	3.2678E−02
lungcancer_3class	Avg	8.3036E−03	1.1518E−02	1.3057E−01	3.6429E−02	7.1935E−02	4.0714E−02	8.6607E−03
	Std	3.7658E−03	4.1974E−03	1.7946E−01	7.1953E−02	1.1721E−01	7.5136E−02	2.8871E−03
penglung	Avg	6.3846E−03	4.1379E−02	6.2543E−02	1.0938E−02	6.0057E−02	4.5119E−02	3.5662E−02
	Std	1.3019E−03	4.8806E−02	7.5764E−02	5.6169E−03	8.0063E−02	4.9652E−02	5.8529E−02
Prostate_Tumor	Avg	5.4771E−02	7.1503E−02	1.4779E−01	7.2852E−02	6.4615E−02	7.1399E−02	5.9989E−02
	Std	6.2381E-02	8.0624E−−02	1.1525E−01	6.7979E−02	6.8109E−02	4.9367E−02	4.3918E−02
Sonar	Avg	1.7333E−02	2.2107E−02	6.5113E−02	4.0571E−02	2.6440E−02	2.9425E−02	2.4750E−02
	Std	4.9348E−03	1.6912E−02	2.1789E−02	2.3100E−02	1.3662E−02	1.8329E−02	1.4840E−02
SRBCT	Avg	6.6789E−03	2.2303E−02	4.1155E−02	2.3002E−02	1.4805E−02	2.3687E−02	6.6811E−03
	Std	1.7049E−03	6.0807E−04	4.6884E−02	3.7227E−02	3.9572E−03	4.3725E−04	1.8935E−03
thyroid_2class	Avg	2.1618E−01	2.2604E−01	2.5094E−01	2.3622E−01	2.4185E−01	2.2907E−01	2.2504E−01
	Std	3.8167E−02	6.2739E−02	5.9681E−02	5.1007E−02	4.7313E−02	5.7220E−02	7.9832E−02
Tumors_9	Avg	2.5445E−02	6.4943E−02	1.9426E−01	5.7946E−02	6.5823E−02	5.6279E−02	6.6829E−02
	Std	4.3415E−02	6.7352E−02	1.6515E−01	9.7354E−02	7.8684E−02	1.0020E−01	7.5872E−02
Tumors_11	Avg	5.3933E−02	7.9013E−02	1.0561E−01	7.0922E−02	8.6107E−02	8.2210E−02	6.1966E−02
	Std	5.6454E−02	3.7298E−02	5.8900E−02	5.4279E−02	6.2308E−02	4.7651E−02	6.1288E−02
USAdata	Avg	2.4118E−01	2.4613E−01	2.8659E−01	2.5302E−01	2.5465E−01	2.5251E−01	2.4553E−01
	Std	2.3091E−02	1.6147E−02	3.0761E−02	1.6995E−02	1.1420E−02	1.8095E−02	2.0967E−02
Vote	Avg	2.2007E−02	2.8333E−02	4.6225E−02	2.8924E−02	2.5031E−02	2.6281E−02	2.5065E−02
	Std	1.6001E−02	2.9362E−02	2.6232E−02	1.9060E−02	1.7305E−02	1.9072E−02	2.2894E−02
wdbc	Avg	1.6500E−02	1.7667E−02	3.6726E−02	2.5609E−02	2.7030E−02	2.5335E−02	2.2667E−02
	Std	6.5475E−03	8.8262E−03	1.4610E−02	1.6207E−02	1.4310E−02	1.0862E−02	1.2771E−02
Wielaw	Avg	6.0897E−02	6.4697E−02	1.3719E−01	9.2155E−02	8.5019E−02	7.7767E−02	6.9519E−02
	Std	4.2724E−02	3.5887E−02	5.4339E−02	4.1255E−02	5.0144E−02	3.3475E−02	3.1863E−02
Wine	Avg	1.0769E−02	1.0769E−02	3.3632E−02	1.4615E−02	1.4231E−02	1.3846E−02	1.2308E−02
	Std	2.4325E−03	3.9723E−03	2.3595E−02	3.9723E−03	3.6488E−03	1.9861E−03	3.5344E−03
Overall Rank	+/=/−	∼	29/1/0	30/0/0	30/0/0	30/0/0	30/0/0	30/0/0
	Avg	1.00	3.70	6.87	4.33	4.53	4.63	2.90
	Rank	1	3	7	4	5	6	2

Fitness balances the classification accuracy and the number of selected features. The lower the value, the higher the classification accuracy can be achieved by selecting a few features. As can be seen from Table 2, bEHHO is the smallest among the thirty UCI data sets, ranking first in the final ranking. On low-dimensional datasets such as blood and Breastcancer, bEHHO is greatly improved compared with other algorithms. Like Brain_Tumor1 and Tumors_11 and other high-dimensional data sets, the fitness of bEHHO is still the lowest. Std is smaller for most of them than the other six algorithms. This is because the addition of hierarchy can enable the algorithm to be fully developed locally, make up for the weakness of the algorithm in the local opening, and strengthen the relationship between populations. Table 3 shows the classification error rate of bEHHO and the other six algorithms. According to Table 3, the proposed bEHHO classification method has the lowest classification error rate on thirty UCI datasets, ranking first in the final overall ranking, which shows that bEHHO has excellent classification performance.

Table 3.

Comparison between the developed bEHHO and other binary metaheuristic algorithms on average error values of KNN.

Dataset	Metric	bEHHO	bPSO	bBA	bSSA	bWOA	bSMA	bHHO
Australian	Avg	8.1292E−02	8.5410E−02	2.0155E−01	8.8370E−02	8.7002E−02	8.9904E−02	8.9904E−02
	Std	3.2624E−02	2.6396E−02	8.5601E−02	2.3010E−02	1.6987E−02	1.9263E−02	2.8974E−02
blood	Avg	0.0000E + 00	0.0000E + 00	1.1429E−01	0.0000E + 00	0.0000E + 00	0.0000E + 00	0.0000E + 00
	Std	0.0000E + 00	0.0000E + 00	1.0581E−01	0.0000E + 00	0.0000E + 00	0.0000E + 00	0.0000E + 00
Brain_Tumor1	Avg	4.1111E−02	5.3333E−02	1.3000E−01	5.2222E−02	6.5556E−02	4.3333E−02	5.4444E−02
	Std	7.1059E−02	7.3479E−02	8.5755E−02	5.5196E−02	5.6522E−02	5.6035E−02	5.7485E−02
Brain_Tumor2	Avg	6.6260E−02	7.6667E−02	2.6500E−01	9.6667E−02	1.2167E−01	1.1167E−01	7.0952E−02
	Std	1.0124E−01	9.9443E−02	1.9696E−01	1.0238E−01	1.0659E−01	1.4908E−01	9.3002E−02
Breastcancer	Avg	8.5513E−03	1.1389E−02	5.7289E−02	1.2817E−02	1.1470E−02	1.5714E−02	1.1511E−02
	Std	1.2036E−02	1.4617E−02	2.5317E−02	1.4157E−02	9.0500E−03	1.5721E−02	1.6316E−02
CNS	Avg	8.3333E−02	1.1429E−01	3.6524E−01	1.1667E−01	1.0095E−01	8.6667E−02	1.1667E−01
	Std	8.7841E−02	1.3645E−01	1.2856E−01	1.1249E−01	8.7943E−02	1.2090E−01	8.0508E−02
Congress	Avg	1.1364E−02	1.3848E−02	1.1263E−01	1.3795E−02	1.1628E−02	1.6068E−02	1.1522E−02
	Std	2.2087E−02	1.6195E−02	7.7276E−02	1.1875E−02	1.9764E−02	1.8920E−02	1.6197E−02
DLCBL	Avg	0.0000E + 00	1.4286E−02	1.3036E−01	1.2500E−02	1.2500E−02	1.2500E−02	1.2500E−02
	Std	0.0000E + 00	4.5175E−02	1.0749E−01	3.9528E−02	3.9528E−02	3.9528E−02	3.9528E−02
glass	Avg	9.3668E−02	1.0648E−01	3.3366E−01	9.8894E−02	1.2949E−01	1.0140E−01	1.1616E−01
	Std	6.6554E−02	5.5435E−02	1.7501E−01	5.6624E−02	5.1048E−02	5.3886E−02	5.3691E−02
Heart	Avg	6.6667E−02	8.1481E−02	2.0741E−01	9.2593E−02	8.1481E−02	7.0370E−02	7.7778E−02
	Std	5.1793E−02	4.8762E−02	8.4096E−02	1.9520E−02	3.4035E−02	4.7655E−02	3.2429E−02
hepatitisfulldata	Avg	6.2500E−03	6.6667E−03	1.6797E−01	1.3333E−02	1.2917E−02	1.2917E−02	1.2500E−02
	Std	1.9764E−02	2.1082E−02	9.1223E−02	2.8109E−02	2.7248E−02	2.7248E−02	2.6352E−02
Ionosphere	Avg	5.5556E−03	1.1517E−02	1.1971E−01	1.7152E−02	1.1354E−02	2.0014E−02	1.4216E−02
	Std	1.1712E−02	2.0335E−02	3.4981E−02	1.4772E−02	1.4665E−02	1.9581E−02	1.4997E−02
JPNdata	Avg	1.2917E−02	3.9167E−02	2.0310E−01	2.5833E−02	2.0000E−02	1.9167E−02	3.9226E−02
	Std	2.7248E−02	4.6114E−02	9.8054E−02	4.5846E−02	4.4997E−02	3.0882E−02	3.3867E−02
Leukemia	Avg	0.0000E + 00	0.0000E + 00	1.0119E−01	0.0000E + 00	0.0000E + 00	0.0000E + 00	0.0000E + 00
	Std	0.0000E + 00	0.0000E + 00	9.8009E−02	0.0000E + 00	0.0000E + 00	0.0000E + 00	0.0000E + 00
Leukemia1	Avg	0.0000E + 00	0.0000E + 00	6.8452E−02	0.0000E + 00	0.0000E + 00	0.0000E + 00	0.0000E + 00
	Std	0.0000E + 00	0.0000E + 00	9.3958E−02	0.0000E + 00	0.0000E + 00	0.0000E + 00	0.0000E + 00
Leukemia2	Avg	0.0000E + 00	1.2500E−02	6.9643E−02	0.0000E + 00	1.4286E−02	1.4286E−02	0.0000E + 00
	Std	0.0000E + 00	3.9528E−02	7.3603E−02	0.0000E + 00	4.5175E−02	4.5175E−02	0.0000E + 00
Lung_Cancer	Avg	1.9549E−02	2.9286E−02	5.9311E−02	3.0104E−02	3.0050E−02	3.1190E−02	2.4311E−02
	Std	2.5279E−02	3.3766E−02	3.1087E−02	2.6027E−02	4.2322E−02	5.2794E−02	3.4100E−02
lungcancer_3class	Avg	0.0000E + 00	0.0000E + 00	3.9167E−01	2.5000E−02	5.8333E−02	2.5000E−02	0.0000E + 00
	Std	0.0000E + 00	0.0000E + 00	2.3257E−01	7.9057E−02	1.2454E−01	7.9057E−02	0.0000E + 00
penglung	Avg	0.0000E + 00	2.4286E−02	9.5794E−02	0.0000E + 00	4.8611E−02	2.5000E−02	2.9167E−02
	Std	0.0000E + 00	5.2186E−02	8.7993E−02	0.0000E + 00	8.6178E−02	5.2705E−02	6.2268E−02
Prostate_Tumor	Avg	4.7273E−02	5.0000E−02	1.8273E−01	6.0000E−02	4.8182E−02	4.9091E−02	4.9091E−02
	Std	6.5807E−02	8.4984E−02	1.5531E−01	6.9921E−02	6.9373E−02	5.1817E−02	5.1817E−02
Sonar	Avg	0.0000E + 00	4.7619E−03	1.3437E−01	1.4286E−02	4.7619E−03	9.3074E−03	5.0000E−03
	Std	0.0000E + 00	1.5058E−02	8.6979E−02	2.3002E−02	1.5058E−02	1.9628E−02	1.5811E−02
SRBCT	Avg	0.0000E + 00	0.0000E + 00	6.9444E−02	1.2500E−02	0.0000E + 00	0.0000E + 00	0.0000E + 00
	Std	0.0000E + 00	0.0000E + 00	1.4164E−01	3.9528E−02	0.0000E + 00	0.0000E + 00	0.0000E + 00
thyroid_2class	Avg	2.0322E−01	2.0833E−01	2.8901E−01	2.1971E−01	2.3023E−01	2.1415E−01	2.0860E−01
	Std	4.1517E−02	6.8626E−02	1.1606E−01	5.5405E−02	5.2935E−02	6.2951E−02	8.6781E−02
Tumors_9	Avg	1.4286E−02	4.3452E−02	4.2190E−01	4.5000E−02	4.6786E−02	3.3333E−02	5.5952E−02
	Std	4.5175E−02	7.0656E−02	2.1689E−01	9.5598E−02	7.7563E−02	1.0541E−01	7.3128E−02
Tumors_11	Avg	4.5425E−02	5.7655E−02	1.3449E−01	5.3391E−02	6.8451E−02	6.0500E−02	5.2659E−02
	Std	5.8326E−02	3.9356E−02	8.8641E−02	5.7890E−02	6.5633E−02	5.0217E−02	6.4383E−02
USAdata	Avg	2.3545E−01	2.4014E−01	3.7112E−01	2.4529E−01	2.4700E−01	2.4527E−01	2.3845E−01
	Std	2.6472E−02	1.9244E−02	7.7078E−02	1.5426E−02	1.2980E−02	1.6981E−02	2.2238E−02
Vote	Avg	1.0007E−02	1.6667E−02	8.9162E−02	1.3341E−02	1.0230E−02	1.0230E−02	1.3226E−02
	Std	1.6122E−02	2.8328E−02	9.6982E−02	1.7231E−02	1.6475E−02	1.6475E−02	1.7077E−02
wdbc	Avg	3.5088E−03	3.5088E−03	4.9096E−02	6.9570E−03	8.8033E−03	8.7741E−03	5.2632E−03
	Std	7.3971E−03	7.3971E−03	2.2996E−02	1.2113E−02	1.2430E−02	9.2510E−03	1.1841E−02
Wielaw	Avg	4.5681E−02	4.9681E−02	2.2952E−01	7.0514E−02	6.6862E−02	5.8000E−02	5.0196E−02
	Std	4.1097E−02	3.7181E−02	9.5825E−02	4.4044E−02	5.2936E−02	3.4888E−02	3.3345E−02
Wine	Avg	0.0000E + 00	0.0000E + 00	1.5139E−01	0.0000E + 00	0.0000E + 00	0.0000E + 00	0.0000E + 00
	Std	0.0000E + 00	0.0000E + 00	1.0110E−01	0.0000E + 00	0.0000E + 00	0.0000E + 00	0.0000E + 00
Overall Rank	+/=/−	∼	23/7/0	30/0/0	24/6/0	25/5/0	25/5/0	23/7/0
	Avg	1.00	2.93	7.00	3.83	3.70	3.43	3.00
	Rank	1	2	7	6	5	4	3

According to the experimental results in Table 3 and Table 4, it is obvious that the proposed bEHHO classification method has the lowest classification error rate and a small number of selected features on thirty UCI datasets. In addition, twenty-three of the thirty datasets are better than the original bHHO, and seven are equal to the original bHHO. This is because the error rates of both bEHHO and bHHO are 0, which indicates that the improvement of bEHHO is meaningful and can have good classification accuracy. It can be seen from Table 4 that bEHHO, compared with other optimizers, uses fewer features on these thirty UCI test sets and has a higher accuracy rate, which indicates that bEHHO can obtain a higher accuracy rate with fewer features.

Table 4.

Comparison between the developed bEHHO and other binary metaheuristic algorithms on average of selected features.

Dataset	Metric	bEHHO	bPSO	bBA	bSSA	bWOA	bSMA	bHHO
Australian	Avg	5.7	6	6.4	6.6	6.3	6.4	5.7
	Std	1.95	1.41	1.51	2.55	1.42	1.08	2.41
blood	Avg	2.75	3.125	7.625	3.625	3.75	5.125	3.375
	Std	2.43	1.89	2.88	2.8253	0.71	0.99	2.39
Brain_Tumor1	Avg	805	2756.9	2420.6	1388.4	1895.6	2876.7	1159.6
	Std	304.1882	45.0542	110.5875	908.2962	550.2685	51.0056	717.1137
Brain_Tumor2	Avg	1591.7	4942.7	4204.7	2216.7	3146.7	5050.9	1736.7
	Std	518.6491	35.4057	106.9673	1965.385	573.201	46.0952	703.063
Breastcancer	Avg	3.3	3.6	3.6	3.7	3.9	3.4	3.6
	Std	1.1595	1.3499	1.6465	1.0593	1.3703	0.84327	0.96609
CNS	Avg	1494.7	3393.2	2867.3	1908	2624.8	3588.5	1621.2
	Std	368.8809	59.01	181.1973	1736.651	692.2772	142.1003	633.9469
Congress	Avg	3.8	3.9	5.9	5.4	5.2	4.9	4.1
	Std	2.3476	1.9692	1.8529	2.4585	2.3944	1.1005	2.331
DLCBL	Avg	680.8	2542.9	2227.1	938.7	1519.6	2628.6	701.7
	Std	123.2818	24.3011	134.8888	721.4128	448.2331	17.4878	130.4812
glass	Avg	3.7	4.3	3.7	4.2	4	4.3	3.8
	Std	0.82327	1.1595	1.1595	1.1353	1.0541	0.67495	0.63246
Heart	Avg	5.8	6.6	6.2	7.7	6.4	6.7	6.6
	Std	2.201	1.5055	1.8135	1.3375	0.84327	1.2517	1.5055
hepatitisfulldata	Avg	6.2	6.2	7.4	7.7	7	6.5	6.4
	Std	1.6865	1.6865	2.7968	3.2335	1.0541	2.1731	2.5473
Ionosphere	Avg	10.6	10.6	11.6	12.8	15.7	13.4	12.5
	Std	3.4059	0.84327	2.2211	4.638	2.7909	3.0984	4.3525
JPNdata	Avg	2.5	2.8	4.2	3.2	3.2	3	3.1
	Std	0.70711	1.0328	1.6193	1.3166	1.3166	1.3333	1.2867
Leukemia	Avg	987.3	3352.6	2842.3	1438.4	2152.5	3447.4	1014.7
	Std	355.3021	30.3762	246.8621	1152.842	394.1317	28.7642	209.4199
Leukemia1	Avg	2.0294E−02	2.4412E−02	3.8047E−02	3.4912E−02	2.6176E−02		2.8235E−02
	Std	788.1	2479.3	2113.6	847.7	1517.3	2559.5	818.4
Leukemia2	Avg	1308.4	5335.1	4577.9	1886	3086.3	5457.5	1537.3
	Std	307.3486	40.5036	181.7712	1668.865	802.4116	29.6732	419.4319
Lung_Cancer	Avg	2041.9	6056	5165.9	2900.6	3776.5	6173.5	2294.1
	Std	688.3479	44.6443	226.5845	2506.599	1501.793	51.7478	863.1049
lungcancer_3class	Avg	9.3	12.9	23.4	14.2	18.5	19	9.7
	Std	4.2177	4.7011	4.1419	8.9914	4.5522	2.4495	3.2335
penglung	Avg	41.5	119	128.3	71.1	90.2	138.9	51.7
	Std	8.4623	8.4984	9.2382	36.5101	24.1882	9.7005	19.2414
Prostate_Tumor	Avg	2072.8	5044.9	4167.5	3331.7	3960.3	5204.7	2806.5
	Std	423.7939	48.2089	279.8906	2371.038	1080.443	77.9872	1738.608
Sonar	Avg	20.8	21.1	22.3	32.4	26.3	24.7	24
	Std	5.9217	4.6774	6.2725	5.9104	6.1653	3.164	9.6724
SRBCT	Avg	308.3	1029.5	962.9	513.6	683.4	1093.4	308.4
	Std	78.6978	28.0684	88.1595	380.8759	182.6662	20.1836	87.4035
thyroid_2class	Avg	3.7	3.7	4.3	4.4	3.7	4.1	4.3
	Std	0.82327	1.6364	1.1595	0.96609	0.94868	1.1005	1.2517
Tumors_9	Avg	1359.8	2709.9	2191.1	1740.2	2448.1	2818.6	1566
	Std	722.5459	54.7387	289.4372	1266.72	846.8756	60.9247	1165.481
Tumors_11	Avg	2702	6076.2	5148.6	5063.6	5283.6	6200.1	2992.9
	Std	1241.907	89.8502	191.0696	1854.343	1128.624	75.1657	925.4537
USAdata	Avg	3.5	3.6	3.8	4	4	3.9	3.8
	Std	0.84984	0.69921	1.6865	0.94281	0.8165	0.99443	0.78881
Vote	Avg	4	4	6.7	5.2	4.9	5.3	4
	Std	2.1082	2.2608	1.1595	2.6583	2.6437	1.7029	2.6247
wdbc	Avg	7.9	8.6	12	11.4	11.2	10.2	10.6
	Std	2.4698	2.5033	3.1269	4.4272	4.341	1.8738	3.5653
Wielaw	Avg	10.5	10.5	12.1	15.1	12.9	13.6	13.1
	Std	4.8132	2.2236	3.4785	4.7947	2.5582	3.0623	4.9766
Wine	Avg	2.8	2.8	5.5	3.8	3.7	3.6	3.2
	Std	0.63246	1.0328	2.1731	1.0328	0.94868	0.5164	0.91894
Overall Rank	+/=/−	∼	24/6/0	29/1/0	30/0/0	29/1/0	30/0/0	28/2/0
	Avg	1.0000	3.80	4.90	4.63	4.50	5.73	2.70
	Rank	1	3	6	5	4	7	2

It can be seen from Table 4 that bEHHO can be classified with fewer features, and bEHHO is mostly smaller than other algorithms in Std, which indicates that bEHHO has strong robustness.

In a word, on thirty UCI test sets, the average classification fitness value, average error rate, and the average number of selected features of the proposed bEHHO classification method rank first, which verifies that bEHHO has excellent classification performance and good robustness in feature selection applications. Table 5 compares the running time of each UCI test set by bEHHO with the other six classification methods. It can be seen from Table 5 that bEHHO runs faster than the original bHHO. This is because we let the better individuals carry out local development while the worse ones continue bHHO operations, which can balance the relationship between global exploration and local development well.

Table 5.

Comparison between the developed bEHHO and other binary metaheuristic algorithms on average running time.

Dataset	Metric	bEHHO	bPSO	bBA	bSSA	bWOA	bSMA	bHHO
Australian	Avg	2.5456E + 00	2.3256E + 00	2.4305E + 00	1.7441E + 00	1.7026E + 00	1.6352E + 00	2.7612E + 00
	Std	3.0487E−01	2.6447E−01	5.2772E−01	2.3030E−01	2.0143E−01	1.9427E−01	3.5615E−01
blood	Avg	1.6421E + 00	1.2184E + 00	1.5277E + 00	1.1446E + 00	1.0455E + 00	1.0615E + 00	1.6892E + 00
	Std	4.5204E−02	3.0819E−02	9.5916E−02	3.4245E−02	1.8316E−02	2.7225E−02	4.2098E−02
Brain_Tumor1	Avg	1.1012E + 01	1.1396E + 01	1.1940E + 01	1.2719E + 01	1.5824E + 01	1.8115E + 01	1.1012E + 01
	Std	3.2280E + 00	2.1412E + 00	2.1669E + 00	2.0747E + 00	2.0209E + 00	1.9798E + 00	3.9661E + 00
Brain_Tumor2	Avg	1.5040E + 01	1.1619E + 01	1.1926E + 01	1.1253E + 01	1.3129E + 01	1.8038E + 01	1.6541E + 01
	Std	2.9740E + 00	2.4696E + 00	2.7923E + 00	2.5122E + 00	1.8231E + 00	1.6887E + 00	3.3561E + 00
Breastcancer	Avg	6.9356E + 00	6.2223E + 00	7.3109E + 00	5.0897E + 00	4.6625E + 00	4.5189E + 00	7.7419E + 00
	Std	6.6432E−01	4.2972E−01	6.2775E−01	4.6987E−01	5.0167E−01	3.9702E−01	6.2923E−01
CNS	Avg	1.2931E + 01	9.4815E + 00	9.6955E + 00	9.5173E + 00	1.0151E + 01	1.4029E + 01	1.3750E + 01
	Std	2.5611E + 00	1.9394E + 00	2.2507E + 00	1.9097E + 00	1.6882E + 00	1.3915E + 00	2.6176E + 00
Congress	Avg	2.1257E + 00	2.0968E + 00	2.1655E + 00	1.4864E + 00	1.4538E + 00	1.4689E + 00	2.4493E + 00
	Std	2.4998E−01	3.2360E−01	4.7292E−01	1.6050E−01	1.6833E−01	1.5932E−01	3.7654E−01
DLCBL	Avg	1.2417E + 01	9.2379E + 00	9.5032E + 00	9.1478E + 00	9.5910E + 00	1.2402E + 01	1.3278E + 01
	Std	2.4010E + 00	1.7698E + 00	2.1729E + 00	1.9147E + 00	1.7359E + 00	1.5505E + 00	2.6585E + 00
glass	Avg	1.8220E + 00	1.8808E + 00	1.9312E + 00	1.2610E + 00	1.1549E + 00	1.1836E + 00	1.9919E + 00
	Std	2.0978E−01	1.9703E−01	5.2488E−01	1.6192E−01	1.3877E−01	1.4529E−01	2.4861E−01
Heart	Avg	1.9941E + 00	1.9673E + 00	1.9944E + 00	1.3395E + 00	1.2062E + 00	1.2014E + 00	2.0972E + 00
	Std	2.3717E−01	2.8066E−01	3.0423E−01	1.7732E−01	1.0552E−01	1.4696E−01	2.4154E−01
hepatitisfulldata	Avg	1.7398E + 00	1.8350E + 00	1.9258E + 00	1.4397E + 00	1.2476E + 00	1.1384E + 00	1.8551E + 00
	Std	2.1706E−01	2.4539E−01	4.4970E−01	2.4617E−01	1.9066E−01	1.4439E−01	1.8870E−01
Ionosphere	Avg	1.9674E + 00	1.8892E + 00	2.0421E + 00	1.2830E + 00	1.2041E + 00	1.2207E + 00	2.0247E + 00
	Std	2.6006E−01	2.7601E−01	4.6228E−01	1.8974E−01	1.1895E−01	1.4617E−01	2.4545E−01
JPNdata	Avg	1.6331E + 00	1.7180E + 00	1.6978E + 00	1.1437E + 00	1.0326E + 00	1.0837E + 00	1.7432E + 00
	Std	2.0065E−01	2.0845E−01	5.1605E−01	1.3682E−01	1.0788E−01	1.3808E−01	2.0772E−01
Leukemia	Avg	1.5707E + 01	1.0494E + 01	1.0939E + 01	1.1428E + 01	1.2320E + 01	1.6703E + 01	1.6902E + 01
	Std	3.2916E + 00	2.0592E + 00	2.1716E + 00	2.2294E + 00	2.2436E + 00	2.4059E + 00	3.3966E + 00
Leukemia1	Avg	1.2111E + 01	8.1235E + 00	8.2039E + 00	8.5480E + 00	8.9884E + 00	1.2237E + 01	1.3391E + 01
	Std	2.4258E + 00	1.7476E + 00	1.7001E + 00	1.4621E + 00	1.5674E + 00	1.4498E + 00	2.8450E + 00
Leukemia2	Avg	2.4101E + 01	1.6840E + 01	1.7137E + 01	1.6824E + 01	1.9497E + 01	2.4402E + 01	2.6033E + 01
	Std	5.0338E + 00	3.5565E + 00	3.9870E + 00	3.7391E + 00	3.3138E + 00	2.8645E + 00	5.3062E + 00
Lung_Cancer	Avg	1.0817E + 02	6.8480E + 01	6.5007E + 01	7.8597E + 01	7.8123E + 01	7.3051E + 01	1.1461E + 02
	Std	2.3803E + 01	1.6325E + 01	1.5167E + 01	2.1295E + 01	1.6161E + 01	1.2095E + 01	2.6157E + 01
lungcancer_3class	Avg	1.6351E + 00	1.7154E + 00	1.6342E + 00	1.0791E + 00	9.7360E−01	1.0613E + 00	1.7208E + 00
	Std	2.1200E−01	2.4175E−01	4.2689E−01	1.4739E−01	1.0079E−01	1.3964E−01	2.0734E−01
penglung	Avg	1.9862E + 00	1.9654E + 00	2.0274E + 00	1.3184E + 00	1.2538E + 00	1.4094E + 00	2.1214E + 00
	Std	2.4947E−01	2.7493E−01	3.3040E−01	1.5691E−01	1.6044E−01	1.6907E−01	2.2316E−01
Prostate_Tumor	Avg	3.2220E + 01	2.2150E + 01	2.2104E + 01	2.3459E + 01	2.5397E + 01	2.8340E + 01	3.5628E + 01
	Std	6.3708E + 00	4.7348E + 00	5.0750E + 00	4.5152E + 00	4.4728E + 00	3.4674E + 00	7.3589E + 00
Sonar	Avg	1.8174E + 00	1.7940E + 00	1.9825E + 00	1.2515E + 00	1.1316E + 00	1.1779E + 00	1.8982E + 00
	Std	2.0724E−01	1.8718E−01	5.5815E−01	1.3860E−01	1.0481E−01	1.4337E−01	2.0551E−01
SRBCT	Avg	8.5203E + 00	5.9353E + 00	7.1348E + 00	6.8742E + 00	6.3304E + 00	9.4137E + 00	8.7569E + 00
	Std	1.4621E + 00	7.6526E−01	1.9298E + 00	1.1554E + 00	1.1581E + 00	1.6755E + 00	1.4430E + 00
thyroid_2class	Avg	2.0127E + 00	2.3603E + 00	1.3378E + 00	1.3640E + 00	1.3088E + 00	1.3332E + 00	2.2146E + 00
	Std	1.7736E−01	2.4255E−01	1.6898E−01	1.9413E−01	1.2477E−01	1.2102E−01	2.6032E−01
Tumors_9	Avg	1.0588E + 01	7.9485E + 00	8.2742E + 00	8.0051E + 00	8.6647E + 00	1.1932E + 01	1.1702E + 01
	Std	2.1545E + 00	1.4337E + 00	1.7759E + 00	1.4812E + 00	1.2187E + 00	1.2733E + 00	2.1247E + 00
Tumors_11	Avg	8.4459E + 01	5.5493E + 01	5.1799E + 01	6.7404E + 01	6.5174E + 01	5.3920E + 01	9.5390E + 01
	Std	1.7815E + 01	1.2820E + 01	1.2082E + 01	1.3190E + 01	1.1985E + 01	1.0258E + 01	2.1725E + 01
USAdata	Avg	6.1842E + 00	4.7895E + 00	4.8207E + 00	4.1431E + 00	4.1826E + 00	3.7407E + 00	6.6627E + 00
	Std	7.7398E−01	5.3575E−01	9.7842E−01	4.6876E−01	5.8177E−01	4.0967E−01	5.6774E−01
Vote	Avg	1.9280E + 00	1.9355E + 00	2.0276E + 00	1.3695E + 00	1.3731E + 00	1.3067E + 00	2.2452E + 00
	Std	1.8745E−01	2.8400E−01	4.5660E−01	1.8172E−01	1.7696E−01	1.7619E−01	2.9602E−01
wdbc	Avg	2.9862E + 00	3.3329E + 00	1.9280E + 00	2.0069E + 00	1.8905E + 00	1.8967E + 00	3.2636E + 00
	Std	3.5512E−01	9.9196E−01	1.9364E−01	2.0643E−01	2.3112E−01	1.8856E−01	4.2315E−01
Wielaw	Avg	1.8882E + 00	1.7782E + 00	1.9197E + 00	1.1672E + 00	1.0826E + 00	1.1197E + 00	1.8652E + 00
	Std	2.6600E−01	2.1713E−01	5.5846E−01	1.2012E−01	1.1491E−01	1.4015E−01	1.4324E−01
Wine	Avg	1.7356E + 00	1.8080E + 00	1.6966E + 00	1.2341E + 00	1.1147E + 00	1.1508E + 00	1.8718E + 00
	Std	1.5206E−01	2.5747E−01	1.3260E−01	1.7424E−01	1.3807E−01	1.2374E−01	1.8610E−01
Overall Rank	+/=/−	∼	8/0/22	11/0/19	0/0/30	0/0/30	7/0/23	29/0/1
	Avg	5.17	3.53	4.20	2.83	2.40	3.23	6.63
	Rank	6	4	5	2	1	3	7

According to the experimental results in Table 2- Table 5, the performance of bEHHO is significantly improved compared with bPSO, bBA, bSSA, bWOA, bSMA, and bHHO. Furthermore, the running time is significantly better than the original bHHO.

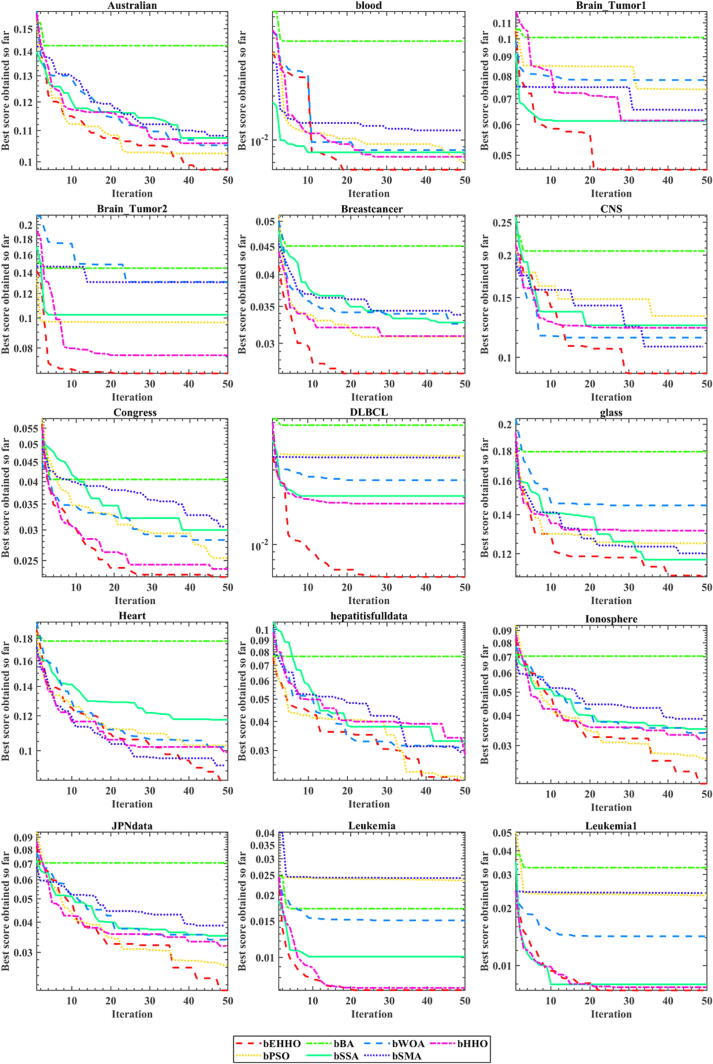
In order to more intuitively and vividly show the excellent classification performance of bEHHO on thirty UCI test sets, Fig. 3 and Fig. 4 show the graph of fitness value calculated by the KNN classifier. The abscissa represents the iteration times of the classification method, and the ordinate represents the average fitness value of the algorithm.

Fig. 3.

Convergence curves of bEHHO and other algorithms for 15 data sets.

Fig. 4.

Convergence curves of bEHHO and other algorithms for 15 data sets.

As can be seen from Fig. 3 and Fig. 4, on thirty UCI datasets, bEHHO has significantly improved compared with other optimizers, and the fitness value has the fastest convergence speed and the highest accuracy. It can be observed that bEHHO performs better on high-dimensional datasets than other optimizers. At the same time, it can be seen from Table 5 that bEHHO does not run long, and the running time on all datasets is shorter than the original bHHO. This is also the purpose of our work to obtain better classification accuracy and precision with faster running time. Although the fitness value of bEHHO is the same as that of bPSO on the Wine dataset, it can be seen from Table 5 that the running time of bEHHO is better than that of bPSO, that is, it can obtain the same optimization effect as bPSO with a shorter running time, which also proves the excellent performance of bEHHO in feature selection. Therefore, if EHHO is applied to other aspects in the future, such as recommender system [115], [116], image segmentation [117], [118], [119], human activity recognition [120], colorectal polyp region extraction [121], location-based services [122], [123], image denoising [124], and road network planning [125], there is also a high possibility that very excellent results will be obtained.

Conclusions and future directions

Our original intention was to handle more complex problems with less running time, so we devised an improved version of HHO, also known as EHHO. The addition of hierarchy can not only solve the weakness of the algorithm in dealing with high-dimensional problems but also enable the excellent individuals in the algorithm to communicate fully. In order to verify the performance of the algorithm, we first test on 23 classical test sets and compare other meta-heuristic algorithms, other excellent improved algorithms, and the algorithm proposed in recent years with the excellent improved HHO. The results show that EHHO is better than these algorithms in accuracy and convergence minimum. Then, to verify the performance of EHHO in practical application problems, we converted EHHO into binary bEHHO by transformation function and tested it on thirty UCI data sets. High-dimensional data sets can well reflect the performance of an algorithm, so we choose more than ten high-dimensional data sets. The final experimental results show that bEHHO is superior to other algorithms in terms of accuracy and feature selection; that is to say, bEHHO can achieve good classification accuracy with fewer features. Compared with the original bHHO, there is also a significant improvement in all indicators, and it can be seen that bEHHO has significantly less running time. This is also in line with our original intention to use less running time and fewer features and achieve good classification accuracy. Therefore, EHHO can be used as an ideal feature selection processing tool. Shortly, we will conduct research in other directions, such as fault diagnosis, image segmentation, and disease diagnosis.

Compliance with ethics requirements

The authors declare that they comply with ethics requirements regarding the publication of article.

CRediT authorship contribution statement

Lemin Peng: Software, Visualization, Investigation, Formal analysis, Writing – original draft, Writing – review & editing. Zhennao Cai: Conceptualization, Methodology, Formal analysis, Investigation, Funding acquisition, Supervision, Writing – original draft, Writing – review & editing. Ali Asghar Heidari: Formal analysis, Software, Visualization, Investigation, Methodology, Validation, Writing – original draft, Writing – review & editing. Lejun Zhang: Software, Visualization, Investigation, Writing – original draft, Writing – review & editing. Huiling Chen: Conceptualization, Methodology, Formal analysis, Investigation, Funding acquisition, Supervision, Project administration, Software, Validation, Visualization, Writing – original draft, Writing – review & editing.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.