ABSTRACT
Elastic recoil drives some of the fastest and most powerful biological movements. For effective use of elastic recoil, the tuning of muscle and spring force capacity is essential. Although studies of invertebrate organisms that use elastic recoil show evidence of increased force capacity in their energy loading muscle, changes in the fundamental properties of such muscles have yet to be documented in vertebrates. Here, we used three species of frogs (Cuban tree frogs, bullfrogs and cane toads) that differ in jumping power to investigate functional shifts in muscle-spring tuning in systems using latch-mediated spring actuation (LaMSA). We hypothesized that variation in jumping performance would result from increased force capacity in muscles and relatively stiffer elastic structures, resulting in greater energy storage. To test this, we characterized the force–length property of the plantaris longus muscle–tendon unit (MTU), and quantified the maximal amount of energy stored in elastic structures for each species. We found that the plantaris longus MTU of Cuban tree frogs produced higher mass-specific energy and mass-specific forces than the other two species. Moreover, we found that the plantaris longus MTU of Cuban tree frogs had higher pennation angles than the other species, suggesting that muscle architecture was modified to increase force capacity through packing of more muscle fibers. Finally, we found that the elastic structures were relatively stiffer in Cuban tree frogs. These results provide a mechanistic link between the tuned properties of LaMSA components, energy storage capacity and whole-system performance.
Keywords: Elastic recoil, Frogs, LaMSA, Power amplification
Highlighted Article: Tuning muscle and spring properties enhanced elastic energy storage in the plantaris longus muscle of Cuban tree frogs.
INTRODUCTION
Fast and powerful movements such as the jump of a flea (Bennet-Clark and Lucey, 1967) or the strike of a mantis shrimp smasher (Patek and Caldwell, 2005) are possible because they use elastic energy storage mechanisms, or latch-mediated spring actuation (LaMSA; Longo et al., 2019). In this mechanism, a latch resists motion of a limb segment (or appendage) while allowing loading muscles to contract slowly and forcefully to store mechanical energy (i.e. work) in the deformations of elastic structures (e.g. tendon, aponeurosis or apodeme; Alexander, 1988). Upon the removal or release of the latch, the elastic structures recoil, delivering stored energy at rates faster than what muscle could do alone (Ilton et al., 2018; Longo et al., 2019; Abbott et al., 2019).
In LaMSA, the temporal decoupling of muscle contraction from movement reduces the shortening velocity of contracting muscles, enabling them to contract against elastic structures with high force. While this decoupling allows loading muscles to operate at a higher proportion of their force capacity, recent evidence also suggests that selection has acted to enhance maximum force capacity of muscles used in LaMSA. For example, the loading muscles of LaMSA systems in some organisms have long resting sarcomere lengths and large physiological cross-sectional areas (PCSAs), indicating potential selection for high muscle force capacity (Blanco and Patek, 2014; Larabee et al., 2017; Booher et al., 2021). Yet it remains unknown whether increased force capacity occurs in the loading muscles of vertebrate systems that use elastic recoil to power movement. The relatively little variation in resting sarcomere length (∼2 μm; Burkholder and Lieber, 2001) in vertebrate muscle suggests that to increase the force capacity of muscle, they may be constrained to changes in PCSA – through changes in either mass, pennation angle or both. An increase in mass should result in an increase in force. In particular, an increase in mass would result in a proportional change in PCSA, and because the force generating capacity of muscle is a function of PCSA, force would also increase. Furthermore, if the pennation angle of a muscle were relatively higher, more fascicles with shorter lengths could be packed into the volume of the muscle, resulting in an increase in PCSA and a net increase in force generating capacity (Sacks and Roy, 1982; Otten, 1988; Azizi et al., 2008; Biewener and Patek, 2018).
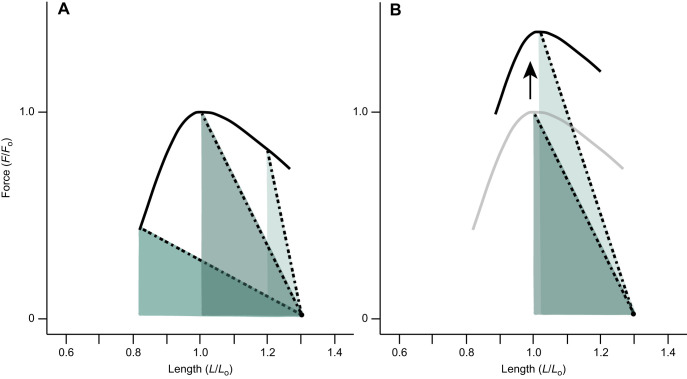
Effective tuning of muscle and spring force capacities is essential for effective function of LaMSA systems (Ilton et al., 2018). Any change in muscle force should be accompanied by a tuned change in spring stiffness to increase elastic energy storage capacity. A spring stiffness matched to the force capacity of the energy loading muscle would allow it to operate along lengths (in the force–length curve) ideal for generating high force and elastic energy storage. Thus, if a muscle contracts against a spring that is not matched to its force capacity, then less energy will be stored. For example, if a muscle contracts against a spring that is relatively too compliant while the latch is engaged, then the muscle would shorten to a sub-optimal length, which would result in more muscle excursion and a reduction in force generation (Fig. 1A). If instead a muscle contracts against a spring that is relatively stiff while the latch is engaged, then the muscle will shorten very little and store less energy because it cannot deform the elastic structures (Fig. 1A). Thus, based on theoretical considerations, any change in a muscle's force capacity would need to be accompanied by a corresponding shift in the mechanical properties of elastic structures.
Fig. 1.
Conceptual figures showing how the relative properties of muscles and springs can affect the amount of elastic energy storage. A series of contractions are shown which all begin at a length of 1.3Lo and shorten against the stretch of a tendon until the contraction reaches a point on the isometric force–length relationship. The slope of the dashed lines indicate spring stiffness, and the area underneath the dashed lines corresponds to the energy stored. (A) A muscle that contracts against relatively stiff elastic structures (right) could store approximately 27% of the maximal energy it could store with tuned springs. A muscle that contracts against relatively compliant elastic structures (left) would store approximately 72% of the maximal energy. Thus, tuning spring stiffness to muscle force capacity should maximize energy storage. (B) The force–length relationship shifted upward for a muscle modified for increased force capacity. With a higher force capacity, a relatively stiffer spring should maximize energy storage.
Frogs are an ideal comparative animal model for investigating functional shifts in muscle-spring tuning in elastic recoil systems. Jumping power varies substantially across frog species and it has been shown that smaller species tend to jump with higher muscle-mass-specific power (Roberts et al., 2011; Astley, 2016; Mendoza et al., 2020). Frogs also happen to occupy a size range that is considered transitional, such that the performance benefits of spring actuation (relative to direct muscle actuation) may be limited, potentially explaining the performance variation observed in the clade (Sutton et al., 2019). In addition, the LaMSA mechanism used by frogs (Roberts and Marsh, 2003) provides the possibility of simultaneously using a combination of both spring and muscle actuation to power jumps by allowing muscles to contribute additional work during limb extension (Sutton et al., 2019; Olberding et al., 2019). The mechanistic diversity observed in frogs provides a unique opportunity to link the properties of LaMSA components to overall jump performance.
In frogs, the plantaris longus muscle–tendon unit (MTU) is an important site of elastic energy storage (Astley and Roberts, 2012; Astley and Roberts, 2014). Here, we used isolated muscle preparations of the plantaris longus MTU to assess the tuning of muscle force capacity and spring properties. We examined the plantaris longus MTU of three species of frogs that vary in jumping power, but not isolated muscle power (Roberts et al., 2011). Moreover, we used this preparation to test whether species differed in energy storage capacity at the plantaris longus MTU. We hypothesized that MTUs that have the highest energy storage capacity will show increased force capacity to the muscle, and spring properties tuned to high muscle force capacity.
MATERIALS AND METHODS
Animals
Six bullfrogs [Rana catesbeiana (Shaw 1802)], five cane toads [Rhinella marina (Linnaeus 1758)] and four Cuban tree frogs [Osteopilus septentrionalis (Duméril and Bibron 1841)] were purchased from herpetological vendors (Table 1). All animals were adults. They were housed individually in large aquaria and were fed calcium-supplemented crickets ad libitum. Animal husbandry and use were approved by the University of California, Irvine Animal Care and Use Committee (protocol AUP 20-129).
Table 1.
Comparison of species plantaris longus muscle morphology (means±s.e.m.)
In-vitro preparation
Animals were euthanized with a double-pithing protocol prior to the isolation of the MTU. In this study, we followed experimental procedures outlined in Azizi and Roberts (2014). First, we removed the skin from the upper hind limb, exposing the musculature. Then, we carefully isolated the sciatic nerve from surrounding tissue. Next, we removed the skin from the lower hind limb to expose the plantaris longus muscle. With a sapphire blade, we carefully made a small incision between two fascicles in the most proximal region of the muscle. We used this incision to implant a sonomicrometry crystal (Sonometrics Corporation, London, ON, Canada). We made a second incision distal to the first sonomicrometry crystal (and proximal to the aponeurosis sheet) along the same two fascicles and implanted a second sonomicrometry crystal. We secured the crystals with 6-0 silk. After instrumentation, we detached the distal tendon from the plantar fascia while keeping the muscle attached to the isolated knee joint. The isolated MTU preparation was secured to a rigid clamp at the knee joint and the distal tendon was placed in a custom-made clamp. The clamp on the distal tendon was attached to a servomotor (310C, Aurora Scientific, Cambridge, MA, USA). Once the MTU was tightly secured, it was placed in a bath of Ringer's solution that was continuously aerated with oxygen and kept at room temperature (22±1°C). Finally, the sciatic nerve was threaded through a custom-made nerve cuff that was connected to a Grass S88D stimulator (Grass Technologies, Warwick, RI, USA) and used to electrically stimulate the muscle.
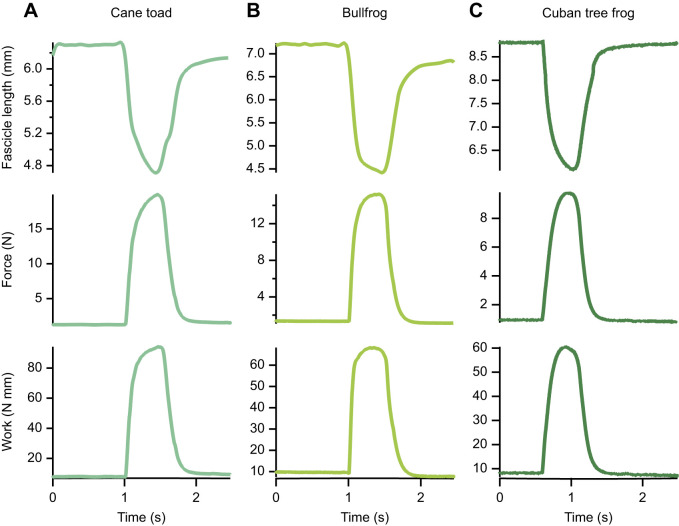
Stimulation voltage was determined through twitch contractions. The stimulation voltage was increased in 1 V increments until the twitch force plateaued (i.e. peak force stopped increasing). We set the stimulation voltage to 1 V above that which resulted in maximal twitch force to supramaximally stimulate the muscle (8–12 V). Tetanic stimulations consisted of 0.2 ms pulses at 80 pulses s−1 for durations of 400 ms. We varied the length of each muscle before each tetanic contraction to characterize the force–length property. Because we varied the length of the muscle prior to stimulation, we also characterized the passive force–length property. Changes in muscle fascicle lengths were measured with sonomicrometry, and the servomotor measured changes in force. Fig. 2 shows representative time series of these contractions for the plantaris longus muscle of all three species. All data were collected at 1000 Hz using a 16-bit data acquisition system (National Instruments USB-6212). After the experiments, we measured muscle mass (in grams), fascicle length (in millimeters) and pennation angle (in degrees). We used these morphological parameters to calculate muscle PCSA assuming a constant muscle density of 1.056 g cm−3 (Mendez and Keys, 1960).
Fig. 2.
Sample time series of fixed end contractions showing fascicle length, force and work in three frog species. (A) Cane toad, (B) bullfrog and (C) Cuban tree frog.
Data processing
Data were processed using Igor Pro software (Wavemetrics, Lake Oswego, OR, USA). The passive force–length curve of the muscle was constructed by plotting fascicle length against the passive force at each varied length prior to stimulation. Therefore, this relationship characterizes the passive properties of the muscle fascicles and not the MTU. Next, the passive force–length data were fit with a standard exponential function following Azizi and Roberts (2010). The total force–length curve was constructed by plotting tetanic force against fascicle length. Note that because the fascicles of the plantaris longus insert into an aponeurosis (a sheet-like tendon along the muscle belly), they shorten during tetanic contractions. Thus, fascicle length and force were measured where force plateaued (Fig. 2). The total force–length data were fit according to Otten (1988).
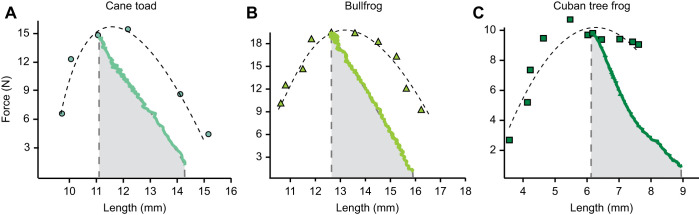
We calculated the work done by muscle fascicles during a series of tetanic contractions, each starting at a different length. During our experiments, the MTU maintained a constant length, so any shortening of the muscle fascicles resulted in an equal stretch of the elastic elements. Thus, to calculate work done, we plotted fascicle length against tetanic force. The area under this curve corresponded to the work done during the contraction. Because we were interested in understanding the maximum work that could be generated by these muscles, we focused primarily on the contraction with the highest work output for each muscle. Note that we measured fascicle shortening at one fascicle, and thus made the assumption that all fascicles undergo similar displacements. Next, to measure the stiffness of the elastic elements, we calculated the slope of fascicle length versus tetanic force curves and normalized them by muscle PCSA. We normalized by PCSA to account for size differences across the three species. Note that our method of normalization does limit comparisons with other studies. Furthermore, we measured elastic element stiffness from muscle fascicle shortening, and previous studies show evidence that this approach may be limiting owing to the mechanical arrangement of muscle and elastic elements (see Herzog, 2019; Zelik and Franz, 2017; Arellano et al., 2019). For each muscle, we measured stiffness of the elastic elements from the contraction with the highest work (Fig. 3). Finally, to compare the force generating capacity of these muscles across species, we normalized peak tetanic force by PCSA to calculate stress and by muscle mass to calculate mass-specific force.
Fig. 3.
Representative force–length curves for three frog species. (A) Cane toad, (B) bullfrog and (C) Cuban tree frog. One representative contraction that produced the highest work is shown for each species. The muscles start on the descending limb of the force–length curve and shorten onto the plateau against the stretch of the tendon. The shaded triangles represent the work (or energy) that was stored into the elastic elements.
Data analysis
All analyses were performed in R (http://www.R-project.org/). We ran an ANOVA on morphological and contractile variables to test for differences across species. Specifically, to test whether species differed in mass-specific stored energy, we performed an ANOVA with mass-specific stored energy as the response variable and species as the effect. Additionally, to test whether species differed in elastic element stiffness, we performed an ANOVA with normalized stiffness as the response variable and species as the effect. To test whether there were differences in muscle stress, we performed an ANOVA with muscle stress as the response variable and species as the effect. Because normalizing force by PCSA accounts for variation related to mass or pennation angle, we performed two more ANOVAs to examine pennation angle and mass-specific peak force in isolation. We did this to understand whether there were differences in muscle architecture or force generating capabilities based on mass, and whether these differences could account for differences in energy storage capacity. One included mass-specific force as the response variable and species as the effect, and the other included pennation angle as the response variable and species as the effect. Lastly, we performed an ANOVA on normalized passive force (i.e. normalized as a percentage of maximal force) across species. We used Tukey's honest significance test (HSD) post hoc analyses to assess comparisons that were significantly different.
RESULTS
The average normalized passive muscle force of the plantaris longus at the contraction that produced the highest work was 10.20%, 7.54% and 8.89% of maximal force for Cuban tree frogs, cane toads and bullfrogs, respectively. The plantaris longus muscle of bullfrogs, cane toads and Cuban tree frogs reached an average peak total force of 21.44, 15.84 and 9.57 N, respectively.
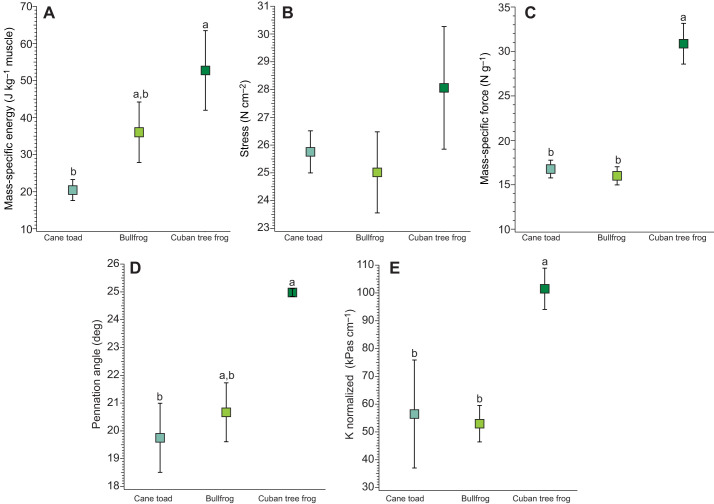
We found that mass-specific stored energy was significantly different across species (F2,15=5.187, P=0.019; Fig. 4A). The plantaris longus of Cuban tree frogs could store mass-specific energies averaging 53 J kg−1 muscle mass, and the plantaris longus of cane toads and bullfrogs stored an average of 22 and 37 J kg−1 muscle mass, respectively. Tukey’s HSD post hoc analysis showed that mass-specific stored energy differed significantly between Cuban tree frogs and cane toads (P=0.015), but not between Cuban tree frogs and bullfrogs (P=0.223) or bullfrogs and cane toads (P=0.187).
Fig. 4.
Summary data plots for cane toads, bullfrogs and Cuban tree frogs. (A) Mass-specific elastic energy, (B) muscle stress, (C) mass-specific force, (D) pennation angle and (E) normalized stiffness. Mass-specific energy was significantly different between Cuban tree frogs and cane toads (P<0.05). Stress did not significantly differ across species. Mass-specific force was significantly different between Cuban tree frogs and cane toads (P<0.001) and between Cuban tree frogs and bullfrogs (P<0.001), but was not significantly different between cane toads and bullfrogs (indicated by lowercase letters). Pennation angle was significantly different between Cuban tree frogs and cane toads (P<0.05). Normalized stiffness was significantly different between Cuban tree frogs and cane toads (P<0.05) and between Cuban tree frogs and bullfrogs (P<0.05), but was not significantly different between cane toads and bullfrogs.
We additionally examined peak muscle stress because energy storage capacity depends on the ability to generate force. We found that peak muscle stress did not differ across species (F2,15=1.651, P=0.225; Fig. 4B), which was consistent with previous studies (e.g. Roberts et al., 2011). Moreover, because normalizing force by PCSA (i.e. to calculate muscle stress) accounts for variation in both pennation angle and muscle mass, we also examined pennation angle and mass-specific peak force in isolation to understand whether there were differences in muscle architecture or force generating capabilities based on mass, and whether these differences could account for differences in energy storage capacity. We found that mass-specific peak force differed significantly across species (F(2,15)=32.61, P=3.45e−06; Fig. 4C). Post hoc analysis showed that mass-specific force was significantly different between Cuban tree frogs and bullfrogs (P=4.30e−06), and between Cuban tree frogs and cane toads (P=1.50e−05), but was not significantly different between cane toads and bullfrogs (P=0.890). Additionally, pennation angle differed significantly across species (F2,15=4.408, P=0.031; Fig. 4D). Tukey’s HSD post hoc analysis showed that pennation angle was significantly different between Cuban tree frogs and cane toads (P=0.027), but not significantly different between Cuban tree frogs and bullfrogs (P=0.095) or bullfrogs and cane toads (P=0.622). Normalized passive force was significantly different across species (F2,15=5.746, P=0.014). Post hoc analysis showed that normalized passive force was significantly different between bullfrogs and Cuban tree frogs (P=0.013), but it was not significantly different between cane toads and Cuban tree frogs (P=0.329) or bullfrogs and cane toads (P=0.153). Finally, normalized spring stiffness was significantly different across species (F2,15=6.049, P=0.012; Fig. 4E). Post hoc analysis showed that normalized stiffness differed significantly between Cuban tree frogs and bullfrogs (P=0.012), and between Cuban tree frogs and cane toads (P=0.027), but not between bullfrogs and cane toads (P=0.961).
DISCUSSION
The plantaris longus of Cuban tree frogs stored more elastic energy than that of the cane toads or bullfrogs (Figs 3, 4). We found that the architecture of this muscle in the Cuban tree frogs enabled higher mass-specific peak forces. Furthermore, we found that the elastic structures in Cuban tree frogs were relatively stiffer than in other species, and well matched to the force capacity of the muscle (Fig. 4). Thus, here we propose that the plantaris longus muscle in Cuban tree frogs was modified for high force generation, and that the surrounding elastic structures were tuned to the force of the muscle to increase energy storage capacity (Fig. 1B).
The observed increase in the mass-specific force capacity of the plantaris longus of Cuban tree frogs likely results from architectural changes (i.e. shorter more pennate fibers) that allow high force production over a small working range. We found that pennation angle was higher and muscle fascicle lengths were shorter in the plantaris longus of Cuban tree frogs than in other species. This architectural arrangement allows more short muscle fascicles to be packed into the same muscle volume, which increases PCSA and mass-specific force (Sacks and Roy, 1982; Otten, 1988; Azizi et al., 2008; Biewener and Patek, 2018). These changes in muscle architecture have implications for locomotor function. For instance, Rosin and Nyakatura (2017) showed that three hindlimb extensor muscles from a rodent jumper specialist had relatively shorter fascicle lengths and higher pennation angles than its non-specialist relative, which would allow for higher mass-specific forces important for jumping. Similarly, Dick and Clemente (2016) showed that varanid lizards mitigate musculoskeletal stresses associated with increased size through functional shifts in muscle architecture that promote higher force production (i.e. higher pennation angles and shorter fascicles). Moreover, in cursorial organisms, the highly pennate architecture of the distal hindlimb muscles functions to generate high force economically to facilitate elastic energy savings (Biewener, 1998; Biewener and Roberts, 2000). Therefore, vertebrate organisms can modify muscle function through changes to muscle architecture and PCSA that have implications for locomotion. Our work suggests that this pathway is also used to increase muscle force in vertebrate systems that use elastic recoil (or LaMSA) to increase elastic energy storage.
Tuning spring stiffness to muscle force capacity maximized energy storage. We found that the plantaris longus of Cuban tree frogs contracted against a spring that was relatively stiffer than that of the other species, and matched to the increased force capacity of its muscle. In frogs, the plantaris longus muscle operates on the descending limb of the force–length curve (Azizi and Roberts, 2010), suggesting that shortening against a relatively stiffer spring would allow the muscle to shorten onto the plateau where the muscle could reach the highest peak forces. Furthermore, studies have shown that the plantaris longus muscle continues to shorten during limb extension (Azizi and Roberts, 2010; Astley and Roberts, 2012), suggesting that after energy storage the muscle would be at a length where it could contribute substantial work directly while contracting onto the ascending limb of the force–length curve (Olberding et al., 2019). Therefore, a spring tuned to the force capacity of the muscle would place the muscle in a position to generate high forces throughout the majority of the energy storage phase, and would result in more energy stored. In contrast, a spring not tuned to the force capacity of the muscle would result in less energy stored. For example, a spring that is relatively too compliant (i.e. not matched to the muscle's force capacity) would allow the muscle to shorten past the plateau and to a length at which it would generate low force (Fig. 1). Alternatively, a spring that is relatively too stiff would result in very little muscle shortening and energy storage (Fig. 1). Although our work suggests that a relatively stiffer spring maximizes energy storage, relatively compliant springs could be ideal in cases where the force capacity of the muscle is constrained (Rosario et al., 2016). Thus, to maximize energy storage, spring stiffness should be tuned to the force capacity of the muscle.
In this study, we examined the energy storage capacity of plantaris longus MTUs of three species of frogs that have been shown to differ in jumping power (Roberts et al., 2011) to assess variable tuning of muscle and spring stiffness and energy storage capacity. We found that species differed in their capabilities to store energy, and more specifically that Cuban tree frogs could store more energy because their muscle and spring were tuned for high energy storage. Thus, our findings support our hypothesis that species would differ in energy storage capabilities. Yet, our findings do not fully resolve the observations of Roberts et al. (2011), which showed that three species of frogs varied substantially in jumping power but not in vitro muscle power. This is largely because in our study, we only examined the work that was stored as potential energy. In ideal systems with Hookean springs and instantaneous-release latches, we could be certain that the energy stored would equal the energy that was returned. However, biological springs are non-Hookean and can lose up to 10% of stored energy as heat to the environment (Ker, 1981). Furthermore, studies show that energy can be lost to latches that do not release instantaneously (Ilton et al., 2018; Divi et al., 2020). The anuran latch is a geometric-release latch that arises through dynamic changes in the muscle's mechanical advantage (Astley and Roberts, 2014; Olberding et al., 2019). As such, the release of energy is not instantaneous and is therefore subject to losses during unlatching (Astley and Roberts, 2014; Abbott et al., 2019; Divi et al., 2020). These components of the jumping mechanism in anurans are sites where additional variation could be introduced into the system, resulting in even larger discrepancies than what we would expect based on energy inputs. Quantifying how the latching (and unlatching) mechanics of the anuran system mediates energy release is an important next step to resolving the observations that there is substantial variation in anuran jumping power (Roberts et al., 2011; Astley, 2016; Mendoza et al., 2020). Variation in anuran jumping power likely also arises because anurans use both spring recoil and direct muscle contributions to actuate jumps (Azizi and Roberts, 2010; Astley and Roberts, 2012; Sutton et al., 2019). Azizi and Roberts (2010) showed that the plantaris longus continues to shorten during limb extension (after storing energy in springs), suggesting that the muscle is contributing work in addition to what is being returned by recoiling springs. Future studies should examine how much work these muscles are contributing to the jump in addition to spring recoil during limb extension, and whether these contributions can explain some of the variation in jumping power that we examined across species.
Several scaling studies have suggested that the use of elastic mechanisms for ballistic movements such as jumping is most beneficial at smaller sizes (Ilton et al., 2018; Sutton et al., 2019; Mendoza et al., 2020). This reliance is largely due to the force–velocity trade-off of muscles, which dictates that a muscle can either contract slowly and forcefully or contract quickly and generate low forces. This property becomes very limiting at small scales (Sutton et al., 2019) because small jumpers need to be able to generate substantial power outputs with little time to maintain jump performances that are comparable to larger jumpers (Ilton et al., 2018; Biewener and Patek, 2018; Sutton et al., 2019; Mendoza et al., 2020). Small jumpers are able to circumvent these limitations by loading energy into elastic structures through slow and forceful contractions and then releasing this energy to actuate movement. In this study, we found that the plantaris longus in Cuban tree frogs could generate more force per unit muscle mass, and that they had relatively stiffer elastic elements than bullfrogs and cane toads, suggesting that the plantaris longus MTU of Cuban tree frogs was modified for high energy storage. Here, we found that the plantaris longus of Cuban tree frogs could store mass-specific energies averaging 53 J kg−1 muscle mass (range: 32–81 J kg−1 muscle mass). Olberding and Deban's (2018) intraspecific scaling study showed that the plantaris longus of Cuban tree frogs could generate mass-specific energies of up to 73 J kg−1 muscle mass, which falls within the range that we measured, and was approximately two times greater than that of the other species measured (average 20 J kg−1 muscle mass for the cane toad and 36 J kg−1 muscle mass for the bullfrog). Cuban tree frogs' impressive energy storage capabilities are likely necessary to provide sufficient mechanical energy within the short time scale available to achieve jump take-off. In contrast, larger jumpers (e.g. such as bullfrogs and cane toads) may not necessitate high energy storage capabilities because they have more time to take off (Biewener and Patek, 2018; Ilton et al., 2018; Sutton et al., 2019; Mendoza et al., 2020).
Conclusions
In conclusion, we examined the capacity of the plantaris longus MTU to store energy across three frog species. We found that Cuban tree frogs were able to store an impressive amount of energy because they had muscles that were modified to generate high mass-specific forces and elastic structures that were tuned to the high force capacity of these muscles. Furthermore, our study showed that the Cuban tree frogs modified muscle force through changes in muscle architecture. As this study focused exclusively on energy storage, future studies should investigate how the unlatching mechanics of the anuran jumping mechanism influences elastic energy return and overall jumping performance. Finally, future studies should quantify how much the hindlimb musculature contributes to the anuran jump during hindlimb extension as this may be an important source of performance variation. Together, these studies will help us understand how shifts in the properties of LaMSA components drive variation in performance.
Acknowledgements
The authors would like to thank Dr Jeff Olberding for help with experimental methods. We thank Dr Natalie Holt and Dr Matt McHenry for helpful discussions. We would also like to thank the members of the Azizi lab, Dr Suzanne Cox, and Dr Monica Daley for helpful feedback on early versions of the manuscript. We acknowledge that this work was done on the unceded original homelands of the Tongva and Kizh nations.
Footnotes
Author contributions
Conceptualization: E.M., E.A.; Methodology: E.M., E.A.; Validation: E.M., E.A.; Formal analysis: E.M.; Investigation: E.M., E.A.; Resources: E.A.; Data curation: E.M.; Writing - original draft: E.M.; Writing - review & editing: E.M., E.A.; Visualization: E.M., E.A.; Supervision: E.A.; Project administration: E.A.; Funding acquisition: E.A.
Funding
This work is supported by the US Army Research Laboratory and the US Army Research Office under contract/grant number W911NF-15-10358. This work was also funded by a University of California, Irvine Eugene-Cota Robles Fellowship to E.M.
References
- Abbott, E. M., Nezwek, T., Schmitt, D. and Sawicki, G. S. (2019). Hurry up and get out of the way! Exploring the limits of muscle-based latch systems for power amplification. Integr. Comp. Biol. 59, 1546-1558. 10.1093/icb/icz141 [DOI] [PubMed] [Google Scholar]
- Alexander, R. M. (1988). Elastic Mechanisms in Animal Movement, Vol. 404. Cambridge: Cambridge University Press. [Google Scholar]
- Arellano, C. J., Konow, N., Gidmark, N. J. and Roberts, T. J. (2019). Evidence of a tunable biological spring: elastic energy storage in aponeuroses varies with transverse strain in vivo. Proc. R. Soc. B 286, 2018-2764. 10.1098/rspb.2018.2764 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Astley, H. C. (2016). The diversity and evolution of locomotor muscle properties in anurans. J. Exp. Biol. 219, 3163-3173. 10.1242/jeb.142315 [DOI] [PubMed] [Google Scholar]
- Astley, H. C. and Roberts, T. J. (2012). Evidence for a vertebrate catapult: elastic energy storage in the plantaris tendon during frog jumping. Biol. Lett. 8, 386-389. 10.1098/rsbl.2011.0982 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Astley, H. C. and Roberts, T. J. (2014). The mechanics of elastic loading and recoil in anuran jumping. J. Exp. Biol. 217, 4372-4378. 10.1242/jeb.110296 [DOI] [PubMed] [Google Scholar]
- Azizi, E. and Roberts, T. J. (2010). Muscle performance during frog jumping: influence of elasticity on muscle operating lengths. Proc. R. Soc. B 277, 1523-1530. 10.1098/rspb.2009.2051 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azizi, E. and Roberts, T. J. (2014). Geared up to stretch: pennate muscle behavior during active lengthening. J. Exp. Biol. 217, 376-381. 10.1242/jeb.094383 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Azizi, E., Brainerd, E. L. and Roberts, T. J. (2008). Variable gearing in pennate muscles. Proc. Natl Acad. Sci. USA 105, 1745-1750. 10.1073/pnas.0709212105 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bennet-Clark, H. C. and Lucey, E. C. A. (1967). The jump of the flea: a study of the energetics and a model of the mechanism. J. Exp. Biol. 47, 59-76. 10.1242/jeb.47.1.59 [DOI] [PubMed] [Google Scholar]
- Biewener, A. A. (1998). Muscle function in vivo: a comparison of muscles used for elastic energy savings versus muscles used to generate mechanical power1. Am. Zool. 38, 703-717. 10.1093/icb/38.4.703 [DOI] [Google Scholar]
- Biewener, A. A. and Roberts, T. J. (2000). Muscle and tendon contributions to force, work, and elastic energy savings: a comparative perspective. Exerc. Sport Sci. Rev. 28, 99-107. [PubMed] [Google Scholar]
- Biewener, A. and Patek, S. (2018). Animal Locomotion. Oxford University Press. [Google Scholar]
- Blanco, M. M. and Patek, S. N. (2014). Muscle trade-offs in a power-amplified prey capture system. Evolution 68, 1399-1414. 10.1111/evo.12365 [DOI] [PubMed] [Google Scholar]
- Booher, D. B., Gibson, J. C., Liu, C., Longino, J. T., Fisher, B. L., Janda, M. and Economo, E. P. (2021). Functional innovation promotes diversification of form in the evolution of an ultrafast trap-jaw mechanism in ants. PLoS Biol. 19, e3001031. 10.1371/journal.pbio.3001031 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burkholder, T. J. and Lieber, R. L. (2001). Sarcomere length operating range of vertebrate muscles during movement. J. Exp. Biol. 204, 1529-1536. 10.1242/jeb.204.9.1529 [DOI] [PubMed] [Google Scholar]
- Dick, T. J. and Clemente, C. J. (2016). How to build your dragon: scaling of muscle architecture from the world's smallest to the world's largest monitor lizard. Front. Zool. 13, 1-17. 10.1186/s12983-016-0133-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Divi, S., Ma, X., Ilton, M., St Pierre, R., Eslami, B., Patek, S. N. and Bergbreiter, S. (2020). Latch-based control of energy output in spring actuated systems. J. R. Soc. Interface 17, 2020-0070. 10.1098/rsif.2020.0070 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herzog, W. (2019). The problem with skeletal muscle series elasticity. BMC Biomed. Eng. 1, 1-14. 10.1186/s42490-019-0031-y [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ilton, M., Bhamla, M. S., Ma, X., Cox, S. M., Fitchett, L. L., Kim, Y., Koh, J.-S., Krishnamurthy, D., Kuo, C.-Y., Temel, F. Z.et al. (2018). The principles of cascading power limits in small, fast biological and engineered systems. Science 360, eaao1082. 10.1126/science.aao1082 [DOI] [PubMed] [Google Scholar]
- Ker, R. F. (1981). Dynamic tensile properties of the plantaris tendon of sheep (Ovis aries). J. Exp. Biol. 93, 283-302. 10.1242/jeb.93.1.283 [DOI] [PubMed] [Google Scholar]
- Larabee, F. J., Gronenberg, W., Suarez, A. V. (2017). Performance, morphology and control of power-amplified mandibles in the trap-jaw ant Myrmoteras (Hymenoptera: Formicidae). J. Exp. Biol. 220, 3062-3071. 10.1242/jeb.156513 [DOI] [PubMed] [Google Scholar]
- Longo, S. J., Cox, S. M., Azizi, E., Ilton, M., Olberding, J. P., St Pierre, R. and Patek, S. N. (2019). Beyond power amplification: latch-mediated spring actuation is an emerging framework for the study of diverse elastic systems. J. Exp. Biol. 222, jeb197889. 10.1242/jeb.197889 [DOI] [PubMed] [Google Scholar]
- Mendez, J. and Keys, A. (1960). Density and composition of mammalian muscle. Metabolism 9, 184-188. [Google Scholar]
- Mendoza, E., Azizi, E. and Moen, D. S. (2020). What explains vast differences in jumping power within a clade? Diversity, ecology and evolution of anuran jumping power. Funct. Ecol. 34, 1053-1063. 10.1111/1365-2435.13545 [DOI] [Google Scholar]
- Olberding, J. P. and Deban, S. M. (2018). Scaling of work and power in a locomotor muscle of a frog. J. Comp. Physiol. B 188, 623-634. 10.1007/s00360-018-1148-3 [DOI] [PubMed] [Google Scholar]
- Olberding, J. P., Deban, S. M., Rosario, M. V. and Azizi, E. (2019). Modeling the determinants of mechanical advantage during jumping: consequences for spring-and muscle-driven movement. Integr. Comp. Biol. 59, 1515-1524. 10.1093/icb/icz139 [DOI] [PubMed] [Google Scholar]
- Otten, E. (1988). Concepts and models of functional architecture in skeletal muscle. Exerc. Sport Sci. Rev. 16, 89-138. 10.1249/00003677-198800160-00006 [DOI] [PubMed] [Google Scholar]
- Patek, S. N. and Caldwell, R. L. (2005). Extreme impact and cavitation forces of a biological hammer: strike forces of the peacock mantis shrimp Odontodactylus scyllarus. J. Exp. Biol. 208, 3655-3664. 10.1242/jeb.01831 [DOI] [PubMed] [Google Scholar]
- Roberts, T. J. and Marsh, R. L. (2003). Probing the limits to muscle-powered accelerations: lessons from jumping bullfrogs. J. Exp. Biol. 206, 2567-2580. 10.1242/jeb.00452 [DOI] [PubMed] [Google Scholar]
- Roberts, T. J., Abbott, E. M. and Azizi, E. (2011). The weak link: do muscle properties determine locomotor performance in frogs? Phil. Trans. R. Soc. B Biol. Sci. 366, 1488-1495. 10.1098/rstb.2010.0326 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosario, M. V., Sutton, G. P., Patek, S. N. and Sawicki, G. S. (2016). Muscle–spring dynamics in time-limited, elastic movements. Proc. R. Soc. B 283, 2016-1561. 10.1098/rspb.2016.1561 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosin, S. and Nyakatura, J. A. (2017). Hind limb extensor muscle architecture reflects locomotor specialisations of a jumping and a striding quadrupedal caviomorph rodent. Zoomorphology 136, 267-277. 10.1007/s00435-017-0349-8 [DOI] [Google Scholar]
- Sacks, R. D. and Roy, R. R. (1982). Architecture of the hind limb muscles of cats: functional significance. J. Morphol. 173, 185-195. 10.1002/jmor.1051730206 [DOI] [PubMed] [Google Scholar]
- Sutton, G., Mendoza, E., Azizi, E., Longo, S., Olberding, J., Ilton, M. and Patek, S. (2019). Why don't large animals exclusively use springs to jump? Because they can jump higher without them. Integr. Comp. Biol. 59, 1609-1618. 10.1093/icb/icz145 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zelik, K. E. and Franz, J. R. (2017). It's positive to be negative: Achilles tendon work loops during human locomotion. PLoS ONE 12, e0179976. 10.1371/journal.pone.0179976 [DOI] [PMC free article] [PubMed] [Google Scholar]