Abstract
This work estimates benchmarks for new approach method (NAM) performance in predicting organ-level effects in repeat dose studies of adult animals based on variability in replicate animal studies. Treatment-related effect values from the Toxicity Reference database (v2.1) for weight, gross, or histopathological changes in the adrenal gland, liver, kidney, spleen, stomach, and thyroid were used. Rates of chemical concordance among organ-level findings in replicate studies, defined by repeated chemical only, chemical and species, or chemical and study type, were calculated. Concordance was 39 - 88%, depending on organ, and was highest within species. Variance in treatment-related effect values, including lowest effect level (LEL) values and benchmark dose (BMD) values when available, was calculated by organ. Multilinear regression modeling, using study descriptors of organ-level effect values as covariates, was used to estimate total variance, mean square error (MSE), and root residual mean square error (RMSE). MSE values, interpreted as estimates of unexplained variance, suggest study descriptors accounted for 52-69% of total variance in organ-level LELs. RMSE ranged from 0.41 – 0.68 log10-mg/kg/day. Differences between organ-level effects from chronic (CHR) and subchronic (SUB) dosing regimens were also quantified. Odds ratios indicated CHR organ effects were unlikely if the SUB study was negative. Mean differences of CHR - SUB organ-level LELs ranged from −0.38 to −0.19 log10 mg/kg/day; the magnitudes of these mean differences were less than RMSE for replicate studies. Finally, in vitro to in vivo extrapolation (IVIVE) was employed to compare bioactive concentrations from in vitro NAMs for kidney and liver to LELs. The observed mean difference between LELs and mean IVIVE dose predictions approached 0.5 log10-mg/kg/day, but differences by chemical ranged widely. Overall, variability in repeat dose organ-level effects suggests expectations for quantitative accuracy of NAM prediction of LELs should be at least ± 1 log10-mg/kg/day, with qualitative accuracy not exceeding 70%.
Keywords: Variability, organ, repeat dose, ToxRefDB
Introduction
Human health risk assessment for chemicals with potential environmental exposures has traditionally relied upon animal study data, but the resources required to evaluate the tens of thousands of chemicals that lack existing toxicity or health effects data (Judson et al., 2009) have demonstrated the clear need for leveraging new approach methodologies (NAMs) data to inform prioritization and assessment. Though NAMs hold promise for increasing the direct human relevance of chemical safety assessment via use of informative human-based models, there are statutory requirements in multiple geographic regions to compare the performance of NAMs to existing methodologies in efforts to bolster scientific confidence and ensure health protection at least equivalent to, if not better than, the current systems. The European Chemicals Agency, Health Canada and Environment and Climate Change Canada, and the US Environmental Protection Agency (EPA) all have created complementary initiatives to promote the use of NAMs for chemical evaluations to reduce reliance on animal testing and determine human health risks using in vitro and in silico methods (Bhuller et al., 2021; ECHA, 2016; ECHA, 2017b; EPA, 2021; HealthCanada, 2021). Reducing the reliance of animal models in favor of NAMs requires a performance comparison, as Section 4(h) of the Frank Lautenberg amendment to the Toxic Substances Control Act stipulates, that reduction and replacement of animals should occur, “to the extent practicable and scientifically justified,” and that NAMs should provide “information of equivalent or better scientific quality and relevance” than traditional models (Lautenberg, 2016). In the EU, the Registration, Evaluation, and Authorisation and Restriction of Chemicals (REACH) legislation (Commission, 2006; ECHA, 2011) Article 13 indicates that NAMs should be employed based on requirements outlined in Annex XI, including: that results are derived from in vitro methods that meet scientific validation requirements; that the NAM is fit for the purpose specified; and, that adequate documentation for the NAM is available. In addressing the uncertainty present in the use of NAMs, interpretation of REACH and the Biocidal Products Regulation (BPR) suggest that NAMs must provide, “an equal level of safety…at least as high as the one supported by the current information requirements” (ECHA, 2017a). Thus, embedded within the statutory impetus for NAM application is a sense that validation and scientific confidence in NAMs may require comparison to existing in vivo studies on which the current regulatory systems rely, in addition to other validation strategies. Indeed, multiple frameworks for scientific confidence in NAMs suggest that characterization of NAM performance, and parallel characterization of traditional animal model performance, is necessary for scientific confidence in some cases (Ball et al., 2022; Parish et al., 2020; Patlewicz et al., 2015; van der Zalm et al., 2022).
One approach to quantify the scientific confidence in NAMs may involve generating a confusion matrix to evaluate the binary presence or absence of some biological effect. Performance metrics such as sensitivity, specificity, and balanced accuracy can then be derived using reference or training set information from in vivo or traditional approaches. Although a pragmatic approach, it is worth noting that complex in vivo outcomes often need to be simplified as inputs for validation and modeling, and additional resources for curation of a small set of chemicals as positive or negative reference chemicals are required. Concordance of effects in in vivo studies of the same duration may be affected by experimental design parameters such as sex and species, in addition to inherent biological variability. However, few available studies examine concordance of animal study reproducibility for toxicology, and available studies in some cases examine the presence of singular outcomes rather than systemic toxicity as a broad group of effects on many organ systems. Indeed, the qualitative reproducibility of positive findings in replicate animal studies such as the local lymph node assay and the rodent uterotrophic assay have been reported to be 78% and 74%, respectively (Hoffmann et al., 2018; Dumont et al., 2016; Kleinstreuer et al., 2016), suggesting that qualitative variability in the reference data may be an important consideration when benchmarking NAM prediction of these outcomes. Karmaus et al. reported that replicate acute toxicity studies resulted in the same hazard categorization with a 60% likelihood, though estimates of quantitative variability in replicate oral 50% lethal doses studies only ranged ±0.24-log10-mg/kg/day (Karmaus et al., 2022). Gottmann et al. (2001b) examined the concordance between rat and mouse carcinogenicity experiments in the National Toxicology Program Carcinogenic Potency Database and in the associated scientific literature, observing that there was only 57% agreement between the two sources in terms of expert opinion of chemical carcinogenicity; when examining replicate mouse and replicate rat carcinogenicity studies, only 49% and 62% were concordant within species, respectively. Though differences in experimental protocols between institutional protocols may have contributed to low concordance observed by Gottman et al., this finding of a lack of reproducibility within and between species highlights a key challenge in using reference chemical data for NAM development, as noted previously (Basketter et al., 2012). Is there an optimal subset or summary of in vivo data that should be used to characterize the binary performance of a NAM intended for human health protection?
Another approach to considering scientific confidence in NAMs involves descriptions of quantitative performance, such as the amount of variance in reference data that can be expected to be explained by a NAM, or the quantitative difference between a NAM-based prediction and a reference value (e.g., the error). In these comparisons, in vivo reference data are often summarized at the chemical level (e.g., minimum, percentile, mean, or median), which obscures the variability in these in vivo estimates of chemical potency and assumes a “true” experimental chemical potency value, which is unknown. In previous work, we aimed to estimate the upper limits of NAM performance based on the variability in in vivo systemic effects in repeat dose studies that could be explained using study metadata. Based on estimates ofvariability in the lowest effect level (LEL) and/or lowest observable adverse effect level (LOAEL) for systemic toxicity as defined for replicate studies of a chemical, the maximum expected performance of a NAM was that new in vivo study-level or chemical-level effect values would fall within approximately ± 1 log10-mg/kg/day of the ”true” value with 95% confidence (Pham et al., 2020; Pradeep et al., 2020).
The work herein aims to further establish qualitative and quantitative benchmarks for understanding the maximum performance for NAMs designed to predict organ-level effects, extending the quantitative variance in systemic effect levels explored previously in (Pham et al., 2020). We hypothesized that the quantitative variability within organ-level LEL values would be lower in comparison to study-level LEL values (Pham et al., 2020) which capture many organ systems. Using a number of different types of “replicate studies” (i.e., replicates by chemical only, by chemical and species, and by chemical and study duration), the concordance among replicate studies for organ-level effects was calculated to improve understanding of the maximum accuracy that could be expected from a NAM for predicting these effects. Given the quantitative variability observed for organ-level effects within subchronic and chronic studies, analyses were performed to better understand: (1) the odds of finding a positive organ-level finding in a chronic study given a subchronic negative at the organ level; and, (2) the quantitative difference in subchronic and chronic organ-level effect values. The size of the quantitative difference in these subchronic and chronic organ-level effect values can be contextualized via comparison to the inter-study variance in replicate subchronic and chronic effect level values, i.e., is the difference in subchronic and chronic organ-level effect values similar to the size of the variance in replicate repeat dose studies? In addition, bioactivity-based points of departure (PODs) for liver and kidney were estimated (i.e., the most commonly affected organs and the organs for which in vitro NAM data were available in the ToxCast database) and compared with organ-level PODs from subchronic and chronic studies. Importantly, this study sets an upper bound expectation on the accuracy that might be expected from predictive modeling of repeat dose, organ-level effects in adult animals and may help inform fit-for-purpose acceptance criteria for organ-level predictions derived from NAMs. Furthermore, the insights derived are critical for managing the expectations of in silico and in vitro NAMs in predicting repeat dose toxicity, permitting the regulatory acceptance of NAMs to proceed with an explicit understanding of the variability that has already been acceptable under the current system of regulatory testing for human health protection.
Methods
Overview of Methods
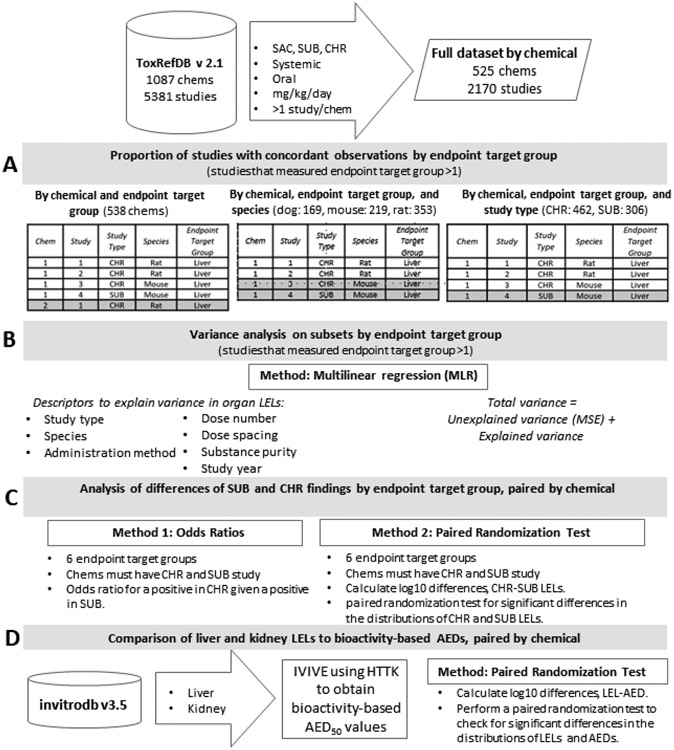
The four major components of the experimental workflow are illustrated in Figure 1. The work described herein addresses fundamental questions of how reproducible qualitative and quantitative organ-level findings in repeat dose animal studies are (Figure 1A and B, respectively) using a dataset developed using ToxRefDB version 2.1. Further, this work informs expectations for NAM performance metrics when predicting organ-level findings via practical questions about implementing NAMs for reduction and replacement of repeat dose studies, including questions regarding whether target organ effects can be identified using subchronic studies, and by logical extension, whether NAM predictions should be made specifically for subchronic versus chronic findings with respect to quantitative potency at target organs (Figure 1C). Finally, this work evaluates how similar organ-level LEL values are to administered equivalent doses (AEDs) based on bioactivity assay data relevant to liver and kidney from the ToxCast database, invitrodb version 3.5, combined with in vitro to in vivo extrapolation of dose (Figure 1D).
Figure 1. Experimental workflow.
The experimental workflow is described in parts A, B, C, and D. In A, different definitions of replicate studies for analysis of concordance are illustrated, where gray denotes the studies that would not be replicates for each grouping. In B, MLR employs descriptors of LEL to estimate explained variance by endpoint target group. In C, the differences between SUB and CHR organ-level findings are explored using odds ratios to describe the qualitative outcomes observed and paired randomization tests to identify quantitative differences. Finally, in D, using IVIVE, AEDs based on organ-relevant bioactivity assays in ToxCast are compared to LELs from ToxRefDB for kidney and liver.
Database used
Data source
ToxRefDB version 2.1 was used as the primary data source for this analysis (USEPA, 2019; Watford et al., 2019). This publicly available database (https://doi.org/10.23645/epacomptox.6062545.v4) contains information curated from studies largely conducted in accordance with or by specifications similar to the US EPA Office of Chemical Safety and Pollution Prevention (OCSPP) Series 870 Health Effects Test Guidelines(USEPA, OCSPP 870 Health Effects Series), for 1087 chemicals and 5381 studies (Figure 1). A major source of these data was curation of reviews of registrant-submitted toxicity studies, known as data evaluation records (DERs), from the Office of Pesticide Programs (OPP) within the OCSPP, with additional data obtained from guideline and guideline-like studies sourced from the National Toxicology Program, the pharmaceutical industry, and open literature. The database includes information regarding the study design, chemical identity, dosing, treatment group parameters, treatment-related (significantly different from control) and critical (adverse) effects, as well as endpoint testing status according to guideline specifications (Martin et al., 2009a; Martin et al., 2009b).
ToxRefDB v2.1 was queried to retrieve only repeat dose studies by the oral route that were categorized as subacute (SAC), subchronic (SUB), or chronic (CHR) in adult rats, mice, or dogs. No restrictions were placed on administration methods (e.g., feed, capsule, gavage/intubation, or water were included if the dose unit was available as or convertible to mg/kg/day). Other administration methods (e.g., intravenous, inhalation) were out of scope on account of a more limited number of studies available. For all 4 components of the workflow outlined in Figure 1, chemicals needed to have more than 1 associated study. The maximum dataset used throughout this study comprised 525 chemicals and 2170 studies (Figure 1, Supplemental File 1).
Endpoint target group lowest effect levels
To understand the reproducibility of organ-level effects, the effect terminology in ToxRefDB v2.1 was leveraged to group data into “endpoint target groups” that correspond to organs. ToxRefDB v2.1 has a hierarchical controlled effect terminology, proceeding as follows: endpoint to effect to treatment group effect. The terms selected were largely driven by efforts to standardize pathological observations from required observations in the studies adhering to the Series 870 test guidelines (Watford et al., 2019). At the endpoint level, the endpoint category (cholinesterase, reproductive, developmental, systemic), endpoint type (clinical chemistry, organ weight, microscopic and gross pathology), and target (or in this case, organ) are defined. An effect is more specific than an endpoint (e.g., for microscopic pathology, the effect may be hypertrophy). Finally, at the treatment group effect level, the life-stage, target site, and free text description from the source document are annotated. For the work herein, endpoint and effect information were used to form endpoint target groups that correspond to the six organs with the highest frequency of positive findings: adrenal gland, kidney, liver, spleen, stomach, and thyroid gland. The endpoint types included in these endpoint target groups include organ weight, gross pathology, and microscopic pathology, with the relative counts of these observations varying by organ (Supplemental Figure 2; Supplemental File 1). For liver, kidney, and thyroid, any clinical chemistry measures that were relevant to the health of these tissues were added to the endpoint targets to form endpoint target groups, whereas the endpoint targets adrenal, spleen, and stomach were not augmented to form endpoint target groups. The following clinical chemistry endpoint targets were added as liver-relevant: alkaline phosphatase, alanine aminotransferase, aspartate aminotransferase, bilirubin, gamma glutamyl transferase and peptides, and globulins. Similarly, for kidney, clinical chemistry endpoint targets were added, including urea nitrogen and urinalysis, as being kidney-relevant. And finally, clinical chemistry measures of thyroid hormones, including thyroid stimulating hormone, triiodothyronine, and thyroxine were annotated as part of the thyroid endpoint target group. All of the endpoint and effect information associated with included endpoint target groups in this work are provided in Supplemental File 1.
Negative data
A feature of ToxRefDB v2.1 is the implementation of guideline profiles that enable the inference of negative findings from studies that were adherent to a standard such as an OCSPP Health Effects 870 Series guideline or specifications from the National Toxicology Program. For studies that can be linked to a guideline profile, endpoints can be understood as required, triggered, or recommended observations, with any endpoints reported but not expressly mentioned in the guideline profile as not required. These guideline profiles allow distinction of data that are missing (not tested) from negative findings that were tested according to the standard, with no effect observed and therefore not reported (Watford et al., 2019). Negative data were inferred programmatically by calling all endpoint target group information that was required to obtain a total number of studies (and endpoints) tested for a given chemical and comparing these totals to the positives reported.
Reproducibility of organ findings
The reproducibility of organ-level findings, of any adversity level or type, was calculated as the value “concordance,” (Figure 1A) as given by Eq. 1 below:
| Eq. 1: |
Where a positive finding is any change (as indicated by treatment-related effects at any dose level) in gross pathology, microscopic pathology, organ weight, or associated clinical chemistry endpoints comprising an endpoint target group, and a negative finding was no change in any of the listed parameters for that organ as inferred from the corresponding guideline profile. To preserve high N in each organ-level calculation, percent concordance was calculated using all studies (where chemical identity defined replicate studies); by chemical and species combination for dog, mouse, and rat (where the unique combination of chemical and species defined replicate studies); and by chemical and study type (where the unique combination of chemical and chronic or subchronic duration defined replicate studies), as illustrated in Figure 1A.
Variance in organ findings across replicate studies
The variance estimation methodology used in this study was similar to the methodology previously reported in Pham et al. (2020), as illustrated in Figure 1B. The goal of this methodology was to approximate “inherent” variance in repeat dose studies that the major experimental design parameters, as indicated by curated study metadata, could not explain. Herein, eight study descriptors were used in multilinear regression (MLR) (Jobson, 2012) for statistical modeling of variance in organ-level effects across replicate studies, including four categorical descriptors (chemical, study type, species, administration method) and four continuous descriptors (number of doses, dose spacing, study year, and substance purity). All study descriptors are summarized in Table 1. Dose spacing by study (i.e., log10-dose spacing) was calculated by averaging the distance between each test chemical dose (excluding the vehicle control). Dose spacing, study year, and substance purity were all centered about the mean, with missing values changed to the mean.
Table 1. Study descriptors used as covariates.
Type indicates categorical or continuous study descriptors used as covariates in multilinear regression (MLR). The conditions defined per study descriptor are described, along with any mathematical adjustments made.
| Study descriptor |
Type | Conditions | Adjustments |
|---|---|---|---|
| Chemical | Categorical (factor) | identified as a “dsstox_substance_id” | |
| Study Type | identified as subacute (“SAC”), subchronic (“SUB”), or chronic (“CHR”) | ||
| Species | identified as “rat”, “mouse”, or “dog” | ||
| Administration Method | identified as “feed”, “gavage/intubation”, “water”, “capsule”, “not specified" [oral], "diet", "whole-body" | included in MLR for full endpoint target dataset; not included for the previously curated ACM dataset due to lack of sufficient levels | |
| Dose Number | Continuous | number of non-control, treatment-related doses | |
| Dose Spacing | the average distance between each dose in the series, centered around the mean | ||
| Study Year | Year the study was reported, centered around the mean | NA changed to mean | |
| Substance Purity | % substance purity reported, centered around the mean | NA changed to mean |
Benchmark dose (BMD) estimates for organ-level effects and study-level points-of-departure were also modeled to understand their statistical variance relative to discrete LELs. BMD values were obtained from ToxRefDB v2.0. Derivation of the BMD values in ToxRefDB v2.0 relied on batch processing with US EPA Benchmark Dose Software (version 2.7) using a Python wrapper, as described previously (Pham et al., 2019; Watford et al., 2019). BMD values from ToxRefDB v2.0 were used in this analysis because the BMD pipeline was not updated for ToxRefDB v2.1. The BMD datasets for variance estimation reflect a smaller N because only ~28,000 of the 92,000 quantitative dose-response datasets in ToxRefDB v2.0 were amenable to BMDS modeling, which requires reporting of dose, sample size (N), and dichotomous or continuous effect mean and variance. As the BMD datasets by organ may contain different and potentially fewer studies than the full LEL datasets by organ, the LEL dataset was subset to include the LELs for the same studies included in the BMD datasets by organ and these LEL subsets were also modeled by MLR.
Additionally, for complete comparison to Pham et al. 2020, in which variance in study-level points-of-departure was estimated, a “curated” set of studies representing stringently defined study replicates, with each study sharing chemical, study type, administration method, and species, from Pham et al. (2020) was used (supplied by Supplemental File 1 of Pham et al. 2020). The organ-level LELs derived for these studies were also modeled.
Total variance
Variance is a statistical measure, defined by the average of the squared differences from the mean, that indicates the “spread” of a population or data set. The total variance estimates in LEL and BMD values were calculated and can be understood as the sum of explained and unexplained variance in the data, as described conceptually by Equation 2.
| Eq. 2 |
Here, we reference unbiased sample variance in Equation 3: total variance, , is given as the sum of the squared deviations of every observation, , from the sample mean, (), divided by the degrees of freedom for the sample (n observations minus 1).
| Eq. 3 |
Multi-linear regression (MLR), explained variance, and unexplained variance
MLR was performed using the linear model function in R (lm(), R version 4.2.1), which uses QR decomposition (Goodall, 2005). MLR was employed to approximate the fraction of total variance in the LEL or BMD values by endpoint target group that could be explained by a simple statistical model. For BMD values, MLR was also employed to examine the variance in study-level BMD values (i.e., the minimum BMD value per study). The explained variance in LELs or BMDs was quantified as the fraction of the total variance that was accounted for by study descriptors used in modeling: chemical identity, study type, species, administration method, dose spacing, number of doses, study year, and % substance purity (Table 1).
The regression modeling using MLR to explain variance in the organ level LEL values is generically presented in Equation 4 as a simplified representation of multilinear regression equations that typically take the mathematical form of the expected y (as = intercept + beta1*variable1 + beta 2*variable2 + beta 3*variable3 + … + betap*variablep). The minimum expected LEL or BMD for an organ (or study, in the case of BMDs) was predicted using a collection of study descriptors, with each of these descriptors multiplied by a beta coefficient, otherwise known as a regression weight or slope value. For categorical variables including chemical, species, and administration method, there will be a coefficient for each unique level. A simplified form, where not all levels of each categorical variable are shown, is presented for conceptual understanding of the model:
| Eq. 4 |
The fraction of the variance that was unexplained by study descriptors was quantified as the estimated residual mean square error (MSE) (Equation 5). In Equation 5, MSE is defined as the residual sum of squares divided by the degrees of freedom for the regression model, where the residual sum of squares is equal to the sum of the squared difference between each observed organ-level or study-level LEL or BMD, Yi, and the predicted value for a given observation, (f(ri)), and the degrees of freedom are equal to the difference between the number of observations, N, and the number of covariates, p (equivalent to the sum of the number of continuous study descriptors and the total number of levels across all categorical study descriptors).
| Eq. 5 |
The unexplained variance includes any variance caused by factors not explained by the available study descriptors, e.g. the unknown differences between specific laboratories that conducted these studies, unknown study conditions (Consulting and Huff, 1989; Sorge et al., 2014) or biological variability of the animals used (Leisenring and Ryan, 1992). The percent of the total variance that can be explained relates to the total variance and the MSE, as indicated in Equation 6. Equation 6 is based on the concept that total variance is equal to the sum of the explained and unexplained variance, with the unexplained variance within observations approximated as MSE. Thus, the % variance explained is equal to the difference of the total variance and the computed MSE, divided by the total variance, and then all multiplied by 100 percent as given below; it is also equivalent to the adjusted coefficient of variation (adjusted R2).
| Eq. 6 |
Differences in organ-level findings based on study duration
Qualitative differences
To understand if SUB organ-level findings were qualitatively different from CHR organ-level findings, the full dataset containing both CHR and SUB studies with positive and inferred negative results based on guideline requirements was filtered to examine chemicals with curated CHR and SUB studies (Figure 1C). This dataset was additionally subset to chemicals with both CHR and SUB studies within the same species as well as within rodent (mouse and rat combined). Organ-level findings were considered binary: a positive or negative finding for a chemical in each study type or study type-species combination was determined based on the presence or absence of any finding for the organ (as described previously for the analysis of concordance). The odds ratios (Tenny and Hoffman, 2022) for a positive in the CHR study given a positive in the SUB study for each organ-level outcome were calculated as (Equation 7a):
| Eq. 7a |
Where is a SUB positive and is a SUB negative for a chemical, organ, and species group of interest, and similarly, is a CHR positive and is a CHR negative for a chemical, organ, and species group of interest. Thus, as an example, represents chemicals positive in both SUB and CHR studies for the organ and species of interest. The odds ratio of a positive in the CHR study given a negative in the SUB study is equal to the inverse of the odds ratio of a positive in both SUB and CHR studies, as given below in Equation 7b.
| Eq. 7b |
The standard error (SE) (Equation 7c) and confidence interval (CI) (Equation 7d) for the odds ratios were also computed with the assumption of a normal error distribution, as given below:
| Eq. 7c |
| Eq. 7d |
Quantitative differences
Quantitative differences between organ-level SUB LELs and CHR LELs for chemicals with both study types were also investigated to understand the potential need for adjustment factors for any prediction of SUB or CHR organ-level effects. The log10 difference between the mean CHR and mean SUB LELs for each of the 6 organs examined were computed to demonstrate the distributions of these raw differences. A paired randomization test based on sampling a permutation distribution 100,000 times was performed to address the hypothesis that the mean CHR and SUB LELs (log10-mg/kg/day) were not significantly different (two-sided test), i.e., the CHR and SUB LELs were interchangeable. This proceeded by evaluating 100,000 random permutations to determine how often the null mean difference was as or more extreme as the observed mean difference of CHR-SUB LELs. Per Equation 8a below, the mean difference between CHR mean and SUB mean LEL values paired by chemical and by organ was calculated as , with the sample size differing by organ. Then, a null distribution of mean differences was constructed by 100,000 random resamples of the CHR-SUB LEL distribution, and the number of times the permutations had mean differences, , that were as or more extreme than the observed mean difference, , was computed (Equation 8b). The number of times the permutations had mean differences, , that were as or more extreme than was divided by the total number of resamples and multiplied by 2 (Equation 8c) to calculate the p-value for this two-sided test, with a p-value of < 0.05 used to denote differences in organ-level SUB and CHR LELs that were significantly different from the null mean difference for that organ. For context, an approximate 95% CI was estimated based on a normal distribution around . If the null mean difference and the mean CHR-SUB difference overlapped, then the null hypothesis was not rejected (i.e., the null mean difference and mean CHR-SUB difference were not different with p-value > 0.05).
| Eq. 8a |
| Eq. 8b |
| Eq. 8c |
Differences in organ findings based on bioactivity-based or animal-based predictions
To understand if the quantitative differences between SUB and CHR LELs by organ are similar to the quantitative differences between bioactivity-based points-of-departure and in vivo LELs by organ, we examined bioactivity-based PODs estimated from publicly available ToxCast data (invitrodb version 3.5) (USEPA, 2022) and their relationship to organ-level LELs reported in ToxRefDB v2.1 (see Figure 1D).
First, assay endpoints in ToxCast corresponding best to liver or kidney were selected, largely based on the cell or cell line utilized (Supplemental File 5). For liver, assay endpoints including gene expression in human hepatocytes and HepaRG cells; nuclear receptor and oxidative stress panel in a metabolically enhanced human hepatocarcinoma (HepG2 subclone); and, high content imaging of cell morphology and health markers in HepG2 were used to indicate liver health. For kidney, a more limited suite of assays was available: assays performed in human embryonic kidney 293 or 293T (HEK293(T)) corresponding to cell cycle were considered an indicator of kidney health, acknowledging that these cells deviate from in vivo kidney phenotype. Assay endpoint data were summarized per chemical and organ indicated (liver or kidney) as the 5th percentile, 50th percentile (median), and mean of the 50% active concentration (AC50) data available. Using these summary potency values, in vitro to in vivo extrapolation of administered equivalent doses (AEDs) was performed using reverse dosimetry assumptions, in vitro high-throughput kinetic data for hepatic clearance and serum protein binding, and a 3-compartment steady state model encoded in R library “httk” (version 2.2.2) (Breen et al., 2021; Pearce et al., 2017). This approach is consistent with to previous analyses (Paul Friedman et al., 2020; Wetmore et al., 2012) and represents a baseline for estimation of AEDs, per Equation 9:
| Eq.9. |
where the is the steady-state plasma concentration for the median individual based on Monte Carlo simulation of the parameter uncertainty and model animal species physiological variability of pharmacokinetic parameters and a 3-compartment steady-state model that assumed 100% bioavailability as a conservative approximation. As multiple assay endpoints may have been relevant as models of liver or kidney, a population of values was created per chemical and organ combination, with summary values (5th percentile and mean ) computed for comparison to in vivo LEL values.
Next, a threshold in vivo organ-level LEL was approximated as the minimum organ-level LELs across any available SUB and CHR studies. The differences (log10-mg/kg/day) between this in vivo organ-level LEL value and the 5th percentile as well as the mean were computed. The paired randomization test procedure was the same as the procedure described above to examine potential quantitative differences between CHR and SUB organ-level LEL values: a paired randomization test with 100,000 permutations was performed to address the hypothesis that the threshold organ-level LEL values (log10-mg/kg/day) were significantly different from the values by comparing to a null mean difference distribution. This proceeded by evaluating these 100,000 random permutations to determine how often the null mean difference was as or more extreme as the observed mean difference of LEL-AED, with p-values < 0.05 used to denote whether the mean LEL-AED difference was significantly different from the null mean difference (see Equations 8a-8c). Both the mean and 5th percentile values by chemical were compared to the minimum LEL from SUB and CHR studies by chemical. The same paired randomization test procedure was also performed for LELs that were allometrically-scaled to human equivalent doses (HEDs) by species using body-weight scaling factors (rat LELs in mg/kg/day * 0.162, mouse LELs in mg/kg/day * 0.135, and dog LELs in mg/kg/day * 0.541) per previously reported methods (Nair and Jacob, 2016).
Supplemental File Descriptions and Software
Supplemental File 1 contains the datasets used in MLR for estimation of variance, including 4 tables: all LELs calculated by endpoint target group (organ level); LELs by organ from the curated LEL set used in Pham et al. 2020; BMDs by organ; and BMDs by study.
Supplemental File 2 contains tabular reporting of input data for concordance analysis and results as percent concordance observed by chemical-endpoint, chemical-endpoint-species, and chemical-endpoint-study type combinations.
Supplemental File 3 contains MLR study descriptors and results for quantitative estimates of variance.
Supplemental File 4 contains odds ratio datasets and results.
Supplemental File 5 contains summarized LEL and HED values, ToxCast assay endpoint information, and calculated values using library(httk) v2.2.2.
Supplemental File 6 contains the R code used for this analysis and figures in this work, available as a knitted R Markdown file (exported as html).
Supplemental File 7 contains Supplemental Figures 1, 2, and 3.
The code (performed with R version 4.2.1) and source data are also available at EPA GitHub (https://github.com/USEPA/CompTox-Reproducibility-Organ-Effects) and EPA Clowder repository (https://clowder.edap-cluster.com/datasets/646d247fe4b08a6b394d2853).
Results
Qualitative concordance
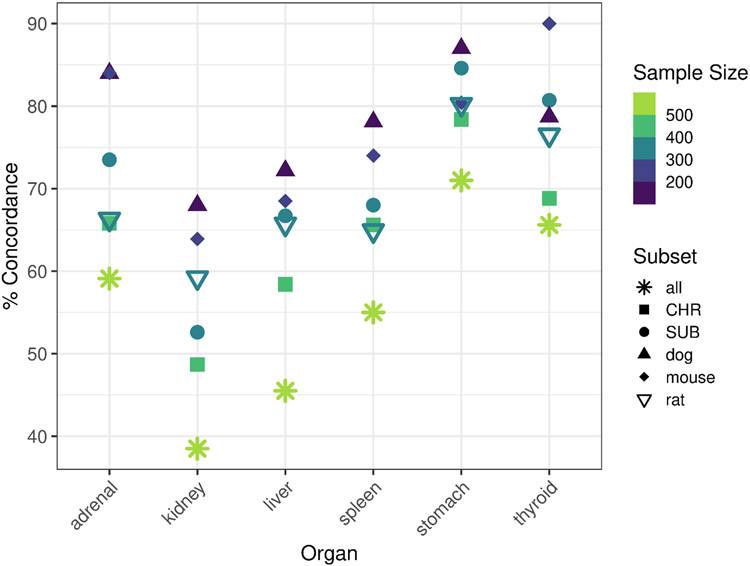
The qualitative concordance of repeat dose study observations (Figure 1A) was evaluated for the six endpoint target groups with the highest frequency of reported effects (Supplemental Figure 1): adrenal gland, kidney, liver, spleen, stomach, and thyroid gland. It should be noted that effects on body weight and clinical signs are in the top five most frequently observed endpoint targets, but these systemic findings are not the focus of this work. Using the full dataset of 538 chemicals corresponding to 2284 studies for all species and repeat dose study types, in which study replicates are considered at the chemical level, demonstrated the lowest qualitative concordance of any replicate study groupings, with 59, 39, 46, 55, 71, and 66% concordance for adrenal, kidney, liver, spleen, stomach, and thyroid gland, respectively, likely because all species were included (Figure 2, with values reported in tabular form in Supplemental File 2). The within-species concordance tended to be greater than the within-study type concordance, as demonstrated by the dog, mouse, and rat subsets of the dataset, which demonstrated qualitative concordance values of 59% or greater, and in some cases approaching 90%; however, these intraspecies comparisons were based on much smaller N (i.e., only 169, 219, and 353 chemicals with replicate data by endpoint target group and species for dog, mouse, and rat). Additionally, higher concordance (approaching 80-90%) corresponded to organs with few positive chemicals; for instance, 87% concordance was observed for stomach in replicate dog studies, but only 2 chemicals were completely positive, 22 chemicals were mixed, and 145 chemicals were completely negative for stomach-related effects in dog studies. Similarly, percent concordance for thyroid gland related effects in mice was 90%, but only 3 chemicals were positive across all studies, 22 chemicals produced mixed results, and 194 chemicals were negative. Whereas organs associated with more “negative” chemicals (i.e., concordance based on absence of findings across studies) tended to be associated with greater rates of concordance in findings across study replicates, the liver and kidney, which demonstrate the highest rates of positive reporting, were associated with the lowest concordance across different definitions of study replication (liver: 46-72% and kidney: 39-68%).
Figure 2. Qualitative reproducibility of organ-level effect observations in repeat dose studies of adult animals.
The % concordance of findings in datasets defined by subset (all = replicate studies defined by chemical; CHR = CHR studies only, multiple species; SUB = SUB studies only, multiple species; dog = dog studies only, multiple study types; mouse = mouse studies only, multiple study types; rat = rat studies only, multiple study types. Sample size (number of chemicals) is indicated by color ranging from 169 (dog studies) to 538 (for “all”).
Quantitative variability
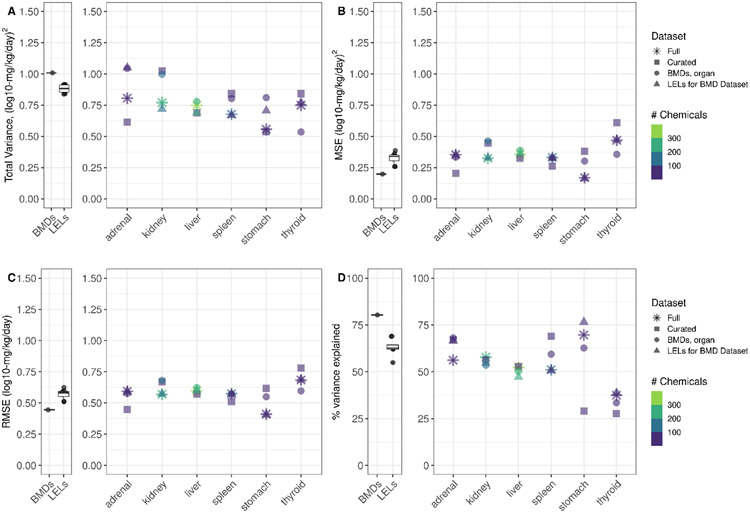
In this work, we compared study-level variance in curated LELs from Pham et al. 2020, study-level variance in the minimum modeled benchmark dose (BMD) values, and organ-level variance with both LELs and BMDs (Figure 1B). In general, estimating the variance in point-of-departure (POD) values at the organ level failed to substantially reduce estimates of variance in the PODs from repeat dose studies (Figure 3, Supplemental File 3). The total variance (Figure 3A) observed at a study-level for LELs in full datasets with different levels of refinement in Pham et al. (2020) ranged from 0.838 to 0.916 (log10-mg/kg/day)2; the variance in minimum BMDs at the study-level was 1.000 (log10-mg/kg/day)2; and the organ-level variance in LEL datasets ranged from 0.538-1.025 (log10-mg/kg/day)2 by organ, potency metric, and dataset, with a mean ± SD of 0.77 ± 0.15 (log10-mg/kg/day)2 across all variance estimates in this work. The number of chemicals and studies included in these estimates was greatest for the “Full” dataset and was greatly decreased for the “Curated” dataset, the “BMDs, organ” dataset, and the “LELs for BMD Dataset.” The “Curated” dataset corresponds to a dataset defined in Pham et al. (2020) with extremely stringent definitions of replicate studies (must share a combined factor of chemical-administration method-species-study type). In this work, the results from the “Curated” set may be least extensible because of the relatively small numbers of chemicals that could be included (4 to 55 chemicals for the “Curated” dataset, depending on organ, versus 58-364 chemicals for the “Full” dataset).
Figure 3. Variance, MSE, RMSE, and % variance explained.
In A-D, the first panel illustrates study-level values for BMDs and LELs (LEL values derived in Pham et al. 2020) for comparison. The second panel for A-D indicate the values at the organ-level, as indicated. In A, total variance estimates for the full organ-level dataset (asterisk), the curated organ-level dataset (square), the BMD dataset by organ (circle), and the LELs corresponding to the BMD dataset (triangle) are shown. In B, C, and D, MSE (unexplained variance), RMSE, and the % total variance explained values for each dataset are shown, respectively. Color indicates the number of chemicals represented in each dataset.
Unexplained variance, approximated by MSE, appears similar between study-level and organ-level estimates among replicate studies. At the study-level, Pham et al. reported MSE values of 0.261-0.387 (log10-mg/kg/day)2 for full LEL datasets. Herein, MSE for study-level BMDs was lower (0.198 (log10-mg/kg/day)2, which corresponded to a slightly higher amount of explained variance (80%) that approached maximal explained variance in study-level PODs. The organ-level MSE estimates (range: 0.169-0.61, mean ± SD: 0.350 ± 0.1) were generally at the higher end of the study-level MSE range. This may be related to the reduced number of chemicals in this work, as replicates at the study-level in Pham et al. included 278 to 563 chemicals for LEL datasets, whereas here the range for the “Full” dataset was 58-364, depending on organ. For thyroid, MSE values appeared higher than other organs, perhaps in part due to the low number of chemicals with thyroid LELs or BMDs (13-79 chemicals).
Of great interest is the finding that an RMSE of 0.5 log10-mg/kg/day serves as a reasonable approximation of inter-study standard deviation in study-level BMDs, study-level LELs from Pham et al. 2020, and herein for organ-level LELs or BMDs (Figure 3). In general, the RMSE values that approximate organ-level variation range within approximately 0.4 to 0.75 log10-mg/kg/day, with a mean ± SD of 0.59 ± 0.09 log10-mg/kg/day. Compared to RMSE values estimated using LEL or BMD values at the study-level (mean ± SD: 0.56 ± 0.06), it seems that an estimate of inter-study standard deviation in both study-level and organ-level PODs of 0.5 log10-mg/kg/day is a reasonable expectation.
The percent variance explained at the study-level was 55-69% for LELs and approximately 80% for BMDs, as noted above. The percent variance explained was variable at the organ level, but generally within 50-75% depending on organ and dataset, except for thyroid, where the percent variance explained was much lower (28-39%). Though the number of chemicals and studies included may have played a factor in the lower percent variance explained for thyroid, the sample sizes for other organs including the adrenal gland and stomach were also low, but without a consistent effect on the percent variance explained.
Differences in SUB and CHR findings
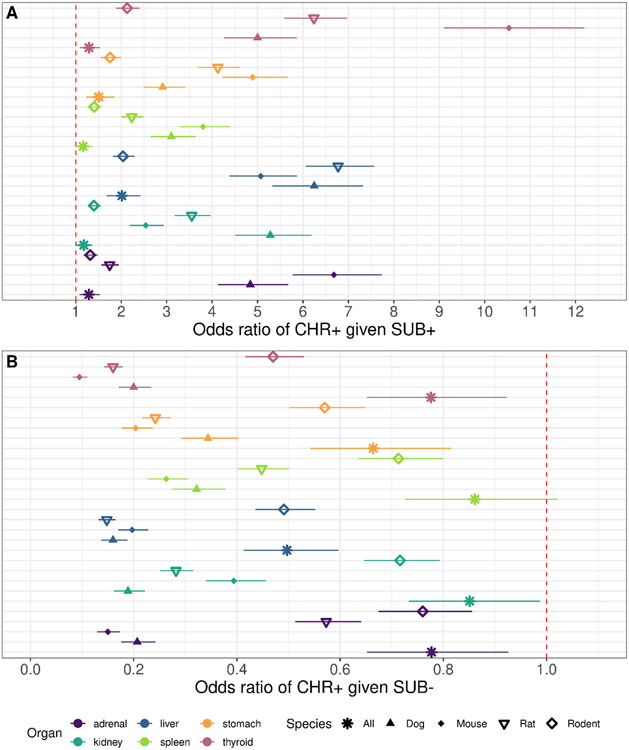
The odds ratios of a positive finding of any magnitude in a CHR study given a positive finding of any magnitude in a SUB study, for all 6 organs included, were greater than 1, indicating that a positive organ-level finding in a SUB study is likely to be recapitulated in the CHR study (Figure 4A). Note that the relative adversity of the findings was not considered in this analysis; rather, any positive finding was considered a positive. In agreement with the findings on qualitative concordance, grouping all species together resulted in odds ratios closer to 1 (in the 1 - 2.5 range) than odds ratios for species-matched SUB and CHR organ level findings (which ranged from 1-12); however, some of these higher odds ratios may not necessarily have been the result of intraspecies concordance alone as they may have been impacted by the very small number of chemicals with positive findings (as in the case of mouse and the thyroid gland, where only 3 chemicals were positive in all studies and 22 chemicals produced “mixed” results). It should be noted that due to the matching procedure performed, the sample size was greatly reduced for the “all” species designation, as this required chemicals to have a SUB and CHR study in mice, rats, and dogs (n=60 chemicals for “all”, versus 313, 179, 152, and 159 chemicals for rat, mouse, dog, and rodent, respectively, where rodent indicates rat and mouse studies together). The invariance of the odds ratio allows for the inverse of the odds ratio calculated for a positive in a CHR given a positive in the SUB to describe the odds ratio for a CHR positive organ-level finding given a SUB negative organ-level finding. Unsurprisingly, all of the odds ratios in Figure 4B for a positive CHR organ-level finding in the absence of a SUB organ-level finding are less than 1, indicating a negative in the SUB indicates a greater likelihood of a negative in the CHR for organ-level findings.
Figure 4. Qualitative concordance between SUB and CHR organ-level effects.
In A, the odds ratio of a positive finding in the CHR study for an organ given a positive finding in the SUB study (subset by species groupings, as indicated by asterisk for all species, filled triangle for dog, filled diamond for mouse, upside down empty triangle for rat, and empty diamond for rodent). Color indicates organ. The dot represents the odds ratio, and the line segment demonstrates the distance from the lower 95% CI bound to the upper 95% CI bound for the odds ratio. Sample sizes for rat, mouse, dog, rodent, all were 313, 179, 152, 159, and 60 chemicals (with SUB and CHR studies available).
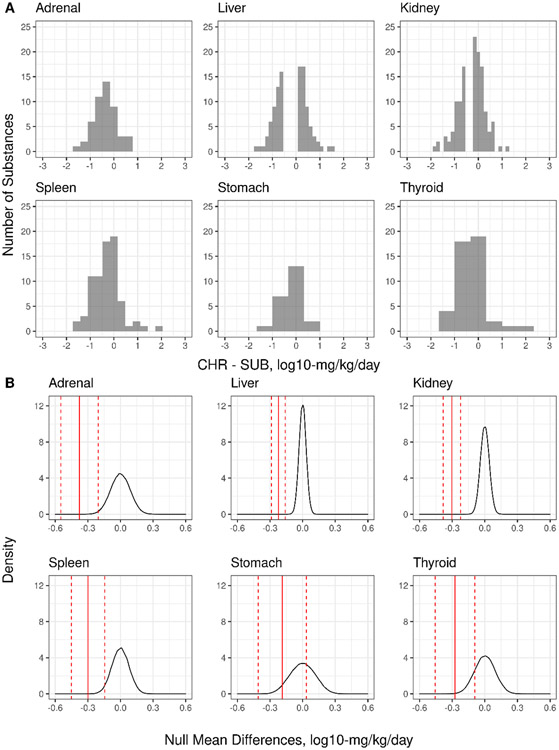
The mean differences between chemical-matched CHR and SUB studies (Table 2) range from −0.187 to −0.377 log10-mg/kg/day, with lower bounds on the 95% confidence interval for this mean difference ranging from −0.286 to −0.548 log10-mg/kg/day. This indicates that on average, for the six endpoint targets included, the mean difference of the CHR and SUB LELs is typically less than −0.5 log10-mg/kg/day. For the adrenal gland, kidney, liver, spleen, and thyroid gland, this mean difference between CHR and SUB organ-level LELs is significantly different from the null mean difference (p <0.05), i.e., the CHR and SUB LELs for these organs are not interchangeable. However, of more interest is the finding that the mean differences for these organ-level LELs appear to be less than the RMSE (representing estimated standard deviation) for LELs among replicate studies as approximated using the RMSE from MLR modeling of the LEL and BMD datasets at both the organ and study-level. It should be noted that the number of chemicals with enough data to understand the relative potency differences between CHR and SUB studies at the organ level are greatest for liver and kidney. In Figure 5A, the distribution of the CHR-SUB LEL differences demonstrate that most of the differences in CHR and SUB organ-level LELs are within ± 1 log10-mg/kg/day, which aligns well with the use of a 10-fold uncertainty factor in common use in risk assessment as a protective practice for the distribution of these differences. Gaps in the distributions for liver and kidney may reflect that these datasets are large for in vivo toxicology, but still relatively “small,” as well as the experimental design motivations that lead to different discrete doses and dose ranges used in CHR and SUB studies for the same chemical. It is likely that study-specific (and thereby, chemical-specific) dose selection and dose spacing influences the shapes of the distributions in Figure 5A, and so the paired differences CHR-SUB differences by chemical were further evaluated using a paired randomization test to understand whether the mean paired differences were statistically different from zero. In 5B, the results of the paired randomization test are visualized, such that the mean ± 95% CI bounds for the mean CHR-SUB LEL difference (red lines) are typically less than the null mean difference of 0 (null mean distribution is a black line). For some organs, like stomach and thyroid, the upper 95% CI bound on the mean CHR-SUB LEL difference approaches zero.
Table 2. Mean differences in CHR and SUB LELs.
The organ, number of chemicals with matched CHR and SUB LELs, the mean difference, p-value, and lower and upper 95% confidence interval (CI) bounds around the mean difference are shown.
| Organ | # Chemicals | Mean difference, CHR – SUB (log10- mg/kg/day) |
p-value | Lower CI bound |
Upper CI bound |
|---|---|---|---|---|---|
| Adrenal | 49 | −0.3768 | <0.0001 | −0.5484 | −0.2052 |
| Kidney | 190 | −0.303 | <0.0001 | −0.3821 | −0.2238 |
| Liver | 251 | −0.2232 | <0.0001 | −0.2871 | −0.1593 |
| Spleen | 75 | −0.2976 | 0.0001 | −0.4502 | −0.1449 |
| Stomach | 23 | −0.1869 | 0.0982 | −0.4077 | 0.034 |
| Thyroid | 45 | −0.2754 | 0.0024 | −0.4576 | −0.0931 |
Figure 5. CHR-SUB LEL difference and the null mean difference.
The distribution of the CHR-SUB LEL differences by organ (A) and the results of the paired randomization test (B) are shown. In B, the solid red line represents the mean CHR-SUB LEL difference, and the dotted red lines represent the upper and lower 95% CI bounds on the mean. The black line represents the null mean difference distribution, centered at zero.
Comparison of in vivo PODs to bioactivity-based PODs
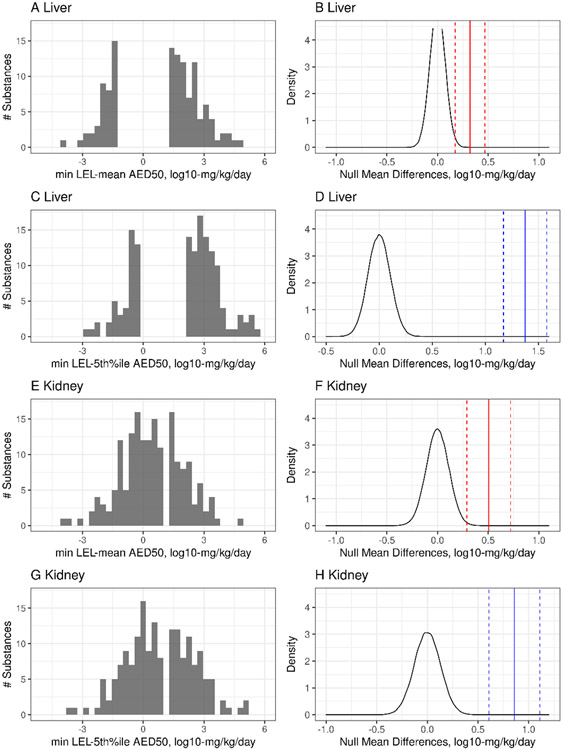
This work also explored the differences between minimum in vivo PODs, summarized as the minimum LEL and HED values by chemical for liver and kidney in SUB and CHR studies, and the 5th percentile or mean estimates from in vitro models of liver and kidney (see distributions of these differences in Figure 6; see Supplemental File 5 for tabular data). Using minimum LEL values for liver and kidney, the LEL – AED difference was minimized using the mean by chemical (0.3203 and 0.5060 log10-mg/kg/day for liver and kidney, respectively) (Table 3 and Figure 6B and 6F). Though the mean LEL-AED difference approached the observed RMSE (i.e., estimated standard deviation) describing variability in in vivo PODs, i.e. approaching 0.5 log10-mg/kg/day, the distributions of the raw LEL-AED difference demonstrated much longer tails (Figure 6A, B, E, F) than the differences in CHR-SUB organ level LELs, with minimum LEL to comparisons at times suggesting differences in excess of 3 orders of magnitude in either direction at the tails (Figure 6A, B, E, F). Using the 5th percentile AED increased the size of the mean LEL-AED differences (1.3755 and 0.8586 log10-mg/kg/day for liver and kidney, respectively) (Figure 6C,D,G,H). We also examined the mean LEL-AED differences with respect to a null mean distribution (Figure 6B, D, F, H). The LEL - AED differences, regardless of whether the mean or 5th percentile were used, were significantly different from the zero-centered null mean distribution (Table 3, p<0.0001) for estimates of liver and kidney effects, using a paired randomization test to compare the LEL-AED difference distributions to the null mean difference distribution. The results herein suggest that the mean LEL-AED difference is similar to the RMSE value computed for replicate SUB or CHR studies that examine organ-level effects, but simultaneously our results indicate the potential for large discrepancies for some chemicals at the tails of this distribution.
Figure 6. LEL-AED50 differences and the null mean difference distribution.
A, B, E, F: the distribution of the minimum LEL – mean AED50 and the matched null mean difference distribution, where the black line represents the null mean difference distribution centered at zero, the solid red line represents the mean difference of the minimum LEL- mean AED50 values, and the dotted red lines represent the upper and lower 95% CI bounds on this mean difference; C, D, G, H: the distribution of the minimum LEL – 5th percentile AED50 and the matched null mean difference distribution, where the black line represents the null mean difference distribution centered at zero, the solid blue line represents the mean difference of the minimum LEL- 5th percentile AED50 values, and the dotted blue lines represent the upper and lower 95% CI bounds on this mean difference. All x-axis units are log10-mg/kg/day.
Table 3. Mean differences in in vivo POD and bioactivity-based AED50 values.
The organ, number of chemicals with matched POD and values, the type of in vivo POD (minimum LEL or HED), the type of summary value being compared (mean or 5th percentile), the mean difference, the p-value on this difference from paired randomization tests, and the lower and upper 95% confidence interval (CI) bounds around the mean difference, are shown in log10-mg/kg/day values.
| Organ | # Chemicals | In vivo POD (log10- mg/kg/day) |
AED type (log10- mg/kg/day) |
Mean difference, in vivo POD - AED (log10- mg/kg/day) |
p-value | Lower CI bound |
Upper CI bound |
|---|---|---|---|---|---|---|---|
| Liver | 365 | min LEL | mean AED | 0.3203 | <0.0001 | 0.1736 | 0.4670 |
| Liver | 365 | min LEL | 5th %-ile AED | 1.3755 | <0.0001 | 1.172 | 1.579 |
| Kidney | 194 | min LEL | mean AED | 0.5060 | <0.0001 | 0.290 | 0.7223 |
| Kidney | 194 | min LEL | 5th %-ile AED | 0.8586 | <0.0001 | 0.608 | 1.110 |
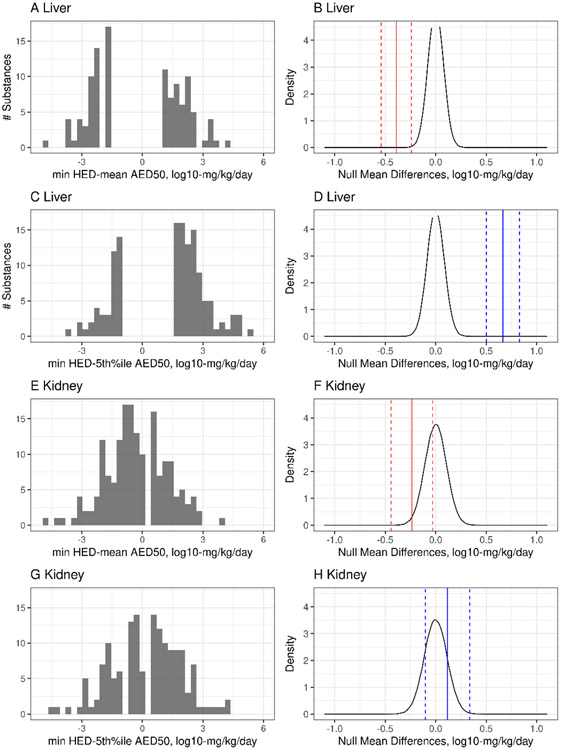
| Liver | 365 | min HED | mean AED | −0.3900 | <0.0001 | −0.5394 | −0.2405 |
| Liver | 365 | min HED | 5th %-ile AED | 0.6652 | <0.0001 | 0.5013 | 0.8291 |
| Kidney | 194 | min HED | mean AED | −0.2357 | 0.0245 | −0.4418 | −0.0295 |
| Kidney | 194 | min HED | 5th %-ile AED | 0.1169 | 0.2953 | −0.1027 | 0.3366 |
The difference between minimum HED values (allometrically scaled LELs based on bodyweight to “human equivalent doses”) from SUB and CHR liver and kidney effects and AED values was also evaluated using the same methodology. Allometric scaling based on bodyweight results in smaller in vivo POD values because the in vivo POD values are multiplied by a species-specific fraction, and as such the size of the mean HED – AED differences (Table 3) were decreased from the mean LEL – AED differences. Indeed, the HED tended to be smaller than the mean , with mean HED – AED differences of −0.3900 and −0.2357 log10-mg/kg/day for liver and kidney, respectively. Using the 5th percentile resulted in a slightly larger mean HED – AED differences of 0.6652 for liver; the mean difference for kidney (0.1169 log10-mg/kg/day) was not significantly different from the null mean difference (p = 0.2953). Using the mean AED in the HED – AED comparison suggests that these mean differences, which were significant for liver and kidney at the α = 0.05 level, are within 0.5 log10-mg/kg/day of the HED values. Yet, again, we observe in Figure 7 that while the mean differences may be less than 0.5 log10-mg/kg/day in some cases, the tails of the raw difference distributions (Figure 7A, C, E, G) suggest longer tails with differences in excess of 3 orders of magnitude for some small fraction of chemicals (15-16 of 365 chemicals for mean liver POD comparisons, depending on use of HED or LEL values, and 9 of 194 chemicals for mean kidney POD comparisons). These subsets represent small sample sizes, so it is difficult to make generalizations about the types of chemicals for which bioactivity-based AEDs were most divergent or the types of uncertainty (experimental, biological, and/or IVIVE-related) that contributed most significantly to these differences; however, several of the chemicals with extreme differences in mean in vivo POD to AED comparisons were shared between liver and kidney (Supplemental File 5). Three of the chemicals with extreme differences in the mean liver comparisons were sulfuron-containing chemicals, which are known to rapidly hydrolyze in DMSO and therefore are not amenable to the in vitro screening paradigms with data currently available in invitrodb version 3.5.
Figure 7. HED-AED50 differences with null mean difference distribution.
A, B, E, F: the distribution of the minimum LEL – mean AED50 and the matched null mean difference distribution, where the black line represents the null mean difference distribution centered at zero, the solid red line represents the mean difference of the minimum LEL- mean AED50 values, and the dotted red lines represent the upper and lower 95% CI bounds on this mean difference; C, D, G, H: the distribution of the minimum LEL – 5th percentile AED50 and the matched null mean difference distribution, where the black line represents the null mean difference distribution centered at zero, the solid blue line represents the mean difference of the minimum LEL- 5th percentile AED50 values, and the dotted blue lines represent the upper and lower 95% CI bounds on this mean difference. All x-axis units are log10-mg/kg/day.
Discussion
In this work, we examined the reproducibility of organ-level effects in repeat doses using publicly available, curated data from oral repeat dose studies that follow health effects guidelines, as these types of studies typically inform regulatory toxicology. We also tested the hypothesis that the variability in the potency of organ-level effects would be less than the variability in the potency of study-level effects, and in doing so, an upper bound on the predictivity of NAMs for in vivo organ-level findings could be described. We examined the qualitative and quantitative concordance of organ-level effects from repeat dose studies of different durations (subchronic versus chronic) to set expectations regarding alternatives to these studies. Finally, we applied an established approach to the estimation of bioactivity-based effect levels, or values, for liver and kidney, and compared these to in vivo effect levels for these organs to understand a current baseline for NAM-based quantitative prediction of target organ effects. Overall, this novel work provides a data-informed perspective on building scientific confidence for NAMs for potential target organ effects by examining how studies following Health Effects guidelines using animals perform in terms of qualitative and quantitative reproducibility.
Understanding the qualitative and quantitative concordance of organ-level effects in replicate animal studies of a chemical may help inform the maximum predictive performance that could be expected from a NAM designed to predict chemical effects on target organs. Often, validation of NAMs utilizes reductionist representations of animal outcomes as “true positives” and “true negatives,” with NAM outcomes providing the “predicted positive” and “predicted negative” quadrants of a confusion matrix for calculation of balanced accuracy. Experts are left to judge: what level of balanced accuracy is suitably “fit-for-purpose” for the toxicology application considered? One possible answer among many may be: balanced accuracy that exceeds the predictive accuracy of replicate animal studies for themselves. Herein, we examined the percent concordance of replicate animal studies, and observed that intraspecies concordance and concordance for organs with largely negative results were the highest concordance values observed. Liver and kidney, with the highest rates of positive effect reporting, demonstrated concordance values from 39-72%. Only organ and species combinations with very limited positive data reported and smaller sample sizes demonstrated concordance values in excess of 70%. Several conclusions can be drawn from these findings. Application of advanced methods for determination of “reference chemicals,” i.e., literature mining, are likely needed for evaluation of NAMs, especially for target endpoints that are less well-studied or only well-characterized for small numbers of chemicals, as many chemicals may produce mixed or equivocal results at the organ-level across replicate studies used in regulatory toxicology. Evaluation of NAMs for organ-level effects may require building knowledge of more mechanistic key events perturbed by chemicals such that current measures (organ weight, histopathology, gross changes) are not being used to measure the success of NAMs that typically indicate bioactivity that would precede adversity. Further, limitations in the in vivo toxicology approach employed to date (few doses, high maximum doses used, only tissue-level changes measured, limited to no understanding of serum concentrations over time within most studies used for regulatory toxicology) may obscure underlying reasons for observations of low concordance across replicate studies. Finally, a general conclusion but perhaps most important of all, is that the current toxicology studies typically used in regulatory toxicology are not themselves 100% concordant between or within species, or between or within study designs, and as such, NAMs should not be expected to recapitulate a summary of in vivo repeat dose study effects with 100% accuracy.
Organs with lower positive reporting rates (i.e., adrenal gland, spleen, stomach, and thyroid gland) appeared to demonstrate higher inter-study concordance, particularly within species or within study type where concordance values for some organs approached 80-90%. This finding may relate to a high negative predictive value of these types of animal studies when the associated true negative rate is low. This finding may also align with previous reports of the high negative predictive value (upwards of 90%) for preclinical rodent studies with similar experimental designs for clinical findings in humans, with variation in the negative predictive value related to the prevalence of clinical findings (Monticello et al., 2017); this previous work suggests that the value of preclinical animal testing for pharmaceuticals may be in identifying drugs with no target organ effects rather than accurate positive prediction. In terms of positive predictive value, Monticello and colleagues note that the requirement to conduct animal studies at doses that produce higher internal exposures than those achieved in human clinical testing increases sensitivity along with the false positive rate and decreases specificity of preclinical animal tests for human effects in the clinic. However, increasing the specificity of preclinical animal studies and thereby potentially increasing the false negative rate for clinical findings might diminish the value of animal studies for identifying drugs free of organ effects in the clinic.
Given inherent limitations in the work herein, which looked at concordance among animal studies without human data for comparison, we looked to the literature for previous estimates of concordance of effects in repeat dose studies to understand if the rates of concordance observed herein were within previously reported ranges. Available studies of concordance of effects were largely focused on carcinogenesis using CHR study designs, including evaluation of site-specific carcinogenesis, replication of carcinogenicity in different species and in different sexes (Table 4). Reports of interspecies concordance of site-specific carcinogenesis (i.e., same target organ site) suggested agreement of 35-37% between mice and rats (Haseman and Lockhart, 1993), though one study suggested interspecies of concordance of carcinogenesis at any site might be 74% between mice and rats (Huff et al., 1991). Concordance within species across different sexes (Haseman and Lockhart, 1993) or within species across different studies (Gottmann et al., 2001a) ranged 49-66% in different reports. Though these previous studies largely focused on studies of carcinogenesis from few institutional sources (i.e., studies primarily from the National Toxicology Program/National Cancer Institute of the US National Institutes of Health), the rates of concordance reported herein are within the range of these previous reports and confirm greater rates of intraspecies concordance than interspecies concordance.
Table 4. Previous observations of concordance of findings in repeat dose studies.
| Comparison type |
Effect type | Species | Description of N | % Concordance |
Reference |
|---|---|---|---|---|---|
| Intraspecies (species-sex) concordance | Site-specific carcinogenesis | Male/Female site-specific carcinogenesis, average of within-mouse and within-rat | 146 chemicals for rat; 159 chemicals for mouse | 65-66 |
Haseman and Lockhart, 1993
https://doi.org/10.1289/ehp.9310150 |
| Interspecies concordance | Site-specific carcinogenesis, average for all sites | Rat/Mouse | 173 site-specific cancer positives in rat divided by positives in mouse, by chemical | 35 |
Haseman and Lockhart, 1993
https://doi.org/10.1289/ehp.9310150 |
| Interspecies concordance | Site-specific carcinogenesis, average for all sites | Mouse/Rat | 167 site-specific cancer positives in mouse divided by positives in rat, by chemical | 37 |
Haseman and Lockhart, 1993
https://doi.org/10.1289/ehp.9310150 |
| Intraspecies concordance | Carcinogen/non-carcinogen | Mouse | NCI/NTP studies vs. CPDB literature component; 70 chemicals | 49 | Gottmann et al., 2001 10.1289/ehp.01109509 |
| Intraspecies concordance | Carcinogen/non-carcinogen | Rat | NCI/NTP studies vs. CPDB literature component; 71 chemicals | 62 | Gottmann et al., 2001 10.1289/ehp.01109509 |
| Interspecies | Carcinogen/non-carcinogen | Rat vs. Mouse | NTP studies, 313 chemicals | 74.4 | Huff et al., 1991 10.1289/ehp.9193247 |
On a quantitative basis, we extended previous work to characterize inter-study variability to examine the variability of organ-level effects among replicate studies by chemical, with the initial hypothesis that variance in organ level effects might be reduced from overall study-level effects that might have been informed by bodyweight changes or clinical signs. Our results failed to support this hypothesis. In general, though total variance in organ-level replicate data may have been reduced depending on the dataset and potency metric used, the RMSE values for organ-level effects were similar to the RMSE values for study-level effects. RMSE is an important metric in this work to understand inter-study standard deviation, and we can define a reasonable minimum prediction interval width with 95% confidence for study or organ-level effects using ± 1.96*RMSE (Pham et al., 2020), which based on the results herein and Pham et al. (2020) may approach ±1 log10-mg/kg/day. This finding informs some benchmark expectations for how well current in vivo methods perform as well as benchmarks for NAMs such as quantitative structure activity relationships (QSARs) or bioactivity assays for capturing in vivo effects from similar reference datasets.
To understand expectations for training set variability versus test set performance with a NAM, and if our results were reasonable, one can look to previous predictive model development using repeat dose studies common to regulatory toxicology. For over 400 chemicals with rat chronic LOAEL compiled from several public databases, the best regression-based, predictive quantitative structure activity relationship (QSAR) model was associated with a RMSE of 0.73 log10-mg/kg/day (representing test set error), approaching the estimated variability of the experimental replicate LOAEL values (0.64 log10-mg/kg/day) used in training (Mazzatorta et al., 2008). Others have found similar results; a QSAR model of chronic oral rat lowest observable adverse effect level (LOAEL) values curated from the Nestlé database and Swiss Food Safety and Veterinary Office Database for a total of 155 training chemicals and 671 test chemicals demonstrated a RMSE (representing test set errors) of 0.65 log10(mg/kg-day), which was similar to the size of the variability in the training data, ±0.59 log10-mg/kg-day (Helma et al., 2018). In both examples, the error in the model approached the error in the training data (Helma et al., 2018; Mazzatorta et al., 2008). A number of attempts to develop QSAR models for repeat dose values from toxicology studies, from different scientific groups using a variety of computational strategies and datasets, have resulted in RMSE values (representing test set errors) that range from 0.41 – 1.12 log10(mg/kg-day) and R2 values that range 0.31-0.84, suggesting that a threshold for minimum variability in potency values from replicate repeat dose regulatory toxicology studies may exist near approximately 0.5 log10-mg/kg/day (Hisaki et al., 2015; Mumtaz et al., 1995; Novotarskyi et al., 2016; Pradeep et al., 2020; Toropova et al., 2015; Veselinovic et al., 2016).
One limitation we sought to address in this work was whether discrete points-of-departure (PODs), i.e., LELs, would demonstrate higher total variance and RMSE than modeled PODs based on the shape of the dose-response curve, i.e., BMDs. Herein, we made comparisons to the estimates of variability made at the study-level for LELs in Pham et al. 2020 and additionally we made estimates of study-level variability in BMDs. Then, we examined both LEL and BMD variability at the organ level. In general, BMDs at the study level demonstrated slightly reduced MSE (unexplained variance) and by extension, percent variance explained approached 80% of the total variance. However, the RMSEs for both the study-level and organ-level BMDs were similar overall to study-level LELs and organ-level LELs, suggesting that the variability in both potency metric types was similar, and that minimum prediction interval widths for BMDs and LELs at the study or organ-level would be similar (e.g., ± 1.96*RMSE, or approximately ± 1 log10-mg/kg/day as RMSEs approach 0.5 mg/kg/day). Of course, use of MLR for estimation of the MSE and RMSE in this work relies on the assumption that the study descriptors employed as covariates contribute independently to variance, and to the extent that these covariates do not contribute independently to variance, MLR may result in an overestimation of MSE or unexplained variance. However, in Pham et al. 2020, use of different regression techniques, datasets of differing refinement, and datasets subset differently, all resulted in RMSE values that were near 0.5 log10-mg/kg/day. For study-level PODs and most organ (adrenal, kidney, liver, spleen, and stomach) PODs, depending on the dataset and potency metric employed, our results herein suggest that approximately 50-80% of variance may be explained by study descriptors curated as metadata in ToxRefDB. Work herein underscores that an RMSE of 0.5 log10-mg/kg/day serves as a reasonable approximation of standard deviation in study-level BMDs, study-level LELs from Pham et al. 2020, and organ-level LELs or BMDs. This confirms the study-level observation made in Pham et al. 2020, suggesting that using BMDs may result in similar RMSE values for study-level LEL replication, and further suggests similar upper bounds on quantitative predictive accuracy for organ-level PODs from animal studies of this kind.
NAMs for predicting quantitative estimates of repeat dose toxicity may include QSARs. As such, to expand the applicability domain of such models, it may be advantageous to consider grouping studies of different durations or designs, as suggested previously (Helma et al., 2018) based on observations of the quantitative similarity of no- and lowest-observable adverse effect levels in subacute, subchronic, and chronic exposure studies in rodents for agrochemicals (Zarn et al., 2011). Note that prediction of a threshold dose for repeat dose toxicity is a distinct goal separate from observation of tumors in animals. Previous work by Pradeep et al. (2020) to develop QSARs for repeat dose PODs, at the study-level, observed that combining all study types, regardless of duration, resulted in the largest applicability domain and best predictive performance. Thus, herein, we looked for potential differences between organ-level effects in SUB and CHR studies. The qualitative concordance of organ-level findings in SUB and CHR studies demonstrated by odds ratios suggest that target organs are likely to be identified in an in vivo SUB study, as the odds ratios for a positive CHR organ-level finding in the absence of a SUB organ-level finding were all less than zero. As such, on a qualitative basis, use of a SUB study is likely sufficient to identify target organ effects. The quantitative relationships present between organ-level findings in SUB and CHR studies suggest that the minimum LELs by organ may differ by an absolute value of 0.19-0.38 log10-mg/kg/day. The size of this difference is smaller than the variation of replicate organ-level LELs as well as study-level LELs (Pham et al., 2020). Thus, to support development of NAM based approaches, e.g., QSAR, repeat dose POD estimation should likely combine SUB and CHR study data in the training data set, as the mean differences between CHR and SUB LEL values by organ are less than or possibly approach estimates of variability in replicate repeat dose studies. In such a scenario, an adjustment could be employed to indicate the study type and conservatively account for potential differences in potency that we observed based on the mean difference in CHR and SUB LELs. In combining CHR and SUB LEL values, it is likely the number of chemicals with potency data and the number of repeat dose potency observations would increase, thus increasing the applicability domain. An additional limitation to consider in a QSAR repeat dose modeling approach is that for a given chemical with a known or predicted long serum half-life and bioaccumulative potential, some adjustment might be considered to account for increasing internal concentrations over a longer period of exposure.
It is possible that existing NAMs that indicate organ-level effects, on average, may predict liver- or kidney-related LELs within estimates of variability in replicate in vivo studies, but caution should be employed in viewing this result. The distribution of differences demonstrated very long tails, signaling that for a subset of chemicals, the differences in LELs and AEDs can be extreme. This finding suggests that in some minority of cases, summarized values are not conservative enough, and in some cases, far too protective (Paul Friedman et al. 2020). Previous work with similar but different methodological details (e.g., different subset of ToxCast data, different version of httk, different set of chemicals, chemical-level PODs rather than organ-level PODs) suggested the median difference between an -based and traditional animal PODs, all at the study-level rather than the organ-level, approached 1 log10-mg/kg/day, but similarly that the tails of the distribution of log10 POD difference were long (−3 to 8 log10-mg/kg/day). The comparisons of in vivo POD to that produced the smallest mean differences (min LEL or min HED to mean ) suggest the mean in vivo POD to difference may approach 0.5 log10-mg/kg/day, and the 95% CI around that mean difference suggests that the mean difference is likely to stay within 1 log10-mg/kg/day. However, to be protective for the set of chemicals where values were up to approximately 3 orders of magnitude greater than in vivo PODs, an uncertainty factor approaching 1000 would likely be needed based on the toxicodynamic (bioactivity) and high-throughput toxicokinetic (HTTK) data used herein to produce values. There is likely some combination of experimental, biological, and IVIVE uncertainty contributing to the chemicals that comprise the long tails of the POD comparison distributions, but there were few chemicals to examine.
Ongoing iterative work to evaluate assumptions used in in vitro to in vivo extrapolation of dose, including in vitro disposition of chemical, bioavailability, metabolism, and decision trees for best application of high throughput toxicokinetics may be helpful in identifying chemicals for which estimates have smaller or greater uncertainty. Previous reviews of generic toxicokinetic modeling using a high-throughput toxicokinetic approach suggest that prediction of toxicokinetic parameters such as peak and area under the curve plasma concentrations may be associated with RMSE values in the 0.5 −1 log10 range (Breen et al., 2021), indicating that uncertainty in toxicokinetic modeling may add to the uncertainty from the bioactivity data, resulting in some cases where the value may be 3 orders of magnitude different from a minimum in vivo POD (which of course reflects only the extreme end of the potential range of in vivo POD values that could be observed in replicate studies). The in vitro bioactivity data used herein may not have covered key targets within the liver and kidney, e.g., functional transport, metabolic, or multi-cellular processes, that would be included in in vitro assays of greater biological complexity. Critically, the comparison also points to the need for a multifaceted approach to quantitative POD prediction when moving beyond the existing paradigm based on long-term animal studies and protective estimates of uncertainty factors, including strategies such as QSAR, read across, and bioactivity. Indeed, short-term animal models including a 5-day exposure with transcriptomic assessment of the liver and kidney may provide POD information within 0.5 to 1 log10-mg/kg/day of apical PODs determined through longer-term studies, and may provide POD confirmation for in silico and in vitro NAM based PODs when warranted (Gwinn et al., 2020).
This work provides additional data-informed benchmarks for NAM performance related to the qualitative and quantitative reproducibility of organ-level effects in vivo in studies used for regulatory toxicology. Organ-level effects were examined as a means of grouping biological findings in the absence of mechanistic information that would enable mapping to specific adverse outcome pathways. The understanding that a prediction of an in vivo systemic effect level, for an organ or for a study, within approximately ± 1 log10-mg/kg/day would demonstrate a very good NAM is important for the acceptance of NAMs for chemical safety assessment. Further, qualitative concordance of biological effects between NAMs and animal studies may range widely, not only due to the variable concordance among animal studies but also because animal studies may demonstrate greater negative predictive value for human effects. In terms of modeling approaches, and alternatives to repeat dose toxicity testing, it is likely that SUB and CHR study data for existing chemicals can be combined to develop repeat-dose POD predictions, which could be adjusted to be more or less conservative in the POD prediction. Finally, this work provides an important contribution to the field in terms of understanding how construction of NAM-based POD estimates may offer equivalent levels of public health protection as the PODs produced by animal methods.
Supplementary Material
Highlights.
Reproducibility of organ-level findings was maximized within species.
Variance explained by study metadata was similar for organ and study findings.
The odds of a CHR study organ effect were <1 if no organ findings were observed in a SUB study.
Mean differences in LEL by exposure duration were similar in size to replicate study variance.
Mean differences in organ LELs and AEDs approached 0.5 log10-mg/kg/day with larger differences observed for some chemicals.
Acknowledgements
The authors would like to acknowledge Kelsey Vitense and Grace Patlewicz from the US EPA Center for Computational Toxicology and Exposure for insightful comments on previous versions of this manuscript.
Abbreviations
- AED
administered equivalent dose
- AED50
administered equivalent dose based on the median steady-state serum concentration
- BMD
benchmark dose
- CHR
chronic study design
- CI
confidence interval
- EPA
U.S. Environmental Protection Agency
- HED
human equivalent dose (allometrically scaled LEL value)
- HTTK
high-throughput toxicokinetics
- LEL
lowest effect level
- MLR
multi-linear regression
- MSE
mean square error
- NAM
new approach method
- POD
point of departure
- RMSE
root residual mean square error
- SAC
subacute study design
- SUB
subchronic study design
Footnotes
Disclaimer: The United States Environmental Protection Agency (U.S. EPA) through its Office of Research and Development has subjected this article to Agency administrative review and approved it for publication. Mention of trade names or commercial products does not constitute endorsement for use. The views expressed in this article are those of the authors and do not necessarily represent the views or policies of the US EPA.
References
- Ball N., et al. , 2022. A framework for chemical safety assessment incorporating new approach methodologies within REACH. Arch Toxicol. 96, 743–766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Basketter DA, et al. , 2012. A roadmap for the development of alternative (non-animal) methods for systemic toxicity testing. ALTEX. 29, 3–91. [DOI] [PubMed] [Google Scholar]
- Bhuller Y., et al. , 2021. Canadian Regulatory Perspective on Next Generation Risk Assessments for Pest Control Products and Industrial Chemicals. Front Toxicol. 3, 748406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Breen M., et al. , 2021. High-throughput PBTK models for in vitro to in vivo extrapolation. Expert Opin Drug Metab Toxicol. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Commission, E., Regulation (EC) No 1907/2006 of the European Parliament and of the Council of 18 December 2006 concerning the Registration, Evaluation, Authorisation and Restriction of Chemicals (REACH), establishing a European Chemicals Agency, amending Directive 1999/45/EC and repealing Council Regulation (EEC) No 793/93 and Commission Regulation (EC) No 1488/94 as well as Council Directive 76/769/EEC and Commission Directives 91/155/EEC, 93/67/EEC, 93/105/EC and 2000/21/EC (Text with EEA relevance) 2006. [Google Scholar]
- Consulting JKH, Huff J, 1989. Sources of Variability in Rodent Carcinogenicity Studies. Fundamental and Applied Toxicology. 12, 793–804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- ECHA, The Use of Alternatives to Testing on Animals for the REACH Regulation. European Chemicals Agency Helsinki, Finland, 2011. [Google Scholar]
- ECHA, New Approach Methodologies in Regulatory Science, Proceedings of a scientific workshop. In: Agency EC, (Ed.), Helsinki, Finland, 2016. [Google Scholar]
- ECHA, Current status of regulatory applicability under the REACH, CLP and Biocidal Products regulations. 2017a. [Google Scholar]
- ECHA, ECHA Strategic Plan 2019-2023. 2017b. [Google Scholar]
- EPA, U. S., New Approach Methods Work Plan (v2). In: Prevention, O. o. R. a. D. a. O. o. C. S. a. P., (Ed.), Washington, DC, 2021. [Google Scholar]
- Goodall CR, 2005. Computational Statistics: Computation using the QR decomposition. Handbook of Statistics. vol. 9. Elsevier, pp. 467–508. [Google Scholar]
- Gottmann E., et al. , 2001a. Data quality in predictive toxicology: reproducibility of rodent carcinogenicity experiments. Environ Health Perspect. 109, 509–14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gottmann E., et al. , 2001b. Data quality in predictive toxicology: reproducibility of rodent carcinogenicity experiments. Environmental Health Perspectives. 109, 509–514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gwinn WM, et al. , 2020. Evaluation of 5-day In Vivo Rat Liver and Kidney With High-throughput Transcriptomics for Estimating Benchmark Doses of Apical Outcomes. Toxicol Sci. 176, 343–354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haseman JK, Lockhart AM, 1993. Correlations between chemically related site-specific carcinogenic effects in long-term studies in rats and mice. Environ Health Perspect. 101, 50–4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- HealthCanada, Science Approach Document: Bioactivity Exposure Ratio - Application in Priority Setting and Risk Assessment. In: Bureau ESRA, (Ed.), Canada, 2021. [Google Scholar]
- Helma C., et al. , 2018. Modeling Chronic Toxicity: A Comparison of Experimental Variability With (Q)SAR/Read-Across Predictions. Front Pharmacol. 9, 413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hisaki T., et al. , 2015. Development of QSAR models using artificial neural network analysis for risk assessment of repeated-dose, reproductive, and developmental toxicities of cosmetic ingredients. J Toxicol Sci. 40, 163–80. [DOI] [PubMed] [Google Scholar]
- Huff J., et al. , 1991. Chemicals associated with site-specific neoplasia in 1394 long-term carcinogenesis experiments in laboratory rodents. Environ Health Perspect. 93, 247–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jobson JD, 2012. Applied Multivariate Data Analysis: Regression and Experimental Design. Springer New York. [Google Scholar]
- Judson R., et al. , 2009. The toxicity data landscape for environmental chemicals. Environmental health perspectives. 117, 685–695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karmaus AL, et al. , 2022. Evaluation of Variability Across Rat Acute Oral Systemic Toxicity Studies. Toxicol Sci. 188, 34–47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lautenberg FR, Frank R Lautenberg Chemical Safety for the 21st Century Act. In: Congress, t. U., (Ed.). Public Law, 2016, pp. 114–182. [Google Scholar]
- Leisenring W, Ryan L, 1992. Statistical properties of the NOAEL. Regulatory Toxicology and Pharmacology. 15, 161–171. [DOI] [PubMed] [Google Scholar]
- Martin MT, et al. , 2009a. Profiling chemicals based on chronic toxicity results from the U.S. EPA ToxRef database. Environmental Health Perspectives. 117, 392–399. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin MT, et al. , 2009b. Profiling the reproductive toxicity of chemicals from multigeneration studies in the toxicity reference database. Toxicological Sciences. 110, 181–190. [DOI] [PubMed] [Google Scholar]
- Mazzatorta P., et al. , 2008. Modeling oral rat chronic toxicity. J Chem Inf Model. 48, 1949–54. [DOI] [PubMed] [Google Scholar]
- Monticello TM, et al. , 2017. Current nonclinical testing paradigm enables safe entry to First-In-Human clinical trials: The IQ consortium nonclinical to clinical translational database. Toxicol Appl Pharmacol. 334, 100–109. [DOI] [PubMed] [Google Scholar]
- Mumtaz MM, et al. , 1995. Assessment of effect levels of chemicals from quantitative structure-activity relationship (QSAR) models. I. Chronic lowest-observed-adverse-effect level (LOAEL). Toxicol Lett. 79, 131–43. [DOI] [PubMed] [Google Scholar]
- Nair AB, Jacob S, 2016. A simple practice guide for dose conversion between animals and human. Journal of basic and clinical pharmacy. 7, 27–31. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Novotarskyi S., et al. , 2016. ToxCast EPA in Vitro to in Vivo Challenge: Insight into the Rank-I Model. Chem Res Toxicol. 29, 768–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parish ST, et al. , 2020. An evaluation framework for new approach methodologies (NAMs) for human health safety assessment. Regul Toxicol Pharmacol. 112, 104592. [DOI] [PubMed] [Google Scholar]
- Patlewicz G., et al. , 2015. Proposing a scientific confidence framework to help support the application of adverse outcome pathways for regulatory purposes. Regul Toxicol Pharmacol. 71, 463–77. [DOI] [PubMed] [Google Scholar]
- Paul Friedman K., et al. , 2020. Utility of In Vitro Bioactivity as a Lower Bound Estimate of In Vivo Adverse Effect Levels and in Risk-Based Prioritization. Toxicol Sci. 173, 202–225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pearce RG, et al. , 2017. httk: R Package for High-Throughput Toxicokinetics. 2017. 79, 26. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pham LL, et al. , 2019. Python BMDS: A Python interface library and web application for the canonical EPA dose-response modeling software. Reprod Toxicol. 90, 102–108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pham LL, et al. , 2020. Variability in in vivo studies: Defining the upper limit of performance for predictions of systemic effect levels. Comput Toxicol. 15, 1–100126. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pradeep P., et al. , 2020. Structure-based QSAR Models to Predict Repeat Dose Toxicity Points of Departure. Comput Toxicol. 16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sorge RE, et al. , 2014. Olfactory exposure to males, including men, causes stress and related analgesia in rodents. Nature Methods. 11, 629–632. [DOI] [PubMed] [Google Scholar]
- Tenny S, Hoffman MR, Odds ratio. In: StatPearls [Internet]. StatPearls Publishing, Treasure Island, FL, 2022. [Google Scholar]
- Toropova AP, et al. , 2015. QSAR as a random event: a case of NOAEL. Environ Sci Pollut Res Int. 22, 8264–71. [DOI] [PubMed] [Google Scholar]
- USEPA, ToxRefDB version 2.0. ftp://newftp.epa.gov/comptox/High_Throughput_Screening_Data/Animal_Tox_Data/current, 2019.
- USEPA, ToxCast database: Invitrodb version 3.5. 2022.
- USEPA, OCSPP 870 Health Effects Series. OCSPP 870 Health Effects Series. [Google Scholar]
- van der Zalm AJ, et al. , 2022. A framework for establishing scientific confidence in new approach methodologies. Arch Toxicol. 96, 2865–2879. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Veselinovic JB, et al. , 2016. The Monte Carlo technique as a tool to predict LOAEL. Eur J Med Chem. 116, 71–75. [DOI] [PubMed] [Google Scholar]
- Watford S., et al. , 2019. ToxRefDB version 2.0: Improved utility for predictive and retrospective toxicology analyses. Reprod Toxicol. 89, 145–158. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wetmore BA, et al. , 2012. Integration of dosimetry, exposure, and high-throughput screening data in chemical toxicity assessment. Toxicol Sci. 125, 157–74. [DOI] [PubMed] [Google Scholar]
- Zarn JA, et al. , 2011. Study parameters influencing NOAEL and LOAEL in toxicity feeding studies for pesticides: exposure duration versus dose decrement, dose spacing, group size and chemical class. Regul Toxicol Pharmacol. 61, 243–50. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.