Energy in functional brain states correlates with cognition in adolescent schizophrenia and healthy persons

Abstract

Schizophrenia is associated with diverse neuroimage-derived phenotypes such as increased ventricular size, gray matter reduction, reduced white matter anisotropy, and functional differences at rest and while performing a task. Well-established functional MRI analysis methods, including observation of statistically significant differences in first-order regional activation as well as second-order functional connectivity modeling based on correlation of blood oxygenation level dependent (BOLD) signal timeseries between pairs of spatially distributed regions, either account for activity in individual regions or pairwise coactivation of regions, respectively. Neither of these methods integrate both first-order and second-order terms to obtain a comprehensive picture of neural dynamics. While it is challenging to incorporate both of these into one framework, the pairwise maximum entropy model (MEM), also called the Ising model, captures both individual and pairwise activity into a single quantity known as energy, which is inversely related to the probability of state occurrence. Here, we apply the MEM framework to task functional MRI data collected on 23 adolescent onset schizophrenia (AOS) since AOS is a more severe form of schizophrenia with more severe cognitive impairments and poorer outcome, in comparison with 53 healthy control subjects while performing the Penn Conditional Exclusion Test (PCET), which measures abstraction and mental flexibility, aspects of executive function that have repeatedly been shown to be impaired in AOS. Accuracy of PCET performance was significantly reduced among AOS compared to controls as expected. Average cumulative energy achieved for a participant over the course of the fMRI negatively correlated with task performance, and the association was stronger than any first-order association. The AOS image-derived phenotype was characterized by spending more time in higher energy brain states that represent lower probability of occurrence and were associated with impaired executive function, suggesting less stable neural dynamics among AOS compared to controls, who spent more time in lower energy states that are more stable. The energy landscapes in both conditions featured attractors that corresponded to two distinct subnetworks, namely fronto-temporal and parieto-motor. Attractor basins were larger in the controls than in AOS; moreover, fronto-temporal basin size was significantly correlated with cognitive performance in controls, although not among the AOS group. These findings demonstrate that the MEM can integrate and reduce the dimensionality of neuroimaging data, providing information about functional brain states while emphasizing rather than obscuring clinical and cognitive associations, and may shed light on the organizing principles of neural dynamics in patients and controls.

1. Introduction

Schizophrenia is a severe brain disorder affecting approximately 3 million persons in the US with a 10% risk for suicide^1–3, a decreased life span by up to 25 years^2,4 and associated costs of more than $155 billion a year⁵. Long-term functional outcome is as low as 14% with existing treatments^6–9. Adolescent onset schizophrenia (AOS) that has phenomenological continuity with adult-onset schizophrenia^10–12 is associated with more prominent developmental and premorbid abnormalities, hence proposed as a more severe form of schizophrenia¹³ with more severe cognitive impairments^{10,11,14–16} especially in working memory^17–20, executive functions^10,11,14,15, and attention^15,16,21,22, with poorer long-term outcomes^10–13 compared to adult-onset schizophrenia. Cognitive deficits respond minimally to antipsychotics^23,24 and are consistently associated with poor long-term outcome^25–28. Further, AOS is less well investigated than adult-onset schizophrenia. Therefore, a better understanding of the pathophysiology of AOS could enable novel treatment strategies to improve outcomes.

Among several approaches available to investigate the pathophysiology of schizophrenia, magnetic resonance imaging (MRI)-based techniques have been extensively used. Functional MRI offers the advantage of examining blood oxygenation level dependent (BOLD) responses as proxy measures of brain activation. Currently, most fMRI studies have examined group differences in the activation of brain regions, namely first-order models²⁹. Another set of studies have examined pairwise correlations of spatially distributed regions and derived functional networks based on co-activation, namely secondorder models. Both of these approaches have highlighted different aspects of brain functioning at rest and during the performance of a cognitive task^30,31. However, these models provide limited information at the systems level. For example, first-order-only analyses cannot elucidate detailed system-level interactions among regions while second-order models do not provide information about regional activation differences. Energy models can comprehensively integrate both the first-order and second-order dynamics. Mathematically, the energy of a brain state represents a combination of first-order activation and second-order coactivation among brain regions³² that best explains the empirical occurrence probability of the state, providing an improvement over separate studies of functional connectivity or regional activation differences between groups.

The pairwise maximum entropy model (MEM)^32,33, also called the Ising model, can represent fundamental properties of the brain: distant regions interact according to an underlying network configuration to produce brain states of varying likelihood. Energy models often decompose complex network dynamics into a set of discrete states. The frequency of occurrence of discrete states can be statistically tested for comparisons between study groups. The term “energy” does not refer to physical energy (measured in joules) nor to metabolic energy (as adenosine triphosphate) but is used in the mathematical context of the model, where energy is inversely related to probability, with higher energy associated with low probability states. This energy term is more specifically referred to as the “integrated energy” of the system configuration when applied to fMRI data³⁴. It provides a representation of time-specific regional brain activation or inactivation while also accounting for the system’s connectivity and pairwise interactions in terms of correlated activations of regions. Energy and cognitive performance may be related³⁵, suggesting that this internal system energy reflects the complexity of the mental work being done.

Although the MEM approach was originally used in physics to model magnetic fields³⁶, different models of MEM have now been used to investigate complex network dynamics associated with cognitive functions. The MEM approach is especially useful to investigate time-varying dynamics during cognitive tasks because the model includes BOLD responses at every repetition time (TR) of the fMRI acquisition. Further, investigation of brain networks using a pairwise MEM and energy landscape provides a very useful model of principles of network organization that can then be compared between different states of the networks or across subject groups. A prior study showed a high number of local minima in a resting fMRI suggesting that in rest states, local minima or the low energy basins that are considered stable and highly probable network configuration cover most of the brain³⁷. Experimentally induced perturbations reduced the number of local minima considerably, while other effects depended on the specifics of the perturbation³⁸. Another resting fMRI study showed different characteristics of the energy landscape in the default mode and frontoparietal networks³⁹. However, to our knowledge the Ising model has not been applied to elucidate complex network dynamics to examine AOS or adult-onset schizophrenia patients using task-fMRI data.

Task-fMRI can provide clinically relevant data on differences in functional and network characteristics that can be used as biomarkers for disease and as treatment targets. Previous studies have reported impaired executive function in schizophrenia patients^10,11,14,15. We selected the Penn Conditional Exclusion Test (PCET) as an fMRI task to test executive function, which is a part of the Penn Computerized Neurocognitive Battery that has been validated in schizophrenia⁴⁰ and healthy⁴¹ subjects and used in many of our previous studies^42–45. PCET is closely related to the Wisconsin card sorting test and to verbal fluency and work behavior such as cooperativeness, work quality, and general impressions⁴⁶.

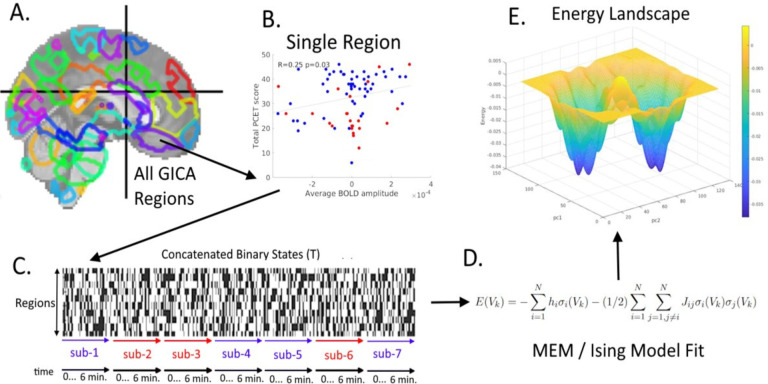
Here, we apply the pairwise MEM to fMRI data while subjects were performing the PCET task in a study of 23 AOS individuals and 53 healthy subjects. The MEM model (Figure 1) is iteratively fit to the entire set of observed brain states using their empirical probabilities to estimate unknown parameters in the MEM. The relationship between MEM energy and cognitive performance assessed as accuracy of inscanner PCET was examined in this sample, motivated by the hypotheses that the average energy attained by an individual over the course of the experiment will be related to PCET accuracy and that the relationship will be stronger than correlation with first-order activation. In addition to supporting these hypotheses, our results show that the AOS and controls visit states at different frequencies, with the AOS group spending more time in higher energy states.

Figure 1:

Methodological Outline. The minimally preprocessed fMRI data is further processed using group independent component analysis (GICA) to find 70 components (A). For each of the 70 components, the correlation of mean individuallevel BOLD signal amplitude with performance on PCET is computed (B) and the regions with nominally significant correlation of BOLD responses to PCET performance are selected (n=9 regions). Blue points are controls; red points are AOS subjects. The temporal activity series of these 9 regions are then binarized at the individual level and concatenated together across all individuals in the study (C), creating the concatenated binary matrix, T. The maximum entropy model (D) is then fit to this matrix. The resulting energy term can be represented in a number of ways, including in terms of principal components (from performing PCA on T), which in particular produces an energy landscape (E). Legend: sub=subjects

2. Methods

2.1. Sample description

We estimated the energy model for a task-fMRI data set collected at the University of Pittsburgh on a Siemens Magnetom 7 Tesla whole-body scanner using a custom 64-channel Tic-Tac-Toe head coil on 23 AOS and 53 healthy controls from the same geographic region. Informed consent was obtained from all participants after providing full description of the study including the risks and benefits. The University of Pittsburgh Institutional Review Board approved the study. Subjects were administered the Structured Depression and Schizophrenia (K-SADS). Consensus diagnosis by medical investigators was made after reviewing all available clinical data including the charts. Controls were 18.9±1.76 years old and 51% female, and AOS were 19.7±1.14 years old and 68% female. HC were significantly younger than AOS (t=2.04; p=0.045) but sex distribution was not statistically different between the groups (χ²=1.86 p=0.17).

2.2. Image Acquisition and Preprocessing

T₁-weighted MP2RAGE scans were acquired in the axial plane (348 slices, 0.55 mm thickness, TE=2.54ms, TR=6 seconds, in-plane resolution=390×390). Functional MRI echo-planar images were acquired in the axial plane (86 slices, 1.5 mm thickness, TE=20ms, TR=3 seconds, in-plane resolution=148×148, 142 volumes). fMRI data was collected while subjects performed the PCET task. Each trial presented four shapes and participants selected the shape that does not belong. The sorting principles changed, with feedback to help subjects develop new strategies. Subjects were expected to select the correct stimulus with the minimum number of errors despite changing sorting principles. Such set shifting was considered to indicate cognitive flexibility, which is subsumed as executive function⁴⁷. The number of correct responses was counted as the measure of accuracy of performance. Schizophrenia subjects have been consistently shown to perform poorly on executive function tasks^48–51.

All the pre-processing steps for the fMRI data were performed using fMRIPrep⁵², which included correction for motion, slice timing, bias, and distortion, and brain extraction before registering to a standard space (MNI 2mm) using the Human Connectome Project approach⁵³. Image registration of fMRI volumes to standard space was performed using co-registration with the T₁-weighted image.

2.3. Region Selection

Group Independent Component Analysis (GICA) was used to define spatial maps⁵⁴. This allowed us to focus on task driven BOLD signals that appear on the inter-subject level⁵⁵. GICA is intentionally performed using a larger selection of components than expected – specifically, 70 components⁵⁶.

We selected a subset of components that showed nominally significant correlation of BOLD responses to the performance on PCET for inclusion in the energy model (Figure 2) because careful selection of regions could contribute to the effectiveness of the model. The region selection step was a purely data-driven to choose informative timeseries for the energy model and to enhance computational tractability through an exponential downscaling of the number of possible states included in the energy computation⁵⁷. The white matter region was included despite the unorthodoxy of white-matter derived BOLD signals⁵⁸ (see discussion).

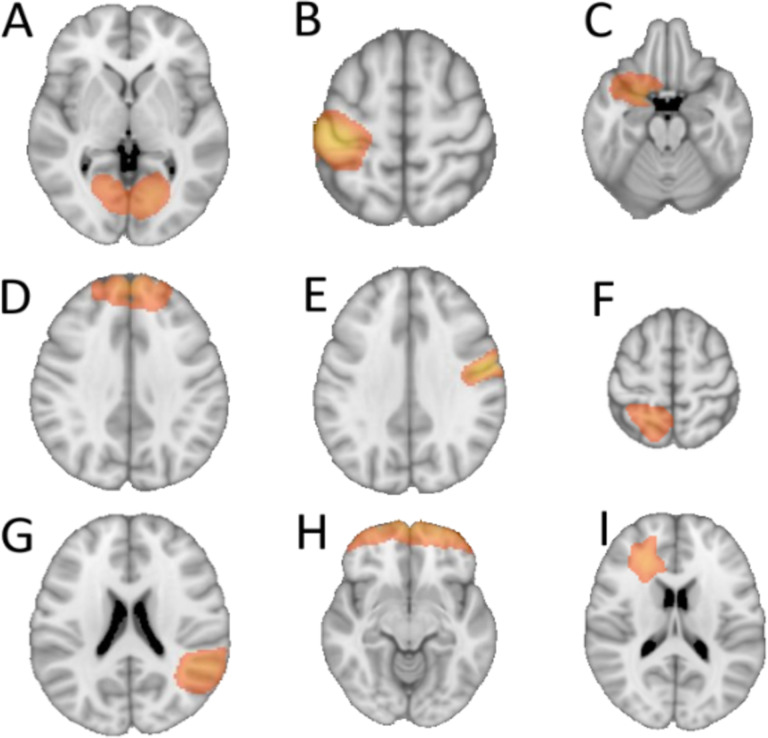
Figure 2:

Spatial representations of the 9 selected brain regions from GICA. The regions roughly correspond to the following anatomical areas: A) calcarine, B) left precentral, C) left olfactory, D) frontal superior medial, E) right postcentral, F) left parietal superior, G) right temporal superior, H) frontal superior orbital, and I) a region labeled as white matter/no label which is located near the left anterior cingulate.

2.4. Concatenation and Binarization

After selecting the regions, all observations were binarized, and then timepoints across all subjects were concatenated together in a structure called T. T is a matrix with N rows representing regions, and M columns equal to the total number of timepoints (TR) in the entire sample, across all subjects; that is, we assume that each subject has the same number of timepoints, p, and take M=S*p where S denotes the threshold choice for binarization can affect the outcome of the energy model (Figure 3). The threshold the number of subjects. Since this binary matrix is ultimately derived from continuous BOLD signal data, value of the z-scored GICA data was zero for all reported results.

Figure 3:

Threshold Effect on Energy. Left: The percent of data in the ‘on’ microstate across all subjects and timepoints after thresholding. Right: Seven thresholds were tested (x-axis), namely mean minus two standard deviations, mean minus one standard deviation, mean minus one-half standard deviation, mean, mean plus one-half standard deviation, mean plus one standard deviation, and mean plus two standard deviations. The middle threshold (mean) was chosen because in the threshold sweep results to the right, mean yielded the most complete “energy landscape” (top row, middle plot), and best fit of the empirical probabilities of state occurrence (bottom row, middle plot).

The seven threshold choices tested for binarizing the independent components (ICs, BOLD-derived; z-scored) at a given moment in time, a given region, and a given subject (more succinctly, a “microstate”) are 0, +/− 0.5, +/− 1.0, and +/− 2.0, since the GICA data is z-scored. The middle or 0 threshold, where roughly half of all microstates are in the “on” position across all subjects and timepoints, was chosen because it produced the most informative energy landscape (see Section 2.5) with the best fit of the energy function to the empirical probabilities of state occurrence. All data in this manuscript uses this threshold.

2.5. Energy Model

Energy, E, is defined for each possible binary state, V_k, according to the Ising model³² as:

$$E\left(V_k\right)=-\sum _{i=1}^N{h}_i{\sigma }_i\left(V_k\right)-\left(\frac{1}{2}\right)\sum _{i=1}^N\sum _{j=1.j\ne i}^N{J}_{ij}{\sigma }_i\left(V_k\right){\sigma }_j\left(V_k\right)$$ (1)

where N is the number of regions, k indexes the state from among the B possible unique binary states where B=2^N, J is the 2-dimensional adjacency matrix that defines the coupling of region pairs, and h is the vector of activation parameters. The model is fitted using a maximum entropy approach. For each index k, V_k is a vector with N elements, V_k = [σ_k1,σ_k2,…,σ_kN], where each element σ_ij (the binary value for a given region at a given state) can be either 1 or 0. The set of all possible unique binary states is defined as: V=[V₁, V₂,…,V_B]. This is not to be confused with T, which concatenates all observed binary states and may feature the same pattern appearing within multiple columns.

While the energy value itself has no absolute interpretation and only relative changes in energy are meaningful, a formula maps energy to probability, P(V_k), which takes the following form:

$$P\left(V_k\right)=\exp \left(-E\left(V_k\right)\right)/\sum _{i=1}^{2^N}\exp \left(-E\left(V_i\right)\right)$$ (2)

The values of h_i and J_ij in equation (1) were iteratively estimated by comparing the actual and estimated values of mean and covariance between the nuclei and adjusting them with learning rate α (0.2). Specifically, we calculated the estimated mean and covariance and performed the iterations of h_i and J_ij as follows:

$$\langle {\sigma }_{jm}\rangle =\sum _{q=1}^{2^{n-1}}{\sigma }_j\left(V_q\right)P\left(V_q\right)$$

$$\langle {\sigma }_j{\sigma }_{lm}\rangle =\sum _{q=1}^{2^{n-1}}{\sigma }_j\left(V_q\right){\sigma }_l\left(V_q\right)P\left(V_q\right)$$

$$h_i^{\mathit{\text{new }}}=h_i^{\mathit{\text{old }}}+\alpha \cdot \mathit{\text{log}}\left(\frac{\langle {\sigma }_i\rangle }{\langle {\sigma }_{im}\rangle }\right)$$

$$J_{ij}^{\mathit{\text{new }}}=J_{ij}^{\mathit{\text{old }}}+\alpha \cdot \mathit{\text{log}}\left(\frac{\langle {\sigma }_{ij}\rangle }{\langle {\sigma }_{ijm}\rangle }\right)$$

We ran 300 iterations of the gradient descent algorithm and that resulted in a good fit between the firstorder (mean activity) and second-order (co-activation) statistics (see Section 2.6).

We also fitted separate MEM to the data corresponding to the control group and to the AOS group. The procedure was identical to that described for the combined data with the exception that the data used to fit the model was exclusively either from controls or AOS.

2.6. Evaluating Fit of the Model

We evaluated the fit of the model by comparing the estimated and actual first-order (mean) and second-order (covariance) features of the data (Supplemental Figure 1). As an additional check, we also examined the relationship between the energy and probabilities of occurrence of each state as estimated by the model and the empirical probability of each state in the data, which also demonstrated a good fit (Supplementary Figure 2). We also ensured that there were more observations than the entropy of the system (in bits). Specifically, the state space (given by B) refers to the number of N x 1 vectors of binary regional activity, across all subjects and timepoints. In this case, N=9, so B=2^N=512. The number of observations refers to the number of vectors in T, which here is 10,792 (twenty times as large) justifying that we had adequate sample for implementing MEM.

2.7. Energy Landscape via Projection onto Principal Components

From equation (1), we derived a vector of energy values along a sequence of time points for each subject. While essential, the time and energy dimensions do not tell the full story. Since the basis for the energy value is the N-dimensional brain state configuration, and moments with the same energy value could correspond to very different brain states, we used Principal Component Analysis (PCA), performed on T, the matrix of observed binary states concatenated across all subjects and time points, to describe states in terms of a lower-dimensional manifold. Further, we projected energy values onto two of these dimensions to create a 3-dimensional “energy landscape” where height and/or color represent energy. The basins of attraction of energy minima correspond to low (usually negative) energy values represented with cooler colors, whereas the peaks correspond to higher (usually positive) energy values.

The PCA isolates the orthogonal eigenvectors that explain the most variance in the data. Our aim was to visualize the energy landscape in the state space of eigenvectors of the data, where two dimensions represent the data projected onto the first 2 principal components (PCs) and the 3^rd dimension represents the energy corresponding to the state. The energy landscape was smoothed with a 2-dimensional Gaussian kernel, with σ=1.5; in brief, the smoothing process introduces a kernel centered at each data point and computes a smooth function by summing over these kernels. The smoothed version was used to visualize the energy manifolds, but all quantification was done on the individual states of the MEM. The same value of σ was used to generate all energy landscapes. PCA was also used to identify the two subnetworks corresponding to the basins observed in the energy landscape. The loading weights of the first two PCs were thresholded (threshold=0.3) to identify the states that corresponded to “fronto-temporal” and “parieto-motor” networks. Fronto-temporal states were defined as states where frontal-superiormedial, olfactory, frontal-superior-orbital and temporal-superior were simultaneously active, whereas parieto-motor states were defined as states where white matter, post-central, pre-central and parietalsuperior were simultaneously active. The binary numerals are converted to base 10 for ease of collation, (e.g., 000000100 is state number 4).

For the MEM for the separate control and AOS data sets, the PCs were calculated separately on each group, before the corresponding data was projected on the PCs for that group.

2.8. Cognitive and Clinical Statistical Comparisons

Energy from the model was compared to cognitive performance and clinical group. The sum of the energies of all states arising for each subject over the entire course of their fMRI was compared, using whole-group and within-group correlations, to the PCET accuracy scores. The 512 states were also binned into 16 equal bins according to energy percentiles. Explicitly, 32 states (6.25% of all states) were classified into the lowest energy bin, 32 into the next-lowest energy bin, and so on. Then, the number of states experienced per energy bin was tallied by group and divided by the total number of states attained, yielding the frequency of occurrence by energy bin. The frequency of occurrence of bins in the bottom half (eight) of all energy bins were compared between AOS and controls using a Wilcoxon rank-sum test, as were frequencies for the top eight bins. A two sample Kolmogorov–Smirnov test was used to determine if the distributions of energy bins attained over time differed between groups.

3. Results

3.1. Activity in the selected regions shows a weak correlation with cognitive performance

From 70 GICA components representing 92 non-contiguous regions, 9 regions (Figure 2) were found to have an average activity at the individual level that significantly correlated with the PCET total score across all participants (Figure 4A), without correction for multiple comparisons. The nine regions have their components’ peak voxels in the following approximate locations in the brain: left calcarine (r=0.23, p<0.05), left precentral (r=0.23, p<0.05), left olfactory (r=0.25, p<0.05), left frontal superior medial (r=–0.25, p<0.05), right postcentral (r=–0.31, p<0.05), left parietal superior (r=–0.25, p<0.05), right temporal superior (r=0.25, p<0.05), left frontal superior orbital (r=–0.23, p<0.05), and a region labeled as white matter/no label which is located near the left anterior cingulate (r=0.30, p<0.05).

Figure 4:

Region Selection and PCET scores. A) For all 70 components from GICA, each subject’s average BOLD signal intensity in that component was plotted against PCET score. The X-axis in each plot is the average z-scored BOLD amplitude-derived component value. The y-axes are the PCET scores. Blue points are healthy control individuals. Red points are AOS individuals. B) PCET score Histograms by group. Blue: controls. Red: AOS. X-axis is total PCET correct. Y-axis is the number of participants in the group who scored the corresponding amount.

3.2. Controls score higher on PCET task as compared to AOS group

Healthy controls showed significantly higher accuracy (35.1±8.4) on the PCET task compared to the AOS group (26.4±8.9) (t=4.0, p<0.001) (Figure 4B).

3.3. Average energy in MEM shows significant negative correlation with cognitive scores

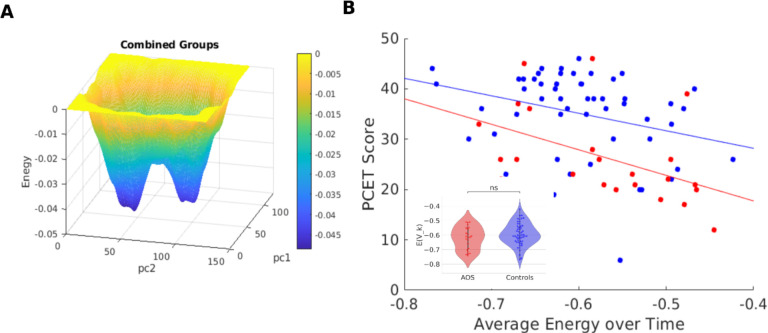
We fitted an MEM to the combined data of fMRI activity from controls and AOS patients (goodness-of-fit shown in Supplemental figure 1). The energy landscape obtained from projecting the data onto the first two PCs of the matrix of activation states observed in all subjects (see Section 2), with energy as the third dimension, is shown in Figure 5A. The energy landscape features two primary attractors in the activity (142 time-points per subject) dynamics during the task, each with a sizeable attraction basin (low energy areas in blue).

Figure 5:

Average Energy versus PCET Score. A) Energy landscape of the combined model. Basins represent more negative energy (cooler colors) and peaks represent more elevated energy (warmer colors). B) The energy values averaged across the entire duration of the fMRI (142 timepoints) for each subject (Blue point: healthy controls; Red points: AOS) show significant negative correlation with PCET scores. Average energy distributions do not show statistical significance between the groups (inset).

The average energy values across the time series of activation states for each subject were not statistically significantly different between AOS and controls (Figure 5B inset) despite the groups’ clear differences in the PCET scores (Figure 4B). However, we found that the average energy value negatively correlated with PCET accuracy (Figure 5B). This relation holds both at the combined group level (N=76, r=– 0.39, p=0.0004) and separately for the control group (N=53, r=–0.30, p=0.03) and AOS (N=23, r=–0.49, p=0.019), as shown in Figure 5B. Thus, our results suggest that the lower average energies are correlated with higher cognitive scores for both clinical groups, suggesting that deeper attractor basins are associated with better cognitive performance.

3.5. Controls experience more low energy states whereas AOS experience more high energy states

Although the groups’ average energy levels do not show a significant difference (Figure 5B-inset), the detailed structure of the activity states and their corresponding energies shows a clear difference between the clinical groups.

When activation states were classified into sixteen equally sized energy bins, states in the lower half of the distribution occur with higher frequency in the time series of control while the time series of AOS consistently included higher frequencies of states in the upper half of the energy distribution (Figure 6A). The Wilcoxon rank-sum test, paired on energy bins, showed significant differences in the occurrence frequencies of the lower energy states (p<0.01, signed rank=36) and higher energy states (p<0.01, signed rank=0). When individual states were compared for differences in occurrence frequency by group without regard to their energies there were no specific, individual states with significantly different occurrence frequency by group after correction for multiple comparisons using false discovery rate.

Figure 6:

Controls experience more low-energy states compared to AOS. A) Using 16 equally sized bins to cluster states based on energy percentiles, we observe that the control group experiences more low energy states and that the AOS group experiences more high energy states. Bin heights within a group sum to 1 across all bins. B) The energy level of the most frequent (modal) energy bin in each subgroup: blue is the control group (N=53) and red is the AOS group (N=23). Time samples are fMRI TR, which are 3 seconds in duration. The yellow regions represent the task blocks, which contain 8 stimuli each. Stimuli are presented every 9 seconds.

When the binary states were ignored and the energy bins (which include multiple states) were examined over time (Figure 6B), the AOS group consistently achieved some of the highest energy states during task blocks. The high energy states during the task occurred at significantly higher frequency for the AOS group than for controls, based on a two-sample Kolmogorov-Smirnov test for distributions of the most frequent (mode) energy bins during task blocks by group (KS-stat=0.20, p=0.0034); mean energy bin during task blocks by group (KS-stat=0.24, p=0.0057) and un-binned average (across subjects) energy over time (KS-stat=0.25, p=0.0035) were also significantly different between groups while the standard deviations were not different by group (Supplemental Figure 4).

3.6. Energy basins correspond to distinct subnetworks: fronto-temporal and parieto-motor

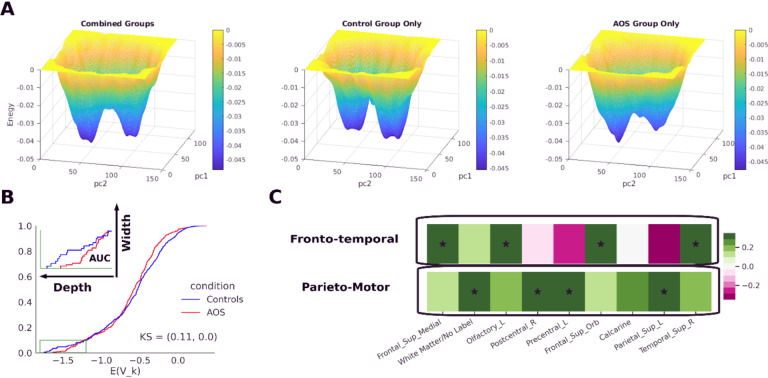
We further investigated the composition of the two basins we observed in the energy landscape (Figure 5A). In order to compare the energy landscapes and the basin features for the clinical groups, we fitted separate groupwise MEMs to the control and AOS data (see section 2.7). The presence of the two basins was consistent even in groupwise models (Figure 7A).

Figure 7:

Energy basins correspond to distinct sub-networks. A) Comparison of energy landscapes for combined model (left) versus separate models for controls (middle) and AOS patients (right). All three manifolds show two primary basins, although the basin depths and energy barrier between basins differ across them. Basins (blue regions) represent more probable, lower energy conglomerates of states. Theoretically, an individual’s brain activation states yield a sequence of positions on the energy landscape during cognition. B) Comparison of the basin areas between MEM of controls versus AOS. The area under the curve (AUC) was calculated for energy cumulative distribution functions based on energy values less than −1.2. The lowest value of the energy CDF in a bin represents the bin depth and proportion of states that lie in that energy bin represents the bin width. The total basin AUC for AOS was 32.94% lower than for the control conditions. C) Principal component analysis over the data shows that these basins represent two distinct sub-networks, I.e., “Fronto-temporal” (Frontal-superior-medial, Olfactory, Frontal-superior-orbital, and temporal-superior regions) and “Parieto-Motor” (White matter, Post-central, Precentral and parietal-superior regions).

Analysis of the separate groupwise models showed that for AOS patients, there was a 32.94% reduction in the basin areas, calculated as area under the energy cumulative distribution function (CDF) for those energy levels less than —1.2, which we defined as the basin boundary (Figure 7B). This result aligns with our previous analysis showing that controls experienced more states in lower energy bins compared to AOS patients.

We further explored if these basins corresponded to distinct sub-networks among the areas, we considered for fitting the model. PCA (Methods section 2.8) showed that the first 2 PCs explain around same amount of variance (PC1: 17%, PC2: 14%) and that the loading weights associated with these two PCs (Figure 8) comprise two distinct sub-networks. The first PC corresponds to a “fronto-temporal” subnetwork that consists of states that show high (above mean) activity in frontal superior medial, olfactory, frontal superior orbital, and superior temporal areas. The second PC corresponds to a “parieto-motor” subnetwork that consists of states that show high activity in postcentral, precentral, superior temporal superior, and white matter areas. The engagement of the two sub-networks is consistent with the cognitive and motor aspects of the PCET task. The area labeled as white matter may consist of axonal fibers connecting these regions and possibly from subcortical areas, which may explain the engagement of the parieto-motor subnetwork.

Figure 8:

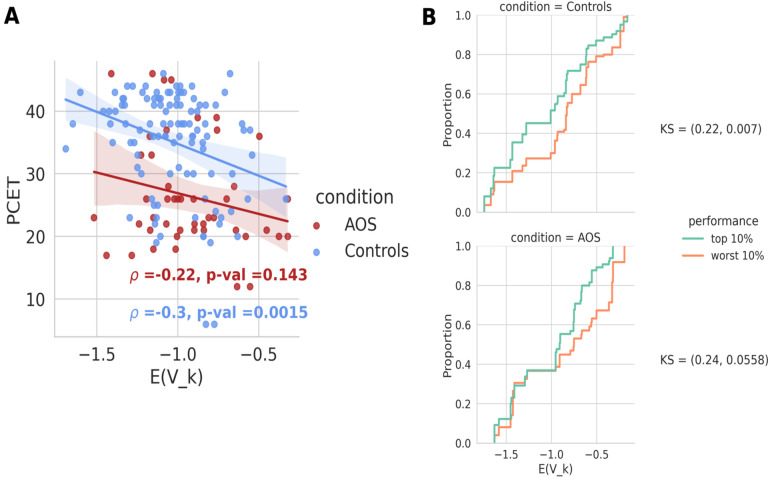
Lower energy of frontal states correlates significantly with higher cognitive score in controls but not in AOS. A) The average energy in frontal states for every subject (control or AOS) was calculated and plotted against the subject’s PCET scores. Controls show a significant negative correlation between the frontal energy values and PCET scores (ρ = - 0.3, p = 0.0015), but this relation did not hold for AOS patients (ρ = – 0.22, p = 0.143). B) The cumulative distribution function for the top 10% of performers in the control group shows a significant shift towards low energy states compared to that of the bottom 10% of performers (top, KS: 0.22, p = 0.007), whereas the distributions for AOS conditions show a shift but do not show a significant difference (bottom, KS: 0.24, p = 0.056).

We used the PCs to identify the states that correspond to activation of each of the two subnetworks, based on how the activated areas in states align with those that load heavily in each PC.

3.7. Deeper and wider frontal basins in controls, but not in AOS, correlated with higher cognitive scores

Our previous analysis showed that lower average energy values were significantly correlated with the PCET scores for both control and AOS subjects. When we limited the analysis of energy values to just the frontal states, we observed a significant negative correlation between the energy values and PCET scores among controls (ρ=—0.3, p=0.0015), suggesting that activation of low-energy frontal states was associated with better cognitive performance among controls. In the AOS group, this relationship was not significant (ρ=—0.22, p=0.14); however, the AOS subjects did show a 30.84% reduction in the basin areas for the frontal states as compared to the controls (Supplementary Figure 5).

We further show the cumulative distribution functions (CDF) of the top 10% and the bottom 10% of performers in both groups (Figure 8B). The CDFs show a clear bias towards lower energies for the top 10% of performers among controls, which differs significantly from the bottom 10% of performers in the control group (KS test, 0.22, p=0.007). The CDFs in the AOS group also featured lower energies for top than bottom performers, but this difference was not significant (KS test, 0.24, p=0.06).

The AOS condition is known to affect the fronto-temporal network, which may be reflected in the overall increased energy values in the fronto-temporal network and impairment in cognitive performance observed in this group.

4. Discussion

In this study, we applied a MEM model to understand the characteristics of energy, which represents an integrated measure of regional activation and coactivation among AOS and healthy subjects, and its relationship to accuracy of executive function performance. We show that the average energy values across the activation time series for each subject correlate with that subject’s PCET accuracy (Figure 5B). This was observed in the data from the combined sample of AOS and healthy controls as well as at the individual group levels. AOS scored lower on accuracy compared to controls throughout the entire range of average energy values suggesting that activation-co-activation pattern among AOS is less optimized and may be unfavorable for optimum executive function performance compared to controls. The relationship showed that the healthy subjects achieved lower energy states more often than AOS and better executive function correlated with lower energy values (Figure 6A). Since lower energy values occur with higher probability and arise more frequently in controls with better cognitive performance, our analysis suggests that cognitive impairments among AOS may be associated with sub-optimal brain activation patterns. Low energy states occurring with higher probability may represent more stable neural dynamics favoring better cognitive functioning. These findings suggest that the application of MEM to examine functional brain network configuration is a useful strategy. This is further supported by our findings on the first-order activations showing only nominal correlations with executive function performance (Figure 4) while MEM model-derived energy values account for a larger variance of performance. Such nominally significant correlations that did not survive multiple test corrections indicate the limitation of first-order statistics of the fMRI BOLD signal activation in explaining higher level behaviors such as cognitive performance and suggest the need for a more comprehensive mathematical model that combines first and second-order statistics of the data. We propose that an MEM that includes these statistics and also yields a quantity, average energy, which can be linked with higher level behavior may be a useful tool for better characterizing the putative mechanisms underlying differences in cognition between the two groups.

While the average energy across the fMRI activation states attained for an individual correlated with their PCET score, and the PCET scores significantly differed between the clinical groups, the average energy levels over the entire time series for each subject did not differ between the clinical groups (Fig 5B inset). This combination of results suggests that although the total energy may not be different between the groups, the time course of energy during performance of a task may be more important. In our analysis, within a common energy landscape derived jointly for the two groups, clustering states into bins according to their MEM energy indicates that the control group attains more low energy states, and the AOS group spends more time in high energy states (Figure 6A). When energy was plotted over the entire length of fMRI data acquisition during task performance for each subject, we observed that during task blocks, members of the AOS group were more likely to reach high energy states than were control group members (Figure 6B).

We observed that the low energy states were more frequent and may be more natural for the brain to reach. It is possible that the more frequent occurrence of such states in individuals with better cognitive performance corresponds to the recognition of a common element across task blocks or reliance on a single successful strategy, whereas the association of higher energy states with poorer performance could correspond to subjects treating each task block as more of a novel challenge and failing to return to and exploit previously successful strategies. When they “solve” the task, they then fall back into a lower, more probable, and more stable state. The more effort a subject put into “solving” the cognitive task, the higher the energy of the activation-coactivation pattern involved may be. Visiting such states may also relate to making incorrect responses; indeed, such higher energy bins may represent a range of different incorrect strategies or may not represent strategies to solve the cognitive task, but instead reflect a lack of coherent, focused engagement of the task, while the lower energy bins may represent convergent correct strategies, although a caveat of these ideas is that neuronal computation does not happen at the level of BOLD signals.

During the course of the task, all subjects showed two primary basins (Figure 7A). PCA shows that these basins corresponded to activation of two distinct sub-networks (Figure 7C), namely the fronto-temporal and parieto-motor that may correspond to cognitive and motor aspects of this task. The lower the average energy was in the front-temporal states, the better the cognitive performance among controls (Figure 8). However, this relationship is lost among AOS suggesting dysfunction of the fronto-temporal network.

Since the nine brain regions are likely to be involved in the task at the level of first-order statistics (Figure 2), and because there are 2⁹=512 possible states given two microstates (on or off) per region, it is apparent that any attempt to classify states as “good” versus “bad” for task performance will be challenging without additional information beyond the states themselves. If all the regional activities were positively correlated with PCET score, one could imagine superficially that being in the “all on” state (given by [1,1,1,1,1,1,1,1,1]) more frequently is “good” for task performance and that the “all off” state (given by [0,0,0,0,0,0,0,0,0]) is “bad” for task performance. This is obviously false in this implementation because the correlations in Figure 4A are both positive and negative. To put forth a more accurate argument, we should first note that in this study the “all off” state has an energy of 0, while the maximum energy state has an energy of 0.2464, and the “all on” state has an energy of –0.2541, while the minimum energy across all states is more negative: –1.7041.

Indeed, an analysis of state frequency by group did not point to any specific states that occur in one group statistically more frequently than in the other group after FDR correction (Supplemental Figure 3). With more data, a natural future step would be to consider subject-level trajectories on the energy landscape defined by the sequence of activation states each subject exhibits during data collection, with possible clustering of trajectories to identify distinct phases and distinct strategies of task performance.

Given the above, it is remarkable that the energy model can classify states (according to their energy) in a clinically significant manner (Figures 5–8). All subjects were included in one model, to provide a common framework within which to compare groups, and the model was blind to the group allegiance, as well as to which states belonged to which moments in time or which individuals. However, interpreting the meaning of all (or any) of the 512 brain states represented is not straightforward, and many of these states may represent small, unknowable noise-driven variations on an underlying set of source states.

The results suggest that impaired PCET ability in AOS individuals is related to what appears to be unfavorable neural dynamics in the fronto-temporal subnetwork consisting of the left olfactory, frontal superior medial, right temporal superior, and frontal superior orbital regions. This is a first-order statistical finding in principle, but due to the nature of multiple comparisons it is difficult to have confidence in these first-order associations. A second-order finding would contextualize the task-associated regions in a network, usually a covariance network where correlations of time series indicate connection strength, but that would, in most implementations, lack temporal specificity. Comparing the strength and smoothness of the correlations in the first-order statistical mappings shown in Figure 4A to the relationship of the same cognitive variable (PCET score) and the integrated first-and-second-order energy term (Figure 5B) indicates the improvement associated with modeling regional coactivation along with individual regional activity using the Ising model. The MEM also reveals that this network has many unequal activation configurations that exist in an energy spectrum where a wide swath of more probable lower energy states is associated with better task performance.

The left precentral and right postcentral, both sensory-motor areas, were also represented in the model. A region labeled as white matter, which is located near the left anterior cingulate, was included as well. Although these three regions may have less direct neurocognitive relevance, we included them in the model because the region selection step was entirely data-driven. Further, subjects respond to the task prompts using a clickable scroll wheel, which justifies inclusion of sensory-motor regions; not engaging the precentral gyrus for instance means not submitting prompt responses and thus doing poorly. Regarding the white matter region, recent arguments have been made that the vascularization of white matter⁵⁸ is relevant for task-related BOLD fMRI analysis⁵⁹, which is plausible given the known role of glia in modulating neuronal signaling⁶⁰.

The performance on PCET has been previously shown to relate to workplace behavior including quality of work, and more generally to verbal fluency and executive function⁴⁶. These domains are impacted by psychotic disorders like schizophrenia. Early detection of schizophrenia is crucial for successful treatment. These results show that an image-derived phenotype associated with poor executive function performance and AOS is an unstable, high-energy interaction between at least nine independent brain regions. Our results highlight that the frontal-motor executive network comprised of these regions is a dynamic entity, where all possible brain state configurations have associated energies that can be used to measure an individual’s propensity towards clinically diagnosed psychosis. While the network studied consisted of nine independent components that do not strictly overlap with any atlas, targeting similar regions in most standard atlases may allow for these findings to be replicated without the GICA. In the future, further research is needed to study full-brain MEMs, for instance using the 360-cortical node Glasser atlas⁶¹. Further, future studies can also focus on elucidating trajectories of brain states⁶² through an “energy landscape”⁶³, where basins represent lower energy and hence higher probability states that theoretically correspond to attractors for the dynamics of neural activity.

Data availability

The data is available through NIMH data repository.

Funding Statement

Funding was provided by NIMH grant numbers: R01MH115026 and R01MH112584 (KMP).