Energy in functional brain states correlates with cognition in adolescent-onset schizophrenia and healthy persons

Abstract

Adolescent-onset schizophrenia (AOS) is a relatively rare and under-studied form of schizophrenia with more severe cognitive impairments and poorer outcome compared to adult-onset schizophrenia. Several neuroimaging studies have reported alterations in regional activations that account for activity in individual regions (first-order model) and functional connectivity that reveals pairwise co-activations (second-order model) in AOS compared to controls. The pairwise maximum entropy model, also called the Ising model, can integrate both first-order and second-order terms to elucidate a comprehensive picture of neural dynamics and captures both individual and pairwise activity measures into a single quantity known as energy, which is inversely related to the probability of state occurrence. We applied the MEM framework to task functional MRI data collected on 23 AOS individuals in comparison with 53 healthy control subjects while performing the Penn Conditional Exclusion Test (PCET), which measures executive function that has been repeatedly shown to be more impaired in AOS compared to adult-onset schizophrenia. Accuracy of PCET performance was significantly reduced among AOS compared to controls as expected. Average cumulative energy achieved for a participant over the course of the fMRI negatively correlated with task performance, and the association was stronger than any first-order associations. The AOS subjects spent more time in higher energy states that represent lower probability of occurrence and were associated with impaired executive function and greater severity of psychopathology suggesting that the neural dynamics may be less efficient compared to controls who spent more time in lower energy states occurring with higher probability and hence are more stable and efficient. The energy landscapes in both conditions featured attractors that corresponded to two distinct subnetworks, namely fronto-temporal and parieto-motor. Attractor basins were larger in the controls than in AOS; moreover, fronto-temporal basin size was significantly correlated with cognitive performance in controls but not among the AOS. The single trial trajectories for the AOS group also showed higher variability in concordance with shallow attractor basins among AOS. These findings suggest that the neural dynamics of AOS features more frequent occurrence of less probable states with shallower attractors, which lack the relation to executive function associated with attractors in control subjects suggesting a diminished capacity of AOS to generate task-effective brain states.

1. Introduction

Adolescent onset schizophrenia (AOS) is associated with more prominent developmental and premorbid abnormalities with more severe cognitive impairments (Frangou, 2010; Holtmaat & Svoboda, 2009; Kester et al., 2006; Rapoport & Gogtay, 2011; Thaden et al., 2006), especially in working memory (Brickman et al., 2004; Karatekin, Bingham, & White, 2009; Karatekin, White, & Bingham, 2008; White, Mous, & Karatekin, 2013), executive functions (Frangou, 2010; Kester et al., 2006; Rapoport et al., 1997; Thaden et al., 2006), and attention (Oie & Hugdahl, 2008; Oie & Rund, 1999; Oie, Sundet, & Rund, 2010; Thaden et al., 2006), and with poorer long-term outcomes (Frangou, 2010; Kumra & Charles Schulz, 2008; Kumra, Shaw, Merka, Nakayama, & Augustin, 2001; Rapoport et al., 1997). Hence, AOS is proposed as a more severe form of schizophrenia (Kumra & Charles Schulz, 2008) although it is phenomenologically continuous with adult-onset schizophrenia (Frangou, 2010; Kumra et al., 2001; Rapoport et al., 1997). Further, neurobiology of AOS is under-investigated compared to adult-onset schizophrenia which is supported by proportionately fewer peer-reviewed publications on AOS compared to adult-onset schizophrenia although AOS is receiving greater attention recently. Despite receiving greater attention, research on AOS constituted approximately 3% of all investigations on schizophrenia reported in peer-reviewed publications in each of the last 5 years (Supplemental figure 1). In addition, although AOS constitutes 12.3% of all schizophrenia (Solmi et al., 2022), the economic and human cost of AOS far exceeds its proportional prevalence (Cloutier et al., 2016). Cognitive deficits are consistently associated with poor long-term outcome (Bora, Gokcen, Kayahan, & Veznedaroglu, 2008; Frith, 1996; Green, 1996; Velligan & Miller, 1999) and respond minimally to antipsychotics (Mishara & Goldberg, 2004; Woodward, Purdon, Meltzer, & Zald, 2005). Therefore, a better understanding of the pathophysiology of AOS could enable novel treatment strategies to improve outcomes, reduce the economic and human cost of AOS, and potentially understand the pathophysiology of onset of schizophrenia in an adolescent developmental context.

Among several approaches available to investigate the pathophysiology of schizophrenia, functional magnetic resonance imaging (fMRI) offers the advantage of examining blood oxygenation level dependent (BOLD) responses as proxy measures of brain activation. Currently, most fMRI studies have examined group differences in the activation of brain regions, namely first-order properties (Gitelman, Ashburner, Friston, Tyler, & Price, 2001), or pairwise correlations of spatially distributed regions and derived functional networks based on co-activations, namely second-order properties. These approaches have highlighted distinct aspects of brain functioning at rest and during task performance (Friston, Holmes, et al., 1994; Friston, Jezzard, & Turner, 1994; Worsley, Evans, Marrett, & Neelin, 1992); however, these models provide limited information at the systems level. First-order models average the BOLD responses over the entire period of a task or a stimulus, losing the temporal evolution of the hemodynamic response. For this reason, first-order-only analyses cannot elucidate detailed system-level interactions among regions. Second-order models rely on correlation between node pairs with the assumption that pairwise node correlations are independent; however, they ignore regional activation levels and often do not provide mechanistic insights. Neither model adequately captures the temporal evolution of neural dynamics as a collective process.

In this work we used the pairwise maximum entropy model (MEM) (Schneidman, 2016; Yeh et al., 2010), which mathematically integrates both first-order and second-order properties across brain regions (Yeh et al., 2010) in a way that relates to the empirical occurrence probabilities of states. That is, the MEM does not rely on pairwise correlation between nodes but instead captures the probabilities of different individual nodes being active, and pairs of nodes being synchronously active, during discrete time bins, thus focusing on collective activity patterns across brain regions (Lamberti et al., 2022). The MEM is therefore considered to be a powerful tool to bridge the gap between micro- and macro-scale activation structure (Fortel et al., 2022). In the MEM, states are defined by binarizing the activation levels of all parcellated brain regions into those that are above threshold or òn’ and those that are below threshold or òff’; a state is therefore a vector of 0’s and 1’s of length equal to the number of regions in the parcellation. The MEM allows us to find the probability distribution of states for which the frequencies with which each region is active and the frequencies with which each pair of regions is co-active best match those observed empirically in the data, without imposing any additional assumptions on the structure of this distribution. The MEM is related to the generalized Ising model (Kloucek et al., 2023), which was originally proposed as a framework to describe the distribution of magnetic dipoles in a magnet over some observation time; the analogy to the brain is that brain regions can be thought of as ‘active’ or ‘inactive’ at a given point in time, can continuously change their activation state, and interact according to an underlying network configuration to produce brain states of varying likelihood. The MEM framework associates an “energy” to each brain state – also called the “integrated energy” of a system configuration when applied to fMRI data (Das et al., 2014) -- but the term “energy” in this setting does not refer to physical energy (in joules) nor to metabolic energy (as adenosine triphosphate). Rather, it is used in a mathematical sense, where energy is inversely related to probability, with higher energy associated with low probability states. In other words, one cannot infer directly from the pattern of active regions in a state whether that state will have high or low energy; rather, the energy level of a state can only be determined from how frequently it arises in a given data set and usually differs across data sets.

Although the MEM approach was originally used in physics to model magnetic fields (Brush, 1967), versions of the MEM have more recently been used in studies associated with cognitive functions. The MEM approach is especially useful to investigate statistics of the time-varying dynamics during cognitive tasks because the model includes BOLD responses at every repetition time (TR) of the fMRI acquisition (Kang, Jeong, Pae, & Park, 2021) providing arguably the best temporal resolution for fMRI data analysis compared to traditional first- or second-order comparisons as well as most models of dynamic functional connectivity. Further, investigation of brain networks using a pairwise MEM and associated energy landscape provides a useful representation of network organization that can be compared between different tasks, conditions, or subject groups. A prior study found multiple local minima in resting fMRI suggesting that in rest conditions, the brain naturally reverts to one of a collection of preferred states (Ezaki, Fonseca Dos Reis, Watanabe, Sakaki, & Masuda, 2020). Experimentally induced perturbations reduced the number of local minima considerably, while other effects depended on the specifics of the perturbation (Kang, Pae, & Park, 2017). Another resting fMRI study showed different characteristics of the energy landscape in the default mode and frontoparietal networks (Watanabe et al., 2014). Energy and cognitive performance may be related (Jeong et al., 2021), in that energy level may reflect the complexity of the mental work being done or the efficiency of strategies adopted to complete a cognitive task; for example, complex tasks or inefficient strategies may lead to high energy and hence low probability states that would not naturally arise in more typical, less complicated settings. In this work, we provide what is to our knowledge the first study to apply the MEM model to elucidate complex network dynamics in AOS or adult-onset schizophrenia patients using task fMRI data.

Task-fMRI can provide data on differences in functional and network characteristics that can be used as biomarkers and as treatment targets. Previous studies have reported impaired executive function in AOS (Frangou, 2010; Rapoport et al., 1997; Thaden et al., 2006) and adult-onset schizophrenia (Gold et al., 2018; Jepsen et al., 2010; Johnson-Selfridge & Zalewski, 2001; Minzenberg, Laird, Thelen, Carter, & Glahn, 2009) patients. We selected the Penn Conditional Exclusion Test (PCET) as an fMRI task to test executive function and select brain regions to build first- and second order models. PCET is a part of the Penn Computerized Neurocognitive Battery that has been validated in schizophrenia (Gur, Ragland, Moberg, Bilker, et al., 2001) and healthy (Gur, Ragland, Moberg, Turner, et al., 2001) subjects and used in our previous studies (Kuo et al., 2018; Prasad et al., 2010; Prasad, Muldoon, Theis, Iyengar, & Keshavan, 2023; Roalf et al., 2013). PCET is closely related to the Wisconsin card sorting test and to verbal fluency and work behavior such as cooperativeness, work quality, and general impressions including quality of work, verbal fluency, and executive function (Kurtz, Wexler, & Bell, 2004).

Here, we applied the pairwise MEM to fMRI data obtained while participants were performing the PCET task. The MEM model (Figure 1) was iteratively fit to the entire set of observed brain states, using their empirical probabilities to estimate unknown parameters in the MEM. The relationship between MEM energy, and cognitive performance assessed as accuracy of in-scanner PCET, and severity of psychopathology were examined. We hypothesized that the average integrated energy associated with the states of an individual over the course of the experiment is related to PCET accuracy and severity of psychopathology. This relationship depends on the first order regional activation over time but is hypothesized to be stronger than the relationship between first-order regional activation over time and PCET score. Energy landscapes are hypothesized to consist of one or more basins, or local minima, representing attractor states that will have both qualitative features such as a description of basins in terms of constituent brain states, and quantitative features such as basin depth that are also related to task performance.

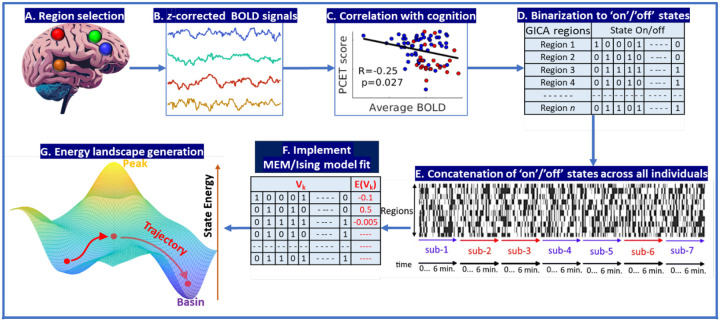
Figure 1:

A schematic of the methodological outline. A. The minimally preprocessed fMRI raw data is used to find components by implementing the group independent component analysis (GICA) to find 70 components. B. For each of the 70 components, the correlation of z-corrected individual-level BOLD signal amplitude with performance on PCET is computed and the regions with nominally significant correlation of BOLD responses to PCET performance are selected (blue points are controls; red points are AOS subjects). D. The temporal activity series of these 9 regions are then binarized using a threshold that determines the ‘on’ and ‘off’ states at the individual level. E. These individual level ‘on’ and ‘off’ states of all regions are concatenated together across all individuals in the study, creating the concatenated binary matrix, T. F. The maximum entropy model is then fit to this matrix. G. The resulting energy term can be represented in a number of ways, including in terms of principal components by performing PCA on T matrix, which in particular produces an energy landscape. Legend: sub=subjects

2. Methods

2.1. Sample description

We enrolled 23 AOS from in- and out-patient clinics of the University of Pittsburgh Medical Center, Pittsburgh and 53 adolescent healthy controls from the community. Adolescent-onset was defined as schizophrenia subjects who had an onset of psychotic symptoms after puberty but before completing 18 years of age. Puberty was assessed using the Peterson Pubertal Developmental Scale and all subjects had to score ≥2 to be eligible for enrolment. Participants diagnosed with intellectual disability according to the DSM-IV, having history of substance use disorder in the last 3 months, head injury with significant loss of consciousness, tumors, encephalitis, and had suffered neonatal asphyxia were excluded. Subjects were administered the Structured Clinical Interview for DSM-IV (SCID-IV) and selected items on the KiddieSchedules for Assessment of Depression and Schizophrenia (K-SADS). Consensus diagnosis by experienced clinical investigators was made after reviewing all available clinical data including the charts. The University of Pittsburgh Institutional Review Board approved the study. Informed consent was obtained from all participants after providing a full description of the study including the risks and benefits. Controls were 19.64±1.63 years old and 68% female, and AOS were 19.8±1.47 years old and 39% female. HC and AOS did not differ significantly in age (t=0.47; p=0.32) but sex distribution was significantly different between the groups (χ²=5.51 p=0.02). We administered Positive and Negative Syndrome Scale (PANSS) (Kay, Fiszbein, & Opler, 1987) was administered to all subjects to assess the severity of psychopathology.

2.2. Image Acquisition and Preprocessing

Imaging data were obtained on a 7 Tesla whole body scanner. T₁-weighted MP2RAGE scans were acquired in the axial plane (348 slices, 0.55 mm thickness, TE=2.54ms, TR=6 seconds, in-plane resolution=390×390). Functional MRI echo-planar images were acquired in the axial plane (86 slices, 1.5 mm thickness, TE=20ms, TR=3 seconds, in-plane resolution=148×148, 142 volumes). fMRI data was collected while subjects performed the PCET task (Figure 2). Our choice of PCET performance is supported by previous studies that relate executive function to workplace behavior (Kuo et al., 2018). These domains are impacted by schizophrenia. Each trial presented four shapes and participants selected the shape that did not belong. The sorting principles changed, with feedback to help subjects develop new strategies. Subjects were expected to select the correct stimulus with the minimum number of errors despite changing sorting principles. Such set shifting was considered to indicate cognitive flexibility, which is subsumed as executive function (Kurtz et al., 2004). The number of correct responses was counted as the measure of accuracy of performance.

Figure 2:

Left: The Penn Conditional Exclusion Task (PCET) used in this study to collect task fMRI data related to executive functions. A) Six task blocks (black boxes) and 7 fixation blocks (white boxes) are shown. The onset time in seconds (numbers in white and black boxes) as well as the corresponding MRI TR (grey box) are shown. Each TR is 3 seconds with total number of TRs = 142; total fMRI duration 7 min and 33 sec. B) Within a task block, 8 stimuli are presented over 48 seconds followed by a fixation block consist of a cross. C) Each stimulus consists of 4 objects with varying features (line thickness, size, and shape). The participant’s responses are provided with feedback (“correct” or “incorrect”) (see text for details). Right: Spatial locations of 9 selected brain regions from GICA. The regions correspond to the following anatomical areas: A) calcarine, B) left precentral, C) left olfactory, D) frontal superior medial, E) right postcentral, F) left parietal superior, G) right temporal superior, H) frontal superior orbital, and I) a region labeled as white matter/no label which is located near the left anterior cingulate.

All the pre-processing steps for the task fMRI data were performed using fMRIPrep (Esteban et al., 2019), which included correction for motion (using mcflirt), slice time correction, susceptibility distortion correction, and brain extraction before registering to a standard space (MNI 152NLin6Asym) using the Human Connectome Project approach (Glasser et al., 2013). Image registration of fMRI volumes to standard space was performed using co-registration with the T₁-weighted image. Furthermore, signal confounds were estimated, encompassing the global mean signal, mean tissue class signal, frame-wise displacement and DVARS (Power et al., 2014). Furthermore, signal confounds were estimated, encompassing the global mean signal, mean tissue class signal, frame-wise displacement and DVARS (Power, Barnes, Snyder, Schlaggar, & Petersen, 2012). DVARS and framewise displacement were calculated and subjects with framewise motion greater than DVARS of 1.5 or framewise displacement above 0.5mm were excluded.

2.3. Region Selection

Group Independent Component Analysis (GICA) was used to define spatial maps (Varoquaux et al., 2010). This allowed us to focus on task driven BOLD signals that appear on the inter-subject level (Salman, Vergara, Damaraju, & Calhoun, 2019). GICA is performed using a larger selection of components than expected to be necessary to explain the task-associated regions. Here, we chose 70 components (Allen et al., 2014), which aims to have sufficiently many components to create a “functional parcellation”, with the understanding that too few components (<20) will result in fused functional parcels, and too many components (>100) will cause reproducibility issues (Abou-Elseoud et al., 2010).

We selected a subset of N components that showed nominally significant correlation of BOLD responses to the performance on PCET for inclusion in the energy model (Figure 2) because careful selection of regions could contribute to the effectiveness of the model. The region selection step was purely data-driven to choose informative timeseries for the energy model and to enhance computational tractability through an exponential downscaling of the number of possible states included in the energy computation (Zhu & Ghodsi, 2006). The white matter region was included despite the unorthodoxy of white-matter-derived BOLD signals (Smirnov, Destrieux, & Maldonado, 2021) (see discussion).

2.4. Concatenation and Binarization

After selecting the N regions to be analyzed, all observations were binarized using a threshold. This process allowed us to represent any time course of BOLD images as a series of states. Here, each state is a vector of N elements, with one element per selected region. Each state is defined by assigning the value of 0 to some elements and the value of 1 to all of the other elements; thus, there are B=2^N total states. A BOLD image in which certain regions exhibited super-threshold activation was assigned the state with 1 values in the elements corresponding to those regions and 0 values in all other elements. For example, an image in which all regions’ activation levels were above threshold would be assigned the state given by the N-vector with all elements equal to 1.

The images, or timepoints, for all subjects were converted into states in this way and concatenated together in a matrix T with N rows representing regions and a number of columns, M, equal to the total number of timepoints (TR) in the entire sample, across all subjects. That is, we assume that each subject has the same number of timepoints, p, and take M=S*p where S denotes the number of subjects.

The threshold choice for binarization can affect the outcome of the energy model (Supplemental figure 2). The seven threshold choices tested for binarizing the BOLD-derived observations, z-scored across all subjects and timepoints, were 0, +/− 0.5, +/− 1.0, and +/− 2.0. For example, a threshold of 0 would produce a matrix T for which roughly half of all elements took the value 1, with correspondingly fewer or more 1 values for higher or lower thresholds, respectively. We chose the threshold of 0 for our subsequent analyses because it produced the most informative energy landscape (see Section 2.5) with the best fit of the energy function to the empirical probabilities of state occurrence. All data in this manuscript uses this threshold.

2.5. Energy Model

We label the state vectors defined in Section 2.4 as V_k, where the index k runs from 1 to B=2^N. Energy, E, is defined for each possible state, V_k, according to the Ising model (Yeh et al., 2010) as:

$$E\left(V_k\right)=-\sum _{i=1}^N{h}_i{\sigma }_i\left(V_k\right)-\left(\frac{1}{2}\right)\sum _{i=1}^N\sum _{j=1.j\ne i}^N{J}_{ij}{\sigma }_i\left(V_k\right){\sigma }_j\left(V_k\right)$$ (1)

where the N-by-N matrix J and the N-vector h are parameters to be determined from the imaging data using a fitting algorithm. In equation (1), each term σ_i(V_K) takes the value 1 if region i exhibits suprathreshold activation in state V_k and takes the value 0 otherwise. While the energy value itself has no absolute interpretation and only relative changes in energy are meaningful, the energy of a state maps to the probability of a state, P(V_k), as follows:

$$P\left(V_k\right)=\mathit{\text{exp}}\left(-E\left(V_k\right)\right)/\sum _{i=1}^B\mathit{\text{exp}}\left(-E\left(V_i\right)\right)$$ (2)

In the fitting algorithm, starting from some initial guesses, the values of h_i and J_ij in equation (1) were iteratively updated by comparing the empirically observed activation and co-activation frequencies (or equivalently mean activation level and covariance) of the imaged brain regions with those estimated from equation (2) and adjusting them with a learning rate, α = 0.2. Specifically, we calculated the estimated mean 〈σ_j〉 and covariance 〈σ_jσ_l〉_m and performed the iterations of h_i and J_ij as follows:

$${\langle {\sigma }_j\rangle }_m=\sum _{q=1}^B{\sigma }_j\left(V_q\right)P\left(V_q\right)$$

$${\langle {\sigma }_j{\sigma }_l\rangle }_m=\sum _{q=1}^B{\sigma }_j\left(V_q\right){\sigma }_l\left(V_q\right)P\left(V_q\right)$$

$$h_i^{\mathit{\text{new}}}=h_i^{\mathit{\text{old}}}+\alpha \cdot \mathit{\text{log}}\left(\frac{\langle {\sigma }_i\rangle }{{\langle {\sigma }_i\rangle }_m}\right)$$

$$J_{ij}^{\mathit{\text{new}}}=J_{ij}^{\mathit{\text{old}}}+\alpha \cdot \mathit{\text{log}}\left(\frac{\langle {\sigma }_{ij}\rangle }{{\langle {\sigma }_{ij}\rangle }_m}\right)$$

where 〈σ_i〉 and 〈σ_ij〉 are the empirically observed mean and covariance, respectively, for regions i and j. We ran 300 iterations of the gradient descent algorithm and that resulted in a good fit between the first-order (mean activity) and second-order (co-activation) statistics (see Section 2.6).

We used this procedure to fit an MEM for the combined control group and AOS group data and also to fit distinct MEMs to the separate data for the control group and the AOS group.

2.6. Evaluating Fit of the Model

We evaluated the fit of the model by comparing the estimated and actual first-order (mean) and second-order (covariance) features of the data (Supplemental Figure 3). As an additional check, we also examined the relationship between the energy and probability of occurrence of each state as estimated by the model and the empirical probability of each state in the data, which also demonstrated a good fit (Supplemental Figure 4). We also ensured that there were more observations than the entropy of the system (in bits). Specifically, the state space size (given by B) refers to the number of N × 1 vectors of binary regional activity, across all subjects and timepoints. In this case, N=9, so B=2^N=512. The number of observations refers to the number of columns in T, which here is 10,792 (approximately twenty times B), justifying that we had an adequate sample for implementing the MEM.

2.7. Energy Landscape via Projection onto Principal Components

From equation (1), we derived a vector of energy values along a sequence of time points for each subject. While essential, the time and energy dimensions do not tell the full story. Since the basis for the energy value is the N-dimensional brain state configuration, and time points with the same energy value could correspond to very different brain states, we used Principal Component Analysis (PCA), performed on T, the matrix of observed binary states concatenated across all subjects and time points, to describe states in terms of a lower-dimensional manifold.

The PCA isolates the orthogonal eigenvectors, or principal components (PCs) that explain the most variance in the data. Our aim was to visualize an energy landscape in a three-dimensional state space, where two dimensions represent the data projected onto the first 2 PCs and the 3^rd dimension represents the energy corresponding to the state. In this space, moving along a PC axis changes the weight on that PC vector; different states are approximated by different weighted sums of the PC vectors and thus different states are projected to corresponding points in PC space. The energy landscape was smoothed with a 2-dimensional Gaussian kernel, with σ=1.5; in brief, the smoothing process introduces a kernel centered at each data point and computes a smooth function by summing over these kernels. The smoothed version was used to visualize the energy manifolds, but all quantification was done on the individual states of the MEM. The same value of σ was used to generate all energy landscapes. The basins of attraction of energy minima correspond to low (usually negative) energy values represented with cooler colors, whereas the peaks correspond to higher (usually positive) energy values represented with warmer colors. PCA was also used to identify two sub-networks corresponding to the basins observed in the energy landscape. The loading weights of the first two PCs were thresholded (threshold=0.3) to identify the states that corresponded to “fronto-temporal” and “parieto-motor” networks. Fronto-temporal states were defined as states where frontal-superior-medial, olfactory, frontal-superior-orbital and temporal-superior were simultaneously active, whereas parieto-motor states were defined as states where postcentral, precentral, parietal-superior and the region corresponding to white matter were simultaneously active. The binary numerals are converted to base 10 for ease of collation, (e.g., 000000100 is state number 4).

For the MEM for the separate control and AOS data sets, the PCs were calculated separately on each group, before the corresponding data was projected on the PCs for that group.

In order to separate the states corresponding to the two sub-networks, each of the two PCs was used as a mask. The mask for PC1 (fronto-temporal network) was considered as all the states where Frontal-Superior-Medial, Olfactory (L), Frontal superior orbital and Temporal-Superior (R) nodes showed suprathreshold activity, represented by the value 1 in the binarized vectors (V_k). Hence, the frontal-temporal network is considered to be active only when all four aforementioned nodes of the network are active. However, the other 5 nodes may be in the inactive (0) or active (1) state, the underlying assumption being that for a sub-network to be active, all the nodes belonging to the sub-network should be concurrently active irrespective of the activity of the nodes outside the sub-network. Similarly, the mask for PC2 (parieto-motor network) was considered as all the states where nodes corresponding to white matter, Postcentral (R), Precentral (L) and Parietal-Superior (L) show suprathreshold activity. The sub-network specific states were used to analyze the energy landscape features specifically associated with the two sub-networks.

2.8. Cognitive, Psychopathological and Clinical Statistical Comparisons

Energy from the model was compared between AOS and healthy controls and to the cognitive performance in each clinical group. Subject-level energy scores, computed as the average energy of all states over the entire course of their fMRI, were compared, using whole-group and within-group correlations, to PCET accuracy scores. The 512 states were also binned into 16 equal bins according to energy percentiles. Explicitly, 32 states (6.25% of all states) were classified into the lowest energy bin, 32 into the next-lowest energy bin, and so on. Then, the number of states experienced per energy bin was tallied by group and divided by the total number of states attained, yielding the frequency of occurrence by energy bin. The frequency of occurrence of bins in the bottom half (eight) of all energy bins were compared between AOS and controls using a Wilcoxon rank-sum test, as were frequencies for the top eight bins. A two sample Kolmogorov–Smirnov test was used to determine if the distributions of energy bins attained over time differed between groups. We used Pearson correlation tests to examine the relationship of energy of each subject with severity of psychopathology assessed using the PANSS. First, we examined the correlation of total PANSS score in relation to total energy obtained from the MEM. Next, we followed up with examination of PANSS scores for each group of symptoms, namely total positive, total negative, total disorganization, and total cognitive score. We also examined the correlation of PCET accuracy scores with the severity of psychopathology as described above. The results are reported after correcting for multiple tests using the Bonferroni correction.

2.9. Single trial trajectories

The PCET task consisted of 6 task blocks of 22 TRs (3 secs each) that were averaged for each participant to obtain their trajectory. The trajectories were smoothened using a box car kernel of length 5. The top 5 performers from the control and poorest performers on the AOS group were chosen on the basis of the 5 highest or lowest PCET scores. The ellipsoid was calculated by finding the average standard deviation across X (PC1), Y (PC2) and Z (Energy) axes corresponding to the AOS and control trajectories.

3. Results

3.1. Controls score higher on PCET task compared to AOS

Healthy controls showed significantly higher accuracy (35.1±8.4) on the PCET task compared to the AOS group (26.4±8.9) (t=4.0, p<0.001) (Figure 3A).

Figure 3:

PCET scores and region selection based on correlation with regional BOLD signals. A) PCET Score Histograms by group. Controls show a right shift in the number of occurrences of higher PCET accuracy compared to patients who mostly concentrated to the left. Blue: controls. Red: AOS. X-axis is total PCET correct. Y-axis is the number of participants in the group who scored the corresponding amount. B) For all 70 components from GICA, each subject’s average BOLD signal intensity in that component was plotted against PCET score. The X-axis in each plot is the average z-scored BOLD amplitude-derived component value. The y-axes are the PCET scores. Blue points are healthy controls. Red points are AOS subjects. The relationship of BOLD signals was complex in that not all regions showed positive correlation of BOLD signal with PCET performance. Notably, frontal, and parietal regions showed negative correlations. None of these correlations survived multiple test corrections using the Bonferroni method.

3.2. Activity in a subset of selected regions shows a significant correlation with cognitive performance

From 70 GICA components representing 92 non-contiguous regions, 9 regions (Figure 2) were found to have an average activity at the individual level that significantly correlated with the PCET total score across all participants (Figure 3B), without correction for multiple comparisons. The nine regions have their components’ peak voxels in the following approximate locations in the brain: left calcarine (r=0.23, p<0.05), left precentral (r=0.23, p<0.05), left olfactory (r=0.25, p<0.05), left frontal superior medial (r=–0.25, p<0.05), right postcentral (r=–0.31, p<0.05), left parietal superior (r=–0.25, p<0.05), right temporal superior (r=0.25, p<0.05), left frontal superior orbital (r=–0.23, p<0.05), and a region labeled as white matter, located near the left anterior cingulate (r=0.30, p<0.05).

In addition, 5 edge weights correlated with total PCET accuracy scores after Bonferroni correction, out of 4186 edges considered across 92 regions (p<1.19e-05). The traditional functional connectomes look almost identical apart from these 5 edges, which are not likely to alter the network in terms of any whole-graph property like characteristic path length, at least for a complete (density=1) network like the one studied here. After covarying for age, sex, and parental education, only the termporal_Mid_L to Cerebellum_7b_L remained significant (r=−0.49, p=1.06503–0.05) (Supplemental Figure 5).

3.3. Average energy in MEM shows significant negative correlation with cognitive scores and severity of psychopathology

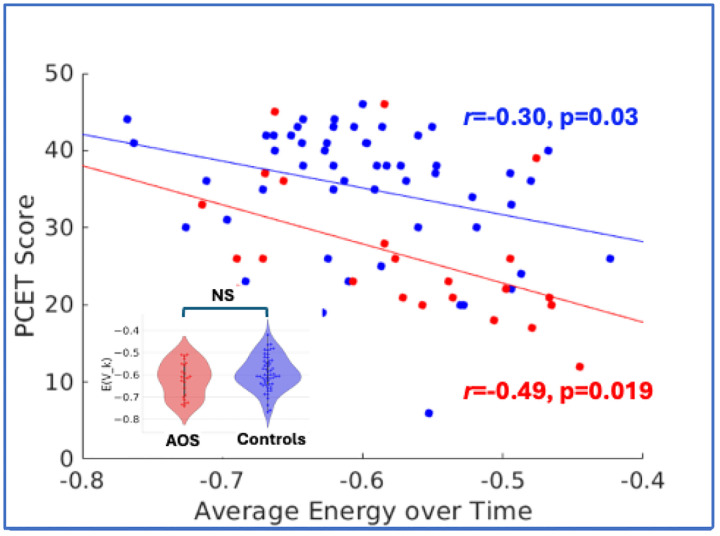
We fitted an MEM to the combined data of fMRI activity from controls and AOS patients (see Supplemental figure 3 for goodness-of-fit). The average energy values across the time series of activation states for each subject were not statistically significantly different between AOS and controls (Figure 4 inset) despite the groups’ clear differences in the PCET scores (Figure 3A). However, we found that the average energy value negatively correlated with PCET accuracy (Figure 4). This relation holds both at the combined group level (N=76, r=− 0.39, p=0.0004) and separately for the control group (N=53, r=−0.30, p=0.03) and AOS (N=23, r=−0.49, p=0.019) (Figure 4). The energy correlated positively with total PANSS score (r=0.24, p=0.038), and within the subgroup of symptoms, energy correlated positively with total cognitive score on the PANSS (r=0.33, p=0.003). Correlation with other categories did not survive multiple comparison correction using the Bonferroni approach. The PCET score correlated negatively with total PANSS score (r=−0.32, p=0.005). Similar negative correlations were observed for total positive (r=−0.38, p<0.001) and total cognitive (r=−0.35, p=0.002) score. Thus, our results suggest that the lower average energies are correlated with higher cognitive scores for both clinical groups, suggesting that more substantial attractor basins are associated with better cognitive performance. These attractor basins also engage specific sub-networks which are described in detail in Section 3.5.

Figure 4:

Average Energy versus PCET Score. The energy values averaged across the entire duration of the fMRI (142 timepoints) for each subject (Blue point: healthy controls; Red points: AOS) show significant negative correlation with PCET scores. Average energy distributions do not show statistical significance between the groups (inset).

3.4. Analysis of combined sample of patients and controls

Although the groups’ overall average energy levels do not show a significant difference (Figure 4 inset), the temporal structure of how (across subjects) energy varies over time was significantly different between groups (KS-stat=0.25, p=0.0035). Moreover, the detailed temporal structure of the activity states and their corresponding energies shows a clear difference between the clinical groups.

To go beyond averages and compare the full distributions of energy levels between the groups, we discretized the state energies into sixteen equally sized energy bins. We found that states in the lower half of the distribution occur with higher frequency in the controls’ time series while the time series of AOS consistently included higher frequencies of states in the upper half of the energy distribution (Figure 5A). The Wilcoxon rank-sum test, paired on energy bins, showed significant differences in the occurrence frequencies of the lower energy states (p<0.01, signed rank=36) and higher energy states (p<0.01, signed rank=0). When individual states were compared for differences in occurrence frequency by group without regard to their energies there were no specific, individual states with significantly different occurrence frequency by group after correction for multiple comparisons using false discovery rate (Supplemental Figure 6).

Figure 5:

Controls experienced more low-energy states compared to AOS. A) Using 16 equally sized bins to cluster states based on energy percentiles, we observed that the control group experienced more low energy states and that the AOS group experienced more high energy states. Bin heights within a group sum to 1 across all bins. B) The energy level of the most frequent (modal) energy bin in each subgroup: blue is the control group (N=53), and red is the AOS group (N=23). Time samples are fMRI TR, which are 3 seconds in duration. The yellow regions represent the task blocks, which contain 8 stimuli each. Stimuli are presented every 9 seconds.

When the binary states were ignored and the energy bins (which include multiple states) were examined over time (Figure 5B), the AOS group consistently achieved some of the highest energy states during task blocks. The high energy states during the task occurred at significantly higher frequency for the AOS group than for controls, based on a two-sample Kolmogorov-Smirnov test for distributions of the most frequent (mode) energy bins during task blocks by group (KS-stat=0.20, p=0.0034); mean energy bin during task blocks by group (KS-stat=0.24, p=0.0057) were also significantly different across groups, while the standard deviations were not different by group (Supplemental Figure 7).

3.5. Energy basins correspond to distinct subnetworks: fronto-temporal and parieto-motor

We computed the energy landscape obtained from projecting the data onto the first two PCs of the matrix of activation states observed in all subjects (see Section 2.7), with energy as the third dimension (Figure 6A). The energy landscape features two primary attractors in the activity (142 time-points per subject) dynamics during the task, each with a sizeable attraction basin (low energy areas in blue).

Figure 6:

Energy basins correspond to distinct sub-networks. A) Comparison of energy landscapes for combined model (left) versus separate models for controls (middle) and AOS patients (right). All three manifolds show two primary basins, although the basin depths and energy barrier between basins differ across them. Basins (blue regions) represent more probable, lower energy conglomerates of states. Theoretically, an individual’s brain activation states yield a sequence of positions on the energy landscape during cognition. B) Principal component analysis over the data shows that these basins represent two distinct sub-networks, I.e., “Fronto-temporal” (Frontal-superior-medial, Olfactory, Frontal-superior-orbital, and temporal-superior regions) and “Parieto-Motor” (White matter, Post-central, Pre-central and parietal-superior regions). C) Comparison of the basin areas between MEM of controls versus AOS. The area under the curve (AUC) was calculated for energy cumulative distribution functions (CDF). The definition of basin depends on the choice of a threshold. An example for threshold = −1.2 is marked with green rectangle, i.e. all states that have energy values lower than −1.2 are considered as basin and the area under the curve (shown as an inset) calculates how many states form a basin. D) % difference in AUC of control vs AUC for AOS group for different values of threshold. The total basin AUC for control was 32.94% higher than for the AOS group as marked by green point and green rectangle in (C).As can be observed, the total basin area in the fronto-temporal network for the control group is higher than the basin area for AOS group for all values of threshold > −0.35.

We further investigated the composition of the two basins we observed in the energy landscape (Figure 6A). In order to compare the energy landscapes and the basin features for the clinical groups, we fitted separate groupwise MEMs to the control and AOS data (see section 2.7). The presence of the two basins was consistent even in groupwise models (Figure 6A).

We further explored if these basins corresponded to distinct sub-networks among the areas used for fitting the model. PCA (Methods section 2.7) showed that each of the first 2 PCs explains around same amount of variance (PC1: 17%, PC2: 14%) and that the loading weights associated with these two PCs (Figure 6B) comprise two distinct sub-networks. The first PC shows strong (well above mean) activation in fronto-temporal brain regions: frontal superior medial, left olfactory, frontal superior orbital, and right superior temporal areas. Thus, we consider this to represent a “fronto-temporal” axis. The second PC corresponds to a “parieto-motor” subnetwork that consists of states that show high activity in right postcentral, left precentral, left parietal superior, and white matter areas. The engagement of the two sub-networks is consistent with the cognitive and motor aspects of the PCET task. The area labeled as white matter may consist of axonal fibers connecting these regions and possibly from subcortical areas, which may explain the engagement of the parieto-motor subnetwork.

We also characterized the difference between the energy landscapes of the control and AOS groups in terms of basin areas using the separate groupwise models. The basin is defined by all states with energies that fall below a chosen threshold, also called a basin boundary. To perform the comparison, we used the cumulative distribution function (CDF) for energies of states in each group as shown in Figure 6C (controls in blue and AOS in red). An example threshold of −1.2 is shown as green rectangle and the inset shows the calculation of the area under the CDF curve (AUC) up to this threshold for both the groups. The AUC for each group quantifies the fraction of states that lie in the basin (i.e., below that threshold), the higher the basin area, the higher the density of states with energy levels lower than the threshold.

We hypothesized that the healthy controls have larger AUCs, and hence a greater fraction of states within basins, than the AOS group. We compared the two groups by calculating the % difference between the AUCs of control and AOS. However, the difference between the basin areas depends on the choice of threshold or the basin boundary. Hence, we compared the basin areas for healthy vs AOS patients for 45 thresholds between the range (−1.7, 0.1) as shown in Figure 6D. For a threshold of −1.2, the basin area for control group was 32.94% higher than basin areas for the AOS patients (shown as the green point on the curve). It can also be observed that the basin area for the control group is greater than for the AOS group for all choices of thresholds > −0.35 (Figure 6D) suggesting that although the comparison of basin areas is dependent on the choice of threshold to define a basin, it is extremely robust to this choice. This result aligns with our previous analysis showing that controls experienced more states in lower energy bins compared to AOS patients.

3.6. Deeper and wider fronto-temporal basins in controls, but not in AOS, correlated with higher cognitive scores

When we limited the analysis of energy values to just the fronto-temporal states (Figure 7A), we observed a significant negative correlation between the energy values and PCET scores among controls (ρ=—0.3, p=0.0015), suggesting that activation of low-energy fronto-temporal states was associated with better cognitive performance among controls. In the AOS group, this relationship was not significant (ρ=— 0.22, p=0.14). However, when the basin area for the AOS group was compared with controls (Figure 7B), the former showed a reduction in basin area for all values of threshold (Figure 7C). An example choice of threshold, = −1.2, also marked as green rectangle in Figure 9B and green point in Figure 7C, AOS subjects showed a 30.84% reduction in the basin areas for the frontal states as compared to the controls.

Figure 7:

Lower energy of frontal states correlates significantly with higher cognitive score in controls but not in AOS. A) The average energy in frontal states for every subject (control or AOS) was calculated and plotted against the subject’s PCET scores. Controls show a significant negative correlation between the frontal energy values and PCET scores (ρ = - 0.3, p = 0.0015), but this relation did not hold for AOS patients (ρ = − 0.22, p = 0.143). B) The cumulative distribution function of energy for just the fronto-temporal networks for controls and AOS groups. The basin area was calculated as area under the curve (AUC) for a particular choice of threshold, example −1.2, marked as green rectangle and shown in the inset. C) The AUC for controls and AOS was compared for different choices of threshold from (− 1.7, 0.1). For a threshold of −1.2, the basin area for controls was 30.8% higher than the basin area for AOS (marked as green point). However, for all values of thresholds, the fronto-temporal basin area for controls was higher than AOS group.

We further show the cumulative distribution functions (CDF) of the top 10% and the bottom 10% of performers in both groups (Supplemental Figure 8). The CDFs show a clear bias towards lower energies for the top 10% of performers among controls, which differs significantly from the bottom 10% of performers in the control group (KS test, 0.22, p=0.007). The CDFs in the AOS group also featured lower energies for top than bottom performers, but this difference showed a trend toward significance (KS test, 0.24, p=0.06).

3.7. Shallower and high energy basins in AOS correspond to more variable single trial trajectories

We further examined individual trial level trajectories for AOS and healthy controls hypothesizing that deeper basins represent stability in neural dynamics; that is, if similar states are frequently and reliably visited, this should be reflected as lower variability in the single trial trajectories. Consequently, shallower basins representing more unstable neural dynamics should correspond to high variability in the single trial trajectories.

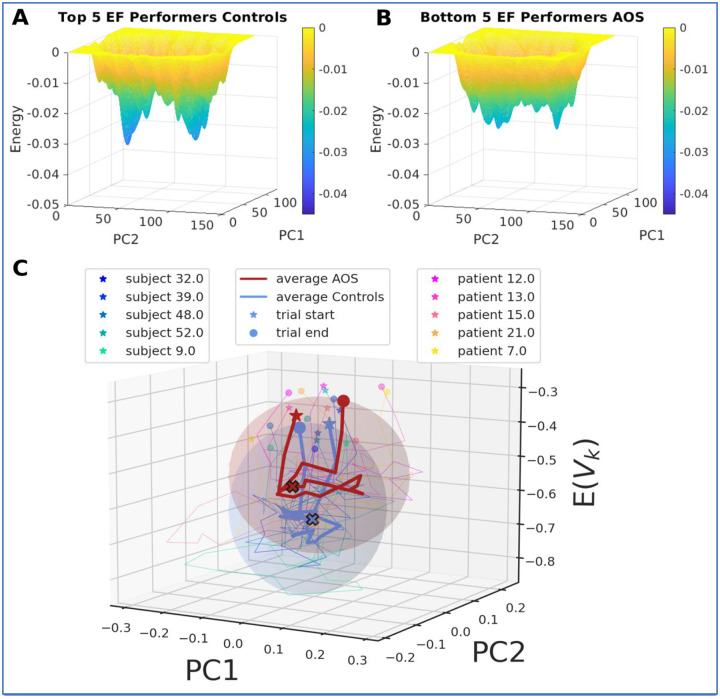
In order to achieve the highest contrast between the groups, we selected the top 5 performers from the control group and the bottom 5 performers among AOS on the PCET task. The states for these selected subjects were projected onto the PC dimensions and smoothed to derive their energy landscapes (Figure 8 A, B). We observed that the top 5 performers among controls showed deep and low energy basins whereas the bottom 5 performers among AOS showed shallow energy basins.

Figure 8:

Average single trial trajectories for AOS have more variance compared to Controls: Energy landscapes for top 5 executive function performers in the PCET task for control group (A) and the poorest 5 performers from the AOS group (B). The energy landscape for controls shows deeper basins with lower energy levels compared to AOS. AOS shows shallower basins and higher energy levels. C) Individual average control trajectories are shown in cooler colors and thin lines (blue to green) and individual AOS trajectories are shown in warmer colors (pink to yellow). The star (*) represents the start of the trial and the circle marks the end of a trial. The average trajectory over all 5 individuals for both groups are shown as thick blue lines for controls and as red lines for AOS. The filled X represent the stimulus onset during the trial. The ellipsoid encompasses the average standard deviation across all 5 controls or AOS subject trajectories in X (PC1), Y(PC2) and Z (energy) axes. A higher radius of the ellipsoid along X and Y axis as seen for AOS suggests higher spread for AOS trajectories over PC1 and PC2.

The average trial trajectory for every subject consisting of 24 timepoints was averaged over 6 such blocks that a subject visited. These individual trajectories for 5 control and 5 AOS subjects are shown as thin lines in cool and warm colors respectively (Figure 8 A, B).

As can be observed, the trial onsets always corresponded to high energy levels, which switched to lowest energy levels at stimulus onset. At the end of the trials, the dynamics return to high energy levels. Although there is a clear switch back to higher energy levels well before the trial end, we could not mark this precisely, because the stimulus stayed on all through the trial and different subjects may mentally deem the trial to finish at different times.

The AOS trial trajectories traverse higher energy levels as compared to controls as expected from their respective energy landscapes. The AOS trial trajectories also show more variability as depicted by the ellipsoid that encompasses the average standard deviation of the spread of trajectories in X (PC1) and Y (PC2) space.

4. Discussion

In this study, we applied for the first time a MEM model to understand the characteristics of energy, an integrated measure of regional activation and coactivation, among AOS and healthy subjects and its relationship to executive function performance and psychopathology. AOS patients experienced more high energy states compared to healthy controls suggesting a relatively less stable activation-coactivation pattern among AOS. In the context of significantly impaired performance on PCET by the AOS compared to controls, we show that the average energy values across the activation time series for each subject correlate with that subject’s PCET accuracy (Figure 4). This was observed in the data from the combined sample of AOS and healthy controls as well as at the individual group levels. The relationship showed that the healthy subjects achieved lower energy states more often than AOS and lower energy values correlated with better executive function (Figure 6), suggesting that a less stable or more variable activation-coactivation pattern may have been unfavorable for optimum executive function performance among AOS compared to controls. For example, low energy states occurring with higher probability may represent more stable neural dynamics favoring better cognitive functioning. In addition, energy positively correlated with severity of psychopathology suggesting that unstable neural dynamics also contributes to more severe symptoms. Greater severity of psychopathology correlated negatively with performance on PCET. Thus, the observed relationship among the energy, executive function performance and severity of psychopathology suggest that high energy states indicative of unstable neural dynamics may be pathophysiologically significant. Further, the PCs of the energy landscape corresponded to the fronto-temporal and parieto-motor networks, where activation of the fronto-temporal network but not the parieto-motor network correlated with executive function performance, highlighting that critical networks underlying cognitive functions can be identified using MEM. The engagement of these two sub-networks is consistent with the cognitive and motor aspects of the PCET task. The area labeled as white matter may consist of axonal fibers connecting these regions and possibly from subcortical areas, which may explain the engagement of the parieto-motor subnetwork. Overall, our findings suggest that the application of MEM to examine functional brain network configuration is a useful strategy especially since improvement in cognitive and social functions following certain treatments can be tracked using longitudinal functional imaging (Keshavan, Eack, Prasad, Haller, & Cho, 2017).

The predominance of high energy states in schizophrenia compared to controls was recapitulated in a transdiagnostic sample of adults with schizophrenia/schizoaffective disorder, bipolar disorder, major depression, and matched healthy controls when we applied the MEM model to the default mode network (DMN) from resting fMRI data. In addition, we observed diagnostically distinct energy state distributions compared to healthy controls in both the unilateral and bilateral DMN system but persons with major depression did not differ significantly compared to controls. More specifically, the schizophrenia group showed higher energy states while the bipolar disorder group showed significantly lower energy states in both unilateral and bilateral DMN compared to controls while persons with major depression showed higher energy in the right DMN only compared to controls. These findings support that high energy states may be associated with schizophrenia even among adults and resting state and may be a distinct marker of schizophrenia (Theis et al., 2024). Replication of these findings can enhance our understanding of the dynamically changing neurobiology during cognitive processing.

The utility of the MEM and associated energy is further supported by our finding that first-order activations showed only nominal correlations that did not survive multiple test corrections (Figure 3) and only a few edge weights showed significant correlation after correction for multiple tests with executive function performance (Supplemental figure 5). These observations highlight the limitations of regional activation differences and coactivation between node pairs in explaining higher level behaviors such as cognitive performance emphasizing the need for a more comprehensive mathematical model that combines first and second-order properties of the data. Moreover, there are limitations to examining functional connectivity alone despite its strengths, e.g., functional connectivity implicitly assumes that the pairwise correlations are independent of each other and identifies two regions as ‘connected’ when they show correlation of BOLD signals even without direct axonal connection or when the two regions receive input from a common afferent (Adachi et al., 2012; Zuo et al., 2012). MEM, however, is a conceptually different approach to infer second-order statistics that relies on pairwise correlation of nodes with an important assumption that the node pairs showing correlations are independent. Our results confirm that MEM model-derived energy values account for a larger variance of performance and that this energy model may be a useful tool for characterizing the putative mechanisms underlying differences in cognition between diagnostic groups since it can be linked with higher level behavior. Since lower energy values occur with higher probability and arise more frequently in controls with better cognitive performance, our analysis suggests that cognitive impairments among AOS may be associated with sub-optimal brain activation-coactivation patterns.

While the average energy across the fMRI activation states attained for an individual correlated with their PCET score, and the PCET scores significantly differed between the clinical groups, the average energy levels over the entire time series for each subject did not differ between the clinical groups (Figure 4). Nonetheless, within a common energy landscape derived jointly for the two groups, clustering states into bins according to their MEM energy suggests that the control group attains more low energy states, and the AOS group spends more time in high energy states (Figure 5A). When energy was plotted over the entire length of fMRI data acquisition during task performance for each subject, we observed that during task blocks, members of the AOS group were more likely to reach high energy states than were control group members (Figure 5B). These findings suggest that although the total energy may not be different between the groups, the time course of energy during task performance may be more important. It is possible that the more frequent occurrence of low energy states in individuals with better cognitive performance corresponds to the recognition of a common element across task blocks or reliance on a single successful strategy possibly using evidence accumulation or other processes, whereas the association of higher energy states with poorer performance could correspond to subjects treating each task block as more of a novel challenge and failing to return to and exploit previously successful strategies. When they “solve” the task, they then fall back into a lower, more probable, and more stable state. The more effort a subject put into “solving” the cognitive task, the higher the energy of the activation-coactivation pattern involved. Visiting such states may also relate to making incorrect responses; indeed, such higher energy bins may represent a range of different incorrect strategies or may not represent strategies to solve the cognitive task, but instead reflect a lack of coherent, focused engagement of the task, while the lower energy bins may represent convergent correct strategies, although a caveat of these ideas is that neuronal computation does not happen at the level of BOLD signals.

During the course of the task, all subjects showed two primary energy minima and attraction basins (Figure 6A). PCA shows that these basins corresponded to activation of two distinct sub-networks (Figure 6B), namely the fronto-temporal and parieto-motor, which may correspond to cognitive and motor aspects of this task. The lower the average energy was in the fronto-temporal states, the better the cognitive performance among controls (Figure 7). However, this relationship is lost among AOS, suggesting dysfunction of the fronto-temporal network. A shallowness of basins among AOS, especially in the fronto-temporal network may support longstanding observation of hypofrontality using fMRI (Callicott et al., 2003; Carter et al., 1998; Glahn et al., 2005), EEG (Mientus et al., 2002) and PET (Buchsbaum & Wu, 1987; Weinberger, Berman, & Zec, 1986) studies. Prior studies supporting hypofrontality relied mainly on first order regional activation differences consisting of decreased activation in the prefrontal regions. Our data extend the finding of hypofrontality to represent brain energy states that include both the first-order activation and second order coactivation suggesting that hypofrontality includes higher occurrence of unstable high energy states that would correspond to critical prefrontal regions inefficiently participating in executive function processing. This is supported by loss of correlation between basin size of fronto-temporal network and executive function performance in AOS, unlike what is observed in controls, suggesting that the higher occurrence of high energy states of the fronto-temporal network may lead to a loss of the functional link between executive function and fronto-temporal network activation.

The left precentral and right postcentral, both sensory-motor areas, were also represented in the model. A region labeled as white matter, which is located near the left anterior cingulate, was also included in the model although these three regions may have less direct neurocognitive relevance because the region selection step was entirely data driven. Further, subjects respond to the task prompts using a clickable scroll wheel, which justifies inclusion of sensory-motor regions; not engaging the precentral gyrus for instance means not submitting prompt responses and thus doing poorly. Regarding the white matter region, recent studies show that the vascularization of white matter (Smirnov et al., 2021) is relevant for task-related BOLD fMRI analysis (Li, Newton, Anderson, Ding, & Gore, 2019), given the known role of glia in modulating neuronal signaling (Fields, Woo, & Basser, 2015). Further, in a prior study we reported that specific white matter tracts connecting some of these regions showed impaired integrity (Prasad, Upton, Schirda, Nimgaonkar, & Keshavan, 2015).

The shallower basins suggest an increase in instability of underlying neural dynamics, i.e. not invoking or visiting the same state reliably, thereby resulting in reduced probability and increased energy levels associated with the state. We hypothesized that the shallower basins would result in more variable single trial trajectories during the task. We indeed found that AOS patients (5 worst performing) not only showed shallow basins (Figure 8B) as compared to controls (Figure 8A) but also higher variability in average trajectories for a single trial (Figure 8C).

The association of energy with severity of psychopathology is intriguing but clinically important. Our study shows that high energy states are correlated not only with impairments in executive functions but also with greater severity of psychopathology. Prior studies have shown that executive function deficits correlated with psychotic symptoms although more strongly with negative and disorganization symptoms than positive symptoms (Dibben, Rice, Laws, & McKenna, 2009; Dominguez Mde, Viechtbauer, Simons, van Os, & Krabbendam, 2009) and are also a major determinant of long-term outcome (Fett et al., 2011; Green, 1996). Our data showed nominally significant correlations of energy with disorganization and negative symptom total scores that did not survive multiple test corrections. More research is needed to further elucidate precise mechanisms that link higher energy states with greater severity of psychopathology and executive function impairments with larger sample sizes.

The results of our study suggest that impaired PCET performance in AOS individuals is related to potentially unfavorable neural dynamics in the fronto-temporal subnetwork consisting of the left olfactory, frontal superior medial, right temporal superior, and frontal superior orbital regions. This is a first-order statistical finding in principle, but due to the nature of multiple comparisons it is difficult to have confidence in these first-order associations. A second-order finding would contextualize the task-associated regions in a network, usually a covariance network where correlations of time series indicate connection strength, but that could lack temporal specificity if dynamic component is not incorporated. Comparing the strength and smoothness of the correlations in the first-order statistical mappings (Figure 3B) to the relationship of the same cognitive variable (PCET score) and the integrated first-and-second-order energy term (Figure 4) indicates the improvement associated with modeling regional coactivation along with individual regional activity using the Ising model. The MEM also reveals that this network has many unequal activation configurations that exist in an energy spectrum where a wide swath of more probable lower energy states is associated with better task performance.

Future research is needed to study full-brain MEMs, for instance using the 360-cortical node Glasser atlas (Glasser et al., 2016) and focus on elucidating trajectories of brain states (Transtrum & Qiu, 2016) through an “energy landscape” where basins represent higher probability states that correspond to attractors for the dynamics of neural activity. Our analysis of state frequency by group did not point to any specific states that occur in one group statistically more frequently than in the other group after FDR correction (Supplemental Figure 8). With more data, a future step would be to consider subject-level trajectories on the energy landscape defined by the sequence of activation states each subject exhibits during data collection, with possible clustering of trajectories to identify distinct phases and strategies of task performance.

Funding Statement

Funding was provided by NIMH grant numbers: R01MH115026 and R01MH112584 (KMP).

Data availability

The data is available through NIMH data repository.