Development of machine learning algorithm for assessment of heat transfer of ternary hybrid nanofluid flow towards three different geometries: Case of artificial neural network

Abstract

The focus of this paper revolves around the examination of flow of ternary hybrid nanofluid, specifically the Al₂O₃–Cu-CNT/water mixture, with buoyancy effect, across three distinct geometries: a wedge, a flat plate, and a cone. The study takes into account the presence of quadratic thermal radiation and heat source/sink of non-uniform nature. To develop the model, the Cattaneo–Christov theory is utilized. The equations governing the flow are solved by applying similarity transformations and employing the "bvp4c function in MATLAB” for numerical analysis and solution. Conventional methods for conducting parametric studies often face challenges in producing significant conclusions owing to the inherent complex form of the model and the method involved. To address the aforementioned issue, this paper explores the potential of machine learning methods to foresee the conduct of the flow characterized by multiple interconnected parameters. By utilizing simulated data, an artificial neural network is trained using the Levenberg-Marquardt algorithm to learn and comprehend the underlying patterns. Subsequently, the trained neural network is employed to estimate the Nusselt number on the surfaces of all three geometries. This approach offers a promising alternative to traditional parametric studies, enabling more precise predictions and insights into the behavior of complex systems. The Nusselt number is highest for THNF flow over the cone. The mean squared error (MSE) values for the ANN algorithm, across all analyzed cases, range from 0 to 0.03972. The findings contribute to an improved understanding of the characteristics and dynamics of ternary hybrid nanofluid flow in various geometries, assisting in the design and optimization of heat transfer systems involving such fluids.

1. Introduction

Ternary hybrid nanofluids (THNFs) have emerged as a promising class of advanced heat transfer (HT) fluids that offer enhanced thermal conductivity and improved HT performance compared to traditional HT fluids. These nanofluids (NFs) are composed of a base fluid, nanoparticles (NPs), and additional additives or surfactants, creating a unique three-component system. By merging different types of NPs and additives, THNFs can be tailored to specific applications to achieve superior thermal properties. The incorporation of NPs into a working fluid considerably enhances the conduction of the NFs. Awwad et al. [1] evaluated the HT property of Al₂O₃/water NF along a vertical plane wall with the help of neural networks. NPs such as metal oxides, carbon-based materials, or hybrid particles, possess a high surface area-to-volume ratio, which facilitates a competent HT rate (Sahoo [2]). Nasir et al. [3] probed the HT rate of water based hybrid NF flow with GO and MoS₂ NPs towards a revolving sphere near a stagnation point. Gul et al. [4] explored the HT characteristics of NF flow with Cu and Al₂O₃ NPs in water in a porous chamber with magnetic field presence. Nasir et al. [5] considered the entropy generation of a Maxwell type hybrid NF flow with multi and single-walled carbon nanotubes over a stretching surface. Moreover, the use of additives or surfactants helps to stabilize the NPs in the fluid, preventing their agglomeration and sedimentation. The superior nature of these NFs provides an additional dimension to their thermal properties. The choice of NPs and additives can be optimized to synergistically enhance the overall thermal conductivity and HT characteristics (Adun et al. [6]). The combination of multiple NPs and additives can lead to unique and advantageous properties that cannot be achieved with hybrid or mono NFs [7]. THNFs have many applications in industries and they are been explored for their potential use in microelectronic cooling structures, solar thermal collectors, heat exchangers, automotive radiators, and many other HT applications (Xuan et al. [8]). The improved thermal properties of these NFs can enhance the overall energy efficiency and performance of these systems, leading to substantial energy savings and improved system reliability [[9], [10], [11]].

Sahoo and Kumar [12], and Sahoo [2,13] conducted a series of experiments on THNF and established mathematical relationships for the different thermophysical properties. The correlations they introduced yielded highly accurate results, which were further verified against experimental data. Bilal et al. [14] explicated the influence of chemical reaction on the THNF flow with titanium dioxide, aluminium oxide, and silicon dioxide NPs suspended in an amalgamation of glycol and water. Elnaqeeb et al. [15] explicated on the THNF flow inside a rectangular-shaped closed domain and studied the implication of suction and stretching with NPs of different densities and shapes. Rauf et al. [16] surveyed the Hall current influence on the flow of micropolar and non-Newtonian THNF between two parallel surfaces. Kumar et al. [17] explicated the significance of the magnetic field on the HT rate of unsteady THNF flow and the influence of magnetic dipole is also investigated. Nasir et al. [18] expounded on the magnetic dipole and non-linear radiation effect on the THNF flow towards a stretching sheet with NPs of different densities and shapes. Adnan and Ashraf [19] studied the influence of a magnetic field together with convective heating on a THNF flow and they presented a comparison of THNF and hybrid NF flow. Singh et al. [20] inspected a THNF flow over a rotating disk with the Cattaneo-Christov model and quadratic thermal radiation. Alnahdi et al. [21,22] studied the flow of blood based THNF using the Casson model inside a divergent or convergent channel and a perforated capillary, respectively. Nasir et al. [23,24] probed the influence of radiation on the THNF flow with titanium dioxide, aluminium oxide, and silicon dioxide NPs suspended in water over stretching surface. Additional research on the topic of THNF flow are cited in the reference list (see Refs. [25,26]).

The wide range of applications for NF and THNF flow over a wedge, flat plate, and cone highlights its significance. These applications encompass various fields such as solar power collectors, spacecraft design, steam generators, fiber technology, and nuclear waste retention vessel design. Zainal et al. [27] investigated a hybrid NF flow towards a flat plate with convection and magnetic field effect. Alzahrani et al. [28] explicated on the impression of solar radiation on hybrid NF flow towards a flat plate. Khan et al. [29] explicated the effect of buoyancy force on a hybrid NF flow over a stretching plate. Hanif et al. [30] considered the HT rate and analyzed the entropy expansion of a hybrid NF flow over a vertical cone. Tlili et al. [31] surveyed the impression of radiation on the engine oil-TC4/NiCr NF flow over a cone rotating around its axis. Bég et al. [32] delved the influence of Navier slip and Stefan blowing on a laminar and steady flow of boundary layer flow past a cone. Yaseen et al. [33] studied the impression of TiO₂ NPs aggregation effect on the HT rate of the Ethylene glycol based NF flow towards a wedge with suction and radiation effect. Mishra and Kumar [34] probed the effect of self-heating on an NF flow towards a wedge in a porous medium. Khan et al. [35] probed the impression of magnetic field and heat flux present with time lag on a Sutterby NF flow over a wedge. Many authors have comparatively analyzed the NF or hybrid NF flow over two or more geometries among a flat plate, a cone, or a wedge. Garia et al. [36] probed the impact of radiation and convection on the water based hybrid NF flow towards a cone and a wedge. They made an observation that the heat source produces contrasting results on the distribution of temperature across the two geometries. Sandeep and Reddy [37] studied the outcome of radiation and magnetic field effect on the Cu-water NF flow towards a wedge and a cone. Jayachandra et al. [38] studied the influence of generalized heat flux and free convection on a NF flow towards a flat plate, a cone and a wedge. Reddy et al. [39] examined how a non-uniform heat sink and source impact the Oldroyd-B NF flow towards a cone or a wedge.

Furthermore, until now very few studies presented the investigations of THNF flow over two or more geometries among a flat plate, a cone, or a wedge. Bilal et al. [40] investigated the THNF flow with MgO, CoFe₂O₄, and TiO₂ NPs dispersed in the water towards a flat plate, a cone, and a wedge. They investigated the flow with the activation energy effect in a Darcy–Forchheimer porous medium. Yaseen et al. [41] explicated the THNF flow with Al₂O₃, Cu, and CNT NPs dispersed in the water towards a flat plate, a cone, and a wedge with linear radiation, and heat source/sink effect. Additionally, they explored the influence of gyrotactic microorganisms on the bioconvective effect. Ramzan et al. [42] investigated the THNF flow with CuO, Al₂O₃, and TiO₂ NPs dispersed in the water towards a cone and a wedge. They scrutinized the impact of the magnetic field, and radiation on the HT rate. An exhaustive assessment of the past studies has indicated that, thus far, no author(s) have published a paper investigating the analysis of the influence of quadratic thermal radiation and non-uniform heat source/sink on THNF flow towards three distinct geometries, namely a flat plate, a cone, and a wedge. This paper aims to present the impact of non-uniform heat source/sink and quadratic thermal radiation on THNF flow with Al₂O₃, Cu, and CNT NPs dispersed in the water towards a flat plate, a cone, and a wedge. The authors have used the aforementioned NPs because of their applications in many fields such as in dielectric materials, conductive materials, drug delivery, electronics, nanocomposites, coatings etc. Each type of nanoparticle bring distinct properties or enhancements to the nanofluid, resulting in a synergistic effect when combined. Moreover, the current research assesses the effectiveness of the soft computing method in forecasting the conduct of a problem that involves numerous interconnected parameters. Conventional methods for conducting parametric studies often face challenges in producing significant results due to the inherent complex form of the model and the techniques involved. To address the aforementioned issue, this paper explores the potential of machine learning methods to predict the performance of a flow model characterized by multiple interconnected parameters. The study focuses on identifying techniques that offer reasonably accurate predictions and employs numerical results to guide an artificial neural network (ANN). This training enables the ANN algorithm to accurately forecast the desired parameters within a broad range. Additionally, the ANN algorithm is applied to accurately determine the Nusselt number values on the surfaces of three different geometries. The results of the paper will be beneficial to fields that employ flow of NF over a plate, a cone, or a wedge such as in medicinal fields, architectural design systems, nuclear waste treatment, carriage processes, etc. The following points delineate the originality, goal, and main investigating points tackled within this research:

• •The mathematical flow model of THNF (Al₂O₃–Cu-CNT/water) is applied to a flat plate, a wedge, and a cone.
• •Investigating the implication of quadratic thermal radiation and non-uniform heat source/sink on THNF flow.
• •Analyze the HT rate of THNF flow across all geometries and identify the specific conditions or geometry in which THNF exhibits the highest heat transfer rate according to the current modeling.
• •The HT rate is compared across all three geometries.
• •Development of a machine learning (ANN) algorithm to predict the HT rate at the surface.

2. Flow model and governing equations

Consider the flow of Al₂O₃–Cu-CNT/water THNF towards a cone, a wedge, and a flat plate in the presence of buoyancy force. In Fig. 1, the visual representation demonstrates that the x-axis and y-axis are aligned in a horizontal and vertical manner relative to the surface. The semi cone angle, denoted by $\alpha$, refers to the angle formed between the side of the cone and its central axis. The cone radius, symbolized by $r$, represents the distance from the centre of the cone to its outer edge. To accurately capture the behavior of THNF, we consider the effects of time lag in HT rate using a model called the “Cattaneo-Christov model”. Also, a variable temperature $T_w=T_{\infty }+a{x}^s$ (“s” signifies the parameter that is associated with the surface temperature) is presumed on the surface. At a distance far away from the surface, the temperature is denoted as $T_{\infty }$, with the wall temperature being greater than the ambient temperature, i.e., $T_w>T_{\infty }$. The temperature gradient between the surface and the neighbouring THNF creates a buoyant force, which is further influenced by the force of gravity. Assuming that the pressure gradient is negligible, Table 1 provides a representation of physical characteristics of the NPs (including metals, metal oxides, and carbon nanotube) in a base fluid, as described in Refs. [43,44]. To evaluate the characteristics of flow and HT in THNF, various physical effects are considered, including non-uniform heat source/sink, quadratic thermal radiation, and suction/blowing effects. Incorporating the above-mentioned assumptions and discussions, the principal PDEs that describe the radiative flow of THNF towards a cone, a wedge, and a flat plate are listed below [[40], [41], [42]]:

Fig. 1.

Physical representation.

Table 1.

Thermo-physical properties of water, Al₂O₃, Cu and CNT nanoparticles [43,44].

	ρ(kg/m3)	Cp(J/KgK)	k(W/mK)	$\beta \left(K^{-1}\right)$	Shape	Sphericity
Water	997.1	4179	0.613	21
Al2O3	3970	765	40	0.85	Spherical	$\psi =1$
Cu	8933	385	401	1.67	Platelet	$\psi =0.612$
CNT	2600	425	6600	$1.6\times {10}^{-6}$	Cylindrical	$\psi =0.52$

Continuity Equation:

$$\frac{\partial \left(r^{n}u\right)}{\partial x}+\frac{\partial \left(r^{n}v\right)}{\partial y}=0$$ (1)

Due to the extremely small thickness of the thermal boundary layer, the radius is denoted by the value $r=x\mathit{sin}\left(\alpha \right)$ to reflect this characteristic.

Momentum Equation:

$$u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}={\nu }_{thnf}\left(\frac{{\partial }^{2}u}{\partial y^2}\right)+\frac{{\left(\rho \beta \right)}_{thnf}}{{\rho }_{thnf}}g\left(T-T_{\infty }\right)\cos \alpha$$ (2)

Energy Equation:

$$u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}+{\tau }_t\left[\begin{array}{l}{u}^2\frac{{\partial }^{2}T}{\partial x^2}+\left(u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}\right)\frac{\partial T}{\partial x}+\left(u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}\right)\frac{\partial T}{\partial y}\\ +2uv\frac{{\partial }^{2}T}{\partial x\partial y}+v^2\frac{{\partial }^{2}T}{\partial y^2}\end{array}\right]=\frac{k_{thnf}}{{\left(\rho C_p\right)}_{thnf}}\frac{{\partial }^{2}T}{\partial y^2}+\frac{1}{{\left(\rho C_p\right)}_{thnf}}Q**-\frac{1}{{\left(\rho C_p\right)}_{thnf}}\frac{\partial q_r}{\partial y}$$ (3)

As per the assumptions discussed earlier, the present model undergoes specific boundary conditions (BCs) that are implemented in the following manner [41,42]:

$$\begin{array}{l}u=u_w=\frac{{\nu }_{f}x}{l^2},v=v_w,T=T_w=T_{\infty }+a{x}^s\text{at}y=0\\ T\to T_{\infty },u\to 0\text{as}y\to \infty \end{array}\}$$ (4)

where, the symbols “$u$ and $v$ represent the constituent of velocity along $x$-axis and $y$-axis, respectively. In addition, $g$, $T$, $q_r$ indicate the gravitational acceleration, temperature, and radiative heat flux, respectively. In addition, $u_w$ and $v_w$ in BCs (Eqn. (4)) are the linear velocity of surface and mass transfer velocity, respectively”. Additionally, the term $Q**$ in Eqn. (3) accounts for the non-uniform heat source/sink effect and is specifically defined in the following manner [45]:

$$Q**=\frac{k_{thnf}{u}_w}{x{\nu }_{thnf}}\left(T_w-T_{\infty }\right)\left[A^{*}{e}^{-\eta }+B^{*}\theta \left(\eta \right)\right]$$ (5)

where in Eqn. (5), the $A^{*}$ specify the space decay coefficient and $B^{*}$ corresponds to temperature dependence. The positive values $A^{*}$ and $B^{*}$ signify heat source phenomena, whereas the negative values $A^{*}$ and $B^{*}$ signify the heat sink phenomena.

Also, the last term on RHS in Eqn. (3) i.e., $q_r$ represents the radiative thermal heat flux using the “Rosseland approximation [46]”. The precision of the Rosseland method becomes evident when analyzing the influence of radiation and it is delineated as [46]:

$$q_r=-\left(\frac{\partial T^4}{\partial y}\right)\left(\frac{4{\sigma }^{*}}{3k^{*}}\right)\text{,}$$ (6)

where in Eqn. (6), the absorption coefficient and Stefan-Boltzmann constant are represented by the symbols $k^{*}$ and ${\sigma }^{*}$, respectively. Following Taylor's expansion formula for $T^4$ about $T_{\infty }$, the radiative temperature is expressed in the subsequent form [46]:

$$T^4\approx T_{\infty }^4+\left(2!\right)T_{\infty }^3\left(T-T_{\infty }\right)+\left(3!\right)T_{\infty }^2{\left(T-T_{\infty }\right)}^2+...$$ (7)

Eqn. (7) is further simplified and the quadratic approximation expressed below is utilized when there is a high temperature difference, as this expression also has a significant impact on the HT [46]:

$$T^4\approx -8T_{\infty }^{3}T+6T_{\infty }^2{T}^2+3T_{\infty }^4$$ (8)

The value of T⁴ expressed in Eqn. (8) is used in Eqn. (6) for further simplification.

The following conditions serve to differentiate the THNF flow towards the cone, wedge, and flat plate [36,41]:

• (a)When $n=1$ and $\alpha \ne 0$, then flow towards a cone.
• (b)When $n=0$ and $\alpha \ne 0$, then flow towards a wedge.
• (c)When $n=0$ and $\alpha =0$, then flow towards a flat plate.

2.1. Correlation for thermophysical properties of ternary hybrid nanofluid

Following the papers of Arif et al. [43], Elnaqeeb et al. [15], and Yaseen et al. [41] the computations for density, heat capacitance, and thermal conductivity of THNF (Al₂O₃–Cu-CNT/water) are done using the following relations:

$$\begin{array}{l}{\rho }_{thnf}=\left(1-{\mathrm{\Phi }}_1-{\mathrm{\Phi }}_2-{\mathrm{\Phi }}_3\right){\rho }_{bf}+{\mathrm{\Phi }}_1{\rho }_{s{p}_1}+{\mathrm{\Phi }}_2{\rho }_{s{p}_2}+{\mathrm{\Phi }}_3{\rho }_{s{p}_3}\text{,}\\ {\left(\rho C_p\right)}_{thnf}=\left(1-{\mathrm{\Phi }}_1-{\mathrm{\Phi }}_2-{\mathrm{\Phi }}_3\right){\left(\rho C_p\right)}_{bf}+{\mathrm{\Phi }}_1{\left(\rho C_p\right)}_{s{p}_1}+{\mathrm{\Phi }}_2{\left(\rho C_p\right)}_{s{p}_2}+{\mathrm{\Phi }}_3{\left(\rho C_p\right)}_{s{p}_3}\end{array}\}$$ (9)

The effective dynamic viscosity of THNF is given by:

$${\mu }_{thnf}=\frac{{\mu }_{n{f}_1}{\mathrm{\Phi }}_1+{\mu }_{n{f}_2}{\mathrm{\Phi }}_2+{\mu }_{n{f}_3}{\mathrm{\Phi }}_3}{{\mathrm{\Phi }}_{thnf}}\text{,}$$ (10)

where, for NP-I (spherical-shaped NPs), NP-II (platelet-shaped NPs), and NP-III (cylindrical-shaped NPs), the viscosity is respectively are as follows:

$$\begin{array}{l}\frac{{\mu }_{n{f}_1}}{{\mu }_{bf}}=1+2.5{\mathrm{\Phi }}_1+6.2{{\mathrm{\Phi }}_1}^2\left(\text{nanoparticle}-\mathrm{I}\right)\text{,}\\ \frac{{\mu }_{n{f}_2}}{{\mu }_{bf}}=1+37.1{\mathrm{\Phi }}_2+612.6{{\mathrm{\Phi }}_2}^2\left(\text{nanoparticle}-\text{II}\right)\text{,}\\ \frac{{\mu }_{n{f}_3}}{{\mu }_{bf}}=1+13.5{\mathrm{\Phi }}_3+904.4{{\mathrm{\Phi }}_3}^2\left(\text{nanoparticle}-\text{III}\right)\end{array}\}$$ (11)

In this study, authors also incorporated the Modified Maxwell model to present the influence of differently shaped NPs on the thermal conductivity of the THNF:

$$\begin{array}{l}{k}_{thnf}=\frac{k_{n{f}_1}{\mathrm{\Phi }}_1+k_{n{f}_2}{\mathrm{\Phi }}_2+k_{n{f}_3}{\mathrm{\Phi }}_3}{{\mathrm{\Phi }}_{thnf}},\text{where}\\ \frac{k_{n{f}_i}}{k_{bf}}=\frac{k_i+\left(n-1\right)k_{bf}+\left(n-1\right){\mathrm{\Phi }}_i\left(k_i-k_{bf}\right)}{k_i+\left(n-1\right)k_{bf}-{\mathrm{\Phi }}_i\left(k_i-k_{bf}\right)},w\text{here}i=1,2,3\text{and}n=\left(\frac{3}{\psi }\right)\text{is}\text{shape}\text{factor}\end{array}$$ (12)

For NP-I (spherical-shaped NPs), NP-II (platelet-shaped NPs), and NP-III (cylindrical-shaped NPs), the thermal conductivity is respectively as follows:

$$\begin{array}{l}\frac{k_{n{f}_1}}{k_{bf}}=\frac{k_1+2k_{bf}+2{\mathrm{\Phi }}_1\left(k_1-k_{bf}\right)}{k_1+2k_{bf}-{\mathrm{\Phi }}_1\left(k_1-k_{bf}\right)}\left(\text{nanoparticle}-\mathrm{I}\right)\\ \frac{k_{n{f}_2}}{k_{bf}}=\frac{k_2+4.7k_{bf}+4.7{\mathrm{\Phi }}_2\left(k_2-k_{bf}\right)}{k_2+4.7k_{bf}-{\mathrm{\Phi }}_2\left(k_2-k_{bf}\right)}\left(\text{nanoparticle}-\text{II}\right)\\ \frac{k_{n{f}_3}}{k_{bf}}=\frac{k_3+3.9k_{bf}+3.9{\mathrm{\Phi }}_3\left(k_3-k_{bf}\right)}{k_3+3.9k_{bf}-{\mathrm{\Phi }}_3\left(k_3-k_{bf}\right)}\left(\text{nanoparticle}-\text{III}\right)\end{array}\}$$ (13)

In the aforementioned correlations (9–13), the symbol $\Phi \left(={\Phi }_1+{\Phi }_2+{\Phi }_3\right)$ denotes the NPs volume fraction (NVF). Also, NVF of Al₂O₃, Cu, and CNT NPs is denoted by ${\mathrm{\Phi }}_1$, ${\mathrm{\Phi }}_2$, and ${\mathrm{\Phi }}_3$. Furthermore, the following subscripts are used for: sp₁ —Al₂O₃, sp₂ — Cu, and sp₃ — CNT NPs. Additionally, there are other symbols representing important thermophysical properties, such as $\mu ,\rho ,\left(\rho C_P\right)$ and $k$ denote the dynamic viscosity, density, heat capacity, and thermal conductivity, respectively. These attributes are associated with ternary hybrid nanofluid, indicated as $thnf$, where $nf$ signifies “nanofluid”. Additionally, subscripts $bf$ and $sp$ represent “base fluid” and “solid NPs”, respectively.

2.2. Similarity transformations

The following suitable similarity variables are employed to the system of equations and BCs [[40], [41], [42]]:

$$\eta =\frac{y}{l},u=\frac{{\nu }_{f}x}{l^2}{f}^{\prime }\left(\eta \right),v=-\left(n+1\right){\nu }_f\frac{f\left(\eta \right)}{l},\theta \left(\eta \right)=\frac{T-T_{\infty }}{T_w-T_{\infty }}$$ (14)

Here, $\eta$ is the similarity variable. Also, it should be noted that $f\left(\eta \right)$ represents the dimensionless stream function, while $\theta \left(\eta \right)$ represents the temperature, respectively. The continuity Eqn. (1) is identically satisfied by utilizing Eqn. (14) in conjunction with Eqns. (9), (10), (11), (12), (13). Additionally, Eqns. (2), (3) along with the BCs (Eqn. (4)), are converted into non-dimensional ODEs. After completing the calculation, the following non-dimensional ODEs and BCs are derived:

$$f{\prime }^2-\left(n+1\right)f{f}^{″}=\frac{{∍}_1}{{∍}_2}{f}^{‴}+\frac{{∍}_3}{{∍}_2}\lambda \theta \cos \alpha$$ (15)

$$sf\text{'}\theta -\left(n+1\right)f\theta \text{'}+\gamma \left[\begin{array}{l}s\left(s-1\right)f{\prime }^2\theta +s\left(\theta f{\prime }^2-\left(n+1\right)\theta f{f}^{″}\right)+\left(n^2+2n+1\right)\theta \text{'}ff\text{'}\\ -2\left(n+1\right)sff\text{'}\theta \text{'}+{\left(n+1\right)}^2{f}^2{\theta }^{″}\end{array}\right]=\frac{1}{{∍}_4\mathit{Pr}}\left({∍}_5-\frac{8}{3}Rd\right){\theta }^{″}+\frac{{∍}_5{∍}_2}{{∍}_4{∍}_1\mathit{Pr}}\left[A^{*}{e}^{-\eta }+B^{*}\theta \right]+\frac{2Rd}{{∍}_4\mathit{Pr}\left({\theta }_r-1\right)}\left(\frac{{\partial }^2}{\partial {\eta }^2}{\left(1+\theta \left(\eta \right)\left({\theta }_r-1\right)\right)}^2\right)$$ (16)

$$\begin{array}{l}{f}^{\prime }\left(0\right)=1,f\left(0\right)=\frac{Su}{\left(n+1\right)},\theta \left(0\right)=1\text{at}\eta =0\\ f^{\prime }\left(\eta \right)\to 0,\theta \left(\eta \right)\to 0\text{as}\eta \to \infty \end{array}\}$$ (17)

in Eqns. (15), (16), (17), the dimensionless parameters are:

“$\mathit{Pr}\left(=\frac{{\left(\rho c_p\right)}_f{\nu }_f}{k_f}\right)$— Prandtl number, $\gamma =\left({\tau }_t\frac{{\nu }_f}{l^2}\right)$ — thermal relaxation parameter, $Su=\left(-\frac{v_{w}l}{v_f}\right)$ — suction/injection parameter, $Rd\left(=\frac{4{\sigma }^{*}{T}_{\infty }^3}{k_f{k}^{*}}\right)$ is thermal radiation parameter, ${\theta }_r\left(=\frac{T_w}{T_{\infty }}\right)$ is temperature ratio parameter, and $\lambda \left(=\frac{G{r}_x}{R{e_x}^2}=\frac{g{\beta }_f\left(T_w-T_{\infty }\right)l^4}{x{{\nu }_f}^2}=\frac{g{\beta }_{f}a{x}^{s-1}{l}^4}{{{\nu }_f}^2}\right)$ — natural convection parameter, where $G{r}_x\left(=\frac{g{\beta }_f\left(T_w-T_{\infty }\right)x^3}{{{\nu }_f}^2}\right)$— local Grashof number, $R{e}_x=\left(\frac{u_{w}x}{v_f}\right)$— local Reynolds number”. Furthermore, ${∍}_1=\frac{{\mu }_{thnf}}{{\mu }_f},{∍}_2=\frac{{\rho }_{thnf}}{{\rho }_f},{∍}_3=\frac{{\left(\rho \beta \right)}_{thnf}}{{\left(\rho \beta \right)}_f},{∍}_4=\frac{{\left(\rho C_p\right)}_{thnf}}{{\left(\rho C_p\right)}_f},{∍}_5=\frac{k_{thnf}}{k_f}$ are constants based on THNF correlations.

To find the similarity solution, the above-described parameters must be dimensionless, so to make $\lambda \left(=\frac{g{\beta }_{f}a{x}^{s-1}{l}^4}{{{\nu }_f}^2}\right)$ dimensionless, the value of parameter “s” is taken as one, i.e. $s=1$.

2.3. Parameter of engineering interest

The engineering parameter under investigation is the Nusselt number $N{u}_x$, having the following description [41]:

$$N{u}_x=\frac{x{q}_w}{k_f\left(T_w-T_{\infty }\right)}$$ (18)

where the expression for heat transfer flux, denoted as $q_w$, is formulated as follows:

$$q_w={-k_{hnf}{T}_y|}_{y=0}+{q_r|}_{y=0}$$ (19)

Using the similarity transformations (Eqn. (14)), and Eqns. (6), (8), (19) in Eqn. (18), the Nusselt number in its reduced form is expressed as:

$$N{u}_x^{*}=-\left({∍}_5+\left(4{\theta }_r-\frac{8}{3}\right)Rd\right){\theta }^{\prime }\left(0\right)$$ (20)

The significance of the Nusselt number (expressed in Eqn. (20)) is that it is used to study the HT rate.

3. Numerical methodology

The present segment examines the numerical methodology employed by the authors in obtaining the solution. By utilizing the "bvp4c function in MATLAB,” the authors successfully resolved the system of equations (Eqns. (15), (16), (17)). The details and functionality of the "bvp4c function” are provided by Shampine et al. [47]. The system of ODEs (Eqns. (15), (16)) with BCs (Eqn. (17)) is transformed into a set of first-order ODEs by implementing the following substitutions:

$$\epsilon \left(1\right)=f,\epsilon \left(2\right)=f^{\prime },\epsilon \left(3\right)=f^{″},\epsilon \left(4\right)=\theta ,\epsilon \left(5\right)={\theta }^{\prime }$$ (21)

The MATLAB code is written with help of Eqn. (21) and it is used for the calculations and obtaining the results is presented below:

$$\begin{array}{c}\epsilon \epsilon 1=\frac{{∍}_2}{{∍}_1}\left[f{\prime }^2-\left(n+1\right)f{f}^{″}-\frac{{∍}_3}{{∍}_2}\lambda \theta \mathit{cos}\alpha \right]\\ \epsilon \epsilon 2=\frac{sf\text{'}\theta -\left(n+1\right)f\theta \text{'}-\frac{{∍}_5{∍}_2}{{∍}_4{∍}_1\mathit{Pr}}\left[A^{*}{e}^{-\eta }+B^{*}\theta \right]-\frac{4Rd}{{∍}_4\mathit{Pr}}\left({\theta }_r-1\right)\theta {\prime }^2+\gamma \left[s\left(s-1\right)f{\prime }^2\theta +s\left(\theta f{\prime }^2-\left(n+1\right)\theta f{f}^{″}\right)+{\left(n+1\right)}^2\theta \text{'}ff\text{'}-2\left(n+1\right)sff\text{'}\theta \text{'}\right]}{\left[\frac{1}{{∍}_4\mathit{Pr}}\left({∍}_5-\frac{8}{3}Rd\right)-\gamma {\left(n+1\right)}^2{f}^2+\frac{4Rd}{{∍}_4\mathit{Pr}}\left(1+\theta \left({\theta }_r-1\right)\right)\right]}\end{array}$$ (22)

The BCs in MATLAB code are written as:

$$\begin{array}{l}\epsilon \left(2\right)=1,\epsilon \left(1\right)=\frac{Su}{\left(n+1\right)},\epsilon \left(4\right)=1\text{at}\eta =0\\ \epsilon \left(2\right)=0,\epsilon \left(4\right)=0\text{as}\eta \to \infty \end{array}\}$$ (23)

The described methodology is employed to determine the unknown slopes and solve Eqns. (22), (23) (see Fig. 2). In the computations, a step length of 0.01 is utilized. To validate the code utilized to derive results, a comparison is conducted with the outcomes of a previous study conducted by Vajravelu and Nayfeh [48] (refer to Table 2). The comparison outcomes exhibit a remarkable level of agreement, affirming the dependability of the current results.

Fig. 2.

Flowchart of numerical method.

Table 2.

Comparison of values of $f^{″}\left(0\right)\&-{\theta }^{\prime }\left(0\right)$ with results of Vajravelu and Nayfeh [48] for the flow over cone when R_d = 0, $\gamma =0$, Su = 0, $B^{*}=0$, ${\mathrm{\Phi }}_1={\mathrm{\Phi }}_2={\mathrm{\Phi }}_3=0$.

Q	Pr	Gr	M	s	$f^{″}\left(0\right)$ (See Ref. [48])	$f^{″}\left(0\right)$ [Present]	$-{\theta }^{\prime }\left(0\right)$ (See Ref. [48])	$-{\theta }^{\prime }\left(0\right)$ [Present]
−5	0.3	−0.5	1	−2.1	−0.155592	−0.15570252	−2.237475	−2.23538986
−5	0.3	−0.5	1	2.1	−0.156001	−0.15588966	−2.232780	−2.23418090
−5	0.3	−0.5	3	2.1	−0.126400	−0.12634921	−2.233732	−2.23472524
−5	1.0	0.5	3	2.1	0.125260	0.12541914	−2.245321	−2.24047000

4. Algorithm of artificial neural network

Artificial neural networks (ANNs) are computational prototypes inspired by biological neural networks. They consist of interconnected artificial neurons (Hassoun [49]). Lately, ANNs have gained popularity due to their ability to effectively model complex and nonlinear functions. The authors have devised a model based on an artificial neural network (ANN) to forecast the Nusselt number in the current flow model. One of the most efficient model is the multilayer perceptron (MLP) network. MLP networks are feedforward neural networks comprising of three layers: the input, hidden, and output layers (see Fig. 3). The input layer neurons collect data, and it is processed and transmitted to the hidden layer and in turn it further processes the information before sending it to the output layer. Every layer is completely interconnected, with each connection assigned specific weights (see Fig. 3). Activation functions are utilized in both the hidden and output layers to activate the neurons. Additional hidden layers can be added as necessary to tackle more complex tasks. The input signal X_i received by the jth neuron in the hidden layer is multiplied by the connection weight and summed together. The obtained sum is subsequently fed into an activation function to stimulate the neurons. The data is processed from the hidden to the output layer in the same pattern. The output of the jth neuron can be expressed as follows:

$$Y_j=f\left(\sum _{i=1}^n{W}_{ji}^n{X}_i+b_j^n\right)$$ (24)

where in Eqn. (24), the activation function is denoted as "f" and "W_ji” represents the weight of the connection from the preceding layer's ith neuron. The training process of the ANN focuses on reducing the errors amid the generated and desired output.

Fig. 3.

Schematic of the ANN model.

A range of activation functions, including logistic, hyperbolic, and exponential functions, can be utilized when represented by the variable "f ". The error propagation algorithm is commonly employed for training neural networks. This supervised learning process involves adjusting the weights between network layers. The learning error rate is determined by comparing the neural network outputs with the expected outputs from the training dataset. It is important to note that the performance of the MLP network is greatly influenced by its configuration. Typically, to minimize the error rate, the optimal network configuration is determined through iterative testing of different options. This process entails conducting experiments with different parameter values, including the choice of activation functions employed in both the hidden and output layers and the number of neurons in the hidden layer. The model's error value is calculated for different parameter values during these experiments. Fig. 4 presents the main structural configuration of the ANN model proposed in this paper. The ANN prediction model in this paper contains eight parameters in the input layer, and output layer contains one output parameter (Nusselt number). The quantity of neurons is a pivotal parameter for an ANN model to work effectively. There is no universally agreed-upon method for determining the precise number of neurons to use in ANNs (Shafiq et al. [50]). As a result, during the design phase of both multilayer perceptron (MLP) networks, different models with varying numbers of neurons have been experimented with and their predictive performance has been evaluated. Based on the data obtained from the analysis, the optimal quantity of neurons that yields the precise prediction act has been identified. The authors have taken the quantity of neurons in the hidden layer same as input parameters. The other particular details of the ANN model developed for this study are provided in the next section.

Fig. 4.

The main structure of the developed ANN model for prediction of Nusselt number.

5. Results and discussion

This segment analyzes the influence of various physical parameters of THNF on the flow and HT characteristics. Our emphasis lies in analyzing the performance of the THNF under different conditions. The numerical procedure, named as bvp4c solver, is employed to tackle the non-linear ODEs. In this model, we investigate the impact of multiple flow parameters over predefined ranges: $0.3\le \lambda \le 2.3$, $0.02\le \mathrm{\Phi }\le 0.04$, $6\le Rd\le 14$, $0.1\le \gamma \le 1.5$, $-1.5\le A^{*}\le -0.7$, $-1.7\le B^{*}\le -0.9$, and $0.1\le Su\le 0.7$. Any alterations made to the fixed parameter values are accompanied by corresponding graphs or tables to demonstrate the resulting variations. Table 3, Table 4, Table 5, Table 6, Table 7 display data regarding the variation of the Nusselt number in response to a range of numerical values of significant physical factors. Fig. 5, Fig. 6, Fig. 7, Fig. 8, Fig. 9, Fig. 10, Fig. 11, Fig. 12, Fig. 13, Fig. 14, Fig. 15, Fig. 16, Fig. 17, Fig. 18 present visual representations that illustrate the effect of various parameters on $f^{\prime }\left(\eta \right)$ and $\theta \left(\eta \right)$, which represent the velocity and thermal profiles, respectively, in different flow conditions. These figures showcase the outcomes and demonstrate how changes in these parameters affect the velocity and temperature. The parameters are initially set to their default values: Pr = 6.2, $\gamma =1.5\text{,}$ A*=-1.5, B*=-1.7, Su = 0.1, $\lambda =1.3$, Rd = 6, and $\mathrm{\Phi }=0.04$.

Table 3.

Numerical values of Nusselt number (rest parameters Pr = 6.2, $\gamma =1.5\text{,}$A*=-1.5, B*=-1.7, Su = 0.1, $\lambda =1.3$).

	Rd	Numerical Result			ANN Prediction
		Cone	Wedge	Plate	Cone	Wedge	Plate
$\text{Training}\text{Data}\{$	6.0	18.51411	18.24206	18.25881	18.73245	18.56103	18.68625
	6.6	19.25598	18.98009	18.99861	19.35620	19.16681	19.27800
	7.2	19.97007	19.69058	19.71088	19.97996	19.77259	19.86976
	7.8	20.65915	20.37630	20.39838	20.60371	20.37837	20.46151
	8.4	21.32562	21.03959	21.06345	21.22746	20.98414	21.05326
	9.0	21.97149	21.68247	21.70812	21.85122	21.58991	21.64500
	9.6	22.59852	22.30667	22.33410	22.47497	22.19569	22.23676
	10.2	23.20824	22.91370	22.94291	23.09872	22.80147	22.82851
	10.8	23.80199	23.50488	23.53586	23.72247	23.40724	23.42026
	11.4	24.38092	24.08138	24.11413	24.34623	24.01302	24.01201
	12.0	24.94609	24.64422	24.67873	24.96998	24.61880	24.60376
	12.6	25.49842	25.19431	25.23058	25.59373	25.22457	25.19552
Testing Data	13.2	26.03874	25.73248	25.77050	26.21749	25.83035	25.78726
	13.8	26.56778	26.25946	26.29923	26.84124	26.43613	26.37901
Validation Data	14.4	27.08622	26.77591	26.81743	27.46499	27.04190	26.97076
	15.0	27.59466	27.28245	27.32570	27.08875	27.64768	27.56251
				MSE	0.03972	0.02754	0.02710

Table 4.

Numerical values of Nusselt number (rest parameters Pr = 6.2, Rd = 6, A*=-1.5, B*=-1.7, Su = 0.1, $\lambda =1.3$).

	$\gamma$	Numerical Result			ANN Prediction
		Cone	Wedge	Plate	Cone	Wedge	Plate
$\text{Training}\text{Data}\{$	0.1	17.81906	17.73235	17.73756	17.84711	17.81785	17.73750
	0.2	17.86799	17.76869	17.77475	17.89237	17.86738	17.77472
	0.3	17.91703	17.80504	17.81196	17.93762	17.91692	17.81195
	0.4	17.96618	17.84140	17.84916	17.98288	17.96645	17.84918
	0.5	18.01543	17.87777	17.88637	18.02813	18.01598	17.88640
	0.6	18.06479	17.91415	17.92359	18.07339	18.06551	17.92363
	0.7	18.11426	17.95055	17.96082	18.11864	18.11504	17.96086
	0.8	18.16384	17.98695	17.99804	18.16390	18.16457	17.99808
	0.9	18.21354	18.02336	18.03528	18.20916	18.21410	18.03531
	1.0	18.26334	18.05978	18.07252	18.25441	18.26363	18.07253
	1.1	18.31326	18.09622	18.10976	18.29967	18.31316	18.10976
	1.2	18.36330	18.13266	18.14702	18.34492	18.36269	18.14699
Testing Data	1.3	18.41345	18.16912	18.18427	18.39018	18.41222	18.18421
	1.4	18.46372	18.20559	18.22154	18.43543	18.46175	18.22144
Validation Data	1.5	18.51411	18.24206	18.25881	18.48069	18.51128	18.25866
	1.6	18.56463	18.27855	18.29608	18.52595	18.56081	18.29589
				MSE	0.00043	0.03754	0.00000

Table 5.

Numerical values of Nusselt number (rest parameters Pr = 6.2, $\gamma =1.5\text{,}$Rd = 6, Su = 0.1, $\lambda =1.3$).

	A*	B*	Numerical Result			ANN Prediction
			Cone	Wedge	Plate	Cone	Wedge	Plate
$\text{Training}\text{Data}\{$	−1.5	−1.7	18.51411	18.24206	18.25881	18.54100	18.27111	18.26134
	−1.46	−1.66	18.31652	18.04260	18.05977	18.32990	18.05757	18.05247
	−1.42	−1.62	18.11668	17.84084	17.85847	18.11878	17.84403	17.84360
	−1.38	−1.58	17.91453	17.63671	17.65481	17.90768	17.63049	17.63473
	−1.34	−1.54	17.70998	17.43013	17.44872	17.69656	17.41695	17.42585
	−1.3	−1.5	17.50293	17.22100	17.24011	17.48545	17.20341	17.21698
	−1.26	−1.46	17.29331	17.00922	17.02888	17.27434	16.98987	17.00811
	−1.22	−1.42	17.08099	16.79469	16.81493	17.06323	16.77633	16.79924
	−1.18	−1.38	16.86589	16.57730	16.59815	16.85212	16.56278	16.59037
	−1.14	−1.34	16.64788	16.35693	16.37843	16.64101	16.34924	16.38150
	−1.1	−1.3	16.42684	16.13346	16.15564	16.42990	16.13570	16.17263
	−1.06	−1.26	16.20265	15.90675	15.92965	16.21879	15.92216	15.96376
Testing Data	−1.02	−1.22	15.97515	15.67665	15.70031	16.00768	15.70862	15.75489
	−0.98	−1.18	15.74420	15.44300	15.46748	15.79657	15.49508	15.54602
Validation Data	−0.94	−1.14	15.50964	15.20563	15.23099	15.58546	15.28154	15.33714
	−0.9	−1.1	15.27129	14.96437	14.99065	15.37435	14.98000	15.00283
					MSE	0.00014	0.00079	0.00153

Table 6.

Numerical values of Nusselt number (rest parameters Pr = 6.2, $\gamma =1.5\text{,}$Rd = 6, A*=-1.5, B*=-1.7, Su = 0.1).

	$\lambda$	Numerical Result			ANN Prediction
		Cone	Wedge	Plate	Cone	Wedge	Plate
$\text{Training}\text{Data}\{$	0.1	18.46570	18.20466	18.20596	18.46772	18.46721	18.18790
	0.3	18.47218	18.20966	18.21302	18.47389	18.47345	18.19762
	0.4	18.47865	18.21465	18.22007	18.48005	18.47969	18.20735
	0.6	18.48512	18.21964	18.22713	18.48622	18.48593	18.21707
	0.7	18.49157	18.22463	18.23417	18.49238	18.49217	18.22679
	0.9	18.49802	18.22961	18.24122	18.49855	18.49841	18.23652
	1.1	18.50446	18.23459	18.24825	18.50471	18.50465	18.24624
	1.2	18.51090	18.23957	18.25529	18.51088	18.51089	18.25596
	1.4	18.51733	18.24455	18.26232	18.51704	18.51713	18.26568
	1.5	18.52375	18.24953	18.26935	18.52321	18.52337	18.27541
	1.7	18.53017	18.25450	18.27638	18.52937	18.52961	18.28513
	1.9	18.53658	18.25948	18.28340	18.53554	18.53585	18.29485
Testing Data	2.0	18.54298	18.26445	18.29042	18.54170	18.54209	18.30458
	2.2	18.54938	18.26942	18.29744	18.54787	18.54833	18.31430
Validation Data	2.3	18.55577	18.27438	18.30445	18.55403	18.55457	18.32402
	2.5	18.56216	18.27935	18.31146	18.56020	18.56081	18.33375
				MSE	0.00000	0.07400	0.00016

Table 7.

Numerical values of Nusselt number (rest parameters Pr = 6.2, $\gamma =1.5\text{,}$Rd = 6, A*=-1.5, B*=-1.7, $\lambda =1.3$).

	Su	Numerical Result			ANN Prediction
		Cone	Wedge	Plate	Cone	Wedge	Plate
$\text{Training}\text{Data}\{$	0.10	18.51411	18.24206	18.25881	18.48955	18.21875	18.23547
	0.14	18.56421	18.29120	18.30797	18.55169	18.27932	18.29608
	0.18	18.61637	18.34230	18.35911	18.61382	18.33989	18.35670
	0.22	18.67063	18.39540	18.41224	18.67596	18.40046	18.41731
	0.26	18.72703	18.45053	18.46741	18.73809	18.46104	18.47792
	0.30	18.78562	18.50774	18.52465	18.80023	18.52161	18.53853
	0.34	18.84643	18.56706	18.58401	18.86237	18.58218	18.59914
	0.38	18.90952	18.62853	18.64553	18.92450	18.64275	18.65976
	0.42	18.97492	18.69221	18.70924	18.98664	18.70332	18.72037
	0.46	19.04269	18.75813	18.77521	19.04877	18.76389	18.78098
	0.50	19.11289	18.82635	18.84348	19.11091	18.82446	18.84159
	0.54	19.18556	18.89692	18.91409	19.17304	18.88504	18.90220
Testing Data	0.58	19.26078	18.96989	18.98712	19.23518	18.94561	18.96281
	0.62	19.33860	19.04533	19.06261	19.29732	19.00618	19.02343
Validation Data	0.66	19.41910	19.12330	19.14063	19.35945	19.06675	19.08404
	0.70	19.50233	19.20386	19.22125	19.42159	19.12732	19.14465
				MSE	0.00090	0.00081	0.00081

Fig. 5.

Effect of $\lambda$ on $f^{\prime }\left(\eta \right)$.

Fig. 6.

Effect of $\mathrm{\Phi }$ on $f^{\prime }\left(\eta \right)$.

Fig. 7.

Effect of Rd on $f^{\prime }\left(\eta \right)$.

Fig. 8.

Effect of $\gamma$ on $f^{\prime }\left(\eta \right)$.

Fig. 9.

Effect of A* & B* on $f^{\prime }\left(\eta \right)$.

Fig. 10.

Effect of Su on $f^{\prime }\left(\eta \right)$.

Fig. 11.

Effect of $\lambda$ on $\theta \left(\eta \right)$.

Fig. 12.

Effect of $\mathrm{\Phi }$ on $\theta \left(\eta \right)$.

Fig. 13.

Effect of Rd on $\theta \left(\eta \right)$.

Fig. 14.

Effect of $\gamma$ on $\theta \left(\eta \right)$.

Fig. 15.

Effect of A* & B* on $\theta \left(\eta \right)$.

Fig. 16.

Effect of Su on $\theta \left(\eta \right)$.

Fig. 17.

Streamlines Pattern for the flow towards

(a) Plate (b) Wedge (c) Cone.

Fig. 18.

Velocity Boundary Layer Pattern for the flow towards

(a) Plate (b) Wedge (c) Cone.

5.1. Analysis of velocity profiles

In Fig. 5, one can note that the velocity $f^{\prime }\left(\eta \right)$ of THNF exhibits a positive correlation with the buoyancy parameter $\lambda$ (natural convection parameter). Here the phenomenon of buoyancy is the driving force behind the movement of fluid in natural convection. In this case, the motion of the THNF is induced by the variation in fluid density, resulting from the temperature gradients. Here, when the parameter $\lambda$ increases, it results in the amplification of buoyancy forces. As a result, the velocity of the THNF experiences a notable increase in all three cases. Fig. 6 illustrates the impact of the nanoparticle's volume fraction (NVF) $\left(\mathrm{\Phi }\right)$ on momentum distribution for THNF. This indicates that the addition of NPs to the conventional fluid results in a rise in velocity. Moreover, the presence of these NPs causes an expansion of the hydrodynamic boundary layer of the THNF in all three scenarios. In addition, upon the addition of NPs to the base fluid, our findings show a distinct velocity pattern among the three cases. Specifically, the flat plate exhibits the highest velocity, followed by the wedge, while the cone exhibits the lower velocity. Fig. 7 focuses on the examination of variations in the radiation parameter Rd and their impact on alterations in velocity profiles. In this case, it is clear that fluid velocity hikes with growth in parameter Rd.

In Fig. 8, the dimensionless velocity is plotted against the variable $\eta$, while systematically varying the thermal relaxation parameter $\gamma$ one at a time, maintaining all other factors constant. The result indicates that increasing the parameter $\gamma$ leads to a fall in the velocity of THNF. Physically, the occurrence of enhanced thermal effects due to the Cattaneo-Christov parameter is main reason behind this phenomenon, effectively slowing down the fluid motion, which decreases the overall velocity profiles. Moreover, the associate boundary layer (BL) experiences a reduction in thickness when the parameter $\gamma$ reaches its maximum value. Fig. 9 demonstrates the effect of varying heat source/sink parameters $A^{*}$ and $B^{*}$ on the momentum distribution for THNF flow over three different geometries. Observing the trends illustrated in the figure, one can deduce that an increase in the heat source/sink parameter leads to an increase in velocity profiles. Moreover, the figure suggests that the heat source/sink parameter is more efficient against the wedge and plate model as compared to the cone model. Fig. 10 visualizes the deviation in velocity fields for varying suction parameter Su. Here, higher Su corresponds to low-velocity profiles for ternary hybrid nanofluid over wedge and plate surface, while a rapid decrease is observed on the same profiles for ternary hybrid nanofluid due to cone surface. This is physically accurate because a smooth surface like a flat plate and wedge enables the THNF to travel without hindrance, ensuring relatively higher velocities. On the other hand, a decrease in velocity is observed as the flow encounters resistance from the curved surface of the cone.

5.2. Analysis of temperature profiles

Fig. 11 showcases the temperature curve, highlighting the effect of varying values of the parameter $\lambda$ on the temperature. Here in this figure, throughout the range of $\eta \in \left[0,5\right]$, the temperature profiles are increased corresponding to the increasing value of $\lambda$. Moreover, the presence of a curved surface, such as a cone acts as an obstacle that disrupts the fluid flow and interaction of particles, causing lower temperature in the region where the THNF flows towards the cone. Fig. 12 investigates how changes in the NVF $\left(\mathrm{\Phi }\right)$ of Al₂O₃, Cu, and CNT NPs affect thermal distribution. The temperature fields are noted to be affected by the NVF. When the parameter $\mathrm{\Phi }$ is raised from 2 % to 4 %, both the temperature of THNF and the associate boundary layer thickness exhibit a decrease. This is due to the fact that an elevation in the NVF boosts thermal conductivity, which, in turn, promotes more efficient heat dissipation from the surface, resulting in a temperature drop. To visually present the influence of increasing estimations of radiation Rd on $\theta \left(\eta \right)$ profiles due to a cone, wedge, and plate, a figure is plotted against $\eta$ and exhibited in Fig. 13. Generally, temperature profiles are significantly influenced by radiation parameter, which holds significant importance. Across all geometries, a significant increment in the boundary layer region was observed with varying values of Rd. Moreover, upon careful analysis of the graph, it becomes evident that the plate geometry consistently exhibits higher temperature compared to the other geometries, regardless of the numerical values assigned to the radiation parameter. From a physical perspective, the combination of radiation emission and conduction effects generates a significant amount of heat throughout the process, leading to a notable enhancement in temperature within the system. By analyzing the graphical representation, it can be deduced that all three geometries (cone, wedge, and plate) exhibit favorable characteristics for HT applications that require elevated temperatures.

Fig. 14 outlines the feature of $\theta \left(\eta \right)$ profiles in relation to the thermal relaxation parameter $\gamma =0.1,0.8,1.5$ for ternary hybrid nanofluid flow over three different configurations. As $\gamma$ increases, the temperature is decreased for THNF due to all geometries. Also, the thickness of temperature BL of the wedge surface is almost identical to that of the plate surface. Physically, the C–C model accounts for the finite speed of heat propagation by introducing a relaxation time parameter. This parameter represents the time it takes for the heat to reach equilibrium within the system. When the relaxation time is increased (larger value of $\gamma$), it means that the system takes longer to reach thermal equilibrium, resulting in slower heat propagation and decreased temperature profiles. The outcomes depicted in Fig. 15 indicate that an increase in the value of the source/sink parameter corresponds to an increase in temperature profiles. In simpler terms, a notable increment is noticed in temperature, when the parameter are changed numerically from $A^{*}=-1.5$ to $A^{*}=-0.7$, and $B^{*}=-1.7$ to $B^{*}=-0.9$ within the region $0\le \eta \le 6$. The response of the growing suction parameter Su on temperature profiles of THNF is displayed in Fig. 16. This graph shows that THNF temperature decreases for all geometries. Physically, growing suction reduces the momentum boundary layer, reducing flow friction, and ultimately causing a temperature drop. It signifies that the parameter Su is associated with a decrease in both the momentum fields and the temperature distribution for THNF.

5.3. Analysis of streamlines and velocity boundary layer patterns

Fig. 17, Fig. 18 (a-c) present the streamlines patterns and velocity boundary layer patterns, respectively, for THNF flow towards all three different geometries. The figure suggests that the stream function value for the flow towards the wedge and plate is almost equal but the value of the stream function for the flow towards the cone is less in comparison to the cone and wedge. Similarly, from Fig. 18 (a-c), it is seen that the velocity boundary thickness is maximum for the flow towards the plate and the velocity boundary thickness is minimum for the flow towards the cone. So, it confirms that the low velocity and boundary layer thickness for the cone is observed because it encounters resistance from the curved surface of the cone.

5.4. Analysis of nusselt number

Table 3, Table 4, Table 5, Table 6, Table 7 provide a comprehensive presentation of the results obtained for the Nusselt number (NN) for THNF flow towards a wedge, a cone, and a flat plate. These tables offer a comparison between the results derived from the numerical method and those obtained using the machine learning algorithm (ANN), presenting them side by side. The radiation parameter Rd has a significant influence on the NN, causing it to increase for all three geometries when the value of parameter Rd is increased. Higher values of this parameter indicate a greater influx of solar radiation directed toward the flow. As a result, the system is exposed to an elevated level of radiation, leading to an increase in the HT rate. For all three geometries, an increase in the thermal relaxation parameter $\gamma$ results in higher values of the NN. This finding suggests that the time lag factor during HT contributes to an enhanced HT rate. The heat source/sink parameters A* and B* have an inverse relationship with the NN, causing it to decrease. This decrease in the NN can be attributed to the growing width of the thermal boundary layer, which occurs as the heat source/sink parameters A* and B* exert a greater influence. The NN is directly influenced by the buoyancy parameter λ and suction parameter Su, causing it to increase as it exerts a dominant behavior. The suction effect disrupts the formation of stagnant or insulating air layers near the surface, allowing for more efficient HT between the surface and the fluid. Furthermore, buoyancy forces lead to fluid motion, which enhances the mixing of fluid near the surface. This increased fluid motion improves HT by bringing fresh fluid in contact with the surface, facilitating the HT away from the surface. The THNF flow towards the cone is seen to exhibit the highest HT rate.

5.5. ANN prediction model and its evaluation

One of the aims of this paper was to utilize a machine learning algorithm (ANN) to estimate the Nusselt number for the flow model. Fig. 3, Fig. 4 illustrate the functioning of the ANN across three consecutive layers. In this research, the modeling of the ANN prediction technique is conducted using MATLAB 2016b, and the training process is executed utilizing the Levenberg-Marquardt algorithm. Eight parameters (X1, X2 ….X8) viz. Rd, Su, Pr, A*, and B*, $\gamma$, $\lambda ,\mathrm{\Phi }$ are incorporated in the input layer. Output layer Y involves the Nusselt number of the THNF. Out of the 16 data sets of numerical simulation used in this analysis, 75 % is used for training and 12.5 % is used for authentication and testing each. The artificial neuron is expressed as $U=\sum _{i=1}^n{W}_{ji}{X}_i$ and Output can be expressed as “$Y_j=f\left(\sum _{i=1}^n{W}_{ji}^n{X}_i+b_j^n\right)$, where ‘j’ corresponds to the neuron, Yj is the output of the jth neuron, ‘i’ corresponds to a layer, b_jⁿ is the bias factor of the jth neuron, Xi corresponds to the input parameters, W_jⁿ is the weight of the jth neuron, n is the number of layers, and f is the activation function”. The ANN prediction model in this paper contains eight parameters in the input layer, and output layer contains one output parameter (Nusselt number) (see Fig. 4). The principal role of the hidden layer is to conduct computations for non-linear problems. In this context, the activation functions used include Sigmoid for the hidden layer and purelin for the output layer. The quantity of neurons is a pivotal parameter for an ANN model to work effectively. The authors have taken the quantity of neurons in the hidden layer same as input parameters.

Once the machine learning algorithms (ANN) have been developed and values are predicted, the next crucial step is to evaluate the performance of these algorithms in terms of prediction. The careful choice of parameters for evaluating prediction performance holds great importance. The prediction performance is determined by calculating the mean squared error (MSE) and regression coefficient (R), which act as metrics for measuring the accuracy of prediction algorithms in comparison to actual data obtained from numerical simulation. The equations provided below are utilized to compute the mean squared error (MSE) and regression coefficient (R) (Shafiq et al. [51,52]):

$$MSE=\frac{1}{n}\sum _{i=1}^n{\left(A{D}_i-F{D}_i\right)}^2$$ (25)

$$R=\frac{n\sum A{D}_{i}F{D}_i-\left(\sum A{D}_i\right)\left(\sum F{D}_i\right)}{\sqrt{n\left(\sum A{D_i}^2\right)-{\left(\sum A{D}_i\right)}^2}\sqrt{n\left(\sum F{D_i}^2\right)-{\left(\sum F{D}_i\right)}^2}}$$ (26)

where in Eqns. (25), (26), n stands for the number of data points forecasted, while FD_i and AD_i are forecasted and actual data values.

A higher level of forecast accuracy is correlated with a lower MSE, indicating improved precision in the predictions (see Table 3, Table 4, Table 5, Table 6, Table 7). By examining Table 3, Table 4, Table 5, Table 6, Table 7, it becomes apparent that the MSE values associated with each dataset are extremely low and, in numerous instances, approach zero. This observation indicates that the machine learning algorithm (ANN) established in this paper has the capability to estimate the Nusselt number with exceptional accuracy, exhibiting minimal errors.

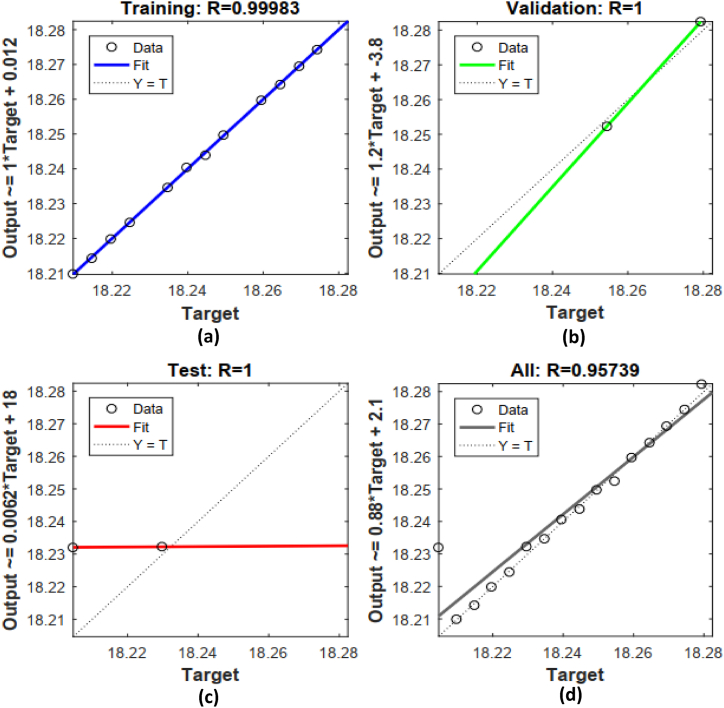
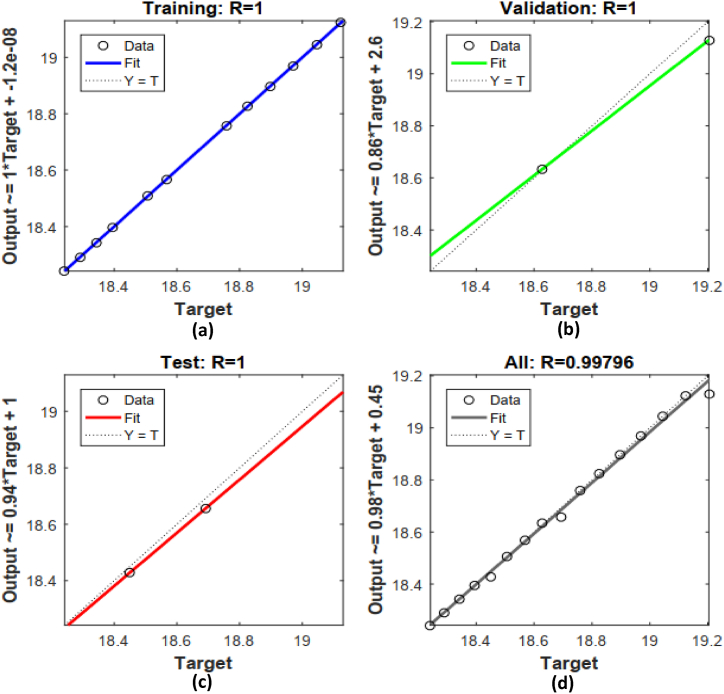
The correlation factor and Regression diagram between the target values and output data serve as additional indicators for assessing the performance of ANN training status. The relationship between the two datasets is quantified by regression. (R). The value of R stands between 0 and 1. R = 0 value implies no relation between the two data sets and R = 1 implies a decent overlap. The authors have presented the alignment between the actual outputs of the ANN and the desired values with the help of Fig. 19, Fig. 20, Fig. 21, Fig. 22, Fig. 23, Fig. 24, Fig. 25, Fig. 26, Fig. 27, Fig. 28, Fig. 29, Fig. 30, Fig. 31, Fig. 32, Fig. 33. In these figures, the horizontal axis represents the target values, whereas the other axis represents the results obtained by ANN. Three key factors are crucial in this figure, namely the “bias (B), slope value (M), and correlation coefficient value (R)”. For an epitome ANN model, its output should perfectly match the target values. In such a scenario, the slope and correlation value will be 1, while the bias value will be 0 (Shafiq et al. [[50], [51], [52]]). Fig. 19, Fig. 20, Fig. 21, Fig. 22, Fig. 23, Fig. 24, Fig. 25, Fig. 26, Fig. 27, Fig. 28, Fig. 29, Fig. 30, Fig. 31, Fig. 32, Fig. 33 show the regression analysis of the (a) training, (b) validation, (c) testing, and (d) overall data w.r.t parameter Rd, $\gamma$, $\lambda \text{,}$ Su, and (A* and B*), respectively for a cone, a wedge, and a plate. In all cases (Fig. 19, Fig. 20, Fig. 21, Fig. 22, Fig. 23, Fig. 24, Fig. 25, Fig. 26, Fig. 27, Fig. 28, Fig. 29, Fig. 30, Fig. 31, Fig. 32, Fig. 33), it is observed that, the regression value is either 1 or very close to 1. The regression (R) value close to 1, express that data points are almost overlapping with the regression line. Furthermore, the points in the graph exhibit minimal scattering, and they are all located precisely on the bisector of the plane. This suggests a good correlation between the analyzed and desired outputs. This observation indicates that the machine learning algorithm (ANN) proposed in this paper has the capability to predict the Nusselt number with exceptional accuracy, exhibiting minimal errors. Fig. 34, Fig. 35, Fig. 36, Fig. 37, Fig. 38 display the error histograms to present the error distributions derived from the ANN model that was developed. The visual representation indicates that the error values at each stage of the ANN model are notably minimal. Nevertheless, it is evident that these errors predominantly cluster around the zero error line. The presence of this pattern in the error histogram graphs verifies that the ANN model was constructed to enable accurate predictions with minimal error.

Fig. 19.

Regression analysis of the data for cone w.r.t parameter Rd (a) Training (b) Validation (c) Testing (d) Overall.

Fig. 20.

Regression analysis of the data for cone w.r.t parameter γ (a) Training (b) Validation (c) Testing (d) Overall.

Fig. 21.

Regression analysis of the data for cone w.r.t parameter λ (a) Training (b) Validation (c) Testing (d) Overall.

Fig. 22.

Regression analysis of the data for cone w.r.t parameter Su (a) Training (b) Validation (c) Testing (d) Overall.

Fig. 23.

Regression analysis of the data for cone w.r.t parameters A* and B* (a) Training (b) Validation (c) Testing (d) Overall.

Fig. 24.

Regression analysis of the data for wedge w.r.t parameter Rd (a) Training (b) Validation (c) Testing (d) Overall.

Fig. 25.

Regression analysis of the data for wedge w.r.t parameter γ (a) Training (b) Validation (c) Testing (d) Overall.

Fig. 26.

Regression analysis of the data for wedge w.r.t parameter λ (a) Training (b) Validation (c) Testing (d) Overall.

Fig. 27.

Regression analysis of the data for wedge w.r.t parameter Su (a) Training (b) Validation (c) Testing (d) Overall.

Fig. 28.

Regression analysis of the data for wedge w.r.t parameters A* and B* (a) Training (b) Validation (c) Testing (d) Overall.

Fig. 29.

Regression analysis of the data for plate w.r.t parameter Rd (a) Training (b) Validation (c) Testing (d) Overall.

Fig. 30.

Regression analysis of the data for plate w.r.t parameter γ (a) Training (b) Validation (c) Testing (d) Overall.

Fig. 31.

Regression analysis of the data for plate w.r.t parameter λ (a) Training (b) Validation (c) Testing (d) Overall.

Fig. 32.

Regression analysis of the data for plate w.r.t parameter Su (a) Training (b) Validation (c) Testing (d) Overall.

Fig. 33.

Regression analysis of the data for plate w.r.t parameters A* and B* (a) Training (b) Validation (c) Testing (d) Overall.

Fig. 34.

Error histograms of developed ANN model w.r.t parameter Rd.

Fig. 35.

Error histograms of developed ANN model w.r.t parameter $\gamma$.

Fig. 36.

Error histograms of developed ANN model w.r.t parameter λ.

Fig. 37.

Error histograms of developed ANN model w.r.t parameter Su.

Fig. 38.

Error histograms of developed ANN model w.r.t parameter A* and B*.

6. Conclusions

The authors have presented a detailed investigation of the flow and HT in three different geometries (cone, wedge, and plate) using THNF flow. The mathematical model incorporates various factors such as quadratic thermal radiation, non-uniform heat source/sink, the Cattaneo-Christov model, suction, and buoyancy effects. Conventional approaches to such a complex problem typically involve parametric studies and computationally intensive efforts. In contrast, this study takes a novel approach by employing machine learning techniques based on the ANN algorithm to analyze the HT. The performance of the algorithm is evaluated using metrics like mean squared error and coefficient of regression. The analysis reveals that the proposed machine learning technique utilizing the ANN algorithm can be applied to solve similar physically related problems. For all the cases examined using the ANN algorithm, the coefficient of regression (R) exceeds 0.99246, which indicates a good relation between forecasted and numerical data. The mean squared error (MSE) values for the ANN algorithm, across all analyzed cases, range from 0 to 0.03972. These findings indicate that the values of MSE are remarkably nearby to zero, implying that the machine learning (ANN) algorithm devised can effectively foresee the Nusselt number with minimal error. The Nusselt number is highest for THNF flow over the cone. The value of stream function for the flow towards the wedge and plate is almost equal but in case of cone, it is less in contrast to the cone and wedge. The velocity boundary thickness is maximum for the plate and the velocity boundary thickness is minimum for the cone.

The present study investigates the flow behavior of a THNF, concentrating on its flow traits while not taking into account the aggregation impact of NPs. Additionally, there is a possibility to enhance the scope of the research by incorporating the effect of NPs aggregation. This could be accomplished through the application of precise thermophysical correlations that have been confirmed to effectively simulate fluid flow.

Data availability statement

No data was used for the research described in the article.

CRediT authorship contribution statement

Ashish Mishra: Conceptualization, Data curation, Software, Writing – original draft, Writing – review & editing. Sawan Kumar Rawat: Conceptualization, Formal analysis, Investigation, Project administration, Supervision, Writing – original draft, Writing – review & editing. Moh Yaseen: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Resources, Software, Validation, Visualization, Writing – review & editing. Manish Pant: Conceptualization, Data curation, Formal analysis, Investigation, Methodology, Software, Validation, Writing – review & editing.

Declaration of competing interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.