Automated delineation of the clinical target volume using anatomically constrained 3D expansion of the gross tumor volume

Abstract

Purpose:

Delineation of the clinical target volume (CTV) is arguably the weakest link in the treatment planning chain. This work aims to support clinicians in this crucial task.

Methods and Materials:

While the CTV itself is ambiguous, it is much easier to identify structures that do not belong to the CTV and serve as barriers to the spread of the disease. We segment the known barrier structures using convolutional neural networks (CNN). The CTV is then obtained by starting from the manually delineated gross tumor volume (GTV) and expanding it while taking into account the barrier structures. Mathematically, we define the CTV as an iso-surface in the 3D map of shortest paths of all voxels from the GTV. The shortest paths are found with the Dijkstra algorithm. While the method is generally applicable, we test it on 206 glioma and glioblastoma cases.

Results:

The auto-segmented barrier structures for the brain cases include the ventricles, falx cerebri, tentorium cerebelli, brain sinuses, and the outer surface of the brain. Manual and auto-segmented barrier structures agree with surface Dice Similarity Coefficients (DSC) ranging from 0.91 to 0.97 at 2mm tolerance. Comparison of manual and automatically delineated CTVs shows a median surface DSC of 0.79.

Conclusions:

Barrier structures for CTV definition can be auto-delineated with outstanding precision using CNNs. An algorithm for automated calculation of the CTV by 3D expansion of the GTV while respecting anatomical barriers has been developed. It shows good agreement with manual CTV definition for brain tumors.

1. Introduction

In radiation oncology, the creation of a patient’s treatment plan involves outlining the tumor target manually on the CT scan. The tumor target includes the radiographically “visible” tumor mass (gross tumor volume or GTV), as well as surrounding tissues which may have been infiltrated by tumor cells (clinical target volume or CTV). The CTV is not radiographically distinguishable from healthy tissues, and therefore it is delineated by estimating the extent of microscopic disease spread based on accumulated knowledge of prior treatment outcomes and histological evidence on the extent of tumor cell spread for a given cancer. The general nature of the published delineation protocols may cause ambiguity and results in a large variability in CTV contours drawn by different clinicians [1, 2, 3, 4]. Automation of CTV delineation may significantly reduce the time burden on experienced oncologists, who currently must manually contour both the tumor mass and microscopic tumor extension for each patient. With automation, the treatment planning workflow can be made more predictable, which can allow for more efficient scheduling. Automation may also improve consistency of delineation by limiting inter-clinician CTV variability. Reproducible CTV margins will be easier to correlate with the location of tumor recurrence. With sufficient data, the size of margins can then be optimized to decrease the risk of recurrence.

Artificial intelligence techniques using convolutional neural networks (CNNs), have shown tremendous promise in medical image processing and automated segmentation of normal anatomy [5, 6, 7, 8, 9, 10] and the GTV [11, 12, 13, 14], with high accuracy and reduced processing time compared to atlas-based segmentation methods [15, 16] commonly used today. Recently, a deep learning approach was developed to automatically delineate CTV for nasopharyngeal [12] and rectal cancer [17]. The authors trained a 2D CNN on a large set of labeled CT images. Both models produced satisfactory segmentation accuracy when compared with manually drawn CTV. In another study, an algorithm based on deep auto-encoders was applied to auto-delineate the high-risk CTV for oropharyngeal cancer [18], and a 3D CNN with U-Net architecture was proposed for all-level-risk oropharyngeal CTV [19]. Another approach to reduce ambiguity of nodal CTV definition for the head and neck cancer is based on applying Bayesian networks to model microscopic tumor spread in the lymph nodes [20, 21].

Guided by the insight that it is easier to identify certain structures that are not tumorous than to identify the actual extent of the disease, we develop a method that combines anatomical definition of “barrier structures” (guaranteed to contain no tumor) using deep learning, and geometrical expansion from the gross tumor volume (GTV, guaranteed to contain tumor cells). The method is not based on direct learning of manually drawn CTV contours. Instead, we mimic the manual contouring process by automated 3D expansion of the GTV that accounts for tissues with different degrees of resistance to tumor spread. The advantage of this method is that the parameters of the constrained expansion can be easily adjusted to fit the set of rules established by clinicians at their institution. A similar approach was considered decades ago [22] as an approximation of the tumor cell spreading. In contrast to the method by Belshi et al, our approach is based on automatically defined barrier structures, and a 3D expansion method that avoids those barrier structures and can take differences of the resistance to tumor spread into account.

In this paper we develop the method for automated expansion of the GTV, and apply it to the delineation of the CTV for highly infiltrative tumors such as glioma and glioblastoma.

2. Materials and methods

2.1. Glioma patients and images

For this study we collected imaging data from 206 glioma and glioblastoma patients who were treated by intensity modulated radiation therapy with curative intent at our institution. The retrospective study was approved by the institutional review board. All patients had three post-operative images available: the planning CT image, and two diagnostic MR images, contrast enhanced T₁-weighted and T₂-weighted FLAIR sequences. Image parameters for the imaging dataset are compiled in Supplementary Table S1 and described in Supplementary Materials.

2.2. Structure sets

According to the target delineation guidelines by the European Organization for Research and Treatment of Cancer (EORTC) and the Radiation Therapy Oncology Group (RTOG) [23], the CTV is defined by adding a margin to the GTV; the recommended margin is 2 cm reduced at anatomical barriers for microscopic spread. The following structures serve as the barriers: brainstem, optic chiasm, ventricles, falx cerebri, tentorium cerebelli, sagittal, transverse, and cavernous sinuses, and skull.

Each patient’s structure set was previously used for treatment planning and included gross tumor volume (GTV) and clinical target volume (CTV) manually delineated by the radiation oncologists on the planning CT and MR image fusion after examination of pre- and post-operative MRI T₁ and T₂ FLAIR sequences. The anatomical barriers such as brainstem and optic chiasm were also included in the set as they are commonly used for treatment plan optimization. The other anatomical barriers not routinely used for treatment planning (ventricles, falx cerebri, tentorium cerebelli, sagittal and transverse sinuses) were delineated manually for a subset of 40 patients (segmentation training set) on CT/MR image fusion. In addition to the anatomical barriers, the brain and cerebellum were manually delineated to support the accurate definition of the CTV; the border of the brain prevents the CTV from expanding into the cavernous sinus. The cerebellum boundary prevents CTV artifacts resulting from the geometry of the tentorium. The skull was segmented based on CT image intensity thresholding.

The GTVs and CTVs manually delineated by radiation oncologists were available for all 206 patients. The segmentation model was trained on 40 patients and was used to auto-delineate the structures on CT images of the remaining 166 patients. The manually drawn GTVs were used as input to an expansion algorithm to create the CTVs for all 206 patients. To evaluate the accuracy of the algorithm, automatically generated CTVs were compared with those delineated by the clinicians, for all 206 patients.

2.3. Convolutional neural network (CNN) model for barrier segmentation

We used the U-Net CNN architecture by Ronneberger et al. [24, 25], see Figure S1 in the Supplementary Materials for details. TensorFlow [26] was used to train the 3D convolutional U-Net. The network architecture and hyperparameters are described in the Supplementary Materials.

2.4. Constrained GTV expansion algorithm

Our algorithm for constrained GTV expansion follows a graph search-based approach. The algorithm takes as input a DICOM structure set containing the GTV and auto-segmented barrier structures for a given patient. This structure set was converted into a 3D label map with the same voxel spacing as the planning CT image. The label map contained integer indices corresponding to different structure types. We constructed a graph from the label map with a cubic grid topology, with one node for each voxel. Face diagonals and space diagonals were also added to the graph. Edge weights were assigned according to the geometrical distance between voxel centers. Specifically, if $\text{Δ}x$, $\text{Δ}y$ and $\text{Δ}z$ are the voxel sizes in the $x$,$y$ and $z$ directions respectively, then the weights for the face diagonals were $\sqrt{\text{Δ}{x}^2+\text{Δ}{y}^2}$, $\sqrt{\text{Δ}{x}^2+\text{Δ}{z}^2}$ and $\sqrt{\text{Δ}{y}^2+\text{Δ}{z}^2}$. The weights for the space diagonals were $\sqrt{\text{Δ}{x}^2+\text{Δ}{y}^2+\text{Δ}{z}^2}$.

For each node, i.e. each voxel $i$, we defined the resistance $R_i$ to tumor spread. Normally we set $R_i=1$. In barrier structures we used high resistance values, $R_i=1000$. The weights for the edges of the graph that directly connect nodes $i$ and $j$ were modified by the factor $R_i\times R_j$. An equivalent way to take barrier structures into account is to remove the nodes belonging to the barrier from the graph.

It should be noted that in other disease sites (but not currently in glioma) one can use other values (other than 1 and 1000) of $R_i$ as well. The resistance factors can depend not only on the location of the respective voxels $i$, but also on the orientation of the respective graph edge. This feature is important for tissues that have a known preferred direction of disease spread, for example muscle tissue in the case of sarcoma.

We used the NetworkX Python package version 2.2 [27] to perform a weighted multi-source Dijkstra’s algorithm search for the shortest path between all GTV nodes and all other nodes in the graph.

2.5. Image post-processing

The convolutional neural network produced brain structures segmentation that sometimes needed corrections. Specifically, to prevent the CTV from extending beyond the skull by ”leaking” through the gaps in the skull that were either real such as surgical defects or artificial, appearing due to under-segmentation, the CTV had to be algorithmically confined within the brain. The confinement within the brain also accounted for the cavernous sinus as an anatomical barrier. Similar imperfection in CTV contours appeared when impermeable barriers that are anatomically connected, such as falx cerebri, brain sinuses, tentorium cerebelli, were separated by the gap upon auto-segmentation so the CTV would not stop at the barrier but extend through it. To patch these gaps, the union structure was created to which a morphological ”closing” operation (dilation followed by erosion) was applied using SciPy Python package version 0.14.0 [28].

2.6. Verification and Validation

We used the surface Dice similarity coefficient (DSC) to evaluate accuracy of auto-delineation. DSC assesses the distance between two surfaces relative to a given tolerance $\tau$, see [9], providing a measure of agreement between the borders of manually and automatically segmented structures:

$$\text{DSC}=\frac{\left(S_m\cap B_a^{\tau }\right)+\left(S_a\cap B_m^{\tau }\right)}{S_m+S_a},$$ (1)

where $S_m$, $S_a$ are areas of the surfaces of structures $m$ and $a$, $B_m^{\tau }$ and $B_a^{\tau }$ are the border regions of thickness $\tau$ for the surfaces of structures $m$ and $a$, and $S_m\cap B_a$ is the surface area of the part of $S_m$ such that any voxel in this part is no farther than $\tau$ from $S_a$. DSC ranges from 0 to 1 representing the fraction of the structure border that has to be manually corrected because it deviates from the ground truth by more than the acceptable distance defined by the tolerance $\tau$.

The results of automated brain structure segmentation were validated via 6-fold cross-validation by calculating the DSC for 6 randomly selected groups of patients. The model for each fold was trained on 34 patients out of 40, leaving six patients for validation. The six folds were non-overlapping and selected at random.

For validation of automatically defined CTV, it was compared to the clinician-drawn CTV using the surface DSC, Eq.(1). The radius of expansion of the GTV to define the CTV boundary varied by the glioma grade as well as by clinician judgement for each case.

3. Results

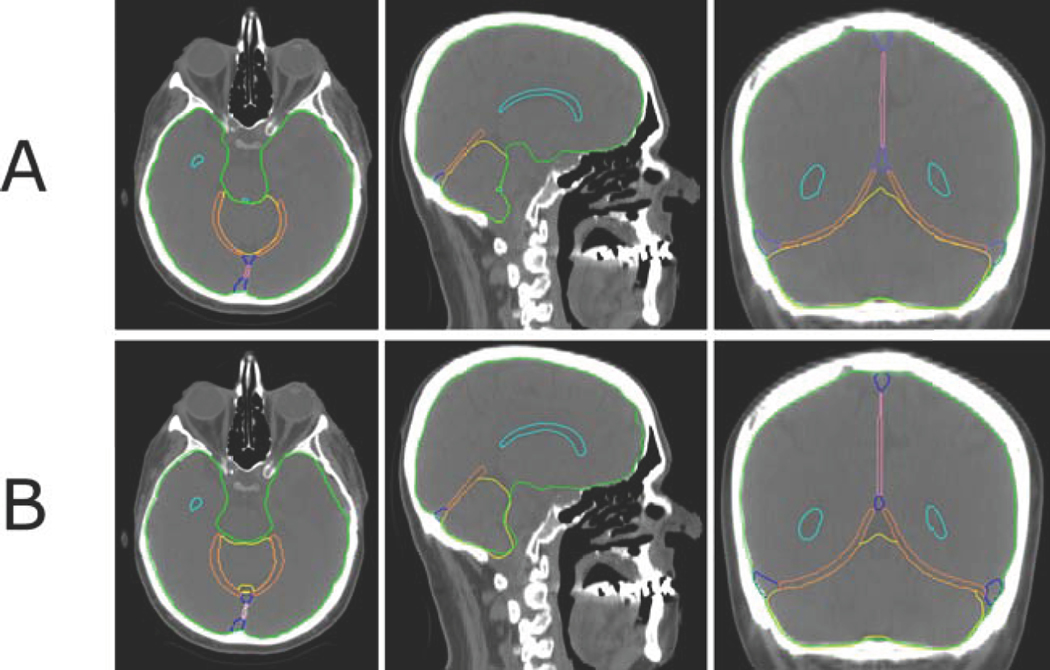
A qualitative comparison of the manually delineated brain structures with the structures generated by the deep-learning model is shown in Figure 1. 2D cuts through a representative CT scan demonstrate the structures included in the model. The manual segmentation was defined by a medical dosimetrist, verified by an experienced neuro-anatomist and arbitrated by a radiation oncologist specializing in glioma treatment.

Figure 1:

Example of auto-segmentation results of the brain structures in comparison with manual delineation. Axial, sagittal, and coronal image slices show the ventricles (cyan), falx cerebri (pink), tentorium cerebelli (orange), sagittal and transverse sinuses (blue), cerebellum (yellow), and brain (green) manually delineated (Panel A) and automatically segmented (Panel B).

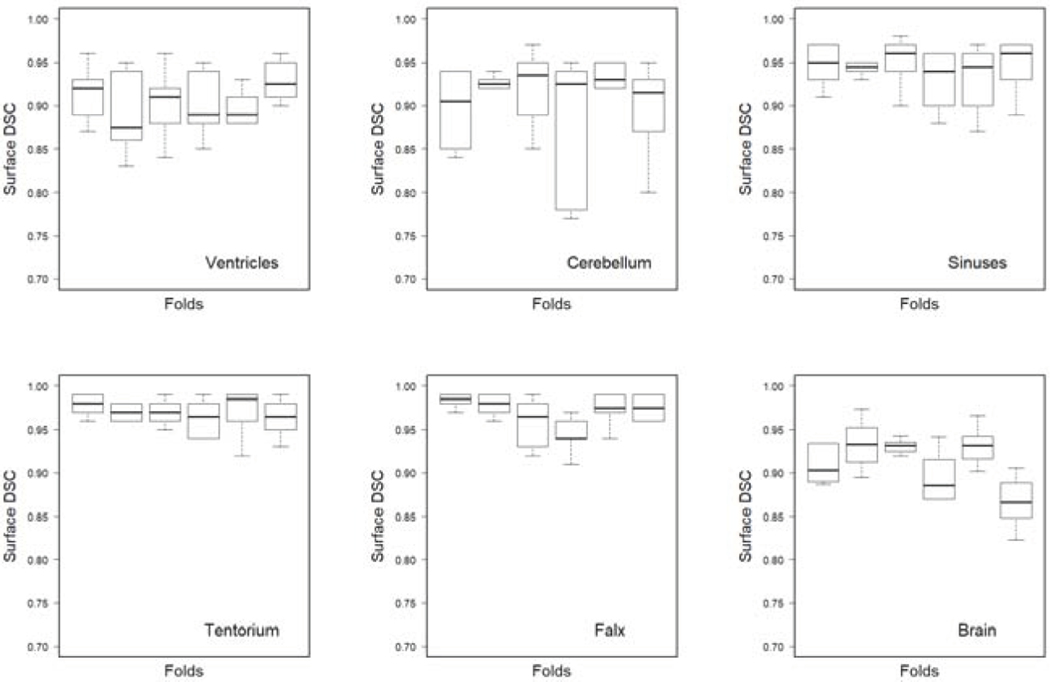
We calculated the DSC according to Eq. 1 using the tolerance $\tau =2\text{mm}$ for each fold and each segmented structure. Figure 2 shows that the variation of the median values of the DSC for most structures across the six folds is similar or less than the variance of DSC across patients within each fold.

Figure 2:

Boxplots of the surface DSC for automated segmentation as compared to the manual delineation at the tolerance level $\tau =2\text{mm}$. The results of 6-fold cross validation are shown for each segmented structure. The model was trained on three input channels per patient, the planning CT image, and two MR images T₁-weighted and T₂-weighted FLAIR.

To study the effect of tolerance $\tau$ on the DSC, we calculated DSC for $\tau$ of 1 mm, 2 mm, and 3 mm for all structures, Table 1. As expected, the value of DSC increases with $\tau$, although increasing $\tau$ over 2 mm has a negligible effect. We hypothesize that this abrupt saturation of DSC with $\tau$ is related to the discretization artifacts and the specific voxel sizes in our dataset.

Table 1:

Surface DSC, median [range], over 36 structure segmentations resulting from the model trained on 34 image sets at different tolerances $\tau$. The 36 segmentations were obtained from 6-fold cross-validation experiment, in disjoint sets of 6 segmentations each.

Structure	$\tau =1\text{mm}$	$\tau =2\text{mm}$	$\tau =3\text{mm}$
Ventricles	0.52[0.29,0.62]	0.905[0.76,0.96]	0.95[0.88,0.99]
Falx	0.505[0.29,0.68]	0.97[0.91,0.99]	0.99[0.95,1]
Tentorium	0.59[0.47,0.68]	0.97[0.86,0.99]	0.99[0.92,1]
Sinuses	0.55[0.47,0.68]	0.95[0.87,0.98]	0.98[0.93,1]
Cerebellum	0.495[0.32,0.6]	0.925[0.77,0.97]	0.98[0.89,1]
Brain	0.59[0.43,0.67]	0.91[0.73,0.97]	0.97[0.76,0.99]

To investigate the benefit of inclusion of the three images (CT and two MR sequences) into the network training with respect to the quality of auto-segmentation, we additionally trained the model with only planning CT and only MR $T_1$ sequences as the input channels, see Figure S2 in the Supplementary Materials. The best quality was achieved with all three images included in the training. The most contributing input was from MR $T_1$ image followed by the planning CT and MR $T_2$ FLAIR sequences with the latter being practically non-contributing.

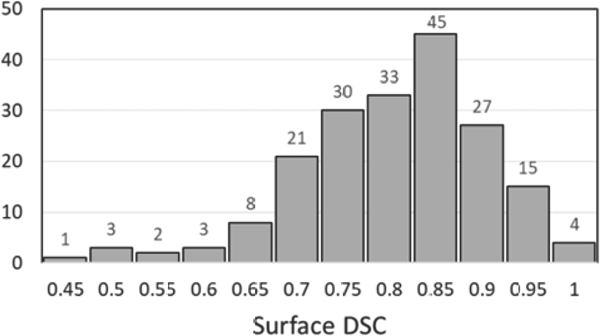
The auto-segmented brain structures were input to the Dijkstra-search-based algorithm for calculating the 3D map of distances from the GTV to other voxels. The calculated distance maps were thresholded at the level of prescribed GTV expansion and the binary labelmaps were compared with the clinican-drawn CTV. The boxplot in Figure 3 demonstrates the surface DSC calculated at the tolerance $\tau =2\text{mm}$ with the median of 0.79 and the range [0.41,0.99]. The algorithm captures clinician-defined CTV margins for the majority of patients. Deviations from the manually drawn margins that resulted in DSC < 0.7 are primarily due to a shift of the margin within the ventricles (up to 5 mm) and beyond the falx cerebri (up to 5 mm). The lowest DSC values (< 0.5) are from the cases of anisotropic margins around the GTV; the decision to expand the GTV differently in different directions is taken by the clinician upon reviewing patient’s medical history for the need to spare surrounding brain tissues.

Figure 3:

Histogram of the surface DSC for automatically defined CTV as compared to the manually delineated CTV at the tolerance $\tau =2\text{mm}$.

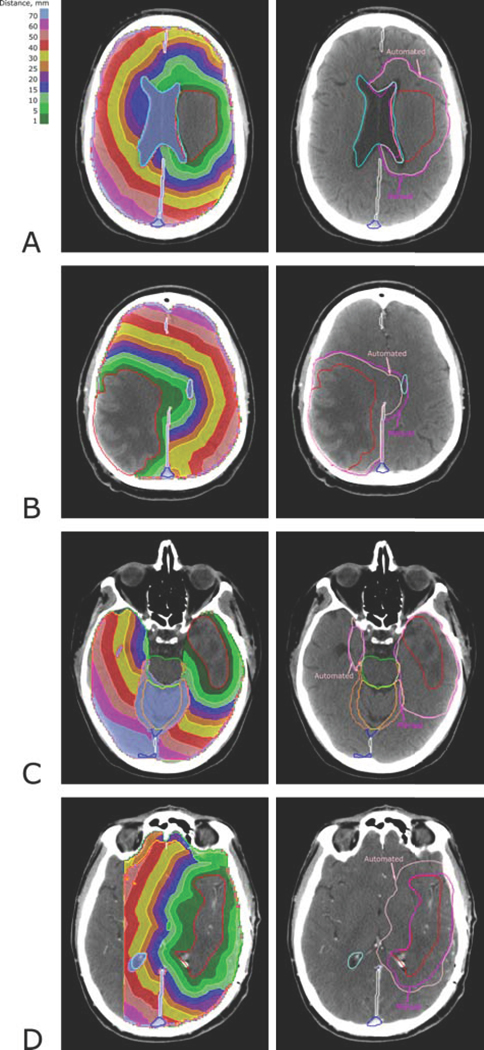
Examples of the distance maps and the CTVs defined by the iso-distance level are shown in Figure 4. In Panel A, a 1 cm marginal expansion of the GTV created the CTV, accounting for the border of the ventricle as an anatomical barrier; in Panel B, two barriers, falx cerebri and ventricle limit the expansion, and in Panel C the CTV is cropped for the cavernous sinus, brainstem, and tentorium cerebelli. Panel D demonstrates the case of mismatching auto- and manually defined CTVs; the clinician-drawn CTV does not account for the microscopic spread laterally on the right and anteriorly to the GTV. This deviation from standard protocol is not captured by the current implementation of our algorithm. Generally, the algorithm can be extended beyond setting different margins (i.e., choosing iso-lines in the distance maps shown in the left column of Figure (4)), to let the user customize the CTV by selecting different values of the resistance $R$ to tumor spread in the surrounding normal tissues. This level of customization was not pursued in this study because of our focus on implementing standard clinical guidelines.

Figure 4:

Examples of the Dijkstra-search-based distance maps (left panels) and the CTV defined by the iso-distance level (pink) corresponding to the clinician-defined CTV margin (magenta) (right panels). The auto-delineated CTV corresponds to the iso-distance levels of 12 mm (A), 12 mm (B), 25 mm (C) and 12 mm (D).

4. Discussion and conclusions

Existing medical image segmentation methods are mostly focused on the segmentation of normal anatomy. Tumor masses are radiographically distinguished from nearby tissues, and can be easily segmented, especially if tumor-specific contrast agents are used. The CTV, however, is defined by clinicians using not only image information but also accumulated knowledge of patterns of disease recurrence, medical history, and, if available, histological evidence of the tumor spread. Thus, CTV cannot be simply segmented from an image using intensity information. Instead, it is created based on empirical rules, capturing the known or agreed-upon patterns of microscopic disease spread.

Direct machine learning of CTV structures from images [12, 17, 18, 19] has been demonstrated for specific disease sites using training sets collected from clinicians practicing at one institution. In this paper, we propose a generalized concept of automation of CTV delineation by mimicking the steps manually performed by radiation oncologists when defining the CTV based on established clinical guidelines, but doing so with the speed, accuracy, and precision of a computer algorithm.

Accurate image segmentation is the key to automatically defining the CTV. Our study showed that applying a deep learning algorithm and the use of multi-modal combined anatomical-functional image information resulted in high quality segmentation of the brain structures. To quantify the segmentation accuracy, we used the surface DSC [9]. For head and neck structures, the authors of [9] achieved an average surface DSC > 0.795. In our study, we find surface DSC ranging from 0.905 to 0.97. The input data we used in this study included images from 2 different CT scanners, and 7 different MRI scanners, representing a reasonable level of heterogeneity between image acquisition systems. We realize, however that our model may not generalize well without tuning of the segmentation algorithms to include images acquired at different institutions.

According to the ESTRO-ACROP guidelines [23] 5 mm margin is added to the ventricles, falx and tentorium to account for shift of these structure borders during radiotherapy treatment. The current implementation of our model does not account for uncertainties in the barrier structures position. In the future we plan to implement robustness against position change with respect to the position defined by auto-segmentation on the planning CT scan. This can be done by either updating the auto-segmentation of the barrier structures on the mid-treatment MRI or by including robustness directly to the model, if we assume that the error in position is known.

The cases with specific tumor location such as near the midbrain are not handled by the current implementation of the algorithm, as in these cases the tumor can grow through the brainstem which is the barrier to the spread from other locations. Also, preferential spread through the corpus callosum was not included in the algorithm. In the future we plan to refine the algorithm to consider anatomical barriers of different degrees of resistance. For example, for the corpus callosum the resistance can be defined as $R<1$ due to preferential tumor spreading within and through the corpus callosum as compared to the adjacent tissues. Previously, the anisotropic growth pattern was addressed in [29]. The general model that includes anatomical barriers partially permeable by the tumor cells will require data processing for estimation of permeability.

The calculated distance maps based on Dijkstra search for the shortest path from the GTV surface to a given voxel can be utilized in treatment plan optimization in a way that deviates from traditional binary CTV-based optimization. As it was recently shown [30], the use of a continuous distribution of the microscopic spread results in dose distributions with a better trade-off between sparing the normal tissues and covering the disease.

In conclusion, convolutional neural networks are able to produce clinically acceptable auto-segmentation of the brain structures that aid definition of the clinical target volume. The 3D distance maps from the GTV that account for impermeability of anatomical barriers define the microscopic spread more accurately than manual contouring on 2D image slices. The margin that defines the CTV can be set at an iso-distance level chosen by the clinician to tailor the extent of irradiated volume to a particular patient.