GPU-Accelerated Flexible Molecular Docking

Abstract

Virtual screening is a key enabler of computational drug discovery and requires accurate and efficient structure-based molecular docking. In this work, we develop algorithms and software building blocks for molecular docking that can take advantage of graphics processing units (GPUs). Specifically, we focus on MedusaDock, a flexible protein-small molecule docking approach and platform. We accelerate the performance of the coarse docking phase of MedusaDock, as this step constitutes nearly 70% of total running time in typical use-cases. We perform a comprehensive evaluation of the quality and performance with single-GPU and multi-GPU acceleration using a data set of 3875 protein–ligand complexes. The algorithmic ideas, data structure design choices, and performance optimization techniques shed light on GPU acceleration of other structure-based molecular docking software tools.

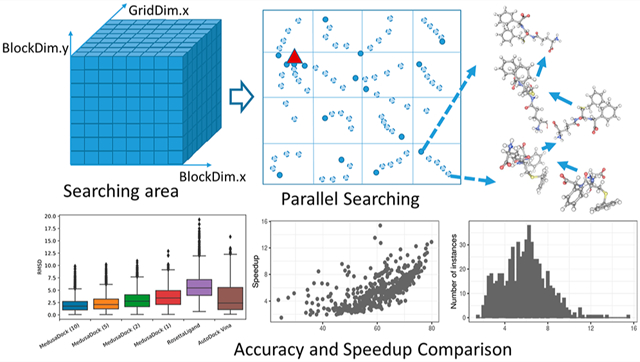
Graphical Abstract

INTRODUCTION

Computational molecular docking is an important subdiscipline in structure-based drug discovery. Modern drug development is slow and expensive, but docking-based approaches could offer low-cost and efficient alternatives for the commonly adopted trial-and-error experiment process in drug discovery, the first stage of the drug development. In the docking-based virtual screening process for drug discovery, small molecules are docked to specific protein targets and ones with the highest binding affinities are selected to be drug candidates. Sampling and scoring are the two key procedures that dictate the performance of docking software. Massive experimentally determined protein–ligand complex structures provide a myriad of options for optimizing the scoring function. With recent developments in infrared spectroscopy, X-ray crystallography, nuclear magnetic resonance spectroscopy, and cryogenic electron microscopy technologies, more protein–ligand complex structures are being determined than ever before, and the focus of protein–ligand docking has shifted to optimizing the scoring functions and improving the sampling procedures.^4–6 For high-throughput virtual screening, significantly expediting the protein–ligand docking process is thus of paramount importance.

Over the last two decades, numerous docking methods have been proposed and evaluated, such as GOLD,^7,8 DARWIN,⁹ MCDOCK,¹⁰ MedusaDock,^11–13 AutoDock,¹⁴ AutoDock Vina,¹⁵ DOCK,¹⁶ FlexX,¹⁷ HADDOCK,¹⁸ ICM,¹⁹ ProDock,²⁰ RosettaLigand,²¹ and SwissDock.²² However, most of them have been mainly designed for CPU-based systems, and only very few^23–25 target GPUs and heterogeneous HPC nodes. AutoDock Vina uses OpenMP to implement a multithreaded version of the Lamarckian genetic algorithm, which is used for searching ligand conformations. It also uses OpenMP to accelerate the individual docking tasks and uses MPI to parallelize virtual screening. There exist multiple works that leverage the GPU architecture to accelerate it. AutoDock-GPU uses an OpenCL-based parallel computing strategy for the Lamarckian genetic algorithm based search in molecular docking in GPUs. The main contribution of this work is proposing a parallel genetic search algorithm targeting GPUs.²⁶ Micevski et al. map GPU threads to ligand atoms directly;²⁷ since the number of ligand atoms is limited, this method leads to a low utilization of the GPU architecture. In comparison, Kannan et al.²⁸ achieve between 10× and 47× speedup by employing the parallel version of a genetic algorithm. However, their approach does not perform any local search (which means it has fewer degrees of freedom) and does not evaluate the accuracy of the result. Their reported results are based on speeding up the kernel without including host data preparation and transfer latency. Serkan et al. also parallelized a genetic algorithm and achieved around 14× speedup.²⁹ They only tested three protein–ligand pairs, and no GPU-specific optimization was employed. VSDocker is similar to AutoDock Vina in that it also utilizes MPI to parallelize the process of virtual screening on a cluster.³⁰ However, VSDocker does not exercise intralevel parallelism within a CPU node. Some software^31,32 target accelerating fast Fourier transform (FFT) calculations used as subroutines in docking. For instance, PIPER³² parallelizes the FFT correlation process and the scoring function on a GPU architecture and achieves around 4.8× speedup. Most of this speedup comes from cuFFT. There also exists docking software accelerated on FPGAs.^33,34 Of note, most existing GPU-based acceleration works^35,36 were only tested on a very small fraction of standard protein–ligand complexes. Their performance results are primarily based on the optimized kernel and may not include end-to-end times.

In this work, we aim to accelerate docking software on clusters with multiple GPUs. We use MedusaDock, a commonly used docking software framework, as a vehicle to study GPU acceleration. Most docking software only support rigid receptor docking. Note that very few tools support flexible docking, which considers the flexibility in receptor side chains; these include MedusaDock, AutoDock Vina, and RosettaLigand. Furthermore, MedusaDock can even allow for the flexibility in receptor backbone. In fact, using a well-studied energy function, MedusaScore,³⁷ with both flexible side chains and backbone docking protocol, MedusaDock can successfully identify the near-native poses for 28 out of 35 ligands in the CSAR2011 (Community Structure–Activity Resource) Docking Benchmark (www.csardock.org), which represents the highest success rate compared to all other methods in near-native pose prediction (<2.5 Å RMSD) in CSAR2011, highlighting the importance of modeling receptor backbone in accurate docking of ligands to a flexible target.¹² A recent version of MedusaDock¹³ allows incorporating experimental constraints to further improve the accuracy.

In this work, we propose a GPU-friendly search algorithm to accelerate MedusaDock. We present several application-specific GPU performance optimization strategies. We exploit parallelism at multiple granularities in the virtual screening process. Our approaches are designed to leverage GPU parallelism at the finest granularity so that we can simultaneously address the high memory use and sequential dependence hurdles. This methodology simplifies the transition to a multi-GPU setting. To fully exploit GPU resources, we pay particular attention to the sampling and scoring procedures. We develop a coarse-grained parallelization strategy that is fully compatible with fine-grained GPU parallelism. We use a large-scale data set of 3875 protein–ligand complexes to evaluate the performance of the GPU-accelerated MedusaDock. We demonstrate that the GPU-accelerated version of MedusaDock preserves, and in some cases even improves, the docking quality results of the original version.

METHODS

MedusaDock.

MedusaDock explores the docking conformational space in three steps: generating a stochastic rotamer library of ligands, repacking the side chain of a protein, and rigid body docking. The first and the second steps prepare the input for the third step of rigid body docking. The rigid body docking step explores the protein–ligand complex by keeping the structure of molecules rigid to rapidly explore all potential complexes. On the basis of the energy scores, MedusaDock will identify several minimum energy complexes for further conformation prediction. Complexes with lower energies are considered to be more stable. Since the scoring function needs to work in concert with the searching algorithm, we target both these parts for efficient GPU execution.

Alternatively, from a program structure perspective, MedusaDock can be divided into three main phases: preparation for coarse docking, coarse docking, and fine docking. The first phase prepares a collection of candidate poses termed STROLL (stochastic rotamer library of ligands). These correspond to the degrees of freedom arising from rotatable bonds in the small molecule. To evaluate the sufficiency of the rotamer library, MedusaDock uses the Kabsch algorithm, which is the standard algorithm to compute the root-mean-square deviation (RMSD) for different STROLL generations.³⁸ Next, in the coarse docking phase, MedusaDock searches for best-fit poses within a docking bounding box. It uses a cluster centroid from the prior step to seed the ligand pose. The ligand and protein structure are kept rigid in this search process, and as a result, the energy outputted may not be accurate.

The coarse docking process iteratively repacks the side chain of the protein to perform rigid docking. Since the lowest energy complex could come from any candidate, many energy poses proposed in this step are saved as candidates for the next step. Next, the coarse-docked poses are sorted and clustered. The RMSD values of low energy poses are continuously calculated and similar poses are removed. The coarse docking step finally chooses a top group of low energy poses (e.g., 10%) for the next fine docking step.

In the fine docking step, both the ligand and the receptor side chain rotamers are simultaneously sampled. All the ligand conformations in each group are changed within 2 Å to enrich the ligand conformations. After the enrichment step, in each group, only the lowest energy complex is selected, so that a small number of candidates are finalized. MedusaDock carefully verifies each conformation and searches around the conformation proposed by coarse docking.

High-Level Parallelization Strategy.

From the analysis and the preliminary result from the Results, it is apparent that coarse docking is the dominant phase in MedusaDock. Specifically, the Monte Carlo method to search the conformation space dominates the overall execution time. The search process begins from a random or a specific state. A state is specified by the position, orientation, and conformation of the ligand and protein side chain. The method then makes random state changes and accepts uphill moves with the probability dictated by the energy function. The algorithm halts when it reaches a local minimum point. This is a crucial time-consuming step in MedusaDock since it includes both randomly moving ligand rotamers as well as expensive energy calculations of the binding complex.

Any fine-grained parallelization of the search should include choosing the starting pose, optimizing and parallelizing the energy calculation, and finally using a reduction operation to determine the lowest energy pose.

Algorithm 1 shows the high-level program flow of the original MedusaDock. The work performed is determined by values of r (number of ligand rotamers), n (number of flexible docking steps), and m (number of random draws). The loop spanning lines 3 through 11 corresponds to the coarse docking phase.

At a high level, the focus of our fine-grain parallelization is to replace the coarse docking inner loop with an alternate search strategy. Ideally, the number of draws must be the same as or lower than the CPU version, and the result quality must be preserved. We want to emphasize that lines 7 and 10 of this algorithm prohibit straightforward parallelization.

Algorithm 2 gives a high-level overview of the parallelization strategy. Instead of m draws, we perform tz searches. We further break down pose search into the shift and rotate steps. We set tz to be larger than m.

Consider a modern GPU with 1000s of computing elements. We use the NVIDIA Tesla P100 GPU for our empirical evaluation and will thus use its configuration as a running example. The P100 GPU has 56 streaming multiprocessors (SMs) with 64 FP32 CUDA cores each. Thus, 3584 compute elements need to be kept busy. As for the memory system, each SM consists of a 64KB private L2 cache/shared memory and a 256 KB register file. All the SMs are connected to eight memory channels controlled by memory controllers, which establish the path to a total of 4096 KB global shared L2 cache. The whole chip has 240 texture units and 16 GB memory in total. It could reach 10.6 TFLOPS of single precision (FP32) as peak performance.

Consider a search strategy based on domain decomposition, or partitioning the search space. Since our goal is to keep 1000s of threads active, one way to create threads is by imposing a 3D grid over the search space and then mapping grid cells to CUDA thread blocks and threads. In Figure 1A, we show a search space division into an 8 × 8 × 8 cube. We correspondingly initialize 7 × 8 × 8 × 8 threads for the GPU implementation, and the number of active threads is bounded by GPU architecture resources. The thread arrangement of the GPU kernel is also shown. We use 64 threads per thread block.

Figure 1.

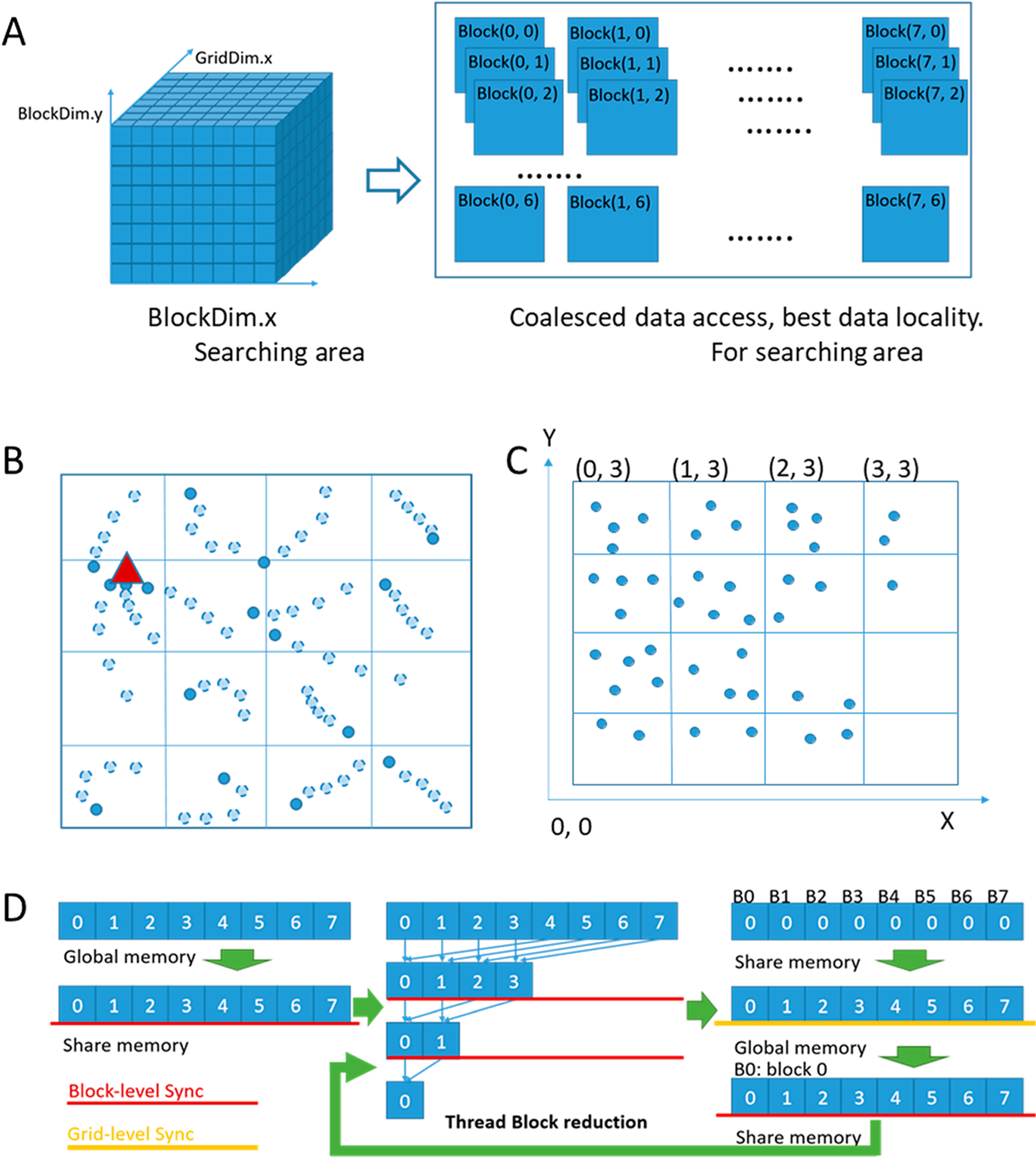
GPU-parallelization of MedusaDock. (A) Mapping the search space to CUDA thread blocks and threads. (B) Illustration of the parallel search process. The triangle indicates a global minimum and dark-shaded circles indicate minima obtained by each thread. Each circle indicates a Monte Carlo draw. (C) Illustration of the atoms grid data structure. (D) Illustrating the multilevel thread block and grid-level synchronization.

We consider the 3D space as 8 × 8 × 8 small cubes. Each thread block processes one cube. A thread randomly shifts the ligand conformations from the initial position within each small cube. The ligand conformations include information such as the center-point position and the rotation degree of the structure. In Figure 1B, we use distinct points to virtually represent each ligand conformation. The conformations differ in their center-point position and rotamer degree. The thread mapping demonstrated in Figure 1A is for optimal data locality and coalesced data access during the searching process. Each shift position is rotated seven times to check for different orientations of the conformation. Within each cube in the 8 × 8 × 8 grid, we again use the Monte Carlo algorithm (m draws on the CPU) to search from each start position.

Figure 1B illustrates the parallel shift and searching process using a 2D 4 × 4 diagram. All the shifts starting in each cube could go in any direction since it is a 3D model. As the figure shows, after several steps of exploring, several threads could reach the same local minimum points. Some other threads may get stuck in their local minimum points. By comparing these local minimum points, we try to reach the global minimum in the entire search space. In our experiments, we define the number of search steps per thread to be 5. We also tried 10 and 20 search steps per thread, but the accuracy improvement (as Table 1 shows) is not commensurate with the increased running time (coarse docking kernel running time grows linearly with the number of search steps). Finally, after finding the minimum energy from the GPU kernel, we add a few additional CPU search steps to explore the neighborhood of the current pose a little bit further. We heuristically find that five additional CPU search steps lead to a sufficient accuracy.

Table 1.

Coarse Docking Energy Evaluation When Varying the Number of Search Steps (on 100 Selected Instances)^a

search steps	similar	OB	OW	better	worse
5	92	7	1	10	4
10	91	8	2	9	6
20	84	12	4	13	9

^aE_cur: the minimum energy of current search step after coarse docking. E_iter1: the minimum energy of 1 search step after coarse docking. Similary, abs(E_cur–E_iter1) < 0.05 × abs(E_iter1). OB: if not similar and E_cur < E_iter1. OW: if not similar and E_cur > E_iter1. Better: E_cur < E_iter1. worse: E_cur > E_iter1.

Since we need the energy of all binding poses to find out the global minimum point, we divide the coarse docking execution in GPU into three parts: randomly shifting and rotating the ligand conformation within the searching space, calculating the energy of the complex, and performing reductions in the GPU to obtain the global minimum energy pose. To reduce the data transfer costs between the host (CPU) and the GPU, we repack the side chain of the receptor first and then search the ligand poses for the specific ligand rotamer in parallel.

Memory Access Optimization.

During the implementation of the coarse docking GPU kernel, since the coarse docking process is quite memory intensive, we take full benefits of the shared memory, register file, and vectorized data access, to optimize the memory access performance. GPU architectures typically have a four-level memory hierarchy. The register file is private per thread and its size is limited per thread block. For the Tesla P100 GPU architecture we use in this study, there is a 256 KB register storage per SM. Note that this is a faster memory storage, when compared to shared memory and global memory. These three memory structures are the only programmable memory on GPUs. L1 and L2 caches on the other hand are not programmable. We store protons of the ligand in the register file, as this part of the data will be frequently accessed during the random move process and energy calculation. Since we are limited by the size of the register file per SM, only proton data can be accommodated in the register file. Initially, we also tried to use shared memory to accommodate the atom data. However, we observed that, for some complicated ligand structure data, shared memory runs out. Moreover, we need to save the partial state to perform the reduction, and the shared memory is very small for this scenario. Also, the grid data needs to be shared across all the thread blocks. Although this data needs to be frequently accessed during energy calculation, it can only be accom-modated in global memory.

The shared memory usage will be explained in the upcoming reduction section. Except for the local memory usage, we use vectorized memory accesses to load and store from global memory. When data access is aligned and consecutive, perfectly matching the three-dimensional data addresses, the memory pressure can be relieved.

Binding Pose Energy Calculation.

Binding pose energy calculation includes all the atom and proton pairs’ van der Waals force field calculation, solvent calculation, and hydrogen bond energy calculation. In this part, if we traverse all the atoms and protons in the receptor for every ligand atom and proton, there would be a lot of unnecessary global memory accesses, decreasing overall performance. Therefore, we build a 3D grid to accommodate the atoms and a 3D grid to accommodate the protons. Figure 1C illustrates the atoms grid in 2D. Since the scope of the force field is limited, using the grid structure, we can easily isolate the atoms that are inside the effect scope. For every atom inside a ligand, we calculate its targeted grid area first, and then using this coordinate information, we can largely reduce the force field effect scope and global memory accesses.

After using the grid data structure, we need to isolate the hydrogen bond energy calculation. Since the hydrogen bond needs to be established during the calculation, this triggers data insertions and deletions inside the grid. Before the GPU kernel launching, we need to copy the data from the CPU host to the GPU device. In this step, vector structures including pointers are not supported. Consequently, we transfer all the vector data structures to an array when copying to the GPU device, including the grid data structure, which is implemented by the vector. The cost of deletion and insertion for an array is very expensive and every thread needs to have its own grid data structure, which significantly increases the overall memory cost. With the 100-instance subset, hydrogen bond-related energy calculations constitute less than 5% of the total binding pose energy. This part of the energy calculation is thus performed on the CPU only.

Parallel Reduction and Optimization.

We develop a custom reduction approach in this work because we seek to avoid overheads when performing the reduction. We also considered reduction functions provided by the Thrust and CUB libraries. Thrust∷reduce() function is a host-side function that cannot work inside a CUDA kernel, and thus it cannot be used for the reduction purpose inside the coarse docking search kernel. CUB’s device (global) level reduction is the same as Thrust (it is also a host-side API). We compared our block-level reduction against the CUB block-level reduction in a synthetic benchmark mimicking the reduction. We observed that our approach is within 2% of CUB’s block reduction. The optimized block-level reduction tries to reduce the block-level synchronizations as much as possible, by resorting to sequential reduction once the remaining data is not too much. Since the optimized block-level reduction performs better, the block level synchronization is the main performance bottleneck in the block-level reduction.

Note that our grid-level reduction consists of global memory as well as shared memory data accesses and communication, grid-level synchronization, block-level reduction, and synchronization. Among these main steps, the grid-level synchronization is the primary time-consuming component. In summary, to optimize the reduction process, reducing synchronizations, especially the grid-level synchronization, is a key consideration. Therefore, we design a multilevel synchronization mechanism to optimize the reduction process.

The first level is the thread-level synchronization. In our parallel search algorithm, we need to run five search steps for each initial point. To avoid grid synchronization after each search step, while keeping the lower energy pose, each thread runs its search and keeps the lower energy pose during the entire searching process (as demonstrated in Figure 1B). The Monte Carlo algorithm generates the next candidate poses independently for each thread, based on the previous poses in such thread. As a result, we only need to randomly move the ligand conformation and calculate the complex energy in the five search steps. The reduction step is no longer required. After these search steps, we need only one global synchronization, to select the global minimum energy poses from the local minimum energy poses among each thread.

Figure 1D shows the second-level synchronization, which consists of thread block-level and grid-level synchronization. To reduce the synchronization overhead across all the threads, we first apply thread block level synchronization, to get the minimum energy pose inside every thread block. Then, we synchronize among all the thread blocks to obtain the global minimum energy pose. The GPU architecture prevents the register file from being shared across the threads, and therefore, we can perform the reduction only in the memory. We take advantage of GPU shared memory to do the reduction in thread block-level, since shared memory can be simultaneously accessed by the thread inside one thread block. Hence, we first copy the data to the shared memory and then perform thread block-level reduction. After that, we copy the data back to global memory, so that the communication between the thread blocks can be performed through global memory. Finally, we copy the data back to shared memory and use one thread block to do the final reduction after maintaining the data consistency.

We tried using cooperative groups to synchronize across the grid for data consistency.

Furthermore, we also tried to use one data allocation in global memory as a lock to manually synchronize across thread block. The experimental results indicated that the manual synchronization is about 14% faster than using cooperative groups. So, we keep the manual synchronization version.

Coarse-Grained Parallelization Using MPI.

We now discuss an additional coarse-grained layer of parallelism that can be exploited to accelerate virtual screening. We use an MPI-based master–worker setup for this work. In this setup, the master process sends tasks to worker processes and is responsible for load balancing. Whenever a worker process is available, the master process dispatches tasks to it. The master process guarantees that all the worker processes are working as long as there is a sufficient number of pending tasks (in this case, protein–ligand complexes). The worker process communicates with the master as soon as its current task is done to request a new task. When all worker processes are done, the master process is notified. If necessary, all the result data are gathered on the master node. Otherwise, worker tasks can write their respective output onto the disk. The same approach works for multi-GPU parallelization as well.

Experimental Setup.

We use a GPU cluster with NVIDIA Pascal GPUs for our evaluation. Specifically, each node of this cluster has two 14-core Intel Xeon E5–2680 v4 (Broadwell) processors. Each processor has 35 MB last level cache, and each node has 256 GB DDR4–2133 memory. While this cluster has more than 70 nodes with this configuration, nearly all our runs use a single node. To benchmark the multi-GPU version, we have some runs using up to 9 GPUs. Each node has one NVIDIA Tesla P100 GPU. We use CUDA 8.0 (nvcc v8.0.61), Intel MPI v16.0.3, and Intel C compiler v16.0.3 to build our code. As previously mentioned, we used a collection of 3875 protein–ligand complexes from PDBbind³⁸ for performance evaluation. It includes a diverse set of protein and ligand structures: the range of protein residues is between 56 and 4,061; the range of ligand atoms is between 6 and 70; the range of ligand protons is between 0 and 23; and finally, the range of ligand hydrogen-bonds is between 0 and 30. We also performed experiments on a subset that consists of 100 protein–ligand pairs obtained from.¹³ The ligands in this data set are generally complex and have a large number of rotatable bonds (average is 22). Further, all these instances are known to be challenging for MedusaDock to process because the RMSD obtained when running with the default options is greater than 2 Å. Specifically, we first performed 1 iteration of the MedusaDock docking attempt with a random seed to dock all protein–ligand pairs in the data set and then calculated the RMSD of the predicted pose. If the pose RMSD is <2 Å, we then deleted the corresponding protein and ligand from the data set. Note that the version of MedusaDock in ref 13 is an experimental one, and the current work optimizes the main bottleneck of the docking procedure in the original MedusaDock.¹¹ In our data sets, we have separated the binders from the decoys. Thus, for each ligand and protein pair, the native ligand structure is not used for docking, and MedusaDock docked the ligand to the protein by using multiple ligand conformations generated by MedusaDock’s internal ligand conformation sampling algorithm.

RESULTS

Application Analysis and Profiling of MedusaDock.

We first perform a preliminary analysis of typical MedusaDock execution for virtual screening. We use a collection of 3875 protein–ligand complexes from PDBbind³⁹ for performance evaluation, and we execute all steps of MedusaDock on a single core of an Intel Broadwell processor. The data set was compiled in Wang and Dokholyan’s prior work.¹³ This data set is derived from the PDBbind database,⁴⁰ which is a comprehensive collection of experimentally solved biomolecule complex structures in the Protein Data Bank. Initially, the refined set of PDBbind 2017, including 4,154 complexes, was downloaded. Complexes with more than one ligand were then removed. The complexes with only one rotatable bond were also excluded from the data set because of the lack of flexibility in the ligand to test the docking method.

We evaluate the wall-clock execution time in hours for processing all protein–ligand pairs (Figure 2A). Additionally, the running time per instance in minutes is shown on the secondary axis. The order of instances is as given in the data set (i.e., we do not reorder complexes by the number of rotatable bonds), and this is a typical execution scenario. We observe that the total execution time is more than 150 h, and multiple instances require 30–50 min for docking.

Figure 2.

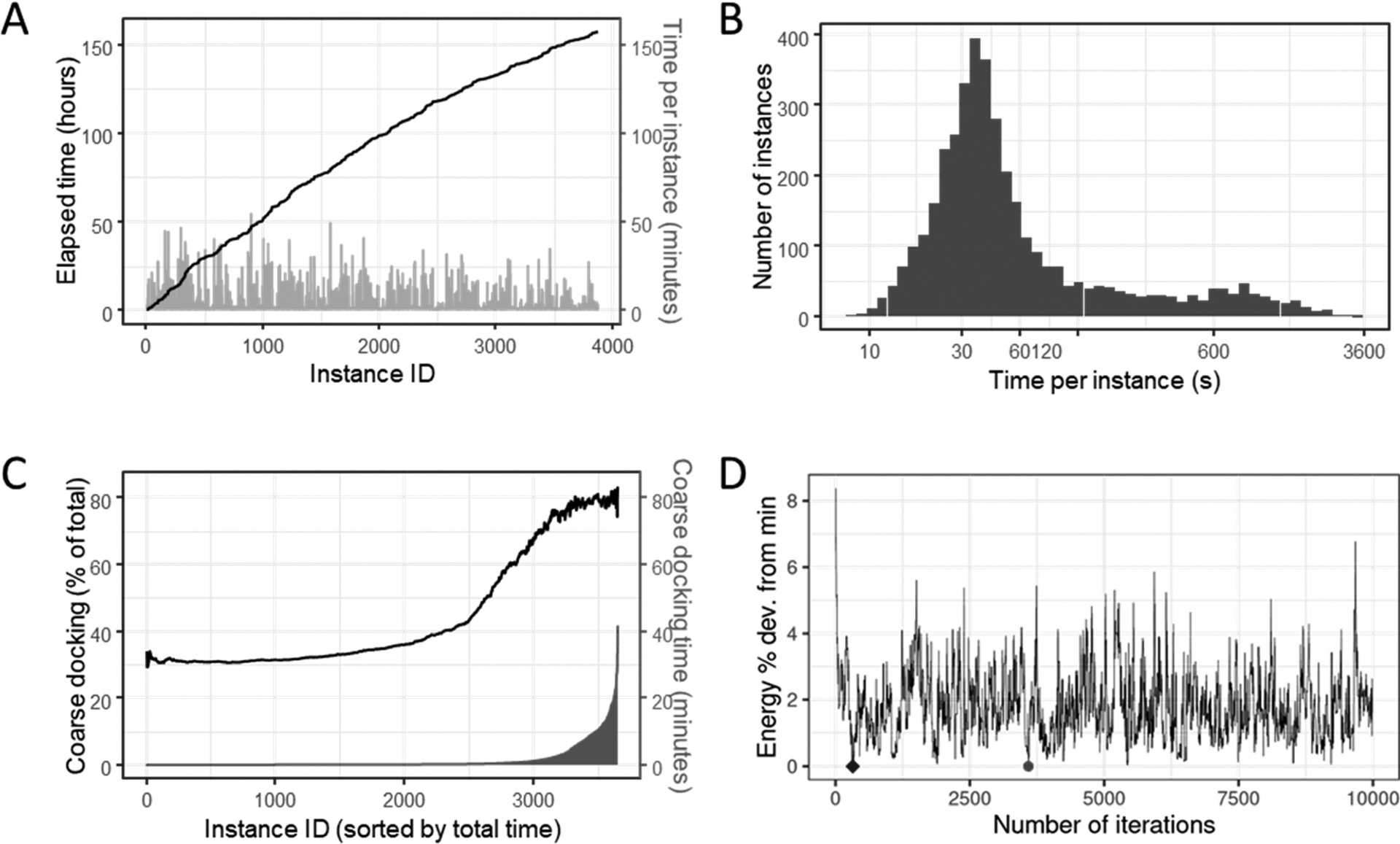
Application Analysis and Profiling of MedusaDock. (A) MedusaDock execution time on the docking of 3875 complexes. Cumulative time is shown in hours and the order of instances is arbitrary. Bars indicate per-instance running times and use the secondary axis. (B) Histogram of per-instance execution times. Note that the X-axis uses a logarithmic scale. (C) Performance of the coarse docking phase: the primary axis shows the fraction of time is spent in coarse docking when instances are sorted by total coarse docking time. The secondary Y-axis and bars indicate per instance running time in minutes. (D) Energy computed for various poses using MedusaDock’s Monte Carlo search algorithm: Y-axis shows the percentage deviation from the minimum obtained with 10 000 iterations, the green circle indicates the minimum energy iteration, and the blue diamond indicates the minimum energy pose in the first 1000 iterations.

Next, we evaluate the distribution of per-instance docking times (Figure 2B). The time per instance varies from 7 s to 55 min, and most instances require less than 90 s. However, about 13.8% of instances require more than 200 s for docking. Hence, it is important to exploit both coarse- and fine-grained parallelism. As mentioned earlier, MedusaDock is composed of three phases, namely, preprocessing, coarse docking, and fine docking. Also, most input instances take less than 1 s for preprocessing, and no instance exceeds 3.1 s. The running time of this phase is therefore negligible.

We also evaluate the percentage of time taken by the coarse docking phase for each instance (Figure 2C). Further, we sort instances by time and indicate the per-instance coarse docking time in minutes. The coarse docking time ranges from 2 s to 46 min. In most cases, if the total execution time is less than 30 s, fine docking is the dominant part of the total execution. On the other hand, if the total execution time is more than 40 s, coarse docking tends to dominate overall time. As the figure shows, for long-running instances, the percentage of time spent in coarse docking can be as high as 80%. Therefore, the coarse docking phase is the primary scalability and efficiency bottleneck in MedusaDock.

The structure of the protein–ligand complex directly impacts the total execution time. For instance, the running time is linearly proportional to the number of rotatable bonds in the ligand. We observe that the average coarse docking time normalized by the number of rotatable bonds is 2.28 s per bond, and standard deviation of this normalized value is 1.45. Also, complicated molecular structures could imply more side chain conformations. In coarse docking, after the best-fit pose is proposed within the docking boundary box, the individual poses need to be sorted and grouped. In the fine docking step, both ligand and receptor side chain rotamers are sampled simultaneously for each conformation. Note that all the conformations in this step are carefully explored. As the number of conformations inside the coarse docking group goes up, the total docking time also proportionally increases.

We note that the time spent in fine docking ranges from 4 s to 13 min. Further, only 3.3% of the docking pairs consume time more than 3 min in this step. Although the total execution time is less than that in the coarse docking step, every candidate will take more time because of the enrichment exploration. Inside coarse docking, MedusaDock uses a Monte Carlo search method to generate candidate poses corresponding to a ligand rotamer. This step is implemented in an inherently sequential manner with dependence between the current and next proposed poses. Parallel Monte Carlo algorithms on GPU have been studied in prior work.^41–43 However, these need to be adapted to work with MedusaDock, and this is not straightforward. When accelerating the code on a GPU, it is important to retain the accuracy of the CPU code. Fine docking is repeated multiple times, once for each candidate pose from the prior step, to determine the best pose. This step is easier to parallelize because there are no inter-iteration dependencies.

We evaluate the energy profile for one representative instance when executing the Monte Carlo search method (Figure 2D). We perform 10 000 docking attempts for each protein–ligand pair and select the minimum energy pose (green circle in Figure 2D) from these 10 000 attempts as the global minimum. If our computational budget were lower, e.g., only 1000 docking attempts, the pose indicated as a blue diamond would be chosen to be the minimum energy pose. For the nine instances considered (details in the artifact appendix), we find that the minimum energy pose in the first 100 draws is within 3.5% (geometric mean) of the global minimum. Note that the number of draws per ligand rotamer is a key performance determinant and is often heuristically chosen.^44–46

Overall Performance.

The GPU-accelerated code (i.e., one GPU and one CPU core) takes about 101.9 h (4.25 days) to process the entire data set of 3875 protein–ligand complexes, while the original code using a single CPU core takes nearly 157 h (or more than six and a half days). This indicates a 1.54× overall speedup with GPU acceleration (Figure 3, parts A and B). The chart on the left shows the speedup achieved for different instances when the instances are sorted in an increasing order of the total docking times for the CPU version. The cumulative elapsed time for the CPU-only and the CPU+GPU codes are also given. The per-instance speedup can vary, and no correlation with running time is immediately discernible from the figure. A speedup histogram is shown on the right. We see that the median speedup is 1.18× and the maximum speed-up for any instance is 2.93 ×.

Figure 3.

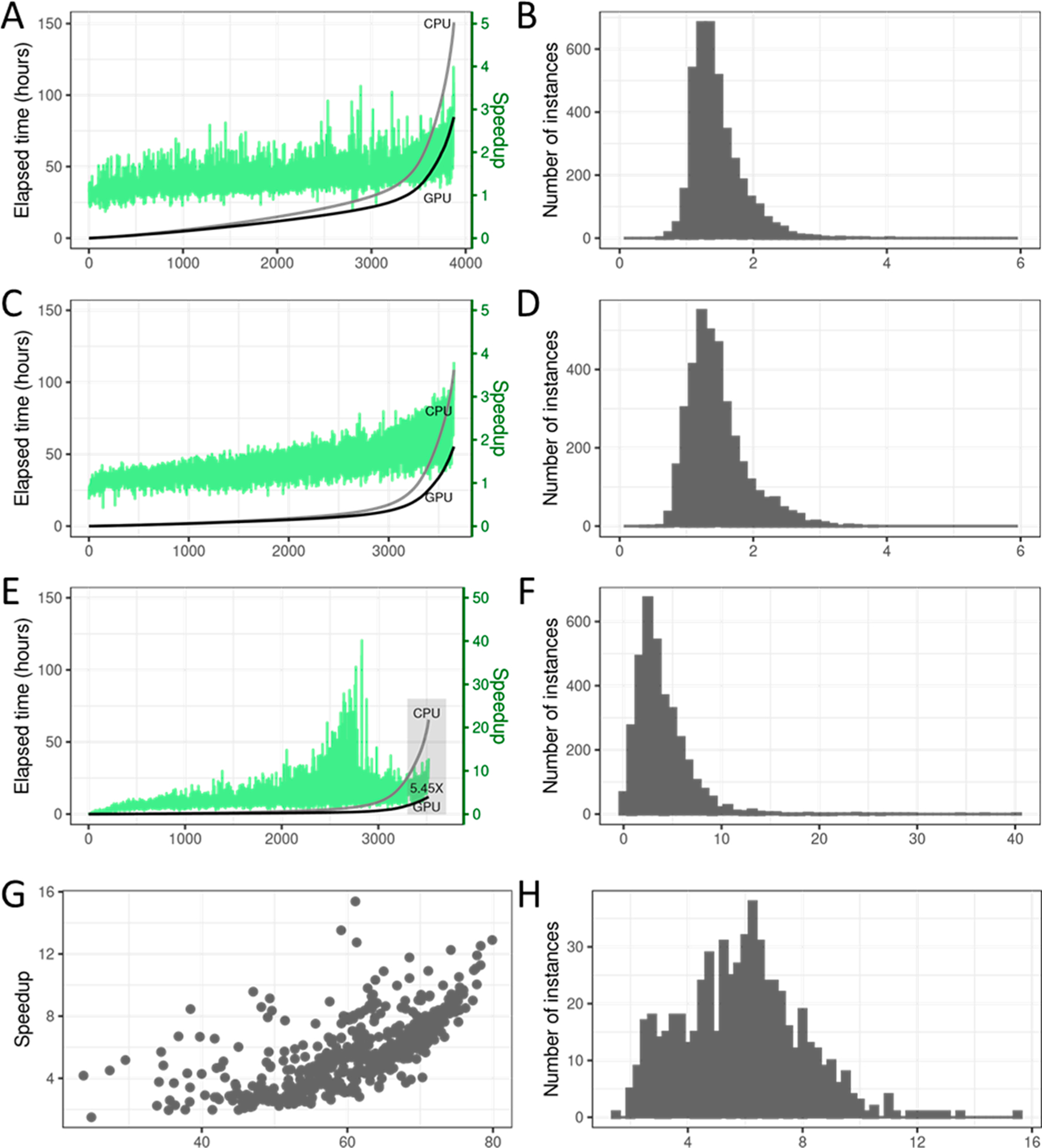
Overall performance on entire collection of 3875 complexes. (A) Elapsed time in hours for CPU-only and the CPU+GPU codes, with per-instance speedups indicated as green bars on secondary axis. (B) Histogram of per-instance speedup (i.e., ratio of CPU-only time and CPU +GPU execution time). (C) Elapsed time in hours for CPU only and the CPU+GPU codes, with per-instance speedups indicated as green bars on the secondary axis. (D) Histogram of per-instance speedup (i.e., the ratio of CPU-only time and CPU+GPU execution time). (E and F) Performance of the pose search step in coarse docking phase: (E) Elapsed time in hours for CPU-only and the CPU+GPU codes, with per-instance speedups indicated as green bars on the secondary axis. (F) Histogram of per-instance speedup (i.e., the ratio of CPU-only time and CPU+GPU execution time). (G and H) Performance of the pose search step in coarse docking phase on instances where the CPU-only search time is greater than 1 min: (G) Possible correlation between parallelized work and GPU speedup achieved. (H) Histogram of per-instance speedup (i.e., the ratio of CPU-only time and CPU+GPU execution time).

To better understand the performance, we compare the cumulative running time of the CPU-only and the GPU-accelerated codes for just the coarse docking phase (Figures 3C and 3D). The CPU-only coarse docking for all instances takes 108.7 h, or 69.2% of the total execution time. The GPU-accelerated code for this step is 1.99× faster, taking 54.5 h. Note that we only modify the coarse docking phase of MedusaDock for GPU acceleration. We notice less variation in per-instance speedup when compared to Figure 3A. In both the charts, the instances are ordered in increasing order of CPU-only execution time. The median speedup when considering only the coarse docking phase is 1.38×. For some instances, the coarse docking phase is not executed at all, and these are omitted. The maximum speed-up for any instance is 3.8×.

Since our GPU search algorithm is different from the original CPU version, we also develop a CPU implementation of the GPU algorithm for comparison. This CPU implementation is not fully tuned, vectorized, or parallelized, but could serve as a starting point for future work. In Table 2, we compare the different approaches. The speedup reported is calculated by summing up the total time taken for the subset of 100 instances. For coarse docking alone, the GPU approach is 7.67× faster than the corresponding CPU implementation. For an individual instance, the peak speedup can reach up to 10.4 ×.

Table 2.

GPU Version Speedup versus GPU Algorithm Implemented on CPU and Original CPU Version^a

	total docking time		coarse docking time
	GPU/GoC	GPU/CPU	GPU/GoC	GPU/CPU
speedup	6.10	1.85	7.67	1.92

^aGoC: GPU algorithm implemented on CPU. CPU: CPU original version. GPU: GPU optimized version.

We next evaluate the performance improvement for the pose search step of the coarse docking phase. Coarse docking has many steps, and our GPU parallelization primarily targets the pose search step, where we use an alternative to the Monte Carlo algorithm. We compare the cumulative time for pose search with a CPU-only implementation with the time for the GPU-accelerated code (Figure 3, parts E and F). We see that pose search is indeed the dominant step in coarse docking, constituting around 60.2% of the cumulative coarse docking time. The cumulative GPU kernel time for this step is 12 h, corresponding to a 5.45× speedup. The per-instance speedups also span a wide range, with the maximum speedup reaching nearly 40×. A histogram of speedups is also given, and the median speedup is 3.23×.

We now isolate the instances for which the coarse docking phase takes more than 1 min. We find the GPU acceleration is primarily due to a reduction in running time for long-running instances (Figure 3, parts C and 3D). We also note higher speedups for instances where pose search takes a greater fraction of the coarsening time (Figure 3, parts G and H). Furthermore, the speedup histogram shows the median speedup moving further to the right in comparison to prior speedup histograms.

We also evaluated MPI parallelization on this large data set. We have two distributed memory MPI versions of the code: a CPU-only version, where we use one processor core per process, and a GPU-accelerated version using a CPU core and a GPU. Both versions use the master–worker paradigm with one master process assigning work (instance identifiers) to worker processes. We execute the CPU-only version on nine compute nodes using 20 cores per node (the remaining cores on a node are reserved for GPU jobs) for a total of 180 worker cores. The running time is 1.5 h, corresponding to a 105× speedup over the single-core run. Due to allocation limits, we cannot execute the code on a large number of GPUs and with the entire data set. When running with nine worker GPUs and 100 picked instances, we achieve an 8× speedup over the single-node GPU-accelerated version. The parallel overhead is negligible for master–worker configurations at such low concurrences, and the MPI version’s strong scaling speedup is decided by the running time of the last process to finish. The time, in turn, depends on the data distribution and the number of instances. For the CPU-only evaluations, we use the distribution shown in Figure 2A, which appears to be random. Tuning the number of instances assigned to each process could reduce load imbalance and further improve performance.

GPU Acceleration Evaluation.

We next assess the impact of memory-centric optimizations and data structure design choices. We evaluate the performance improvement over a baseline implementation with different GPU optimizations for a collection of 10 randomly chosen instances (Figure 4A). The Pgrid optimization corresponds to the use of a grid to simplify proton energy calculations. The results indicate that this optimization achieves a consistent 2% performance improvement (or 1.02× speedup over the baseline) for the 10 test cases. The Agrid optimization captures the influence of the grid structure on atom-related energy calculations. The results are mixed for this optimization, with some instances showing a performance improvement ranging from 7.4% to 18.6% and others showing a performance drop (up to 24%). The ratio of the number of atoms to the number of grid cells is a key indicator of the efficacy of this optimization. This ratio is analogous to the particles-per-cell value in particle-grid n-body calculations. We intuitively expect this value to be high for the optimization to show an impact. Indeed, for the 10 cases, we observe that the ratio needs to be at least 1.5 for this optimization to have a positive impact. Furthermore, we would like the number of atoms per grid cell to be roughly balanced, or else threads processing a higher number of atoms per cell will limit overall performance. Lookups to empty cells are also wasteful. Moreover, the grid data structure increases the indirection in the code. Despite these drawbacks, we expect this optimization to be useful for cases with a higher number of atoms per grid cell.

Figure 4.

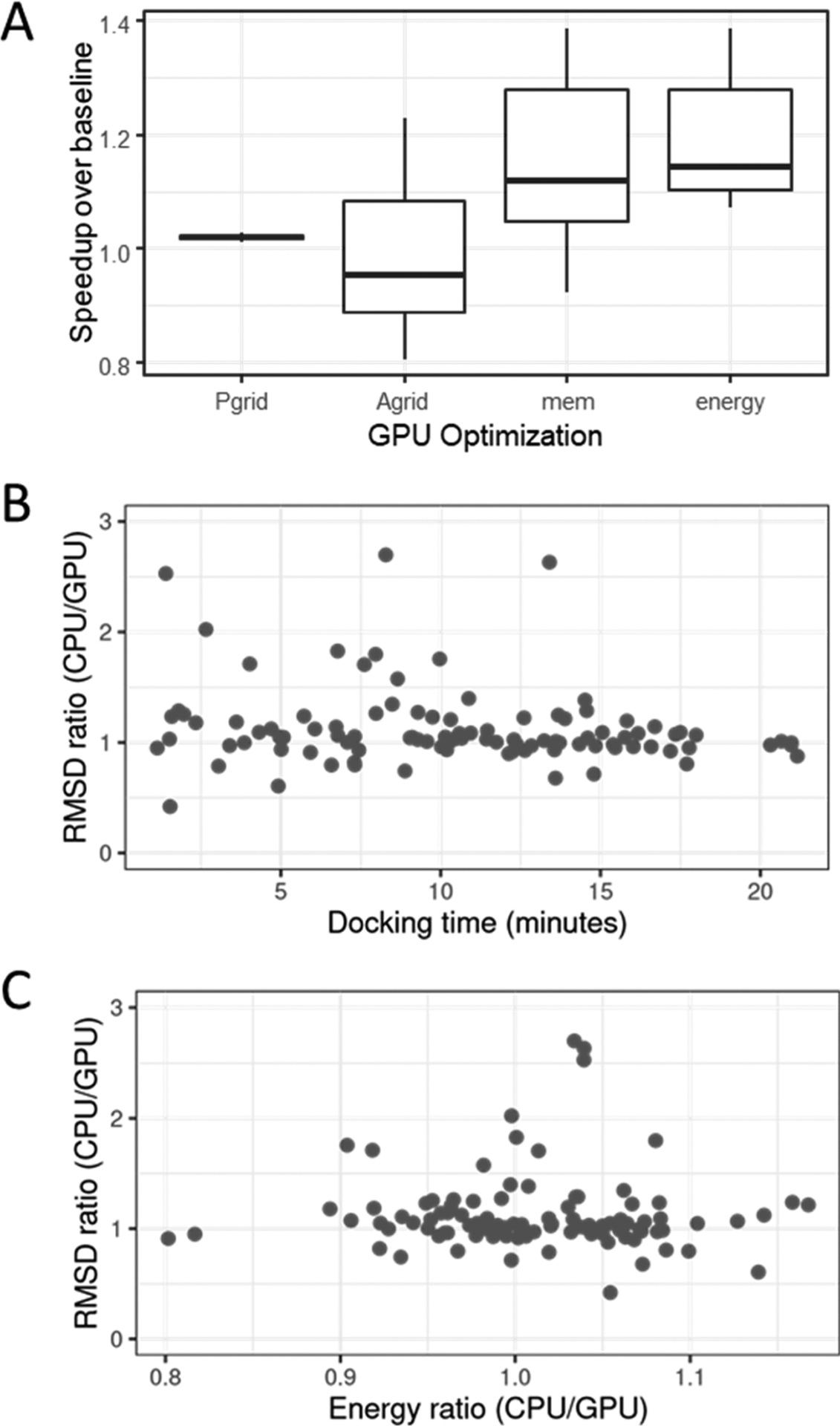
(A) Performance impact of four GPU optimizations over a baseline implementation. Ten instances are randomly chosen. (B) Comparing docking quality for 100 picked instances: possible correlation between RMSD ratio (i.e., RMSD_CPU/RMSD_GPU) and docking time. Values greater than 1 indicate GPU implementation outperforms CPU. (C) Comparing docking quality for 100 picked instances: Energy and RMSD ratios were obtained for various instances.

The mem optimization corresponds to performance improvement with memory-centric optimizations discussed previously. Results indicate an improvement in most cases, with the geometric mean of speedups being 1.15×. The final energy optimization refers to an automatic choice of the atom grid data structure or a grid-free calculation based on the number of atoms per grid cell. This optimization results in a performance improvement in all cases, with the geometric mean being 1.19×.

Additional performance improvements that are intrinsic to our CUDA implementation are not captured in the above analysis. All performance results assume the grid structure and Monte Carlo algorithm default settings given in the previous section. It is possible to trade off accuracy with faster execution times, but we choose our defaults such that they consistently improve on CPU-only performance, as shown in the next subsection.

Docking Accuracy Evaluation.

We perform a comprehensive evaluation of the docking quality using two metrics: the docking energy and the root-mean-square deviation (RMSD) with respect to the experimental pose. For the RMSD, we calculate the minimum RMSD and the RMSD of the pose with the best (minimum) docking energy for each protein–ligand pair. The minimum RMSD reflects if the sampling of the conformation is enough, and the RMSD of the pose with the best docking energy reflects if the scoring of the docking program is good enough to select the best sampled conformation. We first compare the docking energy of the CPU version to the GPU-accelerated version (Table 3). We classify the 3,875 instances into two classes, poses that have similar energy and poses that do not. Using the similarity metric defined in this table (loosely stated, the energies being 10% of each other), we find that more than 81% of instances (3145 out of 3845) have similar energies. Among these instances, the CPU version finds a lower energy pose for a slightly larger fraction (53%). For the cases where the predicted poses are dissimilar, the GPU version slightly outperforms the CPU version. These results suggest that the performance of the sampling procedure of the GPU version of MedusaDock is comparable to the CPU version. We similarly separate minimum RMSD-based quality evaluation into parts using an RMSD threshold of 2 Å (Table 4). There are 471 instances (12.1% of total instances) for which both the CPU and GPU implementations give poses with RMSD less than or equal to 2 Å. For the rest of the cases in this category, the GPU implementation has a slight edge. For the other category of RMSD greater than 2 Å, we define poses to be similar to each other if they differ by an RMSD of 2 Å. A large fraction of total instances (55.2%) falls into this category. For the remaining instances, the GPU implementation again has a slight edge in terms of quality. We further compare the minimum RMSD and the RMSD with minimum docking energy of MedusaDock to RosettaLigand and AutoDock Vina (Figure 5). The result shows that our success rate (the number of protein–ligand pairs that have RMSD < 2 Å in the data set) calculated by minimum RMSD could reach 57.5%, while RosettaLigand and AutoDock Vina could only reach 32.1% and 51.3%. If we calculate the success rate by the RMSD of the conformation with the minimum docking energy, MedusaDock, RosettaLigand, and AutoDock Vina can reach 28.6%, 13.8%, and 24.5%, respectively. Of note, the success rate is low because our data set is challenging since we have deleted all easy-to-dock protein–ligand pairs (see Methods).

Table 3.

Docking Quality Comparison Using Pose Energy^a

counts	|EGPU − ECPU| ≤ δ	|EGPU − ECPU| > δ
total	3145	730
EGPU ≤ ECPU	1462	471
EGPU > ECPU	1683	259

^aδ = 1.1 × max(E_GPU,E_CPU).

Table 4.

Docking Quality Comparison Using Root Mean Square Deviation (RMSD)

	δ = 1.1 × max(EGPU,ECPU)	δ = 1.1 × max(EGPU,ECPU)
total	1268	2607
common	471 (both low)	2138 (similar)
GPU	409 (low GPU-only)	280 (GPU lower)
CPU	388 (low CPU-only)	189 (CPU lower)

Figure 5.

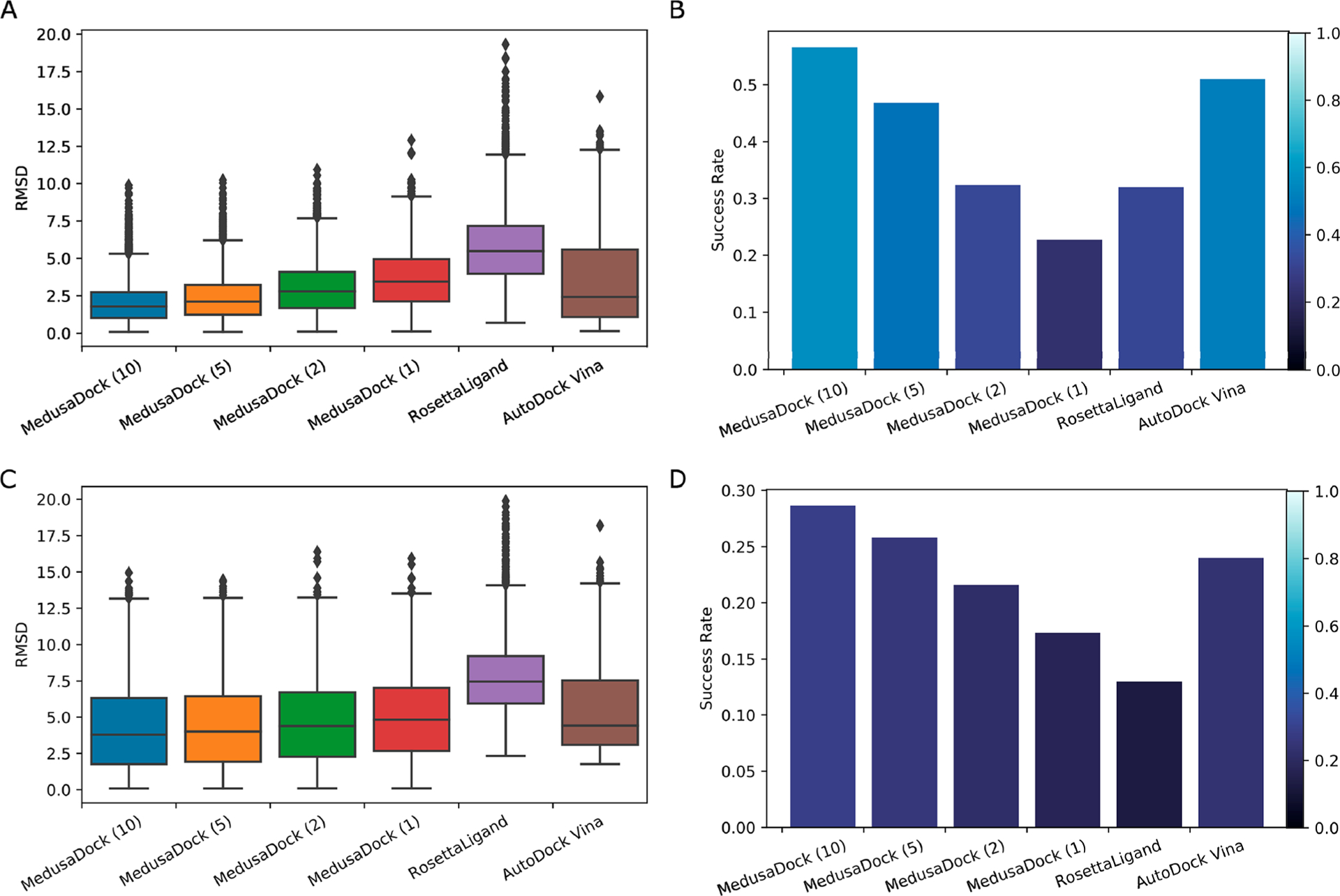
(A) Distribution of the minimum RMSD of MedusaDock GPU version, RosettaLigand, and AutoDock Vina on the PDBBind data set. The number inside the parentheses stands for the number of iterations of the MedusaDock GPU version. (B) Success rate (minimum RMSD < 2 Å relative to experimental data) of different docking software and different running iterations of MedusaDock GPU version on the PDBBIND data set. (C) Distribution of the RMSD with minimum docking energy of MedusaDock GPU version, RosettaLigand, and AutoDock Vina on the PDBBind data set. (D) Success rate calculated by the RMSD with minimum docking energy of different docking software and different running iterations of MedusaDock GPU version on the PDBBIND data set.

Finally, we compare quality metrics to execution time and to each other to check for correlations. We reuse the collection of 100 instances previously used to evaluate multi-GPU performance and do not discern notable correlations (Figure 4, parts B and C).

CONCLUSION

In this work, we proposed coarse- and fine-grained parallelization of computational molecular docking for GPU clusters. We selected the MedusaDock docking software to implement the proposed parallelization strategies. The GPU kernel is carefully optimized, and several application-specific tuning strategies are proposed. We performed a comprehensive evaluation of both running time and result quality to show that the GPU version outperforms the CPU approach in terms of the result quality. Our approach also permits future investigations of time-quality trade-offs.