Abstract
Real-time gait event detection (GED) system can be utilized for gait analysis and tracking fitness activities. GED for various types of terrains (e.g., stair-walk, uneven surfaces, etc.) is still an open research problem. This study presents an inertial sensor-based approach for real-time GED system that works for diverse terrains in an uncontrolled environment. The GED system classifies three types of terrains, i.e., flat-walk, stair-ascend and stair-descend, with an average classification accuracy of 99%. It also accurately detects various gait events, including, toe-strike, heel-rise, toe-off, and heel-strike. It is computationally efficient, implemented on a low-cost microcontroller, works in real-time and can be used in portable rehabilitation devices for use in dynamic environments.
Keywords: Gait event detection (GED), Terrain classification, Adaptive
1. Introduction
Human gait analysis contributes to the development of applications in several domains, such as, fitness, sports, medical, security etc. Gait phase partitioning is often a crucial step in various gait-related applications [1], [2] and is a challenging research area [3], [4], [5]. Human gait events have been assessed using a variety of motion capture methods. These type of studies are usually performed in a motion analysis lab with force platforms and optical motion capture systems. These motion capture devices, however, are non-portable [6], function only in controlled conditions [7], and are thus unsuitable for analyzing successive gait cycles in long-term mobility situations [8].
Recent research indicates that measuring human movement in real world environments is an active area of interest [9]. For gait events detection, force-based devices, such as, the foot switches or force sensitive resistors (FSRs) are widely regarded as the gold standard [8]. However, these sensors are prone to mechanical failure [5], can be unreliable when employed by patients with drop-foot condition, owing to their changing weight when standing [10], and do not offer any information on the orientation of the foot [11].
To overcome some of the limitations of force-based sensors for GED, researchers focused on inertial sensors, which include, gyroscopes [6], [12], [13], accelerometers [14], [15], [16], and inertial measuring units [17], [8], [11]. However, in the presence of vibrations, the accelerometer data becomes unreliable [11]. To cater for this issue, gyroscopes have been used due to their better performance compared to accelerometers. However, gyroscope data tends to drift over time [18]. To get accurate angular data, inertial measuring units that comprise of both accelerometer and gyroscopes have become a popular choice due to their robustness and low-cost. Inertial sensor is usually placed on shank or foot, however, studies suggest that placement on the foot produces more reliable performance in GED [15].
A hidden markov model-based adaptive method for gait detection was proposed in [19]. It used two inertial sensors to detect gait events on flat path. The algorithm was validated by comparing the results with motion capture cameras. A fuzzy logic approach to detect gait events was proposed in [20]. The methodology used three IMU sensors and FSR-based foot insoles and tested the algorithm on level walking area. A real-time rule-based GED system was proposed that used a gyroscope and three FSRs [21]. Similarly, four gait parameters were detected using four motion sensors (two sensors per leg) [22] and the results were compared using a motion capture system. Another study [23] used three sensors (1-FSR, 2-accelerometer) to detect the initial contact of the foot in real-time. A study [24] incorporated three sensors including one gyroscope and two accelerometers, to detect the heel-strike (HS) and toe-off (TO) events using a heuristic algorithm and validated the results using the foot switches. The above-mentioned approaches required multiple sensors that add cost and complexity to the system.
A GED system was developed that used single wearable gyroscope [25]. The system tested the algorithm in a controlled environment (treadmill, walking straight and inclined) and real world terrains (stair-ascend, inclined slope and straight). However, the real-time terrain identification was missing from the system. An infrared-based heel-strike and toe-off detection system [26] was developed and tested on flat-walk, ascending slope, and descending slope and on transitions. However heel-rise and toe-strike were not calculated. Similarly, a force-myography based approached was proposed to detect heel strike and toe off on ground and ramp [27].
A single motion sensor was used to detect only two gait events; heel-strike and toe-off by implementing three different algorithms, i.e., linear discriminant analysis, quadratic discriminant analysis and threshold-based algorithms [32]. The study concluded that the threshold-based algorithm was the most effective among all. Another study [33] used a similar approach as [32], and used threshold-based algorithm, except that they placed the motion sensor on metatarsal bone, just above the toe, instead of placing it on shank [32].
The above-mentioned studies were based on a single algorithm but did not take into account the differences in trajectories and gait sequences for different terrains (flat-walk, stair-ascend, stair-descend). A discrete wavelet transform and fuzzy logic-based approach to classify gait patterns on flat-walking, stair-ascending and stair-descending was proposed that used six inertial sensors [34]. An ambulatory gait parameter calculation system [28] and activity classification system (flat-walk, stair walk, and ramp walk) was developed that used single IMU, however GED was not calculated. A machine learning based classification of five terrains (level ground, stair-ascend, stair descend, ramp ascend, and ramp descend was proposed which used 8 insole pressure sensors one each foot [29] Another discrete wavelet transform based approach [30] was proposed to classify flat walk, stair ascend, and stair descend using IMU.
While the above-mentioned studies have made valuable contributions to Gait Event Detection (GED) or terrain classification, there are still significant opportunities for further advancements in these areas. Many of these tested their algorithms either offline or in controlled environments. GED on stair-ascend and stair-descend is still open to research. Furthermore, most algorithms require high computational power which is also a critical factor in real-time systems. From the above discussion we can infer that a GED should be accurate, computationally efficient, low-cost and should adapt to diverse terrains. In this study, a real-time, two-stage, multi-terrain classification and adaptive GED system is proposed. Table I shows the comparison of the proposed system with relevant existing studies. The proposed system is implemented on a low-cost 32-bit microcontroller and is tested in real-time on healthy subjects, who traverse on diverse terrains. The performance of the proposed method is evaluated with reference to FSRs which are widely regarded as the gold standard for GED [8].
Table I.
Comparison of proposed study with existing Studies.
| Reference | Sensor | Method | Diverse Terrains | Terrain Classification | Gait Event Detection |
Fs (Hz) | ||
|---|---|---|---|---|---|---|---|---|
| Flat-Walk | Stair-Ascend | Stair-Descend | ||||||
| [28] | IMU | Heuristic | Yes | Yes | 100 | |||
| [29] | Pressure sensors + IMU | Machine Learning | Yes | Yes | 50 | |||
| [30] | IMU | Wavelets Based | Yes | Yes | 100 | |||
| [26] | Infrared | Heuristic | Yes | Yes | 86 | |||
| [27] | Force Myography | Heuristic | Yes | Yes | 130 | |||
| [31] | IMU | Heuristic | Yes | Yes | Yes | 125 | ||
| [25] | IMU | Heuristic | Yes | Yes | Yes | 100 | ||
| This study | IMU | Heuristic | Yes | Yes | Yes | Yes | Yes | 50 |
2. Methodology
This section describes the main parts of methodology which includes experimental setup and algorithm development. Experimental setup includes hardware description, data collection, and data analysis procedures. Algorithm development part provides technical explanation of terrain recognition and GED algorithm.
2.1. Experimental setup
The system comprises of a single Inertia Measuring Unit (IMU) sensor MPU6050 with 6 degree of freedom (DOF) with 3-axis gyroscope and a 3-axis accelerometer. The accelerometer has a range of ± 2G and the gyroscope has a range of± 250 deg/s. Two 38 mm square force-sensitive resistors (FSRs) are integrated [35]. The FSRs are calibrated using a potential divider circuitry in such a way that when the toe or heel contacts the ground, a corresponding analog signal value ranging between 0 and 1023 is obtained, with a threshold value of 200 used to determine the state of each gait event. The system has a mini WiFi board with 4 MB flash based on ESP-8266 (WEMOS D1 mini) microcontroller. It receives the data from IMU and two FSRs and executes all the processes and communicates with the laptop using WiFi. All the computations are done in real-time on microcontroller and the data is sent to the laptop for analysis and plotting results. Moreover, a camera is used to capture the gait motion for reference. The data is received on the laptop using open-source Telemetry-Viewer software [36].
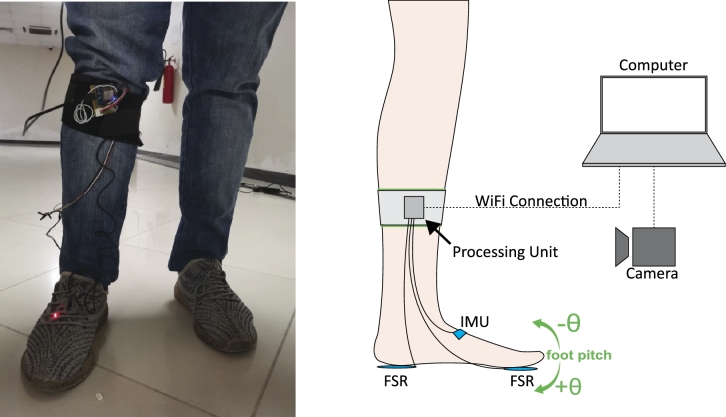
To develop the terrain classification and GED method, a sample dataset was collected from 18 healthy individuals, consisting of 13 males and 5 females aged between 20 and 32 years. The participants' body mass index (BMI) ranged between 18.83 and 29.95, indicating a healthy body composition. Their height varied from 157 to 180 cm, which also is an average range. The participants of our study well-represent the young population. Data was recorded for three terrains, which include, flat-walk, stair-ascend, and stair-descend. The sensor placement is shown in Fig. 1.
Figure 1.
Visual representation of data collection setup.
This study was conducted after the approval of the research ethics committee of the Institute of Space Technology and all the subjects signed an informed consent form. Data collection system comprising an IMU sensor for foot orientation is carefully attached to the right foot of each subject. IMU sensor is placed on the shoe in such a way that planterflexion produces a positive pitch angle and inversion produces a positive roll angle as shown in Fig. 2.
Figure 2.
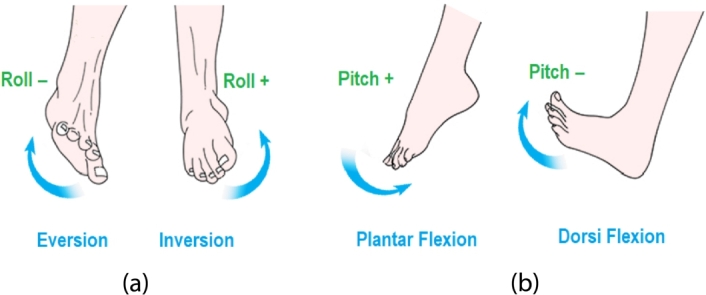
(a) Foot roll angles and (b) Foot pitch angles.
The real-time data is received on a computer through WiFi at a sampling rate of 50 Hz. The is set low to improve the computational efficiency while maintaining the performance of the system. Moreover, a real-time video of the foot orientation is integrated with the data acquisition system for visual reference. The received data consisted of pitch and roll angles of foot, FSR data and timestamp.
The FSR data in this study comprises analog readings obtained from two FSR sensors, which were positioned inside the shoe beneath the heel and toe areas of the subject's foot. These sensors operate on the principle in which the resistance of the sensor increases in proportion to the applied pressure, allowing for the detection of the reference gait event.
The data is collected for a minimum period of 15 minutes from each subject. All subjects were asked to perform the following tasks.
-
•
Walking on 50 m flat surface
-
•
Walking on 12-stride ascending staircase with a uniform step-height of 7 inches (2-4 sessions)
-
•
Walking on 12-stride descending staircase with a uniform step-height of 7 inches (2-4 sessions).
The data from IMU is acquired using an open source library [37] which uses nonlinear complementary filtering [38] to provide accurate angle signal in degrees.
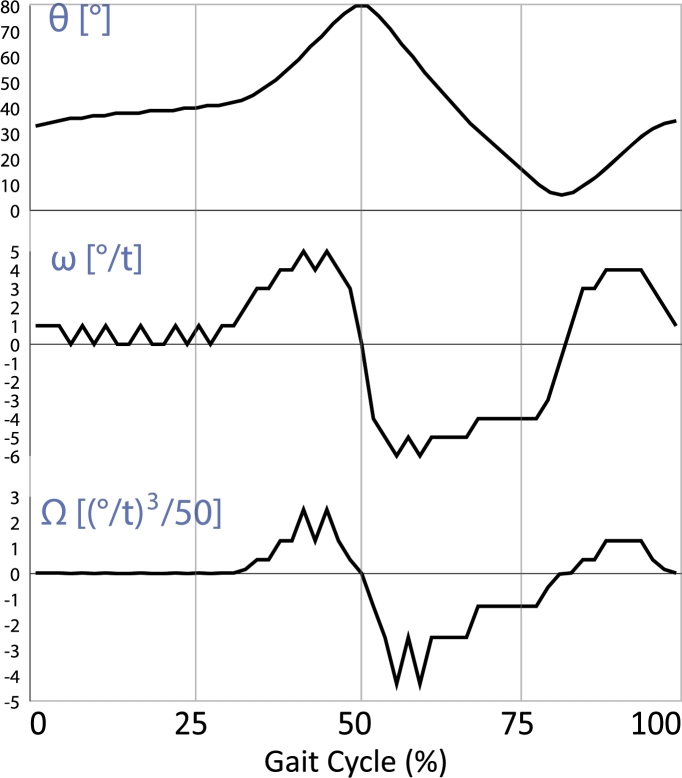
After the data analysis of all terrains it was found that all the information necessary to develop a real-time terrain classification and GED system can be extracted from foot pitch angle θ because of its morphological characteristics. First order derivative [39] of θ is calculated to find the angular velocity ω. In order to remove small fluctuations and magnify major changes in angle, cube of ω is also calculated. For better visualization, the resulting value is down-scaled by a factor of 50 which scales the signal between -5 and 5 as shown in Fig. 3. The cubic angular velocity Ω is expressed in equation (1).
| (1) |
Figure 3.
Foot pitch angle θ, angular velocity ω, and cubic angular velocity Ω for a single stride. Sampling time (t)=0.02 s.
2.2. Human gait cycle
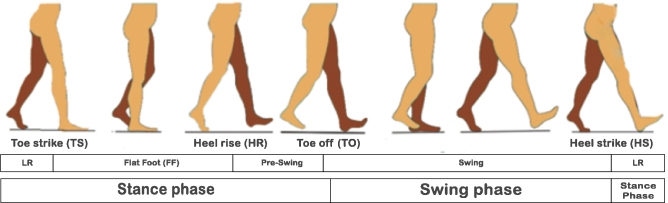
Human gait cycle can be divided into stance phase and swing phase (SW). Stance phase can be further divided into foot-loading (FL), flat-foot (FF) and pre-swing (PS). There are four main gait events that include toe-strike (TS), heel-rise (HR), toe-off (TO) and heel-strike (HS) for each foot as shown in Fig. 4 (a).
Figure 4.
(a): Gait phases and gait events.
TS is the instance in which toe touches the ground. The duration from TS to HR is FF during which foot remains completely on the ground. During this period, there is negligible change in θ. So, Ω is almost zero. HR is the instance where FF period ends. At HR, heel is lifted and a sudden positive increase in Ω is observed and remains positive until TO is achieved. The duration from HR to TO is PS. After the HR, the final contact of foot with the ground is at TO. As soon as the toe is lifted from the ground, ω changes sign from positive to negative and the SW starts. The SW of the foot ends at HS. During SW, ω remains negative. At the point of HS, ω changes sign. The duration in which the foot takes the entire weight of the body, from HS to TS, is FL. During FL, a positive ω is observed for a short duration.
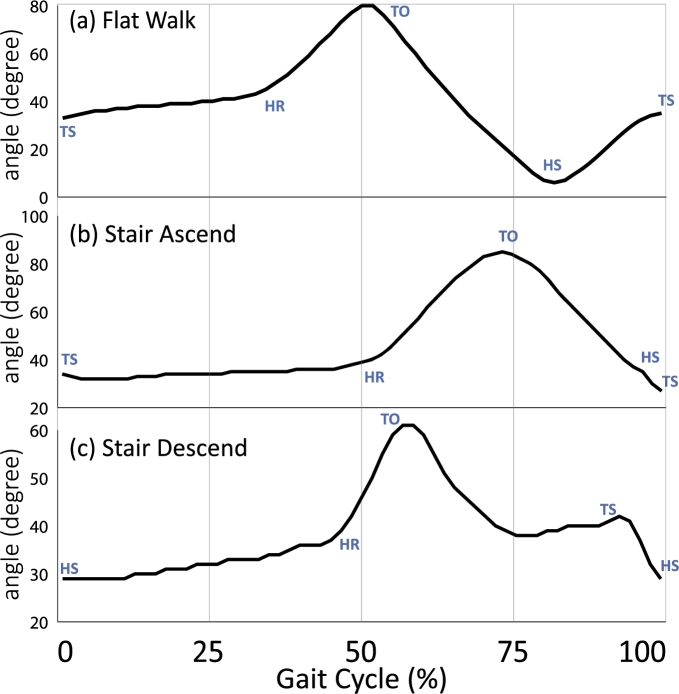
The shape of pitch angle trajectory during stair-walk is different from flat-walk as shown in Fig. 5. However, a clear positive slope after HR can be observed in both stair-ascend and descend data in Fig. 5. Similarly, ω changes sign at TO in both trajectories. During stair-descend, the subject lands foot on toe, therefore, HS comes after TS and the foot loading sequence is inverted. A sudden increase in Ω can be observed during HR in all types of terrains.The θ trajectories of flat-walk, stair-ascend and stair-descend from single subject data are also shown in Fig. 5.
Figure 5.
Multi-terrain θ trajectories in degree (a) Flat-walk θ trajectory (b) Stair-ascend θ trajectory (c) Stair-descend θ trajectory.
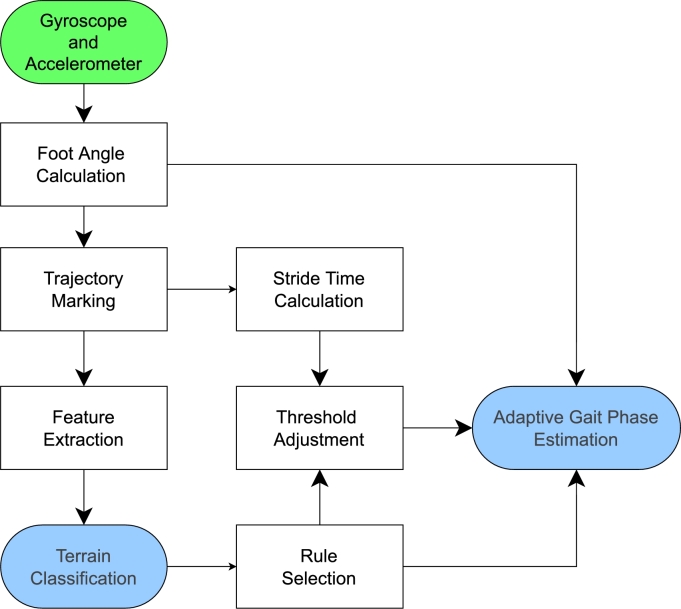
The block diagram of the proposed system is shown in Fig. 6. Initially, pitch signal θ in degrees is calculated from IMU data. Secondly, θ is marked on various points to estimate the morphology of trajectory. Thirdly, the relevant features are calculated based on marker values to classify different terrains into flat-walk, stair-ascend or stair-descend. Finally, based on the classified terrain and walking speed, GED algorithm is fed with the corresponding set of rules.
Figure 6.
Block diagram of proposed GED system.
2.3. Trajectory marking
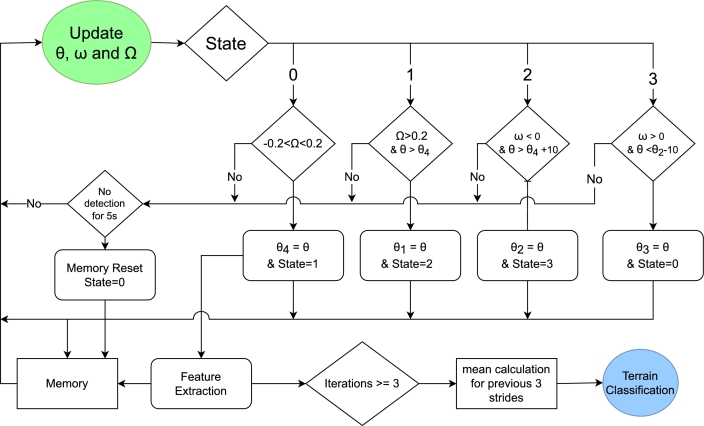
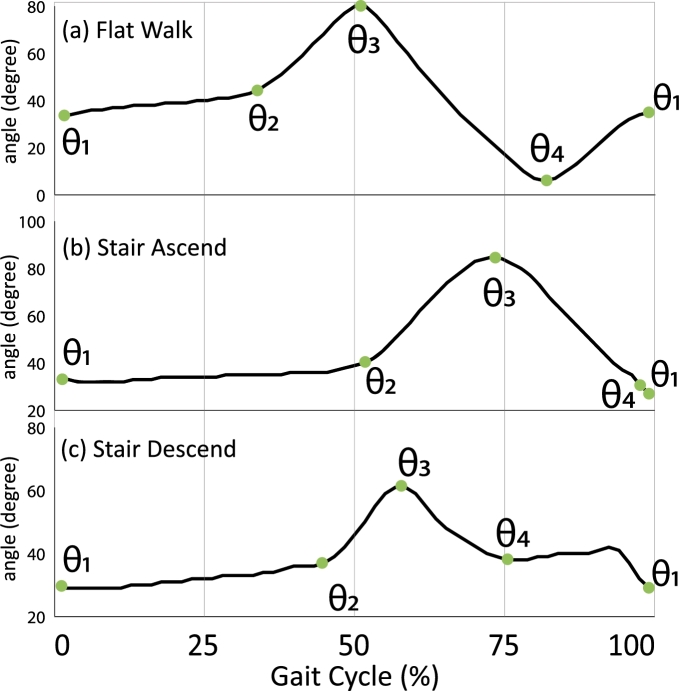
At the start of the iteration, the values for and Ω are updated, after that the state which represents the previous algorithm state is checked. There is a set of conditions for each state. The conditions for each state are explained with the help of flow chart in Fig. 7. The θ values at which the state is changed is stored in memory as and . The morphology of trajectory of θ can be estimated using these values as illustrated in Fig. 8, which represents a single subject's θ for a single stride on different terrains. These values are used for calculating features for terrain classification. If no state is changed for five seconds, the memory resets to initial values.
Figure 7.
Flow chart representing the process of identifying markers of θ.
Figure 8.
Trajectory marking of single subject's θ (degrees) (a) Flat-walk (b) Stair-ascend (c) Stair-descend.
2.4. Feature extraction
Before doing terrain classification, features and are computed using equations (2), (3), (4) and (5) using values of and calculated in Section 2.3.
| (2) |
| (3) |
| (4) |
| (5) |
These morphological features represent the trajectory of angles with respect to different terrains as shown in Fig. 8. These morphological features are easily computed in real-time and are robust. The features are averaged for a maximum of three consecutive strides , where represents the current stride.
2.5. Terrain classification
Based on the features computation in Section 2.4 the terrain can be classified into three classes; flat-walk, stair-ascend and stair-descend. The thresholds for each feature value were selected through empirical data analysis. If the value of <=-5, the terrain is classified as stair-descend, else if >3.5 and <15, then the terrain is classified as stair-ascend, else if >0, >15 and <2, the terrain is classified as flat-walk. These conditions for terrain classification are summarized in Table II.
Table II.
Feature thresholds for terrain classification.
| Flat-Walk | Stair-Ascend | Stair-Descend | |
|---|---|---|---|
| f1 | >0 | - | - |
| - | 3.5 | - | |
| >15 | <15 | - | |
| <2 | - | <=-5 |
2.6. Gait event detection
Once the terrain is classified, a set of rules for corresponding terrain are used for GED. For that, θ, ω, Ω and mean stride time are used and given in equation (6).
| (6) |
The set of rules for each terrain (class) are given in Table III. These set of rules are carefully determined after observing the morphological characteristics of θ trajectories on each terrain from the data gathered from 18 subjects. Some rules vary slightly for different terrains while others are entirely different. In flat-walk, TS is detected when ω is less than 2 and greater than -2. HR is detected when Ω is greater than 0.5, current time (t) has passed 10% time of previous stride time since last TS event. TO is detected when Ω is less than 0. HS is detected when ω is greater than 0 and θ is at least 10 degrees lesser than .
Table III.
Set of GED rules corresponding to each terrain class.
| Terrain | Gait Event | Condition | |||
|
Flat-Walk |
Toe-strike, |
|
|||
| Heel-rise, |
|
||||
| Toe-off, | Ω < 0 | ||||
| Heel-strike, |
|
||||
|
Stair-Ascend |
Toe-strike, | −2 < ω < 2 | |||
| Heel-rise, |
|
||||
| Toe-off, |
|
||||
| Heel-strike, |
|
||||
| Stair-Descend | Heel-rise, |
|
|||
| Toe-off, | Ω < 0 | ||||
| Toe-strike, |
|
||||
| Heel-strike, | −2 < ω < 2 | ||||
2.7. Performance metrics
To evaluate the performance of terrain classification method, the accuracy, sensitivity and specificity are calculated for each class. Accuracy is the proportion of correct classifications and computed by taking the ratio of correct classifications to the total classifications. Sensitivity is the proportion of true positive results and is computed by the ratio of total true positive assessments to total positive assessments. Specificity is the proportion of the true negative results and is computed by the ratio of total true negative assessments to total negative assessments. For the evaluation and validation of GED, the results of our proposed method were compared with the output from reference FSR-based method. Mean absolute error (MAE) was computed by taking the average of absolute errors of each detection event in time. The detected events with MAE greater than 100 millisecond (ms) were marked as missed detection and subsequently detection accuracy for each event was computed. The advance detection percentile, delay detection percentile and exact detection percentiles were also computed for each event.
3. Results
This section presents the performance analysis of terrain detection and GED capabilities of the proposed method. A total of 999 strides from 10 subjects (male/female: 7/3, age (years): , BMI: , Height (cm): ), were observed to test the proposed terrain classification and GED method. Sample size of each subject consisted of a minimum and maximum of 30, 12, 12 and 50, 48, 34 strides for flat-walk, stair-ascend and stair-descend terrains respectively. The total data included 386 flat surface strides, 398 stair-ascend strides and 215 stair-descend strides. Stairs had a uniform step height of 7 inches.
3.1. Terrain identification
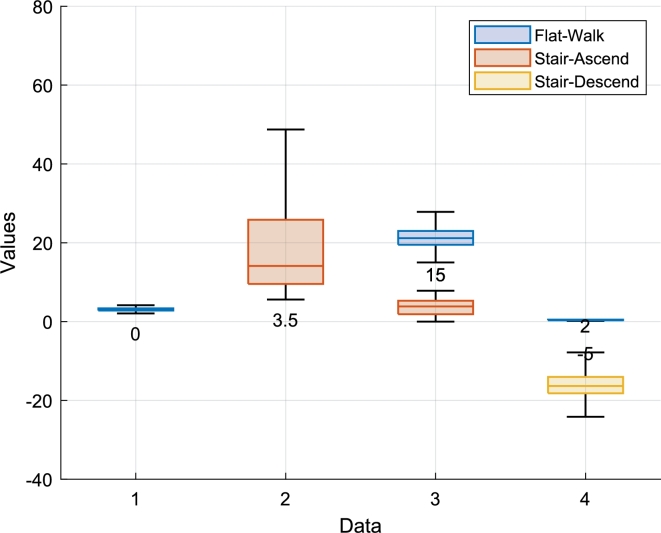
T-test on the four features (, , , and ) was conducted to evaluate their statistical significance in relation to the threshold values as provided in Table II. The t-test results for all four features yielded a p-value of zero. A p-value of zero indicates that the observed differences between the features and the threshold values are highly statistically significant, suggesting a strong association between the features and the threshold values. The occurrence of the features is illustrated in the form of a box and whisker chart in Fig. 10. The confusion matrix of terrain classification is given in Table IV. Table V shows the results for the proposed terrain classification method. The overall accuracy, sensitivity and specificity of the proposed method was found to be 0.990, 0.983 and 0.993 respectively. The highest accuracy of 0.991 was achieved for the stair-descend class, highest sensitivity of 0.99 was achieved for the stair-ascend class and highest specificity of 0.996 was achieved for the stair-descend class. The lowest accuracy of 0.989 was obtained for the stair-ascend class, lowest sensitivity of 0.982 was obtained for the flat-walk class while the lowest specificity of 0.988 was achieved for the stair-ascend class. 4 out of 999 strides including 1 flat-walk, 2 stair-ascend and 1 stair-descend strides were marked as undefined. The undefined values also contributed while calculating the performance metrics of terrain classification method as true negatives and false negatives. The real-time terrain classification system achieved promising results as all performance metrics shown in Table V exceed 97%. The system's accuracy was not affected by subject-to-subject variability, weight shifts and other non-linear factors.
Figure 10.
Boxplot representation of features corresponds to each terrain. The box represents the middle 50% of the data, with the median shown as a line within the box. The whiskers extend from the box to the minimum and maximum values. The values in the figure show the thresholds selected in Table. II.
Table IV.
Confusion matrix for Terrain detection.
| Predicted∖Actual | Flat-Walk | Stair-Ascend | Stair-Descend |
|---|---|---|---|
| Flat-Walk | 379 | 1 | 2 |
| Stair-Ascend | 4 | 394 | 3 |
| Stair-Descend | 2 | 1 | 209 |
Table V.
Performance of proposed terrain classification method.
| Flat-Walk | Stair-Ascend | Stair-Descend | Overall | |
|---|---|---|---|---|
| Accuracy | 0.990 | 0.989 | 0.991 | 0.990 |
| Sensitivity | 0.982 | 0.990 | 0.972 | 0.983 |
| Specificity | 0.995 | 0.988 | 0.996 | 0.993 |
3.2. Gait event detection
A total of 982 strides (only the ones correctly classified by terrain classification method) were observed to test the adaptability and time-effectiveness of the proposed GED method. The data included 379 flat surface strides, 394 stair-ascend strides and 209 stair-descend strides.
The results are summarized in Table VI. During flat-walk, TS event was most accurately detected with MAE 20.686 ms. HS was detected with highest MAE of 38.059 ms. TS and TO achieved the detection accuracy of 100%, HR was detected with 98.378 detection accuracy. HS achieved the lowest accuracy of 98.14% among all events during flat-walk. During stair-ascend, HS event was most accurately detected with MAE 40.109 ms. TS was detected with highest MAE of 41.096 ms. TO achieved the highest detection accuracy of 95.67%, HS and TS were detected with 95.32% and 95.05% accuracies respectively. HR achieved the lowest accuracy of 94.24% among all the events during stair-ascend. During stair-descend, TS event was most accurately detected with MAE 17.170. TO was detected with highest MAE of 62.609 ms. HS achieved the highest detection accuracy of 100%, TS and HR were detected with 97.69% and 92.23% accuracies respectively. TO achieved the lowest accuracy of 91.08% among all the events during stair-ascend.
Table VI.
Performance Metrics of proposed GED system.
| Terrain | Gait Event | Detection Accuracy | Timing Error (ms) |
Timing percentage (%) |
||||
|---|---|---|---|---|---|---|---|---|
| MAE | Advance | Delay | Advance | Delay | Exact | |||
| Flat Walk | TS | 100.000 | 20.686 | 30.000 ± 20.656 | -27.774 ± 11.740 | 4.222 | 69.921 | 25.858 |
| HR | 98.378 | 32.912 | 34.444 ± 16.858 | -38.000 ± 16.934 | 19.459 | 67.568 | 11.351 | |
| TO | 100.000 | 37.203 | 26.667 ± 11.547 | -38.098 ± 12.070 | 0.792 | 97.098 | 2.111 | |
| HS | 98.148 | 38.059 | 41.373 ±19.436 | -26.000 ± 18.974 | 88.624 | 2.646 | 6.878 | |
| Stair Ascend | TS | 95.052 | 41.096 | 49.027 ± 25.492 | -55.000 ± 29.350 | 29.427 | 44.792 | 20.833 |
| HR | 94.241 | 41.944 | 52.340 ± 21.489 | -42.559 ± 18.201 | 12.304 | 77.749 | 4.188 | |
| TO | 95.674 | 43.564 | 58.255 ± 23.702 | -46.951 ± 30.018 | 37.913 | 41.730 | 16.031 | |
| HS | 95.325 | 40.109 | 51.407 ± 26.826 | -50.194 ± 26.123 | 35.065 | 40.260 | 20.000 | |
| Stair Descend | HS | 100.000 | 28.426 | 60.000 ± 31.909 | -28.830 ± 12.780 | 5.556 | 87.037 | 7.407 |
| HR | 92.233 | 54.211 | 62.157 ± 25.158 | -53.514 ± 24.575 | 49.515 | 35.922 | 6.796 | |
| TO | 91.089 | 62.609 | 50.278 ± 24.893 | -78.218 ± 20.995 | 35.643 | 50.000 | 5.446 | |
| TS | 97.696 | 17.170 | 32.222 ± 25.795 | -41.918 ± 28.706 | 8.295 | 33.641 | 55.760 | |
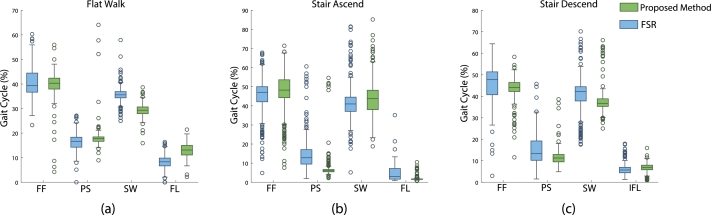
The gait phase calculation is visually represented as box and whisker chart in Fig. 9. The graph shows the percentiles of gait phase calculations. The time difference between two gait events divided by the stride time gives the gait phase percentile. Gait phases include FF, PS, SW and FL. During stair-descend FL is inverted so it is represented as inverse-foot-loading (IFL). The phases calculated with FSR (reference method) are represented in blue colour while the proposed method is represented with green colour.
Figure 9.
Comparison of four gait phase calculations between proposed method (green) and reference FSR method (blue). The box represents the middle 50% of the data, with the median shown as a line within the box. The whiskers extend from the box to the minimum and maximum values. Outliers are values that are significantly higher or lower than the majority of the data points Box and whisker chart for (a) Flat-Walk, (b) Stair Ascend, and (c) Stair Descend.
4. Discussion
In this study an inertial sensor-based multi-terrain classification and GED system is developed. Initially, foot pitch angle θ is calculated. Then the θ is marked on various points to estimate the signal morphology. Next, the relevant features based on marked values are computed and the terrain is classified as either flat-walk, stair-ascend or stair-descend. Finally, the finite state-based GED algorithm adapts to the classified terrain. The results indicate that the overall accuracy, sensitivity and specificity achieved by terrain classification was 99%, 98.3% and 99.3% respectively. GED achieved MAE ranging from 17.170 ms to 62.609 ms.
The critical time period for a gait event to be detected is 100 ms [25], [19]. In this study only two events are detected with MAE above 50 ms (see Table VI) which is significantly less than the critical time period of 100 ms. Detection accuracy values for all the gait events on flat-walk, stair-ascend and stair-descend range from 91.089% to 100%.
Gait analysis using portable inertial sensors has been of primary interest for years. So far most of the proposed methods are either computationally expensive, work offline, or do not take into account real-world terrain diversity. The current study proposes a novel system that performs two functions; terrain classification and GED. Computational efficiency is a major consideration for the development of low-cost real-time systems. To keep the computational requirements to the lowest possible, the proposed method employs basic mathematical operations and works with sampling frequency of 50 Hz while maintaining high performance. The system is tested on a low-cost 32-bit micro-processor. Human gait is a dynamic phenomenon and gait events and phases vary continuously while frequently walking over diverse terrains. While developing GED system, it is crucial to keep track of different terrains which we have effectively done in this work.
The proposed system can be used to study gait in diverse and remote environments where portability and wearability is required. Furthermore, it can be applied for driving motorized exoskeleton. It can also be used by clinicians for analyzing quantitative data from gait measurements, thus enabling them to make informed clinical decisions concerning surgeries (fusions, osteotomy, tendon releases/lengthenings/transfers) [1], orthoses, and physical therapies. This gait analysis can also be used in sports and fitness domains, such as, posture/gait correction and sports biomechanics, as well as for security purposes [2].
5. Conclusion
In this study a real-time inertial sensor-based terrain classification and gait event detection (GED) system is developed. This system is able to classify three walking terrains, which include, flat-walk, stair-ascend and stair-descend. Moreover, our proposed system adapts to the classified terrain to accurately detect gait events including toe-strike, heel-rise, toe-off and heel-strike. The performance of the proposed system was evaluated using a reference GED system, based on force sensing resisters. For flat-walk, stair-ascend, and stair-descend, the terrain classification algorithm attained accuracies of 99%, 98.9%, and 99.1%, respectively. The minimum and maximum detection accuracies were 91.089% and 100%, respectively, with an error of less than 100 ms. GED's minimum and maximum mean absolute timing errors were 17.170 ms and 62.609 ms, respectively. The proposed system works in real-time, it is computationally inexpensive and efficient, and can be employed in portable rehabilitation devices, or exoskeletons, for use in diverse terrains. The proposed system is tested on a low-cost microcontroller with low power requirements. To the best of our knowledge, this is the first study that has performed both terrain classification and GED in real-time and also tested terrain specific GED for stair-descend.
6. Limitations and future work
The proposed system was tested with a group of healthy adult participants with specific demographic characteristics. The study involved a total of 10 subjects, including 7 males and 3 females, with an average age of 24.4 years (± 3.2) and an average body mass index (BMI) of 22.3 (± 2.2). To further improve the generalizability of our findings, we intend to encompass a broader range of subjects, including older age groups and individuals with paretic gait. This will help validate the system's effectiveness for different age groups and clinical scenarios. We intend to use the proposed terrain classification and GED system to design and test a functional electrical stimulator-based rehabilitation device for drop-foot syndrome patients. Moreover, this study can also be extended to design the control system of a motorized prosthetic foot based on the proposed system. Another future research area can be to utilize the proposed system to assist in diagnosing and monitoring of various conditions such as Parkinson's disease, multiple sclerosis, or post-stroke rehabilitation by analyzing gait characteristics and detecting deviations from normal patterns. Machine learning can be used to analyze the system's data for patients recovering from the above medical conditions.
Funding
This study was supported by the Department of Biomedical Engineering of The Chinese University of Hong Kong, Hong Kong.
CRediT authorship contribution statement
Usman Qamar Shaikh: Writing – original draft, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. Muhammad Shahzaib: Writing – original draft, Methodology, Investigation, Formal analysis, Data curation, Conceptualization. Sadia Shakil: Writing – review & editing, Supervision, Resources, Methodology, Funding acquisition, Conceptualization. Farrukh A. Bhatti: Writing – review & editing, Supervision, Conceptualization. Malik Aamir Saeed: Investigation.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
We are grateful to all the volunteers who participated in the study, especially Majid Aziz, who helped with data collection. We are also grateful to Farrell Farahbod, from the open-source software (Telemetry Viewer [36]).
Data availability
The current data used in this study has not been deposited into any publicly available repository. The data will be made available on request.
References
- 1.Feng J., Wick J., Bompiani E., Aiona M. Applications of gait analysis in pediatric orthopaedics. Curr. Orthop. Pract. 2016;27(4):455–464. [Google Scholar]
- 2.Saboor A., Kask T., Kuusik A., Alam M.M., Le Moullec Y., Niazi I.K., Zoha A., Ahmad R. Latest research trends in gait analysis using wearable sensors and machine learning: a systematic review. IEEE Access. 2020;8:167 830–167 864. [Google Scholar]
- 3.Ravi D.K., Gwerder M., Ignasiak N.K., Baumann C.R., Uhl M., Van Dieen W., Taylor Jaap H., Singh N.B. Revealing the optimal thresholds for movement performance: a systematic review and meta-analysis to benchmark pathological walking behaviour. Neurosci. Biobehav. Rev. 2020;108:24–33. doi: 10.1016/j.neubiorev.2019.10.008. [DOI] [PubMed] [Google Scholar]
- 4.König N., Singh N.B., Von Beckerath J., Janke L., Taylor W.R. Is gait variability reliable? An assessment of spatio-temporal parameters of gait variability during continuous overground walking. Gait Posture. 2014;39(1):615–617. doi: 10.1016/j.gaitpost.2013.06.014. [DOI] [PubMed] [Google Scholar]
- 5.Taborri J., Palermo E., Rossi S., Cappa P. Gait partitioning methods: a systematic review. Sensors. 2016;16(1):66. doi: 10.3390/s16010066. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Catalfamo P., Ghoussayni S., Ewins D. Gait event detection on level ground and incline walking using a rate gyroscope. Sensors. 2010;10(6):5683–5702. doi: 10.3390/s100605683. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Sabatini A.M., Martelloni C., Scapellato S., Cavallo F. Assessment of walking features from foot inertial sensing. IEEE Trans. Biomed. Eng. 2005;52(3):486–494. doi: 10.1109/TBME.2004.840727. [DOI] [PubMed] [Google Scholar]
- 8.Alahakone A.U., Senanayake S.A., Senanayake C.M. 2010 IEEE Asia Pacific Conference on Circuits and Systems. IEEE; 2010. Smart wearable device for real time gait event detection during running; pp. 612–615. [Google Scholar]
- 9.Prasanth H., Caban M., Keller U., Courtine G., Ijspeert A., Vallery H., Von Zitzewitz J. Wearable sensor-based real-time gait detection: a systematic review. Sensors. 2021;21(8):2727. doi: 10.3390/s21082727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Bejarano N.C., Ambrosini E., Pedrocchi A., Ferrigno G., Monticone M., Ferrante S. XIII Mediterranean Conference on Medical and Biological Engineering and Computing 2013. Springer; 2014. An adaptive real-time algorithm to detect gait events using inertial sensors; pp. 1799–1802. [Google Scholar]
- 11.Chia Bejarano N., Ambrosini E., Pedrocchi A., Ferrigno G., Monticone M., Ferrante S. A novel adaptive, real-time algorithm to detect gait events from wearable sensors. IEEE Trans. Neural Syst. Rehabil. Eng. 2015;23(3):413–422. doi: 10.1109/TNSRE.2014.2337914. [DOI] [PubMed] [Google Scholar]
- 12.Azhar M.A., Gouwanda D., Gopalai A.A. IEEE-EMBS International Conference on Biomedical and Health Informatics (BHI) IEEE; 2014. Development of an intelligent real-time heuristic-based algorithm to identify human gait events; pp. 573–576. [Google Scholar]
- 13.Formento P.C., Acevedo R., Ghoussayni S., Ewins D. Gait event detection during stair walking using a rate gyroscope. Sensors. 2014;14(3):5470–5485. doi: 10.3390/s140305470. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Rueterbories J., Spaich E.G., Andersen O.K. Gait event detection for use in fes rehabilitation by radial and tangential foot accelerations. Med. Eng. Phys. 2014;36(4):502–508. doi: 10.1016/j.medengphy.2013.10.004. [DOI] [PubMed] [Google Scholar]
- 15.Aung M.S., Thies S.B., Kenney L.P., Howard D., Selles R.W., Findlow A.H., Goulermas J.Y. Automated detection of instantaneous gait events using time frequency analysis and manifold embedding. IEEE Trans. Neural Syst. Rehabil. Eng. 2013;21(6):908–916. doi: 10.1109/TNSRE.2013.2239313. [DOI] [PubMed] [Google Scholar]
- 16.González R.C., López A.M., Rodriguez-Uría J., Alvarez D., Alvarez J.C. Real-time gait event detection for normal subjects from lower trunk accelerations. Gait Posture. 2010;31(3):322–325. doi: 10.1016/j.gaitpost.2009.11.014. [DOI] [PubMed] [Google Scholar]
- 17.Abaid N., Cappa P., Palermo E., Petrarca M., Porfiri M. Gait detection in children with and without hemiplegia using single-axis wearable gyroscopes. PLoS ONE. 2013;8(9) doi: 10.1371/journal.pone.0073152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Diao Z., Quan H., Lan L., Han Y. 2013 Seventh International Conference on Sensing Technology (ICST) IEEE; 2013. Analysis and compensation of mems gyroscope drift; pp. 592–596. [Google Scholar]
- 19.Zhao H., Wang Z., Qiu S., Wang J., Xu F., Wang Z., Shen Y. Adaptive gait detection based on foot-mounted inertial sensors and multi-sensor fusion. Inf. Fusion. 2019;52:157–166. [Google Scholar]
- 20.Negi S., Garg K., Prajapat M., Sharma N. A standalone real-time gait phase detection using fuzzy-logic implementation in Arduino nano. SN Comput. Sci. 2022;3(1):1–7. [Google Scholar]
- 21.Pappas I., Popovic M., Keller T., Dietz V., Morari M. A reliable gait phase detection system. IEEE Trans. Neural Syst. Rehabil. Eng. 2001;9(2):113–125. doi: 10.1109/7333.928571. [DOI] [PubMed] [Google Scholar]
- 22.Lee S.-W., Mase K., Kogure K. 2005 IEEE Engineering in Medicine and Biology 27th Annual Conference. IEEE; 2006. Detection of spatio-temporal gait parameters by using wearable motion sensors; pp. 6836–6839. [DOI] [PubMed] [Google Scholar]
- 23.Hanlon M., Anderson R. Real-time gait event detection using wearable sensors. Gait Posture. 2009;30(4):523–527. doi: 10.1016/j.gaitpost.2009.07.128. [DOI] [PubMed] [Google Scholar]
- 24.Jasiewicz J.M., Allum J.H., Middleton J.W., Barriskill A., Condie P., Purcell B., Li R.C.T. Gait event detection using linear accelerometers or angular velocity transducers in able-bodied and spinal-cord injured individuals. Gait Posture. 2006;24(4):502–509. doi: 10.1016/j.gaitpost.2005.12.017. [DOI] [PubMed] [Google Scholar]
- 25.Figueiredo J., Felix P., Costa L., Moreno J.C., Santos C.P. Gait event detection in controlled and real-life situations: repeated measures from healthy subjects. IEEE Trans. Neural Syst. Rehabil. Eng. 2018;26(10):1945–1956. doi: 10.1109/TNSRE.2018.2868094. [DOI] [PubMed] [Google Scholar]
- 26.Tiwari A., Joshi D. An infrared sensor-based instrumented shoe for gait events detection on different terrains and transitions. IEEE Sens. J. 2020;20(18):10 779–10 791. [Google Scholar]
- 27.Godiyal A.K., Verma H.K., Khanna N., Joshi D. A force myography-based system for gait event detection in overground and ramp walking. IEEE Trans. Instrum. Meas. 2018;67(10):2314–2323. [Google Scholar]
- 28.Song M., Kim J. An ambulatory gait monitoring system with activity classification and gait parameter calculation based on a single foot inertial sensor. IEEE Trans. Biomed. Eng. 2017;65(4):885–893. doi: 10.1109/TBME.2017.2724543. [DOI] [PubMed] [Google Scholar]
- 29.Nguyen N.D., Bui D.T., Truong P.H., Jeong G.-M. Classification of five ambulatory activities regarding stair and incline walking using smart shoes. IEEE Sens. J. 2018;18(13):5422–5428. [Google Scholar]
- 30.Chen M., Yan J., Xu Y. 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems. IEEE; 2009. Gait pattern classification with integrated shoes; pp. 833–839. [Google Scholar]
- 31.Catalfamo Formento P.A.L., Acevedo R.C., Ghoussayni S., Ewins D. 2014. Gait event detection on stair walking using a rate gyroscope. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Ledoux E.D. Inertial sensing for gait event detection and transfemoral prosthesis control strategy. IEEE Trans. Biomed. Eng. 2018;65(12):2704–2712. doi: 10.1109/TBME.2018.2813999. [DOI] [PubMed] [Google Scholar]
- 33.Das R., Hooda N., Kumar N. A novel approach for real-time gait events detection using developed wireless foot sensor module. IEEE Sens. Lett. 2019;3(6):1–4. [Google Scholar]
- 34.Chen M., Yan J., Xu Y. 2009 IEEE/RSJ International Conference on Intelligent Robots and Systems. 2009. Gait pattern classification with integrated shoes; pp. 833–839. [Google Scholar]
- 35.https://cdn.sparkfun.com/assets/c/4/6/8/b/2010-10-26-DataSheet-FSR406-Layout2.pdf Force sensitive resister, fsr 406, [Online]. Available:
- 36.Farahbod F. Telemetryviewer. http://www.farrellf.com/TelemetryViewer/ [Online]. Available:
- 37.GitHub Github tockn/mpu-6050 Arduino library. https://github.com/tockn/MPU6050_tockn.git [Online]. Available:
- 38.Mahony R., Hamel T., Pflimlin J.-M. Nonlinear complementary filters on the special orthogonal group. IEEE Trans. Autom. Control. 2008;53(5):1203–1218. [Google Scholar]
- 39.Mariani B., Rouhani H., Crevoisier X., Aminian K. Quantitative estimation of foot-flat and stance phase of gait using foot-worn inertial sensors. Gait Posture. 2013;37(2):229–234. doi: 10.1016/j.gaitpost.2012.07.012. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Data Availability Statement
The current data used in this study has not been deposited into any publicly available repository. The data will be made available on request.