Receiver operating characteristic curve analysis in diagnostic accuracy studies: A guide to interpreting the area under the curve value

Abstract

This review article provides a concise guide to interpreting receiver operating characteristic (ROC) curves and area under the curve (AUC) values in diagnostic accuracy studies. ROC analysis is a powerful tool for assessing the diagnostic performance of index tests, which are tests that are used to diagnose a disease or condition. The AUC value is a summary metric of the ROC curve that reflects the test’s ability to distinguish between diseased and nondiseased individuals. AUC values range from 0.5 to 1.0, with a value of 0.5 indicating that the test is no better than chance at distinguishing between diseased and nondiseased individuals. A value of 1.0 indicates perfect discrimination. AUC values above 0.80 are generally consideredclinically useful, while values below 0.80 are considered of limited clinical utility. When interpreting AUC values, it is important to consider the 95% confidence interval. The confidence interval reflects the uncertainty around the AUC value. A narrow confidence interval indicates that the AUC value is likely accurate, while a wide confidence interval indicates that the AUC value is less reliable. ROC analysis can also be used to identify the optimal cutoff value for an index test. The optimal cutoff value is the value that maximizes the test’s sensitivity and specificity. The Youden index can be used to identify the optimal cutoff value. This review article provides a concise guide to interpreting ROC curves and AUC values in diagnostic accuracy studies. By understanding these metrics, clinicians can make informed decisions about the use of index tests in clinical practice.

Introduction

Diagnostic accuracy studies are a cornerstone of medical research. When evaluating novel diagnostic tests or repurposing existing ones for different clinical scenarios, physicians assess test efficacy, which is referred to as index tests in diagnostic accuracy analyses. Index tests can encompass a variety of elements, such as serum markers derived from blood samples, radiological imaging, specific clinical findings, or clinical decision rules. Diagnostic studies assess the index test’s diagnostic performance by reporting specific metrics, such as sensitivity, specificity, positive predictive value (PPV), negative predictive value (NPV), positive likelihood ratio (PLR), negative likelihood ratio (NLR), and accuracy. These metrics are compared to the gold standard reference test. Diagnostic ability encompasses not only the index test’s diagnostic prowess (specificity, PPV, and PLR) but also its ability to distinguish healthy individuals from those with the targeted condition (sensitivity, NPV, and NLR).[1-4]

Two Types of Diagnostic Studies

There are two main types of diagnostic studies in medicine: two-by-two tables and receiver operating characteristic (ROC) analysis. The choice between these depends on whether the index test yields dichotomous or continuous results.

Diagnostic Accuracy Studies with Dichotomous Index Test Results

The two-by-two table is used when both the index test and reference test results are dichotomous. As shown in Table 1, sensitivity, specificity, PPV, NPV, PLR, and NLR are calculated based on the data in the table’s four cells. True positive fraction (TPF) and False positive fraction (FPF) are two other important parameters that have a diagnostic character in cases where the index test is positive. TPF reflects the index test’s accuracy in detecting disease (and is equivalent to sensitivity), while FPF gauges the index test’s positivity in nondiseased individuals (and is equivalent to 1 – specificity).[5] In cases where the reference test is also dichotomous, but the index test yields continuous numerical results, the diagnostic study method used is the ROC analysis.[6-8] While the ROC curve and the resultant area under the curve (AUC) offer a concise summary of the index test’s diagnostic utility, clinicians may encounter challenges in interpreting these values. This concise review aims to guide clinicians through the interpretation of ROC curves and AUC values when presenting findings from their diagnostic accuracy studies.

Table 1.

Two-by-two table and calculating parameters of diagnostic test performance

Index test	Reference test		Total
	Diseased	Nondiseased
Positive	a (true positive)	b (false positive)	a + b
Negative	c (false negative)	d (true negative)	c + d
Total	a + c	b + d

Summary parameters of diagnostic test performance: Sensitivity=a/(a + c), specificity=d/(b + d), PPV=a/(a + b), NPV=d/(c + d), TPF=Sensitivity=a/(a + c), FPF=1 − specificity=d/(b + d). PPV: Positive predictive value, NPV: Negative predictive value, TPF: True positive fraction, FPF: False-positive fraction

Diagnostic Accuracy Studies with Numerical Index Test Results

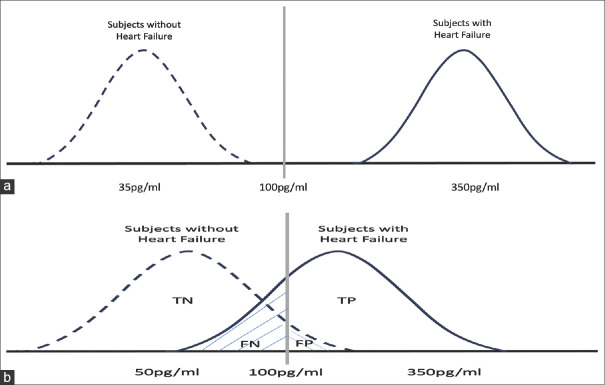
In cases where the index test yields a dichotomous outcome (a single cutoff value), the two-by-two table is sufficient, as discussed earlier. However, when the index test generates continuous (or occasionally ordinal) outcomes, multiple potential cutoff values emerge. Selecting the optimal cutoff value, especially for novel diagnostic tests, poses challenges. With continuous numerical outcomes, diagnostic accuracy studies yield distinct distributions of test results for both diseased and nondiseased groups.[9] For example, a diagnostic accuracy study evaluating B-type natriuretic peptide (BNP) blood levels in diagnosing heart failure could yield the following distributions:

• An ideal diagnostic test would yield sensitivity and specificity of 100%, resulting in nonoverlapping BNP distribution graphs for individuals with and without heart failure [Figure 1a]

• However, real-world scenarios tend to involve overlapping distributions [Figure 1b].

Figure 1.

Two different BNP distribution graphs of the subjects groups with and without heart failure. TN: true negative, TP: true positive, FN: false negative, FP: false positive (a) An ideal diagnostic test would yield sensitivity and specificity of 100%, resulting in non-overlapping BNP distribution graphs for individuals with and without heart failure. (b) real-world scenarios tend to involve overlapping distributions; sensitivity and specificity values are not 100%

Receiver Operating Characteristic Analysis and Receiver Operating Characteristic Curve

ROC analysis involves dichotomizing all index test outcomes into positive (indicative of disease) and negative (nondisease) based on each measured index test value. For instance, if a measured BNP result is 235 pg/ml, ROC analysis would classify all values exceeding 235 as positive and the rest as negative. Relevant diagnostic performance metrics (sensitivity, specificity, PPV, NPV, PLR, and NLR) are then calculated, mirroring the two-by-two table methodology. This process is repeated for all measured values within the ROC analysis. This approach enables the presentation and examination on of these metrics as a table, followed by 33 the graphical depiction of this table, termed the ROC 34 curve [Figure 2].[10-12] The ROC curve plots TPF (sensitivity) and FPF (1 – specificity) values for each index test outcome on an x-y coordinate graph. This curve results from combining coordinate points from each outcome. The diagonal reference line at a 45° angle signifies the diagnostic test’s discriminative power akin to random chance. The upper left corner corresponds to perfect discriminatory power, represented by a TPF of 1 and an FPF of 0 (where sensitivity and specificity both attain 100%).

Figure 2.

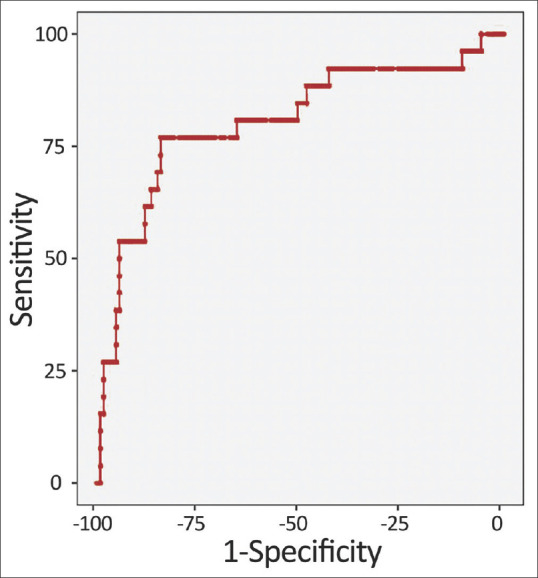
Receiver Operating Characteristic (ROC) Curve

Area under the Curve Value and Interpretation

The AUC value is a widely used metric in clinical studies, succinctly summarizing index test diagnostic performance. The AUC value signifies the likelihood that the index test will categorize a randomly selected subject from a sample as a patient more accurately than a nonpatient. AUC values range from 0.5 (equivalent to chance) to 1 (indicating perfect discrimination).[13]

AUC values serve as a gauge for the index test’s ability to distinguish disease. An AUC value of 1 signifies flawless discernment, while an AUC of 0.5 indicates performance akin to random chance. New researchers often make errors when interpreting the AUC value in diagnostic accuracy studies. This is usually due to an overestimation of the clinical interpretation of the AUC value. For example, an AUC value of 0.65, calculated in a study of the diagnostic performance of an index test, means that the test is not clinically adequate. However, some researchers make the inference that the test is a clinically useful diagnostic test by only looking at statistical significance. In diagnostic value studies, AUC values above 0.90 are interpreted as indicating a very good diagnostic performance of the test, while AUC values below 0.80, even if they are statistically significant, are interpreted as indicating a very limited clinical usability of the test. The classification table of AUC values and their clinical usability is presented in Table 2.

Table 2.

Area under the curve values and its interpretation

AUC value	Interpretation suggestion
0.9 ≤ AUC	Excellent
0.8 ≤ AUC < 0.9	Considerable
0.7 ≤ AUC < 0.8	Fair
0.6 ≤ AUC < 0.7	Poor
0.5 ≤ AUC < 0.6	Fail

AUC: Area under the curve

Notably, attention to the 95% confidence interval and its width, alongside the AUC value, is pivotal in comprehending diagnostic performance.[13,14] For instance, a BNP marker’s AUC value of 0.81 might be tempered by a confidence interval spanning 0.65–0.95. In this scenario, reliance solely on an AUC value above 0.80 may be unwise, given the potential for outcomes below 0.70. Thus, calculating sample size and mitigating type-2 error risk prove vital prerequisites before undertaking diagnostic studies.[15]

A common mistake made at this point is that when two different index tests are wanted to be compared, the index tests are made by considering only the mathematical differences of the single AUC values from each other. This decision should be made not only with the mathematical difference but also by considering whether this mathematical difference is statistically significant. The most common statistical method used to statistically compare the AUC values of different index tests is the De-Long test.

Determination of Optimal Cutoff Value

ROC analysis also facilitates the identification of an optimal cutoff value, particularly when the AUC value surpasses 0.80. The Youden index, often employed, determines the threshold value that maximizes both sensitivity and specificity. This index, calculated as sensitivity + specificity – 1, aids in selecting a threshold where both metrics achieve their peak. Nonetheless, alternative thresholds might be chosen based on cost-effectiveness or varying clinical contexts, prioritizing either sensitivity or specificity.

Conclusion

Studies employing ROC analysis follow reporting guidelines, such as the Standards for Reporting Diagnostic Accuracy Studies (STARD) guideline. The STARD guideline also states that when reporting the diagnostic performance of an index test, not only sensitivity and specificity parameters should be reported, but also NLR and PLR values.[16] However, certain statistical programs might only report sensitivity and specificity parameters in ROC analysis. Therefore, when an AUC value above 0.80 is attained, generating a two-by-two table based on the chosen optimal threshold and reporting all relevant metrics becomes imperative.

Conflicts of interest

None Declared.

Funding

None.