QMrebind: incorporating quantum mechanical force field reparameterization at the ligand binding site for improved drug-target kinetics through milestoning simulations

Abstract

Understanding the interaction of ligands with biomolecules is an integral component of drug discovery and development. Challenges for computing thermodynamic and kinetic quantities for pharmaceutically relevant receptor–ligand complexes include the size and flexibility of the ligands, large-scale conformational rearrangements of the receptor, accurate force field parameters, simulation efficiency, and sufficient sampling associated with rare events. Our recently developed multiscale milestoning simulation approach, SEEKR2 (Simulation Enabled Estimation of Kinetic Rates v.2), has demonstrated success in predicting unbinding (k_off) kinetics by employing molecular dynamics (MD) simulations in regions closer to the binding site. The MD region is further subdivided into smaller Voronoi tessellations to improve the simulation efficiency and parallelization. To date, all MD simulations are run using general molecular mechanics (MM) force fields. The accuracy of calculations can be further improved by incorporating quantum mechanical (QM) methods into generating system-specific force fields through reparameterizing ligand partial charges in the bound state. The force field reparameterization process modifies the potential energy landscape of the bimolecular complex, enabling a more accurate representation of the intermolecular interactions and polarization effects at the bound state. We present QMrebind (Quantum Mechanical force field reparameterization at the receptor–ligand binding site), an ORCA-based software that facilitates reparameterizing the potential energy function within the phase space representing the bound state in a receptor–ligand complex. With SEEKR2 k_off estimates and experimentally determined kinetic rates, we compare and interpret the receptor–ligand unbinding kinetics obtained using the newly reparameterized force fields for model host–guest systems and HSP90-inhibitor complexes. This method provides an opportunity to achieve higher accuracy in predicting receptor–ligand k_off rate constants.

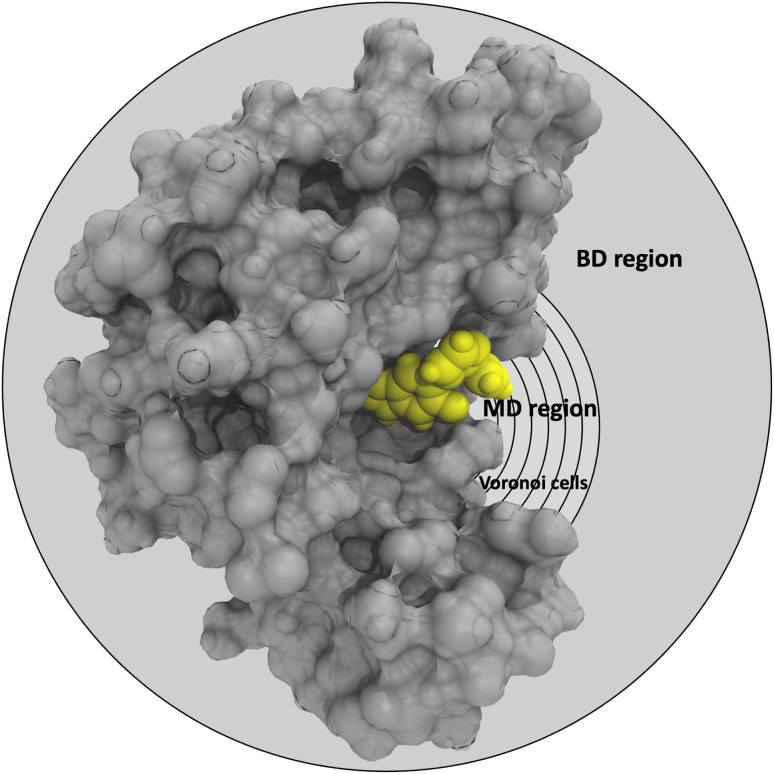
Graphical representation of the partition of the phase-space of the receptor (grey)-ligand (yellow) complex into the MD region (further partitioned into Voronoi cells) and the BD region.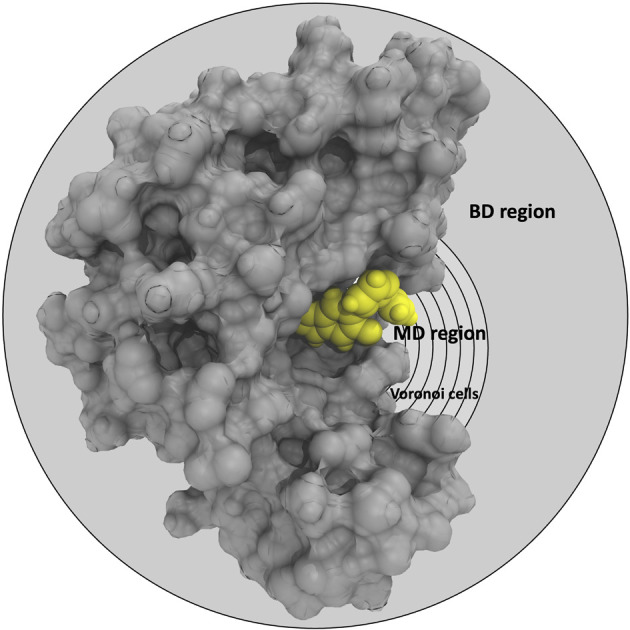

1. Introduction

Receptor–ligand binding and unbinding is a crucial mechanism that governs a range of biological processes, including cellular signaling, enzymatic catalysis, and immunological responses.^1–3 The interaction between the ligand and receptor enables cells to respond to environmental cues, transmit signals, and carry out essential physiological functions.^4–6 A comprehensive understanding of the kinetic and thermodynamic properties of receptor–ligand interactions is essential for designing and optimizing therapeutic agents acting upon specific protein targets.^7–11 Ligands with a higher residence time (or slow dissociation rates) tend to remain in the binding pocket of the receptor for an extended period, leading to prolonged pharmacological effects. On the other hand, ligands with a lower residence time (or fast dissociation rates) are less likely to produce pharmacological effects.^12–17 Similarly, the thermodynamic parameters for receptor–ligand interaction, such as affinity, provide insights into the specificity and stability of receptor–ligand binding and unbinding.^18–21 A complex interplay of kinetic and thermodynamic factors of receptor–ligand (un)binding determines the duration and strength of interaction between the two entities. Leveraging these factors could aid the development of novel therapeutics, leading to efficient drug discovery and development processes.

With recent advancements in computing power and hardware, molecular dynamics (MD) simulations have emerged as a powerful tool for studying the kinetics and thermodynamics of molecular interactions.^22,23 Despite such progress, MD simulations have limitations when studying complex biological processes, such as protein folding and unfolding,^24–26 large protein conformational rearrangements,^27,28 and receptor–ligand binding and unbinding due to the relatively long timescales needed to observe such events.^29–31 These phenomena may occur on a timescale of milliseconds or longer, and it becomes increasingly difficult for MD simulations to rigorously characterize such events. Enhanced MD simulations accelerate the conformational search of the system, thereby allowing rare events to be observed within a reasonable computational time.^32–34 Enhanced MD simulations can be roughly categorized into collective variable (CV) free and CV-based approaches. CV-based approaches include metadynamics,^35–37 Markov state models (MSMs),^38–40 variationally enhanced sampling,^41–43 weighted ensemble,^44–47 and umbrella sampling,^48–50 while CV-free approaches include accelerated molecular dynamics (aMD),^51–53 Gaussian accelerated molecular dynamics (GaMD),^54–56 replica exchange molecular dynamics (REMD),^57–59 and selective integrated tempering.^60,61

Path sampling methods represent a class of enhanced sampling approaches that enable comprehensive exploration of the kinetic properties in biological systems, encompassing phenomena such as receptor–ligand binding and unbinding, protein folding and unfolding, and substantial conformational changes in complex biological systems. The Markovian milestoning with Voronoi tessellations (MMVT) approach in MD simulations partitions the phase space of the receptor–ligand complex into distinct regions called “Voronoi cells”.^62–64 Independent and parallel MD simulations are carried out within each Voronoi cell, with the ligand incrementally displaced from the bound state. This approach is implemented in the computational software toolkit, Simulation Enabled Estimation of Kinetic Rates v.2 (SEEKR2),^65–69 which is further discussed in Section 2.2. Estimation of drug-target residence times of pharmaceutically relevant biomolecular complexes remains difficult for MD-based approaches. However, SEEKR2 has recently succeeded in estimating close-to-experiment residence times for JAK2/STAT5 axis inhibitors with extended residence times (hours or longer) within the target.^69,70

Enhanced MD simulations can be robust methods for investigating complex molecular systems. However, significant challenges are often encountered while predicting the kinetics and thermodynamics of receptor–ligand (un)binding. One such challenge is accurately representing non-covalent interactions at the binding site. While general force fields describe the potential energy landscape across a broad range of biomolecular configurations, incorporating quantum mechanics (QM) to tune the force field parameters can precisely describe non-covalent interactions at the binding site for the conformations examined with QM. Our approach focuses on reparameterizing the potential energy landscape of the receptor–ligand complex within the bound state conformation.

Despite the effectiveness of classical force fields in successfully replicating equilibrium properties and binding affinities, MD simulations face challenges in accurately predicting kinetic parameters.^71,72 Recent investigations have extensively explored this issue, revealing noteworthy disparities between simulation results and experimental data and underscoring the growing realization that classical force fields might need to better capture the complexity of dynamics at transition states.^73,74 Consequently, two promising avenues for improvement have surfaced. The first involves adopting polarizable force fields, a paradigm shift from traditional fixed-charge models.^75–77 Secondly, quantum mechanics/molecular mechanics (QM/MM) simulations show promise to enhance rate prediction accuracy.^77,78 In QM/MM simulations, specific regions (such as the ligand and binding site) are treated at the quantum mechanical level, allowing for precisely describing electronic properties during molecular events. These simulations have demonstrated their potential in modeling the complex kinetics of binding and unbinding processes.^79–82 Furthermore, ongoing research efforts aim to refine parametrization strategies for classical force fields, integrating kinetic information and addressing polarization issues within fixed-charge schemes.^83–85

In this study, we aim to recalibrate the charges of the ligand within the vicinity of its neighboring residues in the binding site, thereby facilitating an accurate representation of interactions between the drug and the target. Subsequently, the QM-enhanced force field parameters are employed in the SEEKR2 simulations to determine the unbinding kinetics of receptor–ligand complexes.

2. Methods

2.1. Quantum mechanical force field reparameterization at the receptor–ligand binding site (QMrebind)

For computing kinetic and thermodynamic properties for receptor–ligand complexes, we have employed different theoretical frameworks to model certain regions of the biomolecular complex under study. Specifically, we applied a higher level of theory (i.e., high-level QM and low-level QM2) to model the active site of the complex and obtain optimized point charges of the ligand, while utilizing classical mechanics to model the remaining protein (Fig. 1). This multiscale approach allows for a more precise and efficient representation of the molecular system within the bound state, which may improve accuracy when modeling the binding and unbinding process. ORCA, a versatile quantum chemistry package that offers a wide range of electronic structure methods, enables the application of different theoretical frameworks for different regions of a molecular system.^86–88 In its latest release, i.e., ORCA 5.0, new features include the three-layered (QM-QM2-MM) ONIOM method with electrostatic and mechanical embedding, covalent bond boundary definitions between the QM and QM2 regions, and automated detection of system topologies with link atoms.^89–91 QMrebind integrates the ORCA QM engine for reparameterizing force field parameters for receptor–ligand complexes.

Fig. 1. Partition of the receptor–ligand complex (Hsp90-ligand 9 complex) into the QM region comprising the ligand (red), the QM2 region comprising the residues surrounding the ligand within a cut-off distance of 5.0 Å (yellow), and the MM region (cyan).

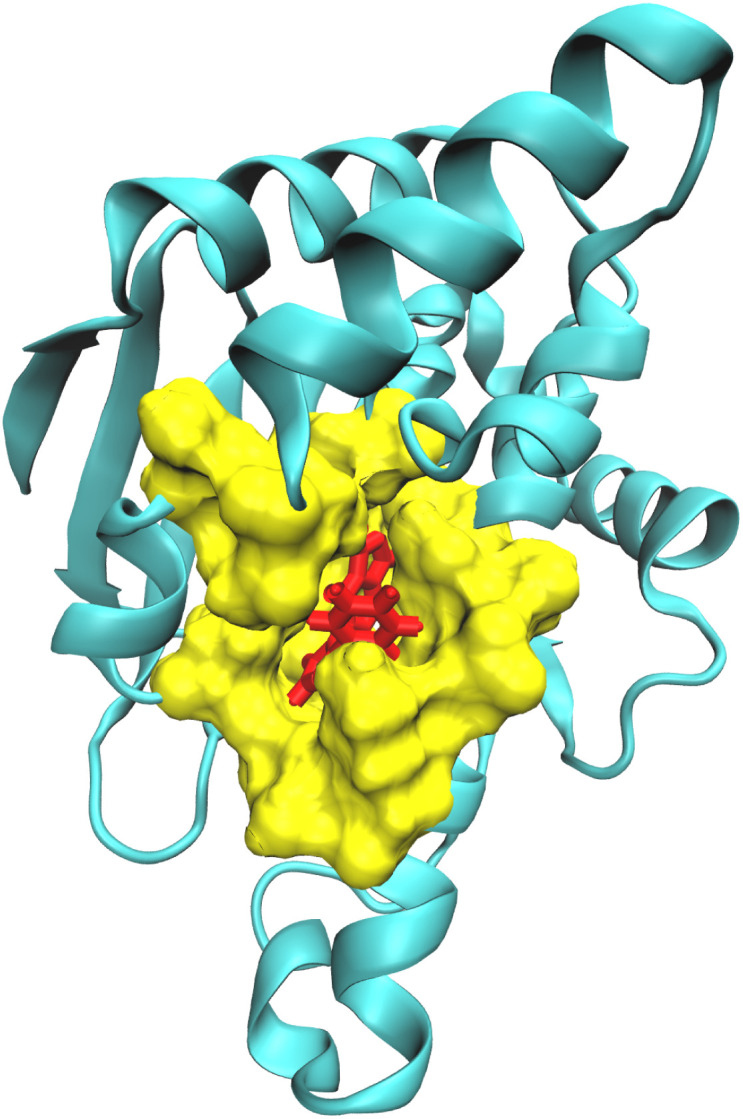
The QMrebind method involves several steps to calculate the charges of the ligand at its binding site (see QMrebind protocol). Initially, a protein data bank (PDB) file of the receptor–ligand complex and its topology file are provided as inputs to the QMrebind software. The user defines a distance cut-off value, which delineates a region of receptor atoms encompassing the ligand within the cut-off distance, typically including only the residues in the binding site. Once the binding site is identified, the ligand is defined as the high-level QM region of the ONIOM method. Residues surrounding the ligand, containing any atom within the cut-off distance, are classified as the low-level QM2 region of the ONIOM method (Fig. 1). All the remaining residues of the receptor comprise the MM region. For the QM region, electronic structure methods such as the Hartree–Fock (HF), density functional theory (DFT), second-order Møller–Plesset perturbation (MP2), and coupled-cluster (CC) theories may be employed.^92–94 A semi-empirical tight-binding method, GFN-XTB or GFN2-XTB, is employed in the QM2 region.^95,96 The GFN2-XTB method accelerates the calculations of noncovalent interaction energies for complex molecular systems by accounting for anisotropic second-order density fluctuation effects.^97,98

QMrebind protocol

(1) Initialization

• A structure (PDB) and topology file for the receptor–ligand complex with the ligand at its binding site is provided as an input.

• The receptor-ligand complex is locally minimized (if not already minimized).

• A user-defined distance cut-off value is defined to identify the receptor region (low-level QM2) surrounding the ligand (high-level QM).

(2) Define QM, QM2, and MM regions within the multiscale ONIOM method

• The ligand at the binding site is defined as the high-level QM region within the three-layered multiscale ONIOM method.

• Residues surrounding the ligand containing any atoms within the cut-off distance are defined as low-level QM2 region within the ONIOM method.

• All protein residues except those within the QM2 region are defined as the MM region.

(3) Assign theories and methods to QM–QM2–MM regions

• An appropriate electronic structure method (HF, DFT, MP2, etc.) and corresponding basis set for the high-level QM region are assigned to describe the quantum behavior of the system.

• A semi-empirical tight-binding method (GFN-XTB/GFN2-XTB) is assigned for the QM2 region.

• The MM region is treated with the generic force field provided in the original topology file.

(4) Define QM–QM2 and (QM–QM2)–MM interactions

• An additive scheme is employed to model (QM–QM2)–MM interactions, treating these regions as independent entities.

• A subtractive scheme is employed to model QM–QM2 interaction, subtracting the contribution of the QM2 region from the total QM–QM2 interaction.

• Electrostatic embedding is employed for QM–QM2 interactions, wherein the high-level QM region interacts with the atomic point charges of the low-level QM2 region.

(5) Employ QM–QM2–MM calculations and charge-fitting schemes

• QMrebind interfaces with ORCA to execute QM–QM2–MM calculations.

• A self-consistent field (SCF) electronic structure calculation is performed for the QM–QM2–MM system.

• Geometry-basis wavefunction (GBW) and the SCF electron density files are saved post-SCF convergence.

• Charge-fitting methods are employed (CHELPG in this study, although Hirshfeld, Löwdin, etc. are available in QMrebind) that utilize the electron density distribution information to calculate charges for the ligand.

(6) Integration of newly obtained ligand charges into a copy of the original parameter/topology file

• Partial charges of the ligand are replaced in a copy of the original topology file with the newly obtained QM charges.

• Tests are conducted using the OpenMM engine to validate the correctness of the reparameterized topology file.

• After successful validation, the reparameterized receptor–ligand topology file can be used in SEEKR2 milestoning simulations.

Two schemes are employed, i.e., subtractive and additive,^90,99 to account for interactions between the QM, QM2, and MM regions. Let the three regions in the receptor–ligand complex be defined as the high-level QM region (H), the low-level QM region (M), and the MM region (L). The QM and QM2 regions employ a subtractive scheme, where the QM–QM2 interaction is calculated by subtracting the contribution of the QM2 region from the total QM–QM2 interaction to ensure the accuracy of the calculations. In a subtractive scheme, three separate energy calculations are performed, i.e., QM calculation for the high layer, (E^QM_H), QM2 calculation for the high and medium layer (E^QM2_HM), and a QM2 calculation for the high layer (E^QM2_H). The total energy for the subtractive scheme, E^sub_QM–QM2, is given by:

E^sub_QM–QM2 = E^QM_H + E^QM2_HM − E^QM2_H 1

An additive scheme models the (QM–QM2)–MM interaction. This scheme assumes the QM–QM2 and MM regions to be independent, and simple pairwise potentials describe their interactions. In an additive scheme, two energy calculations are performed, i.e., a subtractive QM–QM2 calculation for the QM–QM2 region (E^sub_QM–QM2) and a MM calculation, E^MM_L–HM. The total energy for the additive scheme, E^add_{(QM–QM2)–MM}, is given by:

E^add_{(QM–QM2)–MM} = E^sub_QM–QM2 + E^MM_L–HM 2

E ^MM is defined as the sum of MM energy of the MM region (E^MM_L) and the (QM–QM2)–MM interface energy (E^{(QM–QM2)–MM}_L–HM) and is given by:

E^MM_L–HM = E^MM_L + E^{(QM–QM2)–MM}_L–HM 3

Upon substituting the value of E^sub_QM–QM2 and E^MM_L–HM in eqn (2), we get:

E^add_{(QM–QM2)–MM} = E^QM_H + E^QM2_HM − E^QM2_H + E^MM_L + E^{(QM–QM2)–MM}_L–HM 4

In subtractive QM–QM2 calculations, a high-level QM region interacts with a low-level QM2 region treated with the GFN-XTB/GFN2-XTB method. Since the QM2 method, i.e., GFN-XTB/GFN2-XTB, an extended semiempirical tight-binding model, is polarizable, the interaction with the high-level QM region is more accurate.¹⁰⁰ The GFN-XTB method accounts for anisotropic second-order density fluctuation effects, allowing the QM2 region to adjust its electron density dynamically in response to external perturbations (electron distribution) in the QM region,^95,101 allowing for a more realistic description of charge redistribution and electronic polarization during interactions between the high-level QM and low-level QM2 regions. Consequently, subtractive QM–QM2 methods, compared to additive methods, improve accuracy in energy calculations, geometry optimization, and interaction energies by accurately treating electron density differences.

By default, unless specified, ONIOM calculations in the ORCA engine employ the electrostatic embedding scheme, where the high-level QM region interacts with the atomic point charges of the low-level QM2 region. In the electrostatic embedding scheme, partial charges of QM2 atoms are incorporated directly into the Hamiltonian of the QM region, i.e., electrostatic interactions between the QM and QM2 regions are explicitly considered at the QM level. These point charges are determined based on a full system low-level (QM2) calculation, ensuring that they accurately represent the charge distribution of the QM2 atoms.

Different charge schemes implemented into the ORCA QM engine are available to calculate the charges of the ligand at the binding site, including the CHELPG (CHarge-Extra Loop and Gaussian Potentials), Hirshfeld, Löwdin, and Mulliken population analysis. The CHELPG algorithm was used exclusively in this study and involves fitting atomic charges to reproduce the molecular electrostatic potential at a set of grid points surrounding the molecule,¹⁰² subject to the constraint that the sum of charges of all the atoms equals the overall charge of the molecule. Other charge analysis schemes, such as the Hirshfeld, Mulliken and Löwdin population analysis, can also be employed within the framework. The CHELPG method is chosen for reparameterizing ligand charges for the two sets of receptor–ligand complexes in the present study due to its reliability in reproducing molecular electrostatic potentials (ESP). However, as discussed previously, other charge schemes could also be employed for ligand charge parameterization at the binding site. A self-consistent field (SCF) electronic structure calculation is performed for the QM–QM2–MM system to find the electronic wave function that minimizes the electronic energy of the system, accounting for the interactions between the QM and MM regions. Once the SCF calculation converges, necessary output files, including the geometry-basis wavefunction (GBW) and the SCF electron density file, are saved. These files contain information about the molecular structure, electronic structure, and electron density distribution. The CHELPG scheme then calculates the ESP using the data from the GBW and electron density files. It performs a charge fitting procedure to assign atomic charges to each atom in the molecule to best reproduce the calculated ESP at a set of grid points surrounding the molecule. These charges represent the electron density distribution within the molecule based on the electrostatic potential.

As a part of the QMrebind protocol, solvent molecules are not included in the charge calculation at the MM level. Numerous charge derivation methodologies in MD simulations exclude water or other solvent molecules,^84,103,104 ensuring that derived charges are indicative of the inherent electronic properties of the system without being influenced by a liquid-phase, transient, high dielectric medium in its surroundings. Moreover, introducing water molecules into a charge calculation involves consideration of numerous complexities, such as selecting the number of water molecules, their respective orientations, and relative positions, which may introduce accounting for several parameters at once. It should also be noted that such decisions are made on a case-by-case basis and could introduce unnecessary degrees of arbitrariness in reparameterization processes. QMrebind automates the process of interfacing with the QM–QM2–MM multiscale calculation functionality within the ORCA simulation engine. Upon completion of the calculation, newly obtained QM charges for the ligand replace the charges in the initial topology file. Finally, a preliminary MD simulation is run to ensure the correctness of the reparameterized topology file. At this point, the reparameterized system is ready to be simulated with SEEKR2.

2.2. Simulation enabled estimation of kinetic rates v.2 (SEEKR2)

2.2.1. Background and theory

Simulation Enabled Estimation of Kinetic Rates v.2 (SEEKR2) is an open-source software that estimates the kinetics (k_on and k_off) and thermodynamics (ΔG) of molecular processes, most especially receptor–ligand binding and unbinding.^65–69,105 The SEEKR2 program has been validated to accurately compute the kinetic and thermodynamic properties of receptor–ligand (un)binding processes in model host–guest systems and the trypsin-benzamidine complex.^66,67,106 In addition, SEEKR2 has demonstrated the ability to successfully predict the residence times of more complex receptor–ligand systems with extended drug-target residence times, such as the Janus kinase 2 (JAK2) and JAK3 inhibitors, and rank-order them in accordance with their respective residence times.⁶⁹

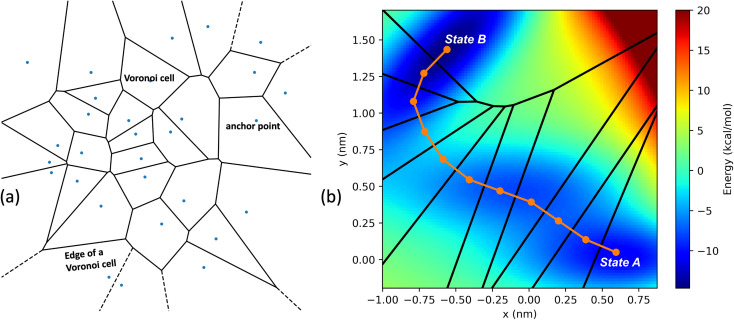
In the SEEKR2 algorithm, the phase space of the receptor–ligand complex is partitioned into two distinct regions based on the distance between the ligand and the binding site of the receptor, i.e., the MD region and the Brownian dynamics (BD) region (Fig. 2). SEEKR2 employs the OpenMM engine to run the MD simulations^107,108 and the Browndye2 engine to run the BD simulations.¹⁰⁹ The MD region is in close proximity to the binding site, where solvent effects and molecular flexibility predominantly mediate the receptor–ligand interactions. Consequently, fully atomistic MD simulations are required in this region to represent the molecular interactions accurately. A Voronoi tessellation approach partitions a given region into multiple smaller regions based on the proximity to a set of anchor points.^110,111 In a Voronoi diagram, the boundaries of the cells corresponding to an anchor point are equidistant to adjacent anchor points, and the vicinity corresponding to the given anchor point is closer to that point than any other input point (Fig. 3a). Fig. 3b illustrates a Voronoi diagram for a simple Muller potential system transitioning between states A and B using a CV that follows a likely reaction pathway between states A and B. The CV is segmented into anchor points. Milestones are defined as surfaces that are equidistant between two adjacent anchor points. The spaces between milestones constitute the Voronoi cells. A Voronoi cell around a particular anchor point is the region in configuration space where every point within this cell is closer to that anchor point than any other. With the SEEKR approach on a biologically relevant receptor–ligand system, the MD region is partitioned into “Voronoi cells” based on the distance between the center of mass (COM) of the ligand and the COM of the alpha-carbon (α-C) atoms of the binding site residues of the receptor. Each Voronoi cell contains a copy of the system where the ligand is at varying distances from the binding site of the receptor, where independent MD simulations are carried out. To generate starting structures of the receptor–ligand complex in each Voronoi cell, steered molecular dynamics (SMD) simulations are propagated that facilitate the controlled movement of the ligand away from its binding site and into the solvent. This process involves gradually pulling the ligand out of the binding pocket with a moving harmonic restraint while maintaining the system in equilibrium and adding no significant stress. Each time the ligand crosses a milestone, a snapshot of the receptor–ligand complex is saved as a starting structure for that particular Voronoi cell for running SEEKR2 simulations. MD simulations with the Markovian milestoning scheme are then employed concurrently within individual Voronoi cells until convergence is reached.^64,112 Reflective boundary conditions are implemented to confine the molecular trajectories within each cell. The mean free passage time (MFPT) is then calculated from the transition matrix, Q̂ obtained from the MMVT-SEEKR2 simulations. Section 2.2.2 provides a comprehensive set of equations employed in the calculation of mean free passage time (MFPT) and the binding free energy profile (ΔG_i) in the context of SEEKR2 simulations.

Fig. 2. Graphical representation of the partition of the phase-space of the receptor (grey)–ligand (yellow) complex into the MD region (further partitioned into Voronoi cells) and the BD region. Voronoi cells are defined based on the CV, which is determined by the distance between the COM of the inhibitor and the COM of the α-carbon atoms of the residues at the binding site.

Fig. 3. (a) An example of the two-dimensional Voronoi diagram generated from a random set of input points illustrating the spatial decomposition based on proximity to a given set of anchor points. Each input point represents an anchor point, and the enclosed region around the point is a Voronoi cell, which is the set of all locations closer to that anchor point than any other. The edges of the Voronoi cell indicate the boundary where any two neighboring sites are equidistant. (b) A simple Muller potential system with an energy barrier between equilibrium states A and B. A collective variable is defined as a series of line segments following a likely reaction pathway along the transition from state A to state B. Specific anchor points on this distance variable form a two-dimensional Voronoi tessellation. After determining the anchor points, milestones are placed equidistant between them. The space between milestones defines each Voronoi cell.

2.2.2. Equations employed in the MMVT-SEEKR2 simulation approach

The SEEKR2 algorithm employs a series of equations to calculate the MFPT and ΔG_i. Let the phase space of a bimolecular complex be divided into N milestones, and Q is the N by N transition rate matrix represented by eqn (5).

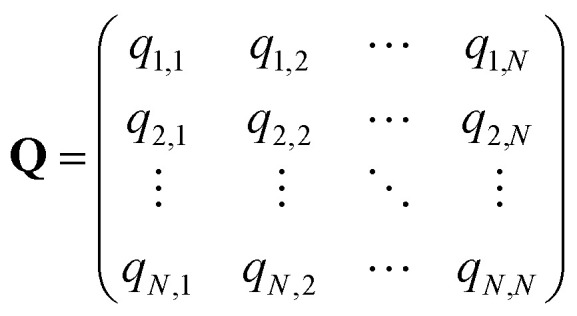5

q _ii and q_ij are the diagonal and off-diagonal elements, respectively, of the transition matrix, Q, N_ij represents the number of transitions between the ith and jth milestone, and R_i is the time spent by a long-timescale trajectory having last touched the ith milestone, then q_ii and q_ij are represented by eqn (6) and (7) respectively.

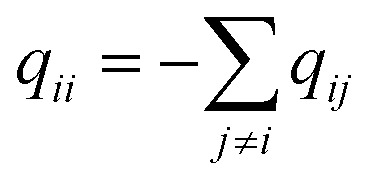6

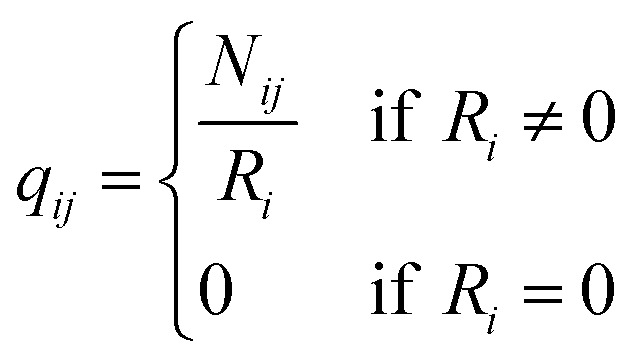7

Let x_α and v_α be the position and velocity of an MMVT trajectory, at any time, t, in the Voronoi cell, V_α. The variables 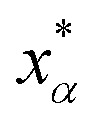and 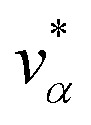are the position and velocity of the trajectory at time, t + Δt, as predicted by the simulation time integrator algorithm (typically, the Langevin integrator). Reflective boundary conditions are employed to keep the trajectories within each Voronoi cell, as represented by eqn (8) and (9), respectively.

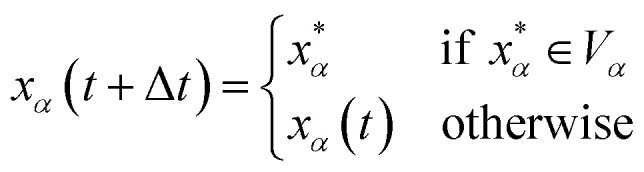8

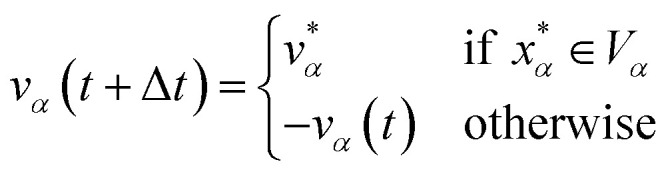9

Let π_α be the probability of an ensemble of unconstrained long-timescale trajectories being in a particular Voronoi cell when the system has reached equilibrium. For Voronoi cell V_α, let T_α be the total simulation time in that cell. A normalizing factor, T, is given by eqn (10).

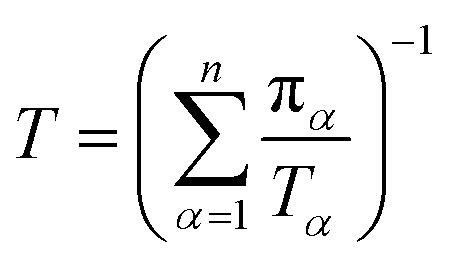10

Let N_ij^α be the number of collisions during the MMVT trajectories with the ith milestone having last touched the jth milestone in V_α, then the total number of transitions between the ith and jth milestones, N_ij is given by eqn (11).

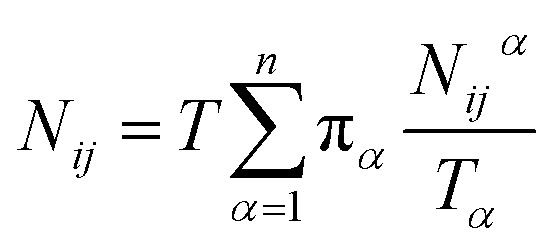11

Let R_i^α be the simulation time in Voronoi cell V_α, having last touched the ith milestone. The time spent by the trajectory having last touched the ith milestone, R_i is given by eqn (12).

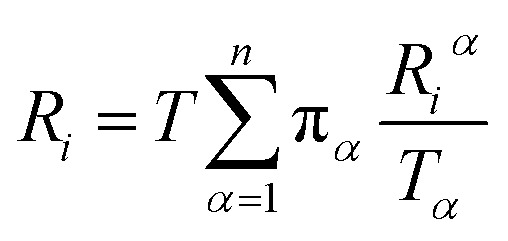12

Let N_α,β be the number of MMVT trajectory collisions in Voronoi cell V_α against its boundary with Voronoi cell V_β, and N_β,α be the number of collisions in Voronoi cell V_β against its boundary with Voronoi cell V_α. The equations to compute π_α are to be found in eqn (13) and (14).

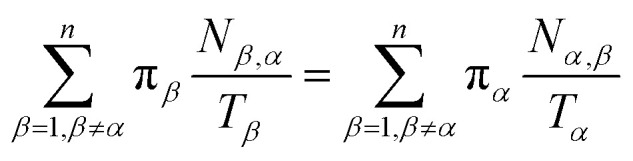13

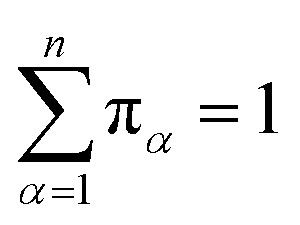14

Let Q̂ be the N-1 by N-1 matrix obtained from the upper left corner of Q, and 1 is a vector of ones, the mean free passage times from all states, T^N is obtained by solving eqn (15).

Q̂T^N = −1 15

Stationary probabilities of the milestones, p are obtained from solving eqn (16).

Qp = p 16

Let R be the gas constant, T be the temperature, p_i and p_ref be the stationary probabilities of the ith and (arbitrary) reference milestone, respectively. The free energy profile of the ith milestone, ΔG_i is given by eqn (17).

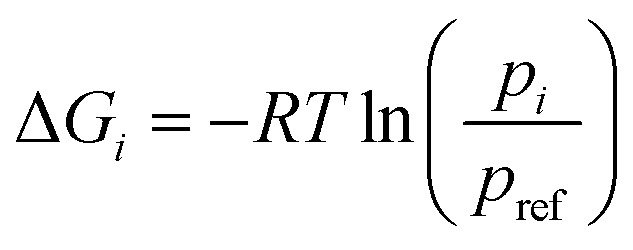17

2.3. Applications to receptor–ligand complexes

2.3.1. Host–guest complexes

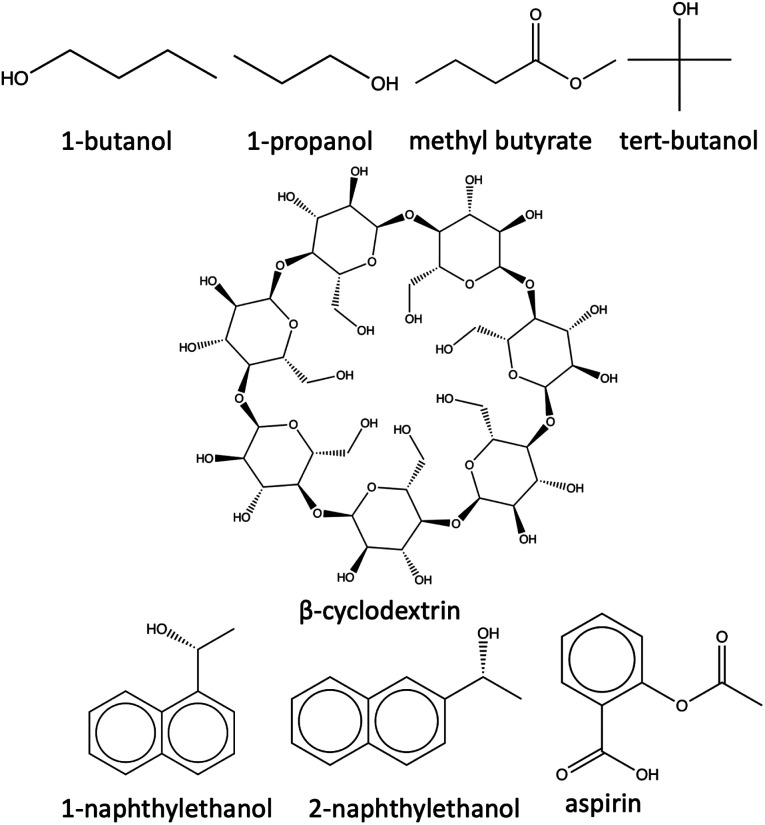
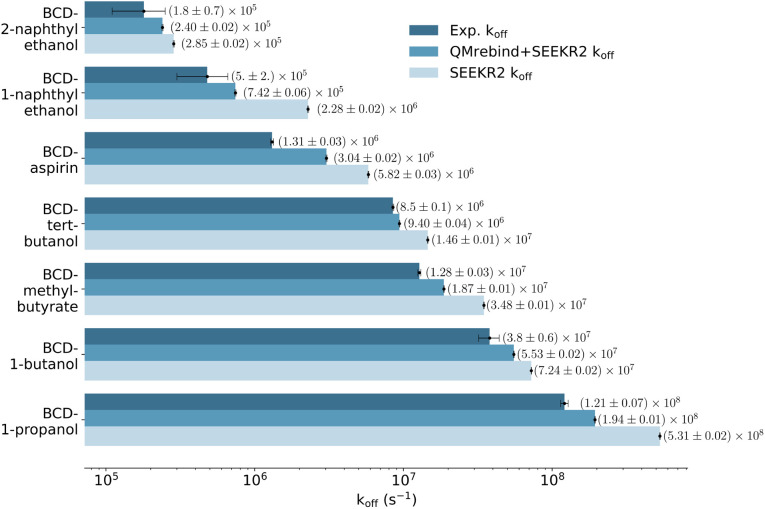
β-Cyclodextrin (host) is a cyclic oligosaccharide characterized by a toroidal shape formed by seven glucopyranose units linked by α-1,4 glycosidic bonds.¹¹³ This macrocyclic molecule possesses a hydrophobic cavity in its central core, which can effectively encapsulate one of the ligand (guest) molecules of suitable size and shape, thus stabilizing their molecular structures and altering their physicochemical properties. These properties make β-cyclodextrin an ideal model system for studying host–guest interactions using novel approaches. The shape, size, and functional groups of the guest molecules affect their binding to the host cavity. Additionally, these ligands have different binding affinities for the host, allowing it to rank-order them according to their unbinding (k_off) rates. The host with seven different ligands, including alcohols (1-butanol, 1-naphtylethanol, 2-naphtylethanol, 1-propanol, and tert-butanol) and esters (aspirin and methyl-butyrate) served as model receptor–ligand complexes for evaluating the effectiveness of the reparameterized force field parameters of the receptor–ligand complexes in the SEEKR2 algorithm (Fig. 4). Receptor–ligand unbinding rates are calculated using the QMrebind + SEEKR2 algorithm and compared against the previously performed SEEKR2 simulations, without QMrebind reparameterization, and experimentally determined unbinding k_off rates.

Fig. 4. Structures of β-cyclodextrin and the seven ligands.

2.3.1.1. System preparation and simulation

The host molecule is initially parameterized using the q4md-CD force field,¹¹⁴ while the guest ligands are parameterized using the general Amber force field (GAFF).¹¹⁵ q4md-CD force field has been designed to accurately represent the geometrical, structural, dynamical, and hydrogen bonding aspects of heterogeneous cyclodextrin-based systems.¹¹⁴ q4md-CD force field incorporates geometrical parameters from the Amber99SB force field to describe protein residues and GLYCAM04 for carbohydrate and organic components (if available). Partial atomic charges are derived using the R.E.D. tools,¹¹⁶ while scaling factors of 1.2 and 2.0 are imposed for the 1–4 electrostatic and 1–4 van der Waals interactions, respectively. The q4md-CD force field has demonstrated better agreement with experimental findings compared to GAFF for cyclodextrin molecules.^117,118

Subsequently, the complexes are solvated with the TIP3P water model and subjected to a non-bonded cut-off distance of 9 Å, and long-range electrostatic interactions were treated with the particle mesh Ewald (PME) method.^119,120 The relatively smaller size of the host–guest complexes necessitates the division into two regions. We treated the ligand molecules quantum mechanically using the Becke-3-parameter-Lee–Yang–Parr (B3LYP) functional,¹²¹ and correlation consistent polarized valence triple zeta (cc-pVTZ)¹²² basis set in the QM region. The host molecule is assigned the QM2 region where the semi-empirical tight-binding method (GFN2-XTB) is employed. For each of the host–guest complexes, 14 CV-based milestones are defined as concentric spheres and are located at distances of 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 7.0, 8.0, 9.0, 10.0, 11.0, 12.0, 13.0, and 14.0 Å respectively from the center of mass (COM) of the host. Starting structures for the SEEKR2 simulations are obtained using the steered molecular dynamics (SMD) simulations, where a moving harmonic restraint of 50 000 kJ mol⁻¹ nm⁻² is applied over the course of 50 ns. Identical CV definitions and milestone spacings have been implemented in the current study as in the previous SEEKR2 implementation,⁶⁷ facilitating a comparison between the two methodologies.

SEEKR2 simulations with the QMrebind-reparameterized force field parameters are run with same milestone spacings for all the complexes. A total of 50 ns of MD simulations are run within each Voronoi cell, totaling a simulation time of 700 ns for 14 Voronoi cells. To obtain statistically meaningful results and assess the reproducibility and robustness of the simulations, three replicas of SEEKR2 simulations are performed for each complex, totaling a simulation time of 2.1 μs. Experimental values for the unbinding rates for the seven host–guest complexes, along with the k_off rates estimated by the SEEKR2 framework, with the QMrebind-reparameterized and generic force field parameters, are provided in ESI Table S1.†

2.3.2. Hsp90-inhibitor complexes

Heat shock protein 90 (Hsp90) is an ATP-dependent molecular chaperone protein that plays a vital role in maintaining the conformational integrity and stability of its client proteins.^123–127 Inhibition of Hsp90 can lead to the degradation of its client proteins, many of which are important oncogenic drivers, making it an attractive target for drug discovery. The N-terminal domain of Hsp90 (N-Hsp90) binds to ATP and co-chaperones, which are essential for regulating its activity.^128,129 By inhibiting the ATPase function of the human N-Hsp90 using ATPase inhibitors, its chaperone activity can be disrupted, which causes the client proteins to degrade and reduce tumor growth. This approach is being investigated as a potential cancer therapy, and several ATPase inhibitors have been developed for this purpose.^130–132

N-Hsp90-inhibitor complexes pose challenges for MD simulations in a variety of ways. The binding and unbinding mechanism of N-Hsp90-inhibitor complexes is complicated and dynamic, involving multiple conformational states and high flexibility of the ATP binding site.^133–135 These conformational changes may occur on timescales beyond the reach of current MD simulations, making it challenging to capture the entire binding/unbinding process accurately. Moreover, such (un)binding events typically involve long timescales, and MD simulations must be run for extended periods, often on the order of microseconds or milliseconds.^30,136,137 Additionally, modeling the interactions between inhibitors and the binding site requires considering various factors, such as polarization at the bound state, complex receptor–ligand binding dynamics, choice of appropriate CVs, and initial starting states. To address such challenges, dividing the conformational space of the receptor–ligand complex into a series of discrete milestones implemented in SEEKR2 and an accurate representation of the non-covalent inhibitor–receptor interactions at the binding site through the QMrebind scheme allows for accurate and efficient sampling of rare events and a greater exploration the conformational space of the receptor–ligand complex.

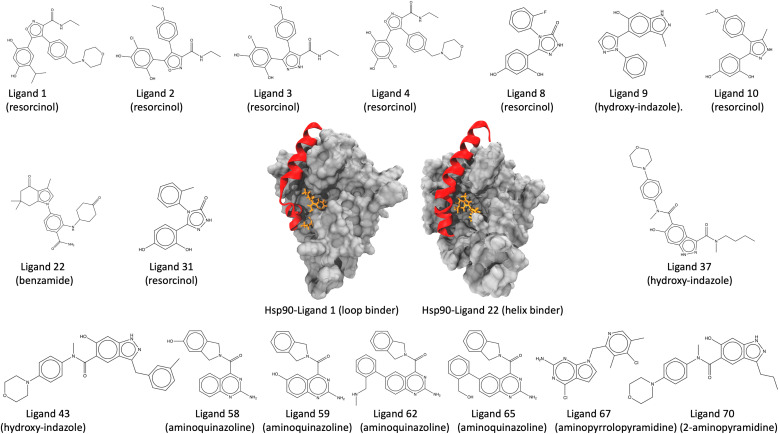
τ-Random acceleration molecular dynamics (τRAMD) is an enhanced sampling computational approach for exploring relevant biomolecular pathways and ranking drug candidates by estimated mean first passage times (MFPT).¹³⁸ Recently, τRAMD has been used to observe the ligand unbinding pathway for a series of 70 N-Hsp90 inhibitors and ranked them according to their relative residence times. N-Hsp90 protein has been shown to acquire different conformations, namely the loop and the helix conformations.¹³⁹ In the loop conformation, inhibitors bind solely to the ATP binding site, while in the helix conformation, inhibitors additionally occupy a hydrophobic transient subpocket situated between α-helix3 and the beta-strands, thereby stabilizing the α-helix3 domain (Fig. 5). This study chooses a subset of 17 inhibitors representing significant diversity in molecular scaffold among 70 inhibitors (Table 1). These inhibitors possess varying residence times within the protein, bind to either the loop or the helix conformation of the protein, and are classified into different groups, including resorcinol, hydroxy-indazole, benzamide, aminoquinazoline, aminopyrrolopyrimidine, and 2-aminopyramidine, based on their structural diversity, scaffold, and chemical motifs (Fig. 5). Absolute unbinding kinetics (k_off) for eight of the 17 are calculated using the original force field parameters input directly into SEEKR2 and the QMrebind + SEEKR2 approach and are compared against the experimental values. PDB and topology files for the Hsp90-inhibitor complexes are obtained from the original study.¹³⁸ In the same study, ligands were parameterized using the Antechamber program, and electrostatic potentials derived from ab initio calculations were employed to fit the restrained electrostatic potential (RESP) atomic partial charges^140–142 at the HF level with a 6-31G*(1d) basis set. While the general Amber force field (GAFF) was applied to the ligands for all non-charge parameters, the protein was parameterized with the Amber14 force field.^115,143

Fig. 5. Structure of the Hsp90-ligand complexes (Hsp90-ligand 1 complex, a loop binder, and the Hsp90-ligand 22 complex, a helix binder) and the 17 inhibitors examined in this study. The inhibitors are further classified into six groups, namely, resorcinol, hydroxy-indazole, benzamide, aminoquinazoline, aminopyrrolopyrimidine, and 2-aminopyramidine, based on their structural diversity, scaffold, and chemical motifs.

Categorizing Hsp90 inhibitors into different functional groups and their binding to specific conformations of the Hsp90 protein.

Hsp90-inhibitor complex	Inhibitor group	Binding conformation
Hsp90-ligand 1	Resorcinol	Loop
Hsp90-ligand 2	Resorcinol	Loop
Hsp90-ligand 3	Resorcinol	Loop
Hsp90-ligand 4	Resorcinol	Loop
Hsp90-ligand 8	Resorcinol	Loop
Hsp90-ligand 9	Hydroxy-indazole	Loop
Hsp90-ligand 10	Resorcinol	Helix
Hsp90-ligand 22	Benzamide	Helix
Hsp90-ligand 31	Resorcinol	Helix
Hsp90-ligand 37	Hydroxy-indazole	Helix
Hsp90-ligand 43	Hydroxy-indazole	Helix
Hsp90-ligand 58	Aminoquinazoline	Helix
Hsp90-ligand 59	Aminoquinazoline	Helix
Hsp90-ligand 62	Aminoquinazoline	Helix
Hsp90-ligand 65	Aminoquinazoline	Helix
Hsp90-ligand 67	Aminopyrralopyrimidine	Helix
Hsp90-ligand 70	2-Aminopyramidine	Helix

2.3.2.1. System preparation and simulation

PDB and topology files for the Hsp90-ligand complexes are obtained from the original study.¹³⁸ Before initiating the QMrebind reparameterization process, structure files are subjected to energy minimization (using only MM) to ensure the stability and optimal conformation of the receptor–ligand complexes. In the reparameterization process, the Hsp90-inhibitor complexes are partitioned into three regions, the high-level QM region, the low-level QM2 region, and the MM region. The inhibitors comprise the QM region, where second-order Møller–Plesset perturbation (MP2) theory is implemented with the cc-pVTZ basis set. The binding site residues having any atoms within a cut-off distance of 5 Å comprise the QM2 region, where the semi-empirical tight-binding method, GFN2-XTB, is employed (refer to ESI Table S2† for an exhaustive list of binding site residues for Hsp90-inhibitor complexes). The rest of the protein comprises the MM region. CVs are defined based on the distance between the COM of the inhibitor and the α-carbon atoms of the residues at the binding site. For each of the Hsp90-inhibitor complexes, 20 CV-based milestones are defined as concentric spheres and are located at distances of 1.00, 1.50, 2.125, 2.875, 3.625, 4.375, 5.125, 5.875, 6.625, 7.375, 8.125, 8.875, 9.625, 10.50, 11.50, 12.50, 13.50, 14.50, 15.50, and 16.50 Å respectively from the COM of the α-C atoms of the binding site residues of the receptor. Starting structures for SEEKR2 simulations are obtained using the SMD simulations, where a moving harmonic restraint of 30 000 kJ mol⁻¹ nm⁻² is applied over the course of 100 ns. A single set of SEEKR2 simulations with the reparameterized and generic force field parameters are run with the same milestone spacings for all the complexes. A total of 400 ns of MD simulations are run within each Voronoi cell, totaling a simulation time of 8 μs for 20 Voronoi cells. For a subset of eight of the Hsp90 inhibitors, the performance of QMrebind + SEEKR2 simulations is evaluated by comparing it with SEEKR2 simulations with generic force fields with the same simulation time, milestone spacings, and collective variable definitions for each of the Hsp90-inhibitor complexes.

3. Results and discussion

3.1. Host–guest complexes

The SEEKR2 and QMrebind + SEEKR2 methods reproduce the rank ordering for receptor–ligand unbinding rates for the seven host–guest complexes (Fig. 6). However, improved accuracies in estimating k_off rates for the host–guest complexes are achieved with the QMrebind + SEEKR2 approach. SEEKR2 simulations with the generic force field tend to slightly overestimate the k_off values for all host–guest complexes, while QMrebind helps to correct this overestimation, resulting in k_off rates that are in closer agreement with experimental measurements (Fig. 6). Additionally, comparable convergences of k_off rates for QMrebind + SEEKR2 simulations with reparameterized force fields and SEEKR2 simulations employing generic force fields are observed (ESI Fig. S1†). For all the seven host–guest complexes, QMrebind + SEEKR2 consistently outperformed SEEKR2 in estimating k_off rates. Such improvements can likely be attributed to more accurate force field parameters for the ligand within the vicinity of the host molecule, as computed by the QMrebind software. There is a peculiar systematic error where the SEEKR2 and QMrebind + SEEKR2 approaches overestimate the experimental k_off values for the host–guest systems. Similar overestimations have also been observed using weighted ensemble sampling¹⁴⁴ and the Ligand Gaussian accelerated Molecular Dynamics (LiGaMD) method.¹⁴⁵

Fig. 6. Unbinding rates or k_off (s⁻¹) for seven host–guest complexes obtained from experiments, QMrebind-reparameterized force field and the generic force field parameters employed in SEEKR2 simulations. Experimental k_off rates for β-cyclodextrin complexed with naphthylethanols were measured using laser flash photolysis.¹⁴⁶ For the other host–guest complexes, the ultrasonic absorption method was employed.^147,148 The horizontal axis is represented in a logarithmic scale, allowing for better visualization of k_off rates that span several orders of magnitude.

3.2. Hsp90-inhibitor complexes

3.2.1. SEEKR2 and QMrebind + SEEKR2 simulations

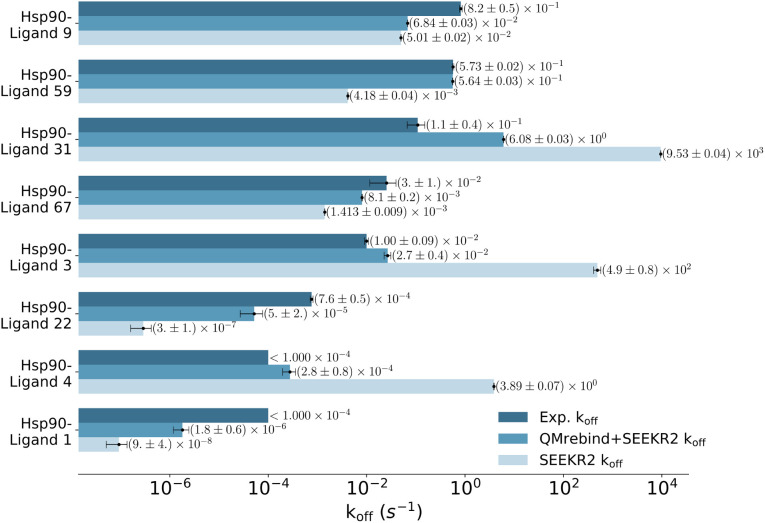
SEEKR2 simulations employing QMrebind-reparameterized force fields outperformed the SEEKR2 simulations employing the generic force fields in more accurately estimating the unbinding rates for all eight Hsp90-inhibitor complexes (Fig. 7). Both force fields within the SEEKR2 framework provided close-to-experimental k_off rates for the Hsp90-ligand 9 complex, with the QMrebind-reparameterized force field slightly outperforming the generic one (ESI Table S3†). For the rest of the seven complexes involving ligands 1, 3, 4, 22, 31, 59, and 67, QMrebind-reparameterized SEEKR2 simulations significantly outperformed generic force field SEEKR2 simulations in estimating the k_off rates. However, for the Hsp90-ligand 22 and 31 complexes, neither of the methods could estimate the k_off rates within an order of magnitude to the experimental values, with the QMrebind-reparameterized force field simulations performing better than the generic force field. In the cases of complexes 1 and 4, the experimental k_off values were only known to be less than 1 × 10⁻⁴ s⁻¹, and unbinding rates obtained with QMrebind + SEEKR2 and SEEKR2 methods seem reasonable within the margin of uncertainty. To further validate the consistent accuracy of QMrebind-reparameterized SEEKR2 simulations in estimating receptor–ligand unbinding rates, an additional set of nine Hsp90-inhibitor complexes is selected. These inhibitors encompassed a diverse range of k_off rates and scaffold diversity (Fig. 4), allowing us to thoroughly assess the accuracy and robustness of the QMrebind-reparameterization method across a broader spectrum of estimating k_off rates for receptor–ligand interactions.

Fig. 7. Unbinding rates or k_off (s⁻¹) for eight Hsp90-inhibitor complexes obtained from experiments are compared to SEEKR2 k_off rates with both the QMrebind-reparameterized force field and the generic force field parameters. In all cases, the QM-parameterized systems reported k_off values closer to the experiment.

Unbinding rate estimates for the eight Hsp90-inhibitor complexes were substantially improved by the use of QMrebind, so that, while they do not match within experimental or theoretical error margins, they often fall within the single order of magnitude criteria for success⁶⁷ and in almost all cases, at least within two orders of magnitude. While the QMrebind + SEEKR2 method has shown k_off prediction accuracy for most of the Hsp90-inhibitor complexes, certain outliers underscore inherent challenges and limitations of this method. For the Hsp90-ligand 37 complex, the estimated k_off of (3.82 ± 0.05) × 10² s⁻¹ is significantly higher than the experimentally determined k_off of (2.0 ± 0.2) × 10⁻³ s⁻¹, and is essentially predicted by QMrebind + SEEKR2 to be a fast unbinder. We choose to define an outlier as any complex whose predicted k_off is greater than two orders of magnitude distant from the experimental k_off. For the outlier complex of ligand 37, reparameterizing partial charges of the ligand via QMrebind did not produce close-to-experiment k_off. The inaccurate k_off estimate for the Hsp90-ligand 37 complex can likely be attributed to other deficiencies within the model. In our assessment, it is possible that starting structures generated via SMD simulations do not always correctly sample the unbinding pathway. Unfortunately, attempts to pull the ligand more slowly out of the binding pocket via SMD simulations to generate starting structures to resolve the problem have not improved the kinetic estimates (data not shown). It is also possible that a better choice of CV, apart from the ligand-binding site COM–COM distance, would produce better kinetics, as it may lead to more extensive sampling within the Voronoi cells. Several attempts have been made to identify the exact causes of these discrepancies, but the solution has, so far, evaded us. Additional investigations, therefore, need to be undertaken to determine the exact causes to resolve such outlier kinetics estimates.

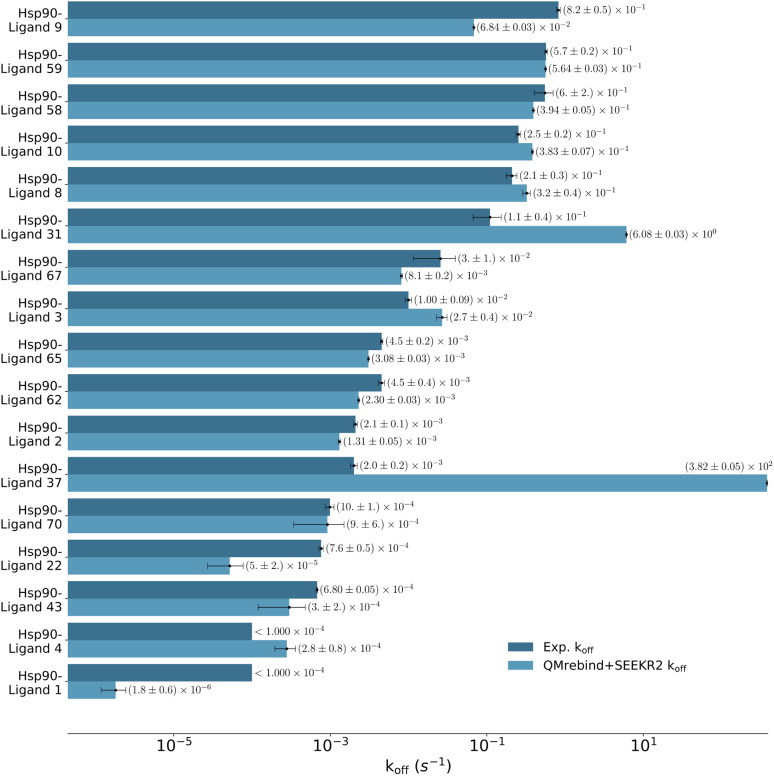
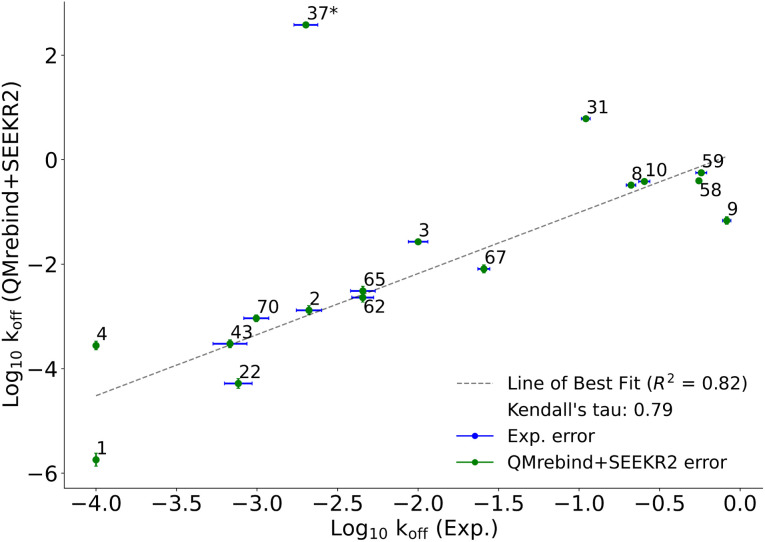
QMrebind-reparameterized SEEKR2 simulations predicted close-to-experimental k_off rates for a majority of Hsp90-inhibitor complexes (Fig. 8). Linear fit and Kendall's tau analysis are performed to evaluate the predictive accuracy of QMrebind-reparameterized SEEKR2 simulations in estimating unbinding rates for a set of 17 Hsp90-Inhibitor complexes. The linear fit (R² = 0.82) among the non-outliers demonstrated a strong correlation between the logarithm of experimental k_off values and QMrebind + SEEKR2 estimated k_off values, showing a good fit to the linear regression model (Fig. 9). Additionally, the computed Kendall's tau (τ = 0.79) displayed a positive and significant ordinal association between the experimental and QMrebind-reparameterized SEEKR2 estimated unbinding rates, supporting the agreement in ranking between both methods (Fig. 9). These analyses establish the improvement allowed by QMrebind-reparameterized SEEKR2 simulations in accurately predicting the unbinding rates for Hsp90-inhibitor complexes with high precision.

Fig. 8. Unbinding rates or k_off (s⁻¹) for 17 Hsp90-inhibitor complexes obtained from experiments and QMrebind-reparameterized force field parameters employed in SEEKR2 simulations. The experimental k_off rates were obtained using Surface Plasmon Resonance (SPR) measurements^138,139,149 (refer to ESI Table S4† for a list of references for experimentally measured k_off for each of the Hsp90-inhibitor complexes). The horizontal axis is represented in a logarithmic scale, allowing for better visualization of k_off rates that span several orders of magnitude.

Fig. 9. Scatter plot comparing the logarithm of experimental k_off values against the QMrebind + SEEKR2 estimated k_off values for Hsp90-inhibitor complexes. Each data point is labeled with its corresponding Hsp90-inhibitor complex ID, and error bars are shown for both data sets (refer to the ESI† of the SEEKR2 article⁶⁷ for detailed analyses on milestoning error estimates). The plot displays a line of best fit to indicate the correlation between the experimental and theoretically calculated k_off, with R² values indicating the goodness of the fit and the computed Kendall's tau statistic, denoting the strength and direction of the ordinal association between the experimental k_off and the QMrebind + SEEKR2 estimated k_off values for 17 Hsp90-Inhibitor complexes. The QMrebind + SEEKR2 k_off value for the Hsp90-ligand 37 complex deviates significantly from its experimental value and is considered an outlier. This complex is excluded from the linear fit and Kendall's tau analysis (refer to ESI Fig. S2† for the line of best fit and Kendall's tau statistics, including complex 37).

3.2.2. Long timescale MD simulations

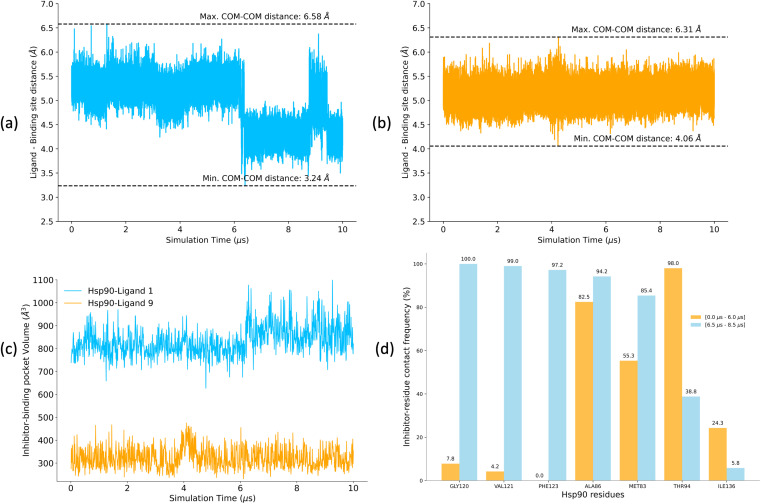
Experimental k_off data indicate distinct residence time profiles for a series of inhibitors in the loop and helix conformations of the Hsp90 protein. Ligands 1 and 4 exhibit prolonged residence times, characterized by k_off values less than 10⁻⁴ s⁻¹, while ligand 9 displays the shortest residence time with a k_off value of (8.2 ± 0.5) × 10⁻¹ s⁻¹ (ESI Table S4†). Unbiased MD simulations are performed for the two Hsp90-inhibitor complexes involving ligands 1 (slowest k_off) and 9 (fastest k_off) to elucidate the underlying factors contributing to discrepancies in residence times. Since these inhibitors are loop binders, direct comparisons can be made to investigate the structural and dynamic determinants governing the receptor–ligand (un)binding kinetics. Initial structures and force field parameters for the Hsp90-inhibitor complexes are obtained from the first Voronoi cell of the QMrebind-reparameterized SEEKR2 milestones. A total of 10 μs of MD simulations are run for each receptor–inhibitor complex at 300 K with a 2 fs timestep and a nonbonded cutoff distance of 10 Å using the Amber20 MD engine.¹⁵⁰ Simulation trajectories are analyzed using the CPPTRAJ module of the Amber 20 package.^151–153

A low k_off denotes an extended residence time for the ligand, characterizing it as a high-affinity binder (as observed for ligand 1). Conversely, ligand 9 exhibits a relatively higher k_off as compared to ligand 1, indicating rapid dissociation from the binding site, classifying it as a low-affinity binder. To explain the variations in residence times, we computed the distances between the center of mass (COM) of the ligands and the COM of α-carbon atoms of the binding site residues for both the Hsp90-ligand 1 and Hsp90-ligand 9 complexes, as depicted in Fig. 10a and b. Changes in the ligand-binding site COM–COM distance during the simulation may suggest shifts in the interaction dynamics between the ligand and the receptor protein. In the context of the Hsp90-ligand 1 complex, a notable decrease in the COM–COM distance is evident at approximately 6 μs into the simulation, suggesting a modification in its interaction pattern with the binding site residues, as illustrated in Fig. 10a. This dynamic behavior could potentially contribute to an increased receptor–ligand interaction or efficient binding, contributing to a smaller k_off. Conversely, the Hsp90-ligand 9 complex showed no significant changes in the ligand-binding site COM–COM distance throughout the simulation (Fig. 10b).

Fig. 10. (a and b) Distances between the center of mass (COM) of the ligand and the COM of α-carbon atoms of the binding site residues for (a) Hsp90-ligand 1 complex and (b) Hsp90-ligand 9 complex calculated for 10 μs of unbiased MD simulations. (c) Pocket volume analysis for Hsp90-ligand 1 and ligand 9 complexes. (d) Contact frequencies of Hsp90 residues when interacting with ligand 1 (within the ligand-binding pocket) over two intervals, i.e., 0–6.0 μs and 6.5–8.5 μs. Contact frequencies are expressed as a percentage of the total number of possible contacts. Only residues with a difference in contact frequencies exceeding 10% between the two simulation intervals are shown.

POVME2 (POcket Volume MEasurer 2) is a powerful computational tool designed to characterize and measure binding pockets within macromolecular and small-molecule complexes.^154–156 POVME2 operates through a series of steps, including grid-based point generation, exclusion of points near receptor atoms, and optional removal of non-contiguous regions. We utilized the POVME2 algorithm to assess the binding pocket volumes for the two complexes for 10 μs of MD simulations. A 1.09 Å cutoff, corresponding to the van der Waals radius of the hydrogen atom, ensured the precise exclusion of non-pocket regions. Larger binding pocket volumes are observed for the Hsp90-ligand 1 complex compared to the Hsp90-ligand 9 complex (Fig. 10c). Ligand 1 possesses a larger and more voluminous molecular structure and is expected to adopt conformations that extend into the binding pocket more than ligand 9 (Fig. 5), leading to an increased volume estimate for the binding pocket. Consequently, the Hsp90-ligand 1 complex might exhibit a more expansive and accommodating binding pocket due to the specific interactions (Fig. 10d) and spatial arrangements between the ligand and the receptor, resulting in a larger calculated binding volume.

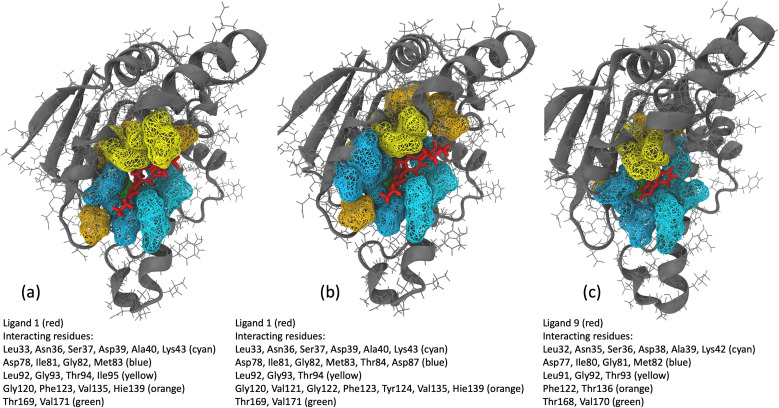
We analyzed interaction dynamics between ligand 1 and a set of key residues (within a cutoff distance of 4 Å) within the ligand-binding pocket of the Hsp90 receptor. Two distinct time intervals were selected (0 μs to 6.0 μs and 6.5 μs to 8.5 μs), where significant differences in the ligand-binding site distance were observed (Fig. 11a and b). More ligand-residue contacts were prevalent during the 6.5 μs to 8.5 μs simulation interval, indicating a dynamic shift in the binding interactions (Fig. 10d and ESI Table S5†). Residues such as Glu32, Ser35, Asn36, Asp39, and Gly80 consistently exhibited higher ligand-residue contact frequencies throughout both intervals (ESI Table S5†), indicating their key roles in maintaining robust interactions with the ligand. Conversely, residues such as Met83, Thr94, Gly120, Val121, and Phe123 displayed significant fluctuations in contact frequency between the two intervals, highlighting dynamic alterations in their binding patterns (Fig. 10d). Changes in receptor–ligand interactions are observed during the later simulation phase (6.5–8.5 μs), where a larger number of residues interacted with the ligand as compared to the initial 6 μs of simulation (Fig. 11a, b, and ESI Table S6†). Such a shift in the interaction landscape with a different ensemble of residues suggests a potential ligand rearrangement within the binding pocket, and a dynamicity of ligand 1 in the binding pocket of the receptor–ligand complex may contribute to an extended residence time of ligand 1. To interpret the binding strength and specificities of the two Hsp90-ligand complexes, residues interacting with the ligand within a cutoff distance of 4 Å were monitored at 0.4 ns intervals for the entire duration of the simulation. It is observed that ligand 1 interacted with a significantly higher number of residues than ligand 9 (Fig. 11a–c and ESI Table S6†). Interactions, such as hydrogen bonds, hydrophobic interactions, and van der Waals forces, potentially account for a higher residence time of ligand 1. On the contrary, reduced ligand-residue interactions for ligand 9 correlate well with its lower residence time, suggesting fewer constraints holding it in the binding pocket.

Fig. 11. (a and b) Hsp90 protein residues interacting with ligand 1 within a cutoff distance of 4 Å for the (a) initial 6 μs of MD simulation and (b) 2 μs (6.5–8.5 μs) of MD simulation interval. (c) Hsp90 protein residues interacting with ligand 9 within a cutoff distance of 4 Å for 10 μs of MD simulation.

4. Conclusion

We have presented a novel approach to enhance the accuracy of SEEKR2 milestoning simulations of bimolecular complexes for predicting receptor–ligand unbinding rates through quantum mechanical reparameterization of the ligand charges at the binding site. The QMrebind force field reparameterization method may also be useful to simulate the binding–unbinding processes of receptor–ligand complexes using other enhanced sampling methods besides SEEKR2, such as RAMD, GaMD, etc. This method provides a multi-scale approach for force field parameterization through quantum mechanical treatment of the ligand at its binding site, thereby increasing the accuracy of simulations in estimating the unbinding rates of the ligands. To evaluate the effectiveness of our approach, we implemented this method within the SEEKR2 simulation framework to estimate the ligand-unbinding rates for seven host–guest complexes and 17 N-Hsp90-inhibitor complexes. Our results showed that the QMrebind-reparameterized force field within the SEEKR2 framework outperformed the generic force field in estimating the kinetic properties of receptor–ligand unbinding for most of the complexes. This comparison highlights the potential of the improved force field parameters to enhance the simulation accuracy. Integration of the QMrebind method into SEEKR2 is straightforward, and it can also be used as a standalone package for reparameterizing force field parameters for unbiased MD simulations and other enhanced MD simulation methods.

Data availability

The QMrebind project is available at https://github.com/seekrcentral/qmrebind, and the SEEKR2 project is available at https://github.com/seekrcentral/seekr2. Data supporting the findings in this study are available as ESI at https://doi.org/10.6075/J09Z9545. The dataset includes SEEKR2 and QMrebind + SEEKR2 simulations for seven host–guest complexes and 17 Hsp90-inhibitor complexes, along with structural and topology files, simulation trajectories, and analysis scripts to obtain the receptor–ligand unbinding rate for each complex.

Author contributions

A. A. O. and R. E. A. conceptualized the project. A. A. O. led the implementation and software development. A. A. O. conducted simulations, visualization, and analysis of the receptor–ligand complexes. A. A. O., L. W. V., and R. E. A. participated in data analysis and interpretation. A. A. O. led the writing, reviewing, and editing of the original draft. L. W. V. provided supporting contributions to the conceptualization, implementation, and software development and helped to write, review, and edit the original draft. R. E. A. provided funding and resource support and supervised the project while contributing to the writing, reviewing, and editing of the manuscript. All authors approved the final version of the manuscript.

Conflicts of interest

The authors declare no conflicting interests.