Generation of Whole-Body FDG Parametric K_i Images from Static PET Images Using Deep Learning

Abstract

FDG parametric K_i images show great advantage over static SUV images, due to the higher contrast and better accuracy in tracer uptake rate estimation. In this study, we explored the feasibility of generating synthetic K_i images from static SUV ratio (SUVR) images using three configurations of U-Nets with different sets of input and output image patches, which were the U-Nets with single input and single output (SISO), multiple inputs and single output (MISO), and single input and multiple outputs (SIMO). SUVR images were generated by averaging three 5-min dynamic SUV frames starting at 60 minutes post-injection, and then normalized by the mean SUV values in the blood pool. The corresponding ground truth K_i images were derived using Patlak graphical analysis with input functions from measurement of arterial blood samples. Even though the synthetic K_i values were not quantitatively accurate compared with ground truth, the linear regression analysis of joint histograms in the voxels of body regions showed that the mean R² values were higher between U-Net prediction and ground truth (0.596, 0.580, 0.576 in SISO, MISO and SIMO), than that between SUVR and ground truth K_i (0.571). In terms of similarity metrics, the synthetic K_i images were closer to the ground truth K_i images (mean SSIM = 0.729, 0.704, 0.704 in SISO, MISO and MISO) than the input SUVR images (mean SSIM = 0.691). Therefore, it is feasible to use deep learning networks to estimate surrogate map of parametric K_i images from static SUVR images.

I. Introduction

¹⁸F-fluorodeoxyglucose (FDG) PET imaging has been widely used for detection, staging, and therapeutic response assessment in oncology [1]. Tumors typically have higher activities of glucose metabolism, leading to higher uptake rates of glucose analogy FDG in tumors than in normal tissues [2–6]. For cancer diagnosis and staging, whole-body PET imaging is typically performed to scan from the base of the skull to mid-thigh, covering most relevant organs [6]. Combined with other imaging modalities, such as CT and MRI, FDG PET imaging help to localize suspected tumor regions and provide more functional information about tumors [7, 8].

Standard uptake value (SUV) is widely used in clinics for PET quantification and is generated from static FDG PET images, acquired typically at 60 minutes post tracer injection [6]. In comparison, parametric K_i value derived from dynamic PET frames is a potentially more quantitative measurement for the FDG metabolic rate than the semi-quantitative measurement of SUV [9, 10]. The derivation of K_i value is based on the theory that the FDG uptake process can be approximated using two-tissue irreversible compartmental model [11, 12]. Through the acquisition of dynamic FDG PET images after tracer injection and the measurement of the arterial tracer activity as the input function, K_i value can be calculated using Patlak graphical analysis for each voxel [12, 13]. As a common physiological metric, the glucose metabolic rate can be converted from the K_i value with the value of the glucose concentration and a correction term of lumped constant [14, 15]. The two-tissue irreversible compartmental model is applicable for many tissue regions over the body, but is not valid in organ regions with dual blood supply, such as liver [16]. Kinetic parameters in these regions could be estimated by more complex models. For example, based on the two-tissue compartmental model, the generalized Patlak analysis estimated K_loss in additional to K_i, with considerations of FDG dephosphorylation. The generalized Patlak analysis can reduce the estimation bias, but encounter higher noise than the standard linear Patlak analysis [17]. The voxel-wise model selection was also implemented to apply different compartmental models in whole-body PET images [18].

Both dynamic PET image acquisition and input function measurement are time-consuming and cause discomfort to the patients [19, 20]. To simplify the process, a dual-time-point K_i calculation method was implemented to reduce the number of frames in linear regression calculation of Patlak analysis [21]. Image-derived and population-based input functions can also replace the input function measurement through arterial blood sampling to reduce discomfort of patients [22, 23]. To further simplify the process, it would be appealing to generate K_i images from single timepoint static PET images.

Deep neural networks have become increasingly popular in medical imaging research, such as image denoising [24], segmentation [25], and detection and classification of tumors [26]. In tasks of denoising low dose PET images, 3D U-Net could achieve superior performance than conventional denoising techniques, such as Gaussian filter [27]. Generative adversarial networks (GAN) [28] are also widely used to denoise images of various modalities, such as low dose CT [29], PET [30] and fast MRI [31]. Various kinds of deep neural networks were also used in image synthesis across different imaging modalities [32]. For example, U-Net, which was originally designed for segmentation tasks of biomedical images, such as segmenting neuronal structures in microscopy images [33], was also developed to generate attenuation maps of PET images from input MRI images [34]. GANs have been used to train SPECT emission images to generate attenuation maps, which can help attenuation correction process without CT [35]. Deep learning networks have been used to predict PET images between different tracers. Based on the correlation between glucose metabolism and synaptic vesicle glycoprotein 2A (SV2A) in the brain, PET images of ¹¹C-UCB-J could be generated from FDG PET images using 3D U-Net [36].

Inspired by the deep learning architecture used for image synthesis between different imaging modalities and tracers, we applied various configurations of 3D U-Nets to synthesize parametric K_i images from static FDG PET images in this study. One recent study used a 3D U-Net structures to generate dynamic PET frames from MR images, where the output dynamic PET frames were further converted to K_i images using Patlak analysis [37]. However, the process of generating K_i images was isolated from the 3D U-Net, and this work focused more on the correlation between MR and dynamic PET images instead of absolute quantification. Another study used 3D U-Net to generate parametric K_i images from static SUV images without input function measurement [38]. The SUV images in their study were acquired by a total-body PET/CT scanner, thus had higher counts than the whole-body PET images from typically clinical PET scanners using continuous bed motion (CBM) or step-and-shoot techniques [38]. A More recent study used an improved cycle-GAN, in additional to U-Net, to generate parametric K_i images from SUV images in the chest regions [39]. Our work implemented similar deep learning networks to generate parametric K_i images in the body trunk without input function measurement. However, we used SUV ratio (SUVR) images, instead of SUV images, as input to training the U-Nets, based on the findings that static SUVR values are better correlated with parametric K_i values than SUV in tumor regions [40]. The static PET images in our study were acquired by a Siemens mCT PET/CT scanner using CBM acquisition and had lower counts than those from total-body scan with long axial FOV. In addition to the U-Net configuration used in [38], we explored U-Net configurations with different sets of input and output image patches to explore if additional information, such V_b values, helped to train U-Nets. Currently, the PET/CT scanners with CBM imaging techniques are still widely used in clinics and our deep learning workflow could be used to generate parametric K_i images from the static PET images acquired by these scanners.

II. Materials and methods

A. Data Generation

There were 25 whole-body FDG dynamic PET scan datasets included in this study. The subjects were scanned on a Siemens Biograph mCT scanner using the multi-pass CBM mode. After the subject’s FDG injection ranging from 256 to 373 MBq, a 6-min single bed scan on the heart was performed to capture the initial phase of input function. Then the whole-body scanning process was performed with 19 CBM passes, with each pass taking 120 seconds for the initial 4 frames from 6 min to 15 min post tracer injection, and 300 seconds for the remaining frames after 15 min post tracer injection [21]. Images were reconstructed into dynamic frames each with the voxel size of 2.036mm×2.036mm×2.027mm. During the acquisition of dynamic frames, blood samples were collected through arterial cannulation after tracer injection and were centrifuged to obtain plasma. The plasma radioactivity of the samples was measured by gamma counters to obtain the arterial input function after decay correction [21].

The static SUV image of each subject was generated as the average of three dynamic SUV frames from 60 minutes to 75 minutes post tracer injection, with the frame index from 14 to 16 [21]. Left ventricle blood pool regions were segmented manually in static SUV images for all subjects, and static SUV images were then normalized by the mean values in the blood pool regions to generate SUVR images. One U-Net configuration was implemented to read three input SUVR patches generated from individual dynamic SUV frames from 60 minutes to 75 minutes, and then normalized by mean values of blood pool in the middle frames. Ground truth K_i images were generated with images of intercept V_b values from all dynamic SUV frames and plasma input functions of the tracer, using Patlak analysis with t* = 20 min [21, 41]. The output K_i images in the training dataset were preprocessed by multiplying the K_i values by 100, so that most output values of U-Nets were in the range of 0 to 10, to improve training efficiency. Both SUVR and K_i images were cropped to only include the subject’s body trunk with a matrix size of 160×288×256. We used patch-based approach in the training and random patches of smaller regions, with a matrix size of 64×64×64, were created from both the SUVR and the K_i images.

B. U-Net Structures

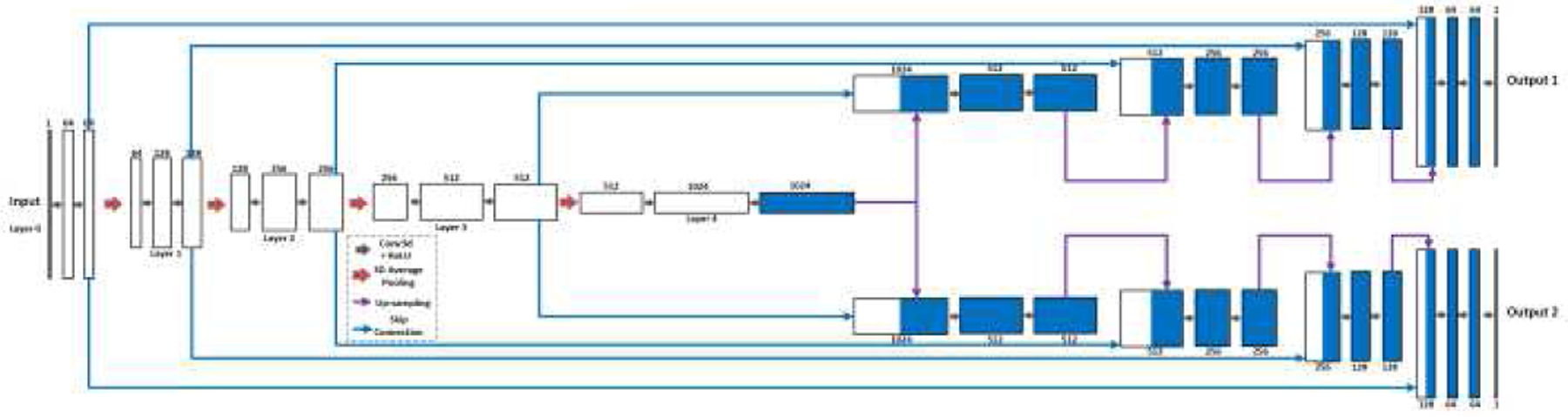
In our work, three deep learning network configurations were implemented using the Pytorch library [42] based on the 3D U-Net structure [36]. All configurations read static SUVR image patches as input and generate their corresponding K_i image patches as output. Fig. 1 shows the first two configurations of U-Nets with different numbers of input SUVR image patches and single output K_i image patch. The U-Net accepting single SUVR patch as input was denoted as single input and single output (SISO). The network with multiple input patches, specifically three SUVR patches corresponding to SUVR images of 60–65 min, 65–70 min, and 70–75 min post-injection, was denoted as multiple inputs and single output (MISO). Three individual SUVR frames provide additional information about the change of tracer activities between 60 minutes and 75 minutes post-injection. We aim to explore if the additional dynamic information could further improve the K_i image prediction. Both U-Net configurations had contraction and expanding paths, with each path having 5 operational layers. Every layer consisted of two 3D convolutional and ReLU operations. The contraction path of the U-Nets encoded the input image patches as smaller features by connecting two consecutive layers with the max-pooling operation, while the expanding path decoded the features with up-sampling operations between two layers. The 3D convolutional operations used 3×3×3 kernels with 1 voxel padding. The first layer had 64 filters, representing 64 features extracted from the input SUVR patches. The number of filters doubled in the next layer, hence there were 128, 256, 512 and 1024 filters in Layers 2, 3, 4 and 5. The output of each layer in the contraction path was concatenated to the layer at the same depth in the expanding path through skip connection. While patches of SUVR and K_i images were used in training process, entire SUVR images of cropped regions in the subjects’ whole body were used as the input of U-Nets in the testing process to generate K_i images.

Fig. 1.

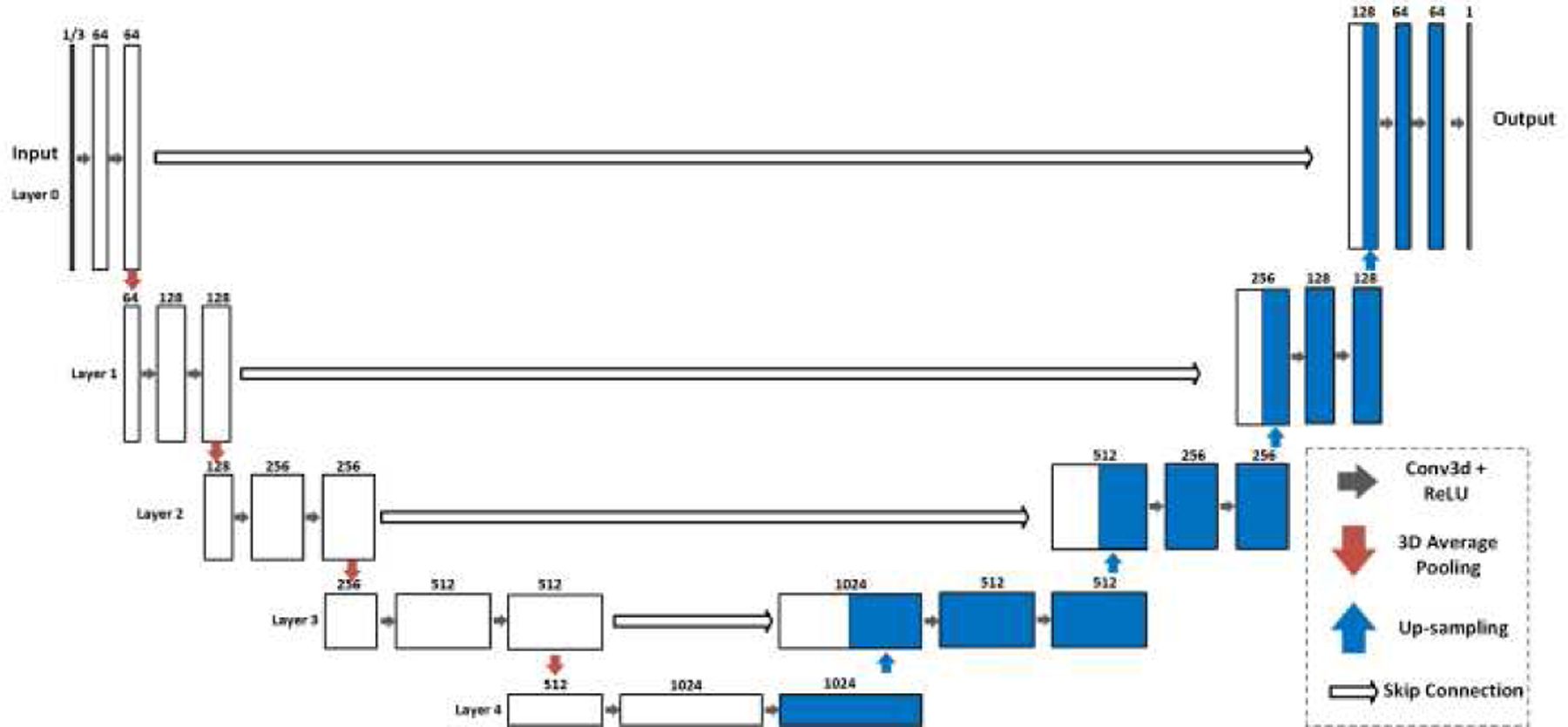
The SISO and MISO U-Nets with 5 operational layers to generate output K_i images from SUVR images. The SISO U-Net reads one SUVR patch as input, while the MISO U-Net has the input of three.

The U-Net can be modified to generate multiple image patches as the multi-task outputs. In Patlak analysis, images of intercept V_b values were generated together with K_i images. In this study, the multi-task U-Net was implemented to incorporate patches of V_b values as the additional output to K_i patches to examine whether V_b values improved the training performance. The multi-task U-Net only accepted single input of SUVR patch, and thus was denoted as single input and multiple outputs (SIMO). This configuration had single contraction path and was divided into two expanding paths after the bottleneck layer between the contraction and the expanding paths. Like the previous two U-Net configurations, the SIMO U-Net used the skip connection to concatenate the output of each contraction path layer to the input of the corresponding expanding path layer.

C. U-Nets Training and Testing

The three configurations of U-Nets were all trained with a NVIDIA Quadro RTX 8000 GPU card. The 25 subjects were partitioned into 5 groups to perform 5-fold cross-validation. In each group, the SUVR and K_i images of 20 subjects were assigned to train the U-Nets, while the SUVR images of the remaining 5 subjects were used as the input of the U-Nets to generate corresponding synthetic K_i images to evaluate the training performance. For every subject, 400 patches of the SUVR and K_i images were randomly generated as the input and output of the U-Nets. All U-Nets were trained with a batch size of 14, and a total of 300 epochs. The SISO and MISO U-Nets used the L1 loss of the scaled K_i patches as the cost function, while in the SIMO U-Net, the cost function was the sum of the L1 losses of scaled K_i and unscaled V_b patches. We did not scale V_b values in the cost function because most of the V_b values were already in the range of 0 to 10. The initial learning rate was set to 10⁻⁴, with decay rate of 0.96 for every epoch. The U-Net is a fully convolutional neural network, including operations of 3D convolution, average pooling, up-sampling and skip connection. Therefore, the U-Net can accept input images with variable sizes, and the image size is only limited by the average pooling operations [33]. In the validation and testing process, the images of body trunks (matrix size of 160×288×256) were set as input of the U-Nets to generate corresponding images of K_i distribution over the body trunks. Due to the limitation of GPU memory, the U-Nets used CPU with a large system memory to generate whole-body K_i images.

D. Evaluation

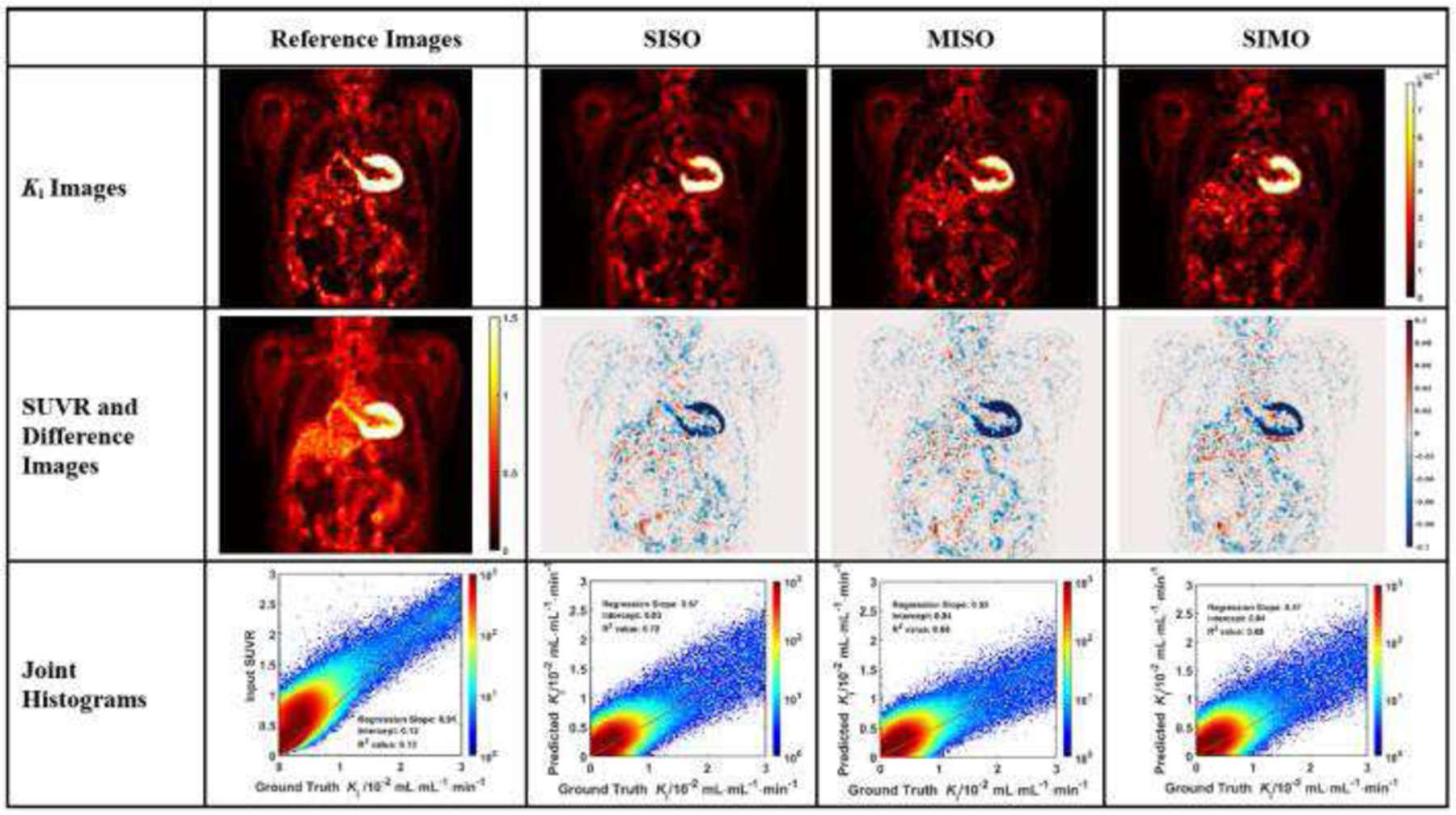
The regions of representative organs, such as liver, heart, kidney, and aorta wall, were first evaluated visually in the coronal view of SUVR, synthetic and ground truth K_i images. Difference images in color map were generated between synthetic and ground truth K_i images, so the regions with high bias between two images can be observed. We also used 2D joint histograms to compare the voxel values in two images. The joint histograms were plotted between synthetic and ground truth K_i images, after removing background voxels, and were compared with the joint histograms between input SUVR and ground truth K_i images.

Two image similarity metrics, structure similarity index (SSIM) and normalized mean square error (NMSE), were used in this study to compare synthetic and ground truth K_i images. The value of SSIM ranges from −1 to 1, and higher values indicate higher similarity between two images [43]. The NMSE is non-negative, and lower values suggest higher similarity. SSIM values were calculated between synthetic and ground truth K_i images and were compared with the values between the corresponding input SUVR and ground truth K_i images to examine whether synthetic K_i images generated from the U-Nets were more similar to ground truth K_i images than SUVR images. The NMSE values were calculated between synthetic images and ground truth K_i images, after removing background voxels, to compare the performance of different U-Nets. Because the definitions of SUVR and K_i are inherently different, thus it is not feasible to calculate the NMSE values between SUVR and K_i images as the reference for evaluation.

Lesion regions were segmented in SUV images by the researchers and verified by a nuclear physician. These regions were evaluated by comparing their mean voxel values in the synthetic and the ground truth K_i images. Among the 25 subjects in the study, 22 of them had hypermetabolic lesions in different parts of the body, such as lung and chest, as displayed in Fig. 7.

Fig. 7.

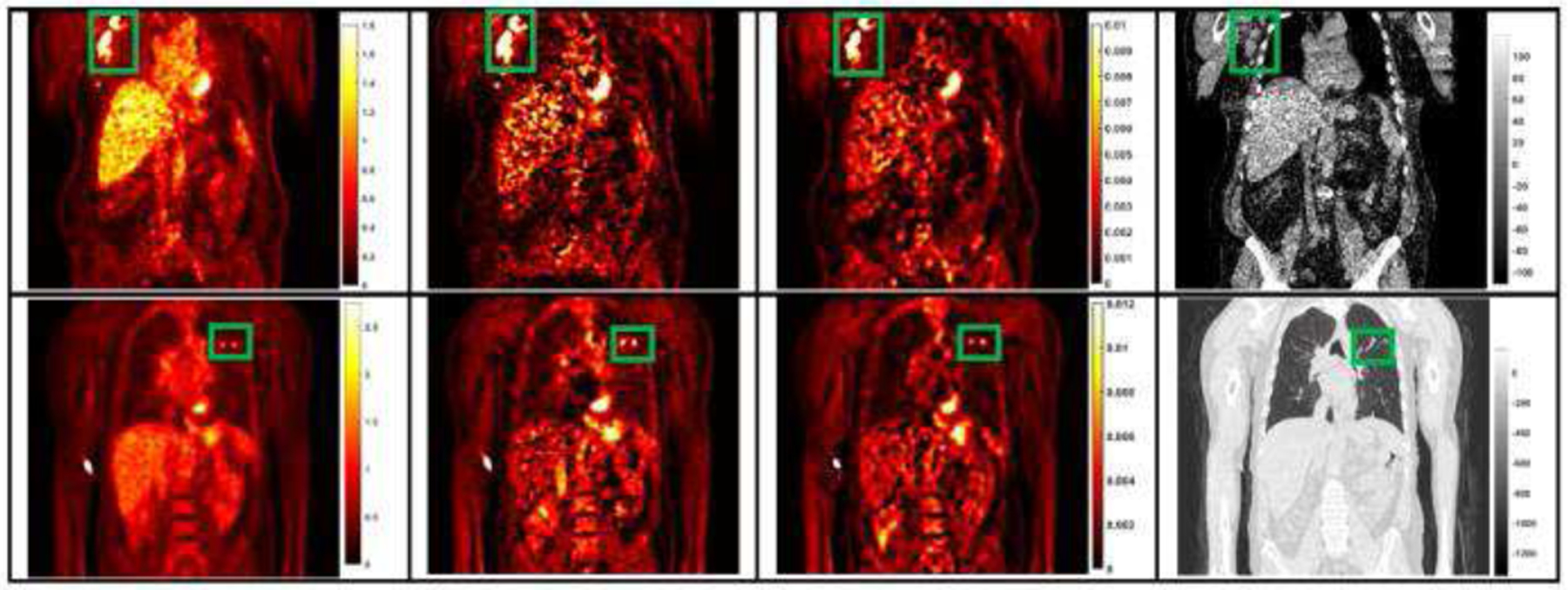
The coronal slices of two sample subject’s SUVR, ground truth K_i, synthetic K_i from SISO, and CT images, with green bounding boxes representing the lesion regions.

III. Results

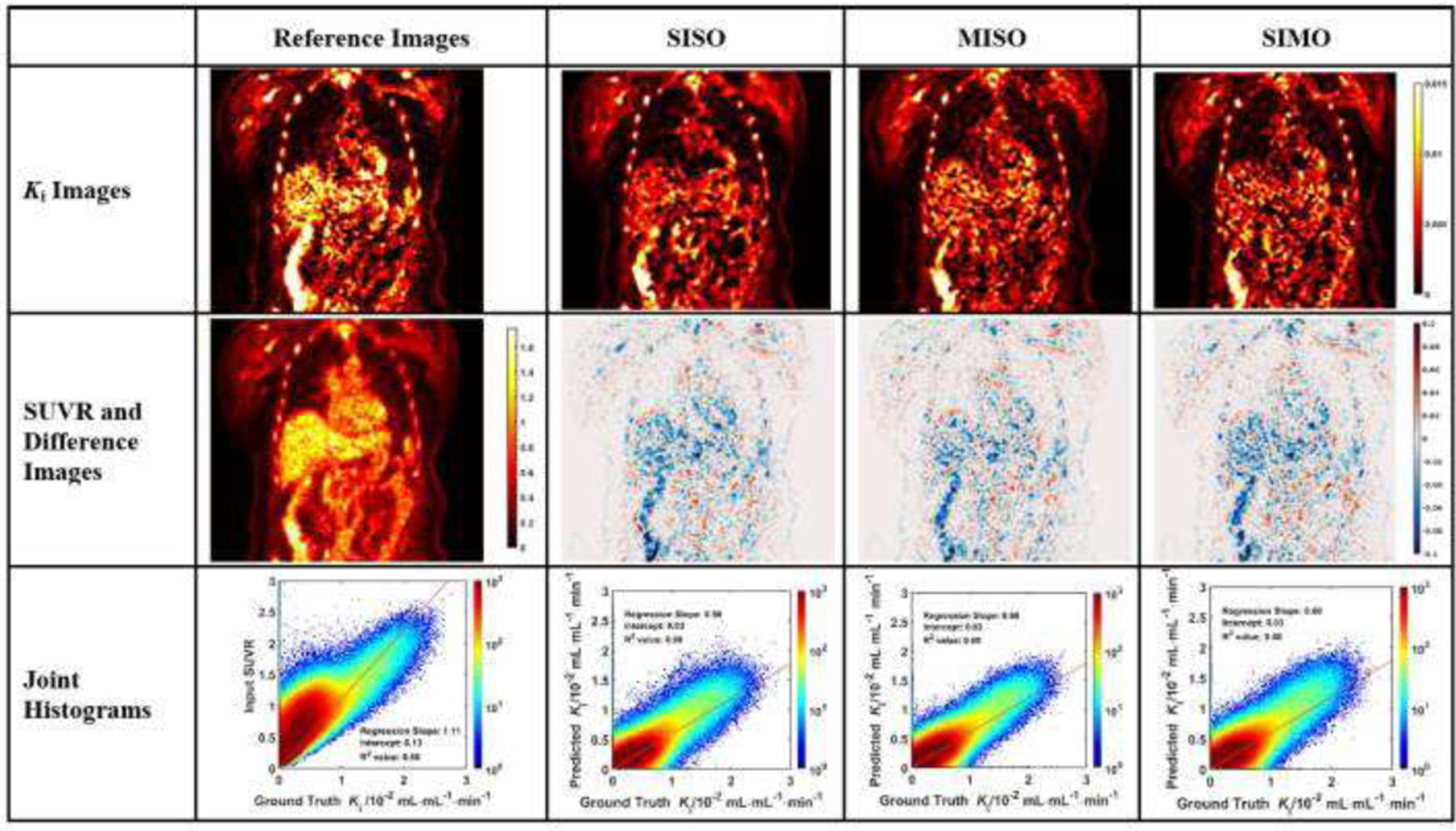
The evaluation of K_i image generation is shown with three sample subjects in Figs. 3 to 5. In each figure, the coronal image slices were chosen to cover the relevant organs, such as liver, heart, and aorta wall. The aorta walls can be visualized more clearly in both synthetic and ground truth K_i images, than in SUVR images. All three networks showed similar difference images, though the myocardial biases appear to be the highest in MISO images.

Fig. 3.

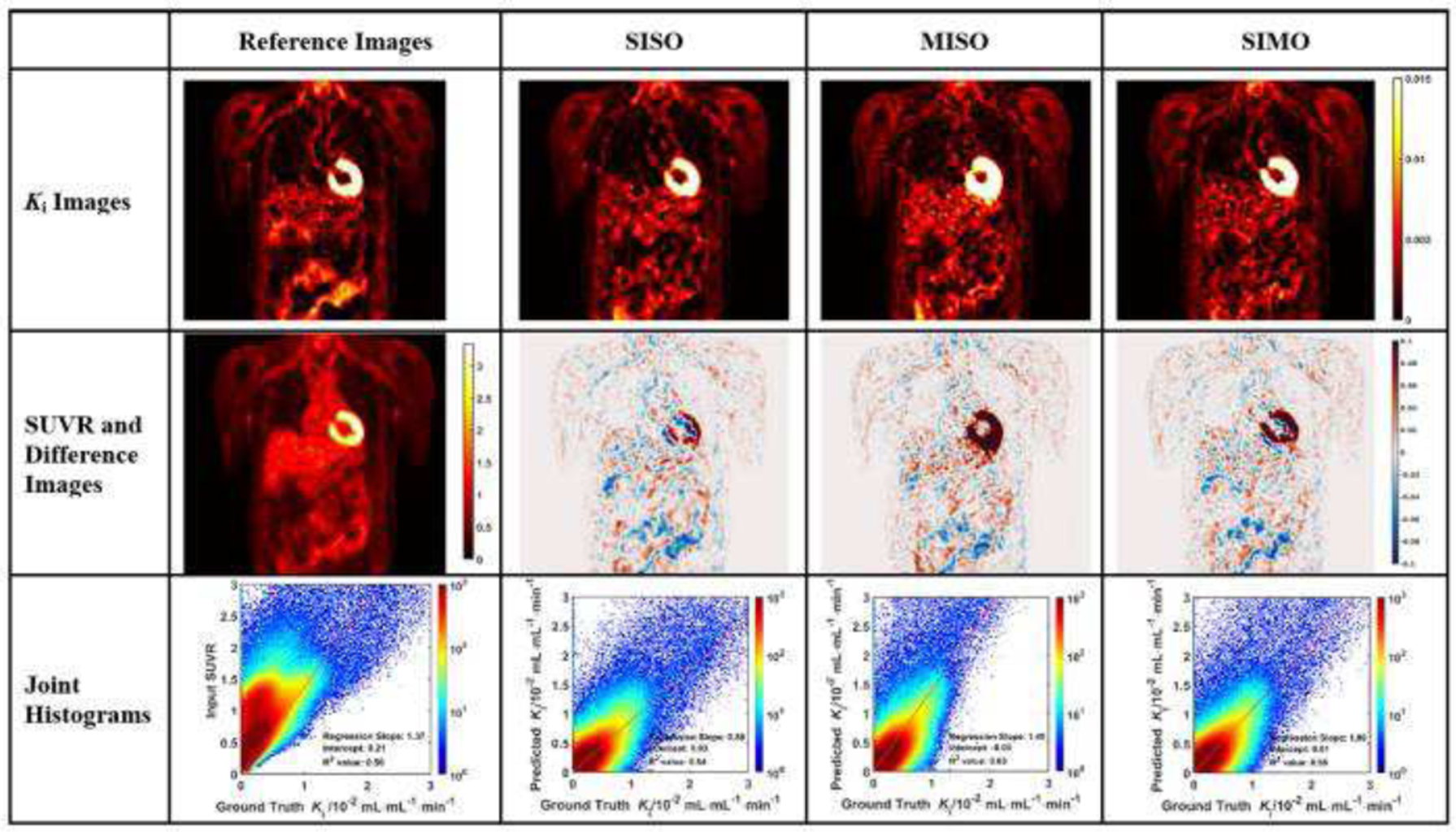
Evaluation analysis of sample subject #1 including the synthetic and reference K_i images, corresponding difference images, SUVR input image, and the joint histograms. In each joint histogram, the regression line was represented by the red straight line, with labels of regression slope, intercept and R² value.

Fig. 5.

Evaluation analysis of sample subject #3 including the synthetic and reference K_i images, corresponding difference images, SUVR input image, and the joint histograms. In each joint histogram, the regression line was represented by the red straight line, with labels of regression slope, intercept and R² value.

In each joint histogram, a regression line was derived between synthetic and ground truth K_i values. Certain body regions, including urinary bladder and injection intravenous lines, were excluded from the linear regression analysis. For each subject, we calculated R² values in the linear regression analysis between the synthetic K_i values generated from various U-Nets and the ground truth K_i values. The R² values of the prediction in the analysis of the SISO U-Net were higher than the R² values of SUVR for most subjects (16 out of 25). In the analysis of the other two U-Net configurations, the R² values of the prediction were generally lower than those of SISO. For the MISO U-Net, 14 out of 25 subjects had higher R² values than the those of SUVR, while 13 out of 25 subjects had higher R² values using the SIMO U-Net than those of SUVR.

Table 1 summarized the statistics of slopes, intercepts and R² values in the linear regression analysis between the synthetic K_i values obtained from various U-Nets and between the input SUVR and the ground truth K_i values. The statistics were also listed for each validation group in the cross-validation process. The R² values were labeled as bold if they were higher than the reference R² values of SUVR. The mean R² value of all subjects in SISO, MISO and SIMO were all slightly higher than that of SUVR. The statistics of each group generally agreed with the results of all subjects that the R² values of U-Net predictions are generally higher than the R² values of SUVR.

TABLE I.

Statistics of Slope, Intercept and R² in the Linear Regression Analysis in Joint Histograms between Input SUVR, Synthetic K_i and Ground truth K_i Images

		SUVR			SISO			MISO			SIMO
		Slope	Intercept	R 2	Slope	Intercept	R 2	Slope	Intercept	R 2	Slope	Intercept	R 2
Total	Mean	1.218	0.155	0.571	0.714	0.0259	0.596	0.740	0.0366	0.580	0.747	0.0357	0.576
	Normalized Standard Deviation	0.235	0.215	0.211	0.366	1.769	0.227	0.423	0.676	0.216	0.367	0.6208	0.239
Group 1	Mean	1.120	0.131	0.606	0.871	−0.014	0.666	0.891	0.022	0.646	0.880	0.023	0.638
	Normalized Standard Deviation	0.401	0.083	0.104	0.609	−6.760	0.097	0.656	1.171	0.209	0.632	0.954	0.198
Group 2	Mean	1.393	0.180	0.562	0.769	0.031	0.555	0.842	0.030	0.577	0.839	0.030	0.566
	Normalized Standard Deviation	0.048	0.214	0.263	0.177	0.879	0.281	0.375	1.236	0.199	0.223	1.014	0.283
Group 3	Mean	1.330	0.172	0.544	0.660	0.046	0.571	0.661	0.049	0.552	0.677	0.052	0.547
	Normalized Standard Deviation	0.158	0.159	0.207	0.128	0.145	0.179	0.160	0.182	0.184	0.138	0.171	0.181
Group 4	Mean	0.944	0.142	0.607	0.576	0.035	0.642	0.544	0.047	0.594	0.595	0.039	0.622
	Normalized Standard Deviation	0.242	0.030	0.135	0.039	0.008	0.132	0.107	0.018	0.126	0.058	0.016	0.148
Group 5	Mean	1.306	0.150	0.538	0.695	0.031	0.548	0.762	0.035	0.53	0.745	0.034	0.509
	Normalized Standard Deviation	0.074	0.212	0.261	0.253	0.751	0.273	0.192	0.616	0.274	0.190	60.646	0.284

Table 2 summarized the statistics of the similarity metrics between synthetic K_i images generated from the U-Nets and ground truth K_i images, compared with the metrics between input SUVR and ground truth K_i images as the reference. The statistics of each validation group were also listed in the cross-validation process. The SSIM values between the synthetic and ground truth K_i images were labeled as bold if they were higher than the reference values. The lowest NMSE values were also labeled in bold among the U-Net predictions. The mean SSIM values between synthetic and ground truth K_i images were higher than that between input SUVR and ground truth K_i images. In the SISO U-Net, 20 out of 25 subjects had higher SSIM scores between synthetic K_i and ground truth K_i images than the scores between input SUVR and ground truth K_i images, while 17 out of 25 in the MISO and 18 out of 25 in the SIMO groups had higher SSIM scores between synthetic and ground truth values. The mean NMSE score between synthetic K_i images from SISO, and ground truth K_i images was lower than those between the synthesis from the other two U-Nets and the ground truth. The K_i images generated from U-Nets were generally more similar to ground truth K_i images than the input SUVR images were, and the SISO U-Net outperformed the other two configurations in terms of SSIM and NMSE.

TABLE II.

Similarity Metrics of SSIM and NMSE between Input SUVR, Synthetic K_i and Ground truth K_i Images

		SUVR		SISO		MISO		SIMO
		SSIM	NMSE	SSIM	NMSE	SSIM	NMSE	SSIM	NMSE
Total	Mean	0.691		0.729	0.139	0.704	0.165	0.704	0.153
	Normalized Std	0.103		0.087	0.580	0.010	0.728	0.010	0.626
Group 1	Mean	0.653		0.675	0.014	0.643	0.016	0.638	0.016
	Normalized Std	0.147		0.072	0.412	0.111	0.552	0.110	0.511
Group 2	Mean	0.727		0.771	0.008	0.759	0.010	0.757	0.009
	Normalized Std	0.068		0.056	0.317	0.058	0.748	0.062	0.450
Group 3	Mean	0.672		0.735	0.007	0.712	0.008	0.713	0.008
	Normalized Std	0.085		0.080	0.218	0.088	0.245	0.087	0.203
Group 4	Mean	0.717		0.713	0.016	0.693	0.020	0.695	0.016
	Normalized Std	0.049		0.054	0.647	0.054	0.733	0.050	0.643
Group 5	Mean	0.689		0.750	0.007	0.713	0.009	0.718	0.009
	Normalized Std	0.142		0.121	0.292	0.130	0.341	0.124	0.271

One-tailed pairwise t-tests were conducted to evaluate the difference of the SSIM and R² values from different U-Nets and the SUVR images. The P values of the t-tested showed that the values of the SSIM and R² from SISO network are significantly larger than those from SUVR, while the values of SSIM and R² from the other two networks showed no significant difference from the reference values of SUVR. Therefore, the t-test also indicated that the SISO U-Net outperformed the SUVR and other two U-Nets in terms of SSIM and R².

The hyperparameters of the U-Nets were optimized using the training and validation datasets. To validate the effectiveness of the hyperparameters, we included a testing dataset with 5 additional subjects to compare their synthetic and ground truth K_i images. The ground truth K_i images were generated using standard Patlak analysis with the image-derived input functions, while the synthetic K_i images were generated using the U-Nets trained in Group 5 in the validation process.

As indicated in Table 4, the U-Nets generally outperformed the input SUVR images in terms of the SSIM and R² values in the testing dataset, even though the R² value of MISO was marginally smaller than that of the SUVR. Therefore, the hyperparameters optimized by the training and validation groups did not overfit and were effective to synthesize the K_i images from subjects outside training and validation datasets.

TABLE IV.

Statistics of SSIM and R² Between the Synthetic and ground truth images in Testing Dataset

		SUVR	SISO	MISO	SIMO
SSIM	Mean	0.739	0.755	0.740	0.742
	Normalized Std	0.059	0.072	0.076	0.074
R 2	Mean	0.696	0.731	0.688	0.770
	Normalized Std	0.133	0.103	0.083	0.080

As shown in Fig. 6, the linear regression analysis of the distributions in lesion regions showed that the R² values of three U-Nets were similar with the R² value of SUVR. The R² value of MISO network was higher than the value of SUVR. Sample lesion regions, labeled by the green bounding boxes, were presented in the coronal image slices in Fig. 7. It can be observed that the synthetic K_i images derived from SISO are visually consistent with the ground truth K_i images and both K_i images have substantially higher lesion contrast than those of SUVR images.

Fig. 6.

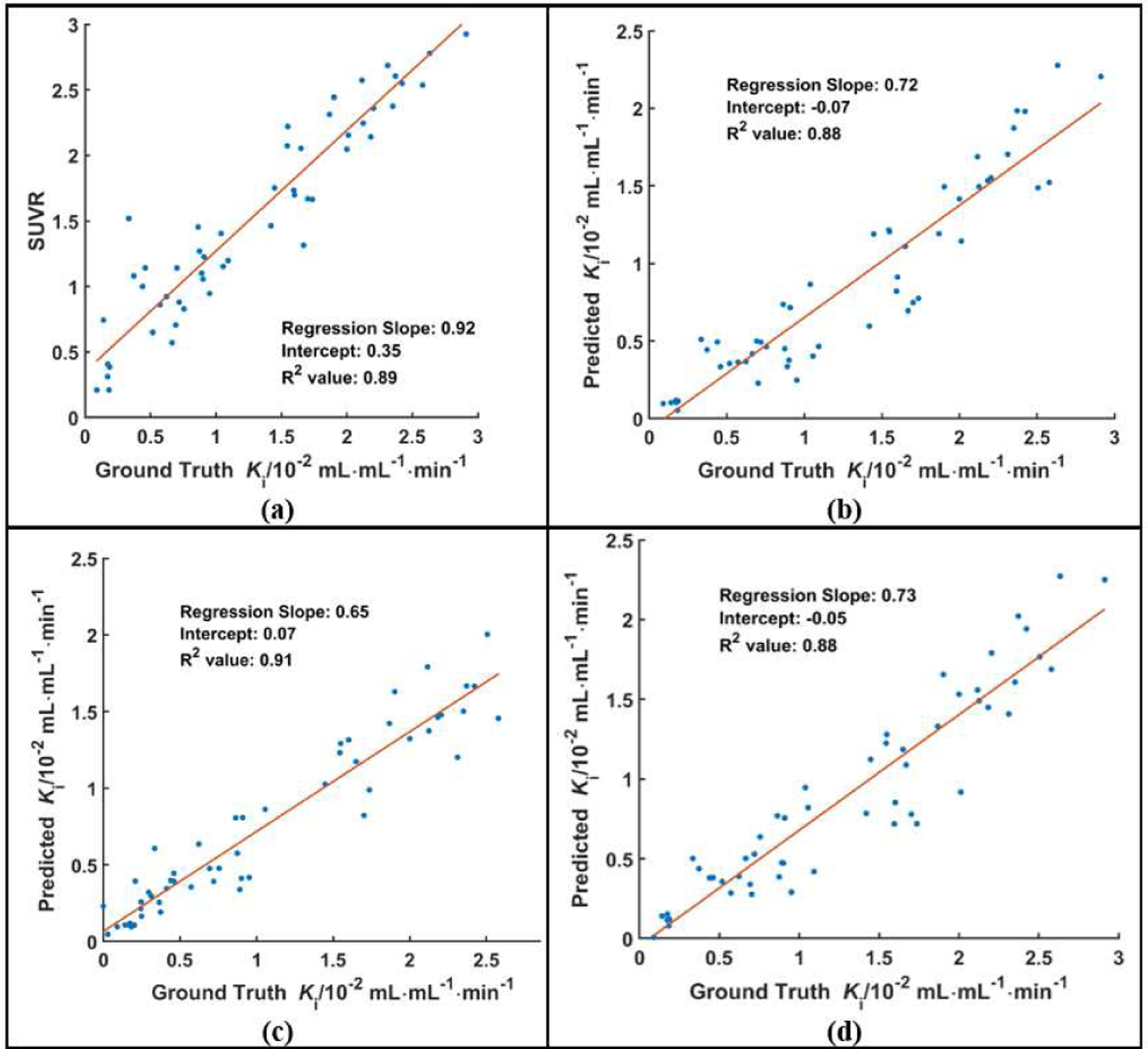
The distributions of the lesion ROI mean values in SUVR (a), synthetic K_i, and ground truth K_i images. The synthetic K_i values were generated from three configurations of U-Nets, which were SISO (b), MISO (c) and SIMO (d).

IV. Discussion

In this study, we developed deep learning methods to generate K_i images from static SUV images using the U-Nets in three configurations. As shown in Figs. 3 to 5, the coronal slices of the synthetic K_i images were visually more consistent with the ground truth K_i slices than the SUVR slices. The aorta walls had higher contrast in both the synthetic and the ground truth K_i slices, than in the SUVR slices. The synthetic K_i images generated from all three U-Nets were visually smoother than ground truth K_i images, likely because SUVR images have lower noise and the subsequent K_i images generated from SUVR images could inherit such low noise level. The difference images showed that the bias between synthetic and ground truth K_i images were small in most regions. Even though higher biases were observed in the regions with high tracer uptake, such as heart and the kidneys, the normalized differences were small.

The linear regression analysis of mean K_i and SUVR values in the body and lesion regions indicated that the synthetic K_i values generated from the U-Nets could correlate slightly better with ground truth K_i values than input SUVR values, in terms of higher R² values, but such differences are not significant. In addition to the linear regression analysis, the comparison of the SSIM values showed that synthetic K_i images were more consistent with ground truth K_i images than input SUVR images. The statistics of each group in the cross-validation process agreed with the statistics from all subjects. Even though in Group 2, the mean R² value of SISO is lower than that of SUVR, SISO network still performed better than SUVR in terms of R² value from all subjects. The statistics in the testing dataset also agree with those in the validation dataset that the U-Nets outperformed the SUVR in terms of mean SSIM and R² values.

Although three configurations were all based on the U-Net architecture, the SISO U-Net generally outperformed the other two configurations. Visually, the synthetic K_i images generated from SISO were less noisy than the images generated from the other two networks, as shown from Fig. 3 to Fig. 5. In the linear regression analysis of the joint histograms, the mean R² value of the prediction in SISO was higher than those of the two other configurations. The mean SSIM value in SISO U-Net was also the highest. However, in the evaluation of the lesion regions, the R² values of U-Net predictions did not have clear differences among all three configurations. The MISO network incorporated more information of the input static SUVR frame than the SISO network. However, individual input frame of MISO was noisier than the single input frame of SISO, which may negatively affect the training performance of MISO network. Therefore, our data suggested that incorporating additional input SUVR or output images of V_b values did not benefit the training performance of U-Nets.

Our work demonstrated that it is feasible to generate parametric K_i images from static SUVR images. The synthetic K_i images generated from various configurations of U-Nets were generally more consistent with ground truth K_i images than input SUVR images, with stronger linear correlations and higher SSIM values. However, the improvement of correlations from the U-Nets over those of SUVR was small and there were still differences between synthetic and ground truth K_i images. As shown in joint histogram analysis from Fig.3 to Fig. 5, the regression slopes between the synthetic and ground truth K_i values were not close to 1 for many subjects. The normalized standard deviation values in Table 1 also showed difference was not minor between the regression slopes across all subjects. Therefore, the synthetic K_i values were not quantitatively accurate compared with ground truth K_i values. In this work, we chose SUVR images instead of SUV images as the network input with the considerations explained in the Appendix that K_i is better correlated with SUVR as compared to SUV. Since input functions vary with subjects, even though population-based input functions can be used [22], values of Θ(T) in the Appendix differ among subjects due to variations of static image acquisition times and input functions. Therefore, the relationship between SUVR and K_i values also varies, and we hope our proposed deep learning methods could recover such underlying relationship. The patient’s motion might also affect the K_i image quality. For example, in Fig. 3, the contour of myocardium is smaller in three synthetic K_i images than in the ground-truth image, probably because this patient’s motion across dynamic frames produced more blurring effect than the static images. In the future, the information of patient’s motion, acquisition times and input functions could be incorporated into deep learning networks to further improve the performance in generating parametric K_i images.

As mentioned in the Introduction, the K_i estimation using standard Patlak analysis is not valid for the tissue regions with double blood supply and FDG dephosphorylation, such as in liver [16]. In these regions, the two-tissue reversible compartmental model is a better tool to estimate the parametric values [17]. And in vascular, lung and skin regions, zero or one compartmental model is favored to reduce the artifacts in the K_i value estimation [18]. Therefore, the bias of K_i estimation from the standard Patlak analysis could also contribute to the errors in our K_i estimation based on the SUVR values. The generalized Patlak analysis could help to reduce the bias of K_i estimation in the regions of non-negligible FDG dephosphorylation. But it could introduce higher noise level than the standard Patlak analysis [17]. Therefore, there are trade-off between noise and bias to select different compartmental models to estimate parametric values.

V. Conclusion

An image synthesis workflow, including three deep neural network configurations based on the 3D U-Net architecture, was developed to generate parametric K_i images from the static SUVR images, which can serve as the surrogate to the K_i estimation from the standard Patlak analysis. This workflow reduced the scan time and eliminated the need of input function measurements in the conventional K_i image generation using dynamic PET data and Patlak graphical analysis.

Fig. 2.

The single input and multiple outputs (SIMO) U-Net with 5 operational layers to generate output K_i and V_b images from SUVR images. The contraction path is shared by both outputs, with the expanding paths split for the outputs.

Fig. 4.

Evaluation analysis of sample subject #2 including the synthetic and reference K_i images, corresponding difference images, SUVR input image, and the joint histograms. In each joint histogram, the regression line was represented by the red straight line, with labels of regression slope, intercept and R² value.

TABLE III.

Significance Test Results (P-value) of R₂ and SSIM Values between Input SUVR, Synthetic K_i and Ground truth K_i Images

	SISO and SUVR	MISO and SUVR	SIMO and SUVR
SSIM	0.0014	0.1485	0.1266
R 2	0.0229	0.3360	0.4137

Appendix

This section summarized the finding of J. van den Hoff, et al., regarding the correlation between the SUVR and K_i values [40]. Patlak analysis was the conventional method to generate K_i values from dynamic data [13], based on the equation of

$$\frac{C_t(t)}{C_a(t)}=K_i\times \frac{{\int }_0^t{C}_a(s)ds}{C_a(t)}+V_b$$

where $K_i=\frac{K_1{k}_3}{k_2{k}_3}$, representing the tracer net influx rate constant in tissue [11], and C_t(t) and C_a(t) were the tracer concentrations in tissue and plasma at time t post-injection [12]. The term on the left side of the equation could be defined as normalized SUV ratio (SUVR) value. The value of K_i can be well correlated to the value of SUVR for a wide range of subjects, with the assumptions that 1) the plasma input functions of different subjects had the similar shapes, which can be expressed as C_a(t) ≈ N × b_a(t); 2) all static SUVR frames were acquired at the approximately the same time post tracer injection; and 3) values of V_b were small compared with SUVR values [40]. Then the correlation can be expressed as $\mathit{\text{SUVR}}\left(T\right)=K_i\times \frac{{\int }_0^T{b}_{a\left(s\right)}ds}{b_{a\left(T\right)}}$. With the fixed time point T, the term $\Theta \left(T\right)=\frac{{\int }_0^T{b}_{a\left(s\right)}ds}{b_{a\left(T\right)}}$ is a constant. Therefore, SUVR is linearly proportional to K_i when the assumptions are met and is preferred over SUV as network input in our study to generate K_i.

In clinical scenarios, plasma input functions vary with subjects, and values of Θ(T) differ accordingly, which makes the relationship among K_i, V_b and SUVR vary among subjects. Acquisition times of the static SUV frames also differ with subjects, in the scale of minutes, which makes values of Θ(T) different across subjects. Values of V_b generated by Patlak analysis are also not negligible compared with SUVR values. Thus, the variations in acquisition times and V_b values could contribute to the errors in deriving K_i directly from SUVR and more training data could further improve the network performance.