Automated Segmentation of Sacral Chordoma and Surrounding Muscles Using Deep Learning Ensemble

Abstract

Background and Purpose.

The manual segmentation of organ structures in radiation oncology treatment planning is a time-consuming and highly skilled task, particularly when treating rare tumors like sacral chordomas. This study evaluates the performance of automated deep learning (DL) models in accurately segmenting the gross tumor volume (GTV) and surrounding muscle structures of sacral chordomas.

Materials and Methods.

An expert radiation oncologist contoured five muscle structures (Gluteus Maximus, Gluteus Medius, Gluteus Minimus, Paraspinal, Piriformis) and sacral chordoma GTV on CT images from 48 patients. We trained six DL auto-segmentation models based on 3D U-Net and Residual 3D U-Net architectures. We then implemented an average and an optimally weighted average ensemble to improve prediction performance. We evaluated algorithms with the average and standard deviation of the Volumetric Dice Similarity Coefficient (VDSC), Surface Dice Similarity Coefficient (SDSC) with 2 and 3 mm thresholds, and Average Symmetric Surface Distance (ASSD). One independent expert radiation oncologist assessed the clinical viability of the DL contours and determined the necessary amount of editing before they could be used in clinical practice.

Results.

Quantitatively, the ensembles performed the best across all structures. The optimal ensemble (VDSC, ASSD) was (85.5±6.4, 2.6±0.8; GTV), (94.4±1.5, 1.0±0.4; Gluteus Maximus), (92.6±0.9, 0.9±0.1; Gluteus Medius), (85.0 ± 2.7, 1.1 ± 0.3; Gluteus Minimus), (92.1 ± 1.5, 0.8 ± 0.2; Paraspinal), and (78.3±5.7, 1.5±0.6; Piriformis). The qualitative evaluation suggested that the best model could reduce the total muscle and tumor delineation time to a 19-minute average.

Conclusion.

Our methodology produces expert-level muscle and sacral chordoma tumor segmentation using DL and ensemble modeling. It can substantially augment the streamlining and accuracy of treatment planning and represents a critical step towards automated delineation of the Clinical Target Volume (CTV) in sarcoma and other disease sites.

1. Introduction

A sarcoma is a rare and heterogeneous group of malignant tumors that arises from mesenchymal tissue, including soft tissue and bone. Among these tumors, chordomas are a particularly rare form of spine sarcoma that often involves the sacrum. Although surgery is considered the mainstay of treatment, patients with locally advanced diseases often cannot be easily resected without severe morbidity. As a result, highdose definitive radiation has emerged as a treatment option for these patients, with comparable local control rates and acceptable toxicity [1].

Target delineation is a critical task in the radiotherapy workflow that can considerably impact the overall treatment outcome, particularly given the increasing dose conformality offered by modern radiotherapy techniques. Accurate delineation is associated with better local tumor control and reduced radiation dose to non-target tissues leading to an improved therapeutic ratio [2].

The delineation of the gross tumor volume (GTV) and clinical target volume (CTV) for sarcomas can be time-consuming, given the often large size of these tumors as well as their propensity to spread along muscle fibers while respecting other anatomic barriers (such as bone or fascial planes). While prior studies have shown reasonable inter-observer variability in the delineation of extremity sarcomas [3], sacral chordomas may represent a particularly challenging contouring task given their anatomic location (with multiple adjacent muscle compartments extending in oblique directions) and propensity to grow to large sizes before the initial diagnosis.

Artificial Intelligence (AI) in healthcare is a driving force for improving patient care and efficiency [4, 5, 6].

AI-assisted segmentation of the GTV and neighboring muscles could substantially reduce the time required to contour these patients and lay the foundations for eventual semi-automatic or fully automatic CTV delineation. However, there is a lack of studies on soft tissue segmentation. Although DL techniques have demonstrated great potential for medical image segmentation, their evaluation is often not pushed enough to enable a translation to clinical practice.

This work investigates these bottlenecks and uses machine learning and DL methodologies to automatically segment sacral chordoma GTV and surrounding muscle structures that serve as tumor spread pathways.

2. Materials and Methods

The contributions of this study are highlighted in the first part of this section. We then describe the critical steps involved in processing patient CT scan data for model training and provide details of the DL architectures and training mechanisms. We also explain how ensemble methods were utilized to improve the performance of individual models. Finally, we describe the qualitative assessment of the automated contours.

2.1. Contributions

Our contributions are the following:

• We train a strong and diverse pool of Convolutional-Neural-Network-based segmentation models using different 3D U-Net architectures, loss functions, and hyperparameters that can simultaneously segment the six different structures of interest with high accuracy. To the best of our knowledge, this is the first time such models are trained on these specific muscle compartments and GTV, which paves the way toward an automated workflow for future CTV delineation. Segmenting patients with a tumor represents the additional challenge of higher muscle shape and texture variability than more traditional segmentation studies because large tumors can lead to substantial deformations of the surrounding healthy tissue anatomy.

• We investigate two methodologies to ensemble the pool of standalone models into a superior consensus model that can outperform any individual ensemble members: (i) an average of standalone models and (ii) an optimally weighted average of these models.

• We evaluate our models quantitatively with the Volumetric Dice Similarity Coefficient, the Surface Dice Similarity Coefficient with tolerance 2 and 3 mm, and the Average Symmetric Surface Distance.

• We provide a qualitative evaluation of our best standalone model and our optimal ensemble contour predictions based on the assessment of an independent expert radiation oncologist. In particular, we provide the estimated amount of time required to edit our automated contours before clinical use and describe the extent and location of the delineation discrepancies.

2.2. Dataset

2.2.1. Patient Selection

48 consecutive patients with sacral chordomas treated with high-dose, definitive proton beam radiation without surgery between 1999 and 2019 who had original simulation CT scans available were retrospectively identified from the Anonymized Database. The CT scans were acquired on GE scanners following the standard protocol for radiotherapy treatment planning in use when the patient was simulated, using 140 kVp for all scans. The image acquisition was performed in prone (n=45) and supine (n=3) positions. The initial CT image resolutions are listed in Table 2. The average patient age was 64, the median was 65, and the range was 31 to 90 years old. 20 patients were females.

Table 2:

Original resolutions of the image sequences of the 48 patients in our cohort.

Resolution (mm)	Number of cases
1 × 1 × 2.5	22
0.9 × 0.9 × 2.5	10
1.3 × 1.3 × 2.5	4
1 × 1 × 3.75	4
0.8 × 0.8 × 3.75	3
0.9 × 0.9 × 3.75	2
1.8 × 1.8 × 2.5	1
0.7 × 0.7 × 2.5	1
1.8 × 1.8 × 5	1

2.2.2. Expert Delineation of Muscles and Sarcoma GTV

The gross tumor volume contours from each patient’s original treatment were extracted and exported into MIM Maestro (MIM Software Inc, Ohio, USA, version 7.0.5) and reviewed by a radiation oncologist. These GTV contours were delineated by six different radiation oncologists over 20 years, with expertise ranging from 5 to 20 years (3 with 20+ years of experience, 2 with 10–15 years, and 1 with 5), and were peer-reviewed to ensure discrepancies were corrected before finalizing the treatment plans. Adjacent muscles of interest, including the gluteus maximus, gluteus medius, gluteus minimus, paraspinal, and piriformis, were manually contoured again for this study by a single radiation oncologist, with left and right muscles recorded as separate contours. Areas inside the body yet outside the muscles of interest and sarcoma GTV were also identified. Similarly, areas within the CT field of view but outside of the patient’s body were identified separately.

5 patients were set aside owing to radiographic obliteration of the piriformis muscles by the primary tumor, meaning these were completely infiltrated by the tumor and thus not distinguishable. However, because these patients still have contours for other muscles (though often still substantially deformed by the GTV), we include them as an outlier test set to evaluate our models’ generalizability to extreme cases. The average GTV volume for in-sample data is 378 cm³ with a standard deviation of 388 cm³. In the outlier test set, the GTV volume average is 1622 cm³, with a standard deviation of 421 cm³. We do not report results on the piriformis muscle group for the outlier test set as there is no ground truth. If one of our models still classifies a few voxels as piriformis during evaluation, we consider such predictions misclassified.

In the end, we randomly split 30 patients in the training set, 5 in the validation set, and 8 in the testing set after putting aside the 5 patients from the outlier testing set.

2.2.3. CT Image Pre-processing

The original CT images comprised samples with different element spacing and image orientation with respect to patient anatomy. To standardize the data into a uniform format suitable for DL networks, we fixed a specific image orientation, aligned all cases, and re-sampled all 3D images to the same element spacing of 2 × 2 × 2 mm, to ensure sufficient resolution for future treatment planning and faster downstream DL model training. We then cropped the images to restrict the field of interest as the smallest bounding box that contained all structures segmented in all patients. We also padded the images on all 3 axes to obtain a common final image dimension of 182 × 157 × 216 voxels. We then re-scaled each CT image so that the overall voxel values of each patient have zero mean and unit variance. Finally, due to the symmetric structure of all contoured muscles, we merged the left and right contours of the same muscle type into a single structure which helped the models capture muscle geometry better (see an illustration in Figure 1).

Figure 1:

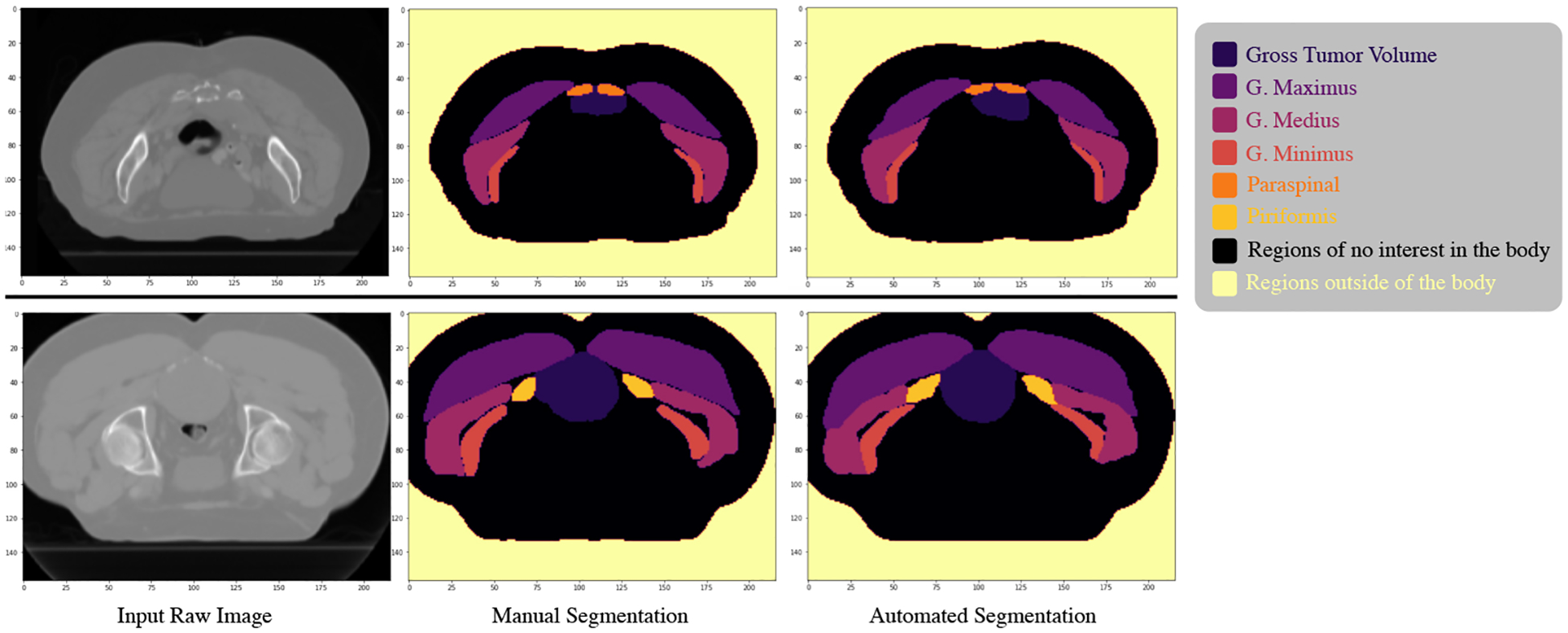
Illustration of an axial CT slice (left) from two different patients after processing the full image. We show the manual segmentation (center) and the final automated segmentation (right) using our optimal ensemble model.

Appendix A provides more detailed explanations of the pre-processing steps.

2.3. Deep Learning Architectures

Recently, DL techniques using neural networks, particularly convolutional neural networks (CNNs), have demonstrated remarkable potential in medical image processing and automated segmentation of normal anatomy [5, 7, 8, 9, 10] and gross tumor volume (GTV) [10, 11, 12, 13, 14], with high accuracy and reduced processing time, outperforming the current atlas-based segmentation methods [15, 16].

2.3.1. 3D U-Net

We based our CNNs used for the DL segmentation tasks on the 3D U-Net architecture [17]. We trained both standard 3D U-Nets and Residual 3D U-Nets [18]. The network’s input is a three-dimensional CT volume of size (182 × 157 × 216) and the ground truth labels of the GTV and muscles. The output is a four-dimensional segmentation mask of size 8 × 182 × 157 × 216 where 8 corresponds to the number of anatomical structures concurrently segmented (GTV, 5 muscle pairs, regions of no interest in the body, and region outside of the body). The 3D U-Net network is divided into 4 downsampling blocks (encoder), 4 upsampling blocks (decoder), and a middle part. All parts of the network use blocks of Group Normalization, 3D convolutions, and rectified linear units (ReLU). We used max-pooling for downsampling and interpolation for upsampling. The difference between the 3D U-Net and Residual 3D U-Net lies in the basic block scheme: the Residual 3D U-Net has 5 block levels in the encoder-decoder path instead of 4, uses summation joining instead of concatenation joining, and transposed convolutions for upsampling. More details on the architectures can be found in Appendix B. We trained the two network architectures with different loss functions, including Dice loss, standard cross-entropy loss, and class-weighted cross-entropy loss.

We adopted a final softmax activation function with cross-entropy-based training losses to produce the segmentation mask of probabilities for each voxel and classification class. We used a final sigmoid activation function when training with a Dice Loss.

Finally, we converted the output probabilities into a discrete label mask to visualize predictions and compute metrics by choosing the class with the highest probability for each voxel.

2.3.2. Training and Validation Mechanism

We trained the models on the 30 image sequences from the training set and validated the performance with the 5 image sequences in the validation set using the Intersection over Union score averaged over all classes (see definition in section (2.5)). For each one of the six (loss, architecture) combinations, we executed a hyperparameter search on the Adam optimizer [19] learning rate and learning rate scheduler, weight decay (L2 weight regularization), image patch shape, and stride shape to obtain the best model performance. For the case of the weighted cross-entropy loss, we also tuned the weights given to each class. The details about the hyperparameter search are given in Appendix B.

During training, we further regularized the models by 7 consecutive data augmentation transformations with on-the-fly random flips on the horizontal and vertical axis, random rotations of 90 degrees, random rotations in the ZY axis, elastic deformation, random contrast changes, additive Gaussian noise, and additive Poisson noise. The ZY rotations were normally distributed with an angle spectrum of 15 degrees in each direction.

Based on validation performance, the best hyperparameter combination was an initial Adam learning rate of 10⁻⁴, decayed by a factor of 0.7 every 15 epochs, a weight decay of 10⁻⁵, a patch shape of 128 × 128 × 128 with a stride shape of 16 × 16 × 32 which gave 60 patches per image. For the weighted cross-entropy loss, the best weights were 0.25 for GTV, 0.1 for G. Maximus, G. Medius, and G. Minimus, 0.15 for Paraspinal, 0.2 for Piriformis, 0.05 for Out-of-the-body regions and In-the-body regions of no interest.

For each (loss, architecture) combination, we chose the model checkpoint with the lowest validation loss to be evaluated on the test set. We stopped the training when there was no improvement in the validation loss for more than 10 epochs, which typically happened after 40–60 epochs. One epoch represents one iteration when the entire training set passes through the neural network. The training was generally completed in two days, using a GPU TeslaV100 and 4 CPU cores.

We obtained six trained models that we included in the pool of base learners for ensemble modeling (see the summary in Figure 2).

Figure 2:

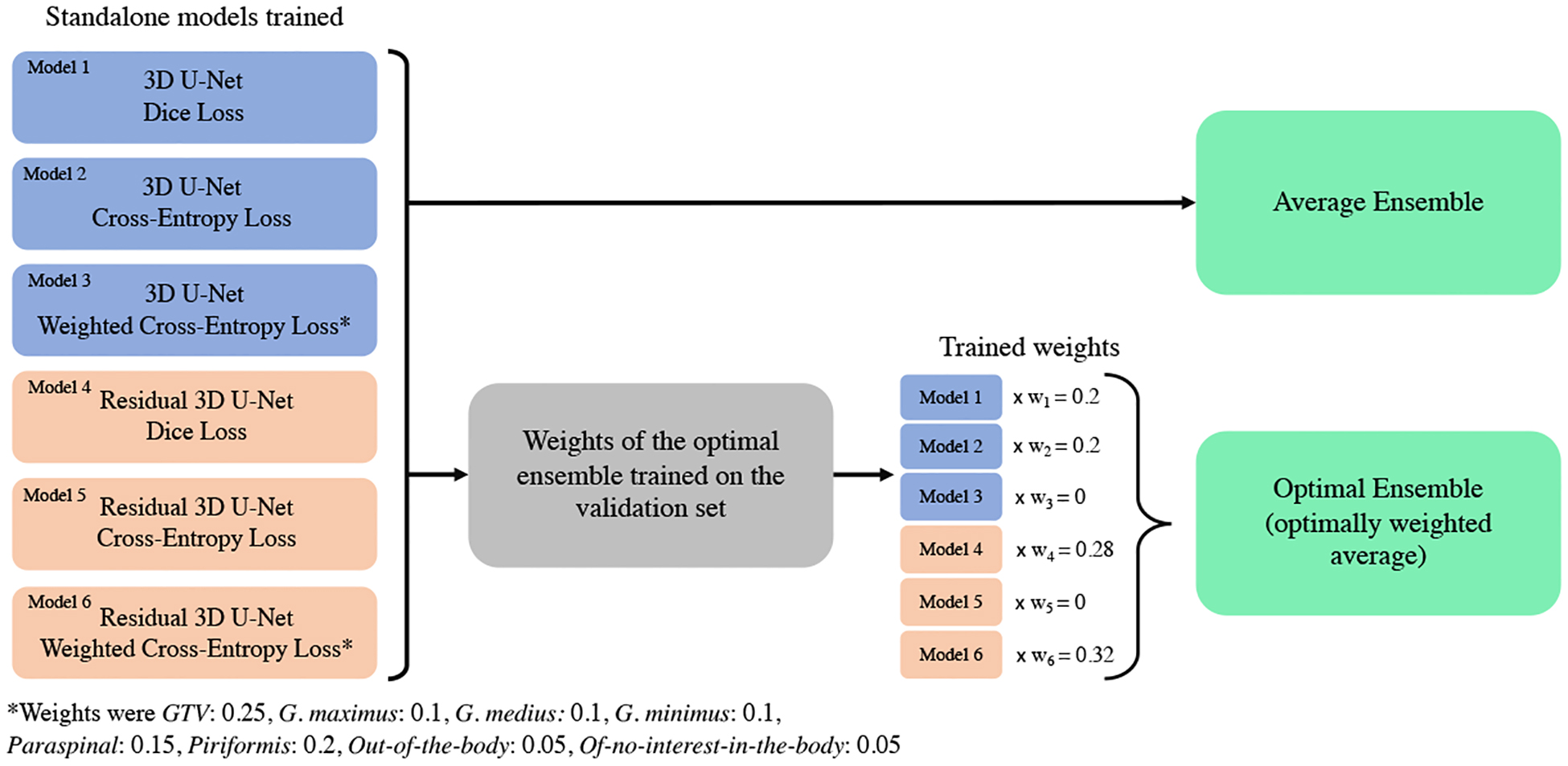
Illustration of the pipeline to utilize the different top standalone models (base learners) into the average and optimal ensemble.

2.3.3. Testing Protocol

At test time, we used the same patch and stride shapes as in training time and mirror-padded the raw data patches by 4 pixels on each axis for sharper prediction near the volume boundaries. We averaged the overlapping patch predictions to avoid checkerboard artifacts in the output prediction masks. We tested the standalone models and the ensemble models in the test set of 8 image sequences and the additional outlier test set of 5 image sequences from patients with very large tumors. The trained models performed the segmentation task in under one minute for each patient.

2.4. Ensemble Modeling

Ensemble methods are a popular technique in machine learning that aims to improve prediction accuracy and robustness by leveraging the diversity of individual models to form a consensus. Individual models are susceptible to data uncertainty, training randomness, and overfitting. However, by combining their knowledge and insights, an ensemble can generate a final consensus that benefits from the “wisdom of the crowd” [20, 21].

In this study, we investigate two stacking [22] ensemble techniques for muscle and sarcoma segmentation: voxel-wise average and optimally weighted average of a specific pool of 3D base learners. We aim to determine if these techniques can lead to superior performance compared to using a single model.

2.4.1. Average Ensemble

For the Average Ensemble, we combined the six top-performing models described in Section 2.3.2 using a simple average of their probability predictions voxel-wise. The final class probabilities of each voxel are the average of the probabilities given by each model. This methodology requires no additional training and has been shown to achieve superior performance in other healthcare segmentation tasks [23, 24, 25].

2.4.2. Optimal Ensemble

We also developed an optimally-weighted combination of the models that we call Optimal Ensemble to further leverage their strengths. Instead of weighting each model equally, we allowed the weights to increase or decrease, including the possibility of setting a model’s weight to 0. The optimal set of weights $\left\{w_1^{\text{*}},w_2^{\text{*}},\cdots ,w_6^{\text{*}}\right\}$ associated with each model was defined as the solution that maximizes the Intersection over Union (see metric definition in Section 2.5) for all eight segmented structures on the validation set:

$$\left\{w_1^{\ast },w_2^{\ast },\cdots ,w_6^{\ast }\right\}:=\arg \underset{\begin{array}{c}{w}_1,\cdots ,w_6\\ \sum _k{w}_k=1\end{array}}{\max }{\text{ IoU }}_{\text{ensemble}}=\arg \underset{\begin{array}{c}{w}_1,\cdots ,w_6\\ \sum _k{w}_k=1\end{array}}{\max }\sum _{i=1}^8\frac{\left|X_e^i\cap X_{\text{ensemble }}^i\right|}{\left|X_e^i\cup X_{\text{ensemble }}^i\right|}\text{, with }$$ (1)

$$X_{\text{ensemble }}=\sum _{k=1}^6{w}_k{X}_{\text{model }k},$$ (2)

where $X_e^i$ represents the expert manual ground truth of the structure $i$, $X_{\text{model }k}$ represents the automated segmentation of model $k$, and $|\cdot |$ corresponds to the cardinality of the set, i.e., the number of voxels equal to 1 in our binary mask scenario.

Contrary to standard weighted average ensembles in machine learning that can be obtained with linear regression (e.g., on a tabular task), this 3-dimensional objective function (1) is not convex. Therefore, we optimized the models’ weights using gradient ascent with the Adam optimizer with a learning rate of 10⁻³ until reaching convergence with a tolerance of 10⁻⁴.

To train the Optimal Ensemble, we optimized the weights using the models’ predictions made on the validation set.

After training ended, 4 models had a non-zero weight: the 3D U-Nets trained with Dice loss $\left(w_1=0.2\right)$ and Cross-Entropy loss $\left(w_2=0.2\right)$, and the Residual 3D U-Nets trained with Dice loss $\left(w_4=0.28\right)$ and Weighted Cross-Entropy loss $\left(w_6=0.32\right)$ (see pipeline summary in Figure 2).

2.5. Metrics

To assess the accuracy of auto-delineation with respect to the ground-truth contours during validation, we used the Intersection over Union (Jaccard score). At test time, we computed four metrics and report their average and standard deviation across the testing sets. We used the Volumetric Dice Similarity Coefficient, the Surface Dice Similarity Coefficient with tolerances of 2 mm and 3 mm, and the Average Symmetric Surface Distance. We chose these four test metrics to provide insights into how well segmentations overlap, how much the structure borders should be corrected, and how far the contour predictions are from the ground truth. We utilized distinct validation and test metrics to make the testing process more robust and check models generalize well, not because they are overfitted to the validation metric.

The Intersection over Union (IoU), also called the Jaccard index, is a similarity measure between a finite number of sets. For two segmentation masks $X_e$ (expert manual ground truth) and $X_a$ (automated segmentation), it can be defined as follows:

$$J\left(X_e,X_a\right)=\frac{\left|X_e\cap X_a\right|}{\left|X_e\cup X_a\right|}=\frac{\left|X_e\cap X_a\right|}{\left|X_e\right|+\left|X_a\right|-\left|X_e\cap X_a\right|}.$$

As mentioned in section 2.3.2, we used the IoU score to compare the models during validation and determine when to stop the training.

The Volumetric Dice Similarity Coefficient (VDSC) is a voxel-wise measure of the overlap of two image regions. It normalizes the overlap size to the average size of the two structures:

$$\text{VDSC}\left(X_e,X_a\right)=2.\frac{\left|X_e\cap X_a\right|}{\left|X_e\right|+\left|X_a\right|},$$

where $X_e$ represents the expert manual ground truth and $X_a$ represents the automated segmentation. The VDSC ranges from 0 to 1, where 1 indicates perfect performance. A larger VDSC corresponds to a higher degree of coincidence between the auto-segmented and ground truth volumes.

The Surface Dice Similarity Coefficient (SDSC) [26] calculates the distance between two surfaces relative to a given tolerance $\tau$, providing a measure of agreement between the borders of manually and automatically defined structures:

$$\text{SDSC}\left(S_e,S_a,B_e,B_a\right)=\frac{\left|S_e\cap B_a\right|+\left|S_a\cap B_e\right|}{\left|S_e\right|+\left|S_a\right|},$$

where $S_e,S_a$ are surface areas of structures $e$ (expert manual ground truth) and $a$ (automated segmentation). $B_e$ (resp. $B_a$) is the surface area of the part of $S_e$ (resp. $S_a$) such that any voxel in this part is no further than $\tau$ from $S_a$ (resp. $S_e$). The SDSC ranges from 0 to 1, representing the fraction of the structure border that must be manually corrected because it deviates from the ground truth by more than the acceptable distance defined by the tolerance $\tau$.

In this study, we report results for the 2 mm and 3 mm distance tolerances $\tau$.

We calculated the shortest distances between structures in the 3-dimensional space. Specifically, the 2 mm SDSC considers a predicted contour that is one perpendicular pixel apart from the ground truth as correct, while the 3 mm SDSC considers a predicted contour that is one diagonal pixel apart (i.e., $2\sqrt{2}\approx 2.83\text{ mm}$) from the ground truth as correct. The selection of 2 mm and 3 mm thresholds was driven by computational and clinical considerations. Since we had previously chosen a 2 mm image resolution to ensure adequate resolution for future treatment planning and faster, more stable deep learning model training, evaluating for a finer threshold was not appropriate. Conversely, selecting a threshold greater than 3 mm was deemed too clinically imprecise for accurate radiotherapy planning.

The Average Symmetric Surface Distance (ASSD) [27] is the average of all the shortest distances from points on the boundary of the machine segmented region to the boundary of the ground truth, and vice versa. The ASSD, therefore, complements the previous metrics by taking voxel localization into consideration. Smaller values represent better segmentation accuracy.

2.6. Qualitative assessment of the segmentation

A separate expert radiation oncologist assessed the average amount of editing time necessary for clinical use of the ground truth, the best standalone model with respect to VDSC (Residual 3D U-Net Dice), and optimal ensemble contours, for five random patients from the test set. We previously anonymized each contour to avoid a biased evaluation. The radiation oncologist examined all muscle and GTV contours on every single slice of each patient to make their evaluation. We also asked this expert radiation oncologist to determine the typical faults made by the models for every structure segmentation.

3. Results

3.1. Quantitative assessment

The performance of the two ensemble models and six base learners is shown in Table 1a. We report the average, standard deviation, and performance range of each model for each metric. We found that the ensembles perform consistently better than the standalone models: they have a higher average and a lower variance. Moreover, each standalone model has at least one poor score for one of the patients and structures, while the ensemble models never suffer such degradation. For instance, among the 6 × 6 = 36 (standalone models, structure) VDSC (respectively ASSD) worst scores (i.e., the minimum of the metric range), the two ensemble models had a better minimum range 31 (resp. 35) times.

Table 1a:

Segmentation results for each structure averaged over the 8 test patients. We provide the standard deviation and range of the results. The best performance for each metric is in bold.

Model	Metric	GTV	G. maximus	G. medius	G. minimus	Paraspinal	Piriformis
3D U-Net Dice	VDSC	82.8 ± 5.7 (73.6,90.1)	93.9 ± 1.5 (91.3,95.8)	92.3 ± 0.8 (91.2,93.4)	84.3 ± 2.5 (79.5,88.8)	90.6 ± 1.1 (88.4,91.9)	74.7 ± 7.3 (62.6,84.5)
3D U-Net Cross-entropy		82.7 ± 6.6 (70.0,89.6)	93.6 ± 2.0 (89.4,95.8)	91.6 ± 1.0 (90.3,93.0)	84.1 ± 2.3 (80.5,87.4)	91.8 ± 0.8 (90.5,92.9)	73.6 ± 6.4 (58.0,79.4)
3D U-Net Weighted cross-entropy		79.3 ± 11.2 (52.2,88.8)	93.5 ± 1.7 (90.7,95.4)	91.7 ± 1.0 (89.9,93.2)	82.9 ± 2.1 (79.1,86.2)	91.2 ± 3.1 (83.6,94.3)	68.9 ± 7.5 (52.2,77.5)
Residual 3D U-Net Dice		81.8 ± 14.7 (43.8,91.0)	94.0 ± 1.7 (90.7,96.0)	92.1 ± 1.1 (90.3,93.4)	83.3 ± 2.6 (79.1,86.5)	90.7 ± 3.0 (83.1,93.0)	77.1 ± 6.1 (68.9,84.5)
Residual 3D U-Net Cross-entropy		83.1 ± 7.1 (71.1,91.4)	93.1 ± 2.6 (87.0,95.6)	90.2 ± 1.6 (87.6,92.4)	80.7 ± 5.2 (70.4,88.0)	91.3 ± 1.8 (87.2,93.8)	72.2 ± 9.3 (49.3,81.9)
Residual 3D U-Net Weighted Cross-entropy		83.4 ± 8.2 (64.7,90.0)	94.0 ± 1.5 (91.0,95.5)	91.4 ± 1.1 (89.5,92.7)	82.8 ± 2.8 (78.6,86.6)	91.5 ± 2.6 (85.6,93.8)	74.5 ± 5.2 (65.9,81.5)
Average Ensemble		85.1 ± 6.5 (70.5,91.5)	94.4 ± 1.6 (91.3,96.1)	92.6 ± 0.9 (91.1,93.7)	85.0 ± 2.7 (81.4,90.1)	92.2 ± 1.3 (89.3,93.3)	77.7 ± 5.4 (66.5,84.9)
Optimal Ensemble		85.5 ± 6.4 (70.7,91.5)	94.4 ± 1.5 (91.6,95.9)	92.6 ± 0.9 (91.1,93.7)	85.0 ± 2.7 (81.7,89.9)	92.1 ± 1.5 (88.6,93.4)	78.3 ± 5.7 (67.4,85.3)
3D U-Net Dice	SDSC 2 mm	61.0 ± 7.5 (49.0,70.2)	90.4 ± 5.0 (80.8,96.6)	91.2 ± 2.2 (86.4,93.9)	86.6 ± 5.1 (77.8,94.3)	88.2 ± 3.5 (82.7,93.8)	80.5 ± 8.7 (63.0,91.9)
3D U-Net Cross-entropy		60.2 ± 8.7 (49.1,73.7)	89.1 ± 5.6 (77.2,93.9)	89.3 ± 2.4 (85.1,93.3)	86.6 ± 3.8 (80.1,91.4)	90.8 ± 4.1 (83.6,96.8)	75.9 ± 8.6 (56.9,86.0)
3D U-Net Weighted cross-entropy		53.4 ± 12.9 (30.6,73.7)	88.6 ± 5.2 (79.7,96.8)	89.3 ± 2.9 (82.3,91.8)	84.3 ± 3.6 (78.2,89.8)	90.3 ± 3.8 (84.3,95.8)	71.5 ± 8.8 (52.0,82.2)
Residual 3D U-Net Dice		61.1 ± 16.9 (21.1,79.5)	90.4 ± 5.9 (77.3,97.1)	90.3 ± 1.9 (87.2,92.7)	85.7 ± 4.0 (78.0,92.1)	88.8 ± 3.8 (82.2,94.2)	81.6 ± 7.8 (71.1,90.8)
Residual 3D U-Net Cross-entropy		62.1 ± 13.4 (35.4,77.7)	87.8 ± 7.6 (69.9,94.5)	84.0 ± 4.0 (78.4,91.6)	82.3 ± 8.5 (63.2,93.5)	90.5 ± 2.9 (85.5,93.8)	72.2 ± 10.8 (46.8,85.5)
Residual 3D U-Net Weighted Cross-entropy		62.3 ± 10.5 (47.9,74.5)	90.9 ± 4.7 (81.6,96.5)	88.3 ± 3.1 (82.7,92.2)	85.1 ± 5.1 (74.1,91.9)	90.7 ± 4.1 (81.3,95.1)	77.9 ± 6.9 (67.9,88.0)
Average Ensemble		65.3 ± 9.1 (54.1,80.5)	91.9 ± 5.1 (80.9,96.8)	91.9 ± 2.5 (86.2,94.5)	88.2 ± 5.1 (77.5,96.1)	92.1 ± 2.5 (86.5,95.2)	82.5 ± 7.2 (67.5,92.5)
Optimal Ensemble		66.2 ± 9.1 (55.1,81.6)	92.2 ± 4.8 (82.0,97.0)	91.9 ± 2.4 (86.6,94.9)	88.3 ± 5.1 (77.4,95.7)	92.0 ± 2.7 (85.6,95.2)	83.9 ± 7.5 (69.5,93.9)
3D U-Net Dice	SDSC 3 mm	68.1 ± 7.1 (57.0,78.0)	94.1 ± 3.8 (86.3,98.1)	95.4 ± 1.8 (91.3,97.5)	91.0 ± 4.0 (84.1,96.9)	93.1 ± 3.0 (87.1,97.1)	86.0 ± 8.0 (69.4,95.4)
3D U-Net Cross-entropy		68.0 ± 8.1 (57.9,81.0)	93.3 ± 4.7 (82.1,96.6)	94.4 ± 2.0 (90.5,97.5)	91.1 ± 3.4 (85.6,95.6)	94.8 ± 2.7 (89.8,98.5)	82.3 ± 8.1 (63.4,90.1)
3D U-Net Weighted cross-entropy		62.0 ± 13.6 (36.0,81.4)	92.9 ± 4.3 (84.4,98.8)	94.4 ± 2.3 (88.5,96.4)	89.4 ± 2.9 (85.1,94.5)	94.3 ± 2.9 (89.3,98.2)	79.3 ± 9.3 (58.0,90.5)
Residual 3D U-Net Dice		68.4 ± 17.5 (25.3,86.2)	94.2 ± 4.6 (83.4,98.5)	94.4 ± 1.6 (91.2,96.0)	90.1 ± 3.6 (82.9,95.8)	92.6 ± 3.1 (87.9,96.2)	87.1 ± 6.7 (77.8,95.3)
Residual 3D U-Net Cross-entropy		69.6 ± 12.3 (44.2,83.5)	92.0 ± 6.7 (75.3,97.1)	89.7 ± 3.5 (83.7,95.1)	87.4 ± 7.4 (70.3,96.4)	94.5 ± 1.9 (91.3,97.1)	78.5 ± 9.9 (54.6,89.4)
Residual 3D U-Net Weighted Cross-entropy		71.0 ± 10.2 (56.1,83.4)	94.6 ± 3.8 (86.0,98.4)	93.4 ± 2.6 (88.2,96.0)	89.6 ± 4.7 (79.7,95.6)	94.5 ± 3.1 (87.4,97.3)	85.3 ± 6.6 (75.5,94.0)
Average Ensemble		72.9 ± 7.9 (63.5,85.8)	95.3 ± 4.1 (85.4,98.7)	95.9 ± 2.0 (90.8,97.4)	91.9 ± 4.2 (82.9,98.2)	95.7 ± 1.8 (91.5,97.3)	87.9 ± 6.6 (73.5,96.1)
Optimal Ensemble		73.7 ± 7.7 (63.3,85.9)	95.5 ± 3.7 (86.9,98.6)	95.8 ± 2.0 (91.0,97.6)	92.0 ± 4.3 (82.6,97.8)	95.5 ± 1.9 (91.0,97.3)	89.0 ± 6.9 (75.1,97.2)
3D U-Net Dice	ASSD	3.7 ± 1.4 (2.1,6.3)	1.2 ± 0.5 (0.6,2.2)	0.9 ± 0.1 (0.8,1.1)	1.2 ± 0.3 (0.8,1.6)	1.1 ± 0.2 (0.6,1.4)	1.9 ± 0.9 (0.9,3.3)
3D U-Net Cross-entropy		3.3 ± 0.9 (2.1,4.7)	1.4 ± 1.0 (0.7,3.9)	1.0 ± 0.1 (0.9,1.2)	1.2 ± 0.3 (0.9,1.7)	0.9 ± 0.3 (0.5,1.4)	2.3 ± 1.0 (1.4,4.6)
3D U-Net Weighted cross-entropy		4.7 ± 3.4 (1.9,13.4)	1.5 ± 0.8 (0.6,3.5)	1.0 ± 0.1 (0.9,1.3)	1.4 ± 0.2 (1.0,1.8)	1.0 ± 0.3 (0.6,1.4)	2.6 ± 1.5 (1.3,6.4)
Residual 3D U-Net Dice		5.0 ± 6.1 (1.6,20.9)	1.2 ± 0.9 (0.6,3.5)	1.0 ± 0.1 (0.8,1.1)	1.3 ± 0.2 (0.9,1.6)	1.0 ± 0.2 (0.6,1.3)	1.6 ± 0.6 (0.9,2.6)
Residual 3D U-Net Cross-entropy		3.5 ± 2.1 (1.9,8.3)	1.7 ± 1.8 (0.7,6.4)	1.3 ± 0.2 (0.9,1.6)	1.5 ± 0.6 (0.8,2.7)	0.9 ± 0.1 (0.8,1.1)	3.4 ± 1.2 (2.2,6.0)
Residual 3D U-Net Weighted Cross-entropy		3.0 ± 0.9 (1.8,4.3)	1.1 ± 0.6 (0.6,2.5)	1.1 ± 0.2 (0.9,1.4)	1.3 ± 0.3 (0.9,1.8)	0.9 ± 0.2 (0.7,1.3)	1.8 ± 0.6 (1.1,2.6)
Average Ensemble		2.7 ± 0.8 (1.6,3.7)	1.1 ± 0.7 (0.6,2.9)	0.9 ± 0.1 (0.7,1.1)	1.1 ± 0.3 (0.6,1.6)	0.8 ± 0.2 (0.6,1.1)	1.6 ± 0.7 (0.9,3.2)
Optimal Ensemble		2.6 ± 0.8 (1.5,3.6)	1.0 ± 0.4 (0.6,2.0)	0.9 ± 0.1 (0.7,1.1)	1.1 ± 0.3 (0.6,1.6)	0.8 ± 0.2 (0.6,1.1)	1.5 ± 0.6 (0.8,2.9)

The average ensemble (resp. optimal ensemble) improves the top-performing standalone model with respect to each metric by an average of 1.5% (resp. 1.7%) on VDSC, 2.8% (resp. 3.3%) on SDSC 2 mm, 2.1% (resp. 2.5%) on SDSC 3 mm, and 11% (resp. 14%) on ASSD.

We saw a very high and stable performance of the ensembles on the Gluteus Maximus, Gluteus Medius, and Paraspinal muscles, with scores above 90% for VDSC, SDSC 2 mm, and SDSC3 mm. We noticed, in general, high performance on the GTV and Gluteus minimus with an average VDSC above 85%. The Piriformis muscle had the lowest performance, although it maintained scores above 77%. Across structures, the VDSC standard deviations were within 1 – 3%, except for GTV (around 6.5% for the ensembles) and Piriformis (in the 5% for the ensembles).

The average ensemble (resp. optimal ensemble) has an average VDSC standard deviation 37% (resp. 36%) lower than the best standalone model with respect to VDSC, an average SDSC 3 mm standard deviation 14% (resp. 15%) lower than the best standalone model with respect to SDSC 3 mm, and an average ASSD standard deviation 0% (resp. 14%) lower than the best standalone model with respect to ASSD.

The different SDSC thresholds show that most contours are within one diagonal pixel away from the ground truth. With the optimal ensemble, the average SDSC 3 mm is higher than 89% for all structures except for the GTV (74%). The average SDSC 2 mm results show that both ensembles have very strong performance for G. Maximus, G. Medius, G. Minimus, and Paraspinal (88%+) and strong performance for the Piriformis (82%+). The average ASSD scores confirm this conclusion: under 1.1 mm for all structures, except Piriformis (under 1.6 mm) and GTV (under 2.7 mm).

The results on the outlier test set, in Table 1b, show the performance of the ensemble models decreases but still maintains a VDSC within 80–90% for all structures and an SDSC 3 mm higher than 80% for all structures except the GTV, where it reaches 51%. The ASSD also increases for all structures, most notably for the GTV (7.0 mm on the outlier test set vs. 2.6 mm on the test set for the optimal ensemble). On the outlier test set, the two ensemble models no longer systematically outperform the best standalone model for every structure. However, they are the only models to maintain consistent performance, at least always close to the best one reported.

Table 1b:

Segmentation results for each structure averaged over the 5 outlier test patients. We provide the standard deviation and range of the results. The best performance for each metric is in bold.

Model	Metric	GTV	G. maximus	G. medius	G. minimus	Paraspinal
3D U-Net Dice	VDSC	81.1 ± 7.4 (69.5,90.7)	85.4 ± 6.6 (73.8,93.3)	88.1 ± 4.6 (79.0,91.6)	83.7 ± 3.4 (77.9,86.7)	78.9 ± 10.4 (67.9,91.8)
3D U-Net Cross-entropy		81.4 ± 6.0 (73.0,90.9)	87.2 ± 2.8 (83.2,91.7)	88.3 ± 3.9 (80.7,91.1)	81.2 ± 3.7 (74.4,84.4)	79.5 ± 9.6 (69.5,92.2)
3D U-Net Weighted cross-entropy		82.7 ± 6.8 (72.8,93.0)	85.0 ± 5.2 (77.0,91.1)	87.8 ± 4.1 (80.6,91.7)	82.5 ± 3.2 (76.7,86.1)	78.0 ± 15.4 (50.5,92.8)
Residual 3D U-Net Dice		82.0 ± 6.9 (72.6,90.9)	87.1 ± 3.9 (81.1,93.0)	88.9 ± 3.4 (82.6,92.2)	81.9 ± 4.2 (74.5,86.1)	84.7 ± 7.2 (71.9,93.2)
Residual 3D U-Net Cross-entropy		78.4 ± 6.8 (68.2,88.3)	85.4 ± 2.6 (81.9,88.4)	84.8 ± 4.8 (75.5,88.7)	79.2 ± 6.5 (66.7,84.8)	81.9 ± 9.8 (64.0,92.1)
Residual 3D U-Net Weighted Cross-entropy		78.8 ± 5.0 (71.4,86.2)	86.5 ± 3.6 (80.2,91.3)	88.5 ± 3.1 (83.2,92.0)	81.7 ± 4.4 (74.2,87.4)	85.7 ± 7.0 (74.7,92.8)
Average Ensemble		82.1 ± 6.4 (72.9,91.7)	87.9 ± 3.1 (82.4,91.5)	89.4 ± 3.3 (83.1,92.0)	83.6 ± 3.6 (77.2,87.5)	83.8 ± 7.0 (75.0,93.1)
Optimal Ensemble		81.9 ± 6.6 (72.6,91.8)	87.8 ± 3.1 (82.4,91.1)	89.4 ± 3.2 (83.3,92.1)	83.4 ± 3.9 (76.4,87.7)	84.9 ± 6.6 (75.0,93.2)
3D U-Net Dice	SDSC 2 mm	41.7 ± 9.6 (27.1,52.6)	71.8 ± 11.7 (54.6,89.4)	82.8 ± 5.6 (72.0,87.5)	84.8 ± 4.3 (77.2,90.3)	68.2 ± 17.2 (40.0,87.6)
3D U-Net Cross-entropy		40.8 ± 8.5 (29.6,52.8)	73.8 ± 7.9 (66.0,87.5)	83.0 ± 5.1 (73.3,87.2)	80.7 ± 6.0 (70.1,87.5)	68.5 ± 16.6 (45.9,90.2)
3D U-Net Weighted cross-entropy		46.9 ± 10.9 (32.8,64.3)	71.2 ± 8.4 (60.4,84.7)	81.6 ± 5.9 (72.3,89.6)	82.7 ± 5.6 (75.6,90.6)	69.2 ± 22.4 (33.6,92.1)
Residual 3D U-Net Dice		45.3 ± 10.2 (34.3,61.7)	76.2 ± 8.6 (66.6,88.4)	83.9 ± 6.7 (72.1,91.7)	83.4 ± 6.1 (74.2,90.3)	78.5 ± 11.6 (61.4,93.3)
Residual 3D U-Net Cross-entropy		35.5 ± 7.3 (26.4,45.5)	72.0 ± 7.1 (64.5,82.1)	74.3 ± 7.8 (59.8,82.0)	77.7 ± 9.6 (60.5,89.2)	74.3 ± 13.4 (50.7,89.9)
Residual 3D U-Net Weighted Cross-entropy		43.8 ± 6.4 (35.1,52.4)	76.8 ± 6.6 (69.1,88.5)	81.6 ± 6.1 (71.2,87.9)	81.9 ± 6.0 (72.3,87.8)	81.2 ± 9.6 (64.2,92.0)
Average Ensemble		44.0 ± 8.7 (31.0,55.9)	76.7 ± 7.7 (67.2,88.8)	85.0 ± 5.3 (75.1,89.7)	85.0 ± 5.5 (76.1,91.0)	76.5 ± 13.4 (56.6,92.4)
Optimal Ensemble		44.2 ± 8.7 (31.6,56.4)	76.9 ± 7.4 (67.9,88.4)	84.9 ± 5.5 (74.7,90.1)	84.9 ± 5.8 (75.4,90.9)	79.3 ± 10.6 (66.3,93.0)
3D U-Net Dice	SDSC 3 mm	49.2 ± 10.8 (33.3,62.8)	78.3 ± 11.0 (61.5,94.1)	88.5 ± 5.1 (78.3,92.2)	90.4 ± 3.3 (84.7,94.1)	74.6 ± 15.9 (49.4,92.5)
3D U-Net Cross-entropy		48.1 ± 9.6 (35.9,62.6)	80.1 ± 6.9 (72.4,91.9)	88.6 ± 4.4 (80.3,92.4)	87.1 ± 5.1 (78.6,92.2)	74.9 ± 16.0 (55.5,94.5)
3D U-Net Weighted cross-entropy		54.0 ± 11.7 (39.2,73.3)	76.7 ± 9.3 (63.4,90.3)	87.4 ± 5.2 (79.1,94.0)	88.4 ± 4.8 (83.1,94.9)	74.3 ± 22.0 (38.1,96.0)
Residual 3D U-Net Dice		52.4 ± 11.6 (39.3,69.6)	81.8 ± 7.8 (71.5,93.0)	89.2 ± 5.8 (79.6,95.6)	89.4 ± 5.3 (81.9,94.3)	83.5 ± 10.8 (64.9,96.3)
Residual 3D U-Net Cross-entropy		42.1 ± 8.3 (31.6,51.9)	78.0 ± 5.8 (70.9,86.2)	81.6 ± 7.1 (68.8,88.2)	84.3 ± 8.9 (67.9,93.9)	79.7 ± 13.7 (54.2,93.7)
Residual 3D U-Net Weighted Cross-entropy		50.0 ± 7.4 (39.8,60.5)	82.3 ± 6.1 (73.6,92.4)	87.7 ± 5.2 (78.6,92.5)	87.4 ± 5.5 (79.4,92.4)	85.8 ± 9.7 (68.2,95.6)
Average Ensemble		51.3 ± 10.0 (36.8,66.1)	82.7 ± 6.8 (73.1,92.7)	90.2 ± 4.5 (82.0,94.4)	90.5 ± 4.5 (84.0,94.7)	82.1 ± 11.7 (67.4,95.9)
Optimal Ensemble		51.4 ± 10.1 (37.1,66.6)	82.8 ± 6.7 (73.2,92.4)	90.1 ± 4.7 (81.7,94.6)	90.3 ± 4.9 (83.2,94.7)	84.6 ± 9.6 (69.9,96.3)
3D U-Net Dice	ASSD	7.1 ± 3.5 (3.5,13.0)	2.8 ± 1.4 (1.0,5.0)	1.9 ± 1.2 (1.1,4.2)	1.3 ± 0.2 (1.0,1.7)	2.5 ± 1.3 (1.1,4.4)
3D U-Net Cross-entropy		6.8 ± 3.1 (3.3,12.1)	2.8 ± 1.2 (1.3,4.9)	1.8 ± 0.8 (1.2,3.3)	1.6 ± 0.4 (1.2,2.2)	4.2 ± 3.9 (1.0,11.4)
3D U-Net Weighted cross-entropy		6.3 ± 3.1 (2.5,11.2)	6.2 ± 7.1 (1.4,20.3)	2.3 ± 1.1 (1.1,4.3)	1.4 ± 0.3 (1.0,1.8)	3.0 ± 2.7 (0.9,8.1)
Residual 3D U-Net Dice		6.8 ± 3.3 (3.1,12.0)	2.4 ± 0.9 (1.1,3.8)	1.7 ± 0.8 (1.0,3.1)	1.5 ± 0.4 (1.0,2.2)	2.8 ± 3.0 (0.8,8.7)
Residual 3D U-Net Cross-entropy		8.1 ± 3.6 (4.3,14.4)	3.3 ± 1.5 (1.9,6.3)	2.4 ± 0.8 (1.7,3.9)	1.9 ± 0.8 (1.1,3.3)	3.2 ± 3.3 (1.0,9.8)
Residual 3D U-Net Weighted Cross-entropy		7.6 ± 2.8 (4.6,12.2)	2.5 ± 0.9 (1.4,4.1)	1.7 ± 0.5 (1.2,2.6)	1.5 ± 0.4 (1.2,2.2)	1.8 ± 1.1 (0.9,3.9)
Average Ensemble		6.9 ± 3.4 (3.0,12.5)	2.3 ± 0.8 (1.4,3.5)	1.6 ± 0.7 (1.0,2.9)	1.3 ± 0.3 (0.9,1.8)	2.0 ± 1.1 (0.8,3.9)
Optimal Ensemble		7.0 ± 3.4 (3.0,12.6)	2.3 ± 0.8 (1.4,3.6)	1.6 ± 0.7 (1.0,2.9)	1.3 ± 0.3 (0.9,1.8)	1.9 ± 1.1 (0.8,3.9)

Qualitative Assessment.

We report the qualitative assessment results in Table 1c.

Table 1c:

Independent qualitative assessment by a separate expert radiation oncologist on 5 random patients from our test set. We report the range and average editing time in minutes necessary for clinical use.

Structure	Ground Truth	Best Model	Optimal Ensemble
GTV	6 (3, 13)	6 (3, 8)	11 (7, 13)
Gluteus Maximus	2 (0, 4)	2 (0, 4)	4 (0, 7)
Gluteus Medius	2 (0, 4)	2 (0, 4)	2 (0, 4)
Gluteus Minimus	3 (1, 4)	3 (1, 4)	3 (1, 4)
Paraspinal	3 (1, 4)	3 (1, 4)	3 (1, 4)
Piriformis	3 (1, 4)	3 (1, 4)	3 (1, 4)

In particular, the best standalone model with respect to VDSC would require the same amount of editing as the ground truth contours for all structures and patients: on average, under 3 minutes for muscles and under 6 minutes for the GTV. The optimal ensemble contours would require, on average, under 3 minutes to correct each structure except for the Gluteus Maximus (4 minutes) and GTV (11 minutes).

Although our automated muscle segmentation can provide reasonably accurate muscle contours, including most muscle origins and insertions, we noted some potential limitations and areas for improvement. Firstly, while the gluteus maximus contours were largely accurate, there were minor areas where their origins were not predicted with complete fidelity. Overall, the paraspinal muscles demonstrated good accuracy in all patients, with only the superior border requiring slight improvements. The gluteus medius and gluteus minimus muscles had some issues with their distal edges but were otherwise generally suitable for clinical use. The piriformis contours demonstrated some inaccuracies where the muscle inserted into the femur. Furthermore, delineating the tumor/bone interface can be difficult, as illustrated in Figure 3a, where the GTV extension through the bone is less defined. Finally, automated delineation of the tumor-muscle interface can also be challenging, mainly where tumor emboli invade muscles, as indicated by the green arrow in Figure 3b.

Figure 3a:

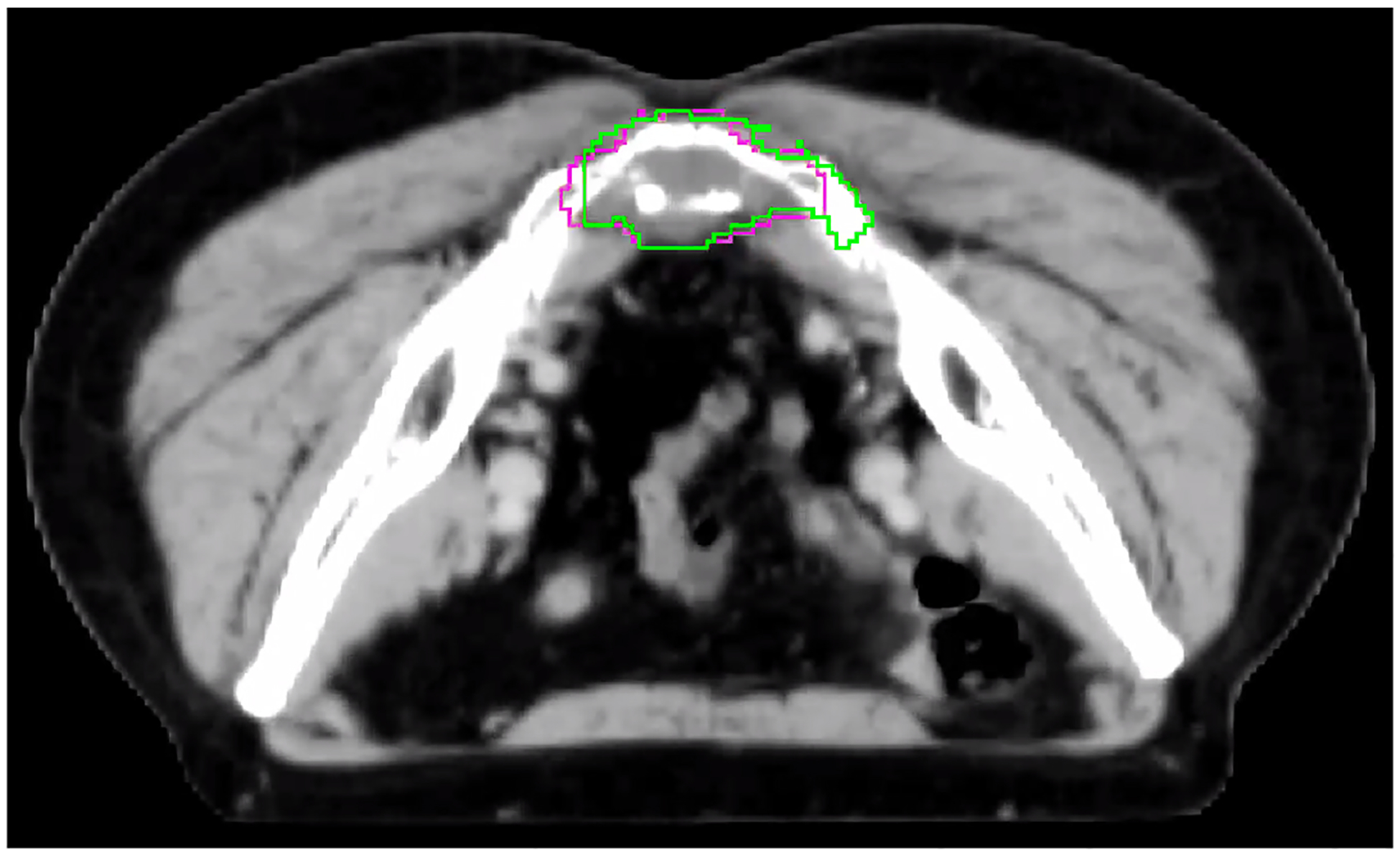
Example of a patient where the extension of the average ensemble GTV contour (magenta) through the bone does not match the ground truth contour (green) and would require adjustments before clinical use.

4. Discussion

4.1. Results Interpretation

The high accuracy for automated contouring of the Gluteus muscles and Paraspinal is likely due to these muscles’ large size and generally consistent structure. The Piriformis has a slightly poorer performance, likely because of the thin shape of this muscle and the difficulty in distinguishing the boundary between the lateral edge of this muscle and the medial edge of the Gluteus Medius on axial imaging. The model achieves remarkably strong performance in general, including on the GTV, despite the variability of its shapes and textures in the images. Moreover, the qualitative assessment confirmed the very satisfactory performance for clinical use.

4.2. Ensemble Models Improve Score Performance and Decrease Variance

By incorporating various model predictions, ensemble models effectively leverage the insights obtained from multiple sources and provide more robust predictions. Table 1a shows that ensemble models largely outperform standalone models for the hardest patients. Ensembles advantageously smooth predictions and may avoid failures cases that a specific model may face for a specific patient. The ensemble models substantially reduced the variance across predictions, which is an important step toward offering physicians robust and stable treatment planning options. We further report t-tests comparing if the ensembles are significantly better than the standalone models in Appendix C.

It also appears possible to obtain valuable auto-delineations of relevant structures for CTV definition using training datasets from only 30 patients. It is remarkable and promising for other rare diseases when it is challenging to acquire large and consistent datasets.

4.3. Advantages of an Automated Approach

Overall, we conclude that AI-assisted muscle contouring and most of the GTV contouring along tumor-fat tissue planes would represent substantial time savings for clinical use. The manual labor of contouring sarcoma tumors and the surrounding muscles of interest is burdensome and tedious for physicians. Clinicians from [Anonymized Hospital] reported a typical 40-minute duration to contour muscles from all groups for one patient. The time required to contour the GTV could range from 10 minutes to an hour depending on its size, the reference sequence (e.g., additional availability of an MRI sequence), and the extent of tumor invasion into adjacent bone and muscle. In comparison, AI-assisted muscle contouring can typically save 30–80 minutes per patient.

Furthermore, at the [Anonymized Hospital], in the case of complex and large soft tissue sarcomas (such as retroperitoneal) or spine or pelvic bone sarcomas, the manual delineation can take up to several hours of the radiation oncologists’ time for a single patient. The automation of the proposed approach is easily applicable and understandable and offers excellent potential to relieve the physicians and free up time. We expect that our segmentation models could be extended to other important structures, such as cauda equina, sacral, sciatic nerves, rectum, and other pelvic organs, if the ground truth labels were available.

4.4. Limitations

On the one hand, the optimal ensemble outperforms, in general, the best standalone model, particularly for the GTV segmentation. On the other hand, the qualitative analysis revealed that the optimal ensemble segmentation of the GTV would require more adjustments than the one from the best standalone model (11 minutes vs. 6 minutes on average). We explain this discrepancy by the subtle flaws in the ground truth contours of the GTV according to the independent assessment. Since the optimal ensemble is trained to replicate the ground truth even more closely, we conjecture that it is more susceptible to intra-observer variability and, thus, is less robust across physicians and may be more biased towards the contouring of those samples. This reflects the limitations of only using quantitative metrics and the importance of complementing with a qualitative clinical use assessment.

Furthermore, since we tackled a rare tumor type, we could only perform our study on a small dataset. While a single radiation oncologist generated the ground-truth contours of the muscle structures, the GTV contours were delineated by six different physicians over 20 years, which may have led to different contouring styles. However, it appeared not to be a problem for our DL models, which displayed great generalization capacity.

The results of Table 1b suggest the models show lower performance when the tumor is huge. This is within expectation as no such cases were present in the training set, and extensive tumor growth can substantially deform adjacent muscles. A larger and more diverse training set would likely improve performance. However, although less accurate, our optimal ensemble remains a valuable tool for fast preliminary segmentation.

We also acknowledge that no dosimetric evaluation was performed. A geometric evaluation like the one investigated in this paper tends to show bigger differences than a dosimetric evaluation because physical phenomena such as radiation scattering blur out geometric differences and lead to more similar radiation dose distributions. Our evaluation can thus be considered a worst-case analysis.

Lastly, further preprocessing of the CT images could potentially improve performance: for example, by increasing the muscle-to-tumor contrast with specific windowing.

Moreover, although we demonstrated that CT images already yield sufficient predictive power, the ideal scenario would combine diagnostic MR images with CT images. MRI offers superior image contrast of soft tissue than CT and would provide an additional modality to analyze the same patient’s muscle and tumor structures. However, our methodology can scale to include other images: MR images can be input as additional channels into the 3D U-Nets, and the ensemble model would work similarly. It is also possible to train models on the MRI alone that could later be combined as distinct standalone models in the ensemble stage.

4.5. Towards Clinical Target Volume (CTV) Delineation

A standard CT simulation scan lacks intrinsic physiologic or anatomic compartment information, making it necessary for annotators to rely on their expertise to identify relevant structures. The CTV delineation process is complex and requires incorporating information about the natural history of a particular tumor’s modes of local extension based on patterns of failure after surgery and/or radiation therapy, as well as anatomic factors that affect tumor dissemination (i.e., fascial barriers to spread).

The automated method of segmenting GTV and surrounding muscles offers several benefits to physicians. The technique represents a critical first step toward automating the CTV delineation process and subsequent treatment planning by accurately identifying natural anatomical barriers and musculoskeletal compartments that are not typically delineated for treatment planning purposes and which otherwise require advanced expertise in recognizing anatomy on CT scans. The automated process also incorporates prior experience information to guide CTV delineation and make it more efficient. Given the rarity of chordomas and other sarcomas in this region, this AI-based tool may prove invaluable in improving target delineation for less experienced clinicians.

5. Conclusion

When combined with ensemble modeling, deep learning methods can effectively solve segmentation problems for rare tumor types, such as sacral chordomas, that typically require substantial clinical expertise for appropriate target delineation. Our analysis of 48 patients demonstrates the ability to reliably auto-segment the GTV and surrounding muscle structures. Overall, we highlight the power of an optimal ensemble which provides a quantifiable advantage, improving the top-performing standalone model by an average of 2% on VDSC and 14% on ASSD. We also qualitatively evaluated and demonstrated a substantial reduction of time spent on manual labor for physicians when using machine-generated contours. Despite the difficulty at the muscle and tumor interface, the automated definitions serve as valuable starting points for clinicians, making the final modifications and confirmation a quick and easy task.

Figure 3b:

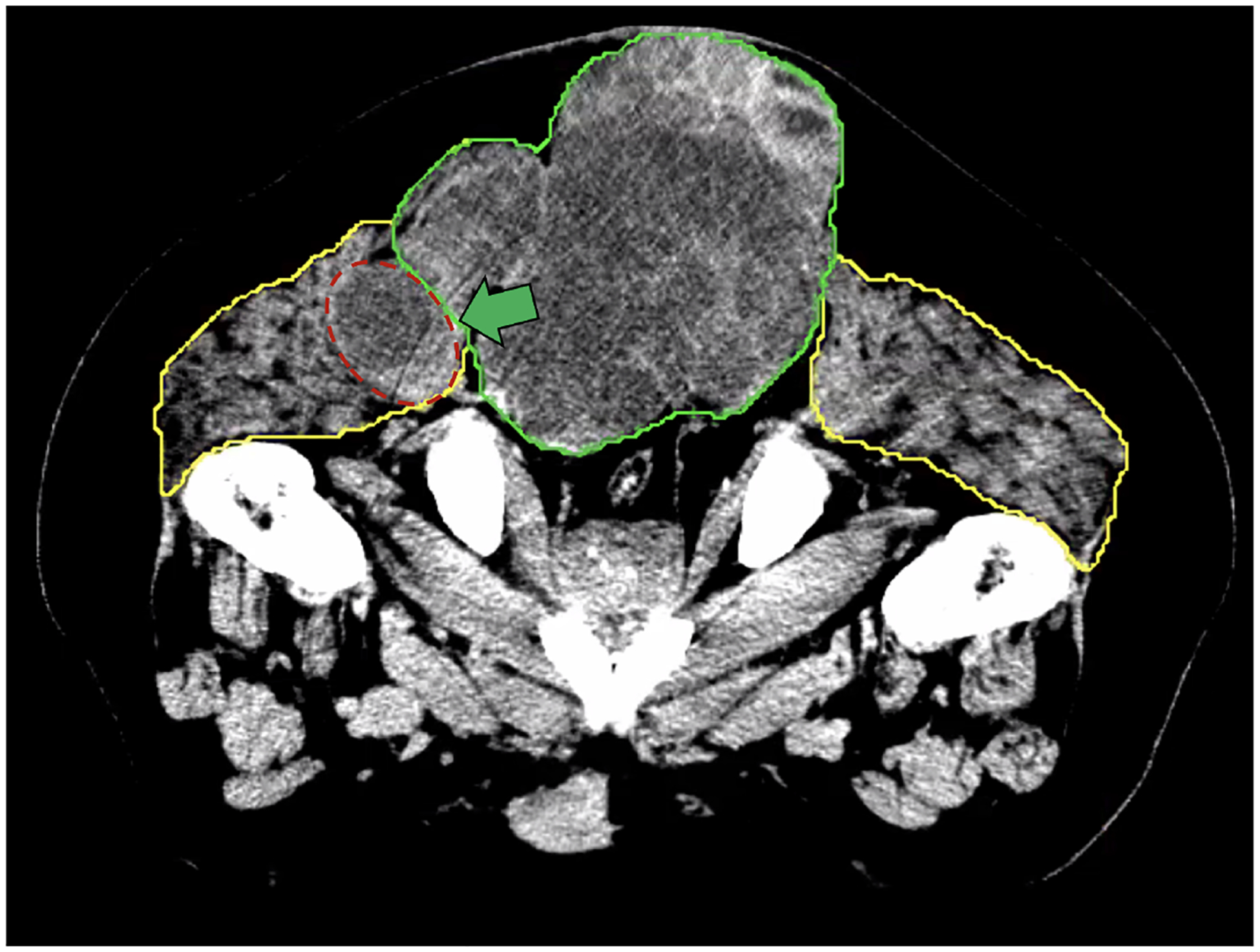
Example of a patient where the interface delineation between the GTV (green contour) and muscle (yellow contour) is harder because tumor emboli are invading into muscle (area with red dashes in the figure).

Table 3b:

Corrected p-values corresponding to each (metric, ensemble, standalone model vs. optimal ensemble) t-test.

ASSD Model Comparison	GTV	G. maximus	G. medius	G. minimus	Paraspinal	Piriformis
3D U-Net Dice	0.168	0.278	0.278	0.285	0.144	0.260
3D U-Net Cross-entropy	0.140	0.193	0.080	0.247	0.247	0.123
3D U-Net Weighted cross-entropy	0.116	0.116	0.000	0.072	0.096	0.002
Residual 3D U-Net Dice	0.252	0.312	0.246	0.252	0.246	0.314
Residual 3D U-Net Cross-entropy	0.053	0.061	0.037	0.037	0.065	0.037
Residual 3D U-Net Weighted cross-entropy	0.247	0.256	0.055	0.246	0.246	0.246
VDSC Model Comparison	GTV	G. maximus	G. medius	G. minimus	Paraspinal	Piriformis
3D U-Net Dice	0.297	0.297	0.297	0.297	0.144	0.297
3D U-Net Cross-entropy	0.292	0.292	0.198	0.292	0.312	0.249
3D U-Net Weighted Cross-entropy	0.215	0.163	0.010	0.085	0.180	0.133
Residual 3D U-Net Dice	0.353	0.353	0.326	0.326	0.326	0.353
Residual 3D U-Net Cross-entropy	0.136	0.153	0.105	0.105	0.205	0.050
Residual 3D U-Net Weighted cross-entropy	0.304	0.304	0.132	0.214	0.304	0.214
SDSC2 Model Comparison	GTV	G. maximus	G. medius	G. minimus	Paraspinal	Piriformis
3D U-Net Dice	0.283	0.283	0.283	0.283	0.132	0.283
3D U-Net Cross-entropy	0.215	0.215	0.129	0.265	0.265	0.129
3D U-Net Weighted cross-entropy	0.173	0.105	0.000	0.084	0.140	0.036
Residual 3D U-Net Dice	0.297	0.297	0.270	0.297	0.270	0.297
Residual 3D U-Net Cross-entropy	0.026	0.039	0.028	0.028	0.058	0.014
Residual 3D U-Net Weighted cross-entropy	0.246	0.258	0.075	0.210	0.246	0.178
SDSC3 Model Comparison	GTV	G. maximus	G. medius	G. minimus	Paraspinal	Piriformis
3D U-Net Dice	0.270	0.343	0.343	0.343	0.270	0.343
3D U-Net Cross-entropy	0.204	0.258	0.204	0.323	0.323	0.204
3D U-Net Weighted cross-entropy	0.156	0.123	0.004	0.115	0.146	0.038
Residual 3D U-Net Dice	0.298	0.298	0.270	0.298	0.174	0.298
Residual 3D U-Net Cross-entropy	0.102	0.143	0.143	0.143	0.196	0.102
Residual 3D U-Net Weighted cross-entropy	0.336	0.336	0.216	0.328	0.336	0.328

Appendix

A. Data

CT Image Acquisition

The CT scans were acquired with a GE scanner following the standard protocol for radiotherapy treatment planning. The image acquisition was performed in prone (n=45) and supine (n=3) positions. The initial CT image resolutions are listed in Table 2.

GTV Contouring Procedure

All GTV contouring procedures were executed by radiation oncologists with specialized expertise in sarcoma treatment. Before 2015, additional staff members participated in the peer review of contours and treatment plans during weekly chart rounds. In 2015, [Anonymized Hospital] introduced a contour review system that incorporated the involvement of an additional radiation oncologist, also with sarcoma subspecialty expertise, before commencing the treatment planning process. At this point, 3–4 radiation oncologists managed these patients, ensuring that at least one participated in contour review. Furthermore, the treatment plans continued to undergo peer review by multiple staff members during weekly chart rounds as before.

CT Image Pre-processing

This section outlines more precisely our pipeline to pre-process the data.

1. CT scans and RT structures were converted to MHA format.

2. We manually fixed some CT image orientations, which were found to be wrongly recorded due to the patient’s prone vs. supine position during CT image acquisition. Moreover, we recentered the offsets of all image sequences to be observed in the same field of view by applying axial translations in 3D Slicer.

3. We rigidly aligned all images to Right-Anterior-Inferior (RAI) anatomical position and applied a transformation to align all patients to one randomly selected reference based on the pelvic bony anatomy. The resulting transformation was applied to the structure files for alignment. We used a rigid registration with 6 degrees of freedom to assign voxel positions of each image relative to one common coordinate system.

4. We resampled image and structure files to the same 2 × 2 × 2 mm resolution with linear interpolation applied to the images and nearest-neighbor interpolation applied to the structures. The 2 × 2 × 2 mm element spacing ensured sufficient resolution for future treatment planning and faster and more stable DL model training.

5. We manually merged all structure segmentation into a single image file.

6. We manually cropped all images to restrict the field of interest as the smallest bounding box that contained all structures segmented in all patients (see Figure 1 as an example). If needed, we padded the images on all 3 axes to obtain a standard final image dimension of 182 × 157 × 216 voxels, where one voxel still corresponds to a 2 mm cube.

7. We re-scaled each image so that voxel values had zero mean and unit variance by calculating the mean and standard deviation of the Hounsfield units of all voxels in a given CT image and then subtracting from each voxel the mean and dividing by the standard deviation.

The final image sequences had 8 anatomical structures: 5 left-right merged muscle structures, sarcoma GTV, other areas inside the body of no interest in this study, and areas outside of the body (see Figure 1).

We converted all data from DICOM image sequences to .mha files for image processing, which we then converted to .h5 files for model training and testing.

B. U-Net Architectures Details

As suggested by [17] and [18], we used the following specific hyperparameters for our 3D U-Nets and Residual 3D U-Nets:

• 64 feature maps at each level of the encoder,

• For each block, a layer order of group normalization, 3D convolution operation, and ReLU activation function,

• 8 groups for the GroupNorm operation,

• 4 levels in the encoder/decoder path for the 3D U-Nets and 5 levels for the Residual 3D U-Nets (since the model effectively becomes a residual net, it allows for deeper networks).

• 1-pixel zero-padding added to all three sides of the input,

• Size of the convolving kernel in the basic blocks: 3,

• Size of the window in the pooling operation: 2,

• Nearest neighbor upsampling in the decoder for 3D U-Nets and transposed convolutions for upsampling in the decoder for Residual 3D U-Nets.

We based our U-Net architecture and training code from [28].

3D U-Net Hyperparameter Search

For each one of the six (loss, architecture) combinations, we concurrently validated the following hyperparameters in the provided sets:

• the Adam optimizer learning rate: [5 ⋅ 10⁻⁵, 10⁻⁴, 3 ⋅ 10⁻⁴, 5 ⋅ 10⁻⁴, 7 ⋅ 10⁻⁴, 10⁻³]

• learning rate scheduler: learning rate×[1, 0.7, 0.5] every [5, 10, 15] epochs

• weight decay (L2 weight regularization): [0, 10⁻⁶, 10⁻⁵, 5 ⋅ 10⁻⁵, 10⁻⁴, 5 ⋅ 10⁻⁴, 10⁻³]

• image patch shape: [128 × 128 × 128, 64 × 64 × 64, 32 × 32 × 32]

• stride shape: [32 × 32 × 32, 32 × 32 × 64, 16 × 16 × 32, 16 × 16 × 16, 8 × 8 × 16]

For the specific case of the weighted-cross-entropy loss, once we found the best hyperparameters corresponding to the standard cross-entropy loss, we fixed these hyperparameters and validated the weights given to each class in the weighted-cross-entropy loss. We tested the following weights with the intuition that we wanted to increase the weight on the hardest classes to predict (GTV, G. minimus, Piriformis): [(0.25,0.1,0.1,0.1,0.15,0.2,0.05,0.05), (0.25,0.05,0.05,0.25,0.05,0.25,0.05,0.05), (0.2,0.1,0.1,0.2,0.1,0.2,0.05,0.05), (0.3,0.05,0.05,0.1,0.1,0.3,0.05,0.05)], where we give tuples corresponding to (GTV, G. Maximus, G. Medius, G. Minimus, Paraspinal, Piriformis, Out-of-the-body regions, In-the-body regions of no interest).

The hyperparameter search revealed the following insights:

• The Adam optimizer learning rate was the best in the ballpark of 10⁻⁴ as smaller led the model to train too slowly, and larger led to less stable training and poorer generalization.

• The learning rate scheduler was not the most crucial hyperparameter, but it was important to decrease the learning rate during the training process to refine the weights.

• The weight decay had to be present but low enough.

• The image patch shape was a critical factor: too small led to much slower training and poorer generalization as the model had less context for predictions.

• The stride shape was less crucial. It was a trade-off to avoid too many or too few samples from each image sequence.

• The weights of the weighted-cross-entropy loss subtly impacted the performance; different combinations had about the same results.

C. Statistical Tests

We conducted t-tests to investigate whether the performance of the average or optimal ensembles surpassed that of each standalone model across the four metrics and six anatomical structures. We employed a two-stage Benjamini and Hochberg procedure for non-negative multiple comparisons correction with a false discovery rate of 0.1 [29]. We conducted the tests for every combination of metric and structure, comparing each standalone model against the average or optimal ensemble. Subsequently, we corrected the p-values model-wise across the six structures under investigation. We reported the corrected p-values in Tables 3a (Standalone Models vs. Average Ensemble) and 3b (Standalone Models vs. Optimal Ensemble). We observe many statistically significant model comparisons at the 0.2 level, indicating that both the average and optimal ensemble models perform significantly better than individual models across several structures and metrics. However, it is important to exercise caution when interpreting the results of the statistical testing due to the limited sample size of the validation cohort. All statistical analysis was executed in Python using the scikit-learn [30] and statsmodels packages [31].

Table 3a:

Corrected p-values corresponding to each (metric, ensemble, standalone model vs. average ensemble) t-test.

ASSD Model Comparison	GTV	G. maximus	G. medius	G. minimus	Paraspinal	Piriformis
3D U-Net Dice	0.210	0.398	0.356	0.374	0.120	0.371
3D U-Net Cross-entropy	0.185	0.248	0.070	0.270	0.248	0.185
3D U-Net Weighted Cross-entropy	0.133	0.133	0.000	0.077	0.077	0.006
Residual 3D U-Net Dice	0.266	0.450	0.228	0.266	0.228	0.517
Residual 3D U-Net Cross-entropy	0.078	0.130	0.064	0.064	0.090	0.078
Residual 3D U-Net Weighted cross-entropy	0.347	0.385	0.050	0.283	0.283	0.347
VDSC Model Comparison	GTV	G. maximus	G. medius	G. minimus	Paraspinal	Piriformis
3D U-Net Dice	0.255	0.255	0.255	0.255	0.055	0.255
3D U-Net Cross-entropy	0.254	0.254	0.198	0.254	0.254	0.254
3D U-Net Weighted Cross-entropy	0.246	0.138	0.010	0.088	0.138	0.138
Residual 3D U-Net Dice	0.397	0.397	0.314	0.314	0.314	0.418
Residual 3D U-Net Cross-entropy	0.156	0.167	0.110	0.110	0.178	0.060
Residual 3D U-Net Weighted cross-entropy	0.337	0.337	0.132	0.234	0.337	0.274
SDSC2 Model Comparison	GTV	G. maximus	G. medius	G. minimus	Paraspinal	Piriformis
3D U-Net Dice	0.268	0.268	0.268	0.268	0.075	0.268
3D U-Net Cross-entropy	0.258	0.258	0.210	0.268	0.268	0.210
3D U-Net Weighted cross-entropy	0.202	0.110	0.000	0.091	0.110	0.056
Residual 3D U-Net Dice	0.362	0.362	0.288	0.332	0.210	0.415
Residual 3D U-Net Cross-entropy	0.031	0.047	0.031	0.032	0.047	0.022
Residual 3D U-Net Weighted cross-entropy	0.284	0.296	0.080	0.232	0.264	0.232
SDSC3 Model Comparison	GTV	G. maximus	G. medius	G. minimus	Paraspinal	Piriformis
3D U-Net Dice	0.342	0.342	0.342	0.342	0.198	0.342
3D U-Net Cross-entropy	0.280	0.293	0.270	0.339	0.293	0.270
3D U-Net Weighted cross-entropy	0.188	0.116	0.004	0.116	0.116	0.058
Residual 3D U-Net Dice	0.392	0.392	0.228	0.386	0.126	0.415
Residual 3D U-Net Cross-entropy	0.135	0.155	0.155	0.155	0.155	0.135
Residual 3D U-Net Weighted cross-entropy	0.385	0.385	0.186	0.360	0.360	0.360

[Data Availability Statement for this Work]

Research data are not available at this time.