Abstract
The emphasis on fairness in predictive healthcare modeling has increased in popularity as an approach for overcoming biases in automated decision-making systems. The aim is to guarantee that sensitive characteristics like gender, race, and ethnicity do not influence prediction outputs. Numerous algorithmic strategies have been proposed to reduce bias in prediction results, mitigate prejudice toward minority groups and promote prediction fairness. The goal of these strategies is to ensure that model prediction performance does not exhibit significant disparity among sensitive groups. In this study, we propose a novel fairness-achieving scheme based on multitask learning, which fundamentally differs from conventional fairness-achieving techniques, including altering data distributions and constraint optimization through regularizing fairness metrics or tampering with prediction outcomes. By dividing predictions on different sub-populations into separate tasks, we view the fairness problem as a task-balancing problem. To ensure fairness during the model-training process, we suggest a novel dynamic re-weighting approach. Fairness is achieved by dynamically modifying the gradients of various prediction tasks during neural network back-propagation, and this novel technique applies to a wide range of fairness criteria. We conduct tests on a real-world use case to predict sepsis patients’ mortality risk. Our approach satisfies that it can reduce the disparity between subgroups by 98% while only losing less than 4% of prediction accuracy.
Keywords: Fairness, Healthcare predictive modeling, Multi-task learning
1. Introduction
Healthcare professionals and policymakers recognize the importance of fairness in healthcare, often defining it as a state, condition, or quality of being fair, just, or free from bias or injustice in providing healthcare services. In recent years, there has been growing interest in ensuring that health policies and systems are designed to achieve good outcomes and be fair and equitable [1]. Fairness in healthcare requires addressing health disparities and reducing inequities in access to care and health outcomes [2]. This requires targeting policies and interventions toward underserved populations, addressing social determinants of health [3], and ensuring that patients receive appropriate and effective care tailored to their needs and preferences [4]. Additionally, the importance of model fairness and data science in healthcare has gained recognition, particularly in ensuring that risk prediction models or automated treatment planning remain fair and efficient for all subpopulations [5].
Predictive models using machine learning or deep learning approaches have achieved great success over the years in healthcare. Recent studies have concentrated on developing machine learning interpretability methods [6] and identifying biases in machine learning models [7]. However, the issue of unfairness in predictive models has been overlooked for many years. Researchers now recognize that decision-making based on machine learning models can result in unfair outcomes and perpetuate existing societal biases [8]. Therefore, developing models that are not only accurate but also objective and fair has become crucial [9]. Several factors can contribute to a machine learning model’s unfairness. Predictive models typically focus on optimizing accuracy rather than fairness, which can lead to biases against certain groups. Bias in datasets or models can also cause unfairness in machine learning models [10]. Machine learning models can reinforce pre-existing unfairness in datasets. For example, suppose specific sub-populations are underrepresented in a healthcare dataset. In that case, the predictive models may perform less accurately for these groups than the dominant subgroup when predicting a particular disease due to a lack of training samples.
The classic fairness-achieving methods in machine learning can be broadly classified into three categories: pre-processing, in-processing, and post-processing methods [9,11]. Pre-processing involves cleaning, transforming, and preparing data before feeding it into the machine learning model, with typical methods including relabeling, generation, and fair representation [12]. In-processing incorporates fairness constraints or objectives directly into the machine learning model’s training process, with regularization techniques and adversarial training being two commonly used approaches. Lastly, post-processing applies a fairness correction technique after the model has made predictions to adjust the outputs for greater equity [13,14]. Each of these categories has its strengths and limitations, and the choice of method depends on the specific use case and data being analyzed. Pre-processing is versatile but limited by the information present in the data, while in-processing is more complex and computationally expensive but offers more direct control over the model’s behavior. Post-processing is typically easier to implement but may not be as effective as in-processing in addressing the root causes of bias in the data or model.
In this work, we aim to propose a fairness-achieving predictive model using in-processing methods. Our goal is to achieve group fairness by mitigating bias concerning protected sensitive attributes such as gender, race, and ethnicity. Instead of using a constrained optimization approach by incorporating fairness constraints as additional regularization terms in the optimization objective function, we propose a new fairness-achieving method based on multitask learning [15]. The key observation is that balancing performances among subgroups is similar to the task balancing problem in multitask learning. This unique perspective of viewing the fairness problem makes our approach fundamentally different from the majority of in-processing methods. Based on this unique finding, we propose a dynamic re-weighting scheme that monitors the unfairness across subgroups during each epoch of the model training process and dynamically adjusts the attention weight on each task. The scheme has two main benefits. First, fairness is optimized implicitly during model training while the model is optimized for prediction accuracy. This does not require formulating fairness constraints into the loss function, which may induce cost on the utility, i.e. performance loss incurred due to adding additional constraints to the optimization problem [16]. Second, instead of directly optimizing fairness metrics in the objective function, we use them to adjust the gradients of tasks. This allows us to optimize a wide variety of fairness metrics without concerns about the non-differentiable nature of the fairness metric formulation. Moreover, the above scheme provides a mechanism that directly optimizes the fairness metric of interest, in contrast to the traditional constraint optimization approach, which only optimizes discrepancies in loss functions among subgroups but is not directly related to the fairness metric of interest (e.g., demographic parity, equalized odds, etc.).
We validate the proposed model’s performance on a mortality risk prediction problem for in-hospital sepsis patients. The patients’ data come from a local academic medical center, and we select nearly 10,000 patients’ three-and-a-half-year medical history data. We demonstrate that the baseline models (without explicitly enforcing predictive fairness) can embed large performance discrepancies among different subgroups. Experimentally, our model achieves predictive fairness with a relatively small sacrifice in accuracy loss compared to traditional methods. To summarize, our contributions include:
A dynamic weighting scheme based on multi-task learning to achieve prediction model fairness
An approach that allows optimizing the specific fairness metric of interest directly
A fairness-achieving method that does not limit by the non-differentiable nature of the fairness metric
The rest of the paper is organized as follows. Section 2 will summarize the related works of bias mitigation methods in healthcare. In Section 3, we will introduce the prediction encoder–decoder model and explain the two main contributions. Section 4 will discuss our data source, data pre-processing, experiment settings, and the comparison study results. Section 5 will conclude this study and discuss a few open questions in Section 6.
2. Related works
Fairness-achieving methods in machine learning can generally be classified into three categories: data pre-processing, in-processing, and post-processing [17]. Pre-processing methods focus on removing discrimination to enhance the training set’s quality before learning a classifier. Correlation Remover is another pre-processing technique that aims to reduce the correlation between sensitive attributes and the target variable in the input data [18]. Jiang et al. demonstrated that training machine learning models on re-weighted datasets could lead to unbiased machine learning classifiers [19]. Kilbertus et al. proposed a solution to improve fairness and utility in situations where ground truth labels depend on specific decisions. They shifted the focus in fair machine learning from “learning to predict” to “learning to decide”, which involves learning to decide with exploring policies while considering fairness constraints and understanding the impact of decisions on future data collection [20]. Xu et al. proposed a fairness-aware generative adversarial network to mitigate discrimination in the training data [21]. Oneto et al. proposed a pre-processing method similar to our work, where they also identified the similarity between the fairness-achieving problem and multi-task learning. Their method differs from ours using low-rank matrix factorization to discover task similarities and encourage shared fair representation across tasks [22]. Tan et al. observed that existing representation methods are model-agnostic, which can generate sub-optimal predictions in terms of both fairness and accuracy. They proposed a model-aware pre-processing method by learning a fair representation of the dataset [23].
Post-processing methods focus on calibrating model predictions to achieve fairness, such as calibrated equalized odds [24]. Noriega-Campero et al. also proposed a calibration method, suggesting that by jointly considering information collection, inference, and decision-making processes, automated decision systems can be designed to more flexibly optimize social objectives, including fairness, accuracy, efficiency, and privacy [25]. Post-processing works well with black-box models where the training data and learning models cannot be modified, but balancing accuracy and fairness can be relatively challenging [17]. Iosifidis et al. proposed a fairness-aware ensemble framework that combines pre-and post-processing steps (generating balanced training samples and shifting the decision boundary) to achieve fairness [26].
In-processing is the area where most works in the literature fall, which involves adding regularization terms and constraints to the overall objective function and fairness metric [27]. Agarwal introduced two in-processing techniques: grid search and exponentiated gradient reduction. Grid search is an approach used to find hyper-parameters by generating a sequence of relabeling and reweightings and training a predictor to find the one that maximumly minimizes the disparity between subgroups. Exponentiated gradient reduction is a fairness-aware algorithm that minimizes subgroup disparities by updating the classifiers’ weights using an exponentiated gradient descent approach [28]. Demographic parity loss adds a fairness constraint to promote different group’s average prediction probability be the same. Chuang and Mroueh propose a data augmentation strategy to regularize the prediction models on paths of interpolated samples to achieve fairness [29]. Ding et al. proposed a fair machine learning framework for liver transplant graft failure prediction, utilizing knowledge distillation and a two-step debiasing method to enhance fairness and accuracy [30]. Build on this work, they proposed another model leveraging multi-task learning and tree distillation to effectively analyze post-transplant causes of death, assisting in clinical decision-making and organ allocation [31]. Liu and Avci incorporated prior knowledge in the model building when integrating feature attributions [32]. Ross et al. penalized the gradients of a neural network using a generalization of the right for the right reasons based on user explanations to train models [33]. Kim et al. proposed a new notion of fairness called metric multifairness, which is achieved by querying an arbitrary metric a bounded number of times. This approach guarantees that similar sub-populations are treated fairly [34]. Another study applied transfer learning and domain adaptation when the protected attributes were unavailable in either source or targeted dataset [35]. A recent study using TabTransformer in a multitask setting achieved promising results in task balancing and fairness-achieving [36]. This approach, similar to ours in leveraging multitask learning for fairness, highlights the versatility of such methods in addressing fairness objectives. Traditional constrained optimization approaches either achieve fairness by penalizing the loss function value discrepancy between different subgroups or by directly introducing the group-wise difference in terms of certain fairness metrics as a regularization term in the loss function to penalize it [37]. The former can be seen as an indirect fairness-achieving method that minimizes the difference in the loss function value but does not guarantee to minimize the real fairness metrics such as equalized odds, equal opportunity, etc. The latter methods are subject to the problem that most fairness metrics are non-convex, non-differentiable functions that will hinder back-propagation in neural network training. Recent works focused on studying transformation methods for commonly used fairness metrics to have such properties, for example, by using the proxy-Lagrangian formulation and searching for approximately optimal and feasible solutions [37]. However, such methods usually require strategic design (by using approximate functions [38,39]) and often sacrifice optimization accuracy, and sometimes the optimization may not even converge due to not having a stationary point.
3. Methods
Multi-task learning has demonstrated success in predicting multiple targets simultaneously. It is particularly effective when tasks are correlated, as multi-task models often outperform single-task models focusing on each task individually. One common approach is hard parameter sharing, which shares hidden layers among all tasks while maintaining task-specific output layers. This approach aims to reduce overfitting and storage costs while improving prediction accuracy [40]. This study uses multi-task learning to achieve prediction fairness among different subgroups. Tasks are defined based on sensitive attributes (such as gender, race, and ethnicity), with each task representing a protected subgroup. We aim to optimize binary cross-entropy loss and balance tasks (subgroups) to achieve comparable predictive performance among them.
3.1. The encoder–decoder multi-task learning model
We started proposing a novel multi-modal encoder–decoder deep learning model for sepsis mortality prediction. The proposed model adopted an encoder–decoder structure and took multi-modal medical data as input. Similar neural network structures have shown great potential in learning from multi-modal longitudinal data and demonstrated impressive performance in tasks such as COVID-19 risk prediction [41] and Multiple Sclerosis disease severity classification [42]. The dual-attention mechanism incorporated into the proposed neural network framework effectively handles EHR databases with multiple tables as input and leverages attention to improve prediction performance and interpretability of results. The uniqueness of the model is its attention mechanism for handling heterogeneous and irregularly sample temporal clinical data.
The model takes the input of data tables, each containing a patient’s medical data history of a certain modality, such as lab tests, treatments, vital sign observations, diagnosis, etc. The rationale behind dividing a patient’s entire structured EHR data into separate homogeneous tables is to enable the encoder neural network to learn distinct patterns from different modalities using separate neural networks. For a patient , each table takes a matrix format of size -by-, where corresponds to the time points in the patient’s observation history (e.g., hospital visits) and denotes the number of features (e.g., the number of lab tests). It is worth noting that the observational variables in each table with features are shared among all patients and remain consistent across different patients.
Encoder.
The encoder network consists of multiple channels, each processing one type of table (modality) and generating a feature map for each patient. Each channel contains a series of stacked 1D convolution layers with the Rectified Linear Unit Activation (ReLU) layers and Random Dropout Layers. The encoder network employs an attention mechanism that learns to place different emphasis on different time points of time series data of the patient and generates a weighted feature map for each type of table. Ultimately, feature maps from different channels are concatenated as the input to the decoder network, and different channels share similar structures with different sizes.
Specifically, the th table of patient ’s input data will go through the encoder channel specified as follows,
| (1) |
| (2) |
where is a -length vector, is the number of repetitions of the layers (the last layer does not go through Dropout and ReLU functions), and is the feature map vector of length generated, which can be seen as a condensed representation of the original data matrix , see Fig. 1.
Fig. 1.
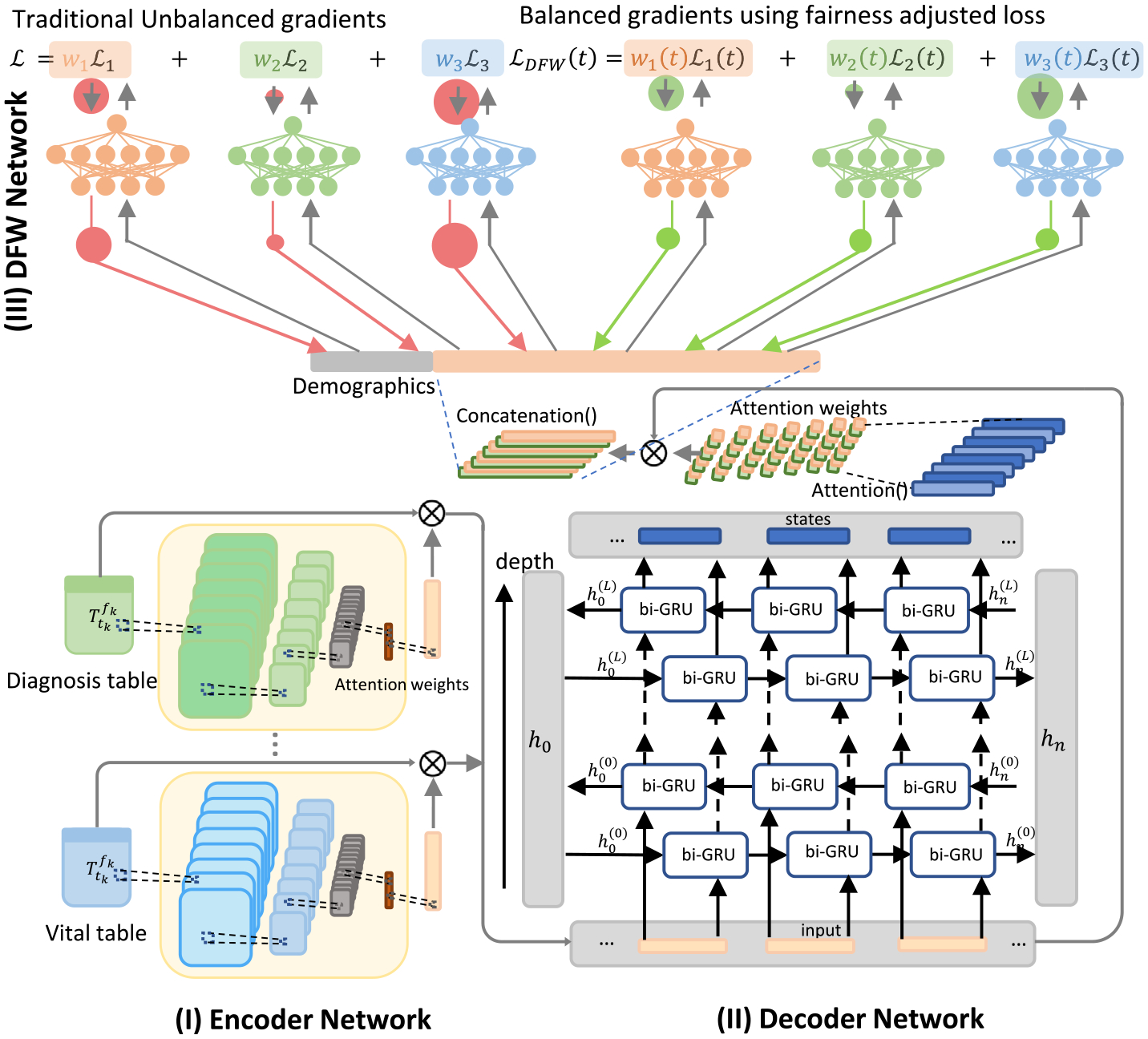
The proposed model structure, consists of (I) an Encoder Network, (II) a Decoder Network, and (III) the DFW Network.
Decoder.
The decoder network takes the format of a bi-directional GRU (Gated Recurrent Unit) network. The feature map outputs from all channels will be zero-padded into the same length (maximal length ) and stacked as a regular matrix to be fed into the Bi-GRU network,
| (3) |
The matrix will go through the decoder bi-directional GRU network followed by a second attention module, specifically
| (4) |
| (5) |
| (6) |
where is a matrix containing state vectors and has shape -by- is the hidden size of the GRU network (2 comes from the bi-direction network). The matrix goes through an attention layer specified by a 1D CNN neural network and generates an attention weight matrix . The attention matrix is multiplied by the state matrix, flattened, and concatenated with the demographics vector . Vector is the final embedding vector of patient , which embeds all medical history information of all modalities.
Suppose the sensitive attribute is denoted as , and a patient belongs to any of the subgroups, for each subgroup , we create a separate prediction head which is a multiple perceptron layer (MLP) with multiple hidden layers. The vector , depends on which subgroup the patient belongs to, will be fed through the corresponding prediction head to predict the final label
| (7) |
where is the predicted risk probability for patient .
3.2. Dynamic re-weighting method
To achieve fairness among different tasks (groups), we propose the idea of task prioritization based on the model task-specific prediction performance. The fairness evaluation metrics (demographic parity, equalized odds, etc.) are evaluated on each subgroup and will be used to re-weighting the gradients during back-propagation for each task.
For multitask loss function, we introduce a dynamic fairness weighting factor dynamically adjust the weight on task at epoch , and the neural network optimizes the following Dynamic Fairness re-Weighted (DFW) loss,
| (8) |
where is the loss function of task .
For the dynamic weight function , we design it to achieve the following purposes: (1) to ensure the gradient for different tasks on the same scale during backpropagation, therefore, the neural network has equal learning speed on each task; (2) to adjust the weight on each task dynamically based on the prediction performance of each task.
Task-wise gradient.
Let be the weight matrix of the last shared layer of the proposed neural network. We define
| (9) |
to be gradient norm of task ’s loss with respect to the weight matrix at epoch , and we use
| (10) |
to denote the epoch-’s average gradient norm.
Task-wise performance.
Let be the task-’s prediction performance metric at epoch . The function is directly related to the model’s fairness, whose format can be easily determined depending on the specific fairness notion of interest, see Table 1. We define
| (11) |
which is the distance of task-’s prediction performance relative to the average performance across all tasks.
Table 1.
The format of function depends on the fairness goals. : predicted risk; : real value.
| Fairness goal | |
|---|---|
| Statistical parity | |
| Equal recall/Equal opportunity | |
| Equal accuracy | |
| Predictive parity/Equal precision | |
| Predictive equality | |
| Equal AUROC | |
| Equal f1-measure |
The proposed dynamic re-weighting scheme achieves fairness by adjusting the magnitudes of each task’s gradient based on the previous training epoch’s performance, specifically, we adjust the task-specific gradient using the following formula
| (12) |
where is a hyper-parameter. Eq. (12) says the gradients of all tasks at training epoch are dynamically balanced according to their performance at training epoch . If a task’s performance is much better than the average performance, measured by , we would like to underweight the neural network’s attention on this task and focus on the other tasks, and vice versa. Table 2 provides an example where the majority of the task’s function falls near some value (0.1) and the others (monitory) tasks’ function values (0.9) deviate from it. The different values of can adjust the ratios of the gradients for tasks 1–9 and task 10 to let the network decide how much attention should be put onto each task.
Table 2.
An example of of different tasks and the dynamic weight enforced on each task’s gradient. At epoch for tasks 1–9 and 0.9 for task 10. 1) , the ratio of the weight (on task 1–9 vs on task 10) is 1.14:1; 2) , the ratio is 1.96:1; 3) , the ratio is 3.85:1; 4) , the ratio is 57:1.
| Task 1 | Task 2 | Task 3 | … | Task 9 | Task 10 | ||||
|---|---|---|---|---|---|---|---|---|---|
| 0.1 | 0.1 | 0.1 | … | 0.1 | 0.9 | 0.18 | −0.08 | 0.72 |
3.3. Fairness metrics
Model bias and fairness can be measured in a wide variety of metrics. Certain metrics can be more important than others, depending on the specific application and the optimization problem. Our fairness-achieving method is general and can be applied to a wide range of fairness metrics. In this study, we focus on the fairness metrics widely used to evaluate the healthcare predictive model’s fairness, including but not limited to equal accuracy, predictive parity, predictive equality, equal true negative rate, equal false negative rate, and equal AUROC. Their definitions are as follows ( : prediction; : true label; : sensitive attribute),
Equal Accuracy:
Equal Recall:
Equal False Positive Rate (FPR):
Equal True Negative Rate (TNR):
Equal Negative Predictive Value (NPV):
Predictive Parity (Equal Precision, Positive predictive value (PPV)):
Predictive Equality (Equal False Negative Rate):
Equal AUROC:
4. Experiments
4.1. Data structure
We collected a large cohort of 17,197 sepsis patients from the UTHealth teaching hospital between January 2018 and June 2021. The selected patients included only those who were admitted to the hospital. To test the prediction accuracy of the proposed framework, we aimed to predict patient mortality 72 h ahead. For deceased patients, we used patients’ temporal data from hospital admission until 72 h before death. For the remaining patients (cured and discharged home), all temporal data from admission to discharge were used. Consequently, we filtered out patients with a hospital stay shorter than 72 h. The final cohort included 9353 patients with 2348 mortality cases. Fig. 2 shows the hospital stay length histogram of the patient cohort. Table 3 demonstrates the statistics of patients’ demographic information.
Fig. 2.
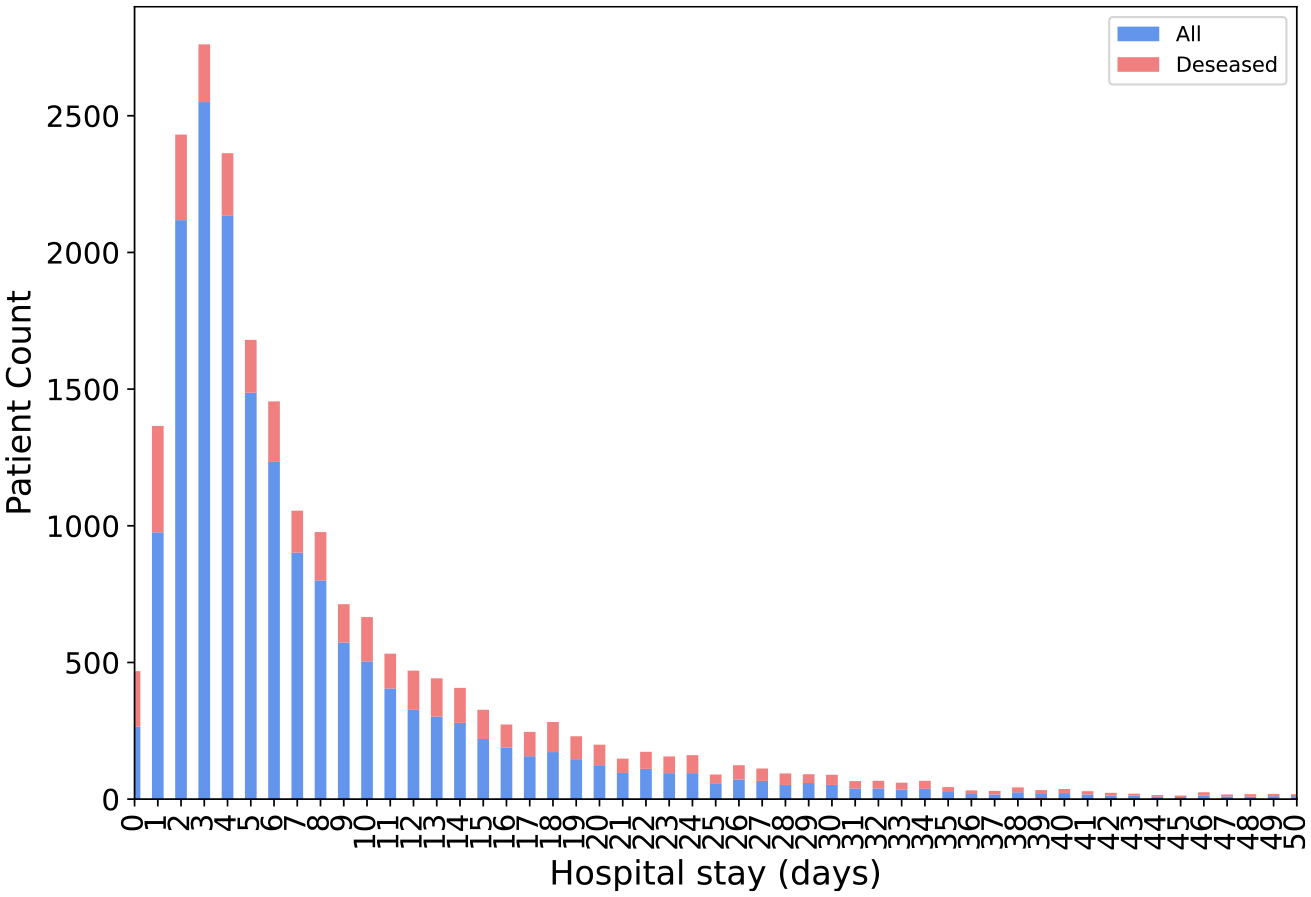
The distribution of all patients’ length of hospital stay (in days).
Table 3.
Patient demographic information is presented in the table, along with chi-squared test p-values that test the independence between the sensitive attribute and mortality.
| Sensitive attributes | Sepsis mortality | Number of patients (% of all patients) | Mortality rate | P values | |
|---|---|---|---|---|---|
| Total | – | 2,348 | 9,353 (100%) | 25.10% | – |
| Gender | Female | 1,002 | 4,282 (45.78%) | 23.40% | |
| Male | 1,346 | 5,070 (54.21%) | 26.55% | 0.0005 | |
| African American | 373 | 1,486 (15.89%) | 25.10% | ||
| Race | Asian | 66 | 217 (2.32%) | 30.41% | |
| Other | 964 | 3,549 (37.95%) | 27.16% | ||
| White | 649 | 2,812 (30.07%) | 23.08% | 0.0077 | |
| Ethnicity | Non-Hispanic | 1,476 | 5,642 (60.32%) | 26.16% | |
| Hispanic | 362 | 1,596 (17.06%) | 22.68% | 0.0008 | |
| Age | <30 | 40 | 844 (9.02%) | 4.74% | |
| 30–45 | 148 | 1,693 (18.10%) | 8.74% | ||
| 46–55 | 228 | 1,483 (15.86%) | 15.37% | ||
| 56–65 | 439 | 1,867 (19.96%) | 23.51% | ||
| 66–75 | 686 | 1,869 (19.98%) | 36.70% | ||
| >75 | 804 | 1,594 (17.04%) | 50.44% | <.0001 |
Patient’s longitudinal EHR data, including laboratory tests, vital sign observations, medication prescriptions, and demographic information, are used as model inputs. The specific feature names are provided in Table 4.
Table 4.
Features used in the predictive model.
| Features | Names |
|---|---|
| Laboratory Tests | Point of care partial pressure of oxygen, Hematocrit test, Mean Corpuscular Hemoglobin Concentration, Mean Corpuscular Volume, Mean platelet volume, Platelet, Red blood cell, Albumin/Globulin Ratio, Albumin Level, Alkaline Phosphatase, CO2, Glucose Level, Potassium Level, Total Protein, Eosinophils, Lymphocytes, Monocytes, Segmental neutrophils, Magnesium Level, Partial Thromboplastin Time, Prothrombin Time, Ionized Calcium Western Blot Test, Basophils, White Blood Count, International Normalized Ratio, Eosinophils, Monocytes, Neutrophils, Hemoglobin test, Mean corpuscular hemoglobin, Red Cell Distribution Width, Alanine Aminotransferase, Aspartate Transferase, Total Bilirubin, Globulin, Anion Gap, Blood urea nitrogen/Creatinine ratio, Blood urea nitrogen, Calcium Level, Chloride Level, Creatinine Level, Sodium Level, Estimated glomerular filtration rate, Phosphorus, Lactic Acid Level, Glucose Point-of-Care, Point of care Source, Point of care pH |
| Vitals Sign Observations | Apical Heart Rate, DCP Generic Code, SpO2 percent, Respiratory Rate, Systolic Blood Pressure, Mean Arterial Pressure, Administration Information, Diastolic Blood Pressure |
| Medicine Prescriptions | Cefepime + sodium chloride, Docusate sodium, Ocular lubricant ointment, Senna, Metronidazole, Acetaminophen, Furosemide, Albuterol ipratropium, Heparin, Insulin, Insulin Lispro Injection, Metoclopramide, Pantoprazole, Potassium chloride, Sodium chloride, Pantoprazole, Polyethylene glycol, Sodium chloride, aspirin, Enoxaparin, Famotidine, Atorvastatin, Docusate sodium, Lactated Ringers, Budesonide, Chlorhexidine, Sodium chloride, Ascorbic acid, Neutral protamine Hagedorn insulin, Meropenem + sodium chloride, Propofol, Sodium chloride, Acetaminophen, Ondansetron, Tramadol, Famotidine, Methylprednisolone, Metoprolol tartrate, Midodrine, Gabapentin, Piperacillin-tazobactam+ sodium chloride, Potassium chloride, Zinc sulfate, Acetaminophen-hydrocodone, Cefepime + water, Sterile, Benzonatate, Fentanyl, Regular insulin, Beneprotein, Dexmedetomidine + sodium chloride |
For each patient, the lab tests, vital signs, and medications are organized into three separate tables to be fed into the neural network. The lab test results and vital sign observations are represented as float number, and medications are represented as 0/1 to represent whether patient takes this medication. The rows of each table represent time stamps, and columns correspond to the features. It is important to note that for each type of table, all patients use the same set of features, ensuring the same number of columns across all patients. However, the number of rows in the tables for different patients may vary depending on the number of measurements performed during their hospital stay, as shown in Fig. 2. As discussed in the method section, the neural network structure does not rely on the row number of the input data, as it employs an attention mechanism to learn weights for different time stamps, mapping inputs of varying sizes to fixed-length vectors.
4.2. Experiment setting
We conducted an experimental study on a cohort of 9353 sepsis patients. The prediction goal was set to predict in-hospital patients’ risk of mortality 72 h ahead while ensuring the model’s prediction fairness among different subgroups. We tested the model’s performance on different subgroups defined by the sensitive attribute (gender, race, and ethnicity).
The hyper-parameters for the proposed model were chosen as follows. For the encoder network, there are three channels, each containing a two-layer CNN network. The specific network parameters are shown in Table 5. The decoder network is a four-layer bidirectional GRU network with a hidden state size of 512. We split the entire dataset into 70% training, 15% validation, and 15% holdout test dataset. The model was trained on the training set for a pre-specified number of epochs, and the best model was selected based on its performance on the validation set. The final performance of the model was reported on the test dataset.
Table 5.
Encoder network parameters (I: input channel size, O: output channel size, K: kernel size, S: stride size, P: padding size, R: (dropout) rate, Avg.: average pooling.).
| Conv1d | ReLU + Dropout | Conv1d | Dropout | Pooling | |
|---|---|---|---|---|---|
| Channel 1 (Lab tests) | I: 1, O: 8, K: 5, S: 2, P: 0 | R: 0.3 | I: 8, O: 1, K: 3, S: 1, P: 0 | R: 0.3 | Avg. |
| Channel 2 (Vital Sign Observ.) | I: 1, O: 8, K: 2, S: 2, P: 1 | R: 0.3 | I: 8, O: 1, K: 2, S: 2, P: 1 | R: 0.3 | Avg. |
| Channel 3 (Medication) | I: 1, O: 8, K: 3, S: 2, P: 0 | R: 0.3 | I: 8, O: 1, K: 3, S: 2, P: 0 | R: 0.3 | Avg. |
We conducted three sets of experiments to answer our research questions from three aspects: (I) We want to see whether the proposed fairness-achieving method works. We monitored the performance metric disparity (related to the chosen fairness notion) among different subgroups to see whether they decreased as the training epoch increased, see Fig. 3; (II) Using our proposed method, whether the model’s performance on the test set demonstrated fairness improvements compared to the baseline model (without using the method), i.e. ablation study, see Fig. 4 and Table 6; (III) Since model fairness is usually achieved with a trade-off in prediction accuracy, we assessed the loss in prediction accuracy for the proposed model, and we compare our fairness-achieving method with several state-of-the-art methods, see Table 7.
Fig. 3.
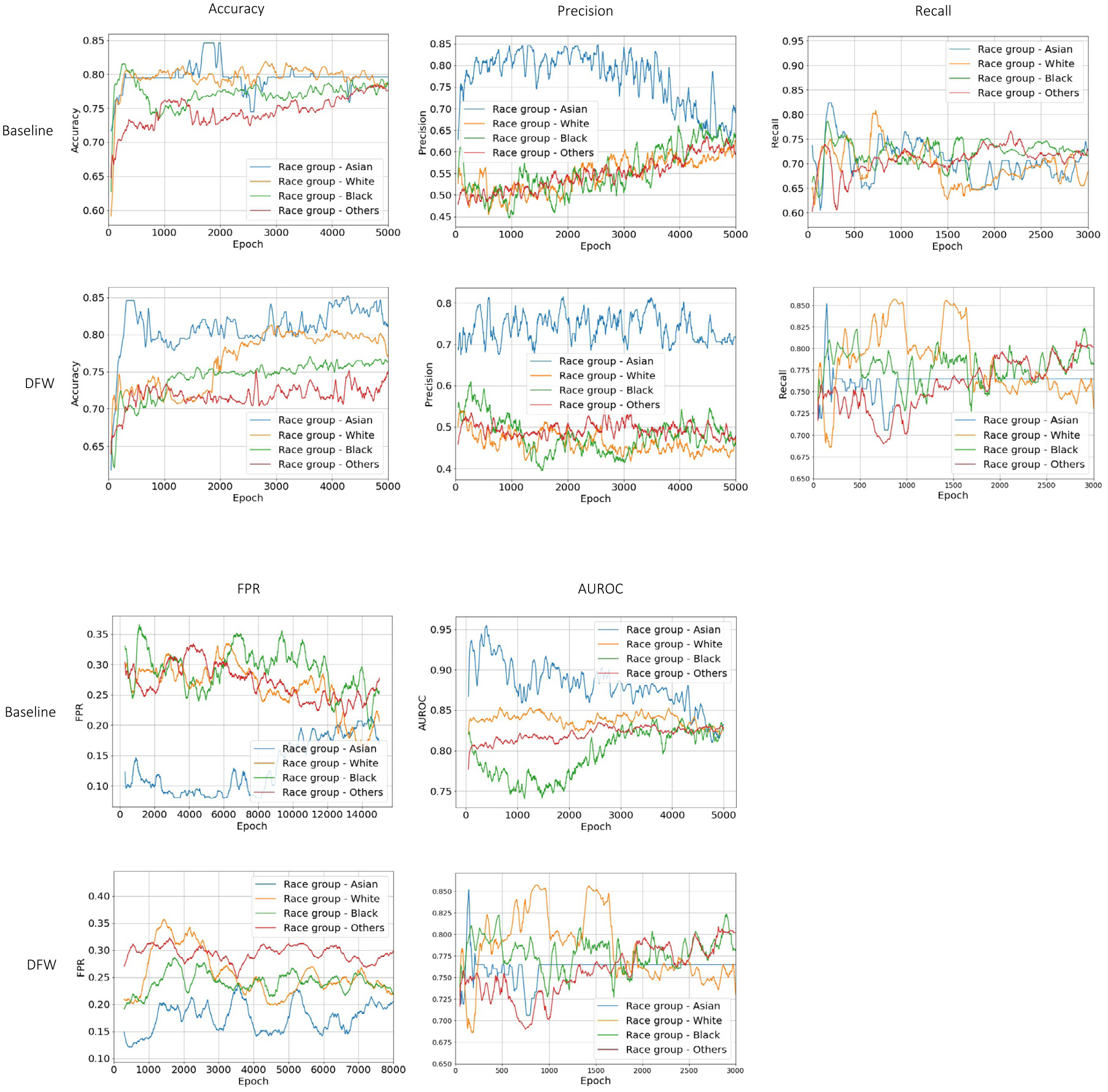
Model fairness performance as training epoch. The figures are examples of the experiment setting when the sensitive attribute is race. DFW: baseline model with the fairness-achieving method. The figure shows performances on the validation set when optimizing for: Equal Accuracy, Predictive Parity (Precision), Recall, FPR, and AUROC, respectively. X-axis: training epoch, Y-axis: the fairness metric being optimized in the DFW method.
Fig. 4.
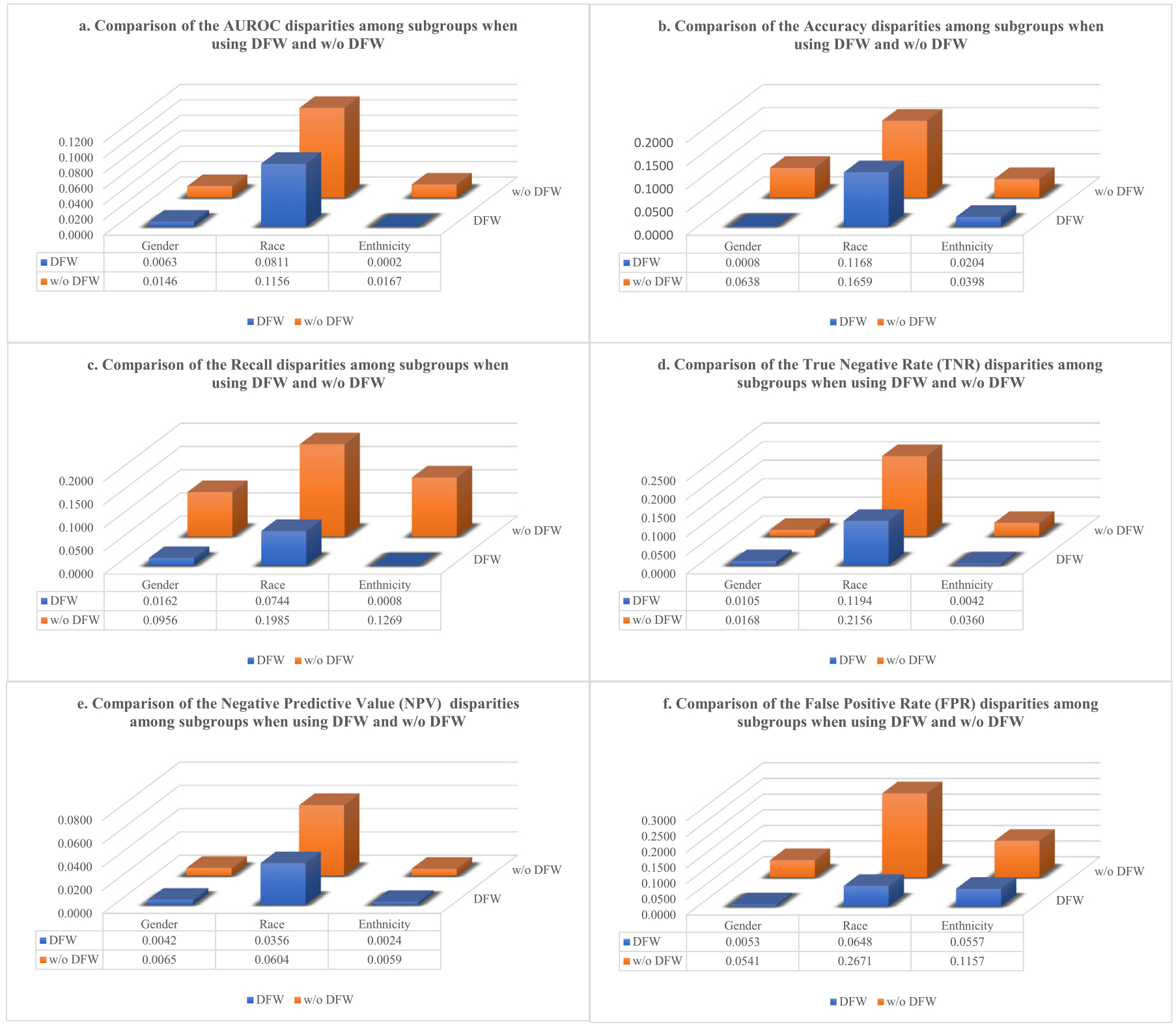
The fairness metric disparity comparison between the proposed model (DFW) and the baseline (w/o DFW) when setting different sensitive attributes, e.g. gender, race, and ethnicity, and optimizing for different fairness metrics: a. equal AUROC, b. equal accuracy, c. equal recall, d. equal TNR (true negative rate), e. equal NPV (negative predictive value), and f. equal FPR (false positive rate).
Table 6.
Comparison of the proposed model with the baseline model on their performance on the test dataset. Each row and column combination corresponds to an experiment setting. DFW: the proposed dynamic fairness re-weighting method. Each row: specifies the definition of the sensitive attribute; Each column: specifies the fairness metric to achieve. The disparity is defined as the largest difference in the fairness metric among different subgroups. A smaller disparity is better (bold).
| DFW | w/o DFW | DFW | w/o DFW | DFW | w/o DFW | DFW | w/o DFW | DFW | w/o DFW | DFW | w/o DFW | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AUROC | Accuracy | Recall | True negative rate (TNR) | Negative predictive value (NPV) | False positive rate (FPR) | |||||||
| Ethnicity | ||||||||||||
| Hispanic | 0.8347 | 0.8573 | 0.7859 | 0.7972 | 0.7632 | 0.8816 | 0.7670 | 0.7885 | 0.9127 | 0.9198 | 0.1649 | 0.1254 |
| Non_Hispanic | 0.8345 | 0.8740 | 0.7655 | 0.8370 | 0.7640 | 0.7547 | 0.7628 | 0.8245 | 0.9151 | 0.9139 | 0.2206 | 0.2411 |
| Disparity(Max-Min) | 0.0002 | 0.0167 | 0.0204 | 0.0398 | 0.0008 | 0.1269 | 0.0042 | 0.0360 | 0.0024 | 0.0059 | 0.0557 | 0.1157 |
| Gender | ||||||||||||
| Female | 0.8109 | 0.8718 | 0.7397 | 0.8089 | 0.7174 | 0.8000 | 0.7428 | 0.7945 | 0.9092 | 0.9251 | 0.2270 | 0.2687 |
| Male | 0.8172 | 0.8572 | 0.7389 | 0.7451 | 0.7336 | 0.7044 | 0.7323 | 0.8113 | 0.9050 | 0.9186 | 0.2217 | 0.2146 |
| Disparity(Max-Min) | 0.0063 | 0.0146 | 0.0008 | 0.0638 | 0.0162 | 0.0956 | 0.0105 | 0.0168 | 0.0042 | 0.0065 | 0.0053 | 0.0541 |
| Race | ||||||||||||
| Asian | 0.8667 | 0.9444 | 0.8611 | 0.9167 | 0.8333 | 0.6667 | 0.8667 | 0.9667 | 0.9310 | 0.9667 | 0.2333 | 0.0333 |
| White | 0.8074 | 0.8288 | 0.7513 | 0.7513 | 0.7589 | 0.8652 | 0.7860 | 0.7511 | 0.9326 | 0.9063 | 0.2249 | 0.1987 |
| African | 0.7856 | 0.8703 | 0.7443 | 0.7508 | 0.8023 | 0.7558 | 0.7534 | 0.8117 | 0.8970 | 0.9167 | 0.2152 | 0.3004 |
| Other | 0.8518 | 0.8601 | 0.7813 | 0.8140 | 0.8155 | 0.8598 | 0.7473 | 0.8159 | 0.9314 | 0.9351 | 0.1685 | 0.1998 |
| Disparity(Max-Min) | 0.0811 | 0.1156 | 0.1168 | 0.1659 | 0.0744 | 0.1985 | 0.1194 | 0.2156 | 0.0356 | 0.0604 | 0.0648 | 0.2671 |
Table 7.
Comparison of the performance of the proposed dynamic fairness re-weighting method (DFW) against three other effective methods applied to the XGBoost model: Grid Search (GS), Exponentiated Gradient Reduction (EGR), and Correlation Remover (CR) on the test dataset. Additionally, we compare the performance of DFW with our baseline model, which incorporates Demographic Parity Loss (DPL). Each row: specifies the definition of the sensitive attribute; Each column: specifies the fairness metric to achieve. The disparity is defined as the largest difference in the fairness metric among different subgroups. A smaller disparity is better (bold).
| GS | EGR | CR | DPL | DFW | GS | EGR | CR | DPL | DFW | GS | EGR | CR | DPL | DFW | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AUROC | Recall | Negative predictive value (NPV) | |||||||||||||
| Ethnicity | |||||||||||||||
| Hispanic | 0.8869 | 0.8264 | 0.8856 | 0.8424 | 0.8347 | 0.6604 | 0.6415 | 0.6604 | 0.8289 | 0.7632 | 0.9104 | 0.9073 | 0.9122 | 0.9350 | 0.9127 |
| Non-hispanic | 0.9125 | 0.8287 | 0.9120 | 0.8607 | 0.8345 | 0.6585 | 0.6690 | 0.6655 | 0.8294 | 0.7640 | 0.8929 | 0.8948 | 0.8943 | 0.9211 | 0.9151 |
| Disparity(Max-Min) | 0.0256 | 0.0023 | 0.0264 | 0.0183 | 0.0002 | 0.0019 | 0.0275 | 0.0051 | 0.0005 | 0.0008 | 0.0175 | 0.0125 | 0.0179 | 0.0139 | 0.0024 |
| Gender | |||||||||||||||
| Female | 0.9205 | 0.8592 | 0.9259 | 0.8549 | 0.8109 | 0.6987 | 0.6923 | 0.6859 | 0.7652 | 0.7174 | 0.9056 | 0.9028 | 0.9026 | 0.9261 | 0.9092 |
| Male | 0.9063 | 0.8205 | 0.8925 | 0.8396 | 0.8172 | 0.6087 | 0.6413 | 0.6467 | 0.7956 | 0.7336 | 0.8841 | 0.8920 | 0.8934 | 0.9179 | 0.9050 |
| Disparity(Max-Min) | 0.0142 | 0.0387 | 0.0334 | 0.0153 | 0.0063 | 0.0900 | 0.0510 | 0.0392 | 0.0304 | 0.0162 | 0.0215 | 0.0108 | 0.0092 | 0.0082 | 0.0042 |
| Race | |||||||||||||||
| Asian | 0.9394 | 0.9167 | 0.9646 | 0.9722 | 0.8667 | 0.7778 | 0.8889 | 0.8889 | 0.7889 | 0.8333 | 0.9130 | 0.9545 | 0.9524 | 0.9200 | 0.9310 |
| White | 0.8717 | 0.8301 | 0.8905 | 0.7905 | 0.8074 | 0.5532 | 0.5957 | 0.6277 | 0.6547 | 0.7589 | 0.8783 | 0.8869 | 0.8955 | 0.8490 | 0.9326 |
| African | 0.8918 | 0.8280 | 0.9169 | 0.7935 | 0.7856 | 0.5000 | 0.6071 | 0.6964 | 0.7194 | 0.8023 | 0.8519 | 0.9091 | 0.9012 | 0.8554 | 0.8970 |
| Other | 0.8889 | 0.8388 | 0.9015 | 0.8502 | 0.8518 | 0.5680 | 0.6748 | 0.6553 | 0.6878 | 0.8155 | 0.8455 | 0.8797 | 0.8737 | 0.8571 | 0.9314 |
| Disparity(Max-Min) | 0.0677 | 0.0887 | 0.0741 | 0.1817 | 0.0811 | 0.2778 | 0.2932 | 0.2612 | 0.1342 | 0.0744 | 0.0675 | 0.0748 | 0.0787 | 0.0710 | 0.0356 |
4.3. Results
Our experiments demonstrate that the proposed model achieves fairness across multiple fairness metrics with only a marginal sacrifice in accuracy. Fig. 3 displays the model’s training process when the sensitive attribute is race, which divides patients into four subgroups: White, Asian, Black, and Others. By aiming to achieve different fairness criteria (equal accuracy, predictive parity, equal recall, equal false positive rate, and equal AUROC), we use the proposed model (DFW) to minimize disparities for each of the above metrics among the four subgroups. After each training epoch , the model evaluates its performance in terms of the metric on different subgroups on the training set and adjusts the dynamic weight before each task’s loss accordingly at the current epoch . To show the proposed model indeed learns to minimize the metric gaps among different subgroups, Fig. 3 shows the evaluations of these metrics on the validation data. As seen in Fig. 3, the proposed methods encourage equal performance among different subgroups as the training proceeds, while the baseline model (without using the proposed fairness-achieving) does not demonstrate such performance.
Fig. 4 shows the fairness disparities of the proposed model compared to the baseline model on the test data. After the training process finishes, the model achieving the best equity on the validation dataset is chosen as the best model to be saved, which is true for both the proposed model (DFW) and the baseline model to keep the comparison fair. The figures in Fig. 4 show the saved model’s fairness performance on the test dataset under different experiment settings. The experiments were performed separately on three different sensitive attributes (gender, race, and ethnicity) when setting different fairness metrics to optimize (equal AUROC, equal accuracy, equal recall, equal TNR, equal NPV, and equal FPR). The disparity is defined as the largest absolute difference of a metric among different subgroups. As seen in the figure, the proposed method’s disparity across all metrics (color blue) has significantly decreased compared to the baseline model (color orange), exhibiting a large improvement in prediction fairness compared to the baseline model.
In Table 6, we compare the trade-off between prediction accuracy and fairness for our proposed method (DFW) and a baseline model without fairness enhancement (w/o DFW) in various experimental settings. The results are obtained by evaluating the best model on the test dataset. Each block entry represents the performance of the two models on a specific fairness metric under a particular sensitive attribute setting. For instance, when optimizing AUROC disparity between different ethnic groups (Hispanic vs. non-Hispanic), our model demonstrates a substantial improvement, achieving a much smaller disparity of 0.0002 compared to the baseline model’s 0.0167. While the proposed model enhances AUROC equality, there is a modest loss in AUROC values for both subgroups: a decrease of 0.0226 (from 0.8573 to 0.8347) for the Hispanic group and 0.0395 (from 0.8740 to 0.8345) for the non-Hispanic group. This sacrifice in AUROC values is acceptable as it results in a significant improvement in AUROC equality between the groups. Our model significantly reduces the AUROC difference by 98%, with less than a 4% loss in AUROC for the two groups.
We compare the proposed model (DFW) and four other effective baseline methods, including Grid Search (GS), Exponentiated Gradient Reduction (EGR), Correlation Remover (CR), and Demographic Parity Loss function (DPL). The first three algorithms are applied to the XGBoost predictive model and the last approach is applied to the same neural network structure of this work. In Table 7, each block entry indicates the performance of the five models on a specific fairness metric under the same sensitive attribute setting. For example, when aiming to achieve equal Recall among different race groups, our model significantly reduces the Recall disparity to 0.0744. In comparison, other effective models GS, EGR, CR, and DPL achieve disparities of 0.2778, 0.2932, 0.2612, and 0.1342, respectively. Additionally, our model outperforms the other four models in terms of Recall on subgroups (White, Black, and Other race), demonstrating our model is able to achieve much better fairness performance with less sacrifice on prediction accuracy. Regarding Recall performance on ethnicity, the DPL method outperforms our proposed model; however, we are closely following it. Similar to the AUROC performance on race, GS has the best performance, but our model is not far behind.
In summary, the proposed model achieves fairness among ethnicity, gender, and race subgroups while maintaining high prediction accuracy across all six evaluation metrics. This performance is not only superior to the baseline model without fairness enhancement (w/o DFW) but is also competitive with other effective models.
5. Conclusion
In this paper, we develop a fairness-achieving framework using multitasking learning by separating subgroups into different learning tasks. Our novel dynamic reweighting scheme achieves model fairness with less prediction accuracy sacrifice comparing traditional fairness-achieving methods. Our new approach, which does not require expressing the fairness metric in a differentiable function, provides a flexible mechanism to optimize fairness across various fairness metrics of practical interest in healthcare.
The proposed fairness enhancing technique is also adaptable for other problems, such as non-binary classification tasks, regression tasks, and ranking tasks. While the task of sepsis mortality risk prediction is interesting, it is not the only application this model can accommodate. In general, it is well-suited for a wide range of predictive modelings in healthcare where fairness is an essential consideration.
Compared to some other fairness-achieving methods that minimize loss discrepancies between different subgroups, our proposed model directly optimizes the specific fairness notion of interest. In contrast, these other methods represent an indirect approach that does not guarantee the exact fairness metric of interest. This limitation on the proposed method implies that two different fairness notions cannot be simultaneously optimized within the current framework, at least not with the existing design of the dynamic re-weighting formula. This challenge could potentially be addressed by adopting a more sophisticated design for the re-weighting function, incorporating multiple fairness notions in a weighted manner, thereby offering a more comprehensive fairness optimization solution.
6. Discussion
Fairness can be due to multiple reasons, and algorithmic fairness is just one aspect of it. In this study, we focus on achieving algorithmic fairness in predictive modeling tasks using a novel task-balancing idea. One promising future direction of this research is to investigate the interpretability of the proposed framework’s decision-making process, i.e., what causes the model to make unfair predictions. Explainable AI techniques can enhance the transparency and accountability of machine learning models and improve the trust and acceptance of their predictions by healthcare providers and patients. By knowing the reasons making the model makes unfair predictions, we can design better fairness-achieving approaches. Another research direction is evaluating the effectiveness and impact of the proposed framework in real-world healthcare settings. Evaluating the framework’s effectiveness in practice can help identify potential challenges and opportunities for improvement and ensure that the model’s predictions are trustworthy and acceptable to the end-users. The framework may be tested on different healthcare applications with varying levels of complexity and heterogeneity to assess its generalizability and scalability to other datasets.
Acknowledgments
XJ is CPRIT Scholar in Cancer Research (RR180012), and he was supported in part by Christopher Sarofim Family Professorship, UT Stars award, UTHealth startup, the National Institute of Health (NIH) under award number R01AG066749, R01AG066749-03S1, R01LM01 3712, and U01TR002062, and the National Science Foundation (NSF), United States #2124789. NZ is supported by the National Science Foundation (NSF), United States #1900990, #1939716, and #2239257.
Footnotes
CRediT authorship contribution statement
Can Li: Data analysis, Model development, Experiments, Writing – original draft. Sirui Ding: Experiments. Na Zou: Writing – review & editing. Xia Hu: Writing – review & editing. Xiaoqian Jiang: Writing – review & editing. Kai Zhang: Data curation, Conceptualization, Methodology, Model development, Writing – original draft, Supervision.
Declaration of competing interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- [1].Williams JS, Walker RJ, Egede LE, Achieving equity in an evolving healthcare system: opportunities and challenges, Am. J. Med. Sci 351 (1) (2016) 33–43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [2].Artiga S, Orgera K, Pham O, Disparities in Health and Health Care: Five Key Questions and Answers, Kaiser Family Foundation, 2020. [Google Scholar]
- [3].Williams DR, Costa MV, Odunlami AO, Mohammed SA, Moving upstream: how interventions that address the social determinants of health can improve health and reduce disparities, J. Public Health Manag. Pract 14 (6) (2008) S8–S17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [4].Parry C, Coleman EA, Smith JD, Frank J, Kramer AM, The care transitions intervention: a patient-centered approach to ensuring effective transfers between sites of geriatric care, Home Health Care Serv. Q 22 (3) (2003) 1–17. [DOI] [PubMed] [Google Scholar]
- [5].Obermeyer Z, Powers B, Vogeli C, Mullainathan S, Dissecting racial bias in an algorithm used to manage the health of populations, Science 366 (6464) (2019) 447–453. [DOI] [PubMed] [Google Scholar]
- [6].Linardatos P, Papastefanopoulos V, Kotsiantis S, Explainable AI: A review of machine learning interpretability methods, Entropy 23 (1) (2020) 18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [7].Lee NT, Resnick P, Barton G, Algorithmic Bias Detection and Mitigation: Best Practices and Policies to Reduce Consumer Harms, Vol. 2, Brookings Institute, Washington, DC, USA, 2019. [Google Scholar]
- [8].Veale M, Binns R, Fairer machine learning in the real world: Mitigating discrimination without collecting sensitive data, Big Data Soc 4 (2) (2017) 2053951717743530 [Google Scholar]
- [9].Pessach D, Shmueli E, A review on fairness in machine learning, ACM Comput. Surv 55 (3) (2022) 1–44. [Google Scholar]
- [10].Meng C, Trinh L, Xu N, Enouen J, Liu Y, Interpretability and fairness evaluation of deep learning models on MIMIC-IV dataset, Sci. Rep 12 (1) (2022) 7166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [11].Xu J, Xiao Y, Wang WH, Ning Y, Shenkman EA, Bian J, Wang F, Algorithmic fairness in computational medicine, EBioMedicine 84 (2022) 104250. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [12].Kim J-Y, Cho S-B, An information theoretic approach to reducing algorithmic bias for machine learning, Neurocomputing 500 (2022) 26–38. [Google Scholar]
- [13].Lohia PK, Ramamurthy KN, Bhide M, Saha D, Varshney KR, Puri R, Bias mitigation post-processing for individual and group fairness, in: Icassp 2019–2019 Ieee International Conference on Acoustics, Speech and Signal Processing, Icassp, IEEE, 2019, pp. 2847–2851. [Google Scholar]
- [14].Petersen F, Mukherjee D, Sun Y, Yurochkin M, Post-processing for individual fairness, Adv. Neural Inf. Process. Syst 34 (2021) 25944–25955. [Google Scholar]
- [15].Vandenhende S, Georgoulis S, Van Gansbeke W, Proesmans M, Dai D, Van Gool L, Multi-Task learning for dense prediction tasks: A survey, IEEE Trans. Pattern Anal. Mach. Intell 44 (7) (2022) 3614–3633. [DOI] [PubMed] [Google Scholar]
- [16].Bertsimas D, Farias VF, Trichakis N, The price of fairness, Oper. Res 59 (1) (2011) 17–31 [Google Scholar]
- [17].Mehrabi N, Morstatter F, Saxena N, Lerman K, Galstyan A, A survey on bias and fairness in machine learning, ACM Comput. Surv 54 (6) (2021) 1–35. [Google Scholar]
- [18].Preprocessing — Fairlearn 0.9.0.dev0 documentation, 2023, https://fairlearn.org/main/user_guide/mitigation/preprocessing.html. (Accessed 12 April 2023).
- [19].Jiang H, Nachum O, Identifying and correcting label bias in machine learning, in: International Conference on Artificial Intelligence and Statistics, PMLR, 2020, pp. 702–712. [Google Scholar]
- [20].Kilbertus N, Rodriguez MG, Schölkopf B, Muandet K, Valera I, Fair decisions despite imperfect predictions, in: International Conference on Artificial Intelligence and Statistics, PMLR, 2020, pp. 277–287. [Google Scholar]
- [21].Xu D, Yuan S, Zhang L, Wu X, Fairgan: Fairness-aware generative adversarial networks, in: 2018 IEEE International Conference on Big Data, Big Data, IEEE, 2018, pp. 570–575 [Google Scholar]
- [22].Oneto L, Doninini M, Elders A, Pontil M, Taking advantage of multitask learning for fair classification, in: Proceedings of the 2019 AAAI/ACM Conference on AI, Ethics, and Society, 2019, pp. 227–237. [Google Scholar]
- [23].Tan Z, Yeom S, Fredrikson M, Talwalkar A, Learning fair representations for kernel models, in: International Conference on Artificial Intelligence and Statistics, PMLR, 2020, pp. 155–166. [Google Scholar]
- [24].Pleiss G, Raghavan M, Wu F, Kleinberg J, Weinberger KQ, On fairness and calibration, Adv. Neural Inf. Process. Syst 30 (2017). [Google Scholar]
- [25].Noriega-Campero A, Bakker MA, Garcia-Bulle B, Pentland A, Active fairness in algorithmic decision making, in: Proceedings of the 2019 AAAI/ACM Conference on AI, Ethics, and Society, 2019, pp. 77–83. [Google Scholar]
- [26].Iosifidis V, Fetahu B, Ntoutsi E, Fae: A fairness-aware ensemble framework, in: 2019 IEEE International Conference on Big Data, Big Data, IEEE, 2019, pp. 1375–1380 [Google Scholar]
- [27].Du M, Yang F, Zou N, Hu X, Fairness in deep learning: A computational perspective, IEEE Intell. Syst 36 (4) (2021) 25–34. [Google Scholar]
- [28].Agarwal A, Beygelzimer A, Dudik M, Langford J, Wallach H, A reductions approach to fair classification, in: Dy J, Krause A (Eds.), Proceedings of the 35th International Conference on Machine Learning, in: Proceedings of Machine Learning Research, vol. 80, PMLR, 2018, pp. 60–69. [Google Scholar]
- [29].Chuang C-Y, Mroueh Y, Fair mixup: Fairness via interpolation, 2021, arXiv: 2103.06503 [Google Scholar]
- [30].Ding S, Tang R, Zha D, Zou N, Zhang K, Jiang X, Hu X, Fairly predicting graft failure in liver transplant for organ assigning, 2023, arXiv:2302.09400 [PMC free article] [PubMed] [Google Scholar]
- [31].Ding S, Tan Q, yuan Chang C, Zou N, Zhang K, Hoot NR, Jiang X, Hu X, Multi-task learning for post-transplant cause of death analysis: A case study on liver transplant, 2023, arXiv:2304.00012 [PMC free article] [PubMed] [Google Scholar]
- [32].Liu F, Avci B, Incorporating priors with feature attribution on text classification, 2019, arXiv:1906.08286 [Google Scholar]
- [33].Ross AS, Hughes MC, Doshi-Velez F, Right for the right reasons: Training differentiable models by constraining their explanations, 2017, arXiv:1703. 03717 [Google Scholar]
- [34].Kim M, Reingold O, Rothblum G, Fairness through computationally-bounded awareness, Adv. Neural Inf. Process. Syst 31 (2018). [Google Scholar]
- [35].Coston A, Ramamurthy KN, Wei D, Varshney KR, Speakman S, Mustahsan Z, Chakraborty S, Fair transfer learning with missing protected attributes, in: Proceedings of the 2019 AAAI/ACM Conference on AI, Ethics, and Society, AIES ‘19, Association for Computing Machinery, New York, NY, USA, 2019, pp. 91–98. [Google Scholar]
- [36].Li C, Jiang X, Zhang K, A transformer-based deep learning approach for fairly predicting post-liver transplant risk factors, 2023, arXiv:2304.02780 [DOI] [PMC free article] [PubMed] [Google Scholar]
- [37].Cotter A, Jiang H, Gupta MR, Wang S, Narayan T, You S, Sridharan K, Optimization with non-differentiable constraints with applications to fairness, recall, churn, and other goals, J. Mach. Learn. Res 20 (172) (2019) 1–59. [Google Scholar]
- [38].Goh G, Cotter A, Gupta M, Friedlander MP, Satisfying real-world goals with dataset constraints, Adv. Neural Inf. Process. Syst 29 (2016). [Google Scholar]
- [39].Gupta M, Bahri D, Cotter A, Canini K, Diminishing returns shape constraints for interpretability and regularization, Adv. Neural Inf. Process. Syst 31 (2018). [Google Scholar]
- [40].Zhang L, Yang Q, Liu X, Guan H, Rethinking hard-parameter sharing in multidomain learning, in: 2022 IEEE International Conference on Multimedia and Expo, ICME, IEEE, 2022, pp. 01–06. [Google Scholar]
- [41].Zhang K, Jiang X, Madadi M, Chen L, Savitz S, Shams S, DBNet: a novel deep learning framework for mechanical ventilation prediction using electronic health records, in: Proceedings of the 12th ACM Conference on Bioinformatics, Computational Biology, and Health Informatics, BCB ‘21, (Article 9) Association for Computing Machinery, New York, NY, USA, 2021, pp. 1–8. [Google Scholar]
- [42].Zhang K, Lincoln JA, Jiang X, Bernstam EV, Shams S, Predicting multiple sclerosis disease severity with multimodal deep neural networks, 2023, arXiv: 2304.04062. [DOI] [PMC free article] [PubMed] [Google Scholar]


