PyEcoLib: a python library for simulating stochastic cell size dynamics

Abstract

Recently, there has been an increasing need for tools to simulate cell size regulation due to important applications in cell proliferation and gene expression. However, implementing the simulation usually presents some difficulties, as the division has a cycle-dependent occurrence rate. In this article, we gather a recent theoretical framework in PyEcoLib, a python-based library to simulate the stochastic dynamics of the size of bacterial cells. This library can simulate cell size trajectories with an arbitrarily small sampling period. In addition, this simulator can include stochastic variables, such as the cell size at the beginning of the experiment, the cycle duration timing, the growth rate, and the splitting position. Furthermore, from a population perspective, the user can choose between tracking a single lineage or all cells in a colony. They can also simulate the most common division strategies (adder, timer, and sizer) using the division rate formalism and numerical methods. As an example of PyecoLib applications, we explain how to couple size dynamics with gene expression predicting, from simulations, how the noise in protein levels increases by increasing the noise in division timing, the noise in growth rate and the noise in cell splitting position. The simplicity of this library and its transparency about the underlying theoretical framework yield the inclusion of cell size stochasticity in complex models of gene expression.

1. Introduction

The origin of random fluctuations (noise) of gene products in cells is currently an important research field [1, 2]. This randomness can explain processes such as cell fate decision [3], survival in complex environments [4], and cell proliferation [1, 5]. Noise from intrinsic sources in gene expression, such as random binding of molecules and spontaneous degradation, can be transmitted to the concentration of the gene product [6, 7]. Other sources of noise, also known as extrinsic, affect all physiological processes of cells; however, their understanding is not yet complete [8]. In this article, we present methods for simulation of one particular extrinsic source of noise: fluctuations in cell size. These fluctuations originated from the randomness of variables such as growth rate, cell division times, and partitioning position.

Fluctuations in cell size have recently been studied thanks to the development of techniques for high-throughput cell imaging and tracking [9, 10]. Among the mechanisms responsible for the transmission of cell size fluctuations to gene expression, we can mention the random segregation of low number molecules during division [11] and variability in reactant concentrations, dilution rates, and division times [12]. However, it is currently not clear how to link gene expression mechanisms to stochastic size dynamics because the relation between expression rates and growth is still being studied [13]. Some attempts have been made [11, 14–16], but the inter-division times do not follow size-dependent statistics, as recently found [17].

In a recently proposed mathematical framework [18], we describe division as a continuous-time Markov chain that can be coupled with gene expression. Here, we synthesize this framework into an easy-to-use tool by developing PyEcoLib; a python based library that can model the stochastic cell size dynamics. This library reproduces most of the known properties of bacterial division, such as division strategies [17, 19], bacterial proliferation [20], known distributions of division times [21], and stochastic fluctuations in both growth rate and septal position [22]. The user can incorporate the library into any simulation script to model gene expression, including size and growth effects on bacterial physiology. PyEcoLib can be found in our repository [23], and can also be installed using the Python Package Index (pip install PyEcoLib).

The structure of this article is as follows: first, we provide an overview of the basic uses implemented in PyEcoLib with figures demonstrating an example of each feature. Next, we provide a detailed explanation of the implemented classes with a focus on the basic class Simulator, which simulates cell size dynamics by discarding descendant cells. We also introduce the more advanced class PopSimulator, which simulates the dynamics of a small cell colony and considers all cells descending from a single ancestor. In addition, PopSimulator generates highly accurate division times, cell growth rates, and sizes of mother and newborn cells, providing the necessary parameters for simulating gene expression from cell size trajectories. Finally, we present the results of simulations that demonstrate how noise in cell size dynamics may increase noise in protein concentration for a basic example of open-loop bursty gene expression.

2. Basic uses for PyEcoLib

The algorithm behind PyEcoLib considers cell size dynamics as a hybrid process, in which the size grows exponentially, and divisions occur as a jump process with a size-dependent rate [18]. As observed in figure 1(A), the division is triggered after the accumulation of a given number of division stages as other similar models [24–26]. Regarding the most recent version, 2.0.3, we can find several uses, among which we can highlight the following applications:

Figure 1.

Schematic model and an example of the basic properties of cell regulation, which can be simulated using PyEcoLib. (A) The division is modeled as a stochastic process that occurs after completion of the M stages. During division, the cell resets the stages to zero. The transition rate from any stage m to another stage $m+1$ is given by ${k{d}^S}^{\lambda }$, where $k_d$ is a constant, s is the cell size, and $\lambda >0$ defines the strength of division control. Throughout the cell cycle, the cell grows exponentially with an exponential growth rate μ and is halved during division. (B) Cell size dynamics. Top: time series of a cell growing and dividing. one of the two descendant cells (gray) is discarded. Bottom: example of cell size trajectories that can be simulated using PyEcoLib. These trajectories can include different sources of noise, such as initial size noise, growth rate noise, and partition noise. (C) The adder division strategy for simulated trajectories. Following this strategy, the cell size added during each cell cycle does not show a correlation with the cell size at birth.

• Generating trajectories of exponentially growing cells following the adder division strategy (figure 1). The trajectories can present any arbitrary small sampling time allowing the study of cell size dynamics with arbitrary precision (figure 1(B), tables 1 and 3).

• Estimate the bacteria division times with arbitrary precision (actually 14 decimal digits). This accuracy level is mainly intended to ensure the computational stability of simulation algorithms that could been built over PyEcoLib outputs. As simulation parameters, we can set the mean cell size, growth rate, and noise in added size. Since the obtained times are highly precise (table 4), they can be coupled to classic stochastic simulation algorithms for gene expression.

• Including variability in the septal position during cell splitting [22]. This can be used to simulate the segregation of molecules (figure 1(B)).

• Setting an arbitrary distribution of cell sizes at the beginning of the experiment with particular applications in statistics of cell proliferation (figure 1(B)).

• Including fluctuations in cell-to-cell growth rate to study the effects of memory across generations on physiological variables of cells (figure 1(B)).

• Computing trends in added size versus size at division for different division strategies (adder, timer-like, sizer-like) that can vary depending on the species of the organism to simulate [19] (figure 2(A) and table 2).

• Estimation of the dynamics of the mean and coefficient of variance of the size distribution for bacteria that grow and divide continuously (figures 2(B) and (C)). This can be useful in estimating some variables of cell regulation, such as the effects of cell regulation noise on size dynamics [27].

• Simulating regulation of cell size along a single lineage (tracking one cell after division and discarding the other cell) or considering the entire population as we explored before [20] (figure 3).

Table 1.

Example of a data set obtained using the function szdyn of the class Simulator in PyEcoLib.

time	Cell1	Cell2	Cell3
0	3	3	3
0.01	3.215	3.215	3.2153
0.02	3.446	3.446	3.446
0.03	3.693	3.693	3.693

Table 3.

Example of a data set obtained in FileName using the function szdyn from the class PopSimulator in PyEcoLib.

Time	Sample	Cell	Size	DivSteps
0	0	0	1	0
0	1	1	1	0
0	2	2	1	0
0	3	3	1	0

Table 4.

Example of a data set obtained in DivEventsFile using the function szdyn from the class PopSimulator in PyEcoLib.

Sample	Cell	Mother	MotherSize	BirthTime	Sb	GrowthRate	DivPar
0	0	0	2.23 864	0.3251 847	1.06 584	0.0385	0.5
1	1	1	2.40 241	0.3786 165	1.15 789	0.0385	0.5
2	2	2	1.62 812	0.4125 762	0.86 721	0.0385	0.5

Figure 2.

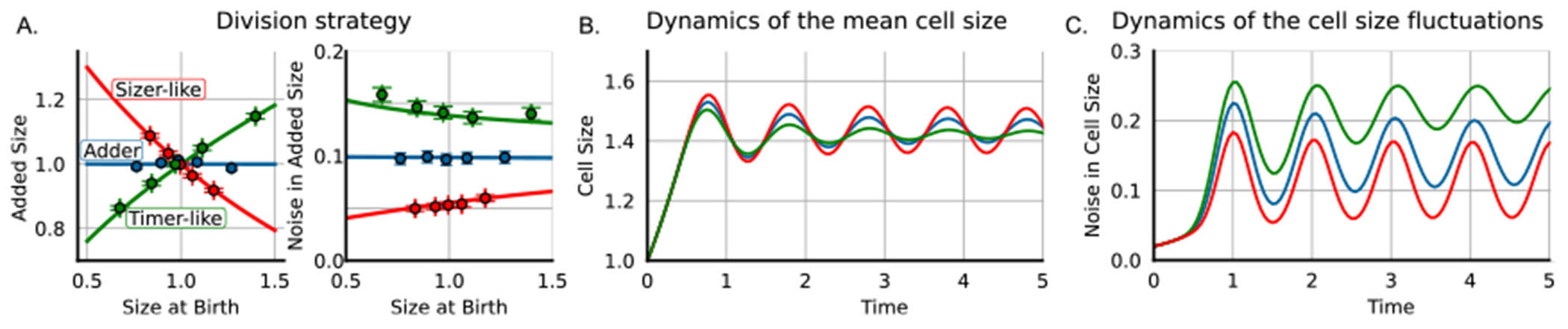
Division strategy and dynamics of the cell size statistics. (A) Cell division strategy left: added size versus size at birth, right: noise in added size versus size at birth. Different colors represent different parameters lamb. red: lamb = 2 (sizer-like strategy), blue: lamb = 1 (adder strategy), green: lamb = 0.5 (timer-like strategy). (B) Mean size across time for different strategies. (C) Noise in cells size as the squared coefficient of variation across time. (Parameters: gr = ln(2), sb = 1, steps = 10, CV2sz = 0.02, CV2div = 0.0, CV2gr = 0.0.)

Table 2.

Example of data obtained using szdynFSP from the class Simulator in PyEcoLib.

Time	Meansize	VarSize
0.01	3.1057	1.60×10−11
0.02	3.1273	9.57×10−11
0.03	3.1491	4.34×10−10
0.04	3.1710	1.61×10−09

Figure 3.

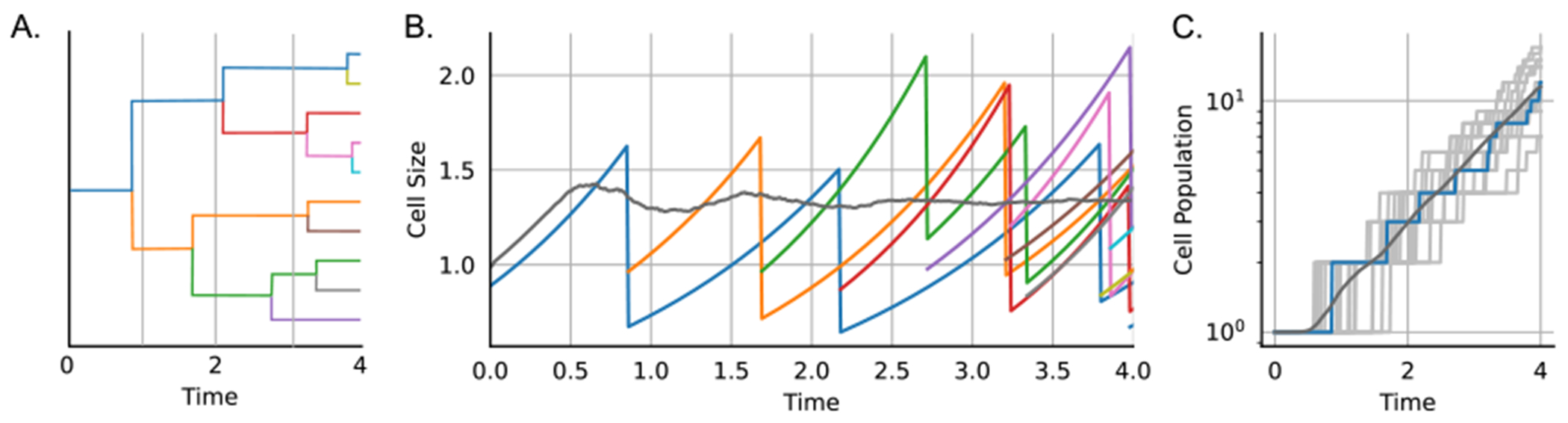
Simulation of the dynamics of a colony using PyEcoLib. (A) Example of the simulated lineage tree over time. Different colors represent different cells. (B) Size dynamics for cells that were presented in (A) with their respective color. The gray line corresponds to the mean cell size for 1000 colonies. (C) Dynamics of the population number for different replicas (gray), while the population of the colony in (A) and (B) is depicted in blue. Parameters: gr = ln(2), sb = 1, steps = 10, nu = 2, CV2gr = 0.01, CV2div = 0.01, V0array = array of gamma-distributed variables with mean = 1 and CV² = 0.03.

In this tutorial, we introduce the PyEcoLib available tools to address the mentioned applications.

3. Classes implemented in PyEcoLib

PyEcoLib is a library implemented in Python version 3.8.1. The user should pre-install the libraries numpy, scipy, math, and platform. PyEcoLib consists on a set of three classes:

• Cell: it is the basic class corresponding to one cell with all parameters such as size, growth rate, division steps (see figure 1(A)), next time to reaction, division exponent, partitioning noise, growth rate noise and division rate. This class has functions used by other classes and the user does not have access to its functions.

• Simulator: this class implements most of the functions to calculate the cell size dynamics. It is implemented in such a way that it considers only one descendant cell after each division. In more technical terms, it tracks only a single lineage of the lineage tree [5]. Among the implemented functions, we can highlight stochastic simulations of cell size dynamics, numerical methods for estimating moments, and numerical and stochastic methods for estimating the division strategy.

• PopSimulator: this class is implemented for stochastic simulation of cell colonies up to approximately five generations. In addition to cell size dynamics, this class can also return the exact time of cell division, as it can be coupled with other simulations of molecular reactions.

In the next section, we explain more thoroughly the features of the classes Simulator and PopSimulator.

3.1. Class Simulator

Simulator is a class implemented in the first version of PyEcoLib (1.0.8). This class contains most of the PyEcoLib functions to study cell size regulation. To import the library, use the folowing line:

from PyEcoLib.simulator import Simulator

An object of this class can be called, as an example, by writing the following lines:

sim = Simulator(ncells = 1000, gr = 0.7, sb = 1, steps = 20, CV2div = 0, CV2gr = 0, lamb = 1, V0array = None)

After defining the name of the object Simulator (denoted sim here), the user simply needs to define the following parameters.

• ncells: number of cells to simulate (positive integer number, 1000 in the example).

• gr: cell growth rate (positive real number). gr is related to the doubling time, that is, the mean time between divisions, by the formula gr = ln(2)/doubling time).

• sb: mean size of the newborn cell (positive real number). After defining this size, the library estimates the division rate so that the mean size at birth is equal to this value.

• steps: division steps (positive integer number). This parameter defines the number of stages that cells have to complete to trigger division (figure 1(A)). The greater the number of steps, the less stochastic the division process. The deterministic division is achieved when the number of steps is infinite. A typical value for this parameter can be 20 steps [17].

3.1.1. Optional parameters for class Simulator

In addition to the parameters mentioned above, there are some other variables that make the simulation more complex and closer to the experimental size regulation, which can be listed as follows.

• V0array: array with the initial sizes of the cells. By default, all cells start at size sb. This array has to have the same dimension as the number of cells.

• CV2div: partitioning noise (figure 1(B)) measured as the squared coefficient of variation (which is given by the variance over the mean squared) of the position of cell splitting (positive number between zero and one third). If this parameter is defined, during each division, the cell partitioning consists of multiplying the cell size times a beta-distributed random variable with mean 0.5 and the specified coefficient of variation. A typical value for CV2div is 0.002 [28]. By default, CV2div is zero, which means that the cell splitting is perfectly symmetric.

• CV2gr: noise from the growth rate (figure 1(B)), measured as the squared coefficient of variation (continuous number between 0 and 1). If this parameter is greater than zero, after every division, the growth rate is picked randomly as a gamma-distributed random variable with the specified mean and the given squared coefficient of variation. By default ((CV2gr) = 0), which means that all cells have the same growth rate. A typical value is 0.005 [29].

• lamb: the division strategy parameter [17] (in the library, lamb is a continuous variable taking values between 0.5 and 2 due to stability of the cycles). By default, lamb is equal to one, which means that the division strategy is adder (see figure 1(C)) [21]. Following the adder strategy, the added size before division is, on average, constant. If lamb < 1, the division strategy is timer-like, that is, the added size, on average, increases with the size at birth. Finally, if lamb > 1 the added size decreases with size at the beginning of the cycle (sizer-like strategy). Under optimal growth conditions, it has been found that lamb = 1 [17]. In slow-growing Escherichia coli cells, lamb is close to 1.5 [17]. Some other rod-shaped cells show different lamb between 0.5 and 2 [19] (see figure 2(A)).

It is important to note that lamb or λ serves as a phenomenological parameter, providing an approximation for division strategies that differ from the adder. This parameter is useful in approximating the observed statistics of cell size regulation [17]. A division rate of ${k{d}^S}^{\lambda }$ where $k_d$ is a constant and s is the cell size results in an adder when $\lambda =1$. This rate resembles the timer strategy when the division rate does not depend on s (that is, $\lambda \to 0$). In contrast, a strong dependence of the division rate on s leads to an sizer strategy (that is, $\lambda \to \infty$). While there exist molecular mechanisms explaining the sizer-like strategy (an strategy between sizer and adder), such as the degradation of FtSZ polymers [30] and the presence of a commitment size to initiate division [20, 31], their implementation can be complex and require a greater number of parameters, which can complicate simulations.

3.2. Implemented functions in class Simulator

In this section, we present and discuss the properties of the main functions implemented in PyEcoLib:

szdyn: this function is used to obtain the stochastic size dynamics for all cells in the simulation. As an example, the user can run this function using the following lines:

sim.szdyn(tmax = 10, sample_time = 0.01, nameCRM = "dataCRM.csv")

Defining a maximum time tmax (in this case 10) and a sampling time sample_time (in this case 0.01), with units of inverse growth rate, the function returns a .csv file with default name dataCRM.csv.

Regarding the output file, the first column is the time from 0 to tmax, sampled periodically with period sample_time. Subsequent columns correspond to the size of each cell at the corresponding times. An example of a data set consisting of three cells is presented in table 1. An example of simulated cell size trajectories is shown in figure 1(B).

Algorithm 1 shows the algorithm implemented in PyEcoLib to calculate the cell size dynamics. The theoretical details behind the used formulas have already been discussed in previous works [17, 18].

szdynFSP: this function estimates numerically the dynamics of the mean and variance of the size distribution. The numerical algorithm used for the calculation of the mentioned moments can be found in previous articles [18, 32]. As an example, szdynFSP can be called using the following lines:

sim.szdynFSP(tmax = 10,sample_time = 0.01,CV2sz = 0.01,nameFSP = "./dataFSP. csv").

The user has to provide the maximum simulation time (tmax) which in this example is tmax = 10. In addition, the sampling time (sample_time), in this example sample_time = 0.01, refers to the frequency with which the user takes measurements. The variability in the starting cell size can be set by the parameter CV2sz (in this example CV2sz = 0.01) corresponding to the squared coefficient of variation of the cell size at the beginning of the simulation (see figure 1(B)). The resulting data frame corresponds to three columns, as shown in table 2.

The first column in table 2 corresponds to the time (taking samples at every sample_time), the second column is the mean size at the corresponding time, while the third column represents the variance of the size distribution at the given time. An example of the dynamics of the mean distribution is shown in figure 2(B), while the dynamics of the variability of cell size is shown in figure 2(C).

SdStat: this function uses numerical methods to return an array of two elements consisting on the mean added size at division (Added) and the squared coefficient of variation of this added size (cv2) as explained in the next line:

Added,cv2 = sim.SdStat(sb = 1.0)# returns (1,0.05)

The main parameter of this function is sb corresponding to the size at birth. We recommend using values close to the given sb defined in the simulator. An example of the results of this function of different sb is shown in figures 1(C) and 2(A) (solid line).

3.3. Class PopSimulator

In the release of the second version of PyEcoLib (2.0.3), we implemented a new class called PopSimulator. This class only contains the function szdyn. Unlike Simulator, which keeps the bacterial number constant throughout the simulation by discarding one of the descendants after division, PopSimulator can simulate the entire population. To import the class, use the following line:

from PyEcoLib.PopSimulator import PopSimulator

An object of class (denoted as sim) can be called using the following line:

sim = PopSimulator(ncells = 1, gr = 0.7, sb = 1, steps = 10, nu = 2)

PopSimulator has the same parameters used in the class Simulator (ncells, gr, sb, steps, CV2div, CV2gr, lamb and V0array) plus the parameter nu. With nu = 1, PopSimulator simulates a class equivalent to Simulator. On the other hand, with nu = 2, all lineages are tracked. when the entire lineage tree is simulated, it is run until a limit tmax<7doubling time such as the population number does not reach a very high value.

To run the function szdyn, the user should write a line as: sim. szdyn(tmax = 5, sample_time = 0.01, FileName = ‘./dynamics.csv’, DivEventsFile = ‘./divevents.csv’).

As specified in the call to the function szdyn, PopSimulator generates two files: one mandatory, called FileName and the other optional, called DivEventsFile. FileName contains the size dynamics for different cells. An example of the data set obtained using this function is presented in table 3.

The first column of table 3 shows the time that is sampled with a period specified with the parameter sample_time. The colony label that corresponds to the column Sample. The cell ID in the column Cell. The cell size of the given cell at that instant in time represented in the column Size and the number of division stages at that time of five in the column DivSteps.

In the optional file, DivEventsFile, szdyn exports the exact time at which each division event occurs. The user should define the path where this file will be stored using the parameter DivEventsFile in szdyn. An example of the first lines of this kind of file is presented in table 4.

DivEventsFile presents the colony ID (Sample), the cell ID (Cell) which is uniquely defined among a colony, the ID of the cell’s mother (Mother) and the size of its mother before the division (MotherSize), the time instant at which the cell got born (BirthTime) measured from the beginning of the simulation; its size at birth (Sb), its growth rate (GrowthRate) that can take an stochastic value depending on the parameter CV2gr defined at defining PopSimulator object. Finally, the division parameter; DivPar (the size of the future daughter cell over the size at division in the division following this division event).

Using the data provided in DivEventsFile, the user can simulate, for example, gene expression knowing exactly when each cell is born, which cell was its mother, what was the size of its mother (if you want to calculate the binomial partition ratio), the size at birth and its growth rate if the user wants to predict the cell size at any time, and DivPar, which tells you how asymmetric their descendant cells are going to be.

4. Example of stochastic simulation that includes gene expression

The field of gene expression that explicitly includes size dynamics has become very active in recent years [33–37]. In this article, we adapt these models by proposing size-dependent protein production, as explicitly explained in some previous articles [38, 39]. Using the division times generated by PyEcoLib, algorithm 2 shows an example of how to pair the PyEcoLib data with more elaborate simulations of gene expression.

Figure 4 shows the results of gene expression simulations using PyEcoLib to obtain division times. For simulation, we consider the protein to be produced by burst events with burst sizes distributed as geometric distributions. Degradation is neglected, and decay in protein concentration occurs only by dilution. Figure 4(A) shows some trajectories of cell size and variability in cell size over time, measured as the squared coefficient of variation. Figure 4(B) shows the number of simulated proteins of different cells assuming a steady-state concentration of 100 proteins per unit of cell size. Fluctuations over time are also presented. Finally, figure 4(C) shows the trajectories, mean, and variability of protein concentration.

Figure 4.

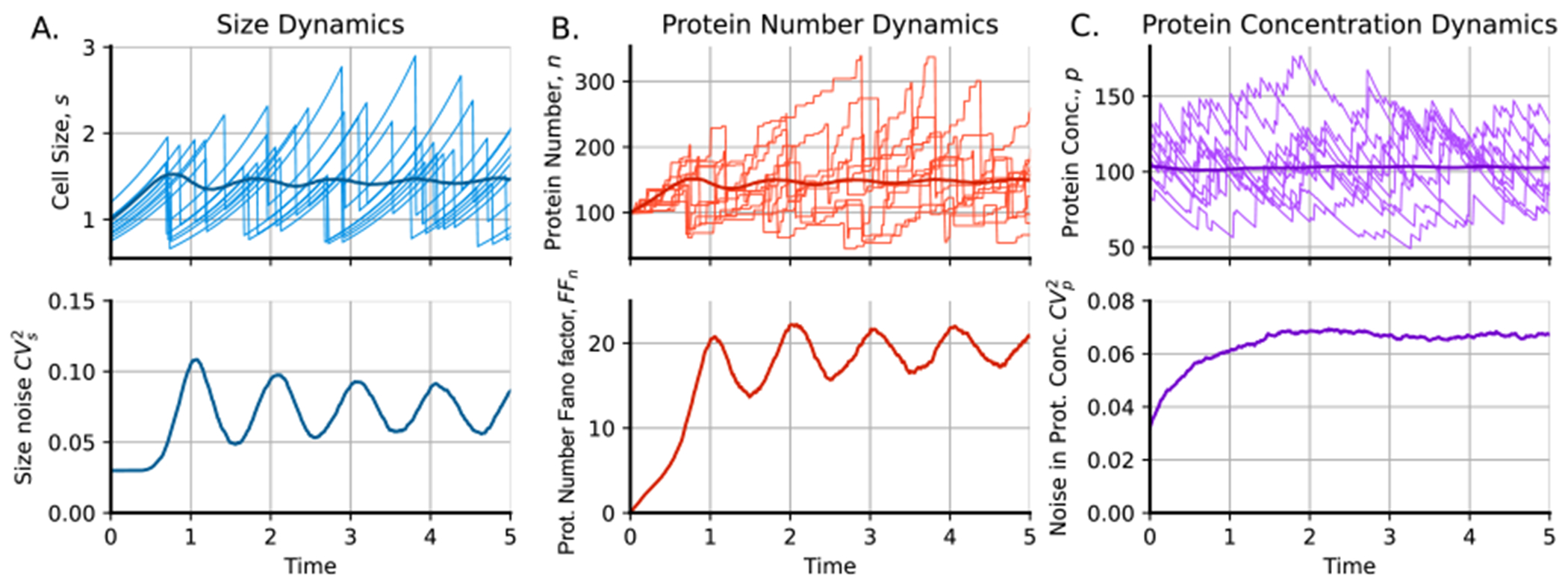
Example of gene expression trajectories including cell size dynamics. (A) Top: some cell size trajectories and mean size in darker blue. Bottom: dynamics of cell size fluctuations as the cell size squared coefficient of variation. (B) Top: some trajectories of the protein number and the mean protein number in darker red. Bottom: dynamics of the noise in protein number as the Fano factor of the protein number (variance over the mean). (C) Top: some protein concentration trajectories and mean protein concentration in darker purple. Bottom: dynamics of the noise in protein concentration as the protein concentration squared coefficient of variation. Parameters: ncells = 5000, sb = 1, gr = ln(2), steps = 10, nu = 1. The protein is produced by burst events that occur at a rate $k_p=10\ln \left(2\right)$ with a burst size distributed following a geometric distribution with mean $\langle b\rangle =10$.

5. Exploring the noise transmission from cell size to protein levels using PyEcoLib

Figure 5 illustrates an advanced application of PyEcoLib, depicting the impact of changes in various parameters of cell regulation on gene expression. The simulation was carried out by following algorithm 2, which can be found in our repository, using the division times obtained through PyEcoLib. The main focus of the study was on the noise in protein concentration while varying the noise in different parameters of cell size regulation, such as division timing, growth rate, and splitting position.

Figure 5.

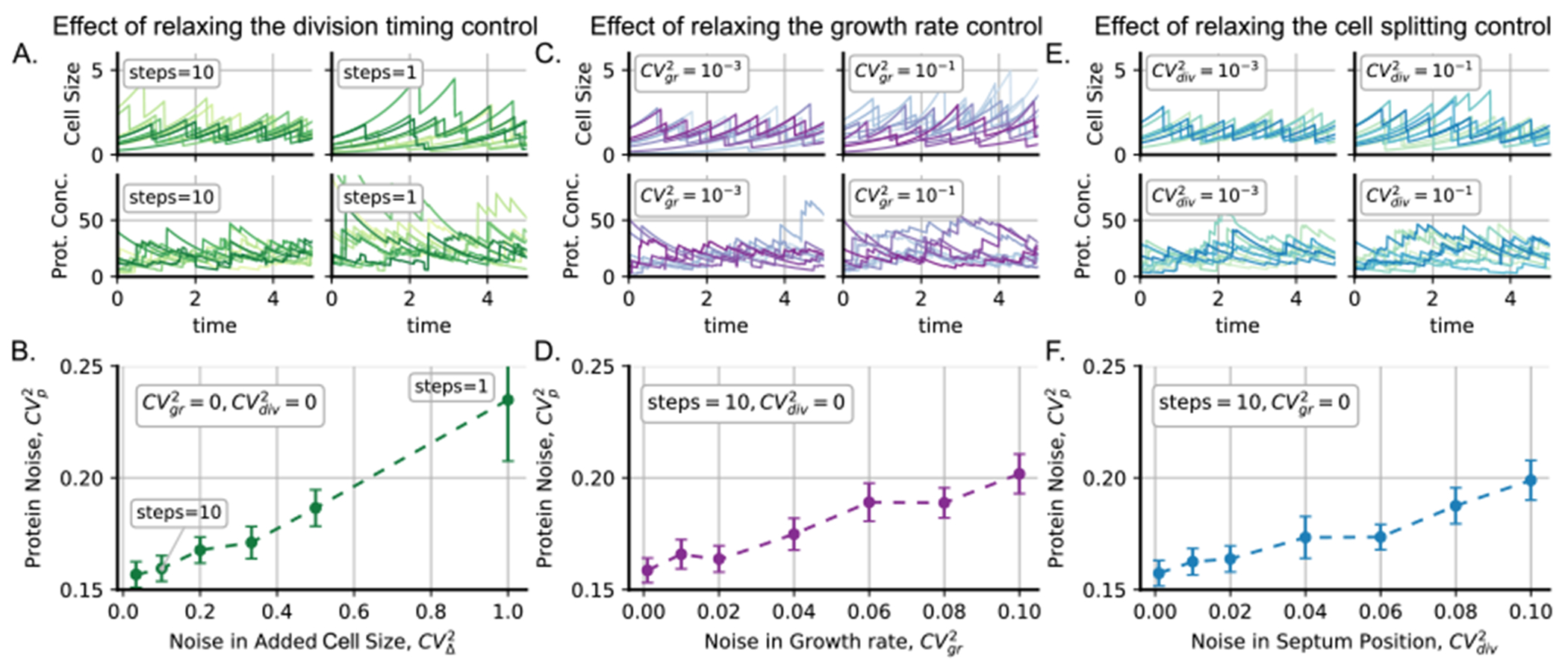
Changing variables that influence noise in cell size regulation can result in variation to the level of noise in protein concentration. (A) Left: some trajectories of cell size and protein concentration for relatively regulated cell cycle timing (steps = 10). Right: trajectories of cell size and protein concentration for a less regulated cell cycle timing (steps = 1). (B) Protein noise as the squared coefficient of variation for different levels of regulation of cell cycle timing measured as the ${CV}^2$ of the added size which theoretically is the multiplicative inverse of the division steps. (C) Left: some trajectories of cell size and protein concentration for relatively regulated growth rate $\left({CV}_{\mathrm{gr}}^2={10}^{-3}\right)$. Right: some trajectories of cell size and protein concentration for relatively less regulated growth rate $\left({CV}_{\mathrm{gr}}^2={10}^{-1}\right)$. (D) Protein noise for different levels of noise in cell growth rate. (E) Left: some trajectories of cell size and protein concentration for relatively regulated cell splitting $\left({CV}_{\text{div}}^2={10}^{-3}\right)$. Right: trajectories of cell size and protein concentration for a less regulated cell splitting $\left({CV}_{\text{div}}^2={10}^{-1}\right)$. (F) Protein noise for different levels of noise in cell splitting position. The protein is produced by burst events that occur at a rate $k_p=4\ln \left(2\right)$ with a burst size distributed following a geometric distribution with mean $\langle b\rangle =5$. Error bars represent the 95% confidence interval of the simulations using bootstrapping methods.

Figure 5(A) shows trajectories of cell size dynamics and protein concentration for different levels of control of division timing. As we explained earlier, the division timing can be controlled by increasing the number of division steps before division. As a result, if the division is triggered by a single step process (steps = 1) the division timing is noisier than for higher division steps (steps = 10). In figure 5(B), we can observe how the noise in protein concentration decreases as the number of division steps increases.

Similar trends can be found in figures 5(C) and (D) when, assuming a given number of division steps (steps = 10) and perfect cell division CV2div = 0, protein concentration noise increases with growth rate noise CV2gr. These graphs were obtained assuming that the dilution rate is equivalent to the growth rate obtained using PyEcoLib, as presented in table 4. Therefore, cells that grow faster also have a faster dilution rate.

Finally, we examined the impact of increasing the noise in cell splitting position over the protein levels. Specifically, we held the division steps (steps = 10) constant and maintained a noiseless growth rate (CV2mu = 0). During division, PyEcoLib generates the size of the mother cell (MotherSize) and the size of the cell after division (Sb) as shown in table 4. It is assumed that the number of molecules during division segregates according to the binomial distribution with parameter Sb/MotherSize. Figure 5(E) illustrates the cell size and protein concentration trajectories, while figure 5(F) displays the trend of increasing noise in protein concentration as the noise in the variable Sb/MotherSize rises. These findings provide valuable insights into the relationship between the noise in cell regulation and protein expression noise, which may prove useful for studying gene expression in different cellular contexts.

6. Discussion

In this article, we present PyEcoLib, a Python-based library that uses the current continuous rate theory of bacterial cell division models [17, 18]. This theory considers division as a time-continuous stochastic jump process triggered by the occurrence of a given number of division steps. PyEcoLib can estimate the stochastic dynamics of cell size from two population perspectives. The first is to keep the population constant by discarding one of the two divisions of descendants cells by each division as experimentally obtained using microfluidic devices [21]. The second perspective consists of tracking all cells in the colony, as done in pico-droplet assays.

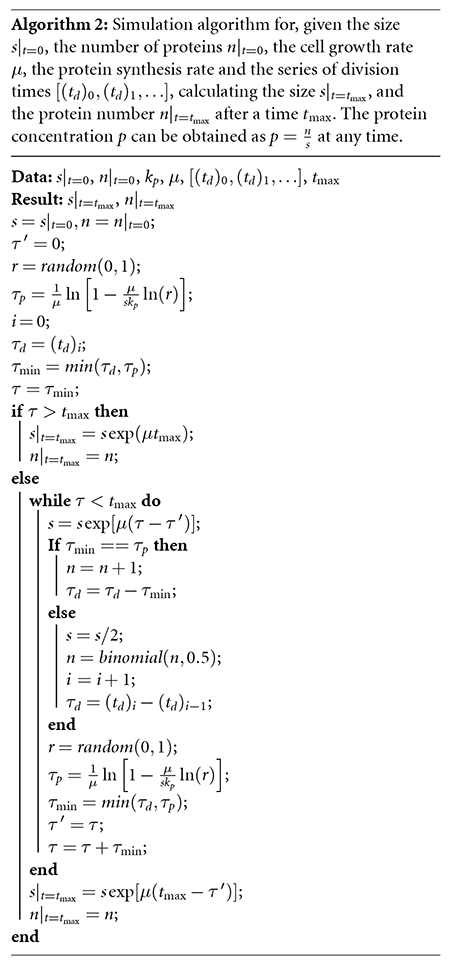
PyEcoLib approximates the population dynamics by simulating cell cycles in a trajectory-wise way. This method is a useful approach to comparing statistics with a finite number of cells in experiments. However, this method is not well-suited for studying the statistics at the population level due to the exponential increase in cell number, which can quickly exhaust CPU and memory resources. To address this issue, we limited the number of cells for the simulation. It should be noted that population-level dynamics can be modeled using the Fokker–Planck equation, master equation, or Kolmogorov equation, which can overcome the challenges posed by CPU and memory limitations [26, 40].

In addition, this library includes some tools to estimate the cell size dynamics, such as simulating most of the division strategies found in E. coli: timer-like, adder, and sizer-like [19, 41] and estimating the distribution of division times, size at division, and size at birth in a population of constant number. PyEcoLib can be coupled to stochastic simulation of gene expression with reactions occurring at arbitrary distributed times. This library can also induce other kinds of noises, such as noise in the placement of the septum ring and the cell-to-cell growth rate [22]. Although the user can set an arbitrary cell size distribution of the precursor cells; PyEcoLib cannot set an arbitrary starting distribution of division steps, and all cells must start from zero division steps.

As shown in figure 4, oscillations in mean size $\langle s\rangle$ and size variability ${CV}_s^2$ were found. As we have shown in previous articles [18], considering only stochasticity in the division steps, these oscillations are maintained over an arbitrarily long period of time. These oscillations are damped when other sources of noise such as the cell-to-cell growth rate variability and the septal position are added.

Including cell size stochasticity in gene expression can be an important tool to understand the origin of fluctuations in molecule concentration. The use of PyEcoLib in more complex gene regulatory architectures can improve understanding of the effects of stochasticity on division timing. Other more complex sources of noise such as division strategy, noise in growth rate, and asymmetric cell splitting can be included in gene expression as well.

In supplementary material the reader can study the implementation of PyEcolib in the notebook SimulatorProt2023.ipynb.

Data availability statement

The data that support the findings of this study are openly available at the following URL/DOI: 10.5281/zenodo.4579183.