AHHME: A model for estimating the holistic cost-effectiveness of antimicrobial resistance interventions in food animal production

Abstract

Antimicrobial resistance (AMR) is considered a global priority for human health, and reducing antimicrobial use in food animals has been suggested as a key area for interventions aiming to reduce resistant infections in humans. In addition to the effect on human health, such interventions may have effects across food animal productivity, healthcare sector costs, and the broader macroeconomy, but these effects are rarely captured in the AMR health economic literature. Without being able to estimate these effects, it is difficult to understand the true cost-effectiveness of antimicrobial stewardship interventions in food animal production, or to correctly design and prioritise such interventions.

We explore and demonstrate the potential use of a novel compartment-based mathematical model to estimate the holistic cost-effectiveness of AMR-related interventions in food animal production from a One Health perspective. The Agriculture Human Health Micro-Economic model (AHHME) uses Markov state transition models to model the movement of humans and food animals between health states. It assigns values to these health states utilising empiric approaches, from the perspectives of human health, food animal productivity, labour productivity and healthcare sector costs. Providing AHHME open-source code and interactive online modelling tools allow for capacity building in AMR intervention modelling.

This model represents a useful framework for capturing the cost-effectiveness of AMR-related interventions in food animal production in a more holistic way: it can allow us to capture the often-overlooked benefits of such interventions in like terms while considering distributional concerns. It also demonstrates that methodological assumptions such as willingness-to-pay thresholds and discount rates can be just as important to health decision models as epidemiological parameters, and allows these assumptions to be altered. We provide example outputs, and encourage researchers and policymakers to use and adapt our code to explore, design, and prioritise AMR-related interventions in their own country contexts.

Highlights

• •We present a mathematical model to estimate the holistic cost-effectiveness of AMR-related interventions in livestock production.
• •It considers four perspectives: livestock productivity, labour productivity, human life years, and healthcare system costs.
• •It shows the importanec of these perspectives, and the sensitivity of cost-effectiveness outputs to methodological parameters.
• •We provide our open-source code and online modelling tool, and encourage others to apply AHHME to their own country contexts.

Acronyms

AMR

Antimicrobial resistance

AMU

Antimicrobial use

WASH

Water, sanitation, and hygiene

AHHME

Agriculture Human Health MicroEconomic Model

QALY

Quality-adjusted life year

WTP

Willingness to pay

QoL

Quality of life

NMB

Net monetary benefit

CEAC

Cost-effectiveness acceptability curve

1. Introduction

Antimicrobial resistance (AMR) imposes a considerable burden of disease globally, affecting human health, economic growth, and food security. This has resulted in international efforts to curb its growth [1,2]. Antimicrobial use (AMU) in food animals has been suggested as a major contributor to the spread of AMR [1]. For this reason, it has been targeted by interventions such as legally restricting the use of antimicrobials in food animal production, encouraging prudent use of antimicrobials, replacing antimicrobials with alternative products,2 or using improvements in animal husbandry, on-farm biosecurity, and on-farm water, sanitation and hygiene (WASH) to reduce the need for antimicrobials [[3], [4], [5]].

However antimicrobials, and especially antibiotics,3 are often used by food animal farmers as disease management and productivity enhancement tools in food animals [6,7], and reducing their use may harm food animal productivity and farmers' incomes. On the other hand, if reduced food animal AMU leads to a lower level of AMR in human infections, then it will provide gains to human health (and subsequently economic productivity) while reducing healthcare costs [8]. Weighing these outcomes against each other is essential to modelling the effect of AMR-related interventions, and is needed in order to correctly design and prioritise such interventions [8]. This will also give us insight into how the costs and benefits of prospective interventions are distributed among actors, helping us to understand important distributional concerns [9].

For this reason, we created the Agriculture Human Health Micro-Economic (AHHME) modelling tool to model and evaluate the cross-sectoral impact of AMS interventions in food animal production, taking a holistic One Health approach as proposed by Naylor et al. [10]. AHHME aims to evaluate the effect of such interventions on a range of relevant sectors, and thus to determine the cost-effectiveness of those interventions and the amount of funding that governments should allocate towards their implementation. It considers the effect of interventions on food animal productivity, human life years lost to disease, healthcare costs, and labour productivity lost to disease. It compares these outcomes in monetary terms, and it can be parameterised in detail to reflect the epidemiological, agricultural, and economic context of the country being considered. We explain in detail how the model works, giving examples of the types of outputs that can be produced and linking to our free open source online resources for using, exploring, and adapting the model.

2. Methods

2.1. Model structure overview

The AHHME model calculates the cost-utility (from the human health perspective) and cost-benefit (from the food animal agriculture sector, labour productivity, and healthcare cost perspectives) of AMR-related interventions in food animal production. It has epidemiological modules for humans and food animals based on a compartmental state-transition model using difference equations to model movement between health states [10]. It assigns monetary values to these health states from different perspectives using economic modules from four perspectives. Namely: human health, healthcare sector costs, labour productivity, and food animal productivity.

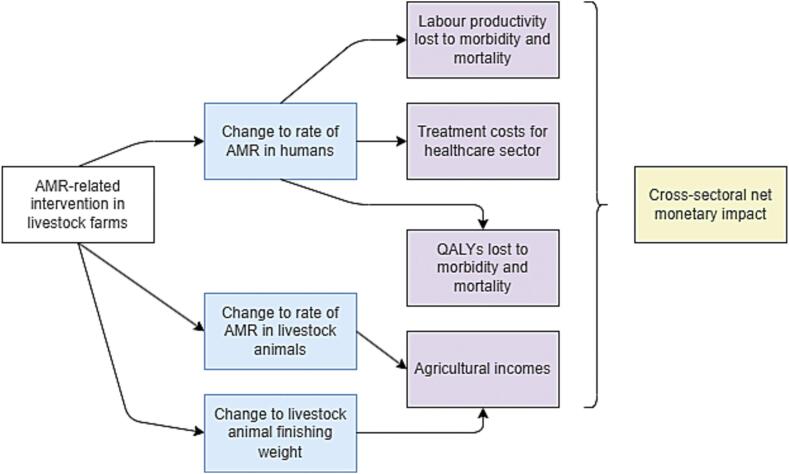
In terms of causal pathways modelled, AHHME considers the impact of a given intervention on the rate of antimicrobial resistance in both humans and food animals, as well as the finishing weight of food animals. It models the resultant change to farmers' incomes, to the number of labour hours lost to illness and death, to the cost of treatment borne by the healthcare sector, and to the life years lost to illness and death (Fig. 1).

Fig. 1.

Causal pathways modelled by AHHME. Blue boxes represent the direct effects of the intervention. Purple boxes represent the four perspectives from which monetary values are assigned to these outcomes. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

AHHME does not mechanistically model the way that farm antimicrobial use interventions influence farm outcomes or the rate of AMR in humans. These intervention impacts vary by intervention and context. Rather, it provides a health-economic framework for understanding the holistic economic impact of these outcomes. The intervention impact on farm outcomes can be parameterised using farm trials or farm-level survey data [[3], [4], [5],[11], [12], [13], [14]]. The intervention impact on human AMR prevalence can be parameterised using mathematical transmission models [15] and ecological panel regression analysis [[16], [17], [18], [19], [20]].

The model is run both with and without the intervention, and compares the number of humans and animals in each health state in the two scenarios. It assigns a monetary value to these health state outcomes from the four perspectives mentioned, and synthesises them to estimate the cross-sectoral monetary benefit of the intervention being simulated at the population level.

While the model currently allows the intervention to directly impact three parameters (blue boxes), the code can be modified to allow the intervention to impact any of the model parameters. The full set of parameters used in the model are listed in Table 1 (below).

Table 1.

List of parameters used for AHHME.

Methodological parameters	Timeframe (years), discount rate, willingness to pay per quality-adjusted life year (QALY)
Demographic parameters	Population, annual population growth rate, portion of population in paid employment, average remaining life years, average remaining working years
Agricultural parameters	Population of each food animal species, portion of animals in each farm type (e.g. industrial, smallholder), average size of farms (by farm type and species), animal selling price per kg by species, number of production cycles per year (by farm type and species), animal mortality without infection (by farm type and species), animal mortality with an antimicrobial-resistant infection (by farm type and species), animal mortality with an antimicrobial-susceptible infection (by farm type and species)
Epidemiological Parameters	Incidence of chosen disease, portion of infections from resistant bacteria, growth rate of portion of resistant infections, fatality from resistant and susceptible infections, chance of sequelae from resistant and susceptible infections, subjective quality of life from resistant infections, susceptible infections, and sequelae, hospital length of stay from resistant and susceptible infections
Economic parameters	Labour productivity, labour productivity annual growth rate, ratio of paid work to total (paid + unpaid) work, cost of providing a hospital bed for one day
Intervention parameters	Effect on rate of AMR in human infections, effect on rate of AMR in animal infections, effect on animal finishing weight (by species and farm type)

Examples values given in the supplementary material

2.2. Epidemiological module

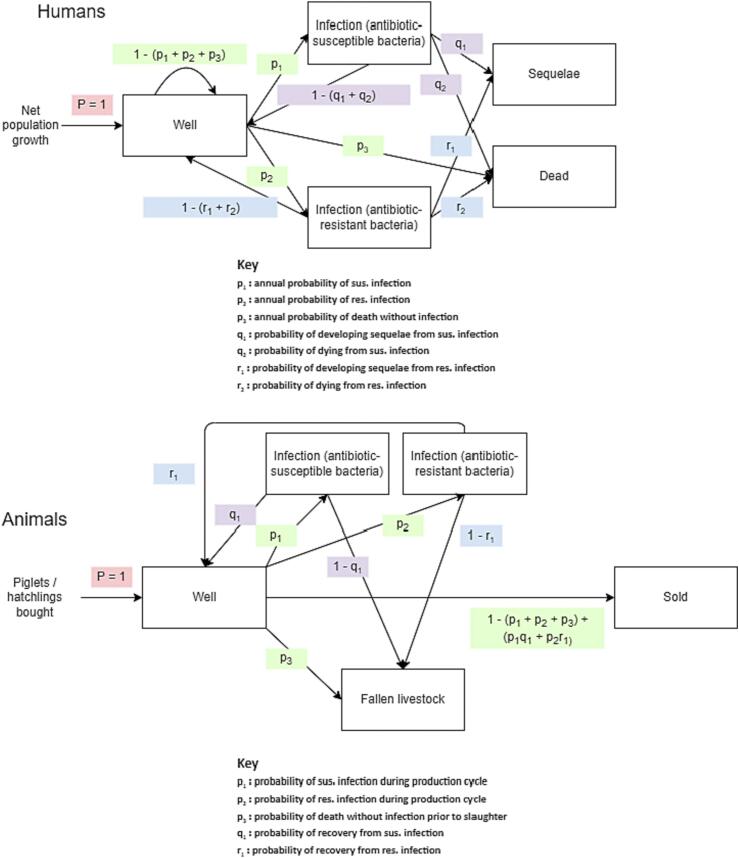
AHHME models human and food animal epidemiology using a population-level Markov chain state-transition model (Fig. 2), which models state transition over one-year periods.4 Humans and food animals begin life in good health. At the beginning of the period, additional humans are born based on the number of net births in the population, and additional food animals are bought by farms based on the growth rate of agricultural output.

Fig. 2.

State Transitions for Humans and Animals.

P = 1 means that individuals who enter the model go directly into the ‘well’ compartment. Green probabilities (p_x) represent transitions out of the ‘well’ compartment. Purple probabilities (q_x) represent transitions out of the ‘susceptible infection’ compartment, and blue probabilities (r_x) represent transitions out of the ‘resistant infection’ compartment.

In a given one-year period, non-infected humans may die without infection, or may develop an infection with (antimicrobial-)susceptible or (antimicrobial-)resistant pathogens. Infected humans may die, recover fully, or develop sequelae.

In a given one-year period, food-producing animals may die without infection, or may develop an infection with (antimicrobial-)susceptible or (antimicrobial-)resistant pathogens. Infected animals may die or recover fully. Those alive and well at the end of the production cycle are sold. The model can be run for as many periods as desired, with the default set to twenty periods (years).

The definition of resistant and susceptible infections in the model depends on the drug-pathogen resistance pairs being modelled. For example, one might model an intervention which reduces use of fluoroquinolones in food animal production, and the resultant effect on the rate of fluoroquinolone resistance in human campylobacterioses. It is possible to model different animal species and farm types, with different parameter sets. By default, the model considers poultry and pig farms, each with two production types (smallholder and industrialised). New modules can be written to add different food-producing animal species and farm types can be added as appropriate, and these farms can be parameterised to behave differently.

Due to the difficulty in mechanistically modelling the ecological relationship between AMU and AMR [8], that relationship is not modelled mechanistically by the model. Instead, the intervention reduces the portion of infections which are resistant by a user inputted value (with separate values for humans and food animals). As with other parameters in the model, this value can have multiple values across different scenarios, and can be drawn from a distribution (more on this in the sensitivity and scenario analysis subsection).

In order to estimate this value, modellers may assume a unit elasticity of resistance with respect to systemwide AMU as in OECD, 2018 [21], may estimate this relationship using mathematical models as in Booton et al. [15], or may do so using ecological panel data regression analysis of public health surveillance data [8,[16], [17], [18], [19], [20]]. The effect of the intervention on the rate of AMR in food animals and on finishing weight can be estimated using farm-level trials of antibiotic stewardship interventions [[3], [4], [5]], or by using system dynamics models of agricultural production systems [22,23].

2.3. Economic modules

After running the model in both the “intervention” and “no intervention” scenario, AHHME sums up the total number of humans and animals in each health state over the study period, discounting future outcomes using the selected discount rate. It then assigns values to these health states from four perspectives: labour productivity, farm productivity, healthcare costs, and human health.

2.3.1. Labour productivity

The labour productivity module calculates the value of labour lost through morbidity and mortality from AMR infections in the whole human population. The labour productivity lost to death can be estimated using either the friction cost or human capital approaches [24], with the approach used being one of the arguments of the main model function. In the former, it is assumed that there exists a pool of unemployed labour and that, once a working person dies, they will be replaced after a searching period (default six months in this model). In this scenario, a death will incur a loss of productivity equal to that which would have been produced in the search period (e.g. six months' productivity). To calculate the average productivity per person per year, we take the average annual labour productivity of a person in paid employment, multiply this by the labour force participation rate, and adjust this by the ratio of paid to total (paid and unpaid) labour. This includes unpaid housework, unpaid carer duties, volunteerism, etc., and estimates of this ratio in different countries can be found in Alonso et al.(25).

In the human capital approach, when a person dies, the loss of productivity is equal to the present value of the labour done by a person of median age during the rest of that person's working life, assuming both a given discount rate and a given rate of per-person labour productivity growth.

Under both approaches, when a person becomes sick but does not die, the loss of productivity is equal to the productivity which would have been created during the time that they are in hospital, assuming given lengths of stay for resistant and susceptible infections respectively. It is assumed by default that people with sequelae have the same life expectancy and labour productivity as those without, although this can be altered (as mentioned earlier, sequelae still affect subjective quality of life and therefore the number of quality-adjusted life years (QALYs) lost to morbidity).

2.3.2. Farm productivity

Because the model allows the intervention to affect the prevalence of AMR in food animal infections (which mechanistically affects the number of animals which survive and are sold) as well as animal finishing weight, the impact of the intervention on farm incomes is straightforward to calculate. The sale price per kg of live weight (which can change over time) is multiplied by the finishing weight of animals, then by the number of animals sold in each production cycle, then by the number of annual production cycles, for each period. This total revenue is discounted and summed over the study period, and the difference in discounted total revenue between the ‘intervention’ and ‘non intervention’ scenarios is the net intervention effect on (food animal) farm productivity.

2.3.3. Healthcare costs

For a given cost of providing a bed day in hospital, and a given length of stay from resistant and susceptible infections, we can estimate the healthcare sector cost from providing hospital beds to people with infections5 of the type being considered, and compare the discounted totals between the ‘intervention’ and ‘non-intervention’ scenarios. By default, there is no healthcare cost for people with sequelae once they are no longer infected, although this can be altered.

2.3.4. Human health

We use a given willingness to pay (WTP) for each quality-adjusted life year (QALY) to assign a monetary value to QALYs lived by people in each health state. This is the money amount that the relevant healthcare system is willing to spend in order to gain one year of life in good health. Different countries may have existing guidelines for the WTP used in their health economic evaluations, and otherwise the WTP can be estimated using the formula suggested in Woods et al.(26). We assign a QALY value to each health state (resistant infection, susceptible infection, sequelae) using subjective quality of life (QoL) estimates, assuming a value of 1 for good health and 0 for death.

The QALYs lost from infection are equal to: $\left({\mathit{QoL}}^{\mathit{good\; health}}-{\mathit{QoL}}^{\mathit{infection}}\right)\ast \mathit{length}{\mathit{of\; infection}}^{\mathit{years}.}$

The QALYs lost from sequelae are equal to the difference between

• a)The discounted present value of the average remaining lifespan if lived in good health, and
• b)The discounted present value of the average remaining lifespan if lived with sequelae

The QALYs lost from death are simply equal to the discounted present value of the QALYs lived in good health for the average remaining lifespan, which can be estimated using life tables.

The total QALYs lost from infection, sequelae and death across the study period are then discounted, summed and multiplied by the WTP threshold. The difference in this value between the ‘intervention’ and ‘non intervention’ scenarios is the value of the intervention from the human health perspective. Assigning monetary values to QALYs in this way allows the human health impact to be considered alongside other perspectives, giving a more holistic picture of the societal impact of AMR interventions.

2.3.5. Calculating final outputs

The value of the intervention for each of the four economic perspectives is presented, as well as their sum, i.e. the total monetary benefit of the intervention. The model also outputs the ‘threshold price’ of the intervention, i.e. the annual implementation cost which would leave the government indifferent between implementing and not implementing the intervention

2.3.6. Sensitivity and scenario analysis

In addition to these main results, our code performs sensitivity and scenario analysis. This includes investigating the threshold price / net monetary benefit under different intervention impact scenarios, using the human capital vs. friction cost approach to estimating productivity losses from illness, etc. If certain parameters fall within a given feasible range, then the model can perform univariate sensitivity analysis using tornado plots. If parameters are uncertain following a given distribution, then the model can also display the distribution of the threshold price following Monte Carlo simulation. If the chosen outcome is net monetary benefit rather than threshold price, a cost-effectiveness acceptability curve (CEAC) can be produced.

3. Example model outputs

Examples of AHHME outputs are displayed below (Table 2, Fig. 3, Fig. 4), where we run the model for hypothetical interventions. For demonstrative purposes, we parameterised the model to settings of different income levels. Taking a population of 100,000,000, we let all other parameters be the population-weighted average of the relevant value among all countries in the low-, middle-, and high-income World Bank lending groups(27). Considering pig and chicken farms, using the human capital approach, and using sepsis as our disease outcome of interest,6 we demonstrate the model applied to a hypothetical intervention which affects animal finishing weight and human AMR prevalence. Examples of interventions that could be modelled include quantitative restrictions on antibiotic use, WASH interventions which limit pathogen transmission to humans, and combinations of AMU reduction with other farm practice interventions such as biosecurity improvements.

Table 2.

Example outputs showing threshold Price of an Intervention (2019 $USD per year) by Scenario. Shading indicates whether the value is positive (green) or negative (red) with a darker shade indicating distance from zero.

Fig. 3.

Example outputs showing tornado plots showing univariate sensitivity of threshold prices to key animal (top) and human (bottom) parameters

Fig. 4.

Example outputs showing distribution of Threshold Price (2019 $USD per year) after Monte Carlo Simulation.

The full distribution for 10,000 model simulations is shown for low-income (red), middle-income (green) and high-income (blue) countries, with the median and range on a log scale. Each simulation used a different parameter combination to estimate the threshold price.

3.1. Code and data availability

All of the code and data used to parameterise and run the model are available on our GitHub(28), as well as example applications of the model and instructions on how to adapt the model to one's own country context. A free interactive Shiny App(29) is also available online, which allows users to explore the model by altering parameters manually and observing the results. We encourage modellers and researchers to use and adapt our code, while the Shiny App may be more useful for policymakers and non-modellers to do more exploratory analysis.

4. Discussion

In this paper, we have constructed and demonstrated the use of a cost-effectiveness analysis tool which can help policymakers to understand the potential benefit of AMR-related interventions in food animal production from a One Health perspective, allowing these interventions to be more accurately designed and prioritised. It can also help to understand the importance of methodological and parameter uncertainty, and can be useful for capacity building in the quantitative evaluation space in One Health.

4.1. Strengths

Our compartmental health-economic model provides a comprehensive estimate of the cross-sectoral cost-effectiveness of AMR-related interventions in food animal production. The literature evaluating AMR-related interventions tends to focus on human health outcomes, and sometimes on healthcare cost as well, but broader impacts such as that on the macroeconomy and on food animal productivity are often overlooked, despite being potentially as important as the direct impact on human health [8]. Taking these outcomes into account, we can more comprehensively estimate the cost-effectiveness of AMR interventions; and can select, design, and prioritise them with greater accuracy and confidence.

By disaggregating the intervention impact by sector, AHHME is also able to consider distributional concerns. For example, it may reveal that the societal benefit of an intervention is likely to be large and positive, but that it will likely affect the food animal sector negatively. This can reveal the need for compensation or insurance, and can give insight into the political feasibility of interventions.

By including detailed options for scenario, sensitivity, and robustness analysis, the model also allows users to explore uncertainty and to have a more realistic impression of the potential impacts of interventions, and of which values need to be parameterised with greater certainty.

4.2. Limitations

Because it is a model, AHHME is by definition a simplification of a complex process. A key limitation to the explanatory power of the model is that it does not mechanistically model the link between antibiotic use and either farm outcomes or population-level resistance prevalence. This shortcoming is not the result of intentional oversimplification but an acknowledgment of a lack of knowledge of, and great contextual variation in, these relationships [8].

A range of other outcomes could not be included in the model. For instance, it does not capture the spillover benefits of AMR reduction for neighbouring countries, or the effect of AMU reduction on the stochastic emergence of new resistant strains, which may be even more important than the effect on the prevalence of existing resistant strains(30,31). We were also unable to model the effect of AMR prevalence on the safety of treatments such as invasive surgery and chemotherapy for cancer7: this relationship has not yet been estimated at the population level and would require a separate and novel investigation beyond the scope of this paper.

We express human health, healthcare sector cost, food animal productivity and labour productivity outcomes in like (monetary) terms. While evaluated QALYs are compared directly to healthcare costs according to health economic evaluation standard practice(32), expansion of this to other economic outcomes (farmers' incomes, labour productivity loss) implies that these can also be compared directly to human life years, an idea which can be challenged on ethical grounds.

Finally, because the model relies on willingness-to-pay thresholds which are specific to a given country and healthcare system context, the results of AHHME can only be used to inform resource allocation within a given country. Comparing results across countries and using this information to inform resource allocation among countries would necessarily involve a differential valuation of human life across countries, which by definition would be racist and unethical.

4.3. Future research

In order to get the greatest use out of the AHHME model, further research should be done: a) on the effect of AMR-related interventions on farm outcomes, using system dynamic models, intervention trials and farm survey data, and b) on the ecological relationship between AMU and AMR using panel data regression on public health surveillance data. Doing this will allow two key model parameters (the intervention impact on farm productivity and on human AMR prevalence) to be more accurately parameterised, increasing the potential value of AHHME. Our current and upcoming research as part of the SEFASI consortium(33) aims to do just that. In addition, our consortium is in the process of developing a new model, named AHHME-B, which uses a similar modelling structure to estimate the societal burden of AMR, considering both the attributable and associated burden.

Above all, we encourage researchers and policymakers to use our open-source code and free interactive app to explore, design, model, and rank AMS interventions in their own contexts. We also encourage researchers to adapt and improve our code, applying it to interventions in other One Health contexts such as human and environmental health.

5. Conclusions

Our AHHME model allows for the cross-sectoral integration that is vitally needed to support intervention analysis and decision-making for the public health priority that is AMR. Our model allows insight into the potential value of AMU reduction interventions in food animals to our society as a whole, and this holistic insight can lead to better-informed intervention design and selection. Future work should tailor this model to specific settings, using local data and considering the policy context and local priorities. This will be best supported by more comprehensive farm-level trials, and use of big data to model the population-level determinants of AMR.

Author contributions

Conceptualisation: ETE, JW, GMK, NRN; data curation: ETE, SDX, TTHL, NRN; formal analysis: ETE, NRN; funding acquisition: ETE, JW, GMK, NRN; investigation: SDX, TTHL; methodology: ETE, GMK, NRN; project administration: JW, GMK, NRN; resources: SDX, TTHL; software: ETE, NRN, GMK; supervision: JW, GMK, NRN; validation: GMK, NRN; visualisation: ETE, GMK, NRN; writing - original draft: ETE; writing - review and editing: ETE, SDX, TTHL, JW, GMK, NRN.

Ethical approval

No ethical approval was sought as this project did not involve human or animal subjects or the collection of new data

Funding

ETE, GMK and NRN's time was funded as part of the SEFASI Consortium, by the MRC under grant code JPIAMR2021–182. The views expressed are those of the author(s) and not necessarily those of the author affiliated institutions and funders, including but not limited to the NHS, the MRC, the Department of Health, or the United Kingdom Health Security Agency.

Declaration of Competing Interest

The authors declare no conflicts of interest

Appendix A. Supplementary data

Supplementary material

Data availability

Data are available on GitHub and linked in the manuscript