Significance
Marine reserves, considered vital for marine biodiversity management, may not always stabilize fish populations as previously believed. Larger reserves can actually promote two types of population oscillations: rapid oscillations due to resource competition and slower oscillations characterized by long transients and regime shifts driven by natural selection. This has implications for reserve design and management, suggesting that smaller reserves may be more effective in stabilizing fish populations. Fisheries managers and policymakers can use this information to strike a balance between population stability and harvesting yields of fish. This study sheds light on the complex interplay of evolution, ecology, and human intervention in marine systems, informing our understanding of the impact of marine reserves on fish populations.
Keywords: marine reserve, transient dynamics, regime shift, evolution, fisheries management
Abstract
Marine reserves are considered essential for sustainable fisheries, although their effectiveness compared to traditional fisheries management is debated. The effect of marine reserves is mostly studied on short ecological time scales, whereas fisheries-induced evolution is a well-established consequence of harvesting. Using a size-structured population model for an exploited fish population of which individuals spend their early life stages in a nursery habitat, we show that marine reserves will shift the mode of population regulation from low size-selective survival late in life to low, early-life survival due to strong resource competition. This shift promotes the occurrence of rapid ecological cycles driven by density-dependent recruitment as well as much slower evolutionary cycles driven by selection for the optimal body to leave the nursery grounds, especially with larger marine reserves. The evolutionary changes increase harvesting yields in terms of total biomass but cause disproportionately large decreases in yields of larger, adult fish. Our findings highlight the importance of carefully considering the size of marine reserves and the individual life history of fish when managing eco-evolutionary marine systems to ensure both population persistence as well as stable fisheries yields.
The widespread problem of over-fishing occurring in many parts of the ocean is causing serious challenges for the preservation of marine biodiversity (1–5). Creating marine reserves is considered a key solution to tackle this issue, which ideally should result in 30% of the oceans being highly protected (6). While marine reserves are increasingly established in various areas around the world (7–10), there is also ongoing debate about their effectiveness compared to traditional management practices (11–14), especially with regard to balancing of conservation and resource utilization (15, 16).
Marine reserves, in which fisheries are forbidden or restricted, are believed to reduce the impact of human activities on fish populations, allowing them to recover and thrive inside the reserve, while at the same time functioning as source populations for larval dispersal (17) that supports stable harvests and improves fisheries yields outside the reserve. Marine reserves have furthermore been argued to enhance ecological resilience (18, 19), even though such beneficial effects may not emerge until a decade after their establishment and their detection may require new monitoring approaches (20). Studies in the Great Barrier Reef Marine Park in Australia indeed confirm that establishing a marine reserve can stabilize population dynamics as well as fisheries yields (21). However, many of the current ecological studies and models used to assess the impacts of marine reserves consider only their short-term consequences on an ecological time scale and do not take into account potential evolutionary responses of the fish populations involved, such as changes in life history traits, gene flow, and genetic diversity (22–24).
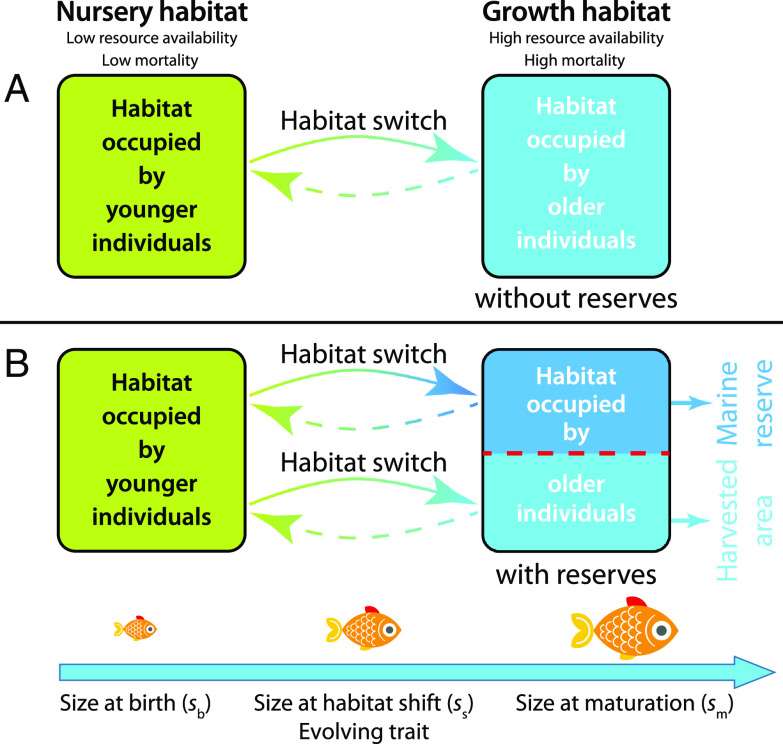
Adaptive evolution is well known to occur in exploited fish populations as a consequence of size- and age-selective harvesting (25). However, the consequences of such fisheries-induced evolution when marine reserves are established may be difficult to predict since many fish species, most prominently anadromous species like salmon and many coral reef fishes (26, 27), use different habitats during different stages of their life history, which exposes them to a multitude of ecological factors that influence fitness. Individuals of the majority of fish species go through an ontogenetic habitat shift during their life history between a “nursery habitat” where they spend the early stage of their life, to a “growth” habitat when they are larger. In the nursery habitat, mortality risks from predation are relatively low, but growth in body size is slow due to competition for limiting food resources. In contrast, in the growth habitat, mortality from predation and fisheries tends to be high, which relaxes competition. Density-dependent effects arising from competition for food are indeed strongest during the early life stages that live in the nursery habitat (28). A recent meta-analysis found substantial evidence for the important role of structured nursery habitats such as sea grass beds, mangroves, and marshes, for enhancing the density, growth, and survival of juveniles of many fish species, including 215 species that are of commercial importance (29).
Because mortality and somatic growth are both dependent on fish body size, small fish face a trade-off between living in the relatively safe nursery habitat and achieving high growth rates in the growth habitat (Fig. 1). The timing of this transition is thus subject to natural selection, allowing the fish to avoid intense food competition as soon as possible while still having a sufficient size to minimize the risk of mortality. Theory (30) predicts that individuals should shift habitats dependent on their body size, which has been experimentally corroborated for a variety of marine species, including the commercially important Nassau grouper (Epinephelus striatus) (31), giant kelpfish (Heterostichus rostratus) (32), blackspot snappers (Lutjanus fulviflamma), and two species of emperor fish (33, 34). Harvesting impacts the evolution of the timing of habitat switch as it makes the growth habitat more risky, especially for larger-sized individuals.
Fig. 1.
Schematic diagram of the fish individual life history under fisheries management without (A) and with (B) the establishment of a marine reserve.
In this study, we explore the long-term consequences of establishing a marine reserve for an exploited fish population, of which the individuals migrate between a nursery and a growth habitat, where they spend consecutive stages of their life history. The nursery habitat is assumed a relatively safe place without harvesting and low mortality rates from natural causes such as predation (from here onward referred to as background mortality), whereas mortality rates due to harvesting as well as natural causes (background mortality) are high in the growth habitat. To this end, we extend a simple consumer–resource model (26), in which the consumer population is structured by individual body size (Materials and Methods). All individuals are born with a body size in the nursery habitat, the habitat occupied by younger individuals. In line with theory (30) and experimental evidence (31–34), we assume they remain in the nursery habitat until their body size reaches a threshold value when they switch to the growth habitat. Individuals with body size will switch to the growth habitat, the habitat occupied by older individuals, where they grow and mature on reaching body size . In contrast to previous models used for marine reserves, e.g., simple discrete models (22, 23), matrix projection models (20, 24, 35), metapopulation models (21, 36), we assume that growth in body size of the individual fish in the nursery habitat, the harvested area, and the marine reserve depends on their feeding rate and hence on the resource density they encounter in these different habitat parts. Reproduction by adult individuals also depends on the food density in the harvested area and the marine reserve, depending on where individuals have settled. Furthermore, in all 3 habitat parts, individuals compete for food and hence deplete food density, as such establishing density-dependent feedback between local population density and individual growth and reproduction operating via food depletion. As a consequence, the time individuals spend in the nursery habitat and the time they take to mature are dependent on resource densities and are affected by the competition for these resources.
We assume harvesting to occur on all individuals in the growth habitat and compare fisheries management strategies without (Fig. 1A) and with (Fig. 1B) the establishment of a marine reserve. For the scenario with a reserve, the growth habitat is separated into two parts consisting of the harvested area and the marine reserve. For the scenario without reserve, the whole zone in the growth habitat is the harvested area. See details in Fig. 1 for an illustration. When leaving the nursery habitat, we assume that individuals settle in either the part of the harvested area or in the marine reserve without any further migration between these two parts.
We use continuous-time dynamics to describe individual resource consumption, somatic growth, survival, and reproduction. To reduce the number of parameters, we analyze the dynamics of a scaled version of the model on an ecological time scale, assuming that individuals switch between the two habitats on reaching a fixed threshold value of body size, as well as on an evolutionary time scale, when we allow the threshold body size at which individuals switch habitats to evolve (see Materials and Methods for details). This threshold at which individuals switch habitat is indicated with the trait value , which is the scaled analogue of the body size at habitat shift in Fig. 1. We use an approach that combines population genetics and adaptive dynamics to assess the eco-evolutionary consequences of the selection process that results from the establishment of a marine reserve in the growth habitat.
Results
Without a marine reserve, high fishing mortality experienced in the growth habitat results in a stable equilibrium state (see = 0 to 50 in Fig. 2) of the fish population and its resource. Evolutionary analysis (Fig. 4A) furthermore reveals that the high fishing mortality also selects for a rather large value of the body size at habitat shift (). Establishing a marine reserve covering 10% of the growth habitat increases fish biomass in the nursery habitat (Fig. 2, Left) due to increases in total population reproduction rate. Total population reproduction increases because the presence of the marine reserve increases the number of adult individuals, while the high resource densities in both the harvested area and marine reserve make that these adults have a high fecundity (Fig. 2, Left). However, the higher fish densities in the nursery habitat deplete the resource to lower levels (Fig. 2, Left), which slows down body size growth and hence delays the recruitment from the nursery to the growth habitat, which further contributes to increased fish density in the nursery habitat. The slowing down of recruitment due to increased competition among individuals in the nursery habitat in turn results in the occurrence of population cycles with a period of approximately 10 time units, which is close to the time delay between the birth of an individual and the moment it leaves the nursery habitat. From a fisheries perspective, the establishment of the marine reserve decreases the fish biomass available for harvesting not only because the harvested area is smaller but mostly because of the emergence of population cycles (average fish biomass in the harvested area decreases from before 10% of the area is protected from harvesting to afterward).
Fig. 2.
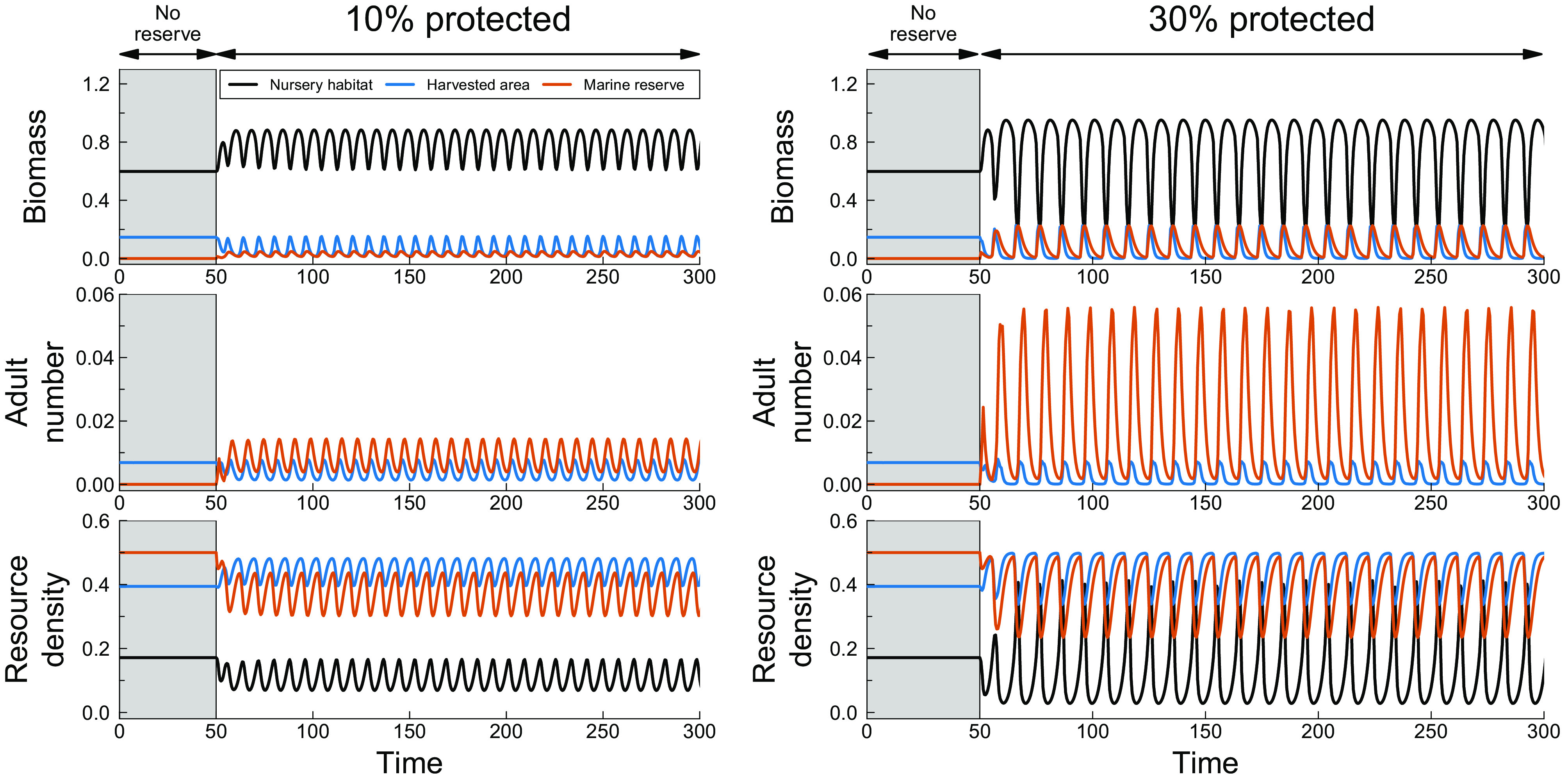
Ecological dynamics of total fish biomass (Top), adult density (Middle) and resource density (Bottom) in the nursery habitat, the harvested area, and the marine reserve following the establishment of a marine reserve at (the reserve does not exist yet during the time interval in gray, , during which the population is in a stable equilibrium state), when the marine reserve covers 10% (Left, ) or 30% (Right, ) of the growth habitat. Evolutionary change in the body size at habitat shift does not occur, which is constant at , corresponding to the evolutionary stable value in the absence of a marine reserve (Fig. 4). Other parameter values are given in Table 1.
Fig. 4.

Equilibrium states and maximum and minimum values occurring during population oscillations of total fish biomass in the nursery habitat (Top) and in the harvested area and marine reserve (Bottom) as a function of the body size at habitat shift in the absence (A) and presence of a marine reserve covering 10% (B) and 30% (C) of the growth habitat. Thick solid lines represent stable equilibrium states, and thin solid lines represent maximum and minimum values during population oscillations. Dashed lines represent unstable equilibrium states. Red dots indicate the evolutionary stable strategy (ESS) for the body size at habitat shift. Green dots marked as limit points (LP) represent saddle-node bifurcation points (tipping points) where regime shifts to an alternative stable or oscillatory state occurs. Red arrows in Top panels indicate the direction of selection in the body size at habitat shift; blue arrows in Top panels (B and C only) indicate the approximate changes in body size at habitat shift and fish biomass that are illustrated in Fig. 3. See Materials and Methods for calculation details. Parameter values as in Table 1.
Establishing a larger marine reserve (30% of the growth habitat) amplifies the population oscillations (Fig. 2, Right) because it leads to substantially larger adult numbers in the reserve. Since resource competition among adults in the harvested area and the marine reserve remains limited, the high adult numbers lead to high offspring production and hence higher densities in the nursery habitat. As a consequence, resource competition in the nursery habitat is intensified (Fig. 2, Right) resulting in population cycles with larger amplitude.
Calculating equilibrium states and population dynamics (see Materials and Methods for details) for different marine reserve sizes (SI Appendix, Fig. S1) confirms the mechanisms underlying the dynamic patterns illustrated in Fig. 2. Larger marine reserve sizes increase the biomass in the nursery habitat, which ultimately leads to population cycles with growing amplitude (SI Appendix, Fig. S1) as a consequence of the increased competition for resources in the nursery habitat. This overexploitation of resources in the nursery habitat is a direct result of protecting part of the adult population from harvesting in the marine reserve.
On an evolutionary timescale, the increase in competition in the nursery habitat following the establishment of a marine reserve imposes selection for an earlier departure at smaller body sizes, leading to evolutionary changes in the trait value . In case there is genetic variation in the trait value (Fig. 3, Left), this trait value decreases over 60 to 70 generations (600 to 700 time units) to an average of , which reduces fish biomass and hence competition in the nursery habitat (Fig. 3, Left). Initially, this stabilizes population oscillations on an ecological time scale (cf. = 1,000 to 1,700 in Fig. 3, Left). Smaller values also increase fish biomass in the harvested area and marine reserve but do not significantly change adult population size. Following the initial decrease in slow, multigenerational cycles arise driven by evolutionary cycling of the trait value , which results in oscillations of the same period in fish biomass in the nursery habitat, harvested area, and marine reserve.
Fig. 3.
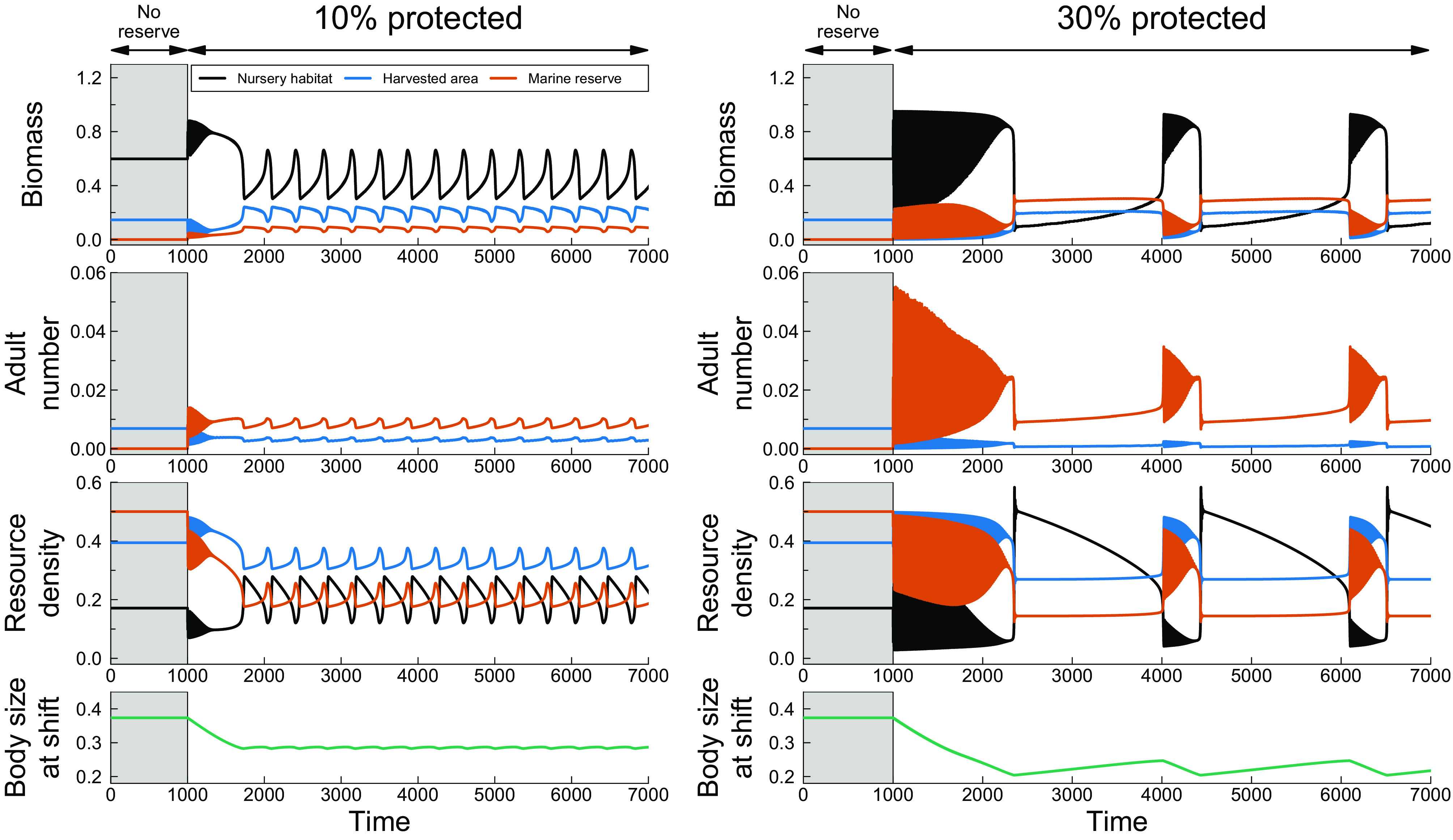
Eco-evolutionary dynamics of total fish biomass (Top Row), adult density (second Row), and resource density (third Row) in the nursery habitat, the harvested area and the marine reserve and the body size at habitat shift (Bottom Row) following the establishment of a marine reserve at = 1,000 (reserve does not exist yet during the time interval in gray, = 0 to 1,000, during which the population is in a stable equilibrium state), when the body size at habitat shift evolves over time and the marine reserve covers 10% (Left, ) or 30% (Right, ) of the growth habitat. Notice that the ecological cycles with a period of approximately 10 time units that are visible in Fig. 2 show up in this figure as solidly colored areas with decreasing amplitude over time. Other parameter values are given in Table 1.
Establishing a larger marine reserve (30% of the growth habitat) results in evolution to even lower values of the body size at habitat shift ( values of 0.2 to 0.25) because the competition in the nursery habitat for resources is in this case more intense. Evolutionary cycles in occur subsequently with a period of hundreds of generations (roughly 2,000 time units), which result in switches between two dynamic patterns in fish biomass. When is low, the harvested area and marine reserve contain high biomass, while biomass in the nursery habitat is low. Biomass remains stable in the harvested area and marine reserve, whereas in the nursery habitat biomass and thus competition increases. Eventually, when reaches higher values, increased competition in the nursery habitat leads to a sudden shift to a dynamic regime where biomass in the nursery habitat is high, and biomass in the harvested area and marine reserve is low. This regime is characterized by population (generation) cycles on ecological time scales with decreasing amplitude as evolves to lower values.
Calculating equilibrium states, population dynamics, as well as selection gradients (see Materials and Methods for details) as a function of the body sizes at habitat shift (Fig. 4) reveals the mechanisms underlying the dynamic patterns illustrated in Fig. 3. In the absence of a marine reserve (Fig. 4A), fish biomass in the nursery and growth habitat show sigmoidal and hump-shaped patterns with body size at habitat shift, respectively. Low fish biomass in the nursery habitat occurs when individuals leave at small sizes, resulting in limited resource competition. In this case, low survival in the growth habitat due to harvesting mortality regulates the population, as few individuals reach maturity, producing low offspring numbers that enter the nursery habitat. Conversely, high fish biomass in the nursery habitat occurs when individuals leave at large sizes, resulting in substantial resource competition. This competition slows down individual growth and limits recruitment to the growth habitat, causing biomass in the growth habitat to decrease after peaking at intermediate body sizes at habitat shift. Population cycles occur due to strong competition in the nursery habitat at large body sizes at habitat shift, even without a marine reserve. Selection favors an increase in body size at habitat shift at small values, when low survival in the growth habitat regulates the population, whereas smaller body sizes at habitat shift are favored at large values, when the population is regulated by resource competition in the nursery habitat. A rather large value of the body size at habitat shift is selected for (i.e., the evolutionary stable state, ESS) where these two factors achieve a balance (Fig. 4A).
In the presence of a marine reserve (Fig. 4 B and C), the two dynamic regimes, in which either low offspring production due to low survival in the growth habitat or strong resource competition in the nursery habitat regulates the population, respectively, still occur at low and high values of the body size at habitat shift. However, the ecological equilibrium curve becomes folded, resulting in alternate stable states for a range of intermediate trait values (Fig. 4 B and C). Larger marine reserve sizes increase the range of trait values with alternate stable states and lead to the occurrence of population cycles at lower values of body size at habitat shift (Fig. 4C). Consequently, with a marine reserve covering 30% of the growth habitat, a stable equilibrium with low survival to adulthood due to early recruitment from the nursery to the growth habitat occurs as alternative to a population cycle regulated by strong competition in the nursery habitat and slow recruitment from the nursery to the growth habitat.
Larger body sizes at habitat shift are still favored when low survival to adulthood due to early recruitment from the nursery to the growth habitat regulates the population at small values, while smaller body sizes at habitat shift are favored when strong competition in the nursery habitat and slow recruitment from the nursery to the growth habitat regulate the population (Fig. 4 B and C) at large body sizes at habitat shift. However, the evolutionary stable state (ESS) of body size at habitat shift would now be unattainable because it corresponds to an unstable ecological equilibrium. As a result, the system alternates between the two dynamic regimes over evolutionary time, with the direction of selection reversing during regime shifts. The overlap between alternate dynamic regimes is smaller with a 10% marine reserve compared to a 30% marine reserve, leading to faster evolutionary cycling (compare Fig. 3, Left and Right). In the case of a 30% marine reserve, the population state regulated by strong competition in the nursery habitat consists of population cycles at a fast ecological time scale, explaining the distinct patterns in Fig. 3, Left.
Our finding that marine reserves promote cycles in fish populations on ecological and evolutionary time scales is robust against changes in parameters. Without evolutionary change in the body size at habitat shift and without a reserve, the population is in a stable equilibrium, as long as the total mortality rate in the growth habitat, from both natural causes and harvesting, is roughly twice the mortality risk in the nursery habitat (SI Appendix, Fig. S2, Top Row). For lower total mortality rates in the growth habitat cycles in population abundance also occur in the absence of a reserve. The implementation of a marine reserve increases the parameter region with population cycles, especially when it covers 30% of the growth habitat (SI Appendix, Fig. S2, Top Row).
When evolution in the body size at habitat shift does occur, the parameter region at low values of background and fisheries mortality in the growth habitat, where cycles in population abundance occur, also increases due to the establishment of a marine reserve (SI Appendix, Fig. S2, Bottom Row). These cycles in abundance are of larger amplitude than without evolution in size at habitat shift. However, at very high total mortality rate in the growth habitat, the body size at habitat shift evolves to become equal to the maturation size, such that individuals stay in the nursery habitat till they mature, after which they move out, reproduce, and quickly die. In this extreme case, the model also predicts cycles in abundance to occur even without a reserve, which are of smaller amplitude and shorter period.
Finally, improving conditions in the nursery habitat by lowering the mortality experienced by small individuals does not qualitatively change the dynamics irrespective of whether the body size at habitat shift evolves or not (SI Appendix, Figs. S3 and S4). The extent of genetic variance in body size at habitat shift affects the rate of evolutionary change, with larger genetic variance speeding up the process (SI Appendix, Fig. S5).
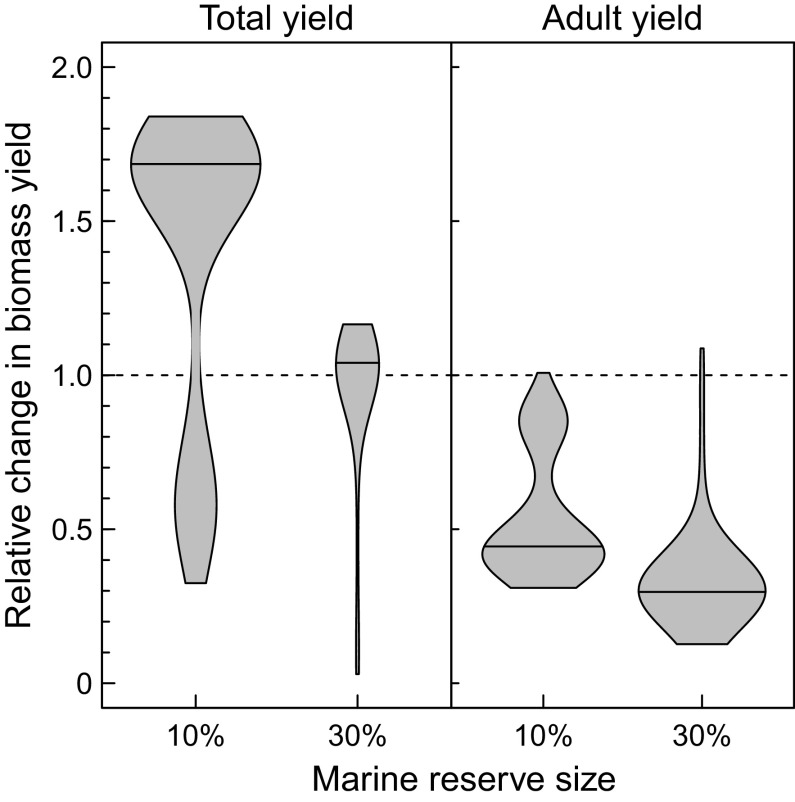
The selection on evolutionary timescales for smaller body sizes at habitat shift following establishment of a marine reserve has consequences for harvesting yields. Leaving the nursery habitat at smaller body sizes results on average in higher maximum sustainable yields of total biomass following marine reserve establishment (Fig. 5), especially when the reserve covers 10% of the growth habitat. However, when 30% of the growth habitat is a marine reserve, the long evolutionary cycles result in low harvesting yields during the larger part of these cycles. These increased total biomass yields are due to increased harvesting of immature fish, while the maximum sustainable biomass yield of adult individuals is on average 2 to 3 times lower after reserve establishment (Fig. 5). This is because fish are exposed to high fishing mortality for a longer period before maturing due to the smaller body size at habitat shift, leading to substantially lower adult biomass densities.
Fig. 5.
Violin plot showing the distribution of harvesting yield per unit time for different sizes of marine reserves. Left: Yield in terms of total biomass (including juveniles and adults); Right: Yield of adult biomass only. Solid lines within the violin shapes indicate median values. Both total and adult biomass yield are expressed as the ratio of the post- and pre-marine reserve yield (the latter being constant in time). Parameter values as in Table 1 except for the harvesting mortality , which equals in the absence of a reserve while and when the marine reserve covers 10% and 30%, respectively, of the growth habitat. These harvesting mortality rates on average provide the maximum sustainable yield in terms of adult biomass (SI Appendix, Fig. S7).
Higher yields in terms of total biomass can be expected over a wide range of harvesting and background mortality rates but only if the body size at habitat shifts evolves (SI Appendix, Fig. S6, Bottom Row). In this case, the maximum sustainable yield will be achieved at higher harvesting rates when a marine reserve is present. In the absence of evolution in the body size at habitat shift, total biomass yields are consistently lower when a marine reserve is established, irrespective of the extent of the reserve (SI Appendix, Fig. S6, Top Row). The yield in terms of adult biomass is however always lower in the presence of a marine reserve, irrespective of whether evolution in the body size at habitat shift occurs or not (SI Appendix, Fig. S7).
Discussion
Marine reserves are ascribed an important role in sustainable fisheries management (1, 37) as they are considered to protect part of an exploited fish population from human impacts. However, with more and larger adults surviving in a reserve, offspring production can be expected to increase, in turn increasing competition and hence decreasing survival in early life stages, which is thought to regulate most exploited fish populations (28). Our theoretical analysis reveals the potential consequences of increased density dependence in early life stages on both ecological and evolutionary time scales for fish populations that spend their early life in a nursery habitat as is common in many marine species (38).
On ecological time scales, early-life competition for resources will reduce individual growth and hence delay recruitment to subsequent life stages. Density-dependent juvenile development rates are well known to promote the occurrence of population cycles with a period close to the generation time of species that are known as generation cycles (39) and commonly occur in size-structured populations due to strong competition (40–44). On evolutionary time scales, increased density dependence in early life stages will favor earlier recruitment from the nursery grounds to habitats inhabited by older individuals, where they often experience higher mortality rates due to harvesting or predation. Hence, marine reserves will impinge on the trade-off between strong competition and low survival early in life and low offspring production due to high harvesting and predation mortality in later stages. Both mechanisms can regulate the population which results in the co-occurrence of alternate dynamic regimes for the same, intermediate values of body size at habitat shift. This bistability between alternate dynamic regimes with opposite directions of selection provides the basis for cycles on evolutionary time scales that are driven by the evolution in body size at habitat shift. These cycles lead to regular regime shifts between the alternate dynamic regimes.
Previous studies of the role of marine reserves, using simple discrete-time models with and without age structure (21–23, 36) or integral projection models (45), suggest that they may promote recovery of exploited fish populations over relatively long time scales although life history traits like age at maturity can affect the speed of recovery and the amplitude of possible oscillations (23, 24). Our results add to these earlier findings as we show that marine reserves may also promote population cycling not only on ecological but also over evolutionary time scales. These population cycles emerge because of the explicit treatment of density dependence in our model in different parts of the habitat. Marine reserves differentially change the strength of density dependence in the different habitat parts, which, as we show, gives rise to these cycles. Our results thus provide a cautionary note about the establishment of especially large-sized marine reserves. Their consequences for ecosystem services may be more detrimental than expected if not at the same time the nursery habitat where small fish live is extended or its resource profitability is improved. While marine reserves are argued to benefit not only conservation but also fisheries, our results show that increases in fisheries yield will only occur after selection for smaller body size at habitat shift and will only increase the yield of smaller, immature fish. If catching larger, adult fish is disproportionately more valuable, establishing a marine reserve will have only negative fisheries consequences.
Previous studies suggest the importance of setting expected timelines to monitor the effect of marine reserve for recovering fish populations (20). The population cycles that our model predicts to occur on both ecological as well as evolutionary time scales complicate assessment of a marine reserve’s effectiveness significantly and may require substantially increasing these timelines. Short monitoring programs or approaches that monitor only one of the different habitats used by the population may provide too positive or too negative a view of the effectiveness of the reserve, depending on the phase of the cycle during which monitoring occurs.
To allow the identification of the mechanisms underlying predictions, our model is based on a suite of simplifying assumptions. We argue however that these simplifications do not significantly influence the qualitative results and insights we present. First, in the growth habitat, both juvenile and adult fish are assumed to experience the same constant background and harvesting mortality rate. Both background and harvesting mortality, however, tend to be size-dependent with background mortality due to predation usually decreasing with body size, whereas harvesting mortality rate increases with body size. Since our finding that marine reserves promote cycles in fish populations depends only on the total mortality rate in the growth habitat, the assumption of equal mortality for both juveniles and adults implies that we assume the size dependency of background and harvesting mortality rate to cancel each other out.
Second, we only consider intraspecific competition for resources and ignore interspecific competition, which is most important for the nursery habitat where competition for resources is strongest. If intraspecific competition is stronger than interspecific competition it is unlikely that other fish species that feed on the same resource would respond sufficiently rapidly to cancel out the large fluctuations in abundance that result from implementing the marine reserve. On the other hand, if interspecific competition would dominate intraspecific competition, we speculate that implementing a marine reserve might have very little effect at all as interspecific competition would quench the positive effect of the reserve on total population reproduction.
Finally, we have focused on the body size at which individuals transition from the nursery to the growth habitat as the only evolvable trait. Empirical evidence shows that ecological conditions indeed influence this trait (31–34) and that individual fish optimize this trait to minimize the ratio between their mortality and growth rate (31), the “ rule”], in line with theoretical predictions (30). Of course, the individual life histories of fish are characterized by many more evolvable traits that may be impacted by fisheries. Empirical evidence from anadromous salmonids, for example, indicates that fishing entails evolutionary changes in a diverse array of life history traits such as body size, migration timing, as well as age of maturation; moreover, these evolutionary changes are detectable within ten or fewer generations (46). Likewise, fisheries-induced evolutionary changes in maturation age, annual growth, and fecundity, which may result in irreversible ecological transitions or decreases in maximum sustainable yield, have been documented for a range of other species (47). How the concurrent evolution in these different life history traits, including the evolution of size at habitat shift, interact to shape population dynamics following the establishment of marine reserves is an open question for future research with potentially different outcomes in terms of population oscillations and fisheries yield.
Despite these simplifying assumptions about fish life history, the mechanism underlying the population cycles on both ecological and evolutionary time scales are general and hence likely robust. Whether or not individuals will settle for life inside or outside a marine reserve or migrate between the areas, an effective marine reserve will increase the density and body size of older, adult individuals in an exploited population. Since larger adults contribute disproportionately to reproduction (48), offspring production will increase, increasing competition on nursery grounds. Irrespective of the details of particular systems, an effective marine reserve will therefore shift the mode of population regulation from on the one hand limited offspring production by small numbers of adults that escape high harvesting and predation mortality to, on the other hand, limited recruitment from the nursery to the growth habitat as a consequence of strong competition and thus low survival early in life. Key to the occurrence of the population cycles, in particular on evolutionary time scales, is the existence of alternative dynamic patterns for a range of trait values with opposing directions of selection in each of them that drives the trait value beyond the tipping point. Such alternative dynamic patterns occur, however, generically in models of populations exhibiting habitat shifts during ontogeny (49, 50), even in size-structured models for salmon populations that are based on a detailed, species-specific dynamic energy budget model (51).
Most importantly, our study highlights that it is crucial for future studies to take into account that one of the most generic elements in fish life history, the habitat shift between a nursery and growth habitat, plays a defining role in the responses of fish stocks to any type of perturbation or management and hence cannot be ignored.
Materials and Methods
We use a minimal, size-structured population model (52), in which individuals are characterized by their body size and compete for resources in different habitats during consecutive stages of their life history. The original model (52) accounts for three key ingredients of the dynamics of a population of individuals exploiting different habitats in consecutive life stages: 1) competition for food and food-dependent development in each habitat resulting in density-dependent growth in body size and density-dependent reproduction; 2) a habitat switch during life history dependent on individual body size; and 3) differences in mortality rate experienced in the different habitats. Individuals are born in the nursery habitat, with a size . Based on theory (30) and experimental evidence (31–34), we assume they remain in the nursery habitat until they reach body size when they switch to the growth habitat. Juvenile individuals mature in the growth habitat and start to reproduce at a body size (). Individual resource consumption, somatic growth, survival, and reproduction follow continuous-time dynamics.
We extend the model by assuming that a fraction of the growth habitat constitutes a marine reserve, in which fisheries are strictly forbidden, and that harvesting only occurs in the remaining fraction of the growth habitat, which we refer to as the harvested area. On reaching body size , a fraction and of the individuals is hence assumed to migrate to and settle in the marine reserve and the harvested area, respectively. We assume that no further migration of individuals between the marine reserve and the harvested area occurs.
In each habitat, density-dependence in somatic growth rate and adult fecundity is mediated by food abundance, since food density declines through foraging by the consumer individuals. Resources are assumed to follow semichemostat growth dynamics (52, 53) with productivity ( or ) and turnover rate when consumers are absent. The dynamics of food density in the nursery habitat (), the harvested area (), or the marine reserve () in the absence of consumers (i.e., fish individuals) is hence given by:
| [1] |
We define as the attack rate on the food resource in habitat and assume individuals to forage following a linear functional response, such that the foraging rate in habitat (, or ) equals . Defining as the proportionality constant relating growth rate in body size to food ingestion rate, somatic growth rate in habitat is given by . Defining as the proportionality constant relating adult fecundity to food ingestion rate, adult reproduction rate is given by in the harvested area and by in the marine reserve. Finally, individuals experience a mortality rate equal to , , and in the nursery habitat, the harvested area and the marine reserve, respectively, with representing the fisheries exploitation rate in the harvested area and the mortality rate in the growth habitat (harvested area and marine reserve) from other causes than fisheries (e.g., predation).
Ecological Dynamics.
Standard methods to formulate size-structured population models from individual life history processes (54) result in the following system of ordinary and partial differential equations (ODEs and PDEs), describing dynamics of food density and population size distribution in the nursery habitat (SI Appendix):
| [2] |
Here, the quantity represents the total population birth rate by all adult individuals (see below). Notice that the size distribution is only defined on the interval and that the integral
represents the total number of consumer individuals in the nursery habitat.
The rate at which individuals reach body size and hence leave the nursery habitat is given by (54). Assuming that a fraction and of these individuals end up in the marine reserve and harvested area, respectively, the dynamics of food density and population size distribution in the marine reserve is described by (see details in SI Appendix, section A)
| [3] |
Notice that the foraging rate of the consumers on the resource has to be corrected by as the integral
represents the total number of consumer individuals in the marine reserve, whereas represents food density.
Similarly, the dynamics of food density and population size distribution in the harvested area is described by (see details in SI Appendix, section A)
| [4] |
Adult individuals in the marine reserve and harvested area reproduce at rates and , such that the total population reproduction rate (cf. Eq. 2) is given by
| [5] |
The model can be nondimensionalized (52) and expressed in terms of scaled body size , which implies that individuals leave the nursery habitat at (scaled) body size and mature at . This nondimensionalization results in the following system of equations (see details in SI Appendix, sections A and B):
| [6] |
| [7] |
| [8] |
| [9] |
| [10] |
| [11] |
| [12] |
| [13] |
| [14] |
The interpretation of the parameters occurring in this nondimensionalized model, their definition in terms of the original model parameters, and their default values in our study are given in Table 1. Default values of the parameters are taken from refs. 40 and 52 and reflect qualitative relationships of mortality and growth rates between the nursery and the growth habitat (31, 33). Because these are scaled parameters, their values can only be interpreted relative to one another. We assume and , the resource productivity in the harvested area and the marine reserve relative to the nursery habitat, to both equal 0.5 as we consider the marine reserve to be an integral part of the growth habitat and the nursery habitat to be the more productive environment. The maximum resource densities in the nursery habitat, harvested area, and marine reserve equal , , and , respectively. The resource growth rate hence acts as a scaling factor of the absolute densities, scaling all maximum resource densities in the same way, which does not qualitatively influence dynamics as this depends on their relative values. The mortality rate in the nursery habitat is assumed to be smaller than the total mortality rate from predation and harvesting () in the growth habitat, although we analyze the effect of different values for both parameters in our study (SI Appendix, Figs. S6 and S7). We take and , the attack rate on resources in the harvested area and the marine reserve relative to the nursery habitat, both equal to 1 because we consider differences in ingestion rate between the nursery and growth habitat to arise from differences in food availability rather than individual foraging capacity. The large value of reflects that many more eggs can be produced with the same amount of energy as required to produce a unit of somatic tissue. In ref. 40, it is furthermore shown that the value of does not qualitatively change dynamics as long as is sufficiently large. Finally, we adopt a rather standard value for the heritability (55), while we analyze the effect of different values of the body size at habitat shift and the width of the trait distribution .
Table 1.
Scaled parameter interpretations, default values, and their definitions
| Symbol | Ecological interpretation | Scaled parameter definition | Default value |
|---|---|---|---|
| Resource growth rate | 1 | ||
| Ratio of resource productivity in the harvested area and the nursery habitat | = 0.5 | ||
| Ratio of resource productivity in the marine reserve and the nursery habitat | = 0.5 | ||
| Background mortality rate in the nursery habitat | 1.0 | ||
| Harvesting mortality in harvested part of the growth habitat | 1.5 | ||
| Background (nonharvesting related) mortality rate in the growth habitat | 0.8 | ||
| Ratio of the attack rate on resources in the harvested area and the nursery habitat | 1 | ||
| Ratio of the attack rate on resources in the marine and the nursery habitat | 1 | ||
| Scaled body size at habitat switch | Evolving trait | ||
| Scaling constant relating adult fecundity to food density relative to somatic growth efficiency | 2,000 | ||
| Heritability | 0.3 | ||
| Relative half-width of the trait distribution (fraction of the average trait value) | 0.1 |
In this nondimensionalized model, the total biomass of consumers in the three different habitats is represented by the integrals:
and the yield in terms of total and adult biomass by:
respectively.
Eco-Evolutionary Dynamics.
The size of a marine reserve impacts mortality rates, altering the trade-off between survival and growth/reproduction when individuals move between habitats. We use quantitative genetics (56) to study the evolutionary dynamics of body size at habitat switch, assuming it is a polygenic trait distributed according to a truncated, approximately normal, distribution (more specifically, a Bates distribution of degree three), with mean and a minimum and a maximum value and , respectively.
To compute the mean trait value of newborn individuals at time , we compute the mean trait value of all adults in the marine reserve and the harvested area, as well as their mean trait value , but weighted by their individual fecundity, which equals and for individuals in the marine reserve and harvested area, respectively. The mean trait value of the newborn offspring is then set equal to:
| [15] |
in which is the heritability with default value . The genetic variation in the trait, , is assumed constant and equal to (but see SI Appendix, Fig. S5). In addition, we compute Evolutionary Stable States (ESSs) using an adaptive dynamics approach for size-structured populations (57).
Numerical Analysis.
As in previous studies (54), we used the Escalator Boxcar Train (EBT) method (54, 58), a numerical approach for size-structured population models, to investigate eco-evolutionary dynamics with and without a marine reserve. In the absence of genetic variation, individuals are grouped into cohorts, which include all individuals born within a short period, and they are characterized by the number of individuals and their average body size. In case of genetic variation, cohorts are subdivided into 11 subcohorts, which all have the same body size at birth () and maturation () but differ in their body size at habitat switch . Individuals within a subcohort are considered identical. Each of the 11 subcohorts is assigned its own trait value: one subcohort with (see above), five with lower and five with higher values than , equidistantly separated by an amount of . Newborn individuals are distributed over subcohorts with different values such that the trait distribution approximates a Bates distribution between and , as described above. The population dynamics are followed by numerically integrating the ODEs for each subcohort separately, which allows for assessing the effects of marine reserves and evolution on fish population dynamics (Figs. 2 and 3). We furthermore use the PSPManalysis software package (59) to numerically compute ecological equilibrium states of the model as a function of model parameters and combine these results with EBT simulations to visualize stable and unstable equilibrium values as well as maximum and minimum densities during limit cycles as a function of the body size at habitat switch (Fig. 4) and the size of the marine reserve (SI Appendix, Fig. S1). The PSPManalysis package also allows to detect ESSs irrespective of whether the equilibrium is ecologically stable or unstable by calculating the selection gradient using the adaptive dynamics approach. Hence, by using a combination of EBT and PSPManalysis package, we detect ESSs in the ecological setting.
Supplementary Material
Appendix 01 (PDF)
Acknowledgments
This research is supported by the National Natural Science Foundation of China (grants 32101235 and 32071609) and Basic Research Program of Shanxi Province (20210302124141) to R.C.
Author contributions
R.C. and Q.-X.L. designed research; R.C. and P.C.C.-P. performed research; P.C.C.-P., S.X., P.J., and A.M.d.R. contributed new numerical/analytic tools; and R.C., Q.-X.L., and A.M.d.R. wrote the paper.
Competing interests
The authors declare no competing interest.
Footnotes
This article is a PNAS Direct Submission.
Data, Materials, and Software Availability
All codes to produce the figures are available in the repository GitHub https://doi.org/10.21942/uva.23057060 (60). Results are theoretical, and numerical analysis was performed using software available in https://staff.fnwi.uva.nl/a.m.deroos/EBT/index.html (61) and https://staff.fnwi.uva.nl/a.m.deroos/PSPManalysis/index.html (62).
Supporting Information
References
- 1.Sala E., et al. , Protecting the global ocean for biodiversity, food and climate. Nature 592, 397–402 (2021). [DOI] [PubMed] [Google Scholar]
- 2.Costello C., et al. , Global fishery prospects under contrasting management regimes. Proc. Natl. Acad. Sci. U.S.A. 113, 5125–5129 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ye Y., Gutierrez N. L., Ending fishery overexploitation by expanding from local successes to globalized solutions. Nat. Ecol. Evol. 1, 1–5 (2017).28812620 [Google Scholar]
- 4.Bruno J. F., et al. , Climate change threatens the world’s marine protected areas. Nat. Clim. Chang. 8, 499–503 (2018). [Google Scholar]
- 5.Edgar G. J., et al. , Global conservation outcomes depend on marine protected areas with five key features. Nature 506, 216–220 (2014). [DOI] [PubMed] [Google Scholar]
- 6.O’Leary B. C., et al. , Effective coverage targets for ocean protection. Conser. Lett. 9, 398–404 (2016). [Google Scholar]
- 7.Magris R. A., et al. , Biologically representative and well-connected marine reserves enhance biodiversity persistence in conservation planning. Conser. Lett. 11, e12439 (2018). [Google Scholar]
- 8.Munguia-Vega A., et al. , Ecological guidelines for designing networks of marine reserves in the unique biophysical environment of the gulf of California. Rev. Fish Biol. Fisher. 28, 749–776 (2018). [Google Scholar]
- 9.Hopf J. K., Jones G. P., Williamson D. H., Connolly S. R., Synergistic effects of marine reserves and harvest controls on the abundance and catch dynamics of a coral reef fishery. Curr. Biol. 26, 1543–1548 (2016). [DOI] [PubMed] [Google Scholar]
- 10.Díaz-Vega J. P., Flores-Arévalo Y., Evaluating marine reserves as a management policy in the central-southern anchovy (Engraulis ringens) fishery of chile. Lat. Am. J. Aquat. Res. 49, 212–226 (2021). [Google Scholar]
- 11.Hastings A., Botsford L. W., Equivalence in yield from marine reserves and traditional fisheries management. Science 284, 1537–1538 (1999). [DOI] [PubMed] [Google Scholar]
- 12.Hilborn R., Traditional fisheries management is the best way to manage weak stocks. Proc. Natl. Acad. Sci. U.S.A. 114, E10610 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Hastings A., Gaines S. D., Costello C., Marine reserves solve an important bycatch problem in fisheries. Proc. Natl. Acad. Sci. U.S.A. 114, 8927–8934 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Crowder L. B., et al. , The impacts of fisheries on marine ecosystems and the transition to ecosystem-based management. Annu. Rev. Ecol. Evol. Syst. 39, 259–278 (2008). [Google Scholar]
- 15.Erisman B. E., et al. , Balancing conservation and utilization in spawning aggregation fisheries: A trade-off analysis of an overexploited marine fish. ICES J. Marine Sci. 77, 148–161 (2020). [Google Scholar]
- 16.De Leenheer P., Optimal placement of marine protected areas: A trade-off between fisheries goals and conservation efforts. IEEE Trans. Autom. Control 59, 1583–1587 (2013). [Google Scholar]
- 17.Harrison H. B., Bode M., Williamson D. H., Berumen M. L., Jones G. P., A connectivity portfolio effect stabilizes marine reserve performance. Proc. Natl. Acad. Sci. U.S.A. 117, 25595–25600 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Barnett L. A., Baskett M. L., Marine reserves can enhance ecological resilience. Ecol. Lett. 18, 1301–1310 (2015). [DOI] [PubMed] [Google Scholar]
- 19.Wilson J. R., Bradley D., Phipps K., Gleason M. G., Beyond protection: Fisheries co-benefits of no-take marine reserves. Marine Policy 122, 104224 (2020). [Google Scholar]
- 20.Kaplan K. A., et al. , Setting expected timelines of fished population recovery for the adaptive management of a marine protected area network. Ecol. Appl. 29, e01949 (2019). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Hopf J. K., Jones G. P., Williamson D. H., Connolly S. R., Marine reserves stabilize fish populations and fisheries yields in disturbed coral reef systems. Ecol. Appl. 29, e01905 (2019). [DOI] [PubMed] [Google Scholar]
- 22.Chen R., Transient inconsistency between population density and fisheries yields without bycatch species extinction. Ecol. Evol. 10, 12372–12384 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Chen R., Tu C., Liu Q. X., Transient perturbations reveal distinct strategies for reserve benefits in life history-dependent ecosystems. Ecol. Modell. 466, 109895 (2022). [Google Scholar]
- 24.White J. W., et al. , Transient responses of fished populations to marine reserve establishment. Conser. Lett. 6, 180–191 (2013). [Google Scholar]
- 25.Heino M., Pauli B. D., Dieckmann U., Fisheries-induced evolution. Annu. Rev. Ecol. Evol. Syst. 46, 1–20 (2014). [Google Scholar]
- 26.Chaparro-Pedraza P. C., de Roos A. M., Density-dependent effects of mortality on the optimal body size to shift habitat: Why smaller is better despite increased mortality risk. Evolution 74, 831–841 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.De La Morinière E. C., Pollux B., Nagelkerken I., Van der Velde G., Post-settlement life cycle migration patterns and habitat preference of coral reef fish that use seagrass and mangrove habitats as nurseries. Estuarine Coastal Shelf Sci. 55, 309–321 (2002). [Google Scholar]
- 28.Zimmermann F., Ricard D., Heino M., Density regulation in Northeast Atlantic fish populations: Density dependence is stronger in recruitment than in somatic growth. J. Anim. Ecol. 87, 672–681 (2018). [DOI] [PubMed] [Google Scholar]
- 29.Lefcheck J. S., et al. , Are coastal habitats important nurseries? A meta-analysis. Conser. Lett. 12, e12645 (2019). [Google Scholar]
- 30.Werner E. E., Gilliam J. F., The ontogenetic niche and species interactions in size structured populations. Annu. Rev. Ecol. Syst. 15, 393–425 (1984). [Google Scholar]
- 31.Dahlgren C. P., Eggleston D. B., Ecological processes underlying ontogenetic habitat shifts in a coral reef fish. Ecology 81, 2227–2240 (2000). [Google Scholar]
- 32.Yeager M. E., Hovel K. A., Structural complexity and fish body size interactively affect habitat optimality. Oecologia 185, 257–267 (2017). [DOI] [PubMed] [Google Scholar]
- 33.Kimirei I. A., et al. , What drives ontogenetic niche shifts of fishes in coral reef ecosystems?. Ecosystems 16, 783–796 (2013). [Google Scholar]
- 34.Kimirei I. A., Nagelkerken I., Mgaya Y. D., Huijbers C. M., The mangrove nursery paradigm revisited: Otolith stable isotopes support nursery-to-reef movements by indo-pacific fishes. PLoS One 8, e66320 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Nickols K. J., et al. , Setting ecological expectations for adaptive management of marine protected areas. J. Appl. Ecol. 56, 2376–2385 (2019). [Google Scholar]
- 36.Hopf J. K., Jones G. P., Williamson D. H., Connolly S. R., Fishery consequences of marine reserves: Short-term pain for longer-term gain. Ecol. Appl. 26, 818–829 (2016). [DOI] [PubMed] [Google Scholar]
- 37.Maxwell S. L., et al. , Area-based conservation in the twenty-first century. Nature 586, 217–227 (2020). [DOI] [PubMed] [Google Scholar]
- 38.Le Pape O., Bonhommeau S., The food limitation hypothesis for juvenile marine fish. Fish Fisher. 16, 373–398 (2015). [Google Scholar]
- 39.Gurney W., Nisbet R. M., Fluctuation periodicity, generation separation, and the expression of larval competition. Theor. Popul. Biol. 28, 150–180 (1985). [Google Scholar]
- 40.de Roos A. M., Persson L., Competition in size-structured populations: Mechanisms inducing cohort formation and population cycles. Theor. Popul. Biol. 63, 1–16 (2003). [DOI] [PubMed] [Google Scholar]
- 41.Hamrin S. F., Persson L., Asymmetrical competition between age classes as a factor causing population oscillations in an obligate planktivorous fish species. Oikos 47, 223–232 (1986). [Google Scholar]
- 42.Sanderson B. L., Hrabik T. R., Magnuson J. J., Post D. M., Cyclic dynamics of a yellow perch (Perca flavescens) population in an oligotrophic lake: Evidence for the role of intraspecific interactions. Can. J. Fish. Aquat. Sci. 56, 1534–1542 (1999). [Google Scholar]
- 43.Persson L., Byström P., Wahlström E., Cannibalism and competition in Eurasian perch: Population dynamics of an ontogenetic omnivore. Ecology 81, 1058–1071 (2000). [Google Scholar]
- 44.Krkošek M., Hilborn R., Peterman R. M., Quinn T. P., Cycles, stochasticity and density dependence in pink salmon population dynamics. Proc. R. Soc. B: Biol. Sci. 278, 2060–2068 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Rees M., Childs D. Z., Ellner S. P., Building integral projection models: A user’s guide. J. Anim. Ecol. 83, 528–545 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Hard J. J., et al. , Evolutionary consequences of fishing and their implications for salmon. Evol. Appl. 1, 388–408 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Jørgensen C., et al. , Ecology: Managing evolving fish stocks. Science 318, 1247–1248 (2007). [DOI] [PubMed] [Google Scholar]
- 48.Barneche D. R., Robertson D. R., White C. R., Marshall D. J., Fish reproductive-energy output increases disproportionately with body size. Science 360, 642–645 (2018). [DOI] [PubMed] [Google Scholar]
- 49.Schreiber S., Rudolf V. H. W., Crossing habitat boundaries: Coupling dynamics of ecosystems through complex life cycles. Ecol. Lett. 11, 576–587 (2008). [DOI] [PubMed] [Google Scholar]
- 50.de Roos A. M., Persson L., Population and Community Ecology of Ontogenetic Development (Princeton University Press, 2013), vol. 51. [Google Scholar]
- 51.P. C. C. Pedraza, Populations crossing habitat boundaries in the face of environmental change. Ph.D. thesis (University of Amsterdam, The Netherlands, 2019).
- 52.Chaparro-Pedraza P. C., de Roos A. M., Ecological changes with minor effect initiate evolution to delayed regime shifts. Nat. Ecol. Evol. 4, 412–418 (2020). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Persson L., Leonardsson K., de Roos A. M., Gyllenberg M., Christensen B., Ontogenetic scaling of foraging rates and the dynamics of a size-structured consumer-resource model. Theor. Popul. Biol. 54, 270–293 (1998). [DOI] [PubMed] [Google Scholar]
- 54.A. M. de Roos, “A gentle introduction to physiologically structured population models” in Structured-Population Models in Marine, Terrestrial, and Freshwater Systems, S. Tuljapurkar, H. Caswell, Eds. (Springer, Boston, MA, 1997), pp. 119–204.
- 55.Law R., Fishing, selection, and phenotypic evolution. ICES J. Marine Sci. 57, 659–668 (2000). [Google Scholar]
- 56.Lande R., A quantitative genetic theory of life history evolution. Ecology 63, 607–615 (1982). [Google Scholar]
- 57.Durinx M., Metz J. H., Meszéna G., Adaptive dynamics for physiologically structured population models. J. Math. Biol. 56, 673–742 (2008). [DOI] [PubMed] [Google Scholar]
- 58.de Roos A. M., Numerical methods for structured population models: The escalator boxcar train. Numerical Methods Part. Diff. Eq. 4, 173–195 (1988). [Google Scholar]
- 59.de Roos A. M., PSPManalysis: Steady-state and bifurcation analysis of physiologically structured population models. Methods Ecol. Evol. 12, 383–390 (2021). [Google Scholar]
- 60.R. Chen et al., Source code: “Marine reserves promote cycles in fish populations on ecological and evolutionary time scales”. https://github.com/amderoos/MarineReserves. Accessed 22 May 2023. [DOI] [PMC free article] [PubMed]
- 61.de Roos A. M., Software: Escalator Boxcar Train (EBTtool). Institute for Biodiversity and Ecosystem Dynamics. https://staff.fnwi.uva.nl/a.m.deroos/EBT/Software/index.html. Deposited 17 April 2023.
- 62.de Roos A. M., Software PSPManalysis: Numerical procedures for the demographic, bifurcation and evolutionary analysis of physiologically structured population models (PSPMs). Institute for Biodiversity and Ecosystem Dynamics. https://staff.fnwi.uva.nl/a.m.deroos/PSPManalysis/index.html. Deposited 28 October 2021.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix 01 (PDF)
Data Availability Statement
All codes to produce the figures are available in the repository GitHub https://doi.org/10.21942/uva.23057060 (60). Results are theoretical, and numerical analysis was performed using software available in https://staff.fnwi.uva.nl/a.m.deroos/EBT/index.html (61) and https://staff.fnwi.uva.nl/a.m.deroos/PSPManalysis/index.html (62).