Abstract

Proteins that do not fold into their functional native state have been linked to diseases. In this study, the influence of the main and side chains of individual amino acids on the folding of the tryptophan cage (Trp-cage), a designed 20-residue miniprotein, was analyzed. For this purpose, we calculated the solvation free energy (SFE) contributions of individual atoms by using the 3D-reference interaction site model with the atomic decomposition method. The mechanism by which the Trp-cage is stabilized during the folding process was examined by calculating the total energy, which is the sum of the conformational energy and SFE. The folding process of the Trp-cage resulted in a stable native state, with a total energy that was 62.4 kcal/mol lower than that of the unfolded state. The solvation entropy, which is considered to be responsible for the hydrophobic effect, contributed 31.3 kcal/mol to structural stabilization. In other words, the contribution of the solvation entropy accounted for approximately half of the total contribution to Trp-cage folding. The hydrophobic core centered on Trp6 contributed 15.6 kcal/mol to the total energy, whereas the solvation entropy contribution was 6.3 kcal/mol. The salt bridge formed by the hydrophilic side chains of Asp9 and Arg16 contributed 10.9 and 5.0 kcal/mol, respectively. This indicates that not only the hydrophobic core but also the salt bridge of the hydrophilic side chains gain solvation entropy and contribute to stabilizing the native structure of the Trp-cage.
Introduction
Understanding protein folding is of fundamental importance in molecular biology. The advent of neural-network-based structure prediction programs such as AlphaFold21 and RoseTTAFold2 enables native structures to be predicted with high accuracy using amino acid sequences. This is expected to greatly accelerate research on protein structures. However, the ability to predict the native structure does not mean that the protein folding mechanism is fully understood. For example, protein folding and misfolding are associated with several diseases. The fact that knowledge of the native structure is insufficient to identify and treat these diseases has motivated many theorists and experimentalists to study the protein-folding problem. We are particularly interested in the interaction between proteins and the surrounding water, which we study numerically.3−7
The 20-residue tryptophan-cage (Trp-cage) miniprotein, designed by Neidigh et al. and consisting of a Trp residue confined by a hydrophobic core, is a useful compact model protein that is often used to study protein-folding and stability.8 Understanding the contribution of the hydrophobic core to the overall stability of the Trp-cage is of significant interest in protein-folding studies and has implications in protein engineering.9−22 This protein is known to fold spontaneously and cooperatively in ∼4 μs,10 whereas a variant thereof folds in ∼1 μs at room temperature.23 The Trp-cage is therefore highly appropriate for studying the folding processes of peptides, both experimentally11,24,25 and theoretically,22,26−36 and in combination.37,38 The Trp-cage has also been used as a test system for various new methods.13,39−55 Many studies have shown that the Trp-cage can also exist in the form of metastable non-native states, which makes it useful for studying complex folding processes.14,42,43,50,53−59
Figure 1 shows the native structure of the Trp-cage variant (DAYAQWLADGGPSSGRPPPS), with a focus on certain side chains. The Leu, Trp, and Pro residues are hydrophobic, whereas Tyr and Arg are hydrophilic. The Trp-cage consists of a short α-helix from residues 2 to 8, a 310-helix from residues 11 to 14, and a C-terminal polyproline II helix packed against the central tryptophan side chain. The side chain of Trp6 is in contact with the side chain of Tyr3,10,12,20,38,60 Leu7, Pro12,16,40 Arg16,58 Pro18, and Pro19,10,11,61 but not in contact with the side chain of Pro17. These side chains form the hydrophobic core of the Trp-cage, which plays a crucial role in maintaining its structural stability.9−2260 The rotamer of the Trp6 side chain is the rate-limiting factor that governs the folding rate.21,62,63 In addition to the hydrophobic core, the formation of a salt bridge between Asp9 and Arg16 also contributes to the structural stability of the Trp-cage.10−12,14,16,27,53,57,61,64−68 The interaction responsible for the formation of the hydrophobic core is driven by the solvation entropy, which indicates a many-body interaction with the surrounding solvent. During the folding process, the side chains that form the salt bridge are dehydrated. Hence, the interactions with the surrounding solvent should be considered during the protein-folding process.69
Figure 1.

Backbone structures with selected side chains. In the native structure, the side chain of Trp6 is in contact with the side chains of Tyr3, Leu7, Pro12, Arg16, Pro18, and Pro19. The side chain of Pro17 is exposed to the solvent without contact with the side chain of Trp6.
The three-dimensional reference interaction site model (3D-RISM) theory is useful for investigating the interaction of a protein with its surrounding solvents. By combining this theory with the atomic decomposition method developed by Chang and Ham,70−72 we calculated the solvation free energy (SFE) and solvation entropy at individual amino acid residues. Previously, we investigated the protein-folding mechanism of chignolin, a 10-amino acid miniprotein, by studying the influence of the main and side chains on the stability of protein. The native and misfolded states were found to have similar total energies but with a different composition, with side-chain interactions and hydrogen bonding playing crucial roles. Thus, we predicted that the mutation of Thr8 to a neutral amino acid could stabilize the misfolded structure over the native structure.5 We calculated the stability of various structures in which the eighth residue was mutated and found that the T8P mutant stabilizes in the misfolded structure. In addition, NMR analysis of the T8P mutant supported these results.6
In this paper, we present a comprehensive analysis of the SFE and the solvation entropy contributions of amino acids in the hydrophobic core and salt bridge of the Trp cage using the atomic decomposition method. Our study aimed to elucidate the specific amino acids and their side chains that contribute significantly to the stability of the Trp-cage. By quantifying the solvation free energy and solvation entropy of each residue, we identified the key residues involved in stabilizing interactions and gained insights into the driving forces behind the structural stability of the Trp-cage.
Method
We introduce total energy G, which is the sum of the conformational energy E and SFE Δμ:
| 1 |
As shown in previous studies, the conformational energy and the SFE are in competition with each other.3−5,73 The Δμ term consists of two components: the solvation energy, Es, and the solvation entropy, ΔS:
| 2 |
where T denotes the temperature. Hereafter, – TΔS with an energy dimension is termed the solvation entropy term. Evaluating the total energy provides a useful measure of protein structural stability.3−75573 These components can be decomposed into the contributions of individual amino acids i, as follows:
| 3 |
and
| 4 |
where n represents the number of amino acids in the protein. These individual contributions are further divided into contributions from the main and side chains,
| 5 |
and
| 6 |
where M and S represent the main chain and side chains, respectively. The solvation energy and entropy terms are similarly divisible.
The conformational energy of a protein is determined by its structure and is influenced by various energy terms, including van der Waals, electrostatic, bond stretching, angle bending, and torsional energies. The van der Waals, electrostatic, and bond stretching energy terms are two-body potentials that are evenly divided among interacting atoms. However, the division of the energy terms for the angle bending and torsional potentials is not well-defined. Nevertheless, their effects are relatively small, because they exhibit low standard deviation. Therefore, for three- or four-body potentials, the energy term is considered to be equally distributed among the interacting atoms. Molecular mechanics and molecular dynamics programs are commonly used to calculate the energy terms.
The SFE represents the change in chemical energy when a solute molecule is transferred from one position in the gas phase to another in the solvent. Several methods can be employed to calculate the SFE, including the 3D-RISM theory.74,75
In this study, we considered the SFE of not only the whole protein but also of individual atoms using the atomic decomposition method.70,72 This method calculates the SFE by considering the solute–solvent interaction and the solvent distribution function around the solute. The interaction potential acting on solvent site γ at position r is denoted by uγ(r). The distribution function of the solvent site, γ, around the solute is expressed by gγ(r)(=hγ(r) + 1), where hγ(r) is the total correlation function. The SFE is given by the Kirkwood charging formula:76
| 7 |
where ργ denotes the average number density of solvent site γ. The coupling parameter, λ, was used to gradually modify the interaction potential from λ = 0 (no interaction) to 1 (full interaction). u(r;λ) varies with λ, and the distribution function under u(r;λ) is denoted by g(r;λ). Δμ represents the SFE of the whole solute, and we aimed to decompose it into the contributions from the individual atoms. uγ(r;λ) is expressed as a sum of the potentials between the atomic site of the solute, α, and the solvent site, γ, as follows:
| 8 |
where rα is the position of the atomic site α and N is the number of atomic sites in the solute. Thus, the following basic expressions are obtained from eqs 7 and 8:
| 9 |
and
| 10 |
Notably, uαγ(r;λ) has been decomposed into the potentials between atom α in the protein and solvent, while g(r;λ) remains the distribution function with respect to the whole protein. The solute–solvent interaction potential, uαγ(r), can be expressed as a combination of Lennard–Jones (LJ) and electrostatic potentials. The SFE contribution, Δμα, can be calculated by using the charging formula with two coupling parameters, λ1 and λ2. Thus, the solute–solvent interaction potential becomes
| 11 |
Here,
| 12 |
and
| 13 |
where ϵαγ and σαγ are the LJ parameters and qα and qγ are atomic charges. Thus, the integration path for λ1 and λ2 is as follows. First, the LJ interaction is performed from 0 to 1 with λ2 = 0, after which the electrostatic interaction is switched on by integrating λ2 from 0 to 1 while keeping λ1 = 1. Finally, Δμα is expressed as
 |
14 |
After calculating Δμα once, it becomes possible to reproduce the contributions of amino acid residues or main/side chains. A similar expression was derived for the solvation entropy,71 but we used the temperature derivative of the SFE at constant solvent density:
| 15 |
To calculate Δμα, we need hγ(r;λ1,λ2), which is obtained using the 3D-RISM theory. For a solute–solvent system at infinite dilution, the 3D-RISM equation can be written as follows:
| 16 |
where hγ(r;λ1,λ2) and cγ(r;λ1,λ2) are, respectively, the 3D total and direct correlation functions
of the solvent site, γ, around the solute under λ1 and λ2, where the asterisk (∗) denotes
a convolution integral in real space, 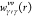 is the site–site intramolecular
correlation function of the solvent, and
is the site–site intramolecular
correlation function of the solvent, and 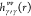 is the site–site total correlation
function of the pure solvent.
is the site–site total correlation
function of the pure solvent.  was precalculated using the 1D-RISM theory
for a pure solvent. The 3D-RISM equation was complemented by the Kovalenko–Hirata
(KH) closure equation, as follows:
was precalculated using the 1D-RISM theory
for a pure solvent. The 3D-RISM equation was complemented by the Kovalenko–Hirata
(KH) closure equation, as follows:
 |
17 |
where β = 1/(kBT) is the reciprocal of the thermodynamic temperature, where kB is the Boltzmann constant and T is the temperature. Finally, the 3D distribution function, gγ(r;λ1,λ2), is defined from hγ(r;λ1,λ2) as follows:
| 18 |
We calculated gγ(r;λ1,λ2) at every integration step of eq 14.
The atomic decomposition method is a powerful method that can calculate the contribution of every single atom in a protein; however, it is computationally expensive. In the present study, a total of 63 calculations were performed for the integration of λ1 and λ2 in eq 14. Thus, we used the reference-modified density functional theory (RMDFT) functional,77−79 which requires only one 3D-RISM calculation to calculate the SFE of the whole protein. We introduced a hard-sphere (HS) reference system to the DFT for polyatomic molecular liquids from which we derived the functional of a solute molecule in water. The RMDFT functional is expressed as follows:
 |
19 |
where
 |
20 |
Here, 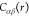 is the site–site direct correlation
function of the pure solvent,
is the site–site direct correlation
function of the pure solvent,  is the intramolecular direct correlation
function,80Lαβ is the length of the bond between the α and β sites,
O denotes the oxygen site of the water solvent,
is the intramolecular direct correlation
function,80Lαβ is the length of the bond between the α and β sites,
O denotes the oxygen site of the water solvent, 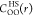 corresponds to the site–site direct
correlation function of the reference HS fluid, FHS[ρO] is the excess intrinsic free energy
functional for the HS fluid,
corresponds to the site–site direct
correlation function of the reference HS fluid, FHS[ρO] is the excess intrinsic free energy
functional for the HS fluid, 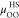 is the excess chemical potential of the
reference HS fluid, δαβ is the Kronecker delta, and ρ is the number density of the
water solvent. Therefore, we require the theory for HS fluids, e.g.,
the effective density approximation (EDA) theory.81 Using this functional, the SFE can be obtained simply by
performing a 3D-RISM calculation under λ1=λ2 = 1.
is the excess chemical potential of the
reference HS fluid, δαβ is the Kronecker delta, and ρ is the number density of the
water solvent. Therefore, we require the theory for HS fluids, e.g.,
the effective density approximation (EDA) theory.81 Using this functional, the SFE can be obtained simply by
performing a 3D-RISM calculation under λ1=λ2 = 1.
Computational Details
In this study, we used the K8A
mutant of the thermostable Trp-cage
variant TC10b.65 Details of the MD simulation
of the Trp-cage on the Anton supercomputer can be found in the Supporting
Information of ref. (82). As the CHARMM22* force field83,84 was used for the MD
simulation, we used the same force field in this study. Structures
were extracted from the MD trajectory for our calculations and used
in intervals of 20 ns, which correspond to every 100 samples. The
total number of sampled structures was 10 440. We used GROMACS85 for calculating the conformational energy. The
SFE of the proteins was calculated using the 3D-RISM theory74,75 with the RMDFT functional77−79 and with the atomic decomposition
method.70,72,73 We used the
TIP3P water model with additional parameters (σ = 0.4 Å
and ϵ = 0.046 kcal mol–1).86,87 The number density of water was 0.033329 –3 for
the thermodynamic states at room temperature (298.15K). We employed
the EDA theory to calculate 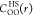 . The optimal HS diameter for the water
oxygen was 2.88 for the RMDFT functional. We chose this diameter so
that the solvation free energies of methane, butane, and isopropane
match the experimental values in the aqueous solvent (the TIP3 model
with additional parameters).77,78 The 3D-RISM/KH equations
were solved on a grid of 2563 points in a cubic cell of
1283 Å3. The atomic decomposition calculations
were performed using 0.05 as the increment width of λ1 and used the following numbers as λ2 ticks: 0.001,
0.005, 0.01, and then from 0.025 to 1.0 in increments of 0.025. The
temperature derivative for the solvation entropy calculation was obtained
during the first-order difference with ΔT =
2 K. We performed the SFE calculation using the 3D-RISM theory with
the original code for multi-GPU processing.88−90
. The optimal HS diameter for the water
oxygen was 2.88 for the RMDFT functional. We chose this diameter so
that the solvation free energies of methane, butane, and isopropane
match the experimental values in the aqueous solvent (the TIP3 model
with additional parameters).77,78 The 3D-RISM/KH equations
were solved on a grid of 2563 points in a cubic cell of
1283 Å3. The atomic decomposition calculations
were performed using 0.05 as the increment width of λ1 and used the following numbers as λ2 ticks: 0.001,
0.005, 0.01, and then from 0.025 to 1.0 in increments of 0.025. The
temperature derivative for the solvation entropy calculation was obtained
during the first-order difference with ΔT =
2 K. We performed the SFE calculation using the 3D-RISM theory with
the original code for multi-GPU processing.88−90
Results and Discussion
First, we describe the computation of the native and unfolded states. The values of the total energy (upper) and the end-to-end distance between the Cα atoms of the N- and C-termini (lower) of the Trp-cage are shown in Figure 2 as a function of Cα-RMSD with respect to the structure with the lowest total energy. The most stable structure has a total energy of −205.5 kcal/mol, and the Cα-RMSD value is 0 Å. Assuming an allowable energy fluctuation of 0.5 kcal/mol per residue, and the fact that the Trp-cage is a 20-residue protein, the overall energy value was estimated to be 10 kcal/mol. We then defined a native state as 29 strctures within 10.0 kcal/mol of the total energy value (i.e, −205.5 kcal/mol). Even if this threshold was changed, it would not result in a qualitative difference in the following discussion. The Cα-RMSD values of these structures were separated and clustered around 1.0 and 1.6 Å. This separation is discussed later. In contrast, the unfolded state was selected as 29 structures with large Cα-RMSD values and end-to-end distances. The structures on the upper right side of the dashed line in the bottom panel of Figure 2 correspond to the unfolded state.
Figure 2.
Upper panel: Total energy as a function of Cα-RMSD with respect to the most stable structure in the simulation. The arrow indicates the most stable structure. Lower panel: End-to-end distance as a function of the Cα-RMSD with respect to the most stable structure in the simulation. The structure above (and to the right) the dashed line was defined as the unfolded state.
Figure 3 shows the backbone structures of the Trp-cage with the side chains of Asp1, Asp9, and Arg16. Figure 3a shows the most stable structure, and Figure 3b shows the structure with the lowest total energy near the Cα-RMSD value of 1.6 in Figure 2. Although the structure in Figure 3b is similar to the most stable structure in Figure 3a, the N-terminus is closer to the C-terminus. The side chain of Asp1 forms a hydrogen bond with the side chain of Arg16. Hereafter, these two structures are referred to as the native1 and native2 structures, respectively. The side chain of Arg16 forms a hydrogen bond with the side chain of Asp9 in the stable structure of the Trp-cage.27,29,37,63,65,68,91,92 In Figure 3b, the side chain of Arg16 forms hydrogen bonds with the side chains of both Asp1 and Asp9. The Trp-cage repeatedly forms and breaks hydrogen bonds between Asp1 and Arg16, moving back and forth between these two structures. The period of this oscillation was ∼60 ns, whereas the hydrophobic core of these structures was retained for a few μs in the MD simulation at 290 K.55 The structural change occurring between these two structures was rapid, making it difficult to distinguish between them. In subsequent calculations, these two structures were processed in their native state.
Figure 3.

Backbone structures with selected side chains: (a) most stable structure and (b) structure with the lowest total energy near the Cα-RMSD value of 1.6 Å. The orange residues are Asp1 and Asp6, and the cyan residue is Arg16.
We then calculated the value of the solvation entropy term, −TΔS, as a function of the Cα-RMSD, as shown in Figure 4. The difference in the solvation entropy, ΔS is known to be attributable to the effect of the excluded volume. The structures in the region with Cα-RMSD values above 10 have a higher value of the solvation entropy term, −TΔS, because the Trp-cage has extended structures, which have a larger excluded volume for water. In the region with Cα-RMSD values between 4 and 8, the solvation entropy term forms a large domain with a range of values approximating 25 kcal/mol. This is due to the presence of various metastable structures that are more compact than the extended structures. The solvation entropy term clearly has a lower value in regions with Cα-RMSD values below 2 Å. The more compact the structure of the Trp-cage, the lower the solvation entropy term, that is, the smaller the excluded volume of water. During the conformational change from native1 to native2, the side chains of Asp1 and Arg16 were dehydrated and formed hydrogen bonds. The solvation entropy, S, increases when the Asp1 side chain forms a hydrogen bond with the Arg16 side chain. The formation of hydrogen bonds by these hydrophilic side chains results in an energy gain from the solvation entropy due to dehydration. The average total energy difference from the native state to the unfolded state was 62.4 kcal/mol, where the positive value indicates that the native state was stable. The difference in the average solvation entropy term was 31.3 kcal/mol, which is half the difference in the average total energy. The solvation entropy contributes significantly to the Trp-cage folding. A comparison of the native1 and native 2 regions reveals that the native2 region has lower values of the solvation entropy term, whereas the native1 region has lower total energy values. The results indicate that for the structures with similar excluded volumes, we need to incorporate other energy terms to investigate the stabilization in details.5
Figure 4.
Solvation entropy term as a function of the Cα-RMSD with respect to the most stable structure in the simulation.
The total energy stability of each residue and its main and side chains are shown in Figure 5. The extent to which the main chain or side chain contributes depends on the residue. All of the residues, with the exception of Gly11, stabilized the native structure. Gly11 forms a short 310-helix with Pro12 and Ser13, and the total energy difference between these helices is positive. However, the 310-helix makes only a small contribution to the structural stability of the Trp-cage, whereas the α-helix, consisting of Ala2–Ala8, contributes significantly. In particular, the contribution of the side chain of Trp6 to the structural stability is 6.8 kcal/mol. The contribution of the hydrophobic core formed by Tyr3, Leu7, Pro12, Pro18, and Pro19 around Trp6 was 15.6 kcal/mol. The side chain of Trp6 also formed a hydrogen bond with the main chain of Arg16, and the contribution of the main chain of Arg16 was 1.5 kcal/mol. The largest contribution to the overall stability of the Trp-cage, 8.4 kcal/mol, was observed for the side chain of Arg16. The contribution of the side chain of Asp9, which forms a salt bridge with Arg16, was 2.5 kcal/mol. The contribution of the salt bridge was 10.9 kcal/mol, the second only to that of the hydrophobic core.
Figure 5.
Differences in the average total energy of each residue of the unfolded state from that in the native state. Gray, white, and black indicate the sum of the main and side chains, main chain, and side chain, respectively.
The total energy, conformational energy, and SFE differences in the (a) main and (b) side chains are shown in Figure 6. Both the main and side chains gain conformational energy at the cost of the SFE during the folding process. This indicated that both the main and side chains were dehydrated to form hydrogen bonds within the protein. However, to increase their energy, the side chains competed more aggressively than the main chains, because the main chains were less exposed to the surrounding solvent than the side chains. Gly, which does not have a side chain, competed in a slightly larger range of energy than the other amino acids. The magnitude of the competition for energy by the side chains varies depending on whether the side chain is hydrophilic or hydrophobic. Hydrophilic side chains gain a greater amount of conformational energy and lose a larger amount of SFE. Therefore, the total energy difference of the hydrophilic side chain was not significantly different from that of the hydrophobic side chains. The hydrophilic side chains, Asp9 and Arg16, lose more SFE because of dehydration but also gain more conformational energy by forming hydrogen bonds within the protein. The hydrophobic residue Trp6 exhibited a smaller conformational energy gain and SFE loss than Asp9 and Arg16. However, the total energy gain was larger for Arg16, Trp6, and Asp9, in that order, depending on the amino acid sequence and native structure.
Figure 6.
Differences in the average total energy (gray), average conformational energy (white), and average SFE (black) in (a) main and (b) side chains of each residue of the unfolded state from that of the native state.
Figure 7 shows the differences in the average solvation entropy term for each amino acid. The contributions of the solvation entropy term of the main and side chains in the entire Trp-cage are 17.4 and 13.9 kcal/mol, respectively. The contribution of the main chain to the solvation entropy is 3.5 kcal/mol larger than that of the side chains. In particular, Gly10 and Gly11, which do not have side chains, have relatively high values of 1.8 and 2.1 kcal/mol, respectively. The contribution of Gly11 was slightly higher because it is buried inside the protein, possibly due to the absence of side chains, which contribute to the compact structure of the Trp-cage. The sum of contributions of these two residues is 3.9 kcal/mol, which is almost equal to the difference between the contributions of the main and side chains. In other words, excluding the contribution of the main chains of the Gly residues, the solvation entropy contributions of the main and side chains are almost equal.
Figure 7.
Differences in the average solvation entropy of each residue of the unfolded state from those of the native state. Gray, white, and black indicate the sum of the main and side chains, main chain, and side chain, respectively.
The contributions of secondary structures, hydrophobic core, and salt bridge were also taken into account. The contribution of the 310-helix from Gly11 to Ser14 is 4.5 kcal/mol and that of the α-helix is 14.3 kcal/mol. Notably, the latter contribution includes those of the side chains of Tyr3, Trp6, and Leu7 (5.1 kcal/mol in total), which form the hydrophobic core. The formations of secondary structures such as α-helix and 310-helix contributed significantly to the increase in the solvation entropy term. The contribution of the hydrophobic core is 6.3 kcal/mol, which corresponds to 20% of the total solvation entropy term. However, the contributions of Pro12, Pro18, and Pro19, amounting to 0.4, 0.0, and 0.8 kcal/mol, respectively, were not significant. As Barua et al. pointed out, Pro/Trp interactions are not essential for the formation of a hydrophobic core.65 Hałabis et al. conducted NMR experiments to show that the Trp6-Arg16 interaction remains, but the Trp6-Pro12 interaction disappears at 313 K.58 The formation of the salt bridge between the Asp9 and Arg16 side chains increases the solvation entropy term by 5.0 kcal/mol. Although these hydrophilic side chains are exposed to the solvent, the formation of salt bridges increases the solvation entropy. This indicates that the solvation entropy, which is the source of hydrophobic interactions, plays a major role in Trp-cage protein folding.
Conclusion
Using the atomic decomposition method, we investigated the contribution of the main and side chains of individual amino acids to folding of the Trp-cage. In particular, we focused on the hydrophobic core centered on the side chain of Trp6 and the salt bridge formed by the side chains of Asp9 and Arg16. The contributions of the hydrophobic core to the total energy and solvation entropy were 15.6 and 6.3 kcal/mol, respectively, and the corresponding contributions by the salt bridge were 10.9 and 5.0 kcal/mol, respectively. The sum of these total energy contributions corresponds to 42% of the total energy gain of the Trp-cage. More specifically, the gain attributable to the solvation entropy was equivalent to 36%. Particularly interesting is that not only the hydrophobic core but also the salt bridge formation of the hydrophilic side chains contributes to the energy gain of the Trp-cage due to the solvation entropy. This insight highlights the pivotal role of solvation entropy and the indirect influence of aqueous solvents on the structural stability of a protein.
The analysis of the energy gain of the main and side chains of the amino acids of proteins using the atomic decomposition method deepens our understanding of the principles of protein stability and folding dynamics. This methodology emerges as a potent tool in investigations related to protein stabilization, destabilization, and conformational ramifications brought about by amino acid mutations. Such detailed analyses are indispensable for the rational design of proteins, enabling enhanced functionalities and, more broadly, a deeper comprehension of protein mutations and their effects on stability. The implications of our study extend beyond mere understanding, potentially paving the way for pioneering endeavors in de novo protein design, conceiving folding architectures previously uncharted in natural systems.
Acknowledgments
This study was supported by JSPS KAKENHI, grant no. JP20H03230 and JP22H04756. The numerical calculations were conducted in part using Cygnus and Pegasus at the Center for Computational Sciences, University of Tsukuba. Molecular graphics were designed using UCSF Chimera, developed by the Resource for Biocomputing, Visualization, and Informatics at the University of California, San Francisco.93
The authors declare no competing financial interest.
References
- Jumper J.; Evans R.; Pritzel A.; Green T.; Figurnov M.; Ronneberger O.; Tunyasuvunakool K.; Bates R.; Žídek A.; Potapenko A.; et al. Highly accurate protein structure prediction with AlphaFold. Nature 2021, 596, 583–589. 10.1038/s41586-021-03819-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baek M.; DiMaio F.; Anishchenko I.; Dauparas J.; Ovchinnikov S.; Lee G. R.; Wang J.; Cong Q.; Kinch L. N.; Schaeffer R. D.; et al. Accurate prediction of protein structures and interactions using a three-track neural network. Science 2021, 373, 871–876. 10.1126/science.abj8754. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maruyama Y.; Harano Y. Does water drive protein folding?. Chem. Phys. Lett. 2013, 581, 85–90. 10.1016/j.cplett.2013.07.006. [DOI] [Google Scholar]
- Maruyama Y.; Mitsutake A. Stability of unfolded and folded protein structures using a 3D-RISM with the RMDFT. J. Phys. Chem. B 2017, 121, 9881–9885. 10.1021/acs.jpcb.7b08487. [DOI] [PubMed] [Google Scholar]
- Maruyama Y.; Mitsutake A. Analysis of Structural Stability of Chignolin. J. Phys. Chem. B 2018, 122, 3801–3814. 10.1021/acs.jpcb.8b00288. [DOI] [PubMed] [Google Scholar]
- Maruyama Y.; Koroku S.; Imai M.; Takeuchi K.; Mitsutake A. Mutation-induced change in chignolin stability from π-turn to α-turn. RSC Adv. 2020, 10, 22797–22808. 10.1039/D0RA01148G. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maruyama Y.; Mitsutake A. Structural Stability Analysis of Proteins Using End-to-End Distance: A 3D-RISM Approach. J 2022, 5, 114–125. 10.3390/j5010009. [DOI] [Google Scholar]
- Neidigh J. W.; Fesinmeyer R. M.; Andersen N. H. Designing a 20-residue protein. Nat. Struct. Biol. 2002, 9, 425–430. 10.1038/nsb798. [DOI] [PubMed] [Google Scholar]
- Gellman S. H.; Woolfson D. N. Mini-proteins Trp the light fantastic. Nat. Struct. Biol. 2002, 9, 408–410. 10.1038/nsb0602-408. [DOI] [PubMed] [Google Scholar]
- Qiu L.; Pabit S. A.; Roitberg A. E.; Hagen S. J. Smaller and Faster: The 20-Residue Trp-Cage Protein Folds in 4 μs. J. Am. Chem. Soc. 2002, 124, 12952–12953. 10.1021/ja0279141. [DOI] [PubMed] [Google Scholar]
- Iavarone A. T.; Parks J. H. Conformational Change in Unsolvated Trp-cage Protein Probed by Fluorescence. J. Am. Chem. Soc. 2005, 127, 8606–8607. 10.1021/ja051788u. [DOI] [PubMed] [Google Scholar]
- Hudáky P.; Stráner P.; Farkas V.; Váradi G.; Tóth G.; Perczel A. Cooperation between a Salt Bridge and the Hydrophobic Core Triggers Fold Stabilization in a Trp-Cage Miniprotein. Biochemistry 2008, 47, 1007–1016. 10.1021/bi701371x. [DOI] [PubMed] [Google Scholar]
- Marinelli F. Following Easy Slope Paths on a Free Energy Landscape: The Case Study of the Trp-Cage Folding Mechanism. Biophys. J. 2013, 105, 1236–1247. 10.1016/j.bpj.2013.07.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meuzelaar H.; Marino K. A.; Huerta-Viga A.; Panman M. R.; Smeenk L. E. J.; Kettelarij A. J.; van Maarseveen J. H.; Timmerman P.; Bolhuis P. G.; Woutersen S. Folding Dynamics of the Trp-Cage Miniprotein: Evidence for a Native-Like Intermediate from Combined Time-Resolved Vibrational Spectroscopy and Molecular Dynamics Simulations. J. Phys. Chem. B 2013, 117, 11490–11501. 10.1021/jp404714c. [DOI] [PubMed] [Google Scholar]
- Han W.; Schulten K. Characterization of Folding Mechanisms of Trp-Cage and WW-Domain by Network Analysis of Simulations with a Hybrid-Resolution Model. J. Phys. Chem. B 2013, 117, 13367–13377. 10.1021/jp404331d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miao Y.; Feixas F.; Eun C.; McCammon J. A. Accelerated molecular dynamics simulations of protein folding. J. Comput. Chem. 2015, 36, 1536–1549. 10.1002/jcc.23964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou C.-Y.; Jiang F.; Wu Y.-D. Folding Thermodynamics and Mechanism of Five Trp-Cage Variants from Replica-Exchange MD Simulations with RSFF2 Force Field. J. Chem. Theory Comput. 2015, 11, 5473–5480. 10.1021/acs.jctc.5b00581. [DOI] [PubMed] [Google Scholar]
- Andryushchenko V. A.; Chekmarev S. F. A hydrodynamic view of the first-passage folding of Trp-cage miniprotein. Eur. Biophys. J. 2016, 45, 229–243. 10.1007/s00249-015-1089-7. [DOI] [PubMed] [Google Scholar]
- Borgohain G.; Paul S. Atomistic level understanding of the stabilization of protein Trp cage in denaturing and mixed osmolyte solutions. Comput. Theor. Chem. 2018, 1131, 78–89. 10.1016/j.comptc.2018.03.013. [DOI] [Google Scholar]
- Chalyavi F.; Schmitz A. J.; Tucker M. J. Unperturbed Detection of the Dynamic Structure in the Hydrophobic Core of Trp-Cage via Two-Dimensional Infrared Spectroscopy. J. Phys. Chem. Lett. 2020, 11, 832–837. 10.1021/acs.jpclett.9b03706. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yasuda T.; Shigeta Y.; Harada R. The Folding of Trp-cage is Regulated by Stochastic Flip of the Side Chain of Tryptophan. Chem. Lett. 2021, 50, 162–165. 10.1246/cl.200699. [DOI] [Google Scholar]
- Coe M. K.; Evans R.; Wilding N. B. Understanding the physics of hydrophobic solvation. J. Chem. Phys. 2023, 158, 034508. 10.1063/5.0134060. [DOI] [PubMed] [Google Scholar]
- Bunagan M. R.; Yang X.; Saven J. G.; Gai F. Ultrafast Folding of a Computationally Designed Trp-Cage Mutant: Trp 2 -Cage. J. Phys. Chem. B 2006, 110, 3759–3763. 10.1021/jp055288z. [DOI] [PubMed] [Google Scholar]
- Ahmed Z.; Beta I. A.; Mikhonin A. V.; Asher S. A. UV-Resonance Raman Thermal Unfolding Study of Trp-Cage Shows That It Is Not a Simple Two-State Miniprotein. J. Am. Chem. Soc. 2005, 127, 10943–10950. 10.1021/ja050664e. [DOI] [PubMed] [Google Scholar]
- Lin M.; Ahmed Z.; Taormina C. R.; Somayajula K. V. A quadrupole/time-of-flight mass spectrometry study of trp-cage’s conformation. J. Am. Soc. Mass Spectrom. 2007, 18, 195–200. 10.1016/j.jasms.2006.09.001. [DOI] [PubMed] [Google Scholar]
- Pitera J. W.; Swope W. Understanding folding and design: Replica-exchange simulations of “Trp-cage” miniproteins. Proc. Natl. Acad. Sci. U.S.A. 2003, 100, 7587–7592. 10.1073/pnas.1330954100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou R. Trp-cage: Folding free energy landscape in explicit water. Proc. Natl. Acad. Sci. U.S.A. 2003, 100, 13280–13285. 10.1073/pnas.2233312100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ota M.; Ikeguchi M.; Kidera A. Phylogeny of protein-folding trajectories reveals a unique pathway to native structure. Proc. Natl. Acad. Sci. U.S.A. 2004, 101, 17658–17663. 10.1073/pnas.0407015102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ding F.; Buldyrev S. V.; Dokholyan N. V. Folding Trp-Cage to NMR Resolution Native Structure Using a Coarse-Grained Protein Model. Biophys. J. 2005, 88, 147–155. 10.1529/biophysj.104.046375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Juraszek J.; Bolhuis P. G. Sampling the multiple folding mechanisms of Trp-cage in explicit solvent. Proc. Natl. Acad. Sci. U.S.A. 2006, 103, 15859–15864. 10.1073/pnas.0606692103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paschek D.; Nymeyer H.; García A. E. Replica exchange simulation of reversible folding/unfolding of the Trp-cage miniprotein in explicit solvent: On the structure and possible role of internal water. J. Struct. Biol. 2007, 157, 524–533. 10.1016/j.jsb.2006.10.031. [DOI] [PubMed] [Google Scholar]
- Juraszek J.; Bolhuis P. G. Rate Constant and Reaction Coordinate of Trp-Cage Folding in Explicit Water. Biophys. J. 2008, 95, 4246–4257. 10.1529/biophysj.108.136267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kannan S.; Zacharias M. Folding of Trp-cage Mini Protein Using Temperature and Biasing Potential Replica—Exchange Molecular Dynamics Simulations. Int. J. Mol. Sci. 2009, 10, 1121–1137. 10.3390/ijms10031121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lai Z.; Preketes N. K.; Mukamel S.; Wang J. Monitoring the Folding of Trp-Cage Peptide by Two-Dimensional Infrared (2DIR) Spectroscopy. J. Phys. Chem. B 2013, 117, 4661–4669. 10.1021/jp309122b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dickson A. III; Brooks C. L. III Native States of Fast-Folding Proteins Are Kinetic Traps. J. Am. Chem. Soc. 2013, 135, 4729–4734. 10.1021/ja311077u. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ota M.; Ikeguchi M.; Kidera A. Itinerary profiling to analyze a large number of protein-folding trajectories. Biophys. Physicobiol. 2016, 13, 295–304. 10.2142/biophysico.13.0_295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iavarone A. T.; Patriksson A.; van der Spoel D.; Parks J. H. Fluorescence Probe of Trp-Cage Protein Conformation in Solution and in Gas Phase. J. Am. Chem. Soc. 2007, 129, 6726–6735. 10.1021/ja065092s. [DOI] [PubMed] [Google Scholar]
- Ren H.; Lai Z.; Biggs J. D.; Wang J.; Mukamel S. Two-dimensional stimulated resonance Raman spectroscopy study of the Trp-cage peptide folding. Phys. Chem. Chem. Phys. 2013, 15, 19457–19464. 10.1039/c3cp51347e. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piana S.; Laio A. A Bias-Exchange Approach to Protein Folding. J. Phys. Chem. B 2007, 111, 4553–4559. 10.1021/jp067873l. [DOI] [PubMed] [Google Scholar]
- Marinelli F.; Pietrucci F.; Laio A.; Piana S. A Kinetic Model of Trp-Cage Folding from Multiple Biased Molecular Dynamics Simulations. PLoS Comput. Biol. 2009, 5, e1000452 10.1371/journal.pcbi.1000452. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zheng W.; Gallicchio E.; Deng N.; Andrec M.; Levy R. M. Kinetic Network Study of the Diversity and Temperature Dependence of Trp-Cage Folding Pathways: Combining Transition Path Theory with Stochastic Simulations. J. Phys. Chem. B 2011, 115, 1512–1523. 10.1021/jp1089596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shao Q.; Shi J.; Zhu W. Enhanced sampling molecular dynamics simulation captures experimentally suggested intermediate and unfolded states in the folding pathway of Trp-cage miniprotein. J. Chem. Phys. 2012, 137, 125103. 10.1063/1.4754656. [DOI] [PubMed] [Google Scholar]
- Kim S. B.; Dsilva C. J.; Kevrekidis I. G.; Debenedetti P. G. Systematic characterization of protein folding pathways using diffusion maps: Application to Trp-cage miniprotein. J. Chem. Phys. 2015, 142, 085101. 10.1063/1.4913322. [DOI] [PubMed] [Google Scholar]
- Omelyan I.; Kovalenko A. MTS-MD of Biomolecules Steered with 3D-RISM-KH Mean Solvation Forces Accelerated with Generalized Solvation Force Extrapolation. J. Chem. Theory Comput. 2015, 11, 1875–1895. 10.1021/ct5010438. [DOI] [PubMed] [Google Scholar]
- Zhang T.; Nguyen P. H.; Nasica-Labouze J.; Mu Y.; Derreumaux P. Folding Atomistic Proteins in Explicit Solvent Using Simulated Tempering. J. Phys. Chem. B 2015, 119, 6941–6951. 10.1021/acs.jpcb.5b03381. [DOI] [PubMed] [Google Scholar]
- Kamiya M.; Sugita Y. Flexible selection of the solute region in replica exchange with solute tempering: Application to protein-folding simulations. J. Chem. Phys. 2018, 149, 072304. 10.1063/1.5016222. [DOI] [PubMed] [Google Scholar]
- Harada R.; Shigeta Y. Temperature-Shuffled Structural Dissimilarity Sampling Based on a Root-Mean-Square Deviation. J. Chem. Inf. Model. 2018, 58, 1397–1405. 10.1021/acs.jcim.8b00095. [DOI] [PubMed] [Google Scholar]
- Harada R.; Shigeta Y. How Does Friction Coefficient Affect the Conformational Sampling Efficiency of Parallel Cascade Selection Molecular Dynamics?. Chem. Lett. 2018, 47, 1119–1122. 10.1246/cl.180464. [DOI] [Google Scholar]
- Harada R.; Shigeta Y. Selection Rules for Outliers in Outlier Flooding Method Regulate Its Conformational Sampling Efficiency. J. Chem. Inf. Model. 2019, 59, 3919–3926. 10.1021/acs.jcim.9b00546. [DOI] [PubMed] [Google Scholar]
- Harada R.; Yoshino R.; Nishizawa H.; Shigeta Y. Temperature–pressure shuffling outlier flooding method enhances the conformational sampling of proteins. J. Comput. Chem. 2019, 40, 1530–1537. 10.1002/jcc.25806. [DOI] [PubMed] [Google Scholar]
- Omelyan I.; Kovalenko A. Enhanced solvation force extrapolation for speeding up molecular dynamics simulations of complex biochemical liquids. J. Chem. Phys. 2019, 151, 214102. 10.1063/1.5126410. [DOI] [PubMed] [Google Scholar]
- Shin K.; Tran D. P.; Takemura K.; Kitao A.; Terayama K.; Tsuda K. Enhancing Biomolecular Sampling with Reinforcement Learning: A Tree Search Molecular Dynamics Simulation Method. ACS Omega 2019, 4, 13853–13862. 10.1021/acsomega.9b01480. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meli M.; Morra G.; Colombo G. Simple Model of Protein Energetics To Identify Ab Initio Folding Transitions from All-Atom MD Simulations of Proteins. J. Chem. Theory Comput. 2020, 16, 5960–5971. 10.1021/acs.jctc.0c00524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Strahan J.; Antoszewski A.; Lorpaiboon C.; Vani B. P.; Weare J.; Dinner A. R. Long-Time-Scale Predictions from Short-Trajectory Data: A Benchmark Analysis of the Trp-Cage Miniprotein. J. Chem. Theory Comput. 2021, 17, 2948–2963. 10.1021/acs.jctc.0c00933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maruyama Y.; Igarashi R.; Ushiku Y.; Mitsutake A. Analysis of Protein Folding Simulation with Moving Root Mean Square Deviation. J. Chem. Inf. Model. 2023, 63, 1529–1541. 10.1021/acs.jcim.2c01444. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Paschek D.; Hempel S.; García A. E. Computing the stability diagram of the Trp-cage miniprotein. Proc. Natl. Acad. Sci. U.S.A. 2008, 105, 17754–17759. 10.1073/pnas.0804775105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rovó P.; Farkas V.; Hegyi O.; Szolomájer-Csikós O.; Tóth G. K.; Perczel A. Cooperativity network of Trp-cage miniproteins: probing salt-bridges. J. Pept. Sci. 2011, 17, 610–619. 10.1002/psc.1377. [DOI] [PubMed] [Google Scholar]
- Hałabis A.; Żmudzińska W.; Liwo A.; Ołdziej S. Conformational Dynamics of the Trp-Cage Miniprotein at Its Folding Temperature. J. Phys. Chem. B 2012, 116, 6898–6907. 10.1021/jp212630y. [DOI] [PubMed] [Google Scholar]
- Du W.; Bolhuis P. G. Sampling the equilibrium kinetic network of Trp-cage in explicit solvent. J. Chem. Phys. 2014, 140, 195102. 10.1063/1.4874299. [DOI] [PubMed] [Google Scholar]
- Lee I.-H.; Kim S.-Y. Dynamic Folding Pathway Models of the Trp-Cage Protein. BioMed. Res. Int. 2013, 2013, 1–9. 10.1155/2013/973867. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu Z.; Tang Y.; Wang H.; Zhang X.; Lei M. Dynamics and cooperativity of Trp-cage folding. Arch. Biochem. Biophys. 2008, 475, 140–147. 10.1016/j.abb.2008.04.024. [DOI] [PubMed] [Google Scholar]
- Chowdhury S.; Lee M. C.; Xiong G.; Duan Y. Ab initio Folding Simulation of the Trp-cage Mini-protein Approaches NMR Resolution. J. Mol. Biol. 2003, 327, 711–717. 10.1016/S0022-2836(03)00177-3. [DOI] [PubMed] [Google Scholar]
- Kannan S.; Zacharias M. Role of Tryptophan Side Chain Dynamics on the Trp-Cage Mini-Protein Folding Studied by Molecular Dynamics Simulations. PLoS One 2014, 9, e88383 10.1371/journal.pone.0088383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simmerling C.; Strockbine B.; Roitberg A. E. All-Atom Structure Prediction and Folding Simulations of a Stable Protein. J. Am. Chem. Soc. 2002, 124, 11258–11259. 10.1021/ja0273851. [DOI] [PubMed] [Google Scholar]
- Barua B.; Lin J. C.; Williams V. D.; Kummler P.; Neidigh J. W.; Andersen N. H. The Trp-cage: Optimizing the stability of a globular miniprotein. Protein Eng., Des. Sel. 2008, 21, 171–185. 10.1093/protein/gzm082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jimenez-Cruz C. A.; Makhatadze G. I.; Garcia A. E. Protonation/deprotonation effects on the stability of the Trp-cage miniprotein. Phys. Chem. Chem. Phys. 2011, 13, 17056–17063. 10.1039/c1cp21193e. [DOI] [PubMed] [Google Scholar]
- Wu X.; Yang G.; Zu Y.; Fu Y.; Zhou L.; Yuan X. The Trp-cage miniprotein with single-site mutations: Studies of stability and dynamics using molecular dynamics. Comput. Theor. Chem. 2011, 973, 1–8. 10.1016/j.comptc.2011.06.018. [DOI] [Google Scholar]
- Byrne A.; Williams D. V.; Barua B.; Hagen S. J.; Kier B. L.; Andersen N. H. Folding Dynamics and Pathways of the Trp-Cage Miniproteins. Biochemistry 2014, 53, 6011–6021. 10.1021/bi501021r. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Best R. B.; Zheng W.; Mittal J. Balanced Protein–Water Interactions Improve Properties of Disordered Proteins and Non-Specific Protein Association. J. Chem. Theory Comput. 2014, 10, 5113–5124. 10.1021/ct500569b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chong S.-H.; Ham S. Atomic decomposition of the protein solvation free energy and its application to amyloid-beta protein in water. J. Chem. Phys. 2011, 135, 034506. 10.1063/1.3610550. [DOI] [PubMed] [Google Scholar]
- Chong S.-H.; Ham S. Component analysis of the protein hydration entropy. Chem. Phys. Lett. 2012, 535, 152–156. 10.1016/j.cplett.2012.03.033. [DOI] [Google Scholar]
- Chong S.-H.; Ham S. Impact of chemical heterogeneity on protein self-assembly in water. Proc. Natl. Acad. Sci. U.S.A. 2012, 109, 7636–7641. 10.1073/pnas.1120646109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maruyama Y.; Takano H.; Mitsutake A. Analysis of molecular dynamics simulations of 10-residue peptide, chignolin, using statistical mechanics: Relaxation mode analysis and three-dimensional reference interaction site model theory. Biophys. Physicobiol. 2019, 16, 407–429. 10.2142/biophysico.16.0_407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beglov D.; Roux B. An integral equation to describe the solvation of polar molecules in l iquid water. J. Phys. Chem. B 1997, 101, 7821–7826. 10.1021/jp971083h. [DOI] [Google Scholar]
- Kovalenko A.; Hirata F. Three-dimensional density profiles of water in contact with a solute o f arbitrary shape: A RISM approach. Chem. Phys. Lett. 1998, 290, 237–244. 10.1016/S0009-2614(98)00471-0. [DOI] [Google Scholar]
- Ben-Naim A.Molecular Theory of Solutions; Oxford University Press: New York, 2006. [Google Scholar]
- Sumi T.; Mitsutake A.; Maruyama Y. A solvation-free-energy functional: A reference-modified density functional formulation. J. Comput. Chem. 2015, 36, 1359–1369. 10.1002/jcc.23942. [DOI] [PubMed] [Google Scholar]
- Sumi T.; Mitsutake A.; Maruyama Y. Erratum: “A solvation-free-energy functional: A reference-modified density functional formulation” [J. Comput. Chem. 2015, 36, 1359–1369]. J. Comput. Chem. 2015, 2009–2011. 10.1002/jcc.24035. [DOI] [PubMed] [Google Scholar]
- Maruyama Y. Correction terms for the solvation free energy functional of three-dimensional reference interaction site model based on the reference-modified density functional theory. J. Mol. Liq. 2019, 291, 111160. 10.1016/j.molliq.2019.111160. [DOI] [Google Scholar]
- Chandler D.; Mccoy J. D.; Singer S. J. Density functional theory of nonuniform polyatomic systems. I. General formulation. J. Chem. Phys. 1986, 85, 5971–5976. 10.1063/1.451510. [DOI] [Google Scholar]
- Sumi T.; Sekino H. A Self-Consistent Density-Functional Approach for Homogeneous and Inhomogeneous Classical Fluids. J. Phys. Soc. Jpn. 2008, 77, 034605. 10.1143/JPSJ.77.034605. [DOI] [Google Scholar]
- Lindorff-Larsen K.; Piana S.; Dror R. O.; Shaw D. E. How fast-folding proteins fold. Science 2011, 334, 517–520. 10.1126/science.1208351. [DOI] [PubMed] [Google Scholar]
- MacKerell A. D. Jr.; Bashford D.; Bellott M.; Dunbrack R. L.; Evanseck J. D.; Field M. J.; Fischer S.; Gao J.; Guo H.; Ha S.; et al. All-atom empirical potential for molecular modeling and dynamics studies of proteins. J. Phys. Chem. B 1998, 102, 3586–3616. 10.1021/jp973084f. [DOI] [PubMed] [Google Scholar]
- Mackerell A. D. Jr.; Feig M.; Brooks C. L. III Extending the treatment of backbone energetics in protein force fields: Limitations of gas-phase quantum mechanics in reproducing protein conformational distributions in molecular dynamics simulation. J. Comput. Chem. 2004, 25, 1400–1415. 10.1002/jcc.20065. [DOI] [PubMed] [Google Scholar]
- Pronk S.; Páll S.; Schulz R.; Larsson P.; Bjelkmar P.; Apostolov R.; Shirts M. R.; Smith J. C.; Kasson P. M.; Van Der Spoel D.; et al. GROMACS 4.5: A high-throughput and highly parallel open source molecular simulation toolkit. Bioinformatics 2013, 29, 845–854. 10.1093/bioinformatics/btt055. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorgensen W. L.; Chandrasekhar J.; Madura J. D.; Impey R. W.; Klein M. L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983, 79, 926–935. 10.1063/1.445869. [DOI] [Google Scholar]
- Pettitt B. M.; Rossky P. J. Integral-equation predictions of liquid-state structure for waterlike intermolecular potentials. J. Chem. Phys. 1982, 77, 1451–1457. 10.1063/1.443972. [DOI] [Google Scholar]
- Maruyama Y.; Hirata F. Modified Anderson method for accelerating 3D-RISM calculations using graphics processing unit. J. Chem. Theory Comput. 2012, 8, 3015–3021. 10.1021/ct300355r. [DOI] [PubMed] [Google Scholar]
- Nukada A.; Maruyama Y.; Matsuoka S.. High performance 3-D FFT using multiple CUDA GPUs. In Proceedings of the 5th Annual Workshop on General Purpose Processing with Graphics Processing Units - GPGPU-5 201257–63 10.1145/2159430.2159437 [DOI] [Google Scholar]
- Maruyama Y.; Yoshida N.; Tadano H.; Takahashi D.; Sato M.; Hirata F. Massively parallel implementation of 3D-RISM calculation with volumetric 3D-FFT. J. Comput. Chem. 2014, 35, 1347–1355. 10.1002/jcc.23619. [DOI] [PubMed] [Google Scholar]
- Patriksson A.; Adams C. M.; Kjeldsen F.; Zubarev R. A.; van der Spoel D. A Direct Comparison of Protein Structure in the Gas and Solution Phase: The Trp-cage. J. Phys. Chem. B 2007, 111, 13147–13150. 10.1021/jp709901t. [DOI] [PubMed] [Google Scholar]
- Scian M.; Lin J. C.; Le Trong I.; Makhatadze G. I.; Stenkamp R. E.; Andersen N. H. Crystal and NMR structures of a Trp-cage mini-protein benchmark for computational fold prediction. Proc. Natl. Acad. Sci. U.S.A. 2012, 109, 12521–12525. 10.1073/pnas.1121421109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pettersen E. F.; Goddard T. D.; Huang C. C.; Couch G. S.; Greenblatt D. M.; Meng E. C.; Ferrin T. E. UCSF Chimera—A visualization system for exploratory research and analysis. J. Comput. Chem. 2004, 25, 1605–1612. 10.1002/jcc.20084. [DOI] [PubMed] [Google Scholar]







