Abstract
Background
Mediation analysis addresses the question of the mechanisms by which an exposure causes an outcome. This article is intended to convey basic knowledge of statistical mediation analysis.
Methods
Selected articles and examples are used to explain the principle of mediation analysis.
Results
The goal of mediation analysis is to express an overall exposure effect as a combination of an indirect and a direct effect. For example, it might be of interest whether the increased risk of diabetes (outcome) due to obesity (exposure) is mediated by insulin resistance (indirect effect), and, if so, how much of a direct effect remains. In this example, insulin resistance is a potential mediator of the effect of obesity on the risk of diabetes. In general, for a mediation analysis to be valid, more confounders must be taken into account than in the estimation of the overall effect size. A regression-based approach can be used to ensure the consideration of all relevant confounders in a mediation analysis.
Conclusion
By decomposing the overall exposure effect into indirect and direct components, a mediation analysis can reveal not just whether an exposure causes an outcome, but also how. For a mediation analysis to be valid, however, multiple assumptions must be satisfied that cannot easily be checked, potentially compromising such analyses as compared to the estimation of an overall effect.
cme plus
This article has been certified by the North Rhine Academy for Continuing Medical Education. Participation in the CME certification program is possible only over the internet: cme.aerzteblatt.de. The deadline for submission is 12 October 2024.
The question of causality lies at the core of empirical medical research, and there are various approaches to examine causal relationships (1, 2). The effect of a new treatment on a clinical endpoint is examined in randomized controlled trials (RCTs), while the effect of exposures on the risk of disease is assessed in cohort studies. Common to these studies is the fact that they examine causal relationships between a treatment or exposure and an outcome. They deal, therefore, with the question of whether an exposure is the cause of an outcome (3–5). Effect estimation is based on the theory of causal inference (6). This mathematical theory makes assumptions which must be satisfied to correctly estimate causal effects (Box). The key difference between observational studies and RCTs is that in RCTs these assumptions are fulfilled by the study design, whereas they are usually not fulfilled in observational studies, subsequently requiring more complex statistical procedures. In most cases, it is not possible to verify whether these assumptions are fulfilled in observational studies despite statistical adjustments.
Box. Necessary assumptions required to estimate causal effects*.
● Exchangeability
Exposed and unexposed study participants must be “exchangeable”. This means that exposed participants would have shown the same endpoint as unexposed had they remained unexposed (and vice versa). Exchangeability is ensured in randomized studies because all potential confounders are equally distributed between the groups. However, if confounders are present in observational studies, then the exchangeability assumption is violated. In such cases, exchangeability can be restored by adjusting for confounders. This so-called conditional exchangeability means that exposed and unexposed are exchangeable within strata of confounders (i.e., adjusted for confounders).
The hypothetical example presented in the main text deals with the causal effect of obesity on the risk of diabetes. In this context, exchangeability means that obese study participants have the same risk of diabetes as non-obese participants if the obese participants were not obese. Given that the confounder “age” increases both the probability of developing obesity and of developing diabetes, the exchangeability assumption could be violated. In comparison with non-obese study participants, obese participants would presumably also have a higher risk of diabetes even without obesity because that were on average older. Consequently, an adjustment should be made for “age” to restore conditional exchangeability.
● Positivity
Both the probability to be exposed and to be unexposed must be positive, i.e., greater than zero. Positivity is ensured in randomized studies by the study design because study participants are allocated to the the treatments groups with predetermined probability. On the other hand, in observational studies, it must be ensured that there are both exposed and unexposed participants. If adjustment is made for confounding in order to achieve exchangeability, then it must also be ensured that the probability to be exposed and unexposed within different strata of confounders is positive.
With reference to the example cited under the heading “Exchangeability”, positivity means that both obese and non-obese individuals participate in the study. If the analysis is adjusted for age, then it should also be ensured that both obese and non-obese individuals are represented in each age group.
● Consistency
The observed endpoint of all study participants under a particular exposure status corresponds to the potential endpoint of the study participants under this exposure status. This assumption may appear trivial at first sight, but it can be violated if there is a possibility of multiple versions of the exposure (for example, weight reduction by a change in dietary behavior or a change in physical activity). If the causal effect of the different versions of the exposure varies, then it is uncertain which version of the exposure the observed endpoint refers to. In randomized studies, the exposure is clearly defined by the randomized group assignment, which is why the assumption of consistency is satisfied here.
In observational studies, on the other hand, there is the possibility that the observed endpoint does not correspond to the potential endpoint. In the example cited under the heading “Exchangeability”, obesity could be prevented by a change in dietary behavior or by a change in physical activity. If these ways of preventing obesity have different effects on the risk of diabetes, then the assumption of consistency is violated. Consequently, the exposure should be defined as clearly as possible.
● No interference
The endpoint of the study participants is not affected by the exposure status of the other participants. This assumption may be violated if the study participants are not independent of one another. This would be the case in the cited example if several members of the same household were included in the study. It is conceivable here that the obesity status of one household member affects the risk of diabetes of another member.
*modified after (6)
One example for the examination of a causal relationship is the question of whether obesity increases the risk of type 2 diabetes. The exact mechanisms leading to this increased risk are not necessarily the initial focus of interest. However, from both a scientific and a medical care perspective, these mechanisms may well be of relevance. For example, it might be of interest to see whether the aforementioned relationship between obesity and diabetes is in part mediated by insulin resistance. This insight could both influence treatment decisions and initiate research projects to develop new therapies to prevent insulin resistance.
Mediation analysis offers a way of investigating these mechanisms (4, 5). It investigates the mechanisms by which an exposure causes an outcome. It therefore not only examines whether there actually is a causal relationship but also how it arises. The focus here is on factors that “mediate” the relationship between exposure and outcome (Latin: “mediator” = go-between or facilitator). In the example above, insulin resistance would be a potential mediator between the exposure “obesity” and the outcome “diabetes”.
Because of this additional complexity of mediation analysis and because such analyses are increasingly applied in medical research, the aim of the present article is to provide a basic understanding of statistical mediation analysis. The focus here is on a correct interpretation of the results and on possible limitations and pitfalls of mediation analysis.
Methods
The principle of mediation analysis will be described here using directed acyclic graphs (DAGs), also known as causal diagrams (7–9), and drawing on selected examples. Moreover, an explanation is provided on how mediation analysis can be biased and how these biases can be avoided.
Results
Causal diagrams and mediation (analysis)
Assumptions about causal relationships are made and presented in causal diagrams based on expert knowledge. These causal diagrams form the basis for addressing a scientific question (7–9). This serves to translate specialized content knowledge into statistical relationships. The insights gained from this can then be applied to data collection and analysis.
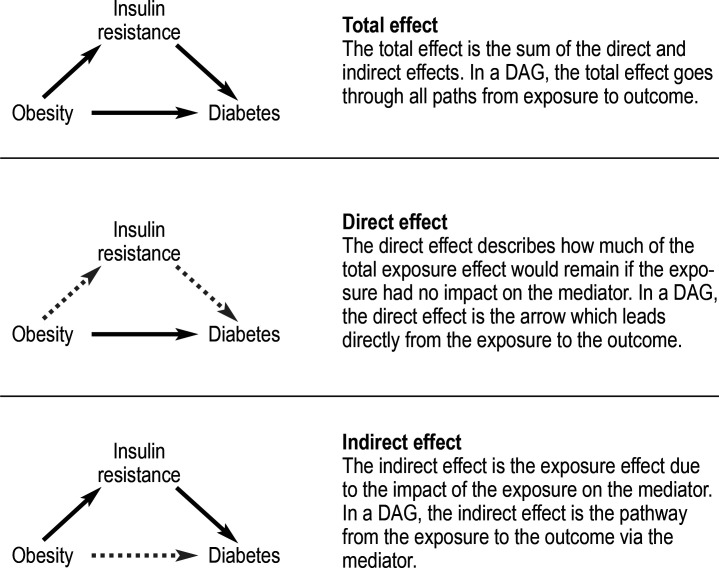
Causal relationships are represented in a causal diagram by directed arrows from the cause (for example, an exposure) to its effect (for example, the outcome). As presented in Figure 1 with reference to the example mentioned above, insulin resistance is a potential mediator for the effect of obesity on diabetes.
Figure 1.
Directed Acyclic Graphs (DAG) to demonstrate mediation analysis—decomposition of the total effect into a direct and an indirect effect
The aim of mediation analysis is to break down, or decompose, the total exposure effect in one or more indirect effects and one direct effect (4, 5). In our example, therefore, the aim would be to decompose the total effect of the risk of diabetes into two parts: one part mediated by the obesity-related risk of insulin resistance (indirect effect) and one part caused directly by obesity (i.e., not via a resistance to insulin). For further clarity, this example is developed in the next section.
A hypothetical example
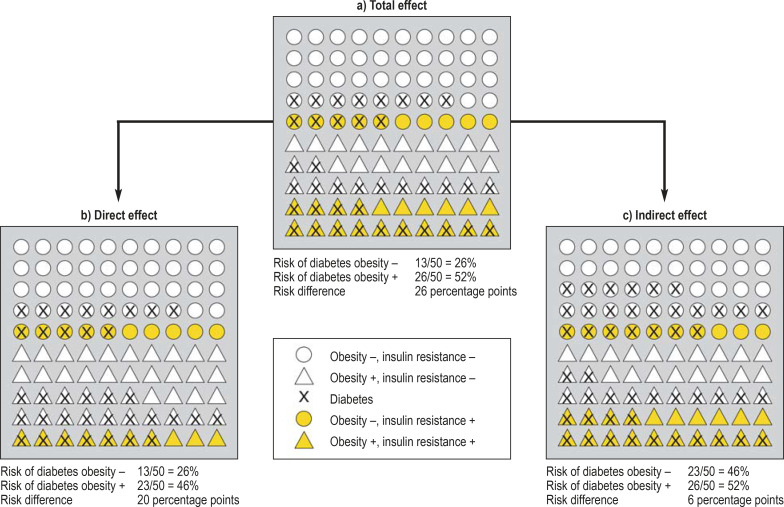
Figure 2 presents a hypothetical, highly simplified study situation involving 100 participants who differ at baseline only with respect to their obesity status. We assume that obesity doubles the risk for insulin resistance as compared with individuals without obesity. Consequently, ten non-obese and 20 obese study participants have insulin resistance in Figure 2a. We also assume that individuals without obesity and without insulin resistance have a 20% risk of developing diabetes and that obesity and insulin resistance increase the risk of diabetes in comparison with individuals without obesity and insulin resistance by 20 and 30 percentage points, respectively. This results in different risks of developing diabetes (Table 1).
Figure 2.
Decomposition of the effect of obesity on the risk of diabetes into a direct and an indirect effect. Presented here are 100 hypothetical study participants of which half are obese. Color is used to distinguish the presence of insulin resistance in the study participants. It is assumed that obesity increases the risk of insulin resistance from 20% to 40%. Accordingly, Figure 2a shows that, of the 50 individuals without obesity (circles), 10 individuals, or 20%, have insulin resistance (yellow circles). On the other hand, twenty individuals, or 40%, in the group with obesity (triangles) have insulin resistance (yellow triangles). Without obesity and without insulin resistance, the risk of diabetes is 20%. Accordingly, in Figure 2a, out of 40 individuals without obesity and insulin resistance (white circles), eight individuals, or 20%, have diabetes (white circles with cross). Obesity and insulin resistance increase the risk of diabetes by 20 and 30 percentage points, respectively. Accordingly, five out of ten individuals, or 50% without obesity but with insulin resistance suffer from diabetes (white circles with cross). Of 30 individuals with obesity but without insulin resistance (white triangles), 12, or 40%, suffer from diabetes. Individuals with obesity and insulin resistance (yellow triangles) have the highest risk of developing diabetes. Here, 14 of 20 individuals, or 70%, suffer from diabetes. To calculate the total effect of obesity on the risk of diabetes, the proportion of study participants with diabetes is compared between individuals with and without obesity. In this example, this results in 13 and 26 people with diabetes in the group without and the group with obesity, respectively, corresponding to a risk of diabetes of 26% and 52%, respectively. The total effect of obesity on the risk of diabetes (Figure 2a) takes into account both the direct risk increase due to obesity and the indirect risk increase via insulin resistance in the presence of obesity. For the direct effect (Figure 2b), the figures were calculated similar to Figure 2a, with the difference that here the effect of obesity on insulin resistance was “eliminated”. This is recognizable by the fact that the number of individuals with insulin resistance in the group with and in the group without obesity is the same (ten yellow circles and ten yellow triangles). The calculation of the figures for the indirect effect (Figure 2c) is also analogous to the total effect, with the difference that here individuals without insulin resistance and obesity have the same risk of diabetes (12 of 30 individuals, 40%) as persons without insulin resistance and with obesity (16 of 40 individuals, 40%). In this case, obesity only influences the risk of diabetes via the increased risk of insulin resistance.
Table 1. The risk of diabetes as a function of the exposure “obesity” and the mediator “insulin resistance”.
| Obesity | Insulin resistance | Risk of diabetes |
| not present (−) | not present (−) | 20% |
| present (+) | not present (−) | 40% |
| not present (−) | present (+) | 50% |
| present (+) | present (+) | 70% |
If these probabilities are applied to the hypothetical study participants in Figure 2a, this results in a risk of developing diabetes of 26% for non-obese and 52% for obese participants, which corresponds to a risk difference of 26 percentage points. So obesity increases the risk of diabetes altogether by 26 percentage points (corresponding to 13 additional cases of diabetes).
The decomposition of the total effect into an indirect and a direct effect is presented in Figures 2b and 2c. In order to calculate the direct effect (Figure 2b), we “eliminate” the impact of obesity on the risk of insulin resistance. In this context, “eliminate“ means that we calculate the figures as in Figure 2a, with the only difference that obesity does not have an impact on the risk of insulin resistance. As a result, the proportion of study participants with insulin resistance is the same in individuals with and in those without obesity (20%). With respect to the causal diagram in Figure 1, proceeding like this corresponds to “eliminating” the arrow from obesity to insulin resistance. Now, if the specified diabetes risks are applied to Figure 2b, there is a risk of developing diabetes of 26% in non-obese and 46% in obese study participants. After “eliminating” the relationship between the exposure “obesity” and the mediator “insulin resistance”, there subsequently remains a direct effect of 20 percentage points (corresponding to ten additional cases of diabetes). In this example, the direct effect answers the question: “How great would the effect of obesity on the risk of diabetes be if obesity had no impact on the development of insulin resistance?”
For calculating the indirect effect (Figure 2c), we assume that obesity has no direct effect on the risk of diabetes and equate the risk of study participants without obesity to the risk of study participants with obesity (40 %). In the absence of insulin resistance, the presence of obesity therefore no longer has a direct impact on the risk of diabetes which it increases only indirectly via an increased risk for insulin resistance. This results in a risk of developing diabetes of 46% in non-obese and 52% in obese study participants. So, after comparing the risk of diabetes in non-obese with that of obese participants, there remains an indirect effect of six percentage points (corresponding to three additional cases of diabetes). The indirect effect answers the question: “How great would the effect of obesity on the risk of diabetes be if obesity were to influence the risk of diabetes exclusively via the development of insulin resistance?”
The sum of the direct and indirect effects gives the total effect of 26 percentage points, or 13 additional cases of diabetes. In mediation analysis, the proportion of the total effect resulting from the indirect effect is often calculated (proportion mediated [PM]). The PM is defined as the ratio of the indirect effect over the total effect. In this example, the PM is six percentage points divided by 26 percentage points, which is 23%. Consequently, in our example, 23% of the total effect of obesity is due to the indirect effect via insulin resistance.
The manual calculation of the direct and indirect effects shown in Figure 2 is used here only to make mediation analysis as comprehensible as possible. In research practice, a wide range of statistical procedures are used for this purpose. For the sake of clarity, we have assumed in our example that there are no confounders (refer to [10] for further information) which might bias the estimation of the effect of obesity on the risk of diabetes. A potential confounder for the relationship between obesity and diabetes would be, for example, physical activity, since it can influence the risk for obesity as well as the risk for diabetes. By mixing the effect of the exposure with the confounder effect, the estimation of the causal relationship between exposure and outcome is biased. A number of statistical methods are available to adjust for potential confounders when estimating causal effects, for example, regression analysis (11). One way to correct for confounding in mediation analysis is illustrated by the following real-world example from diabetes research.
Applied example from diabetes research
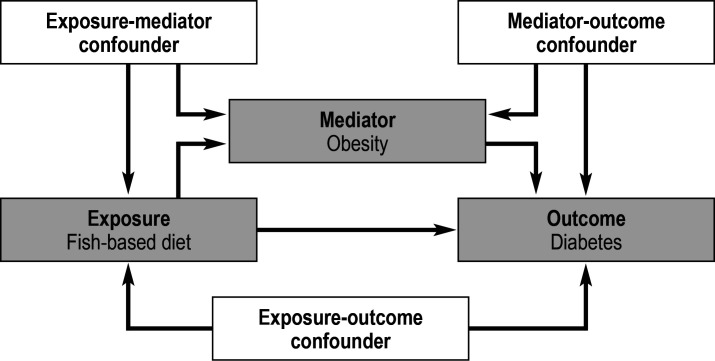
Boonpor et al. (12)) examined the effect of a fish-based diet in comparison with a meat-based diet on the risk of diabetes and to what extent this effect is mediated by obesity. The motivation for this study was the question of whether a fish diet could have other (direct) effects on the risk of diabetes apart from its obesity-inhibiting effect. For this purpose, the data of around 200 000 study participants from the UK Biobank were analyzed. Over a median follow-up period of 5.4 years, 5067 new cases of diabetes were diagnosed in this cohort. The analysis adjusted for several confounders which could bias the relationship between a fish-based diet and the incidence of diabetes. For example, it was assumed that age affects both diet and the risk of diabetes, which would create a bias due to the confounder “age”. The causal relationships examined in this study are presented in Figure 3. Confounders are presented in a causal diagram as characteristics with arrows leading to both the exposure and the outcome. Figures 3 clearly illustrates an important difference between mediation analysis and “conventional” effect estimations in which only the total effect from the exposure to the outcome is of interest. With conventional effect estimations, confounding must be adjusted for by all characteristics that influence both the exposure and the outcome. On the other hand, for valid mediation analysis, the effects of the exposure on the mediator (fish-based diet → obesity) and of the mediator on the outcome (obesity → diabetes) are also relevant. These effects can also be biased by confounding. Consequently, the analysis must include adjustments for exposure-mediator confounders and mediator-outcome confounders in addition to exposure-outcome confounders.
Figure 3.
Directed acyclic graph showing the causal relationship between a fish-based diet, obesity, and diabetes
Regression-based mediation analysis
In their mediation analysis, Boonpor et al. (12) used regression models to adjust for confounding. An introduction to regression analysis is provided by Schneider et al. (11). It is important to note that two regression models are usually computed for mediation analysis. The first regression model estimates the relationship between exposure and outcome and the second between exposure and mediator. With respect to Figure 3, this means that the effect of a fish diet (exposure) on the incidence of diabetes (outcome) is estimated using the first regression model, and the effect of a fish diet on obesity (mediator) is estimated by the second model. Both regression models must adjust for all three confounder sets in Figure 3. Boonpor et al. (12) adjusted for several potential confounders (Table 2). The total, direct, and indirect effect can be estimated using mathematical equations based on the regression coefficients of both regression models (4). Depending on the research question, these equations are more or less complex and are implemented in standard statistical software. The confounder-adjusted analysis demonstrated a lower incidence rate by a factor of 0.56 for a fish-based diet in comparison with a meat-based diet. A reduction by a factor of 0.81 was attributable to the indirect effect via obesity, which corresponded to a PM of 31%.
Table 2. Mediation analysis for the relationship between a fish-based diet, obesity, and the incidence of diabetes (12).
|
Hazard ratio
[95% CI]* |
|
| Total effect | 0.56 [0.43; 0.67] |
| Direct effect | 0.70 [0.53; 0.87] |
| Indirect effect (via obesity) | 0.81 [0.79; 0.83] |
| “proportion mediated” (%) | 30.6 [16.9; 56.0] |
* Effects are specified for a fish-based diet compared with a meat-based diet. Adjusted for age, sex, deprivation, alcohol consumption, smoking, physical inactivity, sleep duration, and type of physical activity.
95% CI, 95% confidence interval
Practical implementation and interpretation of mediation analysis
The regression-based implementation of mediation analyses presented above is incorporated in a user-friendly manner in several statistical programs (for example, SAS, R, or Stata). This method may be used for different types of outcomes and mediators. The correct regression model to use is determined by the scale of the outcome variable in question. For example, relative risks or odds ratios for dichotomous outcomes can be estimated and broken down into direct and indirect effects. In Boonpor et al (12), the outcome was a time-to-event and the mediator a binary variable, so Cox regression and logistic regression were used, respectively.
The selection of confounders can be a challenge when implementing mediation analysis. As already mentioned, three types of confounding variables must be adjusted for in mediation analysis (Figure 3). It is important that the selection of confounders is justified by subject-matter reasons and not only data-driven. One way of making the selection of confounders easier is to use graphical representations of causal relationships in causal diagrams based on expert knowledge. Based on a causal diagram and mathematical rules, freely available software may be used to identify relevant confounders (for example, DAGitty) (13).
Mediation analysis is used for both RCTs and observational studies. However, in the mediation case more assumptions must be fulfilled than with conventional estimations of associations between exposure and outcome. A key assumption when estimating causal effects is that there are no unknown or unmeasured confounders. Usually it is not possible to verify whether this assumption is fulfilled in a given case. Because it is more difficult to fulfill this assumption in mediation analysis due to the three confounder sets which need to be adjusted for, mediation analysis is considered more prone to bias than studies that only estimate the total effect. Mediation analyses in RCTs have the advantage that confounding between the intervention and outcome and between the intervention and mediator are prevented by randomizing the intervention so that confounders can be disregarded for these relationships. However, mediator-outcome confounders must also be adjusted for in RCTs because the mediator is usually not randomized. In general, mediation analyses are therefore more susceptible to bias than conventional effect estimations.
In order to obtain valid effect estimates, it is an advantage if there is a clear chronological order between exposure, mediator, and outcome. Ideally, therefore, a dataset with (at least) three survey dates should be available. Otherwise it might not be guaranteed that, for example, the mediator follows the exposure and not vice versa. If the chronological order of exposure, mediator, and outcome is unclear, then the direction of the causal relationship is also unclear. An unequivocal chronological order is therefore also crucial for the interpretation of mediation analyses. In addition, attention should be paid to whether the confounders were identified with the help of expert knowledge, for example by using causal diagrams, and whether all three types of confounders were adjusted for. As with any study, mediation analyses should also be judged in the light of the overall available evidence.
Discussion
We have used examples to explain how mediation analyses can be implemented to decompose the effect of an exposure or intervention into a direct and an indirect effect. The regression-based approach provides an opportunity to perform mediation analyses. These procedures are flexible for use with various scales of the outcome and mediator and, unlike older methods, can also adjust for an interaction between the exposure and the mediator. However, these procedures do also have their limitations when dealing with more complex issues. For example, situations with more than one mediator require more extensive programming (5).
Therefore, the concepts and methods presented here can only give a brief insight into the principle of mediation analysis. The methodology can be expanded in many ways, for example, by decomposition of the total effect into more than two components (14), and alternatives to the regression-based approach (for example, [15, 16]) are also available. The fundamental principle, however, is the same for all methods: the decomposition of exposure effects into direct and indirect components with the aim of examining not only whether, but also how, an exposure causes an outcome.
Questions on the article in issue 41/2023:
Mediation Analysis in Medical Research
The submission deadline is October 12, 2024. Only one answer is possible per question.
Please select the answer that is most appropriate.
Question 1
Which question does mediation analysis deal with?
Which exposure leads to the observed outcome?
What other outcome can result from the exposure?
Which factors lead to the exposure which is responsible for the outcome?
Based on what mechanism does an exposure lead to a particular outcome?
How pronounced would the outcome be if another exposure interacts?
Question 2
The article draws on the example of the relationship between obesity and diabetes. What is mentioned in the text as a potential mediator?
Increased consumption of glucose
Reduced consumption of glucose
Insulin resistance
Increased production of insulin
Reduced production of insulin
Question 3
One of the necessary assumptions for estimating causal effects is that exposed study participants would have had the same endpoint as unexposed participants if they had actually not been exposed (and vice versa). Which term is used for this?
equality
credibility
dependency
diversity
exchangeability
Question 4
Which of the following aspects are both listed in the article under the necessary assumptions required to estimate causal effects?
positivity and consistency
interference and competition
abstinence and consistency
interference and plausibility
plausibility and competition
Question 5
Causal diagrams are often constructed to explain mediation analysis. What is the technical term for this type of diagram?
Direction Anticipating Graphs (DAG)
Directed Acyclic Graphs (DAG)
Directed Triangular Graphs (DTG)
Direct Acyclic Diagrams (DAG)
Bidirectional Acyclic Graphs (BAG)
Question 6
In the case of the example for a mediation analysis cited in the article, which of the following dimensions answers the following question: “How great would the effect of obesity on the risk of diabetes be if obesity had no impact on the development of insulin resistance?”
the indirect effect
the combined effect
the uncoupled effect
the direct effect
the subtracted effect
Question 7
How is “proportion mediated” (PM) defined in the article?
Difference between indirect and total effect
Ratio of the indirect effect over the total effect
Difference between direct and indirect effect
Sum of indirect and direct effects
Quotient of the total effect divided by the direct effect
Question 8
The article presents an example of a mediation analysis between fish-based diet (in comparison with meat-based diet) and the incidence of diabetes. What is assumed to be the mediator here?
HDL levels
LDL levels
Blood pressure
Heart rate
Obesity
Question 9
How large was the PM in the mediation analysis regarding fish-based diet?
5.8 %
13.7 %
27.1 %
30.6 %
42.1 %
Question 10
During mediation analysis for an RCT, what type of confounder should be considered since they are not yet adjusted for by randomization?
Age as a confounder
Intervention-outcome confounder
Mediator-outcome confounder
Gender as a confounder
Intervention-mediator confounder
Acknowledgments
Translated from the original German by Dr. Grahame Larkin MD.
Footnotes
Conflict of interest statement
OK received fees from Berlin Chemie for biostatistical counseling and education.
The other authors declare that they have no conflicts of interests.
References
- 1.Gianicolo EAL, Eichler M, Muensterer O, Strauch K, Blettner M. Methods for evaluating causality in observational studies—part 27 of a series on evaluation of scientific publications. Dtsch Arztebl Int. 2020;117:101–107. doi: 10.3238/arztebl.2020.0101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Stang A. Eine Einführung in Kausalitätsprinzipien in der biomedizinischen Forschung. Gesundheitswesen. 2014;76:874–882. doi: 10.1055/s-0034-1387509. [DOI] [PubMed] [Google Scholar]
- 3.Richiardi L, Bellocco R, Zugna D. Mediation analysis in epidemiology: methods, interpretation and bias. Int J Epidemiol. 2013;42:1511–1519. doi: 10.1093/ije/dyt127. [DOI] [PubMed] [Google Scholar]
- 4.VanderWeele TJ. Mediation analysis: a practitioner‘s guide. Annu Rev Public Health. 2016;37:17–32. doi: 10.1146/annurev-publhealth-032315-021402. [DOI] [PubMed] [Google Scholar]
- 5.VanderWeele T. Explanation in causal inference: methods for mediation and interaction. Oxford University Press. 2015 [Google Scholar]
- 6.Hernán M, Robins J. Boca Raton: Chapman & Hall/CRC; 2020. Causal inference: what If. [Google Scholar]
- 7.Schipf S, Knüppel S, Hardt J, Stang A. Directed acyclic graphs (DAGs)—Die Anwendung kausaler Graphen in der Epidemiologie. Gesundheitswesen. 2011;73:888–892. doi: 10.1055/s-0031-1291192. [DOI] [PubMed] [Google Scholar]
- 8.Greenland S, Pearl J, Robins JM. Causal diagrams for epidemiologic research. Epidemiology. 1999;10:37–48. [PubMed] [Google Scholar]
- 9.Pearl J. Causal diagrams for empirical Research. Biometrika. 1995;82:669–688. [Google Scholar]
- 10.Hammer GP, Prel J-Bd, Blettner M. Avoiding bias in observational studies: part 8 in a series of articles on evaluation of scientific publications. Dtsch Arztebl Int. 2009;106:664–668. doi: 10.3238/arztebl.2009.0664. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Schneider A, Hommel G, Blettner M. Linear regression analysis—part 14 of a series on evaluation of scientific publications. Dtsch Arztebl Int. 2010;107:776–782. doi: 10.3238/arztebl.2010.0776. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Boonpor J, Petermann-Rocha F, Parra-Soto S, et al. Types of diet, obesity, and incident type 2 diabetes: findings from the UK biobank prospective cohort study. Diabetes Obes Metab. 2022;24:1351–1359. doi: 10.1111/dom.14711. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Textor J, Hardt J, Knüppel S. DAGitty: A graphical tool for analyzing causal diagrams. Epidemiology. 2011;22 doi: 10.1097/EDE.0b013e318225c2be. [DOI] [PubMed] [Google Scholar]
- 14.VanderWeele TJ. A unification of mediation and interaction: a 4-way decomposition. Epidemiology. 2014;25:749–761. doi: 10.1097/EDE.0000000000000121. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Tchetgen Tchetgen EJ. Inverse odds ratio-weighted estimation for causal mediation analysis. Stat Med. 2013;32:4567–4580. doi: 10.1002/sim.5864. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Imai K, Keele L, Tingley D. A general approach to causal mediation analysis. Psychol Methods. 2010;15:309–334. doi: 10.1037/a0020761. [DOI] [PubMed] [Google Scholar]