Skip to main content
NCBI home page
ACS Omega logoLink to ACS Omega
. 2023 Nov 8;8(46):44328–44337. doi: 10.1021/acsomega.3c06937

Development of a Transferable Force Field between Metal–Organic Framework and Its Polymorph

Kyeongrim Kim 1, Jihan Kim 1,*
PMCID: PMC10666274  PMID: 38027331

Abstract

graphic file with name ao3c06937_0010.jpg

Conventionally, force fields for specific metal–organic frameworks (MOFs) are derived from quantum chemical simulations, but this method can be computationally intensive, especially in cases for large MOF structures. In this work, we devise a methodology to reduce the force field derivation costs by replacing the original MOF with a smaller polymorphic structure, with the hypothesis that the force field parameters will be transferrable among chemically identical, polymorphic MOF structures. Specifically, we demonstrate this transferability in MOF-177 structure for H2O and NH3 gas molecules and show that the force field parameters derived from a smaller polymorphic MOF-177 can be used accurately to the original MOF-177 structure. This methodology can accelerate the development of force field parameters for large porous materials, in which computational costs for conventional methods are expensive.

Introduction

Metal–organic frameworks (MOFs) are notable for their large surface areas, high porosity, structural flexibility, and remarkable tunability.1,2 With these properties in hand, MOFs can be adopted for many purposes such as carbon capture, gas storage, catalysis, gas separation, and drug delivery.2−9 Given their highly tunable nature and facile synthesis, tens of thousands of MOFs are experimentally reported,10 and millions of MOFs have been deployed in various computational databases.11−14 In conjunction with the growth of the MOF research field, there has been a growing number of theoretical works devoted to modeling MOF structures. In particular, researchers who are interested in adsorption and diffusion properties use both quantum chemical and classical mechanics to obtain various related properties. And especially for conditions requiring less accuracy but more cost-effectiveness, classical calculations with generic force fields like universal force field (UFF)15 or Dreiding16 are used to model various MOF structures. Furthermore, several common force fields which targeted MOF exclusively such as UFF4MOF17 or BTW-FF18 were also developed for rather precise applications. However, given the chemical diversity of the MOF structures, there are instances where these common force fields fail to accurately describe the interactions between the gas molecule and the MOFs.19 In this case, a new force field that can successfully model the gas properties in the MOFs should be developed.20 In general, accurate quantum chemical calculations are normally implemented as a role of basis function to develop the force field for a given MOF.21 Unfortunately, quantum mechanical simulations can be very expensive, especially for MOFs with a large number of atoms in a unit cell. The cost for density functional theory (DFT) computation grows with the third power of the size of a system,22 which makes it hard to employ DFT calculations for practical usages for large MOFs.

To relieve the burden of expensive calculations for developing accurate force fields, costly reasonable schemes have been studied in recent years and a partly QM-driven force field named MOF-FF23 was developed by Schmid and co-workers. With initial parametrization with the MM3 force field, MOF-FF has been extended to various MOFs adopting the GA algorithm. Quick-FF requiring ab initio constants was also developed by Van Speybroeck et al. to propose a rapid methodology of force field derivation.24 A general force field (VMOF) targeting for reproducing lattice dynamics of MOFs was further devised by Gale et al., which succeeded in simulating thermodynamic properties obtained from DFT calculations.25 In addition, quantum mechanics/molecular mechanics hybrid models have been actively studied for large systems with moderate costs. This methodology is economical and promising, yet problems of automation still exist.26 Although numerous state-of-the-art technologies introduced here are actively utilized for economic force field developments, problems of specificity and applicability remain challenges. In other words, an extension of these force fields is required as they often fail to accurately describe diverse and uncommon building blocks or conditions.19,27 As an example of these widely transferring force fields, there also have been many studies about interchangeable force fields for zeolites and their derivatives.28,29 However, zeolites (especially pure-silica zeolites) all possess the same chemistry since they are made up of SiO4 building blocks, and as such, it makes sense that transferability would be more valid in zeolites compared to MOFs. Therefore, a new methodology of force field development that applies to most MOFs and also inexpensive is expected.

In this work, we devised a new methodology that uses a polymorph of a MOF as a replacement structure to derive the force field parameters. Polymorphs refer to structures that possess the same building blocks but different coordination networks, or topologies.30 Given that various MOFs have reported polymorphism during their experimental synthesis,31−33 it is conceivable that one can potentially generate hundreds of different polymorphs for a given MOF using computational techniques. Upon creating these polymorphs, one can intuit that similar to the case of zeolites, all of these polymorphs will share transferable force fields. If this intuition holds, then one can derive a force field from a polymorph that has a small number of atoms in a unit cell and use these parameters to classically model other polymorphs with a larger number of atoms. Because quantum chemical simulations take far less time for smaller-size MOFs, it is evident that the computational cost for force field derivation can dramatically reduce if transferability indeed holds across polymorphs of a MOF.

With the work, MOF-17734 was selected as the case study target MOF for force field derivation. MOF-177 is composed of Zn4 O(CO2)6 metal clusters and BTB(1,3,5-benzenetribenzoate) linkers and is a promising material for various gas storage and adsorption applications.35,36 More importantly, the unit cell of MOF-177 contains 808 atoms, which makes it a very large MOF and requires expensive DFT simulations to obtain each of the single point energies needed for force field derivation.

The outline of our work is as follows. First, the polymorphs of MOF-177 were generated computationally, and an adequate polymorph of MOF-177 was chosen as our replacement material. In this new polymorph, force field parameters were derived for H2O and NH3 molecules, respectively. These complex molecules were chosen because conventional force fields do not accurately model these polar molecules with quadrupole moments. Finally, these parameters were transferred to the original MOF-177 structure and compared to quantum chemical calculations for verification purposes.

Experimental Section

Force field derivation for MOF-177 was achieved using the following steps, as outlined in this section. Overall, the outline here follows a standard procedure similar to other force field derivation methods37−39 with the only main difference being that the target material of MOF-177 was replaced by its suitable polymorph replacement.

Preparation of MOF-177 and Its Polymorph

An in-house software named PORMAKE14 was used to generate the original MOF-177 structure as well as its polymorph structures. The validity of the MOF-177 structure has been verified by cross-checking the structure with the structures reported in other papers.34,36 Vienna Ab initio Simulation Package (VASP) was employed to relax all of the MOF structures, and the DFT simulations were performed with a generalized gradient approximation functional of Perdew–Burke–Ernzerhof (PBE-GGA).40 Recommended projector augmented wave (PAW) potentials were applied,41 and the cutoff energy for the plane-wave basis was set to 520 eV. For sampling the Brillouin zone, Γ-sampling with a spacing of 0.5Å–1 was used. The conjugate-gradient-based relaxations minimized the forces and the stress tensor was applied with respect to atomic positions, cell shape, and cell volume.42 SCF loops had a convergence criterion of 1 × 10–6 eV, while a maximum of 60 steps were allowed for each run. The relaxation was conducted until the norms of forces became smaller than 0.01 eV/Å. Finally, Zeo++ was used to obtain the void fraction of each structure.

Guest Molecules: NH3 and H2O

In our case study analysis, NH3 and H2O were selected as the guest molecules for deriving new force fields. Since our objective is to show transferability for widely used materials systems, we decided to utilize well-known models for the molecules themselves. For the NH3 molecule, OPLS all-atom (OPLS-AA) force field parameters were used as it can successfully simulate amine hydration by balancing hydrogen bond strengths.43 Regarding the H2O system, the Tip4p-Ew model was adopted, which can replicate Coulomb and Lennard-Jones long-range interactions.44

Computational Details for Energy Calculations

In our research, mainly two types of binding energy calculations were conducted: quantum and classical computations. DFT calculations with VASP were introduced for the reference of the fitting force field parameters. The nonbonded interactions were valued with the following equation.

graphic file with name ao3c06937_m001.jpg

PBE-GGA functional was used with projector augmented wave (PAW) pseudopotentials and periodic boundary conditions to obtain each of these energy terms. For accurate calculations, DFT-D3 methods45 were utilized as the van der Waals correction.

While modifying new force fields, classical simulations were accompanied by testing the resulting fields at each step. Large-scale Atomic/Molecular massively parallel simulator (LAMMPS) was primarily utilized for this kind of computation. With this software, one can get a variety of interaction models for diverse materials, including MOFs.46 The MOF frameworks and guest molecules were considered as individual groups, and pairwise potential energies consisting of van der Waals interactions and Coulomb attractions were computed. The Lennard-Jones potential parts were calculated with a cutoff of 12.5 Å, while the electrostatic interactions were computed with Ewald summations with a cutoff of 10.0 Å. The pairwise interactions were defined as a summation of pairs between each atom from a guest molecule group and every single atom from the frameworks. To be specific, a group of MOF atoms and a group of guest molecules were designated, and pairwise energy, including van der Waals energy, Coulomb energy, and long-range k-space energy, was calculated between these groups. Energy calculations were completed by adopting Lorentz–Berthelot mixing rules. Additionally, data files converted with LAMMPS interface47 were utilized with no pair coefficient section. Instead, pair-related terms were isolated and modified using the force field development process.

Force Field Development

The nonbonded interactions between guests and the MOFs can be described with the following equation in our research

graphic file with name ao3c06937_m002.jpg

In this research, the parameters σ and ϵ for individual atom types of MOF-177 were adjusted, which will be described below. Lennard-Jones potential was targeted for the fitting, rather than the Coulomb potential. The charges of H2O and NH3 were defined as those from the model Tip4p and OPLS-AA, respectively. For the neutralization of MOF-177 and its polymorph, two methods were adopted: Rappe-Goddard charge equilibration (Qeq)48 and extended charge equilibration (EQeq).49Qeq method takes the first ionization potentials, electron affinities, and atomic radii as inputs, which means the determined charges highly depend on the geometry of each atom. EQeq method uses all of the measured ionization energies to get charges. As both of the equilibration methods are widely applied, two systems of charges were established to ascertain the transferability of force fields under diverse conditions.

With the force field parametrization, discussing the atom types for adjustment is necessary. In MOF-177, there are four different elements: metal or zinc, hydrogen, oxygen, and carbon. These atoms were divided into 8 different types which are denoted as Zn, H, C1, C2, C3, C4, O1, and O2. This subdivision was intended to simulate nonbonded interaction energies like van der Waals interaction and Coulomb interaction in classical calculations. Figure 1 shows the definition of atom types for the MOF-177 framework. Specifically, oxygen and carbon atoms were classified by their geometrical conditions; for instance, carbons were divided by whether they were in the terminal of linkers, in central or peripheral benzoate groups, or had no hydrogen. This geometric classification was enabled by using Qeq charges, which determine the values with the geometry. Metal atoms and hydrogen atoms were regarded to share the same local environment, with other atoms belonging to each type.

Figure 1.

Figure 1

Open in a new tab

Atom type definition in metal cluster of MOF-177(a) and in linker(b).

For the derivation of new force fields, a gradient descent algorithm was adopted so that the classical computations can fit well with the reference quantum values. Scipy was used for the optimization, and the specific optimizer was Sequential Least Squares Programming (SLSQP), developed by Dieter. The objective function for the algorithm was a Boltzmann-weighted mean deviation (BMD) which is described below.38

graphic file with name ao3c06937_m003.jpg

Here, n denotes each configuration of a guest molecule, N denotes the total number of configurations, and T stands for temperature. The temperature was set at 300 K, which is considered room temperature. Since the error term is weighted for higher DFT energies in the absolute scale, the fitting is oriented for favorable strong binding sites that have more negative energies.

While the scalar function BMD is minimized for variables, the optimizer requires some constraints or bounds. In this sense, the following bounds were set for the force field parameters: within 0.5 Å for σ parameters, and 1000 times bounds for ϵ parameters. The initial parameters (UFF), a step size of 0.001 for the algorithm, 1 × 10–4 for tolerance, and the previously mentioned bounds could yield unique parameters for each case. One may get several different combinations of parameters with similar loss functions by varying hyper-parameters. Nevertheless, these degenerate solutions show similar parameter values that were empirically observed in our research.

Results and Discussion

Selection of a Polymorph of MOF-177

Using PORMAKE, 44 different polymorphs of the MOF-177 structure were generated. To reduce the computational cost, candidate materials were selected before VASP geometrical optimizations. The primary factor for identifying the candidate was the stability of the polymorphs. As such, polymorphs with RMSD above 0.1 were deemed to be unsuitable due to structural instability and were disregarded as potential candidates. These polymorphs were additionally filtered depending on whether they had atomic composition ratios identical to those of the original MOF-177. To narrow down the possible polymorphs further, only ones with at most a quarter size of MOF-177 were selected. As a consequence, some reasonable candidates were obtained and are shown in Figure 2. All of these candidates consist of the BTB linker and the zinc metal cluster group. Figure 2(a) shows the original MOF-177, and Figure 2(b–d) shows candidate polymorphs.

Figure 2.

Figure 2

Open in a new tab

Topology descriptions for MOF-177 and its polymorphs. (a) qom or the original MOF-177 network; (b–d) candidate polymorphs tsx, rtl, and mcn respectively. The (a)qom network has 808 atoms in its primitive cell, whereas (b) tsx has 101 atoms, and (c) rtl and (d) mcn have 202 atoms in their units.

Next, the identification of polymorphs with a pore environment similar to that of the original MOF-177 was pursued. As given in Table 1, the rtl polymorph has the closest volume profiles compared to the original(qom) MOF-177. In other words, the rtl network might be the best topology which has a similar condition to the original MOF while being quite stable. In this sense, the rtl polymorph (depicted in Figure 2(c)) having 202 atoms in its unit cell was selected as the final candidate to replace the original MOF-177 structure in the force field derivation procedure.

Table 1. Comparison of the Pore Volume between MOF-177 and Its Polymorphs.

  original (qom) rtl tsx mcn
number of atoms 808 202 101 202
void fraction 0.480 0.541 0.216 0.321
volume (cm3/g) 1.157 1.460 0.320 0.597
Open in a new tab

Development of a Force Field for H2O Adsorption

With the reduced (rtl) MOF-177 structure, two different partial charges (Qeq and EQeq) were chosen and different force field parameters were derived for each of these cases. The reason we selected two different charge models is that a priori, it is not clear which charge models should be used for MOF-177 so we wanted to ensure that both charge models lead to accurate energetics upon deriving their respective force fields. For force field development, 123 positions of a H2O molecule were used for fitting. Here, 46 samples were taken from the approaching path determination method,37,38 whereas the rest 77 samples were taken either randomly or with configurations taken from both the Monte-Carlo(MC) and Molecular dynamics(MD) simulation results. Specifically, 30 random sites were utilized for the fitting, while the rest were obtained with MC and MD for obtaining strong binding sites. For the approaching path determination, two types of paths (depicted in Figure S1) were employed for the process: one path from the metal atom to the oxygen atom of the H2O molecule, and the other from the oxygen atom of the (rtl) MOF-177 to the hydrogen of the H2O molecule. Each path contained molecule sites captured with intervals of 0.1 Å (∼15 configurations respectively). H2O sites rotated at intervals of 60° along three different coordinates (2–3 configurations for each rotation vector) were also included for each path. (Details about random sampling, MC, and MD simulations are described in the Supporting Information).

Next, force field parameters were derived by minimizing the error term (BMD) of the classical energies against these 120 DFT energies (Table S1 for the derived force field parameters). The comparisons of the developed force field with those of UFF and DFT are shown in Figures 3 and4. To be specific, Figure 3 focuses on the molecules along the approaching paths, while Figure 4 shows all of the molecules. Analysis of the interaction energies enables us to recognize that the UFF generally overestimates the pairwise interactions in the Qeq-charged system, whereas it shows the opposite in the EQeq-charged system. These deviations are successfully reduced with newly adjusted σ, ϵ parameters in our force field. In Figure 4, one can see that the values from UFF seem to digress more from the benchmarked DFT line compared to the newly calculated force field energies. Specifically, BMD values decrease from 0.3093 to 0.021 ((kJ/mol)2) in the Qeq-charged system, and from 1.254 to 0.0148 ((kJ/mol)2) in the EQeq-charged system.

Figure 3.

Figure 3

Open in a new tab

H2O-(rtl) framework binding energies as a function of the distance between the guest molecule and the framework. (a, b) Qeq-charged systems and (c, d) EQeq systems. The green line stands for the DFT energies calculated from VASP, the dashed yellow line describes UFF which can serve as the control, and our force field is shown with the blue line. These are for two approaching paths: (a, c) Zn and O, and (c, d) O and H paths.

Figure 4.

Figure 4

Open in a new tab

Computed H2O – (rtl)framework binding energies compared to the DFT energies for a fitting set. (a) Qeq-charged system, (b) EQeq-charged system. The dashed green line shows uniformity between quantum-based energies and classically calculated energies. The yellow points show energies obtained with UFF, and the blue points refer to interaction energies calculated with the newly derived force field.

To further evaluate the performance of the new force field, validation with about 50 configurations of the small (rtl) polymorph that were not used in the fitting process was conducted (Figure S2). And for these data points, the new force field parameters agree better with DFT, especially in the low-energy binding regions. (Detailed BMD values are shown in the caption of Figure S2.) With this data, it seems clear that the newly fitted force field parameters do a better job of accurately depicting the energetics compared to conventional force fields.

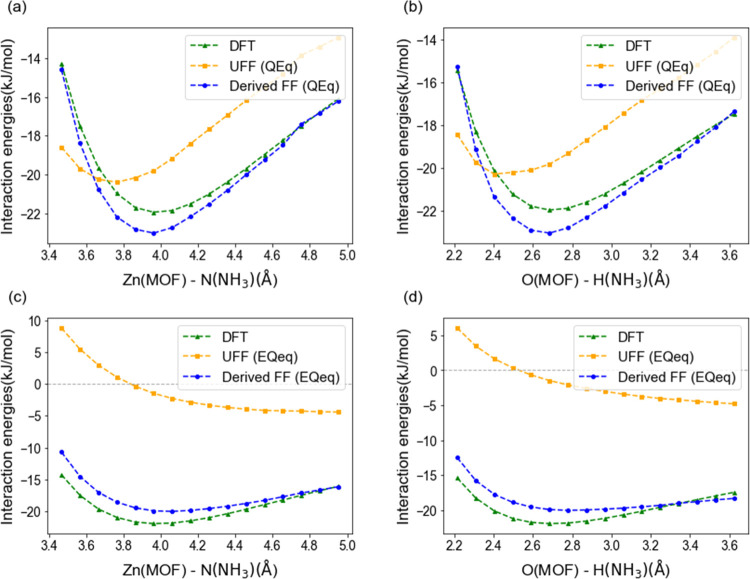
Next, our derived force field parameters were then applied to the original(qom) MOF-177 system to evaluate the transferability. For the evaluation, only a few samples (21 samples) were prepared, as the DFT energy calculations in the original MOF-177 structure are expensive. Figure 5 shows the performance of the parameters for the system in which the H2O molecule interacts with the large MOF-177 configuration set. In Figure 5, the new force field shows good transferability for both the Qeq-charged and EQeq-charged systems. Specifically, some samples are highly overestimated in Qeq-UFF system, whereas the energies are somewhat corrected in the new force field. Samples in the region have close distances between MOF and H2O (∼3 Å between the Zn atom and the O water atom). Namely, UFF seems to be unsuitable for simulating repulsive interactions, and our force field is fitted to supplement the drawback. Also, among the two-charged systems, a dramatic improvement is achieved especially for favorable sites in the EQeq-charged system. With this analysis, it can be concluded that the new force field developed in the small polymorph can be also utilized for the original MOF, and the strength is emphasized when it comes to a more deviating charge system.

Figure 5.

Figure 5

Open in a new tab

Classically obtained H2O -original(qom) MOF-177 binding energies with respect to energies computed with quantum-scale simulations. (a) Qeq-charged system, (b) EQeq-charged system. The dashed line implies that the energies obtained with force fields are in accordance with the DFT values. The yellow dots show the UFF, and the blue dots show the fitted force field. The BMD values changed from 6.124 ((kJ/mol)2) to 1.012 in the Qeq-charged system, and from 8.838 ((kJ/mol)2) to 0.6491 in the EQeq-charged system.

Development of a Force Field for NH3 Adsorption

Force fields were further derived for (rtl) MOF-177 containing NH3 as the guest molecules. Sample construction with 121 sites and BMD minimization were conducted identically to the H2O system. Approaching paths were slightly transformed with respect to related atoms: one path from metal to the nitrogen atom of NH3, and the other path that reaches the hydrogen atom of NH3 from an adjacent oxygen atom of the rtl framework (Figure S3). The resulting force field parameters are listed in Table S2.

Like the H2O case, Figures 6 and7 show the energy comparisons between the classical and the DFT results for the newly derived force field to those from UFF. Approaching paths are plotted in Figure 6, and it seems that the UFF generally underestimates the interaction energies between the MOF and the NH3 in both of these charges. These deviations are reduced in the new force field, indicating its accuracy. In addition, all of the fitting samples are shown in Figure 7. It is noticeable that the UFF for the Qeq-charged system shows pretty good performance (BMD value of 0.1619 ((kJ/mol)2)) compared to the EQeq system (BMD of 2.567) or H2O system (BMD of 0.3093). Nonetheless, fitting procedures do improve the accuracy of the classical calculations in both of the two charges. To be specific, BMDs have decreased to 0.0486 in the Qeq system, and 0.181 in the EQeq system. In the EQeq-charged system, possibly favorable sites were fitted well except for an outlier. The outlier might be inevitable since overall parameters tend to be shifted toward higher energies. As mentioned earlier in the H2O system, validation of the new force field with some sites that were not included in the fitting procedure was also conducted. (The results are shown in Figure S4.) With the process, our new force field was demonstrated to be applicable to the small (rtl) polymorph-NH3 system.

Figure 6.

Figure 6

Open in a new tab

NH3-(rtl) framework binding energies as a function of the distance between the guest molecule and the framework. (a, b) Qeq-charged systems, (c, d) EQeq systems. The dashed green line stands for the DFT energies obtained with VASP, the dashed yellow line describes UFF, and our force field is shown with the blue line. These plots depict two approaching paths: (a) Zn and N and (c, d) paths connecting the O from MOF and H from NH3.

Figure 7.

Figure 7

Open in a new tab

Comparisons of computed NH3-(rtl)framework binding energies with DFT energies for a fitting set. (a) Qeq-charged system and (b) EQeq-charged system. The dashed green line indicates the accordance of DFT energies with energies from a new force field. The yellow points show energies obtained with UFF, and the blue points refer to interaction energies calculated with the newly derived force field.

The results for the original MOF-177 (21 samples) are also depicted in Figure 8. Unlike the H2O system, UFF can simulate the conditions of the Qeq-charged NH3 system with little error, as it does in the small polymorph conditions. However, UFF fails to accurately depict the DFT energies in the EQeq-charged UFF system. Overall, again, the new force field parameters do a good job of transferring to the original MOF.

Figure 8.

Figure 8

Open in a new tab

Comparisons of classically obtained NH3-original(qom) MOF-177 binding energies with energies calculated in quantum-scale simulations. (a) Qeq-charged system, (b) EQeq-charged system. The dashed line implies that the energies obtained with the force field are in accordance with the DFT values. The yellow dots show the UFF, and the blue dots show the fitted force field. The BMD values changed from 0.3778 ((kJ/mol)2) to 0.0704 in the Qeq-charged system, and 9.314 ((kJ/mol)2) to 0.156 in the EQeq-charged system.

Averaged BMD Evaluation for New Force Fields

For the evaluation of the efficiency and transferability of our new force field, resultant Boltzmann-weighted mean distributions were attained, as mentioned above. These values serve as absolute indicators of performance, which enable us to evaluate our force field quantitatively. Consequent results are listed in Table S3, while the overview of all of the values is given in Figure 9. The numbers of samples employed for these values were 123, 50, and 21 sites for fitting, validation, and evaluation, respectively.

Figure 9.

Figure 9

Open in a new tab

BMD values computed in various sets and systems. (a, b) Systems with a H2O molecule, (c, d) NH3 systems. With a classification of charges, (a, c) show Qeq-charged systems, whereas (b, d) are for EQeq-charged systems. For each system, three sets—fitting set, validation set in rtl polymorph, and the evaluation set for original MOF-177—are given. Values from UFF are plotted with yellow bars, and values from the new force field are plotted with blue bars.

From Figure 9, it can be seen that the BMD values of the UFF are higher than those from our new force field. To be specific, BMD values have enhanced up to at least 80% in every case. For the water system, BMD values show 83.5 and 92.7% decreases with Qeq and EQeq, respectively. And for the ammonia system, 81.4 and 98.3% decreases in BMD values are found in Qeq and EQeq charges. This shows the efficacy of developing force field parameters compared to using generic force field parameters. In general, it can be seen that for both UFF and derived force field parameters the BMD values tend to increase upon going from the rtl polymorph to the original MOF-177 structure. These increases are attributed to geometrical factors changing upon moving from one polymorph to another, which implies comparing BMD errors for different polymorphs has little physical significance. In this sense, with the quantitative analysis described in Table S3 and Figure 9, advancements made in the original MOF with the new force field demonstrate transferability.

Conclusions

To demonstrate compatibility between a MOF and its small polymorphs, we have developed force fields for H2O and NH3 molecules inserted in the rtl polymorph of MOF-177. The new force fields can successfully reproduce the interaction energies computed from approaching paths in the small polymorph, demonstrating that the new parameters are accurate enough to be used. And by applying the parameters to the large MOF, our new force fields can be concluded to perform better than UFF in the original MOF-177 as well as they do in the small polymorph. Specifically, the force fields show improvement compared to UFF in all of the systems we derived for.

Our work is meaningful in that transferability between polymorphs is observed, which enables one to reduce the computational costs for classical calculations. As such, with the facility in generating polymorphs for all MOFs, it can become an integral step in force field derivation for other MOF studies that require intensive quantum chemical calculations.

Acknowledgments

This work was supported by the National Research Foundation of Korea (NRF) under grant no. 2021R1A2C2003583

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.3c06937.

  • Description of the sample construction and fitting; details about the force field for H2O adsorption; details about the force field for NH3 adsorption; BMD values for force fields; and favorable binding sites (PDF)

  • Structures of polymorphs (mcn, qom, rtl, tsx) employed in the paper (ZIP)

The authors declare no competing financial interest.

Supplementary Material

ao3c06937_si_001.pdf (989.5KB, pdf)
ao3c06937_si_002.zip (32.3KB, zip)

References

  1. Zhou H.-C. J.; Kitagawa S. Metal–Organic Frameworks (MOFs). Chem. Soc. Rev. 2014, 43 (16), 5415–5418. 10.1039/C4CS90059F. [DOI] [PubMed] [Google Scholar]
  2. Furukawa H.; Ko N.; Go Y. B.; Aratani N.; Choi S. B.; Choi E.; Yazaydin A. Ö.; Snurr R. Q.; O’Keeffe M.; Kim J.; Yaghi O. M. Ultrahigh porosity in metal-organic frameworks. Science 2010, 329 (5990), 424–428. 10.1126/science.1192160. [DOI] [PubMed] [Google Scholar]
  3. Furukawa H.; Cordova K. E.; O’Keeffe M.; Yaghi O. M. The chemistry and applications of metal-organic frameworks. Science 2013, 341 (6149), 1230444 10.1126/science.1230444. [DOI] [PubMed] [Google Scholar]
  4. Elsaidi S. K.; Mohamed M. H.; Banerjee D.; Thallapally P. K. Flexibility in metal--organic frameworks: a fundamental understanding. Coord. Chem. Rev. 2018, 358, 125–152. 10.1016/j.ccr.2017.11.022. [DOI] [Google Scholar]
  5. Sumida K.; Rogow D. L.; Mason J. A.; McDonald T. M.; Bloch E. D.; Herm Z. R.; Bae T.-H.; Long J. R. Carbon dioxide capture in metal--organic frameworks. Chem. Rev. 2012, 112 (2), 724–781. 10.1021/cr2003272. [DOI] [PubMed] [Google Scholar]
  6. He Y.; Zhou W.; Qian G.; Chen B. Methane storage in metal--organic frameworks. Chem. Soc. Rev. 2014, 43 (16), 5657–5678. 10.1039/C4CS00032C. [DOI] [PubMed] [Google Scholar]
  7. Bao Z.; Chang G.; Xing H.; Krishna R.; Ren Q.; Chen B. Potential of microporous metal--organic frameworks for separation of hydrocarbon mixtures. Energy Environ. Sci. 2016, 9 (12), 3612–3641. 10.1039/C6EE01886F. [DOI] [Google Scholar]
  8. Seo J. S.; Whang D.; Lee H.; Jun S. I.; Oh J.; Jeon Y. J.; Kim K. A homochiral metal--organic porous material for enantioselective separation and catalysis. Nature 2000, 404 (6781), 982–986. 10.1038/35010088. [DOI] [PubMed] [Google Scholar]
  9. Sun C.-Y.; Qin C.; Wang C.-G.; Su Z.-M.; Wang S.; Wang X.-L.; Yang G.-S.; Shao K.-Z.; Lan Y.-Q.; Wang E.-B. Chiral Nanoporous Metal-Organic Frameworks with High Porosity as Materials for Drug Delivery. Adv. Mater. 2011, 23 (47), 5629–5632. 10.1002/adma.201102538. [DOI] [PubMed] [Google Scholar]
  10. Wang Q.; Astruc D. State of the art and prospects in metal--organic framework (MOF)-based and MOF-derived nanocatalysis. Chem. Rev. 2020, 120 (2), 1438–1511. 10.1021/acs.chemrev.9b00223. [DOI] [PubMed] [Google Scholar]
  11. Groom C. R.; Bruno I. J.; Lightfoot M. P.; Ward S. C. The Cambridge structural database. Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater. 2016, 72 (2), 171–179. 10.1107/S2052520616003954. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Chung Y. G.; Haldoupis E.; Bucior B. J.; Haranczyk M.; Lee S.; Zhang H.; Vogiatzis K. D.; Milisavljevic M.; Ling S.; Camp J. S.; et al. Advances, Updates, and Analytics for the Computation-Ready, Experimental Metal–Organic Framework Database: CoRE MOF 2019. J. Chem. Eng. Data 2019, 64 (12), 5985–5998. 10.1021/acs.jced.9b00835. [DOI] [Google Scholar]
  13. Wilmer C. E.; Leaf M.; Lee C. Y.; Farha O. K.; Hauser B. G.; Hupp J. T.; Snurr R. Q. Large-scale screening of hypothetical metal--organic frameworks. Nat. Chem. 2012, 4 (2), 83–89. 10.1038/nchem.1192. [DOI] [PubMed] [Google Scholar]
  14. Lee S.; Kim B.; Cho H.; Lee H.; Lee S. Y.; Cho E. S.; Kim J. Computational Screening of Trillions of Metal–Organic Frameworks for High-Performance Methane Storage. ACS Appl. Mater. Interfaces 2021, 13 (20), 23647–23654. 10.1021/acsami.1c02471. [DOI] [PubMed] [Google Scholar]
  15. Rappé A. K.; Casewit C. J.; Colwell K. S.; Goddard W. A. III; Skiff W. M. UFF, a full periodic table force field for molecular mechanics and molecular dynamics simulations. J. Am. Chem. Soc. 1992, 114 (25), 10024–10035. 10.1021/ja00051a040. [DOI] [Google Scholar]
  16. Mayo S. L.; Olafson B. D.; Goddard W. A. DREIDING: a generic force field for molecular simulations. J. Phys. Chem. A 1990, 94 (26), 8897–8909. 10.1021/j100389a010. [DOI] [Google Scholar]
  17. Addicoat M. A.; Vankova N.; Akter I. F.; Heine T. Extension of the universal force field to metal–organic frameworks. J. Chem. Theory Comput. 2014, 10 (2), 880–891. 10.1021/ct400952t. [DOI] [PubMed] [Google Scholar]
  18. Bristow J. K.; Tiana D.; Walsh A. Transferable force field for metal--organic frameworks from first-principles: BTW-FF. J. Chem. Theory Comput. 2014, 10 (10), 4644–4652. 10.1021/ct500515h. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Dzubak A. L.; Lin L.-C.; Kim J.; Swisher J. A.; Poloni R.; Maximoff S. N.; Smit B.; Gagliardi L. Ab initio carbon capture in open-site metal--organic frameworks. Nat. Chem. 2012, 4 (10), 810–816. 10.1038/nchem.1432. [DOI] [PubMed] [Google Scholar]
  20. Haldoupis E.; Borycz J.; Shi H.; Vogiatzis K. D.; Bai P.; Queen W. L.; Gagliardi L.; Siepmann J. I. Ab Initio Derived Force Fields for Predicting CO2 Adsorption and Accessibility of Metal Sites in the Metal Organic Frameworks M-MOF-74 (M = Mn, Co, Ni, Cu). J. Phys. Chem. C 2015, 119 (28), 16058–16071. 10.1021/acs.jpcc.5b03700. [DOI] [Google Scholar]
  21. Fang H.; Demir H.; Kamakoti P.; Sholl D. S. Recent developments in first-principles force fields for molecules in nanoporous materials. J. Mater. Chem. A 2014, 2 (2), 274–291. 10.1039/C3TA13073H. [DOI] [Google Scholar]
  22. Misquitta A. J.; Jeziorski B.; Szalewicz K. Dispersion energy from density-functional theory description of monomers. Phys. Rev. Lett. 2003, 91 (3), 033201 10.1103/PhysRevLett.91.033201. [DOI] [PubMed] [Google Scholar]
  23. Dürholt J. P.; Fraux G.; Coudert F.-X.; Schmid R. Ab initio derived force fields for zeolitic imidazolate frameworks: MOF-FF for ZIFs. J. Chem. Theory Comput. 2019, 15 (4), 2420–2432. 10.1021/acs.jctc.8b01041. [DOI] [PubMed] [Google Scholar]
  24. Vanduyfhuys L.; Vandenbrande S.; Wieme J.; Waroquier M.; Verstraelen T.; Van Speybroeck V. Extension of the QuickFF force field protocol for an improved accuracy of structural, vibrational, mechanical and thermal properties of metal–organic frameworks. J. Comput. Chem. 2018, 39 (16), 999–1011. 10.1002/jcc.25173. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Bristow J. K.; Skelton J. M.; Svane K. L.; Walsh A.; Gale J. D. A general forcefield for accurate phonon properties of metal–organic frameworks. Phys. Chem. Chem. Phys. 2016, 18 (42), 29316–29329. 10.1039/C6CP05106E. [DOI] [PubMed] [Google Scholar]
  26. Csizi K.-S.; Reiher M.. Universal QM/MM Approaches for General Nanoscale Applications. 2022, arXiv:2211.02979. arXiv.org e-Print archive. https://arxiv.org/abs/2211.02979.
  27. Siwaipram S.; Bopp P. A.; Keupp J.; Pukdeejorhor L.; Soetens J.-C.; Bureekaew S.; Schmid R. Molecular insight into the swelling of a MOF: A force-field investigation of methanol uptake in MIL-88B (Fe)–Cl. J. Phys. Chem. C 2021, 125 (23), 12837–12847. 10.1021/acs.jpcc.1c01033. [DOI] [Google Scholar]
  28. Garcia-Sanchez A.; Ania C. O.; Parra J. B.; Dubbeldam D.; Vlugt T. J. H.; Krishna R.; Calero S. Transferable force field for carbon dioxide adsorption in zeolites. J. Phys. Chem. C 2009, 113 (20), 8814–8820. 10.1021/jp810871f. [DOI] [Google Scholar]
  29. Weng T.; Schmidt J. R. Flexible and transferable ab initio force field for zeolitic imidazolate frameworks: ZIF-FF. J. Phys. Chem. A 2019, 123 (13), 3000–3012. 10.1021/acs.jpca.8b12311. [DOI] [PubMed] [Google Scholar]
  30. Stock N.; Biswas S. Synthesis of Metal-Organic Frameworks (MOFs): Routes to Various MOF Topologies, Morphologies, and Composites. Chem. Rev. 2012, 112 (2), 933–969. 10.1021/cr200304e. [DOI] [PubMed] [Google Scholar]
  31. Bon V.; Senkovska I.; Baburin I. A.; Kaskel S. Zr- and Hf-Based Metal–Organic Frameworks: Tracking Down the Polymorphism. Cryst. Growth Des. 2013, 13 (3), 1231–1237. 10.1021/cg301691d. [DOI] [Google Scholar]
  32. Akimbekov Z.; Katsenis A. D.; Nagabhushana G. P.; Ayoub G.; Arhangelskis M.; Morris A. J.; Friščić T.; Navrotsky A. Experimental and Theoretical Evaluation of the Stability of True MOF Polymorphs Explains Their Mechanochemical Interconversions. J. Am. Chem. Soc. 2017, 139 (23), 7952–7957. 10.1021/jacs.7b03144. [DOI] [PubMed] [Google Scholar]
  33. Gándara F.; de la Peña-O’Shea V. A.; Illas F.; Snejko N.; Proserpio D. M.; Gutiérrez-Puebla E.; Monge M. A. Three Lanthanum MOF Polymorphs: Insights into Kinetically and Thermodynamically Controlled Phases. Inorg. Chem. 2009, 48 (11), 4707–4713. 10.1021/ic801779j. [DOI] [PubMed] [Google Scholar]
  34. Chae H. K.; Siberio-Pérez D. Y.; Kim J.; Go Y.; Eddaoudi M.; Matzger A. J.; O’Keeffe M.; Yaghi O. M. A route to high surface area, porosity and inclusion of large molecules in crystals. Nature 2004, 427 (6974), 523–527. 10.1038/nature02311. [DOI] [PubMed] [Google Scholar]
  35. Li Y.; Yang R. T. Gas adsorption and storage in metal- organic framework MOF-177. Langmuir 2007, 23 (26), 12937–12944. 10.1021/la702466d. [DOI] [PubMed] [Google Scholar]
  36. Zhang Y.-B.; Furukawa H.; Ko N.; Nie W.; Park H. J.; Okajima S.; Cordova K. E.; Deng H.; Kim J.; Yaghi O. M. Introduction of functionality, selection of topology, and enhancement of gas adsorption in multivariate metal--organic framework-177. J. Am. Chem. Soc. 2015, 137 (7), 2641–2650. 10.1021/ja512311a. [DOI] [PubMed] [Google Scholar]
  37. Mercado R.; Vlaisavljevich B.; Lin L.-C.; Lee K.; Lee Y.; Mason J. A.; Xiao D. J.; Gonzalez M. I.; Kapelewski M. T.; Neaton J. B.; Smit B. Force field development from periodic density functional theory calculations for gas separation applications using metal--organic frameworks. J. Phys. Chem. C 2016, 120 (23), 12590–12604. 10.1021/acs.jpcc.6b03393. [DOI] [Google Scholar]
  38. Lin L.-C.; Lee K.; Gagliardi L.; Neaton J. B.; Smit B. Force-field development from electronic structure calculations with periodic boundary conditions: applications to gaseous adsorption and transport in metal--organic frameworks. J. Chem. Theory Comput. 2014, 10 (4), 1477–1488. 10.1021/ct500094w. [DOI] [PubMed] [Google Scholar]
  39. Demir H.; Greathouse J. A.; Staiger C. L.; Perry J. J. IV; Allendorf M. D.; Sholl D. S. DFT-based force field development for noble gas adsorption in metal organic frameworks. J. Mater. Chem. A 2015, 3 (46), 23539–23548. 10.1039/C5TA06201B. [DOI] [Google Scholar]
  40. Perdew J. P.; Burke K.; Ernzerhof M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. 10.1103/PhysRevLett.77.3865. [DOI] [PubMed] [Google Scholar]
  41. Kresse G.; Joubert D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. 10.1103/PhysRevB.59.1758. [DOI] [Google Scholar]
  42. Press W. H.; Flannery B. P.; Teukolsky S. A.; Vetterling W. T.. Numerical Recipes; Cambridge Univ.: Cambridge, 1986. [Google Scholar]
  43. Rizzo R. C.; Jorgensen W. L. OPLS All-Atom Model for Amines: Resolution of the Amine Hydration Problem. J. Am. Chem. Soc. 1999, 121 (20), 4827–4836. 10.1021/ja984106u. [DOI] [Google Scholar]
  44. Horn H. W.; Swope W. C.; Pitera J. W.; Madura J. D.; Dick T. J.; Hura G. L.; Head-Gordon T. Development of an improved four-site water model for biomolecular simulations: TIP4P-Ew. J. Chem. Phys. 2004, 120 (20), 9665–9678. 10.1063/1.1683075. [DOI] [PubMed] [Google Scholar]
  45. Grimme S.; Antony J.; Ehrlich S.; Krieg H. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J. Chem. Phys. 2010, 132 (15), 154104 10.1063/1.3382344. [DOI] [PubMed] [Google Scholar]
  46. Thompson A. P.; Aktulga H. M.; Berger R.; Bolintineanu D. S.; Brown W. M.; Crozier P. S.; et al. LAMMPS - a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2022, 271, 108171 10.1016/j.cpc.2021.108171. [DOI] [Google Scholar]
  47. Boyd P. G.; Moosavi S. M.; Witman M.; Smit B. Force-Field Prediction of Materials Properties in Metal-Organic Frameworks. J. Phys. Chem. Lett. 2017, 8 (2), 357–363. 10.1021/acs.jpclett.6b02532. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Rappe A. K.; Goddard W. A. III Charge equilibration for molecular dynamics simulations. J. Phys. Chem. A 1991, 95 (8), 3358–3363. 10.1021/j100161a070. [DOI] [Google Scholar]
  49. Wilmer C. E.; Kim K. C.; Snurr R. Q. An extended charge equilibration method. J. Phys. Chem. Lett. 2012, 3 (17), 2506–2511. 10.1021/jz3008485. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao3c06937_si_001.pdf (989.5KB, pdf)
ao3c06937_si_002.zip (32.3KB, zip)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES