Sedimentation of Free and Attached Cryptosporidium Oocysts and Giardia Cysts in Water

Abstract

Experimental analysis of the sedimentation velocity of Cryptosporidium parvum oocysts and Giardia lamblia cysts was compared with mathematical description of their sedimentation velocities by using measurements of (oo)cyst size and density and the density and viscosity of the sedimentation medium to determine if the sedimentation kinetics of freely suspended oocysts of C. parvum and cysts of G. lamblia can be described by Stokes’ law. The theoretically calculated sedimentation kinetics showed a good agreement with the experimentally observed kinetics. Both showed a decline in sedimentation velocity over time, caused primarily by variation in (oo)cyst density. The initial apparent sedimentation velocities in Hanks balanced salt solution at 23°C was 0.35 μm · s⁻¹ for oocysts and 1.4 μm · s⁻¹ for cysts. (Oo)cysts that enter the surface water environment by discharges of biologically treated sewage may be attached to sewage particles, and this will affect their sedimentation kinetics. Therefore, (oo)cysts were mixed with settled secondary effluent. (Oo)cysts readily attached to the (biological) particles in effluent; 30% of both cysts and oocysts attached during the first minutes of mixing, and this fraction increased to approximately 75% after 24 h. The sedimentation velocity of (oo)cysts attached to secondary effluent particles increased with particle size and was (already in the smallest size fraction [1 to 40 μm]) determined by the sedimentation kinetics of the effluent particles. The observed sedimentation velocities of freely suspended (oo)cysts are probably too low to cause significant sedimentation in surface water or reservoirs. However, since a significant proportion of both cysts and oocysts attached readily to organic biological particles in secondary effluent, sedimentation of attached (oo)cysts after discharge into surface water will probably be a significant factor in the environmental ecology of C. parvum and G. lamblia. Attachment to particles influences not only sedimentation of (oo)cysts in surface water but also their behavior in drinking water treatment processes.

The protozoan parasites Cryptosporidium and Giardia have been implicated as the causative agents of many outbreaks of waterborne intestinal illness (2, 11). Water appears to be an important vehicle for the transmission of these parasites, along with direct contact with infected persons or animals. Both parasites produce a robust (oo)cyst to be able to endure environmental stress and to make the probability of reaching a new, susceptible host as high as possible. The (oo)cysts are shed by infected persons or animals and enter surface water through direct fecal input, discharge of treated and untreated sewage, and runoff from agricultural lands. Transport of infectious (oo)cysts from the source of surface water contamination to areas where exposure of potentially new hosts to surface water occurs, such as bathing areas, abstraction points for drinking water production, and drenching areas for livestock or wildlife, is governed by several hydrodynamical, chemical, and biological factors, i.e., water flow, attachment of freely suspended (oo)cysts to particles, sedimentation and resuspension of free and attached (oo)cysts, and survival of (oo)cysts.

Water flow is the driving force for the transport of the (oo)cysts. Free (oo)cysts will probably behave as particles that are transported by advection. It is likely that a part of the (oo)cysts is attached to larger particles and that their hydrodynamic behavior will be influenced by the characteristics of these particles.

(Oo)cysts can survive for months in surface water. The inactivation rate depends on the presence of an autochthonous microflora (predation or structural or metabolic injury by exoenzymes), temperature, and sunlight intensity (1a, 8, 10).

In stagnant waters, (oo)cysts will slowly settle to the sediment. This may occur in natural environments in which the water flow is low (lakes and slow-flowing streams and rivers in summer) and in man-made environments such as reservoirs for drinking water production (5), settling tanks in sewage treatment or drinking water treatment, and sewers. Sedimentation of particles in water follows Stokes’ law, which implies that sedimentation velocity depends on particle size, difference in density between particles and water, and the viscosity of water. Theoretical calculations by Ives (4) indicate that the sedimentation velocities of single Cryptosporidium oocysts and Giardia cysts in stagnant water are low, i.e., 0.5 and 5.5 μm · s⁻¹, respectively. In natural waters, the (oo)cysts may occur in a freely suspended form, but, since particle concentrations in the wastewater and surface water environments are high, a proportion of the (oo)cysts in surface water will probably be attached to particles such as clay, sand, plankton, algae, and (bio)flocs. The sedimentation velocity of attached (oo)cysts will be affected by the characteristics of the particle (size and density). The sampling techniques (filtration and flocculation) used in previous studies of the presence of Cryptosporidium and Giardia in water (6, 9, 12, 13) have not allowed discrimination between free and attached (oo)cysts; therefore, no data on the occurrence of attached (oo)cysts exist. Since (oo)cysts have a high survivability, settling of (oo)cysts may result in accumulation of (oo)cysts in aquatic sediments. Disturbance of these sediments, by for instance by bathers, ships, or increased water flow, may give rise to high concentration peaks in the water, yielding a relatively high risk of exposure for bathers or breakthrough through drinking water treatment systems.

This paper describes the experimental analysis of the sedimentation velocity of free Cryptosporidium oocysts and Giardia cysts and the mathematics of the sedimentation kinetics by Stokes’ law, as well as the experimental analysis of the kinetics of attachment of (oo)cysts to particles in the effluent of a biological wastewater treatment plant and the sedimentation velocities of (oo)cysts attached to these particles. Wastewater treatment effluent was selected to mimic natural conditions after discharge of treated sewage, since this is one of the major sources of contamination of surface water with Cryptosporidium and Giardia and contains a high level of mainly biological particles. A proportion of the (oo)cysts entering surface water by this route may be expected to be attached to such particles.

MATERIALS AND METHODS

Protozoa.

A bovine strain of Cryptosporidium parvum was obtained from naturally infected calves. Oocysts were purified by cesium density centrifugation and stored in 5% potassium dichromate at 2 to 8°C. Oocysts of a single batch were used at an age of 2 to 8 months. Giardia lamblia cysts were obtained from PRL Dynagenics (Phoenix, Ariz.). This was a human isolate (CH3) that was maintained in gerbils. Cysts were purified from a fecal pellet suspension by zinc sulfate flotation at a specific density of 1.09 and subsequent centrifugation. Cysts were recovered by membrane filtration, fixed in formalin, and washed and stored in distilled water.

Internal characteristics.

The presence of internal characteristics in cysts and oocysts were determined by differential interference contrast (DIC) microscopy at the onset of the experiments. Totals of 300 cysts and 300 oocysts were assayed; 298 of 300 (99.3%) of the C. parvum oocysts showed internal contents. Also, 298 of 300 (99.3%) of the G. lamblia cysts showed internal contents, and 78% had a viable type morphology by the criteria of Sauch (12).

Preparation of suspensions of free (oo)cysts.

Sedimentation experiments were performed with suspensions of 1,000 to 2,000 (oo)cysts of both parasites in 10 ml of Hanks’ balanced salt solution (Gibco BRL, Life Technologies; model no. 24020-091) which was filtered through 0.2-μm-pore-size filters to remove interfering particles (HBSS_f).

The more homogeneous the distribution of (oo)cysts in the suspension prior to sedimentation, the more accurate the determination of the sedimentation kinetics. The homogeneity of the (oo)cyst suspensions was tested by taking 10 1-ml aliquots of the 10-ml suspension. These aliquots were filtered through 25-mm-diameter polycarbonate filters (Millipore RTTP 02500) with a pore size of 1.2 μm. The filters were covered with a mixture of monoclonal antibody-fluorescein isothiocyanate (FITC) conjugates specific for Cryptosporidium (Detect-IF; Shield Diagnostics, Dundee, United Kingdom) and for Giardia (Giardia-Cel; Cellabs, Brookvale, Australia) and incubated for 30 to 45 min at 37°C. Monoclonal antibodies were prefiltered through 0.2-μm-pore-size filters to remove interfering particles. After staining, the filters were washed with HBSS_f and embedded in Dabco (1,4-diazabicyclo[2,2,2]-octane)glycerol mounting medium (adjusted to pH 7 with 1 M HCl). Filters were screened for Cryptosporidium and Giardia (oo)cysts with a Zeiss Axioskop epifluorescence microscope fitted with ×25 and ×100 Plan Neofluar objectives, with an FITC (filter set 09) dichroic mirror and filters.

Preparation of suspensions of (oo)cysts attached to particles.

To test the sedimentation characteristics of attached (oo)cysts, the protozoa were allowed to attach to particles in secondary effluent (effluent of the sedimentation basin after activated sludge treatment) of the biological domestic wastewater treatment plant of Utrecht. Effluent characteristics were as follows: turbidity, 2.4 nephelometric turbidity units; pH 7.4; dissolved organic carbon, 6.4 mg of C/liter; and specific density, 1.001 g/ml at 20.5°C. The majority (>99%) of the particles in the secondary effluent sample were <10 μm; only a small fraction of the particles was larger (as large as >400 μm). The larger particles were open, floc-like structures that consisted mainly of microorganisms.

(Oo)cysts were added to the effluent to a concentration of 3,000 to 6,000 per 10 ml and were allowed to attach for 24 h at 15°C on a rotary shaker table (experiment 1) or for 96 h at 15°C without agitation (attachment during-after settling), after which the settled effluent was aspirated and the pellet was supplemented with unseeded effluent up to the initial volume (experiment 2).

In the sedimentation experiments, the particles with attached (oo)cysts were divided into the following different size categories: 1 to 40, 40 to 80, 80 to 120, and 120 to 200 and >200 μm, as determined with an ocular micrometer.

Depending on the concentration of the particles, a certain proportion of free (oo)cysts would be filtered onto the same area of the membrane surface as a particle and would be hidden or would be apparently attached to the particle. The proportion of apparently attached (oo)cysts can be estimated by determining the surface area of the membrane that is covered with particles. In the worst case (all particles from 10 ml of effluent appear on the membrane), only 7.6% of the membrane was covered with particles. Therefore, no attempts were made to correct for apparent attachment.

Sedimentation experiments.

Sedimentation experiments were performed with 10-ml volumes in glass tubes of 10 by 1.5 cm. The height of the sedimentation column was 65 to 67 mm, and the diameter of the column was 14.0 ± 0.06 mm. Hindered settling (reduction of the sedimentation velocity by the upward flow of displaced fluid) does not significantly (<5%) influence the sedimentation velocity of particles smaller than approximately 1/45 of the column diameter (3). Hence, sedimentation of particles of up to approximately 300 μm can be determined in these columns. The volumetric fraction of the suspended (oo)cysts and of the effluent particles was (much) smaller than 0.003, which was too low to cause a significant reduction in sedimentation velocity.

The columns were placed in a temperature-controlled room at 23°C on a vibration-free surface. At time zero, 10 1-ml samples were taken from the first column to determine the initial (oo)cyst concentration and distribution. The sedimentation suspensions were allowed to settle, and after predetermined time intervals, 9-ml samples were taken from subsequent columns. These samples were taken with a 1-ml pipette with an internal diameter of 3.15 ± 0.04 mm that was attached to the tube of a stereomicroscope stand. With the focusing screws of the microscope stand, the pipette tip was lowered very gently until it was just below the meniscus of the sedimentation solution. The solution was pumped from the column by a peristaltic pump (101 U/R; Watson Marlow, Falmouth, United Kingdom) at a rate of 1 to 1.5 ml · min⁻¹. During sampling, the pipette tip was lowered with the focus screw to follow the descending meniscus. After 9 ml was sampled, the pipette tip was taken out of the column and the sample was pumped at maximum speed through the tubing into a collector tube. The sample was filtered, stained, and examined as described above.

Theoretical sedimentation velocity.

The sedimentation velocity of particles in liquids follows Stokes’ law, which is described by the following equation:

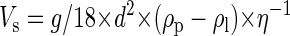1

where V_s is sedimentation velocity (in meters per second), g is gravitational acceleration (9.81 m s⁻²), d is particle diameter (in meters), ρ_p is specific density of the particle (in kilograms per cubic meter), ρ_l is specific density of the liquid (in kilograms per cubic meter), and η is dynamic viscosity of the liquid (in kilograms per meter per second). By measuring particle size and density and the density and viscosity of the liquid, the theoretical sedimentation velocity can be calculated and compared with the experimentally determined sedimentation velocity.

(i) (Oo)cyst size.

The size distribution of the protozoan (oo)cysts was determined by measuring the lengths and widths of 100 (oo)cysts at a magnification of ×1,000 with a calibrated micrometer.

(ii) (Oo)cyst density.

The densities of Cryptosporidium oocysts and Giardia cysts were determined by density gradient centrifugation in Percoll–0.15 M NaCl. The gradient was made by layering Percoll–0.15 M NaCl solutions of decreasing specific densities (1.100, 1.090, and 1.080 to 1.010 g · ml⁻¹). The gradients were loaded with 100 μl of oocyst or cyst suspension in HBSS_f and with dextran Density Marker Beads (Pharmacia DMB 1-7) prepared in 0.15 M NaCl according to the manufacturer’s instructions (30 μl of each density). The gradient was centrifuged at 390 × g for 15 min and allowed to come to a standstill without braking. After centrifugation, marked bands of the density marker beads were observed, but the (oo)cysts did not show up as a visible band. Therefore, 0.5-ml aliquots were gently taken from the gradient by the same procedure used to take the upper 9-ml sample in the sedimentation experiments. The beads and oocysts in these aliquots were pelleted at 13,000 × g for 30 s, and wet mounts of 10 μl of these pellets were made. The number of oocysts or cysts was counted, and the presence of density marker beads was recorded.

(iii) Liquid density.

The specific densities of HBSS_f and secondary effluent were measured at 23°C with a calibrated densitometer in the range of 1,000 to 1,100 kg · m⁻³.

(iv) Viscosity.

The kinematic viscosities of HBSS_f and of the secondary effluent were determined with a calibrated BS/U-tube viscometer for a viscosity range of 0.3 to 3 mm² s⁻¹ according to ISO 3104 (1). The viscosity measurements were performed at 23°C.

The dynamic viscosity (η) was calculated from the kinematic viscosity (ν) by the following equation:

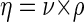2

where η is dynamic viscosity (in kilograms per meter per second), ρ is density of the medium (in kilograms per cubic meter), and ν is kinematic viscosity (in square meters per second).

RESULTS

Homogeneity of suspensions of free (oo)cysts.

In the first experiment, the sedimentation suspension was prepared by mixing a small volume (10 to 120 μl) of cyst and oocyst stock suspensions with a large volume (100 to 150 ml) of HBSS_f by gentle shaking (20×), followed by 15 min of sonification to break any (oo)cyst clumps. Volumes (10 ml) were pipetted into the sedimentation tubes. To determine the homogeneity of the sedimentation suspension, (oo)cysts concentrations of 10 1-ml samples of the 10 ml were counted. A random distribution of the relatively small number of (oo)cysts would result in Poisson-distributed counts, where the variance, ς², in the counts equals the mean, μ (ς²/μ = 1). At 9 df and α = 0.05, the counts can be regarded as homogeneously distributed when ς²/μ < 1.9. The experimental ς²/μ was 18.4 to 20.3. Hence, this mixing protocol did not result in a homogeneous distribution of (oo)-cysts.

A different mixing procedure was used in the second experiment; (oo)cyst suspensions were made by mixing HBSS_f with the stock (oo)cyst suspension on a 1:1 volume basis and by consecutive mixing (1:1) with HBSS_f until the required volume was reached. The resulting ς²/μ values of the sedimentation suspensions in the second experiment were 2.8 for Giardia and 2.5 for Cryptosporidium.

The fraction of the (oo)cysts in the sedimentation suspensions that were clumped was <1%.

Sedimentation experiments with free (oo)cysts.

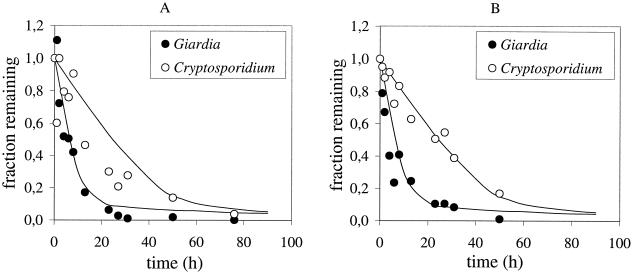
The results of the sedimentation experiments are plotted in Fig. 1A and B. Experiments 1 (Fig. 1A) and 2 (Fig. 1B) were duplicate experiments that differed only in the homogeneity of the (oo)cyst suspensions (see above). The higher degree of homogeneity in experiment 2 appeared to yield less variation in the C. parvum counts, especially in the first 10 h of the sedimentation experiment.

FIG. 1.

Concentration-time curve plot of the duplicate sedimentation experiments A (A) and B (B) with C. parvum oocysts and G. lamblia cysts. The concentration at time t is calculated as a fraction of the initial concentration (concentration_t/concentration₀). The lines represent the Monte Carlo simulation of sedimentation of (oo)cysts according to Stokes’ law. See text for details.

The rate at which the concentration of (oo)cysts decreases is a function of the sedimentation velocity of the (oo)cysts. This rate was, as expected on the basis of their size difference, higher for Giardia cysts than the rate for Cryptosporidium oocysts.

For both protozoa, the rate at which the (oo)cysts settled appeared to decline over time, indicating that a proportion of the (oo)cysts settled relatively slowly.

Theoretical sedimentation velocity.

To compare the observed decline in (oo)cyst concentration with the decline that was expected from Stokes’ equation, the values of the Stokes parameters and their variations were determined for the conditions used in the experiments.

(i) (Oo)cyst size.

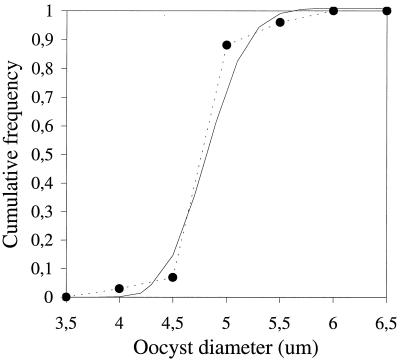
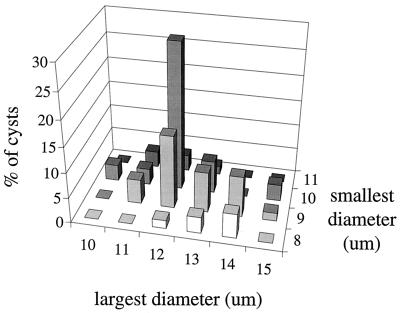
C. parvum oocysts were spherical, with a mean diameter of 4.9 μm. The distribution of the oocyst sizes (Fig. 2) was fitted to a lognormal distribution. The parameters of the fitted distribution were μ̂ = 1.5932 and ς̂ = 0.06276. G. lamblia cysts were elliptical; both the mean largest (length = 12.2 μm) and mean smallest (width = 9.3 μm) diameter are listed in Table 1, together with the mean eccentricity (ratio between length and width) of the cysts, i.e., 1.3. The eccentricity was correlated to the length of the cysts; longer cysts were thinner and shorter cysts were rounder (Fig. 3). To allow for this correlation, cyst lengths and widths were fitted with a bivariate normal distribution. The parameters that describe this distribution are the location vector (l̂ = 12.2 μm; ŵ = 9.3 μm) and the covariance matrix [cov(w,w) = 1.185; cov(w,l) = cov(l,w) = −0.307; cov(l,l) = 0.590], where l is length, w is width, and cov is covariance.

FIG. 2.

Cumulative frequency distribution of the diameters of the spherical C. parvum oocysts. The data points and dashed line represent the experimental size measurements; the solid line is the best-fitting lognormal probability density function.

TABLE 1.

Sizes of C. parvum oocysts and G. lamblia cysts

Parameter	Size (μm)
	Mean (± standard deviation)	Minimum	Maximum
Cryptosporidium oocyst diam	4.9 (0.3)	3.9	5.9
Giardia cysts
Largest diam	12.2 (1.1)	9.8	14.7
Smallest diam	9.3 (0.8)	7.8	10.8
Eccentricity	1.3 (0.2)	1.0	1.8

FIG. 3.

Distribution of the largest and smallest diameters of G. lamblia cysts.

(ii) (Oo)cyst density.

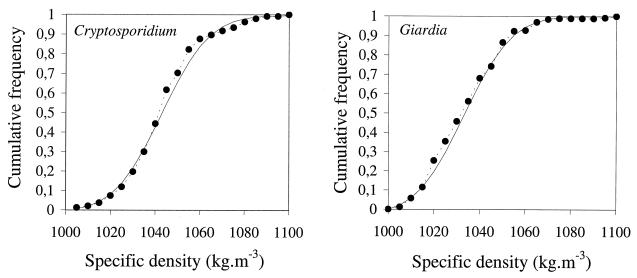
The densities of C. parvum oocysts were determined by duplicate density gradient centrifugation experiments. The density of G. lamblia cysts was determined by the same procedure, but in separate experiments. Student’s t test showed for both protozoa that the hypothesis that the duplicate data sets originated from the same distribution was acceptable (data not shown). The duplicate data sets were therefore pooled. The distributions of densities of the cysts and oocysts are shown in Fig. 4A to B. Since the distribution appeared slightly skewed, a lognormal distribution was fitted to the data. For C. parvum oocysts, the maximum likelihood values for the distribution parameters were μ̂ = 6.943 and ς̂ = 0.01599. The geometric mean density of oocysts was 1,045.4 kg · m⁻³; for cysts, the geometric mean density was 1,036.2 kg · m⁻³.

FIG. 4.

Cumulative frequency distribution of the density of C. parvum oocysts (A) and G. lamblia cysts (B). The data points and dashed lines represent the experimental density measurements; the solid lines are the best-fitting lognormal probability density functions.

(iii) Liquid density.

The specific density of HBSS_f at 22.5°C was 1,005 kg · m⁻³.

(iv) Viscosity.

Duplicate measurements of kinematic viscosity gave a mean of 0.9505 mm² · s⁻¹ (standard deviation, 0.0006 mm² · s⁻¹) for HBSS_f at 23.3°C. The dynamic viscosity was calculated as 0.000955 Pa · s at 23.3°C. Corrected for the average temperature during the sedimentation experiments, the mean dynamic viscosity was 0.000944 Pa · s.

(v) Sedimentation velocity.

To estimate the distribution in sedimentation velocity of cysts and oocysts on the basis of these parameter values, a Monte Carlo simulation of the sedimentation experiment was performed. In this simulation, a sedimentation column of 9 ml, with the same dimensions as those for the experimental column, was assumed to contain a homogeneously distributed suspension of cysts and oocysts, both in a concentration of 100 ml⁻¹. A total of 1,000 random samples were drawn from the lognormal density distribution and the lognormal or multinormal size distribution. For Giardia, the average of length and width was used in Stokes’ equation, since Brownian motion will probably result in a randomization of the orientation of the cysts during settling. The resulting parameter values were entered in Stokes’ equation, along with the mean values for the dynamic viscosity and density of HBSS_f. This resulted in a Stokes’ velocity of 1,000 cysts and oocysts at each time interval. By giving each of the 1,000 (oo)cysts a random initial position in the sedimentation column (by random sampling from a uniform distribution for the height of the column), the fraction of (oo)cysts that remained in the upper 9 ml could be calculated for 96 time intervals of 1 h. The resulting decline of the (oo)cyst concentration is plotted in Fig. 1, together with the experimental data. The plots show that, as with experimental sedimentation, the theoretically calculated sedimentation velocities decrease over time for both cysts and oocysts. The initial apparent sedimentation velocities were 0.35 μm · s⁻¹ for oocysts and 1.4 μm · s⁻¹ for cysts. Similar Monte Carlo simulations with the mean density (fixed) and random samples from the size distributions and with mean size (fixed) and random samples from the density distribution showed that the sedimentation kinetics were determined primarily by the variation in density for both parasites.

Attachment of (oo)cysts.

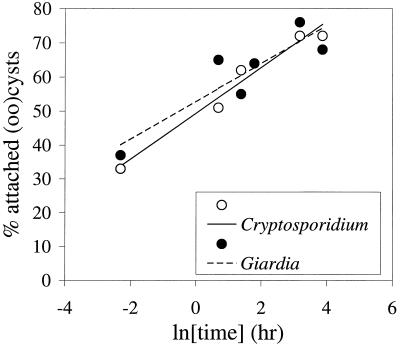
To determine the kinetics of attachment, (oo)cysts were added to secondary effluent, mixed, and incubated at 15°C under continuous mixing. The percentage of C. parvum oocysts and G. lamblia cysts that attached to the particles in secondary effluent was determined as a function of time. Attachment kinetics were assumed to follow an exponential relation; the percentage attachment was therefore plotted against the natural logarithm of the incubation time (Fig. 5). Although no (oo)cysts were attached before the suspensions were prepared, approximately one-third of both cysts and oocysts was attached to particles from secondary effluent at the time at which the first sample was taken, which was immediately after mixing. Apparently, during the preparation of the suspension, the (oo)cysts attach readily to the particles. The percentage attachment appeared to reach a maximum after approximately 24 h; prolonged incubation (48 h) did not result in a higher percentage of attached (oo)cysts. This may be due to detachment of attached (oo)cysts caused by shear forces by the fluid movement.

FIG. 5.

Attachment rate of Cryptosporidium oocysts and Giardia cysts to particles from biologically treated sewage effluent.

Sedimentation experiments with attached (oo)cysts.

Also in the sedimentation experiments with attached (oo)cysts, the homogeneity of the (overall, i.e., suspended and attached) counts was tested. The ς²/μ values of the counts of the 10 1-ml aliquots were 2.2 for oocysts and 6.4 for cysts (caused by 1 low count) in the first experiment and 3.3 for oocysts and 1.3 for cysts in the second experiment.

The sedimentation velocities of free (oo)cysts and (oo)cysts attached to particles in the different size categories were calculated by linear regression of the concentration decrease in the upper 9 ml of the sedimentation column over time. The linear area of the concentration-time curve was determined optically from a concentration-time curve plot. The observed sedimentation velocities of the free cysts and oocysts in this system were 1.5 and 0.40 μm · s⁻¹, respectively, which is comparable to the sedimentation velocity of free (oo)cysts in HBSS_f.

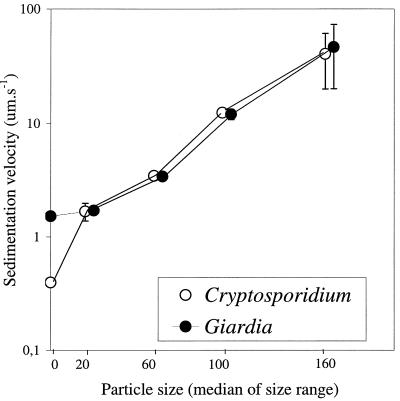
When (oo)cysts were attached to effluent particles, their sedimentation velocity increased with particle size (Fig. 6). Attached C. parvum oocysts and G. lamblia cysts had similar sedimentation velocities. The sedimentation velocity of the (oo)cysts appeared (already in the smallest size fraction [1 to 40 μm]) to be determined by the sedimentation velocity of the particles.

FIG. 6.

Sedimentation velocity of Cryptosporidium oocysts and Giardia cysts attached to particles in biologically treated sewage effluent of different size ranges. Error bars represent the minimum and maximum sedimentation velocities in duplicate experiments.

DISCUSSION

The results of this study show that the sedimentation kinetics of free G. lamblia cysts and C. parvum oocysts can be adequately described by the size and density of the (oo)cysts and the density and viscosity of the sedimentation medium. The theoretical sedimentation kinetics, which were calculated from independent measurements of the (oo)cyst and medium characteristics as used in these experiments, provide an adequate fit with the sedimentation kinetics observed in these experiments. This fit was better for C. parvum when a more homogeneous initial oocyst suspension was used in the sedimentation experiments.

Both the experimental and the theoretical sedimentation kinetics show a decline in apparent sedimentation velocity over time. The density measurements showed that the (oo)cyst population in the sedimentation experiments consisted of cysts and oocysts with various densities. According to Stokes’ law, (oo)cysts with a high density have a higher sedimentation velocity than that of (oo)cysts with a low density. At the onset of the sedimentation experiment, the observed sedimentation velocity would be the net result of the sedimentation of all (oo)-cysts. As time progressed, the denser (oo)cysts settled and the observed sedimentation velocity was composed more and more by the sedimentation velocity of (oo)cysts with a relatively low density. The simulated experiments with (oo)cysts with a constant size or density indicated that the observed variation in the sedimentation velocity was determined primarily by the variation in density.

The variation in (oo)cyst density was not apparent from the (oo)cyst morphology as observed by DIC microscopy; 99.3% of both cysts and oocysts showed internal contents. Further differentiation in high- or low-density (oo)cysts was not possible by DIC microscopy. A possible effect of experimental handling on (oo)cyst morphology was not tested. However, handling of (oo)cysts was mild, and the observed sedimentation kinetics compared favorably with the calculated sedimentation kinetics by using the measured density distribution of the (oo)cysts used in the experiments. The similarity between the calculated and the measured sedimentation kinetics provides validation of both the sedimentation experiments and the measurements of the (oo)cyst size and density distribution.

In aquatic environments, variation in density is likely to occur due to variations in age (depletion of internal resources) and exposure to stressors. In our experiments, all (oo)cysts were all of the same age and had encountered similar conditions in the laboratory. Density variation may also affect the recovery efficiency of centrifugation and flotation protocols that are used in the methods to detect C. parvum and G. lamblia in water (6, 9). The (oo)cysts in the low-density range will probably be less efficiently recovered by centrifugation techniques, while the denser (oo)cysts are less efficiently recovered by flotation techniques. Since the flotation medium (Percoll-sucrose) is used at a density of 1,090 to 1,100 kg · m⁻³, this will probably not result in significant losses of (oo)cysts, since more than 95% of the (oo)cysts have a density of less than 1,090 kg · m⁻³ (Fig. 4). However, LeChevallier et al. (7) showed that increasing the Percoll-sucrose density to 1,150 kg · m⁻³ improved the recovery efficiency.

Mixing of small volumes with large volumes is a common practice in the preparation of stock suspensions of (oo)cysts for experiments to determine the recovery efficiency of detection methods. As we have shown, this protocol does not result in homogeneous suspensions and may give rise to a high degree of variation in the (oo)cyst concentration measurements, as observed in the initial hours of the first sedimentation experiment (Fig. 1). The mixing protocol using consecutive 1:1 dilutions until the required volume was obtained consistently gave a homogeneity that was close to random distribution, and less variation between counts was observed in the second sedimentation experiment (Fig. 1). This latter protocol is therefore to be preferred for the preparation of (oo)cyst suspensions. Although the obtained distribution in our experiments was not completely homogeneous, the variation in counts was small enough to allow determination of the sedimentation velocities (Fig. 1). These observed sedimentation kinetics are validated by the calculated sedimentation velocities by using independently obtained size, density, and viscosity data for (oo)cysts and sedimentation liquid.

The initial apparent sedimentation velocities in HBSS at 23°C were 0.35 μm · s⁻¹ for oocysts and 1.4 μm · s⁻¹ for cysts. These are lower than the sedimentation velocities that were calculated by Ives (4) in water at 20°C with Stokes’ law and point estimates of (oo)cyst size and density. The estimated density of cysts and oocysts (1,050 kg · m⁻³) used by Ives were higher than the observed average density in this study. Also, the diameter of Giardia cysts that Ives used (14 μm) is considerably larger than that observed in this study. Both result in higher calculated sedimentation velocities. The most important difference between the sedimentation velocities calculated by Ives (4) and those in this study is that our sedimentation velocities are not based on point estimates of (oo)cyst size and density but on the observed distribution of size and density in our (oo)cyst population. Since size and especially density showed a considerable variation, this latter approach results in more accurate estimates of the sedimentation velocity.

The observed sedimentation velocities are very low and will probably not result in significant sedimentation in natural aquatic habitats. Turbulence caused by water flow, wind, temperature, and movement of aquatic organisms is more likely to influence the movements of (oo)cysts in water than gravitational settling.

Discharges from activated sludge treatment systems of sewage are an important source of surface water contamination with Giardia and Cryptosporidium. Giardia cysts and Cryptosporidium oocysts were shown to rapidly attach to particles from secondary effluent of a biological wastewater treatment plant. In the protocol used in this study, approximately 35% of both cysts and oocysts almost instantly attached and as much as approximately 70% attachment was attained after 24 h. Attachment kinetics depend on the probability of particle collision, the probability of attachment of colliding particles, and the firmness of the attachment. The attachment probability partly depends on the surface characteristics of cysts and oocysts. These may have been altered by the purification and storage procedures. The observed attachment kinetics are therefore valid only for the experimental conditions.

The sedimentation characteristics of (oo)cysts that were attached to effluent particles were, already in the smallest size fraction (1 to 40 μm), governed by the sedimentation characteristics of the particles. The particles were mainly bioflocs, with an irregular and open structure. The nature of the particles and the sample location (after secondary settling of activated sludge) imply that the density of these particles is relatively low. The density of the effluent particles can be deduced from Stokes’ equation; assuming their density is not related to their size, the sedimentation velocity is a function of d². The function V = c · d², where d is the median of the size ranges, yielded an adequate fit (r = 0.99 by nonlinear regression by the Levenberg-Marquardt method) to the data of particles in the size range of from 0 to 200 μm. From constant c, the viscosity and the specific density of effluent, the apparent specific density of the effluent particles can be calculated to be 1,003 to 1,004 kg · m⁻³, which was only slightly denser than the effluent (1,001 kg · m⁻³). This also explains why although attachment of Giardia cysts to the smallest size fraction resulted in a particle with more than double the diameter of free cysts, the sedimentation velocity increased from only 1.5 to 1.7 μm · s⁻¹.

A significant proportion of the (oo)cysts attached (rapidly) to biological particles in secondary effluent, and the sedimentation kinetics of the attached (oo)cysts were determined by the sedimentation characteristics of the particles. The sedimentation velocity of free (oo)cysts is probably too low to cause significant sedimentation in natural aquatic habitats. These observations imply that attachment is an important factor in the environmental ecology of Cryptosporidium and Giardia that needs further research. Attachment to particles will influence not only sedimentation of (oo)cysts in surface water environments, but probably also survival of (oo)cysts and their removal during drinking water treatment by filtration, soil passage, and disinfection processes.