Skip to main content
PMC home page
RSC Advances logoLink to RSC Advances
. 2023 Nov 24;13(49):34475–34481. doi: 10.1039/d3ra07275d

Tuning ferroelectric photovoltaic performance in R3c-CuNbO3 through compressive strain engineering: a first-principles study

Zu-Da He a, Wen-Ce Li a, Jin-Long Yang a, Hua-Kai Xu a, Xiang-Fu Xu a, Guo-Xia Lai a, You-Da Che a, Wei-Ling Zhu a, Xiao-Dong Yang a,✉, Xing-Yuan Chen a,✉
PMCID: PMC10667965  PMID: 38024997

Abstract

Most ferroelectric oxides exhibit relatively wide bandgaps, which pose limitations on their suitability for photovoltaics application. CuNbO3 possesses potential ferroelectric properties with an R3c polar structure that facilitate the separation of charge carriers under illumination, promoting the generation of photovoltaic effects. The optical and ferroelectric properties of R3c-CuNbO3, as well as the effect of strain on the properties are investigated by first-principles calculation in this paper. The calculated results indicate that R3c-CuNbO3 possesses a moderate band gap to absorb visible light. The interaction of Cu–O and Nb–O bonds is considered to have a crucial role in the photovoltaic properties of CuNbO3, contributing to the efficient absorption of visible light. The bandgap of CuNbO3 becomes smaller and the density of states near the conduction and valence bands becomes relatively uniform in distribution under compressive conditions, which improves the photoelectric conversion efficiency to 29.9% under conditions of bulk absorption saturation. The ferroelectric properties of CuNbO3 are driven by the Nb–O bond interactions, which are not significantly weakened by the compressive strain. CuNbO3 is expected to be an excellent ferroelectric photovoltaic material by modulation of compressive strain due to the stronger visible light absorption and excellent ferroelectric behavior.

First-principles calculations reveal that CuNbO3 with an R3c structure under compressive strain exhibits enhanced visible light absorption and maintains robust ferroelectric behavior.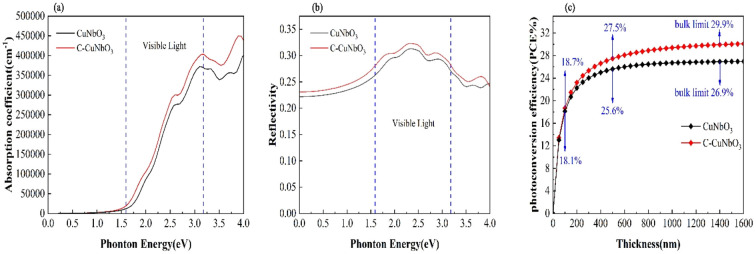graphic file with name d3ra07275d-ga.jpg

1. Introduction

Oxide-group materials have wide potential application in ferroelectric, photocatalysis and photovoltaic fields.1,2 Perovskite materials with R3c structure show a unique application prospect in the field of ferroelectric photovoltaics due to the internal electric field.3,4 For example, BiFeO3 and LiNbO3 with R3c structure have internal ferroelectric polarization electric fields, which can promote carrier separation without the p–n junction.5,6 Some ferroelectric oxides with a narrow band gap, such as Bi2FeCrO6, CuGaO2, ABiO3 (A = Ca, Cd, Zn, and Mg) and Pb(Fe1/2V1/2)O3, exhibit strong visible light absorption, which is advantageous for achieving high photoconversion efficiency.7–10 However, the band gap of most R3c-structured ferroelectric oxides is usually large and it is difficult for them to effectively absorb visible light.11,12 Niobium oxide (CuNbOx) films have been shown to be excellent p-type semiconductors that can be stabilized as hole transport layers, significantly improving the efficiency of perovskite solar cells.13 In addition, CuNbO3 with perovskite structure is also considered as a potential semiconductor material for photovoltaic and photoelectrochemical conversion.14 Narayanasamy successfully synthesized the C/2m structure of CuNbO3 by pulsed laser deposition technology, and applied it to dye-sensitized solar cells, achieving good photovoltaic performance.15 First-principles calculations show that CuNbO3 with C/2m structure can absorb visible light, and the optical properties are closely related to the Cu-d, Nb-d, and O-p energy level transitions.16,17 At the same time, Fukuda et al. synthesized CuNbO3 with an R3c structure, a polarized structural material with potential ferroelectric properties, although its light absorption properties have not been studied in detail.18 In addition to the choice of materials, strain is also a key factor in regulating the physical properties of materials. Strain can induce and regulate changes in the physical properties of materials, such as ferroelectric depolarization, piezoelectricity, magnetoresistance, electrical capacitance, and photovoltaic performance.19–22 By adjusting lattice parameters and electronic structure, strain can affect the band structure, ferroelectric polarization strength and optical properties to improve the photoelectric properties of the material.23,24 The wide band gap ferroelectric oxides, such as BiFeO3 (ref. 25) and InFeO3,26,27 have been shown to achieve significant bandgap adjustment while maintaining high ferroelectric polarization, which enhances the absorption of visible light and achieves excellent ferroelectric photovoltaic performance. In this paper, CuNbO3 with an R3c structure has been investigated by density functional theory for the ferroelectric photovoltaic performance. The calculated result indicated that CuNbO3 with an R3c structure is a new promising ferroelectric photovoltaic oxide. CuNbO3 with an R3c structure has a good ferroelectric polarization strength and can absorb visible light, which could improve the photovoltaic efficiency under the compressive strain conditions.

2. Computational method

All calculations in this paper are primarily conducted by using density functional theory implemented in the Vienna Ab initio Simulation Package (VASP) software, employing the pseudopotential plane wave method.28,29 Exchange–correlation interactions are treated by using the Perdew–Burke–Ernzerhof (PBE) functional combined with Hubbard U correction (PBE+U).30 The Hubbard U correction is particularly vital for the accurate calculation of the electronic structure with 3d transition metals.31 The plane-wave cutoff is set at 550 eV, and the K-point sampling density within the Brillouin region is maintained at 0.03 Å−1. The crystal structure was relaxed until the force acting on the atoms reached a magnitude lower than 0.001 eV Å−1. The Hubbard U value for the Cu element in R3c-CuNbO3 is set at 6 eV, with similar reports of Hubbard U correction available for other copper-based oxides.17,32,33 The calculated results indicate that the band gap of R3c-CuNbO3, obtained through the PBE+U approach, is approximately 1.7 eV. This value closely aligns with the band gap obtained using the HSE06 functional and is consistent with the experimental band gap of the C/2m structure CuNbO3.14 Considering that the PBE+U method offers an accurate calculation of the electronic structure for 3d elemental materials and is more cost-effective, we have chosen to employ the PBE+U approach for subsequent calculations involving energy, electronic structure, band structure, ferroelectric and optical properties.

3. Calculation of the structure

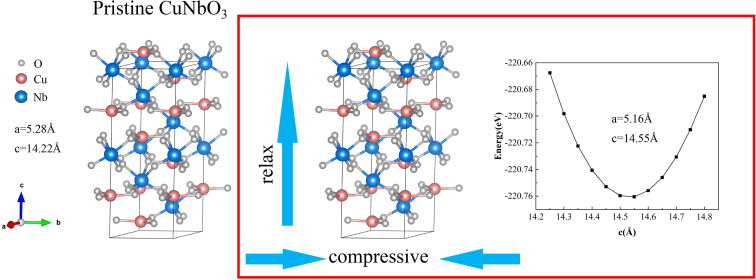
The introduction of strain was achieved by simultaneous optimization of the ab-axis and c-axis lengths, as depicted in Fig. 1. The calculated results are summarized in Table 1. The calculated pristine CuNbO3 lattice parameters are closed to the experimental values. MgSnO3 and LiNbO3 share structural similarities with CuNbO3. With the possibility of growing R3c-MgSnO3 films on LiNbO3 substrates,6,34 the lattice constant of LiNbO3 (5.15 Å) was chosen to optimize the lattice parameters of R3c-CuNbO3, introducing lattice strain. This choice is based on the smaller lattice constant of LiNbO3 compared to CuNbO3 (5.28 Å), leading to compressive strain within the CuNbO3 lattice. Using the lattice parameter a of LiNbO3 as a reference, the lattice parameter a and b of R3c-CuNbO3 was adjusted to 5.15 Å through fitting, optimizing the lattice parameter c. The c-axis of R3c-CuNbO3 under compressive strain (C–CuNbO3) is changing from 14.22 Å to 14.55 Å. To assess mechanical stability under compressive strain, the strain stress method35 within VASP software was employed to calculate the elastic constants of CuNbO3 with the R3c space group. Six independent elastic constants exist within the R3c space group structure, including C11, C12, C13, C14, C33 and C44. Based on the crystal mechanics stability criteria proposed by Mouhat and Coudert et al.,36 mechanical stability dictates that these independent elastic constants must adhere to specific inequalities.

C11 − C12 > 0, C11 + C12 > 0, C33 > 0, C44 > 0, (C11 + C12)C33 − 2C132 > 0 1

Fig. 1. The calculated structure of pristine and compressive R3c-CuNbO3.

Fig. 1

Open in a new tab

The calculated and experimental lattice parameters.

a (Å) b (Å) c (Å)
CuNbO3(exp)14 5.24 5.24 14.00
CuNbO3 (cal) 5.28 5.28 14.22
C–CuNbO3 (cal) 5.15 5.15 14.55
Open in a new tab

The calculated results, as presented in Table 2, confirm that both pristine CuNbO3 and C–CuNbO3 satisfy these inequalities, signifying their mechanical stability. The changes in the elastic constants of C–CuNbO3 could be attributed to the compressive strain, which enhances the interatomic interactions, leading to bond shortening and an increase in the elastic constants. A similar situation exists for R3c-InFeO3 and R3c-MgSnO3 in our earlier research reports, where the compressive strain causes the bond length to become shorter resulting in a larger elastic constant.27,37 Cu–O bond lengths are transitioned from 2.03 Å to 1.99 Å, whereas Nb–O bond lengths are changed from 2.14 Å to 2.12 Å under compressive strain in R3c-CuNbO3.

The calculated elastic constants and the unit given in GPa.

C 11 C 12 C 13 C 14 C 33 C 44
CuNbO3 204.167 138.897 88.539 6.668 193.172 31.948
C–CuNbO3 236.263 171.384 104.460 4.204 216.713 31.433
Open in a new tab

4. Calculation of optical properties

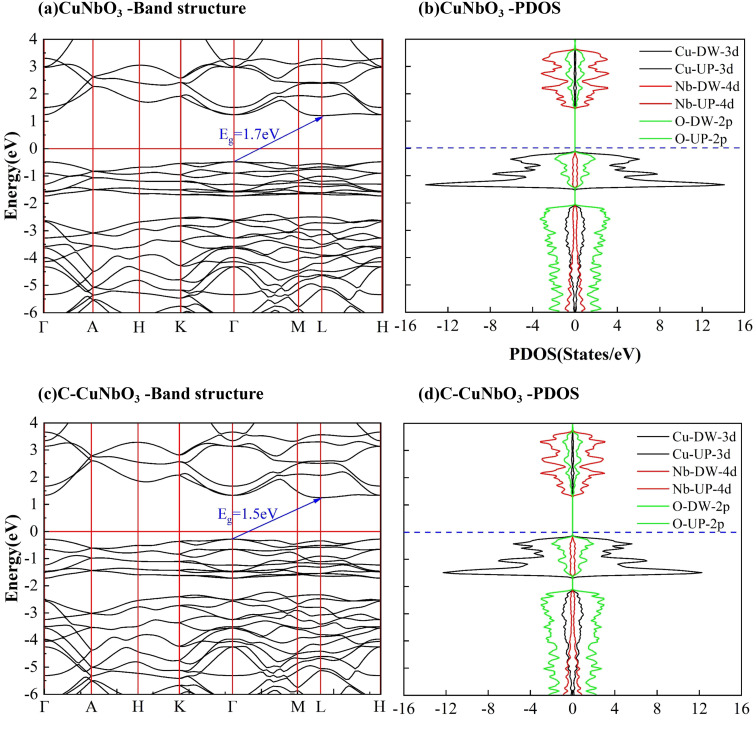
The optical and electronic properties of the material are closely correlated with its band structure. As illustrated in Fig. 2(a) and (c), the calculated band gaps for pristine CuNbO3 and C–CuNbO3 are 1.7 eV and 1.50 eV, respectively, both of which are indirect band gaps. Notably, the band gap of R3c-CuNbO3 closely aligns with the experimentally reported value for C/2m-structured CuNbO3 (2.0 eV).14 The band gap of R3c-CuNbO3 is smaller compared to the ferroelectric materials with R3c structure such as BiFeO3 (2.7 eV),38 MgSnO3 (4.0 eV),39 and ZnSnO3 (3.7 eV).39 It shares the potential for strong visible light absorption with narrow bandgap ferroelectric oxides like Bi2FeCrO6 (1.8 eV),9 CuGaO2 (1.46 eV),8 and ABiO3 (A = Ca, Cd, Zn, and Mg) (2.0 eV).7 Under compressive conditions, the band gap of R3c-CuNbO3 decreases to 1.50 eV. The valence band maximum of both pristine CuNbO3 and C–CuNbO3 (Fig. 2(b) and (d)) is primarily composed of Cu-3d orbitals and O-2p orbitals, while the conduction band minimum is predominantly occupied by Nb-4d orbitals and O-2p orbitals. The bonding states of Cu–O and the anti-bonding states of Nb–O play a pivotal role in the optical properties of R3c-structured CuNbO3. The influence of compressive strain results in a reduction of the interatomic distance in C–CuNbO3. The density of states (DOS) near the valence and conduction bands become relatively uniform distribution, resulting in a reduced bandgap and facilitating electron transitions. The band gap and dielectric function are intricately linked to the optical properties of the material. The optical properties can be obtained from the real (ε1) and imaginary (ε2) parts of the dielectric function within the Random Phase Approximation (RPA). The refractive index n and the extinction coefficient κ are determined from ε1 and ε2 with the photon energy E as follows.40

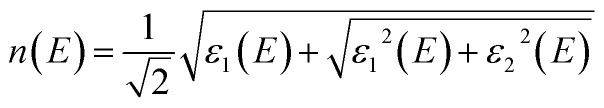4. 2
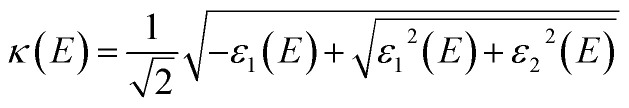4. 3

Fig. 2. The calculated energy band structure and partial density of states (PDOS) of (a and b) pristine and (c and d) compressive R3c-CuNbO3.

Fig. 2

Open in a new tab

The reflectivity R and absorption α coefficient were calculated from n and κ.40

4. 4
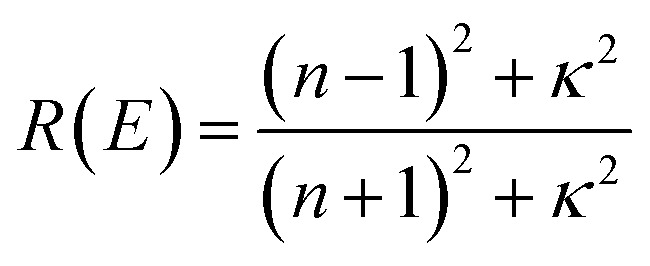4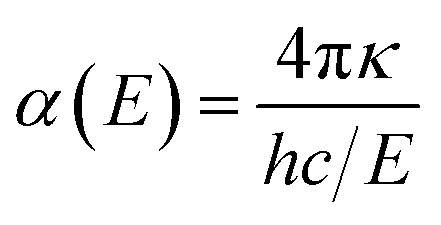. 5

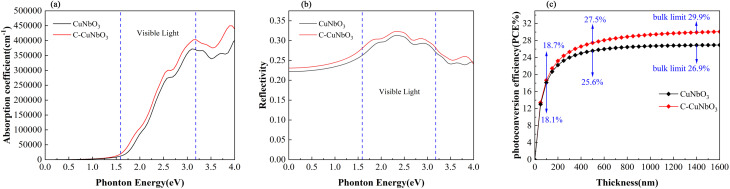
Pristine R3c-CuNbO3 exhibits a significant absorption coefficient within the visible light range, reaching 105 cm−1 in the Fig. 3a. In contrast, under compressive strain conditions, C–CuNbO3 displays a reduced band gap and stronger absorption in the visible light range compared to pristine CuNbO3, which is highly advantageous for photovoltaic applications. The photovoltaic conversion efficiency was estimated to evaluate photovoltaic potential of CuNbO3. The following approach was employed to calculate the photovoltaic conversion efficiency (PCE).41

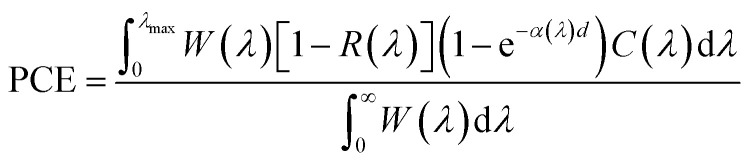4. 6

Here, λ represents the wavelength of light, λmax is the maximum absorption wavelength related to the band gap Eg as follows.

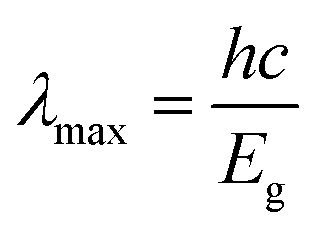4. 7

W(λ) represents the solar spectrum irradiance (AM1.5), where d represents the thickness of the material. The calculated absorption α and reflectivity R coefficient are shown in the Fig. 3a and b. C(λ) is the conversion factor, reflecting the ratio of photon energy converted to electron energy. It is related to the excitation energy of electron–hole pairs passing through the minimum band gap as follows.

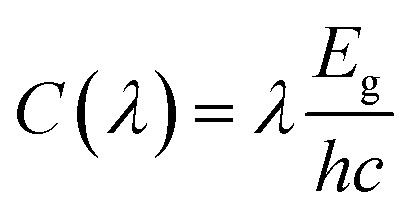4. 8

Fig. 3. The calculated (a) optical absorption coefficient, (b) reflection coefficient, and (c) photoelectric conversion efficiency. The range of visible light is indicated between the two dashed lines.

Fig. 3

Open in a new tab

The calculated photovoltaic conversion efficiencies are illustrated in Fig. 3c. For pristine CuNbO3 and C–CuNbO3 with a thickness of 100 nm, the photovoltaic conversion efficiencies are 18.1% and 18.7%, respectively. The photovoltaic conversion efficiencies for pristine CuNbO3 and C–CuNbO3 with thickness of 500 nm are 25.6% and 27.5%, respectively. Both materials exhibit significantly high photovoltaic conversion efficiencies. The application of compressive strain further enhances the photovoltaic conversion efficiency of CuNbO3 from 26.9% to 29.9% under conditions of bulk absorption saturation. The calculations of the optoelectronic properties suggest that R3c-CuNbO3 is a promising photovoltaic material, with strain-induced enhancement of light absorption leading to increased photovoltaic conversion efficiency.

5. Calculation of ferroelectric properties

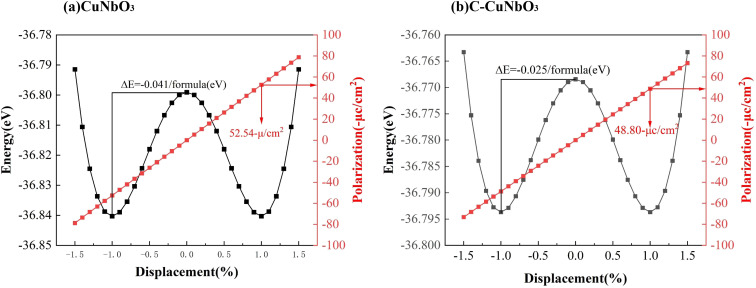
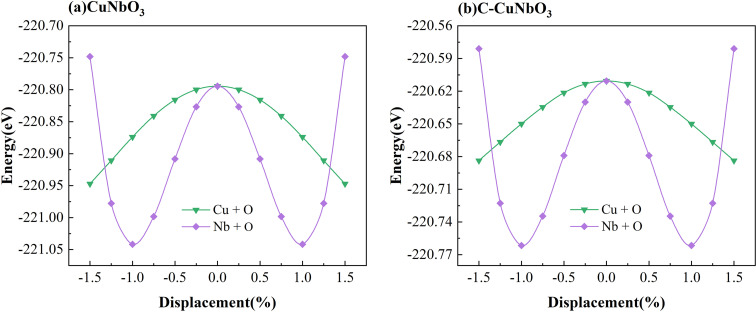
The ferroelectric polarization strength of both pristine CuNbO3 and C–CuNbO3 is determined by using the Berry phase method within the framework of modern polarization theory.42,43 As shown in Fig. 4, the R3c space group is designated as the ferroelectric phase (state 1), while the centrosymmetric reference phase is labeled as R3̄c (state 0). The double-well potential energy curves and ferroelectric polarization strength are obtained by linearly interpolating between the centrosymmetric phase (state 0) and the polar phase (state 1). These energy curves suggest that R3c-CuNbO3 could exhibit promising ferroelectric properties similar to well-documented ferroelectric materials like BiFeO3, ZnSnO3 and MgSnO3 in the literature.44–46 Under compressive strain conditions, the ferroelectric polarization value of R3c-CuNbO3 decreases from 52.54 μC cm−2 to 48.80 μC cm−2. In Table 3, the Born effective charges (BEC) and atomic displacements away from centrosymmetric positions are calculated to investigate the ferroelectric properties of CuNbO3. Born effective charges quantify the induced dipole moment of an atom in response to a slight displacement from its equilibrium position caused by the applied electric field. Greater Born effective charges generally correspond to more pronounced polarization effects, indicating increased susceptibility to atomic displacement in response to an applied electric field. The calculated results reveal that the BEC of Nb is larger than that of Cu (1e+), at approximately 8e+, and this significantly contributes to the ferroelectric polarization of R3c-CuNbO3. The calculated displacements show relatively substantial movements of Nb and O atoms in R3c-CuNbO3. Energy change diagrams for different atomic movements are also provided in Fig. 5, displaying a prominent double-well trend in atomic movement between Nb and O atoms, further affirming the pivotal role of Nb–O interaction in ferroelectric properties of R3c-CuNbO3. In Table 3, it is observed that the offset for O in pristine CuNbO3 is approximately 0.09 Å, while the Nb offset is about 0.12 Å. For C–CuNbO3, the O offset is roughly 0.08 Å, and the Nb offset is approximately 0.10 Å. Under compressive strain conditions, the ferroelectric polarization strength of CuNbO3 experiences a slight reduction due to the diminished displacement offsets. However, it still exhibits excellent ferroelectric properties, evident from the distinct double-potential well curve and robust ferroelectric polarization strength. The introduction of compressive strain in CuNbO3 enhances its light absorption, coupled with outstanding ferroelectric behavior, rendering it a highly promising ferroelectric photovoltaic oxide material.

Fig. 4. The calculated ferroelectric polarization strength and energy changes as the atom interpolation shifts of (a) pristine and (b) compressive R3c-CuNbO3.

Fig. 4

Open in a new tab

The calculated Born effective charges (e) and atomic offset (Å) away from centrosymmetric positions.

BECxx BECyy BECzz Offset (Δz)
CuNbO3 O −2.98 −2.98 −2.80 −0.09
Cu 1.05 1.05 1.09 0.01
Nb 7.92 7.92 7.30 0.12
C–CuNbO3 O −2.99 −2.99 −3.02 −0.08
Cu 0.93 0.93 1.03 −0.01
Nb 8.03 8.03 8.04 0.10
Open in a new tab

Fig. 5. The calculated energy changes as Cu–O and Nb–O movement of (a) pristine and (b) compressive R3c CuNbO3.

Fig. 5

Open in a new tab

6. Conclusion

The optical and ferroelectric properties of R3c-CuNbO3, as well as the impact of compressive strain, have been investigated by density functional theory. The calculated results showed that R3c-CuNbO3 has a more suitable band gap for absorbing visible light compared to ferroelectric materials with the R3c structure, such as BiFeO3, ZnSnO3, and MgSnO3. The interactions between Cu–O and Nb–O bonds play a crucial role in establishing the favorable bandgap in R3c-CuNbO3. The bandgap of R3c-CuNbO3 decreased under compressive strain, leading to increased uniform distribution DOS near the valence and conduction bands, improving photovoltaic conversion efficiency to 29.9% under conditions of bulk absorption saturation. The photoelectric conversion efficiency of CuNbO3 can be enhanced by the compressive strain interaction, without weakening its ferroelectric properties driven by Nb–O bond interactions. CuNbO3 under compressive strain exhibits enhanced visible light absorption and retains its exceptional ferroelectric characteristics, leading to a promising ferroelectric photovoltaic material.

Conflicts of interest

The authors declared that they have no conflicts of interest to this work. We declare that we do not have any commercial or associative interest that represents a conflict of interest in connection with the work submitted.

Supplementary Material

Acknowledgments

This work was supported by National Natural Science Foundation of China (Grant No. 12074441), the Natural Science Foundation of Guangdong Province, China (Grant No. 2021S055, 2022A1515010989), Guangdong Provincial Key Areas Special Project for Regular Higher Education Institutions (Grant No. 2023ZDZX3014, 2022ZDZX3015), Guangdong University Student Climbing Project (Grant No. pdjh2023b0357), Natural Science Foundation of Guangdong University of Petrochemical Technology (Grant No. 2019rc009).

References

  1. He J. Liu Y. Qu J. et al., Boosting photocatalytic water oxidation on photocatalysts with ferroelectric single domains. Adv. Mater. 2023;35(14):2210374. doi: 10.1002/adma.202210374. [DOI] [PubMed] [Google Scholar]
  2. Gao C. Li W. Jing L. et al., Enhanced Fill Factor and Power Conversion Efficiency of Single Oxide Ferroelectric Photovoltaic Devices with Designed Nanostructures. Adv. Funct. Mater. 2023:2213178. [Google Scholar]
  3. Choi T. Lee S. Choi Y. J. et al., Switchable ferroelectric diode and photovoltaic effect in BiFeO3. Science. 2009;324(5923):63. doi: 10.1126/science.1168636. [DOI] [PubMed] [Google Scholar]
  4. Han X. Ji Y. Yang Y. Ferroelectric photovoltaic materials and devices. Adv. Funct. Mater. 2022;32(14):2109625. [Google Scholar]
  5. Yi H. T. Choi T. Choi S. G. et al., Mechanism of the switchable photovoltaic effect in ferroelectric BiFeO3. Adv. Mater. 2011;23(30):3403. doi: 10.1002/adma.201100805. [DOI] [PubMed] [Google Scholar]
  6. Somma C. Reimann K. Flytzanis C. et al., High-field terahertz bulk photovoltaic effect in lithium niobate. Phys. Rev. Lett. 2014;112(14):146602. doi: 10.1103/PhysRevLett.112.146602. [DOI] [PubMed] [Google Scholar]
  7. He J. Franchini C. Rondinelli J. M. Ferroelectric oxides with strong visible-light absorption from charge ordering. Chem. Mater. 2017;29(6):2445. [Google Scholar]
  8. Song S. Kim D. Jang H. M. et al., β-CuGaO2 as a strong candidate material for efficient ferroelectric photovoltaics. Chem. Mater. 2017;29(17):7596. [Google Scholar]
  9. Nechache R. Harnagea C. Li S. et al., Bandgap tuning of multiferroic oxide solar cells. Nat. Photonics. 2015;9(1):61. [Google Scholar]
  10. Wu Z. Zhang Y. Ma K. et al., Strong visible-light photovoltaic effect in multiferroic Pb (Fe1/2V1/2)O3 bulk ceramics. Phys. Status Solidi RRL. 2014;8(1):36. [Google Scholar]
  11. He J. Franchini C. Rondinelli J. M. Lithium niobate-type oxides as visible light photovoltaic materials. Chem. Mater. 2016;28(1):25. [Google Scholar]
  12. Grinberg I. First-Principles Studies of Band Gap Engineering in Ferroelectric Oxides. Isr. J. Chem. 2020;60(8–9):823. [Google Scholar]
  13. Ye X. Wen Z. Zhang R. et al., High-performance and stable inverted perovskite solar cells using low-temperature solution-processed CuNbOx hole transport layer. J. Power Sources. 2021;483:229194. [Google Scholar]
  14. Joshi U. A. Palasyuk A. M. Maggard P. A. Photoelectrochemical investigation and electronic structure of a p-type CuNbO3 photocathode. J. Phys. Chem. C. 2011;115(27):13534. [Google Scholar]
  15. Narayanasamy P. Chidambaram S. G. Mahendran M. et al., Fabrication of copper-niobium-oxygen complexes as a photocathode for p-type dye-sensitized solar cell. Int. J. Energy Res. 2021;45(13):19623. [Google Scholar]
  16. Harb M. Masih D. Takanabe K. Screened coulomb hybrid DFT investigation of band gap and optical absorption predictions of CuVO3, CuNbO3 and Cu5Ta11O30 materials. Phys. Chem. Chem. Phys. 2014;16(34):18198. doi: 10.1039/c4cp02497d. [DOI] [PubMed] [Google Scholar]
  17. Crespo C. T. CuNbO3 as a solar energy converter to fuel and electricity. Sol. Energy Mater. Sol. Cells. 2018;179:305. [Google Scholar]
  18. Fukuda M. Yamada I. Murata H. et al., Perovskite-type CuNbO3 exhibiting unusual noncollinear ferrielectric to collinear ferroelectric dipole order transition. Chem. Mater. 2020;32(12):5016. [Google Scholar]
  19. Wu Z. Zhang Y. Fang C. et al., Magnetostriction-strain-induced enhancement and modulation of photovoltaic performance in Si-p–n/TbxD y1− xFe2 composite. Phys. Status Solidi A. 2014;211(3):641. [Google Scholar]
  20. Jia Y. Tian X. Si J. et al., Modulation of strain, resistance, and capacitance of tantalum oxide film by converse piezoelectric effect. Appl. Phys. Lett. 2011;99(1):011905. [Google Scholar]
  21. Fang C. Wang C. Wu Z. et al., Uniaxial stress-induced ferroelectric depolarization in <001>-oriented 0.72Pb(Mg1/3Nb2/3)O3-0.28PbTiO3 single crystal. J. Alloys Compd. 2015;647:14. [Google Scholar]
  22. Gong S. Wu Z. Jia Y. et al., Strong strain modulation on magneto-resistance of La0. 85Sr0. 15MnO3 film via converse piezoelectric effect. J. Alloys Compd. 2018;752:402. [Google Scholar]
  23. Sando D. Yang Y. Paillard C. et al., Epitaxial ferroelectric oxide thin films for optical applications. Appl. Phys. Rev. 2018;5(4):041108. [Google Scholar]
  24. Pesquera D. Parsonnet E. Qualls A. et al., Beyond substrates: strain engineering of ferroelectric membranes. Adv. Mater. 2020;32(43):2003780. doi: 10.1002/adma.202003780. [DOI] [PubMed] [Google Scholar]
  25. Liu H. L. Lin M. K. Cai Y. R. et al., Strain modulated optical properties in BiFeO3 thin films. Appl. Phys. Lett. 2013;103(18):317. [Google Scholar]
  26. Souza J. S. Alves L. L. Lima A. F. Effects of tensile strain on the electronic, optical and ferroelectric properties of a multifunctional R3c InFeO3 compound. Comp. Mater. Sci. 2022;215:111788. [Google Scholar]
  27. Xu X. F. Lai G. X. Su K. R. et al., First-principles study on the elastic, electronic and photocatalytic properties of multiferroic material InFeO3 under strain. Int. J. Mod. Phys. B. 2021;35(21):2150215. [Google Scholar]
  28. Blöchl P. E. Projector augmented-wave Method. Phys. Rev. B: Condens. Matter Mater. Phys. 1994;50:17953. doi: 10.1103/physrevb.50.17953. [DOI] [PubMed] [Google Scholar]
  29. Kresse G. Furthmüller J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B: Condens. Matter Mater. Phys. 1996;54:11169. doi: 10.1103/physrevb.54.11169. [DOI] [PubMed] [Google Scholar]
  30. Liechtenstein A. I. Anisimov V. I. Zaanen J. Density-functional theory and strong interactions: Orbital ordering in Mott-Hubbard insulators. Phys. Rev. B: Condens. Matter Mater. Phys. 1995;52(8):R5467. doi: 10.1103/physrevb.52.r5467. [DOI] [PubMed] [Google Scholar]
  31. Kulik H. J. Cococcioni M. Scherlis D. A. et al., Density functional theory in transition-metal chemistry: A self-consistent Hubbard U approach. Phys. Rev. Lett. 2006;97(10):103001. doi: 10.1103/PhysRevLett.97.103001. [DOI] [PubMed] [Google Scholar]
  32. Heinemann M. Eifert B. Heiliger C. Band structure and phase stability of the copper oxides Cu2O, CuO, and Cu4O3. Phys. Rev. B: Condens. Matter Mater. Phys. 2013;87(11):115111. [Google Scholar]
  33. Sterling T. C. Reznik D. Effect of the electronic charge gap on LO bond-stretching phonons in undoped La2CuO4 calculated using LDA+U. Phys. Rev. B: Condens. Matter Mater. Phys. 2021;104(13):134311. [Google Scholar]
  34. Fujiwara K. Minato H. Shiogai J. et al., Thin-film stabilization of LiNbO3-type ZnSnO3 and MgSnO3 by molecular-beam epitaxy. APL Mater. 2019;7(2):022505. [Google Scholar]
  35. Le Page Y. Saxe P. Symmetry-general least-squares extraction of elastic data for strained materials from ab initio calculations of stress. Phys. Rev. B: Condens. Matter Mater. Phys. 2002;65(10):104104. [Google Scholar]
  36. Mouhat F. Coudert F. X. Necessary and sufficient elastic stability conditions in various crystal systems. Phys. Rev. B: Condens. Matter Mater. Phys. 2014;90(22):224104. [Google Scholar]
  37. Xu X. F. et al., Tuning mechanical properties, ferroelectric properties and electronic structure in R3c-MgSnO3 by compressive strain: A first-principle study. Phys. B. 2021;618:413143. [Google Scholar]
  38. Ihlefeld J. F. Podraza N. J. Liu Z. K. et al., Optical band gap of BiFeO3 grown by molecular-beam epitaxy. Appl. Phys. Lett. 2008;92(14):142908. [Google Scholar]
  39. Fujiwara K. Minato H. Shiogai J. et al., Thin-film stabilization of LiNbO3-type ZnSnO3 and MgSnO3 by molecular-beam epitaxy. APL Mater. 2019;7(2):022505. [Google Scholar]
  40. Fox M., Optical Properties of Solids, 2002 [Google Scholar]
  41. Shi G. Kioupakis E. Electronic and optical properties of nanoporous silicon for solar-cell applications. ACS Photonics. 2015;2(2):208. [Google Scholar]
  42. Resta R. Macroscopic polarization in crystalline dielectrics: the geometric phase approach. Rev. Mod. Phys. 1994;66(3):899. [Google Scholar]
  43. Spaldin N. A. A beginner's guide to the modern theory of polarization. J. Solid State Chem. 2012;195:2. [Google Scholar]
  44. Neaton J. B. Ederer C. Waghmare U. V. et al., First-principles study of spontaneous polarization in multiferroic BiFeO3. Phys. Rev. B: Condens. Matter Mater. Phys. 2005;71(1):014113. [Google Scholar]
  45. Zhang J. Yao K. L. Liu Z. L. et al., First-principles study of the ferroelectric and nonlinear optical properties of the LiNbO3-type ZnSnO3. Phys. Chem. Chem. Phys. 2010;12(32):9197. doi: 10.1039/b920065g. [DOI] [PubMed] [Google Scholar]
  46. Chen X. Y. Tan J. Q. Su K. R. et al., First-principles study of R3c-MgSnX3 (X=O, S and Se) for photovoltaic and ferroelectric application. Phys. Lett. A. 2022;422:127774. [Google Scholar]

Articles from RSC Advances are provided here courtesy of Royal Society of Chemistry

RESOURCES