Cell-Matrix Elastocapillary Interactions Drive Pressure-based Wetting of Cell Aggregates

Abstract

Cell-matrix interfacial energies and the energies of matrix deformations may be comparable on cellular length-scales, yet how capillary effects influence tis sue shape and motion are unknown. In this work, we induce wetting (spreading and migration) of cell aggregates, as models of active droplets onto adhesive substrates of varying elasticity and correlate the dynamics of wetting to the balance of interfacial tensions. Upon wetting rigid substrates, cell-substrate tension drives outward expansion of the monolayer. By contrast, upon wetting compliant substrates, cell substrate tension is attenuated and aggregate capillary forces contribute to internal pressures that drive expansion. Thus, we show by experiments, data-driven modeling and computational simulations that myosin-driven ‘active elasto-capillary’ effects enable adaptation of wetting mechanisms to substrate rigidity and introduce a novel, pressure-based mechanism for guiding collective cell motion.

I. INTRODUCTION

The balance between cell-cell and cell-extracellular matrix (ECM) forces determines the collective motion of cells, influencing essential life processes, including embryonic development [1–4] and the spreading of cancer [5–8]. The propensity for tissues to flow [9–11], fuse [12] and distribute their stresses at the surface [13] has led to modeling tissue as a fluid. Thus, cell-ECM interactions are often abstracted as interfacial energies between liquid droplets and elastic substrates [14–18]. Likewise, the spreading and migration of cells and tissues has drawn analogy to the wetting of liquid droplets on hydrophilic substrates [14, 16, 19–22]. In some cases, the magnitude of cell interfacial energies and elastic deformation energies of the ECM are comparable on the scale of micrometers, suggesting a role for elasto-capillary effects in their mechanical response [23–25]. However, the impact of elasto-capillary effects on the adhesion and wetting of cells and tissues is unclear. Further, cell-cell and cell-matrix interfacial tensions are not constant, but depend upon non-equilibrium stresses generated by the actomyosin cytoskeleton [18, 26, 27], and hence are termed ‘active’ [28]. Active stresses are associated with anomalous effects, such as dependence upon mechanical load, substrate stiffness, or boundary conditions [13, 29–32]. Thus, non-constant interfacial tensions and capillary effects may challenge the applicability of equilibrium models including Johnson-Kendall Roberts (JKR) and Young Dupré in representing the mechanics of the cell-ECM interface [33–36]. As a result, how interfacial tensions and capillary effects coordinate the shape and motion of tissue is unclear.

In this work, we explore the role of elasto-capillary interactions on the wetting of cell aggregates and the expansion (migration) of a cell monolayer film underneath the aggregate, in analogy to the wetting of liquid droplets. First, we establish the presence of strong capillary deformations in the adhesion of aggregates to compliant substrates, by measuring the indentation of the substrate during initial contact. Second, we demonstrate the extent that capillary deformations contribute to the internal pressure of the aggregate during adhesion. Finally, we show how internal pressures, monolayer-induced traction forces and substrate-dependent frictional interactions determine the rate of wetting across both compliant and rigid substrates. In doing so, we identify a switch in the motive forces for the onset of wetting. Overall, these results highlight a novel role for myosin-driven active cell surface tensions and pressures in driving the dynamics of collective cell motion.

II. AGGREGATE WETTING IS TISSUE SIZE AND SUBSTRATE RIGIDITY DEPENDENT

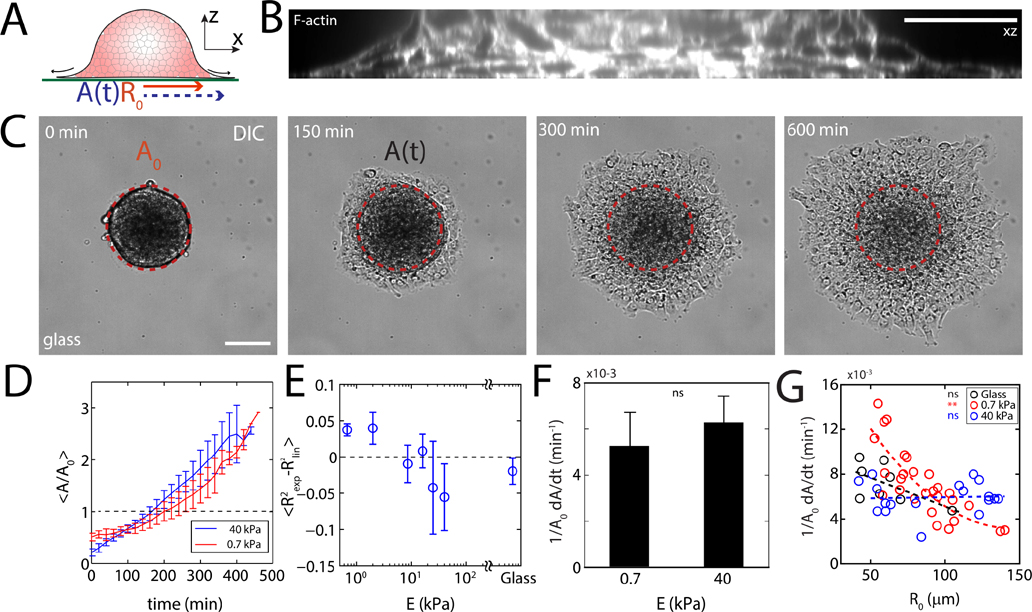
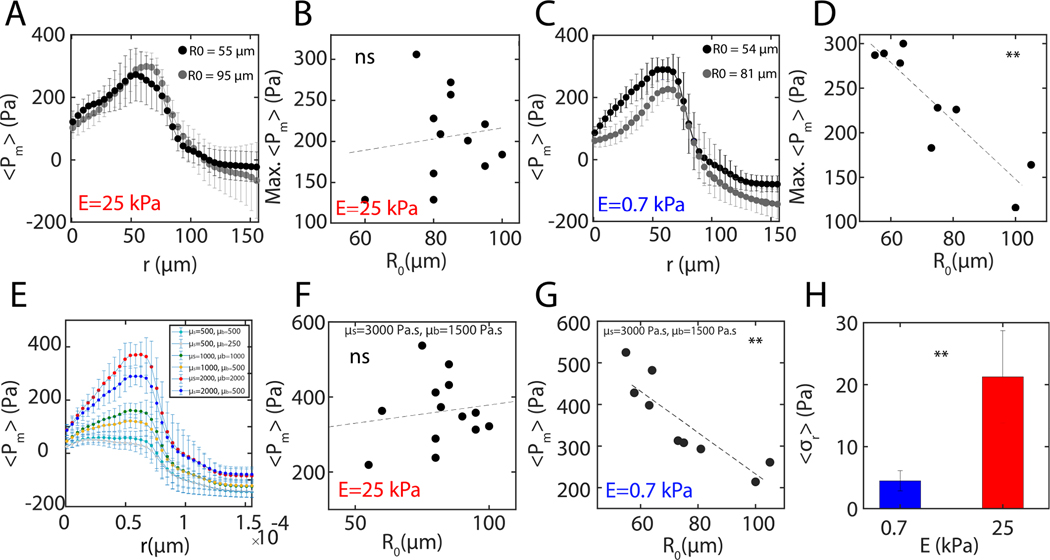
Aggregates of S180 Sarcoma cells, approximately 100–300 μm in diameter, are added to fibronectin-coated polyacrylamide gels that vary in rigidity (E) with constant added surface adhesion ([fibronectin] = 1 mg/mL) (Fig 1A, B, Supplementary Figs 1, 2, Supplementary Tables 1, 2, 3, Appendix E). The diameter of cells in the aggregates is 5–10 μm. Aggregates with initial radius $R_0$ and maximal cross-sectional area $A_0$, are visualized using Differential Interference Contrast (DIC) as well as fluorescent actin (Ftractin-EGFP) microscopy. Aggregates adhere and spread homogeneously (Supplementary Fig 3, Supplementary Video 1, 2, 3), expanding a monolayer, resembling the wetting of a liquid droplet and the expansion of a precursor film (Fig 1C) [14, 16]. Defining a monolayer strain $ϵ\left(t\right)=A\left(t\right)/A_0$ over time $t$ shows a linear expansion of the monolayer on rigid substrates and a weakly exponential expansion on soft substrates (Fig 1D, Supplementary Fig 4). Comparing the goodness of fits for both linear and exponential approximations $\left(R^2\right)$, the change from linear to exponential spreading dynamics occurs at approximately 8.6–10.0 kPa indicating a stiffness-induced shift in the mode of migration (Fig 1E). However, the instantaneous strain rates $\dot{ϵ}$ (defined as $\frac{1}{A_0}\frac{dA}{dt}$) are similar in magnitude for $A>A_0$ for soft $(\mathrm{E}=0.7\mathrm{k}\mathrm{P}\mathrm{a})$ and stiff $(\mathrm{E}=40\mathrm{k}\mathrm{P}\mathrm{a})$ substrates (Fig 1F). Further, we show that on soft substrates, the strain rate $\dot{ϵ}$ depends strongly on the size of the aggregate (Fig 1G), although size-dependence cannot be assigned on very stiff substrates (40 kPa and glass). Previous reports of aggregate spreading on a glass surface do not conclusively demonstrate a size-dependent strain rate, although its existence cannot be excluded [18]. Douezan et al. have shown that balancing the rates of energy gained by adhesion and energy lost by slippage gives rise to a spreading behavior where the adhesion area increases linearly with time [18]. However, a nonlinear behavior suggests that the balance of adhesion and slippage may be insufficient to describe motion on soft substrates and additional forces are involved. Thus, we measure the spatio-temporal patterns of velocity and traction stress exerted on the substrate.

FIG. 1. Substrate stiffness and aggregate size determine wetting dynamics.

(A) Diagram of an aggregate spreading on a fibronectin-coated polyacrylamide gel. (B) z-profile of F-actin stained aggregate adhered to glass. (C) DIC image of an aggregate spreading on glass. $A_0$ is the projected area of an un-deformed aggregate, and A is the instantaneous contact area over which the monolayer has spread. (D) Normalized spread area $\left(A/A_0\right)$ as a function of time and stiffness. (E) Difference in fitting $R^2$ values as a function of stiffness. (F) Spreading rate $\frac{1}{A_0}\frac{dA}{dt}$ measured between $A=A_0$ and $A=2A_0(\mathrm{n}=13$ for 0.7 kPa and $\mathrm{n}=10$ for 40 kPa). (G) Spreading rate as a function of aggregate size for 0.7 kPa substrate (red, $\mathrm{n}=27),$ 40 kPa substrate (blue, $\mathrm{n}=18$), and glass (black, $\mathrm{n}=8$). Scale bars are $50\mu m$. *P < 0.05, **P < 0.01, ***P < 0.001. ns is non-significant. Error bars are mean ± standard deviation.

III. SPATIAL TRACTION STRESS PATTERNS DEPEND ON SUBSTRATE STIFFNESS

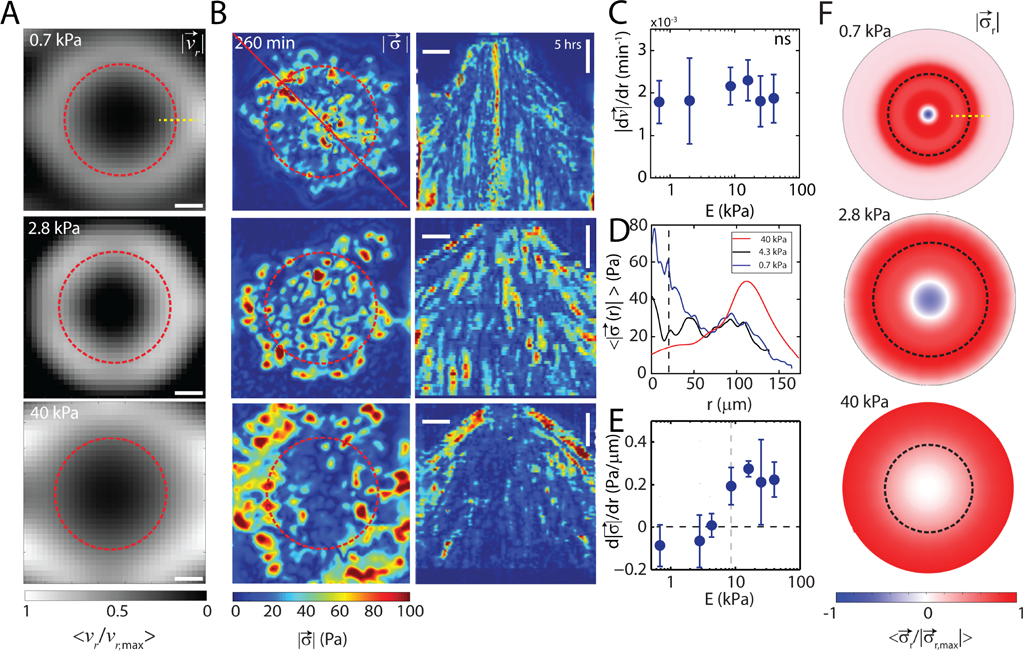
Next, we measure the radial velocity field and the traction stress field that characterizes the pattern of monolayer motion and force generation for a wide range of substrate stiffnesses. Particle Image Velocimetry (PIV) is used on basal $(\mathrm{z}=0\mu m)$ images of cellular F-actin to measure the cell accumulated radial displacements which are normalized by the elapsed time yielding a scalar velocity field, $v_r$ (Fig 2A). From this measurement, we observe that the magnitude of the radially outward flow increases from the center of the aggregate to the periphery of the monolayer. Furthermore, the gradient in velocity $\frac{d|\overrightarrow{v}|}{dr}$ is invariant with the stiffness of the substrate (Fig 2C). All spatial derivatives are calculated when the emerging monolayer reaches the edge of the microscope field of view and are measured 25 μm from the center.

FIG. 2. Traction stresses are attenuated during wetting to soft substrates.

(A) Normalized radial velocity fields $(|{\overrightarrow{v}}_r|/|{\overrightarrow{v}}_{r,max}|)$ for cumulative displacement of cell motion. F-actin images are used for flow calculation. (B, left) Magnitude of stress vectors $(|\overrightarrow{\sigma }|)$ calculated via TFM of an aggregate spreading on substrates of stiffness 0.7 kPa (top), 2.8 kPa (middle), and 40 kPa (bottom). (B, right) Corresponding kymograph of data in (B, left).(C) Velocity gradient $\frac{d|\overrightarrow{v}|}{dr}$, as a function of substrate stiffness, E $(\mathrm{n}=12)$. (D) Radial stress distribution of a spread aggregate on substrates with stiffness 0.7kPa, 2.8kPa, and 40kPa $(\mathrm{n}=3)$. (E) Stress gradient $\frac{d|\overrightarrow{\sigma }|}{dr}$ as a function of substrate stiffness, E $(\mathrm{n}=12)$. (F) Normalized radial stresses $(|\overrightarrow{{\sigma }_r}|/|{\overrightarrow{\sigma }}_{r,max}|)$ for the substrate stiffnesses in A. Red indicating inward tractions, blue indicating outward tractions. dashed black line indicates the contact line of aggregates. Yellow dashed lines in A and F indicate region where the gradients are calculated. ns is non-significant. Scale bar is 50 μm. Error bars are mean ± standard deviation.

Traction force microscopy (TFM) is used to measure the in-plane components of the surface stresses $\overrightarrow{\sigma }$ generated in the substrate by cell motion [37]. The distribution of the magnitude of the stress field $|\overrightarrow{\sigma }|$ has a strong dependence on substrate stiffness. On rigid substrates ($\mathrm{E}>8.6\mathrm{k}\mathrm{P}\mathrm{a})$, stresses are principally concentrated at the periphery of the monolayer and are nearly absent in the central region central to the aggregate (Fig 2B, bottom). By contrast, on soft substrates $(\mathrm{E}<2.8\mathrm{k}\mathrm{P}\mathrm{a})$, stresses at the monolayer periphery are nominal, but elevated central to the aggregate (Fig 2B top). For intermediate substrate stiffness $(\mathrm{E}=2.8-8.6\mathrm{k}\mathrm{P}\mathrm{a})$, the magnitude of the stress is uniformly distributed in space (Fig 2B, middle). The radial component of the stress field for soft and intermediate stiffness substrates shows outward stresses (Fig 2F top and middle) which are absent on stiff substrates (Fig 2F bottom, Supplementary Fig. 5). These results are in stark contrast to monolayer spreading experiments where stresses are inward and localized at the edges, even on soft substrates [13, 30–32]. While the velocity gradient is approximately constant, the stress gradient varies continuously with substrate stiffness (Fig 2D, 2E). Thus, the driving force for rapid wetting absent of elevated boundary stresses is unknown, and a localization of stresses away from monolayer boundaries and opposite stress directions may indicate fundamentally distinct modes of motion on soft and rigid substrates.

IV. AGGREGATE ADHESION INDUCES SIZE-DEPENDENT ELASTO-CAPILLARY EFFECTS IN SPREADING DYNAMICS

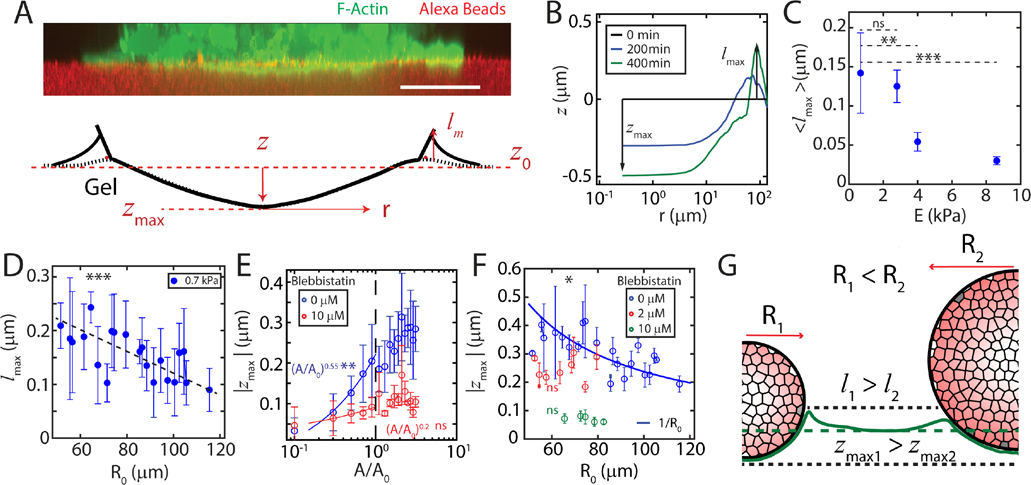
The localization of stresses under the aggregate for $\mathrm{E}=0.7\mathrm{k}\mathrm{P}\mathrm{a}$ substrates resembles the accumulation of pressure on a soft surface under an indenter, as described by contact mechanics [34]. Indeed, the deformation is not limited to the plane, as the aggregate acts like a soft spherical punch deforming the substrate in the $-\hat{z}$ dimension (Fig 3A). The aggregate indents the substrate under it by a distance $z_m$ and pulls up a meniscus at the contact line by $l_m$, both of which increase during the early phase of indentation $\left(A<A_0\right.$, Fig 3B, Supplementary video 4,5). The maximum meniscus height along the contact line, $l_{max}$ (Fig. 3B), directly scales with the elasto-capillary length in experiments with an adhesive indenter [24, 38–40]. We observe that in our experiments $l_{max}$ depends on the size of the aggregate as well as the stiffness of the substrate (Fig 3C, D).

FIG. 3. Aggregate adhesion induces capillary deformations in the substrate.

(A, top) A reconstructed z-slice showing F-actin in a cell aggregate (green) indenting a 0.7 kPa substrate (red). (A, bottom) A schematic showing relative magnitudes of out-of-plane deformations $(l,z)$. (B) z-indentation as a function of radial distance from the center of an aggregate. (C) Mean elasto-capillary length for all aggregates, as a function of substrate stiffness, E. The indentation measured at 8.6 kPa corresponds to noise in the measurement of indentation. (D) Meniscus height as a function of aggregate size on $\mathrm{E}=0.7\mathrm{k}\mathrm{P}\mathrm{a}$. (E) Maximum indentation as a function of scaled contact area, $A/A_0$ for untreated (blue) and 10 μM Blebbistatin treated (red) aggregates. (F) Maximum indentation, $z_{max}$, as a function of aggregate radius, $R_0$. Pharmacological treatment with Blebbistatin vanishes Laplace-like behavior. $0\mu M(\mathrm{n}=75)$, $2\mu M(\mathrm{n}=30)$, $10\mu M(\mathrm{n}=20)$. (G) Diagram of aggregates of different sizes inducing different out-of-plane deformations. Scale bar is $50\mu M$. *P < 0.05, **P < 0.01, ***P < 0.001. ns is non-significant. $z_0$ is set to 0 for all measurements.

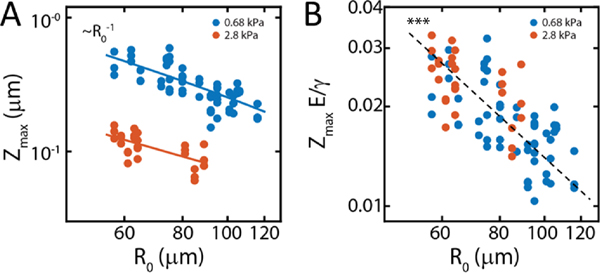
To compare the mechanics of indentation across aggregates of different sizes, we replace time with the re-scaled contact area (Fig 3E, Supplementary Fig 6). Thus the increase in contact area in time can be considered an indentation by punches of different sizes. At early times $\left(A<A_0\right)$, the indentation increases rapidly, reaching approximately 75% of the maximum by $A\approx A_0$. The Johnson Kendall Roberts (JKR) model in contact mechanics predicts the deformation of a surface caused by an elastic punch in the presence of adhesion [34]. In the original JKR model, the energy stored in substrate deformation is greater than the adhesive energy, and a scaling of $z_{\mathrm{m}\mathrm{a}\mathrm{x}}\sim A$ is expected. However, we observe a roughly $z_{\mathrm{m}\mathrm{a}\mathrm{x}}\sim A^{1/2}$ relationship, consistent with a modified form of the JKR model, where deformation and adhesive energies are comparable [39] (Fig 3E). Thus, capillary effects contribute significantly to the mechanics of aggregate-substrate interaction.

The law of Laplace relates surface tension and internal pressure. It predicts that a droplet adhered to a substrate should induce an indentation that decays inversely as the size of the droplet. Indeed, dependent upon myosin activity, we find a $\left|z_{max}\right|\sim 1/R_0$ relationship between the size of the aggregate and the indentation in the gel as has also been observed in passive droplets [22, 24, 39] (Fig 3F, Supplementary Fig 7). This relationship is retained for a range of substrate stiffness, although the magnitude decreases with increasing substrate stiffness (Appendix Fig 7). Strong capillary interactions and a Laplace-like behavior are suggestive of elevated internal pressures (Fig 3G). However, the magnitude of the capillary deformations are modest (0.1 – 0.4μm). It is unclear if these deformations are large enough to contribute to the internal pressure of the aggregate. Therefore, we next seek to use capillary deformations and the effective stiffness of the gel to estimate aggregate surface tension and evaluate its impact on aggregate pressure.

V. ELASTO-CAPILLARY EFFECTS INCREASE AGGREGATE PRESSURE

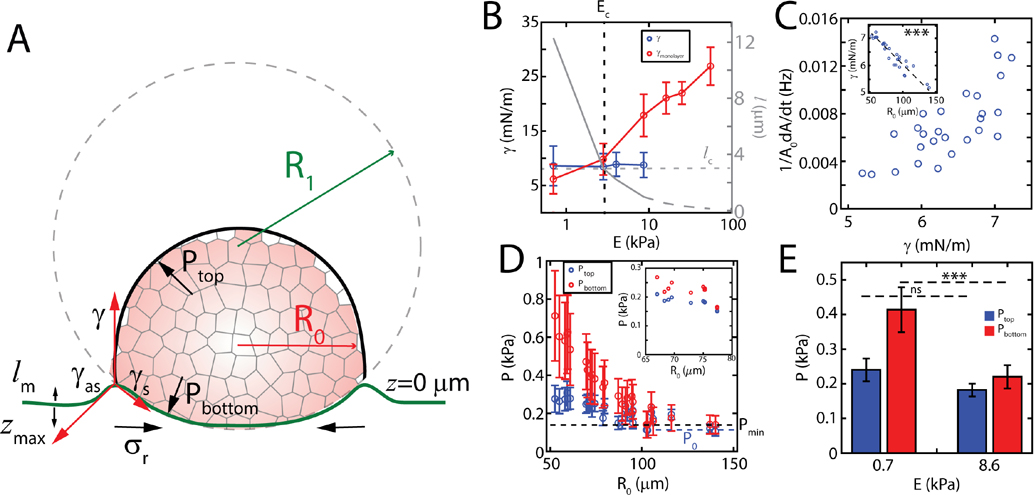
To estimate the contribution of elasto-capillary interactions to pressure of the aggregate we estimate the aggregate surface tension using force balance at the contact line and find it to be given by:

$$\gamma =\sqrt{\text{∮}{\sigma }_{r}ds\cdot E_{\mathrm{e}\mathrm{f}\mathrm{f}}\left(2l_{max}+z_{max}\right)}$$ (1)

where the line integral is along the contour of the contact line, ${\sigma }_r$ is radial traction stress measured within the contact line, $E_{eff}$ is the effective Young’s modulus of the substrate and $l_{\mathrm{m}\mathrm{a}\mathrm{x}}$ and $z_{max}$ are the maximum meniscus height and the maximum indentation, respectively (Fig 4A, Appendix A, Fig 8). As the gel thickness is comparable to the size of the aggregate, a 0.7 kPa gel has an effective stiffness of 3.7 kPa [41]. First, we observe that $\gamma$ ranges from 7 mN/m to 5 mN/m, comparable to previous measurements with micropipette on aggregates of the same cell line [42, 43](Fig 4B). Second, on average over all aggregate sizes we observe that $\gamma$ is independent of substrate stiffness, as traction stress increases with substrate stiffness while $l_{\mathrm{m}\mathrm{a}\mathrm{x}}$ and $z_{max}$ decrease with stiffness (and depend on aggregate size). Assuming that the surface tension stays constant for all stiffnesses, the effective elasto-capillary length, $l=\gamma /E$, decays monotonically with increasing substrate stiffness (Fig 4B). However, $\gamma$ retains the size dependence from $l_{\mathrm{m}\mathrm{a}\mathrm{x}}$ and $z_{max}$, and varies inversely with the size of the aggregate (Fig 4C inset), consistent with the size dependence of myosin activity (Supplementary Fig 8) [43, 44].

FIG. 4. Capillary forces increase aggregate internal pressure.

(A) A schematic describing the decomposition of forces and pressures at $A=A_0$ on deformable substrates. (B) Effective surface tension as a function of substrate stiffness when measured from monolayer stress (red), and active elasto-capillary deformations (blue) $(\mathrm{N}=10$ samples per data point). Effective elasto-capillary length as a function of substrate stiffness calculated from experimental data (solid grey) and under assumption that surface tension stays constant (dashed grey). $l_c$ and $E_c$ are the critical elasto-capillary length and critical substrate stiffness, respectively, where the transition between modes of migration occurs. (C) Aggregate spreading rate as a function of the aggregate surface tension on a 0.7 kPa substrate $(\mathrm{N}=27)$. Surface tension as a function of aggregate size (inset). (D) Pressure on top and bottom section of an aggregate at 0.7 kPa and 8.6 kPa (inset). The dashed black line represents the minimum pressure, $\left(P_{min}=135.8\pm 4.4\mathrm{P}\mathrm{a}\right)$, required to overcome traction. The dashed blue line is basal pressure, $\left(P_0=109.6\pm 6.2\mathrm{P}\mathrm{a}\right)$, for largest aggregates. Error bars are error propagated from measurements of $l_{max}$ and $z_{max}$. (E) Mean pressure on top and bottom sections as a function of substrate stiffness ($\mathrm{N}=9$ for 0.7 and 8.6 kPa each). Error bars are mean ± standard deviation.

Considering the stresses that localize at the monolayer boundary, it is possible to compute an ‘effective’ surface tension for the monoloayer (${\gamma }_{\text{monolayer}}$), which is defined as the radial traction force at the boundary (approximately one cell diameter outside and inside the contact line) normalized by the length of the boundary [13, 30, 32]. With this measurement, we can compare the surface tension generated by the aggregate to the effective surface tension generated by the monolayer as a function of substrate stiffness (Fig 4B). For $E>E_c\approx 2.8\mathrm{k}\mathrm{P}\mathrm{a}$, ${\gamma }_{\text{monolayer}}>\gamma$, which corresponds to elasto-capillary lengths larger than a critical length $l>l_c\approx 3\mu \mathrm{m}$. By contrast, for $E<E_c,\gamma >{\gamma }_{\text{monolayer}}$ [13], which happens when $l<l_c$. Thus, for very soft substrates, the aggregate surface tension is larger than that generated by the expanding monolayer. The decay in surface tension is captured by equation (1) and experimental measurements in Fig 3, where $l_{max}$ decay nonlinearly with $E_{\text{eff}}$. Gradients in aggregate surface tension has also been shown to drive internal flows in laser ablation studies. In these studies, ablation at the contact line (between the aggregate and monolayer) induces retraction of the aggregate nearly exclusively at the contact line for $\mathrm{E}=0.7\mathrm{k}\mathrm{P}\mathrm{a}$, compared to retraction across the contact area for $\mathrm{E}=40\mathrm{k}\mathrm{P}\mathrm{a}$ (Supplementary Fig 10, Supplementary Video 6). Thus, the aggregate surface tension gradient couples to motion in the soft regime. Likewise here, by comparing the $\gamma$ to the spreading rate, we find that fast spreading is correlated to high surface tension (Fig 4C, Supplementary Fig 8,9).

From the estimates of $\gamma$, and the Laplace relationship established by the size-dependence of $l_{max}$, we calculate the pressure along the top surface $\left(P_{\text{top}}\right)$ and bottom surface $\left(P_{\text{bottom}}\right)$ of the aggregate (Appendix A). For stiff substrates, these two pressures are comparable and are nearly independent of the size of the aggregate (Fig 4D, inset). However, for 0.7 kPa gels, $P_{\text{bottom}}<P_{\text{top}}$, and the overall pressure of the aggregate is increased by indentation, yet decreases with the size of the aggregate (Fig 4D, E). In this case, the pressure decays to a ‘basal’ pressure, $P_0=110\pm 6\mathrm{P}\mathrm{a}$ which is the pressure of the aggregate unaltered by indentation. Using an energy minimization argument we also calculated the minimum pressure $P_{min}=136\pm 4\mathrm{P}\mathrm{a}$, required to overcome the traction on an undeformed substrate (Appendix A). Estimation of both $P_0$ and $P_{min}$ assume that the contact angle of the aggregate with the substrate is $\pi /2$ and the radius of the contact area is same as that of the undeformed aggregate. Further, these pressure estimates from indentation using Laplace’s law agree with estimates of pressure using the modified JKR approach (Appendix D). Next, we seek to determine the role of the internal pressure in the expansion of the monolayer.

VI. INTERNAL PRESSURE DRIVES SIZE-DEPENDENT CELLULAR FLOWS ON SOFT SUBSTRATES

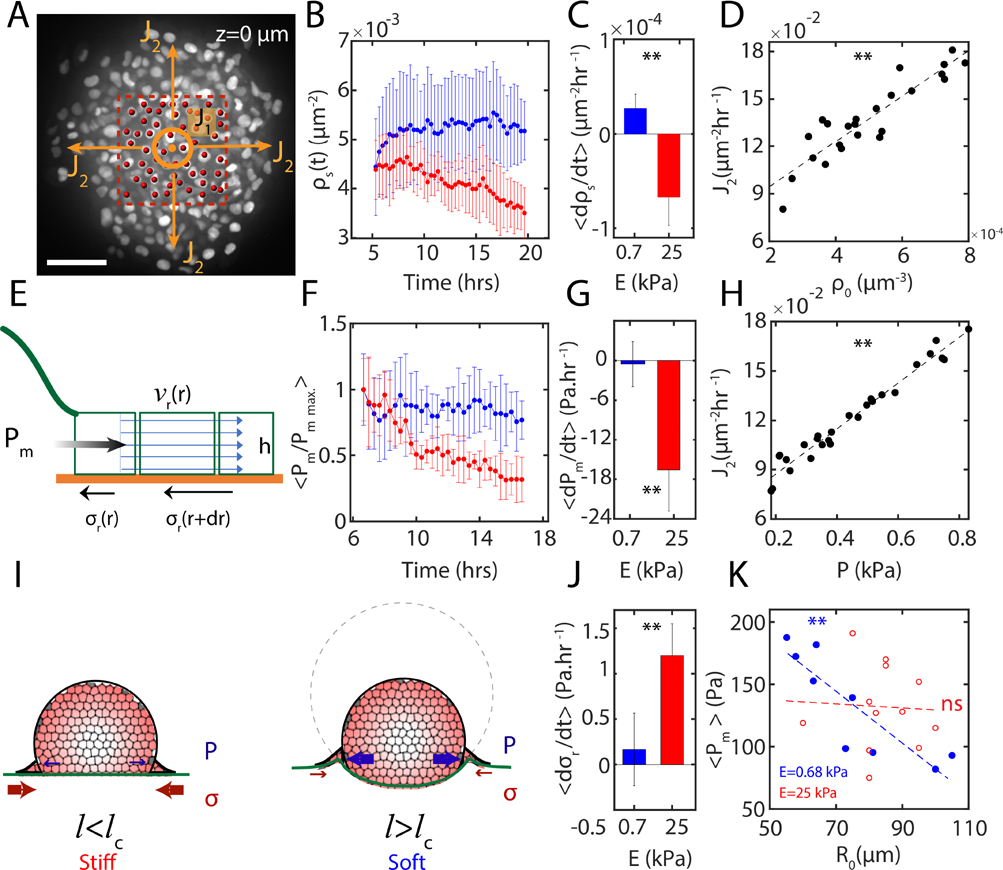
Cells from the bulk of the aggregates feed the contact surface through a downward flux of cells normal to the substrate in the $\mathrm{z}$ direction $\left(J_1\right)$ and they eventually escape the area beneath the aggregate once they get to the contact line through a planar flux $\left(J_2\right)$ (Fig 5A). Measurements of cell number density $\left({\rho }_s\right)$ at the $z=0\mu \mathrm{m}$ surface, underneath the nuclei stained aggregates (red box in Fig 5A), shows increasing or constantly maintained ${\rho }_s$ with time on soft substrates $(\mathrm{E}=0.7\mathrm{k}\mathrm{P}\mathrm{a})$. By contrast, ${\rho }_s$ decreases over time on stiff substrates $(\mathrm{E}=40\mathrm{k}\mathrm{P}\mathrm{a}$) (Fig 5B), indicating compressibility of the ‘flow’. With $N$ being the number of cells passing through the aggregate cross-section per unit time, $A_0^{-1}dN/dt=J_1-J_2,J_1/J_2>1$ for soft substrates, as opposed to $J_1/J_2<1$ for stiff substrates. Thus, the rate of change of cell surface densities is significantly different based on the substrate stiffness (Fig 5C). On soft substrates, the flux increases with the initial cell density of aggregates $\left({\rho }_0\right)$ (Fig 5D) which also shows similar correlation with the measured internal pressure $\left(P\right)$ from gel indentation (Fig 5H).

FIG. 5. Internal pressure drives size-dependent cellular flows on soft substrates.

(A) Image of a spreading nuclei-stained aggregate at $z=0\mu \mathrm{m}$, the substrate surface. Red dashed box shows the area underneath the aggregate where $\left({\rho }_s\right)$ measurements were done. Central circle represents the normal vector of inlet flux $\left(J_1\right)$ on the plane, arrows showing the outlet flux of cells $\left(J_2\right)$. (B) ${\rho }_s$ as a function of time for spreading on soft $(\mathrm{E}=0.7\mathrm{k}\mathrm{P}\mathrm{a}$, blue) and stiff $(\mathrm{E}=40\mathrm{k}\mathrm{P}\mathrm{a}$, red) substrates. (C) Significant difference in the rates of change of ${\rho }_s$ on soft $\left(\mathrm{E}=0.7\mathrm{k}\mathrm{P}\mathrm{a}\right.$, blue) and stiff (E=40 kPa, red) substrates. (D) $J_2$ as a function of ${\rho }_0$ on soft substrate $(\mathrm{E}=0.7\mathrm{k}\mathrm{P}\mathrm{a})$. (E) A schematic of the components of the data-driven fluid model to calculate the internal pressure. (F) Normalized internal pressure (within $0<r<40\mu m$ of aggregate) calculated from the data-driven model $\left(P_m\right)$ as a function of time for soft $(\mathrm{E}=0.7\mathrm{k}\mathrm{P}\mathrm{a}$, blue) and stiff ($\mathrm{E}=25\mathrm{k}\mathrm{P}\mathrm{a}$, red) substrates. (G) Significant difference in the mean rate of change of internal pressure for aggregates spreading on soft ($\mathrm{E}=0.7\mathrm{k}\mathrm{P}\mathrm{a}$, blue) and stiff ($\mathrm{E}=25\mathrm{k}\mathrm{P}\mathrm{a}$, red) substrates. (H) $J_2$ as a function of $P$. (I) Schematic for pressure-driven and traction-driven flows, which depends upon the stiffness of the substrate, $E$. (J) Significant difference in the mean rate of change of traction stresses for aggregates spreading on soft ($\mathrm{E}=0.7\mathrm{k}\mathrm{P}\mathrm{a}$, blue) and stiff $(\mathrm{E}=25\mathrm{k}\mathrm{P}\mathrm{a}$, red) substrates. (K) Mean internal pressure calculated within $0<r<40\mu m$ of aggregates as a function of aggregates initial radius $\left(R_0\right)$ in steady state spreading of aggregates on soft ($\mathrm{E}=0.7\mathrm{k}\mathrm{P}\mathrm{a}$, blue) and stiff ($\mathrm{E}=25\mathrm{k}\mathrm{P}\mathrm{a}$, red) substrates.

Next, we sought to identify the extent that pressure contributes to the expansion of the monolayer. Due to large displacements during spreading and flow-like, collective motion of cells, we developed a continuum force balance model, treating the flow of cells as a thin fluid film. The model computes the internal pressure field $\left(P_m\right)$ driving the spreading dynamics of the monolayer, by counterbalancing the monolayer shear and bulk stresses, and the active cellular traction stresses applied on the substrates (Appendix B). A schematic of the model (Fig 5E) shows the variables used in the model: $v_r\left(r\right)$ is the radial velocity field obtained from PIV measurements on nuclei-stained cells spreading experiments, ${\sigma }_r\left(r\right)$ is the radial traction stress field on PAA gels exerted by spreading cells, $P_m$ is the driving pressure and $h$ is the monolayer thickness. In this model, the monolayer expansion was modelled using a compressible thin fluid film, characterized by shear and bulk viscosities. The pressure profiles were computed after the initial spreading of the monolayer $\left(A>A_0\right.$, after approximately 6 hours) where we characterize the behavior as fluid-like and before the aggregate fully spreads and flattens out. We calculate these profiles for a range of shear and bulk viscosities.

The viscosity of tissue is an active topic of investigation, and the estimates vary over several order of magnitudes from 1 Pa.s to 10⁶ Pa.s (Appendix G). As the viscosity of the spreading monolayer is an input in our model, by performing a parameter sweep we chose the corresponding shear viscosity ${\mu }_s$ of 2000 Pa.s and bulk viscosity ${\mu }_b$ of 1000 Pa.s, that gave pressure values consistent with our experimentally measured pressures from indentation (Fig 4E), pressure estimates of freely suspended aggregates [42, 43, 45] as well as cells [46]. We verified that the change in viscosities did not change the qualitative response of the pressure profile driving the flow (Fig 9, Supplementary Figure 13). Therefore, for the purpose of the main results presented in this work, we use the viscosities stated above.

The internal pressure is averaged between $0<r<40\mu m$ from the center of aggregate. For soft substrates, the pressure remains high and drives outward flow (Fig 5F, blue). By contrast, on rigid substrates, there is a 50% decrease in internal pressure (Fig 5F, red). Therefore, the pressure exhibits distinct rates of change based on substrate stiffness (Fig 5G), consistent with our independent measurements on the surface number density of cells (Fig 5B, C). However, the radial traction stresses increase more for aggregates spreading on stiff substrates compared to soft substrates (Fig 5J). Thus, there are opposite trends in the change in internal pressure and the traction stresses during aggregate spreading.

The internal pressure profiles peak near the contact line where $r\approx R_0$ regardless of the stiffness of their substrate and show minimum negative values on the monolayer indicating expansion (Appendix B, Fig 9). The average internal pressure is inversely size-dependent for aggregates spreading on soft substrates and shows no significant size-dependence for aggregates spreading on stiff substrates (Fig 5K). The pressure is size-dependent for all values of monolayer viscosity and retains the same general spatial pattern.

A schematic of the traction-driven spreading mechanism on stiff substrates and pressure-driven spreading mechanism on soft substrates is shown in Fig 5I. To better understand cell-level interactions leading to switching between different spreading mechanisms, we next build a cell-based computational model, where cell-cell and cell-ECM interactions can be controlled independently.

VII. CELL-SUBSTRATE FRICTION DETERMINES MECHANISM OF MOTION

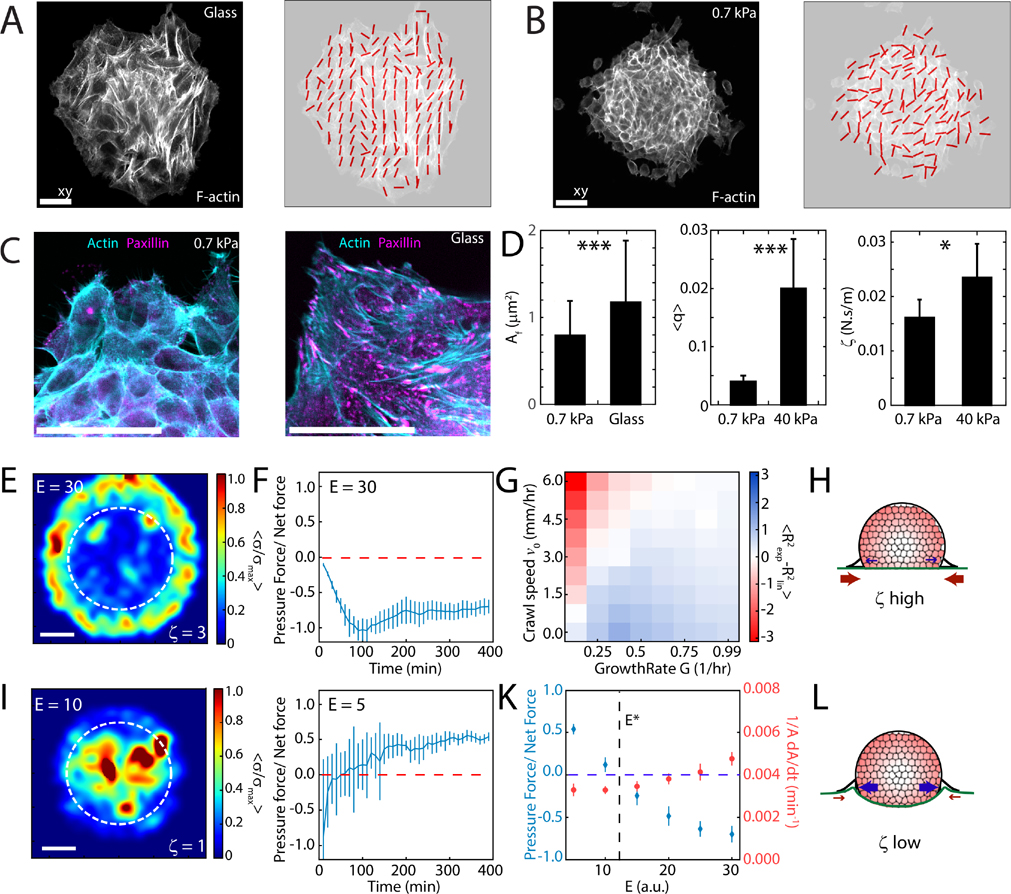
Traction stress depends upon the alignment of F-actin [47] and depends upon substrate stiffness [48]. On rigid substrates, F-actin is aligned (Fig 6A), consistent with the elevated traction stresses as reported earlier (Fig 2B and 2F). By contrast, on soft substrates (0.7 kPa), F-actin is unaligned (Fig 6B), consistent with lower traction stresses. Relatedly, on rigid substrates (glass), focal adhesions are elongated and mature. By contrast, on soft substrates, focal adhesions are nascent and small (Fig 6C). As there is an association between focal adhesion size and stability [49], the difference in focal adhesion size may be associated to a difference in cell-substrate friction [4, 29, 32]. As the traction force is frictionally transmitted, we can calculate a friction coefficient $\zeta$, by taking the ratio of the traction force to the spreading speed. We find that the frictional coefficient is lower on 0.7 kPa gels compared to 40 kPa gels, consistent with the difference in F-actin alignment and focal adhesion size (Fig 6D).

FIG. 6. Friction differentiates pressure-driven from traction-driven motion.

Confocal images and alignment vector field showing ordering of F-actin cytoskeleton on glass (A) and 0.7 kPa substrate (B). (C) F-actin and Paxillin stains within an aggregate spreading on 0.7 kPa gel and glass. Scale bars are 25 μm. (D) Focal adhesion size, mean ordering parameter and effective friction coefficient on soft and stiff substrates $(\mathrm{N}=7$ for 0.7 and 40 kPa each). Traction force results from Vertex Model for stiff, (E) $\mathrm{E}=30$ and soft, (I) $\mathrm{E}=10$ substrates. Area outlined by dashed white line indicates the region of cell addition. Scale bar is 20 μm. (E) On rigid substrates ($\mathrm{E}=30$), friction is high, and self-propulsion accounts for most of the total traction force that drives motion. (I) On soft substrates $(\mathrm{E}=5)$ friction is low, and pressure accounts for most of the total traction force that drives motion. (F,G, and J) The balance of crawling and growth reproduces exponential and linear behaviors on soft and stiff substrates respectively. (K) The balance of pressure to self-propelled forces changes as a function of substrate rigidity E, with nominal changes to spreading rate $\left(ϵ\right)$. (H, L) Schematic for pressure-driven and traction-driven flows, which depends upon the friction coefficient $\zeta$ (and stiffness, E) of the substrate. Error bars are mean ± standard deviation.

To determine how the balance between traction and pressure drives collective cell motion, we developed a vertex-based computational model [50, 51] to describe the spreading of the monolayer as a function of substrate stiffness, cell-substrate friction and individual cell mechanical properties. In this model, the monolayer is represented by a network of vertices, connected by tensed junctions that represent cell-cell interfaces [52]. Each cell has a self-propulsion force and exists in mechanical force balance with its neighbors and the substrate underneath. The influx of cells from the 3D aggregate is represented by cell addition localized to a fixed, central, and circular 2D region interior to the boundary (Appendix C). As a simple assumption, the cell incorporation rate within this region is independent of substrate stiffness (E, unitless) although the single cell self-propulsion force and cell-substrate friction coefficient correlates positively with E (Appendix C,D, Fig 10, Supplementary Fig 12). With these model properties, the monolayer spreads and traction stresses grow to localize either to the monolayer boundary $(\mathrm{E}>15)$ or to the interior $(\mathrm{E}<10)$ consistent with our experiments (Fig 6E,I, Supplementary Fig 12). We further demonstrate that the redistribution of the traction forces is driven by an interplay between a gradient in crawl speed and rate of insertion of cells to the substrate. Hence, this is a behavior unique to aggregate spreading and is not observed in monolayer spreading experiments (Appendix C). Respectively, internal pressures either decay $(\mathrm{E}>15)$ or grow $(\mathrm{E}<15)$ in time (Fig 6F,J) positively correlated to the density of cells within the monolayer (Supplementary Fig 12). Thus, motion may be principally traction-driven $(\mathrm{E}>15)$ or guided by pressure $(\mathrm{E}<15)$ where traction stresses are nominal (Fig 6G–L).

VIII. DISCUSSION

In this work, we demonstrate that substrate stiffness can induce a switch in the dynamics of aggregate wetting, suggestive of distinct stiffness-dependent mechanisms driving motion. In parallel, we show that the switch in dynamics corresponds to a change in the traction stress gradients and the balance of interfacial tensions at the contact line.

First, on soft substrates, we establish the existence of strong elasto-capillary interactions. To this end, we show that aggregate adhesion induces capillary deformations, and that the deformations are consistent with the law of Laplace, as well as a JKR model in which surface adhesion energies are comparable to bulk deformation energies [39]. Second, we show that these deformations, while nominal, contribute to the internal pressure of the aggregate. We then suggest that internal pressure provides a motive force for motion, aiding in the migration of the monolayer. Evidence includes the existence of radially-outward, substrate stiffness-dependent traction stress in the center of the monolayer, underneath the aggregate. This observation differs from that in monolayer colony studies in which no outward stresses are present [13, 29–32]. Further, the pressure by indentation has a strong dependence upon aggregate size, consistent with the size-dependent ‘strain rate’ of the monolayer in this regime. Finally, we show by force balance that internal pressures reproduce the observed pattern of cell motion and substrate traction stress.

The pressure of the aggregate in part, arises from the indentation of the substrate. Therefore, elasto-capillary effects contribute to the pressure that drives motion in this regime. From force balance, a minimum of approximately 136 Pa ($P_{min}$) is required to exceed the radial traction stress (Fig 4D, averaged over aggregate size). This estimation is a lower bound to $P_{min}$ under the assumption that the deformation from sphere to hemisphere would also increase the internal Laplace pressure of unadhered aggregates (Appendix A). The basal aggregate pressure $P_0$, which is not elevated by indentation (e.g. for large aggregates) is approximately 109 Pa. By these estimates $\left(P_0<P_{min}\right)$, we suggest elasto-capillary effects may also be necessary to elevate the internal pressure to drive robust pressure-driven flow under these experimental conditions. Controlling the generation of inplane traction stress at the boundary and out-of-plane deformations independently is a focus for future studies.

Previous works have suggested that during aggregate dewetting, a lengthscale arises from a competition between boundary stresses and contractility in the monolayer [31]. By contrast, here, we show a size-dependence in wetting on soft substrates and a corresponding size-dependence in aggregate internal pressure consistent with the elastocapillary effects. This suggests different physical mechanisms may drive wetting and dewetting.

In summary, upon wetting of stiff substrates, mature focal adhesions and organized F-actin contribute to high friction and generate large traction stresses at the boundary of the monolayer, driving outward expansion. By contrast, upon wetting a soft substrate, boundary stresses are attenuated due to the inability of immature focal adhesions to generate significant friction or traction. In the absence of strong traction, internal pressure can guide outward flows. These results indicate that pressure and traction stresses are compensatory mechanisms in the spreading of cell aggregates.

Appendix A: Estimating aggregate surface tension from indentation and elasto-capillary response data

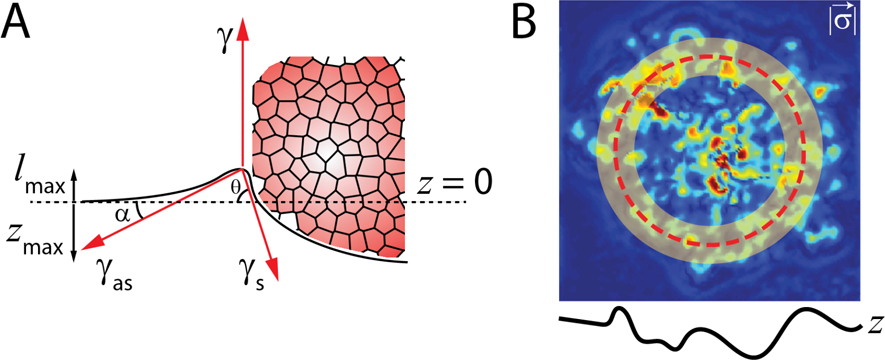
Here we present the derivation for estimating aggregate surface from force-balance at the contact line. We use the schematic in Fig 8, where the dashed line represents the substrate at $\mathrm{z}=0$, which is the undeformed reference plane. The height of meniscus at the point of contact is $l_m$, and maximum indentation under the aggregate is $-z_{max}$. From balance of forces around the contact line:

$${\gamma }_{as}\mathrm{c}\mathrm{o}\mathrm{s}\left(\alpha \right)={\gamma }_s\mathrm{c}\mathrm{o}\mathrm{s}\left(\theta \right)=\text{∮}{\sigma }_{r}ds,$$ (A1)

$${\gamma }_{as}\mathrm{s}\mathrm{i}\mathrm{n}\alpha +{\gamma }_s\mathrm{s}\mathrm{i}\mathrm{n}\theta =\gamma ,$$ (A2)

where $\gamma$ is the tension at the aggregate-media (fluid) interface, ${\gamma }_{as}$ is the tension at the media-substrate interface, ${\gamma }_s$ is the tension at the substrate-aggregate interface (Fig 8A), ${\sigma }_r$ is the magnitude of the radial component of the traction stress measured within the contact line and the line integral is along the contact line contour (Fig 8B). Using the first set of relations in (A1) we eliminate ${\gamma }_{as}$ from (A2):

$${\gamma }_s(\mathrm{c}\mathrm{o}\mathrm{s}\theta \mathrm{t}\mathrm{a}\mathrm{n}\alpha +\mathrm{s}\mathrm{i}\mathrm{n}\theta )=\gamma$$ (A3)

Using the second set of relations from (A1) we eliminate ${\gamma }_s$ from (A3)

$$(\mathrm{t}\mathrm{a}\mathrm{n}\alpha +\mathrm{t}\mathrm{a}\mathrm{n}\theta )\text{∮}{\sigma }_{r}ds=\gamma$$ (A4)

To estimate the tangent of two contact angles we make the approximation that outside the aggregate meniscus height decays from $l_{\mathrm{m}\mathrm{a}\mathrm{x}}$ to 0 over elasto-capillary length scale, whereas on the inside it decays from $l_{\mathrm{m}\mathrm{a}\mathrm{x}}$ to $-z_{max}$.

$$\therefore \mathrm{t}\mathrm{a}\mathrm{n}\alpha =\frac{l_{\mathrm{m}\mathrm{a}\mathrm{x}}{E}_{eff}}{\gamma },\mathrm{t}\mathrm{a}\mathrm{n}\theta =\frac{\left(l_{\mathrm{m}\mathrm{a}\mathrm{x}}+z_{max}\right)E_{eff}}{\gamma }$$ (A5)

Using (A5) in (A4), we get:

$$\gamma =\sqrt{\text{∮}{\sigma }_{r}ds\cdot E_{eff}\left(2l_{\mathrm{m}\mathrm{a}\mathrm{x}}+z_{max}\right)}$$ (A6)

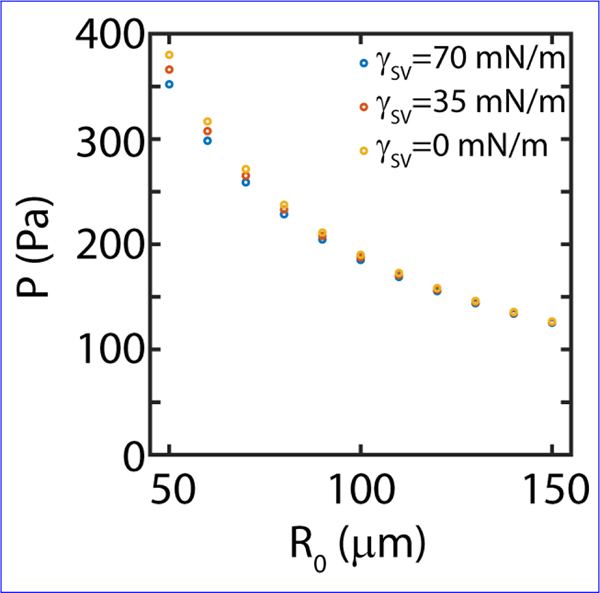
It is interesting to note that the aggregate surface tension turns out to be a geometric mean of contributions from radial and the $z$-direction. As traction stresses are measured from in-plane deformations, we use gel stiffness to be 0.7 kPa. However, elastocapillary contributions are measured from out of plane deformations; hence to account for the finite thickness of the substrate, we use an effective gel stiffness of 3.7 kPa [41]. Using the value of $\gamma$ from (A6) and substituting in equation (A3) gives us an estimate of surface tension at the aggregate-substrate interface

FIG. 7. Indentation follows a $1/R_0$ decay on substrates of different stiffnesses.

(A) Maximum indentation at $R=R_0$ as a function of aggregate size $R_0$ and substrate stiffnesses (0.7 kPa and 2.8 kPa). In both cases we observe that the indentation behavior is well approximated by a $1/R_0$ decay. (B) Maximum indentation scaled by elasto-capillary length scale, $\gamma /E$ as function of size $R_0$. Collapse of the data to a single regime indicates that indentation is proportional to elasto-capillary length. Each point represents a single experiment.

FIG. 8. Estimation of Aggregate surface tension from 3D deformation data:

(A) A schematic showing force balance at the meniscus. The surface tension of the adhered aggregate was estimated by measuring the z-indentation, meniscus height, and radial traction forces. $\gamma$ is the tension at the aggregate-media interface, ${\gamma }_{as}$ is the tension at the substrate-media interface, ${\gamma }_s$ is the tension at the substrate-aggregate interface. (B) Traction forces are calculated in the transparent yellow circular region of the TFM maps. Red dashed line show $r=R_0$. The width of yellow region is 25 μm.

$${\gamma }_s=\frac{\gamma }{(\mathrm{c}\mathrm{o}\mathrm{s}\theta \mathrm{t}\mathrm{a}\mathrm{n}\alpha +\mathrm{s}\mathrm{i}\mathrm{n}\theta )},$$ (A7)

which can be further reduced to

$${\gamma }_s=\frac{\gamma \sqrt{{\left(l_{\mathrm{m}\mathrm{a}\mathrm{x}}+z_{max}\right)}^2+l_c^2}}{\left(2l_{\mathrm{m}\mathrm{a}\mathrm{x}}+z_{max}\right)}$$ (A8)

where $l_c$ is the critical elasto-capillarity length. The pressure on top and bottom surfaces can then be calculated by using Laplace’s relation $P=2\gamma /r$, where $\gamma$ is the surface tension at the surface of interest and $\mathrm{r}$ is the radius of curvature of that surface.

Using a free energy argument, we can also calculate the minimum internal pressure, $P_{min}$ required to overcome the traction in the absence of any elasto-capillary deformations. The free energy of the adhered aggregate can be written as

$$E=-P_{min}V\left(r\right)+{\gamma }_{monolayer}A\left(r\right)$$ (A9)

where $V\left(r\right)$ and $A\left(r\right)$ are the volume and contact area of the aggregate, respectively when its radius is $r$, and ${\gamma }_{monolayer}$ is the line tension at the contact line. Taking a derivative of the above equation and equating it to zero for a spherical aggregate of radius $R_0$, with a circular projected area, yields $P_{min}=2{\gamma }_{monolayer}/R_0$. For a hemispherical cap of similar dimension, above analysis yields $P_{min}={\gamma }_{monolayer}/R_0$. As adhesion of the aggregate leads to the deformation of the aggregate and a further increase in the pressure, we choose $P_{min}=2{\gamma }_{monolayer}/R_0$ as the lower bound of the pressure required to overcome traction.

Appendix B: Internal pressure calculation using a data-driven continuum fluid model

To determine how the internal pressure counterbalances the monolayer shear, bulk, and active cellular stresses, we developed a continuum fluid model that describes the local force balance of the spreading monolayer. The different terms in the force balance equation are informed by experimental data on the velocity fields of spreading aggregates and traction force field from traction force microscopy (TFM) measurements. Let $s_{ij}$ denote the 3D stress tensor of the monolayer. Local force balance in the monolayer leads to the equation:

$$\frac{\partial s_{iz}}{\partial z}+\frac{\partial s_{ij}}{\partial x_j}=0,$$ (B1)

where $i,j=\{x,y\}$. Integrating across the monolayer height we get

$${\int }_0^h\left(\frac{\partial s_{iz}}{\partial z}+\frac{\partial s_{ij}}{\partial x_j}\right)dz=0.$$ (B2)

The monolayer is stress free at the top surface and has equal stress in magnitude but in the opposite direction to the stresses measured from TFM [53]. This leads to the following simplification:

$$s_{iz}(h)-s_{iz}(0)+\frac{\partial }{\partial x_j}{\int }_0^h{s}_{ij}dz=0$$ (B3)

$$0-{\sigma }_i+\frac{\partial }{\partial x_j}{\int }_0^h{s}_{ij}dz=0$$ (B4)

$$\frac{\partial }{\partial x_j}{\int }_0^h{s}_{ij}dz={\sigma }_i$$ (B5)

where ${\sigma }_i$ is the substrate traction stress vector. For thin monolayers with height $h$, we can write the z-averaged planar stress as:

$${\mathrm{\Sigma }}_{ij}=\frac{1}{h}{\int }_0^h{s}_{ij}(x,y,z)dz$$ (B6)

where ${\mathrm{\Sigma }}_{ij}$ is the thickness averaged 2D stress tensor. Therefore from (B5) and (B6) we will have the following effective force-balance equation:

$$h\frac{\partial {\mathrm{\Sigma }}_{ij}}{\partial x_j}={\sigma }_i.$$ (B7)

We assume the following constitutive equation for the monolayer, which is modeled as an active fluid with shear viscosity ${\mu }_s$ and bulk viscosity ${\mu }_b$:

$${\mathrm{\Sigma }}_{ij}={\mu }_b(\frac{\partial v_k}{\partial x_k}){\delta }_{ij}+\frac{{\mu }_s}{2}\left(\frac{\partial v_i}{\partial x_j}+\frac{\partial v_j}{\partial x_i}\right)-P_m{\delta }_{ij}.$$ (B8)

In the above, $v_i$ is the velocity field, $P_m$ is the active pressure field in the monolayer, $\delta$ is the Kronecker delta, $i$ the the main index and $k$ is the dummy index. By plugging (B8) into (B7):

$$-\frac{\partial P_m}{\partial x_i}+{\mu }_s\frac{{\partial }^2{v}_i}{\partial x_j\partial x_j}+{\mu }_b(\frac{{\partial }^2{v}_k}{\partial x_i\partial x_k})=\frac{{\sigma }_i}{h}$$ (B9)

Since the monolayer expansion has an axial symmetry around the center of aggregate, writing the $r$-component in cylindrical coordinate gives:

$$-\frac{\partial P_m}{\partial r}+{\mu }_s\left[\frac{1}{r}\frac{\partial }{\partial r}\left(r\frac{\partial v_r}{\partial r}\right)\right]+{\mu }_b\frac{\partial }{\partial r}\left[\frac{1}{r}\frac{\partial }{\partial r}\left(r{v}_r\right)\right]=\frac{{\sigma }_r}{h}$$ (B10)

$$-\frac{\partial P_m}{\partial r}+\left({\mu }_s+{\mu }_b\right)\left(\frac{{\partial }^2{v}_r}{\partial r^2}+\frac{1}{r}\frac{\partial v_r}{\partial r}\right)-{\mu }_b\frac{v_r}{r^2}=\frac{{\sigma }_r}{h}$$ (B11)

where $v_r=v_r\left(r\right)$ and ${\sigma }_r={\sigma }_r\left(r\right)$ are the radial velocity and traction stress components, respectively. Integration and further simplification of equation (B11) gives:

$$\begin{gathered} P_m(r)=P_m(0)+\left({\mu }_s+{\mu }_b\right)\left(\frac{v_r}{r}+\frac{\partial v_r}{\partial r}\right)+{\mu }_s{\int }_0^r\frac{v_r}{r^2}dr \\ -{\int }_0^r\frac{{\sigma }_r}{h}dr-{\left.\left({\mu }_s+{\mu }_b\right)\left(\frac{\partial v_r}{\partial r}+\frac{v_r}{r}\right)\right|}_{r=0} \end{gathered}$$ (B12)

$v_r$ was obtained by particle image velocimetry (PIV) analysis on the time-lapse movies of spreading of nucleilabeled aggregates and calculating the radial component followed by averaging radially over rings of different radii from the center of aggregate. Moreover, the active traction force field, ${\sigma }_r$, was obtained from traction force microscopy (TFM) measurements on the same experiments. The fields were then smoothen to reduce noise. We verified that at long time scales, the velocity profile scales as $r^2$, allowing us to integrate equation B12 without encountering divergence at $r=0$ due to $1/r^2$ term (Supplementary Fig 11). We also integrate from $r>{10}^{-6}$ for consistency across all data sets.

We used Eq. (B12) to numerically calculate the radial pressure profile from the center of aggregates towards the monolayer edge. The pressure profiles were then analyzed after the initial spreading of the monolayer and before the aggregate fully spreads and flattens out, which is until the time a shadow of the bulk of aggregate is visible in the central region. We used $h=5\mu \mathrm{m}$ for thickness and estimated the viscosity parameters of ${\mu }_s=2000$ Pas and ${\mu }_b=1000\mathrm{P}\mathrm{a}.\mathrm{s}$ for our analysis by fitting for viscosities which are consistent with the pressure estimated from indentation measurements. We further show that our main results do not depend upon the choice of viscosities.

Appendix C: Active vertex model for monolayer spreading

In the vertex model for cell monolayer, each cell is modelled by a 2D polygon, with edges representing cell-cell interfaces, and vertices three-way junctions. The tissue has a total mechanical energy given by:

$$E=\sum _{\alpha }\frac{1}{2}K{\left(A_{\alpha }-A_0\right)}^2+\sum _{\alpha }\frac{1}{2}\mathrm{\Gamma }{\left(P_{\alpha }-P_0\right)}^2$$ (C1)

where $\alpha$ represents the cell identity [50, 51]. The first term represents the area elasticity of the cell, with elastic modulus $\mathrm{K}$, cell area $A_{\alpha }$, and preferred area $A_0$. The second term represents a combination of actomyosin contractility and interfacial tension, where $\mathrm{\Gamma }$ is the contractility, $P_{\alpha }$ is the perimeter, and $P_0$ is the preferred cell perimeter. The mechanical force acting on each vertex $i$ with position $x_i$ is given by:

$${\mathbf{F}}_i=\frac{\partial E}{\partial {\mathbf{x}}_i}$$ (C2)

where ${\mathbf{x}}_i$ is the vertex’s position.

Active crawling forces.

Each cell has a polarity vector ${\mathbf{p}}_{\alpha }$ that defines the direction of active crawling forces [52]. Cells on the monolayer boundary have their polarity aligned outwards, attempting to spread out, with ${\mathbf{p}}_{\alpha }=\frac{{\mathbf{r}}_{\alpha }}{\mid {\mathbf{r}}_{\alpha }|}$, where $r_{\alpha }$ is the vector from the cell center to the midpoint of its outside edge. Cells in the bulk of the monolayer align their polarities with their neighbors:

$$\frac{\partial {\mathbf{p}}_{\alpha }}{\partial t}=k_p\sum _{\beta }\left(\frac{{\mathbf{p}}_{\beta }}{n_{\beta }}-\frac{{\mathbf{p}}_{\alpha }}{n_{\alpha }}\right)$$ (C3)

where $\beta$ label the neighbors of cell $\alpha$, $k_p$ is the rate of alignment, $n_{\alpha }$ and $n_{\beta }$ are the number of neighbors for cells $\alpha$ and $\beta$ respectively, ensuring that total polarity is conserved since each cell polarity at rate $k_p{\mathbf{p}}_{\alpha }$, which its neighbors gain. In a continuum description, this would be equivalent to $\frac{\partial {\mathbf{P}}_a}{\partial t}=k_p{\nabla }^2{\mathbf{p}}_a$.

Assuming overdamped motion, force balance is given by:

$$\mu \frac{\partial {\mathbf{x}}_i}{\partial t}=\mu {\nu }_0⟨{\mathbf{p}}_{\alpha }⟩+{\mathbf{F}}_i$$ (C4)

Where $\mu$ is the friction coefficient, which we assume to be an increasing function of substrate stiffness, $v_0$ is the active crawling speed, and $⟨{\mathbf{p}}_{\alpha }⟩$ is the average polarity vector of cells containing vertex $i$. The traction force on each vertex is given by: $\mu \left(\frac{\partial {\mathbf{x}}_i}{\partial t}-{\nu }_0\right)⟨{\mathbf{p}}_{\alpha }⟩={\mathbf{F}}_i$. We assume that friction increases with substrate stiffness, and for simplicity we assume a linear dependence: $\mu \left(E\right)=\tau E$, where $\tau$ is a constant. This linear dependence emerges from a kinetic model of focal adhesions [54], which predicts that cell-substrate adhesions provide a frictional drag that increases linearly with substrate elastic modulus. Finally, the tissue pressure force is the sum of the radial components of traction force

$${\sigma }_r=\sum _i{F}_i\cdot x_i/\left|x_i\right|$$ (C5)

Similarly, the net force is equal to the sum of pressure and traction forces, with the total net force given by

$$N{F}_r=\sum _i\left(F_i+\mu v_0<p_{\alpha }>\right)\cdot x_i/\left|x_i\right|$$ (C6)

Aggregate dynamics.

We model the effects of cells entering the monolayer from the aggregate by inserting new cells within the initial aggregate area, a circular region of radius $R_a$ that is fixed in time. Each cell within this area is subdivided into two cells stochastically, with addition rate $\mathrm{G}$, and the newly inserted cell is given zero initial polarity. Thus, if the monolayer area is smaller than the aggregate area, then the growth rate of the monolayer is given by $G\frac{A_m}{A_a}$, where $A_m$ and $A_a$ are the monolayer and aggregate areas respectively, giving rise to the observed exponential growth on soft gels. Changes in spreading dynamics as stiffness is varied could arise from differences in crawling forces. Since cells are more polarized on stiff gels (Fig 6A,B), in this model we assume that cells crawl faster on stiff gels. We incorporate this into the model by having the crawl speed scale with substrate stiffness, thus: $v_0\left(E\right)=E{c}_0$, where $c_0$ is a constant [55–57].

Model implementation.

The model is implemented in Surface Evolver, and solved numerically using the forward Euler method, with time step dt [58]. When an edge between to cells become smaller than a threshold length $L^{\mathrm{*}}$, and would become shorter the next time step, the edge undergoes a $T_1$ transition, in which the two cells lose contact, and a new edge is formed between the two initially non-adjacent cells connected to the edge. This new edge has the length as the previous edge, but is rotated 90 degrees about the midpoint. To simulate the spreading aggregate, a random tissue of 127 cells is generated, using a Voronoi tessellation, within a circle of the size of a typical aggregate. The tissue is then relaxed to mechanical equilibrium, without growth or cell crawling, before the simulation begins. Due to the contractility of the cell, the monolayer is roughly at rest. Once we begin the simulation using stress free boundary conditions, allowing the tissue to spread out, and we simulate 400 minutes of spreading.

Model parameters.

In simulations we normalize length scales by $A_0^{1/2}$ and energy by $K{A}_0^2$. We assume that the length scale is given by $A_0^{1/2}=5\mu \mathrm{m}$, and use real time units. Tissue parameters were taken from our previous model for a MDCK monolayer [4]. The aggregate radius is taken from experiments. The growth rate is taken to fit the exponential growth of area on soft gels. The remaining parameters are chosen to give a quantitative fit to our experimental data. For parameter values, see Table in Appendix D.

FIG. 9. Pressure profiles obtained using continuum fluid model.

Pressure profiles of aggregates spreading on soft (A) and stiff (C) substrates, showing a size-independent maximum pressure for aggregates spreading on stiff substrates (B) and size-dependent maximum pressure for aggregates spreading on soft substrates (D). To check of the results on internal pressure from the data-driven model were independent the choice of ${\mu }_s$ and ${\mu }_b$, using a set of combinations of the viscosities, qualitatively similar pressure profiles were obtained (E). Mean central pressure as a function of $R_0$ with a different set of viscosities (${\mu }_s=3000\text{Pa.s}$ and ${\mu }_b=1500\text{Pa.s}$) remained uncorrelated for stiff substrates $(\mathrm{E}=25\mathrm{k}\mathrm{P}\mathrm{a})$ (F) and exhibited a significant inverse correlation for soft substrates ($\mathrm{E}=0.7\mathrm{k}\mathrm{P}\mathrm{a}$) (G). Magnitude of traction stresses on soft $\mathrm{E}=0.7\mathrm{k}\mathrm{P}\mathrm{a}$ vs stiff $\mathrm{E}=25\mathrm{k}\mathrm{P}\mathrm{a}$ substrates (H).

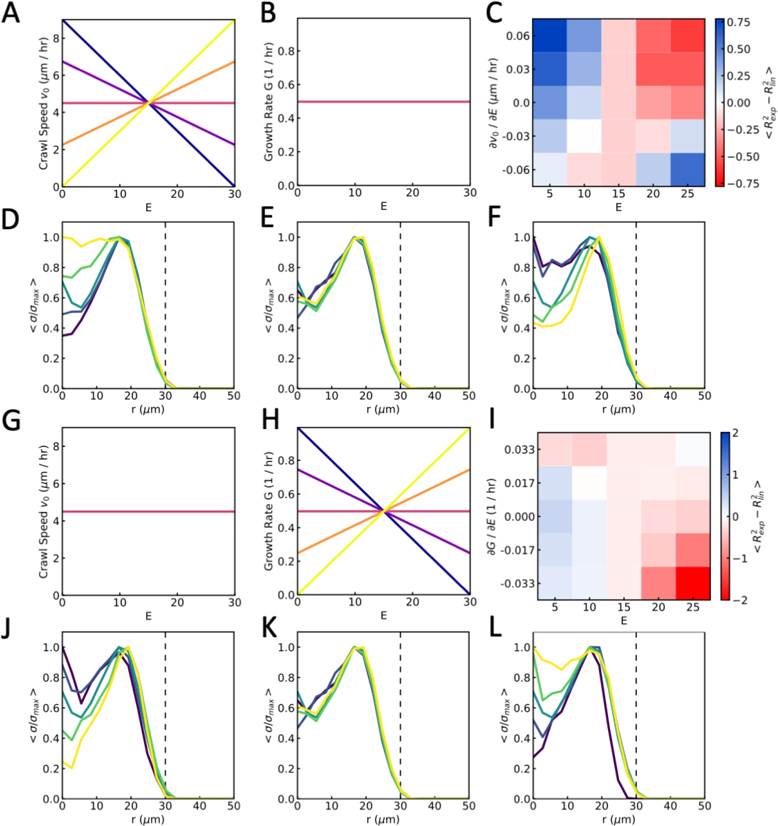
Cell influx and locomotion guide stress distribution under monolayer.

To test how our model results change with the dependence on crawl speed on substrate stiffness, we varied the gradient of speed with respect to stiffness, from positive, as used in our simulations, to negative at fixed growth rate (Fig 10A,B). We find that the transition from exponential growth to linear growth as stiffness increases can be achieved with a crawl speed independent of stiffness (Fig 10C). Moreover, when crawl speed decreases with stiffness we begin to see the opposite behavior, with exponential growth at high stiffness, and linear at low stiffness.

However, when we study the distribution of traction forces underneath the spreading monolayer, we find that a gradient of crawl speed with substrate stiffness is needed to recapitulate the transition from internal traction forces to border localized. Without a gradient, the traction force profile takes the same form on soft and stiff gels (Fig 10E). When the crawl speed increases with stiffness, we see the transition from internal traction forces to border localized as stiffness increases (Fig 10F). Similarly, if the crawl speed decreases with stiffness, we see this transition as we decrease stiffness (Fig 10D). Thus, to capture both the change from exponential to linear growth, and the localization of traction forces from the monolayer center to the border, we find that cell crawl speed must increase with substrate stiffness.

While we find that increasing crawl speed with substrate stiffness captures the experimental results, another mechanism may be a change in the influx of cells from the aggregate. To test if this idea may capture the spreading dynamics, we varied the gradient of growth rate with substrate stiffness for a fixed crawl speed (Fig 10G,H). With no stiffness dependence, we observe the transition from exponential growth to linear growth as stiffness increases as before, but by reducing growth rate with stiffness, we find that this transition is emphasized. Conversely, if we make growth rate higher on stiff gels, then we see exponential growth in area on stiff gels and linear growth on soft (Fig 10I).

When looking at the traction force distributions, we find that forces are localized to the boundary when the growth rate is low relative to crawl speed, and localized to the center when the growth rate is high (Fig 10J–L). Thus, another mechanism that may capture the spreading dynamics in both area growth and traction force distribution is a decreasing cell influx rate with increasing stiffness, increasing the relative strength of motility-driven spreading from cell crawling against pressure-driven spreading for cell influx.

FIG. 10. Differential growth or traction can capture spreading dynamics.

(A-F) Results from simulations in which cell crawl speed depends on substrate stiffness and growth rate is constant. (A) Cell crawl speed, and (B) growth rate as a function of substrate stiffness (E), for different gradients corresponding to C. (C) Average difference in fitting $R^2$ values, using exponential against linear curves, as a function of substrate stiffness and crawl speed gradient ($\mathrm{n}=5$). (D-F) Average traction stress $\left(\sigma \right)$ as a function of distance from the center of the monolayer, r $(\mathrm{n}=5)$, from soft to stiff substrates (dark to light) when (D) crawl speed decreasing with stiffness, $\frac{\partial v_0}{\partial E}=-0.06$, (E) constant crawl speed $\frac{\partial v_0}{\partial E}=0$, and (F) crawl speed increasing with stiffness $\frac{\partial v_0}{\partial E}=0.06$. (G-L) Results from simulations in which growth rate depends on substrate stiffness and cell crawl speed is constant. (G) Cell crawl speed, and (H) growth rate as a function of substrate stiffness (E), for different gradients corresponding to I. (I) Average difference in fitting $R^2$ values, using exponential against linear curves, as a function of substrate stiffness and growth gradient $(\mathrm{n}=5)$. (J-L) Average traction stress $\left(\sigma \right)$ as a function of distance from the center of the monolayer, r $(\mathrm{n}=5)$, from soft to stiff substrates (dark to light) when (J) growth rate decreasing with stiffness, $\frac{\partial G}{\partial E}=-0.033$, (K) constant growth rate $\frac{\partial G}{\partial E}=0$, and (L) growth rate increasing with stiffness $\frac{\partial G}{\partial E}=0.033$.

Appendix D: Pressure measurement using JKR

We verified our results on pressure measurement using an independent estimate of pressure using a modified JKR approach [39]. Assuming that for a substrate where the solid surface tension of the substrate is important, the change in energy on indentation, $\mathrm{U}$, can be written as

$$U=\frac{cE{R}^{1/2}{d}^{5/2}}{\left(1-{\nu }^2\right)}+\pi \gamma SV{d}^2-2\pi WRd$$ (D1)

Where $E$ is effective stiffness of substrate-indenter material, $R$ is the radius of indenter, $d$ is the indentation distance, $\nu$ is the Poisson ratio, $\gamma SV$ is the solid surface tension of the substrate, and $W$ is energy gained due to adhesion per unit area. Taking a derivative with respect to $\mathrm{d}$ and writing the first term in terms of force of indentation, we get

$$cF+2\pi {\gamma }_{SV}d-2\pi WR=0$$ (D2)

We know from Douezan et al. (PNAS, 2011) that linear spreading on a hard substrate is related to $W$, by the following relation

$$W=\frac{A\zeta }{t}$$ (D3)

Where $A$ is the area of spread aggregate, $t$ is the time taken by a monolayer to spread to area $A$, and $\zeta$ is the friction coefficient. Using our results from fig. 1D and 6D, we estimate $W$ to be 9.5 mN/m. Using the measured value of indentation for an aggregate of radius $R$, we can then estimate the force, and hence pressure due to substrate deformation using the above equation.

For top and bottom surfaces of aggregate, we can compare the forces due to adhesion as that is the dominant term. This is due to the fact that adhesion term scales with $R$, whereas solid surface tension term scales with $\mathrm{d}$.

$$c{F}_{Top}=2\pi W_{cell-cell}Rc{F}_{Bottom}=2\pi W_{cell-substrate}R$$ (D4)

As we know that $W_{cell-substrate}>W_{cell-cell}$ otherwise, the aggregate cannot spread as it will be favorable for cells to stay inside aggregate than to adhere to the substrate.

Appendix E: List of parameters

TABLE I:

Default normalized parameters used in simulations

Parameter	Symbol	Value
Contractility	$\mathrm{\Gamma }$	0.166
Preferred parameter	$P_0$	1.5
Crawl speed constant	$c_0$	0.001/min/kPa
Polarity alignment rate	$k_p$	1.0/min
Cell addition rate	$G$	0.9375/min
Aggregate radius	$R_a$	5
Viscoelastic timescale	$\tau$	0.1s/kPa
Simulation timestep	$dt$	0.05min
T1 length	$L_{\mathrm{*}}$	0.05

FIG. 11. Pressure measurement on the bottom surface of the aggregate using JKR.

Laplace independent measurement of pressure on the bottom surface of aggregate using JKR approximation, agrees qualitatively and quantitatively with Laplace based measurements.

Appendix F: Materials and Methods

1. Cell Culture and Aggregates Preparation

We use murine sarcoma E-cadherin expressing cells with a doubling time of approximately 24 hours. Cells are cultured at 37 °C under 95% air/ 5% CO2 atmosphere in culture medium consisting of Dulbecco’s Modified Eagle Medium (DMEM) enriched with 10% calf serum and 5% penicillin streptomycin. Cell aggregates are prepared from confluent cell cultures using a suspension-spinning method. Aggregates ranging from 100 to 300 μm in diameter (Supplementary Fig 2) are obtained from 5 mL of cell suspension in CO₂-equilibrated culture medium at a concentration of 4×10⁵ cells per mL in 25 mL Erlenmeyer flasks, which are placed on a gyratory orbital shaker at 75 rpm at 37 °C for 30–50 hrs. The flasks are pretreated with 2% dimethylchlorosilane in chloroform to prevent adhesion of cells to the glass surface.

2. Cell transfection for Actin

Murine sarcoma S180 cells were stably transfected with plasmid construct encoding for F-TRActin-EGFP (Addgene Plasmid #58473). Briefly, cells were transfected using FuGENE HD Transfection reagents where 2 μg of the DNA plasmid was added to the transfection reagent and added to a cell dish. Cells were incubated for over 24 hrs with the plasmid to complete the transfection process. Following 1 week of incubation with a selection media containing G418 (Mirus Bio LLC) at 1mg/mL, population of cells were isolated and flow sorted with BD FACSAria II flow cytometer. The isolated population were cultured and expanded in DMEM (supplemented with 10%FBS, 1%Pen/strep) and used for experiments.

3. Cell transfection for Nuclear-GFP

GFP tagged with an NLS (nuclear localization sequence) was introduced in a lentivirus plasmid using Gibson assembly. GFP-NLS expression is driven in this plasmid by the PGK promoter. For virus production, envelope plasmid pMD2.G, packaging plasmid psPAX2, and library plasmid were added at ratios of 1:1:2.5, and then polyethyleneimine (PEI) was added and mixed well. The solution stood at room temperature for 5 min, and then the mixture was added into 80–90% confluent HEK293FT cells and mixed well by gently agitating the plates. Six hours post-transfection, fresh DMEM supplemented with 10% FBS and 1% Pen/Strep was added to replace the transfection media. Virus-containing supernatant was collected at 48 hours, and was centrifuged at 1500 g for 10 min to remove the cell debris; samples were aliquoted and stored at −80 °C. Lentivirus was added to the media of sarcoma cells (30% confluency) with polybrene (Millipore-sigma TR-1003-G) at a concentration of 5μg/ml. After 2 days of incubation GFP-positive cells were sorted on a BD FACSAria II.

4. Immunofluorescence staining

Adherent and non-adherent aggregates were fixed with a solution of 4% paraformaldehyde in 1X PBS for 15 min and permeabilized with 0.2% Triton X-100 for 20 min. The cells were then blocked with 2% bovine serum albumin (BSA) in 1X PBS (PBS-2%BSA) at room temperature for 1 hr, incubated with primary antibodies for Paxillin (Recombinant Anti-Paxillin antibody [Y113], Abcam ab32084; 1:250 dilution) and Myosin (Phospho-Myosin Light Chain 2 (Ser19) Antibody, Cell Signaling Technologies ( #3671); 1:250 dilution) in PBS-2%BSA for 48 hrs at 4 °C. The sample were incubated for 48 hrs at 4 °C for secondary antibodies Alexa Fluor 647 (Donkey anti- Rabbit, Abcam ab 150075, 1:500 dilution) and Alexa Fluor 555 (Anti-mouse IgG (H+L), F(ab’)2 Fragment, 1:500 dilution). Phalloidin staining was performed with Alexa Fluor 488 Phalloidin (Life Technologies; 1:200) diluted in PBS with 2% BSA for 48 hrs at 4 °C. Images were taken with 2X (air), 40X and 60X oil immersion objective. Analysis was performed with ImageJ and Imaris (Bitplane).

5. Blebbistatin treatment

Myosin II inhibitor ((−) Blebbistatin) was purchased from Sigma Aldrich (B0560) and reconstituted in dimethyl sulfoxide (DMSO) at high stock concentration of 17.1 mM. Different dilution concentrations were used for experiments as 10 μM, 25 μM and 50 μM unless otherwise noted.

6. Polyacrylamide Gel Preparation

Traction force microscopy experiments were carried out on polyacrylamide (PA) substrates polymerized onto 25mm diameter (#1.5, Dow Corning) coverslips. Briefly, the coverslips are treated with a combination of aminopropylsilane (Sigma Aldrich) and glutaraldehyde (Electron Microscopy Sciences) to make the surface reactive to the acrylamide. The ratios of polyacrylamide to bisacrylamide for the gels used in this study are 7.5%:0.03% (0.7kPa), 7.5%:0.1% (2.8kPa), 7.5%:0.153% (4.3kPa), 7.5%:0.3% (8.6kPa), 12%:0.145% (16kPa), 12%:0.19% (20kPa), 12%:0.25% (25kPa), 12%:0.46% (40kPa) and 12%:0.6% (55kPa). A concentration of 0.05% w/v ammonium persulfate (Fisher BioReagents) and 20nM beads (Molecular Probes) are embedded in the gel mixture prior to polymerization. A 15 μl volume of the polyacrylamide solution is added to the coverslip and covered with another coverslip, which has been made hydrophobic through treatment with Rain-X. The gels are polymerized on the coverslips for 30 minutes at room temperature. The gels are then reacted with the standard 1mg/mL Sulfo-SANPAH (Thermo Fisher Scientific, 22589) [59]. The surface of the gels is then coated with fibronectin (F002, Sigma-Aldrich) with 1 mg/ml concentration (Supplementary Fig 1, Supplementary Table 1, 2). Lower concentrations of fibronectin changes dynamics of wetting to dewetting and partial wetting conditions. The reaction proceeds for 12 hrs overnight incubation in the dark, and the coverslips are then rinsed and stored in 1X PBS.

7. Traction force microscopy

Traction force microscopy is used to measure the forces exerted by cells on the substrate. ‘Force-loaded’ images (with cells) of the beads embedded in the polyacrylamide gels were obtained using a 60× oil-immersion objective (Leica Microsystems). The ‘null-force’ image was obtained at the end of each experiment by adding trypsin to the cells for 1 hr. Images were aligned to correct drift (StackReg for ImageJ) and compared to the reference image using PIV software (http://www.oceanwave.jp/softwares/mpiv/) in MATLAB to produce a grid spacing of 7.0 μm. Forces can be reliably measured between 0.7 and 40 kPa and are calculated using custom-written code by Ulrich Schwarz.

8. Particle Tracking

Individual nuclei are monitored by spot tracking of the center of fluorescence intensity in Imaris (Bitplane). For quantifying alignment of nuclei in an aggregate, the edges of nuclei were marked manually. The orientation was then detected by fitting the enclosed region with an ellipse. The direction of orientation is then the principal axis of the fitted ellipse.

9. Indentation and meniscus height measurement

A z-stack of substrate with fluorescent bead was obtained in absence of any cell. The image acquisition started with focal plane 10 μm inside the substrate and finished at 10 μm out of it. A calibration profile quantifying intensity as a function of distance from undeformed substrate was obtained. The relation was inverted to give height as a function of measured intensity. During experiments, intensity difference between undeformed substrate and deformed substrate (with aggregate) is calculated and the calibration curve is used to convert intensity changes into deformation profile.

10. Director field calculations

The director field $\hat{n}$ is calculated using custom MATLAB code as described previously [60]. Briefly, a director field is created from images of fluorescently labeled F-actin and the images are divided into small, overlapping 8.6 μm by 8.6 μm windows, and the local orientation director is calculated for each window [61]. Each window is then Gaussian filtered and transformed into Fourier space using a 2D fast Fourier Transform (FFT). Then, the axis of the least second moment is calculated from the second order central moments of the transformed window. The angle of the local F-actin director is defined as orthogonal to this axis.

11. Nematic order calculation

The local degree of alignment is calculated between adjacent windows within 3×3 kernels. The local nematic order is calculated for the central window in each kernel using the modified order parameter equation $q=<{cos}^2\theta >$, where $\theta$ is the difference in F-actin orientation between the central window and the 8 surrounding windows. This process is repeated for all possible 3×3 kernels over an image, yielding a nematic director field with defined director magnitude and orientation for each window over an image. Perfect alignment between adjacent regions within an F-actin network results in an order parameter equal to one.

12. Particle Image Velocimetry

Particle image velocimetry (PIV) is applied in MATLAB (MathWorks) to fluorescent F-actin images, (mPIV, https://www.mn.uio.no/math/english/people/aca/jks/matpiv/) yielding displacement and velocity vector fields.

13. Focal adhesion size calculation

The spatial dimension of focal adhesion spots was determined using a point detection tool in Imaris software (Bitplane).

14. Statistical tests

All statistical comparisons between two distributions were done with a two-sided t-test. When distributions are presented as a single value with error bars, the value is the mean of the distribution, and the error bars are the standard deviations. We use the symbols *, ** and *** for p < 0.05, 0.01 and 0.001, respectively. When fitting lines to data, we quote the p-value as significance values to rejections of the null hypothesis.

15. Cell-based computational model

For a full description of the computational active vertex model see the Appendix C and E.

16. Data availability

Data that support plots and other findings within this manuscript are available from the corresponding author upon reasonable request.

17. Code availability

Custom codes that were used to analyze experimental data within this manuscript are available from the corresponding author upon reasonable request.

Appendix G: List of parameters

TABLE II:

Viscosity values from literature.

Experiment	Value	Ref.
Tissue Growth	0.002–1 Pa.s	Hass et al. [62]
Cell Lysates	0.03 Pa.s	Newton et al. [63]
Cell monolayer sheet	0.5 Pa.s	Serra-Picamal et al. [30]
Tissue Phantoms	0.04–1.3 Pa.s	Girnyk et al. [64]
E-coli membrane	1 Pa.s	Mika et al. [65]
Liver	1–40 Pa.s	Deffieux et al. [66]
Liver, Heart, Limb	10–100 kPa.s	Forgacs et al. [67]
Mouse Tissue	200 kPa.s	Mgharbel et al. [68]
Zebrafish tissue	300–400 kPa.s	Serwane et al. [69]
Aggregate fusion	440 kPa.s	Marmottant et al. [70]
Epithelia	0.1–10 MPa.s	Blanch-Mercader et al. [71]
Dewetting Epithelia	1 MPa.s	Perez-Gonzalez et al. [31]