Utilizing restricted mean duration of response for efficacy evaluation of cancer treatments

Abstract

In oncology clinical trials, response-based endpoints (time to response, objective response, duration of response [DOR]) are commonly used to detect therapeutic effect to support proof-of-concept or submission decisions. The restricted mean DOR (RMDOR) was recently proposed as a composite nonparametric method to efficiently quantify the treatment effect related to tumor reductions, which offers an intuitive way to perform statistical inference in cross-arm comparison and has since been applied in some Phase III studies. In this paper, we provide further technical details and asymptotic properties of the RMDOR method and discuss the selection of the truncation time. A simulation study is conducted comparing the performance of the proposed method with existing standard methods in hypothesis testing and quantification of treatment efficacy. We use two oncology Phase III examples to illustrate the method. An R package PBIR and a SAS macro are available to perform statistical inference based on the RMDOR.

1 |. INTRODUCTION

With the emergence of novel therapies including kinase inhibitors, monoclonal antibodies, and antibody–drug conjugates, great advancement in cancer treatment has been made over the past two decades. Together with the effort of prevention, screening and early diagnosis, some types of cancer or cancer indications have become a chronic disease.

For clinical researchers and drug developers, a commonly asked question is: what does a desirable future cancer treatment look like? From patients’ and physicians’ perspective, a future cancer treatment may not necessarily be a “cure” for all patients, but should effectively reduce the disease burden and control the disease so that patients can live a “normal” life for a prolonged period of time. What are the characteristics of a desirable cancer treatment for patients and doctors? First of all, it needs to be life extending, and overall survival (OS) is the gold standard to evaluate the effectiveness of a therapy, although it is getting more difficult to demonstrate statistical significance in a future randomized clinical trial, especially for earlier lines of therapies.¹ Second, there should be a high likelihood of tumor response (defined as substantial reduction in tumor size, or complete disappearance of disease [i.e., complete remission]). No patients want to carry a large burden of tumors in daily life. Also once receiving the therapy, time to response ideally should be fast, and the amount of time being in the state of tumor response should be long-lasting (i.e., the response should be durable). These three characteristics (high response rate, fast time to response, durable response) are commonly used to assess effect on imaging-based endpoints in oncology studies. Other desirable characteristics include manageable adverse drug reaction, and improved or not worsening health-related quality of life (HRQOL).

Given the high censoring rate related to the OS endpoint and the confounding effect of subsequent anti-cancer therapies, intermediate endpoints are frequently used in cancer trials to support Go/No-Go decisions and drug approvals. The most commonly used intermediate endpoint for OS is progression-free survival (PFS), which is another imaging-based endpoint. Although PFS is a widely accepted intermediate endpoint, it has limitations, in particular to assess some immunotherapies.² One reason for that is PFS measures the duration of disease stabilization so it does not distinguish tumor reduction from no change or slight increase. However, disease stabilization may not translate to long-term survival benefit.² In a recent paper in European Journal of Cancer,³ Pasalic and colleagues criticized PFS as a suboptimal predictor for OS among metastatic solid tumor clinical trials. Using ClinicalTrials.gov, they identified 1239 phase III oncologic RCTs, 260 of which were metastatic solid tumor trials with a superiority design. There was only a 38% conversion rate of positive PFS-to-OS benefit.

Objective response (OR), complete response (CR), duration of response (DOR), and duration of complete response (DOCR) are frequently used secondary endpoints in solid tumor and hematologic malignancy cancer trials.^4–6 They have the potential to play a more important role in future oncology studies as they measure the direct effect of a drug on the tumor and durability of the effect. In a thought-provoking commentary in the Lancet,⁷ Pilie and Jonasch argue that if the desired goal is to increase the proportion of patients achieving a durable CR, perhaps it is time to formally incorporate this endpoint in registrational studies and to consider durable CR as a surrogate for OS in the increasingly complex therapeutic landscape.

The conventional approach to analyze DOR or DOCR is to look at the descriptive statistics among responders. Although DOR among responders has a good clinical interpretation, one normally does not make formal statistical inference comparing DOR between treatment arms. This is because response is an outcome after randomization which correlates with both the treatment and the DOR. As a result, such comparison violates the intent-to-treat (ITT) principle, and does not have good causal interpretation for the potential treatment benefit because responders from different arms have different prognoses at their response time. For example, consider an ineffective treatment that achieves response in patients who have low disease burden at baseline and are less likely to experience disease progression. For this ineffective treatment, the DOR among responders only may seem impressive even though most patients did not benefit. Even if we are interested in the DOR among responders only, the standard approach of constructing Kaplan–Meier curves and reporting the median DOR, without formal statistical inference, does not allow us to draw conclusions about treatment efficacy.

A valid statistical comparison of DOR should be based on all patients. A simple approach assigning zero to DOR for non-responders causes dependent censoring issue,^8,9 rendering the Kaplan–Meier method invalid. Ellis and colleagues¹⁰ proposed a MLE-based parametric method to calculate the mean DOR among all patients. However, strong parametric assumptions are typically unverifiable and the result will be model dependent. A nonparametric approach was recently proposed^8,9 to evaluate the restricted mean DOR (RMDOR) within a time window of interest, which offers an intuitive and clinically meaningful way to perform statistical inference in cross-arm comparison and has since been applied in some phase III oncology studies.^11,12 Hu and colleagues¹³ later compared the RMDOR with conventional ORR, PFS as efficacy endpoints in simulated Phase 2 screening trials. Their simulations suggest the DOR is a more sensitive and useful intermediate endpoint than PFS and ORR for predicting Phase 3 success, and should be considered in future randomized Phase 2 trials.

In this paper, we provide further technical details and asymptotic properties of the RMDOR method and summarize the guiding principles for selecting the truncation time point. A simulation study is conducted comparing the performance of the proposed method with existing standard methods in hypothesis testing and quantifying treatment efficacy. We use two oncology Phase III examples to illustrate the RMDOR method. An R package PBIR and a SAS macro are introduced to perform statistical inference based on RMDOR. We conclude with a discussion.

2 |. METHOD

2.1 |. Notations and set up

To quantify the efficacy of an experimental treatment, the disease history of a patient can be partitioned into three states:

1. State 1: Time from the start date (date of randomization or start of treatment) to response, disease progression or death, whichever is earlier.

2. State 2: Time from end of State 1 to disease progression or death.

3. State 3: Time from end of State 2 to death, or post-progression survival (PPS).

This idea of partitioning of time interval is similar to Q-TWiST (quality-adjusted time without symptoms and toxicity), a method that has been used in health economic outcome research.¹⁴ For each individual patient, the combined duration of States 1–3 is OS, denoted as $T[D]$. Let $T[P/D/R]$ and $T[P/D]$ be response/progression-free survival (RPFS) and PFS, respectively. Notably, RPFS is an important intermediate outcome for subsequent derivation. The duration of States 1–3 can then be written as:

1. State 1: $T[P/D/R]$.

2. State 2: $T[P/D]-T[P/D/R]$.

3. State 3: $T[D]-T[P/D]$.

The role of PPS (i.e., duration of State 3) as a determinant of OS has been a medical research interest in various cancer types, which has a complex association with PFS and effective subsequent-line and salvage therapies.^15,16 It is not a topic of interest here. In this paper, we focus on State 2, the DOR.

As mentioned in the Introduction, the traditional DOR analysis is descriptive, among responders only. Ignoring non-responders, however, can result in biased assessment of the duration, especially when the ORR of the two treatment groups differ. Instead of assessing the median DOR among responders, Huang and colleagues^8,9 proposed an ITT analysis to analyze the restricted mean (expected) DOR (RMDOR) for all patients who receive the study treatment within the maximum follow-up window. This approach takes into account TTR, ORR, DOR all together in the ITT population. The summary measure is the duration a patient is expected to spend at State 2 (from response to progression or death). For a responder, this is equivalent to the DOR by traditional definition. For a non-responder, the observed DOR is zero according to the new definition. One important advantage of this approach is that it enables an ITT analysis with increased sensitivity. For example, a doubling in ORR and a doubling in DOR among responders translates to approximately a 4-fold increase in expected “time in response.”¹⁷

The RMDOR, or literally expected DOR in State 2 (truncated by time $\mathrm{\tau }$) can be expressed as

$$E[\text{min}(T[P/D],\tau )-\text{min}(T[P/D/R],\tau )]=E[\text{min}(T[P/D],\tau )]-E[\text{min}(T[P/D/R],\tau )]={\int }_0^{\tau }S(t;P/D)dt-{\int }_0^{\tau }S(t;P/D/R)dt={\int }_0^{\tau }S(t;P/D)-S(t;P/D/R)dt={\int }_0^{\tau }\text{Pr}(T[P/D/R]<t<T[P/D])dt$$

where $S(t;P/D)$ and $S(t;P/D/R)$ are the survival functions for PFS and RPFS time, respectively, and the RMDOR is the area between the PFS curve and the RPFS curve from 0 to $\tau$.

In the equation above, $\mathrm{Pr}(T[P/D/R]<t<T[P/D])$ is essentially the probability of being in response (PBIR) at time $t$ (i.e., probability of being in State 2), or the response rate at current time t.⁹ The statistical properties of PBIR have been studied in the literature^18–20 and will not be discussed further here. In this paper, we focus on the statistical properties of the RMDOR.

2.2 |. Statistical inference based on restricted mean duration of response

Assume time-to-event data for patient $i$ are denoted as $\left\{\left(X_i=T_i\wedge C_i,{\delta }_i=I\left(T_i\le C_i\right)\right),i=1,\dots ,n\right\}$, where $X_i$ is the observed value (time to event $T_i$ or time to censoring $C_i$) and ${\delta }_i$ is the indicator for the event of interest. Without loss of generality and in the setting of analyzing RMDOR, it can be PFS $T[P/D]$ or RPFS $T[P/D/R]$. In other words, our observed data consist of $\left(T_i^{P/D}\wedge C_i,{\delta }_i^{P/D},T_i^{P/D/R}\wedge C_i,{\delta }_i^{P/D/R}\right)$. The AUC of the Kaplan–Meier curve $\theta$ for $\left\{X_i,{\delta }_i\right\}$ has an expansion in the form of

$$\begin{gathered} \sqrt{n}\left(\widehat{\theta }-\theta \right)=-\frac{1}{\sqrt{n}}\sum _{i=1}^n\frac{\left\{{\int }_{t_i}^{\tau }{S}_T(u)du\right\}d{M}_i(t)}{S_X(u)} \\ =-\frac{1}{\sqrt{n}}\sum _{i=1}^n\left\{\frac{\left\{{\int }_{X_i}^{\tau }{\widehat{S}}_T(u)du\right\}{\delta }_i}{{\widehat{S}}_X(X_i)}-n^{-1}\sum _{j=1}^n\frac{\left\{{\int }_{X_j}^{\tau }{\widehat{S}}_T(u)du\right\}I(X_i\ge X_j){\delta }_j}{{\widehat{S}}_X{(X_j)}^2}\right\} \end{gathered}$$

Let

$${\widehat{\xi }}_i=\frac{\left\{{\int }_{X_i}^{\tau }\widehat{S}(u)du\right\}{\delta }_i}{{\widehat{S}}_X(X_i)}$$

Then

$$\sqrt{n}(\widehat{\theta }-\theta )=-\frac{1}{\sqrt{n}}\sum _{i=1}^n\left\{{\widehat{\xi }}_i-n^{-1}\sum _{j=1}^n\frac{{\widehat{\xi }}_{i}I(X_i\ge X_j)}{{\widehat{S}}_X(X_j)}\right\}$$ (1)

The RMDOR $\mu$ is the area between the 2 km curves of PFS and RPFS. It can be shown to follow the normal distribution asymptotically

$$\frac{\sqrt{n}(\widehat{\mu }-\mu )}{\sigma }\sim 𝒩(0,1)$$ (2)

where $\sigma$ is the SD of $\widehat{\mu }$.

The two curves of PFS and RPFS are correlated with each other. Therefore, ${\sigma }^2$ does not equal to the sum of two variances of estimators for the restricted mean survival time (RMST)^21–23 of $T[P/D]$ and $T[P/D/R]$.

To derive the variance analytically, we follow the counting process approach by using the martingale representation of the Kaplan–Meier estimator.²⁴

For the difference of AUCs of two Kaplan–Meier curves (PFS, RPFS), $\widehat{\mu }$, we have the following expansion

$$\sqrt{n}(\widehat{\mu }-\mu )=-\frac{1}{\sqrt{n}}\sum _{i=1}^n\left\{{\widehat{\xi }}_i^a-n^{-1}\sum _{j=1}^n\frac{{\widehat{\xi }}_i^{a}I\left(X_i^a\ge X_j^a\right)}{{\widehat{S}}_X^a\left(X_j^a\right)}-{\widehat{\xi }}_i^b+n^{-1}\sum _{j=1}^n\frac{{\widehat{\xi }}_i^{b}I\left(X_i^b\ge X_j^b\right)}{{\widehat{S}}_X^b\left(X_j^b\right)}\right\}+o_p(1)$$

and ${\sigma }^2$, the variance of $\widehat{\mu }$, can be estimated as

$${\widehat{\sigma }}^2=\frac{1}{n^2}\sum _{i=1}^n{\left\{{\widehat{\xi }}_i^a-n^{-1}\sum _{j=1}^n\frac{{\widehat{\xi }}_i^{a}I\left(X_i^a\ge X_j^a\right)}{{\widehat{S}}_X^a\left(X_j^a\right)}-{\widehat{\xi }}_i^b+n^{-1}\sum _{j=1}^n\frac{{\widehat{\xi }}_i^{b}I\left(X_i^b\ge X_j^b\right)}{{\widehat{S}}_X^b\left(X_j^b\right)}\right\}}^2$$ (3)

The superscript ${}^a$ and ${}^b$ indicate the corresponding survival data with respect to $T[P/D]$ and $T[P/D/R]$, respectively. We can then make statistical inference for the RMDOR within the study follow-up time $(0,\tau )$ for a group of patients or for the comparison of two groups of patients.

With this consistent estimator of ${\sigma }^2$, the 95% confidence interval of the RMDOR can be constructed as

$$[\widehat{\mu }-1.96\widehat{\sigma },\widehat{\mu }+1.96\widehat{\sigma }]$$

In a two-group comparison, we may estimate the RMDOR in group $j$ by ${\widehat{\mu }}_j$ and the variance of ${\widehat{\mu }}_j$ by ${\widehat{\sigma }}_j^2$, where $j\in \{\mathrm{0,1}\}$. Thus the difference in RMDOR can be estimated by ${\widehat{\mu }}_1-{\widehat{\mu }}_0$ and the 95% confidence interval for the difference can be constructed as

$$\left[{\widehat{\mu }}_1-{\widehat{\mu }}_0-1.96\sqrt{{\widehat{\sigma }}_1^2+{\widehat{\sigma }}_0^2},{\widehat{\mu }}_1-{\widehat{\mu }}_0+1.96\sqrt{{\widehat{\sigma }}_1^2+{\widehat{\sigma }}_0^2}\right]$$

Furthermore, we may test the equivalence of two RMDOR based on the Wald test statistic

$$Z=\frac{{\widehat{\mu }}_1-{\widehat{\mu }}_0}{\sqrt{{\widehat{\sigma }}_1^2+{\widehat{\sigma }}_0^2}}$$

Under the null hypothesis of no difference in RMDOR between two groups, the $Z$-statistic follows a standard normal distribution, and we would reject the null at the two-sided significance level of 0.05, if $|Z|>1.96$. Similarly, we can estimate the ratio of two RMDOR by ${\widehat{\mu }}_1/{\widehat{\mu }}_0$, whose large sample distribution can be derived via the delta-method on $\mathrm{l}\mathrm{o}\mathrm{g}\left({\widehat{\mu }}_1/{\widehat{\mu }}_0\right)$. The associated 95% confidence interval can be constructed as

$$\left[\frac{{\widehat{\mu }}_1}{{\widehat{\mu }}_0}\text{exp}\left(-1.96\sqrt{\frac{{\widehat{\sigma }}_1^2}{{\widehat{\mu }}_1^2}+\frac{{\widehat{\sigma }}_0^2}{{\widehat{\mu }}_0^2}}\right),\frac{{\widehat{\mu }}_1}{{\widehat{\mu }}_0}\text{exp}\left(+1.96\sqrt{\frac{{\widehat{\sigma }}_1^2}{{\widehat{\mu }}_1^2}+\frac{{\widehat{\sigma }}_0^2}{{\widehat{\mu }}_0^2}}\right)\right]$$

The corresponding test statistic based on the ratio of the two RMDOR is

$$Z=\frac{\text{log}({\widehat{\mu }}_1)-\text{log}({\widehat{\mu }}_0)}{\sqrt{\frac{{\hat{\sigma }}_1^2}{{\hat{\mu }}_1^2}+\frac{{\widehat{\sigma }}_0^2}{{\widehat{\mu }}_0^2}}}$$

We developed an R package PBIR which has a function mduration to analyze the RMDOR and is available on CRAN: https://cran.r-project.org/web/packages/PBIR/. A SAS macro was also written to perform statistical inference based on the RMDOR in the 1-arm and 2-arm settings (see Appendix), and is available online as Supporting Information appended to the article.

2.3 |. Selection of the truncation time $\tau$

The requirement of a truncation time $\tau$ has been overly (sometimes unfairly) criticized for the RMST in the literature. For any global statistic (e.g., hazard ratio [HR]) summarizing the overall treatment benefit with respect to a time-toevent endpoint, a data dependent time window is always required. The selection of a time window and its impact on the RMST has been thoroughly investigated and discussed in the literature.^25–27 It has been pointed out that for any given dataset of a randomized clinical trial, the maximum time window for the RMST is always as least as wide as that for the HR.

The principle of selecting the truncation time $\tau$ in a single treatment group for the RMDOR is that one can make a valid inference for the RMST with respect to both time to $P/D/R$ and time to $P/D$. Following Tian et al.,²⁵ suppose that ${\tau }_C=\mathrm{i}\mathrm{n}\mathrm{f}\{\tau \mid \mathrm{P}\mathrm{r}(C\ge \tau )=0\}$ is the upper end of the support of the censoring time $C$. In general, for event time $T$ of interest, if

$$\text{Pr}(T>{\tau }_C)=0,$$ (4)

the proposed inference on RMST up to any truncation time point is valid. If Condition 4 does not hold but

$$\underset{t\to {\tau }_C}{\text{lim}}\frac{f_C(t)}{{({\tau }_C-t)}^{1+\delta }}>0$$ (5)

for any $\delta >0$, the inference on RMST up to any truncation time point no greater than the last follow up time is still valid, where $f_C(t)$ is the density function of the censoring distribution. If Condition 4 is satisfied, then the Kaplan–Meier estimate reaches zero with a probability approaching 1 as the sample size increases and there is no restriction in selection $\tau$ for RMST. Condition 5 concerns the censoring distribution. In clinical trials, censoring is often dominated by administrative censoring induced by staggered entry. In such a case, if we assume that patients entered the study uniformly over the accrual period, the regularity Condition 5 is trivially satisfied. Noting the fact that $T[P/D/R]\le T[P/D]$, there are three scenarios:

1. If the observed RPFS curve (i.e., the Kaplan–Meier curve for $[P/D/R]$) has not reached zero (that is, the largest observed time to $P/D/R$ or censoring is not a $P/D/R$ event time), the truncation time can be as large as the largest observed RPFS time. The corresponding regulatory condition is 5.

2. If the observed RPFS curve has reached zero but the observed PFS curve has not reached zero (that is, the largest observed time to $P/D/R$ or censoring is a $P/D/R$ event time, but the largest observed time to $P/D$ or censoring is not a $P/D$ event time), the truncation time can be as large as the largest observed PFS time. The corresponding regulatory condition is 5 as $\mathrm{Pr}\left(T[P/D/R]>{\tau }_C\right)=0$ and $\mathrm{Pr}\left(T[P/D]>{\tau }_C\right)>0$.

3. If both the observed RPFS curve and the PFS curve have reached zero, there is no restriction in selecting the truncation time point. The mean of DOR without any time constraint can be estimated. The corresponding regulatory condition is 4 as $\mathrm{Pr}\left(T[P/D]>{\tau }_C\right)=0$.

To select the common truncation time $\tau$ in the randomized clinical trial setting, one can follow the steps below after selecting the truncation time for each arm (Arm A and Arm B):

1. If both the RPFS curve and the PFS curve have crossed zero for both arms, use the maximum of the $\tau$ for each of the arms.

2. Else if both the RPFS curve and the PFS curve have crossed zero for Arm A, use the $\tau$ of Arm B.

3. Else if both the RPFS curve and the PFS curve have crossed zero for Arm B, use the $\tau$ of Arm A.

4. If none of the above conditions is met, use the minimum of the $\tau$ for each of the arms.

The main merits of using the proposed data-driven choice of the cut-off value in RMDOR are (1) to avoid the subjective choice of the cut-off value and (2) to utilize as much information in the observed data to summarize the survival profile as possible. The major limitation is that the validity of the corresponding statistical inference depends on the regularity Condition 5, which ensures that the area under the Kaplan–Meier curve is sufficiently stable even toward the tail of curve. On the other hand, if a well-accepted and clinically meaningful cut-off value such as 24 months can be selected prior to the analysis and specified in the analysis plan, this fixed time point can be more desirable for its simplicity and transparency. The main drawback of using a fixed cut-off point is that we may lose valuable follow-up information beyond this time point. Lastly, in most applications, the powers of analyses based on these two choices of cut-off value are not very different, if the additional follow up beyond the fixed time point is limited in the cohort.

3 |. EXAMPLES

In this section, we illustrate the application of the RMDOR in two real oncology examples.

3.1 |. Example 1: Phase 3 study in renal cell carcinoma

The JAVELIN Renal-101 trial (NCT02684006) is a multi-center, randomized, open-label, Phase 3 study that compared avelumab plus axitinib with sunitinib as first-line treatment among patients with advanced renal cell carcinoma (RCC). Patients were randomly assigned, in a 1:1 ratio, to avelumab/axitinib $(N=442)$ or sunitinib $(N=444)$. PFS and OS were the two primary endpoints, with alpha split unevenly between them. Secondary efficacy endpoints included OR and DOR. The study achieved its primary objective for PFS at the first interim analysis in September 2018 with significantly prolonged PFS in the experimental combination arm ($\mathrm{H}\mathrm{R}=0.69$ [95% CI: 0.56, 0.84]; $p\le 0.001)$²⁸.

An ad-hoc analysis of the RMDOR was performed using the updated data at the second interim analysis in 2019.¹¹ Figure 1 displays graphically the RMDOR as the area between the PFS Kaplan–Meier curve and the RPFS Kaplan–Meier curve for the experimental arm and control arm, respectively. The RMDOR for the avelumab plus axitinib arm and the sunitinib arm was 9.3 months (95% CI: 8.3, 10.3) and 5.1 months (95% CI: 4.2, 6.0), respectively. The difference in RMDOR between the two arms was 4.2 months (95% CI: 2.9, 5.6, $p\le 0.001$), favoring the avelumab plus axitinib arm. The truncation time $\tau$ was selected as 26.25 months following the data-driven min-max principle outlined in Section 2.3.

FIGURE 1.

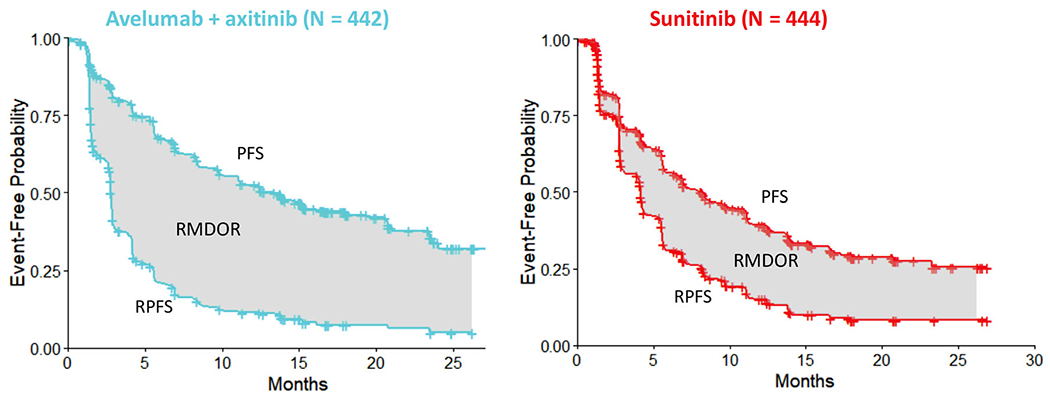
A Phase 3 example in first-line renal cell carcinoma evaluating avelumab plus axitinib versus sunitinib. The restricted mean DOR (RMDOR) is the area between the progression-free survival (PFS) curve and the response/progression-free survival (RPFS) curve up to follow up time $\tau$. The RMDOR for the experimental arm (avelumab plus axitinib) and the control arm (sunitinib) was 9.3 months (95% CI: 8.3, 10.3) and 5.1 months (95% CI: 4.2, 6.0), respectively. The difference in RMDOR between the two arms was 4.2 months (95% CI: 2.9, 5.6), and the truncation time $\tau$ was 26.25 months

Although statistical significance could not be claimed due to the ad-hoc nature of the analysis, a clear benefit for avelumab plus axitinib versus sunitinib was observed in this ITT analysis. It provides an easy-to-interpret global summary measure for the response-based endpoints, estimated using data from all subjects, including responders and non-responders. The RMDOR method supported the regulatory submission of avelumab plus axitinib for the first-line RCC indication to the European Medicines Agency (EMA) in 2019, and the assessment report including this analysis can be found on the EMA website.²⁹

3.2 |. Example 2: Phase 3 study in non-muscle invasive bladder cancer

The CREST study¹² is a Phase 3, multi-center, multinational, randomized, open label, parallel, 3-arm study to evaluate sasanlimab in combination with bacillus Calmette-Guerin (BCG induction with [Arm A] or without [Arm B] BCG maintenance) versus BCG (induction and maintenance, Arm C) in participants with high-risk, BCG naïve non-muscle invasive bladder cancer (NMIBC). Randomization is stratified by geographic region and the presence of carcinoma in situ (CIS: yes or no) at baseline. For patients with CIS at randomization, CR and DOCR are key secondary endpoints.

The planned sample size is 999 subjects (333 in each arm). To adequately analyze CR and DOCR and make valid statistical comparison between arms, RMDOR is the primary analysis method for DOCR and is applicable to approximately 25% of subjects who have CIS at randomization. As a result, the analysis will be performed for 167 subjects in each comparison (Arm A vs. Arm C, Arm B vs. Arm C). The RMDOR and its 95% CI will be calculated for each arm. For each comparison between study arms, difference in the RMDOR and the p value will be calculated. The conventional analysis of DOCR among subjects with CR will also be performed in a descriptive manner.

Unlike the JAVELIN trial example, the RMDOR analysis is prospectively pre-specified in the statistical analysis plan. The study is expected to be completed in 2024.

4 |. A SIMULATION STUDY TO COMPARE THE RESTRICTED MEAN DOR WITH OTHER METHODS

4.1 |. Simulation setup

We conduct a simulation study to compare the different endpoints (PFS, DOR) and analysis/testing methods (HR, log-rank test, median, RMST, RMDOR) in the randomized clinical trial setting.

The total sample size of a two-arm simulated trial is assumed to be 100, 300, or 600 with 1:1 randomization ratio. The sample size of 100 subjects is typical for a randomized Phase 2 screening study, while $N=300$ and $N=600$ are aligned with the common size of a Phase 3 confirmatory study in most indications in solid tumors and hematologic malignancies. Accrual follows a uniform distribution with constant accrual rate that completes within 12 months. To evaluate the sensitivity of each method to the long-term benefit, analysis is performed at three study time points from the start of accrual: 25, 50, and 75 months. For simplicity, only non-informative administrative censoring is introduced. $\tau$ is selected as the minimum of maximum follow up in each arm for the RMST analysis of the PFS endpoint. For the RMDOR method, $\tau$ is selected following the data-driven principles in Section 2.3. Likewise, the maximum time window for each simulated dataset is utilized for the HR and log-rank test.

Hu and colleagues¹³ demonstrate that under moderate sample size $(N=100\text{or}200$) the Type I error rate is controlled with the RMDOR. Since the large sample properties of Kaplan–Meier based survival functions are well established, we will not further evaluate the Type I error rate and instead in this simulation study focus on the sensitivity of each method to the short-term and long-term treatment effect in terms of power and estimation of effect size. Two scenarios are considered with 2000 simulations for each of them.

In Scenario 1, the ORR is assumed to be 50% in Arm A (new drug) and 30% in Arm B (standard of care). For simplicity, an exponential distribution is assumed for PFS, time-to-response (TTR) and DOR for the responders. In Arm A, the median PFS is assumed to be 10 months for the non-responders. For 80% of the responders, the median TTR is 2 months, median DOR is 12 months. For the remaining 20% of the responders, a long-term benefit is added, with median TTR of 2 months and median DOR of 60 months. In Arm B, the median PFS is 10 months for the non-responders (same as in Arm A). For 90% of the responders, median TTR is 4 months, median DOR is 8 months. For the remaining 10% of the responders, a long-term benefit is assumed, with median TTR of 4 months and median DOR of 60 months.

In Scenario 2, the ORR is assumed to be similar between the two arms: 25% in Arm A and 20% in Arm B. In Arm A, the median PFS is assumed to be 13 months for the non-responders. For 50% of the responders, the median TTR is 2 months, median DOR is 12 months. For the remaining 50% of the responders, a long-term benefit is added, with median TTR of 2 months and median DOR of 60 months. In Arm B, the median PFS is 10 months for the non-responders (<Arm A). For 90% of the responders, median TTR is 4 months, median DOR is 8 months. For the remaining 10% of the responders, a long-term benefit is assumed, with median TTR of 4 months and median DOR of 60 months.

4.2 |. Simulation results

The results of the 2000 simulations for each scenario are summarized in Table 1, Figure 2 and Table 2, Figure 3, respectively.

TABLE 1.

Simulation results under Scenario 1 for the summary and comparison of quantitative statistical measures of treatment benefit

		PFS				RMDOR
N	Follow-up (months)	Median difference	RMST difference	HR	RMST ratio	RMDOR difference	RMDOR ratio
100	25	1.99	1.17	0.86	0.92	3.85	0.45
	50	2.04	2.64	0.83	0.87	5.75	0.44
	75	2.04	3.68	0.82	0.83	6.70	0.44
300	25	1.98	1.25	0.84	0.91	3.99	0.43
	50	1.98	2.80	0.81	0.85	5.99	0.41
	75	1.98	3.81	0.80	0.82	7.07	0.40
600	25	1.96	1.30	0.84	0.91	4.02	0.43
	50	1.97	2.90	0.80	0.84	6.07	0.40
	75	1.97	3.97	0.79	0.81	7.20	0.39

Note: For PFS, median difference (treatment vs. control) and RMST difference (Arm A vs. Arm B) are used as the absolute measures, while HR (Arm A vs. Arm B) and RMST ratio (Arm B vs. Arm A) are used as the relative measures. For DOR, RMDOR difference (Arm A vs. Arm B) is used as the absolute measure, while RMDOR ratio (Arm B vs. Arm A) is used as the relative measure. For HR, RMST and RMDOR, the maximum time window from each simulated dataset is used.

Abbreviations: DOR, duration of response; HR, hazard ratio; PFS, progression-free survival; RMDOR, restricted mean DOR; RMST, restricted mean survival time.

FIGURE 2.

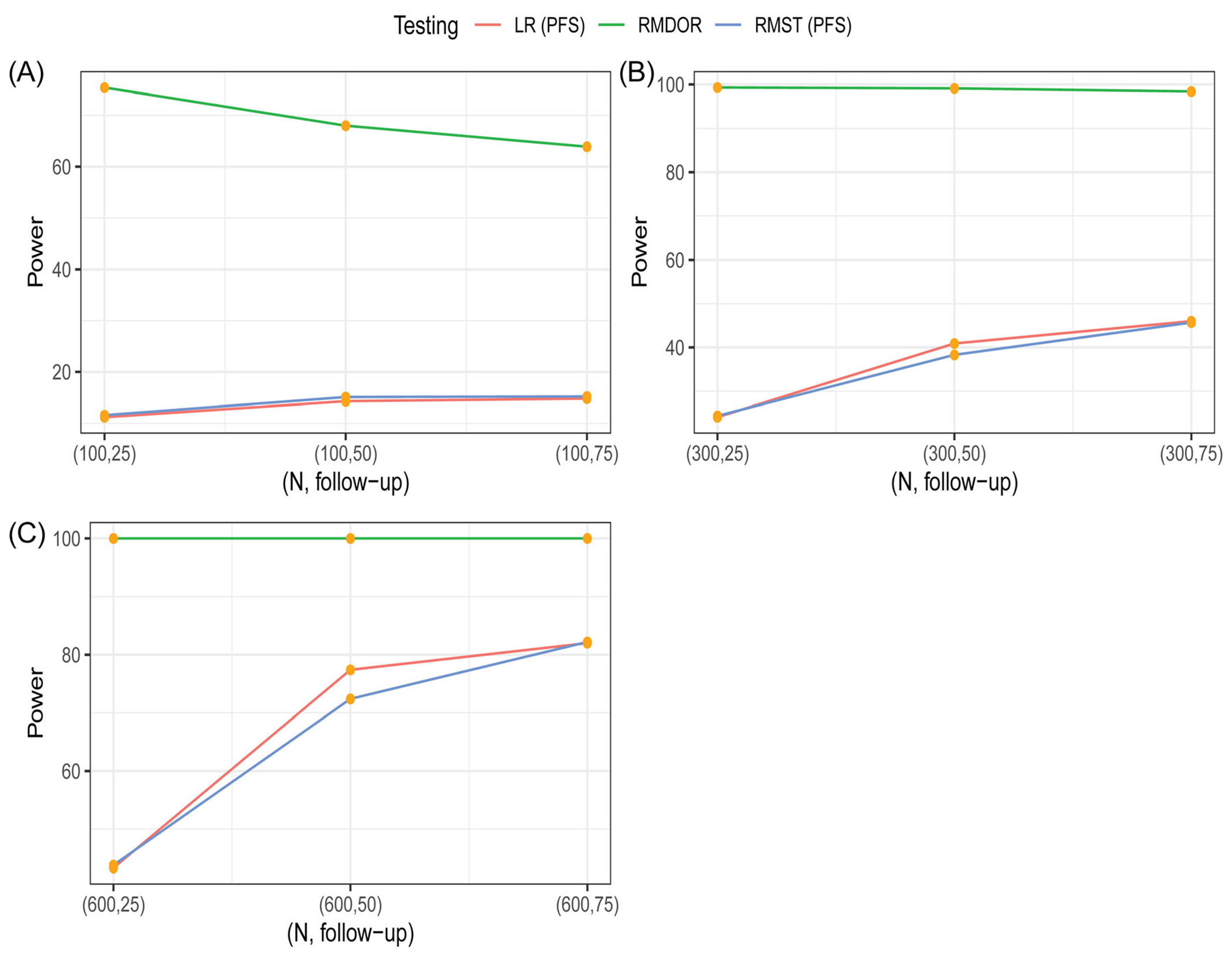
Comparison of statistical power to detect an efficacy improvement of Arm A over Arm B among various methods based on simulations under Scenario 1. The testing methods are log-rank (LR) test for difference in progression-free survival (PFS), restricted mean survival time (RMST) test for difference in restricted mean PFS, restricted mean DOR (RMDOR) test for difference in RMDOR

TABLE 2.

Simulation results under Scenario 2 for the summary and comparison of quantitative statistical measures of treatment benefit

		PFS				RMDOR
N	Follow-up (months)	Median difference	RMST difference	HR	RMST ratio	RMDOR difference	RMDOR ratio
100	25	3.87	2.18	0.74	0.86	1.85	0.57
	50	4.17	4.76	0.71	0.77	3.40	0.51
	75	4.17	6.53	0.70	0.72	4.43	0.48
300	25	4.33	2.34	0.72	0.84	2.00	0.51
	50	4.28	5.05	0.69	0.75	3.73	0.44
	75	4.28	6.76	0.68	0.70	5.01	0.39
600	25	4.28	2.41	0.71	0.84	2.00	0.50
	50	4.28	5.21	0.68	0.74	3.77	0.43
	75	4.28	6.97	0.67	0.69	5.09	0.38

Note: For PFS, median difference (treatment vs. control) and RMST difference (Arm A vs. Arm B) are used as the absolute measures, while HR (Arm A vs. Arm B) and RMST ratio (Arm B vs. Arm A) are used as the relative measures. For DOR, RMDOR difference (Arm A vs. Arm B) is used as the absolute measure, while RMDOR ratio (Arm B vs. Arm A) is used as the relative measure. For HR, RMST and RMDOR, the maximum time window from each simulated dataset is used.

Abbreviations: DOR, duration of response; HR, hazard ratio; PFS, progression-free survival; RMDOR, restricted mean DOR; RMST, restricted mean survival time.

FIGURE 3.

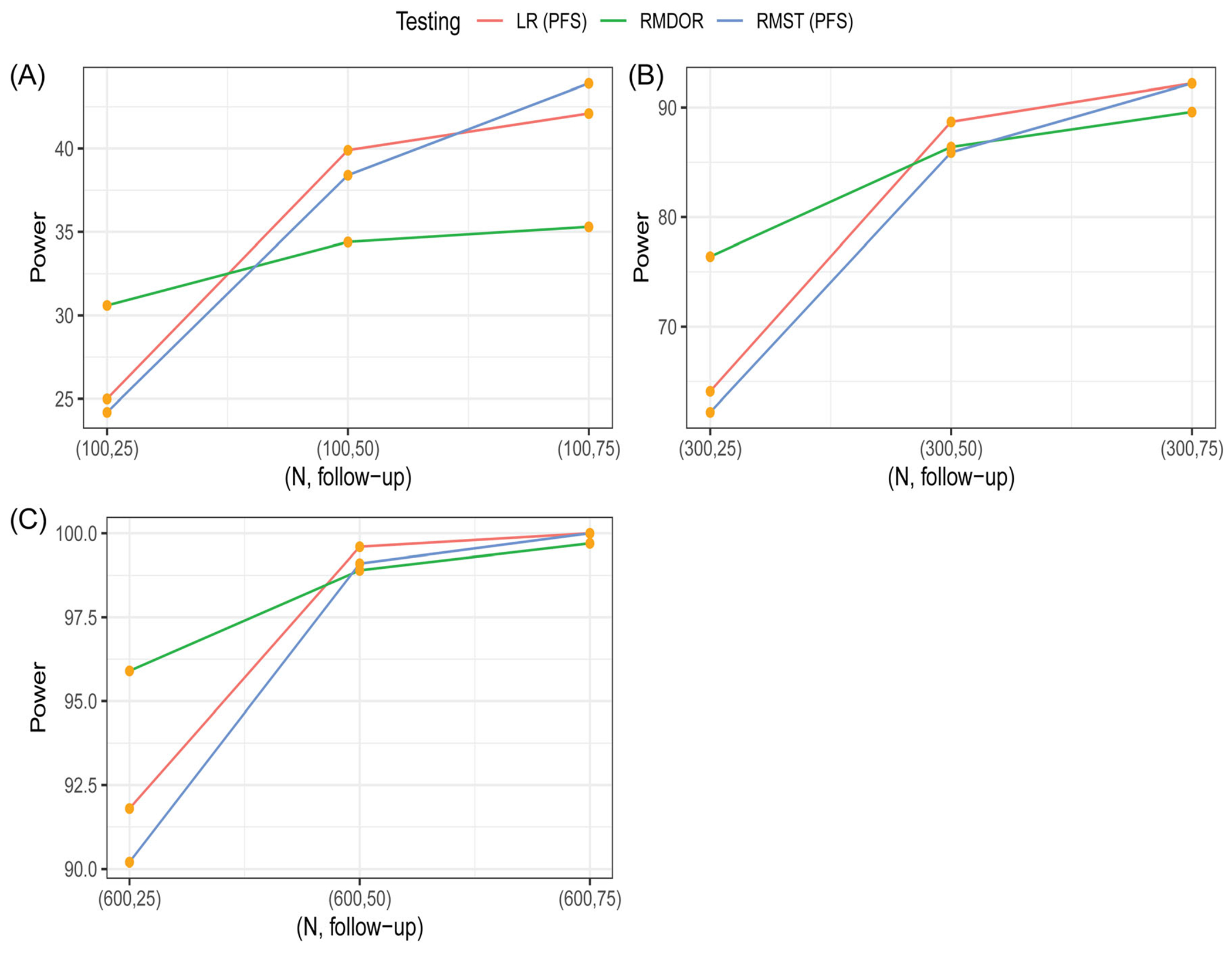
Comparison of statistical power to detect an efficacy improvement of Arm A over Arm B among various methods based on simulations under Scenario 2. The testing methods are log-rank (LR) test for difference in progression-free survival (PFS), restricted mean survival time (RMST) test for difference in restricted mean PFS, restricted mean DOR (RMDOR) test for difference in RMDOR

Scenario 1 is more favorable to the class of response-based endpoints, with shorter TTR, higher ORR, and longer DOR among responders for Arm A versus Arm B. For example, when $N=300$, at 25 months, for the PFS endpoint, the HR is 0.84, median difference is 1.98 month, with the power of the log-rank test only at 24%. With longer follow-up at 50 and 75 months, the median difference stays the same and the HR has moderate changes, which is expected due to the fact that the proportional hazard assumption does not hold with a mixed distribution of responders and non-responders. If we look at the RMST of PFS, the difference between two arms is 1.25, 2.8, and 3.8 months for follow-up time of 25, 50, and 75 months, respectively. So with longer follow-up, the effect size increases, and the RMST can appropriately capture the long-term effect owing to some durable responses. The power of RMST is similar to the power of log-rank test at each timepoint. With respect to the proposed RMDOR in the ITT population, at 25 months, the mean difference is 4 months, bigger than both the 1.98 months’ difference in median and the RMST difference for PFS. At longer follow up of 75 months, the mean difference in DOR is 7 months, much longer than the median difference and RMST difference for PFS. Interestingly, the RMDOR ratio and RMST ratio are relatively stable with longer follow-up time (50 and 75 months), similar to the HR. The power is almost 100% at each timepoint. This is because TTR is short between 2 and 4 months, and with a much higher ORR in the treatment arm, a large treatment benefit can be detected early based on the difference of two AUCs for PFS and RPFS curves.

Scenario 2 is more favorable to the PFS endpoint where clinically meaningful improvement in PFS is observed for both responders and non-responders in Arm A. However, the ORRs are similar (25% vs. 20%) so making this scenario less favorable to the response-based analysis. Nevertheless, the RMDOR is still a competitive method in hypothesis testing and estimation. For the PFS endpoint, HR and medians are not sensitive to the durable responses with longer follow-up even though there is a longer-term benefit. In contrast, both RMST for PFS and RMDOR are able to capture the long-term effect. For example, when $N=300$, with 75 months of follow-up, the PFS RMST difference is 6.76 months and the RMDOR difference is 5 months. Similar to Scenario 1, the RMST ratio and RMDOR ratio are relatively stable when follow-up time is 50 and 75 months. All the testing methods have similar power, with the RMDOR being more sensitive to the short term benefit with higher power at 25 months.

When the sample size is 100, the typical size for a randomized Phase II screening study for Go/No-Go decision making, the RMDOR method performs very well compared to other testing methods in both scenarios, especially with a shorter follow-up of 25 months. This is because the RMDOR is sensitive to both short-term and long-term effect, particularly in the event of a higher ORR associated with the investigational drug and when TTR is much shorter than PFS. In Scenario 1, unlike the other methods, the RMDOR still has high power with $N=100$ (Figure 2), because of doubling of ORR and longer DOR among responders, making it an ideal endpoint for proof-of-concept studies with moderate sample size. Even in Scenario 2 when the ORR is similar between the two arms, the RMDOR performs impressively well and has higher power than the Log-rank test and RMST test for PFS when the follow-up time is 25 months.

Since the performance of RMDOR is robust with a small sample size, then naturally the performance of the method with well-established asymptotic properties is guaranteed in larger studies, as demonstrated in the simulation study when $N=300$ and $N=600$. Therefore, the RMDOR is also an appealing method in a Phase III pivotal study to assess the benefit of a treatment that can quickly reduce tumor size and maintain that effect for a prolonged period. This is not to conclude that the RMDOR is advantageous to summary measures for PFS in all circumstances, but to offer a useful alternative tool as either the primary analysis method or a supportive method for quantitative benefit assessment, in particular for a pivotal study where response-based endpoints are clinically relevant and formal statistical inference needs to be made.⁵

This simulation study demonstrates the potential benefit of using the RMDOR as a novel statistical measure to quantify treatment effect by efficiently quantifying higher ORR, faster TTR and longer DOR among responders. It is also more sensitive to both short-term benefit and long-term benefit, making it an ideal endpoint for both Phase 2 screening trials and Phase 3 registrational trials.

5 |. DISCUSSION

As achieving statistically significant improvement in OS becomes an increasingly daunting goal in oncology randomized clinical trials due to high censoring and confounding of post-progression anti-cancer therapies, early novel end-points that could be measured relatively quickly but still be able to characterize the clinical benefit are important to optimize drug development with go/no-go decisions, minimize the exposure of ineffective therapies to cancer patients, and expedite the development of oncology drug and biologic products. The commonly used PFS endpoint may not always be a good intermediate endpoint for OS.^2,3 The RMDOR is a promising quantitative measure that directly assesses the effect of a tumor targeting therapy and may reliably predict long term survival benefit. Simulations show that it may have high power to detect treatment effect even with short-term follow-up if the novel therapy can induce tumor response early with high probability.

Both the mean DOR among all patients and the mean DOR among responders have intuitive clinical interpretations. The former is the expected DOR for a patient receiving a treatment, something a physician can explain before the patient receives the treatment, whereas the latter represents the expected DOR among patients who have achieved a response, something a physician can explain after the patient achieves a response. There are pros and cons to each of these approaches, but we believe the former is a better summary for the entire population because it is a composite summary measuring the TTR, ORR and DOR altogether. Furthermore, the comparison of DOR among responders between treatment arms does not have a causal interpretation given that the response status is itself a post-randomization outcome, and the response populations in the two treatment arms can differ greatly.

For study design and sample size calculation based on the RMDOR method, the power of the hypothesis test with a given sample size can be estimated by calculating

$$\text{Pr}\left(\frac{|{\widehat{\mu }}_1-{\widehat{\mu }}_0|}{\sqrt{{\widehat{\sigma }}_1^2+{\widehat{\sigma }}_0^2}}>Z_{\alpha }\right)=\text{Pr}\left(N(0,1)>Z_{\alpha }-\frac{|{\mu }_1-{\mu }_0|}{\sqrt{{\sigma }_1^2+{\sigma }_0^2}}\right)$$

where $Z_{\alpha }$ is the efficacy boundary of standard normal test at significance level $\alpha$. To determine the value of $\left({\mu }_j,{\sigma }_j\right)$, one needs to specify the joint distribution of $(T[P/D],T[P/D/R],C)$ in arm $j\in \{\mathrm{0,1}\}$ under hypothesized alternative. With the given distribution, one may calculate $\left({\mu }_j,{\sigma }_j\right)$ analytically via the difference between two RMSTs and Equation (3). But this computation can be complicated depending on the specified distribution, similar to the case for the RMST.³⁰ In practice, it is often easier to perform a numerical simulation to estimate relevant quantities via the Monte-Carlo method. The sample size of a future study can then be chosen such that the estimated power achieves the desired level such as 90%. In general, the use of data driven choice of the truncation time point needs to be specified in the study analysis plan, which should also include an explicit plan for study completion that can be based on the total number of events, the standard error estimate (i.e., information) of the RMDOR in the pooled data, average and maximum follow-up times or their combinations. The further extension to the group sequential design is possible but more complicated, since the truncation time points at the interim and final analyses may need to be different, which introduces some difficulties in quantifying the between group difference.

Although the RMST and RMDOR are able to capture the long-term benefit associated with the treatment, the choice of the truncation time has a substantial impact on the results for the absolute measure (difference).²⁶ The sensitivity of trial results to $\tau$ may cause interpretation concern and limit cross-trial comparisons, which of course is also applicable to the HR. Nevertheless, the relative measures in terms of RMST ratio and RMDOR ratio are relatively stable, similar to the HR. The HR may be less sensitive to the truncation point because it is calculated based on a shorter time window (Section 2.3). We recommend that both the difference and the ratio are reported for restricted mean based methods.

The RMDOR works best for heterogeneous populations where the experimental drug is effective and durable for only a fraction of patients (responders), but less or little effect for subjects who do not respond to the treatment. In such cases, PFS is not efficient compared to the RMDOR to measure the short-term and long-term therapeutic benefit. However, for cytostatic drugs that provide benefit not in the form of (prolonged) tumor shrinkage, but by keeping disease stable for a prolonged period, response-based analysis (ORR or RMDOR) does not capture fully the efficacy profile due to omission of prolonged stable disease which is well represented by PFS. In this situation, however, such a cancer treatment does not offer any cure and may not improve the quality of life of patients or lead to long-term survival.

The proposed DOR estimator can be represented as the area between 2 km curves and thus has very nice statistical properties. Based on our limited experience, the Gaussian distribution can be used to approximate its distribution accurately, even when the study sample size is modest.²⁵ As a consequence, the endpoint-based statistical inference procedure discussed in the paper is reliable in practice.

The ultimate goal of a cancer treatment is to reduce disease burden or achieve complete remission of cancer cells so that patients will have a better quality of life and ultimately cancer can be cured with prolonged and sustainable disease-free duration. The response-based endpoints and summary measures are objective outcomes that may correlate well with quality of life and OS. A meta-analysis to examine the surrogacy of the proposed RMDOR method for OS based on historical trials is warranted.

APPENDIX

SAS MACRO FOR THE RMDOR

The calculation of the restricted mean DOR (RMDOR) is available as a SAS macro _macro_RMST_DOR.sas, available online as Supporting Information appended to the article.

The input dataset must be tuned in order for this SAS macro to run correctly:

• For two-arm comparison, the treatment arm indicator must be numeric, with value 1 for treatment and 0 for control.

• The dataset must include time to response or censoring and binary response/censoring indicator. The censor indicator variable must be numeric, with value 1 indicating response and 0 indicating no response. For responders, time to response (days) = date of first documenting response – date of randomization + 1; For non-responders, time to response (days) can be a missing value or a number larger than progression-free survival (PFS). By definition, PFS time ≥ response/progression-free survival time. For study in which no adequate baseline assessment is part of the censoring algorithm for PFS, subjects may be assessed as responders while censored at randomization for PFS due to no adequate baseline assessment. For such cases subjects can be censored at date of randomization for time to response.

• The dataset must include PFS and PFS binary event/censoring indicator. The event indicator variable must be numeric, with value 1 indicating event (e.g., PD or death) and 0 indicating no event.

• The unit for time to response or censoring and PFS must be the same.

DATA AVAILABILITY STATEMENT

Data sharing is not applicable to this article as no new data were created or analyzed in this study.