A Deep Learning Based Anti-aliasing Self Super-resolution Algorithm for MRI

Abstract

High resolution magnetic resonance (MR) images are desired in many clinical applications, yet acquiring such data with an adequate signal-to-noise ratio requires a long time, making them costly and susceptible to motion artifacts. A common way to partly achieve this goal is to acquire MR images with good in-plane resolution and poor through-plane resolution (i.e., large slice thickness). For such 2D imaging protocols, aliasing is also introduced in the through-plane direction, and these high-frequency artifacts cannot be removed by conventional interpolation. Super-resolution (SR) algorithms which can reduce aliasing artifacts and improve spatial resolution have previously been reported. State-of-the-art SR methods are mostly learning-based and require external training data consisting of paired low resolution (LR) and high resolution (HR) MR images. However, due to scanner limitations, such training data are often unavailable. This paper presents an anti-aliasing (AA) and self super-resolution (SSR) algorithm that needs no external training data. It takes advantage of the fact that the in-plane slices of those MR images contain high frequency information. Our algorithm consists of three steps: 1) We build a self AA (SAA) deep network followed by 2) an SSR deep network, both of which can be applied along different orientations within the original images, and 3) recombine the multiple orientations output from Steps 1 and 2 using Fourier burst accumulation. We perform our SAA+SSR algorithm on a diverse collection of MR data without modification or preprocessing other than N4 inhomogeneity correction, and demonstrate significant improvement compared to competing SSR methods.

1. Introduction

High resolution (HR) magnetic resonance images (MRI) provide more anatomical details and enable more precise analyses, and are therefore highly desired in clinical and research applications [8]. However, in reality MR images are usually acquired with high in-plane resolution and lower through-plane resolution (slice thickness) to save acquisition time. Thus in these images, the high frequency information in the through-plane direction is missing. Some MRI protocols acquire 3D images as stacks of 2D images, which introduce aliasing that appears as high-frequency artifacts in the images. Interpolation is frequently used (both on the scanner and in postprocessing) to improve the digital resolution of acquired images, but this process does not restore any high frequency information. The partial volume artifacts that remain in these images make them appear blurry and degrade image analysis performance as well [2,8].

To address this problem, a number of super-resolution (SR) algorithms have been developed, including neighbor embedding regressions [11], random forests (RF) [9], and convolutional neural networks (CNNs) [5–7]. Generally, CNN methods need paired atlas images to learn the transformation from low resolution (LR) to high resolution (HR). They work well with natural images, but a lack of adequate training data (an LR/HR atlas) is a major problem when applying these approaches to MRI. There are two reasons for the lack of adequate training data. First, acquisition of HR data with isotropic voxels is time consuming—potentially taking hours, depending on the desired resolution—in order to also achieve adequate signal-to-noise ratio. Such long acquisitions are prohibitive from a subject comfort point of view and are also highly prone to motion artifacts. Second, MR images have no standardized tissue contrast, so application of an SR approach trained from a given atlas may not readily apply to a new subject from scan that has different contrast properties. It is therefore desirable that any SR approach for MRI not require the use of an external atlas.

To avoid the requirement of external training data, researchers have developed self super-resolution (SSR) methods [3,4,14,16]. SSR methods use the mapping between the high in-plane resolution images and simulated lower resolution images, to estimate high resolution through-plane images. Previous SSR methods [4,14,16] have achieved good results on medical images. Jog et al. [4] built an SSR framework that extracts training patches from the LR MRI and blurred LR₂ images, trains a RF regressor, and applies the trained regressor to LR₂ images in different directions. The resultant images are LR, but have low resolution in different directions. Thus, each of them contributes high frequency information to a different region of Fourier space. Finally, these images are combined through Fourier burst accumulation (FBA) [1] to obtain an HR image. We have previously reported [16] a method that replaces the RF framework of Jog et al. [4] with the state-of-art SR deep network EDSR [7]. This approach applies the trained network to the original LR image instead of the LR₂ images as in Jog et al. [4]. Weigert et al. [14] reported an SSR method for 3D fluorescence microscopy images based on a U-net and showed improved segmentation. None of these previous works address anti-aliasing (AA).

In this paper, we report an approach for applying both anti-aliasing (AA) and super-resolution (SR) by building the first self AA (SAA) method in conjunction with an SSR deep network. We build upon our own [16] framework and the work of Jog et al. [4], with two major differences. First, the previous approaches constructed the LR₂ data by applying a truncated sinc in $k$-space simulating the incomplete signal in $k$-space of LR images for 3D MRI. However, for 2D MRI, this process does not simulate aliasing artifacts and therefore cannot provide training data for removing aliasing. We therefore modify this filtering to suit our desired deep networks. Second, we build two deep networks, one for SAA and one for SSR.

2. Method

Our algorithm needs no preprocessing step other than N4 inhomogeneity correction [12] to make the image intensity homogeneous. The pseudo code is shown in Algorithm 1, and we refer to our algorithm as Synthetic Multi-Orientation Resolution Enhancement (SMORE). Consider an input LR image having slice thickness equal to the slice separation. The spatial resolution (approximate full-width at half-maximum) and voxel separation of this image is assumed to be $a\times a\times b$ where $b>a$. Without loss of generality, we assume that the axial slices are $a\times a$ HR slices. We model this image as a low-pass filtered and downsampled version of the HR image $I(x,y,z)$ which has spatial resolution and voxel separation $a\times a\times a$. Our first step is to apply cubic b-spline (BSP) interpolation to the input image yielding $I_z(x,y,z)$ which has the same spatial resolution $a\times a\times b$ as the input but voxel separation $a\times a\times a$. Aliasing exists in the $z$ direction in this image because the Nyquist criterion is not satisfied (unless the actual frequency content in the $z$ direction is very low, which we assume is not the case in normal anatomies.) We denote the ratio of the resolutions as $k=b\text{/}a$, which need not be an integer. Similar to Jog et al. [4], the idea behind the algorithm is that 2D axial slices $I_z(x,y)$ can be thought of as $a\times a$ HR slices, whereas sagittal slices $I_z(z,y)$ and coronal slices $I_z(z,x)$ are $b\times a$ LR slices. Blurring axial slices in the $x$-direction produces ${\tilde{I}}_{xz}(x,y)$ with resolution of $b\times a$ which we can use with $I_z(x,y)$ as training data. Any trained system can then be applied to $I_z(z,y)$ or $I_z(z,x)$ to generate HR sagittal and coronal slices. We choose an state-of-art deep network model EDSR [7] as it won the Ntire 2017 super-resolution challenge [10]. We describe the steps of SMORE in details below.

Training Data Extraction:

To construct our training data, we desire aliased LR slices ${\tilde{I}}_{xz}(x,y)$ that accurately simulate the resolution $b\times a$ and have aliasing in the $x$-axis. For 2D MRI, we need to model the slice selection procedure, thus we use a 1D Gaussian filter $G_{\sigma }(x)$ in the image domain with a length round($k$) and full-width at half-maximum (FWHM) of $k$. The filtered image $I_{xz}(x,y,z)$ has the desired LR components without aliasing. To introduce aliasing, the image is downsampled by factor of $k$ using linear interpolation to simulate the large slice thickness. We denote this image as ${\downarrow }_x^k\left(I_{xz}(x,y,z)\right)$. To complete the training pair we upsample this image by a factor $k$ using BSP interpolation to generate LR₂ which can be represented as ${\uparrow }_x^k\left({\downarrow }_x^k\left(I_{xz}(x,y,z)\right)\right)$,

Algorithm 1:

SMORE Pseudocode

but for brevity denoted as ${\tilde{I}}_{xz}(x,y,z)$. To increase the training samples, we rotate $I_z(x,y,z)$ in the $xy$-plane by $\theta$ and repeat this process to yield $I_z^{\theta }(x,y,z)$. In this paper we use six rotations where $\theta =n\pi /6$ for $n=0,\dots ,5$, but this generalizes for any number and arrangement of rotations.

EDSR Model:

We train two networks, one for SAA and one for SSR. 1) To train the SAA network, $32\times 32$ patch pairs are extracted from axial slices in ${\tilde{I}}_{xz}(x,y,z)$ and $I_{xz}(x,y,z)$ (i.e., aliased LR₂ and LR, respectively). We train a deep network SR model, EDSR, to remove this aliasing. We use small patches to enhance edges without structural specificity so that this network can better preserve pathology. Additionally, small patches allow for more training samples. 2) To train our SSR network, $32\times 32$ patch pairs are extracted from axial slices in ${\tilde{I}}_{xz}(x,y,z)$ and $I_z(x,y,z)$. These patch pairs train another EDSR model to learn how to remove aliasing and improve resolution. Although training needs to be done for every subject, we have found that fine-tuning a pre-trained model is accurate and fast. In practice, training the two models for one subject based on pre-trained models from an arbitrary data set takes less than 40 minutes in total for a Tesla K40 GPU.

Applying the Networks:

Our trained SSR network can be applied to LR coronal and sagittal slices of $I_z(x,y,z)$ to remove aliasing and improve resolution. However, experimentally we discovered that if we apply our SSR network to patches of a sagittal slice $I_z(x,z)$, and subsequently reconstruct a 3D image, then the result only removes aliasing in sagittal slices. To address this, we apply our SAA network to coronal slices to remove aliasing there, and then apply our SSR network to sagittal slices. Subsequently, the aliasing in both the coronal and sagittal planes of our SMORE result are removed. We repeat this procedure by applying SAA in sagittal slices and then SSR to the coronal slices to produce another image. As long as SAA and SSR are applied to orthogonal image planes, we can do this for any rotation $\alpha$ in the $xy$-plane. The list of SAA and SSR results are finally combined by taking the maximum value for each voxel in $k$-space for all rotations $\alpha$. This is the $l_{\infty }$ variant of Fourier burst accumulation (FBA) [1], which assumes that high values in $k$-space indicate signal while low values indicate blurring. Since aliasing artifacts appears as high values in $k$-space, this assumption of FBA necessitates our SAA network. Our presented results use only two $\alpha$ values, 0 and $\pi /2$.

3. Experiments

Evaluation on simulated LR data:

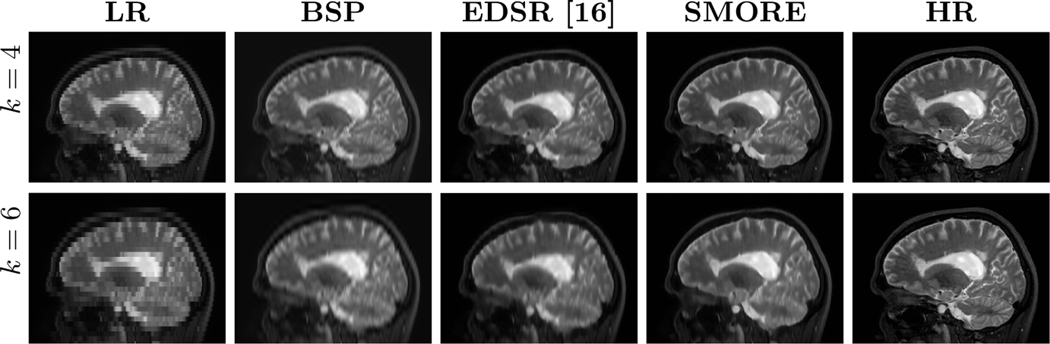
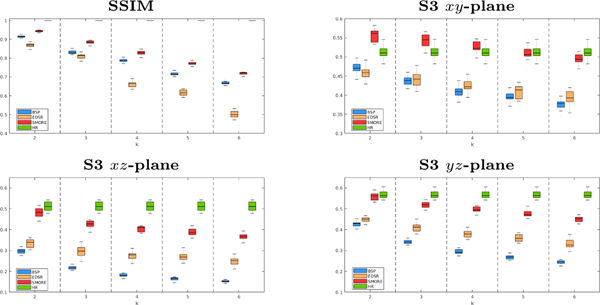
We compare SMORE to our previous work [16], which uses a different way of training data simulation and uses EDSR to do SSR on MRI without SAA, on T₂-weighted images from 14 multiple sclerosis subjects imaged on a 3T Philips Achieva scanner with acquired resolution of $1\times 1\times 1$ mm. These images serve as our ground truth HR images, which are blurred and downsampled by factor $k=\{2,\dots ,6\}$ in the $z$-axis to simulate thick-slice MR images. The thick-slice LR MR images, and the results of cubic B-spline interpolation (BSP), our competing MR variant of EDSR [16], and our proposed SMORE algorithm are shown in Fig. 1 for $k=4$ and 6. Visually, SMORE has significantly better through-plane resolution than BSP and EDSR. For SMORE, the lesions near the ventricle are well preserved when $k=4$. With $k=6$, the large lesions are still well preserved but smaller lesions are not as well preserved. The Structural SIMilarity (SSIM) index is computed between each method and the $1\times 1\times 1$ mm ground truth. And the mean value masked over non-background voxels is shown in Fig. 2. We also compute the sharpness index S3 [13], a no-reference 2D image quality assessment, along each cardinal axis with the results also shown in Fig. 2. Our proposed algorithm, SMORE, significantly outperforms the competing methods.

Fig. 1.

Sagittal views of the $k$ mm LR image, the cubic B-spline (BSP) interpolated image, an MR variant of EDSR [16], our proposed method SMORE, and the HR ground truth image with lesions anterior and posterior of the ventricle.

Fig. 2.

For $k=2,\dots ,6$, we have evaluation of BSP (blue), an MR variant of EDSR [7] (yellow), our proposed method SMORE (red), and the ground truth (green).

Evaluation on acquired LR data:

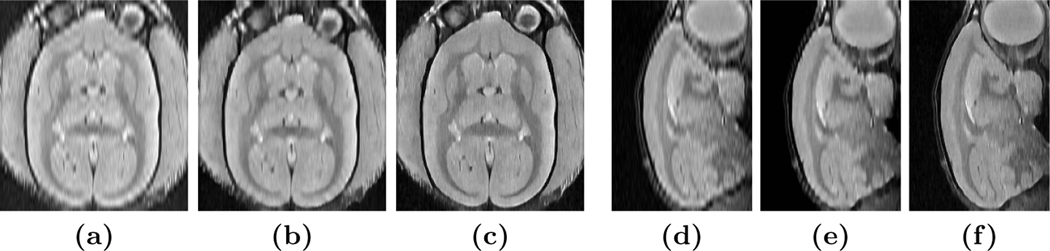
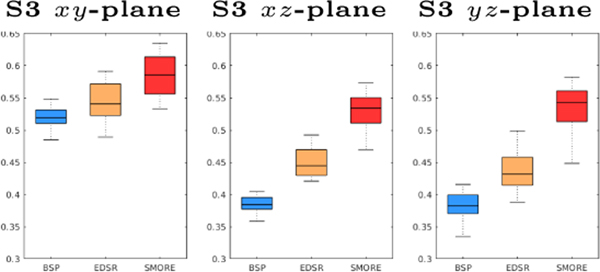
We applied BSP, our previous MR variant of EDSR [16], and our proposed SMORE method on eight PD-weighted MR images of marmosets. Each image has a resolution of $0.15\times 0.15\times 1$ mm (thus $k\approx 6.667$), with HR in coronal plane. Results are shown in Fig. 3. We observe severe aliasing on the axial and sagittal plane of the input images, with an example shown in Fig. 3(a) and (d). Although there is no ground truth, visually SMORE removes the aliasing and gives a significantly sharper image (see Figs. 3(c) and (f)). To evaluate the sharpness, we use the S3 sharpness measure [13] on these results (see Fig. 4).

Fig. 3.

Experiment on $0.15\times 0.15\times 1$ mm LR marmoset PD MRI, showing axial views of (a) BSP interpolated image, (b) MR variant of EDSR [16], (c) SMORE, and sagittal views of (d) BSP, (e) MR variant of EDSR, and finally (f) SMORE.

Fig. 4.

S3 evaluation for the $0.15\times 0.15\times 1$ marmoset data, with BSP (blue), an MR variant of EDSR (yellow), and our proposed method SMORE (red).

Application to multi-view image reconstruction:

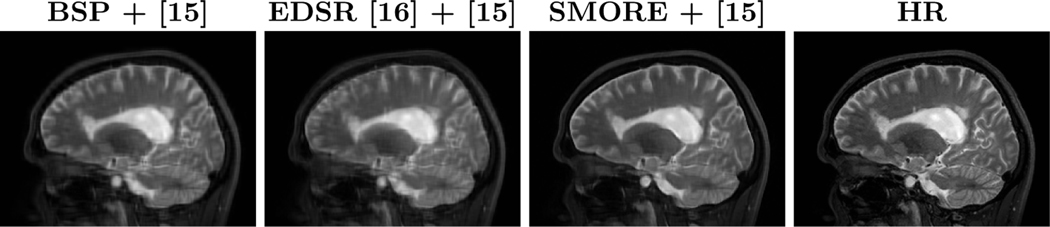
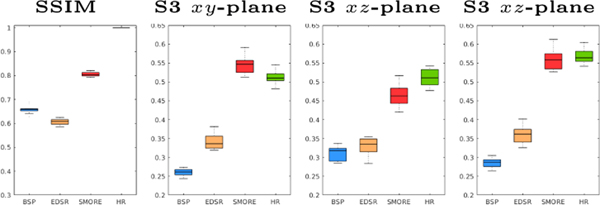
Woo et al. [15] presented a multi-view HR image reconstruction algorithm that reconstructs a single HR image from three orthogonally acquired LR images. The original algorithm used BSP interpolated LR images as input. We compare using BSP for this reconstruction with the MR variant of EDSR [16] and our proposed method SMORE. We use the same data as in Sec. ??, which have ground truth HR images. Three simulated LR images with resolution of $6\times 1\times 1$, $1\times 6\times 1$, and $1\times 1\times 6$ are generated for each data set. Thus $k$ = 6 and the input images are severely aliased. We apply each of BSP, EDSR, and SMORE to these three images and then apply our implementation of the reconstruction algorithm [15]. Example results for each of these three approaches are shown in Fig. 6. SSIM is computed for each reconstructed image to its $1\times 1\times 1$ mm ground truth HR image, with the mean of SSIM over non-background voxels being shown in Fig. 5. We also compute the sharpness index S3 along each cardinal axis with the results also shown in Fig. 5. Our proposed algorithm, SMORE, significantly outperforms the competing methods.

Fig. 6.

Sagittal views of the reconstructed image [15] using three inputs ($k=6$) from results of BSP, MR variant of EDSR [16], our proposed method SMORE, and the HR ground truth image.

Fig. 5.

SSIM and S3 for the reconstruction result using three inputs ($k=6$). We have results from BSP (blue), an MR variant of EDSR (yellow), our proposed method SMORE (red), and the ground truth (green).

4. Conclusion and Discussion

This paper presents a self anti-aliasing (SAA) and self super-resolution (SSR) algorithm that can resolve high resolution information from MR images with thick slices and remove aliasing artifacts without any external training data. It needs no preprocessing step other than inhomogeneity correction like N4. The results are significantly better than competing SSR methods, and can be applied to multiple data sets without any modification or parameter tuning. Future work will include an evaluation of its impact on more applications such as skull stripping and lesion segmentation.