Abstract
Drug delivery via dry powder inhaler (DPI) is a complex process affected by multiple factors involving gas and particles. The performance of a carrier-based formulation depends on the release of active pharmaceutical ingredient (API) particles, typically characterized by fine particle fraction (FPF) and dispersion fraction (DF). Computational Fluid Dynamics coupled with Discrete Element Method (CFD-DEM) can capture relevant gas and particle interactions but is computationally expensive, especially when tracking all carrier and API particles. This study assessed the efficacy of two coarse-grained CFD-DEM approaches, the Discrete Parcel Method and the representative particle approach, through highly-resolved CFD-DEM simulations. The representative particle approach simulates all carrier particles and a subset of API particles, whereas the Discrete Parcel Method tracks parcels representing a specified number of carrier or API particles. Both approaches are viable for a small carrier-API size ratio which requires modest degrees of coarse-graining, but the Discrete Parcel Method showed limitations for a large carrier-API size ratio. The representative particle approach can approximate CFD-DEM results with reasonable accuracies when simulations include at least 10 representative API particles per carrier. Using the representative particle approach, we probed powder characteristics that could affect FPF and DF in a model problem and correlated these fractions with the maximum carrier-API cohesive force per unit mass of API particles.
Keywords: Dry powder inhaler, Computational fluid dynamics, Discrete element method, Coarse-graining
1. Introduction
Dry powder inhalers (DPIs) deliver active pharmaceutical ingredients (APIs), such as bronchodilators, as dry powder formulations to specific regions in human respiratory systems such as the upper airway and lungs (Newman and Busse, 2002; Atkins, 2005; Smyth and Hickey, 2005; Chan, 2006; Islam and Gladki, 2008; Daniher and Zhu, 2008; Wong et al., 2012; Donovan et al., 2012; Cui et al., 2014; Tong et al., 2015; Yang et al., 2015; van Wachem et al., 2017; Sommerfeld et al., 2019; Bass et al., 2020). DPI has a wide range of applications in treating respiratory diseases such as pneumonia, asthma, tuberculosis, and chronic obstructive pulmonary disease (Newman and Busse, 2002; Atkins, 2005; Chan, 2006; Islam and Gladki, 2008). A typical DPI fluidizes the API particles with air from the inlet and passes them to the mouthpiece. This process utilizes energy either from the patient’s inspiration (passive device) or an external energy source (active device) (Islam and Gladki, 2008). This study focuses on passive devices, which represent a majority of the approved commercial DPI products (Lee et al., 2009; Sommerfeld et al., 2019). Specifically, we present a method referred to as the “representative particle approach” to simulate fluidization and deagglomeration in a DPI. This approach tracks all the carrier particles’ motion and a subset of the API particles, as described in greater detail below.
In order for API particles to be transported beyond the mouth, throat, and bronchial regions, their sizes have to fall in the 1–5μm size range (Bisgaard et al., 2001; Daniher and Zhu, 2008), which poses challenges as particles in this size range are extremely cohesive and hard to fluidize (Begat et al., 2004). The effect of cohesion can be mitigated through aggregation so that the resultant agglomerates can be airborne and easily transported by airflow (Yang et al., 2015). Although agglomerates formed with purely API particles are available (Nguyen et al., 2014; Yu et al., 2017), many formulations are carrier-based, which will be the focus of this study. Carrier-based formulations utilize bigger 50–200μm carrier particles to form agglomerates with the small API particles (Timsina et al., 1994; French et al., 1996; Smyth and Hickey, 2005; Donovan and Smyth, 2010; Yang et al., 2015; Nguyen et al., 2018; Sommerfeld et al., 2019) and then deagglomerate to release API particles for drug delivery. The drug delivery efficiency thus depends on the fine particle fraction (FPF), which is the fraction of API particles released as agglomerates smaller than 5μm (Tong et al., 2010).
Agglomeration and deagglomeration are essential for carrier-based DPI formulations. Interparticle cohesive forces, including van der Waals (vdW) force and electrostatic force (Zellnitz et al., 2019; Yang et al., 2015; Peng et al., 2016; Zellnitz et al., 2019), attach small API particles to big carrier particles. In this study, we focus on carrier-API agglomerates formed with vdW force. Deagglomeration in DPI is governed by mechanical impact and turbulence (Telko and Hickey, 2005; Donovan et al., 2012; Ruzycki et al., 2013; Ariane et al., 2018). Both agglomerate-agglomerate and agglomerate-wall collisions weaken the agglomerate structure and release the API particles (Thornton and Liu, 2004; Ariane et al., 2018), while turbulence can disperse the agglomerates and also directly dislodge the API particles from the carrier particles (Yang et al., 2015).
Models of varying levels of complexity have been used to simulate the flow and deagglomeration processes in DPIs. Studies (Coates et al., 2005; Donovan et al., 2012; Kannan et al., 2017) used Computational Fluid Dynamics (CFD) to simulate gas flow in DPI, assuming that the gas flow behavior is unaffected by the presence of the particles. The fate of test Lagrangian carrier particles injected in the flow is then followed to infer FPF from the number of carrier-wall collisions and collision velocity distribution. However, these simulations do not explicitly capture the deagglomeration process, which is crucial for carrier-based formulations.
One commonly used approach to include particle-particle interactions is the Discrete Element Method (DEM) that models individual particles as soft spheres that can slightly overlap with each other (Cundall and Strack, 1979; Tsuji et al., 1993). DEM explicitly models vdW forces, electrostatic interactions, contact forces, and rolling friction, which are crucial for agglomeration and deagglomeration processes (Thornton et al., 1999; Moreno et al., 2003; Tong et al., 2015). Particle agglomeration and deagglomeration, without gas flow, have been studied via DEM simulations (Moreno-Atanasio and Ghadiri, 2006; Nguyen et al., 2014; Yang et al., 2015).
Computational Fluid Dynamics coupled with the Discrete Element Method (CFD-DEM) has the advantage of capturing gas flow, gas-particle interactions, and particle-particle interactions in DPI. Early studies employing the CFD-DEM approach involved only a few thousand API particles (Tong et al., 2010) or a few carrier-based agglomerates (Yang et al., 2014), which are below the actual number of particles in the system. The CFD-DEM approach has also been used to study the dynamics of carrier particles (Alexopoulos et al., 2013; Sommerfeld and Schmalfuß, 2016) to demonstrate the importance of including gas flow, gas-particle interactions, and particle-particle interactions. The cost of the CFD-DEM simulation increases with the number of particles in the system (Wong et al., 2012; Sommerfeld et al., 2019). Current computing resources can readily simulate the gas and all the carrier particles’ motion via the CFD-DEM approach. However, the same is not valid for the API particles. A typical dosage usually involves tens or hundreds of millions of API particles (van Wachem et al., 2017; Nguyen et al., 2018), rendering a full simulation impractical.
In order to expand the simulating capability of CFD-DEM, Cui et al. (2014) used a multi-scale approach by treating API particle concentration as a continuum passive scalar. This approach only tracks carrier particles, which makes CFD-DEM simulation easily affordable and fast. Constitutive models, required as inputs in this approach, are formulated for the detachment of API particles from micro-scale simulations, which involve a single or a few carrier-API agglomerates at different impact conditions. Tong et al. (2015) and van Wachem et al. (2017) expanded this approach by including constitutive models for detachment of API particles by fluid-flow and their reattachment. Nguyen et al. (2018) used the multi-scale approach to simulate DPI formulations in a model inhaler and found that this approach can predict FPF by using apparent surface energy. The adequacy of such constitutive models extracted from micromechanical tests can be a source of uncertainty in this powerful approach.
Besides the multi-scale approach, a commonly used coarse-graining CFD-DEM approach is the Discrete Parcel Method. In the Discrete Parcel Method, each parcel represents a specified number of primary particles. Parcel-parcel and parcel-wall interaction forces are computed by the force models similar to those in the DEM by treating inter-parcel interactions as effective equivalents of inter-particle interactions (Bierwisch et al., 2009; Radl and Sundaresan, 2014; Washino et al., 2018; Tausendschön et al., 2020 ). This approach tracks a smaller number of entities in the system, thus reducing the computational cost.
In this study, we develop and validate a novel particle-based coarsening method called the “representative particle approach”, where one tracks all the carrier particles and a subset of API particles referred to as the “representative” particles. Each “representative” API particle represents a specified number of primary API particles. This approach reduces the number of particles tracked in the simulation, thus decreasing the computational cost compared to the full simulation. These simulations will necessarily be more expensive than the passive scaler-based approach alluded to earlier but offer the possibility of assessing the accuracy by changing the number of representative particles simulated.
We assess the accuracy of the represntative particle approach through agglomerate-wall and agglomerate-agglomerate collision tests with different collision conditions. We examine the combined effect of multiple collisions and gas flow by analyzing the dispersion behavior in a model inhaler geometry using realistic carrier-based formulations. We also compare the dispersion behavior in the model inhaler of this approach against the more conventional Discrete Parcel Method.
In the comparison, we first simulate a formulation with a relatively small carrier-API size ratio, allowing us to simulate all the particles using CFD-DEM. We then conduct simulations using (i) the Discrete Parcel Method and (ii) the representative particle approach at different levels of coarse-graining. We will demonstrate that both approaches can capture the FPF of the original system reasonably well.
In a more demanding formulation with a relatively large carrier-API size ratio, the total number of particles in the original system is extremely large, rendering full-scale simulation unaffordable. Reducing the total number of entities tracked in the system requires high degrees of coarsening. We will present the pitfalls of using Discrete Parcel Method to simulate this formulation. On the other hand, the representative particle approach tracks all the carrier particles, thus avoiding potential issues. We will demonstrate that the representative particle approach is a promising way of capturing the original system’s release behavior with reasonable accuracy and reduced computational cost, as long as the simulation includes a sufficient number of representative API particles per carrier particle (which is ∼ 10). Using the representative particle approach, we will correlate API particle release with the ratio of the maximum carrier-API cohesive force to API particle mass in a model problem.
2. Models and Methods
2.1. Fluid Phase Model
The LES approach adopted in our simulations is known to be more accurate, especially in the near-wall region, in the transitional and turbulent flow regimes , which are common in DPI(Ilie et al., 2008). The fluid phase momentum equation is given by (Sagaut and Germano, 2005; Mallouppas and van Wachem, 2013; van Wachem et al., 2017).
| (1) |
where is the fluid volume fraction, is the fluid density and is the filtered fluid velocity. is filtered pressure gradient. is the interphase momentum exchange between gas phase and solid phase. is the undisturbed fluid velocity at the location of particle . The filtered fluid phase stress is expressed as
| (2) |
where is taken to be simply of fluid as a default. This approximation fails at high particle loadings, but at high particle loadings the effect of gas phase turbulence on fluid and particle flow is much weaker than that of the drag force and so the error is inconsequential.
The subgrid scale fluid stress is written as (Pope, 2000)
| (3) |
where is the subgrid scale viscosity, which can be modeled as,
| (4) |
In Eq. 4, is the Smagorinsky constant given by Dynamic Germano-Lilly model (Germano et al., 1991; Lilly, 1992)
| (5) |
with the following definitions
| (6) |
| (7) |
where the symbol refers to a test filtered quantity with a filter size of (Mallouppas and van Wachem, 2013).
2.2. Particle Phase Model
2.2.1. Discrete Element Method
In Discrete Element Method (Cundall and Strack, 1979; Tsuji et al., 1993), the particles are described by Newton’s equations of motion.
| (8) |
| (9) |
Here, , , and refer to the mass, the moment of inertia, translational and angular velocities of particle respectively. and are the normal and tangential contact forces between particle and particle . and are the normal and tangential contact forces between particle and a wall. is the van der Waals force from the interaction between particle and particle . is the van der Waals force between particle and a wall. is the total force acting on particle by gas. is the gravitational force. is the torque acting on particle due to particle . is the torque acting on particle from a wall.
The contact force for particle-particle and particle-wall interaction is quantified using a Hertzian spring-dashpot model; see Gu et al. (2016) for further details. Softening correction is not included in this study as the real Youngs’ modulus is used in all the cases. The cohesion force is modeled using a cohesion model based on the Hamaker constant. The magnitude of van der Waals force between particle and particle is modeled by the following (Hamaker, 1937; Galvin and Benyahia, 2014)
| (10) |
where is the Hamaker constant and is the distance between the particle surfaces. A maximum cutoff distance is used to accelerate the simulation (Gu et al., 2016). The van der Waals force is not accounted for is a separation distance commensurate with intermolecular spacing where the van der Waals cohesive force is assumed to saturate. Even when the separation distance is smaller than this value, the van der Waals force is capped at the value evaluated at , which is 1nm in this study (Galvin and Benyahia, 2014; Gu et al., 2016). The van der Waals force between particle and particle can be modeled as (Gu et al., 2016),
| (11) |
The van der Waals force between particle and a wall experienced by particle can be modeled as (Gu et al., 2016),
| (12) |
2.2.2. Representative particle approach
In order to reduce the number of entities tracked in the simulation, we propose the following representative particle approach. While still tracking all the carrier particles, we only track a representative subset of API particles, where each simulated API particle represents primary API particles, and is known as the coarsening factor. Essentially, we interpret each representative particle as primary particles located in the same location, , and with the same velocity, .
The representative particle approach is different from the more conventional Discrete Parcel Method in the following aspects. In the Discrete Parcel Method, each parcel represents primary particles, and in the context of DPI formulations, both the carrier and API particles would be coarse-grained in the same manner. In the representative particle approach, only API particles are ”coarse-grained”, whereas all carrier particles are still tracked in the simulation. When resolving particle collisions, a parcel is treated as a bigger particle with an equivalent volume of primary particles, whereas in the representative particle approach, particle sizes are the same as the original system. (When the Discrete Parcel Method is coupled with CFD, the fluid-particle interaction force is still computed using the primary particle diameter and multiplied by to get the force on the parcel.) In the Discrete Parcel Method, both the number of carrier parcels and API parcels would be reduced to of those in the original system. In the representative particle approach, the number of carrier particles is the same as the original system, whereas the number of representative API particles is reduced to of that in the original system. These comparisons are summarized in Table 1 and illustrated in Fig. 1. In the representative particle approach, API particle diameter remains the same after coarsening, as shown in Fig. 1b.
Table 1.
Comparison between the Discrete Parcel Method approach and the representative particle approach. is the diameter of a primary particle. and are the numbers of carrier and API particles, respectively in the original system. is the coarsening factor.
| Discrete Parcel Method | Representative Particle Approach | |
|---|---|---|
| Methodology | primary particles → 1 parcel (for both carrier and API) | primary API particles → 1 representative API particle |
| Particle diameter (in DEM) | ||
| Number of carrier particles | ||
| Number of API particles |
Fig. 1.
Schematic illustrations of a) the Discrete Parcel Method and b) the representative particle approach. The original system in this example consists of 3 carrier particles with a diameter of 70.0μm and 387 API particles with a diameter of 5.0μm. After coarse-graining (with ) using the Discrete Parcel Method in (a) and the representative particle approach in (b), the system consists of a) one carrier parcel with a diameter of 101.0μm and 129 API parcels with a diameter of 7.2μm and b) 3 carrier particles with a diameter of 70.0μm and 129 representative API particles with a diameter of 5.0μm. In the rerpresentative particle approach, API particle diameter remains the same after coarse-graining.
In the representative particle approach, the DEM equation for carrier particles is as follows. is the coarsening factor for API particles.
| (13) |
In this equation, is the mass of carrier particle . is the translational velocity of carrier particle . and are the normal and tangential contact forces between carrier particle and carrier particle . and are the normal and tangential contact forces between carrier particle and representative API particle . and , where and are the normal and tangential contact forces between carrier particle and one primary API particle at the same position as representative API particle . The contact forces between carrier particle and representative API particle are equivalent to the contact forces between carrier particle and primary API particles.
is the van der Waals force between carrier particle and carrier particle . is the van der Waals force between carrier particle and representative API particle . , where is the van der Waals force between carrier particle and one primary API particle at the same position as representative API particle . Similarly, the van der Waals force between carrier particle and representative API particle is equivalent to that between carrier particle and primary API particles. , and are the normal contact force, tangential contact force, and van der Waals force between carrier particle and wall . is the total force acting on carrier particle by gas. is the gravitational force.
The DEM equation for representative API particles is as follows
| (14) |
In this equation, is the mass of representative API particle , where as the mass of one representative API particle is equivalent to primary API particles. is the translational velocity of representative API particle . and are the normal and tangential contact forces between representative API particle and carrier particle . and , where and are the normal and tangential contact forces between carrier particle and one primary API particle at the same position as representative API particle , consistent with Eq. 13. and are the normal and tangential contact forces between representative API particles and . and , where and are the normal and tangential contact forces between two primary API particles which are at the same positions as representative API particles and , respectively. Since there are on both sides of the equation, the contact forces between two representative API particles are equivalent to those between two primary API particles.
is the van der Waals force between representative API particle and carrier particle . , where is the van der Waals force between carrier particle and one primary API particle at the same position as representative API particle , consistent with Eq. 13. is the van der Waals force between representative API particles and . , where is the van der Waals force between two primary API particles, which are at the same positions as representative API particles and , respectively. Similar to contact forces, the van der Waals force between two representative API particles is equivalent to that between two primary API particles.
, and are the normal contact force, tangential contact force and van der Waals force between representative API particle and wall . , and , where , and are the normal contact force, tangential contact force and van der Waals force between wall and a primary API particle at the same position as representative API particle . Thus, particle-wall interactions between one representative API particle and a wall are equivalent to those between primary API particles and a wall. is the total force acting on representative API particle . , where is the total force acting by gas on one primary API particle at the same position as representative API particle . Since there are on both sides of the DEM equation, the effect of total gas-particle interactions on one representative API particle is equivalent to that on one primary API particle. However, the effect of total gas-particle interactions by one representative API particle on gas is equivalent to that by primary API particles.
2.3. Physical parameters
In this study, the physical parameters are based on lactose (van Wachem et al., 2017; Nguyen et al., 2018) and are listed in Table 2. The diameter of carrier particles is chosen to be 70μm, which is in the range of commonly used carrier particle sizes (Tong et al., 2015; Nguyen et al., 2018; Ariane et al., 2018). The diameters of API particles used in this study are 2μm and 5μm respectively. Both 2μm and 5μm are commonly used API particle sizes (Yang et al., 2014; Tong et al., 2015; Nguyen et al., 2018). The Hamaker constants considered in this study range between 10−20J and 10−19J, which are reasonable values for lactose particles (Nguyen et al., 2018)
Table 2.
Physical parameters of the particles used in this study, unless otherwise specified.
| Diameter of carrier particle (μm) | 70 |
| Diameter of API particle (μm) | 2 or 5 |
| Particle density (kg/m3 ) | 1520 |
| Young’s modulus (Pa) | 109 |
| Poisson’s ratio | 0.35 |
| Coefficient of restitution | 0.85 |
| Sliding friction coefficient | 0.45 |
| Rolling friction coefficient | 0.05 |
It is assumed in our study that the actual (“real”) Young’s modulus of both the carrier and API particles is 109Pa, which is based on material properties of lactose particles (Nguyen et al., 2018). It is a common practice to reduce the Young’s modulus in DEM simulations to reduce computational cost. It is known that, in order to avoid falsification of contact dynamics, the models for cohesive interaction (Kobayashi et al., 2013; Gu et al., 2016), tangential contact, and rolling friction (Washino et al., 2018; Chen et al., 2019) must be appropriately adjusted when one introduces artificial softening of the particles. The readers are referred to these papers for the details of these softening corrections. These softening corrections can be done independently of the coarse-graining approach introduced in the paper. We have used the real Young’s modulus in all the simulations and defer the use of softening corrections to future studies.
2.4. Formation of carrier-API agglomerates
A carrier-API agglomerate is formed by uniformly inserting API particles to the region in close vicinity to a carrier particle and then turning on the vdW cohesion force to initiate agglomerate formation. The resultant agglomerate consists of a partial monolayer of API particles on the surface of a carrier particle. Fig. 2 shows typical carrier-API agglomerates formed using this approach. The mass fraction of API particles in the figure is 0.045, which is typical for a carrier-based DPI formulation (Tong et al., 2016; Nguyen et al., 2018), where there are around 130 API particles with a diameter of 5μm or 2000 API particles with a diameter of 2μm per carrier particle.
Fig. 2.
Carrier-API agglomerates formed with one carrier particle with a diameter of 70μm and a) 130 API particles with a diameter of 5μm or b) 2000 API particles with a diameter of 2μm. The mass fraction of API particles is 0.045. API particles are evenly inserted around the carrier particle. Agglomerate formation is achieved by applying cohesion force between the carrier and API particles.
2.5. Inhaler geometry, initial condition and boundary condition
All simulations were done using the screen-haler geometry, which is an experimental model geometry used to study formulation and dispersion properties (van Wachem et al., 2017; Nguyen et al., 2018). This test geometry is adequate for developing general modeling approaches. The dimension of the screen-haler is shown in Fig. 3a.
Fig. 3.
Simulation setup: a) Dimension of the screen-haler used in this study. For the initial condition, a 3.5mg formulation consisting of carrier-API agglomerates is settled as a pile. 99% of the particles are within the initial pile indicated by the red box. b) Inhalation profile: flow rate starts from 0 and increases at a constant rate reaching the peak inspiratory flow rate (PIFR) at . (c) CFD grid in the cross-section of the screen-haler. In the core region, the mesh is nearly Cartesian with grid size close to ( is the carrier particle diamter). There is a wall layer with a thickness of around . The wall layer consists of 8 grids with decreasing grid sizes as they approach the wall.
We load the dose in the inhaler by running a pure DEM simulation, where a specified number of carrier-API agglomerates are randomly inserted in a cylindrical cone region and then allowed to settle down completely. This step is necessary for loading the formulation into the inhaler as a packing. The position of the cylindrical cone is 39mm away from the outlet. At the end of the settling simulation, more than 99% of the agglomerates can be found in the initial pile, as indicated by the region within the red box in Fig. 3a. This procedure resembles previous studies (van Wachem et al., 2017), except that instead of simulating carrier particles, carrier-API agglomerates are simulated in the DEM-only simulation.
Fig. 3b shows the inhalation profile used in this study. The flow rate increases at a constant slope until the peak inspiratory flow rate (PIFR) at time . After , the flow rate remains constant at PIFR. This resembles the inhalation profile used in van Wachem et al. (2017), which is a typical profile based on invitro analyses of nonsmoking healthy adults (Delvadia et al., 2016). For this study, the peak inspiratory flow rates are 70L/min and 40L/min respectively, with .
Fig. 3c shows the CFD grid for the cross-section of the screen-haler. In the core region, the mesh is almost Cartesian with a grid size of close to (where is the carrier particles’ diameter). To better resolve the near-wall region, we refine the near-wall cells by employing a wall layer as shown in Fig. 3c. We chose the thickness of the wall layer and the number of grids in the wall layer based on sensitivity analysis, which we will cover in detail in Section 3.2.
The gas-phase equations are solved using an OpenFOAM-based Computational Fluid Dynamics solver (Userguide, 2013), while the particle phase equations are solved via the LIGGGHTS platform (Kloss et al., 2012). The two-phases are coupled via CFDEMcoupling (Kloss et al., 2012).
3. Results and Discussion
The inhaler efficiency and performance can be determined from fine particle fraction (FPF), which is the fraction of emitted fine particle found in clusters smaller than 5μm. Besides fine particle fraction, we also analyzed dispersion fraction (DF), which is defined as the fraction of API particles detached from carriers (Yang et al., 2014). These two indicators will be used as overall performance metrics to assess the accuracy of the coarse-graining approach. We also examine other qualitative and quantitative metrics as described in this section.
3.1. Microscale tests
We conduct microscale dispersion tests to verify that the representative particle approach yields release behavior consistent with the original case. These tests are DEM-only simulations involving one or two API-carrier agglomerates. Each API-carrier agglomerate is formed as described in Section 2.4. We considered four different types of collisions, as illustrated schematically as well as quantitatively in Fig. 4. Panels a and b show the results corresponding to normal (90°) and oblique (45°) collisions between a carrier-API agglomerate and a flat wall. Panels c and d show the results corresponding to normal (90°) and oblique (45°) collisions between two carrier-API agglomerates.
Fig. 4.
Dispersion fraction (DF) for microscale tests involving 1 or 2 agglomerates, each formed with 1 carrier () and 130 API () (mass fraction of API = 0.045, Hamaker constant ): a) agglomerate-wall impact (90°); b) agglomerate-wall impact (45°); c) agglomerate-agglomerate impact (90°); d) agglomerate-agglomerate impact (45°). Each data point is based on the mean of 10 different tests with varied configurations of API particles on the carrier particle. Error bar shows the standard deviation.
Since van Wachem et al. (2017) suggests collision-induced dispersion is largely affected by the normal component of the impact velocity, we chose the normal component instead of the magnitude of relative impact velocity as the abscissa in Figs. 4(b) and 4(d). The normal component of impact velocity ranges between 0 and 1m/s, where the maximum fine particle fraction (FPF) and dispersion fraction (DF) are around 70%, respectively. As the normal component of impact velocity increases, the variations in FPF and DF will become weaker and approach unity, at which point both DF and FPF are not sensitive to the coarsening factor, . Therefore, calculations of DF and FPF at higher impact velocities are not shown.
For Figs. 4a and 4b, the initial distance between the center of the carrier-API agglomerate and the flat wall was 0.02cm. For Fig. 4c, the initial distance between the centers of two carrier-API agglomerates was 0.04cm. For Fig. 4d, the normal component of the initial distance (same direction as the normal component of impact velocity) between the centers of two carrier-API agglomerates was 0.04cm. Each data point is based on the mean of 10 different tests, with the initial distribution of API particles on the carrier particle’s surface varied. The error bar shows the standard deviation of the 10 tests.
It is clear from Figs. 4a and 4b that the dispersion fraction (DF) resulting from agglomerate-wall collisions is not affected by the coarsening very much. Although there is some variability in the estimated DF with the coarsening factor , the variation is not systematic, and it mostly lies within the range of the standard deviation. We arrive at the same conclusion from Figs. 4c and 4d, illustrating dispersion fractions (DF) resulting from collisions between two agglomerates. The same trend also applies to fine particle fractions (FPFs), which are around 95% of the dispersion fraction for all cases, thus not shown in the Figure. The DF in Figs. 4a and 4b are nearly the same, and so are those in Figs. 4c and 4d. This trend suggests collision-induced dispersion is indeed largely affected by the normal component of impact velocity, which supports the finding of van Wachem et al. (2017).
3.2. Sensitivity Analysis
We conduct sensitivity analyses to probe the effect of wall layer resolution and fluid time step using a 3mg formulation with PIFR = 70L/min (, , mass fraction of API = 0.045, , using the representative particle approach). Table 3 shows the simulation conditions for 5 different cases with different combinations of CFD time steps, wall layer thicknesses and numbers of grids in wall layer. Here we used value, a dimensionless wall distance, to quantify the grid resolution in the near-wall region. value is defined as
| (15) |
where is the friction velocity at the wall, is the distance to the wall, and is the kinematic viscosity of the fluid. Table 3 shows the thickness of the grid nearest to the wall as a multiple of the value at the highest Reynolds number in that simulation.
Table 3.
Sensitivity analysis on CFD time step, wall layer resolution characterized by wall layer thickness (measured in terms of carrier particle diameter, ), number of grids in the wall layer, and the thickness of the grid nearest to the wall as a multiple of the value at the highest Reynolds number in that simulation. Dispersion fraction (DF) and fine particle fraction (FPF) are consistent for the range of conditions considered here.
| Run | CFD time step (s) | Wall layer thickness (as multiple of ) | Number of grids in wall layer | Near-wall grid size as multiple of | DF | FPF |
|---|---|---|---|---|---|---|
| 1 | 1 × 10−5 | 6 | 8 | 1 | 0.350 | 0.295 |
| 2 | 5 × 10−6 | 6 | 8 | 1 | 0.354 | 0.296 |
| 3 | 1 × 10−6 | 6 | 8 | 1 | 0.330 | 0.275 |
| 4 | 1 × 10−5 | 3.5 | 6 | 0.75 | 0.349 | 0.301 |
| 5 | 1 × 10−5 | 3 | 8 | 0.5 | 0.350 | 0.296 |
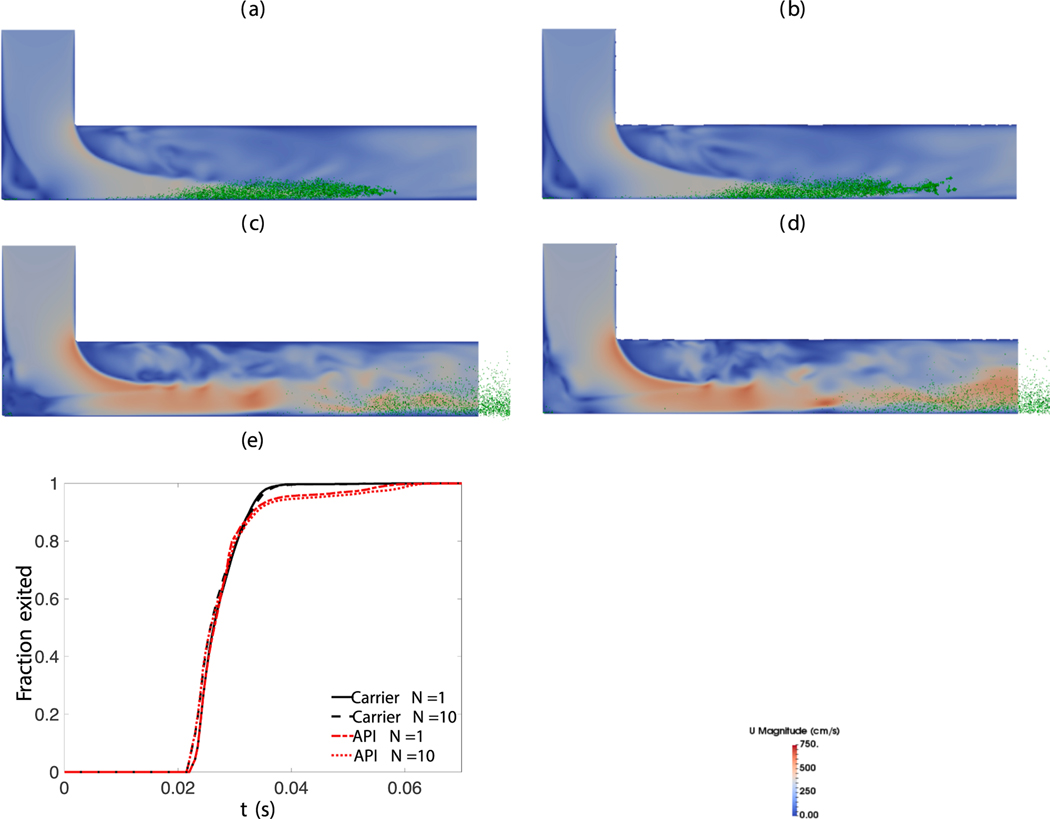
Table 3 shows that fine particle fraction and dispersion fraction remain relatively constant (within ±10% of the FPF/DF value) for runs with different CFD time steps and wall layer resolutions. Fig. 5 shows the gas velocity magnitude (shown by the color code of the two-dimensional cross-section) and carrier particle locations (shown as green points) captured by simulation snapshots at 0.02s, as well as exiting profiles for carrier and API particles. The snapshots provide qualitative guidance that the simulation results are unaffected by the grid and time resolutions. In the snapshots, some carrier particles can be seen in a small region just outside of the exit. Since we only use this region for computing FPF and DF of particles that just exited the domain, we do not simulate the gas phase in this region. We include this region in the DEM simulations to visualize better the region over which the particles exit the inhaler. The exiting profiles lend further quantitative assurance (over and above those shown in Table 3) about the adequacy of the grid resolution and the time step used in the simulations. Therefore, we generate all the simulation results presented in subsequent analyses using a CFD time step of 10−5s, with a wall layer thickness of consisting of 8 grids.
Fig. 5.
Sensitivity analysis: (a)-(e) show two dimensional cross-sectional snapshots of gas phase (shown as colored surface with color code representing gas velocity magnitudes) and carrier particles (locations shown as green points) at 0.02s obtained in Runs 1–5 (see Table 3).The exiting profiles for the carrier and API particles are shown in (f) and (g), respectively.
In the near-wall region, the size of the mesh closest to the wall is smaller than 0.3 . This ensures a value smaller than 0.75, at the highest Re. With such small mesh sizes, unrealistically large fluctuations could arise in solid volume fractions, which may lead to numerical instability. In order to avoid this issue, we have used a mapping scheme when mapping solid volume fraction from DEM data to CFD mesh as described in Radl et al. (2015). This mapping scheme divides the volume of a particle into 29 equal volume regions, each associated with a centroid. The number of centroids in each CFD cell determines how the solid volume of the particle is distributed in different CFD cells. For a mesh size of around 0.3 , this mapping scheme effectively smoothens the solid volume fraction in neighboring CFD cells (Radl et al., 2015).
3.3. Comparing the Discrete Parcel Method and the representative particle approach
The total number of carrier and API particles in a typical DPI application is, as mentioned earlier, very large and some form of coarse-graining is essential to render the simulations affordable. This section compares the Discrete Parcel Method and the representative particle approach using three test examples. The first test problem considers the screen-haler geometry with a 3.5mg formulation with PIFR = 70L/min (, , mass fraction of API = 0.045). The first row in Table 4 shows the numbers of carrier and API particles in a full simulation with no coarse-graining (i.e., coarsening factor ). The other rows show the numbers of carrier and API entities in coarse-grained simulations. The entities in the Discrete Parcel Method are referred to as parcels; the numbers of carrier and API parcels decrease with increasing coarsening factors. In contrast, in the representative particle approach, we simulate the same number of carrier particles irrespective of the extent of coarsening; coarsening only decreases the number of API particles (referred to as the representative API particles) simulated. In this set of test simulations, we chose the Hamaker constant to be 1 × 10−19J for all the materials involved, so that the resultant FPF falls in the range between 20% and 60%, which are typical values measured experimentally (Newman and Busse, 2002; Mitchell et al., 2007; Nguyen et al., 2018). Fig. 6 shows FPF and DF for cases considered in Table 4
Table 4.
Numbers of i) carrier and API parcels in the Discrete Parcel Method approach (parcel) and ii) carrier particles and representative API particles in the representative particle approach (representative) for different coarsening factors. The formulation is 3.5mg. The mass fraction of API particles is 0.045. , .
| Discrete Parcel Method | Representative Particle Approach | ||||
|---|---|---|---|---|---|
|
| |||||
| Coarsening factor | Number of carrier parcels | Number of API parcels | Coarsening factor | Number of carrier particles | Number of representative API particles |
| 1 | 1.3 × 104 | 1.7 × 106 | 1 | 1.3 × 104 | 1.7 × 106 |
| 8 | 1.6 × 103 | 2.1 × 105 | 10 | 1.3 × 104 | 1.7 × 105 |
| 15.625 | 8.3 × 102 | 1.1 × 105 | 18.57 | 1.3 × 104 | 9.1 × 104 |
| 27 | 4.8 × 102 | 6.3 × 104 | 26 | 1.3 × 104 | 6.5 × 104 |
Fig. 6.
a) Fine particle fraction (FPF) and dispersion fraction (DF) for a screen-haler with a 3.5mg formulation and PIFR = 70L/min (, , mass fraction of API = 0.045, Hamaker constant ) predicted using the Discrete Parcel Method (parcel) and the representative particle approach (representative); b) computational cost measured in terms of CPU hours for simulating 0.07s of inhalation, by when most of the particles have left the screen-haler (see Figs. 5f and 5g).
Fig. 6a shows that the FPF and DF are 0.307 and 0.423, respectively, in the full simulation, in which each carrier particle contained 130 API particles initially (without any coarsening). In the Discrete Parcel Method, the DF was found to increase with coarsening factor , while the FPF registered a decrease. In contrast, in the representative particle approach, the DF manifested a non-monotonic dependence on , while the FPF gradually increased with N. The DF and FPF values estimated using both the Discrete Parcel Method and the representative particle approach were within ∼ 10% of those for the full simulation for up to . Fig. 6b shows the computational cost of these simulations. Simulations with cost around 12% of that of the original system. In other words, for this formulation, when the coarsening factor is smaller than 10, both the Discrete Parcel Method and the representative particle approach are able to capture DPI release behavior to within ± 10% of the full simulation result at considerably reduced computational costs.
The increase of FPF with coarsening factor in the representative particle approach can be attributed to the decreasing number of representative API particles in the system. Even though the DFs in coarse-grained cases are comparable to that in the original system, the representative API particles are further apart in simulations with higher coarsening factors, making it harder for them to interact with each other and agglomerate. Therefore, out of the API particles dispersed from carriers, a higher percentage would end up as singlets, leading to higher FPFs in more coarse-grained systems.
The changes of FPF and DF with coarsening factor in the parcel approach are attributed to changes in initial pile structures due to lower numbers of carrier parcels in systems with higher coarsening factors. These changes are discussed below for a second example with smaller API particles.
Table 5 shows the number of entities tracked in the second example involving a 3.5mg formulation consisting of 70μm carrier particles and 2μm API particles using the Discrete Parcel Method and the representative particle approach. While the formulation in the previous example contained 1.7 million particles, the present case consists of more than 26 million particles due to a larger carrier-API size ratio. A large number of particles dramatically increases the cost of computation without coarse-graining. In order to reduce the computational cost, coarsening factors need to be large (more than 100 in this case) to limit the total number of entities tracked in this system. In the Discrete Parcel Method, this would significantly reduce the number of carrier parcels in the simulation, which falsifies the initial pile structure, as shown in Fig. 7. On the other hand, the representative particle approach avoids this issue by conserving the number of carrier particles for all coarsening factors.
Table 5.
Numbers of i) carrier and API parcels in the Discrete Parcel Method and ii) carrier particles and representative API particles in the representative particle approach for different coarsening factors. The formulation is 3.5mg. The mass fraction of API particles is 0.045. , .
| Discrete Parcel Method | Representative Particle Approach | ||||
|---|---|---|---|---|---|
|
| |||||
| Coarsening factor | Number of carrier parcels | Number of API parcels | Coarsening factor | Number of carrier particles | Number of representative API particles |
| 1 | 1.3 × 104 | 2.6 × 107 | 1 | 1.3 × 104 | 2.6 × 107 |
| 100 | 1.3 × 102 | 2.6 × 105 | 100 | 1.3 × 104 | 2.6 × 105 |
| 200 | 65 | 1.3 × 105 | 200 | 1.3 × 104 | 1.3 × 105 |
| 400 | 33 | 6.6 × 104 | 400 | 1.3 × 104 | 6.5 × 104 |
Fig. 7.
Initial piles formed with a 3.5mg formulation (, , mass fraction of API = 0.045, ) for a) the representative particle approach with ; b) the representative particle approach with ; c) the Discrete Parcel Method with and d) the Discrete Parcel Method with .
Fig. 7 compares the initial piles formed using the representative particle approach and the Discrete Parcel Method for two different coarsening factors. As the representative particle approach always involves the same number of carrier particles, the pile’s shape is essentially independent of the coarsening factor. However, this is not the case in the Discrete Parcel Method. Fig. 7 clearly shows that the shape of the initial pile is dramatically affected by coarsening in the Discrete Parcel Method, rendering it unacceptable. Such falsifications of the initial pile structure in the Discrete Parcel Method can be expected to affect subsequent release behavior. Because of the significant changes in the initial pile structure with coarsening, we concluded that the Discrete Parcel Method is unreliable (especially when a large carrier-API size ratio is involved) and decided to focus only on the representative particle approach in this example.
In order to compute the FPF in a system with , we analyzed the fraction of API particles found in released API clusters. Fig. 8a shows that the cluster size distribution did not vary noticeably with coarsening factor values considered. Since FPF is defined as the fraction of segments smaller than 5μm, we assumed that the fraction of API particles in clusters with 15 or fewer API particles is FPF. (The volume of 15.6 particles with a diameter of 2μm is the same as that of one particle with a diameter of 5μm.) This method obviously does not account for the shape of the API clusters; nevertheless, Fig. 8a shows that FPF would be independent of the coarsening factor even if a different cluster size is used to determine the FPF.
Fig. 8.
a) Fraction of API particles which have been dislodged from the carrier particles that exit the inhaler as clusters of different sizes for coarsening factor , 100 and 200; b) Fine particle fraction (FPF), dispersion fraction (DF) and computational cost (measured in terms of CPU hours for simulating 0.07s in screen-haler). 3.5mg formulation and PIFR = 70L/min (, , mass fraction of API = 0.045, ).
Fig. 8a shows that the majority of the API cluster released contains fewer than 10 particles, which is below the 15-particle cluster mentioned above. Fig. 8b shows that there is little difference between FPF and DF. However, lowering further would likely decrease FPF slightly as an increase in the number of the representative particles would increase the likelihood of the formation of API agglomerates. Fig. 6a shows that in the representative particle approach, the difference between DF and FPF decreases with increasing . Fig. 8b shows that the DF is remarkably consistent over a fairly wide range of coarsening factors. As in the previous example, the computational cost decreases appreciably with the degree of coarsening, as shown in Fig. 8b.
For the 5μm API particles considered in the first example (Fig. 6a), the representative particle approach was accurate (to within ∼ 10% error) if was not much larger than 10, while for the 2μm API particles considered in the second example (Fig. 8b) it was found that could be as large as 200 with minimal sacrifice in accuracy. We can rationalize these two different values of using the number of representative API particles per carrier, , included in the simulation. Fig. 9 shows the FPF and DF for both formulations. Even though FPF and DF values vary between the different formulations due to differences in particle size and Hamaker constant, the FPF and DF remain relatively constant when simulations include more than 10 representative API particles per carrier particle. When simulations are performed with , both FPF and DF manifest deviations. Based on this observation, we suggest that one should set in the representative particle approach.
Fig. 9.
Fine particle fraction (FPF) and dispersion fraction (DF) predicted by simulations with different numbers of representative API particles per carrier particle, . Simulations were performed with 3.5mg formulations with PIFR = 70L/min: Case 1: , , mass fraction of API = 0.045, . Case 2: , , mass fraction of API = 0.045, .
Fig. 10a-d show simulation snapshots from the first test example for i) the original system and ii) a coarse-grained system using representative particle approach . Fig. 10e shows the exiting profile for these two cases. It is clear that the dynamics of the coarse-grained system () are essentially the same as that for the original system. The exiting profiles are also comparable between the original and coarse-grained systems using the representative particle approach. The exiting time is around 0.06s for both cases, which is consistent with experimental observation for the screen-haler (Nguyen et al., 2018). This agreement is not surprising because both the original system and the coarsened system simulate the fluid and all the carrier particles, which contribute the most to the overall flow characteristics; furthermore, the coarse-grained simulations do account for all the mass of the API particles, so there is little reason for any difference in overall flow behavior. The majority of the API particles have been released at the initial stage of inhalation that is far before the peak of inhalation velocity, which is a common trend observed in inhalers (Dorosz et al., 2021).
Fig. 10.
Simulation snapshots for the 3.5mg formulation with PIFR = 70L/min (, , mass fraction of API = 0.045, ): a) original system () at 0.01s; b) the representative particle approach () at 0.01s; c) original system () at 0.02s; d) the representative particle approach () at 0.02s; e) fraction of carrier particles and API particles/representative API particles exited the inhaler.
Figs. 11a and 11b show cumulative dispersion fractions (DFs) at different axial distances starting from the initial pile for a 3.5mg formulation (, , mass fraction of API = 0.045, ) with two different peak inspiratory flow rates (PIFR), 70L/min and 40L/min.
Fig. 11.
Cumulative dispersion fraction (DF) for the screen-haler in axial distance from the pile for peak inspiratory flow rate (PIFR) of (a) 70L/min and (b) 40L/min. The last point at 39mm corresponds to DF at the outlet.
Each curve in Figs. 11a and 11b shows the cumulative DFs at different distances from the initial pile obtained from the same DPI simulation. The agglomerates can undergo more collisions and be subject to greater deagglomeration due to the gas phase at larger axial distances, which is indeed revealed by these figures. Since the distance between the initial pile and the outlet in our simulation is 39mm, the last point at 39mm corresponds to DF at the outlet. DF for both PIFRs showed good consistencies between the original case () and the coarse-grained cases using the representative particle approach (, , and ) at every axial position. The same trend also applies to fine particle fractions (FPFs), which are not showed in the Figure. This comparison provides indirect evidence that the representative particle approach can capture the combined effect of dispersion due to multiple collisions and flow-induced dispersion as the particles move downstream.
Because of the extremely large number of API particles in the formulation with a large carrier-API size ratio (, , mass fraction of API = 0.045), the original system in the second example could not be simulated due to excessive computational cost. This led us to consider a third system which had the same carrier-API size ratio as the second example, but a much smaller API loading. Fig. 12 shows the FPF and DF for a 3.5mg formulation with PIFR = 70L/min (, , mass fraction of API = 0.003, ) for cases with different coarsening factors. The FPF and DF for the original case without any coarse-graining are shown at . Compared with original case (FPF = 0.815, DF = 0.823), FPF and DF at coarsening factor , 5 and 10 show good agreement. This shows that the representative particle approach is able to capture the release behavior in the original system for different carrier-API size ratios and API mass fractions. With , the recommendation made earlier about is still met with .
Fig. 12.
Fine particle fraction (FPF) and dispersion fraction (DF) for a 3.5mg formulation with PIFR = 70L/min (, , mass fraction of API = 0.003, ) using the representative particle approach. Both DF and FPF remain relatively constant with respect to coarsening factors.
It is instructive to compare the DF and FPF for the cases shown in Fig. 8 and Fig. 12, which only differed in API loading. In Fig. 8 with an API mass fraction of 0.045, DF and FPF are 0.613 and 0.608, respectively (for ). When the mass fraction of API is lowered to 0.003 in Fig. 12, DF and FPF increase slightly to 0.823 and 0.815. This observation is directionally consistent with experimental observations in Tong et al. (2016).
3.4. Effect of wall cohesion
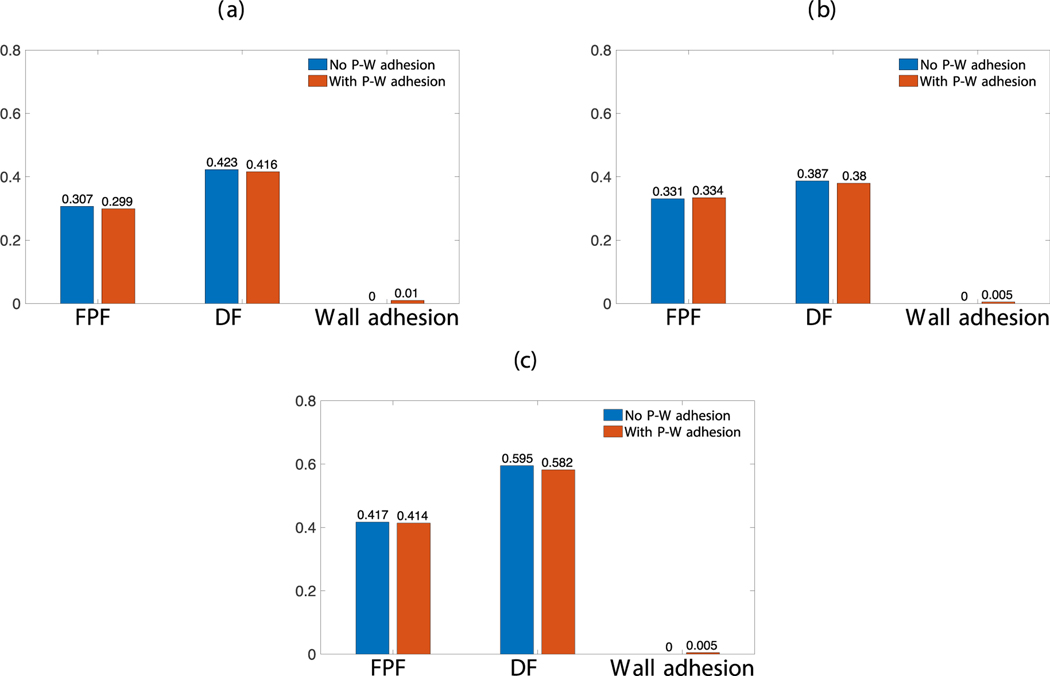
In the results reported in the previous sections, the particle-wall (P-W) adhesive interaction was turned off. In this subsection, simulations were conducted with this interaction turned on to probe its effect on API release and wall-deposition behavior. Fig. 13 illustrates the effect of turning on P-W adhesion in the two different formulations. Fig. 13a and Fig. 13b correspond to a formulation with , , mass fraction of API = 0.045, . The P-W adhesion did not affect the FPF and DF appreciably, trapping about 1% of the API particles in the full simulation (Fig. 13a) and 0.5% in the coarse-grained () simulation (Fig. 13b). Fig. 13c corresponds to a formulation with , , mass fraction of API = 0.045, (), which led to the same conclusion as well.
Fig. 13.
Fine particle fraction (FPF), dispersion fraction (DF) and fraction of API particle attached to wall for a 3.5mg formulation with PIFR = 70L/min. (a) and (b) correspond to , , mass fraction of API = 0.045, . (a) full simulation (); b) coarse-grained simulation with . (c) corresponds to , , mass fraction of API = 0.045, , . Hamaker constants between the carrier and API particles and wall were taken to be the same as those between every particle pair.
It is clear from Fig. 13 that with a reasonable choice of Hamaker constant value for P-W interaction, the amount of wall adhesion is almost negligible and does not affect the general release behavior. Admittedly, a better model for capturing wall adhesion should also include corrections for gas-particle interactions in the near-wall region (Jin et al., 2016), or even electrostatic interactions between particles and the wall (Song and Mehrani, 2017; Sippola et al., 2018). We will defer these to future studies.
3.5. Effect of API particle size and cohesive strength
In this subsection, we examine how the API particle size and cohesive characteristics affect the release behavior of a 3.5mg formulation with PIFR = 70L/min (, mass fraction of API = 0.045). We conducted several cases with different combinations of API particle sizes (), minimum separation distance used in van der Waals’ force calculation, (s), API particle densities (), and gas velocity ramp rates in the initial inhalation profiles () for a range of Hamaker constant values. Table 6 summarizes these simulation groups.
Table 6.
Simulation parameters for probing the effect of API particle size (), minimum separation distance used in van der Waals’ force calculation (), API particle density (), and gas velocity ramp rate in the initial inhalation profiles () on fine particle fraction (FPF) and dispersion fraction (DF). In each group, simulations were conducted using a number of different Hamaker constant values.
| Group | (μm) | (nm) | (kg/m3) | (m/s2) |
|---|---|---|---|---|
| 1 | 2 | 1.0 | 1520 | 150 |
| 2 | 5 | 1.0 | 1520 | 150 |
| 3 | 5 | 0.5 | 1520 | 150 |
| 4 | 5 | 1.0 | 912 | 150 |
| 5 | 5 | 1.0 | 1520 | 75 |
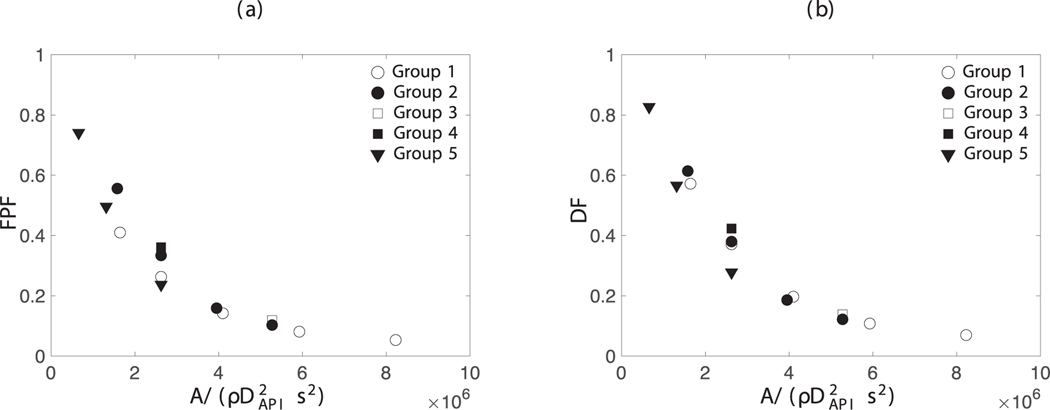
Fig. 14 shows that we can collapse both DF and FPF in various cases reasonably well onto a single curve if using as the abscissa, where is the Hamaker constant used for calculating cohesive force magnitude in Eq. 10. Note that the maximum cohesive force between an API particle and a very large carrier particle at contact scales as ; then the maximum cohesive force at contact per unit mass of API particle scales as .
Fig. 14.
a) Fine particle fraction (FPF) and b) dispersion fraction (DF) for a 3.5mg formulation with PIFR = 70L/min (, mass fraction API = 0.045). Simulation parameters in each group are summarized in Table 6.
The abscissa in this figure, , has a dimension of . It then raised a question as to whether one can identify an appropriate acceleration to render the abscissa dimensionless. Dimensional analysis suggests the gas velocity ramp rate and the gravitational acceleration . Unfortunately, neither one proved to be an appropriate choice. Simulations performed by changing or by a factor of two did not support using either one as the reference acceleration to render the abscissa in Fig. 14 dimensionless.
The extent of deagglomeration depends on many different factors, including strength and frequency of carrier-carrier and carrier-wall collisions, gas turbulence, and residence time in the inhaler, making it hard for a single dimensionless group to capture such a complicated phenomenon based on dimensional analysis. Thus, we do not pursue the search for a dimensionless group that captures deagglomeration behavior in this study. Nevertheless, it is an interesting and useful finding that deagglomeration behavior indicated by DF and FPF in the screen-haler can be captured by a dimensional ratio of the maximum carrier-API cohesive force and the API particle mass. There are recent indications that inter-particle forces arising from different mechanisms are additive in particulate flows (Vo et al., 2020). Suppose several different inter-particle forces, such as van der Waals’ forces, liquid-bridge forces due to humidity effects, and electrostatic forces, are present in a DPI system. In that case, the abscissa in Fig. 14 can be replaced (at least as a first approximation) as the sum of all contributions to the inter-particle force per unit mass of the API particle, which can be used as guidance for choosing particle size and carrier particle material (thus inter-particle interaction characteristics). This suggestion should be verified in future studies.
4. Conclusions
Drug delivery via dry powder inhaler is a complex process affected by the mechanics of both gas and particle phases. A carrier-based formulation’s performance depends on how well the API particles are released, which are typically characterized by the FPF and DF. Gas-phase turbulence, gas-particle interaction, particle-particle interactions, and particle-wall interactions play important roles in the deagglomeration of carrier-API agglomerates. The CFD-DEM approach offers the potential to probe the effects of these interactions. A CFD-DEM simulation that tracks all the carrier and API particles is computationally costly, and hence researchers have sought simplifications. The least expensive CFD-DEM computations of DPI flow track only the carrier particles via DEM and treat the API particles as passive continuum scalars (Cui et al., 2014; Tong et al., 2015; van Wachem et al., 2017). This approach employs micro-scale simulations to develop the constitutive models required for the continuum equation for the API particles.
In the present study, we have assessed the efficacy of two coarse-grained CFD-DEM approaches, which do not require the above-mentioned micro-scale continuum model development. One of these approaches is the Discrete Parcel Method (Bierwisch et al., 2009; Radl and Sundaresan, 2014; Washino et al., 2018; Tausendschön et al., 2020 ) where both the API and carrier particles are coarsened into parcels. In the second approach, referred to as the representative particle approach, one simulates all the carrier particles (as in the least expensive approach mentioned above) and a subset of the API particles (instead of treating them through a continuum scalar). Towards this end, we first assessed model accuracy of the representative particle approach using agglomerate-wall and agglomerate-agglomerate collision tests. We then performed full simulations of all the carrier particles and API particles in some model problems using the screen-haler geometry of the DPI. We performed coarse-grained simulations using both approaches. As one would expect, the computational cost associated with both approaches decreases dramatically with the increasing extent of coarsening.
Both approaches are viable in the first example considered, which had a carrier-API size ratio of 14 when only a modest degree of coarsening was needed. When this ratio was 35, a much greater level of coarsening was necessary to bring the computational cost to affordable levels, which led the parcel approach to yield unrealistic initial pile geometries as shown in Fig. 7. As a result, we recommend the representative particle approach as the more desirable among these two approaches. Our simulations reveal that the representative particle approach approximates the results of the full simulation when there are at least 10 representative API particles included in the simulation per carrier particle (e.g., see Fig. 9).
We then performed a number of simulations using the representative particle approach for several different combinations of particle characteristics and gas velocity ramp rate. We found that DF and FPF obtained in these simulations can be correlated with the maximum carrier-API cohesive force per unit mass of the API particles (Fig. 14). Fig. 14 is clearly limited to the screen-haler geometry considered in this study and the specific mass loading of carrier and API particles. It would be interesting to see if such collapse emerges in other DPI geometries (where each geometry will correspond to a different curve) and other carrier particle sizes and mass loading. Such a parametric investigation could also reveal how the cohesive acceleration used as abscissa in Fig. 14 can be properly non-dimensionalized.
All the work has been done in a simple screen-haler geometry and it would be interesting to explore the performance characteristics of commercial devices using this representative particle approach. It would be interesting to expand the representative particle approach to other inter-particle forces such as electrostatic interaction, other types of adhesion, and liquid-bridge force between particles. It has been suggested that different inter-particle forces are additive in particulate flows (Vo et al., 2020). This suggestion raises a question as to whether other inter-particle interactions can be lumped into this cohesive acceleration in the overall analysis of the DPI performance, which would be both interesting and useful to probe.
Acknowledgements
Financial assistance for the project by the U.S. Food and Drug Administration (FDA) (Grant 1U01FD006514) is gratefully acknowledged. We gratefully acknowledge the many valuable suggestions and critiques made by Ross Walenga from the Office of Generic Drugs and Maziar Kakhi from the Office of Pharmaceutical Quality at the US FDA during the course of this study. One of us (Sankaran Sundaresan) gratefully acknowledges the inspiration and financial support provided by the William R. and Jane G. Schowalter Research Fund and his former PhD student Sanjay Dasgupta.
Footnotes
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Alexopoulos A, Milenkovic J, Kiparissides C, An integrated computational model of powder release, dispersion, breakage, and deposition in a dry powder inhaler, in: Computer Aided Chemical Engineering, volume 32, Elsevier, 2013, pp. 139–144. [Google Scholar]
- Ariane M, Sommerfeld M, Alexiadis A, 2018. Wall collision and drug-carrier detachment in dry powder inhalers: using dem to devise a sub-scale model for cfd calculations. Powder Technol. 334, 65–75. [Google Scholar]
- Atkins PJ, 2005. Dry powder inhalers: an overview. Respiratory care 50, 1304–1312. [PubMed] [Google Scholar]
- Bass K, Farkas D, Hassan A, Bonasera S, Hindle M, Longest W, 2020. High-efficiency dry powder aerosol delivery to children: Review and application of new technologies. J. Aerosol Sci. 105692. [DOI] [PMC free article] [PubMed]
- Begat P, Morton DA, Staniforth JN, Price R, 2004. The cohesive-adhesive balances in dry powder inhaler formulations i: direct quantification by atomic force microscopy. Pharmaceutical research 21, 1591–1597. [DOI] [PubMed] [Google Scholar]
- Bierwisch C, Kraft T, Riedel H, Moseler M, 2009. Die filling optimization using three-dimensional discrete element modeling. Powder technology 196, 169–179. [Google Scholar]
- Bisgaard H, O’Callaghan C, Smaldone GC, 2001. Drug delivery to the lung. CRC Press. [Google Scholar]
- Chan H-K, 2006. Dry powder aerosol delivery systems: current and future research directions. Journal of aerosol medicine 19, 21–27. [DOI] [PubMed] [Google Scholar]
- Chen S, Liu W, Li S, 2019. A fast adhesive discrete element method for random packings of fine particles. Chem. Eng. Sci. 193, 336–345. [Google Scholar]
- Coates MS, Chan H-K, Fletcher DF, Raper JA, 2005. Influence of air flow on the performance of a dry powder inhaler using computational and experimental analyses. Pharmaceutical research 22, 1445–1453. [DOI] [PubMed] [Google Scholar]
- Cui Y, Schmalfuß S, Zellnitz S, Sommerfeld M, Urbanetz N, 2014. Towards the optimisation and adaptation of dry powder inhalers. International journal of pharmaceutics 470, 120–132. [DOI] [PubMed] [Google Scholar]
- Cundall PA, Strack OD, 1979. A discrete numerical model for granular assemblies. geotechnique 29, 47–65. [Google Scholar]
- Daniher DI, Zhu J, 2008. Dry powder platform for pulmonary drug delivery. Particuology 6, 225–238. [Google Scholar]
- Delvadia RR, Wei X, Longest PW, Venitz J, Byron PR, 2016. In vitro tests for aerosol deposition. iv: Simulating variations in human breath profiles for realistic dpi testing. Journal of aerosol medicine and pulmonary drug delivery 29, 196–206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Donovan MJ, Smyth HD, 2010. Influence of size and surface roughness of large lactose carrier particles in dry powder inhaler formulations. International journal of pharmaceutics 402, 1–9. [DOI] [PubMed] [Google Scholar]
- Donovan MJ, Kim SH, Raman V, Smyth HD, 2012. Dry powder inhaler device influence on carrier particle performance. Journal of pharmaceutical sciences 101, 1097–1107. [DOI] [PubMed] [Google Scholar]
- Dorosz A, Żaczek M, Moskal A, 2021. Dynamics of aerosol generation and release–dry powder inhaler performance considerations. J. Aerosol Sci. 151, 105673. [Google Scholar]
- French DL, Edwards DA, Niven RW, 1996. The influence of formulation on emission, deaggregation and deposition of dry powders for inhalation. J. Aerosol Sci. 27, 769–783. [Google Scholar]
- Galvin JE, Benyahia S, 2014. The effect of cohesive forces on the fluidization of aeratable powders. AIChE J. 60, 473–484. [Google Scholar]
- Germano M, Piomelli U, Moin P, Cabot WH, 1991. A dynamic subgrid-scale eddy viscosity model. Phys. Fluids A 3, 1760–1765. [Google Scholar]
- Gu Y, Ozel A, Sundaresan S, 2016. A modified cohesion model for cfd–dem simulations of fluidization. Powder Technol. 296, 17–28. [Google Scholar]
- Hamaker H, 1937. The london–van der waals attraction between spherical particles. physica 4, 1058–1072. [Google Scholar]
- Ilie M, Matida E, Finlay W, 2008. Asymmetrical aerosol deposition in an idealized mouth with a dpi mouthpiece inlet. Aerosol Sci. Technol. 42, 10–17. [Google Scholar]
- Islam N, Gladki E, 2008. Dry powder inhalers (dpis)–a review of device reliability and innovation. International journal of pharmaceutics 360, 1–11. [DOI] [PubMed] [Google Scholar]
- Jin C, Potts I, Reeks M, 2016. The effects of near wall corrections to hydrodynamic forces on particle deposition and transport in vertical turbulent boundary layers. Int. J. Multiph. Flow 79, 62–73. [Google Scholar]
- Kannan RR, Przekwas A, Singh N, Delvadia R, Tian G, Walenga R, 2017. Pharmaceutical aerosols deposition patterns from a dry powder inhaler: Euler lagrangian prediction and validation. Medical engineering & physics 42, 35–47. [DOI] [PubMed] [Google Scholar]
- Kloss C, Goniva C, Hager A, Amberger S, Pirker S, 2012. Models, algorithms and validation for opensource dem and cfd–dem. Progress in Computational Fluid Dynamics, an International Journal 12, 140–152. [Google Scholar]
- Kobayashi T, Tanaka T, Shimada N, Kawaguchi T, 2013. Dem–cfd analysis of fluidization behavior of geldart group a particles using a dynamic adhesion force model. Powder technology 248, 143–152. [Google Scholar]
- Lee SL, Adams WP, Li BV, Conner DP, Chowdhury BA, Lawrence XY, 2009. In vitro considerations to support bioequivalence of locally acting drugs in dry powder inhalers for lung diseases. The AAPS journal 11, 414–423. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lilly DK, 1992. A proposed modification of the germano subgrid-scale closure method. Phys. Fluids A 4, 633–635. [Google Scholar]
- Mallouppas G, van Wachem B, 2013. Large eddy simulations of turbulent particle-laden channel flow. Int. J. Multiph. Flow 54, 65–75. [Google Scholar]
- Mitchell J, Newman S, Chan H-K, 2007. In vitro and in vivo aspects of cascade impactor tests and inhaler performance: a review. Aaps Pharmscitech 8, 237–248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Moreno-Atanasio R, Ghadiri M, 2006. Mechanistic analysis and computer simulation of impact breakage of agglomerates: effect of surface energy. Chemical engineering science 61, 2476–2481. [Google Scholar]
- Moreno R, Ghadiri M, Antony S, 2003. Effect of the impact angle on the breakage of agglomerates: a numerical study using dem. Powder Technol. 130, 132–137. [Google Scholar]
- Newman S, Busse W, 2002. Evolution of dry powder inhaler design, formulation, and performance. Respiratory medicine 96, 293–304. [DOI] [PubMed] [Google Scholar]
- Nguyen D, Rasmuson A, Thalberg K, Bjo IN, et al. , 2014. Numerical modelling of breakage and adhesion of loose fine-particle agglomerates. Chem. Eng. Sci. 116, 91–98. [Google Scholar]
- Nguyen D, Remmelgas J, Bjorn IN, van Wachem B, Thalberg K, 2018. Towards quantitative prediction of the performance of dry powder inhalers by multi-scale simulations and experiments. International journal of pharmaceutics 547, 31–43. [DOI] [PubMed] [Google Scholar]
- Peng T, Lin S, Niu B, Wang X, Huang Y, Zhang X, Li G, Pan X, Wu C, 2016. Influence of physical properties of carrier on the performance of dry powder inhalers. Acta pharmaceutica sinica B 6, 308–318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pope S, 2000. Turbulent Flows, 6th ed. Cambridge University Press, Cambridge. [Google Scholar]
- Radl S, Sundaresan S, 2014. A drag model for filtered euler–lagrange simulations of clustered gas–particle suspensions. Chem. Eng. Sci. 117, 416–425. [Google Scholar]
- Radl S, Gonzales BC, Goniva C, Pirker S, State of the art in mapping schemes for dilute and dense euler-lagrange simulations (2015).
- Ruzycki CA, Javaheri E, Finlay WH, 2013. The use of computational fluid dynamics in inhaler design. Expert opinion on drug delivery 10, 307–323. [DOI] [PubMed] [Google Scholar]
- Sagaut P, Germano M, 2005. On the filtering paradigm for les of flows with discontinuities. J. Turbul. N23.
- Sippola P, Kolehmainen J, Ozel A, Liu X, Saarenrinne P, Sundaresan S, 2018. Experimental and numerical study of wall layer development in a tribocharged fluidized bed. J. Fluid Mech. 849, 860–884. [Google Scholar]
- Smyth HD, Hickey AJ, 2005. Carriers in drug powder delivery. American journal of drug delivery 3, 117–132. [Google Scholar]
- Sommerfeld M, Schmalfuß S, 2016. Numerical analysis of carrier particle motion in a dry powder inhaler. J. Fluids Eng. 138. [Google Scholar]
- Sommerfeld M, Cui Y, Schmalfuß S, 2019. Potential and constraints for the application of cfd combined with lagrangian particle tracking to dry powder inhalers. Eur. J. Pharm. Sci. 128, 299–324. [DOI] [PubMed] [Google Scholar]
- Song D, Mehrani P, 2017. Mechanism of particle build-up on gas-solid fluidization column wall due to electrostatic charge generation. Powder technology 316, 166–170. [Google Scholar]
- Tausendschön J, Kolehmainen J, Sundaresan S, Radl S, 2020. Coarse graining euler-lagrange simulations of cohesive particle fluidization. Powder Technol. 364, 167–182. [Google Scholar]
- Telko MJ, Hickey AJ, 2005. Dry powder inhaler formulation. Respiratory care 50, 1209–1227. [PubMed] [Google Scholar]
- Thornton C, Liu L, 2004. How do agglomerates break? Powder Technol. 143, 110–116. [Google Scholar]
- Thornton C, Ciomocos M, Adams M, 1999. Numerical simulations of agglomerate impact breakage. Powder Technol. 105, 74–82. [Google Scholar]
- Timsina M, Martin G, Marriott C, Ganderton D, Yianneskis M, 1994. Drug delivery to the respiratory tract using dry powder inhalers. International journal of pharmaceutics 101, 1–13. [Google Scholar]
- Tong Z, Yang R, Chu K, Yu A, Adi S, Chan H-K, 2010. Numerical study of the effects of particle size and polydispersity on the agglomerate dispersion in a cyclonic flow. Chem. Eng. J. 164, 432–441. [Google Scholar]
- Tong Z, Kamiya H, Yu A, Chan H-K, Yang R, 2015. Multi-scale modelling of powder dispersion in a carrier-based inhalation system. Pharmaceutical research 32, 2086–2096. [DOI] [PubMed] [Google Scholar]
- Tong Z, Zhong W, Yu A, 2016. Cfd-dem study the effect of carrier-drug mass ratio on the aerosolisation process in original and modified dry powder inhalers. In: International Conference on Discrete Element Methods. Springer, pp. 957–965. [Google Scholar]
- Tsuji Y, Kawaguchi T, Tanaka T, 1993. Discrete particle simulation of two-dimensional fluidized bed. Powder technology 77, 79–87. [Google Scholar]
- Userguide O, Version 2.2. 2, 2013.
- van Wachem B, Thalberg K, Remmelgas J, Niklasson-Björn I, 2017. Simulation of dry powder inhalers: combining micro-scale, meso-scale and macro-scale modeling. AIChE J. 63, 501–516. [Google Scholar]
- Vo TT, Nezamabadi S, Mutabaruka P, Delenne J-Y, Radjai F, 2020. Additive rheology of complex granular flows. Nature communications 11, 1–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Washino K, Chan EL, Tanaka T, 2018. Dem with attraction forces using reduced particle stiffness. Powder Technol. 325, 202–208. [Google Scholar]
- Wong W, Fletcher DF, Traini D, Chan H-K, Young PM, 2012. The use of computational approaches in inhaler development. Advanced drug delivery reviews 64, 312–322. [DOI] [PubMed] [Google Scholar]
- Yang J, Wu C-Y, Adams M, 2014. Three-dimensional dem–cfd analysis of air-flow-induced detachment of api particles from carrier particles in dry powder inhalers. Acta Pharmaceutica Sinica B 4, 52–59. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J, Wu C-Y, Adams M, 2015. Numerical modelling of agglomeration and deagglomeration in dry powder inhalers: a review. Current pharmaceutical design 21, 5915–5922. [DOI] [PubMed] [Google Scholar]
- Yu J, Wong J, Ukkonen A, Kannosto J, Chan H-K, 2017. Effect of relative humidity on bipolar electrostatic charge profiles of dry powder aerosols. Pharmaceutical research 34, 1707–1715. [DOI] [PubMed] [Google Scholar]
- Zellnitz S, Pinto J, Brunsteiner M, Schröttner H, Khinast J, Paudel A, 2019. Tribocharging behaviour of inhalable mannitol blends with salbutamol sulphate. Pharmaceutical research 36, 1–11. [DOI] [PMC free article] [PubMed] [Google Scholar]