Abstract
The dose/exposure‐efficacy analyses are often conducted separately for oncology end points like best overall response, progression‐free survival (PFS) and overall survival (OS). Multistate models offer to bridge these dose‐end point relationships by describing transitions and transition times from enrollment to response, progression, and death, and evaluating transition‐specific dose effects. This study aims to apply the multistate pharmacometric modeling and simulation framework in a dose optimization setting of bintrafusp alfa, a fusion protein targeting TGF‐β and PD‐L1. A multistate model with six states (stable disease [SD], response, progression, unknown, dropout, and death) was developed to describe the totality of endpoints data (time to response, PFS, and OS) of 80 patients with non‐small cell lung cancer receiving 500 or 1200 mg of bintrafusp alfa. Besides dose, evaluated predictor of transitions include time, demographics, premedication, disease factors, individual clearance derived from a pharmacokinetic model, and tumor dynamic metrics observed or derived from tumor size model. We found that probabilities of progression and death upon progression decreased over time since enrollment. Patients with metastasis at baseline had a higher probability to progress than patients without metastasis had. Despite dose failed to be statistically significant for any individual transition, the combined effect quantified through a model with dose‐specific transition estimates was still informative. Simulations predicted a 69.2% probability of at least 1 month longer, and, 55.6% probability of at least 2‐months longer median OS from the 1200 mg compared to the 500 mg dose, supporting the selection of 1200 mg for future studies.
Study Highlights.
WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?
The associations between dose/exposure and oncology end points like overall response rate, progression‐free survival, and overall survival (OS) are typically analyzed independently from each other.
WHAT QUESTION DID THIS STUDY ADDRESS?
Multistate models naturally connect multiple clinical end points by describing the transitions and transition times from enrollment to response, progression, and death. This study explored a scenario where transition‐specific dose effects were evaluated and jointly informed the probability of achieving clinically meaningful separations of OS between two dose levels.
WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?
Trends of relatively higher probability of response, as well as lower probability of progression and death upon progression was found in patients receiving 1200 mg versus 500 mg bintrafusp alfa. Simulations indicated a ~70% probability of clinically meaningful OS improvement from the higher tested dose compared to the lower dose.
HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?
This analysis show‐cased multistate model as a powerful tool in oncology dose‐optimization setting, and potential opportunities for cross end point bridging, patient selection for individualized therapy, and real‐time predictions of state change.
INTRODUCTION
Project Optimus, driven by the US Food and Drug administration (FDA), emphasizes the importance of a good understanding of the dose/exposure‐response relationship during the early development of anticancer drugs. 1 The associations between dose/exposure and efficacy for end points like best overall response (BOR), progression‐free survival (PFS), and overall survival (OS) are most of the times estimated separately using logistic regression for BOR and Cox proportional hazards models for PFS and OS. However, these classic analyses suffer from static and compartmentalized views. In particular, logistic regression analysis for BOR overlooks longitudinal information, such as the time to response, duration of response, and time of progression, which hinders its connection to patient clinical benefit in PFS and OS. Similarly, it is difficult to link dose effect on PFS to OS when estimated separately. The potential inconsistencies in the results make it challenging to gain a reliable and integrated understanding of the underlying dose/exposure‐efficacy relationship. 2
To overcome these limitations, this study used a multistate model, which describes the transitions and transition times from enrollment to response, progression, and death. This approach naturally integrates multiple clinical end points within one modeling framework, leveraging the totality of longitudinal clinical outcome data (time to response, PFS, and OS). 3 , 4 Moreover, the assumption of proportionality in the Cox model for OS analysis, where the hazard ratio of death between doses remains constant overtime, may not hold true. This could lead to biased estimates of dose/exposure effects, as intermediate events of response and progression can substantially change the risk of death and associated drug effects. With a multistate model, transition‐specific drug effects can be investigated, providing a granular evaluation of dose/exposure–efficacy relationships. Such an approach enables the derivation and comparison of expected patient benefits from different dose levels via simulations in support of dose‐optimization decisions.
Another problem encountered in oncology exposure‐response analyses is immortal time bias, which arises when relating predictors measured post‐baseline to time‐to‐event end points. 5 Examples of such predictors include drug clearance and exposure, or maximal reduction of a biomarker like tumor size. The multistate modeling framework protected the reliability of conclusion from immortal time bias by testing predictors in a prospective manner: only information before a state observation was used to predict the transition out of the state or staying within the same state at the next observation(s). An application example was published by Krishnan et al., 4 where the past change in tumor size from baseline derived from a longitudinal tumor growth inhibition (TGI) model was used to forecast the transition from SD to response.
Bintrafusp alfa is an investigational first‐in‐class bifunctional fusion protein with a molecular structure composed of the extracellular domain of the TGF‐βRII receptor designed to function as a transforming growth factor beta (TGF‐β) “trap” fused to a human IgG1 antibody blocking programmed death‐ligand 1 (PD‐L1). Two randomized doses (500 mg vs. 1200 mg) were tested in an expansion cohort of a phase I study, which enrolled 80 patients with non‐small cell lung cancer (NSCLC) receiving monotherapy bintrafusp alfa as second‐line (2 L) treatment. 6 A previous analysis found that initial bintrafusp alfa clearance had a inversed correlation with efficacy (BOR/PFS). 7 This trend has also been observed for multiple approved PD‐1/PDL‐1 inhibitors, 8 , 9 , 10 for which clearance was found to decrease over time with extent inversely correlated with treatment response. 11 , 12 , 13 A potential explanation is that clearance is affected by the underlying physiological state that parallels the disease severity. 14 For example, patients with cancer cachexia suffer from a negative energy balance with high proteolytic clearance, and have reduced treatment benefit and/or shorter survival. 15 , 16 These phenomena makes clearance a potential predictor of tumor response and survival, and at the same time challenges the evaluation of causal exposure‐efficacy relationship. 11 , 14 , 17 The apparent concentration‐response relationship would be a combination of the causal concentration‐response relationship and the clearance‐response relationship, making its interpretation very challenging. Therefore, dose instead of concentration was tested as predictor of efficacy in this analysis.
The objectives of this analysis were to develop a multistate modeling and simulation framework to describe the phase I clinical end points data originating from the above‐described study of two randomized doses in patients with NSCLC, and to evaluate potential dose‐efficacy relationship. Besides dose, evaluated predictors of multistate transition rates include: (i) time, (ii) baseline covariates, (iii) individual systemic clearance (CL) derived from a population pharmacokinetic (PK) model, and (iv) observed and derived tumor dynamic metrics from a TGI model.
MATERIALS AND METHODS
Patients and data
The 2L NSCLC expansion cohort of the phase I trial (ClinicalTrials.gov Identifier: NCT02517398) enrolled patients (n = 80) with advanced NSCLC, randomized 1:1 to receive 500 or 1200 mg of bintrafusp alfa every 2 weeks until investigator‐assessed disease progression, unacceptable toxicity, or trial withdrawal. The trial was conducted following the International Good Clinical Practice Standards consistent with the International Conference on Harmonization (ICH) Topic E6 GCP and the Declaration of Helsinki. Informed consent was retrieved from all patients.
The PK sampling schedule is provided in Table S1. Tumor evaluations were scheduled at screening (baseline), during treatment (every 6 weeks in the first year and thereafter every 12 weeks), and at post‐treatment follow‐ups. Tumor lesion sizes and response categories were determined by the local investigator, followed by an Independent Endpoint Review Committee (IRC), according to Response Evaluation Criteria in Solid Tumors (RECIST) version 1.1. 18 Once progressive disease (PD) was observed for one patient, following observation of SD or response were treated as continued progression.
Baseline covariates prespecified for analysis included age, body weight, race, sex, smoking, Eastern Cooperative Oncology Group (ECOG) status, metastases, liver metastases, CRP, LDH, neutrophil‐to‐lymphocyte ratio, PD‐L1 expression in tumor cells, TGF‐β1 plasma concentration, number of nontarget lesions, histology, previous medication with biologics and previous medication with antibiotics, and concomitant corticosteroids.
Development of PK and TGI model
For details refer to the Appendix S1. In summary, a published PK model 19 was adapted to describe the plasma concentrations of bintrafusp alfa available from the 2L NSCLC expansion cohort. The potential time‐varying CL was evaluated by testing the empirical model of CL change over time 20 or by including observed tumor size as time‐varying covariate. The longitudinal measurements of tumor size (sum of longest diameters [SLD] of target lesions per IRC) were described by the TGI model. 21 Subsequent covariate analysis explored dose, CL, and baseline covariates in explaining the interindividual variability of TGI model parameters.
Development of the multistate model
The developed model consisted of six states informed by tumor response and survival data. The longitudinal intermediate state observations were derived from the repeated measurements of overall tumor response per IRC according to RECIST 1.1 criteria:
: Stable disease (SD: stable disease)
: Response (PR: partial response or CR: complete response)
: Progression (PD: progressive disease)
: Unknown (treatment and tumor evaluation were terminated without preceding PD documented, thus the current state of tumor response remains unknown).
The observations of absorbing states were derived from the survival data:
: Dropout (lost to follow‐up for survival but not right‐censored nor have died during the observed study period)
: Death
The derived multistate observations from representative patients are shown in Figure 1a. The state and transition diagram are shown in Figure 1b. The states were modeled as compartments with the amount being the probability of occupying the state. All patients were assumed to be in SD () at treatment initiation, and therefore an amount (or probability) of 1 was given to at time 0. This probability was then distributed across the six states following the differential Equations (1), (2), (3), (4), (5), (6). The sum of probabilities equals to 1 at any timepoint (Equation 7). After each observation, the probabilities of all states were reset to zero, and a probability of 1 was given to the observed state. Example NONMEM code and dataset are included in the Appendix S2.
FIGURE 1.
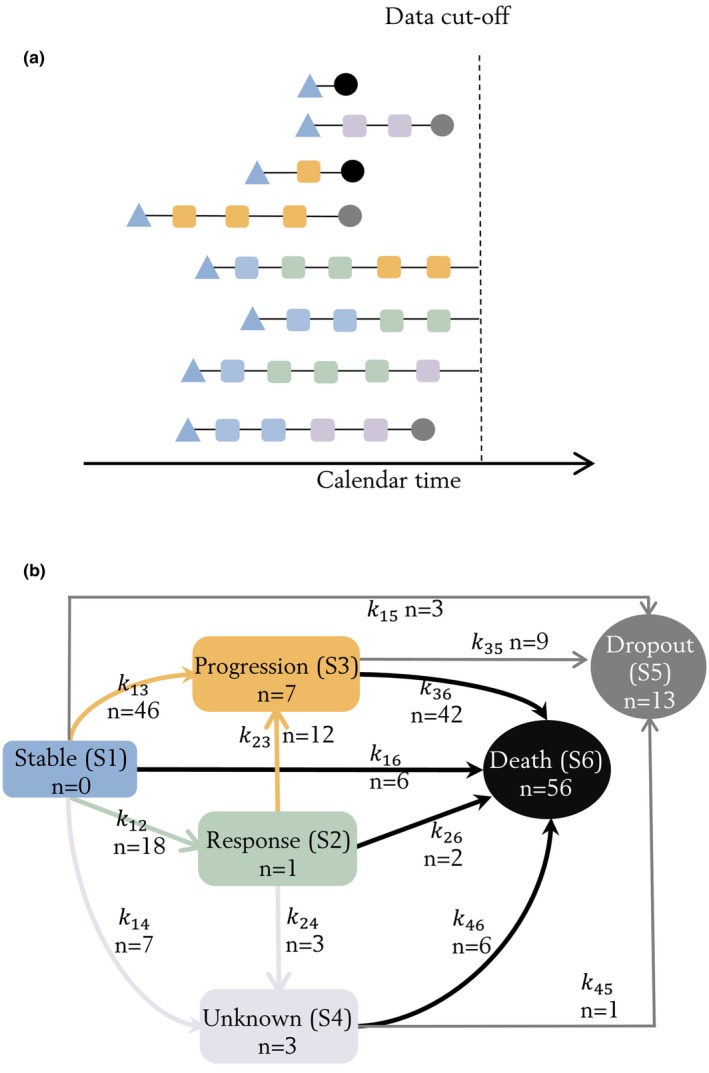
Multistate observations demonstrated with example patients (a). The blue triangles represent the initial state of stable disease (SD) at treatment initiation. The triangle shape indicated that the state of patient was assumed to be SD at first dose administration, as tumor assessment was conducted at screening before the initiation of treatment. The squares represent states observed from repeated overall tumor response evaluations (once every 6 weeks): blue state observations were stable disease (SD); green response state observations were partial response (PR) or complete response (CR); yellow progression state observations were progressive disease (PD); pink unknown state observations (pink) were imputed if the tumor evaluation was terminated without preceding PD documented. The circles represent absorbing states observed as survival events: gray dropout states were observed at the date of last date known to be alive; black death states were observed at the date of death. State and transition diagram (b). Each compartment is a state and the arrows are observed transitions between states. All patients were assumed to have SD (S 1) at treatment initiation (time = 0), and could stay stable (S 1), respond (S 2) or progress (S 3). Patients with response (S 2) could stay in response (S 2) or progress (S 3). State of patients who discontinued treatment without progression (S 1/S 2) would transit to unknown (S 4). If survived pass the data cutoff date, patients could be censored at the intermediate states (S 1/S 2/S 3/S 4). Patients would transit to the absorbing states if dropped out from survival follow‐up (S 5) or died (S 6). Patients who are still alive at the data cutoff date were right censored at their current state. The number of patients who experienced a certain transition between each state, or censored at the intermediate states is represented by n for each arrow or in each box, respectively.
The transitions of patients were assumed to be unidirectional (e.g., patients that moved from response [] to progression [] cannot move back to response [] after progression). This property was introduced by defining only a forward transition hazard from state to () at time t, and resetting the probability () of observed state to 1 and all other states to 0 after each observation.
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
Both a constant (exponential) and a time‐varying characterized by Weibull function were assessed (Equations 8 and 9):
| (8) |
| (9) |
where both t as time since treatment initiation or as time since entering the state were evaluated. and >1 indicates a decreasing and increasing hazard with time, respectively. If transition to death () was estimated with high uncertainty or close to 0 it was fixed to the Gompertz‐Makeham distribution to allow for a hazard no lower than the expected age‐specific hazard of death. 23
The ability of covariates in describing data through influencing the transition rate constant was tested with a proportional hazard model. For example, for individual with continuous covariate the transition hazards will be:
| (10) |
where is the baseline transition hazard, is the coefficient of the effect of X on transition from state i to j. is the population median value of X for baseline covariate, and median value of X at baseline for time‐varying covariates.
Preselected baseline covariates, PK model‐derived Empirical Bayes Estimates (EBEs) of individual CL and observed or TGI model‐derived tumor dynamic metrics were tested on all estimable transitions in a univariable analysis. Additionally, time in response and time to progression were tested on the transition hazard k 36 (progression → death).
Derivation of EBEs of individual clearance
The prospective evaluation (Proseval) tool 23 in PsN 24 was used to update the EBEs of individual CL continuously as more observations became available given the same set of population parameters from the final PK model. This methodology is in contrast to calculating the individual CL with all available longitudinal PK observations in a sequential or joint modeling approach. 25 The latter could introduce bias in a setting where potential time‐varying clearance correlates with disease severity, as the information of how clearance vary with time obtained in the future would be involved in the forecast of current disease status.
Derivation of tumor dynamics metrics
Both observed and TGI model derived tumor dynamic metrics (baseline SLD, relative change in SLD [i] from baseline, [ii] from tumor nadir, and [iii] between the two previous measurements), and model derived tumor growth rate and shrinkage rate constant were tested as prospective predictors as described by Krishnan et al. 4 Specifically, the state for a patient at time is not observed until the SLD at time has been measured, therefore the SLD value at time should not be used to inform predictors forecasting the state at time . Therefore, to predict the state observation at time , the current analysis only used SLDs observed before time , EBEs of TGI model parameters informed by past‐observed SLDs using Proseval, and model‐predicted SLD at time based on the EBEs.
Dose–response analysis
Two parallel approaches were prespecified to quantify the dose effects: (1) a p value driven covariate analysis of dose on transition rates, similar to other predictors; And (2) estimation of dose‐specific transition rates, in which dose was predefined as a predictor on each transition. The second approach helps to avoid selection bias due to conditioned inclusion based on multiple testing, thus ensured an unbiased estimate of the impact of dose on efficacy end points.
Derivation of PFS and OS
The clinical end points PFS and OS were derived from multistate records. PFS was defined as the time from treatment initiation to progression (), or transition to death () from stable ()/response (). If a patient transited to unknown (), dropout (), or was right censored without a preceding PD or death event, PFS was censored the date of the last available tumor evaluation. If a patient transited to unknown () state at the first post‐treatment initiation tumor assessment (i.e., no post‐baseline tumor size [TS] assessment was conducted), and no death occurs, PFS is censored at day 1. OS was defined as the time from treatment initiation to the transition to dropout ()/ death (), or the data cutoff date if right‐censored in an intermediate state.
Simulations
A multistate model with dose‐dependent transition parameters was used to evaluate its combined effect on clinical outcomes including PFS and OS via simulations. Five hundred simulation replicates were generated by sampling parameter vectors from the posterior distribution obtained with Sampling Importance Resampling, 26 thus accounting for parameter uncertainty. Each sample of the parameter vector was applied for a virtual population of significant size (n = 5000) generated by resampling covariates from the analysis population (n = 80) stratified by dose. Using such large size of the virtual population, ensured that any variation between the results of the simulated replicates would be attributed to the uncertainty of the multistate model parameters acquired in the estimation step.
Data analysis
NONMEM (version 7.4.4) 27 was used with runs executed by Perl‐speaks‐NONMEM (PsN, version 5.2.0). 24 R (version 4.0.4) and Xpose4 (version 4.7.1) were used for the exploratory analysis and model assessment. 28 , 29 For the multistate model, LAPLACE LIKE was used for estimation and p < 0.05 was set as statistical significance level. For PK and TS model, see Appendix S1. Models' predictive performance was evaluated by visual predictive checks (VPCs). If a statistical significance was driven by few (≤3) individuals, the relationship was reported but not included in the final model to minimize the risk of false positivity due to influential individuals in combination with multiple testing.
RESULTS
Patients and data
Baseline characteristics of enrolled patients are summarized in Table 1. The 998 assayed plasma concentrations indicated dose‐proportional PKs and close to complete separation of systemic exposures between the two dose groups (Figures S1 and S2). SLD of target lesions per IRC were available for 76 out of 80 patients at baseline (screening) with a median of 57 mm (range 13–262 mm) and plotted in Figure S3. The time interval between the baseline measurement and the first dose administration was on average 17.6 days (1.4–48.4 days). At least one SLD measured after treatment initiation was available for 73 patients and the median TS follow‐up was 12 weeks (range 2–177 weeks). The SD or PR observed after an initial PD was treated as continued PD. The number of such patients observed was one and one, respectively. OS data were collected for a median of 52 weeks (range 1–180 weeks) after the start of bintrafusp alfa treatment. Fifty‐six patients (70%) had death events with a median time to death of 47 weeks (range 1.3–166).
TABLE 1.
Summary of patient characteristics stratified on dose, presented as mean (standard deviation) [minimum; maximum] {number of subjects missing} or number of subjects (%).
| Baseline characteristics | 500 mg | 1200 mg |
|---|---|---|
| (n = 40) | (n = 40) | |
| Age (years) | 63.9 (8.9) | 62.1 (11.1) |
| [43.0; 85.0] | [38.0; 79.0] | |
| Body weight (kg) |
68.0 (15.6) [41.9; 109.0] |
70.8 (13.8) [44.3; 107.8] |
| Sex | ||
| Female | 16 (40%) | 7 (18%) |
| Male | 24 (60%) | 33 (82%) |
| Race | ||
| White | 25 (62%) | 14 (35%) |
| Black/African Americans | 0 (0%) | 1 (3%) |
| Asian | 15 (38%) | 25 (62%) |
| Smoking status | ||
| Never used | 13 (32%) | 5 (12%) |
| Former/regular | 27 (68%) | 35 (88%) |
| C‐reactive protein (mg/L) |
27.1 (26.7) [1.0; 88.2] {3} |
30.8 (70.0) [0.4; 429.1] |
| Lactate dehydrogenase (U/L) |
327.2 (152.9) [80.0; 769.0] {1} |
301.3 (202.5) [144.0; 1259.0] {1} |
| Neutrophil‐to‐lymphocyte ratio | 4.1 (1.9) | 3.7 (2.4) |
| [0.9; 9.1] | [1.6; 14.0] | |
| TGF‐β1 plasma concentration (ng/L) |
7058.3 (10,101.9) [625.0; 32,904.2] {7} |
6254.4 (13,832.8) [625.0; 77,104.5] {1} |
| PD‐L1 tumor cell expression (%) | 35.6 (29.6) | 37.5 (31.3) |
| [2.0; 100.0] {2} | [0.0; 95.0] {3} | |
| ECOG score | ||
| 0 | 13 (32%) | 7 (18%) |
| 1 | 27 (68%) | 33 (82%) |
| >1 | 0 (0%) | 0 (0%) |
| Metastases | ||
| Yes | 33 (82%) | 32 (80%) |
| No | 7 (18%) | 8 (20%) |
| Liver metastases | ||
| Yes | 7 (18%) | 4 (10%) |
| No | 33 (82%) | 36 (90%) |
| Number of non‐target lesions |
5.2 (2.5) [1.0; 11.0] |
4.5 (2.3) [1.0; 10.0] |
| Histology | ||
| Non‐squamous | 32 (80%) | 31 (78%) |
| Squamous | 8 (20%) | 9 (22%) |
| Previous medication with biologics a | ||
| Yes | 7 (18%) | 9 (22%) |
| No | 33 (82%) | 31 (78%) |
| Previous medication with antibiotics b | ||
| Yes | 14 (35%) | 11 (28%) |
| No | 26 (65%) | 29 (72%) |
| Concomitant corticosteroids | ||
| Yes | 20 (50%) | 23 (58%) |
| No | 20 (50%) | 17 (42%) |
Abbreviation: ECOG, Eastern Cooperative Oncology Group.
Biologics treatment received prior to therapy with bintrafusp alfa.
Systemic antibacterial medication received at any time in the period from 1 month (29 days) before until 1 month (29 days) after randomization for any duration.
PK and TGI models
A two‐compartment model with time‐constant first‐order linear elimination described the PK data (parameter estimates given in Table S2; VPC in Figure S4). No time‐varying clearance was identified. The longitudinal SLDs were described by a TGI model with a K G of 1.43 mm/week, a k D of 0.0306 per week, and a half‐life of drug effect disappearance of 124 weeks (Table S2; VPC in Figure S5). No significant association was found among dose, CL, or baseline covariates with tumor dynamic parameters. For detailed description of the results (see Appendix S1).
Multistate model
The multistate data consisted of 406 observations derived from 326 post‐baseline tumor response categories (75 SD, 127 PR, and 124 PD) and 80 absorbing events (56 deaths, 13 dropouts, and 11 censored at data cutoff), leading to 155 transitions between states (Figure 1a) and 251 transitions within states. The observed transitions to dropout () were well‐described by the dropout completely at random assumption (). Alternative assumptions (e.g., dropout rate is dependent on current state) were tested but did not improve the description of data. Ten patients moved to the unknown state (), including patients who discontinued treatment due to adverse events (n = 2), physician's decision (n = 1) or investigator‐assessed progression (n = 6), and a patient who had missing data (n = 1). The (SD → death) was fixed to the Gompertz‐Makeham distribution due to high parameter uncertainty. The shape parameter of (SD → progression) and (progression → death) were lower than 1, indicating decreased probability of progression and death upon progression over time since treatment initiation.
In the univariable analysis, neither dose nor CL was found statistically significant in predicting transitions. The statistically significant predictor–transition relationships are reported in Table S3. The only predictor included in the final model was metastases at baseline that increased by 4.18‐fold (95% confidence interval [CI], 1.45, 12.06). Race was associated with dropout rate, which is likely confounded by study sites, as all patients (n = 13) dropped out were Asians from four Asian sites out of 25 global sites (Table S4), and thus this relationship was not retained. The remaining identified relationships were driven by one or two influential individuals. For example, a bigger model‐predicted increase of SLD at progression from baseline and higher tumor growth rate K G were associated with higher k 36 (progression → death), which was not included in the final model due to predefined inclusion criteria (>3 influential individuals). The final multistate model estimates (Table 2) provided an adequate fit of the transitions as well as the joint PFS and OS (VPCs shown in Figure S6).
TABLE 2.
Parameter estimates and uncertainty of the multistate models.
| Parameter | Transition | Final multistate model estimated value | Final multistate model with dose‐dependent estimated value | ||
|---|---|---|---|---|---|
| (95% CI) a | (95% CI) a | ||||
| 500 mg q2w | 1200 mg q2w | ||||
|
|
Stable disease → Response |
0.032 (0.021, 0.050) |
0.037 (0.020, 0.080) |
0.029 (0.019, 0.054) |
|
| Stable disease → Progression |
0.157 (0.086, 0.341) 0.427 (0.247, 0.631) |
0.371 (0.148, 2.339) 0.292 (0.072, 0.568) |
0.089 (0.053, 0.187) 0.584 (0.330, 0.891) |
||
|
|
Stable disease → Unknown |
0.012 (0.006, 0.023) |
0.020 (0.010, 0.050) |
0.007 (0.003, 0.020) |
|
|
|
Stable disease → Death | – | |||
|
|
Response → Progression |
0.013 (0.008, 0.022) |
0.012 (0.006, 0.027) |
0.013 (0.008, 0.028) |
|
|
|
Response → Unknown |
0.003 (0.001, 0.008) |
0.002 (0.001, 0.009) |
0.004 (0.002, 0.012) |
|
|
|
Response → Death |
0.002 (0.0008, 0.006) |
0.002 (0.001, 0.010) |
0.002 (0.001, 0.009) |
|
| Progression → Death |
0.023 (0.015, 0.044) 0.631 (0.439, 0.862) |
0.028 (0.016, 0.091) 0.542 (0.320, 0.771) |
0.015 (0.010, 0.031) 0.941 (0.510, 1.378) |
||
|
|
Unknown → Death |
0.008 (0.004, 0.015) |
0.007 (0.004, 0.020) |
0.007 (0.003, 0.018) |
|
|
|
Stable disease and Progression and Unknown → Dropout |
0.003 (0.002, 0.005) |
0.001 (0.001, 0.004) |
0.004 (0.003, 0.008) |
|
|
|
Stable disease → Progression |
−1.431 (−2.570, −0.497) |
−1.430 (−2.398, −0.489) |
||
Abbreviation: CI, confidence interval.
Obtained from Sampling Importance Resampling.
Exponential distribution (week‐1).
Weibull distribution, , t is time since treatment initiation.
Fixed to the Gompertz‐Makeham distribution.
Coefficient of the metastasis at baseline on
Dose response analysis
In the univariable analysis, dose did not achieve statistical significance as a predictor for any transition rate (p > 0.01). Based on the final multistate model, dose‐dependent transitions were estimated (ΔOFV = −14.2, df = 11, p = 0.22). The parameter estimates (Table 2) suggested a trend of relatively higher probability of response, as well as a lower probability of progression and death upon progression, in patients receiving 1200 mg vs. 500 mg q2w. The VPCs stratified on dose (Figure 2) showed a good predictive performance of the model for both dose groups.
FIGURE 2.
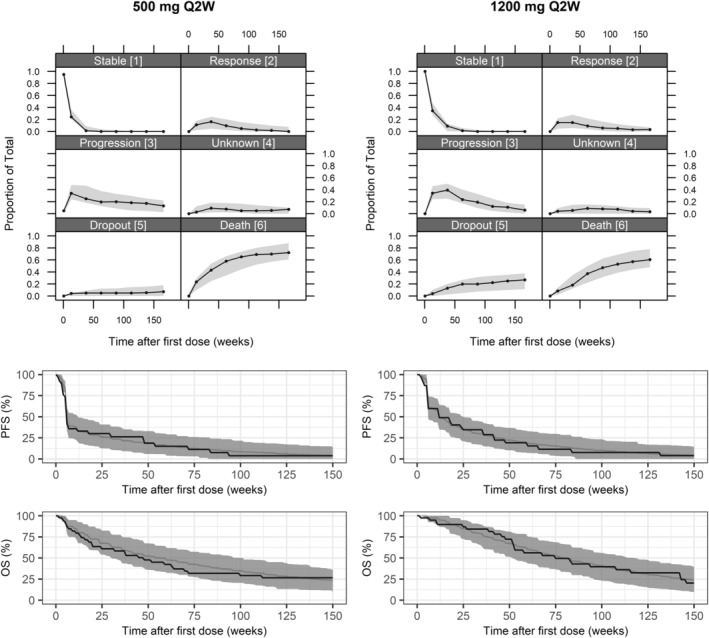
Visual predictive checks (VPCs) of the proportion of patients in each state and Kaplan–Meier curve of progression‐free survival (PFS) and overall survival (OS), stratified on patient receiving 500 or 1200 mg every 2 weeks (q2w) of bintrafusp alfa. In the VPCs of proportion of remaining patients in the different states, solid lines represent the observed data, and gray shaded areas are 95% confidence intervals (CIs) from 500 simulations. In the Kaplan–Meier VPC, the black solid line represents the observed data, the gray solid line represents the median and the gray shaded area is 95% CIs from 500 simulations.
Simulations
Over the 500 simulated replicates, the median (95% CI) of simulated overall response rate (ORR) was 20% (10, 32) and 27% (15, 42), PFS was 1.4 (1.3, 1.5) and 2.6 (1.3, 3.7) months, and OS was 11.0 (7.4, 16.5) and 13.7 (9.5, 17.8) months for 500 and 1200 mg, respectively. These values are in line with the observed ORR of 15% and 28%, median PFS of 1.4 and 2.7, and median OS of 9.5 and 12.2 months for the two dose groups (Figure 3). More survival benefits for patients with higher dose is predicted during the first 6 months, however, the difference diminishes over time. As shown in Figure 4, the simulation results predicted a 69.2% and 55.6% probability of at least 1 and 2 months longer median OS, respectively, for the 1200 mg compared to the 500 mg dose. The probability that 500 mg has the same or better efficacy as 1200 mg in terms of median OS is 21.8%. In an early development setting, these results provide a strong rationale to proceed with the 1200 mg dose.
FIGURE 3.
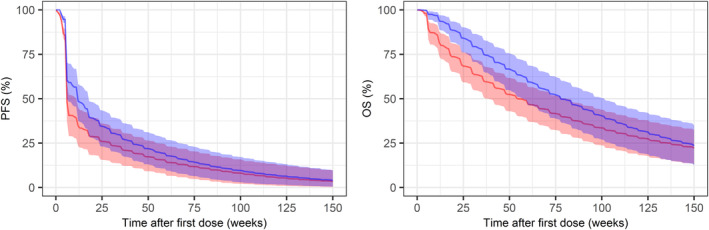
Comparison of simulated Kaplan–Meier curves of progression‐free survival (PFS) and overall survival (OS) between dose groups (1200 mg q2w vs. 500 mg q2w). Kaplan–Meier plot of expected PFS and OS for virtual patients with second‐line non‐small cell lung cancer receiving 500 mg (red) or 1200 mg (blue) every 2 weeks (q2w) of bintrafusp alfa. The solid lines represent the median and the shaded areas are 90% simulation interval from 500 simulated trials.
FIGURE 4.
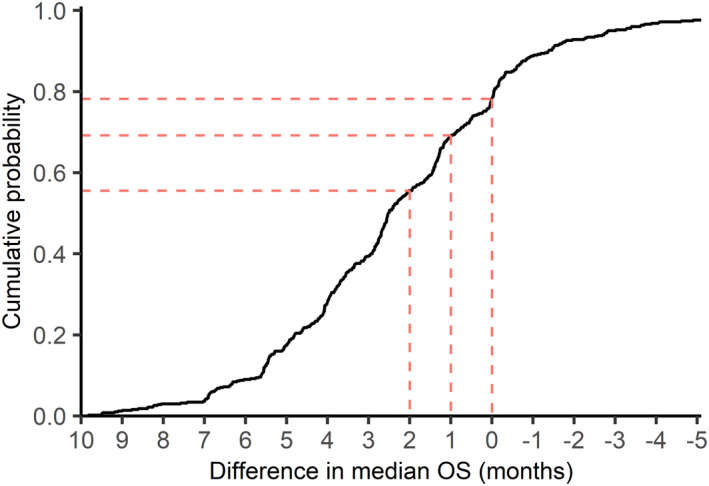
Cumulative probability of the difference in median overall survival (OS) between two dose groups (1200 mg vs. 500 mg) in months. Cumulative probability for a difference in median OS of X was calculated as the percentage of simulated trials with the median OS of the 1200 mg dose arm is longer than X months compared to the median OS of the 500 mg dose arm.
DISCUSSION
To the best of our knowledge, this is the first study to use a multistate modeling and simulation framework for evaluating dose–response relationships of anticancer drug. Survival analysis with multistate model has useful application in statistics and epidemiology, 30 and was first introduced for pharmacometric analysis of OS in clinical oncology research setting by Krishnan et al., 4 as a method accounting for the influence of intermediate events on hazard of death, and link predictors measured post‐baseline (e.g., tumor dynamic metrics) to OS without introducing immortal time bias. In this analysis, multistate model with dose‐specific transition rates was established and provided an adequate fit of the observed transitions, and jointly the PFS and OS for the patients with NSCLC receiving 2L bintrafusp alfa in both the 500 mg and the 1200 mg group, based on which the simulation step supported the selection of 1200 mg dose for future studies.
Bias in the estimation of treatment benefit can be reduced naturally with multistate modeling framework. In a recent publication, “second‐line treatment” was treated as a state and enabled the separation of the confounding effect of subsequent therapy from the investigated effect of primary treatment on OS. 31 In this study, the framework was expanded to incorporate the unknown state to accommodate patients who were lost to follow‐up for tumor assessment (n = 10, 12.5%) due to treatment termination before progression or have missing tumor response data, thus avoided assuming such patients retained in the stable or response state. Furthermore, the dropout state was added to account for patients lost to survival follow‐up (n = 13, 16.25%). These modifications ensured an unbiased assessment of transition hazards and corresponding effect of dose and coefficient of covariates.
With the ability to examine individual transition between states, multistate models enhanced the power to identify predictors that are particularly relevant for certain transitions but not necessarily for others. The hazard of progression () and death upon progression () were found to decrease over time, indicating patients progressed shortly after receiving the first dose had a higher probability to die. The presence of metastases at baseline was predictive of early progression and a high probability of death upon progression, in line with earlier reports on presence of metastasis being associated with high treatment failure and mortality rate. 32 , 33 However, the small size of the dataset in this analysis likely limited the power for discerning potential predictor‐transition associations. No predictor was retained for (SD → response, 18 transitions observed) and (response → progression, 12 transitions observed). A majority of stable to progression transitions (35 out of 46) happened at the first tumor assessment, before which no tumor metrics besides baseline size was learned, thus decreased the power of tumor dynamic metrics in forecasting . Despite the statistical significance level not being reached, some trends were noted (Table S5). Decreased baseline PD‐L1 expression correlates with lower (SD → response), and higher (SD → progression), (response → progression), and (progression → stable disease), all with 95% CI of hazard ratio including 1. These results are in line with the role of PD‐L1 as a predictive biomarker in cancer immunotherapy and the mechanism of action of bintrafusp alfa. 34 , 35 , 36 Although time‐varying CL was not found, the possibility of its existence was not necessarily excluded, considering the relatively small number of patients (n = 80). Trends of associations were observed between increased individual CL and lower , and higher , , and (Table S5), which are in agreement with the previous reported high initial CL associated with low probability of BOR and high risk of PFS events. 7 However, a larger dataset would be required to confirm reliably the significance of these trends.
When analyzing covariates that potentially have a small impact on many transitions, a p value driven analysis may fail to incorporate such covariate–transition relationships, especially under limited sample size, despite their substantial cumulative effect on PFS and OS. Additionally, a conditioned inclusion based on multiple tests may result in selection bias. To address these issues, a model with covariate‐specific transition rates can be prespecified, which ensured an unbiased estimation of covariate effects of interest. In this study, such a model was estimated for dose, based on which the simulations suggested that patients receiving a dose of 1200 mg q2w had cumulatively better PFS and OS in the first half year of the study, with a probability of ~70% for at least a 1‐month's difference in median OS for the two dose, considering parameter uncertainties. The higher dropout rate in the 1200 mg dose may be confounded by study sites (Table S4), indicating that the true probability of favoring the 1200 mg is potentially higher than what was calculated. Therefore, despite dose failing to be significant for each individual transition, the combined effect quantified through the integrated aspect of the event time‐course was still pronounced and informative, taken together with previously reported safety results, 7 , 37 supported the decision of moving forward with the higher dose.
Viewed in the context of Project Optimus, this study proposed a new methodology for evaluating the dose‐efficacy relationship in oncology trials. All longitudinal information was integrated to discriminate the clinical benefit of different dosages. The relationships between dose and multiple clinical end points (e.g., ORR, PFS, and OS) were bridged and quantified in one modeling practice. Moreover, the simulation step provides insight into the “learning” of the dose–response relationship, which is not a statistical testing problem, but rather a quantification of the probability of achieving better outcomes with one dose versus another based on integration of all available data. 38 Together with clinical safety data and associated exposure‐safety relationships, the framework described here can be powerful as a component of a Totality of Evidence approach to dose optimization for oncology therapies that is based on a robust characterization of dose/exposure‐response relationships. 38 , 39 , 40 Furthermore, integration of covariates (e.g., tumor genomics) into these models can present opportunities for informing patient selection hypotheses in precision medicine development. Taken together, we view the approach described here as an important component of the pharmacometrics toolkit in oncology drug development and encourage our readers to reflect on potential opportunities for future applications across cancer indications to inform cross‐endpoint bridging, patient selection, and dose optimization.
CONCLUSION
The developed multistate model adequately described the transitions between different disease states in patients with NSCLC receiving 500 mg versus 1200 mg of bintrafusp alfa. Results from simulations based on developed multistate model with dose‐specific estimation of transitions showed an ~70% probability of clinically meaningful median OS improvement from the 1200 mg dose compared to the 500 mg dose arm.
AUTHOR CONTRIBUTIONS
H.L., A.‐M.M.‐G., S.J., L.E.F., A.K., K.V., and M.O.K. wrote the manuscript. H.L., A.‐M.M.‐G., S.M.K., S.J., L.E.F., P.G., K.V., Y.V., A.K., and M.O.K. designed the research. H.L. performed the research. S.M.K., S.J., L.E.F., and M.O.K. analyzed the data.
FUNDING INFORMATION
This work was supported by Merck KGaA, Darmstadt, Germany, and the Swedish Cancer Society (20 1226 PjF).
CONFLICT OF INTEREST STATEMENT
A.‐M.M.‐G. and A.K. are employees of Merck Healthcare KGaA, Darmstadt, Germany. P.G. is an employee of Merck Institute of Pharmacometrics, Lausanne, Switzerland, an affiliate of Merck KGaA. Y.V. and K.V. are employees of EMD Serono, an affiliate of Merck KGaA. All other authors declared no competing interests for this work. As Deputy Editor in Chief of CPT: Pharmacometrics and Systems Pharmacology, Lena Friberg was not involved in the review or decision process for this paper.
Supporting information
Appendix S1
Appendix S2
Figure S1
Figure S2
Figure S3
Figure S4
Figure S5
Figure S6
Table S1
Table S2
Table S3
Table S4
Table S5
ACKNOWLEDGMENTS
The authors thank the patients and their families, the investigators, co‐investigators, and study teams who contributed to the clinical study that provided the data. We also thank Sebastian Ueckert for his help in data management and specifically NONMEM data compiling.
Liu H, Milenković‐Grišić A‐M, Krishnan SM, et al. A multistate modeling and simulation framework to learn dose–response of oncology drugs: Application to bintrafusp alfa in non‐small cell lung cancer. CPT Pharmacometrics Syst Pharmacol. 2023;12:1738‐1750. doi: 10.1002/psp4.12976
Akash Khandelwal and Mats O. Karlsson shared senior authorship.
REFERENCES
- 1. Project Optimus [Internet]. https://www.fda.gov/about‐fda/oncology‐center‐excellence/project‐optimus
- 2. Goring S, Varol N, Waser N, et al. Correlations between objective response rate and survival‐based endpoints in first‐line advanced non‐small cell lung cancer: a systematic review and meta‐analysis. Lung Cancer. 2022;170:122‐132. [DOI] [PubMed] [Google Scholar]
- 3. Beyer U, Dejardin D, Meller M, Rufibach K, Burger HU. A multistate model for early decision‐making in oncology. Biom J. 2020;62(3):550‐567. [DOI] [PubMed] [Google Scholar]
- 4. Krishnan SM, Friberg LE, Bruno R, Beyer U, Jin JY, Karlsson MO. Multistate model for pharmacometric analyses of overall survival in HER2‐negative breast cancer patients treated with docetaxel. CPT Pharmacometrics Syst Pharmacol. 2021;10:1255‐1266. doi: 10.1002/psp4.12693 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Khandelwal A, Grisic A‐M, French J, Venkatakrishnan K. Pharmacometrics golems: exposure‐response models in oncology. Clin Pharmacol Ther. 2022;112:941‐945. doi: 10.1002/cpt.2564 [DOI] [PubMed] [Google Scholar]
- 6. Paz‐Ares L, Kim TM, Vicente D, et al. Bintrafusp alfa, a bifunctional fusion protein targeting TGF‐β and PD‐L1, in second‐line treatment of patients with NSCLC: results from an expansion cohort of a phase 1 trial. J Thorac Oncol. 2020;15(7):1210‐1222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7. Vugmeyster Y, Wilkins J, Koenig A, et al. Selection of the recommended phase 2 dose for bintrafusp alfa, a bifunctional fusion protein targeting TGF‐β and PD‐L1. Clin Pharmacol Ther. 2020;108(3):566‐574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Wang X, Feng Y, Bajaj G, et al. Quantitative characterization of the exposure‐response relationship for cancer immunotherapy: a case study of nivolumab in patients with advanced melanoma. CPT Pharmacometrics Syst Pharmacol. 2017;6(1):40‐48. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Turner DC, Kondic AG, Anderson KM, et al. Pembrolizumab exposure‐response assessments challenged by Association of Cancer Cachexia and Catabolic Clearance. Clin Cancer Res. 2018;24(23):5841‐5849. [DOI] [PubMed] [Google Scholar]
- 10. Baverel PG, Dubois VFS, Jin CY, et al. Population pharmacokinetics of durvalumab in cancer patients and association with longitudinal biomarkers of disease status. Clin Pharmacol Ther. 2018;103(4):631‐642. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Liu C, Yu J, Li H, et al. Association of time‐varying clearance of nivolumab with disease dynamics and its implications on exposure response analysis. Clin Pharmacol Ther. 2017;101:657‐666. doi: 10.1002/cpt.656 [DOI] [PubMed] [Google Scholar]
- 12. Li H, Yu J, Liu C, et al. Time dependent pharmacokinetics of pembrolizumab in patients with solid tumor and its correlation with best overall response. J Pharmacokinet Pharmacodyn. 2017;44(5):403‐414. [DOI] [PubMed] [Google Scholar]
- 13. Wilkins JJ, Brockhaus B, Dai H, et al. Time‐varying clearance and impact of disease state on the pharmacokinetics of Avelumab in Merkel cell carcinoma and urothelial carcinoma. CPT Pharmacometrics Syst Pharmacol. 2019;8:415‐427. doi: 10.1002/psp4.12406 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Dai HI, Vugmeyster Y, Mangal N. Characterizing exposure‐response relationship for therapeutic monoclonal antibodies in immuno‐oncology and beyond: challenges, perspectives, and prospects. Clin Pharmacol Ther. 2020;108(6):1156‐1170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Porporato PE. Understanding cachexia as a cancer metabolism syndrome. Oncogenesis. 2016;5(2):e200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Mondello P, Lacquaniti A, Mondello S, et al. Emerging markers of cachexia predict survival in cancer patients. BMC Cancer. 2014;14:828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Poon V, Lu D. Performance of cox proportional hazard models on recovering the ground truth of confounded exposure‐response relationships for large‐molecule oncology drugs. CPT Pharmacometrics Syst Pharmacol. 2022;11(11):1511‐1526. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Eisenhauer EA, Therasse P, Bogaerts J, et al. New response evaluation criteria in solid tumours: revised RECIST guideline (version 1.1). Eur J Cancer. 2009;45(2):228‐247. [DOI] [PubMed] [Google Scholar]
- 19. Wilkins JJ, Vugmeyster Y, Dussault I, Girard P, Khandelwal A. Population pharmacokinetic analysis of bintrafusp alfa in different cancer types. Adv Ther. 2019;36(9):2414‐2433. [DOI] [PubMed] [Google Scholar]
- 20. Petitcollin A, Bensalem A, Verdier M‐C, et al. Modelling of the time‐varying pharmacokinetics of therapeutic monoclonal antibodies: a literature review. Clin Pharmacokinet. 2020;59(1):37‐49. [DOI] [PubMed] [Google Scholar]
- 21. Claret L, Girard P, Hoff PM, et al. Model‐based prediction of phase III overall survival in colorectal cancer on the basis of phase II tumor dynamics. J Clin Oncol. 2009;27(25):4103‐4108. [DOI] [PubMed] [Google Scholar]
- 22. Missov TI, Lenart A. Gompertz–Makeham life expectancies: expressions and applications. Theor Popul Biol. 2013;90:29‐35. [DOI] [PubMed] [Google Scholar]
- 23. Uppsala Pharmacometrics Group . Proseval function of peral‐speaks‐NONMEM userguide [Internet]. https://github.com/UUPharmacometrics/PsN/releases. Accessed September 12, 2022.
- 24. Nordgren R, Freiberga S, Ueckert S, Yngman G, Karlsson M. PsN: an open source toolkit for non‐linear mixed effects modelling. 2004.
- 25. Zhang L, Beal SL, Sheiner LB. Simultaneous vs. sequential analysis for population PK/PD data I: best‐case performance. J Pharmacokinet Pharmacodyn. 2003;30(6):387‐404. [DOI] [PubMed] [Google Scholar]
- 26. Dosne AG, Bergstrand M, Harling K, Karlsson MO. Improving the estimation of parameter uncertainty distributions in nonlinear mixed effects models using sampling importance resampling. J Pharmacokinet Pharmacodyn. 2016;43(6):583‐596. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Beal SL, Sheiner LB, Boeckmann AJ, Bauer RJ. NONMEM 7.4 Users Guides (1989–2019). ICON plc; 2019. https://nonmem.iconplc.com/nonmem744 [Google Scholar]
- 28. R Core Team . R: A Language and Environment for Statistical Computing. R Foundation for Statistical Computing; 2021. https://www.R‐project.org [Google Scholar]
- 29. Dullum MK, Resano FG. Xpose: a new device that provides reproducible and easy access for multivessel beating heart bypass grafting. Heart Surg Forum. 2000;3(2):113‐117. discussion 117–8. [PubMed] [Google Scholar]
- 30. Meira‐Machado L, de Uña‐Alvarez J, Cadarso‐Suárez C, Andersen PK. Multi‐state models for the analysis of time‐to‐event data. Stat Methods Med Res. 2009;18(2):195‐222. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Krishnan SM, Friberg LE, Mercier F, et al. Multistate pharmacometric model to define the impact of second‐line immuno‐therapies on the survival outcome of IMpower131 study. Clin Pharmacol Ther. 2023;113:851‐858. doi: 10.1002/cpt.2838 [DOI] [PubMed] [Google Scholar]
- 32. Huang Y, Zhu L, Guo T, et al. Metastatic sites as predictors in advanced NSCLC treated with PD‐1 inhibitors: a systematic review and meta‐analysis. Hum Vaccin Immunother. 2021;17(5):1278‐1287. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Dillekås H, Rogers MS, Straume O. Are 90% of deaths from cancer caused by metastases? Cancer Med. 2019;8(12):5574‐5576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Davis AA, Patel VG. The role of PD‐L1 expression as a predictive biomarker: an analysis of all US Food and Drug Administration (FDA) approvals of immune checkpoint inhibitors. J Immunother Cancer. 2019;7(1):278. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Zamora Atenza C, Anguera G, Riudavets Melià M, et al. The integration of systemic and tumor PD‐L1 as a predictive biomarker of clinical outcomes in patients with advanced NSCLC treated with PD‐(L)1blockade agents. Cancer Immunol Immunother. 2022;71(8):1823‐1835. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36. Passiglia F, Bronte G, Bazan V, et al. PD‐L1 expression as predictive biomarker in patients with NSCLC: a pooled analysis. Oncotarget. 2016;7(15):19738‐19747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Vugmeyster Y, Grisic A‐M, Wilkins JJ, et al. Model‐informed approach for risk management of bleeding toxicities for bintrafusp alfa, a bifunctional fusion protein targeting TGF‐β and PD‐L1. Cancer Chemother Pharmacol. 2022;90(4):369‐379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38. Fourie Zirkelbach J, Shah M, Vallejo J, et al. Improving dose‐optimization processes used in oncology drug development to minimize toxicity and maximize benefit to patients. J Clin Oncol. 2022;40(30):3489‐3500. [DOI] [PubMed] [Google Scholar]
- 39. Venkatakrishnan K, Cook J. Driving access to medicines with a totality of evidence mindset: an opportunity for clinical pharmacology. Clin Pharmacol Ther. 2018;103(3):373‐375. [DOI] [PubMed] [Google Scholar]
- 40. Venkatakrishnan K, van der Graaf PH. Toward project optimus for oncology precision medicine: multi‐dimensional dose optimization enabled by quantitative clinical pharmacology. Clin Pharmacol Ther. 2022;112(5):927‐932. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Appendix S1
Appendix S2
Figure S1
Figure S2
Figure S3
Figure S4
Figure S5
Figure S6
Table S1
Table S2
Table S3
Table S4
Table S5


