Clinical decision support for chemotherapy‐induced neutropenia using a hybrid pharmacodynamic/machine learning model

Abstract

Consensus guidelines recommend use of granulocyte colony stimulating factor in patients deemed at risk of chemotherapy‐induced neutropenia, however, these risk models are limited in the factors they consider and miss some cases of neutropenia. Clinical decision making could be supported using models that better tailor their predictions to the individual patient using the wealth of data available in electronic health records (EHRs). Here, we present a hybrid pharmacokinetic/pharmacodynamic (PKPD)/machine learning (ML) approach that uses predictions and individual Bayesian parameter estimates from a PKPD model to enrich an ML model built on her data. We demonstrate this approach using models developed on a large real‐world data set of 9121 patients treated for lymphoma, breast, or thoracic cancer. We also investigate the benefits of augmenting the training data using synthetic data simulated with the PKPD model. We find that PKPD‐enrichment of ML models improves prediction of grade 3–4 neutropenia, as measured by higher precision (61%) and recall (39%) compared to PKPD model predictions (47%, 33%) or base ML model predictions (51%, 31%). PKPD augmentation of ML models showed minor improvements in recall (44%) but not precision (56%), and data augmentation required careful tuning to control overfitting its predictions to the PKPD model. PKPD enrichment of ML shows promise for leveraging both the physiology‐informed predictions of PKPD and the ability of ML to learn predictor‐outcome relationships from large data sets to predict patient response to drugs in a clinical precision dosing context.

Study Highlights.

• WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?

Current practice for identifying patients at risk of neutropenia uses a simple scoring system, which can miss some patients. More sophisticated methods proposed include pharmacokinetic/pharmacodynamic (PKPD) models, which are semimechanistic but involve limited covariate information, or machine learning (ML) models, which are not physiologically informed but can learn complex predictor‐outcome relationships, to predict neutrophil counts or neutropenia.

• WHAT QUESTION DID THIS STUDY ADDRESS?

This study proposes a novel hybrid PKPD‐ML approach, applied here to predict absolute neutrophil counts during chemotherapy.

• WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?

This study demonstrates that PKPD‐enrichment of ML models, in which PKPD model predictions and individual parameter estimates are incorporated as ML model features, improves predictive performance relative to ML or PKPD alone.

• HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?

This work suggests that hybrid models hold promise for predicting patients at risk of neutropenia at the point of care, and could be extended to other clinical care decision making applications.

INTRODUCTION

A common side effect of chemotherapy is neutropenia, characterized by a drop in absolute neutrophil count (ANC), which can be associated with infection and poor treatment outcomes. Current National Comprehensive Cancer Network guidelines recommend prophylactic administration of granulocyte colony‐stimulating factor (G‐CSF) when the patient's risk of neutropenia exceeds 20% on the Multinational Association for Supportive Care in Cancer (MASCC) risk index, which incorporates age, symptoms, blood laboratory tests, and comorbidities. ¹ For patients presenting with low ANC at the time of their next cycle, treatment may also be delayed to allow their ANC to rebound. Despite these guidelines, neutropenia rates remain high, with reported rates of febrile neutropenia ranging from 11% to 13% of patients, resulting in changing or delaying chemotherapy in 9.5% of patients, ² , ³ and in‐hospital mortality rates of 9.5% for those patients admitted for febrile neutropenia. ⁴ Broad prophylactic use of G‐CSF comes at a high financial cost and risks patient discomfort, but more targeted dosing is challenged by high variability in patient response to chemotherapy and G‐CSF.

Clinical decision support tools based on predictive models can potentially identify patients at risk of neutropenia and suggest treatment modifications. ⁵ , ⁶ , ⁷ Models that allow individualization of risk scores have been proposed. ⁸ , ⁹ However, these models dichotomize neutropenia risk and do not incorporate administration of G‐CSF in their risk scores, preventing prediction of when ANC may rebound sufficiently for the beginning of the next round of chemotherapy.

One option is to use pharmacokinetic/pharmacodynamic (PKPD) models to semi‐mechanistically model changes in ANC arising from chemotherapy and G‐CSF use. In this approach, the coefficients governing these systems of ordinary differential equations can be tailored to a patient based on their ANCs collected during therapy using Bayesian methods. ⁷ Chemotherapy courses with or without use of G‐CSF can then be modeled, estimating the risk of neutropenia as well as predicting when subsequent cycles can be safely resumed. Whereas similar model‐informed precision dosing (MIPD) approaches have been implemented at the point of care for other disease areas and clinical interventions, ¹⁰ , ¹¹ , ¹² few models exist that describe the impacts of both G‐CSF and chemotherapy on ANCs ¹³ and their predictive ability in real‐world settings is unclear.

Because covariates are added to PKPD models in an onerous, statistically rigorous selection process, these models typically incorporate relatively few predictors. Instead, they rely chiefly on measurements of the dependent variable (e.g., ANCs) to tailor models to a patient through Bayesian updates. As a result, at the start of therapy, model predictions reflect the average patient, and then adapt to the individual patient as additional data becomes available. Factors known to influence the probability of neutropenia, such as those factors included in the MASCC risk index, are rarely directly included in these models.

A second approach is to use machine learning (ML) to predict future ANCs. ML presents an advantage over PKPD approaches in that these methods are better equipped to incorporate the wealth of information available in the electronic health records (EHRs), perhaps better reflecting the complex and multiplicative physiological relationships governing ANC during chemotherapy. Unlike PKPD models, however, ML models have no “built‐in” understanding of biological relationships. Because they must learn biological principles from the data, ML models sometimes make biologically implausible predictions. ¹⁴

Here, we propose a new method that combines the strengths of PKPD and ML approaches in a hybrid model. We start with the development of a PKPD model and an ML model based on a large, real‐word data (RWD) set. We next create a PKPD‐enriched ML model, using individual patient PKPD parameter estimates as additional features (Figure 1a). Because RWD is typically sparsely sampled, we then use the PKPD model to simulate richly sampled treatment courses, augmenting the number of data points available for model training (Figure 1b). We evaluate the ability of these models to accurately predict ANCs, as well as their ability to demonstrate good precision and recall in prediction of grade 3 or 4 neutropenia.

FIGURE 1.

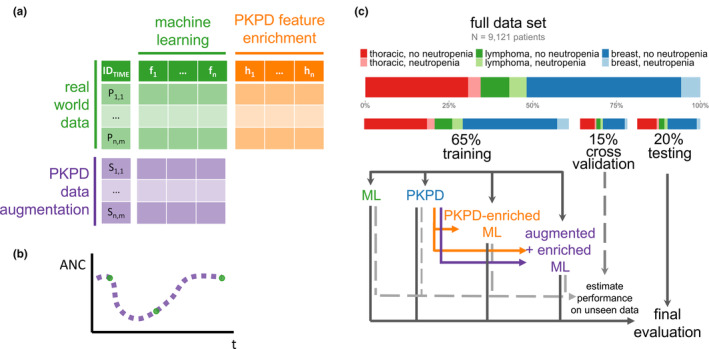
Experimental design. (a) PKPD model outputs, including predictions and parameter estimates, can be added as new features to an ML model to create a PKPD‐enriched hybrid ML model, effectively adding additional columns to tabular data. PKPD simulations can also augment data available for ML model training to create an augmented model, effectively adding more rows to tabular data. (b) PKPD simulations can be densely sampled, allowing for ML models to better learn time dynamics based on prior knowledge of human physiology. (c) Randomization into training, cross‐validation, and testing splits was performed to ensure an equal balance of primary diagnosis and rate of neutropenia (ANC <1 k/μL) in each data split. Models were developed on the training data set, and candidate models were evaluated on the cross‐validation data set with final models evaluated on the test data set. ANC, absolute neutrophil count; ML, machine learning; PKPD, pharmacokinetic/pharmacodynamic.

METHODS

Data source

EHR data describing routine clinical care were retrospectively extracted, de‐identified, and analyzed for patients treated at Memorial Sloan Kettering Cancer Center. This study was approved by Memorial Sloan Kettering Cancer Center's Institutional Review Board (approval #22‐094). Patients were included in the analysis if they were treated with a chemotherapeutic agent for metastatic thoracic cancer (non‐small cell, small cell, or mesothelioma), metastatic breast cancer, or lymphoma (diffuse large B‐cell lymphoma or follicular lymphoma) using chemotherapeutic agents between 2016 and 2020. Patients were excluded from analysis if they were treated for more than one of these cancers during this period, or if they received only immunotherapy or bone modifying agents. A pragmatic literature review was conducted to identify commonly available patient characteristics and laboratory values with possible power in predicting neutropenia ⁶ , ⁸ , ⁹ , ¹⁵ , ¹⁶ , ¹⁷ , ¹⁸ , ¹⁹ , ²⁰ , ²¹ , ²² , ²³ , ²⁴ , ²⁵ , ²⁶ (Table S1), and these data were included in addition to medication administration records describing chemotherapeutic agents, G‐CSF, and immunotherapy. ANCs were excluded from analysis if their values were greater than 15 k/μL, or showed variation greater than 4 k/μL per 24 h period in the absence of G‐CSF administered within the preceding 72 h ²⁷ because these values were deemed physiologically unlikely and adversely impacted model estimation. Patients were randomly assigned into testing, internal cross‐validation, and training data sets (Figure 1c).

PKPD model development

PKPD models adapted from models reported in the literature were implemented and estimated in NONMEM (version 7.4, ICON plc) using the Stochastic Approximation Expectation Maximization estimation method. The data were subset to include only the first three cycles of chemotherapy on record for a given patient, because patients change over time and interoccasion variability led to model instability. To build one model that covered a variety of regimens, each dose for each medication was scaled to the patient's body surface area, and then normalized to the average dose for that drug across the training population. For multiple drugs administered within a 24‐h period, the average normalized dose was implemented as a single dose where the amount was the mean of the normalized dose amounts for those drugs administered within that period. Dose “amounts” were therefore centered around 1 and most administrations fell between 0.3 and 3.

First, covariate‐free versions of candidate models were developed to identify a reasonable model structure, confirmed by visual inspection of ANC‐time curves and dependent variable‐individual prediction plots. Next, the ability of available covariates to explain individual estimates and residuals was explored using general additive models, and covariates with the most statistically significant ability to explain variability were stepwise included in the model until no further covariates were found to provide explanatory power. Baseline ANC was incorporated as a covariate acting on the baseline level of circulating cells ($\mathrm{CIR}{\mathrm{C}}_0$; see Figure S1), using the method proposed by Dansirukul et al., ²⁸ which recognizes the residual variability in baseline measurements. For other covariates, knowledge of typical PK and biology were used to identify likely relationships between covariates and PKPD parameters. Covariates were scaled to the median value in the training data set and all covariates were implemented as a power model.

Model predictions were evaluated using the Perl‐Speaks‐NONMEM tool proseval, ²⁹ which iteratively uses the first n observations to predict the (n + 1)th observation, mimicking clinical practice, where information from the future cannot be used to guide decision making.

Machine‐learning model development

The ML problem was structured as a regression to predict the next ANC given patient characteristics, laboratory values, chemotherapy dose information, and ANC values at the time of dosing. These model features are detailed in Table S2. The training data were sampled to better represent regions of particular importance for predicting neutropenia: values under 1.3 k/μL were triplicated and values greater than 2 k/μL were randomly downsampled. XGBoost was selected due to its good performance in tabular data sets, ³⁰ including in PK applications ³¹ , ³² and in chemotherapy response prediction. ³³ XGBoost models are ensembles of decision trees, with each iteratively added tree correcting the error of its predecessors, and are trained using regularization to prevent overfitting. The XGBoost model was trained using fivefold repeated cross‐validation with five repeats and a space‐filling search for hyperparameter tuning. To remain consistent with the PKPD model, data were limited to the first three cycles of chemotherapy.

Model evaluation

Model predictions were evaluated using root mean square error (RMSE) and mean percent error (MPE) of predicted ANC values relative to measured ANC values. The models were also evaluated according to their ability to predict grade 3 or 4 neutropenia (ANC <1 k/μL) using accuracy, precision, and recall. All reported metrics and figures reflect performance on the test data set. The code for the models and evaluation metrics are available in the supplementary information.

RESULTS

Patients and data collection

The total number of patients that met the inclusion criteria was 9121. ANCs indicating grade 3 or 4 neutropenia (values ≤1 k/μL) were rare in the data set, at just 4.7%, although 16% of patients experienced grade 3 or 4 neutropenia at any time during therapy (Table 1). Because the data were collected during routine clinical care, most ANCs were measured around the time of medication administration, and so there were proportionally few samples collected mid‐cycle (10%–11% of total).

TABLE 1.

Patient characteristics, disaggregated by data split.

Characteristic	Training	Cross‐validation	Testing	Overall
Number of patients	5952	1339	1830	9121
Breast	3080	682	947	4709
Lymphoma	804	182	246	1232
Thoracic	2068	475	637	3180
Absolute neutrophil counts
N total	21,831	4949	6292	33,030
N per patient	3 (1–59)	3 (2–36)	3 (1–47)	3 (1–59)
Value (k/μL)	4.8 (0.1–15)	4.9 (0.1–15)	4.9 (0.1–15)	4.8 (0.04–15)
Quantity below 1 k/μL	534	98	132	763
Patients with ≥1 value below 1 k/μL	241	44	61	346
Quantity mid‐cycle (>24 h after and >7 days before a dose)	2437	524	623	3584
Quantity measured day 1–day 4	869	173	214	1256
G‐CSF use
Total number of administrations	7725	1742	2349	11,808
Number of patients with ≥1 dose	2923	656	869	4448
Patient demographics
Age (years)	57.7 (19.6–89.4)	58.2 (22.1–89.2)	58.7 (21.2–86.1)	58.0 (19.6–89.4)
Patient‐reported sex
Female	4509	999	1388	6896
Male	1443	340	442	2225
Race
American Indian or Alaska Native	6	2	0	8
Asian	546	98	170	814
Black or African American	514	112	153	779
Native Hawaiian or other Pacific Islander	3	0	3	6
White	4413	1003	1367	6783
Other	236	54	70	360
Unknown	234	70	67	371
Ethnicity
Hispanic or Latinx	460	104	135	699
Not Hispanic or Latinx	5288	1185	1631	8104
Unknown	204	50	64	318
Additional laboratory tests and covariates
Serum albumin (g/dL)	4.2 (1.7–5.3)	4.2 (1.9–5.3)	4.2 (2.2–5.1)	4.2 (1.7–5.3)
Weight (kg)	71 (28–187)	72 (32–151)	71 (35–164)	71 (28–187)
White blood cells	6.3 (0.1–494)	6.2 (0.1–116)	6.3 (0.1–73)	6.3 (0.1–494)

Note: Values shown are median (min–max) or number.

Abbreviation: G‐CSF, granulocyte colony stimulating factor.

PKPD model development

A pragmatic literature search was conducted to identify PKPD models describing the relationship among G‐CSF, chemotherapy, and ANC that supported a broad range of chemotherapy regimens and aligned with our patient population. The model described by Melhem et al. ¹³ was identified and implemented. To tailor the model to our patient population, we attempted to re‐estimate model parameters, however, the resulting estimates proved unstable. Possibly, these difficulties were due to the high complexity of this model, which was developed on clinical trial data. Instead, the Friberg model, ³⁴ which external validation has shown to describe ANC dynamics well during chemotherapy, ³⁵ was adapted to include the stimulatory effect of subcutaneous G‐CSF acting on proliferation (ST1) and maturation (ST2) of stem cells (Figure S1). Because the data set lacked drug serum concentrations, PK parameters were fixed to values identified in the literature (see Table 2), and only PD parameters were estimated, and so this approach could also be considered a kinetic‐PD approach. The feedback parameter could not be stably estimated and was fixed to values from the literature. Interindividual variability (IIV) was added to all other PD terms, however, IIV on ST2 could not be estimated and so was removed from the model. Covariate screening identified albumin as a covariate acting on MTT, and age acting as a covariate on SLOPE and ST1, consistent with prior neutropenia PD models ³⁶ (Figure 2a). Regimen effects, modeled as one‐hot encoded covariate effects acting on MTT and SLOPE, were considered for all regimens represented by at least 50 patients in the training data set, and regimen effects that could be estimated with reasonable precision were retained in the model (Figure 2b). These retained regimen effects included only regimens with at least 230 patients, justifying our threshold of 50 patients. After inclusion of these covariates, no other covariates (such as cancer type, sex, or serum creatinine) appeared correlated with residual error or IIV based on visual inspection. The final parameter estimates for the model are shown in Table 2. The model showed good ability to describe the data, as assessed by visual predictive checks (Figure S2a–c), and showed improved predictive ability compared to the model found in the literature (precision: 47% vs. 20%, recall: 31% vs. 18%, RMSE: 2.76 k/μL vs. 2.98 k/μL, MPE: 26% vs. 14%; Figure S2d).

TABLE 2.

Final pharmacokinetic/pharmacodynamic model parameters.

Parameter	Estimate	RSE (%)	Unit	Description
Pharmacokinetic parameters
$\mathrm{C}{\mathrm{L}}_{\text{chemo}}=\theta$	5	–	L/h	Clearance of chemotherapeutic agent, fixed
$V=\theta$	50	–	L	Volume of distribution, fixed
$k_A=\theta \bullet {\left(0.153\right)}^{\mathrm{PEG}}$	0.123	–	h−1	Absorption rate of subcutaneous G‐CSF, fixed to values reported by Melhem 2018 13
$\mathrm{C}{\mathrm{L}}_{\text{GCSF}}=\theta \bullet {\left(0.258\right)}^{\mathrm{PEG}}$	13.3	–	L/h	Clearance of G‐CSF, fixed to values reported by Melhem 2018 13
$F={\theta }^{\mathrm{PEG}}$	0.646	–		Bioavailability of PEG relative to filgrastim, fixed to values reported by Melhem 2018 13
Pharmacodynamic parameters
$\text{SLOPE}=\theta \bullet S_{\text{drug}}\bullet S_{\mathrm{age}}$	107	2.8		Killing effect of drug on stem cells
$S_{\mathrm{age}}={\left(\raisebox{1ex}{$\mathrm{AGE}$}\!\left/ \!\raisebox{-1ex}{$57.2$}\right.\right)}^{\theta }$	0.752	11		Effect of age on $\text{SLOPE}$
$S_{\text{drug}}={\theta }^{\mathrm{REG}}$	0.269–1.74	2.7–24		Effect of chemo regimen on $\text{SLOPE}$, see Figure 2
$\mathrm{MTT}=\theta \bullet M_{\text{drug}}·M_{\mathrm{alb}}$	126	1.4	h	Mean transit time between bone marrow compartments. $k_{\mathrm{TR}}=4/\mathrm{MTT}$
$M_{\mathrm{alb}}={\left(\raisebox{1ex}{$\mathrm{ALB}$}\!\left/ \!\raisebox{-1ex}{$4.1$}\right.\right)}^{\theta }$	0.326	6.0		Effect of serum albumin on $\mathrm{MTT}$
$M_{\text{drug}}={\theta }^{\mathrm{REG}}$	0.458–1.89	2.3–9.7		Effect of chemo regimen on $\mathrm{MTT}$, see Figure 2
$\mathrm{FB}=\left\{\begin{array}{c}{\left(\frac{\mathrm{CIR}{\mathrm{C}}_0}{\mathrm{ANC}}\right)}^{\theta };\mathrm{ANC}<\mathrm{CIR}{\mathrm{C}}_0\hfill \\ 1;\mathrm{ANC}\ge \mathrm{CIR}{\mathrm{C}}_0\end{array}\right.$	0.16	‐		Feedback on stem cell proliferation rate based on current ANC relative to baseline ANC. Fixed to the mean value reported for γ by Kloft 2006 26
$\mathrm{S}{\mathrm{T}}_1=\theta ·P_{\mathrm{age}}$	0.960	4.9		Stimulatory effect of G‐CSF on stem cell proliferation
$P_{\mathrm{age}}={\left(\raisebox{1ex}{$\mathrm{AGE}$}\!\left/ \!\raisebox{-1ex}{$57.2$}\right.\right)}^{\theta }$	0.160	17		Impact of age on stimulatory effect of G‐CSF on stem cell proliferation
$\mathrm{S}{\mathrm{T}}_2=\theta$	0.701	6.2		Stimulatory effect of G‐CSF on stem cell maturation
Inter‐individual variability
${\omega }_{\text{SLOPE}}$	78.0	3.7	%	Interindividual variability on $\text{SLOPE}$
${\omega }_{\mathrm{MTT}}$	32.9	1.5	%	Interindividual variability on $\mathrm{MTT}$
${\omega }_{\mathrm{S}{\mathrm{T}}_1}$	9.99	1.8	%	Interindividual variability on $\mathrm{S}{\mathrm{T}}_1$
${\omega }_{\mathrm{CIR}{\mathrm{C}}_0}$	40.4	0.20	%	Interindividual variability in baseline $\mathrm{CIR}{\mathrm{C}}_0$ relative to measured ANC at baseline, fixed to the residual variability 28
Residual variability
σ	40.4	0.20	%	Proportional residual error on the log scale

Abbreviations: AGE, patient age (years); ALB, serum albumin (g/dL); ANC, absolute neutrophil count (k/μL); G‐CSF, granulocyte colony stimulating factor; PEG, use of pegfilgrastim; RSE, relative standard error; $S_{\text{drug}}$, $M_{\text{drug}}$: See Supplementary model code and Figure 2.

FIGURE 2.

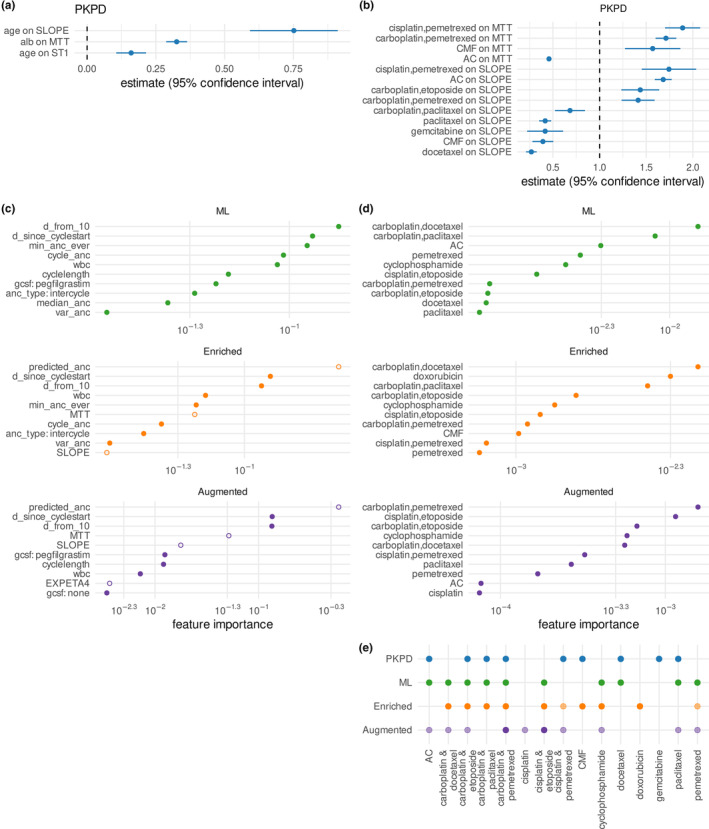
Covariate and feature effects in PKPD, ML, and hybrid models. (a) Effect sizes of age and albumin (alb) on PD parameters. (b) Effect sizes of regimens on PD parameters. (c) Top 10 most important features in ML and hybrid models, excluding regimen effects, as determined by the information gain associated with each feature. Closed circles indicate features derived from electronic health records and open circles indicate PKPD‐enriched features. (d) Top 10 most important regimen features in ML and hybrid model (e) Overlap between regimens identified as predictive in the four models. For the ML and hybrid models, features with an importance under 0.001 have been shaded semi‐transparently (see panel d). ANC, absolute neutrophil count; ML, machine learning; PD, pharmacodynamic; PKPD, pharmacokinetic/pharmacodynamic.

ML and hybrid model development

First, an XGBoost regression model was trained on 32 features derived only on data available from the EHR (Table S2). Because neutropenic ANCs values were rare (Table 1), initial models showed high rates of false negative predictions of neutropenia. Recall of neutropenic ANCs was improved by fitting the model using a pseudo‐Huber loss function, which penalizes errors below the selected threshold more strongly than errors above a selected threshold. Downsampling high observations and upsampling low observations produced a model that showed a good balance across all error metrics considered (Figure S3). The final ML model predominantly used features related to prior ANC observations and time dynamics, such as the relative number of days of the predicted ANC from the expected day 10 nadir, as well as use of G‐CSF (Figure 2c, green circles). Chemotherapy regimen was also important for model predictions (Figure 2d, green circles) and aligned with regimens identified as predictive for the PKPD model (Figure 2e).

For the enriched ML model, MAP Bayesian estimation of individual PKPD parameters was iteratively performed using PsN proseval to avoid data leakage, and these individualized parameters as well as the predicted ANCs were added as four additional features to the base ML model (Figure 1, Table S2). For this hybrid PKPD/ML model, the features derived from the PKPD model were highly important (Figure 2c, open orange circles).

Finally, an augmented ML model was developed by training the model on a data set comprised of both simulated data and RWD (see Figure 1). The simulated data were created by using the PKPD model to simulate ANC in response to chemotherapy for synthetic copies of the patients in the training data set, sampling ANC every day. Initial experiments showed that the combination of PKPD‐enriched features in addition to data augmentation produced better results than augmentation alone (Figure S4a), so subsequent efforts combined both enrichment (i.e., using features derived from the PKPD model predictions) and augmentation (i.e., using simulated data). Adding larger quantities of simulated data deteriorated model performance (Figure S4b). Instead, model performance was improved by using simulated data solely from the first 4 days after each dose of chemotherapy (Figure S4c). This period corresponds to high variability in ANC, where ANC may still be rebounding after previous doses or where G‐CSF doses, which are typically given within the first 48 h after chemotherapy, produce rapid rises in ANC. ³⁷ This period is also relatively poorly represented in the data set, making up just 3.8% of all ANC samples (Table 1). The final augmented model used the same features as the enriched model, with simulated data selected from the first 4 days of therapy added to the training data set (corresponding to an 81% increase in data set size), upsampled, and downsampled as for the RWD set. The importance of features derived from the PKPD model rose (Figure 2c, purple circles), with all four PKPD enrichment features presenting in the top 10 most important features. In contrast, regimen feature importance decreased (Figure 2d, purple circles), possibly because the neutropenic effects of many regimens well‐represented in the data set were already incorporated into the individual PKPD parameter estimates for SLOPE and MTT.

Model performance

The PKPD model and the ML model performed similarly in their ability to predict grade 3 or 4 neutropenia (Figure 3a), as quantified by accuracy (96.6%, 96.6%), precision (47%, 51%), and recall (33%, 31%). Accurate prediction of ANC value is crucial for predicting when a patient's neutrophils will rebound to appropriate levels for resuming therapy, the ML model showed lower prediction error and bias, as quantified by RMSE (2.75 k/μL, 2.57 k/μL) and MPE (26%, 15%). Variability in the data was relatively high; the ML model showed better correlation between measured and iteratively predicted values (Figure 3b; R ² of 38% vs. 33%). Compared to the PKPD model and the ML model, the enriched ML model showed improvements in all error metrics considered (accuracy: 97.0%, precision: 61%, recall: 39%, RMSE: 2.42 k/μL, MPE: 13%, and R ²: 44%). The impact of augmentation on predictive performance was mixed; whereas augmentation improved recall and MPE (44%, 11%), it showed a slight degradation in performance relative to the enriched model in accuracy, precision, RMSE, and R² (96.9%, 56%, 2.51 k/μL, and 41%). In other words, the ML and PKPD models correctly identified one out of every three patients that developed neutropenia, whereas the hybrid models identified two out of every five patient (enriched model) and four out of every nine patients (augmented model). For every two patients predicted to develop neutropenia by the ML and PKPD models, one patient would truly develop neutropenia. For the hybrid models, this ratio improved to three out of every five patients predicted to develop neutropenia.

FIGURE 3.

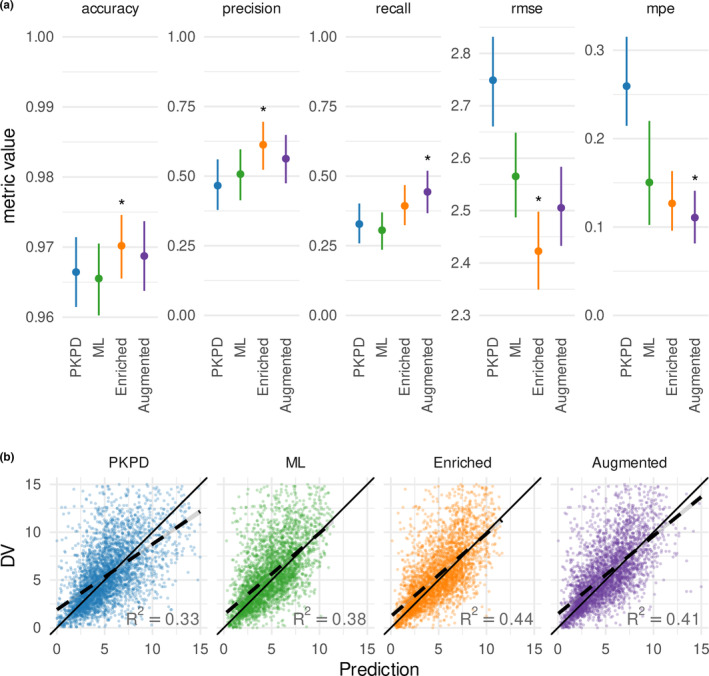
Performance of PKPD, ML and hybrid models. (a) Prediction performance is summarized according to accuracy, precision, recall, rmse, and mpe. Asterisks indicate the model with the best performance on that error metric. Lines indicate the spread between the 5th and 95th percentile and points indicate the median of 1000 bootstrapped samples. (b) Observation (DV)‐predictive IPRED plots for each model. ANC, absolute neutrophil count; DV, dependent variable; IPRED, individual predictions, made iteratively using only data available prior to the time of the observation; ML, machine learning; mpe, mean percent error; PKPD, pharmacokinetic/pharmacodynamic; rmse, root mean square error.

All four models showed reasonable ability to describe ANC dynamics (Figure S5). The PKPD model showed the expected nadir followed by a rebound after chemotherapy (see also Figure S2), although its peaks and nadirs were often muted. The ML model showed the expected nadirs, but predicted levels often did not rebound as expected. The hybrid models combined the strengths of both models, showing both the physiologically expected nadir and rebound as well as more accurately predicting the extent of the nadir. The augmented model often tracked the PKPD model very closely, especially in the first few days after a chemotherapy dose, suggesting over‐reliance on PKPD predictions relative to other information.

DISCUSSION

The combination of mechanistic models and ML to harness the strengths of both approaches has been previously proposed. ³⁸ In recent years, there have been a few applications of this strategy for clinical decision support in precision dosing. For example, ML models have been developed to improve estimation of individual PK parameters or correct PK model biases, ³¹ , ³² , ³⁹ to select an appropriate PK model ⁴⁰ or combine PK model predictions, ⁴¹ or to create a composite PD parameter for a PK‐PD model. ⁴² To our knowledge, this is the first example of a hybrid model that uses Bayesian PKPD predictions as features for an ML model. We demonstrate that this PKPD‐enriched hybrid approach shows good ability to describe ANC dynamics during chemotherapy, and predicts with higher precision and recall and lower prediction error than ML or PKPD models alone.

PKPD modeling techniques were developed to describe time variation in biomarkers based on sparse data and small data sets, which challenge ML algorithms. Feeding PKPD predictions into a relatively simple ML model helps bridge this gap in a sparsely sampled RWD set. Future work could compare the performance of this hybrid approach with more complex ML approaches in different levels of data sparsity. For example, Choo et al. ⁵ proposed a deep learning time series approach for describing ANC dynamics during chemotherapy, however, this model was developed on data an order of magnitude more densely sampled than our data, and may not be practical for many clinical applications with sparser sampling. One limitation of our study is that the data set lacked drug concentrations, and so our PKPD model relied on PK parameters reported in the literature. These assumptions add uncertainty in the relationship between drug doses and ANC described by the PKPD model. However, the ability of the model enriched with PD predictions and PD parameter estimates to outperform both the PKPD model and the ML model nevertheless speaks to the promise of this approach. It would be interesting to see to what extent enriching an ML model with drug concentration predictions and PK parameter estimates would improve a hybrid PKPD‐ML model.

Applying a hybrid PKPD/ML model to support clinical decision making will require implementation into MIPD software, such as shown in Figure 4. Because the hybrid PKPD/ML model includes many predictive features, to avoid burdensome data entry at the point‐of‐care, it is important that such a tool be integrated with the EHR. ⁴³ Although our model uses commonly available data, in some clinical scenarios, some quantities may be unknown. For some missing data, such as laboratory results with minor impacts on model predictions, imputation with typical values may be appropriate, and resulting uncertainty can be incorporated in prediction uncertainty communicated to the user. The regulatory landscape for ML‐based tools is still evolving and varies between jurisdictions. In general, the more a clinician relies on the predictions and other information presented by CDS software and the less the clinician can verify the predictions, the more regulatory oversight required. In the United States, a majority of artificial intelligence/ML applications approved by the US Food and Drug Administration were classified as Software as a Medical Device. ⁴⁴

FIGURE 4.

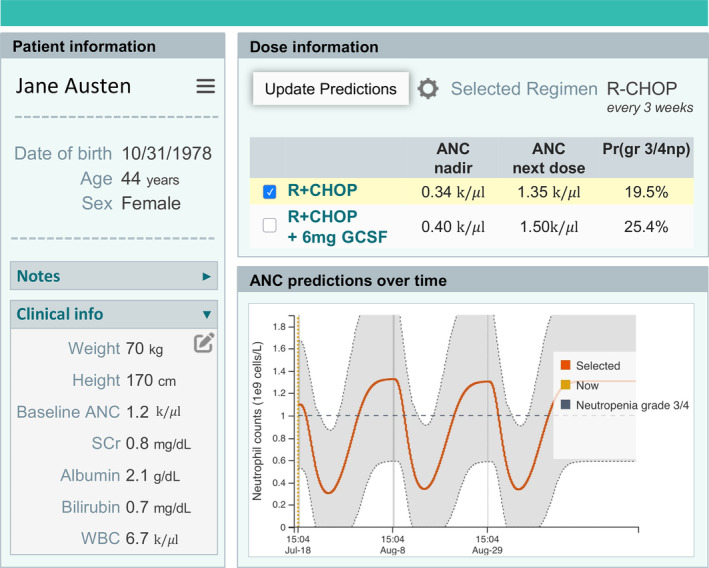
Schematic showing an example dashboard for informing clinical decision support using a hybrid PKPD‐ML model. The software collects patient data and displays them in the left side bar. Given a user‐selected regimen, the model then predicts absolute neutrophil counts with or without administration of G‐CSF, and estimates the probability of grade 3 or 4 neutropenia at the time of the next dose. ANC, absolute neutrophil count; G‐CSF, granulocyte colony stimulating factor; ML, machine learning; PKPD, pharmacokinetic/pharmacodynamic.

Augmentation of our training data using simulations from the PKPD model reduced prediction bias and improved recall but worsened performance on other metrics. This method required substantial manual tuning; larger quantities of synthetic data degraded performance substantially as the hybrid ML model learned to mimic the PKPD model used to generate the data. Familiarity with the clinical application was also necessary to identify which sampling methods would provide informative synthetic data: augmentation of the first 4 days after a dose, which is poorly sampled but where ANC changes are highly dynamic, showed better performance than other augmentation schemes investigated. Although ANCs collected during this time period proportionally made up a small part of the data set, the RWD training set informing our models was large, comprising 5952 patients and 21,831 ANC measurements. Therefore, although this part of the ANC‐time curve was sparsely sampled, there were still ample data points to inform the models. Possibly, data augmentation would provide more benefit in smaller data sets, where there are fewer examples available for an ML model to use to learn the shape of a biomarker‐time curve. However, because ML models can simply re‐learn the PKPD model and its inherent model misspecifications, this approach should be used cautiously and predictions should always be evaluated on RWD.

One drawback of our approach is that the PKPD model used for enrichment was developed on the same data as the ML models. As a result, some of the information captured by the PKPD parameters is duplicated by other ML features. For example, the enriched ML models include regimen‐related features as well as the PKPD parameters SLOPE and MTT, which themselves incorporate chemotherapy regimen. This relationship can be seen in the changes in regimen feature importance between the enriched model and the base ML model. The relative performance of the augmented and enrichment models might differ if there was less shared information between the PKPD and the ML model.

Synthetic data simulated from PKPD models necessarily only includes relationships between covariates and PD that are described in the PKPD model. Whereas each row of synthetic data provides new information about the expected shape of the ANC‐time curve, these new rows contain no information about the relationship between ANC and predictors not included in the PKPD model. Synthetic data can therefore dilute the information available about relationships that are present in the RWD but not the PKPD model. This phenomenon can be seen in the high dependency of the augmented model on PKPD predictions of ANCs and reduced importance of other predictive features (Figure 2c). This drawback is not true of PKPD enrichment of ML models, in which additional information is added to the RWD without diluting existing feature‐PD information.

The PKPD model proved difficult to estimate stably, probably due to the noisiness of RWD. Residual error was relatively high; a similar model trained on clinical trial data reported residual error of 29.8% versus 40.4% reported here. ¹³ High residual error downweighs the role of measured ANC samples during Bayesian estimation, causing the PKPD parameter estimates to hew more closely to population values. This behavior may account for the somewhat muted ANC dynamics observed in individual predicted curves. In this situation, flattening model priors could possibly improve model predictions. ³¹ However, despite its higher residual error, the PKPD model developed here produced more accurate ANC predictions in this patient population compared to the literature model, demonstrating good fit‐for‐purpose.

Model predictions should be considered in the context of physiological and mechanistic plausibility. The covariate impact of some regimens on SLOPE was counterintuitive. For example, severe neutropenia is common in patients receiving docetaxel, ⁴⁵ however, we found docetaxel reduced the impact of chemotherapy on ANC. To mitigate the highly neutropenic effects of docetaxel and similar drugs, prophylactic G‐CSF is typically prescribed. Likely, the relative contributions of regimens like docetaxel and G‐CSF on ANC were, as a result, not identifiable from the available data, and clinical judgment should be used when considering deviations from standard practice.

This study explores the benefits of a hybrid PKPD‐ML approach and examines some of the model development considerations for developing models of this type. To facilitate development of this technique, the treatment period considered was limited to only three cycles. Although these cycles correspond to a high proportion of neutropenia cases, patients typically remain on chemotherapy far beyond three cycles. Future research should explore methods of following patients across their full treatment course. This is particularly important when switching to a new chemotherapy regimen, because the patient's ability to tolerate the new regimen is uncertain and of high clinical interest, and likely varies based on past chemotherapy exposure. It would also be interesting to extend the approach presented here by enrichment with multiple PKPD models to create an ensemble PKPD‐enriched ML model. Overall, the combination of semi‐mechanistic PKPD models and ML techniques holds promise for aiding clinical decision making.

AUTHOR CONTRIBUTIONS

J.H.H., D.M.H.T., and R.J.K. wrote the manuscript. J.H.H., D.M.H.T., and V.B. performed the research. J.H.H., D.M.H.T., R.J.K., S.G., J.J.B., P.R., and B.D. designed the research and analyzed the data.

FUNDING INFORMATION

J.J.B., P.R., and B.D. were supported by the NIH/NCI Cancer Center Support Grant P30 CA008748. B.D. also acknowledges grant support from the Emerson Collective. No other funding was received for this work.

CONFLICT OF INTEREST STATEMENT

J.H.H., D.M.H.T., V.B., S.G., and R.J.K. are employees of InsightRX, which develops precision dosing software. B.D. is on the advisory board of Varian Medical Systems and holds stock or stock options in Roche. All other authors declared no competing interests for this work.

Supporting information

Appendix S1

Appendix S2

Hughes JH, Tong DMH, Burns V, et al. Clinical decision support for chemotherapy‐induced neutropenia using a hybrid pharmacodynamic/machine learning model. CPT Pharmacometrics Syst Pharmacol. 2023;12:1764‐1776. doi: 10.1002/psp4.13019