An Update to the Kaiser Permanente Inpatient Risk Adjustment Methodology Accurately Predicts In-Hospital Mortality: a Retrospective Cohort Study

Abstract

Background

Methods to accurately predict the risk of in-hospital mortality are important for applications including quality assessment of healthcare institutions and research.

Objective

To update and validate the Kaiser Permanente inpatient risk adjustment methodology (KP method) to predict in-hospital mortality, using open-source tools to measure comorbidity and diagnosis groups, and removing troponin which is difficult to standardize across modern clinical assays.

Design

Retrospective cohort study using electronic health record data from GEMINI. GEMINI is a research collaborative that collects administrative and clinical data from hospital information systems.

Participants

Adult general medicine inpatients at 28 hospitals in Ontario, Canada, between April 2010 and December 2022.

Main Measures

The outcome was in-hospital mortality, modeled by diagnosis group using 56 logistic regressions. We compared models with and without troponin as an input to the laboratory-based acute physiology score. We fit and validated the updated method using internal-external cross-validation at 28 hospitals from April 2015 to December 2022.

Key Results

In 938,103 hospitalizations with 7.2% in-hospital mortality, the updated KP method accurately predicted the risk of mortality. The c-statistic at the median hospital was 0.866 (see Fig. 3) (25th–75th 0.848–0.876, range 0.816–0.927) and calibration was strong for nearly all patients at all hospitals. The 95th percentile absolute difference between predicted and observed probabilities was 0.038 at the median hospital (25th–75th 0.024–0.057, range 0.006–0.118). Model performance was very similar with and without troponin in a subset of 7 hospitals, and performance was similar with and without troponin for patients hospitalized for heart failure and acute myocardial infarction.

Conclusions

An update to the KP method accurately predicted in-hospital mortality for general medicine inpatients in 28 hospitals in Ontario, Canada. This updated method can be implemented in a wider range of settings using common open-source tools.

Supplementary Information

The online version contains supplementary material available at 10.1007/s11606-023-08245-w.

INTRODUCTION

The Kaiser Permanente inpatient risk adjustment methodology (KP method) is a well-validated and widely used method to predict inpatient mortality using routinely collected administrative and laboratory data.^[1,2] This method generates a predicted probability of in-hospital mortality that can be used for high-quality risk adjustment in research, and quality assessment of different healthcare institutions that has been tied to funding in some jurisdictions.^[3–7] The KP method can be applied to heterogeneous non-disease-specific cohorts and is not restricted to location (e.g., ICU). The KP method has been validated in an external population and demonstrated strong performance; however, this cohort included only two hospitals and had a low mortality rate of 3.3%.^[8]

In practice, it can be difficult to use the KP method, as it requires information that is not available in most health administrative databases. First, it requires longitudinal outpatient comorbidity data to obtain the Comorbidity Point Score (COPS). Second, it requires locally developed groupings of ICD-9-CM codes, which are no longer used in most international contexts. Third, a more recent KP method involves the use of an updated LAPS2 score incorporating vital signs, mental status, and end-of-life care directives,^[2] which are seldom available in health administrative datasets. Fourth, LAPS and LAPS2 require troponin values to calculate the laboratory-based acute physiology score (LAPS). New high-sensitivity cardiac troponin assays were introduced in 2010 and have replaced conventional troponin assays in many healthcare institutions.^[9,10] High-sensitivity cardiac troponin cannot readily be harmonized to older troponin assays due to their nonlinear relationship, which makes it impossible to calculate LAPS or LAPS2 as presently formulated.^[9]

The objectives of this study are to update and validate the KP method to predict in-hospital mortality in a heterogeneous population of contemporary general medical inpatients. We update the KP method by replacing the COPS and diagnosis groupings with open-source tools that are easily implemented, and we assess models with and without troponin as an input to the LAPS. We fit and validate the updated method in 28 hospitals from Ontario, Canada.

METHODS

Data Source

We conducted a retrospective cohort study using data from 12 academic and 16 large community hospitals in Ontario, Canada, that are part of GEMINI.^[11] GEMINI is a hospital research collaborative that collects administrative and clinical data from hospital information systems with 98–100% accuracy of selected data elements compared to manual chart review.^[12]

Study Population

We included adults 18 years or older who were admitted to or discharged from general medicine. General medicine hospitalizations account for approximately 40% of all emergency admissions at study hospitals^[11] and represent a markedly heterogeneous population with no single condition representing more than 5.1% of all hospitalizations.^[13] We performed analyses in two cohorts. Cohort 1: We compared models with and without troponin as an input to the LAPS in a cohort of 7 hospitals (5 academic, 2 large community) from April 2010 to December 2020 (Cohort 1). General medicine includes many hospitalizations for cardiovascular conditions^[13] where troponin may have particular prognostic value. This analysis was limited to hospitals where the specific manufacturer of the troponin assay was known, in order to allow standardization across assays.^[14] This serves as a real-life example of the barriers to implementing existing KP methods in practice. Cohort 2: We fit and validated our updated KP method in general medicine patients from 28 Ontario hospitals (12 academic, 16 large community) from April 2015 to June 2022 (Cohort 2).

Implementing the Kaiser Permanente Inpatient Risk Adjustment Methodology

Complete details on the derivation and validation of the original KP method have previously been published.^[1,8] The variables included in the original derivation are age, sex, admission urgency (elective or emergent), service (medical or surgical), admission diagnosis, severity of acute illness as measured by the LAPS, and chronic comorbidities as measured by the COPS. Hospitalizations are grouped by diagnosis and separate logistic regression models are fit within each diagnosis group, allowing for diagnosis-specific intercepts and for each risk factor to have diagnosis-specific coefficients.

The LAPS is a continuous variable calculated by assigning points based on different laboratory values.^[1] The theoretical range of the LAPS is 0 to 256, with higher scores denoting greater mortality risk. The KP method has been updated to include LAPS2 (including lactate and vital signs), mental status, and end-of-life care directives.^[2] At our study hospitals, vital signs, mental status, and end-of-life care directives were documented in paper (vital signs, end-of-life care) or not standardized (mental status) for much of the study period and not available for analyses. Thus, we implemented the original KP method with LAPS instead of LAPS2.

We defined diagnosis groups using the Clinical Classifications Software Refined (CCSR) based on a hospitalization’s most responsible discharge ICD-10-CA discharge diagnosis code.^[15] The CCSR method groups all ICD-10 codes into mutually exclusive clinical categories and has been adapted for use with Canadian ICD-10-CA codes by GEMINI^[16] and is available as open-source software.^[17] Diagnosis groups with fewer than 150 deaths were grouped together and separated by observed in-hospital mortality rate (> 75th, 50th–75th,  < 50th percentiles) into three catch-all groups. These ranges were selected to ensure all models had sufficient events for parameter estimation and model convergence. The 150-event threshold is anti-conservative with respect to our 11 degrees of freedom; this is to maximize the number of diagnosis-specific models, and because we could examine generalizability in our analyses.

We used the Charlson comorbidity index score^[18] as our comorbidity score because it is widely used and open-source packages exist for easy calculation (in place of the COPS, which is a custom implementation based on ICD-9-CM codes). We only included emergency department and pre-admission diagnosis codes from the index hospitalization, as opposed to COPS, which requires pre-admission outpatient data that may not be available in some datasets. Van Walraven et al. have shown similar performance of the Elixhauser and Charlson scores in the KP method,^[8] and we utilized the Charlson score as it is easier to implement. Furthermore, Crooks et al. have demonstrated that using either inpatient or outpatient diagnostic codes to calculate the Charlson comorbidity index can be equally effective.^[19] We did not include medical vs surgical service as a variable because our cohort is restricted to general medicine. We calculated the LAPS using the same weights as the derivation paper, except we did not impute arterial pH, troponin, or total white blood cell count using a 2-step approach and we treat each admission as distinct (no linking of transfers).^[1] LAPS was calculated using the most extreme laboratory values between emergency department triage and time of admission. Laboratory tests that were not performed were assumed to be normal, consistent with other risk adjustments of inpatient mortality.^[20] Age was squared and modeled as a restricted cubic spline, sex as nominal, admission urgency as nominal, LAPS as linear, and comorbidity score as linear. Two-way interaction terms were included between age squared, LAPS, and comorbidity score.^[1,8]

Evaluating Performance of the KP Method Without Troponin

We excluded hospitalizations from Cohort 1 during time periods when high-sensitivity cardiac troponin assays were performed, to allow us to compare the performance of the KP method with and without conventional troponin assays. Models were fit with and without troponin and performance metrics were calculated using Harrell’s bias correction and 1000 bootstrap iterations.^[21–24] Metrics focused on both discrimination and calibration and included the c-statistic, Brier score, Nagelkerke’s R₂, calibration slope, calibration intercept, and visual depiction of bias-corrected calibration curves. Bootstrap details are available in the Appendix.

Additionally, we investigated model performance in a subgroup of hospitalizations for cardiac conditions (CCSR groups for heart failure and acute myocardial infarction). Troponin is known to be prognostic in these conditions^[25,26] so we expected these models to be most affected by removing troponin.

Evaluating Performance and Generalizability of the Updated KP Method

Models without troponin were fit in Cohort 2 and evaluated using internal-external cross-validation.^[27] This involved removing a single hospital from the training data and evaluating the performance of the model on that held-out hospital, as if it were a new hospital to the network. This procedure was repeated 28 times, once for each hospital. Model performance metrics were the same as described above, but the Brier Skill score replaced the Brier score, using the Brier score from the observed mortality rate of the held-out hospital as a reference. Given that the primary interest of this analysis was to evaluate model calibration in external hospitals, we also calculated the 50th, 95th, and 99th percentiles of absolute vertical distance between the calibration curve and diagonal line of perfect calibration (E50, E95, E99) and the integrated calibration index (ICI).^[28] Calibration curves allowed 1/4 of points influence the smoother to ensure that deviations from ideal calibration were easily visible (~ 2/3 of points is typical^[28–30]). Prior to validation, we tested whether (i) removing interactions and (ii) adding nonlinear terms for LAPS improved Akaike Information Criterion (AIC) of diagnosis-specific models and performance on internal-external cross-validation.

All analyses were performed in R version 4.1.0 using or adapting code from the rms package.^[31,32]

Ethics Approval

Research ethics board approval was obtained from all participating hospitals.

RESULTS

Cohort Characteristics

In the overall cohort (Cohort 2, 28 hospitals), there were 938,103 unique hospitalizations and 67,849 deaths (7.2%). Median age was 72 years (25th–75th 57–83), 50.0% were female, 30.5% had a Charlson comorbidity index score  ≥ 2, 2.0% of hospitalizations were elective, and median LAPS (without troponin) was 15 (25th–75th 5–27). The most common diagnosis groups were heart failure (5.0%), pneumonia (4.1%), urinary tract infections (3.8%), chronic obstructive pulmonary disease and bronchiectasis (3.7%), and neurocognitive disorders (3.1%) (Table 1). Cohort 2 included 53 diagnosis groups with at least 150 deaths, resulting in 56 logistic regression models (including the 3 catch-all groups).

Table 1.

Cohort Characteristics

	Cohort 2 28 hospitals (N = 938,103)	Cohort 1 7 hospitals (N = 206,155)
Age, median [Q1–Q3]	72.0 [57.0–83.0]	72.0 [57.0–83.0]
Female, n (%)	469,431 (50.0%)	101,606 (49.3%)
LAPS, median [Q1–Q3]	–	17 [6–30]
LAPS without troponin, median [Q1–Q3]	15 [5–27]	16 [5–29]
Charlson comorbidity index score at admission, mean (SD)	1.20 (1.75)	1.13 (1.67)
Elective admission, n (%)	19,111 (2.0%)	1054 (0.5%)
In-hospital mortality, n (%)	67,849 (7.2%)	14,265 (6.9%)
Top 10 CCSR diagnosis groups*, n (%)
Heart failure	47,049 (5.0%)	10,428 (5.1%)
Pneumonia (except that caused by tuberculosis)	38,296 (4.1%)	10,077 (4.9%)
Chronic obstructive pulmonary disease and bronchiectasis	35,918 (3.8%)	8482 (4.1%)
Urinary tract infections	34,762 (3.7%)	9296 (4.5%)
Neurocognitive disorders	29,258 (3.1%)	6837 (3.3%)
Septicemia	27,245 (2.9%)	4748 (2.3%)
Cerebral infarction	25,443 (2.7%)	7117 (3.5%)
Diabetes mellitus with complication	22,243 (2.4%)	4215 (2.0%)
Acute and unspecified renal failure	20,853 (2.2%)	3895 (1.9%)
Gastrointestinal hemorrhage	20,037 (2.1%)	4737 (2.3%)

Cohort 2 includes 12 academic and 16 community hospitals from April 2015 to June 2022

Cohort 1 includes 5 academic and 2 community hospitals from April 2010 to December 2020

^*Top 10 CCSR diagnosis groups are ranked based on Cohort 2

Abbreviations: LAPS, laboratory-based acute physiology score; CCSR, Clinical Classification Software Refined

Cohort 1, our 7 hospital cohort, included 353,489 unique hospitalizations and 14,265 deaths (6.9%). High-sensitivity troponin tests were introduced in April 2011, January 2012, November 2014, February 2015, and November 2019 in the 5 academic hospitals and were not introduced at the 2 community hospitals during our study period. After excluding time periods with high-sensitivity troponin testing, our cohort included 206,155 unique hospitalizations. LAPS values were similar with and without troponin (quantiles with troponin: 0, 6, 17, 30, 152; quantiles without troponin: 0, 5, 16, 29, 152) (Table 1). This cohort included 20 diagnosis groups with at least 150 deaths, resulting in 23 logistic regression models. No patients in Cohort 1 had missing data, and one patient in Cohort 2 was excluded due to missing age.

Evaluating Performance of the KP Method Without Troponin

The KP method accurately estimated the risk of inpatient mortality with and without troponin as an input to the LAPS. Bias-corrected c-statistics were 0.874 (95%CI 0.872–0.877) with troponin and 0.873 (95%CI 0.871–0.876) without troponin, indicating strong discrimination (Table 2). Brier scores demonstrated high accuracy in predicted probabilities and were nearly identical with and without troponin (both 0.050, 95%CI 0.050–0.051). Nagelkerke’s R² values were also similar. The exclusion of troponin from LAPS did not meaningfully affect model calibration, which was strong, as evidenced by calibration intercepts, slopes, and curves (Table 2; Fig. 1).

Table 2.

Bias-Corrected Performance of the Kaiser Permanente Inpatient Risk Adjustment Methodology, With and Without Troponin

	With troponin		Without troponin
	Apparent	Bias-corrected (95% CI)	Apparent	Bias-corrected (95%CI)
c-statistic (ROC)	0.877	0.874 (0.872–0.877)	0.876	0.873 (0.870–0.876)
Brier score	0.050	0.050 (0.050–0.051)	0.050	0.050 (0.050–0.051)
Nagelkerke’s R2	0.345	0.343 (0.337–0.349)	0.347	0.341 (0.335–0.347)
Intercept	0.000	− 0.029 (− 0.059 to 0.001)	0.000	− 0.030 (− 0.060 to 0.001)
Slope	1.000	0.984 (0.969–0.998)	1.000	0.983 (0.969–0.997)

Apparent metrics are based on models in the training data. Bias-corrected metrics are based on models from 1000 bootstrap iterations. Results are based on Cohort 1

Figure 1.

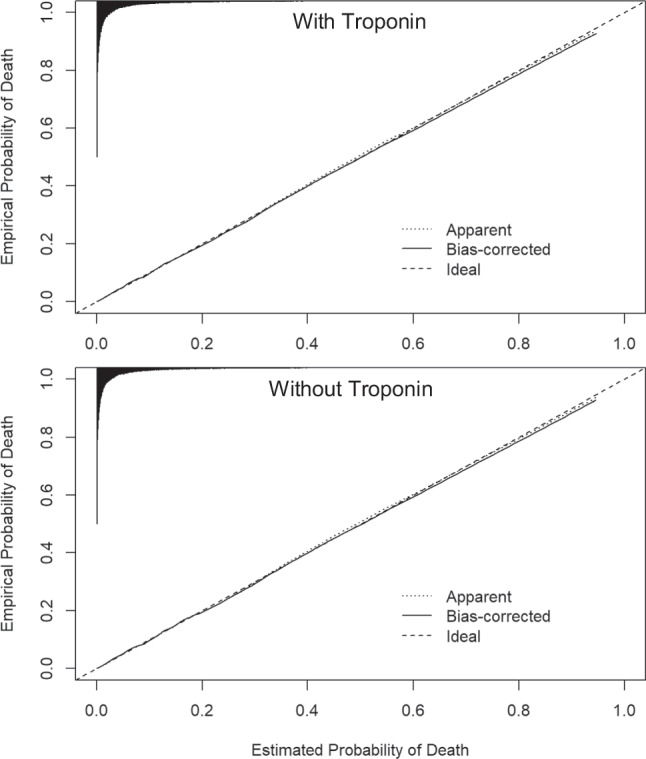
Bias-corrected calibration with and without troponin. Apparent calibration is based on models in the training data. Bias-corrected calibration accounts for optimism through 1000 bootstrap resamples. The histogram on the top denotes the distribution of predicted probabilities and is not scaled to the y-axis.

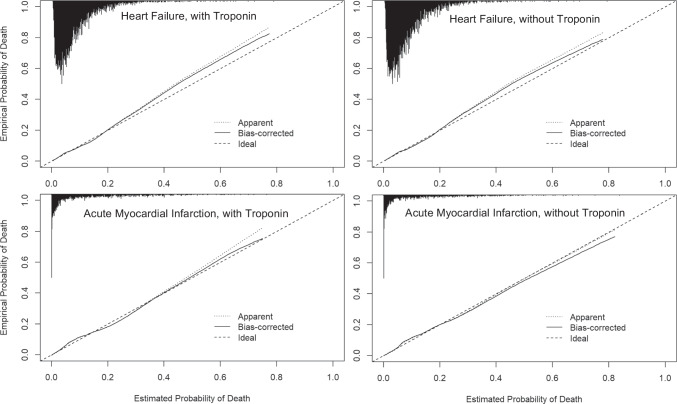
The KP method had similar performance with and without troponin in heart failure. For example, the bias-corrected c-statistic with troponin was 0.721 (95%CI 0.703–0.739) and without troponin was 0.717 (95%CI 0.700–0.735) (Table 3 and Fig. 2 for full results). Calibration curves demonstrated that exclusion of troponin led to small improvements in the agreement between high predicted probabilities and observed mortality in the heart failure model, although both models with and without troponin slightly underestimated risk of mortality at high predicted probabilities (Fig. 2). The KP method had similar discrimination with and without troponin in acute myocardial infarction (c-statistic with troponin: 0.834, 95%CI 0.810–0.858; without troponin: 0.838, 95%CI 0.815–0.860). Calibration was strong with and without troponin, though without troponin the risk of mortality at high predicted probabilities was slightly overestimated.

Table 3.

Bias-Corrected Performance of the Heart Failure and Acute Myocardial Infarction Models, With and Without Troponin

		With troponin		Without troponin
		Apparent	Bias-corrected (95% CI)	Apparent	Bias-corrected (95%CI)
Heart failure	c-statistic (ROC)	0.725	0.721 (0.703–0.739)	0.722	0.717 (0.700–0.735)
	Brier score	0.069	0.069 (0.065–0.074)	0.069	0.070 (0.066–0.074)
	Nagelkerke’s R2	0.123	0.116 (0.093–0.136)	0.117	0.111 (0.088–0.130)
	Intercept	0.000	− 0.051 (− 0.248 to 0.164)	0.000	− 0.055 (− 0.264 to 0.159)
	Slope	1.000	0.975 (0.887–1.072)	1.000	0.973 (0.879–1.069)
Acute myocardial infarction	c-statistic (ROC)	0.841	0.834 (0.810–0.858)	0.845	0.838 (0.815–0.860)
	Brier score	0.073	0.074 (0.066–0.083)	0.074	0.075 (0.067–0.083)
	Nagelkerke’s R2	0.293	0.273 (0.219–0.318)	0.298	0.279 (0.227–0.323)
	Intercept	0.000	− 0.082 (− 0.316 to 0.199)	0.000	− 0.081 (− 0.321 to 0.196)
	Slope	1.000	0.944 (0.814–1.081)	1.000	0.944 (0.814–1.081)

Apparent metrics are based on models in the training data. Bias-corrected metrics are based on models from 1000 bootstrap iterations. Results are based on Cohort 1

Figure 2.

Bias-corrected calibration of the heart failure and acute myocardial infarction models, with and without troponin. Apparent calibration is based on models in the training data. Bias-corrected calibration accounts for optimism through 1000 bootstrap resamples. The histogram on the top denotes the distribution of predicted probabilities and is not scaled to the y-axis.

Evaluating Performance and Generalizability of the Updated KP Method

Our implementation of the updated KP method is based on the original formula. See Appendix for details of our model comparisons (i) without interactions and (ii) with nonlinear terms for LAPS.

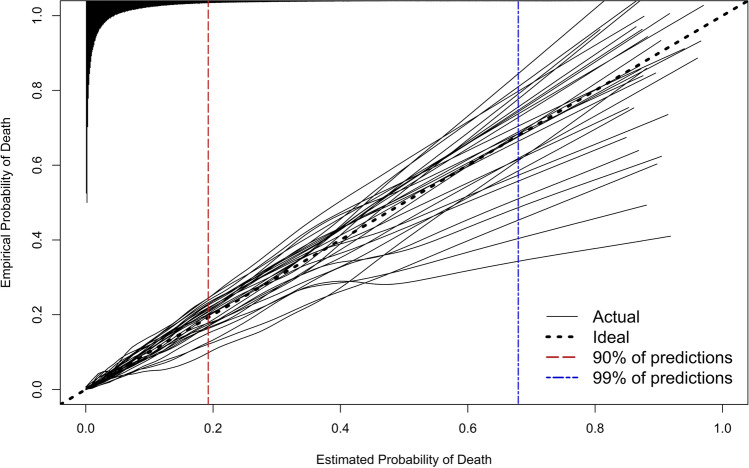
The updated KP method accurately estimated the risk of mortality for the vast majority of patients in all 28 hospitals, with strong discrimination and calibration (Fig. 3). The median c-statistic in held-out hospitals was 0.866 (see Fig. 3) (25th–75th 0.848–0.876), the median Brier Skill score was 0.200 (25th–75th 0.162–0.240), and the median Nagelkerke’s R² was 0.315 (25th–75th 0.277–0.363). The median calibration intercept was 0.096, but there was substantial variation in intercepts (25th–75th − 0.220 to 0.209, range  − 0.927 to 0.345) that reflected both under- and over-estimation at specific hospitals, partially reflecting substantial variability in hospital mortality rates (25th–75th 5.9–8.9%, range 4.2–11.7%, correlation 0.45).

Figure 3.

Performance on internal-external cross-validation for each held-out hospital. Each point is a hospital. Relative size of the points is proportional to the number of admissions at that hospital. The Brier Skill score was calculated using the Brier score from the observed mortality rate of the held-out hospital as the reference. E95 denotes the 95th percentile absolute vertical distance between the calibration curve and perfect calibration. Note that ICI and E95 are in the same units, but the y-axes are scaled differently.

Calibration was strong across the range of predicted probabilities for nearly all patients at all hospitals (Fig. 4). The ICI at the median hospital was 0.013 (25th–75th 0.007–0.017), interpreted as the median hospital having a weighted mean absolute difference between predicted and observed probabilities of 0.013 (i.e., a 1.3% weighted mean error in predicted probability of mortality). The median absolute difference between predicted and observed probabilities (E50) was 0.004 at the median hospital (25th–75th 0.002–0.009, range 0.001–0.018), E95 at the median hospital was 0.038 (25th–75th 0.024–0.057, range 0.006–0.118), and E99 was 0.068 (25th–75th 0.053–0.134, range 0.020–0.386), indicating very strong agreement between predicted and observed probabilities for the vast majority of patients at all hospitals. All performance metrics for each held-out hospital are superimposed on hospital-specific calibration curves in Figure A1.

Figure 4.

Calibration on internal-external cross-validation for each held-out hospital. The histogram on the top denotes the distribution of predicted probabilities and is not scaled to the y-axis. Ninety percent of predicted probabilities are to the left of the red vertical dashed line, and 99% of predicted probabilities are to the left of the blue vertical dashed line. Performance metrics superimposed on each held-out hospital’s calibration curve are available in Figure A1.

DISCUSSION

An updated version of the KP method accurately predicted inpatient mortality among heterogeneous general medicine inpatients at 28 hospitals in Ontario, Canada. Our internal–external cross-validation provides a realistic assessment of generalizability that directly matches the use case of a new hospital with a new data distribution adopting the method in their own patients.

We validated several changes to the KP risk adjustment method that greatly simplify its deployment in modern settings. First, we show that it can be used without troponin measurements, which eliminates the need for standardization across conventional troponin assays and enables use in settings that have switched to high-sensitivity troponin measurement, which is not readily standardized to conventional troponin measures.^[9,10] Second, we show the method works well with the Charlson comorbidity index score using only diagnosis codes from the current hospitalization rather than the COPS, which requires a custom calculation with outpatient data and ICD-9-CM codes. Third, we show the method works well without the two-step imputation to calculate the LAPS. Fourth, we show that the KP method can be deployed using the open-source CCSR software to classify diagnoses. Our findings support the external validity of the KP method in a diverse and contemporary cohort and highlight simple adaptations to enhance its adoption.

Risk adjustment methods have many use cases in research and quality improvement. Researchers can employ the updated method to adjust for clinical severity of patient populations when evaluating the effect of different in-hospital exposures on mortality. Administrators, quality improvement teams, and funders interested in quality assessment and inter-institutional comparison can use this method to account for institutions with different patient populations. We provide R functions to generate predictions based on our updated implementation, and corresponding mapping files and code in the Appendix. Anyone interested in adopting our updated method for clinical research or quality improvement applications should carefully evaluate performance in their own data and decide whether their particular aim merits recalibration of the models. Consider an example where predictions are applied to a new hospital and they systematically underestimate mortality across the range of predicted probabilities. Underestimation may be due to systematic differences in quality of care at that institution, in which case recalibrating the intercept may mask quality of care differences and be undesirable for quality assessment applications. However, poor calibration might also reflect that models do not generalize well to the patient population, and recalibration may be desirable for research applications focused solely on accurate predictions. The decision to recalibrate models, and the nature of that recalibration, should be informed by theoretical aspects of the particular use case and knowledge about one’s own patient cohort.

Few available models have been validated to accurately predict mortality in heterogeneous inpatient populations. While the Veterans Affairs (VA) inpatient risk adjustment method has similar performance to the KP method in VA data,^[20] there are several limitations to its use outside of the VA population. First, it requires marital status, which is not routinely available in health administrative data. Second, it requires data from the entire hospitalization, including ICU admission, which has the potential to introduce reverse-causality to the predictions. Third, it was developed and validated in a population that has over 94% males, which is not reflective of most health jurisdictions. Tremblay et al. have also created a simplified inpatient mortality risk prediction based on the KP method.^[33] However, its generalizability could not be assessed because data were from a single institution, and granular calibration was not assessed. Additionally, as with the original KP method, it utilized ICD-9 codes and older troponin assays. Most other inpatient risk adjustment techniques apply only to patients in the intensive care unit or with a small number of specific conditions.^[34–36]

Our results are similar to a prior external validation study.^[8] Our cohort (2015–2022) differed substantially from the prior validation cohort (1998–2002, 3.3% mortality rate). The median LAPS of the previous validation cohort was 0 in comparison to 17 in our study. The most prevalent diagnoses in the previous validation cohort were neurologic disorders (12.9%), arthritis (10.5%), and non-malignant gynecologic disease (8.5%) in comparison to congestive heart failure (5.1%), pneumonia (4.9%), and urinary tract infection (4.5%) in our study. Strong performance of the KP method in both of these external populations, separated by two decades, highlights strong generalizability. This generalizability is further demonstrated by our 28 validations in held-out hospitals with mortality rates ranging from 4.2 to 11.7%.

Limitations

One limitation of this study is that diagnosis groups were categorized according to discharge diagnosis. This is because admitting diagnosis is not reliably available in Canadian administrative hospital data. This is a primary limitation to the deployment of our implementation in real-time clinical practice. We considered defining diagnosis groups based on emergency department diagnosis codes, but this would have required excluding patients who were not admitted through the emergency department. At present, use of our method is restricted to applications where predictions are applied after a patient has been discharged from hospital. We note that prior research has shown that admission and discharge diagnoses are highly correlated within administrative data^[37,38]; thus, we believe it is likely this approach would generalize to real-time deployments, but that will require careful validation. Though the performance of the KP method was excellent in our study, Escobar et al. have demonstrated that the inclusion of lactate in an updated LAPS2 score, vital signs, and advanced directives further improve model performance.^[2] We did not include these additional predictors because vital signs and advanced directives are often unavailable in large administrative databases.^[20,39]

Conclusion

We updated and validated the Kaiser Permanente inpatient risk adjustment methodology in a large external population of heterogeneous general medicine patients. Using internal-external cross-validation with 28 hospitals, we demonstrate that the updated KP method accurately predicts inpatient mortality after several steps that simplify its use, including using common open-source tools, excluding troponin, and using ICD-10 diagnosis codes. This updated implementation of the KP method has strong discrimination, is well-calibrated, and can be used for all comers to general medicine in a variety of research and quality measurement applications.

Supplementary Information

Below is the link to the electronic supplementary material.

Author Contribution

Surain B Roberts: conceptualization, investigation, methodology, formal analysis, software, visualization, writing—original draft, writing—review and editing.

Michael Colacci: investigation, visualization, writing—original draft, writing—review and editing.

Fahad Razak: resources, data curation, supervision, writing—review and editing.

Amol A Verma: conceptualization, investigation, methodology, resources, data curation, supervision, writing—original draft, writing—review and editing.

Funding

This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors. Amol Verma receives salary support as the Temerty Professor of AI Research and Education in Medicine. The development of the GEMINI data platform has been supported with funding from the Canadian Cancer Society, the Canadian Frailty Network, the Canadian Institutes of Health Research, the Canadian Medical Protective Association, Green Shield Canada Foundation, the Natural Sciences and Engineering Research Council of Canada, Ontario Health, the St. Michael’s Hospital Association Innovation Fund, and the University of Toronto Department of Medicine, with in-kind support from partner hospitals and Vector Institute. Funders had no role in the design, conduct, or interpretation of this study.

Data Availability

We are unable to provide unlimited open access to GEMINI data because of data sharing agreements and research ethics board protocols with participating hospitals. However, researchers can request access to GEMINI data through an established process approved by our institutional research ethics boards. Please see full details at https://www.geminimedicine.ca/access-data.

Declarations

Ethics Approval

Research ethics board approval was obtained from all participating hospitals.

Conflict of Interest

SBR and MC have no disclosures. Outside of this research, FR and AV are part-time employees of Ontario Health (Provincial Clinical Leads).