Knowledge-driven learning, optimization, and experimental design under uncertainty for materials discovery

Summary

Significant acceleration of the future discovery of novel functional materials requires a fundamental shift from the current materials discovery practice, which is heavily dependent on trial-and-error campaigns and high-throughput screening, to one that builds on knowledge-driven advanced informatics techniques enabled by the latest advances in signal processing and machine learning. In this review, we discuss the major research issues that need to be addressed to expedite this transformation along with the salient challenges involved. We especially focus on Bayesian signal processing and machine learning schemes that are uncertainty aware and physics informed for knowledge-driven learning, robust optimization, and efficient objective-driven experimental design.

The bigger picture

Thanks to the rapid advances in artificial intelligence, AI for science (AI4Science) has emerged as one of the new promising research directions for modern science and engineering. In this review, we focus on recent efforts to develop knowledge-driven Bayesian learning and experimental design methods for accelerating the discovery of novel functional materials as well as enhancing the understanding of composition-process-structure-property relationships. We specifically discuss the challenges and opportunities in integrating prior scientific knowledge and physics principles with AI and machine learning (ML) models for accelerating materials and knowledge discovery. The current state-of-the-art methods in knowledge-based prior construction, model fusion, uncertainty quantification, optimal experimental design, and symbolic regression are detailed in the review, along with several detailed case studies and results in materials discovery.

Developments in the application of signal processing and machine learning methods for the discovery of novel materials can shift the current trial and error practices to informatics-driven discovery, which can reduce cost and time. This work reviews the recent developments in knowledge-driven Bayesian learning, model fusion, uncertainty quantification, optimal experimental design, and automated knowledge discovery in a historical context of robust signal processing and robust decision-making in materials science applications.

Introduction

Accelerating the development of novel functional materials with desirable properties is a worldwide imperative because it can facilitate advances in diverse fields across science, engineering, and biomedicine with significant potential contributions to economic growth. For example, the US Materials Genome Initiative (MGI) calls for cutting the cost and time for bringing new materials from discovery to deployment by half by integrating experiments, computer simulations, and data analytics.^1,2 However, the current prevailing practice in materials discovery primarily relies on trial-and-error experimental campaigns or high-throughput virtual screening approaches by computational simulations, neither of which can efficiently explore the huge materials design space to develop materials that possess targeted functional properties.

To fundamentally shift the current trial-and-error practice to an efficient informatics-driven practice, there have been increasing research efforts to develop signal processing (SP) and machine learning (ML) methods that may ultimately enable autonomous materials discovery and expedite the discovery of novel materials at a substantially reduced cost and time.^3,4,5 When applying SP and ML methods in materials science, several unique challenges arise, which include (1) a limited amount of data (if any) for investigating and exploring new materials systems, (2) data of varying and inconsistent quality because of technical limitations and a lack of common profiling prototypes, (3) significant complexity and uncertainty in existing computational simulation and surrogate models,⁶ and (4) incomplete domain knowledge.

To cope with the aforementioned challenges and to effectively discover novel functional materials with the desired target properties, robust decision-making strategies are critical for efficient exploration of the immense materials design space through effective learning, optimization, and experimental design under significant uncertainty. Directly applying existing data-driven SP and ML methods falls short of achieving these goals, and comprehensive theoretical and methodological developments tailored to address these unique challenges are crucial. Some salient issues that need to be addressed include the following:

• (1)Knowledge-based prior construction: mapping scientific knowledge into a prior distribution that reflects model uncertainty to alleviate the issues stemming from data scarcity
• (2)Model fusion: updating the prior distribution to a posterior distribution with multiple uncertain models and data sources of different data quality
• (3)Uncertainty quantification (UQ): quantification of the cost of uncertainty relative to one or more objectives for efficient materials discovery
• (4)Optimization under uncertainty (OUU): derivation of an optimal operator from the posterior distribution
• (5)Optimal experimental design (OED): efficient experimental design and data acquisition schemes to improve the model to explore the materials design space more effectively
• (6)Knowledge discovery: closing the knowledge gap in the current model, such as composition-process-structure-property (CPSP) relationships relevant to the materials discovery objectives, based on newly acquired data or increased model knowledge

In this article, we will review the recent advances related to the aforementioned research issues. Especially, we will provide an in-depth review of Bayesian SP and ML approaches for knowledge-driven learning, objective-based UQ, and efficient experimental design for materials discovery under substantial model and data uncertainties. The core foundation underlying these strategies is a Bayesian framework that enables mathematical representation of the model and data uncertainties, encoding available domain knowledge into a Bayesian prior, seamlessly integrating experimental (or simulation) data with the domain knowledge to obtain a posterior, quantifying the impact of the uncertainty on the objective, and effective design of strategies that can reduce this uncertainty. It is important to note that the guiding principle of the aforementioned Bayesian framework is to have a (knowledge-based) prior represent an uncertainty class of models. The prior characterizes the state of our knowledge about the model representing the system, based on which we can design operators to achieve the scientific objectives. Artificial intelligence for science (AI4Science) has emerged as an enormous modern research field. Because of the rapidly evolving nature of this field, it is challenging to provide a comprehensive review of all ongoing research efforts, and the readers are strongly encouraged to refer to additional resources, including recent publications in AI4Science^7,8,9,10 as well as those in AI/ML-augmented materials discovery.^11,12,13

In the following sections, we first introduce the UQ framework that encompasses the various components in knowledge-driven learning, optimization, and experimental design. This will be followed by in-depth discussion of the individual research themes, where we will review the latest research results along these directions.

Bayesian learning, UQ, and experimental design

Engineering generally aims at optimization to achieve operational objectives when studying complex systems. Because all but very simple systems must account for randomness, modern engineering may be defined as the study of optimal operators on random processes. Besides the mathematical and computational challenges that arise with classical system identification (learning) and operator optimization (control or filtering, for example) problems, such as nonstationary processes, high dimensions, and nonlinear operators, another profound issue is model uncertainty. For instance, with linear filtering there may be incomplete knowledge regarding the covariance functions or power spectra in the case of Wiener filtering. In such cases, not only must optimization of the operator (i.e., filter in this example) be relative to the original cost function but also relative to an uncertainty class of random processes. This naturally leads to the need for postulation of a new cost function that integrates the original cost function with the model uncertainty. If there is a prior (or posterior) distribution governing the likelihood of a model within the uncertainty class, then one can choose an operator that minimizes the expected cost over all possible models in the uncertainty class. In what follows, we first lay out the mathematical foundations pertinent to quantifying and handling model uncertainty and then review relevant existing literature, with recent efforts focusing on materials science research.

Mathematical backgrounds

The design of optimal operators can take different forms depending on the random process constituting the scientific model and the operator class of interest. The operators might be filters, classifiers, or controllers. The underlying random process might be a random signal/image for filtering, a feature-label distribution for classification, or a Markov process for control. Optimal operator design involves a mathematical model representing the underlying (materials) system and a class of operators from which the best operator that minimizes the cost function reflecting the objective should be selected. It takes the general form

$${\psi }_{\text{opt}}=\arg \underset{\psi \in \mathbf{\Psi }}{\min }C\left(\psi \right)\text{,}$$ (Equation 1)

where $\mathbf{\Psi }$ is the operator class, and $C\left(\psi \right)$ is the cost of applying operator ψ on the system. The genesis of such an operator design formulation can be traced back to the Wiener-Kolmogorov theory in SP for optimal linear filters developed in the 1930s,^14,15 where the operational objective is to recover the underlying signals given noisy observations with the minimum mean squared error (MSE). In this class of filtering problems, the operators mentioned above are filters. The underlying system can be modeled by a joint random process $\left(X\left(t\right),Y\left(s\right)\right)$, $t\in T,s\in S$. Optimal filtering involves estimating the signal $Y\left(s\right)$ at time s via a filter ψ given observations ${\left\{X\left(t\right)\right\}}_{t\in T}$. A filter $\psi \in \mathbf{\Psi }$ is a mapping on the space of possible observed signals, and a cost function takes the form $C\left(Y\left(s\right),\hat{Y}\left(s\right)\right)$, with $\hat{Y}\left(s\right)=\psi \left(X\right)\left(s\right)$. For fixed $s\in S$, an optimal filter is defined by Equation 1 with $C\left(\psi \right)=C\left(Y\left(s\right),\psi \left(X\right)\left(s\right)\right)=E\left[{\left(Y\left(s\right)-\psi \left(X\right)\left(s\right)\right)}^2\right]$. Similar operator design formulations have been adopted in control¹⁶ and, more recently, in ML,¹⁷ where the corresponding operators are controllers that can desirably alter the system behavior or predictive models for system properties of interest (e.g., classifiers). For example, the operator may be a predictor that tries to characterize the property of a given material based on input features (such as its composition and structure).

When the true model is not known with certainty, it would be prudent to consider the entire uncertainty class $\mathrm{\Theta }$ of possible models that contains that true model $\theta \in \mathrm{\Theta }$, where θ may be typically a parameter vector specifying the model rather than aiming at accurate inference of the true model. Given $\mathrm{\Theta }$, the goal would then be to design a robust operator that guarantees good performance over all possible models. For example, there have been significant research efforts taking a minimax strategy to design robust operators:

$${\psi }_{\text{minimax}}^{\mathrm{\Theta }}=\arg \underset{\psi \in \mathbf{\Psi }}{\min }\underset{\theta \in \mathrm{\Theta }}{\max }{C}_{\theta }\left(\psi \right)\text{,}$$ (Equation 2)

Where $C_{\theta }\left(\psi \right)$ characterizes the cost of the operator ψ for model θ. Taking filtering as an example, $C_{\theta }\left(\psi \right)=C\left(Y\left(s;\theta \right),\psi \left(X\right)\left(s;\theta \right)\right)$, where θ denotes the model parameters for the signal and observation random processes. Such a minimax robust strategy is risk averse because it aims to find an operator whose worst performance over an uncertainty class of models $\mathrm{\Theta }$ is the best among all operators in $\mathbf{\Psi }$^18,19. Minimax robustness has been applied in many optimization frameworks; for example, for filtering^20,21,22,23 with a general formulation in the context of game theory,²⁴ as well as recently in ML.^25,26 One critical downside of minimax robustness is that, in avoiding the worst-case scenario, the average performance of the designed operator can be poor, in particular when the prior knowledge about the uncertainty class $\mathrm{\Theta }$ is available and the worst-case model is unlikely. There has been extensive research on alleviating this potential issue by developing risk measures, such as conditional value at risk in a recently proposed risk quadrangle scheme,¹⁸ to achieve better trade-off between the attainment of the operational objective and the aversion of potential risk because of uncertainty.

Unlike such minimax robust strategies, we focus on Bayesian robust strategies that try to optimize the expected performance in the presence of uncertainty. This leads to the design of the intrinsically Bayesian robust (IBR) operator, which is defined as

$${\psi }_{\text{IBR}}^{\mathrm{\Theta }}=\arg \underset{\psi \in \mathbf{\Psi }}{\min }{E}_{\mathrm{\Theta }}\left[C_{\theta }\left(\psi \right)\right]\text{,}$$ (Equation 3)

where the expectation is with respect to a prior probability distribution $\pi \left(\theta \right)$ of the uncertain model $\theta \in \mathrm{\Theta }$. While not as risk averse as minimax robust operators, these Bayesian robust operators guarantee optimal performance on average. The prior $\pi \left(\theta \right)$ probabilistically characterizes our prior knowledge as to which models are more likely to be the true model than the others. If there is no prior knowledge beyond the uncertainty class itself, then a uniform (non-informative) prior may be used.

Related works

Before we delve into the Bayesian framework for learning, UQ, and experimental design, here we provide a literature review of related topics. We first review the history of operator design, in particular related to filtering, classification, and control. For optimal operator design in filtering, Kalman-Bucy recursive filtering was proposed in the 1960s²⁷ after the Wiener filter.^14,15 Optimal control began in the 1950s, as did classification as now understood. In all three areas, it was quickly recognized that often the underlying scientific model would not be known—hence the development of adaptive linear/Kalman filters and adaptive controllers.^28,29 Classification became dependent on classification rules that make no effort to estimate the true feature-label distribution.¹⁷ From the perspective of model uncertainty classes, control theorists delved into Bayesian robust control for Markov decision processes in the work of Bellman and Kalaba,³⁰ Silver,³¹ and Martin^30,31,32 in the 1960s, but computation was prohibitive, and adaptive methods prevailed. Optimal linear filtering was approached via minimax in the late 1970s in the work of Kuznetsov,²⁰ Kassam and Lim,²¹ Poor,²² and Verdu and Poor.²⁴ Model-constrained Bayesian robust (MCBR) MSE linear filtering and classification appeared in the early 2000s.^33,34

When considering uncertainty in optimization, there has been extensive research in designing different risk metrics for UQ. For example, different values at risk¹⁸ and quantities of interest (QoIs)¹⁹ have been proposed based on different statistics when modeling random processes or the corresponding model parameters as random variables, including the ones based on prediction variance³⁵ and predictive entropy.^36,37 With these risk metrics, different robust operator design strategies have been studied to derive risk-averse operators that can achieve good performance.^{19,25,26,35,37,38,39} While introducing additional risk metrics enables balancing the trade-off between the operational objectives and the potential risk (or regret) because of uncertainty, incorporating different metrics with different strategies can be subjective. For example, there may be large predictive variance or entropy, but it may not always directly affect the operational objectives and, thereafter, consequent decision-making.

Bayesian learning and experimental design offers one solution for robust design under uncertainty.^{19,40,41,42,43,44} In this framework, UQ can be naturally measured by the loss of performance because of the utilization of a robust operator to cope with uncertainty. This leads to an experimental design strategy where experiments are selected to optimally reduce this performance loss, following the early thinking of Bayesian robust filtering and control.^15,30,31,32 Such an experimental design framework, rooted in the foundation of modern engineering, closes the loop from scientific knowledge on a complex system, models for the complex system under uncertainty, data generated by the system, and experiments to enhance the current system knowledge to better attain the objectives. In this paper, we focus on this closed-loop framework, which distinguishes itself from (1) other existing schemes that are purely data driven^45,46,47,48 or (2) experimental design frameworks based on high-throughput simulations, such as $\mathrm{\Pi }$ 4U⁴⁹ and DAKOTA.⁵⁰

Data-driven frameworks heavily depend on the availability of data, upon which “black box” surrogate models are trained. They typically model the operators (used to achieve the objectives) of interest rather than modeling the system itself when designing experiments. For example, in materials discovery, many existing methods rely on Bayesian optimization (BO), which uses Gaussian processes (GPs) as surrogate models to directly approximate the target materials properties as “black box” functions.^51,52,53 While BO may be useful for optimizing the properties, the acquired data do not improve our knowledge regarding the materials system. As a consequence, there is often a scientific gap in making prior assumptions on these “black box” models and their uncertainty.⁵⁴ To better integrate scientific knowledge, such as materials’ process-structure-property relationships, as detailed under “Knowledge-driven prior construction,” the model uncertainty should be directly imposed on the system model that incorporates inter-relationships among the underlying random processes. For simulation-based frameworks, including $\mathrm{\Pi }$ 4U and DAKOTA, UQ, sensitivity analysis, and experimental design are mostly based on forward model simulations, which do not provide a natural way to propagate the data generated by the selected experiments back to the system to fill the gap in our system knowledge and to improve the current model, which is precisely what our proposed paradigm aims to do. The emphasis here is that (1) the uncertainty is placed directly on the underlying random process (i.e., current knowledge regarding the materials system) and not on surrogate models that reflect operational performance on this uncertain process and that (2) the experimental design is centered around attaining specific objectives. A wide range of approaches can emerge, depending on the assumptions made regarding the uncertainty class, action space, and experiment space. Popular Bayesian experimental design policies, such as knowledge gradient (KG)^46,47 and efficient global optimization (EGO),⁴⁵ are special cases in this framework under their modeling assumptions. These approaches often adopt generic surrogate models with the uncertainty placed on the reward function; therefore, there is no direct connection between the prior model assumptions and the underlying process/system.

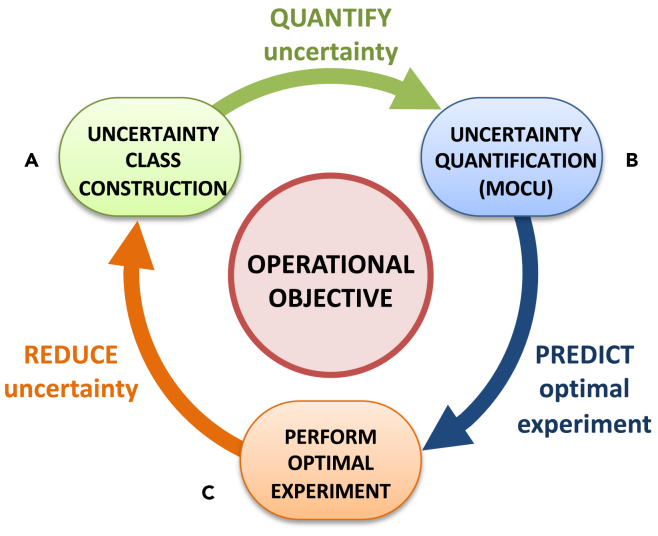
Because of these characteristics, Bayesian frameworks have been increasingly used to address a wide range of materials discovery problems.^{55,56,57,58,59} BO’s ability to balance the exploration and exploitation is ideally suited in materials discovery tasks because queries to the materials design space (either through computations or experiments) are extremely resource intensive. Most approaches focused on materials discovery are myopic in the sense that increased knowledge of the materials space being explored is not necessarily part of the objective. In other cases, Bayesian learning is used to increase knowledge of the physics underlying observed physical phenomena without much attention being put on improving the materials’ performance relative to the existing state of the art.^{60,61,62,63,64} In materials discovery applications, the complexity and stochasticity because of substantial model and data uncertainty call for SP and ML approaches in a Bayesian setting that can provide a unified closed-loop framework for objective-based learning and optimal design of robust operators and effective experiments under uncertainty. This is illustrated in Figure 1.

Figure 1.

Illustration of the knowledge-driven optimal experimental design (OED) cycle for materials discovery

IBR operator and mean objective cost of uncertainty (MOCU)-based UQ

In this section, we focus on the objective-based UQ (objective-UQ) framework using the MOCU,^65,66 which measures the expected loss with respect to the final operational objective because of the model uncertainty. Uncertainty is directly imposed on the model representing the underlying system and not on the parameters of the operator, as typically done in the ML community. Because the uncertainty is on the system model, reduction of this uncertainty inevitably leads to improving our knowledge regarding the system, leaving no discrepancy between what is learned (through data acquisition or experiments) about the model and what we know about the underlying system (and the relevant science).

Consider a stochastic model $\mathcal{M}$ with uncertainty class $\mathrm{\Theta }$ composed of possible parameter vectors. Let C be a cost function and $\mathrm{\Psi }$ a class of operators on $\mathcal{M}$. For each operator $\psi \in \mathrm{\Psi }$, $C_{\theta }\left(\psi \right)$ denotes the cost of applying ψ on the model parametrized by $\theta \in \mathrm{\Theta }$. An IBR operator on $\mathcal{M}$ is an operator ${\psi }_{\text{IBR}}\in \mathrm{\Psi }$ so that the expected value over $\mathrm{\Theta }$ of the cost $C_{\theta }\left(\psi \right)$ is minimized by ${\psi }_{\text{IBR}}$ as formulated in Equation 3,⁶⁷ the expected value being with respect to a prior probability distribution $\pi \left(\theta \right)$ capturing model uncertainty over $\mathrm{\Theta }$. Here, each parameter vector $\theta \in \mathrm{\Theta }$ corresponds to a model, and $\pi \left(\theta \right)$ quantifies the likelihood that a model is $\mathrm{\Theta }$ and therefore reflects prior knowledge. If there is no prior knowledge beyond the uncertainty class itself, then it is taken to be uniform with all models being equally likely. Given a data sample S sampled independently from the full model, the IBR theory can be used with a posterior distribution ${\pi }^{\ast }\left(\theta \right)=\pi \left(\theta |S\right)$, giving the optimal Bayesian operator. Because of the optimality of the IBR operator ${\psi }_{\text{IBR}}$ over $\mathrm{\Theta }$, $E_{\mathrm{\Theta }}\left[C_{\theta }\left({\psi }_{\text{IBR}}\right)\right]\le E_{\mathrm{\Theta }}\left[C_{\theta }\left(\psi \right)\right]$ for any operator ψ. For $\theta \in \mathrm{\Theta }$, the objective cost of uncertainty relative to θ is the difference between $C_{\theta }\left({\psi }_{\text{IBR}}\right)$ and $C_{\theta }\left({\psi }_{\theta }\right)$. Averaging this loss differential provides our basic UQ, the MOCU:⁶⁵

$$\text{MOCU}\left(\mathrm{\Theta }\right)=E_{\theta }\left[C_{\theta }\left({\psi }_{\text{IBR}}\right)-C_{\theta }\left({\psi }_{\theta }\right)\right]\text{,}$$ (Equation 4)

where ${\psi }_{\theta }$ denotes the optimal operator with respect to the model specified by the model parameter θ. The expectation is computed with respect to the distribution $\pi \left(\theta \right)$ of the model θ in the uncertainty class $\mathrm{\Theta }$.

While the entropy of the prior (or posterior) has been commonly used to measure model uncertainty, entropy, however, does not focus on the objective. In other words, there may be large entropy, but it may not directly affect the operational objective because it may not affect the expected cost in Equation 13. Unlike entropy, MOCU aims to quantify the uncertainty that practically “matters” as it pertains to a specific objective (Figure 1).

IBR (with a prior) and optimal Bayesian (with an updated posterior given observed data) operator design have been applied in modern engineering, statistics, and ML. Based on different operators (for example, for filtering, classification, and control) and their corresponding cost functions, the research focus has been mostly on solving the corresponding inference and optimization problems, known as Bayesian learning or Bayesian inverse problems.^68,69,70 When systems understanding and operator design are the objectives of modeling complex systems, Bayesian experimental design and decision-making are often with respect to the uncertainty class of models and the cost function related to the operator of interest. More importantly, MOCU provides a natural measure for the cost of uncertainty that quantifies the potential operator performance degradation because of uncertainty, directly focusing on operational objectives. Therefore, this IBR-MOCU framework not only provides the robust operator design and objective-oriented UQ but also leads to experimental design to choose an experiment to optimally reduce performance loss by adding to existing scientific knowledge. The IBR-MOCU paradigm follows in line from the early thinking of Wiener and Kolmogorov, and it extends and unifies previous work on robust filtering, classification, and control. The historical context of the IBR-MOCU framework is depicted in Figure 2.

Figure 2.

Illustration of the historical context of the intrinsically Bayesian robust (IBR) framework and the concept of mean objective cost of uncertainty (MOCU)

In the following sections, we focus on recent developments on the corresponding components of this IBR-MOCU framework, including prior construction, model fusion, OED, and automated feature engineering for knowledge discovery in the context of materials science applications.

Knowledge-driven prior construction

The first challenge of applying SP/ML methods in the MOCU framework to materials science is modeling and quantifying uncertainty because there rarely exist sufficient data for satisfactory system identification because of the enormous search space and the complicated CPSP relationships.⁴ Small samples are commonplace in materials applications, in particular when the research focus is to discover novel complex functional materials. Thereafter, if prior knowledge, such as physics principles, may help constrain the SP/ML model space, it is critical to utilize these in systems modeling.^71,72,73 While Bayesian methods naturally model the uncertainty because of their distribution-based nature to treat model parameters as random variables, the salient obstacle confronting Bayesian methods is how to appropriately impose model prior.

Regarding prior construction, Jaynes⁷⁴ has remarked, “… there must exist a general formal theory of determination of priors by logical analysis of prior information—and that to develop it is today the top priority research problem of Bayesian theory.” However, the most common practice of Bayesian methods is to adopt either non-informative or conjugate prior for computational convenience. When there are limited data or strong scientific prior knowledge, it is precisely then that the formal structure as commented by Jaynes⁷⁴ is critical for appropriate prior construction.

In this section, we first briefly review traditional prior construction methods and then focus on the formal structure for prior construction involving a constrained optimization, in which the constraints incorporate existing scientific knowledge augmented by slackness variables. The constraints tighten the prior distribution in accordance with prior knowledge while at the same time avoiding inadvertent over-restriction of the prior, an important consideration with small samples.

Traditional priors

Starting from Jeffreys’⁷⁵ non-informative prior, there was a series of information-theoretic and statistical methods: maximal data information priors (MDIP),⁷⁶ non-informative priors for integers,⁷⁷ entropic priors,⁷⁸ reference (non-informative) priors obtained through maximization of the missing information,⁷⁹ and least informative priors.⁸⁰ As discussed in the literature,^81,82,83 the principle of maximum entropy can be seen as a method of constructing least informative priors,^84,85 though it was first introduced in statistical mechanics for assigning probabilities. Except in the Jeffreys’⁷⁵ prior, almost all of the methods are based on optimization: maximizing or minimizing an objective function, usually an information theoretic one. The least informative prior⁸⁰ is found among a restricted set of distributions, whereas the feasible region is a set of convex combinations of certain types of distributions. Zellner⁸⁶ proposed several non-informative and informative priors for different problems. All of these methods emphasize the separation of prior knowledge and observed sample data.

A priori knowledge in the form of graphical models (e.g., Markov random fields) has also been widely utilized to either constrain the model space (for example, in covariance matrix estimation in Gaussian graphical models)^87,88 or impose regularization terms.⁸⁹ In these studies, using a given graphical model illustrating the interactions between variables, different problems have been addressed; e.g., constraints on the matrix structure^87,90,91 or known independencies between variables.^88,92 Nonetheless, these studies rely on a fundamental assumption: the given prior knowledge is complete and hence provides one single solution. However, in many applications, the given prior knowledge is uncertain, incomplete, and may contain errors. Therefore, instead of interpreting the prior knowledge as a single solution (e.g., a single deterministic covariance matrix), we aim to construct a prior distribution on an uncertainty class.

CPSP relationships in materials science

A central tenet in the field of materials science and engineering is that the processing history controls the material’s internal structure, which, in turn, controls the effective (macroscale) properties or performance characteristics exhibited by the material. Exploration and exploitation of the materials space thus necessitate the generation of CPSP linkages.^93,94 Given the multiscale nature of the material’ structures,⁹³ such (abstract) sets of CPSP linkages can be visualized as a large connected and nested network of models that mediate the flow of information about the material’s state and behavior up and down the scales.

Any single model in this large network of models can be formally expressed as $f\left(\mu ,\phi \right)$, where μ represents the appropriate CPSP variables (i.e., related to process history, material structure, or material property), and φ denotes variables describing the physics controlling the material phenomenon of interest. Established domain knowledge can be used to construct a prior on φ. Seeking $f\left(\mu ,\phi \right)$ allows us to explicitly capture physics in formulating our ML/AI models. This allows us to use physics-based simulation data to train $f\left(\mu ,\phi \right)$ by independently varying μ and φ. Given the enormous challenges associated with the development of concurrent multiscale CPSP relationships, materials analysis tends to be carried out (most of the time) at different, not necessarily strongly coupled scales. At the mesoscale level and beyond (i.e., larger than the atomic scale), several efforts have been made to predict materials’ behavior by using data-driven approaches. Most successful efforts at this scale have exploited low-dimensional representation of microstructure information to build effective property models.⁹⁵ To date, however, there is not much work on the direct use of physical principles to constrain the models used to establish these CPSP linkages. In this regard, more success has been achieved when considering the structure-property connections at the atomic scale.

From the atomic point of view, materials are fundamentally composed of atoms of similar or different types of chemical elements located on real-space sites. The equilibrium atomic structures of materials are reached through the minimization of total energy originated from the complex interaction among ions and electrons in the presence/absence of the external field. It consists of the Coulomb and kinetic energy of electrons and ions and the additional important contributions from quantum mechanical effects, such as (1) exchange energy because of the fermionic spin statistics of electrons, (2) static and dynamical correlation energy beyond the single Slater determinant approximated electronic wave functions, and (3) nuclear quantum effects when tunneling and delocalization of ions become important.⁹⁶ Recently, a graph convolutional neural network has been applied to describe crystal and molecular structures of materials because atoms and bonds can be perfectly represented by graph nodes and edges, respectively. Recent examples include the crystal graph convolutional neural networks (CGCNN),⁹⁷ the improved CGCNN (iCGCNN),⁹⁸ the materials graph network (MEGNet),⁹⁹ etc. An underlying physical prior hypothesis is the locality of interactions; that is, the physical knowledge of interest can be learned from the local chemical interactions. For example, in the CGCNN,⁹⁷ the feature vector ${\mathit{v}}_i$ for atom i is updated via iterative convolution as

$${\mathit{v}}_i^{\left(t+1\right)}={\mathit{v}}_i^{\left(t\right)}+\sum _{j,k}\sigma \left({\mathit{z}}_{{\left(i,j\right)}_k}^{\left(t\right)}{\mathit{W}}_f^{\left(t\right)}+{\mathit{b}}_f^{\left(t\right)}\right)\odot g\left({\mathit{z}}_{{\left(i,j\right)}_k}^{\left(t\right)}{\mathit{W}}_s^{\left(t\right)}+{\mathit{b}}_s^{\left(t\right)}\right)\text{,}$$ (Equation 5)

where $z_{{\left(i,j\right)}_k}^{\left(t\right)}={\mathit{v}}_i^{\left(t\right)}\oplus {\mathit{v}}_j^{\left(t\right)}\oplus {\mathit{u}}_{{\left(i,j\right)}_k}$ is the concatenated neighbor vector consisting of atom i’s feature vector ${\mathit{v}}_i$, feature vector ${\mathit{v}}_j$ of atom j located on the k-th bond of atom i, and the corresponding bond feature $u_{{\left(i,j\right)}_k}$. σ is a sigmoid function, and g is a nonlinear softmax activation function. $\mathit{W}$ and $\mathit{b}$ denote the convolution weight matrix and bias of the corresponding layer, respectively. In these convolutional filters, the summation only runs through the local neighboring sites via local coordination determination⁹⁷ or Voronoi tessellation.⁹⁸ The results from these graph convolutional neural network approaches are promising because it is generally true that the physical interaction decreases as the distance of $\left(i,j\right)$ atom pair (i.e., bond length), increases. This a priori physical knowledge is built inside these graph networks as an implicit constraint. While the bare Coulomb operator decays slowly with $1/r$, the destructive interference of electronic wave functions in many-particle systems leads to the nearsightedness of electronic matter in the absence of long-range ionic interactions;^100,101 i.e., local electronic properties, such as electron density, depend mostly on the effective external potential at nearby locations. However, for ionic systems, the long-range Coulomb interaction can have a non-negligible contribution to the total energy and atomic forces even when the $\left(i,j\right)$ atom pair is separated far away, and further consideration to include these long-range interactions will be of great importance to more accurate describe the physical properties of ionic materials. In addition to these interaction-based physics principles, another important consideration when developing ML methods for materials systems is to make sure that the input feature and the derived descriptor representations should be invariant to the symmetries of the system, such as rotation, reflection, translation, and permutation of atoms of the same species. Kernel-based methods and topological invariants based on group theory have been recently investigated to help improve the accuracy of predictions in the ML modeling of solid state materials.¹⁰²

Maximal knowledge-driven prior (MKDIP) construction

Knowledge-driven prior construction utilizes first principles and expert domain knowledge to alleviate the model/data uncertainty and the small sample size issues through constraining the model space or deriving the uncertainty class of models based on physical and chemical constraints. Incorporating scientific knowledge to directly constrain Bayesian predictive models can achieve robust predictions, which would be impossible by using data alone. In materials science, there is a substantial body of knowledge in the form of phenomenological models and physical theories for prior construction. Such knowledge can be used in choosing features or descriptors and constrain the model space for predicting novel materials with desired properties.

To translate more general materials knowledge into Bayesian learning, a general prior construction framework can be developed to map the known physical, chemical, and structural constraints into prior distributions in Bayesian learning. We have proposed such a framework, capable of transforming any source of prior information to prior probabilities given an uncertainty class of predictive models.^{103,104,105,106} We call the final prior probability constructed via this framework an MKDIP. The new MKDIP construction constitutes two steps: (1) functional information quantification, where prior knowledge manifested as functional relationships is quantified as constraints to regularize the prior probabilities in an information theoretic way, and (2) objective-based prior selection, where, by combining sample data and prior knowledge, we build an objective function in which the expected mean log likelihood is regularized by the quantified information in step (1). As a special case, where we do not have any sample data, or where there is only one data point available for constructing the prior probability, the proposed framework is reduced to a regularized extension of the maximum entropy principle (MaxEnt).¹⁰⁷

By introducing general constraints, which can appear as conditional statements based on expert domain knowledge or physics principles, the idea here is to maximally constrain the model uncertainty with respect to the prior knowledge characterized by these constraints. To give a simple example, assuming that we know a priori, based on physics principles, that certain microstructural properties R for a target material are determined by its composition X, we then can derive the corresponding constraint $E_{\pi }\left[H_{\theta }\left(R|X\right)\right]\le \xi$, where $H_{\theta }\left(R|X\right)$ denotes the conditional Shannon entropy of R given X under the probabilistic model determined by θ. If our prior knowledge is correct, then $H_{\theta }\left(R|X\right)\to 0$ for any appropriate model. Hence, under the uncertainty characterized by the prior distribution $\pi \left(\theta \right)$, we aim to derive the MKDIP with the expected conditional entropy as small as possible. Depending on different types of prior knowledge, we can write different forms of such constraints. Specifically, the MKDIP construction integrates materials science and statistical learning by (1) model prior knowledge quantification, where general materials knowledge, from physical theories or expert domain knowledge, is quantified via quantitative constraints or conditional probabilities and (2) optimization, where MKDIP construction requires solving the constrained optimization problems depending on different applications and data types of available observed measurements. When sufficient data exist, we can also split the data for prior construction and for updating the posterior, appropriately integrating prior knowledge and existing data.

In particular, MKDIP aims to derive the solution to the following optimization problem:

$$\arg \underset{\pi \in \mathrm{\Pi }}{\min }{E}_{\pi }\left[C_{\theta }\left(\xi ,D\right)\right]\text{,}$$ (Equation 6)

where $\mathrm{\Pi }$ is the set of all proper priors, and $C_{\theta }\left(\xi ,D\right)$ is a cost function that depends on 1 θ, the random vector parameterizing the underlying probability distribution; (2) ξ, our state of (prior) knowledge; and (3) D, partial observations. Alternatively, by parameterizing the prior probability as $\pi \left(\theta ;\gamma \right)$, with $\gamma \in \mathrm{\Gamma }$ denoting the hyperparameters, the MKDIP can be found by solving

$$\arg \underset{\gamma \in \mathrm{\Gamma }}{\min }{E}_{\pi \left(\theta ;\gamma \right)}\left[C_{\theta }\left(\xi ,D\right)\right]\text{.}$$ (Equation 7)

We have considered cost functions $C_{\theta }$ that can be decomposed into three terms:¹⁰⁶

$$C_{\theta }\left(\xi ,D\right)={\lambda }_1\left[\left(1-\beta \right)g_{\theta }^{\left(1\right)}\left(\gamma \right)+\beta g_{\theta }^{\left(2\right)}\left(D\right)\right]+{\lambda }_2{g}_{\theta }^{\left(3\right)}\left(\xi \right)\text{,}$$

where β, ${\lambda }_1$, and ${\lambda }_2$ are non-negative regularization parameters. Here, $g^{\left(1\right)}(·)$ denotes the information-theoretic cost, which can take different forms, including MaxEnt;¹⁰⁷ $g^{\left(2\right)}(·)$ is the cost that involves the partially observed data when they are available, including regularized MDIP and regularized expected mean log likelihood prior;¹⁰³ and, more critically, $g^{\left(3\right)}(·)$ denotes the knowledge-driven constraints that convert prior knowledge into functional constraints to further regularize the prior as detailed in Boluki et al.¹⁰⁶ Using this cost function, we formulate the MKDIP construction problem as the following optimization problem:

$$\begin{array}{c}{\mathrm{argmin}}_{\gamma \in \mathrm{\Gamma }}{\mathrm{E}}_{\theta }\left[\left(1-\beta \right){\mathrm{g}}_{\theta }^{\left(1\right)}\left(\gamma \right)+\beta {\mathrm{g}}_{\theta }^{\left(2\right)}\left(\mathrm{D}\right)\right]\\ \text{Subject}\text{to}:{\mathrm{E}}_{\theta }\left[{\mathrm{g}}_{\theta ,\mathrm{i}}^{\left(3\right)}\right]>0;\mathrm{i}\in \left\{1,\dots ,{\mathrm{n}}_{\mathrm{c}}\right\}\text{,}\end{array}$$ (Equation 8)

where $g_{\theta ,i}^{\left(3\right)}$, $\forall i\in \left\{1,\dots ,n_c\right\}$, are constraints resulting from our state of knowledge ξ via the mapping $\mathcal{T}$: $\xi \to E_{\theta }\left[g_{\theta ,i}^{\left(3\right)}\right]>0$, $\forall i\in \left\{1,\dots ,n_c\right\}$; for example, based on the aforementioned composition-structure relationship $E_{\pi }\left[H_{\theta }\left(R|X\right)\right]$. The overall MKDIP scheme is illustrated in Figure 3.

Figure 3.

Illustration of knowledge-based prior construction via MKDIP

In contrast to non-informative priors, MKDIP aims to incorporate the available prior knowledge and uses part of the data to construct an informative prior. While, in theory, the observed data can be entirely used in the optimization problem in Equation 8, in practice one should be cautious to avoid overfitting to the given data. The MKDIP construction here introduces a formal procedure for incorporating prior knowledge. It allows the incorporation of the knowledge of functional relationships and any constraints on the conditional probabilities. Finally, we shall note that deriving the solution to the MKDIP optimization problem Equation 8 can be challenging because of the non-convexity of the objective function and constraints. Nevertheless, feasible and local optimal solutions, especially with the specific distribution families and constraint forms, can be derived.¹⁰³

Integrating prior knowledge in materials science

Xue et al.⁵² have applied Bayesian learning and experimental design based on materials knowledge using results from the Landau-Devonshire theory for piezoelectric materials. In particular, a Bayesian regression model,⁵⁴ constrained by the Landau functional form and the constraints on morphotropic phase boundaries (MPBs), was developed to guide the design of novel materials with the functional response of interest and to help navigate the search space efficiently so that the desired composition can be achieved in a few trials. The Landau-Devonshire theory has been widely used to reproduce phase diagrams for many piezoelectrics and to investigate their performance at the MPB. The ferroelectric nanodomain phases can be characterized by different polarization vectors, $\overrightarrow{p}=\overrightarrow{n}p$, where $\overrightarrow{n}={\left[n_1,n_2,n_3\right]}^T$ is a unit vector in the direction of polarization, and p is its magnitude.¹⁰⁸ The free energy, g, of the ferroelectric system (e.g., ${BaTiO}_3$ -based piezoelectrics) can be described by a Landau polynomial that depends on the modulus of the polarization vector (p) and the polarization direction ($\overrightarrow{n}$) at a given temperature τ:

$$g\left(p,\overrightarrow{n};\tau \right)=\frac{\alpha }{2}\left(n_1^2+n_2^2+n_3^2\right)p^2+\frac{{\beta }_1}{4}{\left(n_1^2+n_2^2+n_3^2\right)}^2{p}^4+\frac{{\beta }_2}{4}\left(n_1^4+n_2^4+n_3^4\right)p^4+\frac{{\gamma }_1}{6}{\left(n_1^2+n_2^2+n_3^2\right)}^3{p}^6+\frac{{\gamma }_2}{6}\left(n_1^6+n_2^6+n_3^6\right)p^6+\frac{{\gamma }_3}{6}\left(n_1^2{n}_2^2{n}_3^2\right)p^6\text{,}$$

where the coefficients α, β′s, and γ′s are materials dependent and often determined from experiments; for example, ${\beta }_2\left(\tau ,x\right)$ depends on the temperature (τ) and composition (x). The MPB is a phase boundary where the two phases (i.e., tetragonal [T] and rhombohedral [R] phases in ${\text{BaTiO}}_3$-based piezoelectrics) coexist and have degenerate free energy. Therefore, at MPB ($\tau ={\tau }_{MPB}$ and $x=x_{MPB}$), $g_T=g_R$, which leads to

$${\beta }_2\left({\tau }_{MPB},x_{MPB}\right)+\frac{24{\gamma }_2-{\gamma }_3}{27}{p}_{eq}^2\left({\tau }_{MPB},x_{MPB}\right)=0\text{,}$$

$p_{eq}^2\left(\tau ,x\right)$ denotes the polarization at equilibrium and has the functional form $\rho \left(\tau -{\tau }_C\left(x\right)\right)$, where ρ is a constant, and ${\tau }_C\left(x\right)$ is the composition-dependent Curie temperature. Based on these relationships (more details can be found in Xue et al.⁵²), the MPB curve has the following quadratic form:

$${\tau }_{MPB}\left(x\right)={\omega }_1{x}^2+{\omega }_{2}x+C_1\text{,}$$

where ${\omega }_1$, ${\omega }_2$, and $C_1$ are the corresponding model parameters to learn from experimental data. This serves as the prior knowledge to constrain our Bayesian regression model to map the material composition x to the MPB curves.

As illustrated in Figure 4, with the minimal collected data (only 20 characterized BaTiO₃-based piezoelectrics), the Bayesian regression model with the aforementioned functional constraints provides reliable phase boundaries and faithful uncertainty estimates. More importantly, we demonstrated our approach for finding BaTiO3-based piezoelectrics with the desired target of a vertical MPB. We have predicted, synthesized, and characterized a solid solution, (Ba_0.5Ca_0.5)TiO₃-Ba(Ti_0.7Zr_0.3)O₃, with piezoelectric properties showing better temperature reliability than other BaTiO₃-based piezoelectrics in our initial training data.

Figure 4.

Bayesian learning and experimental design constrained by the Landau functional for discovery of BaTiO₃-based piezoelectrics as described in the text

Shown are predicted (solid lines) and experimental (dots) phase diagrams for BZT-m50-n30, together with uncertainty estimates, from Bayesian regression. The solid lines show the mean phase boundaries, and the dashed lines mark the 95% confidence intervals. Notice the uncertainty reduction given more data.

When the prior knowledge, including different functional forms and constraints, is available, the MKDIP framework can help take the best advantage of them to explicitly determine the predictive models as well as their corresponding predictors for specific functional responses of interest. Besides such explicit functional-form prior knowledge, which allows us to directly constrain predictive models, the existing prior knowledge on CPSP relationships may simply be in the form of correlation, conditional relationships, and inequality constraints. To enable users, especially materials domain experts, to easily explore and integrate existing phenomenological knowledge into Bayesian learning, infrastructure and friendly user interfaces should be developed to help prior construction via active knowledge acquisition from either materials scientists or even more recent large language foundation models as the unprecedented knowledge base.^9,13 The current practice is mostly hand crafted based on different problems and how data scientists work with their collaborating materials scientists. More interfacing efforts between data scientists and materials domain experts are required to achieve more synergistic collaboration in materials science.

Bayesian model averaging (BMA) with experimental design

With a derived surrogate model, we would like to exploit it in combination with experiments to accelerate the development of new materials. However, often, because of incomplete prior knowledge, there are multiple feasible surrogate models within the uncertainty class. We further explore a Bayesian experimental design framework that is capable of adaptively selecting or aggregating competing models connecting materials composition and processing features to performance metrics through BMA.^109,110

Review on Bayesian model fusion

Bayesian model fusion methods have been studied extensively to achieve better predictive accuracy as well as robust risk and uncertainty estimates.^{70,109,111,112} There are different Bayesian model ensemble strategies stemming from the Bayes’ theorem from Bayesian inference,⁷⁰ including Bayesian model selection, Bayesian model combination, and BMA. They all start with an ensemble of candidate models as the uncertainty model class and then update the model posterior probabilities given observed data. The main difference among these different strategies lies in how the updated posterior probabilities guide the way to derive posterior predictive probabilities. For example, Bayesian model selection aims to identify the best predicting model(s) with different criteria, including the Bayesian information criterion (BIC) and Akaike information criterion (AIC).^113,114 Bayesian model combination often samples the best model subsets based on the updated model posterior, hoping to achieve better convergence.¹¹⁵ In this paper, we focus on BMA, which essentially relies on the weighted ensemble of the models in the uncertainty class by the model posterior.^109,112 The theoretical properties of BMA have been studied in the literature. For example, BMA can achieve better prediction performance than any model in the uncertainty class.^109,116 The corresponding implementations addressing model uncertainty have also been investigated for more effective and efficient inference procedures.¹¹²

BMA with MOCU for OED

For Bayesian experimental design in general, there can be three categories of objective functions to guide the experimental design. In the first case, we have a parametric model where the parameters come from an underlying physical system. One such example is in biomedicine, where the objective function is the likelihood of the cell being in a cancerous state, given a state-space model based on genetic regulatory pathways.¹¹⁷ Another example is in imaging (for example, for image reconstruction or filtering), where the parameters characterize the image appearance, and the objective function is an error measure between two images.

In the second category, the features are given, and the parameters come from a surrogate model used in place of the actual physical model but are believed to be appropriately related to the physical model. For example, in the materials science applications under “OED with MOCU,” the surrogate model is based on the time-dependent Ginzburg-Landau (TDGL) theory and simulates the free energy given dopant parameters, the objective function is the energy dissipation, and the action is to find an optimal dopant and concentration.⁵ To see how the approach in Dehghannasiri et al.⁵ fits the above general theory, the reader can refer to Boluki et al.¹¹⁸

In the third category, we do not know the physical model, and we lack sufficient knowledge to posit a surrogate model with known features/forms relating to our objective. This case arises in many scenarios where the objective function is a “black box” function. Nevertheless, we can adopt a model, albeit one with known predictive properties. This model can be a kernel-based model, such as a GP.¹¹⁹ Moreover, this model can consist of a set of possible parametric families, a kernel-based model with different possible feature sets, or even kernel-based models with different choices for the kernel function. In such scenarios, we do not a priori have any knowledge about which feature set or model family would be the best, and reliable model selection cannot be performed before starting the experiment design loop because of the limited number of observed samples. Considering the average prediction from models based on different feature sets or model families weighted by their posterior probability of being the correct model, namely BMA, is one possible approach.

In the context of materials discovery, we can frame the model averaging problem in a hierarchy to define a family of uncertain model classes in which, for example, different features contribute differently to functional property prediction differently. With such a hierarchical Bayesian model, BMA, essentially weighing all the possible models by their corresponding probability of being the true model, is embedded in BO for OED to realize a system not only capable of autonomously and adaptively learning the surrogate predictive models for the most promising materials of desired properties but also utilizing the models to efficiently guide exploration of the design space. With more acquired data, the uncertainty of different models will be quantified, and improved predictive models as well as efficient experimental design can be attained.

Again, assume an uncertainty class $\mathrm{\Theta }$ with the probability measure $\mathrm{\Pi }$, characterizing predictive models on a design space $\mathcal{X}$. The experimental design goal is to optimize an objective function $f:\mathrm{\Theta }\times \mathcal{X}\to \mathbb{R}$. For example, we want to find a design $\mathbf{x}\in \mathcal{X}$ that minimizes an unknown true objective function $f\left(\mathbf{x};{\theta }_t\right)$ over $\mathcal{X}$, where ${\theta }_t\in \mathrm{\Theta }$ denotes the true model. When there is no strong prior knowledge on functional forms of the objective function, often GP regression (GPR) is adopted and iteratively updated given data from performed experiments ${\mathcal{D}}_n$: $P\left(f|\mathbf{x};{\mathcal{D}}_n\right)\sim GP\left(y|\mu ,K\right)$, where $\left\{\mu ,K\right\}$ denote the corresponding mean and kernel parameters. To account for potential model uncertainty, BMA can be used for more robust modeling of the objective function:

$$P\left(f|\mathbf{x};{\mathcal{D}}_n\right)=\sum _{i=1}^{L}P\left(i|{\mathcal{D}}_n\right)P\left(f|\mathbf{x};{\mathcal{D}}_n,{\mu }_i,K_i\right)\text{,}$$ (Equation 9)

where i is the index of the candidate models in the uncertainty class.

As explained under “Bayesian learning, UQ, and experimental design,” a robust design is an element ${\mathbf{x}}^R\in \mathcal{X}$ that minimizes the average of the objective function across all possibilities in the uncertainty class relative to a probability distribution governing the corresponding space. This probability at each experimental design iteration is the posterior distribution given the observed data points available up to that step. Mathematically,

$${\mathbf{x}}_n^R=\underset{\mathbf{x}\in \mathcal{X}}{\mathrm{argmin}}{E}_{\theta }\left[f\left(\mathbf{x};\theta \right)|{\mathcal{D}}_n\right]\text{,}$$ (Equation 10)

where ${\mathcal{D}}_n$ denotes the observed data till the nth iteration. MOCU in this context can be defined as the average gain in the attained objective between the robust design and the actual optimal designs across the possibilities:

$${\text{MOCU}}_n^{\mathcal{X}}\left(\mathrm{\Theta }\right)=E_{\theta }\left[f\left({\mathbf{x}}_n^R;\theta \right)-f\left({\mathbf{x}}_{\theta }^{\ast };\theta \right)|{\mathcal{D}}_n\right]\text{,}$$ (Equation 11)

where ${\mathbf{x}}_{\theta }^{\ast }$ denotes the optimal action for a given model parameterized by θ, including both GPR parameters and additional parameters from BMA. Note that, if we actually knew the true (correct) model, then we would simply take the optimal design for that model, and MOCU would be 0. Denoting the set of possible experiments by $\mathrm{\Xi }$, the best experiment ${\xi }_n^{\ast }$ at each time step (in one-step look-ahead scenario) is the one that maximally reduces the expected MOCU following the experiment; i.e.,

$$\begin{array}{c}{\xi }_n^{\ast }=\underset{\xi \in \mathrm{\Xi }}{\mathrm{argmin}}{E}_{\xi }[E_{\theta }\left[f\left({\mathbf{x}}_{n+1}^R;\theta \right)|\xi ,{\mathcal{D}}_n\right]]-E_{\theta }\left[f\left({\mathbf{x}}_n^R;\theta \right)|{\mathcal{D}}_n\right]\text{.}\end{array}$$ (Equation 12)

In most cases in materials discovery, each experiment is synthesizing the corresponding materials design and measuring its actual properties (or their noisy versions). Thus, the experiment space is equivalent to the design space.

It is beneficial to recognize that MOCU can be viewed as the minimum expected value of a Bayesian loss function, where the Bayesian loss function maps an operator (the materials design in this context) to its differential objective value (for using the given operator instead of an optimal operator), and its minimum expectation is attained by an optimal robust operator that minimizes the average differential objective value. In decision theory, this differential objective value has been referred to as the regret. Under certain conditions, MOCU-based experimental design is, in fact, equivalent to KG and EGO.¹¹⁸

BMA for materials science applications

We have integrated BMA with the MOCU-based experimental design to deploy an autonomous computational materials discovery framework that is capable of performing optimal sequential computational experiments to find optimal materials and updating the knowledge on materials system model at the same time. One of our recent exercises¹²⁰ consisted of implementing the BMA approach for robust selection of computational experiments to optimize properties of the MAX phase crystal system.¹²¹ Employing BMA approaches using a set of GPR functions based on different feature sets, we demonstrated that the framework was robust against selection of poor feature sets because the approach considers all the feature sets at once, updating their relative statistical weights according to their ability to predict (successful) outcomes of unrealized simulations. More critically, we have demonstrated the effectiveness of our computational materials discovery platform for single and multiobjective optimization problems.

This framework has been used efficiently for objective-oriented exploration of materials design spaces (MDSs) through computational models and, more importantly to guide experiments by focusing on gathering data in sections of the MDS that will result in the most efficient path to achieving the optimal material within resource budgets. Additionally, the BO approach was successfully combined with BMA for autonomous and adaptive learning, which may be used to auto-select the best models in the MDS, thereby eliminating the requirement of knowing the best model a priori. Thus, this framework constitutes a paradigm shift in the approach to materials discovery by simultaneously (1) accounting for the need to adaptively build increasingly effective models for the accelerated discovery of materials while (2) accounting for the uncertainty in the models themselves. It enables a long-desired seamless connection between computation and experiments, each informing the other, while progressing optimally toward the target material.

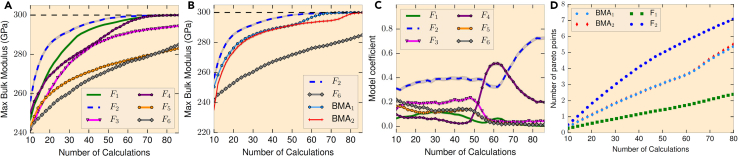
In our implementation for MAX phase crystal systems, after training the GPs based on the current and previous observations, solving for the GP hyperparameters to maximize the marginal likelihood of the observed data, each GP provides a Gaussian distribution over the objective function value of each design. Averaging several GPs based on their posterior model probabilities is like mixing weighted Gaussian distributions over the objective value of each design. Based on the sum of weighted Gaussian distributions, the MOCU-based utility function or other acquisition functions, including expected improvement (EI) with a single objective⁴⁵ or expected hypervolume improvement (EHVI) with multiobjectives,¹²² can be calculated for all possible designs, and the maximizer is chosen as the next experiment. In our experiments, six sets of basic compositional and structural features were chosen a priori without assuming any knowledge of their suitability for the underlying true model that generates data. We have investigated whether the updated model posterior in BMA captured the expected CPSP relationships.¹²⁰ The goal of experimental design is to discover MAX phases with maximum bulk modulus and minimum shear modulus, which were computed through density functional theory (DFT) calculations^123,124 for 1,500 randomly sampled MAX ternary carbide/nitride crystals. Among these DFT-calculated results, there were 10 MAX phases belonging to the Pareto front when considering the design goals. All of the reported performances of Bayesian experimental design were based on the average values of 1,500 runs starting from the random initial sets of 10 training samples. In Figure 5A, we show the change of the average maximum bulk modulus with the iterations of sequential experimental design. It is clear that, among six models with different features, the feature set $F_2$ achieves the best experimental design performance because the average maximum bulk modulus is consistently higher than the other models. On the other hand, $F_6$ has the worst performance. When adopting BMA (either based on first-order or second-order maximum likelihood inference [BMA1 or BMA2, respectively]), it is clear that BMA achieves robust performance even when some models may not have good predictive power (Figure 5B). With the increasing number of iterations, it is also clear that the posterior probability of the best model, $F_2$, gets higher (Figure 5C). Last but not least, as shown in Figure 5D, our BMA-based multiobjective experimental design can approach the Pareto front within a small number of sequential design iterations considering the vast MAX ternary carbide/nitride space. All of these experimental results on the maximization/minimization of mechanical properties of MAX phases suggest that BMA-based model fusion can lead to considerable reduction in the number of experiments/computations that need to be carried out to identify the desired solutions to this specific materials design problem.

Figure 5.

Bayesian experimental design with BMA for MAX phases as described in the text

(A) The change of average maximum bulk modulus for the original six feature sets with the number of design iterations.

(B) The change of average maximum bulk modulus comparing BMA surrogates with the best and worst feature sets.

(C) The change of posterior model probabilities corresponding to six feature sets.

(D) The average number of sampled Pareto front points when considering bulk modulus and shear modulus.

Along these directions, we can develop robust Bayesian learning methods by model fusion that exploit correlations among sources/models. Together with a multiinformation source optimization framework driven by scientific knowledge, they will reliably and efficiently identify, given the current knowledge, the next best information source to query and guide the materials design.¹²⁵

OED with MOCU

In the context of OED, it has a long history in science and engineering as a properly designed experimental procedure that provides much greater efficiency than simply making random probes. Indeed, Francis Bacon’s call for experimental design in 1620 is often taken to be the beginning of modern science.¹²⁶

MOCU-based OED

Because the MOCU^65,66 can be used to quantify the objective-based uncertainty, it provides an effective means to estimate the expected impact of potential experiments on the objective (i.e., operational goal) through the reduction of model uncertainty. Suppose we are given a set of potential experiments from which the next experiment could be chosen. Which among the possible experiments should be selected if we wish to optimally improve the operational performance of the operator based on the expected experimental outcome? A natural way to select the best possible experiment would be to choose the one that would lead to the minimum expected remaining MOCU after observing its outcome. To be more specific, let $\xi \in \mathrm{\Xi }$ be an experiment in the experimental design space $\mathrm{\Xi }$. Given ξ, the MOCU conditioned on this experiment can be computed as

$$\text{MOCU}\left(\mathrm{\Theta }|\xi \right)=E_{\theta |\xi }\left[C_{\theta }\left({\psi }_{\text{IBR}}^{\mathrm{\Theta }|\xi }\right)-C_{\theta }\left({\psi }_{\theta }\right)\right]\text{,}$$ (Equation 13)

where ${\psi }_{\text{IBR}}^{\mathrm{\Theta }|\xi }$ is the IBR operator that is optimally robust for the uncertainty class of models $\mathrm{\Theta }|\xi$ that is now conditioned on this experiment ξ, and the expectation is taken with respect to the conditional distribution $\pi \left(\theta |\xi \right)$. The expected remaining MOCU can be evaluated by

$$R\left(\mathrm{\Theta }|\xi \right)=E_{\xi }\left[\text{MOCU}\left(\mathrm{\Theta }|\xi \right)\right]\text{,}$$ (Equation 14)

and the optimal experiment ${\xi }^{\ast }$ is the one that minimizes the expected remaining MOCU in Equation 14 so that it satisfies

$${\xi }^{\ast }=\underset{\xi \in \mathrm{\Xi }}{\mathrm{argmin}}R\left(\mathrm{\Theta }|\xi \right)\text{.}$$ (Equation 15)

While this strategy does not guarantee that the selected experiment will indeed minimize the uncertainty impacting the objective among all experiments (because the experimental outcome is not known in advance with certainty), it will be optimal on average. Recently, this MOCU-based experimental design scheme has been developed for a variety of systems and applications, which include enhancing the performance of gene-regulatory network intervention with partial network knowledge,^117,127 synchronization of an uncertain Kuramoto model that consists of interconnected oscillators with uncertain interaction strength,^128,129 optimal sequential sampling,¹³⁰ Bayesian classification through active learning,^44,131 and robust filtering of uncertain stochastic differential equation (SDE) systems.⁴²

For materials discovery via OED guided by MOCU, as shown in Equation 15, optimization algorithms have to be developed based on the structure of the input design space as well as the properties of the MOCU computation based on different problem settings. For example, if we are investigating pool-based high-throughput screening or discovery problems with a finite set of candidates, either exhaustive search as in typical BO implementations^5,53,131 or dynamic programming algorithms based on KGs^{47,132,133,134} can be developed for solving the optimization problems. When the input design space is continuous and the gradient of MOCU can be estimated, gradient-based local search algorithms can be implemented, as discussed in Zhao et al.¹³⁵ There are also other solution strategies that can be used to solve OED guided by MOCU, including sampling and genetic and other evolutionary algorithms.¹³⁶

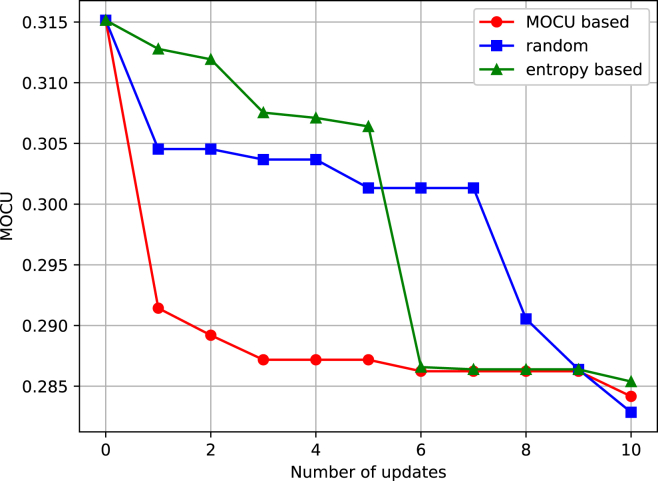
Figure 6 shows the performance of the MOCU-based OED strategy in reducing the uncertainty that impacts the synchronization cost of a Kuramoto model that consists of 5 oscillators, where the coupling strength between oscillators is uncertain and known only up to a range.¹²⁸ In this example, an experiment picks an oscillator pair and observes whether the selected oscillator pair is synchronized in the absence of external control. The observation can be used to reduce the range of the uncertain coupling strength between the oscillators. For this Kuramoto model, there exist $\left(\begin{array}{c}5\\ 2\end{array}\right)$ potential experiments in the experimental design space $\mathrm{\Xi }$, and Figure 6 shows how MOCU decreases as a function of experimental updates. As can be seen, the MOCU-based OED strategy leads to a sharp reduction in uncertainty within a few updates, outperforming random selection (which selects one of the possible experiments from $\mathrm{\Xi }$ with uniform probability) or an entropy-based approach (which selects the experiment for the oscillator pair whose coupling strength has the largest uncertain range).

Figure 6.

Experimental design results based on a 5-oscillator Kuramoto model with uncertain coupling strength between the oscillators as described in the text

The MOCU-based OED scheme quickly reduces the model uncertainty that impacts the performance.

OED for shape memory alloy (SMA)

In materials design, the MOCU-based OED strategy has been applied to a computational problem for shape memory alloy (SMA) design with desired stress-strain profiles for a particular dopant at a given concentration utilizing the TDGL theory.⁵ The TDGL model simulates the free energy for a specific dopant with a specified concentration, given the dopant’s parameters, which is considered an oracle in the experiments. Because the computational complexity of the TDGL model is enormous, an uncertain surrogate model is first trained to approximately predict a dissipation energy for a specified dopant and concentration. In particular, based on TDGL, a reciprocal function is adopted to model the energy dissipation at a specific temperature as a function of dopant potency, dopant spread, and dopant concentration. The experimental design goal is to discover SMAs with the minimum energy dissipation, and therefore this surrogate model is used as the cost function to define MOCU to efficiently guide throughout the experimental design iterations for an optimal dopant and concentration. With the MOCU defined based on this Landau mesoscale surrogate for SMAs as the cost function, the expected remaining MOCU, given the corresponding dopant and its corresponding concentration levels, can be computed by the definition in Equation 14. The optimal experiment can then be determined to minimize the expected remaining MOCU under model uncertainty as in Equation 15.

In the reported experiments,⁵ MOCU-based OED was compared with the pure exploitation and random selection policies. Averaged over 10,000 simulations, our MOCU-based OED strategy, which strives to minimize the uncertainty in the model pertaining to the design objective, identified the dopant and concentration with the optimal dissipation after only two iterations on average, while either exploitation or random selection policies cannot find the optimal dopant even after 10 iterations. Getting optimal results after fewer iterations is especially crucial in materials discovery, where measurements by either high-throughput simulation models or synthesis and profiling experiments are expensive and time consuming.

Automatic feature engineering (AFE)

Finally, with accumulated knowledge and data from experimental design based on objective-UQ using MOCU, we may help fill in the missing gap of the understanding in materials systems under study. In materials science, the fundamental paradigm is the existence of causal relationships connecting composition and processing (i.e., the modifications to a material’s current state), structure (i.e., the multiscale arrangement of the material), and properties (i.e., the response of the material to an external stimulus); i.e., CPSP relationships. The navigation of this CPSP space is enormously resource intensive, regardless of whether this query is on physical experiments or computational ones. As a result, it typically takes more than 20 years to identify, develop, and finally deploy one material in real-world applications—a key bottleneck for the MGI.^1,3,4 Attempting to use physics-agnostic models to build these relationships is limited by the scarcity of the training data itself. Moreover, one would be interested in discovering derived relationships that connect features to properties/behavior because these relationships can further be used to design/discover materials with optimal properties. Besides designing and discovering promising new materials with desired functional properties, identifying critical input features (related to composition, process, structure) that determine function properties as well as principled CPSP relationships can provide a systematic understanding of the underlying physics for different materials systems. Such knowledge can be explored and updated, as illustrated in the previous examples under “Integrating prior knowledge in materials science” and “BMA for materials science applications.” One such knowledge discovery strategy is AFE, which enables us to use physics constraints on learning surrogate models while facilitating the discovery of fundamental materials design rules at the same time.

Engineered features obeying physics principles provide valuable interpretability that is critical to help new knowledge discovery and consequent critical decision-making. It is worth noting that, in scientific ML (sciML) involving complex systems, training data tend to be scarce and noisy because obtaining data can be difficult, time consuming, and costly. Materials problems clearly reflect these challenges.

Related work in feature engineering

Feature representation learning has been studied extensively in the SP/ML community, including “white box” methods based on specific basis families (Fourier and wavelet are two representatives) and data-driven “black box” methods, such as dictionary learning and deep learning.^137,138,139 Although “black box” deep AFE models¹⁴⁰ have shown great potential to improve the corresponding ML algorithm performance, we focus on feature engineering, aiming to derive features based on explicit functional forms in this survey. Desirable feature engineering should attain considerable improvement of prediction performance and generalizability as well as good interpretability with little manual labor. Among the existing methods, deep feature synthesis¹⁴¹ extracts features based on explicit functional relationships without experts’ domain knowledge through stacking multiple primary features and implementing operations or transformations on them, but it suffers from efficiency and scalability problems because of its brute-force way to generate and select features. Kaul et al.¹⁴² proposed Autolearn by regression-based feature learning through mining pairwise feature associations. While it avoids overfitting, to which deep learning-based FE methods are amenable, and improves the efficiency by selecting subsets of engineered features according to stability and information gain, it does not directly produce interpretable features. Khurana et al.¹⁴³ introduced Cognito, which formulates the feature engineering problem as a search on the transformation tree with an incremental search strategy to explore the prominent features and later extended the framework by combining reinforcement learning (RL) with a linear functional approximation¹⁴⁴ to improve the efficiency. A similar framework has recently been developed in Zhang et al.,¹⁴⁵ where the deep reinforcement learning (DRL) policy is learned on a tree-like transformation graph. It improves the policy learning capability compared with Cognito. However, both frameworks do not explicitly incorporate available prior knowledge into the AFE procedures.

For AFE in materials science applications, we are interested in finding the actuating mechanisms of the materials’ functional properties of interest by identifying a set of physically meaningful variables and their relationships.¹⁴⁶ Such a set of physical variables with corresponding parameters that uniquely describe the materials’ properties of interest can be denoted as “descriptors.” Discovering descriptors in materials science can help better predict target functional properties with potential interpretability for a given complete class of materials.¹⁴⁷ Several methods have been developed, such as a method based on compressed sensing¹⁴⁷ and the more recent Sure Independent Screening and Sparse Operation (SISSO)¹⁴⁸ by brute-force search to generate and select subsets of generated features by sure independent screening¹⁴⁹ together with sparse operators such as least absolute shrinkage and selection operator (LASSO).¹⁵⁰ These methods pose a scalability challenge with the exponentially growing memory requirement to store intermediate features and high computational complexity to search for features.

Physics-constrained AFE

In our recently developed AFE framework,¹⁵¹ a feature generation tree (FGT) was constructed with physics constraints to explore the engineered feature (descriptor) space more efficiently based on first principles, which was demonstrated in several materials problems to be able to take advantage of prior chemical and physical knowledge of the materials systems under study.

Our FGT-based AFE framework focuses on sciML applications, where interpretability is critical to help consequent critical decision-making under data scarcity and uncertainty. Specifically, AFE strategies have been developed by combining FGT exploration with Deep Reinforcement Learning (DRL)¹⁵² to address the interpretability and scalability challenges. Instead of employing a brute-force way to perform algebraic operations on the raw features in a given dataset and then selecting important descriptors, we combine the descriptor generating and selecting processes together by constructing FGTs and developing the corresponding tree exploration policies guided by a deep Q network (DQN). An efficient exploration of the prominent descriptors can be attained in the growing feature space based on the allowed algebraic operations. Our FGT-based AFE strategies construct interpretable descriptors based on a list of operations according to the DRL learned policies, which are more scalable and flexible with the performance-complexity trade-off with the help of adjustable batch size for generating intermediate features. More critical to materials science and other sciML problems, our FGT provides a flexible framework for incorporating prior knowledge (e.g., physics constraints) to generate and select features. This is important for knowledge discovery via interpretable learning with physics constraints under data scarcity and uncertainty because the space connecting intrinsic materials attributes/features to materials behavior is vast, sparse, and complex in nature.

In particular, let ${\mathbf{x}}_0$ denote the finite set of p variables as raw or primary features $\left\{{\mathbf{x}}_0^1,\dots ,{\mathbf{x}}_0^p\right\}$ and y the target output vector. AFE is to develop an algorithm to construct sets of engineered features as interpretable and predictive descriptors $F_i=\left\{g_1\left({\mathbf{x}}_0,c_1\right),g_2\left({\mathbf{x}}_0,c_2\right),\dots \right\}$ based on explicit functional forms with allowed algebraic operations that accurately predict y. The set of algebraic operations φ in an operation set O can be constructed based on prior knowledge; for example, with the following unary and binary operations: $\mathbf{O}=\left\{\mathit{exp}(·),\mathit{log}(·),{(·)}^2,{(·)}^3,{(·)}^{-1},\sqrt{·},\sqrt[3]{·},+,-,\times ,÷\right\}$. For each function $g\left({\mathbf{x}}_0,c\right)$, c denotes the complexity of the corresponding generated descriptor—the number of algebraic operations. For example, the function $\mathit{exp}\left({\mathit{x}}_0^0\right)\times {\left({\mathit{x}}_0^1\right)}^2+\sqrt{\left({\mathit{x}}_0^2\right)}$ has a complexity of 5. The operation set O can be pre-defined based on the prior knowledge about the system under study. If we denote the primary features ${\mathbf{x}}_0$ by $F_0$, then $F_i$ denotes the iteratively generated set of descriptors with the maximum allowed complexity $c_i$. Our goal is to find an optimal descriptor set $F^{\ast }$ that maximizes the prediction performance score; for example, by classification or regression accuracy, $A_L\left\{F^{\prime },y\right\}$:

$$F^{\ast }=\underset{\forall f^k\in F,f^k\in \mathbb{F}}{\mathrm{argmax}}{A}_L\left\{F,y\right\}\text{,}$$ (Equation 16)

where L denotes the prediction model (for example, linear regression or Support Vector Machine (SVM) for interpretability with generated descriptors), and $f^k$ is any descriptor (including primary features) in $\mathrm{F}$, the set of all generated features with the maximum allowed complexity $c_{\mathit{max}}$.

The combinatorial optimization problem in Equation 16 is NP hard. We solve it approximately by introducing the FGT to iteratively construct the descriptor space and transform the problem into a tree search problem for efficient AFE. Each node in the FGT represents a set of descriptors $F_i$, and each edge represents an operation φ. We denote ${\left(F^d\right)}^{\ast }=\left\{{\left(f^1\right)}^{\ast },{\left(f^2\right)}^{\ast },\dots ,{\left(f^d\right)}^{\ast }\right\}$ as the top d optimal features when we choose the cardinality of $F^{\ast }$ as d and ${\left(f^d\right)}^{\ast }$ as the selected optimal feature for the dth dimension of ${\left(F^d\right)}^{\ast }$. The FGT exploration aims to search for the best descriptors ${\left(f^1\right)}^{\ast },{\left(f^2\right)}^{\ast },\dots$ one by one based on the testing accuracy given the observed data. The corresponding complete AFE procedure constructs the feature subspace $F^d$ sequentially as the search space of each ${\left(f^d\right)}^{\ast }$ exploration, starting from the root node $F_0$ with the primary feature set. At each node $F_i$, we would like to learn a generation policy π to choose an operation ${\phi }_i$ to generate the new descriptor set $F_j\left(j>i\right)$ as the corresponding child node, with which the current optimal ${\left(F^d\right)}^{\prime }$ and $A_L\left\{{\left(F^d\right)}^{\prime },y\right\}$ will be updated accordingly. The FGT will grow by repeating the operations above until it reaches the maximum complexity $c_{\mathit{max}}$.

To learn the FGT generation policy π, we adopt a DQN with experience replay.¹⁵² Formally, we define the states, actions and rewards as follows:

• •state $F_i^d$, denoting a set of primary features or generated descriptors when looking for the dth optimal descriptor;
• •action $\pi \left(F_i^d\right)={\phi }_i$, denoting an operation in the set O;
• •reward: $R\left(F_i^d,{\phi }_i\right)=\underset{F^{\prime }}{\max }{\left(1.001-A_L\left\{F^{\prime },y\right\}\right)}^{-1}$, where $0\le A_L\left\{F^{\prime },y\right\}\le 1$.

The pseudo-code for learning DQN-based FGT exploration is given in Algorithm 1. To have a flexible exploration procedure for performance-complexity trade-off and incorporation of prior knowledge, each ${\left(f^d\right)}^{\ast }$ in $F^{\ast }$ can be chosen from the top n features with highest rewards in the corresponding feature subspace $F^d$, composing a candidate set $S^d$. So ${\left(F^{d-1}\right)}^{\ast }$ can have multiple combinations according to the whole candidate sets $\mathbb{S}=\left\{S^1,\dots ,S^{d-1}\right\}$, and $F^{\prime }$ also has multiple combinations according to different ${\left(F^{d-1}\right)}^{\ast }$ and $f^d$. Consequently the reward is computed as the maximum reward over $F^{\prime }$.

Algorithm 1. DQN for AFE.

• 1: input: Primary features $F_0$, Action set O

• 2: for $d=\mathrm{1,2},\dots$ do

• 3:  Construct new DQN

• 4:  Clear Buffer

• 5:  for $episode=\mathrm{1,2},\dots ,N$ do

• 6:   for $i=\mathrm{0,1},\dots \text{,}$ do

• 7:    ${\phi }_i=ϵ$-Greedy Method($F_i,ϵ$)

• 8:    $F_{i+1}^d,R_i,c_{i+1}=$ FGT_Grow $\left\{F_i^d,{\phi }_i,c_i\right\}$

• 9:    Buffer $\leftarrow \left\{F_i^d,F_{i+1}^d,{\phi }_i,R_i,c_{i+1}\right\}$

• 10:    Train DQN with experience replay

• 11:    if $R_i>threshold$ then

• 12:     goto Output

• 13:    end if

• 14:    if $c_i\ge c_{\mathit{max}}$ then

• 15:     break

• 16:    end if

• 17:   end for

• 18:  end for

• 19:  $\mathbb{S}\leftarrow$ Candidate set $S^d$ with n features of highest $R_i$

• 20: end for

• 21: Output: Optimal feature set $F^{\ast }$ chosen from $\mathbb{S}$

Note that when we apply binary operations on $F_i$, beside the one feature in the $F_i$, we have to choose another feature in the generated descriptor space, leading to the exponentially exploding number of new descriptors. To achieve appropriate performance-complexity trade-off, we introduce flexible batch sampling to randomly sample a feature subspace B from $\mathbb{F}$ as a “batch set” each time and enumerate $f^s$ only from B and take the maximum reward from all of the combinations as the reward. When prior knowledge is available as physics constraints on applying corresponding operations to specific feature groups, this batch sampling procedure can naturally take care of them.

AFE to learn interatomic potential models for copper

First-principles DFT^123,124 has been extensively applied in materials science, physics, and chemistry. However, it is often constrained to simulate materials with 100–1,000 atoms for several thousands ab initio molecular dynamics steps, covering about 10 picoseconds. In contrast, classic interatomic potentials have been widely adopted in the past, allowing large-scale molecular dynamics simulation of millions of atoms for millions of time steps (that is, covering $>$10 nanoseconds). However, the construction of the functional form and the optimization of the corresponding parameters of classic potentials are highly nontrivial. Recently, developing and training neural network potentials based on first-principles DFT calculations of relatively small systems has become an important research direction in the atomistic simulation in combination with active learning.^{153,154,155,156} Very recently, a feature engineering method has been pursued where genetic programming was applied to develop fast and accurate classic interatomic potentials with explicit functional forms from physically meaningful hypothesis space.¹³⁶ Particularly, genetic programming was applied to optimize the exact functional form of pairwise and many-body potentials as well as other potential forms, highlighting an important avenue toward the development of physics-constrained models with analytic functional form.

Different from the above genetic programming approach, we have adopted our FGT-based AFE and evaluated its ability to find potential models from data generated by DFT. To compare with the genetic programming symbolic regression approach,¹³⁶ we used the same 150 snapshots of 32-atom DFT molecular dynamics simulations on fcc copper in Hernandez et al.,¹³⁶ where each snapshot was generated every 100 steps with a time step of 1 fs. We adopted the same 150 snapshots, including 50 snapshots from ab initio molecular dynamics performed at 300 K in the canonical (NVT) ensemble, 50 snapshots at 1,400 K in the NVT ensemble, and 50 snapshots at 1,400 K in the isothermal-isobaric (NPT) ensemble with pressure at 100 kPa. The 150 total energies calculated by Hernandez et al.¹³⁶ were considered the target output of interest,¹⁵⁷ with the random split of 125 structures and their corresponding total energies for training, and the remaining 125 structures and total energies for validation, for feature engineering.

We have compared our AFE with the recently developed physics-informed genetic programming method¹³⁶ to arrive at analytical many-body classical interatomic potential models. Figure 7 shows the plots of predicted total energy of these different copper structures vs. the simulated total energy based on primary features (left), genetic-programming-generated descriptors (center), and AFE-generated descriptors (right) on the same held-out testing data. With the same simulated molecular dynamics data and experimental setup in the paper, our AFE has achieved the total energy prediction with a mean absolute error (MAE) of 3.73 meV/atom within 12 h. By contrast, the reported model GP1 by genetic programming in Hernandez et al.¹³⁶ had a prediction MAE of 4.13 meV/atom after 360 CPU hours on the same training and test sets.

Figure 7.

Copper energy regression results for different interatomic potential models

Our proposed AFE strategies approximate the expected future reward of engineered descriptors through DQN-based policy learning and replace the exhaustive feature generation by DQN-guided FGT exploration considering physics prior knowledge. Consequently, our AFE enhances scalability and computational efficiency without sacrificing prediction performance, as demonstrated in the reported experiment as well as other materials systems in Xiang et al.¹⁵¹ The results of these real-world materials science experiments have demonstrated the potential of our DQN-guided FGT exploration in reducing the runtime and enhancing the scalability for AFE. More importantly, the engineered descriptors are interpretable with the corresponding lists of algebraic operations on the original primary features. Our physics-constrained AFE aims at generalizable learning under data scarcity and uncertainty. Interpretable instead of “black box” learning helps new knowledge discovery and better decision-making.

Conclusions and future work

When facing real-world complex systems in various science and engineering domains—such as complex materials systems, which are our focus in this paper—where acquisition of ample data is practically difficult and formidably expensive, currently existing ML methods fail to produce reliable and generalizable predictions. To cope with the current shortcomings of existing SP and ML schemes in materials discovery, there is a pressing need for novel methods that enable robust optimal decision-making under challenging conditions, such as small data size, enormous system complexity, nonstationarity, as well as data and model uncertainty. In this paper, we have presented recent efforts in knowledge-driven learning, optimization, and experimental design, and we have also provided their historical context against the rich research history in the SP community revolving around robust filtering and control, which can probably be dated back to the 1950s. Specifically, we have shown several examples in an objective-based UQ framework—via MOCU—to develop sciML methods to address the aforementioned challenges in accelerating materials discovery, focusing on learning and experimental design under uncertainty. The problems of studying complex systems will persist in diverse science and engineering disciplines, and we expect that the learning and optimization schemes based on objective-based UQ presented in this paper would provide a useful guideline for developing new sciML methods that more effectively incorporate scientific knowledge, design surrogate ML models that are better suited for the given systems under study, and devise computational solutions that are more scalable and efficient.