Halide Perovskite Artificial Solids as a New Platform to Simulate Collective Phenomena in Doped Mott Insulators

Abstract

The development of quantum simulators, artificial platforms where the predictions of many-body theories of correlated quantum materials can be tested in a controllable and tunable way, is one of the main challenges of condensed matter physics. Here we introduce artificial lattices made of lead halide perovskite nanocubes as a new platform to simulate and investigate the physics of correlated quantum materials. We demonstrate that optical injection of quantum confined excitons in this system realizes the two main features that ubiquitously pervade the phase diagram of many quantum materials: collective phenomena, in which long-range orders emerge from incoherent fluctuations, and the excitonic Mott transition, which has one-to-one correspondence with the insulator-to-metal transition described by the repulsive Hubbard model in a magnetic field. Our results demonstrate that time-resolved experiments provide a quantum simulator that is able to span a parameter range relevant for a broad class of phenomena, such as superconductivity and charge-density waves.

The paradigm of quantum simulations^1,2 has been pioneered by the development of ultracold-atom systems³⁻⁶ and extended to the solid state via nano- and heterostructured^1,7−9 devices and, more recently, twisted bidimensional materials.¹⁰⁻¹³ An additional promising path consists in coupling a quantum material with the photons of a cavity,^14,15 which opens the possibility to optically drive and control the emergence of collective phenomena and long-range coherence. Intense efforts are currently being dedicated to the development of photonics-based platforms aimed at replicating the many-body physics of quantum correlated materials. External optical control of the microscopic parameters entering the relevant Hamiltonian, such as doping, hopping, and interaction strength, is key to tackle open problems relevant to solid-state physics.

The most fundamental properties of many correlated materials, such as copper oxides,¹⁶ are captured by the Hubbard model, which describes charges moving in a lattice and subject to an on-site Coulomb repulsion U. When U is of the order of the bandwidth (4t, t being the hopping), the Hubbard model reproduces the correlation-driven metal-to-insulator Mott transition, thus capturing the insulating nature of copper oxide parent compounds.¹⁷ When a small number of free carriers is injected (doping), the model hosts the emergence of a wealth of long-range phases,^18,19 such as charge density waves and high-temperature superconductivity, characterized by the macroscopic phase locking of fundamental incoherent fluctuations. More recently, the introduction of light-excitation protocols has unveiled the possibility of inducing nonequilibrium superconducting-like states²⁰ or enhanced charge density waves,²¹ whose relation with equilibrium thermodynamical phases is still not clarified. The understanding of these phenomena in real materials is still a major challenge that is driving the search for synthetic systems where to reproduce the physics of doped Mott insulators and investigate, in a controlled way, the manifestation of long-range collective phenomena in both equilibrium and nonequilibrium conditions mediated by long-range electromagnetic interactions.

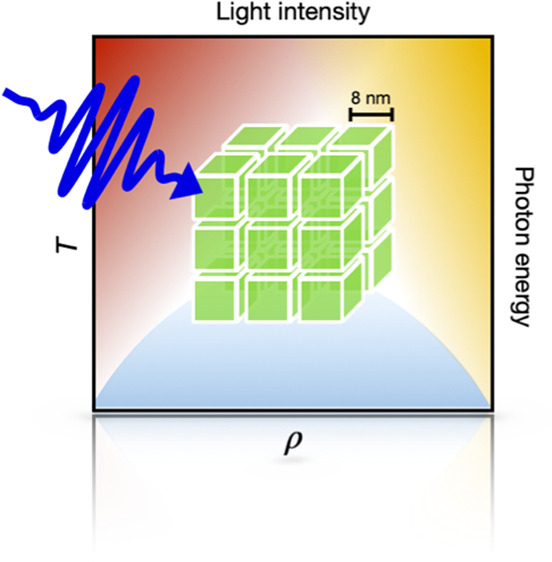
In this work, we introduce macroscopic lattices constituted by lead halide perovskite nanocubes as a new photonic platform to artificially implement the Hubbard model, which describes the local excitonic physics within each nanocube. At the same time, the long-range interactions among excitons in different nanocubes drive the emergence of collective phase-coherent states. We perform broadband time-resolved optical measurements and demonstrate the possibility of spanning different quantum phases, namely, the excitonic Mott insulating phase, the super-radiant collective state, and the metallic electron–hole liquid phase, on the same artificial solid system by continuously tuning the light excitation intensity.

Lead halide perovskite nanocubes (NC) feature appealing optoelectronic properties,²²⁻²⁴ characterized by great tunability and quantum confined excitons,²⁵⁻²⁸ and can self-organize into a highly ordered three-dimensional superlattice.^29,30 The use of these artificial solids as a platform to simulate the many-body problems that characterize quantum correlated materials is based on the possibility of simultaneously controlling short-range correlations, which determine the Mott insulating ground state, and long-range interactions, which are responsible for the emergence of collective phases such as superconductivity or charge-density waves. To this purpose, we introduce the total Hamiltonian:

1

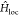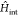where describes the local interactions within each single nanocube and is defined on the perovskite cubic lattice with periodicity a, whereas describes the interunit cell interactions and is defined on the superlattice with periodicity Λ > a (see Figure 1).

Figure 1.

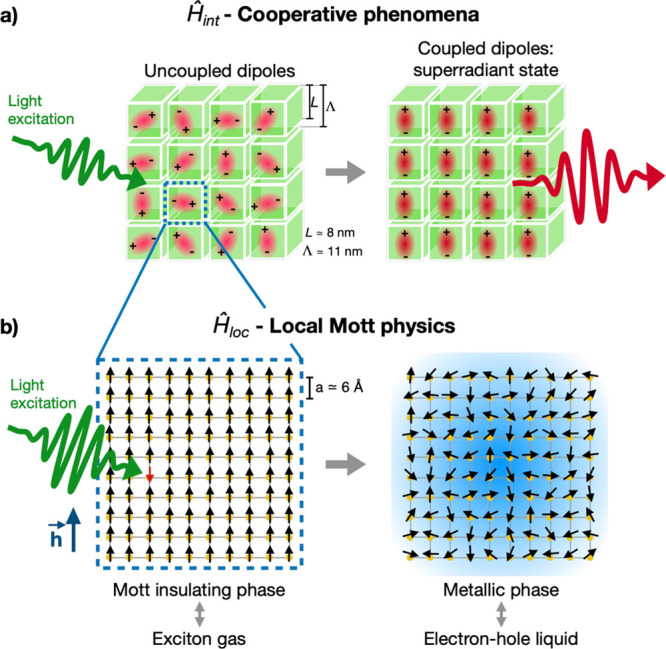
Cartoon describes how perovskite nanocube artificial solids can be harnessed to simulate cooperative phases in the vicinity of the Mott insulator-to-metal transition. (a) Cooperative effects, such as super-radiance, emerge from long-range interactions when coupled via an external light field. (b) Local interactions govern the photoinduced transition from an exciton gas and an electron–hole liquid in a semiconductor, realizing a Mott transition that can be fully mapped onto a repulsive Hubbard model in a magnetic field h.

The first element to realize is given by the electromagnetic field that drives the long-range interaction among excitons in different nanocubes, which can be expressed by³¹⁻³³

2

where 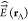is the electromagnetic field and 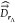the dipole operator at the superlattice site r_Λ. If the electromagnetic field is traced out, eq 2 can be written as an effective dipole–dipole interaction term, whose strength is characterized by a long-range |r_Λ,n – r_Λ,m|^–1 decay,³² |r_Λ,n – r_Λ,m| being the distance between the n^th and m^th dipoles. The 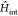term is responsible for a rich family of collective phenomena, broadly indicated as super-radiant.³⁴ As sketched in Figure 1a, super-radiance occurs when the electromagnetic-field-driven interaction leads to phase coherence of N quantum emitters. A typical manifestation is the collective emission of radiation (superfluorescence), which is both enhanced and faster than the emission from individual nanocubes, with the radiative rate scaling as N² for large N.^34,35 Groundbreaking photoluminescence (PL) experiments recently reported evidence of superfluorescence effects in halide perovskites.^30,36−41 The main manifestations of this collective phenomenon are (i) the superlinear dependence of the emission amplitude with respect to the intensity of the exciting external field;^30,36,37,39 (ii) the emergence of a narrow red-shifted peak in the PL spectrum, which is assigned to the cooperative emission from a subpopulation of nanocubes within a single superlattice.^30,36−39 These cooperative effects are suppressed at high temperatures in nanocube superlattices due to thermal noise that undermines quantum coherence.^32?

The second element necessary to reproduce the physics of correlated materials is described by 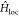. It is well-known that short-range electronic interactions can give rise to a transition from an exciton gas (EG) to a liquid of weakly interacting electrons and holes (EHL), achieved when a very large number of excitons is photoinjected in bulk and low-dimensional semiconductors.⁴²⁻⁴⁶ This transition is believed to almost perfectly realize the insulator-to-metal Mott transition, i.e., a transition driven by the weakening of the electronic interactions without any symmetry breaking. 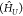It has been demonstrated^47,48 that the Hamiltonian describing the EG → EHL transition in photoexcited semiconductors has a one-to-one correspondence (see Supporting Information section S1) with the repulsive Hubbard model in a magnetic field, in which the electron spins play the role of the electron–hole excitations:⁴⁸

3

where

4

n_iσ is the occupation number at site i of electrons with spin ↑ and ↓; 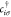and c_iσ are creation and annihilation operators for an electron of spin σ at site i. 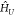is a repulsive Hubbard model, identical to that capturing the insulator-to-metal Mott transition in transition metal oxides^16,49 and the insulating ground state of cuprate parent compounds.¹⁷ In this effective description, the total number of excitons (n_eh) is mapped into the number of flipped spins with respect to the ferromagnetic background, i.e., n_eh = ∑_i⟨n_i↓⟩/N (N being the total number of particles). The exciton density is therefore controlled by the Lagrange multiplier h, which acts as an auxiliary magnetic field inducing the effective magnetization m = 1–2n_eh. For large h, the auxiliary repulsive model is fully polarized (m = 1), which corresponds to the absence of excitons in the original model (eq S1). The sudden reduction of h, which injects a finite number of spin excitations (m < 1), mimics the sudden photoinjection of excitons (n_eh > 0).

The physics generated by 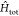is here investigated by broadband transient reflectivity measurements. We performed experiments on artificial lattices constituted by L = 8 nm CsPbBr₃ nanocubes (Bohr exciton diameter ∼7 nm²⁷) arranged in cubic superlattices of periodicity Λ = L + l = 11 nm, where l is the thickness of the ligand layer between two neighboring NCs. The size of each superlattice is of the order of a few micrometers (1–10 μm). Ultrashort light pulses are used to impulsively inject optical excitons, whose density is controlled by the light intensity. The broadband probe (2.1–2.5 eV photon energy) measures the femto/picosecond time evolution of the optical properties following the impulsive excitation. In particular, we employ a resonant pumping scheme in which the pump photon energy (≃2.41 eV) is tuned to the exciton energy, thus limiting the direct generation of free carriers in the conduction band.

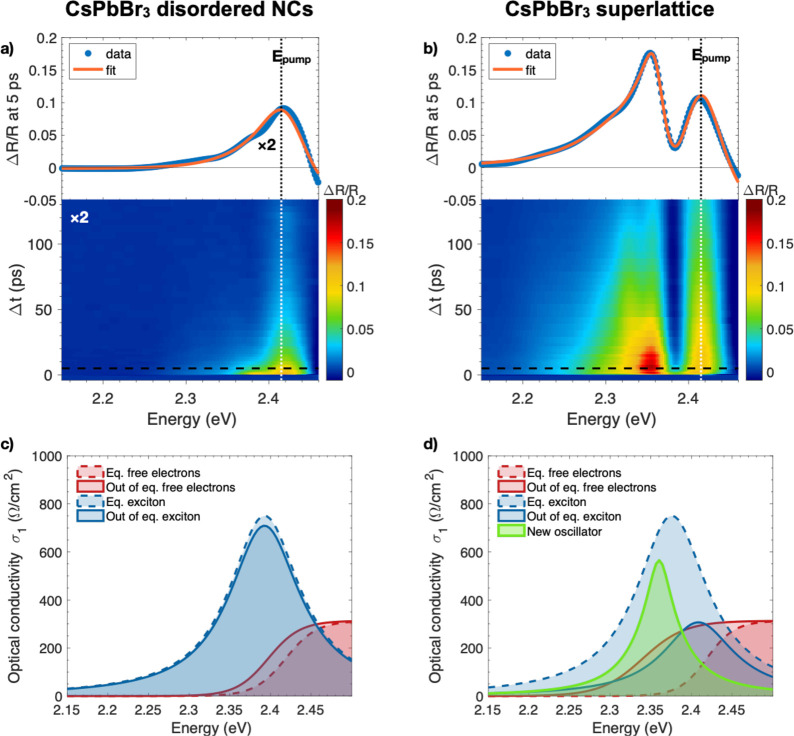
Figure 2 panels a and b display the typical data collected from pump–probe experiments (see Supporting Information section S5 for experimental details) on CsPbBr₃ disordered NCs and NC superlattices, respectively. For the disordered sample (see Figure 2a), the transient reflectivity signal ΔR/R is characterized by a positive reflectivity variation of the order of 5% centered at 2.41 eV. The same experiment performed on NC superlattices (see Figure 2b) displays a larger signal amplitude, with a similar spectral response around 2.41 eV and, additionally, a more structured spectral response extending down to ≃2.20 eV probe energy. The origin of these structures in the ΔR/R signal is assessed by performing a differential fit, which consists of modifying the parameters of the model describing the equilibrium optical properties that are responsible for the observed reflectivity variation. The starting point is the equilibrium optical conductivity that is obtained from a Kramers-Krönig constrained model matching the experimental absorbance of the samples and the temperature dependent trends reported in the literature (Supporting Information S6). In the 2–2.5 eV energy range, the model is dominated by the conduction band edge absorption (red dashed line in Figure 2c) and the exciton peak (blue dashed line), modeled through a Drude-Lorentz oscillator. The outcome of the differential fitting procedure is depicted in Figure 2 panels c and d, where the solid lines represent the out-of-equilibrium components of the optical conductivity σ₁ necessary to fit the experimental ΔR/R signal (see the orange solid lines in the top panels of Figure 2a,b and Supporting Information S8 for details about the robustness of the fitting procedure). In order to reproduce the measured spectral response of CsPbBr₃, for both samples it is necessary to assume (i) a decrease of the excitonic spectral weight and a concomitant blue-shift of the exciton energy and (ii) an increase of in-gap free-electron states accounted for by a red-shift of the semiconducting band gap. In addition to the (i,ii) contributions observed in both samples, the feature observed in the 2.2–2.4 eV energy range solely for NC superlattices (see Figure 2b) requires an additional narrow structure (iii) that we model through a new oscillator (green line in Figure 2d) appearing in the out-of-equilibrium optical conductivity.

Figure 2.

Ultrafast transient reflectivity of CsPbBr₃ disordered NCs sample (left panels) and NC superlattice sample (right panels), measured at 17 K, 230 μJ/cm² excitation fluence and pump photon energy resonant with the excitonic line, i.e., E_pump = 2.41 eV. The bottom (a) and (b) panels report the two-dimensional pump–probe maps displaying the ΔR/R signal (see color scale on the right) as a function of the delay (Δt) and probe photon energy. The top panels (a) and (b) report the ΔR/R signal (blue dots) as a function of the probe photon energy at fixed delay time, Δt = 5 ps (horizontal dashed line in the color maps). The orange solid lines represent the differential fit to the data. (c) and (d) optical conductivity (σ₁) at equilibrium (dashed lines) and out-of-equilibrium at Δt = 5 ps (solid lines) obtained from experimental absorbance and fit of ΔR/R spectra. The colors represent the different contributions to the total optical conductivity: (i) main excitonic line (blue); (ii) across gap optical transitions (red); and the photoinduced peak emerging at low temperature in ordered NC superlattices (green).

The narrow additional peak (green area in Figure 2d) emerging out-of-equilibrium in NC superlattices features characteristics very similar to the superfluorescence recently observed in perovskite superlattices by means of low-temperature photoluminescence.^36,37 While the detailed analysis of this new resonance is discussed in Supporting Information section S9, here we only summarize the main results that allow us to assess its cooperative origin. First, the new resonance appears as a narrower and red-shifted peak as compared to the equilibrium excitonic line. The new peak has a ≃ 40 meV line width, to be compared to the 100 meV width of the main excitonic line, and is centered around 2.36 eV, corresponding to a red-shift δ with respect to the instantaneous position of the main excitonic resonance. By comparing results obtained on nine different NC superlattice samples with the same nominal characteristics, we obtain a value of δ that varies between 40 and 80 meV. Second, a detailed fluence (F) dependence (see Figure S17b) shows peculiar behaviors of the different spectral features in ΔR/R for F < 150–200 μJ/cm². For photon energies ℏω > 2.37 eV, i.e., far from the photoinduced additional peak, the transient reflectivity scales with a power law with exponent (0.91 ± 0.07), which corresponds to a linear behavior. In contrast, the spectral region corresponding to the additional photoinduced peak (ℏω < 2.37 eV) features a clearly superlinear fluence dependence, corresponding to a superlinear exponent (1.43 ± 0.05), in agreement with what is expected for super-radiant phenomena.^30,36,39,41 It is useful to compare the present results with those obtained on disordered NCs, in which collective super-radiant phenomena should be quenched⁵⁰⁻⁵² due to disorder-driven dephasing. As reported in the Supporting Information section S9, in this case, the fluence-dependence of the signal is always linear, independent of the energy region considered. Third, the reflectivity variation corresponding to the spectral feature at 2.36 eV is considerably reduced at room temperature. The temperature-dependent data (Figure S17c) report a suppression of the photoinduced peak at temperatures as high as 200 K, which is compatible with the thermally driven loss of coherence of super-radiant emitters.³²

The physics of the excitonic Mott transition from EG to EHL can be experimentally accessed in the high photodoping limit, which is achieved at light fluences on the order of ∼200 μJ/cm². As shown above, in this regime the transient optical response of NC superlattices is dominated by a decrease of the excitonic spectral weight and the corresponding increase of in-gap free electron states, as captured by the effective red-shift of the semiconducting gap (see Figures 2d and 3a). The transient increase of in-gap states at the expenses of the intensity of the exciton peak demonstrates that, at high fluence, the NC superlattices no longer support well-defined excitons but rather delocalized electron–hole excitations. To assess the nature of this high-excitation regime, we calculated from the differential model (see Supporting Information S8) the spectral weight variation associated with the direct across-gap transitions ΔSW_free. At Δt = 5 ps we obtain ΔSW_free/SW_exc ≃ 0.2, with SW_exc being the spectral weight of the excitonic peak already present in the equilibrium optical conductivity, which indicates that approximately 20% of the initial SW_exc is transferred into in-gap free electrons states. This spectral weight transfer can be considered as the direct signature of the excitonic Mott transition, which is ubiquitously characterized by the appearance of new in-gap metallic states at the expenses of the correlated lower and upper Hubbard bands, corresponding to a single localized exciton and delocalized electron–hole excitations separated by the binding energy E_b (see Figure 3b).⁴⁸ The time-resolved dynamics contains important information about the temporal evolution of the newly created metallic states and the recovery of the initial excitonic gas. Since during the relaxation the excitonic density n_eh decreases due to the slow recombination across the semiconducting gap, at some time the system will undergo the transition from the photoinduced EHL state back to the EG insulating phase. In Figure 3c we plot the temporal evolution of the fraction of the excitonic spectral weight that is transferred to the free carrier states. At low fluence (∼30 μJ/cm², green markers in Figure 3c), the spectral weight of the photoinduced metallic states is very limited and exponentially decays with a time scale of 130 ps (black solid line in Figure 3c). This slow relaxation is in agreement with what expected for the recombination of electrons and holes across the gap and with the fluorescence time scale.^36,53 At large fluences (∼230 μJ/cm², red markers in Figure 3c), we observe additional spectral weight variation, which exceeds that present in the low-fluence data. This additional ΔSW_free component rapidly relaxes with a time scale of ∼20 ps, thus allowing us to estimate the critical number of excitations necessary for re-establishing the insulating EG phase. Assuming that n_eh spontaneously decays with the time scale of 130 ps, the change in slope of the ΔSW_free/SW_exc dynamics at ∼20 ps corresponds to a threshold value 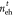= 0.5% (see section S7). A similar conclusion is obtained by analyzing the data on disordered NCs, which display a similar change in the slope of the ΔSW_free/SW_exc dynamics (see Figure 3c).

Figure 3.

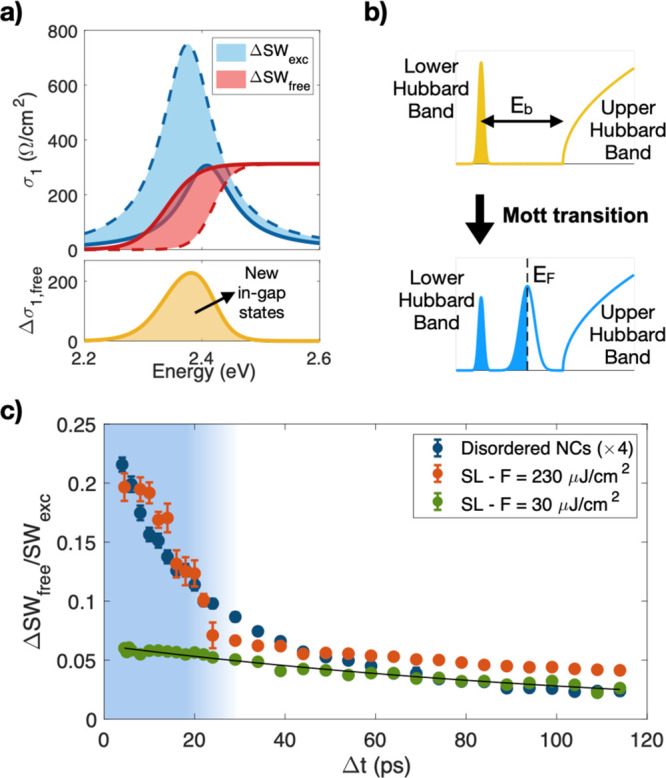
(a) Top panel: plot of the equilibrium (dashed lines) and out-of-equilibrium (solid lines) optical conductivity obtained from fitting the experimental data at Δt = 5 ps. The blue filled area represents the excitonic spectral weight decrease, which is counterbalanced by the appearance of new states below the conduction band minimum, described by a red-shift of the band edge (red filled area). Bottom panel: difference between out-of-equilibrium and equilibrium σ_1,free, which represents the contribution from the conduction band states to the optical conductivity. (b) In terms of the excitonic problem, the insulating phase of the magnetized Hubbard model maps the existence of well-defined localized excitonic states (lower Hubbard band), separated from the upper Hubbard band by an energy amount E_b. When the excitonic density n_eh exceeds a critical value, the Mott transition to a liquid of delocalized electrons and holes takes place and is characterized by the emergence of metallic states at the Fermi level. (c) Time evolution of the spectral weight transfer from the exciton state to free carrier states, estimated as ΔSW_free/SW_exc. The black line denotes an exponentially decaying function fitted to the data. The blue area highlights the region where an excess of ΔSW_free is observed for a large excitation fluence.

The experiments presented above allow access to a region of the zero-temperature phase diagram of 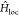+ 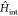that is relevant for describing real correlated materials.^49,54 As discussed in ref (48), the parameters controlling the electronic phases of photoexcited halide perovskites are the excitation density n_eh, which is mapped into the magnetization m through 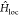, and the binding energy E_b, which is mapped into the Coulomb repulsion U. For small excitation densities (n_eh < 1%) and moderately large Coulomb repulsion (U > 3.8t, with t being proportional to the hopping parameter, following the notation of ref (48)), the phase diagram is characterized by the boundary between an excitonic insulating gas and a mixed state with phase separation between EG and EHL, as shown in Figure 4.⁴⁸ The resonant excitation of the excitonic line directly modifies n_eh without creating an additional effective electron–hole population, which would require a finite temperature description. At the same time, the excitonic energy undergoes a transient blueshift, δE_b (see Figure 2 and related discussion), that is, maximum at short delays (∼5 ps) and progressively decreases as the system relaxes and returns to the initial state. The observed blue shift is likely related to a dynamical weakening of the exciton binding energy as a consequence of the increased screening after the light excitation. The determined time-dependent values of n_eh and δE_b define a trajectory in the phase diagram, in which the energy scales are expressed as a function of the unknown effective hopping t. The determination of 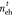= 0.5% as the density threshold for the instability of the EG, allows us to anchor the time-dependent trajectory and fix the range of the U/2t values spanned by the time-resolved experiment. Figure 4 shows the trajectory in the phase diagram for the high-fluence experiment. At very short delays, the NC superlattices are driven into a nonequilibrium state corresponding to U/2t ≈ 1.6 and n_eh = 0.6%, which is characterized by phase separation between insulating EG and metallic EHL regions. In this regime, cooperative phenomena start to be quenched (see Figure S17b) due to the progressive growth of metallic domains. During the relaxation dynamics, the system undergoes a dynamical transition back to the EG insulating phase before the initial parameters (U/2t ≈ 2.8 and n_eh = 0) are recovered on longer time scales. When combined together, our results demonstrate the possibility to explore the region of the magnetized Hubbard model 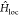that is the most relevant to describe many-body effects in correlated materials (U/t = 3.2–5.6). Although in the present case we access the insulator-to-metal transition in 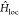only in the presence of a magnetic field h, the observed phenomenology is a very general property of correlated materials, such as iron-based superconductors, superconducting copper oxides and fullerides, which develop superconductivity and other long-range collective phases, e.g., charge density waves, nematicity, antiferromagnetism, and spin density waves, when the Mott insulating state is lightly doped.^19,55

Figure 4.

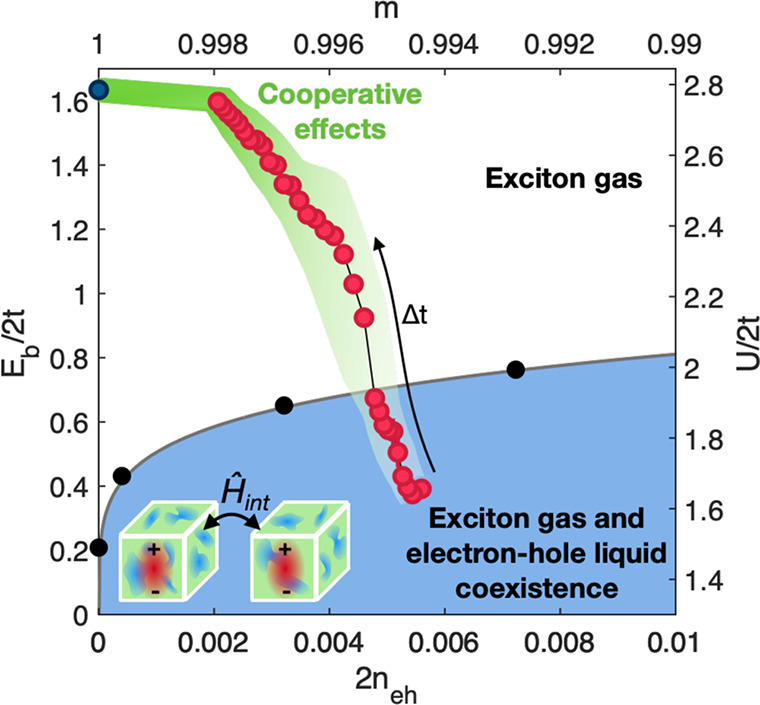
Phase diagram showing the electron gas (EG) and electron–hole liquid (EHL) regions. The electron–hole density 2n_eh and the exciton binding energy E_b correspond to magnetization m and on-site interaction U in the equivalent Hubbard model. The black points are taken from ref (48). The red dots are the experimental data points representing the trajectory the system follows while relaxing to the equilibrium EG phase from the photoinduced EHL phase. The plotted values are the binding energy values extracted from the time-resolved fit of the pump–probe data on NC superlattices at 230 μJ/cm² fluence, as a function of the estimated electron–hole density at the corresponding Δt. The green shaded area represents the phase-space region compatible with the outputs of the time-resolved experiment when the error bars associated with n_eh and E_b are considered.

We have demonstrated here that halide perovskite NC artificial solids represent a unique platform to investigate the emergence of long-range cooperative phases in lightly doped Mott insulators. Future nonresonant experiments will allow to directly create a nonequilibrium electron–hole population at a very high effective temperature, thus providing a platform to simulate the magnetized Hubbard model at finite temperatures and with controllable disorder and lattice size. The possibility to manipulate local correlations and long-range orders on similar time (5–100 ps) and spatial (Λ ≃ 10a) scales can thus trigger the development of fully tunable synthetic quantum correlated materials. As compared to cold-atoms based or solid-state platforms, halide perovskite NC superlattices represent an easy to handle solution, which presents many interesting advantages: (i) they allow continuous tuning of the excitonic density and span collective phenomena and Mott insulating phases in a region of the phase diagram that is directly relevant for correlated quantum materials; (ii) the 1/r scaling of the effective long-range interaction drives a direct all-to-all coupling of a large number of dipoles, on the order of 10⁶, in a spatially confined geometry; (iii) this platform can be easily integrated onto small-scale optoelectronic systems operating in the visible range; (iv) the spontaneous cavity formed by the superlattice itself^40,56 can be naturally exploited to investigate long-range orders in cavity-coupled lattices.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.nanolett.3c03715.

• Theoretical mapping of the excitonic Mott transition; sample preparation; absorbance and photoluminescence spectra, XRD patterns and optical microscopy of disordered NCs and NCs superlattices samples; analysis of aging effects; description of the pump–probe experimental setup; details of the transient reflectivity data fitting; estimation of exciton density; discussion of the experimental evidence of cooperative effects (PDF)

The authors declare no competing financial interest.