Modern Alchemical Free Energy Methods for Drug Discovery Explained

Abstract

This Perspective provides a contextual explanation of the current state-of-the-art alchemical free energy methods and their role in drug discovery as well as highlights select emerging technologies. The narrative attempts to answer basic questions about what goes on “under the hood” in free energy simulations and provide general guidelines for how to run simulations and analyze the results. It is the hope that this work will provide a valuable introduction to students and scientists in the field.

This Perspective is a treatise that brings together and describes the most critical components of alchemical free energy (AFE) methods and places them into the context of free energy simulations used in drug discovery. For broader discussion of methods in the field, the reader is referred to several excellent texts^1,2 and reviews.³⁻⁹ This is an active field with a long history that can be difficult to navigate, especially for new students and practitioners.¹⁰ This work endeavors to answer basic questions about what goes on “under the hood” in free energy simulations and is subjective in the sense that it draws from methods that have been developed in the author’s lab and implemented in the most recent AMBER suite of programs,¹¹ including emerging technologies available for testing as part of the AMBER Drug Discovery Boost package.¹²

1. What Is an Alchemical Free Energy Simulation?

Molecular dynamics (MD) simulations¹³ have been traditionally used to explore the equilibrium and dynamical properties of a single state of a system. Free energy simulations are a distinct class of simulations that explore a process whereby one state of the system changes into a different state.¹ In practice, this usually implies performing a series of simulations that sample both end states and usually the free energy surfaces and/or pathways connecting the states. There are two general categories of free energy simulations that have been subsequently described.

The first category is referred to as the “free energy surface” (FES) or “potential of mean force” (PMF) profile methods that explore a reduced-dimensional free energy profile along some appropriate set of coordinates that describe the real chemical process being studied. Often a goal of these methods is to determine the minimum free energy pathways between states. The pathway establishes the mechanism for the chemical process and thus is of interest together with the free energy values along the path and the associated critical points (e.g., transition states and intermediates) from which kinetic parameters can be determined and predictions can be made. Example applications¹⁴ include the study of catalytic mechanisms of enzymes,^15,16 transport of ions through membrane ion channels,¹⁷ or folding of protein¹⁸ or RNA¹⁹ molecules. This method can also be used to study binding of small molecules in host–guest systems²⁰ or to biological targets^21,22 and has the advantage that it can provide estimates of on/off rates that may be correlated with drug potency.²³

The second category is referred to as “alchemical free energy” methods²⁴ and is illustrated in Figure 1. Here the primary interest is in the overall free energy difference for the process and not the chemical mechanism itself. As the free energy is a state function, changes in free energy are independent of the path taken to effect the transition between states. AFE methods leverage artificial “alchemical” pathways that are more computationally efficient in determining the free energy differences between end states. In this way, one can gain efficiency and robustness in the computation of the free energy difference between states but at the cost of forfeiting information about the real chemical pathways connecting the states. Example applications include the transfer of a molecule from one environment to another (e.g., from the gas phase to aqueous solution), the change in protonation state of a titratable residue in a protein or nucleic acid, or the binding of a drug-like molecule (ligand) to a protein target⁴ (as is the focus of this Perspective).

Figure 1.

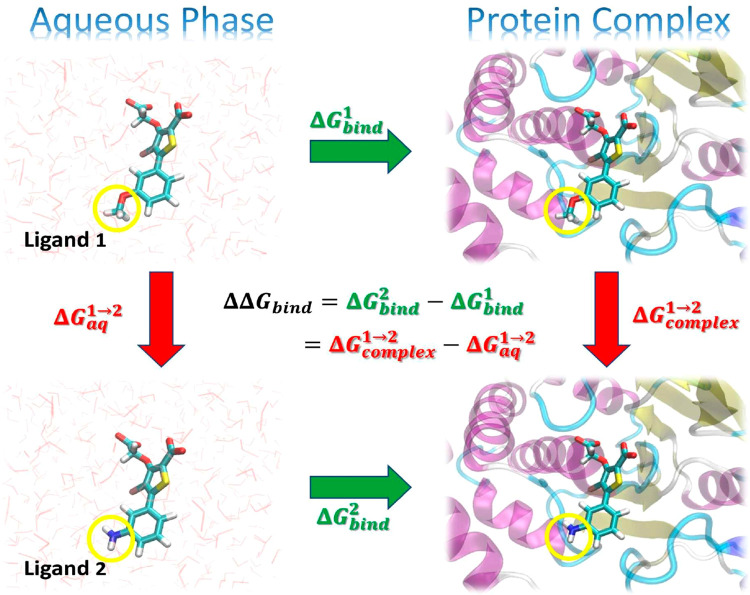
Illustration of a thermodynamic cycle for the relative binding free energy (RBFE, ΔΔG_bind) between two ligands (“Ligand 1” and “Ligand 2”). The green arrows represent the absolute binding free energy (ABFE, ΔG_bind) of each ligand (indicated by the superscript), which involves changing the environment from unbound in the aqueous phase to bound in a complex with the protein target. These quantities are experimentally measurable but are challenging to directly compute, as the change in the environment can be considerably complicated. The red arrows represent alchemical transformations where Ligand 1 is mutated into a similar Ligand 2 in the same environment. These transformations are frequently more amenable to practical computations. The yellow circles in the figures indicate the region of each ligand that undergoes the most significant changes in the alchemical transformation and would likely be modeled using a “softcore potential” during the alchemical transformation.

Formally, these two categories of methods share common theoretical foundations in statistical mechanics and methods for their solution when one recognizes that the main difference is in the choice of real (chemical) or artificial (alchemical) pathways used to connect states. In this way, many of the exact same underlying techniques can be used for either the FES or AFE simulations. For example, for either category one can perform simulations at a set of fixed (constrained) values along the pathway²⁵ such that the mean values of the derivatives (forces) at each point along the path can be numerically integrated to obtain the change in free energy as the reversible work. In the FES category, this is referred to as a PMF calculation,²⁶ whereas in the AFE category this is referred to as a thermodynamic integration (TI) calculation.^27,28 Alternatively, one can monitor fluctuations of the pathway coordinates use biasing potentials (e.g., in a set of “umbrella sampling” simulations²⁹) and reassemble the free energy profile from these multiple distributions using variational approaches such as the unbinned weighted histogram analysis method³⁰ (UWHAM), Bennett’s acceptance ratio (BAR)³¹ or its multistate generalization (MBAR)^32,33 or network-wide extensions with cycle closure,³⁴ and variational free energy profile³⁵⁻³⁷ (vFEP) methods. In the first category, these are known as biased sampling/free energy profile methods^26,37,38 (e.g., “umbrella sampling”²⁹ and metadynamics^39,40), whereas in the second category, this approach is encompassed in so-called λ-dynamics.^41,42 The take-home message here is that FES and AFE methods have the same foundational underpinnings, and most methods developed for one category can be transferred in some way to the other.

2. How Are AFE Simulations Used in Drug Discovery?

Computational predictions are a vital part of drug discovery, and with increasing access to high-performance computing, together with advances in machine learning technology, the role of these predictions in computer-aided drug design is increasing at a rapid pace. Arguably, the most rigorous and, in principle, most accurate of these methods are AFE simulations for prediction of the binding affinity of ligands (e.g., small drug-like molecules) to their macromolecular (e.g., protein or RNA) targets. Drug discovery companies use AFE simulations in the lead optimization phase to predict the RBFEs of proposed ligands and design selectivity to circumvent off-target effects.⁹ Predictions are used to prioritize compounds for the next stage of development:³ costly synthesis and testing in the lead optimization cycle, followed by preclinical drug development and, if successful, advancement to clinical trials. As only a small fraction of trial compounds make it to approved drugs (with an average cost of getting a new drug to market of over $1 billion),⁴³ even small increases in the accuracy of design predictions will have great impact on the cost and efficiency of drug development.^44,45

3. What Are the Different Ways We Can Compute Alchemical Free Energies?

The change in free energy between two thermodynamic states can be rigorously computed using a free energy perturbation⁴⁶ (FEP) or TI^27,28 formulation or through nonequilibrium work (NEW) simulations using the Jarzynski equality⁴⁷ and its equation variations.⁴⁸⁻⁵⁴ Both the TI and NEW approaches require the formulation of a transformation pathway between states in order to connect them. Only the FEP approach formally requires performing simulations only of one or both of the thermodynamic end states in order to obtain the free energy differences between the states. However, the “end-state-only” FEP approach is only reliable in practice if the two end states have large phase space overlap⁵⁵⁻⁵⁸ (e.g., as in so-called indirect reference potential “book-ending” approaches;⁵⁸ see below). For ligand–protein binding, the FEP approach requires breaking down the pathway into smaller λ intervals, similar to the TI method. It should be noted that there exist other approximate (nonrigorous) “end-state-only” methods that require sampling only at the two thermodynamic end points, such as the MM-GB/SA, MM-PB/SA,⁵⁹ and LIE⁶⁰ methods, which are not discussed in this Perspective.

Hence, for drug discovery applications, the TI, FEP, and NEW methods all require a parametric pathway to be introduced to connect thermodynamic states. Often the parameter in this path is designated by the variable λ and varies between 0 and 1. As the end states are generally chemically distinct molecules with different compositions, the pathway is nonphysical and hence referred to as an “alchemical” transformation. This is achieved by defining a λ-dependent potential energy function U(r^N; λ), where U(r^N; 0) = U₀(r^N) and U(r^N; 1) = U₁(r^N) are the end-state potential energy functions (e.g., think of them as representing the “Ligand 1” and “Ligand 2” states in Figure 1), and the parameter λ transforms state 0 into state 1 in such a way as to be continuously differentiable in the interval [0, 1] (e.g., as depicted by the vertical red arrows in Figure 1). Here the coordinate r^N represents the N Cartesian coordinates for each particle as well as any lattice vector information that defines the periodic boundary conditions for the system. While the free energy is a state function and formally is invariant to the pathway connecting states, in practice the TI, FEP, and NEW methods are all extremely sensitive to the pathway and the phase space overlap⁵⁵⁻⁵⁸ of states along the pathway.

Thermodynamic Integration

In the TI method, the free energy change, ΔA_0→1, between states “0” and “1” can be achieved through integration of the thermodynamic derivative as

1

where the second integral involves the derivative of the potential energy U with respect to the parameter that smoothly connects the end states λ = 0 and 1 and the averaging brackets indicate equilibrium sampling of the state characterized by subscript λ. For each λ-window “λ_k”, mean values of 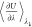are collected, and the sum in eq 1 indicates numerical integration over M quadrature points λ_k (k = 1, ..., M) with associated weights w_k. The weights can be chosen in accord with a particular quadrature, such as the trapezoidal rule, Simpson’s rule, or various Gaussian quadrature rules.⁶¹ Alternatively, spline functions⁶¹ (e.g., cubic splines) or polynomials⁶² can be fitted to the 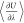profiles and integrated analytically.

Free Energy Perturbation

In the FEP method, the free energy change can be computed as

2

where λ_k < λ_k+1, λ₁ = 0, and λ_M = 1. The interval free energy change ΔA_{λk → λk+1} can be computed from one of several FEP equation variations given by

3

designated “forward” exponential averaging,

4

designated “reverse” exponential averaging, or

5

designated as the “BAR” method, where ΔU_k,k+1 = U(r^N; λ_k+1) – U(r^N; λ_k), β = (k_BT)⁻¹ is the inverse temperature (where k_B is the Boltzmann constant and T the absolute Kelvin temperature), f(x) = 1/(1 + e^x) is a Fermi function, and C is an arbitrary constant. Formally these expressions are equivalent in the limit of infinite sampling. The first and second expressions require conformation sampling (simulation) from one of the two end states of the interval [λ_k, λ_k+1] (as indicated by the subscript on the averaging bracket) and are sometimes referred to as the Zwanzig equation⁴⁶ or “exponential averaging”. The third expression is the BAR equation³¹ and requires sampling from both end states and solving for C such that the first term vanishes (by equating the numerator and denominator) in order that C becomes the statistical best (minimal variance) estimate of the free energy ΔA_{λk → λk+1} for the interval. For MBAR^32,33 analysis, FEP data consist of an M × M matrix of ΔU_k,k′ values (k, k′ = 1, ..., M) for each sampling time point (noting that the diagonal values of this matrix are zero).

In principle, the FEP formula (eq 2) can be applied without taking recourse into intermediate λ states; i.e., in the limit that M = 2, only the end states λ = 0 and/or 1 need to be sampled (no intermediate λ-window simulations are required). However, in practice, this “end-state-only” approach is only feasible if there is a very high degree of phase space overlap⁵⁵⁻⁵⁸ between the λ = 0 and 1 states (which is not the case for AFE simulations in drug discovery). Nonetheless, this can be an attractive approach when one wishes to correct a free energy obtained from simulations performed by using a “low-level” (computationally efficient) Hamiltonian to a “high-level” (computationally intensive) Hamiltonian while avoiding the need to perform an expensive simulation at the high level. These end-state-model Hamiltonian corrections are sometimes referred to as “book-ending” corrections⁵⁸ (as part of an “indirect” AFE approach^{49,53,63−65}) and typically have only modest sampling requirements because the chemical identity of the species does not change, just the potential energy model. Even so, often an intermediate low-level “reference potential” is still needed in order to achieve sufficient phase space overlap for the calculations to be reliable by considering only the end states,⁵⁸ or alternatively, nonequilibrium methods have been shown to be promising^{49,53,63−65} (see below). The take-home message here is that for AFE calculations typically encountered in drug discovery (not “book-ending” corrections), the FEP approach requires simulations of intermediate λ states (λ-windows) with essentially the same requirements as for the TI method.

Nonequilibrium Work

In the NEW methods, the free energy change is computed from a series of nonequilibrium simulations where the work is calculated for transforming λ from 0 to 1 over a time interval τ. Here, by “nonequilibrium” simulations it is recognized that the time interval is not sufficiently long that it can be assumed that the system has reached equilibrium at every sampled λ value in the interval 0 ≤ λ ≤ 1. Let us define the work of such a transformation that departs from starting coordinates r^N(0) = r^N₀ at t = 0 and takes place over the time interval [0, τ] as

6

where in the integral both the coordinates r^N and λ are functions of time and it is implicit that λ will vary from 0 to 1 over the time interval. If one sets the dλ/dt rate to be constant over the interval (i.e., dλ/dt = 1/τ), then the above equation simplifies to

7

Here the subscripts {r^N₀, τ} on the averaging brackets emphasize that the average is taken from a nonequilibrium simulation of duration τ departing from initial coordinates r^N₀. In order to calculate the free energy ΔA_0→1, one performs a series of short nonequilibrium work simulations by sampling the initial conditions {r^N₀} from the equilibrium end-state distribution(s), and computes the free energy change analogously to eqs 3–5:

8

9

10

where the subscripts in the averaging brackets indicate the equilibrium end state distribution from which the initial conditions are sampled for the nonequilibrium simulations. Equation 8 was the original equality proven by Jarzynski,⁴⁷ from which much work has followed, including the formula developed by Crooks⁴⁸ (eq 10).

The nonequilibrium work free energy formulation forms an elegant connection between the thermodynamic integration and free energy perturbation formulas. In the limit that the nonequilibrium work simulation is performed over an infinite amount of time, such that the equilibrium work is actually measured (and the results become independent of initial conditions and do not require averaging), the above formulas become identical to the thermodynamic integration formula of eq 1:

11

Alternatively, in the limit that the nonequilibrium work is performed over a vanishingly short amount of time, such that the coordinates r^N remain fixed, the above formula becomes identical to the change in potential energy:

12

where ΔU_0,1(r^N) = U(r^N; 1) – U(r^N; 0). In this limit, substitution of eq 12 into the nonequilibrium work free energy equations (eqs 8–10) recovers the free energy perturbation equations (eqs 3–5).

4. What is the Best Method to Use: FEP (BAR/MBAR), TI, or NEW?

The conservative, and perhaps less satisfactory answer to this question is almost universally “it is case-dependent”, as each method has advantages and disadvantages. The more aggressive answer is “use more than one method at the same time and perform consistency checks”. What follows is a short discussion of various pros and cons of the different methods as well as general recommendations for establishing robust best practices.

TI versus FEP (BAR/MBAR)

The FEP and TI methods are closely related and have similar computational requirements, and for most codes the overhead for calculating TI, BAR, and MBAR free energy estimates at the same time is negligible. MBAR statistics for a particular λ-window k requires evaluation of ΔU_k,k′ at other λ-windows k′ ≠ k. Not all pairs of state distributions (i.e., not all possible k′ ≠ k) need to be considered in the MBAR analysis (e.g., one could consider only |k′ – k| ≤ n in the analysis, where n is an integer representing the number of nearest-neighbor λ-windows). In the BAR method, only intervals between nearest-neighbor λ-windows are considered. The traditional TI method, on the other hand, requires ∂U/∂λ statistics only for the λ-window being sampled (although methods have been proposed that enable additional statistics to be collected at neighboring λ-windows as well⁶⁶). For well-behaved calculations, MBAR is often the most rapidly convergent of the methods; however, for edge cases, BAR may be more robust. In other cases, the exponential term in the integrand of the FEP (BAR/MBAR) methods can become unstable and more difficult to average due to large fluctuations in the ΔU_k,k′ values, whereas the ∂U/∂λ integrand in the TI method may be less sensitive and yield more stable averages. In any case, the statistical quantities required for the BAR, MBAR, and TI methods are not prohibitive to compute at the same time (as they typically only have to be collected every 1000 time steps or so). It is thus recommended that free energies be calculated from all three analysis methods and used as a consistency check that can help to flag potential problematic edge cases. If, for example, the differences between TI, BAR, and MBAR free energy values are larger than their corresponding statistical error estimates, then likely there is a problem in the calculation that needs to be addressed (see below).

TI/FEP versus NEW

As mentioned previously, the NEW methods form a conceptual connection between the TI and FEP methods, but aspects of their practical application can be different. NEW methods have been successfully applied to a number of problems, most notably single-molecule force microscopy⁶⁷ and related physical and chemical processes and MM → QM transformations in “book-ending” corrections.^{49,53,63−65} Ony fairly recently have NEW methods seen application in direct AFE simulations for drug discovery,⁶⁸ and hence, they are currently less mature than TI and FEP methods and have less well-demonstrated behavior. NEW calculations critically depend on the ability to first sufficiently sample the equilibrium end state distributions that are then used to launch short nonequilibrium switching simulations. The switching time, together with the number of switches (i.e., the number of initial conditions sampled from the equilibrium end state distribution), determines the reliability of the resulting free energy estimate. In practice, the switching time depends on how quickly the environment is able to relax and accommodate the λ perturbation and how much this relaxation affects the free energy estimate. These properties can vary widely between aqueous and protein environments and even more so between relative and absolute binding free energy calculations, often in ways that are not easily predictable. These issues not withstanding, a computational advantage of the NEW methods is that the ensemble of switching simulations are all independent of one another and can be performed in parallel. As the switching simulations are themselves short with respect to those needed by TI and FEP methods, this can translate into potentially very short wall-clock turnaround for users that have substantial on-demand parallel resources such as are available on the cloud (albeit for a high price tag). However, a significant advantage of current TI and FEP methods over the NEW methods is that the former are easily integrated with modern enhanced equilibrium sampling methods such as the ACES⁶⁹ approach discussed below. It is likely that as NEW approaches for AFE calculations continue to evolve they will become an increasingly important tool. As the field is still in the early stages in this regard, the remainder of this Perspective will focus on practical aspects of the more established equilibrium TI and FEP approaches used for drug discovery applications.

5. What Are the Considerations That Go into Performing a Set of AFE Simulations?

There are many steps that go into a setting up AFE simulations in a drug discovery workflow,⁴ ranging from developing structural models for the protein target (if full experimental structures have not been determined at sufficiently high resolution) and ranking docking poses for proposed ligands at the start to making predictions about off-target binding in order to engineer selectivity. In this Perspective, discussion is focused on AFE simulations (RBFE or ABFE) for a set of ligands binding to a single protein target, where the presumed starting point is that reliable starting structures have been prepared for each ligand–protein complex and relaxed and equilibrated in a realistic solvated environment under relevant conditions of temperature, pressure, pH, and ionic strength. The same starting point must also exist for the unbound ligands in aqueous solution as part of the thermodynamic cycle (Figure 1) and, in the case of ABFE calculations, also the unbound (apo) state of the target. To arrive at such a starting point requires practical considerations that have been discussed in detail elsewhere^4,70,71 and are now only briefly mentioned.

First, one should endeavor to depart from a high-fidelity structure of the protein (or other biological target molecule) obtained from experiment (e.g., X-ray crystallography, NMR, or cryo-EM), preferably in ligand-bound form so as to provide information about the ligand binding mode and any target rearrangement that might be induced upon binding. If such structures are not available, then recourse can be taken into homology or integrative structural modeling⁷²⁻⁷⁴ or computational predictions (e.g., Rosetta⁷⁵ or AlphaFold2^76,77). In real-world drug discovery applications, it is unlikely that structures exist for the ligand–protein complexes for which binding affinities are to be predicted, and initial structures typically come from docking and scoring procedures⁷⁷⁻⁸¹ or alignment of ligands of a congeneric series with the known structure of the most chemically similar cocrystallized ligand based on shape similarity, followed by energy refinement.⁷¹ The next goal is to generate a realiable model of the conformational ensemble in a realistic environment under relevant temperature, pressure, pH, and ionic strength conditions. Here it is important to ensure that all residues and functional groups of both ligands and target are in their most probable tautomeric form/protonation state⁸² (which may differ in different environments). Further, it is important to include placement of key water molecules and ions, e.g., solvent components observed crystallographically or predicted by computational methods.⁸³⁻⁸⁶ One common mistake made in calculations is to neutralize a charged protein or nucleic acid with only minimal counterions, as opposed to additionally adding a background of (counterion/co-ion) salt at relevant concentration (e.g., 0.14 M). Not only is this unrealistic, it is also more difficult to sample.^87,88 Once the solvation environment has been established, carefully controlled molecular dynamics procedures using appropriate force fields for the target, ligands, and solvation environment are typically used to allow relaxation of the solvent and ultimately the ligand/target structures (e.g., from their experimental crystal environments) to aqueous solution under constant temperature and pressure conditions. As more than half of drug targets are membrane proteins, additional considerations are needed for AFE simulations in these more complex heterogeneous environments.⁸⁹⁻⁹¹

Once the individual ligand–protein complexes have been prepared and equilibrated in a realistic environment under relevant conditions, AFE simulations can be performed to obtain the relative or absolute binding free energy. This is the main focus of the current Perspective. The following are decisions the practitioner needs to make prior to setting out to run a set of AFE calculations:

• How to construct the thermodynamic graph network.

• How to define the alchemical transformation pathways.

• How to optimize alchemical enhanced sampling.

Each of these is considered in more detail below. It should be emphasized that for each of these topics, there are different strategies that can be taken and different methods that can be brought to bear to solve the problem. In the present discussion, emphasis is placed on those methods for which the author has had first-hand experience in developing and/or applying. Nonetheless, there are alternative methods and approaches that are likely equally effective but that are not reviewed here.

5.1. How to Construct the Thermodynamic Graph Network

The construction of thermodynamic graph networks is a topic for which there are many different strategies.⁹² Early strategies built upon the idea that networks of ligands would be connected using a minimal spanning tree (smallest number of edges) to reduce computational cost, and the edges would be chosen to avoid large perturbations (i.e., connect/transform the most structurally similar ligands). In such transformations, a maximum common substructure⁹³ between two ligands was often identified to define the atom mapping procedure, i.e., the mapping of each atom in one ligand to a structually similar atom in the second ligand (the equivalent mapped atoms would usually share the same coordinates during the transformation). By maximizing the common substructure, the number of remaining atoms would be minimized. These atoms would have to be either created or annihilated in the transformation and often required the use of specialized “softcore” potentials and treatment with separable coordinates during the transformation.

With the concurrent advancement of new AFE methods, high-performance computing hardware, and efficient software implementations, this once established paradigm is now being revisited to some degree. As will be discussed in more detail below, the construction of more “dense” thermodynamic graph networks⁹⁴ enables analysis of cycle closure conditions as well as integration of experimental free energy contraints for known ligands. Network AFE simulations can be performed adaptively with resources allocated dynamically in order to improve precision of the free energy predictions.^95,96 Further, the choice of atoms treated by softcore potentials and using a dual topology are leveraged in alchemical enhanced sampling methods such as ACES.⁶⁹ Hence, while large perturbations should still be avoided if possible, it is sometimes advantageous to choose a smaller “common substructure” or “common core” region (and hence a larger region treated with softcore potentials and separate coordinates within the dual topology) in order that flexible substituents (such as functional groups or rings attached to the common core by single bonds) can be selected for enhanced sampling. These will be discussed in more detail below.

RBFE or ABFE?

When constructing a thermodynamic graph network, one consideration is whether to use relative or absolute binding free energy calculations or a combination of the two. In the case of ABFE calculations, the entire ligand is in some way “annihilated”, or more precisely, it is transformed into a noninteracting “dummy atom” state,⁹⁷⁻⁹⁹ which creates a void space that the environment must then strive to fill during the transformation. Further, specialized restraints need to be imposed in the dummy state such that the noninteracting ligand remains bound in the pocket so that it will retain better phase space overlap with the neighboring λ states.^100,101 One might naively argue that ABFE calculations are more preferable as they are not subject to “cycle closure conditions”, as are RBFE calculations in thermodynamic graph networks that contain redundancies in path connections. However, the reality is that ABFE simulations are much more computationally intensive, as the nature of the transformations is much larger, and the fact that the consistency of results cannot be checked with cycle closure conditions is a significant concern rather than an advantage of the method.

RBFE calculations, on the other hand, enable dense thermodynamic graphs to be constucted and cycle closure conditions to be leveraged to increase overall calculation precision and potentially accuracy as well in the case of inclusion of experimental free energy constraints for known ligands.^34,94 When RBFE calculations are being performed optimally, there is only modest rearrangement of the environment along the alchemical transformation pathway and minimal generation of void space that needs to be occupied by the environment. Moreover, RBFE simulations do not have the same issues as ABFE simulations of maintaining position in the binding pocket when the ligand is in the pure dummy atom state, as such a state does not exist for the RBFE case where there is a shared “common core” of atoms.¹⁰² Alternatively stated, as the two ligand real-state end points are stably bound in an RBFE simulation, the corresponding partial dummy state ligand also will remain bound, as it shares a common core of atoms with the bound ligand that prevents it from diffusing away.

In some cases, RBFE calculations can be performed even when the ligands do not share a “common core” (where atoms in one ligand cannot be directly mapped into those of the other) but are nonetheless similar in overall shape and binding mode (i.e., there is substantial overlap of the ligand shapes and excluded volumes). In this situation, one can perform RBFE simulations as counterpoised ABFE simulations,¹⁰³ i.e., two ABFE transformations performed in opposite directions along the λ dimension within the same simulation. This method will retain the advantage that there is minimal relaxation of the environment and need to occupy void space that is created during the transformation; however, as the ligands no longer share a common core of atoms, Boresch-type restraints^100,101 must be imposed to prevent the dummy atom states⁹⁹ from drifting out of the binding pocket. This form of RBFE calculation between ligands that do not share a common core will be referred to as “core-hopping RBFE”.

Hence, the following is a hierarchy of complexity of AFE calculations of ligands and recommendations of what type of calculation (RBFE, core-hopping RBFE, or ABFE) to perform:

• RBFE: For transformations between ligands that share a common core of atoms (molecular scaffold), such as a congeneric series, and have similar binding modes, i.e., the ligands have strongly overlapping shapes and excluded volumes when bound.

• Core-hopping RBFE: For transformations between ligands that do not share a common core of atoms (molecular scaffold) but have similar shapes and binding modes, i.e., the ligands have strongly overlapping excluded volumes when bound but lack a straightforward atom mapping to a common core.

• ABFE: For transformations of a single ligand for which no other ligand has a similar shape and binding mode, i.e., no other ligand has a strongly overlapping excluded volume when bound.

• ABFE: For transformations of a single representative ligand within a subnetwork of RBFE calculations such that the relative binding free energy values can be connected to those of other ligand subnetworks for which RBFE calculations between subnetworks are not practical (e.g., that have different/nonoverlapping binding modes).

It should be mentioned that there are emerging methods that may further modify the above paradigm. One such promising method is the alchemical transfer method (ATM),¹⁰⁴ a novel approach based on a coordinate transformation that swaps the positions of two ligands. The method has been tested successfully on ligands with diverse scaffolds and offers the advantage of being applicable with any potential energy function.^105,106

5.2. How to Define the Alchemical Transformation Pathways

There are many strategies for performing free energy simulations^4,8,107 and in turn for choosing appropriate alchemical transformation pathways. Here the focus is on “concerted” alchemical transformations (sometimes referred to as “one-step” or “unified” procedures) where all nonbonded terms (e.g., electrostatic and Lennard-Jones) occur synchronously. This differs from “stepwise” transformations (sometimes referred to as “multistep” or “split” procedures), where transformation of electrostatic and Lennard-Jones terms occur asynchronously, for example, in a three-step “decharge/LJ/recharge” transformation. Concerted transformations are particularly useful in RBFE calculations, as they avoid weakly bound states that may require additional restraints and are easily integrated with enhanced sampling tools such as replica exchange and ACES. Formally, the lines that separate concerted and stepwise transformations are somewhat arbitrary and can be tuned by so-called “λ-scheduling”, where different energy terms can be turned off/on independently over different subintervals of the global [0, 1] λ interval.^12,102

Alchemical free energy simulations typically require at least some atoms to be effectively created or annihilated during the transformation process. This is achieved by transforming atoms into so-called “dummy atoms”⁹⁷⁻⁹⁹ that do not interact with the real atoms of the physical system except through select bonded interactions such that they do not introduce a net potential of mean force on any of the real atoms. Transformations of real atoms into dummy atoms can be especially challenging if there is poor phase space overlap of neighboring states along the transformation coordinate,^{56,58,99,108,109} giving rise to chronic problems such as end-point catastrophes, particle collapses, and large gradient jumps.¹⁰² This issue can also occur in transformations between two real atoms that have significantly different force field parameters.

A number of strategies have been explored to develop stable transformation pathways in alchemical free energy simulations, including the use of so-called “softcore potentials” with separation-shifted scaling,^110−112 parameter interpolation,¹¹³ short-range switching,¹¹⁴ or capping the short-range interactions^115,116 and nonlinear mixing of the end-point potentials.^117−121 Recent studies have shown that adverse effects of these problematic transitions can lead to large variance and in some cases order/disorder transitions along the alchemical path that can hinder sampling and convergence of free energy estimates.¹¹⁶ Very recently, a λ-enveloping distribution sampling method,^107,122,123 which is related to approaches to optimize minimum-variance pathways in alchemical transformations,^124−126 has been explored as an alternative coupling scheme to more conventional λ-intermediate states.

Recently, we developed a new framework¹² for the design of optimized alchemical transformation pathways.¹²⁷ The methods extended and improved the use of so-called “smoothstep” softcore potentials¹²⁸ to address chronic problems of particle collapse and large gradient jumps.¹²⁷ Important improvements include (1) consistent power scaling of Coulomb (Coul) and Lennard-Jones (LJ) interactions with unitless control parameters to maintain balance of electrostatic attractions and exchange repulsions, (2) introduction of a pairwise form based on the LJ contact radius for the effective interaction distance with separation-shifted scaling, and (3) rigorous smoothing of the softcore potential at the nonbonded cutoff boundary. The new softcore potentials and optimized alchemical transformation pathways¹²⁷ improve phase space overlap between neighboring states and have been leveraged in the development of the new alchemical enhanced sampling (ACES) method⁶⁹ for accelerated convergence of conformational ensembles and free energy estimates.

5.3. How to Optimize Alchemical Enhanced Sampling

The term “enhanced sampling” has been used in many contexts.^129−137 As the dynamic degrees of freedom in a molecular simulation are usually the atomic positions, sampling is intimately connected to different conformations of the system. It is important to distinguish “conformational sampling” of a target distribution from “conformational searching” for a structural ensemble or pathway that optimally satisfies some property of interest that is part of the search criteria (e.g., a stable docking pose, metal ion binding site, or protein/nucleic acid conformational state). In the context of free energy simulations, enhanced sampling implies sampling in regions that contribute substantially to the free energy change of interest but that are only seldom visited by Boltzmann sampling (e.g., by conventional molecular dynamics) of any one state along the transformation pathway. This subclass of methods is referred to as “importance sampling” methods. As an example, if a ligand can adopt multiple orientations in the binding pocket of a protein, then a method able to sample each with the correct occupation is important to obtain an accurate estimate of the binding free energy. On the other hand, an enhanced sampling method used to study protein folding pathways that explore conformations of folded and unfolded states likely would be counterproductive to the sampling needed to converge the free energy estimate for ligand–protein binding where only the folded state significantly contributes. In this sense, importance sampling must focus on the degrees of freedom responsible for converging the free energy change of interest while avoiding unnecessary “enhanced sampling” of other degrees of freedom.^1,138

There is a vast array of enhanced sampling methods for AFE simulations,^{129−132,132−136,139,140} including replica exchange (RE)^141−143 and multiple-replica strategies that use adaptive biasing forces,¹⁴⁴ umbrella sampling (US),^29,145 parallel or simulated tempering,^{141,142,146,147} metadynamics,¹⁴⁸ self-guided molecular dynamics,¹⁴⁹ replica exchange with solute tempering (REST¹⁵⁰ or REST2¹⁵¹), multicanonical algorithm (MUCA),^152−154 orthogonal space random walk (OSRW),¹⁵⁵ λ-enveloping distribution sampling (EDS/λ-EDS),^122,123,156 thermodynamic integration with enhanced sampling (TIES), and others.^{9,54,132,134,153,157,158}

We recently introduced⁶⁹ an ACES method in AMBER that integrates the following novel features:

• Localized enhanced sampling states through tuning of intra- and intermolecular energy terms, e.g., noninteracting “dummy” states⁹⁹ with modified internal energy terms that eliminate kinetic traps;

• Robust alchemical transformation pathways to connect real and enhanced sampling states using new smoothstep softcore potentials, nonlinear Hamiltonian mixing, and flexible λ-scheduling capabilities;¹⁰²

• Efficient Hamiltonian replica exchange MD (HREMD) frameworks that maintain equilibrium between λ-windows and enable enhanced sampling.

The ACES approach⁶⁹ has advantages due to its dual-topology nature¹⁶⁰ that allows it to overcome local “hot spot” problems encountered with REST/REST2.¹⁶¹ As the ACES region of the λ = 0 real state (e.g., Ligand 1) is being “annihilated” with respect to its interactions with the environment and transformation into an enhanced-sampled “dummy” state,⁹⁹ the ACES region of the λ = 1 real state (e.g., Ligand 2) is being “created”. This concerted “counterdiffusion” of alchemical states produces minimal rearrangement of the environment along the λ path. Further, the computational overhead of the method is negligible relative to more conventional AFE simulations with HREMD. Although ACES can be used along with REST2-like methods added to further enhance sampling of the end states (which incurs added computational cost), results suggest that there is little gain beyond using ACES alone.⁶⁹

Enhanced sampling methods such as ACES can reduce issues associated with ligands that exhibit multiple orientations or binding poses, especially when the free energy barriers between these conformational states are sufficiently low that interconversion is observed within the time scale of the simulations. On the other hand, if this cannot be achieved, then alternative strategies need to be pursued.⁷⁰ One straightforward, albeit time-consuming, way to deal with this situation is to calculate the free energy associated with each binding mode separately and use Boltzmann weighting to account for their collective free energy.¹⁶² Emerging end-state alchemical reservoir methods will enable the precalculation of multiple ligand binding modes that can be integrated with existing enhanced sampling methods, such as ACES.

6. What Are Some General Recommendations for Performing AFE Simulations?

The following are some general recommendations for setting up and running simulations (further details are outlined in a recently reported workflow⁹⁴):

• Carefully equilibrate each end state (node) prior to setting up an alchemical transformation (edge) simulation between the nodes. Use the same equilibrated structures of a given node consistently for any edge containing the node.

• Construct “dense” thermodynamic graphs that have sufficient redundancy to enable network-wide analysis³⁴ of cycle closure conditions and yield meaningful internal consistency checks.

• Use optimized alchemical transformation pathways, including smoothstep softcore potentials¹⁰² and, if necessary, advanced λ scheduling features in order to maximize phase space overlap between windows.

• Apply robust enhanced sampling methods such as ACES⁶⁹ that leverage an HREMD framework to ensure that different λ-windows are kept in equilibrium.

Simulation results should be tested for convergence through block analysis, and statistical error estimates should be made^{1,33,34,163−165} that include multiple independent trials of ACES runs. The next section discusses potential caveats and offers suggestions for analysis to help troubleshoot and improve the reliability of predicted results.

7. How Do I Know If There Are Problems with My AFE Calculations?

AFE simulations, aside from issues associated with the accuracy of the force fields used, can encounter a number of caveats that limit their predictive capability. In what follows, we consider the most common use case in drug discovery: AFE simulations for a set of ligands arranged in a thermodynamic graph network, where the nodes in the graph represent real states and edges that connect nodes represent alchemical transformations between the real states. The real states thus form the “end states” (or “real-state end points”) for a given alchemical transformation. Within this context, the following are some guiding principles:

• Are the end-state (node) conformational ensembles and associated energy distributions correct and consistent within the network, i.e., are they the same for every connecting alchemical transformation (every edge containing the same node)?

• For a given alchemical transformation (edge), are the λ-window simulations sampling consistent conformational ensembles and energy distributions, i.e., are the λ-windows in equilibrium with one another?

• For the degree of sampling that is achieved, is the alchemical transformation pathway stable, i.e., do the ∂U/∂λ distributions fluctuate stably (i.e., appear unimodal with small variance and show no signs of phase transition behavior in the λ-dimension) and is there sufficient phase space overlap between λ-windows to allow a reliable estimate of the free energy?

Of these guiding principles, often the most difficult one to correct is the first. In typical calculations, edges are computed in separate (independent) simulations, e.g., a HREMD simulation using ACES or the REST/REST2 method. For example, consider a particular node (“node 1”) that is connected to three other nodes (“nodes 2, 3, and 4”) in a thermodynamic graph, and let us label the edges connecting to node 1 as “edge (1–2), edge (1–3), and edge (1–4)”. Suppose that for each edge an HREMD simulation is performed such that the λ-windows, including the end states, are in equilibrium with one another. If simulations for each edge are performed separately, then it is not guaranteed (or even probable) that the end state distributions for node 1 derived independently from edge (1–2), edge (1–3), and edge (1–4) HREMD simulations will be statistically indistinguishable. In principle, one could set up a large network of HREMD simulations, where the edges are connected through a common node. This strategy imposes a constraint that the entire network of HREMD simulations be run in some way synchronously (even if exchanges are made asynchronously) and does not easily allow for the network to be extended to include new edges and nodes. An alternate strategy is to precompute the end state (node) distributions and store them as end-state alchemical reservoirs and then use them as ensemble baths for each node (i.e., have the reservoirs exchanging at the end state during an edge transformation so as to ensure a consistent end state distribution). A technical challenge arises as to how to rigorously map the set of noninteracting “dummy atoms” that are needed for an alchemical (edge) tansformation onto a reservoir conformation where such dummy atoms are not present. These end-state reservoir methods are forthcoming and promise to considerably enhance the level of precision achievable in AFE simulations for drug discovery.

Once a strategy has been decided in terms of construction of a thermodynamic graph network, atom mapping procedure, and alchemical transformation pathway, the following are some valuable checks that can be performed:

• Perform comprehensive statistical error analysis^{1,33,34,163−165} (of both correlated data samples and independent trials) such as block bootstrapping and forward/reverse sampling.

• Compare TI and MBAR free energy estimates for consistency within their estimated statistical errors.³⁴ If the variance between estimates is outside of reasonable error bounds, this is suggestive of problems that need to be addressed. Tracking how the MBAR result changes by progressively removing states in the analysis (approaching the BAR limit) could offer additional insight into the stability of the free energy estimate.

• Analyze the ⟨∂U/∂λ⟩_λ profiles as a function of λ and the variance at each λ-window. Windows that exhibit kinks and/or deviations from otherwise smooth profiles or that have anomalously large variances or bimodal ∂U/∂λ distributions are likely problematic. A possible solution is to find a more suitable alchemical transformation pathway by considering alternative softcore potentials, atom mapping, λ scheduling (which may include sequential creation/annihilation of functional groups one at a time as opposed to all at once), or introduction of new chemical or alchemical intermediates (i.e., new nodes in the thermodynamic graph).

• Analyze phase space overlap, HREMD acceptance ratios, and round-trip statistics. Phase space overlap is typically correlated with the HREMD acceptance ratios and should never dip to values close to zero (values below 0.2 are of concern). HREMD simulations should see many walkers making “round trips” from one real state to the other and back again. Two common origins of poor phase space overlap are (1) the spacing between λ windows is too large and (2) first-order phase transitions in the λ-dimension can result in bimodal ∂U/∂λ distributions. In the first case, a possible solution is to find more optimal λ spacing such that the phase space overlap is larger and more uniform, and if needed, increase the number of λ-windows appropriately. In the second case, it may be necessary to introduce new chemical or alchemical intermediates to further break up edges that exhibit these phase transitions.

• Analyze cycle closure conditions as independent consistency checks and perform Lagrange multiplier analysis to identify potentially problematic edges. If such an edge is identified, consider excluding it in the analysis (which might require adding a new edge to reconnect a node that was severed).

8. What Are Some Other Considerations and Future Directions?

There are a vast number of outstanding issues that are being actively addressed by a variety of groups at the forefront of the field. Some selected for mention here include the following:

• Methods to handle interfacial and buried (kinetically trapped) water molecules that can fluctuate in occupancy upon binding.⁸³⁻⁸⁵

• Charge-changing ligand perturbations and counterbalancing salt effects.^166−170

• Alternative tautomers^82,171 and protonation states¹⁷² of both ligand and target molecules.^82,173,174

• Binding sites involving metal–ligand interactions.^175,176

• Covalent inhibition.^177,178

As the methods evolve to meet these and other challenges, it will become increasingly important to perform large-scale assessments^179,180 and conduct community-wide blind challenges.^181,182

Emerging technologies that promise to improve the accuracy and precision of AFE calculations in drug discovery include the development of end-state ensemble reservoirs that can be used within networks to ensure consistent end states as well as continued evolution of sampling methods. Finally, there are a number of exciting advances in the development of new force fields that promise higher levels of accuracy, most notably classical polarizable force fields^183−187 and machine learning potentials (MLPs).^188−191 Of particular promise are the new methods that combine fast, approximate quantum-mechanical (QM) models with MLP corrections to achieve high accuracy (QM/Δ-MLPs).^{174,192−197} These methods are “universal” in the sense that unlike molecular mechanical force fields (including polarizable force fields), they do not assume a predetermined bonding topology and are able to accurately model different tautomers and protonation states. This is highly significant, as 30% of the compounds in vendor databases and 21% drug databases have potential tautomers^198,199 and it has been estimated that up to 95% of drug molecules contain ionizable groups.¹⁹⁸

What is clear is that there is a driving need to continue to advance the state-of-the-art AFE simulations to improve both precision and accuracy to meet the evolving challenges in the design of new therapeutics. It is our hope that the current Perspective is useful in providing some insight into modern alchemical free energy methods and their role in drug discovery.

The author declares no competing financial interest.