Theoretical Insight into the Effect of Phosphorus Oxygenation on Nonradiative Decays: Comparative Analysis of P-Bridged Stilbene Analogs

Abstract

Incorporation of the phosphorus element into a π-conjugated skeleton offers valuable prospects for adjusting the electronic structure of the resulting functional π-electron systems. Trivalent phosphorus has the potential to decrease the LUMO level through σ*−π* interaction, which is further enhanced by its oxygenation to the pentavalent P center. This study shows that utilizing our computational analysis to examine excited-state dynamics based on radiative/nonradiative rate constants and fluorescence quantum yield (Φ_F) is effective for analyzing the photophysical properties of P-containing organic dyes. We theoretically investigate how the trivalent phosphanyl group and pentavalent phosphine oxide moieties affect radiative and nonradiative decay processes. We evaluate four variations of P-bridged stilbene analogs. Our analysis reveals that the primary decay pathway for photoexcited bis-phosphanyl-bridged stilbene is the intersystem crossing (ISC) to the triplet state and nonradiative. The oxidation of the phosphine moiety, however, suppresses the ISC due to the relative destabilization of the triplet states. The calculated rate constants match an increase in experimental Φ_F from 0.07 to 0.98, as simulated from 0.23 to 0.94. The reduced HOMO–LUMO gap supports a red shift in the fluorescence spectra relative to the phosphine analog. The thiophene-fused variant with the nonoxidized trivalent P center exhibits intense emission with a high Φ_F, 0.95. Our prediction indicates that the ISC transfer is obstructed owing to the relatively destabilized triplet state induced by the thiophene substitution. Conversely, the thiophene-fused analog with the phosphine oxide moieties triggers a high-rate internal conversion mediated by conical intersection, leading to a decreased Φ_F.

1. Introduction

The effective use of quantum chemical calculations for developing novel photofunctional molecules has received growing interest.¹⁻³ Computing energy levels of excited states and their oscillator strengths for electric dipole transitions using time-dependent density functional theory (TD-DFT) has become a standard practice in synthetic work. Besides these properties, the functionalities of the organic dyes and their photophysical performances are influenced by the decay behavior of photoexcited molecules, which proceeds via radiative and nonradiative transitions.⁴⁻⁷ Thus, a more in-depth theoretical characterization of the dyes by detailing these processes is desirable. In particular, the computational method to analyze the excited-state dynamics based on the simulation of nonradiative decay rate constants (k_nr) and fluorescence quantum yield (Φ_F) is in urgent demand. The nonradiative decay occurs at the intersection of potential energy surfaces or that between vibronic states. Synthetically, tuning electronic structures of organic dyes by chemical modification with main group elements is a promised approach to impact the decay behavior.⁸⁻¹⁰ However, there is still limited availability of computational approaches to estimate the rate constants affected by chemical tuning. Hence, incorporating quantum chemical technology to accurately predict k_nr and Φ_F into exploring tuned molecular dyes is yet a crucial endeavor.

Among the main group elements, incorporation of a phosphorus atom into an organic π-conjugated skeletons through a synthetic approach has recently been the subject of significant interest.¹⁰⁻¹⁷ These phosphorus-containing π-skeletons serve as synthetically manipulable building blocks, giving rise to novel classes of organic (opto)electronic materials that exhibit notable functionalities and performances. Prominent examples include bioimaging probes exhibiting exceptional photostability¹⁸⁻²⁰ and near-infrared (NIR) fluorescence,²¹⁻²³ thermally activated delayed fluorescence (TADF) dyes boasting high quantum efficiency,²⁴ and organic photovoltaic cells demonstrating enhanced power conversion efficiency.²⁵ Such successful applications of organophosphorus systems have piqued a growing interest.

A distinctive characteristic of phosphorus (P) in the development of organic π-conjugated materials is its structural and electronic nature, which varies according to the oxidation state of the P center in the moieties.^10,13,16,26 The trivalent phosphorus involves a lone pair that is not effectively delocalized. Phosphole, a phosphorus counterpart of pyrrole, is an example that includes a P center with this type of covalency. The site hosting the lone pair provides various fine-tuning opportunities through chemical modifications, including oxidation to phosphine oxides or sulfides, complexation with boranes, and coordination with metal atoms.¹¹⁻¹⁴ However, the trivalent P-moieties exhibit a limited n-π orbital interaction, leading to a diminished aromatic character. This outcome is a result of the P center adopting a trigonal pyramidal geometry, which triggers a characteristic σ*−π* interaction, thus stabilizing the LUMO energy level.^11,27 Consequently, the phosphole ring serves not as an electron-donating unit but as a potent electron-withdrawing/accepting unit. This characteristic makes them desirable as building blocks in the construction of n-type (electron-acceptor) materials.

Pentavalent phosphorus can be generated by oxidizing the trivalent P center—such as oxygenation to phosphine oxides (for instance, phosphole oxide). The σ*−π* interaction between the P atom and the π framework is further enhanced by the presence of the P–O bond. Previous ab initio orbital analyses^28,29 clearly showed that the bonding nature of phosphine oxides is more aptly described as R₃P⁺–O^– rather than R₃P=O. This interpretation stems from the orbital view that the P–O bond comprises a strongly polarized σ bond and an additional ionic interaction associated with oxygen π orbital back-bonding. It correlates with the short length of the PO bond and underlies its greater bonding strength compared with the traditional single bond. Such extended orbital conjugation in phosphine oxides plays a fascinating role in reducing the LUMO energy level compared to that of the trivalent P-moieties. As a result, the PO-containing π-conjugated skeleton, such as phosphole oxide, can be desirable as a building block in the construction of n-type (electron-acceptor) materials.^12,14,15

Therefore, adjusting the covalency of phosphorus through chemical modifications, such as oxidation, represents a promising strategy for fine-tuning the electronic properties of organophosphorus π-conjugated systems. In this regard, one of the authors conducted experimental studies on the phosphorus-containing ladder-type π-conjugated molecules and analyzed the relationship between structure and properties.^26,30 In this paper, we aim to augment these findings by delving deeper into the theoretical aspects of the extraordinary effects of oxidation on P-containing organic dyes experimentally observed in a previous work.

As trivalent phosphorus systems, two types of ladder π-conjugated molecules were created: bis-phosphanyl-bridged stilbene (P-Ben in Figure 1) and its thiophene-fused counterpart (P-Thio′ in Figure 1), in which the benzene rings of P-Ben are replaced with thiophene rings. In terms of the pentavalent phosphorus species, the corresponding oxides were synthesized: bisphosphoryl-bridged stilbene (PO-Ben) and its thiophene-fused derivative (PO-Thio′). Notably, the spectroscopic measurements revealed that the oxidation of the P-centers led to completely divergent impacts on the resulting alternations of photophysical properties between the benzene and thiophene series, as discussed below.

Figure 1.

Chemical structures of the molecules investigated in this study. The fluorescence quantum yields experimentally determined^26,30 are provided in the parentheses. P-Thio and PO-Thio are modeled molecules utilized in this study.

The crucial discovery from refs (30) and (26) is twofold. First, the oxidation of P-Ben to PO-Ben resulted in a red shift in absorption and fluorescence, which correlates with the lowered LUMO level by the oxidation. Concurrently, this transformation led to a significant enhancement in the fluorescence quantum yield (Φ_F) from 0.07 to 0.98 (Figure 1). This suggests that the phosphole-oxide could serve as an effective building unit for designing fluorescent dye molecules with a high Φ_F. Based on discovering its properties in PO-Ben, one of the authors developed a fluorescent bioimaging marker involving the phosphine oxide moiety.^31,32 The marker has high photostability due to its high Φ_F, which is crucial for imaging the mitochondrial ultrastructure in living cells. However, regarding the thiophene-fused counterparts, the effect of the oxidation on Φ_F is reversed; the Φ_F for P-Thio′ and PO-Thio′ was found to be 0.95 and 0.04, respectively (Figure 1). This inconsistent trend of Φ_F upon the oxidation of phosphole to phosphole-oxide cannot be explained by the conventional understanding of the organophosphorus electronic nature. While it has been widely acknowledged that thiophene has a higher-lying HOMO level, making it a stronger electron donor than benzene, it remains unclear why this difference instigates an opposite trend of Φ_F for oxygenation in the thiophene and benzene series.

In this study, we aim to clarify the unique photophysical trends of trivalent and pentavalent P-bridged stilbene analogs using quantum chemical and excited-state dynamics calculations. Detailed theoretical models of the radiative and nonradiative decay processes are constructed based on the calculated excited-state potential energy surfaces (PESs) and excited-state dynamics. There are various ways to estimate decay rate constants, including nonadiabatic molecular dynamics simulations, perturbative methods such as Fermi’s golden rule or Marcus theory, and Eyring’s equation to determine the activation energy at the excited state. Out of these methods, the perturbative approach has been applied in recent years for studying relatively slow decays. Barone and Santoro et al. utilized time-independent and time-dependent formalisms to simulate the absorption and radiative spectra, incorporating the effects of vibronic transitions.³³⁻³⁹ Shuai et al. developed a computational approach based on the time-dependent formalism called the thermal vibration correlation function (TVCF) method, which allows the efficient evaluation of rate constants for radiative decay, internal conversion (IC), and intersystem crossings (ISCs).^7,40−42 These rate constant calculations have been employed to study the Φ_F of the organic π-conjugated molecules,^39,43−45 some of which also searched the conical intersection. This approach builds upon primary formalisms and techniques developed in prior studies, including the correlation function approach by Lin⁴⁶⁻⁴⁸ and the generating function approach by Lax and Kubo.⁴⁹⁻⁵¹

To handle ISCs in molecules mediated by small spin–orbit coupling matrix elements (SOCMEs), Shuai et al. incorporated a formalism based on second-order perturbation theory,⁷ which was also employed in a recent study by Kim et al.^52,53 Alternatively, Marian et al. developed a method for using the first-order derivatives of SOCMEs within the framework of the Herzberg–Teller expansion.^6,54,55 The related methods have been made available in the ORCA program.⁵⁶ Lastly, Liang et al. used this kind of calculation to investigate ISCs in the TADF emitter.⁵⁷

This study demonstrates that the predicted rate constants of the decay processes using the perturbative excited-state dynamics theory adequately account for the trend of Φ_F transitioning from P-Ben (P-Thio′) to PO-Ben (PO-Thio′). In the case of PO-Thio′, we focus on another nonradiative decay process facilitated by a conical intersection (CI), revealing that the computed minimal-energy CI (MECI) is sufficiently stable, consistent with a small Φ_F. Gaining an understanding of the electronic-level mechanisms underlying the variations in Φ_F for these systems could yield advanced insights into the fine-tuning of organophosphorus dyes. This study underscores the effectiveness of our computational approach in conducting a detailed analysis of P-containing organic dyes.

2. Method

In this study, we employed rate constant simulations grounded on first-principles molecular modeling to analyze how the oxygenation of the phosphorus atom in P-bridged stilbene analogs impacts their nonradiative decay rates. The molecules incorporated in the calculations are depicted in Figure 1. To expedite the computational investigation, we utilized model molecules P-Thio and PO-Thio as substitutes for experimentally studied P-Thio′ and PO-Thio′. The assumption behind this substitution is that the triisopropylsilyl (TIPS) moieties do not influence the decay processes. With the optimized geometries in the S₁ and several low-lying triplet states, we computed the rate constants of the transitions from the initial S₁ state to the pertinent destination states. These rate constants were then used as fundamental physical parameters to characterize the effects on nonradiative decay.

We have calculated the rate constants for fluorescent decay, the S₁ → S₀ IC, and ISC to each triplet state T, which we denote as k_r, k_ic, and k_isc(T), respectively, for four molecules: P-Ben, PO-Ben, P-Thio, and PO-Thio. In this study, the TVCF method serves as a central tool for estimating the rate constants of various electronic transitions in a simplified, yet effective way. The basics of the TVCF approach are briefly reviewed in the Supporting Information (SI). For the calculations of k_r and k_isc(T), the transition dipole moments and SOCMEs are required within the TVCF framework. These coupling quantities were processed with two levels of vibronic treatments based on the Franck–Condon (FC) and Herzberg–Teller (HT) approximations. Our calculations excluded the involvement of intermediate states in the description of the ISC process.^6,7,52,53 The total rate constant of the ISC transition from the S₁ to the triplet state was calculated as a sum of those to the triplet’s spin-substates:⁶ Ε_M=–1,0,1k_isc(T^M). The calculations of k_ic necessitate the nonadiabatic coupling matrix elements (NACMEs), which were considered at the FC level, following the approach taken by Shuai et al.

Furthermore, we investigated the energetic accessibility of PO-Thio to a CI. The optimized geometries of the S₁ state and the MECI for PO-Thio were ascertained at the level of the extended multistate complete-active-space second-order perturbation theory (XMS-CASPT2).⁵⁸ The activation energy required to reach the MECI at the S₁ state was estimated by using these structures. By considering both the rate constant predictions derived from the TVCF method and the MECI activation energy, we conducted a comparative analysis of the P-bridged stilbene analogs.

3. Computational Details

Throughout our electronic structure calculations, we considered each molecule as a single isolated system in the gas phase. We performed geometry optimizations and Hessian calculations on the S₀, S₁, and several lowest-lying triplet states at the (TD-)PBE0/cc-pVDZ level of theory.⁵⁹⁻⁶¹ We chose this functional based on the computed absorption and fluorescence energies and subsequent Stokes shift (see the SI). The transition dipole moments, their analytical derivatives, and NACMEs were computed at the minimum of the S₁ state using the same computational approach. The SOCMEs were determined at the ZORA-TD-PBE0/ZORA-def2-TZVP level of theory⁶²⁻⁶⁴ using a Breit-Pauli type Hamiltonian with a mean-field approximation for the 2-electron term.⁶⁵ In these SOC calculations, we used the SARC/J basis⁶⁶ for the density fitting to the Coulomb term and a chain-of-spheres exchange for the exchange term to expedite the calculation (RIJCOSX).^67,68 The derivatives of the SOCMEs were evaluated using numerical differentiation at the S₁ minimum under the same computational condition. At the DFT-optimized geometries, the similarity transformed equation-of-motion coupled-cluster model at the singles and doubles under the approximation with the domain-based local pair natural orbital (DLPNO-STEOM-CCSD)⁶⁹⁻⁷² calculations with the cc-pVTZ basis set were conducted using the ORCA 5.0.1 program⁵⁶ to validate the estimations of the adiabatic energies (ΔE) at the TD-PBE0 level. In this wave function calculation, we used the RIJCOSX approximation with the def2-universal/J and cc-pVTZ/C auxiliary basis sets for RHF and DLPNO-STEOM-CCSD treatments. To circumvent a technical issue in version 5.0.1, the SOCMEs were recalculated using the ORCA 5.0.2 program. All other TD-DFT calculations were conducted using the Gaussian 16 rev. B01 program.⁷³

3.1. Decay Rate Constant Calculations

The rate constants were calculated by using our in-house code, written in the Python programming language. We incorporated a module adapted from Psi4⁷⁴ to prepare the normal modes in internal coordinates. The matrix operations associated with the internal coordinate space were programmed in line with the β version of FCClasses 3.0.^75,76 More detailed information about the methods we used to compute rate constants can be found in the Supporting Information.

Throughout our rate constant calculations, the harmonic approximation to the PESs was based on the adiabatic Hessian model. We didn’t test the vertical Hessian model^35,36 due to the limitations of our implementation. The validity of the adiabatic Hessian PES treatment was assessed by checking the reorganization energies (Table S3). The vibrational modes at the initial and final states were employed, considering the Duschinsky rotation,⁷⁷ where the shift vector and Duschinsky matrix were computed in the redundant internal coordinate space.^35,38,78,79 We did not use a scaling factor for the vibrational frequencies. The vibrational state at the initial state was set based on the Boltzmann distribution, assuming a temperature of 300 K. The delta function dephasing in Fermi’s golden rule was represented by a Gaussian function with a half-width-half-maximum (HWHM) of 50 cm^–1. The importance of the choice of the line shape function was discussed in ref (39), where a Lorentzian broadening was shown to largely affect the k_ic versus adiabatic energy plot. In our system, Lorentzian broadening with a HWHM of 0.033 cm^–1, which was determined based on the fluorescence lifetime of PO-Thio′ (1.0 ns), was found to show a negligible effect on our Φ_F estimation (Figure S4b). The correlation function was evaluated over a time range from 0.05 to 10000.15 fs, with a time step of 0.1 fs. The correlation function for the negative time was inserted using the complex conjugate of the positive time region.

The rate constants k_r, k_ic, and k_isc are obtained as functions of the separate entities ρ(t) and ΔE (further details are available in the SI). The correlation function ρ(t) was constructed by using the harmonic vibrational states ascertained at the PBE0 level of theory. In the rate constant calculations, we used ΔE as a variable, allowing us to substitute with different values of the adiabatic energy gap based on the chosen electronic structure method.⁸⁰ The adiabatic energy ΔE was estimated at the TD-PBE0 level and was re-evaluated using the DLPNO-STEOM-CCSD theory, referred to as STEOM, only if the predicted percentage of active character resulted in an acceptable ratio. We excluded the T₁ state because it lies below the S₁ state with a large energy gap. Triplet states that lie more than 10.0 kcal/mol above the S₁ state were not considered as the destination electronic state of the ISC process.

3.2. MECI Determination for PO-Thio

In the XMS-CASPT2 calculations, all of the valence π-orbitals in the thiophene-fused structure were included in the active space, corresponding to 14 electrons in 12 orbitals, i.e., (14e,12o). The active space of PO-Thio is depicted in Figure 2. We employed the cc-pVDZ basis set with the RI approximation using the cc-pVDZ/JK auxiliary basis set.⁸¹ During the geometry optimizations, three electronic states were computed by the state-averaged (SA-)CASSCF scheme within these active spaces. A perturbative correction was considered for these electronic states, using the so-called SS-SR contraction scheme, where an imaginary level-shift^82,83 of 0.3 E_h was employed, while the IPEA shift⁸⁴ was not used. As per the original method,⁵⁸ the zeroth-order Hamiltonian for the perturbative correction was constructed using the state-averaged density. During the MECI geometry optimization, the analytical interstate coupling^83,85 was employed. To evade numerical instability in geometry optimization, the threshold for the overlap of the internally contracted basis was set to 1 × 10^–7.⁸⁶ These geometry optimizations at the XMS-CASPT2 level were conducted using the QSimulate-QM program.^87,88

Figure 2.

Active orbitals in the extended multistate complete-active-space second-order perturbation theory calculations for PO-Thio at the optimized S₁ state geometry at the XMS-CASPT2 level. These 12 orbitals are occupied by 14 electrons (14e,12o).

After identifying the minimum of the S₁ state and MECI geometries, we prepared a set of linearly interpolated internal coordinates (LIIC) between them to obtain potential energy curves (PECs) from single-point calculations on these coordinates. For the LIIC geometries, we conducted calculations at the 3SA-XMS-CASPT2 level using the orz program. In these calculations, the first-order wave functions were expanded in the MS-MR contraction scheme. The active space and basis sets used were identical with those in the geometry optimization using QSimulate-QM.

4. Results and Discussion

In this discussion, we examine the influence of oxygenation on the phosphorus atom in the P-bridged stilbene analogs and its effect on their nonradiative decay rates. We begin by comparing calculated absorption and fluorescence energies with experimental data to validate the accuracy of our TD-DFT method. We then detail the computed transition rate constants in P-Ben to illuminate its low fluorescence quantum yield, Φ_F. Next, we contrast the computed rate constants across the four molecules, P-Ben, PO-Ben, P-Thio, and PO-Thio, to decipher their decay mechanisms. The impact of oxygenation on the phosphorus atom is analyzed based on the energy levels of the electronic states and Kohn–Sham orbitals. Finally, we explore a potential alternative nonradiative decay route for PO-Thio, accessible via a CI.

4.1. Absorption and Fluorescence Energies

Table 1 presents a comparison between the computed vertical absorption and fluorescence energies and the experimental results alongside the corresponding Stokes shift values. The TD-PBE0 calculations were successful in accurately reproducing both absorption and fluorescence energies with a maximum absolute error of a mere 0.16 eV. Single-point calculations using the DLPNO-STEOM-CCSD method tended to slightly overestimate the energies in comparison to the predictions at the TD-PBE0 level. Despite the computed results showing an overestimation of the Stokes shift, the predicted PES of the S₁ state around the minimum is well depicted at these computational levels. Note that the peak top energy of the simulated spectrum is more suitable for comparison with the peak top of the experimentally obtained spectrum than the computed vertical transition energy. In our current case, the vertical fluorescence energies were found to be similar in value to the simulated peak top energies (Table S1).

Table 1. Comparison between Computationally Estimated and Experimentally Obtained Energies of Absorption, Fluorescence, and Stokes Shift, Expressed in eV.

	PBE0ab			STEOMac			expd
	abs	fluo	shift	abs	fluo	shift	abs	fluo	shift
P-Ben	3.59	2.92	–0.67	3.76	3.07	–0.70	3.53	2.99	–0.54
PO-Ben	3.20	2.42	–0.78	3.39	2.58	–0.80	3.14	2.58	–0.56
P-Thio	3.12	2.45	–0.66	3.27	2.57	–0.70	2.95	2.40	–0.55
PO-Thio	2.66	1.89	–0.77	2.85	2.03	–0.82	2.52	2.03	–0.49

^aGeometries at the TD-PBE0/cc-pVDZ level.

^bEnergies at the TD-PBE0/cc-pVDZ level.

^cEnergies at the DLPNO-STEOM-CCSD/cc-pVTZ level.

^dTaken from refs (30) and (26).

4.2. Calculated Rate Constants for P-Ben

The optimized geometries pertinent to the photophysical behavior of P-Ben were obtained for the S₁ state and two lower-lying triplet states. The natural transition orbitals (NTOs),⁸⁹ crucial for characterizing the obtained states, are illustrated in Figure 3a. The S₁ state represents the π–π* transition in the stilbene skeleton, and can be assigned as the HOMO–LUMO transition relative to the S₀-state closed-shell electronic configuration. One of the identified triplet states involves the phosphorus lone-pair orbitals, exhibiting the n(P)-π* transition, and is denoted as T(n-π*). Interestingly, another pertinent low-lying triplet state was discovered, characterized by the π–π* excitation occurring at the side phenyl ring, denoted as T(Ph-Ph). At the TD-PBE0 level, the T(n-π*) and T(Ph-Ph) states were calculated to be more stable than the S₁ state by 7.1 and 2.1 kcal/mol, respectively; these values were 7.0 and 5.3 kcal/mol, respectively, at the STEOM level. These small energy differences should enable these triplet states to participate in ISC and contribute to decreasing the Φ_F.

Figure 3.

(a) Natural transition orbitals (NTOs) of P-Ben at each optimized geometry. The upper line represents the lowest unoccupied NTOs (LUNTO), while the lower line represents the highest occupied NTOs (HONTO), along with their corresponding eigenvalues. The relative energies with respect to the minimum of the S₁ state at the TD-PBE0 level are provided below each HONTO plot. (b) Schematic illustrating the vibronic transitions from the S₁ state in P-Ben.

The rate constants of fluorescent decay, the S₁ → S₀ IC, and the ISCs from the S₁ state to both the T(n-π*) state and the T(Ph-Ph) state were calculated. These are denoted as k_r, k_ic, k_isc(nπ), and k_isc(PP), respectively, as displayed in Figure 3(b). The total nonradiative decay rate constant was estimated as k_nr = k_ic + k_isc(nπ) + k_isc(PP). The calculated k_r and k_nr values are compared with the experimentally estimated values from previous researches^26,30 (Table 2).

Table 2. Comparison of Computationally Estimated and Experimentally Obtained Rate Constants and Fluorescence Quantum Yield of P-Ben, Presented in Units of s^–1.

	cal (PBE0)ab	cal (STEOM)ac	expd
kr	7.4 × 107	9.3 × 107	5.0 × 107
kic	6.1 × 103	9.0 × 102	—
kisc(nπ)	8.9 × 107	8.7 × 107	—
kisc(PP)	1.6 × 108	4.8 × 108	—
knr	2.5 × 108	5.6 × 108	6.6 × 108
ΦF	0.23	0.14	0.07

^aGeometries and Hessians at the TD-PBE0/cc-pVDZ level.

^bEnergies at the TD-PBE0/cc-pVDZ level.

^cEnergies at the DLPNO-STEOM-CCSD/cc-pVTZ level.

^dEstimated assuming a lifetime of the S₁ state is 1.4 ns and a fluorescence quantum yield of 0.07, as reported in ref (26). Please note that an additional lifetime of 9.8 ns mentioned in ref (30) was not considered.

Using TD-PBE0 level calculations, k_r was estimated to be 7.4 × 10⁷ s^–1, which agrees well with the experimental k_r. The FC term in the TVCF rate constant formula contributes significantly to k_r, accounting for 90% of its total value, as this transition is dipole-allowed. The IC rate constant was determined to be 6.1 × 10³ s^–1, which is considerably lower than k_r due to the large energy gap (ΔE = 3.26 eV) between the involved states. The ISC rate constants, k_isc(nπ) and k_isc(PP), were predicted to be 8.9 × 10⁷ and 1.6 × 10⁸ s^–1, respectively. The FC term contributes significantly to these ISC rate constants as well, with 92% and 54% of the total values, respectively. This indicates that the HT treatment of the spin-vibronic coupling contributes to k_isc(nπ) and k_isc(PP) by factors of 8% and 46%, respectively. This may be attributed to the large values of the spin–orbit coupling matrix elements (SOCMEs), with the averaged SOC, given by 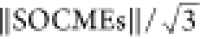, calculated to be 1.77 and 1.11 cm^–1, respectively, at the minimum of the S₁ state.

Based on the computed rate constants, the fluorescence quantum yield (Φ_F) of P-Ben was estimated to be 0.23. Although slightly higher than the experimental value of 0.07, we can conclude that the present calculations qualitatively reproduce the low Φ_F observed for P-Ben. It should be noted that the values of k_isc(nπ) and k_isc(PP) can be multiplied by 2.0 because P-Ben contains two phosphorus atoms and two phenyl rings. If this adjustment is made, then the resulting Φ_F value of 0.13 is closer to the experimental value.

The relative energies calculated at the DLPNO-STEOM-CCSD level provide further support for our results. The adiabatic energy difference between the S₁ and S₀ states, ΔE(S₁-S₀), was estimated to be 3.48 eV, slightly higher than the 3.26 eV obtained at the TD-PBE0 level. The inclusion of the ω³ prefactor in the fluorescence spectrum contributed to an enhanced fluorescence spectrum and a slightly larger k_r. However, the overestimation of ΔE(S₁-S₀) resulted in a decreased IC rate constant. The ΔE(S₁-T(nπ*)) value at the STEOM level was comparable to that at the TD-PBE0 level, thus not significantly affecting the ISC rate constants k_isc(nπ). However, the ΔE(S₁-T(Ph-Ph)) value at the STEOM level was higher than that at the TD-PBE0 level, leading to a larger k_isc(PP). The increase in k_isc(PP) may be influenced by the large reorganization energy (0.67 eV). It is worth noting that the energy gap law, where a smaller energy gap corresponds to a larger rate constant, applies to transitions with small displacements. Based on these re-evaluated rate constants, we estimated the Φ_F to be 0.14, which accurately reproduces the low Φ_F observed for P-Ben.

In summary, our computations successfully reproduced the experimental observation that the Φ_F value of P-Ben is significantly lower than unity. This result can be attributed to the efficient ISC processes between the S₁ state and two triplet states, which exhibit comparable energies and substantial SOCMEs, consistent with the El-Sayed rule. One of the triplet states is characterized by a local excitation within the phenyl ring coordinated with the phosphorus atom, and it plays a significant role in the nonradiative decay process.

4.3. Comparison among the P-Bridged Stilbene Analogs

Now, let us shift our focus to the rate constants of the ISCs, k_r, and k_ic, computed for the remaining P-bridged stilbene analogs: PO-Ben, P-Thio, and PO-Thio (Table 3 and Figure 4). Comparing these values to those of the ISCs of P-Ben would be particularly interesting. Furthermore, additional types of triplet states, distinct from those observed in P-Ben, were also obtained for the other three molecules, as detailed in the SI. It is worth noting that computed k_nr considers the contributions from these triplet states.

Table 3. Rate Constants for the Transitions from the S₁ State of the P-Bridged Stilbene Analogs.

	P-Ben	PO-Ben	P-Thio	PO-Thio
kr	7.4 × 107	3.9 × 107	5.3 × 107	2.1 × 107
kic	6.1 × 103	1.5 × 106	1.4 × 105	1.2 × 108
kisc(nπ)	8.9 × 107	—a	2.8 × 105	—a
kisc(PP)	1.6 × 108	1.0 × 106	7.2 × 105	—b
knr	2.5 × 108	2.7 × 106	2.2 × 106	1.2 × 108
ΦF	0.23	0.94	0.96	0.14

^aOxygenation of the phosphorus atoms removes the n-π* type triplet state.

^bNot computed due to the T(Ph-Ph) state being computed to be more unstable than the S₁ state by 21.0 kcal/mol.

Figure 4.

Importance analysis of the simulated rate constants, k_r, k_ic, and k_isc, shown in Table 3 for P-Ben, PO-Ben, P-Thio, and PO-Thio.

The TD-PBE0-level calculations successfully captured the experimental trend observed in the Φ_F of the P-bridged stilbene analogs. Specifically, P-Ben and PO-Thio were predicted to have low Φ_F, while PO-Ben and P-Thio exhibited high Φ_F. The computed rate constants shed light on the underlying mechanisms. It was found that either the oxygenation of the phosphorus atoms or the substitution with thiophene rings led to a decrease in k_isc, which in turn resulted in an increase in the Φ_F. This decrease in k_isc can be attributed to the relative destabilization of the destination triplet states as a consequence of the stabilized S₁ state, despite the increased SOC, as illustrated in Figure 5. Notably, the T(n-π*) state is absent in PO-Ben due to conversion of the n(P) orbital to the σ(P–O) bond. This absence narrows the ISC pathway compared with P-Ben, further reducing k_isc. Furthermore, the relative destabilization of the triplet states in PO-Thio was found to be more significant than that in PO-Ben and P-Thio, indicating a diminished ISC transfer to the triplet states. Surprisingly, the Φ_F of the PO-Thio was found to be reduced due to an alternative nonradiative pathway facilitated by the IC process from the S₁ to S₀ state, characterized by a large k_ic (1.2 × 10⁸ s^–1).

Figure 5.

(a) Adiabatic energy levels of the S₁, T(n-π*), and T(Ph-Ph) states of the molecules in this study. The energy values were obtained from TD-PBE0/cc-pVDZ level calculations. Note that the T(n-π*) levels are not shown for PO-Ben and PO-Thio because they do not possess any lone pairs on the P atoms. (b) The spin–orbit coupling (SOC) between the S₁ and triplet states of interest at the S₁min is presented. Please note that the SOC values for PO-Thio are not included as the triplet states of interest were found to be highly unstable.

To investigate the source of the relative destabilization of the triplet states, we examined the energy levels of the Kohn–Sham orbitals obtained at the S₁ structure. These orbital energy levels, depicted in Figure 6a, are given relative to the MO level of π* associated with the side phenyl rings. We made this comparison under the assumption that the MO level remains relatively unchanged across the four types of molecules.

Figure 6.

(a) Energy levels of the specific Kohn–Sham orbitals involved in the decays. The energy level values are given relative to the π* orbital in the side phenyl rings and are reported in eV. These values were obtained from the PBE0/cc-pVDZ level calculations at the optimized S₁ state geometry. Additionally, the HOMO–LUMO gap is provided for each molecule. (b) Energy levels of the HOMO and LUMO of stilbene (Stil), P-Ben, and PO-Ben. The positions highlighting the orbital interactions with the phosphanyl/phosphoryl groups are indicated by black arrows. (c) A schematic illustrating the interaction is provided for each orbital. The geometry of stilbene was optimized at the TD-PBE0/cc-pVDZ level. Isosurface value of 0.03 was used to visualize the MOs.

The oxygenation process of P-Ben to PO-Ben leads to the stabilization of the LUMO level, as discussed in the previous studies.^13,30 This stabilization is attributed to the inductive effect of the phosphine oxide group and the interaction between the σ*(P–O) orbital and the LUMO of the stilbene skeleton.⁹⁰ A graphical representation of this orbital interaction is illustrated in Figure 6c. It demonstrates that the σ* orbital provided by the P atom facilitates the conjugation between the π-type LUMOs and the noncovalent orbital space. Consequently, the HOMO–LUMO gap is reduced from 3.53 eV (P-Ben) to 3.16 eV (PO-Ben), resulting in stabilization of the S₁ state in PO-Ben. However, the energy level of the T(Ph-Ph) state remains unchanged between P-Ben and PO-Ben because the MO levels of the π and π* orbitals associated with the side phenyl rings are retained during the oxygenation process. This discrepancy in stability between the S₁ and T(Ph-Ph) states accounts for the relative destabilization of the T(Ph-Ph) state in PO-Ben.

We can analyze the impact of replacing the benzene rings with thiophene rings in P-Ben to P-Thio in a similar manner. Both P-Thio and P-Ben possess a lone pair on their phosphorus atoms, which have similar energy levels. The substitution with the thiophene ring does not modify the MO levels of π and π* associated with the side phenyl rings. The LUMO level remains unchanged. However, the substitution destabilizes the HOMO level, resulting in a reduction of the HOMO–LUMO gap from 3.53 eV (P-Ben) to 3.00 eV (P-Thio). This reduction causes the stabilization of the S₁ state in P-Thio, and it leads to the relative destabilization of the T(Ph-Ph) state.

PO-Thio undergoes both oxygenation of the P atoms and substitution with the thiophene-fused skeleton, resulting in the most significant stabilization of its S₁ state and relative destabilization of its triplet states compared to the other molecules. This highly stabilized S₁ state may accelerate the IC to the S₀ state, thereby leading to its low Φ_F. However, by correcting the adiabatic energy at the STEOM level by 0.26 eV, k_ic decreases by a factor of 0.13, resulting in a Φ_F value of 0.65. This value is noticeably different from the experimental observation (see the SI for more detail). This suggests that the IC-based decay mechanism under the TVCF framework may not fully explain the observed low Φ_F.

4.4. Decay of PO-Thio through CI

We proposed an alternative hypothesis that the nonradiative pathway of PO-Thio occurs through the CI pathway. To investigate this hypothesis, we searched for the MECI geometry of PO-Thio using the 3SA-XMS-CASPT2 level of theory. Figure 7 compares the optimized geometries of the S₁ state minimum (S₁min) and S₀-S₁ MECI, and Table 4 presents some characteristic changes in internal coordinates. At the XMS-CASPT2 level, we found an S₁-S₀ MECI of PO-Thio that is only 3.6 kcal/mol less stable than the S₁min. At the S₁min, the thiophene-fused skeleton adopts a nearly planar conformation, with a dihedral angle of C1–C13–C14–C10, denoted as D(1–13–14–10), at −180.0°. However, at the MECI geometry, the conformation deviates from planarity, exhibiting a dihedral angle of −117.3°. Additionally, the bond length between C13 and C14, denoted as B(13–14), increases from 1.413 to 1.565 Å, indicating a bond elongation of 0.15 Å and a reduction in bond order. These significant changes in internal coordinates suggest that this MECI can be characterized as a twisting of the polyene chain with the thiophene ring behaving as a bridged diene.

Figure 7.

(a) Optimized S₁ and S₁–S₀ MECI geometries of PO-Thio at the XMS-CASPT2 level. The upper line displays the top view, while the lower line shows the side view of the geometries. The relative energies at the S₁ state are provided below the pictures. (b) The atom labeling for PO-Thio is illustrated. The labels are shown exclusively for the thiophene-fused skeleton, with hydrogen atom labels omitted.

Table 4. Characteristic Changes in Internal Coordinates from S₁min to MECI Geometry.

bond (B)				dihedral angle (D)
	S1min	MECI	Δ/Å		S1min	MECI	Δ/deg
B(1–39)	1.702	1.748	+0.045	D(1–13–14–10)	–180.0	–117.3	+62.7
B(2–15)	1.813	1.857	+0.044	D(7–10–14–13)	–0.8	–24.3	–23.5
B(3–4)	1.367	1.398	+0.031	D(14–13–7–6)	177.9	132.9	–44.9
B(7–10)	1.433	1.472	+0.039	D(13–14–2–15)	–177.9	172.9	–9.3
B(10–40)	1.702	1.754	+0.051
B(13–14)	1.413	1.565	+0.153

We aimed to estimate the rate constant of the MECI-driven decay using Eyring’s equation.⁹¹ To do this, we needed to estimate the activation energy required to reach the MECI. We computed the PECs along the LIIC between the S₁min and MECI geometries at the 3SA-XMS-CASPT2 level of theory. These PECs provide an upper limit of the activation energy. Figure 8 presents the PECs plotted as a function of the (D(1–13–14–10)).

Figure 8.

Potential energy curves (PECs) of the S₀ and S₁ states along the linearly interpolated internal coordinates (LIIC) connecting the S₁min and MECI geometries. The energies were calculated at the 3SA-XMS-CASPT2/cc-pVDZ level by using the MS-MR contraction scheme. The left figure shows the PECs of both S₀ and S₁ states, while the right figure zooms in on the S₁ PEC for a closer examination.

The energy along the LIIC reached its highest point at the MECI geometry in the S₁ state, indicating the absence of a transition state between the S₁min and MECI. The S₁ state at the MECI geometry was estimated to be 4.5 kcal/mol less stable than the S₁min, representing the activation energy required to reach the MECI geometry. Assuming that the S₁-excited PO-Thio must transit to the S₀ state at the MECI geometry, the experimental activation free energy was estimated to be 5.2 kcal/mol based on the experimentally measured k_nr (9.6 × 10⁸ s^–1).²⁶ However, there were computational challenges in calculating the free energy correction in the MECI geometry. Despite this, our prediction of the activation energy suggests that the decay through this MECI likely contributes to lowering the Φ_F of PO-Thio.

We further investigated the electronic states at the geometries of the S₁min and CI regions to understand the nature of the CI. To distinguish between the ground and excited states at the CI structure, we employed a geometry slightly displaced from the MECI, referred to as n-MECI. The (D(1–13–14–10)) for n-MECI and MECI were −120.3° and −117.3°, respectively.

Upon analyzing the XMS-CASPT2 state-rotation matrix, we found that the S₀ and S₁ states at S₁min are predominantly composed of CASSCF S₀ and S₂ states, respectively. However, in the n-MECI geometry, the states were mainly composed of CASSCF S₀ and S₁ states. Figure 9 displays the natural orbitals with characteristic occupation numbers, and further details can be found in the SI. Based on the occupation numbers of the natural orbitals at the S₁min geometry, the nearly closed-shell S₀ state was primarily described by a single closed-shell determinant, with occupation numbers ranging from 0.0 to 0.25 or from 1.75 to 2.0. Conversely, the CASSCF S₂ state was characterized as a HOMO–LUMO single excitation relative to the S₀ state. At the n-MECI geometry, the S₀ state became an open-shell singlet state, while the S₁ state exhibited a closed-shell character. The open-shell orbitals for the S₀ state comprised the bonding and antibonding π-orbitals of the central C–C bond. This clearly indicates that the π bond in the stilbene skeleton is bent and divided in half.

Figure 9.

Characteristic CASSCF natural orbitals and their occupation numbers for the S₁min and n-MECI geometries, denoted as R(S₁min) and R(n-MECI), respectively. Two orbitals with occupation numbers closest to 1.0 are selected for each state. The states in the upper line predominantly contribute to the XMS-CASPT2-level S₁ state, while the orbitals in the lower line mainly contribute to the S₀ state.

To gain insight into the qualitative nature of the crossing states at the CI, we examined the important electronic configurations that characterize the CASSCF states and their corresponding quasi-canonical orbitals, as shown in Figure 10a. At the S₁min geometry, quasi-canonical HOMO and LUMO were delocalized around the thiophene-fused skeleton. However, at the n-MECI geometry, these orbitals became localized either on the right or left side of the skeleton. Notably, the HOMO and LUMO at the n-MECI geometry exhibited a resemblance to the SOMO of the pentadienyl radical, as depicted in Figure 10b. This suggests that at the n-MECI geometry, the S₀ state consists of two pentadienyl radicals, while the S₁ state is separated into the pentadienyl cation and its anion, forming a zwitterionic state. The separation of the quasi-canonical HOMO and LUMO on the thiophene-fused skeleton appears to be one of the factors contributing to the emergence of a CI, as discussed by Nakai et al.⁹²

Figure 10.

(a) Characteristic part of the major configuration in the CASSCF states at the S₁min and n-MECI geometries, with the remaining electrons occupying lower-level active MOs in a closed-shell arrangement. The figure displays the configuration weight and corresponding quasi-canonical orbitals. (b) SOMO of the pentadienyl radical and its chemical structure computed at the UPBE0/cc-pVDZ level. The geometry was optimized to mimic the orientation found in PO-Thio.

Furthermore, it appears that the pentadienyl anion on the right side of the structure was stabilized by the presence of the electron-withdrawing phosphole-oxide group. This stabilization effect can be estimated by removing the two O atoms at the n-MECI geometry, which leads to an increase in the S₀-S₁ energy gap from 0.19 to 0.93 eV at the 3SA-XMS-CASPT2 level of theory. This finding suggests that the presence of the phosphole-oxide groups plays a crucial role in stabilizing the zwitterionic S₁ state (see the SI for more information). The calculated stabilization of the S₁ state may explain why reaching the MECI point requires relatively little energy.

5. Conclusions

This report presents a theoretical analysis of the photophysical behaviors of the trivalent and pentavalent P-bridged stilbene analogs which have been of interest in synthetic research involving phosphorus-containing ladder-type π frameworks. Our computational approach to excited-state dynamics has proven to be a useful tool for obtaining detailed information about the photophysical characteristics of P-containing organic dyes. We employed a perturbative approach with TVCF formalism to calculate the rate constants of radiative and nonradiative transitions from the S₁ state to various destination states. The aim is to provide a numerical understanding of the effects of P atom oxygenation on the photophysical properties of these analogs on the basis of the predicted rate constants and Φ_F.

Our calculations characterized the fluorescence as the dipole-allowed LUMO–HOMO transition and satisfactorily reproduced the radiative decay rate constants. The calculations considered the dominant role of Franck–Condon vibronic contributions, although our rate constant formalism incorporates up to the Herzberg–Teller type spin-vibronic coupling. The resulting rate constants successfully reproduced the experimentally observed Φ_F values for P-Ben, PO-Ben, P-Thio, and PO-Thio. Based on the computed rate constants, we can explain the differences in Φ_F between the four molecules as follows:

• The Φ_F of P-Ben was estimated to be low, which qualitatively agrees with the experimental observation. Our findings indicate that the nonradiative decay of P-Ben predominantly occurs through ISC processes, leading to the T(n(P)-π*) and T(π(Ph)-π*(Ph)) states. These triplet states were found to be energetically lower than the S₁ state.

• In a previous experimental study, it was observed that PO-Ben, formed by oxygenating the phosphorus atoms of P-Ben, exhibits a high Φ_F (0.98). This high Φ_F in PO-Ben can be attributed to the stabilization of the S₁ state, which is a result of the stabilized LUMO level due to the enhanced σ*−π* interaction. This stabilization causes the T(Ph-Ph) state to become relatively destabilized, leading to a suppression of ISC in PO-Ben. Additionally, the transformation of the lone pairs at the phosphorus sites in P-Ben into σ(P–O) bonds in PO-Ben further contributes to the suppression of the ISC process.

• The substitution of the stilbene skeleton in P-Ben with the thiophene-fused skeleton, resulting in P-Thio′, has been found to significantly increase the Φ_F to 0.95. This increase in Φ_F can be attributed to the stabilization of the S₁ state, which is a consequence of the destabilized HOMO in P-Thió. Our calculations indicate that this substitution leads to a decrease in the rate constant of the ISC process. The relative destabilization of the triplet states in P-Thio′ plays a more prominent role in reducing the ISC rate constant compared to the increased SOCME values.

• Contrary to the oxygenation of P-Ben to PO-Ben, the oxygenation of P-Thio′ to PO-Thio′ decreased the Φ_F to 0.04. Our calculations revealed that for PO-Thio, the S₁ → S₀ IC plays a significant role in reducing the Φ_F value.

We further investigated the nonradiative decay pathway through the CI for PO-Thio. The MECI of PO-Thio was located using the 3SA-XMS-CASPT2-level analytic gradients, and it was found to be 3.6 kcal/mol less stable than the minimum of the S₁ state. At the optimized MECI geometry, the π-conjugated skeleton was found to be bent at the central C–C bond. The PECs along the LIIC ranging from S₁min to MECI indicated that the activation energy could be approximated by the energy difference between MECI and S₁min. The computationally determined relative energy is in good agreement with the experimentally inferred activation free energy (5.2 kcal/mol), although the Gibbs free energy correction was not considered in this analysis. In the CI region, the S₀ state is characterized as an open-shell electronic structure, while the S₁ state is closed-shell. Notably, the closed-shell S₁ state at the CI region exhibits a zwitterionic character, where the anion on the right side of the structure appears to be stabilized by the electron-withdrawing phosphole-oxide group.

We performed a comparative analysis to investigate the differences in the Φ_F among the various P-bridged stilbene analogs using computational excited-state simulations. Our computational predictions revealed that the primary nonradiative decay pathway for P-Ben is through ISC, while for PO-Thio, it is the IC process via CI. These findings provide valuable insights into the control and modulation of radiative and nonradiative decay processes in phosphorus-containing π-conjugated molecules. This study, using the perturbative approach for theoretical analysis to estimate k_nr and Φ_F, could pave the way for a new molecular design strategy based on quantum chemical calculations.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsphyschemau.3c00038.

• Natural transition orbitals and rate constants of PO-Ben, P-Thio, and PO-Thio, CASSCF natural orbitals of PO-Thio, and Cartesian coordinates of the molecules (PDF)

Author Contributions

CRediT: Naoto Inai conceptualization, data curation, formal analysis, investigation, methodology, software, validation, visualization, writing-original draft, writing-review & editing; Shigehiro Yamaguchi conceptualization, investigation, supervision, validation, writing-review & editing; Takeshi Yanai conceptualization, formal analysis, funding acquisition, investigation, project administration, resources, software, supervision, validation, visualization, writing-original draft, writing-review & editing.

The authors declare no competing financial interest.