Abstract
Cathode degradation of Li-ion batteries (Li+) continues to be a crucial issue for higher energy density. A main cause of this degradation is strain due to stress induced by structural changes according to the state-of-charge (SOC). Moreover, in solid-state batteries, a mismatch between incompatible cathode/electrolyte interfaces also generates a strain effect. In this respect, understanding the effects of the mechanical/elastic phenomena associated with SOC on the cathode performance, such as voltage and Li+ diffusion, is essential. In this work, we focused on LiCoO2 (LCO), a representative LIB cathode material, and investigated the effects of biaxial strain and hydrostatic pressure on its layered structure and Li+ transport properties through first-principles calculations. With the nudged elastic band technique and molecular dynamics, we demonstrated that in Li-deficient LCO, compressive biaxial strain increases the Li+ diffusivity, whereas tensile biaxial strain and hydrostatic pressure tend to suppress it. Structural parameter analysis revealed the key correlation of “Co layer distances” with Li+ diffusion instead of “Li layer distances”, as ordinarily expected. Structural analysis further revealed the interplay between the Li–Li Coulomb interaction, SOC, and Li+ diffusion in LCO. The activation volume of LCO under hydrostatic pressure was reported for the first time. Moreover, vacancy formation energy calculations showed that the Li intercalation potential could be decreased under compressive biaxial strain due to the weakening of the Li–O bond interaction. The present findings may serve to improve the control of the energy density performance of layered cathode materials.
Keywords: biaxial strain, hydrostatic pressure, layered cathode material, ionic diffusion, vacancy
1. Introduction
Rechargeable Li+ batteries (LIBs) not only power most of today’s portable electronic devices but have also led to a revolution in electric vehicles. Such strong market incentives demand higher energy storage capabilities and power characteristics of LIBs. The main focus lies on cathodes, which have the determining role in defining LIB properties.1−3 Meanwhile, structural degradation, which results in capacity and voltage fading, is one of the main problems affecting the performance of cathodes. Because Li+ is rapidly extracted and inserted in cathodes during the charging and discharging processes, the lattice parameters of the crystalline structure rapidly change. This charge/discharge cycle induces stresses and strains that can potentially cause microcracking.4,5 For example, Tan et al.6 observed the crystal damage in the LiNi0.9Co0.05Mn0.05O2 (NCM) cathode during the charging process. By using in situ XRD characterization, they observed internal strain and stress accumulation upon Li+ extraction.
Apart from stress inside the cathode structures, strain phenomena also happen at the interface between cathodes and solid electrolytes due to the interface lattice mismatch.7−9 Previous works discussed how such strain could weaken the interface interaction and eventually retard the battery performance.10,11 As the focus shifts toward the development of all-solid-state LIBs, the application of external pressure becomes crucial to enhance the contact area between the Li electrode and solid electrolyte, ensuring smooth battery operations. This pressure typically ranges from dozens to hundreds of MPa or even several GPa.12,13
On the other hand, previous research has demonstrated that Li+ diffusion can be greatly enhanced in solid-electrolyte and anode materials under external biaxial strain.14−16 This manipulation of the lattice via strain effects raises fundamental scientific questions because it is an effective way of modulating ionic conductivity in oxide materials. Regarding the effects of strain on Li+ cathode materials, LiFePO4 has been studied via various simulation methods. Lee et al.16 performed density functional theory (DFT) calculations and predicted that a 4% biaxial tensile strain would increase the room-temperature electronic and Li+ ion conductivities 15- and 50-fold, respectively. Similarly, Tealdi et al.17 conducted classical molecular dynamics (MD) simulations to investigate the strain effects on the ion conduction and defect formation in olivine Li+- and Na+-based cathode materials. They predicted a sudden drop in the activation energy of Li+ diffusion at room temperature for tensile strain applied within a certain plane, leading to a significant enhancement in the ionic conductivity. For the investigation of such strain and stress effects, theoretical simulation has been regarded as an effective tool that allows us to understand the strain and stress mechanisms at the atomistic level.18
LiCoO2 (LCO), as a representative cathode material that has been commercialized for nearly 30 years, still shows great potential for further enhancement of its energy density.19 Even though it is one of the most prominent layered intercalated Li+ cathode materials, LCO was reported to display complicated internal strain and stress patterns generated during charging/discharging processes.20−22 Additionally, the effect of hydrostatic pressure—which inevitably arises during the assembly of battery components—remains poorly understood. As such, an understanding of the strain and stress effects on Li+ diffusion under different charging states is still lacking.
In this article, we aim to investigate the impact of external biaxial strain and hydrostatic pressure on the Li+ diffusion behavior of LCO with varying state-of-charge (SOC) by means of first-principles calculations based on density functional theory (DFT). We hope that the present work will advance knowledge of the complex role played by strain and stress effects in LCO during charge/discharge cycles as well as in other similar layered materials employed as battery cathodes.
2. Computational Methods
First-principles calculations based on DFT were carried out using the generalized gradient approximation of Perdew–Burke–Ernzerhof (GGA-PBE) as it is implemented in the Vienna Ab initio Simulation Package (VASP) software.23 The projector-augmented wave method (PAW) was employed to represent the ionic cores by considering the following electronic states as valence: Li 1s, 2s, and 2p; Co 4s and 3p; and O 2s and 2p.24 A “Hubbard-U” scheme was used to correct the localized electronic states of Co. In this paper, the U value used for Co is 4.91 eV.25 In terms of bulk structures, the LCO unit cell (R3̅m space group) was fully optimized and relaxed until the total energies were converged to within 1 meV/atom and the forces in the atoms were all below 0.01 eV/Å by using an energy cutoff of 650 eV and a Monkhorst–Pack k-point grid of 10 × 10 × 2. The relaxed LCO unit cell lattice had the parameters a = b = 2.83 Å and c = 14.15 Å, which are in good agreement with previous theoretical and experimental studies.26−28
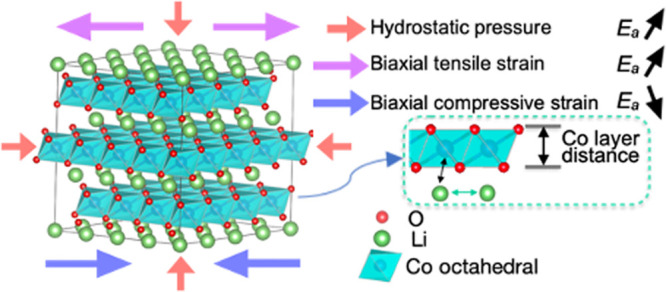
Biaxial strain is defined as η = (a – a0)/a0, where a0 represents the equilibrium in-plane lattice parameter (shown in Figure 1 a,b). A positive η is regarded as tensile biaxial strain, whereas a negative η is regarded as compressive. Energy-minimized structures were subjected to biaxial strains ranging from −4% (compressive) to +4% (tensile) in the a, b plane while the out-of-plane lattice parameter c was fully relaxed. The range of biaxial strains applied in our study was determined based on the findings of a recent experimental investigation by Zhu et al., where they observed ∼4% residual strain aligned parallel to the LCO < 003> plane.29 The same strain range was also observed and discussed in a recent study by Wang et al.30 These strained energy-minimized structures were used as the initial configurations in subsequent electronic structure and ion migration calculations. Similar methodologies were reported in previous studies of Li+ cathode and solid oxide fuel cell materials.17,31
Figure 1.
Schematic view of external (a) biaxial tensile strain, (b) biaxial compressive strain, and (c) hydrostatic pressure (HP) applied to LiCoO2.
In terms of the hydrostatic pressure (HP), shown in Figure 1c, around 1 GPa was exerted on the energy-minimized structures, which were subsequently reoptimized and employed in further calculations. We simulated biaxial stress on the a, b plane by simultaneously applying strain in both lattice vectors and HP by applying a pressure of ∼1 GPa along the three axes. The stress induced is shown in Figure S1. The strain along the a and c axes as a function of biaxial strain can be found in Figure S2.
Nudged-elastic band (NEB) calculations were conducted to estimate the Li+ migration pathway and activation energy barrier (Ea) within the vacancy-mediation regime.32 An energy cutoff of 520 eV and a simulation cell containing 192 atoms (Li48Co48O96) before vacancy creation were used. Two pathways, with one and two Li vacancies (where Li vacancy concentrations are 0.98 and 0.96), respectively, were examined.
First-principles molecular dynamics (FPMD) simulations based on DFT were performed in the canonical (N, V, T) ensemble with a time step of 1 fs. In a trade-off between the computational cost and accuracy, only the Γ-point grid for Brillouin zone sampling and an energy cutoff of 400 eV were set for all FPMD calculations. The selected volumes and geometries were those determined at zero-temperature conditions; hence, we neglected thermal expansion effects. The temperature in the FPMD simulations kept fluctuating around a preset value by employing the Nosé–Hoover thermostat. The calculations comprised a total simulation time of ∼100 ps. We performed three FPMD simulations for each of T = 800, 1000, 1200, and 1400 K, considering an η of −4, 0, and +4%. All configurations were visualized using the VESTA software.33 Additional FPMD calculations for energy cutoffs of 600 and 800 eV were performed for 20 ps at 1200 K to obtain the average stress tensors. We compared the results to those obtained with an energy cutoff of 400 eV and found that the average stress tensors (xx, yy, and zz) calculated with the lower cutoff vary within ±2%, indicating the plausibility of using 400 eV as the cutoff energy for the following FPMD calculation. The Li+ ionic diffusion coefficient (D*) is estimated based on the mean squared displacement (MSD) using the following formula:
| 1 |
where N and d indicate the number of Li+ included and the dimensionality in the system, respectively. t0 and ri(t) refer to the initial time and the displacement of the ith Li+ at time t. The activation energy (Ea) was assumed to follow the Arrhenius equation:
| 2 |
where D0 is the pre-exponential factor and kB is the Boltzmann constant. Ea and D0 are adopted by the extrapolation from the temperatures FPMD was performed at to room temperature (300 K) because of the poor Li+ diffusion of LCO at lower temperatures. Such a strategy has been employed in previous simulation works for solid electrolytes.34,35
Ionic conductivities were obtained with the Nernst–Einstein relationship:
| 3 |
where C and e are the concentration and charge of Li+ ions. For the calculation of vacancy formation energies, EV, we removed one Li from the simulation supercell.
All point defects were assumed to be neutrally charged, and EV was computed using the following formula:
| 4 |
where Edefect is the total energy of the system containing the Li vacancy, Eperfect is the total energy of the system without any defect, and μi is the chemical potential of Li metal, which was estimated from the formation energy of bulk bcc Li metal as equal to −1.904 eV.
3. Results and Discussion
3.1. Zero-Temperature Activation Energy for Li+ Diffusion under Biaxial Strain
The NEB method was used to calculate the migration energy barrier (Ea) as a function of the biaxial strain. Two possible diffusion pathways were considered based on the structural similarity of LCO with the layered material α-NaFeO2, namely, the oxygen dumbbell hop (ODH) and the tetrahedral site hop (TSH),36−38 as shown in Figure 2a–d. In the case of the ODH, Li+ hops via a single Li vacancy. As for the TSH pathway, which requires two or more vacancies, Li+ migrates along a curved path through a tetrahedral site.
Figure 2.
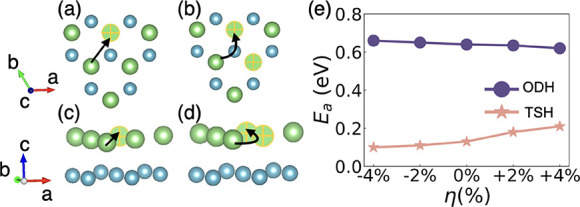
Left panel: (a) top view and (c) front view of the ODH diffusion path; (b) top view and (d) front view of the TSH diffusion path. Green and cyan spheres indicate Li and Co ions. Li vacancies are marked with a cross. Black arrows point in the migration direction. Only the Li+ migration region of the system is shown for clarity. Right panel: (e) NEB migration energy barrier (Ea) results of LCO expressed as a function of biaxial strain for the ODH and TSH diffusion mechanisms, where the positive (negative) ratio corresponds to tensile (compressive) strain.
Figure 2e shows Ea results obtained as a function of the biaxial strain. It is demonstrated therein that the Ea estimated for the TSH diffusion path is always significantly lower than that of the ODH mechanism, in agreement with previous DFT results.39 Nevertheless, Ea varies differently under biaxial strain for both mechanisms. In particular, the Ea of the ODH mechanism is reduced under increasing strain, dropping by 0.02 eV from η = 0 to +4%. In contrast, at η = +4%, the Ea of the TSH mechanism greatly increases by ∼61% compared to the value estimated at zero strain (i.e., from 0.13 to 0.21 eV). Moreover, upon compressive biaxial strain, Ea for the ODH mechanism increases slightly by 0.02 eV at η = −4%, whereas it decreases by roughly the same amount for the TSH mechanism.
Moreover, the application of uniaxial strain along the c axis yields strain along the a and b plane directions as characterized by the Poisson’s ratio (∼0.24 in our calculation) of LCO. To confirm this, we proceeded to implement uniaxial strain conditions of −2 and +2%, approximating the c axis lengths corresponding to biaxial strains of −4 and +4%, respectively. Subsequently, we conducted additional NEB calculations, specifically focusing on the TSH diffusion pathway—the dominant mechanism, discussed in further detail in Section 3.2—to corroborate our supposition. The relaxed lattice parameters corresponding to these uniaxial strain conditions are outlined in Table S1b for reference. The outcomes, as depicted in Figure S3, illustrate that tensile uniaxial strain along the c axis leads to a reduction in the Ea (from 0.13 to 0.06 eV), whereas the application of compressive strain is observed to impede the diffusion process, resulting in a higher Ea (from 0.13 to 0.25 eV). This indicates that uniaxial strain might have a similar effect to biaxial strain. Acknowledging the observed similarities, our emphasis remains directed toward biaxial strain, as it has been extensively investigated in recent research concerning the strain effects induced by rapid charging in LCO.29
The estimated strain-induced Ea trends indicate that compressive biaxial strain could promote the overall ionic conductivity in LCO because the TSH mechanism exhibits the lowest Ea compared to that of ODH and other possible diffusion mechanisms identified in a previous study. Additionally, the TSH mechanism has been suggested to become dominating in Li+ diffusion as the concentration of Li vacancies increases.36,40 Nevertheless, in the zero-temperature NEB calculations, possible lattice vibrations are totally neglected, which could be very important for the ionic diffusion.40,41 To fully test the reliability of our Ea results obtained with the zero-temperature NEB approach, FPMD simulations were conducted, as they take lattice thermal excitations into consideration without the need for assuming any particular diffusion path.42
3.2. Li+ Diffusion at Finite Temperatures under Biaxial Strain
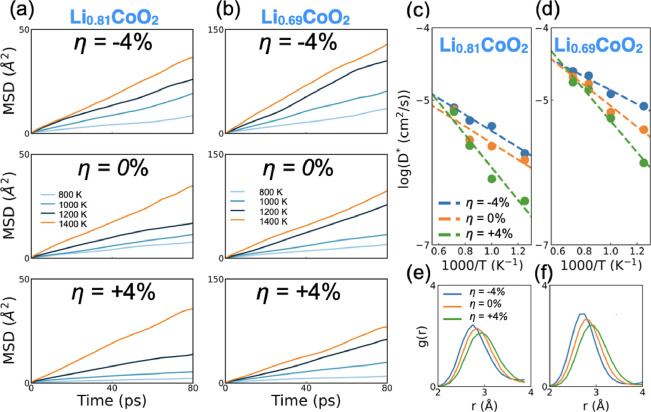
Supercells containing 183 atoms (Li0.81CoO2) and 177 atoms (Li0.69CoO2) were used in the FPMD simulations to characterize the interplay between SOC and Li+ diffusion. Specifically, three and five Li atoms were removed from each Li plane on average, respectively. The calculated out-of-plane lattice parameter c of bulk LixCoO2 (x = 0.81 and 0.69) increased to 14.19 and 14.25 Å, respectively, as compared to perfectly stoichiometric LCO (14.15 Å), whereas a showed negligible variation (Table S1a), reaching a good agreement with previous studies.26,28,43 The highest Li vacancy concentration was fixed at 33.3% because we would like to avoid the phase transition toward a monoclinic phase.44 The Li ordering was initialized randomly. In general, in Li0.69CoO2 at η = −4%, the c axis increases up to 14.60 Å (under no strain, the value is 14.25 Å), whereas at η = +4%, it is reduced to 13.94 Å. Based on the energy profiles shown in Figure S4, all of the FPMD simulations reached equilibrium after 20 ps. Therefore, the first 20 ps was disregarded in the subsequent analysis of ion diffusion.
Time-averaged mean squared displacements (MSDs) and the corresponding fit to the Arrhenius equation are shown in Figure 3a–d, and Table 1 includes the Ea values determined for each strain case. The diffusion of Li+ is visualized via the atomic trajectories generated in the FPMD simulations (Figure S5). The barriers obtained at η = 0% with different Li vacancy concentrations are in quantitative agreement with previous analogous37,45 first-principles and experimental studies.37,45 The self-diffusion coefficients estimated at 300 K (Table S2), D*300 K, for Li0.81CoO2 and Li0.69CoO2 are 5.3 × 10–9 and 4.2 × 10–9 cm2/s, respectively, in good agreement with experiments.46 Because of the high computational cost for FPMD, it was not feasible to sample a detailed range of Li contents in our study. Nevertheless, the agreement between our findings and previous work serves as a testament to the soundness of our selection and subsequent analysis.
Figure 3.
(a, b) Mean squared displacement calculated for Li+ ions with FPMD simulations performed at 800, 1000, 1200, and 1400 K and considering different epitaxial strain conditions, namely, η = −4, 0, and +4% for Li0.81CoO2 and Li0.69CoO2. (c, d) Arrhenius plots of the self-diffusion coefficient in Li0.81CoO2 and Li0.69CoO2. (e, f) Radial distribution functions of Li–Li distances averaged from 20 to 100 ps in the FPMD simulations at 1200 K for η = −4, 0, and +4% for bulk Li0.81CoO2 and Li0.69CoO2.
Table 1. Activation Energy (Ea), Conductivity (σ), and Co Layer Distance Measured with FPMD Simulations for Li0.81CoO2 and Li0.69CoO2 at η = −4, 0, and +4%.
| Ea (eV) | σ300 K (S cm–1) | Co layer distance (Å) | |
|---|---|---|---|
| Li0.81CoO2 | |||
| η = −4% | 0.22 ± 0.02 | 1 × 10–3 | 2.13 |
| η = 0% | 0.23 ± 0.05 | 8 × 10–4 | 2.04 |
| η = +4% | 0.45 ± 0.06 | 8 × 10–7 | 1.96 |
| Li0.69CoO2 | |||
| η = −4% | 0.21 ± 0.01 | 5 × 10–3 | 2.10 |
| η = 0% | 0.27 ± 0.03 | 5 × 10–4 | 2.00 |
| η=+4% | 0.35 ± 0.02 | 5 × 10–5 | 1.91 |
We note that the Ea's obtained from FPMD simulations at η = 0% are slightly higher than those obtained with NEB calculations for the TSH mechanism (0.13 eV), namely, 0.23 eV for Li0.81CoO2 and 0.27 eV for Li0.69CoO2. To make them comparable, additional NEB calculations for Li0.69CoO2 were performed for comparison with NEB results, with Ea for the TSH diffusion pathway seeing an increasing trend for η = 0% (from 0.13 to 0.19 eV). The origins of this outcome can be understood as follows: (1) the TSH mechanism is the dominant one in the presence of vacancies,36 and (2) the effective positive charge of the Co ions increases when the concentration of Li vacancies increases, thus electrostatically hindering Li+ diffusion.37Table 1 also shows that the Ea estimated for Li0.81CoO2 at η = −4% (0.22 eV) is close to the η = 0% value (0.23 eV), whereas under biaxial tensile strain, it is doubled (0.45 eV). It is noteworthy that in the case of Li0.81CoO2, compressive strain does not have a significant effect on Ea. (The corresponding ionic conductivity, σ, was found to increase slightly with respect to the zero-strain case, although the small increment can be ascribed to a fitting error.) Meanwhile, when the Li deficiency is further increased, the compressive strain clearly enhances the Li+ diffusion. In particular, Ea decreases by 0.06 eV for η = −4% in comparison to the zero-strain case. Likewise, the accompanying ionic conductivities increase by 1 and 2 orders of magnitude (Table 1). The additional NEB calculations for Li0.69CoO2 also confirm this trend (0.17 eV for η = −4% and 0.19 eV for η = 0%), whereas the reverse is true for tensile strain.
To gain insight into the variations in the Li+ migration properties, we conducted an analysis of the local structure parameters. First, we performed a comparison of the Li layer distances and Co layer distances (shown in Figure S6) under η = −4, 0, and +4%. A linear correlation between the Co layer distance and Ea can be observed, as shown in Table 1. For example, the Co layer distance is reduced by approximately 4% under η = +4%, resulting in an Ea increase of nearly 100 and 30% for Li0.81CoO2 and Li0.69CoO2, respectively. On the other hand, η = −4% results in a larger Co layer distance and consequently leads to a lower Ea, especially in Li0.69CoO2 (a layer expansion of approximately 6% leads to an Ea reduction of 20%). Notably, a larger Co layer distance results in smaller electrostatic repulsive interactions during Li+ migration along the TSH pathway, which could promote Li+ diffusion.36,47 Furthermore, Li layer distances (Table S3) also show a trivial increase under compressive strain, which could also provide additional room for Li+ diffusion through the TSH mechanism, leading to lower Ea. Additionally, we analyzed the Li–Li radial distribution functions (RDFs), as depicted in Figure 3e,f. As the a and b axes were compressed or enlarged, the peaks of the RDFs shifted toward the left or right, along with increased or decreased maximum populations of Li–Li distances, which were consistent with the η = −4 and +4% conditions, respectively. In the compressive situation, the Li–Li distances thus decrease, which increase Coulomb repulsion and destabilize the Li at its site, consequently resulting in a lower energy barrier. Such a shortened Li–Li distance could promote Li+ diffusion and conduction.
The Li+ diffusion enhancement effect observed under compressive biaxial strain strongly depends on the Li vacancy concentration.48 As previously mentioned, the Ea and σ300 K calculated for Li0.81CoO2 at η = −4% do not appreciably vary from the values obtained at zero strain (see, e.g., the Li+ trajectory densities in Figure S5). The specific vacancy concentration at which the Li+ diffusion enhancement effect occurs under compressive biaxial strain is currently unknown and requires further investigation. Nevertheless, it is still plausible that compressive strain can promote the Li+ diffusion via creating Li/Co layer distance variation and increasing the Li–Li Coulomb repulsion. Previous studies have reported such cases of increased diffusivity with similar mechanisms due to compressive strain for various materials.49−51
3.3. Li+ Diffusion under Hydrostatic Pressure (HP)
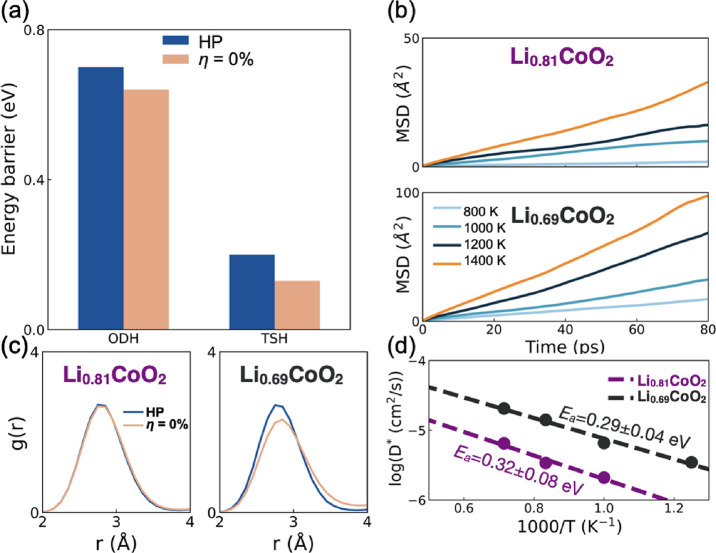
We also investigated Li+ diffusion under 1 GPa of HP in LCO, as such a scenario occurs during the packaging of batteries and in different performance and safety tests.52 NEB calculations show that upon 1 GPa of hydrostatic pressure, the activation energy for Li+ diffusion of both the ODH and TSH pathways increases by 0.02 eV (Figure 4a).
Figure 4.
(a) Calculated DFT-NEB energy barrier (Ea) for Li+ diffusion along two different pathways (ODH and TSH) for LCO under hydrostatic pressure (HP) and strain-free cases. (b) Mean square displacement (MSD) calculated for Li+ ions from FPMD simulations performed at 800, 1000, 1200, and 1400 K under an HP of 1 GPa in Li0.81CoO2 and Li0.69CoO2. During the first 20 ps of the FPMD simulations, the system was equilibrated; hence, this interval of time was excluded from our analysis. (c) Radial distribution functions (RDFs) of Li–Li distances averaged from 20 to 100 ps in the FPMD simulation at 1200 K for η = 0% and HP in bulk Li0.81CoO2 and Li0.69CoO2. (d) Arrhenius plots of the Li+ self-diffusion coefficients in Li0.81CoO2 and Li0.69CoO2 under 1 GPa HP.
To further investigate the Li+ migration behavior, FPMD simulations were also performed to mix all the diffusion pathways and take lattice thermal excitations into consideration. Figure 4b shows the MSD results obtained for Li0.81CoO2 and Li0.69CoO2 in our FPMD simulations. Note that we disregard the case of 800 K for Li0.81CoO2, when fitting D(T) to the Arrhenius equation due to the negligible MSD (average MSD per atom of less than 3 Å2 over 80 ps). Ea for Li+ migration rises from 0.23 (Table 1) to 0.32 eV in Li0.81CoO2, but it decreases to 0.29 eV in Li0.69CoO2 (Figure 4d).
Analysis of the local structure parameters was performed to understand the diffusion-suppressing effect of HP. Table S4 indicates that under HP, the c lattice parameters of Li0.81CoO2 and Li0.69CoO2 decrease by 0.06 and 0.08 Å, respectively, compared to the unstressed system (Table S1a). Table S5 shows that only the Li layer distance undergoes a minor contraction, whereas the Co layer distance remains relatively unchanged. This leads to an increase in Ea for Li+ migration. However, our observations also reveal that the a and b lattice parameters of Li0.81CoO2 and Li0.69CoO2 decrease by 0.3 and 0.5%, respectively. Combined with RDF analysis (refer to Figure 4c), we find that the Li–Li peak shifts to the left, indicating a shortened Li–Li distance when the Li vacancy concentration increases in Li0.69CoO2 (this effect is not seen for Li0.81CoO2). This indicates a stronger Coulomb repulsion, which could offset the negative effect of smaller Li layer distances and promote Li+ diffusion, thus explaining why Ea drops in Li0.69CoO2. Although the activation energy in Li0.69CoO2 is lower than that of Li0.81CoO2, it is still higher than that of the unstressed system (0.27 eV, Table 1), suggesting that the application of HP could lead to a decrease in Li+ diffusion in LiCoO2.
Similar to Ea, which characterizes the Li ionic diffusivity through an Arrhenius-type relation (eq 2), a characteristic activation volume (Va) for conduction can describe the pressure-dependent evolution of ionic conductivity.53Va and Ea are interconnected, with Va capturing the changes in Ea as stress is applied. Given the influence of Co and Li layer distance variations, it is also important to consider the role of Va in the migration process, which provides additional insights into the migration mechanism and the interplay between the material structure and the migration pathway.54 We performed additional NEB calculations of LCO to obtain the Ea under 2, 3, 4, and 5 GPa of HP. Va is obtained as follows:55
| 5 |
where p is the pressure and T is the temperature. The Va for LCO under hydrostatic pressure is obtained as 2.6 ± 0.1 cm3/mol. Note that we only considered the TSH diffusion pathway as it is the dominant one in LCO under the presence of vacancies (see Sec 3.2). The Va can be further extended in tensor form utilizing the conventional concept of the elastic stiffness tensor in the elastic theory, as follows:
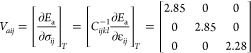 |
6 |
where Cijkl is the elastic stiffness tensor of LCO, σij the stress tensor, and εij the strain tensor under HP.
We refer to Supporting Discussion 2 for a more detailed derivation of Equation 6. To the best of our knowledge, it is the first time that the Va and its tensor form of LCO are reported. A nonzero activation volume serves as an indicator of a disparity between the available free volume within the structure and the volume necessary for efficient ion migration. A positive Va shows that Li+ ions need to open up the space for diffusion, as described in previous studies for Li10GeP2S12 (+2.17 cm3/mol),55 Na3PS4 (+1.78 cm3/mol for high temperature),54 and t-Li7SiPS8 (+1.7–2.0 cm3/mol).56 On the other hand, a negative Va, indicating an enhanced ionic diffusivity under increasing pressure, is also observed in certain cases, for example, Ag3SI (−2.3 ± 0.4 cm3/mol) and Li-β-Al2O3 (−0.7 cm3/mol).57 Our Va shows consistent results with our AIMD calculation, i.e., that Li+ diffusion decreases under external HP, given the shrinkage of the diffusion space. Inspired by the work carried out by Jagad et al.,58 we explored a two-step fitting by adding HP and Va into the Arrhenius equation. Comparing one-step and two-step fitting (Figure S8), Ea for Li0.81CoO2 increased slightly from 0.32 to 0.34 eV, whereas Ea for Li0.69CoO2 does not show a significant change between two fitting procedures. Moreover, D0 of Li0.81CoO2 decreases from 3 × 10–10 to 1.8 × 10–10 cm2/s, whereas that of Li0.81CoO2 remains relatively constant. Despite these minor effects, our conclusion on the tuned Li+ diffusion under HP in LCO remains unchanged. For consistency with biaxial strain effects, we thus retained the one-step fitting results.
3.4. Li Vacancy Formation Energy under Biaxial Strain and HP
The formation energy (EV) of a Li vacancy (VLi) is a critical quantity in the evaluation of Li+ transport because VLi affects the intercalation potential and rate capability of cathode materials. Note that the calculated EV is given with respect to the Li metal (see Section 2). The effects of biaxial strain and HP on EV were estimated for LiCoO2. As shown in Figure 5, the average EV calculated for LiCoO2 amounts to 4.21 eV at η = 0%, which is in good agreement with previous DFT studies.8,59,60EV for LiCoO2 is reduced by 0.2 eV under η = −4% and increased by 0.15 eV under η = +4% with respect to the η = 0% case. We expressed EV as a function of biaxial strain and obtained the xx (or yy) component of the elastic dipole tensor (both 4.74 eV) with respect to the biaxial strain,61,62 as shown in Figure S9. Moreover, the variation of EV suggests that compressive strain makes it easier to remove Li+ from the cathode material, which leads to a lower intercalation potential. Regarding the application of HP, we found that the average EV of LCO is 0.05 eV lower than that of the analogous uncompressed system. Bader charge analysis (Table S7) shows that under compressive biaxial strain, the Li+ ions concede on average less charge to the nearby O ions than under tensile strain, thus indicating weaker bonding interactions. A weaker interaction results in a lower EV and easier Li+ extraction. Lastly, the nearest average Li–Li distances under different strain cases were evaluated. In the compressive case (η = −4%), the average distance is reduced by 0.07 Å, indicating a stronger Li–Li Coulomb repulsion interaction, which also contributes to a lower EV. Meanwhile, in the tensile case (η = +4%), the distance is increased by 0.11 Å, correspondingly resulting in a higher EV. A lower EV can limit the performance of energy storage devices by reducing the intercalation voltage and, ultimately, the energy density of the cathode material.
Figure 5.
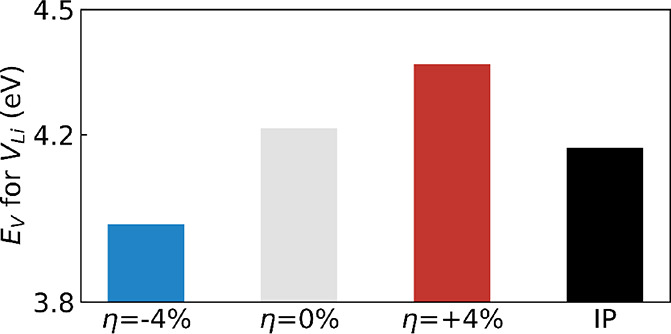
Formation energy (EV) of a single Li vacancy for LiCoO2 under η = −4, 0, and +4% and HP.
4. Conclusions
We have presented a comprehensive first-principles study of the Li+ diffusion properties of SOC LCO under biaxial strain and an HP of around 1 GPa. By performing both NEB and FPMD calculations, we found that compressive biaxial strain tends to enhance Li+ diffusivity, whereas tensile biaxial strain suppresses it. FPMD simulations show that compressive strain does not tend to promote Li+ diffusion when Li deficiencies are low, whereas tensile biaxial strain always tends to hinder the diffusion. Our results demonstrated that, under compressive strain, the Co layer distance was greatly increased, leading to an easier diffusion of Li+ along the TSH pathway by reducing the activation energy. Moreover, a stronger Coulomb interaction between Li-ions also contributed to Li+ diffusion. In contrast, HP could decrease Li+ diffusion in LCO, primarily by reducing the Li layer distance, with Coulomb repulsion between Li-ions partially offsetting this effect. However, the resulting increase in Ea of Li+ migration ultimately results in a decrease in Li+ diffusion. The results thus highlight the interplay among mechanical strain, variations in Li/Co layer distance, Li–Li distance, state-of-charge, and Li+ diffusion in LCO. A Va ∼2.6 ± 0.1 cm3/mol for LCO under HP is reported for the first time, indicating that Li migration requires additional space. Moreover, the calculated formation energies of a single Li vacancy show that Li vacancies are more likely to be created under compressive biaxial strain than under tensile strain, which could subsequently lead to a lower energy density. This trend is due to a weaker Li–O interaction, as demonstrated by the Bader charge analysis and supported by a strong Li–Li Coulomb interaction. Meanwhile, HP has a relatively minor effect on the formation of a single Li vacancy. The present results provide guidance on LCO cathode control, in which the strain effect should be taken into account, and can be generalized to other layered oxide cathodes to stimulate research efforts in this direction.
Acknowledgments
This work was supported in part by JSPS KAKENHI grant JP19H05815, MEXT as “Program for Promoting Research on the Supercomputer Fugaku” grants JPMXP1020200301 and JPMXP1020230325, Data Creation and Utilization Type Material Research and Development Project grant JPMXP1121467561, as well as JST COI-NEXT grant JPMJPF2016. The calculations were performed on the supercomputers at NIMS (Numerical Materials Simulator) and the supercomputer Fugaku at the RIKEN through the HPCI System Research Project (project IDs: hp220059 and hp220177). Z.Z. would like to thank Ane Eline Herlyng for proofreading
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsami.3c14444.
Stress tensor components for LCO as a function of the biaxial strain and hydrostatic pressure; strain along the a and c axes for LCO as a function of biaxial strain; NEB migration energy barrier for TSH pathway in LCO as a function of uniaxial strain; energy evolutions and corresponding energies averaged in FPMD; Li+ trajectory of FPMD; lattice parameter, layer distance, and diffusion coefficient for LCO under different concentrations, strains, and hydrostatic pressures; band gap and effective mass for LCO under biaxial strain and hydrostatic pressure; (Supporting Discussion 1) electronic conductivity of LCO under biaxial strain and hydrostatic pressure; and (Supporting Discussion 2) activation volume defined in tensor form (PDF)
Author Contributions
Z.Z. and Y.T. conceived the study with the help of C.C., B.G., L.D., and T.M. Calculations were performed by Z.Z. Contributions were made by Y.T., C.C., B.G., L.D., and T.M. in relation to the analysis and discussion of the results. The manuscript was written by Z.Z. with input/comments/feedback from other authors.
The authors declare no competing financial interest.
Supplementary Material
References
- Qin Z.; Zhang Y.; Luo W.; Zhang T.; Wang T.; Ni L.; Wang H.; Zhang N.; Liu X.; Zhou J.; Chen G. A Universal Molten Salt Method for Direct Upcycling of Spent Ni-Rich Cathode towards Single-Crystalline Li-Rich Cathode. Angew. Chem., Int. Ed. 2023, 62 (25), e202218672 10.1002/ange.202218672. [DOI] [PubMed] [Google Scholar]
- Ugata Y.; Yukishita K.; Kazahaya N.; Takahashi S.; Yabuuchi N. Nonflammable Fluorinated Ester-Based Electrolytes for Safe and High-Energy Batteries with LiCoO2. Chem. Mater. 2023, 35 (9), 3686–3693. 10.1021/acs.chemmater.3c00374. [DOI] [Google Scholar]
- Goodenough J. B.; Kim Y. Challenges for Rechargeable Li Batteries. Chem. Mater. 2010, 22 (3), 587–603. 10.1021/cm901452z. [DOI] [Google Scholar]
- Fergus J. W. Recent Developments in Cathode Materials for Lithium Ion Batteries. J. Power Sources 2010, 195 (4), 939–954. 10.1016/j.jpowsour.2009.08.089. [DOI] [Google Scholar]
- Zhou J.; Notten P. H. L. Studies on the Degradation of Li-Ion Batteries by the Use of Microreference Electrodes. J. Power Sources 2008, 177 (2), 553–560. 10.1016/j.jpowsour.2007.11.032. [DOI] [Google Scholar]
- Tan Z.; Li Y.; Xi X.; Jiang S.; Li X.; Shen X.; Zhang P.; He Z.; Zheng J. A Novelty Strategy Induced Pinning Effect and Defect Structure in Ni-Rich Layered Cathodes towards Boosting Its Electrochemical Performance. Journal of Energy Chemistry 2022, 72, 570–580. 10.1016/j.jechem.2022.05.037. [DOI] [Google Scholar]
- Tokranov A.; Sheldon B. W.; Lu P.; Xiao X.; Mukhopadhyay A. The Origin of Stress in the Solid Electrolyte Interphase on Carbon Electrodes for Li Ion Batteries. J. Electrochem. Soc. 2014, 161 (1), A58. 10.1149/2.009401jes. [DOI] [Google Scholar]
- Gao B.; Jalem R.; Ma Y.; Tateyama Y. Li+ Transport Mechanism at the Heterogeneous Cathode/Solid Electrolyte Interface in an All-Solid-State Battery via the First-Principles Structure Prediction Scheme. Chem. Mater. 2020, 32 (1), 85–96. 10.1021/acs.chemmater.9b02311. [DOI] [Google Scholar]
- Mukhopadhyay A.; Tokranov A.; Xiao X.; Sheldon B. W. Stress Development Due to Surface Processes in Graphite Electrodes for Li-Ion Batteries: A First Report. Electrochim. Acta 2012, 66, 28–37. 10.1016/j.electacta.2012.01.058. [DOI] [Google Scholar]
- Hao F.; Fang D. Diffusion-Induced Stresses of Spherical Core-Shell Electrodes in Lithium-Ion Batteries: The Effects of the Shell and Surface/Interface Stress. J. Electrochem. Soc. 2013, 160 (4), A595. 10.1149/2.054304jes. [DOI] [Google Scholar]
- Suthar B.; Northrop P. W. C.; Braatz R. D.; Subramanian V. R. Optimal Charging Profiles with Minimal Intercalation-Induced Stresses for Lithium-Ion Batteries Using Reformulated Pseudo 2-Dimensional Models. J. Electrochem. Soc. 2014, 161 (11), F3144. 10.1149/2.0211411jes. [DOI] [Google Scholar]
- Ngandjong A. C.; Lombardo T.; Primo E. N.; Chouchane M.; Shodiev A.; Arcelus O.; Franco A. A. Investigating Electrode Calendering and Its Impact on Electrochemical Performance by Means of a New Discrete Element Method Model: Towards a Digital Twin of Li-Ion Battery Manufacturing. J. Power Sources 2021, 485, 229320 10.1016/j.jpowsour.2020.229320. [DOI] [Google Scholar]
- Lim H. D.; Park J. H.; Shin H. J.; Jeong J.; Kim J. T.; Nam K. W.; Jung H. G.; Chung K. Y. A Review of Challenges and Issues Concerning Interfaces for All-Solid-State Batteries. Energy Storage Materials. 2020, 25, 224–250. 10.1016/j.ensm.2019.10.011. [DOI] [Google Scholar]
- Hao F.; Chen X. First-Principles Study of Lithium Adsorption and Diffusion on Graphene: The Effects of Strain. Mater. Res. Express 2015, 2 (10), 105016 10.1088/2053-1591/2/10/105016. [DOI] [Google Scholar]
- Zhang Q.; Tang C.; Zhu W.; Cheng C. Strain-Enhanced Li Storage and Diffusion on the Graphyne as the Anode Material in the Li-Ion Battery. J. Phys. Chem. C 2018, 122 (40), 22838–22848. 10.1021/acs.jpcc.8b05272. [DOI] [Google Scholar]
- Lee J.; Pennycook S. J.; Pantelides S. T. Simultaneous Enhancement of Electronic and Li+ Ion Conductivity in LiFePO4. Appl. Phys. Lett. 2012, 101 (3), 033901 10.1063/1.4737212. [DOI] [Google Scholar]
- Tealdi C.; Heath J.; Islam M. S. Feeling the Strain: Enhancing Ionic Transport in Olivine Phosphate Cathodes for Li- and Na-Ion Batteries through Strain Effects. J. Mater. Chem. A 2016, 4 (18), 6998–7004. 10.1039/C5TA09418F. [DOI] [Google Scholar]
- Cheng Y.-T.; Verbrugge M. W. Diffusion-Induced Stress, Interfacial Charge Transfer, and Criteria for Avoiding Crack Initiation of Electrode Particles. J. Electrochem. Soc. 2010, 157 (4), A508. 10.1149/1.3298892. [DOI] [Google Scholar]
- Lyu Y.; Wu X.; Wang K.; Feng Z.; Cheng T.; Liu Y.; Wang M.; Chen R.; Xu L.; Zhou J. An Overview on the Advances of LiCoO2 Cathodes for Lithium-Ion Batteries. Adv. Energy Mater. 2021, 11 (2), 2000982 10.1002/aenm.202000982. [DOI] [Google Scholar]
- Diercks D. R.; Musselman M.; Morgenstern A.; Wilson T.; Kumar M.; Smith K.; Kawase M.; Gorman B. P.; Eberhart M.; Packard C. E. Evidence for Anisotropic Mechanical Behavior and Nanoscale Chemical Heterogeneity in Cycled LiCoO2. J. Electrochem. Soc. 2014, 161 (11), F3039–F3045. 10.1149/2.0071411jes. [DOI] [Google Scholar]
- Mukhopadhyay A.; Sheldon B. W. Deformation and Stress in Electrode Materials for Li-Ion Batteries. Prog. Mater. Sci. 2014, 63, 58–116. 10.1016/j.pmatsci.2014.02.001. [DOI] [Google Scholar]
- Choi Y.-M.; Pyun S.-I. Effects of Intercalation-Induced Stress on Lithium Transport through Porous LiCoO2 Electrode. Solid State Ionics 1997, 99 (3–4), 173–183. 10.1016/S0167-2738(97)00253-1. [DOI] [Google Scholar]
- Kresse G.; Furthmüller J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54 (16), 11169–11186. 10.1103/PhysRevB.54.11169. [DOI] [PubMed] [Google Scholar]
- Blöchl P. E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50 (24), 17953–17979. 10.1103/PhysRevB.50.17953. [DOI] [PubMed] [Google Scholar]
- Zhou F.; Cococcioni M.; Marianetti C. A.; Morgan D.; Ceder G. First-Principles Prediction of Redox Potentials in Transition-Metal Compounds with LDA + U. Phys. Rev. B 2004, 70 (23), 235121 10.1103/PhysRevB.70.235121. [DOI] [Google Scholar]
- Laubach S.; Laubach S.; Schmidt P. C.; Ensling D.; Schmid S.; Jaegermann W.; Thißen A.; Nikolowski K.; Ehrenberg H. Changes in the Crystal and Electronic Structure of LiCoO2 and LiNiO2 upon Li Intercalation and de-Intercalation. Phys. Chem. Chem. Phys. 2009, 11 (17), 3278–3289. 10.1039/b901200a. [DOI] [PubMed] [Google Scholar]
- Wu L.; Zhang J. Ab Initio Study of Anisotropic Mechanical Properties of LiCoO2 during Lithium Intercalation and Deintercalation Process. J. Appl. Phys. 2015, 118 (22), 225101 10.1063/1.4937409. [DOI] [Google Scholar]
- Kramer D.; Ceder G. Tailoring the Morphology of LiCoO2: A First Principles Study. Chem. Mater. 2009, 21 (16), 3799–3809. 10.1021/cm9008943. [DOI] [Google Scholar]
- Zhu Y.; Wu D.; Yang X.; Zeng L.; Zhang J.; Chen D.; Wang B.; Gu M. Microscopic Investigation of Crack and Strain of LiCoO2 Cathode Cycled under High Voltage. Energy Storage Mater. 2023, 60, 102828 10.1016/j.ensm.2023.102828. [DOI] [Google Scholar]
- Wang L.; Li B.; Chen J.; Li J.; Luo Y.; Lv T. Coupled Effect of SOC and SOH on Tensile Behaviors of Lithium-Ion Battery Electrodes. J. Energy Storage 2023, 68, 107782 10.1016/j.est.2023.107782. [DOI] [Google Scholar]
- Tealdi C.; Mustarelli P. Improving Oxygen Transport in Perovskite-Type LaGaO3 Solid Electrolyte through Strain. J. Phys. Chem. C 2014, 118 (51), 29574–29582. 10.1021/jp509413w. [DOI] [Google Scholar]
- Henkelman G.; Uberuaga B. P.; Jónsson H. A Climbing Image Nudged Elastic Band Method for Finding Saddle Points and Minimum Energy Paths. J. Chem. Phys. 2000, 113 (22), 9901–9904. 10.1063/1.1329672. [DOI] [Google Scholar]
- Momma K.; Izumi F. VESTA 3 for Three-Dimensional Visualization of Crystal, Volumetric and Morphology Data. J. Appl. Crystallogr. 2011, 44 (6), 1272–1276. 10.1107/S0021889811038970. [DOI] [Google Scholar]
- Deng Z.; Zhu Z.; Chu I. H.; Ong S. P. Data-Driven First-Principles Methods for the Study and Design of Alkali Superionic Conductors. Chem. Mater. 2017, 29 (1), 281–288. 10.1021/acs.chemmater.6b02648. [DOI] [Google Scholar]
- He X.; Zhu Y.; Epstein A.; Mo Y. Statistical Variances of Diffusional Properties from Ab Initio Molecular Dynamics Simulations. npj Comput. Mater. 2018, 4 (1), 18. 10.1038/s41524-018-0074-y. [DOI] [Google Scholar]
- Van der Ven A.; Ceder G. Lithium Diffusion Mechanisms in Layered Intercalation Compounds. J. Power Sources 2001, 97–98, 529–531. 10.1016/S0378-7753(01)00638-3. [DOI] [Google Scholar]
- Van der Ven A.; Ceder G. Lithium Diffusion in Layered LixCoO2. Electrochem. Solid-State Lett. 2000, 3 (7), 301. 10.1149/1.1391130. [DOI] [Google Scholar]
- Liu X.; Shi J.; Zheng B.; Chen Z.; Su Y.; Zhang M.; Xie C.; Su M.; Yang Y. Constructing a High-Energy and Durable Single-Crystal NCM811 Cathode for All-Solid-State Batteries by a Surface Engineering Strategy. ACS Appl. Mater. Interfaces 2021, 13 (35), 41669–41679. 10.1021/acsami.1c11419. [DOI] [PubMed] [Google Scholar]
- Kang K.; Ceder G. Factors That Affect Li Mobility in Layered Lithium Transition Metal Oxides. Phys. Rev. B 2006, 74 (9), 094105 10.1103/PhysRevB.74.094105. [DOI] [Google Scholar]
- Li J.-J.; Dai Y.; Zheng J.-C. Strain Engineering of Ion Migration in LiCoO2. Front. Phys. 2022, 17 (1), 13503. 10.1007/s11467-021-1086-5. [DOI] [Google Scholar]
- Ning F.; Li S.; Xu B.; Ouyang C. Strain Tuned Li Diffusion in LiCoO2 Material for Li Ion Batteries: A First Principles Study. Solid State Ion 2014, 263, 46–48. 10.1016/j.ssi.2014.05.008. [DOI] [Google Scholar]
- Sagotra A. K.; Chu D.; Cazorla C. Influence of Lattice Dynamics on Lithium-Ion Conductivity: A First-Principles Study. Phys. Rev. Mater. 2019, 3 (3), 035405 10.1103/PhysRevMaterials.3.035405. [DOI] [Google Scholar]
- Yaqoob N.; Mücke R.; Guillon O.; Kaghazchi P. Delithiation-Induced Oxygen Vacancy Formation Increases Microcracking of LiCoO2 Cathodes. J. Power Sources 2022, 533, 231316 10.1016/j.jpowsour.2022.231316. [DOI] [Google Scholar]
- Chen Z.; Dahn J. R. Methods to Obtain Excellent Capacity Retention in LiCoO2 Cycled to 4.5 V. Electrochim. Acta 2004, 49 (7), 1079–1090. 10.1016/j.electacta.2003.10.019. [DOI] [Google Scholar]
- Nakamura K.; Ohno H.; Okamura K.; Michihiro Y.; Moriga T.; Nakabayashi I.; Kanashiro T. 7Li NMR Study on Li+ Ionic Diffusion and Phase Transition in LixCoO2. Solid State Ion 2006, 177 (9–10), 821–826. 10.1016/j.ssi.2006.02.021. [DOI] [Google Scholar]
- Sugiyama J.; Mukai K.; Ikedo Y.; Nozaki H.; Månsson M.; Watanabe I. Li Diffusion in LixCoO2 Probed by Muon-Spin Spectroscopy. Phys. Rev. Lett. 2009, 103 (14), 147601 10.1103/PhysRevLett.103.147601. [DOI] [PubMed] [Google Scholar]
- Kang K.; Meng Y. S.; Bréger J.; Grey C. P.; Ceder G. Electrodes with High Power and High Capacity for Rechargeable Lithium Batteries. Science (1979) 2006, 311 (5763), 977–980. 10.1126/science.1122152. [DOI] [PubMed] [Google Scholar]
- Qi Y.; Hector L. G.; James C.; Kim K. J. Lithium Concentration Dependent Elastic Properties of Battery Electrode Materials from First Principles Calculations. J. Electrochem. Soc. 2014, 161 (11), F3010. 10.1149/2.0031411jes. [DOI] [Google Scholar]
- Zou Z.; Ma N.; Wang A.; Ran Y.; Song T.; Jiao Y.; Liu J.; Zhou H.; Shi W.; He B.; Wang D.; Li Y.; Avdeev M.; Shi S. Relationships Between Na+ Distribution, Concerted Migration, and Diffusion Properties in Rhombohedral NASICON. Adv. Energy Mater. 2020, 10 (30), 2001486 10.1002/aenm.202001486. [DOI] [Google Scholar]
- Kozinsky B.; Akhade S. A.; Hirel P.; Hashibon A.; Elsässer C.; Mehta P.; Logeat A.; Eisele U. Effects of Sublattice Symmetry and Frustration on Ionic Transport in Garnet Solid Electrolytes. Phys. Rev. Lett. 2016, 116 (5), 055901 10.1103/PhysRevLett.116.055901. [DOI] [PubMed] [Google Scholar]
- Düvel A.; Heitjans P.; Fedorov P.; Scholz G.; Cibin G.; Chadwick A. V.; Pickup D. M.; Ramos S.; Sayle L. W. L.; Sayle E. K. L.; Sayle T. X. T.; Sayle D. C. Is Geometric Frustration-Induced Disorder a Recipe for High Ionic Conductivity?. J. Am. Chem. Soc. 2017, 139 (16), 5842–5848. 10.1021/jacs.7b00502. [DOI] [PubMed] [Google Scholar]
- Barai A.; Guo Y.; McGordon A.; Jennings P. A Study of the Effects of External Pressure on the Electrical Performance of a Lithium-Ion Pouch Cell. 2013 Int. Conf. Connected Vehicles Expo (ICCVE) 2013, 295–299. 10.1109/ICCVE.2013.6799809. [DOI] [Google Scholar]
- Hoshino H.; Yanagiya H.; Shimoji M. Effect of Hydrostatic Pressure on the Electrical Conductivity of Ag3SBr and β-Ag3SI. Journal of the Chemical Society, Faraday Transactions 1: Physical Chemistry in Condensed Phases 1974, 70, 281–286. 10.1039/f19747000281. [DOI] [Google Scholar]
- Famprikis T.; Kudu O. U.; Dawson J. A.; Canepa P.; Fauth F.; Suard E.; Zbiri M.; Dambournet D.; Borkiewicz O. J.; Bouyanfif H.; Emge S. P.; Cretu S.; Chotard J. N.; Grey C. P.; Zeier W. G.; Islam M. S.; Masquelier C. Under Pressure: Mechanochemical Effects on Structure and Ion Conduction in the Sodium-Ion Solid Electrolyte Na3PS4. J. Am. Chem. Soc. 2020, 142 (43), 18422–18436. 10.1021/jacs.0c06668. [DOI] [PubMed] [Google Scholar]
- Fu Z. H.; Chen X.; Zhao C. Z.; Yuan H.; Zhang R.; Shen X.; Ma X. X.; Lu Y.; Liu Q. B.; Fan L. Z.; Zhang Q. Stress Regulation on Atomic Bonding and Ionic Diffusivity: Mechanochemical Effects in Sulfide Solid Electrolytes. Energy Fuels 2021, 35 (12), 10210–10218. 10.1021/acs.energyfuels.1c00488. [DOI] [Google Scholar]
- Schneider C.; Schmidt C. P.; Neumann A.; Clausnitzer M.; Sadowski M.; Harm S.; Meier C.; Danner T.; Albe K.; Latz A.; Wall W. A.; Lotsch B. V. Effect of Particle Size and Pressure on the Transport Properties of the Fast Ion Conductor t-Li7SiPS8. Adv. Energy Mater. 2023, 13 (15), 2203873 10.1002/aenm.202203873. [DOI] [Google Scholar]
- Radzilowski R. H.; Kummer J. T. The Hydrostatic Pressure Dependence of the Ionic Conductivity of β-Aluminas. J. Electrochem. Soc. 1971, 118 (5), 714. 10.1149/1.2408152. [DOI] [Google Scholar]
- Jagad H. D.; Harris S. J.; Sheldon B. W.; Qi Y. Tradeoff between the Ion Exchange-Induced Residual Stress and Ion Transport in Solid Electrolytes. Chem. Mater. 2022, 34 (19), 8694–8704. 10.1021/acs.chemmater.2c01806. [DOI] [Google Scholar]
- Haruyama J.; Sodeyama K.; Han L.; Takada K.; Tateyama Y. Space–Charge Layer Effect at Interface between Oxide Cathode and Sulfide Electrolyte in All-Solid-State Lithium-Ion Battery. Chem. Mater. 2014, 26 (14), 4248–4255. 10.1021/cm5016959. [DOI] [Google Scholar]
- Hoang K.; Johannes M. D. Defect Chemistry in Layered Transition-Metal Oxides from Screened Hybrid Density Functional Calculations. J. Mater. Chem. A Mater. 2014, 2 (15), 5224–5235. 10.1039/C4TA00673A. [DOI] [Google Scholar]
- James C.; Wu Y.; Sheldon B.; Qi Y. Computational Analysis of Coupled Anisotropic Chemical Expansion in Li2-XMnO3-δ. MRS Adv. 2016, 1 (15), 1037–1042. 10.1557/adv.2016.48. [DOI] [Google Scholar]
- Gillan M. J. The Elastic Dipole Tensor for Point Defects in Ionic Crystals. Journal of Physics C: Solid State Physics 1984, 17 (9), 1473. 10.1088/0022-3719/17/9/006. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.