Abstract
Accurate prediction of the temporal and spatial characteristics of COVID-19 infection is of paramount importance for effective epidemic prevention and control. In order to accomplish this objective, we incorporated individual antibody dynamics into an agent-based model and devised a methodology that encompasses the dynamic behaviors of each individual, thereby explicitly capturing the count and spatial distribution of infected individuals with varying symptoms at distinct time points. Our model also permits the evaluation of diverse prevention and control measures. Based on our findings, the widespread employment of nucleic acid testing and the implementation of quarantine measures for positive cases and their close contacts in China have yielded remarkable outcomes in curtailing a less transmissible yet more virulent strain; however, they may prove inadequate against highly transmissible and less virulent variants. Additionally, our model excels in its ability to trace back to the initial infected case (patient zero) through early epidemic patterns. Ultimately, our model extends the frontiers of traditional epidemiological simulation methodologies and offers an alternative approach to epidemic modeling.
Keywords: COVID-19, Agent-based method, Antibody dynamics, Epidemic prediction, Targeted epidemic-control measures, Epidemiological investigation
1. Introduction
The COVID-19 pandemic has exerted profound adverse effects on worldwide public health security and economic stability. The virus exhibits ongoing evolution, as evidenced by clinical data revealing its heightened transmissibility (He et al., 2021; Tian et al., 2022). This poses a substantial obstacle to public prevention strategies, particularly within jurisdictions that espouse dynamic zero policies. Recent outbreaks attributable to the Delta variant in Xi'an, China, and the Omicron variant in Tianjin have starkly illustrated the deleterious impact of the virus on societal and economic operations within a compressed timeframe of several weeks to a month (Taylor, 2022).
Mathematical models have proven to be valuable tools for predicting and assessing the trends of the COVID-19 epidemic. Currently, two primary modeling approaches are employed in forecasting the spread of the disease: ordinary differential equation (ODE) models, specifically compartment models, and agent-based models. ODE models can be categorized into various subtypes, such as SIR (susceptible, infected, recovered) (Dos Santos et al., 2021; Roberto Telles et al., 2021), SEIR (susceptible, exposed, infected, recovered) (Godio et al., 2020), and SEIQR (susceptible, exposed, infected, quarantined, recovered) (Mishra et al., 2020), depending on the specific compartments included. These models exhibit exceptional capabilities in fitting empirical data and making predictions. In fact, as early as 2017, researchers extended the SIR model by incorporating asymptomatic individuals and seasonal factors (Tang et al., 2017). Since the emergence of the COVID-19 outbreak, researchers have continuously enhanced these traditional models. For instance, Lai Yingcheng proposed the SHIJR model, which introduces a time delay function to improve the accuracy of disease progression prediction (Long et al., 2020; Zhai et al., 2021), while Wang Hao and Jiang Jifa developed a stochastic discrete-time SIR model (Schreiber et al., 2021). Additionally, researchers have also made efforts to account for unreported cases (Griette et al., 2019, 2021). Nonetheless, ODE-based compartment models possess certain limitations, particularly their inability to consider system heterogeneity (Chowell et al., 2016). Although they demonstrate satisfactory fitting outcomes, employing these models with early-stage data often results in underestimated initial susceptible population figures. Moreover, due to their failure to incorporate geographical distribution and individual contact characteristics, these models lack precision in predicting the spatial dynamics of epidemic development (Afzal et al., 2022; Chowell et al., 2016).
The agent-based model is another valuable tool employed for predicting the spread of COVID-19, benefiting from its ability to leverage rapid computational capabilities. This model focuses on examining the probability of incidence among individual agents, thereby providing a comprehensive understanding of epidemic characteristics across the entire population (Banisch, 2016; Wilensky & Rand, 2010). In contrast to traditional ODE models, the agent-based model offers a more accurate representation of system heterogeneity. These approaches have found widespread applications in diverse fields such as supply chain optimization (Macal et al.), the decline of ancient civilizations (Kohler et al., 2005), and dynamic modeling of the immune system (Folcik et al., 2007). Following the outbreak of COVID-19, numerous researchers have adopted the agent-based approach for prediction, prevention, and control of the disease. For instance, Hoertel et al. proposed an agent-based model incorporating random perturbations to simulate the early stages of COVID-19 in France (Hoertel et al., 2020). Hinch et al. developed “OpenABM-Covid19,” an agent-based framework for studying non-pharmaceutical interventions against COVID-19 in the UK (Hinch et al., 2021). Erik Cuevas introduced a model that assesses the transmission risk by considering changes in individual locations (Cuevas, 2020).
Meanwhile, there has been a growing recognition of the impact of fluctuating population immunity on the development of the epidemic, leading many traditional compartment models to incorporate factors related to the temporal dynamics of immunity (Crellen et al., 2021; Ghosh et al., 2022; Pérez-Alós et al., 2022). Accounting for the temporal changes in immunity allows for a more realistic depiction of the evolving susceptible population over time, thus enabling more reliable predictions of epidemic trends. By incorporating information on vaccination and secondary infection into an age-structured SEIRS model of SARS-CoV-2 transmission, Anass Bouchnita et al. utilized the model to provide scenario projections for public health agencies in Texas and the COVID-19 Scenario Modeling Hub as new Omicron subvariants emerged (Bouchnita et al., 2023). However, population immunity is directly linked to antibody levels, and the decline of these antibody levels does not exhibit a simple mathematical relationship with time. Therefore, these models still face significant limitations when it comes to accurately predicting localized variations in the epidemic.
Drawing upon previous research achievements, we incorporated valuable insights to inform our current study. We have developed a continuous Markov chain model that leverages individual characteristics to simulate the spatiotemporal development of epidemics (Xu et al., 2022). Our model encompasses three primary features. Firstly, we incorporate individual contact information, guided by extensive big data, to predict epidemics more effectively. Secondly, we account for time-varying infection probabilities for individuals. Lastly, we consider epidemic resurgence by incorporating individual age and the decay of immunity following natural infection or vaccination. Building upon our initial model, we have made significant improvements to reflect the evolving epidemic landscape and introduce new functionalities. These enhancements primarily encompass two aspects. Firstly, we have integrated the capability to trace the origin of the epidemic and potential transmission chains based on current disease incidence. Secondly, to enhance the predictive accuracy of our model, we have integrated information from individual antibodies and viruses into the overarching population network, drawing upon our prior research findings (Xu et al., 2022, 2023a). By explicitly incorporating antibody dynamics for each individual, we model the gradual decline in antibody levels and simulate infection risk deterministically based on the interaction between antibodies and viruses. This refinement allows us to more accurately predict and evaluate disease progression and transmission risks for both individual cases and population dynamics.
Since the late spring of 2020, China has implemented targeted control measures and a dynamic zero policy as part of its epidemic prevention and control strategies. This approach involves the identification and isolation of positive patients and their close contacts within susceptible infection groups, utilizing nucleic acid tests to promptly detect positive cases and effectively disrupt transmission chains (Liang et al., 2022). Initially, this strategy exhibited favorable outcomes in terms of cost-effectiveness during 2020 and 2021. However, its effectiveness has gradually waned, particularly with the emergence of the omicron variant. Consequently, since March 1st, 2022, COVID-19 has spread rapidly across mainland China, leading more local governments to abandon precision-based prevention and control policies aimed at complete infection containment. The objective of this study is to establish a precise mathematical model capable of predicting the local development of the epidemic, while evaluating the efficacy of different prevention policies currently implemented in China, including lockdowns, quarantine measures for positive cases, and the dynamic zero approach. Furthermore, we seek to explore the effects of these various prevention strategies and elucidate the reasons behind the diminished efficiency of isolating close contacts in the context of dynamic zero initiatives.
2. Methods
2.1. An overview of our agent-based model
Our agent-based model consists of two main components. The first part, as detailed in Section 2.2, focuses on the dynamic changes in viral load after infection for each individual. Taking into account the interaction between virus and antibodies, the invasion of the virus leads to an increase in the concentration of neutralizing antibodies in the body. The antibodies ultimately neutralize and clear the virus, as illustrated in Fig. 1.
Fig. 1.
An illustration of our agent-based model.
The second part pertains to the interactions among individuals, as described in Section 2.3. Each infected individual releases virus particles into the environment, with the number of particles released proportional to the viral load in their body. Simultaneously, each individual may inhale virus particles released by infected individuals. The amount of inhaled particles is proportional to the viral load released into the environment and the frequency of contact between individuals.
By employing this agent-based model, individual infection events can give rise to group infection events. When a virus invades an individual in the population, under the condition of low antibody concentration, the virus has an opportunity to rapidly proliferate. The infected individual also releases virus particles into the environment, leading to the infection of individuals in close contact. However, transmission is not guaranteed. When individuals in contact have high levels of antibodies, the interaction between the virus and antibodies prevents potential infections, as high antibody concentrations rapidly neutralize the invading virus. Such individuals are not categorized as susceptible in our traditional mathematical models. Nevertheless, our model's advantage lies in its ability to quantitatively describe the dynamics of antibodies, thereby capturing changes in individual susceptibility over time. The aggregation of contact frequencies for each person yields the contact matrix for the entire population.
Control measures exert inhibitory effects on population infections by selectively altering the contact matrix. For example, implementing a large-scale distancing policy that increases social distance and reduces social interactions is equivalent to proportionally reducing the values of each element in the distance contact matrix. However, such control measures are not absolute; otherwise, our daily lives would be severely disrupted. Thus, reducing contact frequencies close to zero is challenging. This concept is discussed in pseudocode in Section 2.4.1. We can also simulate the occurrence of isolation. When a person is isolated, all elements in the contact matrix related to this individual are set to zero during the isolation period, effectively severing all connections with the external environment. This is described in the pseudocode in Section 2.4.2. Similarly, we can simulate more extensive control measures, such as isolating confirmed cases and their close contacts, as discussed in Section 2.4.3. In this case, not only do we set the contact vector of the infected individual to zero, but we also set the contact matrix of the population in close contact with them to zero. Specific examples of these measures are provided in Fig. 1. The relevant contact matrices return to their original states after the completion of isolation.
2.2. Modeling virus-antibody dynamics at individual level
A simple mathematical representation of the immune response is described in the diagram below.
In Fig. 2, x denotes the amount of antibody-antigen (virus) complex, y denotes the total number of antibodies, and z denotes the number of viruses. Six processes are displayed in our model. The first reaction represents the proliferation or the replication of virus with a reaction constant . The second reaction represents the binding reaction between virus and antibody, with a forward reaction constant β and reverse constant γ. The third reaction represents the removal of antibody-virus complex with a reaction constant δ. The fourth reaction represents the induction of new antibody by the antibody-virus complex with a kinetic constant ε. In immunology, those virus-antibody complexes are on the surface of B-cells since the antibody are initially produced by B-cells and will attach to the plasma membrane of B cells. Those complexes would further bind to the helper cells because the antibody has another structure binding region toward those receptors. Those helper cells will present the antigen part, which is a virus in this case, to the T-cell. The physical placement should be B-cells bind to those helper cells and further present themselves close to T-cells. The T-cells will handle those antigen substances; if those substances are not self-originated, they would secret signal molecules to promote the proliferation or the division of B-cells who attached on them. Therefore, B-cell finally get proliferated, so are the antibodies generated by their B-cell. The fifth reaction represents the degradation of virus with a constant ζ. The sixth reaction represents the degradation of antibody with a rate constant η. p denotes antigen-like substances in the environment whose concentration is supposed to be constant; q denotes antibodies bound to antigen-like substances in the environment. Reaction 7 represents the binding reaction between antibody and environmental antigenic substances with a forward constant θ and a reverse constant λ. Reaction 8 represents the remove of antibody-antigen complex q with a reaction rate δ which is supposed to be same as the remove of antibody-virus complex. Reaction 9 represents the induction of new antibody by q with rate . Therefore, a set of equations is derived as following:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
Fig. 2.
A diagram of host-virus interaction.
Based on the model described by Equations (1), (2), (3), it can be observed that the concentration of antibodies will eventually diminish to zero. This decay is attributed to the presence of a decay coefficient, denoted as ζ, which ensures that the antibodies fade away within a short time frame. However, in contrast to this observation, certain antibodies are capable of persisting in the human body for extended periods, offering lifelong protection. This phenomenon forms the fundamental basis for vaccine development. Immunologists commonly refer to these long-lasting B-cells or T-cells as “memory cells”. Although empirical studies have confirmed that these “memory cells” are distinct subclasses of immune cells (Inoue et al., 2018; Kurosaki et al., 2015), they exhibit similar half-lives to normal CD8+ cells (van den Berg et al., 2021). Consequently, the sustained antibody levels from “memory cells” can be attributed to a continuous stimulation triggering the proliferation of these memory cells. We propose that this stimulation arises from the presence of environmental antigen-like substances. These substances, which can be derived from various sources such as food, air, or even endogenous factors, exhibit weak binding affinity with neutralizing antibodies. Termed “environmental antigen-like substances”, they elicit weak signals upon presentation to T-cells, thereby promoting the proliferation of memory B-cells or T-cells. Due to their weak binding and the close similarity of protein sequences between these substances and our own body, their antigenicity is relatively low. Accordingly, the secreted stimulation signals by T-cells remain correspondingly weak. A dynamic equilibrium is established at a certain time point where the decay of memory cells is counterbalanced by the generation of new memory cells. A comprehensive elucidation of the virus-antibody interaction model can be found in our previous publication (Xu, Wei, Zhang, & et al, 2023).
2.3. Modeling infections at population level
We proceed to incorporate the virus-antibody interaction within our agent-based model. In our previous study (Xu et al., 2022), we introduced a continuous Markov-chain model for simulating epidemics. This model considers a population consisting of N individuals, each exhibiting varying contact probabilities with others. The probability of infection is directly proportional to the contact probability, with the infection probability being equal to the contact probability itself. Notably, the contact probability between an individual and themselves is assigned a value of zero. Consequently, a matrix of size N × N is constructed, exhibiting the following properties:
| (6) |
| (7) |
where stands for the interaction possibility between individual i and individual j. An accurate contact matrix can be obtained by tracking the individual contact probability in a natural population group. For example, each person's mobile phone can be recorded to obtain the population contact matrix within a particular time phase. The contact matrix is temporal and dynamic, which means it changes over time. However, it is difficult to obtain such accurate data at present. Therefore, the contact frequency is determined according to the relative distance between individuals, as shown in Equation (11).
| (8) |
where is the maximal contact possibility between agent i and agent j. In particular, the values of , , and n are preliminarily determined according to the initial reproduction constant R0 of the virus. According to the contact matrix, we can further determine the number of environmental invasive viruses received by a specific individual in a specific period of time.
| (9) |
represents the inhaled virus of individual i from infected people j. represents the overall released virus from infected person j. is positive related to the virus loading in corresponding infected agent with a correlation factor .
An extensive set of ordinary differential equations is further constructed. Assuming that the number of individuals in the population is N, the antibody virus complex in individual i is represented as , the concentration of antibodies is represented as , virus concentration is represented as , environmental antigenic substances concentration is represented as and the antibody-environment antigen complex is represented as .
| (10) |
| (11) |
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
This system of equations contains 5 N variables, where the last term in Equation (12) represents the overall number of viruses transmitted to this individual by other individuals in the whole population. We can generate random kinetic parameters that conform to the real population distribution through the first step of simulation. For such a large system of ordinary differential equations, we can solve it quickly by increasing the step size.
In order to interpret the simulation outcomes in terms of individual morbidity and total population morbidity, we establish distinct thresholds to identify infections presenting specific symptoms and compute the corresponding infected populations exhibiting such symptoms. Specifically, we introduce a threshold for nucleic acid testing to distinguish between positive and negative cases. When the value exceeds this threshold, an individual will yield a positive nucleic acid test result. We define this threshold as 104. Moreover, we categorize asymptomatic patients within the range of 104 to 5∗104, individuals with mild symptoms within the range of 5∗104 to 5∗105, and severe cases within the range of 5∗105 to ∞. The selection of these thresholds is based on the composition of each symptom during different stages of the epidemic. Notably, the proportion of asymptomatic patients gradually rises to over 95% during Omicron infection, while the prevalence of severe and mild cases steadily declines over time. We acknowledge that the selection of these thresholds is reasonable but necessitates systematic fitting. Different criteria exist for defining asymptomatic cases in clinical practice; in this study, we define asymptomatic patients as those without pneumonia. By examining the correlation between virus quantity within host cells and exhibited symptoms, we can obtain comprehensive insights into the characteristic evolution of specific groups during the epidemic.
2.4. Estimating the effects of different prevention strategies
2.4.1. Lock-down strategy
The main components of the lock-down measures include reducing social interactions and increasing social distancing. In our model, we multiply the population interaction matrix with a factor which ranges from 0 to 1 to mimic the lock-down effect. The contact frequency of the whole population engages a non-discriminatory declination. The stricter the policy, the smaller the value. Specific examples can be illustrated in Fig. 1, where the implementation of lock-down measures results in an equal decrease in the frequency of contact among individuals A, B, C, and D.
| (18) |
2.4.2. Extensive nucleic acid testing and quarantine positive cases
The primary measure of this approach lies in promptly identifying positive cases, and mass nucleic acid testing is the most effective means of detecting infected individuals. When an individual's viral load exceeds the threshold for nucleic acid testing, they will be screened and appropriate isolation measures will be implemented. During the isolation period (14 days), the values associated with their contacts in the population's contact matrix become zero. After the isolation period concludes, the contact matrix returns to its initial state. Specific examples can be referred to in Fig. 1.
The pseudocodes are presented as follows:
| for i = 1:M (M represents the overall steps) |
| for j = 1:N (N represents the overall number of people in the population) |
| if > C (C is the qPCR threshold) |
| end |
| End |
| end |
represents the antibody-virus complex level of individual j at i-th time point. represents the antibody level of individual j at i-th time point. represents the virus level of individual j at i-th time point. represents the environmental antigen level of individual j at i-th time point. represents the antibody-environmental antigen complex level of individual j at i-th time point.
2.4.3. Extensive nucleic acid testing and quarantine both positive cases and their close contacts
This approach represents the specific implementation strategy of China's dynamic zero-covid policy and is also known as China's targeted prevention and control strategy. It also requires mass nucleic acid testing to identify positive cases. Once a positive case is detected, not only does the individual undergo a 14-day isolation period, but also those who have been in contact with them are required to undergo a 14-day isolation period. After the isolation period ends, if the isolated individuals test negative in nucleic acid testing, the isolation measures are lifted. If they test positive, an additional 14-day isolation period is imposed. In our model, this approach is reflected by setting the contact frequency to zero for the overall contact matrix involving positive cases and their close contacts, and restoring it to its original state after the isolation measures are lifted. Specific examples are presented in Fig. 1.
The pseudocodes are presented as follows:
| for i = 1:M (M represents the overall steps) |
| for j = 1:N (N represents the overall number of people in the population) |
| if > C (C is the nucleic acid testing threshold) |
| if |
| end |
| end |
| end |
| end |
represents the antibody-virus complex level of individual j at i-th time point. represents the antibody level of individual j at i-th time point. represents the virus level of individual j at i-th time point. represents the environmental antigen level of individual j at i-th time point. represents the antibody-environmental antigen complex level of individual j at i-th time point.
2.5. Tracing the epidemic origin based on current infection information
An important task in epidemic prevention and control is epidemiological investigation, which aims to effectively identify the source of infection and the transmission chain. Traditional epidemiological investigations only focus on tracing close and secondary contacts, identifying the original case based on the contact matrix. This retrospective approach does not consider the influence of population immunity on the infection. By providing contact information of the population, our model can better conduct the investigation of the disease source.
The overall idea of our algorithm is to globally traverse all individuals in a population consisting of N individuals. The index case could be any individual from 1 to N. The outbreak generated by a specific initial case i will lead to a specific distribution of the epidemic within a time period from 1 to M. By comparing this epidemic distribution with the actual distribution, the similarity reflects the probability that individual i is the index case, which we represent as cos_similarity (S(i,j), Starget) in our pseudocode. Through this approach, we can identify the most likely original case.
We can create a morbidity landscape for the entire population at different time intervals. Each person can be assigned a value based on their current symptoms. For example, a severe case would be assigned a value of 1, mild symptoms would be assigned 0.5, asymptomatic infection would be assigned 0.25, and negative cases would be assigned 0. Therefore, a matrix S can be generated to represent the symptoms of each individual at different time points. S(i,j) represents the symptoms of individual i at the j-th time point. The actual epidemic distribution can be represented as S target. We attempted to determine the probability of each individual becoming the original zero patient. This probability can be represented as a vector P.
The pseudocode is as follows:
| for i = 1:N (N is the population size, i = k stands for the individual k is the zero patient) |
| for j = 1:M (M is overall step sizes or the overall time points) |
| S(i,j) (It can be derived based on(10), (11), (12), (13), (14), (15)) |
| Pro(i,j) = cos_similarity(S(i,j), Starget) |
| end |
| P(i) = Max(Pro(i,:)). |
| end |
cos_similarity (S(i,j), Starget) stands for the cosine similarity between two vectors. P(i) stands for the probability of individual i to become original zero patient.
3. Results
3.1. Parameter estimation based on clinical data
In previous studies, we presented a theoretical framework elucidating the dynamics of antibodies and proposed a methodology to estimate the duration of antibody-mediated protection based on this model (Xu, Wei, Zhang, & et al, 2023). By analyzing data obtained from clinical experiments, we successfully calibrated specific parameters to capture the temporal characteristics of antibodies in distinct populations. An important characteristic of our model is the absence of units associated with these parameters, which might pose a challenge for some readers. However, we deliberately omitted units as they are not essential for simulation purposes. Instead, what remains crucial is the dynamic interplay between antibodies and the viral agent. Moreover, obtaining precise units directly from experimental data is not feasible. For instance, although the CT value in nucleic acid testing provides an indication of viral load, it is arduous to quantitatively determine the actual viral burden within the host organism solely based on the CT value. The interaction between antibodies and viruses exhibits a complex and multifaceted binding pattern. Furthermore, determining the absolute concentration of antibodies at different time points is challenging since most experimental data are reported in terms of antibody titer.
The principal objective of our model is to faithfully simulate the reciprocal dynamics between antibodies and viruses, thereby obviating the need to incorporate units within the mathematical framework. Through manipulation of diverse parameters, particularly the mean and variance, we can capture the inherent characteristics governing the dynamics of antibodies within a given population. By comparing empirical statistical data, we can estimate the distribution of antibody dynamics parameters across the entire population. Although these parameters lack immediate physical interpretation, they provide a more precise depiction of waning immunity and the potential for reinfection across varying temporal contexts in distinct individuals.
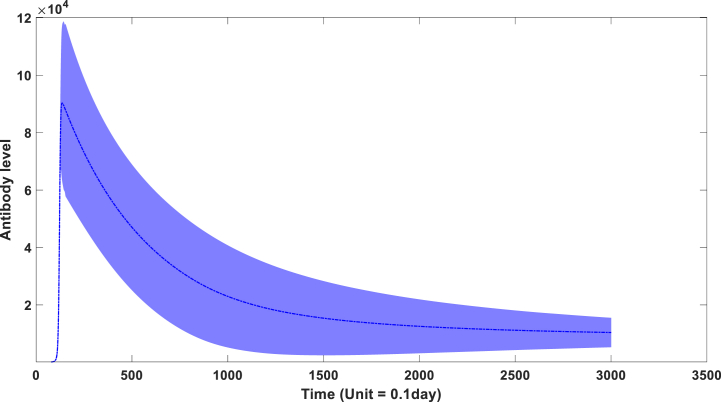
We postulate a constant concentration of the environmental antigenic substance in our model. The key variation arises from inter-individual differences in the binding capacity of antibodies (β). Furthermore, the binding kinetics (θ) between the environmental antigenic substance and antibodies also exhibit variability across individuals. Fig. 3A visually depicts the population-level performance characteristics of antibody kinetics based on these parameters. A longitudinal seroprevalence study involving 3217 healthcare workers in the UK (Lumley et al., 2021) provided empirical evidence of declining levels of IgG antibodies targeting the SARS-CoV-2 nucleocapsid within a few months. As displayed in Fig. 3A, a substantial decrease in IgG levels becomes apparent following their peak attainment. However, this decline manifests in a non-linear fashion, with the rate of descent gradually diminishing before stabilizing approximately 200 days post-infection. Remarkably, these simulation outcomes closely align with clinical observations indicating that IgG levels reach their zenith approximately 20 days following infection before gradually declining at a decelerating pace over time.
Fig. 3a.
the dynamic behavior of antibodies in the overall population through time. (The blue zone around mean curve stands for 95% confidence interval).
The peak concentration of antibodies is primarily determined by the parameter β, whereas the rate of antibody waning is mainly governed by θ. Fig. 3A graphically represents the temporal dynamics of population-level antibody levels, while Fig. 3B illustrates the corresponding changes in overall protective efficacy. Based on our model, we can infer that in the absence of viral mutation, an initial COVID-19 vaccine efficacy of 100% in a human population (10,000 simulations) would diminish to 97.21% after 100 days, 65.44% after 150 days, 39.28% after 200 days, and 28% after 240 days. The simulation results in Fig. 1B are broadly consistent with clinical evidence concerning vaccine effectiveness (Chemaitelly et al., 2021; Cohn et al., 2022; Tartof et al., 2021). A cohort study conducted among US veterans from February 1st to October 1st, 2021, discovered a time-dependent decline in vaccine effectiveness against infection (VE-I) (P < 0.01), even after adjusting for age, sex, and comorbidities. VE-I decreased for all vaccine types, with the most substantial declines observed for Janssen, followed by Pfizer-BioNTech and Moderna. Specifically, in March, VE-I was 86.4% (95% CI, 85.2–87.6%) for Janssen, 89.2% (95% CI, 88.8–89.6%) for Moderna, and 86.9% (95% CI, 86.5–87.3%) for Pfizer-BioNTech. By September, VE-I had dropped to 13.1% (95% CI, 9.2–16.8%) for Janssen, 58.0% (95% CI, 56.9–59.1%) for Moderna, and 43.3% (95% CI, 41.9–44.6%) for Pfizer-BioNTech (Cohn et al., 2022). A retrospective cohort study evaluating the effectiveness of mRNA BNT162b2 vaccine reported a decline in effectiveness against infections from 88% (95% CI 86–89) during the first month following full vaccination to 47% (43–51) after 5 months. Notably, among sequenced infections, vaccine effectiveness against delta variant infections remained high during the initial month after full vaccination (93% [95% CI 85–97]) but decreased to 53% after 4 months (Tartof et al., 2021). Similar trends were observed in a cohort study conducted in Qatar (Chemaitelly et al., 2021). Consequently, in subsequent simulations, we will employ these parameter combinations to investigate the epidemic progression under various prevention and control measures. Table 1 provides the parameters and initial values of variables.
Fig. 3b.
The protection performance of antibodies in the overall population through time.
Table 1.
parameters and initial values of variables in this model.
| Parameter | Value | Description | Source |
|---|---|---|---|
| α | Constant of reaction 1 | No need | |
| β | ∼N (10−5, 2∗10−6) | Forward reaction constant of reaction 2 | Estimated based on initial values from (Xu et al., 2023a, 2023b) |
| γ | 10–14 | Reverse reaction constant of reaction 2 | (Xu et al., 2023a, 2023b) |
| δ | 0.1 | Constant of reaction 3&8 | Estimated |
| ε | 2 | Constant of reaction 4&9 | Xu et al (2023a, 2023b) |
| ζk | 1 | Constant of reaction 5 | Xu et al (2023a, 2023b) |
| ηs | 0.02 | Constant of reaction 6 | Xu et al (2023a, 2023b) |
| θ | ∼N (1.8∗10−8, 1∗10−9) | Forward reaction constant of reaction 7 | Estimated based on initial values from (Xu, Wei, Zhang, & et al, 2023) |
| λ | 10–14 | Reverse reaction constant of reaction 7 | Xu et al (2023a, 2023b) |
| μ | Cofactor between released virus and the virus loading in the host | No need | |
| 5∗10−5 | Time-dependent declination factor of α (represents declining virulence through time) | Estimated | |
| 4∗10−4 | Time-dependent increase factor of μ(represents increasing transmission through time) | Estimated | |
| i | 1 | Initial value of α | Xu et al (2023a, 2023b) |
| 10–7 | Initial value of μ | Estimated | |
| 0 | Initial value of antibody-virus complex in each agent | Xu et al (2023a, 2023b) | |
| 102 | Initial value of antibody level in each agent | Xu et al (2023a, 2023b) | |
| 0 | Initial value of virus level in each agent | Xu et al (2023a, 2023b) |
3.2. Simulation of epidemic development at population level
This study is predicated on four assumptions:
-
Ⅰ
In this model, individual immunity to certain infectious diseases exhibits heterogeneity. This heterogeneity is captured by varying β values, which reflect the kinetics of neutralizing antibody binding to the virus. To account for individual behavior and its impact on epidemic dynamics at the population level, a normal distribution of β values is employed. Fig. 3A visualizes the temporal dynamics of population-level antibody levels, while Fig. 5B illustrates the corresponding 3D landscape of population antibody behaviors.
-
Ⅱ
The introduction of virus mutation factors into the model results in a reduction in virus proliferation capacity (indicated by a decreasing α value over time) and an increase in virus release (indicated by an increasing in Equation (13)). These evolutionary changes may lead to the emergence of viral variants with lower virulence but higher transmissibility. Consequently, the replication constant α diminishes over time, while increases. The model also accounts for the antibody attenuation effect through the antibody degradation constant η. The antibody dynamics depicted in Fig. 3A reflect these trends.
-
Ⅲ
Infections exhibit varying transmission potentials at different time points. An infected individual produces antibodies and becomes contagious. Equation (9) incorporates , which represents the overall released virus from infected person j. The quantity captures the transmission potential of an infected individual and is linearly correlated with the viral load level in the host's body. The virus dynamics across different host bodies are presented in Fig. 5A, showing highly fluctuating, individualized, and time-dependent patterns.
-
Ⅳ
Individuals recover from infection cycles without mortality, thereby maintaining a constant overall population size.
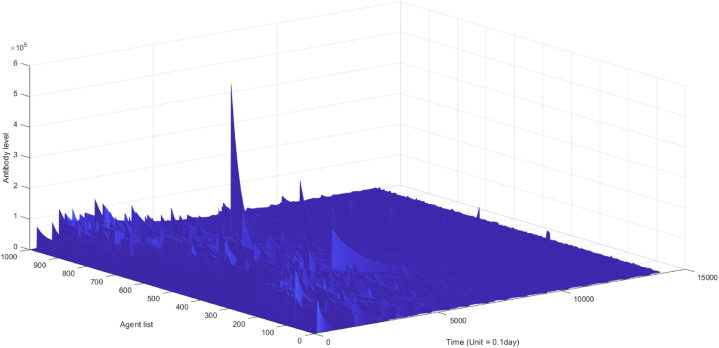
Fig. 5b.
the landscape of antibody dynamics in the actual scenario (n = 1000).
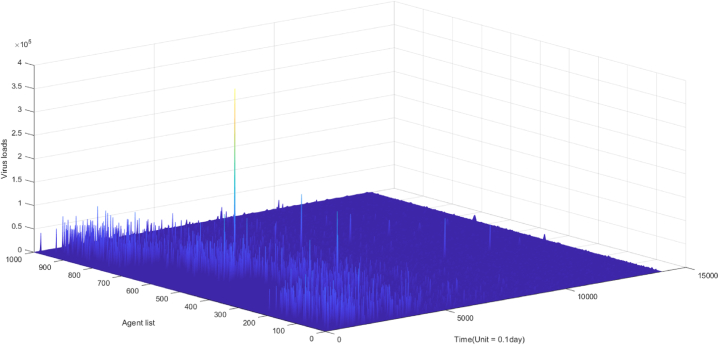
Fig. 5a.
the landscape of virus dynamics in the actual scenario (n = 1000).
Using the parameter combination proposed in Section 3.1, a group of 1000 individuals was randomly distributed across four regions based on a specific functional relationship between contact frequency and distance, as explained in our earlier publication (Ghosh et al., 2022) and defined in Equation (8) of the methodology section. By incorporating individuals' locations, a population contact matrix was derived, assuming only one individual acted as the initial infected person (patient zero) at the start time. Two scenarios were simulated based on Equations 10–17 in the methodology section. The first scenario represents the spread of the epidemic under ideal conditions, assuming no virus mutation over time (Fig. 4A). Supplementary Video 1A provides temporal and spatial information on all infected individuals. The second scenario approximates real-world epidemic development, considering the impact of virus mutation. Experimental and statistical evidence has demonstrated that SARS-CoV-2 is evolving to exhibit lower virulence and higher transmissibility (Alizon & Sofonea, 2021; Lan et al., 2021; Xu, Wei, Zeng, & et al, 2023). This scenario is depicted in Fig. 4B, with supplementary Video 1B showcasing the temporal and spatial distribution of infections. In Video 1, asymptomatic infections are depicted by light-colored gray level 0.25, mild symptom infections by medium-gray level 0.5, and severe cases are represented by dark gray (scale of darkness: 1).
Fig. 4a.
The development of epidemic in ideal condition (n = 1000).
Fig. 4b.
The development of epidemic in actual case (n = 1000).
Fig. 5a, Fig. 5b, Fig. 5c depicts the landscape of virus dynamics and antibody dynamics. Fig. 5A illustrates the temporal dynamics of virus dynamics in diverse individuals over a period of 1400 days, while Fig. 5B showcases the antibody dynamics in each individual during the same duration. Additionally, Fig. 5C demonstrates the dynamics of virus-antibody interaction in a specific individual. Based on observations from Fig. 5a, Fig. 5cA and C, it can be inferred that initial infections consistently manifest high viral loads in the absence of neutralizing antibodies, leading to a higher proportion of severe cases and a lower proportion of asymptomatic cases in the early stages of the epidemic, as exemplified in Fig. 4B. However, subsequent infections exhibit reduced fatality and lower viral loads due to the induction of neutralizing antibodies, as indicated in Fig. 3B. This methodology not only enables the determination of infection onset time and hotspots, but also facilitates quantitative descriptions of transmission risk and infection severity for each infected individual. In our model, infection symptoms are correlated with viral load within the host's body, which can be quantified by the quantity of antibody-antigen complexes. We propose several symptom thresholds, including a low threshold for a positive nucleic acid test (104), a moderate threshold for mild symptoms (5∗104), and a high threshold for severe cases (5∗105). Experimental evidence has revealed a significant positive correlation between symptoms and in vivo viral content, as manifested by the low cycle threshold (CT) value of viral amplification in severe patients (Gorzalski et al., 2020; Kim et al., 2020).
Fig. 5c.
an illustration of the antibody and virus dynamics in specific agent (500th person in this case).
The severity of infection diminishes progressively over time, influenced by two contributing factors. Firstly, the declining efficacy of virus proliferation, characterized by a reduction in virus virulence as indicated by the decreasing α value in our model. Secondly, the augmented presence of antibodies within the population, leading to subsequent infections essentially being reinfections with lower peak virus loads. Consequently, a greater proportion of asymptomatic cases emerges owing to the heightened levels of antibodies, as depicted in Fig. 4B.
3.3. Evaluation of the efficiency of different epidemic prevention strategies
Utilizing the proposed model, we conducted an assessment of the impact associated with various epidemic prevention strategies. In order to simulate epidemic scenarios under distinct prevention approaches, we employed a model that closely emulates real-world conditions. Specifically, our model incorporates a dynamic virus proliferation parameter α, as elucidated in section 2.3, which exhibits a progressively decreasing trend over time. Furthermore, considering pertinent clinical data, we accounted for the fluctuating transmission parameter and the heightened formation of virus particles over time. Consequently, we evaluated the efficacy of three standardized epidemic prevention methods.
The first strategy entails the implementation of enhanced social distancing measures along with a reduction in social contact frequency. This can be achieved through multifarious measures such as widespread usage of masks and the enforcement of lockdown policies. The second strategy involves the widespread utilization of nucleic acid testing on a large scale, subsequently followed by the isolation of individuals who test positive. The third strategy encompasses the deployment of quantitative polymerase chain reaction (qPCR) tests for all individuals residing in high-risk areas, followed by the subsequent isolation of individuals who test positive, as well as their close contacts. This particular approach has been referred to as “targeted control” by the Chinese government.
We conducted a simulation of disease onset within a small population consisting of 1000 individuals over a span of 1400 days, specifically focusing on the absence of vaccination and the subsequent increase in antibodies solely through natural infection. The outbreak was initiated by patient 0 on the first day, and for the initial six weeks, the number of infected individuals remained relatively low. Various prevention measures were implemented starting from the seventh week onwards.
The first prevention strategy involved the reduction of social frequency by adjusting the overall contact matrix to 20% of its original value. It is worth noting that a smaller value could be employed for a more stringent lockdown policy; however, this would come with additional side effects. The efficacy of this strategy is illustrated in Fig. 6A, while the dynamic geographic epidemic distribution can be observed in Video 2. It is important to highlight that while reducing social distance and contact frequency can effectively control the epidemic, the strategy does pose negative consequences on both the economy and social life. Furthermore, its success is contingent upon the strictness of the lockdown policy.
Fig. 6a.
the effect of 80% lock-down on the epidemic development.
Fig. 6A demonstrates that reducing contact frequency by 80% through a lockdown policy can effectively control the epidemic for the initial 300 days. However, as the virus's transmission capacity increases, a more stringent lockdown becomes necessary to prevent a widespread outbreak. A complete lockdown accompanied by population quarantine theoretically has the potential to eliminate any mutant strains; however, its implementation is impractical. Additionally, the risk of imported cases must be taken into consideration.
Furthermore, Fig. 6A indicates that the effectiveness of lockdown measures varies depending on the specific mutant strains. For high-transmission strains, preventive and control measures such as lockdowns and mask-wearing may delay the large-scale outbreak of the epidemic. However, they are unable to alter the overall trend of the outbreak or reduce the peak number of infections. Considering the costs associated with lockdown measures, it is evident that such an approach is not a feasible long-term solution.
The second policy for epidemic prevention involves implementing large-scale nucleic acid tests and isolating individuals who test positive. In our model, we simulate this strategy by setting the contact frequency to zero for a duration of 14 days when the virus concentration in a host exceeds 104. If the virus concentration drops below this threshold after two weeks, the original contact matrix is reinstated, indicating a negative nucleic test result. However, if the threshold is not reached, an additional 14-day isolation period is implemented. It is crucial to continuously monitor and evaluate the virus loading amount within each individual through frequent nucleic acid tests. The effectiveness of this strategy is illustrated in Fig. 6B, while the dynamic geographic epidemic distribution is presented in Video 3.
Fig. 6b.
the effect of positive case quarantine on the epidemic development.
This prevention strategy solely quarantines individuals who test positive and is comparatively less costly and more feasible to implement. Many countries have adopted this approach in their efforts to combat SARS-CoV-2. Nonetheless, as depicted in Fig. 6B, the impact of prevention and control measures is limited. Even for variants with a lower transmission capacity, this measure does not effectively suppress the spread of the epidemic.
The third policy for epidemic prevention involves conducting nucleic acid tests for individuals in high-risk areas and isolating both positive patients and their close contacts. In our model, this is achieved by setting the contact matrix to zero for individuals with a viral level exceeding 104, as well as their close contacts, for a duration of 14 days. The virus levels of individuals residing in high-risk areas must be regularly monitored and evaluated through nucleic acid tests. The efficacy of this strategy is depicted in Fig. 6a, Fig. 6b, Fig. 6c, while a dynamic geographic distribution of the epidemic is presented in Video 4.
Fig. 6c.
the effect of targeted-control policy on the epidemic development.
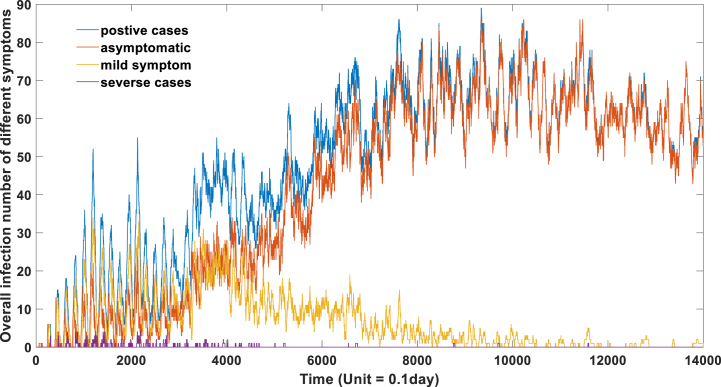
In comparison to the first approach, the cost of the third strategy is relatively low, yet its preventive and control measures yield significant results, as observed in Fig. 6C. This targeted containment strategy proves effective in controlling the epidemic during the initial 500 days, which explains China's attainment of the dynamic zero goal in 2020 and 2021 through targeted containment measures. However, it is important to note that while the isolation of close contacts surpasses the effectiveness of the first two strategies, its capacity for control remains limited and reliant on the virus's transmission potential. The effectiveness of this strategy gradually diminishes with increased virus transmissibility, particularly with the emergence of highly transmissible variants.
As evidenced in Fig. 6C, after 500 days, the epidemic spreads extensively, underscoring the strategy's dependence on the virus's transmission potential. Different expectations should be set for this strategy during different phases of the COVID-19 epidemic. If the virus's transmissibility is significantly heightened, solely isolating close contacts will prove insufficient in effectively curbing the surge of the epidemic. Broader quarantine measures, such as isolating secondary close contacts, may become necessary, thereby augmenting the challenges and costs of prevention efforts.
While the practical value of prevention has gradually waned with the decline in virus virulence, concerns persist regarding the potential emergence of more virulent strains in the future. Our previous research predicted the delicate trade-off between virulence and transmission in the evolution of SARS-CoV-2, elucidating its evolutionary trajectory and demonstrating that future virulence will not be significantly enhanced. By integrating this agent-based model, we have demonstrated the limited efficacy of precise prevention and control measures against highly infectious viruses. Imposing extensive and prolonged large-scale quarantine policies is also impracticable. Therefore, coexistence with SARS-CoV-2 becomes necessary, gradually alleviating people's fear of COVID-19 infection while acknowledging the merits of early prevention and control measures, which can mitigate the impact of highly virulent variants during the early stages of an epidemic. Both the first and third strategies substantially reduce the proportion of severe cases and overall mortality rates in the population, as evidenced by the comparison between Fig. 5a, Fig. 5b, Fig. 5c, Fig. 6c.
A comparison of the three different prevention policies is summarized in Fig. 7. As depicted, all three strategies would eventually become ineffective and lead to an epidemic outbreak as the virus transmission capacity continuously increases. However, large-scale lock-down (dashed blue line) and China's targeted-control policy (solid yellow line) are more effective in preventing early infections compared to the positive case quarantine strategy (solid red line).
Fig. 7.
A comparison of those three different prevention policies.
3.4. Epidemiological investigation to unearth patient number zero based on the early epidemic distribution
While SARS-CoV-2 has undergone evolutionary changes, resulting in a highly transmissible yet less virulent variant, the significance of precise prevention and control strategies remains pertinent due to the potential emergence of new viruses exhibiting high virulence but controllable infectivity. A vital component of the targeted-control approach involves identifying the source of the epidemic and concealed transmission chains based on known patterns of the outbreak. Conducting epidemiological investigations serves to identify potential positive cases and their close contacts, thereby emphasizing the importance of tracing patient zero utilizing early epidemic information. In our model, we offer a systematic and scientifically grounded approach to uncover the initial infection and elucidate the complete transmission chain. Through the utilization of the population contact matrix and early epidemic distribution, we are capable of quantitatively assessing the probability of patient zero for each individual (Xu et al., 2022). An illustrative example is provided to demonstrate the traceability of our model.
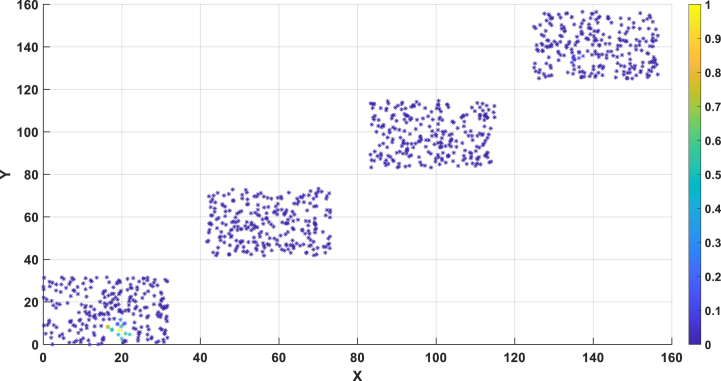
A detailed representation of the spatial distribution of the one thousand individuals can be found in Fig. 8B. In Fig. 8B, there are four blocks, each representing a community or small town. The spatial positions of individuals within each block were generated using random numbers in MATLAB, within a 30 × 30 area. Specifically, for the first block, the X and Y coordinates of individual positions were randomly generated between 0 and 30, including decimal values. For the second block, the X and Y coordinates of individual positions were randomly generated between 43.33 and 73.33, including decimal values. For the third block, the X and Y coordinates of individual positions were randomly generated between 86.66 and 116.66, including decimal values. And for the fourth block, the X and Y coordinates of individual positions were randomly generated between 130 and 160, including decimal values. Fig. 8A illustrates the location information of infected individuals at a specific moment. Through this approach, we attempted to identify the index case, maximizing the likelihood of reproducing the observed distribution of infected individuals at that specific time.
Fig. 8b.
the probability of patient zero for each individual in the overall population. X represents people's location in X-axis. Y represents people's location in Y-axis.
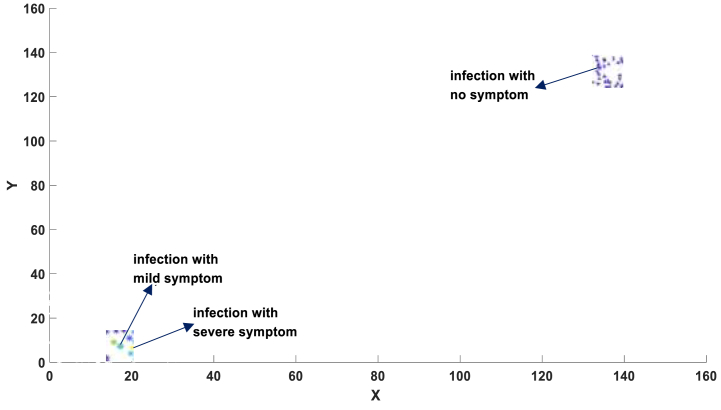
Fig. 8a.
Location of patients with symptom information.
Fig. 8A presents the infection distribution of 1000 individuals, representing the morbidity landscape with symptom information at 30 days (300-time units) since the initial infection of patient No.1. The landscape comprises three categories of patients: severe, mild, and asymptomatic, with their precise locations depicted in Fig. 8A.
By applying the techniques outlined in section 2.5, we traced the origin of this epidemic and presented the results in Fig. 8B, which illustrates the probability of patient zero for each individual in the population. Our method precisely identifies patient zero and the virus transmission chain, as indicated by the highest probability assigned to individual No.1 (100%) in Fig. 8B, accurately reflecting the actual situation.
4. Discussion
This study builds upon our prior research and introduces a Markov chain model to forecast the progression of an epidemic (Xu et al., 2022). In contrast to traditional ODE models and other agent-based models, the Markov-chain model offers several advantages. It characterizes individuals as distinct entities and incorporates contact information across a population to furnish more precise and dependable forecasts regarding epidemic development. The model challenges the conventional theory of herd immunity in the context of COVID-19 by projecting multiple waves of the epidemic resulting from declining immunity over time following initial infection or vaccination. These projections have been substantiated by subsequent developments in the epidemic. Nevertheless, a significant constraint of the Markov chain model lies in the absence of a simple mathematical function to account for the waning effects of antibodies, as illustrated in Fig. 3B. To overcome this limitation, we have devised a dynamic theory encompassing antibody dynamics that integrates antibody-related information into the prediction of the infection spectrum within the population (Xu, Wei, Zhang, & et al, 2023). Our agent-based model generates a unique landscape specific to a given population contact matrix and the dynamic parameters governing antibodies for each individual within the cohort. By explicitly incorporating antibody concentration and viral load, our model adeptly forecasts the likelihood of infection and the quantity of released viruses at different time intervals, thereby markedly enhancing the accuracy of the Markov chain model.
Our model posits three pivotal factors contributing to the resurgence of the COVID-19 epidemic: geographic diffusion, antibody degradation, and virus mutation effects. While geographic diffusion plays a crucial role in precipitating multiple waves in the COVID-19 pandemic, our small-scale model, limited by computational constraints, only simulates 1000 individuals and thus omits its impact. Regarding the SARS-CoV-2 virus, as expounded upon in our prior research (Xu, Wei, Zeng, & et al, 2023), its overall evolutionary trajectory during the initial stages tends towards augmented infectivity and diminished virulence. This evolutionary progression may transpire in an intermittent fashion; nonetheless, our model employs continuously changing parameters over time to capture this variation for the sake of simplicity. Throughout the evolutionary process, numerous strains will emerge, each harboring multiple subtypes. While our model cannot precisely forecast specific mutation sites, it can elucidate the ramifications of mutations on virulence and transmissibility. A key component of this entails the matter of virus assembly efficiency. When the virus exhibits low assembly efficiency, its RNA evinces feeble binding activity with its structural proteins, resulting in exposed RNA and heightened replication and translation efficacy. During this stage, the virus manifests heightened virulence, denoted by relatively magnified values of α within our parameters. Nevertheless, owing to diminished assembly efficiency, the abundance of fully assembled virus particles diminishes, subsequently yielding a relatively reduced quantity of released virus particles within the environment, correspondingly reflected by a comparatively smaller value of μ. The variability of the virus assumes a critical role in our simulations and serves as the foundation for examining diverse control measures. A more refined modeling approach may encompass the virus's life cycle and explicit incorporation of viral mutations and assembly processes. However, such an undertaking would undoubtedly amplify the intricacy of the present model, as each potential random mutation would engender a distinct strain necessitating supplementary independent structures in the programming process. Nonetheless, we aspire to enhance this model in the future by not only treating infected individuals as autonomous entities but also considering myriad virus strains as independent agents. Such bidirectional heterogeneity will unquestionably engender more insightful prognostications.
Our model encompasses the advantages of the Markov-chain model while offering a more comprehensive representation of morbidity dynamics. It incorporates antibody levels, virus levels, spatial distribution, and symptom classification for each individual at any given time, thereby presenting a more detailed landscape of disease progression. Moreover, it demonstrates commendable contact tracing capabilities, enabling the estimation of patient-zero probabilities within a small-scale population based on recent contacts and morbidity status. This feature facilitates the identification of hidden transmission pathways and potential future-positive cases, rendering it a valuable tool for epidemiological investigations and epidemic control.
According to our model, stringent lockdown measures effectively curb the spread of the epidemic, whereas relaxed lockdown policies may prove insufficient in this regard. However, it is important to recognize that large-scale lockdowns entail significant costs, and thus, we do not advocate for their widespread adoption as a strategy for future infectious disease control. While extensive qPCR testing and quarantining of positive patients may not yield the desired epidemic control outcomes, expanding the scope of quarantine to include close contacts can yield substantially better prevention results. This observation elucidates why China's targeted-control policy in 2020 and 2021, whereby quarantine measures were implemented for close contacts, was successful in reducing severe cases and fatalities. Our model affirms and acknowledges the effectiveness and feasibility of China's targeted-control policy, while also recognizing its eventual loss of efficacy with increased virus infectivity.
Finally, it is worth noting that various factors, such as specific government policies (Han et al., 2021) and weather patterns (Ganslmeier et al., 2021), exert an influence on the development of the epidemic. In this regard, our agent-based model, which incorporates antibody information, serves as a viable alternative for simulating COVID-19 epidemic scenarios.
Supplementary Materials: Videos 1 to 4 are displayed in supplementary materials. Matlab codes can be accessed at: https://github.com/zhaobinxu23/antibody_dynamics_agent-based_model.
Funding
This research was funded by DeZhou University, grant number 30101418.
CRediT authorship contribution statement
Zhaobin Xu: Conceptualization, Funding acquisition, Methodology, Writing – original draft. Jian Song: Writing – review & editing. Weidong Liu: Methodology. Dongqing Wei: Writing – review & editing.
Declaration of competing interest
All authors declare no conflict of interest.
Acknowledgements
We thank Dr. Zuyi Huang from Villanova University, Qiangcheng Zeng, Zhenlin Wei and Tianxiang Chen from Dezhou University for helpful conversations, comments, and clarifications.
Handling editor: Raluca Eftimie
Footnotes
Peer review under responsibility of KeAi Communications Co., Ltd.
Supplementary data to this article can be found online at https://doi.org/10.1016/j.idm.2023.11.001.
Appendix A. Supplementary data
The following is the Supplementary data to this article:
References
- Afzal A., Saleel C.A., Bhattacharyya S., et al. Merits and limitations of mathematical modeling and computational simulations in mitigation of COVID-19 pandemic: A comprehensive review[J] Archives of Computational Methods in Engineering. 2022;29(2):1311–1337. doi: 10.1007/s11831-021-09634-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alizon S., Sofonea M.T. SARS-CoV-2 virulence evolution: Avirulence theory, immunity and trade-offs[J] Journal of Evolutionary Biology. 2021;34(12):1867–1877. doi: 10.1111/jeb.13896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Banisch S. Springer Verlag; 2016. Markov chain aggregation for agent-based models. [Google Scholar]
- van den Berg S.P.H., Derksen L.Y., Drylewicz J., et al. Quantification of T-cell dynamics during latent cytomegalovirus infection in humans. PLoS Pathogens. 2021;17(12) doi: 10.1371/journal.ppat.1010152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bouchnita A., et al. Projecting Omicron scenarios in the US while tracking population-level immunity. medRxiv. 2023:2023. doi: 10.1016/j.epidem.2024.100746. -08. [DOI] [PubMed] [Google Scholar]
- Chemaitelly H., Tang P., Hasan M.R., et al. Waning of BNT162b2 vaccine protection against SARS-CoV-2 infection in Qatar[J] New England Journal of Medicine. 2021;385(24):e83. doi: 10.1056/NEJMoa2114114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chowell G., Sattenspiel L., Bansal S., et al. Mathematical models to characterize early epidemic growth: A review[J] Physics of Life Reviews. 2016;18:66–97. doi: 10.1016/j.plrev.2016.07.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cohn B.A., Cirillo P.M., Murphy C.C., et al. SARS-CoV-2 vaccine protection and deaths among US veterans during 2021[J] Science. 2022;375(6578):331–336. doi: 10.1126/science.abm0620. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crellen T., Pi L., Davis E.L., et al. Dynamics of SARS-CoV-2 with waning immunity in the UK population[J] Philosophical transactions of the royal society b. 2021;376(1829) doi: 10.1098/rstb.2020.0274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cuevas E. An agent-based model to evaluate the COVID-19 transmission risks in facilities[J] Computers in Biology and Medicine. 2020;121 doi: 10.1016/j.compbiomed.2020.103827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dos Santos I.F.F., Almeida G.M.A., De Moura F. Adaptive SIR model for propagation of SARS-CoV-2 in Brazil[J] Physica A: Statistical Mechanics and Its Applications. 2021;569 doi: 10.1016/j.physa.2021.125773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Folcik V.A., An G.C., Orosz C.G. The basic immune simulator: An agent-based model to study the interactions between innate and adaptive immunity. Theoretical Biology and Medical Modelling. 2007;4(39) doi: 10.1186/1742-4682-4-39. http://www.tbiomed.com/content/4/1/39 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ganslmeier M., Furceri D., Ostry J.D. The impact of weather on COVID-19 pandemic[J] Scientific Reports. 2021;11(1):1–7. doi: 10.1038/s41598-021-01189-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ghosh S., Banerjee M., Volpert V. Immuno-epidemiological model-based prediction of further COVID-19 epidemic outbreaks due to immunity waning[J] Mathematical Modelling of Natural Phenomena. 2022;17:9. [Google Scholar]
- Godio A., Pace F., Vergnano A. SEIR modeling of the Italian epidemic of SARS-CoV-2 using computational swarm intelligence[J] International Journal of Environmental Research and Public Health. 2020;17(10):3535. doi: 10.3390/ijerph17103535. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gorzalski A., Hartley P., Laverdure C., Kerwin H., Tillett R., Verma S., Rossetto C., Morzunov S., van Hooser S., Pandori M.W. Characteristics of viral specimens collected from asymptomatic and fatal cases of COVID-19. J. Biomed. Res. 2020;34:431. doi: 10.7555/JBR.34.20200110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griette Q., Demongeot J., Magal P. A robust phenomenological approach to investigate COVID-19 data for France[J] Mathematics in Applied Sciences and Engineering. 2019:1–12. [Google Scholar]
- Griette Q., Demongeot J., Magal P. What can we learn from COVID-19 data by using epidemic models with unidentified infectious cases?[J] Mathematical Biosciences and Engineering: MBE. 2021;19(1):537–594. doi: 10.3934/mbe.2022025. [DOI] [PubMed] [Google Scholar]
- Han C., Li M., Haihambo N., et al. Mechanisms of recurrent outbreak of COVID-19: A model-based study[J] Nonlinear Dynamics. 2021;106(2):1169–1185. doi: 10.1007/s11071-021-06371-w. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He X., Hong W., Pan X., et al. SARS-CoV-2 omicron variant: Characteristics and prevention[J] MedComm. 2021 doi: 10.1002/mco2.110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinch R., Probert W.J.M., Nurtay A., et al. OpenABM-Covid19—an agent-based model for non-pharmaceutical interventions against COVID-19 including contact tracing[J] PLoS Computational Biology. 2021;17(7) doi: 10.1371/journal.pcbi.1009146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoertel N., Blachier M., Blanco C., et al. A stochastic agent-based model of the SARS-CoV-2 epidemic in France[J] Nature medicine. 2020;26(9):1417–1421. doi: 10.1038/s41591-020-1001-6. [DOI] [PubMed] [Google Scholar]
- Inoue T., Moran I., Shinnakasu R., et al. Generation of memory B cells and their reactivation[J] Immunological Reviews. 2018;283(1):138–149. doi: 10.1111/imr.12640. [DOI] [PubMed] [Google Scholar]
- Kim S.E., Jeong H.S., Yu Y., Shin S.U., Kim S., Oh T.H., Kim U.J., Kang S.-J., Jang H.-C., Jung S.-I. Viral kinetics of SARS-CoV-2 in asymptomatic carriers and presymptomatic patients. International Journal of Infectious Diseases. 2020;95:441–443. doi: 10.1016/j.ijid.2020.04.083. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kohler T.A., Gumerman G.J., Reynolds R.G. Simulating ancient societies. Scientific American. 2005;293(1):77–84. doi: 10.1038/scientificamerican0705-76. [DOI] [PubMed] [Google Scholar]
- Kurosaki T., Kometani K., Ise W. Memory B cells[J] Nature Reviews Immunology. 2015;15(3):149–159. doi: 10.1038/nri3802. [DOI] [PubMed] [Google Scholar]
- Lan F.Y., Filler R., Mathew S., et al. Evolving virulence? Decreasing COVID-19 complications among Massachusetts healthcare workers: A cohort study[J] Pathogens and Global Health. 2021;115(1):4–6. doi: 10.1080/20477724.2020.1847778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liang W.N., Liu M., Liu J., et al. The dynamic COVID-zero strategy on prevention and control of COVID-19 in China[J] Zhonghua Yixue Zazhi. 2022;102(4):239–242. doi: 10.3760/cma.j.cn112137-20211205-02710. [DOI] [PubMed] [Google Scholar]
- Long Y.S., Zhai Z.M., Han L.L., et al. 2020. Quantitative assessment of the role of undocumented infection in the 2019 novel coronavirus (COVID-19) pandemic[J] arXiv preprint arXiv:2003.12028. [Google Scholar]
- Lumley S.F., Wei J., O'Donnell D., et al. The duration, dynamics and determinants of SARS-CoV-2 antibody responses in individual healthcare workers[J] Clinical Infectious Diseases. 2021 doi: 10.1093/cid/ciab004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Macal, CM. Emergent structures from trust relationships in supply chains. In: Macal C, Sallach D and North M (eds). Proceedings of agent 2004: Conference on social dynamics: Interaction, reflexivity and emergence. Argonne National Laboratory: Chicago, IL, 7–9 October, pp 743–760..
- Mishra A.M., Purohit S.D., Owolabi K.M., et al. A nonlinear epidemiological model considering asymptotic and quarantine classes for SARS CoV-2 virus[J] Chaos, Solitons & Fractals. 2020;138 doi: 10.1016/j.chaos.2020.109953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pérez-Alós L., Armenteros J.J.A., Madsen J.R., et al. Modeling of waning immunity after SARS-CoV-2 vaccination and influencing factors[J] Nature Communications. 2022;13(1):1614. doi: 10.1038/s41467-022-29225-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roberto Telles C., Lopes H., Franco D. SARS-COV-2: SIR model limitations and predictive constraints[J] Symmetry. 2021;13(4):676. [Google Scholar]
- Schreiber S.J., Huang S., Jiang J., et al. Extinction and quasi-stationarity for discrete-time, endemic SIS and SIR models[J] SIAM Journal on Applied Mathematics. 2021;81(5):2195–2217. [Google Scholar]
- Tang Y., Xiao D., Zhang W., et al. Dynamics of epidemic models with asymptomatic infection and seasonal succession[J] Mathematical Biosciences and Engineering. 2017;14(5&6):1407. doi: 10.3934/mbe.2017073. [DOI] [PubMed] [Google Scholar]
- Tartof S.Y., Slezak J.M., Fischer H., et al. Effectiveness of mRNA BNT162b2 COVID-19 vaccine up to 6 months in a large integrated health system in the USA: A retrospective cohort study[J] The Lancet. 2021;398(10309):1407–1416. doi: 10.1016/S0140-6736(21)02183-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taylor L. 2022. Covid-19: Omicron drives weekly record high in global infections[J] [DOI] [PubMed] [Google Scholar]
- Tian D., Sun Y., Xu H., et al. The emergence and epidemic characteristics of the highly mutated SARS-CoV-2 Omicron variant[J] Journal of Medical Virology. 2022 doi: 10.1002/jmv.27643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilensky U., Rand W. MIT Press; 2010. An introduction to agent-based modeling modeling natural, social, and engineered complex systems with NetLogo. [Google Scholar]
- Xu Z., Wei D., Zeng Q., et al. More or less deadly? A mathematical model that predicts SARS-CoV-2 evolutionary direction[J] Computers in Biology and Medicine. 2023 doi: 10.1016/j.compbiomed.2022.106510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu Z., Wei D., Zhang H., et al. A novel mathematical model that predicts the protection time of SARS-CoV-2 antibodies[J] Viruses. 2023;15(2):586. doi: 10.3390/v15020586. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xu Z., Zhang H., Huang Z. A continuous markov-chain model for the simulation of COVID-19 epidemic dynamics[J] Biology. 2022;11(2):190. doi: 10.3390/biology11020190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhai Z.M., Long Y.S., Tang M., et al. Optimal inference of the start of COVID-19[J] Physical Review Research. 2021;3(1) [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.