Accelerating Alchemical Free Energy Prediction Using a Multistate Method: Application to Multiple Kinases

Abstract

Alchemical free-energy methods based on molecular dynamics (MD) simulations have become important tools to identify modifications of small organic molecules that improve their protein binding affinity during lead optimization. The routine application of pairwise free-energy methods to rank potential binders from best to worst is impacted by the combinatorial increase in calculations to perform when the number of molecules to assess grows. To address this fundamental limitation, our group has developed replica-exchange enveloping distribution sampling (RE-EDS), a pathway-independent multistate method, enabling the calculation of alchemical free-energy differences between multiple ligands (N > 2) from a single MD simulation. In this work, we apply the method to a set of four kinases with diverse binding pockets and their corresponding inhibitors (42 in total), chosen to showcase the general applicability of RE-EDS in prospective drug design campaigns. We show that for the targets studied, RE-EDS is able to model up to 13 ligands simultaneously with high sampling efficiency, leading to a substantial decrease in computational cost when compared to pairwise methods.

Introduction

Free energy is one of the most fundamental quantities in chemistry. Any spontaneous chemical process (under constant pressure or temperature) is accompanied by a decrease in free energy. In the context of drug design, the properties of a drug candidate must satisfy specific criteria, which can be related to differences in free energy, e.g., binding affinity, selectivity, solubility, and passive membrane permeability.¹ During hit-to-lead optimization, accurate prediction of binding affinities allows prioritization and reduction of the number of compounds to synthesize.^2,3 Approximate methods such as docking have been used for decades to estimate binding affinities,⁴ although they fail to account for entropic contributions,⁵ ligand and/or protein flexibility,⁶ or the role of specific water molecules in binding.⁷⁻⁹ Recent advances in computing power have enabled the routine application of rigorous free-energy methods based on molecular dynamics (MD) simulations such as free-energy perturbation (FEP)¹⁰ in both academic and industrial settings.^11,12

While calculating the physical binding pathway of an inhibitor is possible,^14,15 it is computationally more feasible to estimate relative binding free energies (RBFE)¹⁶ by performing “alchemical” transformations between analogous inhibitors (Figure 1 and eq 1)

1

Figure 1.

Thermodynamic cycle to estimate the relative binding free energy between inhibitors A and B. Simulating the alchemical pathway (bold black arrows) is computationally more feasible than the physical pathway (gray arrows). The relative binding free energy is obtained with eq 1. Figure inspired by Aldeghi et al.¹³

The main drawback of such pairwise methods is that the number of calculations to perform grows quadratically (at most) with the number of compounds to be screened,^17,18 as accuracy relies on the simulation of many of the (ⁿ₂) possible pairwise combinations (see discussion in Results and Discussion below).¹⁹ To limit this combinatorial problem in practice, automated workflows have been developed to estimate the smallest and/or most efficient perturbation map for a given set of ligands.¹⁹⁻²² Despite these efforts, finding a general solution is no trivial task and remains an open question.^19,23,24 In this context, simulating many such alchemical transformations from the same MD simulation would thus significantly decrease the computational costs of the free-energy method, further improving their applicability in the drug design process.

The existing multistate free-energy methods can be grouped into three main families. The first set of methods is based on λ-dynamics,²⁵⁻²⁸ the second group is based on enveloping distribution sampling (EDS),^29,30 and the third class is based on “single-step” perturbation.³¹⁻³³ The latter is typically restricted to systems with a good phase space overlap. In the first method, the system follows well-defined pathways to transition from state to state, whereas no such constraints are imposed in EDS (i.e., it is “pathway independent”), which may provide additional flexibility for sampling. Transitions in alchemical space may be accelerated by coupling these methods to enhanced sampling algorithms, enabling a more rapid convergence of the free-energy differences. λ-dynamics based methods have been combined with the tailor-made adaptive landscape flattening algorithm,³⁴ while EDS has been combined with well-established algorithms, giving rise to replica-exchange EDS (RE-EDS)³⁵⁻³⁹ and accelerated EDS.^40,41 In this work, we aim to showcase the transferability of the RE-EDS method to multiple protein targets with distinct binding pockets. To that end, we have constructed a data set of inhibitors for four different kinases, containing a wide range of chemical functional groups and scaffolds.

The kinase family of enzymes catalyzes the phosphorylation of proteins, contributing to the mediation of a wide range of critical biological processes such as metabolism, transcription, cytoskeletal rearrangement, apoptosis, and intercellular communication.⁴² Deregulation of kinase function has been linked to various diseases such as autoimmune, cardiovascular, inflammatory, and nervous diseases as well as cancer.^43,44 Over the past 20 years, drug discovery programs have focused heavily on developing inhibitors targeting kinases, accounting for a significant part (20–33%) of drug discovery efforts worldwide.⁴⁵ While 68 FDA-approved drugs targeting more than 20 kinases already exist, research in the field remains very active, highlighted by the large number of additional compounds currently undergoing clinical trials.⁴⁶ In this work, we have applied the RE-EDS method to a series of inhibitors of the following four kinases: checkpoint kinase 1 (CHK1),⁴⁷ NF-κB inducing kinase (NIK),⁴⁸ p21-activated kinase 1 (PAK),⁴⁹ and the proviral insertion in murine lymphoma kinase 1 (PIM).⁵⁰ All four enzymes belong to the most common subclass of serine/threonine kinases.⁴⁵ All inhibitors examined in this work (Figure 3) bind in the hinge region connecting the terminal N- and C-lobes, in competition with the natural adenosine triphosphate (ATP) cofactor.⁵¹

Figure 3.

Four kinases and the set of inhibitors used in this study. For CHK1, PIM, PAK, and NIK, the core is shown together with the different substituents and the corresponding label. For CHK1, we studied two subsets separately, indicated by dashed lines. Molecules C.4 and C.5 are part of both subsets.

In summary, the main objective of this work is to demonstrate the transferability of the RE-EDS method to multiple protein targets with distinct binding pockets, highlighting it as a viable and computationally less demanding alternative to conventional pairwise free-energy calculations. We present methodological improvements that enable us to expand both the scope and number of alchemical perturbations that can be performed in a single RE-EDS simulation, further showcasing its suitability to calculate RBFE in prospective drug design campaigns. All simulations in this work were performed with two small-molecule force fields (GAFF⁵² and OpenFF⁵³), which allows us to discern deviations stemming from lack of sampling and from force-field inaccuracies. Note that we have studied a subset of the inhibitors of CHK1 (subset a) with RE-EDS and the GROMOS force field in our previous work.⁵⁴ We discuss the current limitations of RE-EDS and compare them to other state-of-the-art free-energy methods. While our study focuses on biologically relevant kinases, RE-EDS can of course also be applied to other protein families as well as solvation free energies (ΔG_solv) of small organic molecules,^38,39 or to investigate water thermodynamics in binding pockets.⁵⁵

Theory

RBFE calculations involve the simulation of the alchemical transformation of a molecule into another and the adaptation of the environment in which this alteration is taking place (e.g., protein binding pocket). State-of-the-art pairwise free-energy methods introduce a coupling parameter λ to connect end states together. Independent simulations are then carried out at discrete λ-points along the path connecting the two end states, and free-energy differences can be obtained using the Zwanzig equation,¹⁰ thermodynamic integration,⁵⁶ or MBAR estimator.^57,58

Replica-Exchange Enveloping Distribution Sampling

In EDS, the different end states are connected in a reference state R with the form^29,30

2

where 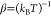, s is the smoothing parameter, and E_i is the energy offset for each end state i. The force acting on a particle k is calculated by using eq 3, which is simply a weighted contribution of the forces exerted by all end states (eq 4). Note that the calculation of the reference potential (eq 2) requires N energy evaluations (one for each end state) per step, while the interactions between the unperturbed particles in the system have to be calculated only once if a strictly pairwise decomposable approach like reaction field^59,60 is used for the long-range electrostatic interactions

3

4

Essentially, forces will be largest for the end state for which the current conformation is most compatible, and forces exerted by states in unfavorable conformations (e.g., overlap with the protein or solvent molecules) are scaled to approximately zero, without requiring soft-core potentials.^34,61 This reference potential-energy surface “envelops” the potential-energy surfaces of all end states, ensuring that all minima of the individual end states are minima of the reference state (Figure 2A). In order to sample the minima corresponding to all end states in a reasonable amount of simulation time, two parameters were introduced to the EDS reference state:³⁰ the energy offsets (E_i), which enable equal sampling of all end states, and the smoothness parameter (s), which reduces energy barriers to enhance transitions. Finding appropriate reference-state parameters is not trivial, as the ideal energy offsets (at s = 1, assuming infinite simulation) correspond to the free-energy differences we seek to calculate.⁶² Similarly, the s-values alter the shape of the reference potential-energy surface and need to be chosen carefully.^62,63 Excessive reduction of the s parameter leads to a distortion of the reference potential-energy surface such that its minima no longer map to minima corresponding to physical conformations for any of the end states. We denote this unphysical regime “undersampling” (yellow curve in Figure 2B).⁶³

Figure 2.

(A) “Enveloping” nature of the reference potential V_R (in dark gray), which encloses the minima of the potential-energy surfaces of three small molecules (colored dashed curves). If no energy offsets or s-values are used to scale minima or barrier heights, transitions between states C and B are unlikely (indicated with a red cross). (B) Effect of lowering the s-value on a reference potential V_R (all colored lines), with energy offsets chosen such that all minima are aligned at s = 1. Gray areas indicate regions of phase space that are sampled, and black dots and arrows represent possible replica exchanges in RE-EDS.

In RE-EDS,³⁵⁻³⁷ multiple EDS simulations with different s-values are carried out in parallel, and exchange trials are performed between neighboring replicas every few steps. All sets of conformations (starting at distinct s-values) are thus able to “visit” replicas at lower s-values that enable transitions between end states, as well as higher s-values where physically meaningful conformations are sampled. Free-energy differences between all pairwise combinations of end states i and j can then be recovered by employing the Zwanzig equation (eq 5) from the simulation data gathered at s = 1, or more optimally by combining data from all replicas with MBAR.⁵⁸ Coupling EDS to replica exchange was found to simplify the choice of appropriate s parameters,³⁶ and affords enhanced transitions between the states

5

Obtaining accurate free-energy differences thus relies on the ability to sample conformations relevant to all end states in the simulation at s = 1. Doing so is crucially dependent on the energy offsets and s-parameters, which are determined prior to the production run. Ries et al.³⁷ have recently proposed an improved automated workflow to optimize these parameters. The pipeline is discussed in more detail in the Methods Section.

Methods

Data Sets

The main focus of this work is to demonstrate the transferability of the RE-EDS methodology to different protein targets as well as its capability to simulate a wide range of distinct chemical perturbations. Increasingly complex sets of inhibitors were chosen to showcase the generality of RE-EDS. Details of the assay conditions and crystal structure preparation are given for the different targets in the respective publications (NIK,^64,65 PAK,^66,67 PIM,⁶⁸ CHK1⁶⁹).

We built sets of congeneric inhibitors for each target, with at least one crystal structure of the inhibitor–protein complex available, which could be used as the starting structure. We also followed guidelines by Mey et al.⁷⁰ in the construction of the data sets to avoid known sources of error in free-energy calculations (e.g., small spread of experimental binding affinities, inhibitors with multiple protonation/tautomeric state at pH 7, unknown stereoisomer in the experimental assay, etc.). For backward comparison, we simulated the same set of CHK1 inhibitors from our previous work (Ries et al.³⁷), and in addition constructed a larger set of 13 ligands from the same experimental data.⁶⁹ The four kinases and the selected inhibitors are shown in Figure 3.

Topology Preparation and Parameterization

All initial topologies were prepared with the AmberTools⁷¹ suite of programs. Unresolved residues in the crystal structure were added using SWISS-MODEL,⁷² and buried water molecules (if any) were retained. Solvent molecules were added, ensuring a minimum distance of 1.2 nm between solute atoms and the edge of the box. All protein parameters were taken from the AMBER ff14SB force field,⁷³ and the TIP3P water model was used.⁷⁴ The inhibitors were modeled with two different small-molecule force fields using AM1-BCC⁷⁵ charges: the general AMBER force field (GAFF) 1.8,⁵² and the Open Force Field (OpenFF) version 2 (“Sage”).^53,76 Topologies with both force fields, as well as initial coordinates, were generated in the AMBER format and then translated into the GROMOS format using the amber2gromos program.³⁸

Alchemical free-energy calculations may be performed with different representations of the perturbed region. We chose to represent this region with a “hybrid topology”,^77,78 where common core atoms between inhibitors are represented once, and all varying substituents are represented separately. We opted for this representation to avoid hindering any motion of the common core with distance restraints (known to introduce some biases or cause slow convergence^79,80), which are necessary to keep ligands overlaid with one another in RE-EDS simulations with the “dual topology” representation.^37,78 Note that the same atom may have a different partial charge (and Lennard-Jones parameters) according to the various end states in the hybrid topology representation. This allows to take into account electron withdrawing (or donating) effects of a perturbed group on the core region while maintaining an integer net charge for each ligand, and without requiring any charge renormalization protocol as in some λ-dynamics implementations.⁸¹

Hybrid topologies were generated by combining the topologies of the individual inhibitors using the RDKit⁸² and PyGromosTools⁸³ to select an appropriate core structure with a maximum common substructure (MCS) search and adding the different substituent atoms and parameters (bonded and nonbonded) to the initial topology. An example Jupyter notebook to build such a hybrid topology can be found in the GitHub repository (https://github.com/rinikerlab/reeds/blob/main/examples/input_preparation/hybrid_topology_maker.ipynb). For the NIK data set, additional calculations using a dual topology representation (as in our previous work³⁷) were investigated for comparison, imposing weak harmonic distance restraints (k_restraint = 5000 kJ mol^–1 nm^–2) between selected core atoms of each inhibitor to prevent drifts (see Figure S3 in the Supporting Information). All results obtained with RE-EDS discussed in this work correspond to those using hybrid topologies, unless explicitly labeled. The starting coordinates for the hybrid topologies were built by taking protein coordinates from a reference crystal structure and ligand coordinates from prealigned crystal structures if available (PAK, NIK), or by generating coordinates for the substituents using the constrained embedding functionality in the RDKit (CHK1, PIM).

Simulation Details

All simulations were performed using the GROMOS software package.⁸⁴ The program is freely available on www.gromos.net. The simulations were propagated using a leapfrog algorithm with an integration time step of 2 fs. All bond lengths were constrained with the SHAKE algorithm⁸⁵ and a relative tolerance of 10^–4. Nonbonded interactions were calculated up to an atomic cutoff of 1 nm (the pair list was updated every step), and electrostatic contributions beyond the cutoff were modeled by a reaction field⁶⁰ with a relative permittivity ε_RF = 66.7.⁸⁶ The simulations were carried out in the NpT thermodynamic ensemble by maintaining a temperature of 298 K and a pressure of 0.06102 kJ mol^–1 nm^–3 (≈1 atm) with a Berendsen thermostat and barostat, respectively.⁸⁷ The translational and rotational motions of the center of mass of the box were removed every 1000 steps. Energies and coordinates of the system were recorded every 1000 steps (2 ps).

RE-EDS Simulations

RE-EDS simulations were performed using the pipeline introduced by Ries et al.^37,54 (Figure 4). In the following sections, we briefly describe each step of the RE-EDS pipeline. The complete set of simulation details (lengths, initial conformations given, number of parameter optimization iterations, etc.) is given in Section S2 of the Supporting Information.

Figure 4.

Schematic overview of the steps to calculate free-energy differences with RE-EDS. The steps during the parameter estimation and optimization phases are needed to acquire information about the system to improve the s-values (circled in yellow) or the energy offsets (circled in blue).

First, starting coordinates have to be generated where the environment (solvent, protein) is well adapted for each of the end states. Starting from optimized coordinates was shown to improve the accuracy of RE-EDS calculations,⁷⁸ in particular when an experimental crystal structure is not available for all end states. This procedure, termed “end-state generation”, consists of N-independent EDS simulations in which energy offsets are chosen to enforce sampling of one specific end state. The lowest energy conformation in each of these simulations is then used as an input for all subsequent RE-EDS simulations (“starting state mixing”, SSM). In parallel, the lower-bound search consists of very short EDS simulations performed at different s-values to determine when the system reaches undersampling. Then, a first guess for the energy offsets is estimated from free-energy differences in the undersampling regime (eq 5) of an RE-EDS simulation with default parameters (i.e., E_i = 0, logarithmically distributed s-parameters between 1.0 and the lower bound). Typically, a gap region with low exchange frequencies is observed during this step (see Figure S1 in the Supporting Information), which can be crudely filled prior to the optimization phase, making the latter more efficient (see details in Supporting Information Section S2).

Subsequently, the distribution of s-values and energy offsets are further optimized in an iterative process, until specific criteria are met: no replica-exchange bottlenecks and approximately equal sampling of all end states at s = 1. Each iteration consists of a short RE-EDS simulation from which exchange probabilities or sampling distributions are extracted to guide the update of RE-EDS parameters. The parameters can be refined separately one after the other as proposed by Ries et al.³⁷ (e.g., s-optimization followed by energy-offset optimization), or may be updated simultaneously (“mixed optimization” as described in this study). Optimization of the s-distribution may be achieved by either adding replicas in regions of s-space with low exchange rates based on local criteria (N-LRTO algorithm³⁶) or by redistributing the replicas in s-space to maximize the replica-exchange probability over the entire range of s-values (N-GRTO algorithm³⁶). Note that the N-GRTO algorithm could also be used to add replicas, but this was not done in this study. If there are already some transitions between all replicas with the initial s-distribution, the N-GRTO algorithm is more robust and often requires fewer replicas than N-LRTO. The latter algorithm was developed mainly for cases with severe exchange bottlenecks, where N-GRTO fails. Optimization of the energy offsets is accomplished with the “energy-offset rebalancing” approach,³⁷ which updates the energy offsets based on the current sampling of each end state (at s = 1). Sampling is determined with the “maximally contributing”³⁷ criterion, which assigns the current frame to the end state which contributes most to the forces (largest w_i in eqs 3 and 4). Finally, the RE-EDS production phase is carried out with the parameters obtained, and the final free-energy differences are extracted from the simulation at s = 1 (or all s-values when using MBAR).

Replica-exchange trials were carried out every 50 steps. After the parameter optimization phase, production runs of 5 ns were performed, of which the first 1 ns was discarded as equilibration. Five replicates with different initial velocities were performed, from which average values were obtained and standard deviations were used to represent statistical uncertainty.^88,89 To calculate the final free-energy differences, the data acquired at all s-values were incorporated using the MBAR procedure.⁵⁸ For this, the values of the reference potential energy of each replica need to be re-evaluated with the reference potential parameters (s-values and/or energy offsets) of all other replicas, allowing us to optimally connect all thermodynamic states together. This re-evaluation can be simply done as a postprocessing step. Free-energy differences with respect to the reference state at s = 1 (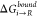 and 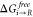) are then passed into eq 6.

TI Simulations

For the NIK data set, we performed additional TI calculations for comparison. Here, only OpenFF was tested. TI calculations were performed using 21 evenly spaced λ-values between 0 and 1. Five replicates with different initial velocities were performed for 5 ns at each λ-value. Hamiltonian replica-exchange trials were performed every 50 steps between neighboring λ-values to enhance sampling.⁹⁰

Comparison to Experiment

All simulated RBFE values were compared to experimental values (K_i or IC₅₀) by first converting them to absolute binding free energies (ABFE) based on the known experimental binding free energies of the N inhibitors (eq 6), following the procedure introduced by Wang et al¹⁷

6

We noted that this conversion, which is simply a shift with respect to average values, does not alter the interpretation of the results in a prospective study (experimental affinities unknown) as the ranking of inhibitors and the differences among them remain identical. All experimental values can be found in Section S1 in the Supporting Information.

We also followed recommendations from Mey et al.⁷⁰ to perform a bootstrapping analysis. This was performed by drawing new simulated binding free energies from normal distributions with standard deviations equal to those obtained from the five repeats that started with different velocities. Note that the alignment with respect to the experimental values was not repeated after adding noise to the data based on the observed errors.

We calculated both the mean unsigned error (MUE) and correlation metrics for the ABFE values obtained using the scheme described above as well as the root-mean-squared error (RMSE) of the RBFE values (including all possible pairwise relative differences). Since the error metrics depend on the range of experimental values included, we also provide a reference “null model” where each prediction is equal to the mean of the experimental data set.

Results and Discussion

First, we present the modifications made to the RE-EDS pipeline and discuss the resulting gains in efficiency. Second, we examine the binding free energies calculated with RE-EDS for each data set and explain observed deviations. Subsequently, we discuss our results more generally, with an emphasis on the differences between the inhibitors/binding pockets studied and how these relate to differences in the RE-EDS simulations. Finally, we compare the cumulative simulation time with state-of-the-art methods and discuss future improvements expected to amplify the gains in computational cost provided by RE-EDS.

Improvements to the RE-EDS Pipeline

In this work, we build upon the pipeline described by Ries et al.³⁷ to set up the system and optimize the reference-state parameters (Figure 4). Modifications to the workflow are proposed, which allowed us to fine-tune and shorten the parameter optimization phase. First, we take advantage of the information regarding exchanges (or lack thereof) between replicas during the energy offset estimation step to preoptimize the s-distribution. Typically, the default logarithmic s-distribution contains a “gap region” where the replica-exchange probability is low (see Figure S1 in the Supporting Information), especially for simulations with the ligands in the protein binding pocket. Previously,^36,37 this problem was tackled using the N-LRTO algorithm to add replicas in the exchange bottleneck region until sufficient exchanges were obtained. By using the information about the location of the gap region from the energy offset estimation step and placing a large number of s-values in this gap region (uniformly on a log scale) prior to the s-optimization step, we were able to bridge the gap sufficiently to directly use the N-GRTO algorithm to optimize the s-distribution. We found that adding replicas in the gap region to reach a total of 32 replicas worked well for all systems studied here (details in Supporting Information Section S2). This hyperparameter is analogous to the number of λ-values in FEP/TI simulations (often 21 values).

We found that the optimal set of energy offsets may depend on the current s-distribution. As a result of this coupling of parameters, an optimized set of parameters (e.g., energy offsets) may require reoptimization upon changes to the other parameters (e.g., s-values). To facilitate the optimization of connected parameters, we explored the adjustment of both sets simultaneously (termed “mixed optimization”). This is particularly important if the initial guess for energy offsets leads to preferential sampling of only one end state, which we observed in one of our simulations (Figure 5). In this example, we noticed that the s-distribution changed significantly between iterations 1 and 3 where ligand C.11 is predominantly sampled and shifted again when the updated energy offsets led to more equal sampling of the end states between iterations 3 and 6. More generally, we found that the s-distribution converges close to an ideal solution within a few iterations (2 or 3, see Figure S2 in the Supporting Information), and the remaining iterations mostly involve fine-tuning the energy offsets. This suggests that applying the N-GRTO algorithm to an optimal s-distribution does not further modify it, supporting the robustness of the mixed optimization protocol.

Figure 5.

Mixed optimization of the RE-EDS parameters for the CHK1 data set (ligands in water) with the GAFF. (Upper left): Average number of round trips made by all replicas. The error bars correspond to the standard deviations among the replicas. Sampling of the end states in the uppermost replica (s = 1). (Right): Distribution of the replicas in s-space.

In summary, we recommend optimization of the parameters via a mixed optimization protocol. In this work, the parameter optimization phase typically represents around 20% of the total simulation time (see the discussion below). Note that the 500 ps used for each iteration was chosen based on our experience from previous simulations.^36,37 The procedure in its current form may still be further refined, which will be part of future work. Faster convergence toward optimal parameters may for example be obtained by performing an initial set of short optimization steps, followed by longer iterations to fine-tune the parameters.²⁷

Binding Free Energies for the Kinase Inhibitors

To start, we will present our results for the NIK data set which was evaluated using both a dual topology (as used in our previous work^36,37,63) and a hybrid topology (more suitable for R group modifications). The three other kinases will be discussed in the order of increasing complexity in terms of the magnitude and number of alchemical perturbations as well as the flexibility of the binding site.

NF-κB Inducing Kinase (NIK)

The NIK data set displays the greatest variety in structural modifications among the inhibitors with ring opening (e.g., ligand N.1 compared to the others), a fusion of rings (e.g., N.1, N.3, N.4, and N.6), and a second site of modification (e.g., N.4 and N.6), adding different layers of complexity.

In the case of NIK, the results obtained with GAFF are within the margin of error with an MUE of 3.8 kJ mol^–1, in contrast to OpenFF with an MUE of 7.7 kJ mol^–1 (Figure 6 and Table 1). The largest deviation compared to the experiment with OpenFF was found for ligand N.1 (15.3 kJ mol^–1). Supporting these observations, the ranking correlation metrics are better for GAFF with a Spearman ρ of 0.6 and Kendall τ of 0.4 compared to 0.0 and 0.1, respectively, with OpenFF (using also a dual topology). Detailed analysis pointed to insufficient sampling of the protein reorganization as the main source of error. First, we analyzed the binding poses of the six different ligands based on the crystal structures and identified the key interactions between the protein and ligand. In all six crystal structures, the catalytically important DFG activation loops are well aligned (Figure S5 in the Supporting Information), indicating that the inhibitors interact in a fashion similar to that part of the binding pocket. On the other hand, the Arg410 side chain adopts various conformations in the crystal structures, some with and some without a hydrogen bond with either the ligand, Glu475, or Leu474. In the RE-EDS simulations, we find three key conformations of the protein with respect to Arg410, which we denote “open”, “closed 1″, and “closed 2” (Figure 7). The system adopted an open or closed conformation approximately 50% of the time with both GAFF and OpenFF. However, the “closed 2” form in which Arg410 interacts with Leu474 as well as the ligand occurs more prominently in the simulations with OpenFF (Figure 7D), which may explain the differences between the two force fields. As the crystal structures vary among the different inhibitors, it is not trivial to interpret them, but there is no evidence for the presence of this “closed 2” form (Figure S5).

Figure 6.

Results obtained for the NIK data set: Comparison of the calculated and experimental binding free energies. Dark and light-gray regions correspond to margins of error of 1 and 2 kcal mol^–1, respectively. Error bars correspond to standard deviations over the five random seeds. (A) Results from RE-EDS simulations with dual topologies were obtained with the GAFF (purple) and OpenFF (blue), and reference H-RE TI calculations (orange) were performed for comparison with those with OpenFF. (B) Comparison of the results of RE-EDS simulations with the OpenFF (blue) using dual and hybrid topologies.

Table 1. Statistical Metrics Used to Evaluate the Accuracy of Binding Free Energies Calculated for the NIK Data Set^a.

method	simulation	MUE [kJ mol–1]	RMSE [kJ mol–1]	Kendall τ	Spearman ρ
RE-EDS	GAFF (dual)	3.8 [3.64–4.04]	7.3 [6.92–7.72]	0.4 [0.36–0.47]	0.6 [0.56–0.69]
RE-EDS	OpenFF (dual)	7.7 [7.59–7.93]	14.3 [14.11–14.53]	0.0 [-0.03–0.03]	0.1 [0.10–0.19]
RE-EDS	OpenFF (hybrid)	7.0 [6.90–7.19]	13.1 [12.83–13.34]	0.1 [0.06–0.10]	0.3 [0.26–0.28]
H-RE TI	OpenFF (dual)	5.3 [5.14–5.48]	10.6 [10.33–10.91]	0.1 [0.06–0.15]	0.2 [0.13–0.25]
null model		6.0	10.1	0	0

^aMUE and correlation metrics (τ and ρ) relate to absolute binding free energies, whereas RMSE corresponds to all pairwise relative binding free energies. Numbers reported correspond to the mean, with upper and lower bounds of the 95% confidence interval in square brackets.

Figure 7.

(A–C) Three key conformations of Arg410 are seen in the simulations of the protein binding to ligand N.1. (D) Distributions of the distance between Arg410 and Glu475 (left) and between Arg410 and Leu474 (right) from the combined trajectories (five repeats concatenated). Blue and purple lines correspond to simulations with OpenFF and GAFF, respectively.

To further investigate whether force-field deficiencies or sampling are the main causes of deviations, we performed H-RE TI simulations with the same force field (OpenFF). We found overall good agreement with the RE-EDS results (Figure 6A), but a lower MUE of 5.3 kJ mol^–1 compared to the experiment. We note that the binding affinity of the largest outlier in the RE-EDS simulations (N.1) is also predicted poorly by H-RE TI, and the increased accuracy mainly stems from slightly better predictions for other ligands (N.2, N.3, N.4, and N.6). This suggests that incomplete sampling in the simulations with OpenFF may at least be partially responsible for the deviations observed. In agreement with our previous analysis, we find that the Arg410 side chain position in the H-RE TI calculations varied for the different ligands (Figure S7 in the Supporting Information), suggesting that this degree of freedom may indeed be the source of part of the observed deviations in both RE-EDS and H-RE TI simulations.

The sampling issues may also be related to the motion slower than the trajectory, which is supported by observations from Shih et al.,⁹¹ who reported that FEP+ results for inhibitors of the NIK kinase may differ by up to 8.4 kJ mol^–1 when using a starting structure prepared with a different workflow to model the missing loop residues. Finally, we note that the simulations with a hybrid topology perform slightly better than those with a dual topology representation (Table 1 and Figure 6B). This result may be explained by the larger number of round trips observed in the simulations with a hybrid topology (∼5.6 round trips per ns) than with dual topology (∼2.3 round trips per ns), thus favoring transitions between states.

Consequently, we recommend the use of the hybrid topology representation for binding free-energy calculations of ligands with a common core due to the advantages this confers (e.g., no hindering of motion with distance restraints),^77,78 as shown below for the other data sets.

p21-Activated Kinase 1 (PAK)

The PAK data set was constructed to highlight the transformations of five-membered and six-membered aromatic and nonaromatic heterocycles as might be explored in lead optimization. Note that the substituent modified here is in the buried region of the binding pocket, which is generally considered to be more challenging to simulate, as the rearrangement of the protein pocket may be slow on the simulation time scale. However, all functional groups occupy a very similar volume and all ligands form the same key hydrogen bond between the carbonyl group oxygen of the modified substituent and Lys299 (Figure 8B). Overall, the binding free energies obtained with GAFF and OpenFF are in good agreement with experimental values, with a MUE of 1.9 and 2.8 kJ mol^–1, respectively (Table 2), and all but one data point lie within the chemical accuracy limit⁷⁰ of 1 kcal mol^–1 (=4.184 kJ mol^–1) (Figure 8A). While the MUE is higher for OpenFF than for GAFF, the ranking of the ligands (Spearman ρ and Kendall τ) is more accurate with OpenFF. We note that the RMSE values are generally higher than MUE values but follow the same trend, which we observe for all data sets in this study.

Figure 8.

Results obtained for the PAK data set. (A) Comparison of calculated and experimental binding free energies obtained with GAFF (purple) and OpenFF (blue) with hybrid topologies. Dark- and light-gray regions correspond to margins of error of 1 and 2 kcal mol^–1, respectively. Error bars correspond to standard deviations over the five random seeds. (B) Binding pose of the RE-EDS system in a conformation favorable for ligand K.1. The core and perturbed functional group for ligand K.1 are shown in black, whereas the nonsampled states are shown in light gray. The side chain of Lys299 is shown as dark-green sticks. (C,D) Time series of the dihedral angle between the core and the perturbed substituent of ligand K.1 in the simulations with GAFF (purple, C) and OpenFF (blue, D). Gray points correspond to the dihedral angle at all time steps, whereas colored points correspond to frames where ligand K.1 is actively sampled in the reference state. (E) Probability distribution of the distance between the carbonyl oxygen of ligand K.1 and the terminal nitrogen atom of Lys299 from frames in which ligand K.1 is actively sampled. The gray region corresponds to distances compatible with the presence of the stabilizing hydrogen bond.

Table 2. Statistical Metrics Used to Evaluate the Accuracy of Binding Free Energies Calculated for the PAK Data Set^a.

force field	MUE [kJ mol–1]	RMSE [kJ mol–1]	Kendall τ	Spearman ρ
GAFF	1.9 [1.80–2.01]	3.3 [3.14–3.50]	0.4 [0.33–0.46]	0.5 [0.45–0.60]
OpenFF	2.8 [2.66–2.89]	5.8 [5.62–6.00]	0.6 [0.57–0.65]	0.7 [0.71–0.76]
null model	2.1	3.7	0	0

^aMUE and correlation metrics (τ and ρ) relate to absolute binding free energies, whereas RMSE corresponds to all pairwise relative binding free energies. Numbers reported correspond to the mean, with upper and lower bounds of the 95% confidence interval in square brackets.

The largest deviation compared to the experiment was observed for ligand K.1 with OpenFF. Inspection of the rotation around the bond connecting the modified substituent and the core in the simulations with GAFF and OpenFF (Figure 8C,D) showed some differences in dihedral-angle sampling between the force fields, which led to small differences for adopting the key hydrogen bond with Lys299 (Figure 8E), which occurs when the dihedral angle is around 120°. Although the hydrogen bond was present in both simulations, the population differences may explain the larger deviation of ΔG_bind with OpenFF. This finding highlights the importance of accurate torsion parameters for binding free-energy calculations.

Checkpoint Kinase 1 (CHK1)

The CHK1 data set consists of two subsets of 5 and 13 ligands, respectively. The first subset of five ligands is the same as studied by Wang et al.⁹² with FEP+, Jespers et al.²¹ with QligFEP, and Ries et al.³⁷ with RE-EDS in combination with the GROMOS force field. The five ligands include challenging ring growth and ring opening modifications. The second subset was prepared from the same set of published experimental values,⁶⁹ choosing molecules for which the experimental IC₅₀ values were spread over a broader range. This second subset focuses on the alchemical modifications of aromatic rings (five-membered, six-membered, and fused rings).

The results for the smaller subset are very good with MUE values of 1.7 and 1.5 kJ mol^–1 for GAFF and OpenFF, respectively (Figure 9 and Table 3), which is lower than the previous results obtained with GROMOS force-field parameters (MUE of 2.2 kJ mol^–1). This confirms the hypothesis that deviations seen in Ries et al. can be attributed mostly to force-field parameterization (done manually based on similar molecules). These results are also very similar to those obtained for the same system with other methods (FEP+⁹² and QligFEP²¹) (Figure S8 in the Supporting Information). Note that the standard deviations in the RE-EDS simulations with GAFF and OpenFF are generally smaller than those observed with FEP+ and QligFEP as not all possible pairwise transformations were simulated with the latter methods.

Figure 9.

Results obtained for the CHK1 data sets. (A) Comparison of calculated and experimental binding free energies for the smaller subset with five inhibitors. Dark- and light-gray regions correspond to margins of error of 1 and 2 kcal mol^–1, respectively. Error bars correspond to standard deviations over the five random seeds. Results are shown with GAFF (purple) and OpenFF (blue) with hybrid topologies, as well as results taken from Ries et al.⁵⁴ performed with the GROMOS force field and dual topology (green) for comparison. Additional comparisons to other state-of-the-art methods can be found in Figure S8 in the Supporting Information. (B) Results obtained for the larger subset of 13 inhibitors (hybrid topologies).

Table 3. Statistical Metrics Used to Evaluate the Accuracy of Binding Free Energies Calculated for the CHK1 Data Sets^a.

simulation	MUE [kJ mol–1]	RMSE [kJ mol–1]	Kendall τ	Spearman ρ
GAFF (subset 1)	1.7 [1.61–1.78]	3.1 [2.93–3.27]	0.3 [0.27–0.38]	0.5 [0.36–0.55]
OpenFF (subset 1)	1.5 [1.39–1.67]	2.7 [2.44–2.90]	0.5 [0.39–0.52]	0.7 [0.60–0.71]
GROMOS FF (subset 1)	2.2 [2.16–2.30]	4.1 [4.03–4.23]	0.3 [0.20–0.39]	0.4 [0.30–0.49]
null model (subset 1)	1.5	2.8	0	0
GAFF (subset 2)	4.2 [4.16–4.24]	7.4 [7.29–7.45]	0.3 [0.31–0.34]	0.5 [0.47–0.51]
OpenFF (subset 2)	3.7 [3.69–3.78]	6.8 [6.69–6.88]	0.5 [0.52–0.56]	0.7 [0.67–0.71]
null model (subset 2)	4.8	8.6	0	0

^aMUE and correlation metrics (τ and ρ) relate to absolute binding free energies, whereas RMSE corresponds to all pairwise relative binding free energies. Numbers reported correspond to the mean, with upper and lower bounds of the 95% confidence interval in square brackets. Errors used to perform the bootstrapping analysis correspond to standard deviations over the five random seeds, with the exception of simulations with the GROMOS force field where they had been estimated using Gaussian error approximation.⁵⁴ The MUE and RMSE values presented here do not match exactly those reported in ref (54) due to the different re-centering procedures to obtain MUE values and different error propagation.

Results for the subset of 13 ligands show overall good performance and demonstrate that more ligands can be included in the same RE-EDS simulation. For both force fields, we find average errors below the margin of error (1 kcal mol^–1) and the correlation coefficients show a reasonable ranking of the ligands (Table 3). All metrics indicate OpenFF performing slightly better for these data sets. Most of the remaining deviations can likely be attributed to the force field, as the sampling of all end states is almost uniform (Figure S9 in the Supporting Information). Sampling is facilitated in this system by the modified substituent being solvent-exposed. As rearrangement of water molecules occurs on a faster time scale than rearrangement of protein side chains or loops, the transition between the end states should be easier.

Proviral Insertion in Murine Lymphoma Kinase 1 (PIM)

The PIM data set was constructed to further validate the ability of RE-EDS to simulate more than 10 alchemical modifications of five- and six-membered rings with potentially bulky substituents (e.g., –CN in M.3, and –CF₃ in M.4). In general, the 13 ligands were sampled well in all simulations (except one, see discussion below), while the resulting binding free energies show overall a slightly larger deviation from experimental values compared to the CHK1 data set (Table 4). Akin to the PAK data set, we find that the MUE indicates a (slightly) better performance of GAFF (4.6 kJ mol^–1) over OpenFF (4.9 kJ mol^–1), while the correlation metrics are better for OpenFF (e.g., ρ = 0.5 compared to 0.3 with GAFF), showing that the ligands were ranked more accurately despite being further away from experimental reference values.

Table 4. Statistical Metrics Used to Evaluate the Accuracy of Binding Free Energies Calculated for the PIM Data Set^a.

simulation	MUE [kJ mol–1]	RMSE [kJ mol–1]	Kendall τ	Spearman ρ
GAFF	4.6 [4.56–4.71]	8.5 [8.38–8.69]	0.2 [0.15–0.17]	0.3 [0.24–0.27]
OpenFF	4.9 [4.83–4.94]	8.6 [8.55–8.72]	0.3 [0.28–0.30]	0.5 [0.43–0.46]
null model	3.0	5.3	0	0

^aMUE and correlation metrics (τ and ρ) relate to absolute binding free energies, whereas RMSE corresponds to all pairwise relative binding free energies. Numbers reported correspond to the mean, with upper and lower bounds of the 95% confidence interval in square brackets.

The five repeats of the production runs showed larger deviations for the PIM system than for CHK1 (compare Figures S9 and S10 in the Supporting Information). These differences result directly from less frequent transitions between the end states, which depend strongly on the nature of the binding pocket. Upon inspection of the binding pose (see Figure 10), we hypothesize that accommodation of the bulky –CF₃ of ligand M.4 requires a rearrangement of the neighboring Arg122 side chain, which could explain the larger standard deviations in ΔG_bind observed for this ligand (rearrangement of Arg122 is unlikely to occur in short ns simulations typically performed in free-energy calculations). When comparing the rotation around the bond connecting the core and perturbed substituent of ligand M.4 (see Figures S11 and S12 in the Supporting Information), we found that this dihedral angle remained close to the initial conformation (−CF₃ pointing toward Arg122, dihedral angle of 360°) over the whole simulation with OpenFF, while it rotates with GAFF in the “dummy state” (i.e., when the system samples other end states) such that the bulky –CF₃ substituent points in the other direction, which is an unfavorable conformation hindering transitions to that end state. We note that this does not impact the other ortho-substituted ligands (M.4, M.10, M.12, and M.13) as those are symmetric. For the PIM data set, ligand M.4 was sampled in one of the five random repeats with GAFF >0.1% of the time due to this issue. Thus, the average values for 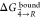, which were subsequently converted to ΔG_bind, were obtained based only on four repeats (Figure 10 and Table 4). A more detailed discussion of the implications of a lack of sampling of end states is provided in the following section.

Figure 10.

(A) Comparison of calculated and experimental binding free energies for the PIM data set. Dark- and light-gray regions correspond to margins of error of 1 and 2 kcal mol^–1, respectively. Error bars correspond to standard deviations over the five random seeds. Results are shown with GAFF (purple) and OpenFF (blue) with hybrid topologies. (B) SSM conformations (minimum energy conformers from a 1 ns simulation) for ligands M.1 (black) and M.4 (light gray). Alignment was performed by using the atoms of the maximum common core to showcase the shift in the position of the Arg122 side chain (colored as the corresponding ligand) required to accommodate the bulkier –CF₃ substituent.

General Discussion

Sources of Errors

The results shown demonstrate that the RE-EDS methodology can be applied to different protein–ligand systems, allowing to rank ligands based on ABFE values (obtained from shifting RBFE with respect to experimental values) within the 1 kcal mol^–1 margin of error, which is the common performance criterion for free-energy methods (see recent large-scale comparisons^11,17,27,93). RMSE values of RBFE were on the other hand consistently higher and ranged from approximately 1 to 4 kcal mol^–1 depending on the data set and force field, with most values being below 2 kcal mol^–1. As with standard free-energy methods like FEP or TI, deviations may stem from either incomplete sampling, inaccurate force-field parameters, or a combination thereof, and it is often difficult to disentangle them.⁹⁴

In the presented simulations, the main source of deviations appeared to be related to dihedral-angle rotations when a ligand is not actively sampled in the RE-EDS simulation (i.e., the protein environment does not “see” it). If an unfavorable configuration is reached in this “dummy state”, transitions to this end state become more difficult. Sampling of degrees of freedom with time scales similar to that of the simulation is a known problem for free-energy methods.^24,94 In its current implementation in GROMOS, the EDS reference state (eq 2) includes only the nonbonded potential energy. Inclusion of the dihedral-angle terms may be a way to address this issue for RE-EDS.

Simulation Time Requirements

Calculating binding free energies with RE-EDS provides a significant decrease in computational time compared to standard pairwise methods like FEP or TI. The performance enhancement obtained grows with the number of ligands (n) included simultaneously (Figure 11 and Table S6 in the Supporting Information). Note that the hyperparameters for FEP/TI (21 λ-values with 5 ns each) were chosen based on common procedures, although there is no strict consensus on the best parameters to use, and it is generally accepted that they are system-dependent.^11,12,70,95 Furthermore, we report estimates for FEP/TI with both the minimum number of pairwise calculations (n – 1) and for the maximum number ((ⁿ₂)) of edges, as the actual number of calculations will lie in between and depends on the user. Recent work from Pitman et al. suggests that the minimum number of edges to simulate from a perturbation graph scales with respect to O(n log n),¹⁸ based on a rigorous statistical analysis assuming normally distributed errors (with σ = 1.0 kcal mol^–1) on a set of synthetic data. Simulating a more challenging system may, however, require the inclusion of a larger number of edges to satisfy the same stability in precision. Multiscale methods like RE-EDS, on the other hand, will likely have a better scaling because the interactions between the unperturbed particles in the system have to be calculated only once and not for each pair of ligands.

Figure 11.

Comparison of the cumulative sampling time in the RE-EDS simulations performed in this work (colored diamonds) to the expected range of corresponding FEP/TI sets of simulations (gray). The black dashed line corresponds to the minimum number of edges to simulate a perturbation graph to maintain a stable precision in free-energy differences.¹⁸

The results shown in Figure 11 are for a single production run. It is, however, widely acknowledged that performing multiple repeats (as done in this study) provides more accurate results.^88,89 The speed-up provided by RE-EDS is amplified when repeats of the production run are performed because the preparation phase does not need to be repeated (Table S7 in the Supporting Information). Although not all ligands were sampled in all repeats for the more complex PIM data set, we would like to emphasize that it was still possible to estimate all binding free energies with reasonable accuracy. Importantly, the lack of sampling of one specific ligand in a simulation did not impact in any way the results for the other end states.

In this work, we simulated up to 13 ligands simultaneously with RE-EDS. While this number can in theory be increased further, it becomes at some point more efficient to subdivide the set into smaller subsets with one or two overlapping ligands, as shown by Rieder et al.³⁸ for solvation free energies. The exact point where splitting the data set becomes more efficient depends on the specific system and the complexity of the ligand transformations.

Conclusions

In this study, we have applied the multistate free-energy method RE-EDS to calculate protein–ligand binding free energies of a set of four kinases and their inhibitors (42 in total). The ligands involved relatively large modifications, changes in ring size, ring opening, and buried and solvent-exposed substituents. The results demonstrate that the method is suitable to estimate relative binding affinities for >10 ligands simultaneously, giving a substantial decrease in cumulative simulation time compared to conventional methods like FEP and TI. We have presented a set of improvements made to the RE-EDS pipeline, in particular a combined optimization of the energy offsets and s-distribution.

Akin to other free-energy methods, results obtained with RE-EDS are also affected by force-field deficiencies and practical limitations in the simulation time restricting the sampling of all accessible conformations. For the sets of molecules studied in this work, we did not observe a clear superiority of one of the two force fields studied. These observations are in line with the benchmarking study reported by OpenFF developers where GAFF and OpenFF show similar performance.⁵³ In addition to deviations arising from larger conformational changes of the protein (e.g., reorganization of a loop), which cannot be expected to be sampled within a few nanoseconds,⁹⁶ we have identified that dihedral-angle rotations of the ligand in the “dummy state” may hinder transitions to this ligand, affecting sampling and thus the resulting free-energy differences. This issue will be addressed in future developments of the methodology.

In conclusion, RE-EDS has been shown to be an attractive and efficient free-energy method, with a pipeline readily available on GitHub⁵⁴ and freely available implementations in GROMOS⁹⁷ and OpenMM.³⁹

Data Availability Statement

The reeds module for parameter optimization is freely available on GitHub at https://github.com/rinikerlab/reeds. The equilibrated protein–ligand coordinates and topology files for the simulations can be obtained at https://github.com/rinikerlab/reeds_applications/tree/main/projects/kinase_inhibitors, as well as example input files for the RE-EDS simulations.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acs.jcim.3c01469.

• Experimental binding affinities; RE-EDS simulation details; additional information for PAK, NIK, CHK1, and PIM data sets; and computational scaling and costs (PDF)

Author Present Address

^† Boehringer Ingelheim Pharma GmbH & Co KG, Medicinal Chemistry, Birkendorfer Str 65, Biberach an der Riss 88397, Germany

The authors declare no competing financial interest.