Design of a Parabolic Trough Collector Solar Field for a Pilot CO₂ Capture Plant from Natural Gas Combined Cycle Power Plant Flue Gas

Abstract

A parabolic trough collector solar field was designed to supply the heat needed to regenerate the CO₂-rich monoethanolamine in a solar-assisted carbon capture system. Process design modeling was performed for 90% of the CO₂ removal from 1% of the flue gas produced by a 255 MWe natural gas combined cycle power plant. Calculations with and without 24 h of thermal energy storage by increasing the solar collector size needed and providing a buffer vessel to store hot heat transfer fluid were performed. A dynamic analysis of the solar field using the hourly solar forecast was performed to investigate how heat transfer fluid mass flow changes during January and June to maintain the desired parabolic solar field outlet temperature needed for CO₂ reboiler operation. The calculations provided here present an explicit method to calculate relevant solar field design parameters that can be scaled up and used in solar energy-assisted gas capture processes.

1. Introduction

Emissions of carbon dioxide (CO₂) due to fossil fuel combustion are considered an important contributor to global warming.^1,2 Availability of natural gas due to the shale revolution³ has resulted in its relatively high availability at competitive prices that have contributed to the reduction in usage of other fossil fuels, such as coal, while limited access to sufficient feedstock and high transportation costs have constrained the capacity of biomass-powered power plants.⁴ Commercially available and well-investigated technology for CO₂ capture from flue gas is based on monoethanolamine (MEA) absorption and regeneration.⁵⁻⁹ In particular, the MEA carbon capture system consists of two columns, an absorber and stripper, a heat exchanger to recover the energy from the hot stream, and a reboiler equipped in the base of the stripper.¹⁰ The energy needed for MEA regeneration in the reboiler is significant and can be viewed as limiting the full implementation of the CO₂ capture technology; MEA regeneration energy consumption as low as 3.6 GJ/tonne CO₂ for flue gas capture designs has been suggested via theoretical calculations and in pilot plants.¹¹ Since steam is drawn from the cycle to regenerate the MEA solvent, it results in an efficiency reduction and decreased net produced power.

In particular, solar energy could be integrated^12,13 with the power plant in four different scenarios. The particular choice of solar energy collection and delivery to contribute to the power plant operation, especially to supplement CO₂ capture, can vary depending on several factors including the region where it operates, the specific fuel or capacity of the plant, and the plant electrical demand profile, among others. A process integration study by Sharma et al. suggested that under design conditions of 275 °C hot oil from a solar field header, solar energy with the molten salt storage option can be used to preheat feedwater from the deaerator of a 600 MW power plant, while the CO₂ stripper reboiler is only powered by the steam drawn after the auxiliary turbine.¹⁴ This concept was further elaborated by the Abbas group where a solar oil-feedwater preheater, combined with auxiliary gas boosting and thermal storage and powered by a solar collector field, was integrated into a solar-repowered postcombustion carbon capture unit of a 600 MWe power plant at 100% capacity rate and 90% capture rate in Australia.¹⁵ This model was augmented by a control logic system that accessed weather library data. This allowed dynamic plant performance profiles to be produced. This type of dynamic approach was further used by Qadir et al. to perform the economic analysis of a CO₂ capture plant retrofitted to preheat high-pressure feedwater.¹⁶ This was consistent with other detailed dynamic designs where a 600 MW supercritical coal-fired plant was supplemented with a trough solar collector system for feedwater preheating.¹⁷

In addition to the steady-state models, case studies exist where the solar power plant design approach is based on the DNIs available in the region, the optical properties of the parabolic trough, a constant heat transfer fluid (HTF) mass flow, and a desired solar field outlet temperature to determine the number of collectors per loop and the total number of solar field collectors.^18,19 Bishoyi and Sudhakar showed that detailed parameters of the solar field, thermal storage, and power block need to be accounted for to obtain an accurate plant configuration based on the US National Renewable Energy Lab’s (NREL’s) Systems Advisor Model (SAM) data.¹⁸ Work by the Abbas group showed estimated economics of direct solvent regeneration via solar thermal energy supplied by parabolic troughs^16,20 for up to 700 h simulations using a combination of steady-state calculations and dynamic DNI-adjusted solar thermal plant models. Notably, these dynamic simulations that account for DNI were location-specific with emphasis on solar energy-rich Australia,²¹ and case studies that can validate solar collector potential use in other geographical locations are missing. These advanced solar integration models to supplement CO₂ stripper have been recently described in detail,^15,16,20 but they rely mostly on secondary models, such as response surface methodology, to generate nonlinear reduced models of stripper operation as regressed from the experimental data.¹⁶ These models are unique to the operating unit and do not have transferability, e.g., the regression is unique to the specific application. It can be suggested that more transferable models, based on the fundamental properties of aqueous MEA solutions, instead need to be used to ensure full transferability of the calculations. This approach has only recently been applied for a solar energy-assisted flue gas amine-based CO₂ capture process²² but did not include the explicit solar field model parameters as it was only based on the implicit solar flux.

In the present work, solar energy collection was modeled to supplement the energy needed to capture CO₂ from 1% of the flue gas of an NGCC plant with 90% efficiency and complemented with an integrated HTF (Therminol VP-1) storage for an uninterrupted 24 h operation of a 255 MWe NGCC power plant located in Poza Rica, Mexico. For this purpose, a parabolic trough solar field with two HTF storage tanks was used as the best design option due to its availability, costs, and efficiency. The capacity of the CO₂ capture was designed according to industry-standard carbon capture, utilization, and storage (CCUS) projects.²³ Design calculations and results for a field without thermal energy storage (no TES) and with 24 h of TES with a backup steam boiler are presented, and a comprehensive economic analysis is provided. The comparative economic evaluation was performed to assess the potential savings obtained when solar trough collectors are incorporated into a regenerated CO₂-rich amine solvent. In particular, we first outline flue gas calculations for the 1% 255 MWe NGCC power plant in Sections 2.1 and 2.2, the details of the solar field calculations in Sections 2.2 and 2.3, calculations of the solar energy storage unit in Section 2.5, the final design of the solar heat exchanger in Section 3, dynamic simulation results in Section 4, and economic evaluation in Section 5.

2. CO₂ Removal from Flue Gas and Solar Trough Field Modeling

2.1. Power Plant Model Verification

A benchmark NGCC plant was used consisting of a combustion turbine generator and two heat recovery steam generators to supply heat to a single steam turbine generator cycle. This cycle contains high-pressure, intermediate pressure, and low-pressure sections, an independent economizer, an evaporator, and a superheater for each pressure. CO₂ capture was achieved via a modeled MEA-based system, which was connected to the flue gas stream exiting heat recovery steam generators. It comprised the absorber/stripper columns connected via a crossflow heat exchanger. Heat is supplied to the stripper via a low-pressure steam extraction supplemented, in this work, by a solar energy carrier. A good numerical agreement between the model of both the power plant and CO₂ capture unit was found including operating temperatures and heat duties, critical parameters in the current work. The full model was first designed in our previous work by Bravo et al.²⁴ where it was benchmarked against the NGCC model equipped with a CO₂ capture unit available in detail by NETL.²⁵

2.2. Flue Gas Mass Flow Specification

A reference 555 MWe NGCC power plant was used as a base case, which was previously selected and validated using rigorous modeling simulations.²⁴ The model parameters obtained were scaled down to a 255 MWe NGCC power plant similar to that operating in Poza Rica, Mexico. In particular, scaling calculations in (eq 1) allowed us to determine the fuel mass flow needed to operate the 255 MWe NGCC power plant

1

where P is the power plant capacity, w is natural gas mass flow, η is power plant efficiency, and ΔH is the natural gas enthalpy of the reaction. A 1% flue gas removal scenario was analyzed due to the interest in building a reduced-scale prototype to demonstrate the MEA carbon capture technology in Mexico. The 1% of flue gas mass flow was augmented by 10% due to the losses during the scaling of the gas and steam turbines leading to (eq 2)

2

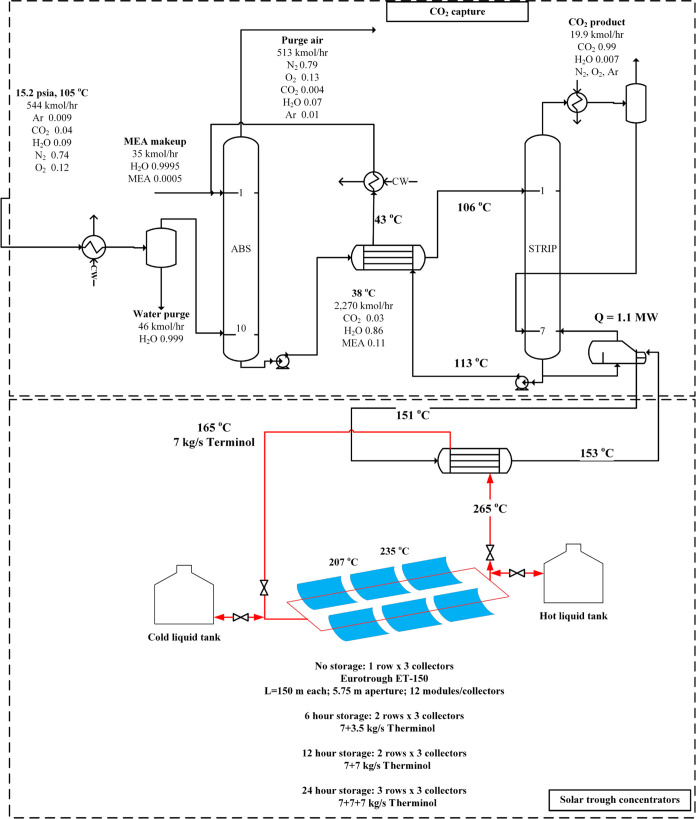
where ṁ_FGr is the reference power plant flue gas mass flow and ṁ_fr is the reference power plant natural gas mass flow. Using the value of 1% of flue gas capture and maintaining its temperature, pressure, and mole fractions from the reference power plant, Aspen Plus simulations were performed on an MEA-based carbon capture system and the pilot plant stripper reboiler duty, Q̇_r, was calculated. Figure 1 shows the Aspen Plus model used to simulate carbon capture of the 1% flue gas flow.

Figure 1.

Steady-state simulation results for absorber/stripper-based MEA scrubbing of CO₂ from flue gas powered with hot liquid generated in solar trough concentrators. MEA, monoethanolamine; CW, cooling water; ABS, absorber; and STRIP, stripper.

In particular, 544 kmol/h of flue gas containing 967 kg/h of CO₂ was treated in a 10-stage absorber column using an 11% MEA solution at 90% capture efficiency. This system is comprised of adsorption and desorption (stripping) columns. The flue gas is supplied to absorber stage 10 at the absolute pressure of 15.3 psia and contains 4% of CO₂. Flue gas is cooled, and the condensed water is flashed before the column. 2286 kmol/h of 30% MEA CO₂-lean solution is circulated into the absorber stage 1. The CO₂-rich solvent was stripped in a 7-stage stripper, resulting in the reboiler duty, Q̇_r = 1.1 MW. The reboiler duty in the stripper is 4.6 GJ/tonne CO₂, typical of that used in amine separation systems. In steady-state, Q̇_r was supplied using 153 °C steam generated in the evaporator that utilized 265 °C hot liquid from the solar trough concentrators designed in this study. The simulation results are summarized in Table 1. The results obtained from Aspen Plus for 1% of the flue gas are reliable since the model was based on the strictly validated model presented previously²⁴ and scaled down for this specific research case. All of the results obtained from Aspen Plus are based on numerical simulations, and no experimental data were used in this research project.

Table 1. Aspen Plus Simulation inputs to Model the CO₂ MEA Capture System and the Modeling Results^a.

inputs
power plant capacity, P	255,000 kJ/s
power plant efficiency, η	0.502
natural gas enthalpy of reaction, ΔH	886 kJ/mol
natural gas weight, w	0.016 kg

results
natural gas mass flow, ṁf	9.2 kg/s
1% flue gas mass flow, ṁFG	4.3 kg/s
pilot plant stripper reboiler duty, Q̇r	1.1 MW

^aResults are for the 1% flue gas from the 255 MWe NGCC power plant.

2.3. Design of the Parabolic Trough Solar Field

Available previous modeling and economic evaluation suggested that, on a process level, the use of parabolic troughs as solar energy collectors was the most economically and energetically feasible option to supplement an MEA carbon capture system.²⁴ In the current modeling study, a Eurotrough ET150 was used as a basis to model the parabolic collector. With an effective length of 142.2 m and a width of 5.75 m, an Eurotrough ET150 provides an aperture area of 817.5 m² and a heat removal factor of 0.963. In conjunction, the modeling work utilized a Siemens UVAC 2010 solar receiver with an absorber tube inside of a glass envelope. The latter prevents the absorber from convective losses since hydrogen surrounds the absorber tube and works as an insulator. A reflectance of 0.92, an intercept factor of 0.92, a transmittance of 0.945, and an absorbance of 0.94 were assumed in this study.²⁶ Finally, Therminol VP-1 was selected as the HTF. Therminol VP-1 is a clear, water-white liquid that is a biphenyl/diphenyl oxide (DPO) eutectic mixture that can be used as a liquid or as a boiling-condensing heat transfer medium up to 400 °C.²⁷ Liquid heat capacity at 260 °C is 2.207 kJ/(kg·K). A flow rate, ṁ_c, of 7 kg/s of HTF mass flow was used in the simulations as calculated in the following sections describing the modeling work.

2.4. Solar Trough Energy-Powered CO₂ Stripper System without Thermal Energy Storage Using Static DNI

We began with modeling the solar trough collector system necessary. To calculate the number of collectors per loop and the total number of collectors in the solar field, a single collector heat production was calculated according to the methodology by Yasin and Draidi.²⁸ The methodology used in this section relies on the formulizm presented by Duffie and Beckman.²⁹ First, the absorbed solar radiation was calculated according to (eq 3)

3

where a DNI—direct normal irradiance—of 900 W/m² was used (maximum value from Figure 2), ρ is reflectance, γ is an intercept factor, τ is transmittance, α is absorbance, and κ is the incident angle modifier.

Figure 2.

National Solar Radiation Database hourly DNI forecast for the months of (a) January and (b) June as implemented in SAM.³⁰

A useful heat gain of one collector was calculated via (eq 4) as

4

where F_R is the collector heat removal factor, A_a is the aperture area of the collector in m², A_r is the receiver area in m², U_L is a heat loss coefficient in W/m²·°C, T_i is HTF solar field inlet temperature in °C, and T_a is the ambient temperature in °C.

Knowing Q̇_c, the outlet temperature after one collector was calculated as

5

where ṁ_c is the HTF mass flow through a collector in kg/s, T_oc is HTF solar field outlet temperature in °C, and C_p is the HTF heat capacity in kJ/kg K at T_oc.

From the temperature difference across each collector and the known solar field temperature difference, the number of collectors per loop can be obtained as

6

where T_o is the HTF temperature at the solar field outlet in °C. Using the reboiler duty obtained from the carbon capture Aspen Plus simulation shown in Figure 1 and the efficiency of the HTF–steam heat exchanger, η_x, the number of collectors required in the solar field, N_T can be calculated via (eq 7)

7

The corresponding number of loops, L, required in the solar field is

8

Finally, the total HTF mass flow in kg/s in the solar field is

9

which is also the HTF mass flow through the HTF–steam heat exchanger which produces the steam that goes to the MEA reboiler. The input and results from the calculations in eqs 3 to 9 are tabulated in Table 2.

Table 2. Solar Field Design without Thermal Storage: Inputs and Calculation Results.

receiver inlet pipe diameter, Di	0.065 m
receiver outlet pipe diameter, Do	0.07 m
receiver area, Ar	31.27 m2
collector effective length, Lc	142.2 m
collector width, Wc	5.75 m
collector aperture area, Aa	817.5 m2
direct normal irradiance, DNI	10.80 kWh/m2
sunlight hours per day, td	12 h
receiver absorbance, a	0.94
receiver reflectance, r	0.92
receiver intercept factor, g	0.92
receiver transmittance, t	0.945
incident angle modifier, k	1
absorbed solar radiation, S	0.677 kW/m2
heat loss coefficient, UL	0.0055 kW/m2°C
collector heat removal factor, FR	0.963
HTF outlet temperature, To	265 °C
HTF inlet temperature, Ti	165 °C
HTF average temperature, Tav	236 °C
ambient temperature, Ta	31 °C
HTF mass flow per loop, mc	7.0 kg/s
HTF heat capacity at Tav, Cp	1.8 kJ/kg K
collector useful heat gain, Qc	510 kJ/s
HTF first collector outlet temperature, Toc	207 °C
number of collectors per loop, NL	3
solar field total number of loops, L	1
solar field number of collectors, Nf	3
solar field area, As	2452 m2
HTF mass flow in the solar field, mT	7.0 kg/s

2.5. System with Thermal Energy Storage

A system consisting of two storage tanks was used to simulate a solar field with thermal energy storage. Namely, one was used for hot HTF and one for cold HTF to store enough HTF to supply the HTF–steam heat exchanger when only diffuse irradiance is available or during the night.

Using an HTF C_p in kJ/kg K at T_o in °C, the solar field temperature difference, T_o – T_i, and the desired storage time, t_n in seconds, the mass in kg needed to store the required thermal energy was calculated as (eq 10)

10

From the calculated value of the stored mass, the volume in m³ of each tank is obtained as

11

where ρ is the HTF density in kg/m³. The mass flow in kg/s from the cold tank to the hot tank needed to fill the hot tank during the sunlight period t_d in seconds was calculated using (eq 12)

12

Knowing the mass flow from the cold tank to the hot tank during the sunlight period, the number of collectors needed just for storage was calculated as

13

The number of loops required just for storage was obtained using (eq 14)

14

Therefore, the solar field’s total number of loops was (eq 15)

15

From the value calculated in eq 15, the solar field’s total number of collectors is obtained as

16

Finally, the solar field’s total area in m² was calculated using (eq 17)

17

Input and results for t_n = 6, 12, and 24 h of storage are tabulated in Table 3. 24 h storage represents a case where all of the heat to the reboiler can be supplied using only hot HTF. It can be seen that for a complete 24 h operation, if the sun is not present, a tank of 637 m³ is sufficient, provided there is a solar field to collect the energy consisting of 3 loops and 9 collectors in total.

Table 3. Calculated TES Parameters for 6, 12, and 24 h HTF Storage.

storage hours per day, tn [h]	6	12	24
HTF mass needed for storage, m [kg]	151,200	302,400	604,800
Hot storage tank volume, V [m3]	159	318	637
HTF mass flow from cold to hot tank, md [kg/s]	3.5	7	14
Number of loops needed for storage, Ls	1	1	2
solar field total number of loops (rows), LT	2	2	3
solar field total number of collectors, N	6	6	9
solar field area, As [m2]	4905	4905	7357
summarized solar field design parameters
no storage
Eurotrough ET-150
L = 150 m each, 5.75 m aperture, and 12 modules/collectors
6 h storage
2 rows × 3 collectors
7 + 3.5 kg/s therminol
12 h storage
2 rows × 3 collectors
7 + 7 kg/s therminol
24 h storage
3 rows × 3 collectors
7 + 7 + 7 kg/s therminol

3. Design of Heat Transfer Fluid–Steam Heat Exchanger

To satisfy the reboiler duty demanded by the carbon capture system, it is necessary to design the HTF–steam heat exchanger, which can only be realistically modeled using a quasi-dynamic approach described here. Using the design parameters in Table 1, calculations were performed to determine the HTF mass flow and the product of the heat exchanger’s overall heat transfer coefficient, which can supply the right amount of heat rate to evaporate the saturated liquid. Saturated steam at 153 °C is used in the stripper reboiler. The steam mass flow demanded by the stripper reboiler duty in kg/s was calculated using (eq 18)

18

The product of the overall heat transfer coefficient and the heat transfer area is

19

where h_g is the enthalpy of the saturated vapor in kJ/kg, h_f is the enthalpy of the saturated liquid in kJ/kg, η_x is the assumed HTF–steam heat exchanger efficiency (0.85), and T_s is the saturation steam temperature in °C. Input and results are tabulated in Table 4.

Table 4. HTF–Steam Heat Exchanger Design Input and Results.

steam temperature, Ts	153 °C
saturated vapor enthalpy at Ts, hg	2619.3 kJ/kg
saturated liquid enthalpy at Ts, hf	274.4 kJ/kg
steam mass flow, ms	0.5239 kg/s
heat exchanger UA, UA	35.3 kW/°C

4. Model Results for the Simulations of the Solar Trough Field-Integrated CO₂ Capture System Using Dynamic DNI

Once the number of collectors and the size of the storage tanks are known, a simulation using the hourly DNI forecast tabulated by the National Solar Radiation Database was performed to determine how much energy the designed solar field can supply to the stripper reboiler. The amount of energy supplied by the solar field will change as a function of the DNI, which varies depending on the time of the day and the month of the year. For a demonstrative purpose, the months of January and June have been presented since these are commonly the months of the year with the lowest and highest values of DNI, respectively.

4.1. Dynamic Solar Trough Field Design without TES

Solar energy is the best option to supply the heat needed in the stripper reboiler to regenerate the MEA because of its straightforward integration with the reboiler unit. Solar energy reliability depends on the particular region of installation and its weather, which are factors that cannot be controlled. The solar parameters were first defined as a basis of the model, and the operation of the designed solar field using the National Solar Radiation Database hourly DNI forecast was used to obtain the amount of thermal energy that the solar field can produce with very close-to-real DNI conditions in Poza Rica, Mexico. Figure 2a,b shows the DNI forecast for January and June, respectively.

Initially, a constant DNI, as assumed during the design process shown in Figure 1, is not feasible and it will be necessary to vary the HTF mass flow, ṁ_T, to have a constant solar field outlet temperature of 265 °C. Controlling ṁ_T guarantees the complete evaporation of the steam in the HTF–steam heat exchanger. Since the steam mass flow, ṁ_s, is controlled as a function of the variable DNI, the energy supplied to the stripper will not always be enough to satisfy the reboiler demand.

A comparison between the thermal energy produced by the parabolic solar field based on the dynamic DNI forecast and the thermal energy produced for the reboiler for January and June is shown in Figure 2. The calculated dynamic operational parameters of the simulation, such as solar heat, Q_s, generated, HTF mass flow rate, boiler heat duty Q_b, and steam mass flow are also included in Figure 3.

Figure 3.

Comparison between thermal energy produced by the solar field needed in the reboiler for (top) January and (bottom) June as well as the related operational parameters. The horizontal yellow line shows the total duty needed during continuous reboiler operation. Panels (a, b) represent solar heat, panels (c, d) represent heat transfer fluid mass flow, panels (e, f) represent boiler heat, and panels (g, h) represent steam mass flow in January and June, respectively.

In this dynamic simulation, where the solar trough field is combined with a CO₂ reboiler, a constant value of 7 kg/s for the HTF mass flow was used, which should remain, according to the steady-state calculations, constant if the DNI value is constant at 900 W/m². Figure 3c,d shows that the HTF mass flow, ṁ_c, changes dynamically with DNI. It can be seen that the HTF mass flow will increase when the DNI increases and will decrease when the DNI decreases to maintain its outlet temperature constant at 265 °C. It can be noted that when the solar field is capable of collecting more energy than the amount needed in the reboiler, this energy is wasted because no storage option has been considered.

To guarantee an uninterrupted 24 h supply of the energy needed in the reboiler and to compensate for unfavorable weather conditions, it was necessary to add a steam boiler as a backup as shown in Figure 3e–h. The steam boiler could provide the heat needed in the reboiler to ensure a heat supply at moments when the DNI was zero. Since the conditions in the reboiler were specified as saturated steam at 153 °C, the steam boiler was designed to work under conditions of saturated steam at 160 °C. These conditions lead to the selection of a steam boiler that should supply 1.302 MWth and produce saturated steam at 160 °C with a steam mass flow of ∼0.55 kg/s accounting for 85% boiler efficiency. The difference between the energy supplied from the solar field and the overall consumption in the reboiler is then supplied by the boiler. Figure 3e,f shows the energy supplied by the steam boiler to keep a constant heat supply to the reboiler during January and June, respectively. Based on the values of energy supplied to the reboiler by the steam boiler, the steam mass flow rate supplied by the steam boiler was also calculated. Figure 3g,h shows the steam mass flow needed to be supplied by the steam boiler to keep constant the heat needed in the reboiler to regenerate the MEA. A deeper analysis of the results in Figure 3 suggests that solar heat supplied in the mode without TES suffers from long periods, where steam is needed. In January, a period of 1 week took place, where the CO₂ capture system effectively operated using steam only.

4.2. Dynamic Solar Trough Field Design with TES

A solar field without a TES system will not achieve the full capacity needed to remove CO₂ since it needs to obtain extra thermal energy during periods when the DNI is lower than the design value. A solution to this problem is to implement a two-tank system with one tank operating at 165 °C (the cold tank) and the other tank at 265 °C (the hot tank), where HTF can be stored. During the day, the energy collected by the parabolic troughs will supply energy to the reboiler, and the extra energy will heat the HTF which will be stored in the hot tank during a charging period. During periods of low DNI, the hot tank will supply hot HTF to compensate for the lack of energy collected by the parabolic troughs in the discharging process. During the night, the hot tank will be further discharged to supply the heat needed in the reboiler to keep the MEA regeneration process uninterrupted for at least 24 h. Other parameters need to be maintained including controlling the HTF flow rate to keep its temperature at 265 °C at the outlet of the solar field and using the formulas from Sections 2.3 and 2.5. Figure 4 shows the total amount of thermal energy collected by the solar field with energy storage during January and June. Upon availability, part of this energy will be used in the reboiler, and the extra will be stored.

Figure 4.

Energy exchanged in the reboiler by the solar field as well as other operating parameters with a 24 h two-tank storage system for the months of (top) January and (bottom) June. The horizontal yellow lines signify the HTF amount needed to ensure uninterrupted CO₂ removal for at least 24 h without an external steam supply. (a, b) Solar heat, (c, d) solar reboiler duty, (e, f) heating fluid mass flow, and (g, h) hot heat transfer fluid storage tank mass in January and June, respectively.

In particular, the modeling results tabulated in Table 4 are for the solar field design considering thermal storage to achieve uninterrupted 24 h operation. By accounting for the dynamic DNI changes with time, the energy supplied by the solar field (including the extra parabolic troughs used for thermal storage) can be calculated. Figure 4 shows the energy exchanged in the reboiler by the solar field with a 24 h two-tank storage system for January and June. Total heat generated by the solar trough field, Q_S, peaks at 5 MW as shown in Figure 4a,b. It can also be seen that solar energy contribution to the reboiler duty in Figure 4c,d is nonmonotonic, e.g., sometimes it becomes negligible even with the 24 h storage. This is especially prominent during January, as shown in Figure 4c. A procedure similar to that used in the previous section to calculate the controlled HTF mass flow to keep its temperature at 265 °C when it leaves the solar field is used in this section. Figure 4e,f show how the HTF mass flow through the reboiler changes during January and June. During the day, the DNI fluctuations force the system to circulate a variable HTF mass flow. Sometimes these fluctuations can change from very high to very low values in a short or long period. Figure 4g,h show a comparison between the total mass capacity of the hot tank and the amount of HTF inside the hot tank during January and June. Even though the solar field was designed to store thermal energy to satisfy the demand for 24 h, this does not occur all of the time. There are some occasions when the DNI levels are too low for extended periods, especially during January. In these cases, the hot tank is discharged during the day rather than being charged, and the amount of mass inside of it reaches the lowest level; in some cases, this low level remains for a longer time.

To guarantee a steady supply of the energy needed in the reboiler, even though the weather conditions are unfavorable, it was necessary to include the steam boiler as a backup. The heat capacity of the steam boiler should be at least the heat needed for the reboiler. Since the steam conditions in the reboiler are specified as saturated steam at 150 °C, the steam boiler should work under conditions of at least saturated steam at 160 °C. These conditions lead to a steam boiler that should be able to supply 1.302 MWth and produce saturated steam at 160 °C with a steam mass flow of 0.55 kg/s. Figure 5 shows the energy supplied by the steam boiler to keep a constant heat supply to the reboiler during the months of (top) January and (bottom) June as well as the steam mass flow needed to be produced by the boiler to keep constant the heat needed in the reboiler to regenerate the MEA.

Figure 5.

Energy supplied by the steam boiler to keep a constant heat supply to the reboiler during the months of (top) January and (bottom) June as well as the steam mass flow needed. (a, b) represent boiler heat, and (c, d) represent steam mass flow in January and June, respectively.

5. Overall Process Economics for CO₂ Removal

An economic analysis was first performed to assess the value of the CO₂ trading price (or the taxed amount incurred) and compared it to the cost of the operation per year with 0 and 24 h HTF storage. The results are listed in Table 5. We next calculated the electricity not generated due to the draw of the intermediate pressure steam before the turbine for CO₂ stripping as lost revenue as shown in Figure 6a. Finally, the difference between the annual CO₂ capture cost implemented with and without the 0 and 24 h HTF storage solar field was calculated and shown in Figure 6b and Table 7. The analysis period was 10 years. The inflation rate assumed was 2.5%. The nominal interest rate was 5% per year. An effective tax rate of 40% per year was used. No depreciation was assumed.

Table 5. Comparative Economics of the 1% Flue Gas CO₂ Capture Process Using a Solar Concentrator with and without 24 h HTF Storage.

solar field economics
solar field storage [h]	0	24
cost of heat [$/kWhth]	0.0619	0.0382
heat per year [kWhth/year]	1,685,310	5,491,792
cost of operation per year [$/year]	104,321	209,786

CO2 trade price
CO2 captured per year [tonCO2/year]	7171
trade value of CO2 [$/tonCO2]	50–100
trade value of CO2 per year [$/year]	358,550–717,100

Figure 6.

(a) Revenue lost due to CO₂ capture for the different wholesale prices of generation. (b) Savings for different wholesale prices of generated electricity and solar field with and without energy storage.

Table 7. Cost of Operation of Solar Field without Energy Storage and with 24 h Energy Storage.

solar field storage hours [h]	0	24
heat sink [MWth]	124	124
solar multiple	1.3	1.4
cost of heat [$/KWhth]	0.0449	0.0427
heat per year [kWhth/year]	210,480,224	239,313,920
cost of operation per year [$/year]	9,450,562	10,218,704

5.1. Economics of the 1% Total Flue Gas Process

From Aspen Plus simulations, the amount of CO₂ captured per year from 1% of the total flue gas was found to be 7171 tons. A capacity factor of 85% for the power plant was assumed to calculate the amount of CO₂ captured per year from 1% of the total flue gas. Assuming a levelized cost of CO₂ capture of $50–100 per ton of CO₂,³¹ the amount to pay per year if no carbon capture system was implemented would range from $358,550 to $717,100. From simulations performed using System Advisor Model (SAM) software,³⁰ a levelized cost of heat (LCOH) of $0.0619 and $0.0382 for the cases of solar fields without energy storage and with 24 h of energy storage were found, respectively, as shown in Table 5. Also, from SAM, the values of annual energy produced by the solar field without energy storage and with 24 h of energy storage were found as 1,685,310 kWh_th and 5,491,792 kWh_th, respectively. Using this information from SAM, the costs to operate the solar field without energy storage and with 24 h of energy storage were found as $104,321 and $209,786, respectively.

It can be concluded from the data available in Table 5 that the cost of implementing a solar field to supply the energy needed in the stripper reboiler of a carbon capture system is about 3× lower than the Levelized cost of CO₂ capture if the carbon capture system is not implemented.

5.2. Economics of the Total Power Plant with and without CO₂ Capture Using Solar Trough Collectors

The parameters used to calculate the cost of capturing CO₂ are obtained when the power plant is scrubbing the CO₂ of all of the flue gas produced by the power plant. Typical operational parameters such as the heat rate and power output are used for the calculation. The heat rate and the power output of the 255 MW_e power plant are 6798 Btu/kWh_e and 255,000 kW_e for the case without carbon capture, respectively, and 7,968 Btu/kWh_e and 230,751 kW_e for the case when the plant operates with a carbon capture system, respectively.

The cost of generation of a kWh_e, assuming a power plant capacity of 85% and a price of the natural gas of $4, is $0.0272 and $0.0319 for the power plant with and without a carbon capture system, respectively. The energy generated per year is 1,898,730,000 kWh_e and 1,718,170,762 kWh_e for the cases without carbon capture and with carbon capture, respectively. The cost to operate the power plant per year can be found as the product of the cost to generate 1 kWh_e and the energy generated per year. The cost to operate the power plant per year without carbon capture and with carbon capture is $51,630,266 and $54,761,539, respectively. These data are summarized in Table 6. Additionally, the revenue lost due to capturing CO₂ needs to be calculated. It will be assumed three different values of the wholesale price of generated electricity, $0.04, $0.05, and $0.06/kWh_e. Calculating the difference between the energy generated per year of the cases without and with carbon capture, the energy deprived to be generated, due to the energy requirement by the reboiler of the carbon capture system, and sold to the grid due to capturing CO₂ is 180,559,238 kWh_e. The loss of revenue due to CO₂ capture is $7,222,370, $9,027,962, and $10,833,554 for the assumed wholesale prices of generated electricity of $0.04, $0.05, and $0.06, respectively. By subtracting the cost to operate the power plant without carbon capture from the cost to operate the power plant with carbon capture and adding the revenue lost due to CO₂ capture, the cost to capture CO₂ per year can be calculated for the assumed values of the wholesale price of generated electricity of $0.04, $0.05, and $0.06, it is found to be $10,353,642, $12,159,234, and $13,964,827, respectively. These results are shown in Figure 6a.

Table 6. Power Plant Operation Parameters^a.

power plant case	baseline	baseline + CO2 capture
heat rate [Btu/kWhe]	6798	7968
power output [kWe]	255,000	230,751
cost of electricity [$/kWhe]	0.0272	0.0319
electricity per year [kWhe/year]	1,898,730,000	1,718,170,762
cost of operation per year [$/year]	51,630,266	54,761,539

^aNatural gas price of $4/MMBtu, the capacity factor of 0.85, and operating for 7446 h per year.

Costing was performed by the system advisor model (SAM) to calculate the levelized cost of heat (LCOH) to operate a solar field without energy storage and with 24 h of energy storage to supply the heat needed in the stripped reboiler to regenerate the solvent. The simulation assumptions take an analysis period of 10 years and a nominal debt interest rate of 5% per year. The LCOH for a solar field without energy storage and with 24 h of energy storage was found as $0.0449 and $0.0427, respectively, as shown in Table 7. The values of annual energy produced by the solar field without energy storage and with 24 h of energy storage were found as 210,480,224 kWh_th and 239,313,920 kWh_th, respectively. Using these costing results, the costs to operate the solar field without energy storage and with 24 h of energy storage were found as $9,450,562 and $10,218,704, respectively.

By comparing the values of the cost to capture CO₂ per year with the cost to operate a solar panel without energy storage and with 24 h of energy storage, it can be found that the lowest saving is 1.3% for the case of wholesale prices of generated electricity of $0.04 and a solar field with 24 h of energy storage and the highest saving is 32.3% for the case of wholesale prices of generated electricity of $0.06 and a solar field without energy storage shown in Figure 6b.

6. Conclusions

An explicit methodology to design a solar trough collector field for the stripper reboiler was developed to capture 90% of CO₂ from the 1% flue gas of the Poza Rica NGCC power plant. A solar field was designed to assist the carbon capture system and prevent it from impacting the efficiency and power rating of the NGCC plant. The results obtained showed a reboiler duty of 1.1 MW needed at an efficiency of 85% for an HTF–steam heat exchanger. The calculations adopted the use of commercially validated Eurotrough ET150 and Siemens UVAC 2010 solar collector and receiver, respectively, while the HTF selected was Therminol VP-1. A basis of the calculation was a constant HTF mass flow of 7 kg/s with a solar field inlet temperature of 165 °C and an outlet temperature of 265 °C.

The resulting average temperature in each collector of 236 °C was calculated, which resulted in the use of three collectors per loop to guarantee the design temperature increase of 100 °C through the solar field. The calculated total number of loops needed in the solar field without TES was one, and the total area of the solar field calculated was 2452 m². When the solar field was designed with TES a two-tank storage system was considered: one tank to store hot HTF and a second one to store cold HTF. Using the calculated 1.1 MW reboiler demand, 604,800 kg of HTF was needed to store 24 h of thermal energy. This mass resulted in a storage volume of 637 m³ per tank. The number of collectors needed to operate with the 24-h uninterrupted operation was 9, which resulted in a total number of loops of 3. This total number of collectors represents an area of 7,357 m² of the solar field. The design in this work can still be considered pseudodynamic, thus providing pathways for a complete pressure-driven dynamics simulation using PID controllers.

This design represents a practical approach to offset power losses taking place during the 255 MW NGCC plant power generation that is retrofitted with a carbon capture system. It provides a practical estimate for a pilot plant CO₂ capture retrofit due to the direct scalability of the energy parameters obtained. Finally, it will also facilitate the estimation of the solar field designs needed to capture and recover other important waste gases, such as NH₃ in the anaerobic waste processing facilities, via vacuum stripping of the liquid digestate.³²⁻³⁴

Author Contributions

J.B.: investigation (lead), conceptualization (supporting), writing—original draft (equal), and writing—review and editing (equal); C.R.: investigation (supporting), writing—original draft (equal), and writing—review and editing (equal); J.B.: conceptualization (lead), methodology (supporting), supervision (lead), writing—original draft (equal), and writing—review and editing (equal).

The authors declare no competing financial interest.