The effect of pre-aggregation scale on spatially adaptive filters

Abstract

Choropleth mapping continues to be a dominant mapping technique despite suffering from the Modifiable Areal Unit Problem (MAUP), which may distort disease risk patterns when different administrative units are used. Spatially adaptive filters (SAF) are one mapping technique that can address the MAUP, but the limitations and accuracy of spatially adaptive filters are not well tested. Our work examines these limitations by using varying levels of data aggregation using a case study of geocoded breast cancer screening data and a synthetic geore-ferenced population dataset that allows us to calculate SAFs at the individual-level. Data were grouped into four administrative boundaries (i.e., county, Zip Code Tabulated Areas, census tracts, and census blocks) and compared to individual-level data (control). Correlation assessed the similarity of SAFs, and map algebra calculated error maps compared to control. This work describes how pre-aggregation affects the level of spatial detail, map patterns, and over and under-prediction.

1. Introduction

1.1. Challenges in health mapping

Disease mapping is a useful technique for visualizing and communicating the burden of disease to health stakeholders including government agencies, nonprofits and the general public. There are a myriad of techniques for creating disease maps with choropleth mapping being a popular approach. Choropleth maps are easy to construct; however, they suffer from two known problems in disease mapping: (1) the small number problem, and (2) the Modifiable Areal Unit Problem (MAUP) (Arbia and Petrarca, 2011; Fotheringham and Wong, 1991; Openshaw and Taylor, 1979). Small numbers occur in sparsely populated areas, small areal units, or when working with rare diseases. Small numbers can result in highly variable - and therefore unreliable - estimates of disease risk (Nakaya, 2000; Takiar et al., 2009). Small numbers can also lead to areal units being labeled as suppressed in maps produced by government health agencies. Small number problems have been addressed with fixed-sized filters (Turnbull et al., 1990) and statistical methods, such as Bayesian smoothing, headbanging, and geographically weighted regression (Bernardinelli and Montomoli, 1992; Best et al., 2005; Lawson, 2013; Mungiole et al., 1999). However, the MAUP remains a problem for analyzing and visualizing disease pattern.

The MAUP demonstrates that the number or size of spatial units breaks-up spatial data in artificial ways that obscure true patterns (Arbia and Petrarca, 2011; Openshaw and Taylor, 1979). Visualizations or maps whose estimates are derived from areal unit aggregations - such as counties or zip codes - can be statistically unrepresentative of the underlying continuous pattern of disease risk, and changing the geographic unit of analysis (e.g., from county to zip code) changes the number and/or scale of units and perpetuates these artifacts. Further, reliance on predefined administrative boundaries limits our understanding of disease burden at the local level. For example, if data is pre-aggregated to the county level, it is difficult to make reliable estimates at lower levels, such as Zip Code Tabulated Areas (ZCTAs). New methods that produce reliable estimates at the local level, while simultaneously controlling for the effect of the MAUP, are needed.

There are several mapping approaches known to attenuate the effects of the MAUP. Working with individual data removes the aggregation bias, but is impractical for measures like rate calculation (with a numerator and denominator). Individual data also have additional privacy concerns that must be addressed unlike aggregated datasets (Hampton et al., 2010; Olson et al., 2006; Stinchcomb, 2004). Some statistical approaches, like geographically weighted regression, attempt to account for the MAUP by spatially weighing the relationships between observations. This approach can provide a more representative model of the underlying spatial heterogeneities in the data (Matthews and Yang, 2012). Regionalization techniques address MAUP through the creation of new geographic units; new units are systematically created using rules based on geographic adjacency, the similarity of attributes, or a threshold of population or disease events. These new geographic areas produce stable disease rates while maximizing homogeneity in underlying attributes (Wang et al., 2012). However, regionalization techniques may be biased as researchers could choose new units that support their hypotheses (Swift et al., 2008). Finally, researchers can conduct extensive sensitivity analyses by constructing maps of various units and scales and comparing them, but this process increases the time of study and there is no agreed-upon reference for truth.

Spatially Adaptive Filters (SAF) are an estimation technique that attempts to overcome these problems by (1) implementing a minimum population threshold that produces reliable estimates for sparsely populated or small areas and (2) creating a surface that describes the burden of disease irrespective of administrative boundaries. Spatially Adaptive Filters have accurately described the variation of cancer incidence and mortality patterns (Beyer and Rushton, 2009; Tiwari and Rushton, 2005). A limitation of the previous literature is that the adaptive filters used pre-aggregated data. Our work adds to the literature by working with data at the individual level and comparing those results to various levels of pre-aggregation on spatially adaptive filters. To accomplish this, we will use breast cancer screening data from the Minnesota Department of Health. We use aggregations at the census block, census tract, ZCTA, and county levels to compare the resulting SAFs (i.e., estimates). Correlations and visualizations are used to assess change between the aggregation and individual-level SAF map as the control. Comparisons between SAF interpolated maps and choropleth maps are also conducted.

1.2. Description of the case study

Cancer is a leading cause of mortality among U.S. women, and 30% of women’s new cancer diagnoses in 2020 will be breast cancers (American Cancer Society, 2018; Hahn et al., 2018). Screening is effective at reducing breast cancer mortality, but uptake of screening has stalled in recent years; national breast cancer screening rates fell slightly (3%) among women 50 to 74 years old (Hall et al., 2018; Office of Disease Prevention and Health Promotion, 2019). The National Breast and Cervical Cancer Early Detection Program (NBCCEDP) is one path to increase breast cancer screening (Lantz and Mullen, 2015). NBCCEDPs are implemented by state-level governments and provide free breast and cervical cancer screening to low-income women who are uninsured or underinsured.

To measure impact, NBCCEDPs require data on screening services utilization. Estimates of the number of women eligible for screening and screening utilization have been performed at the national and state levels (Howard et al., 2015; Tangka et al., 2006). Nation-level estimates suggest 10% to 20% of eligible women are screened by NBCCEDPs. There is a wide variation of screening rates among states with a range of 3.2–53% of the eligible population screened (Howard et al., 2015; Subramanian et al., 2015; Tangka et al., 2006). These estimates may be useful at a national level but are inadequate for local health administrators and community advocacy groups. Hughes et al. (2021) provide a more detailed assessment using spatial modeling of Minnesota’s NBCCEDP, “Sage“. Their results revealed that Sage had an average breast cancer screening rate of 37.21% in Minnesota. Furthermore, the analysis reported significant variation in the uptake of services. The program is designed to serve the entire state, but the interpolated raster cell estimates of the utilization of mammography services ranged within the state from 0% to 100%. These results indicate tremendous variation in local use of services.

2. Data and methods

2.1. Datasets

2.1.1. Breast cancer screening instances (numerator)

Utilization of Sage breast cancer screening services was defined as instances of women screened every year (numerator) over the eligible population (denominator). Under Sage guidelines, every woman in Minnesota is eligible for screening services if they have income below 250% of the federal poverty level. A more detailed description of the Sage numerator and denominator is found in Hughes et al. (2021). This work performed a secondary analysis of observational data for the purpose of program evaluation and was not considered human subjects research.

Sage maintains a database of women screened and their residential addresses at the time of screening. Five years of data were pooled to ensure a sufficient sample size in sparsely populated areas. From 7/1/2010 to 6/30/2015 (five fiscal years), we identified 74,226 instances of screening with address information. Sage clients were geocoded using the Minnesota Department of Health geocoder and we accepted a match score of 60 or greater. A match score, range 0–100, is given to the client’s street address, which is compared to a reference dataset of roads (Goldberg, 2013). The majority of addresses (73%) had a geocode score of 80 or greater. Address scores of this range were accepted as historical client addresses were being retrospectively geocoded using a current geocoding service.

Individuals in datasets that do not have complete address information can be difficult to incorporate into spatial analyses. Some Sage clients, 10%, did not have sufficient address information for geocoding, yet all clients did supply zip code. It is common practice to geocode individuals to a zip code using the zip code tabulated areas (ZCTA) (Rushton et al., 2006). There are two common options for handling records that have only zip code/ZCTA data. The first is to place individuals at the ZCTA centroid, and the second is randomly assigning individuals within a ZCTA. Both options can lead to unrealistic clustering of individuals that skews results at an analysis below the zip code level. As the goal was to analyze datasets from a range of pre-aggregations, we did not want to bias the data toward ZCTAs, and developed a third option.

We developed an algorithm in PostgreSQL 10 and PostGIS 2.2 to systematically distribute individuals within a geographic boundary, in this case, a ZCTA. For all individuals within a ZCTA, the algorithm will determine the distance necessary for placing each point equidistant from any other point within the ZCTA. The algorithm begins with a set of distances that it will use to create an evenly spaced lattice. The distances are determined by taking the extent of the polygon and dividing it by the number of features that need to be placed within the boundary. For example, a ZCTA that has a spatial extent of 100 and needs to place four clients would have an initial space definition of 25. The algorithm then would calculate a lattice that was equally spaced and test to see if all necessary points are within the polygon. If the points are not within the boundary the algorithm would divide that distance in half and test again. The process repeats until a lattice is created that contains the number of required features.

2.1.2. Eligible population (denominator)

Census datasets have historically been the primary source for denominator datasets but have limitations. First, they use pre-existing administrative boundaries. Second, census data have privacy limitations, so to reduce the chance of identification, they do not provide detailed demographic cross-tabulations (e.g., the number of uninsured African American women between the ages of 50–55) for small areas such as the census block. To address this concern, we employed the RTI 2010 U.S. Synthesized Population dataset (RTI international, 2012; Wheaton et al., 2009). The synthetic population is a dasymetric modeled representation of the U.S. 2010 census. The dasymetric model employed is derived from the American Community Survey Public Use Microdata (U.S. Census, 2018). The model dataset provides geocoded households with characteristics like income, and household individuals with age, race, and sex characteristics.

Our Sage denominator population was determined by the Sage eligibility criteria, that is, women aged 40 or greater and household income is less than or equal to 250% of the federal poverty level. Additionally, this program provides screening services for age-appropriate American Indian or Alaska Native women regardless of income. To account for five years of screening data, the denominator population was multiplied by 5.

2.1.3. Creating pre-aggregation datasets

The numerator and denominator populations were both individually spatially joined to four sets of geographic units in Minnesota: county, ZCTA, census tract, or census block. Geographic unit shapefiles are from the U.S. Census (Manson et al., 2020). The individual-level data were retained to serve as a control.

2.2. Spatial adaptive filters and interpolation

Spatially adaptive filters consist of three datasets: (1) a defined set of grid points which are the centers of the filters and where rate calculations are assigned, (2) geographic coordinates for the eligible population, and (3) a distance matrix, which is an ordered collection of distances between grid points and the eligible population. We employed a regularly spaced grid, with a defined distance of 5000 m, across the entire state of Minnesota. Each grid point (Fig. 1) represents the center of an adaptive filter whose size grows until it reaches or surpasses the standardized population threshold of the eligible population. The population threshold value is determined by a sample size calculation (Cai et al., 2012). We accepted a standard error of 0.10, which gives a population threshold value of 500. Each filter grows in size until it encompasses the geographic locations of (at least) 500 eligible women for the denominator. When the filter size is determined, all the instances of screening that fall inside the filter serve as the numerator. The ratio calculation is completed by using a spatial join that assigns numerator/denominator for each grid point. The sizes of the filters vary, with smaller circles located in densely populated areas and larger circles in more rural areas (Fig. 1). The following equation was used to derive the minimum population threshold required to achieve a standard error of 0.10.

Fig. 1.

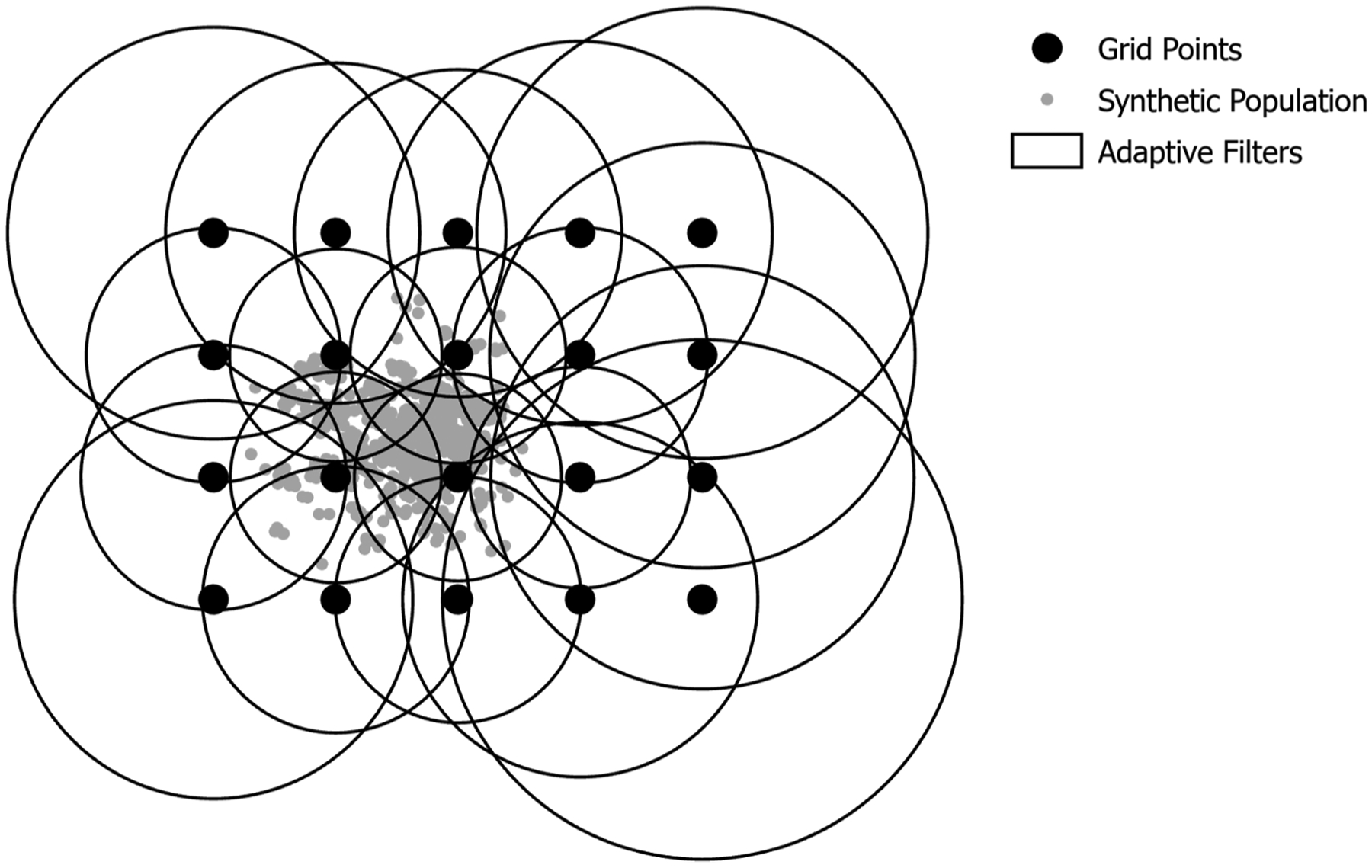
Example of spatially adaptive filters.

Eq. (1), Sample Size Calculation

$$E_i\ge \frac{Z^2{}_{1-\propto }}{{\left({\widehat{R}}_i-1\right)}^2}$$

Where E_i is the required minimum population threshold needed to achieve a standard error of 0.10, Z is the standardized normal distribution Z statistic at our desired alpha level cutoff (0.10) and R_i is our estimated standardized morbidity ratio (Cai et al., 2012).

To ensure a fair comparison between the four pre-aggregated spatially adaptive filter estimates and the individual-level spatially adaptive filter estimates, each was computed using the same grid and the same population threshold. However, pre-aggregation will affect the size of the calculated SAF as its size is determined by meeting or surpassing the population threshold. Fig. 2 provides a 1-dimensional example of spatially adaptive filter calculation at the individual, census Block, and ZCTA levels. Filter size determination begins at the grid point and expands from left to right until it reaches the threshold of 500 eligible women. With individual data the filter size determination is exact and only 500 women are included in the denominator every time. However, when working with pre-aggregated units (i.e., census block, ZCTA, and county) the filter size is not as precise. The filter grows until it meets or surpasses the population threshold of 500 eligible women and since unit inclusion is binary (in or out) the threshold can quickly be surpassed based on the population of the unit.

Fig. 2.

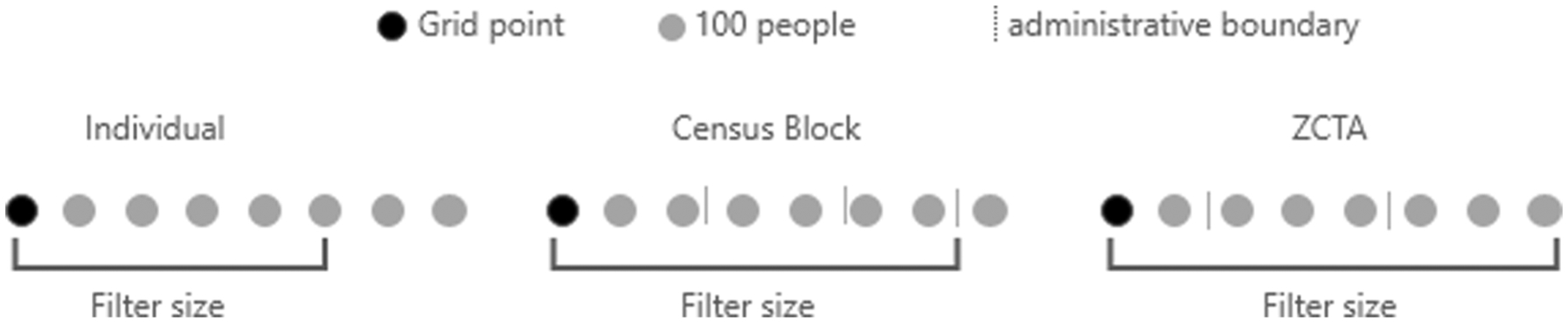
1-Dimensional view of filter determination based upon unit aggregation.

Spatially adaptive filters have not been rigorously applied in disease mapping due to the computational complexity necessary when creating a distance matrix and performing spatial joins between two datasets. For example, a sparse grid with 1,000 points and 5,000 geographic locations results in a distance matrix holding 5 million distance calculations. Our grid contained 9,486 points and computed distance matrices with as little as 87 to 231,520 (county centroids to individual-level coordinates) geographic locations. Centroids were calculated using the geometric centroid and distances were determined by projecting both the grid and geographic centroids into UTM Zone 15 North. Our largest distance matrix and spatial join contained over 2 billion distance calculations. We used the big data platform Apache Spark due to the number of calculations necessary for this analysis. Apache Spark is an in-memory parallel computation environment that uses Resilient Distributed Datasets to partition data into small segments for effective parallel computing. The library GeoSpark is used for handling geospatial data types and providing spatial functions (Yu et al., 2018).

After the SAF were calculated in GeoSpark, we interpolated the screening utilization rate using secondary geospatial software (ArcGIS Pro version 1.4). The surface is interpolated using an inverse distance weighted algorithm with a defined raster cell size of 500 m.

2.3. Comparative methods

Multiple comparative methods were used to examine how pre-aggregation affects both SAF estimates and interpolated visualizations. Our analyses began by observing the effect of the MAUP on our datasets, we report descriptive statistics of the spatial distribution of the numerator (instances of screening) and denominator (eligible population) populations. Next, we report properties of the spatially adaptive filters and how they vary when using different pre-aggregated datasets, for example, the average spatial extent of the filters. This forms a basis for understanding how pre-aggregation and SAF can alter estimates and visualizations.

Our analysis concludes with two comparative measurements. R (version 3.5.2) was used to calculate Pearson’s correlation among screening utilization grid point estimates (R Core Team, 2020). Pearson’s correlation is a measure of the similarity between two sets of SAF screening estimates. Next, differences between interpolated screening rates, or raster cell estimates, are performed, by using map algebra to create error maps. Absolute error maps were produced using R (version 3.5.2), to identify locations as well as the magnitude of changes between two rasters (Hijmans, 2020). The individual map is considered the control for the absolute error maps.

3. Results and discussion

We examined the distribution of Sage clients and eligible population for each pre-aggregation dataset and observed the effect of the MAUP (Table 1). Some geographic scales (e.g. ZCTA, Tract, or Block) had multiple units with zero instances of screening and/or eligible population. Some geographic scales have far more than others, suggesting that pre-aggregations may bias the analysis in artificial ways that could affect downstream visualizations, especially in the case of choropleth mapping. The bias is due to how the geographic units are derived. All census-derived units (i.e., census blocks, block groups, and tracts) have minimum and maximum population thresholds they must adhere to U.S. Census (2013), which results in geographic units that are more homogeneous and standardized. However, ZCTA are generalizations of zip code delivery routes that have population data allocated to them.

Table 1.

Description of the spatial distribution of sage clients and eligible population.

Geographic Scale	Geographic Units with Number of Clients > 0	Geographic Units with Eligible Population > 0	Total Number of Geographic Units
County	87	87	87
ZCTA	844	867	969
Tract	1328	1330	1336
Block	27,186	50,516	259,777

Pre-aggregation affected the size of SAFs (Table 2). The median number of geographic features needed to meet the population threshold of 500 was influenced by geographic scale. For example, filters derived using data aggregated to the county have a median value of 1.0, as most filters reached or exceeded the minimum population value by using a single county. The number of features needed to reach the population threshold increased as the geographic scale decreased. The average eligible population found within a filter follows a similar trend. As we increase the spatial resolution (county to individual) our denominator becomes more exact. Table 2 confirms the logic we expected in Fig. 2, where larger geographic units have eligible populations that easily exceed the threshold of 500 eligible women.

Table 2.

Description of spatially adaptive filters.

Geographic Scale	Min Filter Size (m)	Max Filter Size (m)	Median Number of Features Needed	Average Eligible Population
County	126.12	96,955.10	1	6747.32
ZCTA	140.02	75,097.25	2	1235.59
Tract	120.92	84,647.37	2	890.72
Block	368.33	74,126.94	52	510.22
Individual	377.94	74,109.83	500	500.00

The results depicted in Table 3, show that pre-aggregation has a strong effect on the relationship between the SAF grid point estimates. Geographic units with similar scales are more correlated. Correlations varied from 0.498 (Individual : County) to 0.970 (Individual : Block). Decreasing the spatial resolution (Individual to County) reduced the correlation of the grid point estimates. This suggests that a significant amount of the original overall pattern of information is lost with increasingly large pre-aggregations.

Table 3.

Correlations of spatial adaptive filters (Grid Points) by aggregation.

	Individual	Blocks	Tracts	ZCTA	County
Individual	1	0.970	0.650	0.681	0.498
Blocks		1	0.654	0.683	0.499
Tracts			1	0.718	0.689
ZCTA				1	0.617
County					1

We gain greater insight as to how pre-aggregation alters estimates by interpolating and visualizing the estimated breast cancer screening rates to raster cell estimates. Raster cell estimates were used to create standardized map visualizations for each pre-aggregation and the individual-level datasets (Fig. 3). While the overall spatial pattern of breast cancer screening utilization for each pre-aggregation level is consistent, one can immediately see deviations. Larger pre-aggregations are smoother and show less variation, which likely obscures detailed information. For all maps, the average utilization rate is lowest in the North-West and South-West portions of the state and is depicted by the darker browns. One region that has consistently high rates of utilization is in the Central-Western portion of the state. Only the individual and Block-level maps estimate breast cancer utilization rates above 40%.

Fig. 3.

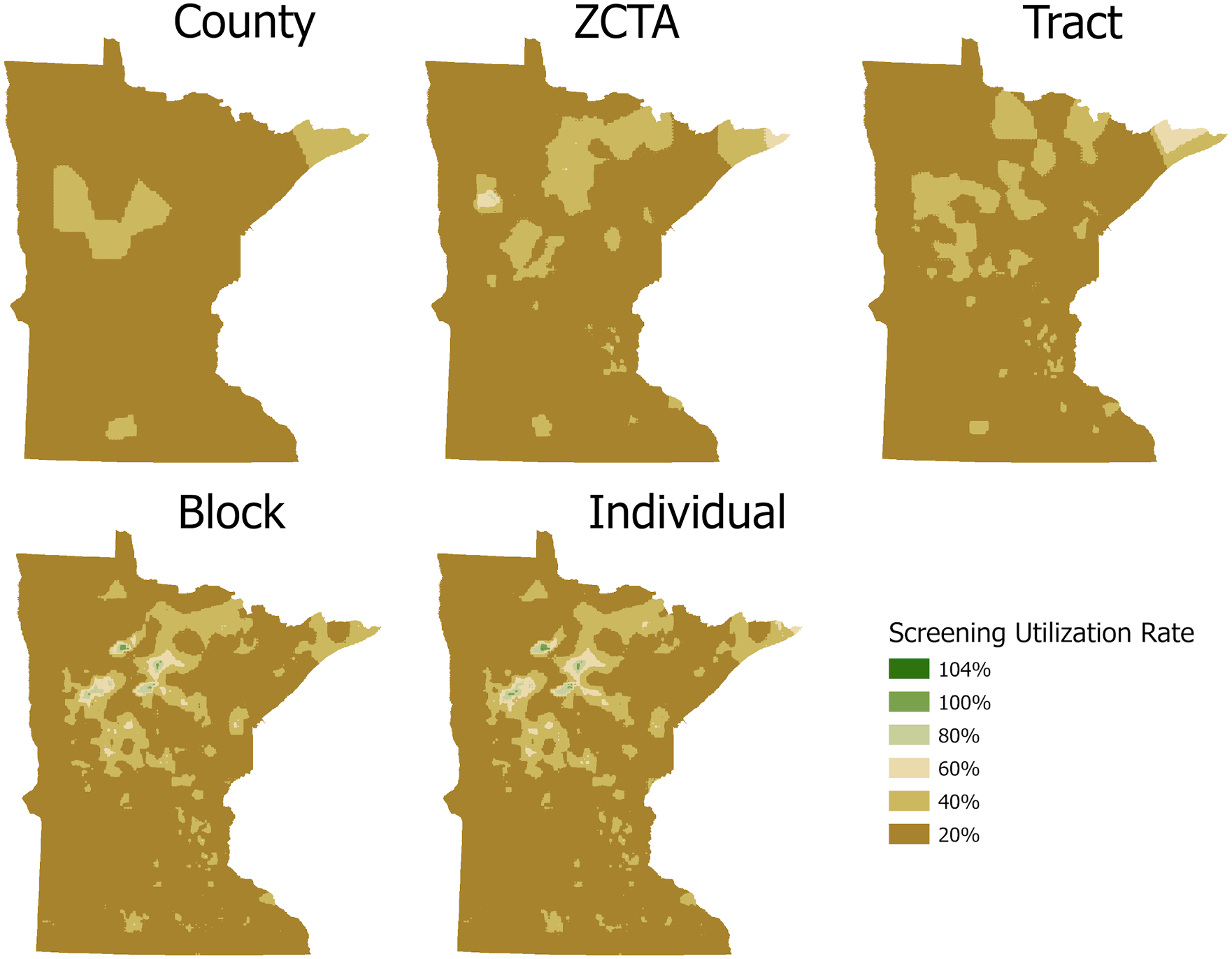
Breast cancer screening utilization rates by aggregation.

Table 4 provides summary statistics of the interpolated maps of raster cell estimates. The county map has the smallest deviation and the smallest range of estimate values. As we increase the spatial resolution of the pre-aggregated units, we begin to see more variation in the resulting dataset.

Table 4.

Screening utilization maps statistics.

	Min	Max	Mean	St. Deviation
County	1.0%	31.7%	11.1%	5.7%
ZCTA	0.3%	61.5%	11.7%	7.3%
Tract	1.0%	47.2%	12.2%	7.5%
Block	0.0%	100%	12.9%	9.6%
Individual	0.0%	104%	13.1%	10.0%

To determine how much error occurs with aggregation, we calculate the absolute error. We used the individual-level map as the control and calculated absolute errors for all other maps, which are any deviation from the individual-level map. The individual values serve as the reference, so positive values indicate underprediction and negative values are areas where overprediction has occurred. Areas that are zero indicate alignment between datasets.

Absolute error maps are beneficial because unlike the correlation statistics, which provide summary results for the entire dataset, they describe the individual raster cell errors that occur.Fig. 4 shows the full state view of the county, ZCTA, census tract, and census block error maps. The county, ZCTA, and census tract errors are largest in the north-central region of the state (Fig. 5). This region is characterized by the largest under predictions; error rates are up to 1.0. An error rate of 1.0 could result, for example, if the ZCTA or census tract map predicted a value of 0.2 and the individual map values were 1.2 for the same raster cell. This clearly describes how pre-aggregation has “smoothed“the rate. Other notable errors found in the ZCTA and census tract maps are the overprediction errors in the North-East corner of the state. When examining the census block error map there is little error, however, the over and under prediction errors are found in similar regions for the ZCTA and census tract error maps.

Fig. 4.

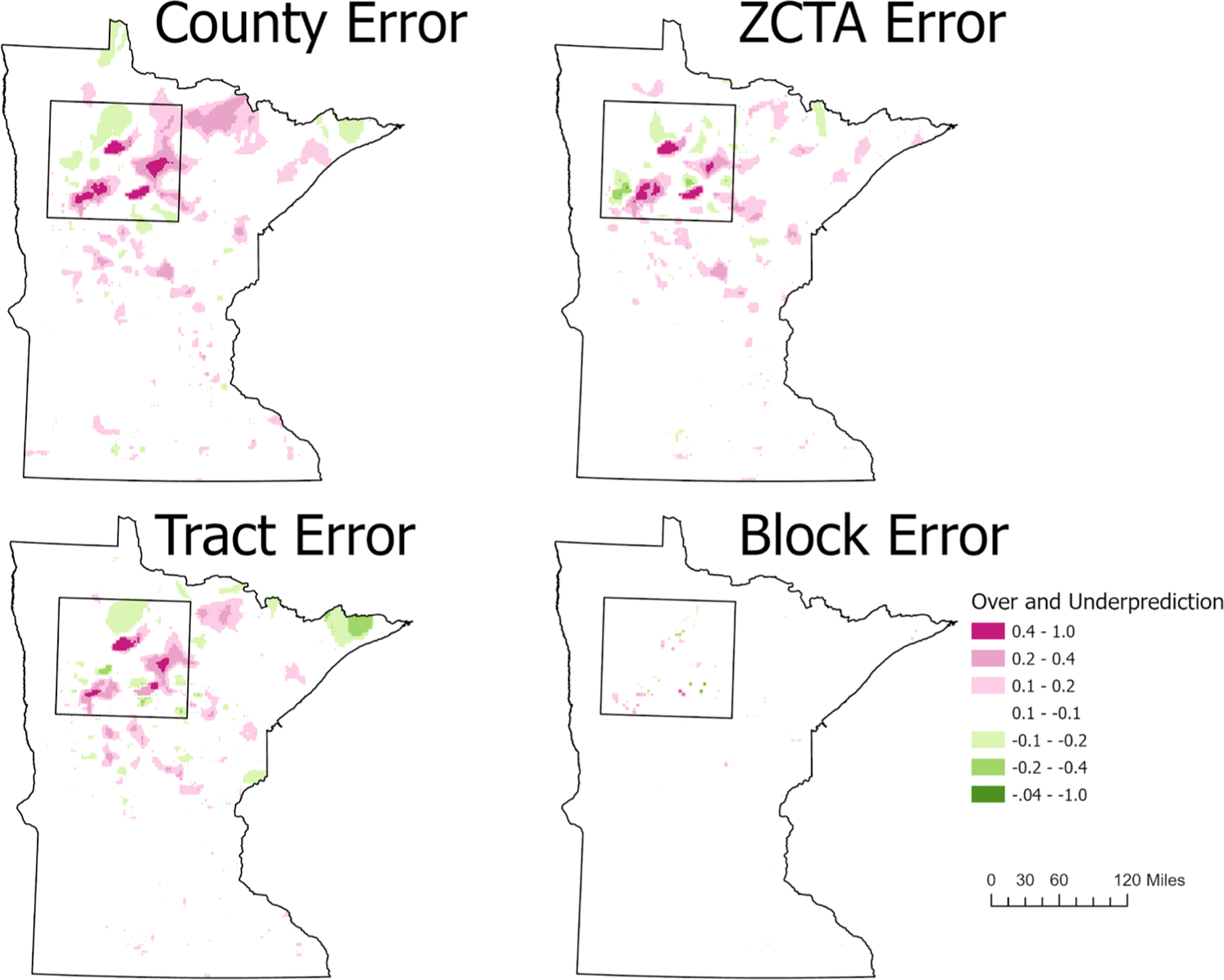
Absolute error maps: depicting the effect of scale on predictive accuracy using the individual values as reference. Positive values representg underpredictions (pink) and negative values representing overpredictions (green).

Fig. 5.

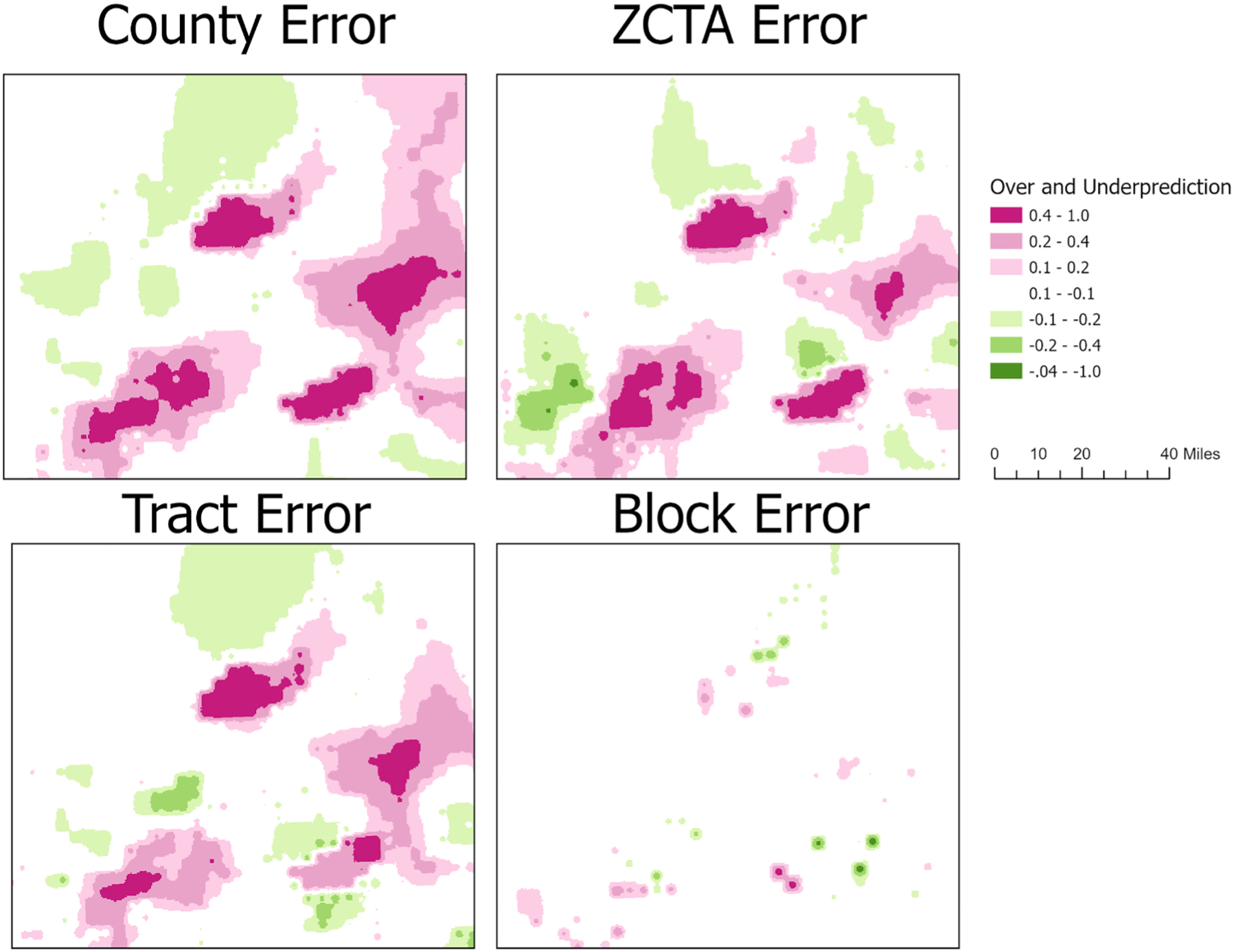
Absolute error maps: depicting the effect of scale on predictive accuracy using individual values as reference. positive values represen underpredictions (pink) and negative values representing overpredictions (green).

Table 5 provides measures of statistical measures of central tendency for each of the error maps. The Individual-County error map has the most error, and accordingly, it has the largest standard deviation and the largest count of over and under predicted raster cells (Table 5,Fig. 4). As the spatial resolution increases, therefore decreasing the size of the units, we show that the error decreases. The Individual-Block error map has the least error overall, however, it does have the largest under prediction for a single raster cell, with a value of −0.549. The error maps for the ZCTA and Tract have similar central tendency measures, however, the tract aggregation overpredicted twice as many raster cells. The majority of those cells (31,127) had very small prediction errors between 0.1 and 0.2.

Table 5.

Summary statistics of error rasters.

	Minimum	Maximum	Mean	St. Deviation	Number of overpredicted raster cells	Number of underpredicted raster cells
Individual-County	−0.228	0.915	0.020	0.086	29,695 (3.39%)	104,052 (11.9%)
Individual-ZCTA	−0.475	0.896	0.014	0.070	18,824 (2.15%)	62,837 (7.18%)
Individual-Tract	−0.306	0.944	0.008	0.073	36,039 (4.12%)	55,482 (6.34%)
Individual-Block	−0.549	0.564	0.001	0.017	1336 (0.15%)	2,938 (0.33%)

4. Limitations

We developed a non-deterministic algorithm that evenly spaces the population across a ZCTA boundary. However, we did not test if different instances of the distribution affected any downstream calculations. This is a limitation of the analysis and the scope of the work, but we have used the same dataset implementation in all our analyses. Secondly, we did not perform a sensitivity analysis on the 5000 m grid, which was used to calculate the spatially adaptive filters. Varying the grid density and size could change the patterns of the map and should be explored in future work. Our analysis is conducted only in the state of Minnesota. Therefore, the population distribution of census blocks, census tracts, ZCTA, or counties in other states may lead to other results. Completing similar analyses in other locations would be a great avenue of future investigation; although individual-level datasets for health behaviors or disease are rare.

5. Conclusion

Disease mapping’s primary contribution is to provide visual evidence of the burden of disease. However, maps derived from pre-aggregated data have limited ability to describe the pattern and burden of disease risk at the local level. Choropleth maps are limited in their ability to accurately describe the prevalence of disease risk for small areas. Additionally, there are no methods that easily allow us to precisely compare choropleth maps that use different spatial scales. A main contribution of our work is that by using the SAF with this pre-aggregation approach, we begin to examine how much information is lost. Previously, our understanding of the variation of disease risk has been limited to the development of new techniques. Our work performs a sensitivity analysis using the various spatial scales to quantify the amount of information potentially lost. Maintaining the accuracy of this information is important for understanding the potential burden of disease upon communities of interest. The techniques we have applied can create maps that provide reliable local information to address public health concerns and direct resources to those communities.

We demonstrate that spatially adaptive filters are an appropriate method for mapping disease for small areas as they limit the effect of the small number and modifiable areal unit problems. However, we also show that SAF are affected by MAUP through pre-aggregation. The employment of the RTI synthetic dataset allowed us to reveal high-resolution patterns of disease risk, which in turn allowed for the quantification of error. Our current work lays the foundation for future work to explore how disease prevalence, geographic feature size, and grid size affect our ability to better understand the true pattern of disease risk.

SAF can work with individual-level data to produce statistically reliable results without losing spatial accuracy. Our work also demonstrates that SAF, like many other smoothing techniques such as Bayesian smoothing, headbanging, and geographically weighted regression can also be applied to very small-scale geographic units that have inflated counts of zero values and would fail, with choropleth mapping, to produce reliable and informative maps. Additionally, our work shows that working with larger pre-aggregated units can greatly impact the quality and informativeness of resulting maps even when using SAF. Even when using the same grids and population threshold the interpolated patterns for the SAF estimates are strikingly different. Pre-aggregation smooths out the variation for some of the most vulnerable communities and this smoothing effect is seen in the sparsely populated areas around the state. If one must use pre-aggregated data, we recommend using the smallest unit size aggregation possible.