Common pitfalls and mistakes in the set-up, analysis and interpretation of results in network meta-analysis: what clinicians should look for in a published article

Abstract

Objective

Several tools have been developed to evaluate the extent to which the findings from a network meta-analysis would be valid; however, applying these tools is a time-consuming task and often requires specific expertise. Clinicians have little time for critical appraisal, and they need to understand the key elements that help them select network meta-analyses that deserve further attention, optimising time and resources. This paper is aimed at providing a practical framework to assess the methodological robustness and reliability of results from network meta-analysis.

Methods

As a working example, we selected a network meta-analysis about drug treatments for generalised anxiety disorder, which was published in 2011 in the British Medical Journal. The same network meta-analysis was previously used to illustrate the potential of this methodology in a methodological paper published in JAMA.

Results

We reanalysed the 27 studies included in this network following the methods reported in the original article and compared our findings with the published results. We showed how different methodological approaches and the presentation of results can affect conclusions from network meta-analysis. We divided our results into three sections, according to the specific issues that should always be addressed in network meta-analysis: (1) understanding the evidence base, (2) checking the statistical analysis and (3) checking the reporting of findings.

Conclusions

The validity of the results from network meta-analysis depends on the plausibility of the transitivity assumption. The risk of bias introduced by limitations of individual studies must be considered first and judgement should be used to infer about the plausibility of transitivity. Inconsistency exists when treatment effects from direct and indirect evidence are in disagreement. Unlike transitivity, inconsistency can be always evaluated statistically, and it should be specifically investigated and reported in the published paper. Network meta-analysis allows researchers to list treatments in preferential order; however, in this paper we demonstrated that rankings could be misleading if based on the probability of being the best. Clinicians should always be interested in the effect sizes rather than the naive rankings.

Introduction

One of the most frequent clinical decisions is the selection of the most appropriate treatment from a number of options.¹ Network meta-analysis is probably the best statistical tool we have to answer this question because it allows for estimation of comparative efficacy and ranking interventions even if they have not been investigated head to head in randomised controlled trials.² Clinicians, however, should be particularly careful when appraising network meta-analysis and should usually avoid simple conclusions, as evidence-based practice is not ‘cookbook’ medicine.^{3 4} Network meta-analysis is quickly gaining popularity in the literature, but quality is variable.⁵ Several tools have been developed to evaluate the extent to which the findings from a network meta-analysis would be valid and useful for decision-making.⁶ However, applying these tools is a time-consuming task and often requires specific expertise. Clinicians have little time for critical appraisal and so need to understand the key elements that help them select network meta-analyses that deserve further attention, optimising time and resources. In this paper, we propose a practical framework to assess the methodological robustness and reliability of results from network meta-analysis. A brief description of the key terms used throughout the paper is available in table 1.

Table 1.

Description of key terms and concepts related with network meta-analysis

Terms	Explanation	Method of evaluation/estimation
Transitivity assumption	The assumption of transitivity implies that interventions and populations in the included studies are comparable with respect to characteristics that may affect the relative effects.	Primarily, the evaluation is based on the clinical understanding of the disease, the competing interventions and the outcomes of interest. Once the data have been collected, it can be assessed statistically by comparing the distribution of the potential effect modifiers, when enough studies (eg, at least five) are available for each comparison.
Consistency assumption	The assumption of consistency implies that the direct and indirect evidence are in statistical agreement for every pairwise comparison in a network. When transitivity is likely to hold, this is expected to be expressed in the data via consistency. However, the absence of statistical inconsistency is not evidence for the plausibility of the transitivity assumption.	Several methods have been suggested for the evaluation of consistency, which infer on the presence or absence of statistical inconsistency based on statistical tests (eg, z-test, χ2 test). For a review of the available approaches, see Donegan, 2013. The absence of statistically significant disagreement between direct and indirect estimates is not evidence for the plausibility of consistency, since the tests are often underpowered.
Hierarchical model approach	This model relates the relative effects observed in the studies with the respective ‘true’ underlying effects and combines the available direct and indirect evidence for every comparison via the ‘consistency equations’.	–
Multivariate meta-analysis model approach	This model considers the different observed direct comparisons as different outcomes and imposes the consistency assumption by assuming a common reference arm in all studies, which might be ‘missing at random’ in some of them.	–
Ranking probability	The probability for a treatment of being ranked in a specific position (first, second, third, etc) in comparison with the other treatments in a network.	The ranking probability is estimated as the number of simulations that a treatment is ranked in a specific place (ie, first, second, third, etc) over the total number of simulations. It can be estimated either within a Bayesian framework (using MCMC simulations) or in a frequentist framework (using resampling methods).
p (best)	The probability for a treatment of being the best (eg, the most effective or safe) in comparison with any other treatment in a network.	p (best) is estimated as the number of simulations that a treatment is ranked first over the total number of simulations.
Mean/median rank	The average/median of the distribution of the ranking probabilities (for all possible ranks) for a treatment. Lower values correspond to better treatments.	Using the estimated ranking probabilities.
SUCRA	Surface under the cumulative ranking curves (SUCRA) expresses the percentage of effectiveness/safety that a treatment has, when compared with an ‘ideal’ treatment that would be ranked always first without uncertainty.	Using the estimated ranking probabilities.
Contribution of a study to the direct estimate	The contribution of a study to the direct estimate is the percentage of information that comes from a specific study in the estimation of a direct relative effect using standard pairwise meta-analysis.	This contribution is estimated by re-expressing the weights (eg, the inverse variance weights) of the studies as percentages.
Contribution of direct comparison to the network estimates	The contribution of a direct comparison to the network estimate is the percentage of information that comes from a specific direct (summary) relative effect with available data in a network in the estimation of the relative effects using network meta-analysis.	The network estimates are indeed a weighted average of the available direct estimates in a network. Re-expressing these weights as percentages gives the contribution of each direct comparisons to every network estimate. Then, the contribution of a study to the network estimates is estimated by combining the study-specific contributions (to the direct estimates) and the comparison-specific contributions (to the network estimates).
Loop-specific approach for inconsistency	The loop-specific approach is a ‘local’ approach that estimates inconsistency in every closed loop of a network, separately.	Inconsistency is estimated as the difference between the direct and indirect estimates for one of the comparisons in the loop. Then, a z-test is employed to assess the statistical significance of this difference.
Design-by-treatment model	The design-by-treatment model is an ‘inconsistency model’ for network meta-analysis that relaxes the consistency assumption and infers for the presence of inconsistency in the entire network jointly (ie, ‘global’ test).	This models accounts for two types of inconsistency: the ‘loop’ and the ‘design’ inconsistency. Loop inconsistency is the disagreement between the different sources of evidence (eg, direct and indirect), while design inconsistency is the disagreement between studies with different designs (eg, two-arm vs three-arm trials). A χ2 test is employed to infer about the statistical significance of all possible inconsistencies in a network.

MCMC, Markov chain Monte Carlo.

Methods

We selected a network meta-analysis about drug treatments for generalised anxiety disorder (GAD),⁷ which was published in 2011 in the British Medical Journal and has been previously used as a working example in another paper.⁸ Twenty-seven randomised controlled trials were included in this review, which provided outcome data on 10 competing treatments (duloxetine, escitalopram, fluoxetine, lorazepam, paroxetine, pregabalin, quetiapine, sertraline, tiagabine, venlafaxine) and placebo. Network meta-analysis technique was employed to synthesise the available data, using both a Bayesian hierarchical model and a frequentist meta-regression approach. Three clinical outcomes were considered: response and remission for efficacy, and dropout rate due to adverse events as a measure of tolerability. Results were reported as ORs and the relative ranking of interventions was based on the probability for each treatment of being the best. Fluoxetine resulted to be the most efficacious treatment (62.9% probability of being best), while sertraline ranked first in terms of tolerability (49.3% probability of being best). We reanalysed the 27 studies included in this network following the methods reported in the original article and compared our findings with the published results (details on the statistical model can be found in the online  supplementary web appendix). To illustrate how inappropriate methodological approaches and suboptimal presentation of results can affect conclusions from network meta-analysis, we have divided our paper into three sections, according to the specific issues that should always be checked. For the purpose of this article, we present and discuss here only some of the findings from our analyses, but full results are reported in the online  supplementary web appendix.

Results

Understanding the evidence base

Which is the network of treatments?

As for all systematic reviews and meta-analyses, the construction of the evidence base for a network meta-analysis should derive from a coherent and clear set of inclusion criteria, which define the competing interventions, the study characteristics and the patient population. It is worth noting that, for the same clinical question, researchers might be interested in comparing all the available interventions for the condition under investigation or only a subset of them. Interventions that are not of direct interest for the clinical question (eg, non-licensed drugs or placebo) can be added to the network to increase the amount of data and provide additional indirect evidence. In theory, both approaches are equally methodologically valid, but different interventions under consideration mean different networks of treatments and, therefore, potentially different results.⁹ To help reduce the potential for selection bias and the risk of incorrect results, a prespecified rationale for including or excluding interventions from the network should be reported in the study protocol, which should be made available (as URL link or web-only supplementary material). In the GAD network meta-analysis, we first checked the selected interventions and the included studies, to assess whether they were appropriate to answer the review question. The paper reported that ‘in this systematic review we compared the efficacy and tolerability of all drug treatments for generalised anxiety disorder by combining data from published randomised controlled trials. We also carried out a subanalysis comparing the five drugs currently licensed for generalised anxiety disorder in the United Kingdom (duloxetine, escitalopram, paroxetine, pregabalin, and venlafaxine)… 46 trials met the inclusion criteria, but only 27 contained sufficient or appropriate data to be included in the analysis’. It is not clear, though, what was meant by ‘sufficient and appropriate data’ and why some interventions such as alprazolam and buspirone were not incorporated in the analyses. These two drugs were used at a therapeutic dose in two three-arm studies that were included in the network (see references 24 and 35 in Table A of the Supplementary web material in Baldwin et al ⁷); however, alprazolam and buspirone arms were excluded from the analyses without any justification. The availability of a review protocol would have clarified the selection of interventions and reduced the risk of selection bias.

Is the transitivity assumption likely to hold?

The synthesis of studies making a direct comparison of two treatments makes sense only when the studies are sufficiently similar in important clinical and methodological characteristics (eg, severity of illness at baseline, treatment dose, sample size and study quality—the so-called effect modifiers). Similarly, for an indirect comparison (such as A vs B) to be valid, it is necessary that the sets of direct comparisons (A vs C and B vs C) are similar in their distributions of effect modifiers. Only when this is the case can we assume that the intervention effects are transitive (ie, the previously mentioned subtraction equation holds).¹⁰ Transitivity can be viewed as the extension of clinical and methodological homogeneity to comparisons across groups of studies that compare treatments.² In a network meta-analysis, the inclusion criteria should be wide enough to enable generalisation of the findings, but also sufficiently narrow to ensure the plausibility of the transitivity assumption. Transitivity can be assessed statistically by comparing the distribution of effect modifiers across the available direct comparisons when there are sufficient data,¹¹ but inference on its plausibility should also be based on the clinical understanding of the evidence. For this reason, a clear and transparent presentation of the inclusion criteria is necessary in all network meta-analyses. This information should be reported in Method section of the paper, and all the primary studies described in detail in the Results section.¹²

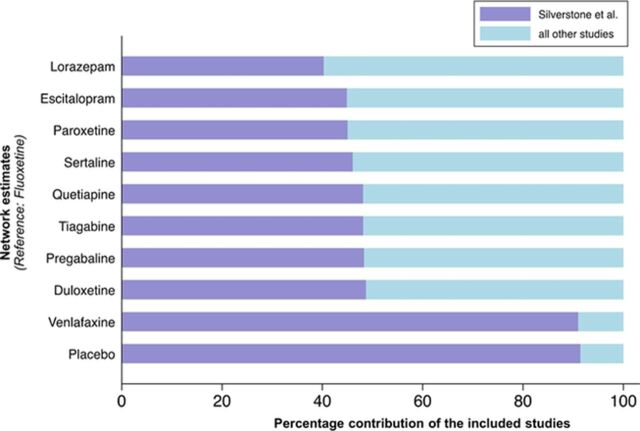
In our working example, the systematic review found only one randomised controlled trial of fluoxetine. This was a three-arm study, which compared fluoxetine with venlafaxine and placebo.¹³ This was actually an analysis of a subgroup of patients from another randomised trial,¹⁴ in whom the formal assessment of GAD in comorbidity with major depression was made retrospectively (thus increasing the risk of selection bias) and for whom the randomisation was not stratified according to the comorbid diagnosis of GAD (stratified randomisation is usually employed in a trial in order to achieve approximate balance of patients with two—or more—characteristics that may influence the clinical outcome, without sacrificing the advantages of randomisation). Due to its non-properly randomised design, the rationale for including this study in the network was questionable. Moreover, it probably violated the transitivity assumption, as its population was likely to be substantially different from other included studies, which excluded patients with any current and primary Diagnostic and Statistical Manual of Mental Disorders-IV Axis I diagnosis other than GAD, including major depressive disorder, within the previous 6 months. To assess how much the fluoxetine study influenced the relative effects and ranking of treatments, we evaluated the contribution of each direct comparison in the network¹⁵ and found that for the primary efficacy outcome, this study contributed to 9% of the total amount of information and more than 30% in the relative effects of all interventions versus fluoxetine (figure 1). As this study was the only trial providing evidence about fluoxetine, superiority of this drug over other interventions is therefore at least doubtful and the validity of the findings for the whole network is thrown into doubt.

Figure 1.

Percentage contribution of the Silverstone study in the network estimates of the relative effects for all interventions versus fluoxetine for the response outcome. The percentage contribution of the included studies was estimated assuming for all comparisons the heterogeneity standard deviation estimate obtained from the Bayesian hierarchical model (=0.26).

Checking the statistical analysis

Has consistency been assessed properly?

There are several statistical approaches for carrying out a network meta-analysis (eg, hierarchical models,¹⁶ meta-regression models¹⁷), and all of them, when the underlying assumptions hold, yield comparable results. All existing statistical models for network meta-analysis are based on the integration of the direct and all possible indirect estimates (ie, ‘mixed evidence’), assuming that the different sources of evidence (direct and indirect) are in agreement within the treatment network; this is the so-called consistency assumption.² Consistency is the statistical manifestation of transitivity, and the validity of the findings from network meta-analysis is highly dependent on the plausibility of this assumption. Statistical inconsistency is inextricably connected to statistical heterogeneity and both need to be explicitly evaluated in a network meta-analysis. Inconsistency should be low enough to ensure validity of the results and heterogeneity should be low enough to make the results relevant to a clinical population of interest. Inconsistency can occur in one in eight networks⁶ and inconsistency models are used to evaluate it in a network meta-analysis.¹⁸ Despite its fundamental importance, however, researchers often assess the consistency assumption, if at all, using inappropriate methods.⁵

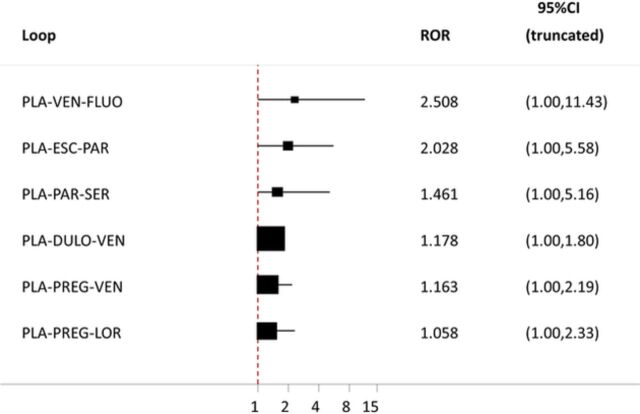
In our working example, it is reported that the authors ‘tested the validity of the mixed treatment model by comparing the consistency of results between the mixed treatment meta-analyses and the direct comparison meta-analyses.’ This is not a valid method for assessing inconsistency because the network estimates (mixed treatment meta-analyses) are a combination of the direct (direct comparison meta-analyses) and indirect estimates and consequently they are not expected to differ much, even in the presence of substantial inconsistency. We applied two tests in our reanalysis, the design-by-treatment interaction test¹⁸ (p value=0.85) and the loop-specific approach¹⁹ (figure 2), and both did not reveal statistically significant inconsistency; however, the large uncertainty in the estimation of the ratio of ORs (RORs) between direct and indirect estimates in three out of six loops would require further exploration (figure 2). It is probably not by chance that the loop including the Silverstone study (fluoxetine, placebo, venlafaxine) had the largest upper CI limit (ROR=2.51, 95% CI 1.00 to 11.43) and this reinforced our concerns about the inclusion of this study in the network.

Figure 2.

Inconsistency results of the loop-specific approach for the outcome of response. Squares represent the ratio of ORs (RORs) between the direct and indirect estimates and the black horizontal lines the respective 95% CI truncated to the null value of 1 (red line). DULO, duloxetine; ESC, escitalopram; FLUO, fluoxetine; LOR, larazepam; PAR, paroxetine; PLA, placebo; PREG, pregabaline; SER, sertraline; VEN, venlafaxine.

Checking the reporting of findings

How was the relative ranking of treatments estimated?

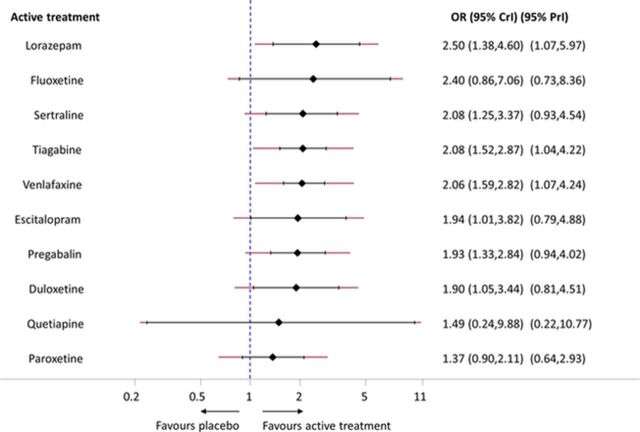
Even though often challenging, presenting the results of network meta-analysis in a way readers can understand has to be the norm. From a decision-making point of view, the most important clinical output of network meta-analysis is the set of relative effects between all pairs of interventions and it can be reported in a league table²⁰ or by using other graphical displays.²¹ According to our reanalysis, in terms of response, all drugs—except fluoxetine, quetiapine and paroxetine—appeared to be statistically significantly more effective than placebo (figure 3). However, no important differences existed between the 10 interventions in terms of efficacy (table 2) and the predictive intervals in figure 3 indicated that only for lorazepam, tiagabine and venlafaxine, the estimated heterogeneity (τ=0.26 (0.00, 0.53)) was small enough to suggest their possible beneficial effect in a future study.²²

Figure 3.

Median ORs of all active treatments versus placebo for the response outcome. The black horizontal lines represent the 95% credible intervals (CrI) and the red lines represent the respective 95% predictive intervals (PrI). The vertical blue dotted line shows the null value (OR=1).

Table 2.

Relative ORs between active treatments estimated from the Bayesian hierarchical model for the outcomes of response (lower triangle) and withdrawals (upper triangle). Values larger than 1 favour the treatment in the column for response and the treatment in the row for withdrawals. Treatments have been ordered from top to bottom according to their relative ranking for efficacy

LOR	0.32 (0.03–2.21)	0.78 (0.31–1.99)	0.31 (0.11–0.93)	0.77 (0.33–1.75)	0.60 (0.24–1.51)	0.48 (0.24–0.94)	0.70 (0.28–1.84)	–	0.93 (0.39–2.19)
1.04 (0.31–3.44)	FLUO	2.41 (0.37–23.03)	0.95 (0.13–9.80)	2.34 (0.41–20.48)	1.84 (0.28–17.64)	1.47 (0.24–13.61)	2.16 (0.34–20.92)	–	2.84 (0.46–25.92)
1.31 (0.57–3.08)	1.27 (0.39–4.35)	DULO	0.40 (0.15–1.07)	0.98 (0.46–2.04)	0.77 (0.40–1.42)	0.61 (0.28–1.30)	0.89 (0.39–2.09)	–	1.19 (0.55–2.51)
1.20 (0.56–2.68)	1.15 (0.37–3.83)	0.91 (0.46–1.87)	SER	2.47 (0.95–6.02)	1.93 (0.71–5.00)	1.55 (0.58–3.79)	2.24 (0.82–6.05)	–	2.99 (1.15–7.39)
1.21 (0.62–2.31)	1.16 (0.41–3.36)	0.92 (0.47–1.75)	1.01 (0.55–1.73)	VEN	0.78 (0.37–1.63)	0.63 (0.33–1.16)	0.91 (0.43–2.04)	–	1.21 (0.70–2.10)
1.29 (0.52–3.13)	1.24 (0.36–4.39)	0.98 (0.48–1.97)	1.08 (0.47–2.34)	1.06 (0.52–2.22)	ESC	0.80 (0.37–1.70)	1.17 (0.51–2.76)	–	1.55 (0.73–3.28)
1.30 (0.71–2.36)	1.24 (0.42–3.87)	0.98 (0.48–1.98)	1.08 (0.56–1.98)	1.07 (0.69–1.70)	1.00 (0.47–2.17)	PREG	1.46 (0.67–3.34)	–	1.95 (0.99–3.86)
1.82 (0.87–3.83)	1.76 (0.58–5.58)	1.39 (0.66–2.87)	1.52 (0.77–2.88)	1.50 (0.91–2.57)	1.41 (0.65–3.14)	1.41 (0.80–2.51)	PAR	–	1.33 (0.59–2.86)
1.67 (0.23–11.62)	1.61 (0.19–13.56)	1.28 (0.18–8.71)	1.39 (0.20–9.22)	1.39 (0.21–8.89)	1.30 (0.18–9.20)	1.30 (0.19–8.46)	0.92 (0.13–6.04)	QUE	–
1.20 (0.61–2.38)	1.16 (0.40–3.52)	0.91 (0.47–1.79)	1.00 (0.54–1.78)	0.99 (0.69–1.49)	0.93 (0.45–1.97)	0.93 (0.57–1.52)	0.66 (0.39–1.13)	0.72 (0.11–4.87)	TIAG

DULO, duloxetine; ESC, escitalopram; FLUO, fluoxetine; LOR, lorazepam; PAR, paroxetine; PREG, pregabalin; QUE, quetiapine; SER, sertraline; TIAG, tiagabine; VEN, venlafaxine.

The relative ranking of treatments is often used because it offers a concise summary of the findings. The hierarchy of competing interventions should be based on the network meta-analysis estimates presented in the Results section. The most popular ranking approach is based on the ‘ranking probabilities’, that is, the probabilities for each treatment to be placed at a specific ranking position (best treatment, second best, third best and so on) in comparison with all other treatments in the network.²³ Similarly to other measures of relative effect, ranking probabilities have a degree of uncertainty.⁷ Alternative measures that incorporate the entire distribution of the ranking probabilities include the mean (or median) ranks²¹ and the surface under the cumulative ranking curves (SUCRA)²³ (see table 1 for a definition and description). By contrast, other approaches ignore the uncertainty in the relative ranking and focus only on the first position (like the ‘probability of being the best’). This way of ranking treatments can lead to misleading conclusions, because the probability of being the best does not account for the uncertainty in the estimate and can spuriously give higher ranks especially for treatments with little evidence available. This was the case of the original analysis of the data set in our example,⁷ where fluoxetine resulted the most effective treatment for both response (62.9%) and remission (60.6%). However, it is very likely that the advantage of fluoxetine in the hierarchy was the consequence of using an inappropriate ranking measure that did not properly account for statistical uncertainty. In our reanalysis, we ranked the treatments using the SUCRA percentages and found different results: lorazepam ranked first in terms of response (75.8%) and escitalopram for remission (80.8%) (table 3). Fluoxetine was still among the drugs with potentially better efficacy profile; however, the small differences in the SUCRA values suggest that the most sensible conclusion would have been that there is too large uncertainty around the hierarchy of treatments (see online supplementary web appendix for full details).

Table 3.

Values of the surface under the cumulative ranking curve (SUCRA) for response, withdrawals and remission

Treatment	Response	Withdrawals	Remission
Duloxetine	61.1%	18.3%	39.0%
Escitalopram	53.3%	51.0%	80.8%
Fluoxetine	67.6%	71.4%	80.3%
Lorazepam	75.8%	16.6%	–
Paroxetine	51.2%	30.7%	56.6%
Placebo	5.0%	91.9%	1.2%
Pregabalin	52.3%	65.5%	–
Quetiapine	40.5%	91.9%	–
Sertraline	60.3%	82.4%	60.0%
Tiagabine	22.9%	39.4%	17.4%
Venlafaxine	60.1%	32.9%	64.8%

Conclusions

The validity of the results from network meta-analysis depends on the plausibility of the transitivity assumption. As in pairwise meta-analysis, the risk of bias introduced by limitations of individual studies must be considered first and judgement should be used to infer about the plausibility of transitivity. Possible effect modifiers could always be clinical (similarity in patients’ characteristics, interventions, settings, length of follow-up, outcomes) and also methodological (similarity in study design and risk of bias). Sometimes, differences in the distribution of these moderators across studies are large enough to make network meta-analysis invalid. Inconsistency exists when treatment effects from direct and indirect evidence are in disagreement. Unlike transitivity, inconsistency can be always evaluated statistically. Network meta-analysis should describe in the protocol a clear strategy to deal with inconsistency, which should be always scrutinised for errors at the raw data level.

Clinicians usually want to know the preferential order of treatments that could be prescribed to an average patient. In this paper, we demonstrated that rankings could be misleading if based on the probability of being the best (see online supplementary web appendix box 1,  for a hypothetical example showing how imprecise estimate and large variance can lead to wrong conclusions, if this method is used). In a properly conducted network meta-analysis, ranking measures and probabilities are a convenient way to present results and the corresponding hierarchy of treatments. Good rankings, however, do not necessarily imply large or clinically important differences. Despite the ease of presentation, ranking measures should be presented and interpreted only in light of the estimated relative treatment effects. Clinicians should always be interested in the effect sizes and look at the SUCRAs (together with their degree of uncertainty) rather than the naive rankings.

Further implications for researchers and journal editors

The methodological approach can affect the magnitude of estimated effect associated with an intervention and consequently materially change the study findings.²⁴ Researchers should recognise the complexity of conducting a high-quality network meta-analysis, which require a multidisciplinary team with clinical and technical expertise to adequately cover each step of the research project, including skills in literature search, data extraction and statistical analysis.²⁵

As for all systematic review and standard meta-analyses, results from network meta-analyses should be replicable. Published papers must include all of the information that readers need to completely understand how the study was conducted, independently assess the validity of the analyses and reach their own interpretations.²⁶ The availability of the review protocol and the codes for statistical analyses should become soon a mandatory requirement for all network meta-analyses (mostly needed for the peer review process), as it is important to avoid misconceptions regarding the undertaken analysis.